Understanding death risks of Covid-19 under media awareness strategy: a stochastic approach

Abstract

The coronavirus disease 2019 (COVID-19) is rapidly spreading in the world and the mortality rate is getting higher and higher. Due to the outbreak of such epidemic disease, many countries imposed stricter measures among which is social distancing and enforced isolation. The present study tries to establish a realistic model to characterize the dynamics of COVID-19 and explicitly parameterize the intervention effects of control measures. In so doing, it takes into account stochastic perturbation and investigates the effects of media coverage on the transmission dynamics. This paper seeks to study the existence and uniqueness of the global positive solution to the proposed model and establish conditions for extinction and persistence in mean of the disease. Numerical simulations are presented to show the theoretical results obtained from this study.

1 Introduction

In their history, pandemics have taken different forms and shapes and gone viral throughout the globe. For instance, in the 20th century, there appeared two prominent types of pandemics following the Spanish Influenza of 1918. These are the Asian flu of 1957 and the Hong Kong flu of 1968, while in the 21st century, there emerged another four types, namely N1H1 in 2009, known as (bird flu), (SARS) in 2002, which stands for Severe Acute Respiratory Syndrome, Middle East Respiratory Syndrome (MERS) in 2012, and last but not least Ebola which attained maximum intensity in 2013–2014. A detailed listing of information related to the afore-mentioned types of pandemics is beyond the scope of the current study. However, the following article website presents the comprehensive information about this issue under question [6].

The recent form of the pandemic persisting these days and that is permeating and jeopardizing humankind life is known as the novel COVID-19. The current existing pandemic named COVID-19, which closely resembles a viral pneumonia malady, marked its initial appearance in Wuhan, China, in December 2019. Since that time and up to the the 30th May 2020, this disease has gone viral all around the world infecting thus a considerable number of people.

There is a unanimous agreement among scientists that COVID-19 is an infectious disease that is caused by severe acute respiratory syndrome. Research endeavors are still exploring the features that characterize COVID-19 attack, its strength of infecting individuals and future predictions pertaining to the long term epidemic. In this respect, Qing and Gallagher [13] maintain that COVID-19 is a new phenomenon in the scientific world and many of its features are still unfathomable and are under scrutiny due to its new tensions and strains.

The term COVID-19 was coined by the World Health Organization (WHO) in February 2020 [17]. McKay et al. [10] asserted that COVID-19 has gone viral in all corners of the globe and that no place is left safe from its contagion. In seven months after its appearance, almost 12 million individuals were contaminated and more than 500 thousand people deceased so far [17]. Given that it became a major global concern, COVID-19 was declared a pandemic on March 11, 2020 [17].

In order to prevent COVID-19 infection and slow its transmission, many governments are acting proactively by maintaining trade restrictions and quarantine requirements. Like never before, humanity has been suffering a great deal ever since the emergence of COVID-19 pandemic. The current crisis has led several public authorities worldwide to cripple all sorts of internal movements. Social contacts and peoples’ movements are thus strictly limited.

Given that it is a new phenomenon in the scientific world, the novel coronavirus is posing lots of challenges for worldwide researchers. Indeed, much efforts need to be coordinated in order to understand the current COVID-19’s biological character and its mode of attack. Again, to combat COVID-19 is to block its spread through the implementation of the afore-mentioned preventive measures.

As far as the mathematical models of infectious disease transmission dynamics are concerned, there are plenty of them in the literature. These models play a key role in measuring possible infectious disease control and mitigation strategies. the novel COVID-19 is a contagious disease caused by a new virus which sets off the worldwide alarm bells and requires a specific model taking into consideration its identified features and aspects.

Numerous approaches have been made to get a thorough understanding of the novel coronavirus (COVID-19) but for modeling biological phenomenon, it is important to use stochastic models due to its realistic approach in order to yield more valuable output. In this respect, Zhao and Chen [15] recommend to use the SUQC model (Susceptible, Un-quarantined infected, Quarantined infected, Confirmed infected) to typify the underlying forces of COVID-19 and clearly determine the intervention effects of control measures. Four SUQC model variables, which are related to their features, are used to specify the flux of people within four possible states, namely the Susceptible, Un-quarantined infected, Quarantined infected, Confirmed infected. SUQC system can be used as an epidemic model to measure parameters and variables pertaining to the effects of quarantine or confirmation methods on the epidemic, and pave the way to a better control of the outbreak.

The remaining part of this paper is delineated as follows: In Section one, we propose a stochastic epidemic model for the COVID-19 transmission dynamics to describe the changing behavior of the epidemic diseases in a realistic sense. We attempt to improve the recommended model in [15] by primarily including the stochastic perturbation. Subsequently, we investigate the effects of media coverage on the transmission dynamics. In Sect. 2, we show the existence and uniqueness of a global positive solution of the model. Extinction and persistence in mean will be discussed in Sects. 3 and 4 respectively. In Sect. 5, we present some numerical simulations to clarify obtained analystical results and conclude the paper by a discussion.

2 The model

Coronavirus disease 2019 (COVID-19) is an infectious disease caused by severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2), which is generating a worldwide emergency situation and needs a model taking into account its known specific characteristics. In particular, it would be convenient to develop a model which incorporates the following:

• The effect of undetected infected people and the effects of quarantine.

• The effects of control measures, which is more suitable for analysis than other existing epidemic models.

• The high infectivity during incubation, and the intervention effects of implemented quarantine and control measures.

There are some mathematical models in the literature that try to describe the dynamics of the evolution of COVID-19. Zhao and Chen [15] propose SUQC model (Susceptible, Un-quarantined infected, Quarantined infected, Confirmed infected) to typify the underlying forces of COVID-19 and clearly determine the intervention effects of control measures. SUQC distinguishes the infected individuals (observed data) to be un-quarantined, quarantined but not confirmed, and confirmed. SUQC can be used as an epidemic model to measure parameters and variables pertaining to the effects of quarantine or confirmation methods on the epidemic, and pave the way to a better control of the outbreak.

The SUQC model distinguishes the confirmed infected individuals (observed data), the total infected individuals, and the parameter confirmation rate is affected by medical resources and the sensitivity of diagnosis methods. Furthermore, the number of recovered and died individuals due to the disease is included in the number of confirmed cases in the SUQC model. In addition to that, we take into account the (natural) dead in each compartment as well as the newborns while keeping the population constant.

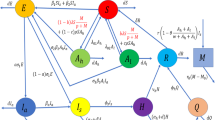
The total population is divided into four classes: the susceptible S, infected and un-quarantined individuals U, the quarantined infected individuals Q, and the confirmed infected cases C. In the model, U goes directly to C, or goes through Q indirectly.

The infected individuals are classified into un-quarantined, quarantined and confirmed. And only the unquarantined can infect the susceptible individuals. SUQC distinguishes the confirmed infected individuals (observed data), the total infected individuals, and the parameter confirmation rate is affected by medical resources and the sensitivity of diagnosis methods. The limitation of detection methods and the medical resources can greatly delay the confirmation process, insomuch the confirmation proportion $\frac{C}{I}$ is less than 1 and time-varying.

In this paper, we modify the model that appears in the work of Zhao and Chen [15] by adding the recovery class R which contains the individuals who have been infected and then recovered, as well as those who no longer spread the disease. This compartment class sees some augmentatin in terms of individuals recovering from their infection and a decrease as regards individuals who surrender to death due to loss of immunity. Let N be the size of the population i.e. $N = S + U + Q + C + R$ , and we assume that N is constant, i.e., fixed over time. Another thing is that COVID-19 mortality rate seems higher compared to other diseases and that the number of deaths is on the rise across the globe. Hence, we assume a different mortality rates to the model compartments, namely $\mu _1$, $\mu _2$, $\mu _3$, $\mu _4$ and $\mu _5$.

At any given time, $t \ge 0$, the numbers S(t), U(t), Q(t), C(t) and R(t) denote the fractions of the total population belonging to the classes of susceptibles, infected and un-quarantined individuals, the quarantined infected individuals, the confirmed infected cases, the recovered individuals (resp.). With the above variables, $I (t) = U (t) + Q (t) + C (t)$ represents the actual cumulative number of individuals infected at the time t. The limitation of detection methods and the medical resources can greatly delay the confirmation process, insomuch the confirmation proportion $\frac{C}{I}$ is less than 1 and time-varying.

It should be noted that C stands for cumulative confirmed cases and not for active ones. It could be then considered as the sum of active infective agents and removed cases (recovered or died due to the COVID-19).

Among the most useful tools, according to several works that contribute to the control of epidemic spreading, we cite media awareness. So, in order to investigate the effects of media coverage on the transmission dynamics, we introduce a general incidence function g(S, U) induced by media awareness, by means of the following incidence function:

$$\begin{aligned} g(S,U)=\left( \alpha -\alpha _1 f(U)\right) \frac{SU}{N}, \end{aligned}$$

where $\alpha _1$ is the contact rate before media alert; the term $\alpha _1 f(u)$ measures the effect of reduction of the contact rate when infectious individuals are reported in the media. Since the coverage report cannot prevent disease from spreading completely, we have $\alpha \ge \alpha _1 > 0$. The function f(U) is a continuous bounded function that takes into account disease saturation or psychological effects such that $f(0)= 0$, $f^{\prime } > 0$ and $\lim _{U \rightarrow \infty } f(U)=1.$

The deterministic system has the following form:

$$\begin{aligned} {\left\{ \begin{array}{ll} \dot{S} = \varLambda N - g(S,U)- \mu _1 S , \\ \dot{U}= g(S,U)-\gamma _1 U - \mu _2 U - ( 1-\gamma _1) \delta U - \lambda _1 U , \\ \dot{Q} = \gamma _1 U - \left( \gamma _2+ ( 1-\gamma _2) \sigma \right) Q -\mu _3 Q- \lambda _2 Q , \\ \dot{C}= \left( \gamma _2+ ( 1-\gamma _2) \sigma \right) Q+ ( 1-\gamma _1) \delta U -\mu _4 C - \lambda _3 C ,\\ \dot{R}= \lambda _1 U+ \lambda _2 Q +\lambda _3 C - \mu _5 R , \end{array}\right. } \end{aligned}$$

(1)

where $\alpha$, $\gamma _1$, $\gamma _2$, m and $\sigma$ are positive constants such that $\alpha \in [0,\infty )$ and $\gamma _1,\gamma _2 \in [0,1]$.

The basic reproduction number $\mathcal {R}_0$, which is a threshold quantity that determines whether an epidemic occurs or the disease simply dies, is given by:

$$\begin{aligned} \mathcal {R}_0= & {} \frac{\alpha \varLambda }{\mu _1(\mu _2 + \gamma _1 +\lambda _1+(1-\gamma _1)\delta )}. \end{aligned}$$

The physical reality shows that the epidemic dynamics are inevitably disturbed by ambient noise. In this paper, our approach is to make the proposed system more realistic. This fact leads us to include stochastic perturbation, which is analogous to that of Imhof and Walcher [7] in order to show how the noise affects our epidemic model and the transmission dynamics. At this point, we assume that stochastic perturbations are of a white noise type which are directly proportional to S(t), U(t), Q(t),C(t) influenced on the $\dot{S}(t)$, $\dot{U}(t)$, $\dot{Q}(t)$, $\dot{C}(t)$ in the model (1).

Finally, since R(t) does not appear in the equations of system (1), it is quite adequate to consider only the equations for S(t) , U(t), Q(t), and C(t). Hence, the system that we propose in this study while introducing white noises and taking into account the effects of media coverage on the transmission dynamics with the transformations $\frac{S}{N}=s, \frac{U}{N}=u,\frac{Q}{N}=q,$ and $\frac{C}{N}=c,$ can be written as

$$\begin{aligned} {\left\{ \begin{array}{ll} ds =\left[ \varLambda - g(s,u)- \mu _1 s \right] dt + \sigma _1 s dB_1 (t), \\ du= \left[ g(s,u)-\gamma _1 u - \mu _2 u - ( 1-\gamma _1) \delta u - \lambda _1 u \right] dt + \sigma _2 u dB_2 (t), \\ dq = \left[ \gamma _1 u - \left( \gamma _2+ ( 1-\gamma _2) \sigma \right) q -\mu _3 q - \lambda _2 q \right] dt + \sigma _3 q dB_3 (t), \\ dc=\left[ \left( \gamma _2+ ( 1-\gamma _2) \sigma \right) q + ( 1-\gamma _1) \delta u- \mu _4 c - \lambda _3 c\right] dt + \sigma _4 c dB_4(t) , \end{array}\right. } \end{aligned}$$

(2)

where $B_i,i=\cdots ,4$ are independent standard Brownian motions defined on a complete probability space $(\varOmega , \mathcal {F}, \mathcal {P})$ with a natural filtration $\{\mathcal {F}_t \}_{t \ge 0}$ (i.e., it is increasing and right continuous while $\mathcal {F}_0$ contains all $\mathcal {P}$-null sets) with intensities $\sigma _i , i=\cdots ,4$.

The parameters of the considered model have characteristics presented in table 1.

Table 1 Model parameters description

Throughout this paper, we will use the following notations. $\mathbb {R}^d$ denotes the d-dimensional Euclidean space, and |x| denotes the Euclidean norm of a vector x and $\mathbb {R}_+^d$ denote the positive cone in $\mathbb {R}^d,$ i.e., $\mathbb {R}_+^d=\{x\in \mathbb {R}^d:\; x_i>0\;, i=1,\;2\dots ,\;d\}$.

We define a d-dimensional stochastic differential equation (SDE)

$$\begin{aligned} \mathrm {d}X(t)=F(t,X(t))\mathrm {d}t+G(t,X(t))\mathrm {d}B(t), \end{aligned}$$

(3)

where $F:\mathbb {R}^d \rightarrow [t_0;+\infty [ \times \mathbb {R}^d$,  $G:[t_0;+\infty [ \times \mathbb {R}^d \rightarrow \mathcal {M}_{d,m}(\mathbb {R})$, and B(t) is an d-dimensional Brownian motion defined on the probability space $(\varOmega , \mathcal {F}, \mathcal {P})$ with the filtration $\{\mathcal {F}_{t} \}_{t\ge 0}$ satisfying the usual condition. Denote $S_h = \{ x \in \mathbb {R}^d: \;| x | < 0 \},$ the differential operator $L$ acts on a function $V\in C^{1,2}(\mathbb {R}^+ \times S_h; \mathbb {R}^+)$ is of the form

$$\begin{aligned} L V (t,x)= & {} V_t (t,x) + V_x (t,x)F(t,x) +\dfrac{1}{2}\text {trace}\left[ G^T(t,x)V_{xx }(x, t)G(x,t)\right] . \end{aligned}$$

(4)

By the Itô’s formula, if $X(t) \in S_h$, we have

$$\begin{aligned} dV(t,X(t))= & {} L V (t,X(t)) \mathrm {d} t + V_x (t,X(t))\mathrm {d} B(t), \end{aligned}$$

(5)

where

$$\begin{aligned} V_t=\dfrac{\partial V}{\partial t}, \quad V_x=\left( \dfrac{\partial V}{\partial x_1}, \,\dfrac{\partial V}{\partial x_2},\dots ,\dfrac{\partial V}{\partial x_d} \right) \quad V_{xx} =\left( \dfrac{\partial V^2}{\partial x_i \partial x_j}\right) _{d\times d}. \end{aligned}$$

(6)

3 Existence and uniqueness of the global positive solution

In order to investigate the dynamical behavior of the disease, the first disconcerting thing is whether the solution is global and unique. Using Lyapunov’s analysis method, we will show that the model (2) has a positive local solution, then we will show that this solution is global. The next theorem gives us the existence and uniqueness of the global positive solution.

Theorem 1

For any given initial value $(s(0),u(0),q(0),c(0))\in \mathbb {R}_{+}^{4}$, the model (2) has a unique global solution $(s(t),u(t),q(t)),c(t)) \in \mathbb {R}_{+}^{4}$ for all $t\ge 0$ almost surely.

Proof

Since the coefficients of the system (2) are locally Lipschitz continuous and for any given initial value $(s(0),u(0),q(0),c(0))\in \mathbb {R}_{+}^{4}$, there is a unique local solution (see [14]) (s(t), u(t), q(t), c(t)) for $t \in [0,\tau _e),$ where $\tau _e$ is the explosion time [14]. So, to show this solution is global, we need to show that $\tau _e = \infty$ a.s. First, we show that s(t), u(t), q(t), c(t) do not explode to infinity in a finite time.

Let $k_0>0$ such that be sufficiently large so that $s(0)\in \left[ \frac{1}{k_0},k_0\right] , \; u(0)\in \left[ \frac{1}{k_0},k_0\right]$, $q(0)\in \left[ \frac{1}{k_0},k_0\right] , \; c(0)\in \left[ \frac{1}{k_0},k_0\right]$. Then, for each integer $k \ge k_0$, we define the stopping time

$$\begin{aligned} \tau _k=\inf \left\{ t\in [0,\tau _e):s(t)\notin \left( \frac{1}{k},k\right) \,\text {or}\, u(t)\notin \left( \frac{1}{k},k\right) \,\text {or} \, q(t) \notin \left( \frac{1}{k},k\right) \,\text {or}\,c(t)\notin \left( \frac{1}{k},k\right) \right\} , \end{aligned}$$

where throughout this paper we set $\inf \emptyset = \infty$ (as usual $\emptyset$ denotes the empty set). We remark that $\tau _k$ is increasing as $k\uparrow \infty$. Set $\tau _\infty = \lim _{k\rightarrow \infty }\tau _k$, whence, $\tau _{\infty }\le \tau _e$ a.s. To complete the proof, it is required to show that $\tau _{\infty }=\infty$ a.s. If $\tau _\infty =\infty$ a.s is true, then $\tau _e = \infty$ and $(s(t),u(t),q(t), c(t))\in \mathbb {R}_{+}^{4}$ a.s for $t \ge 0$. If this statement is false, then there exists a pair of constants $T>0$ and $\varepsilon \in (0 ,1)$ such that

$$\begin{aligned} \mathcal {P}\{\tau _{\infty } \le T\} >\varepsilon . \end{aligned}$$

(7)

Thus there is an integer $k_1 \ge k_0$ such that

$$\begin{aligned} \mathcal {P}\{\tau _k \le T \} \ge \varepsilon ,\quad \forall k \ge k_1. \end{aligned}$$

Let $x(t) = (s(t), u(t), q(t), c(t))$ and consider the $C^2$-function $V_1 : \mathbb {R}_+^4\rightarrow \mathbb {R}_+$ as follows

$$\begin{aligned} V_1(x(t))= & {} \left( s-a-a\log \left( \frac{s}{a}\right) \right) + \left( u-\log (u) \right) \nonumber \\&+ \left( q-\log (q) \right) +\left( c-\log (c)\right) -3, \end{aligned}$$

(8)

for a positive constant a. We note that $V_1$ is a nonnegative function verified from the fact that $\forall y \in \mathbb {R}^+_* \quad y - \log y - 1 \ge 0 .$ Then by the Dynkin formula [2], we obtain for all $k \ge k_1$ that

$$\begin{aligned} \mathbb {E} V_1(x(T\wedge \tau _k)) = V_1(x(0)) +\mathbb {E}\int _0^{T \wedge \tau _k} L V_1(x(t)) dt, \end{aligned}$$

(9)

where $L V_1$ is given by

$$\begin{aligned} LV _1(x(t))= & {} \left( 1-\frac{a}{s}\right) \left[ \varLambda - g(s,u)- \mu _1 s(t) \right] +a \frac{ \sigma _1^{2}}{2}\\&+\left( 1-\frac{1}{u(t)}\right) \left[ g(s,u)-\gamma _1 u(t) - \mu _2 u(t)- \lambda _1 u - ( 1-\gamma _1) \delta u(t) \right] +\frac{\sigma _2^{2}}{2}\\&+\left( 1-\frac{1}{q(t)}\right) \left[ \gamma _1 u(t) - \lambda _2 q - \left( \gamma _2+ ( 1-\gamma _2) \sigma \right) q(t) -\mu _3 q(t) \right] +\frac{\sigma _3^{2}}{2}\\&+\left( 1-\frac{1}{c(t)} \right) \left[ \left( \gamma _2+ ( 1-\gamma _2) \sigma \right) q(t)+ ( 1-\gamma _1) \delta u(t)-\mu _4 c(t) - \lambda _3 c \right] +\frac{\sigma _4^{2}}{2}. \end{aligned}$$

Hence

$$\begin{aligned} LV _1(x(t))= & {} a \mu _1 - \mu _2 u +\varLambda + \mu _2+\mu _3+\mu _4+\lambda _1+\lambda _2+\lambda _3+\gamma _1+\gamma _2 - \mu _1 s(t)-\lambda _1 u\\&-\lambda _2 q -\lambda _3 c - \frac{a \varLambda }{s} - \mu _3 q+ \mu _4 c + ( 1-\gamma _2) \sigma - (\alpha -\alpha _1 f(u)) s +( 1-\gamma _1) \delta \\&-\frac{\gamma _1 u(t)}{q(t)} + a (\alpha -\alpha _1 f(u)) u - \frac{(\gamma _2+( 1-\gamma _2) \sigma )q(t)}{c(t)}- \frac{( 1-\gamma _1) \delta u(t)}{c(t)}\\&+\frac{a \sigma _1^{2}+\sigma _2^{2}+ \sigma _3^{2} +\sigma _4^{2}}{2}, \end{aligned}$$

which implies that

$$\begin{aligned} LV _1 (x(t))\le & {} a \mu _1 +\left( a \alpha -\mu _2 -\lambda _1\right) u(t)+\mu _2+\mu _3+\mu _4+\lambda _1+\lambda _2+\lambda _3 +\varLambda +\gamma _1+\gamma _2\\&+( 1-\gamma _1) \delta +( 1-\gamma _2) \sigma +\frac{a \sigma _1^{2}+\sigma _2^{2}+ \sigma _3^{2} +\sigma _4^{2}}{2}. \end{aligned}$$

Choose $a= \frac{\mu _2 +\lambda _1 }{\alpha }$ such that $\left( a \alpha - \mu _2 -\lambda _1 \right) u=0$, it yields

$$\begin{aligned} LV _1(x(t))\le & {} K, \end{aligned}$$

(10)

where is the following positive number

$$\begin{aligned} K=&\frac{(\mu _2 +\lambda _1) \mu _1}{\alpha } +\mu _2+\mu _3+\mu _4+ \lambda _1+\lambda _2+\lambda _3 +\varLambda +\gamma _1+\gamma _2 +( 1-\gamma _1) \delta \\&+( 1-\gamma _2) \sigma + \frac{(\mu _2 +\lambda _1 )\sigma _1^{2}}{2 \alpha } +\frac{ \sigma _2^{2}+ \sigma _3^{2} +\sigma _4^{2}}{2}. \end{aligned}$$

Substituting (10) into (9), we obtain

$$\begin{aligned} 0\le \mathbb {E}[V_1(x(\tau _k \wedge T))]\le V_1(x(0))+ K T. \end{aligned}$$

(11)

Similar to the method developed in the study conducted by [1, 9], we obtain

$$\begin{aligned} \infty >V_1(x(0))+K T=\infty , \end{aligned}$$

which is a contradiction. So,we must have $\tau _e =\infty$  a.s. Consequently, s(t), u(t), q(t) and c(t) are positive and the solution of (2) is global. The proof is complete. $\square$

4 Extinction

The main problem in epidemiology is how we investigate the infectious disease behavior so that the epidemic will be vanished in a long term. In this section, we investigate sufficient conditions for the extinction of the disease of the system (2). Let $\mathcal {R}_0^e$ be the quantity

$$\begin{aligned} \mathcal {R}_0^e = \mathcal {R}_0 - \frac{ \sigma _2^2 }{2( \mu _2 + \gamma _1 +\lambda _1 +(1 -\gamma _1) \delta ) }. \end{aligned}$$

Before presenting the main result of this section, we need some lemmas that we state as follows:

Lemma 1

(See [12]) Let A(t) and U(t) be two continuous adapted increasing process on $t \ge 0$ with $A(0) = U(0) = 0$ a.s. Let M(t) be a real-valued continuous local martingale with $M(0) = 0$ a.s. Let $X_0$ be a nonnegative $\mathcal {F}_0$-measurable random variable such that $EX_0 < \infty$. Define $X(t) = X_0 + A(t) - U(t) + M(t)$ for all $t \ge 0$. If X(t) is nonnegative, then $\lim _{t\rightarrow \infty } A(t) < \infty$ implies $\lim _{t\rightarrow \infty } U(t) < \infty$, $\lim _{t\rightarrow \infty } X(t) < \infty$ and $- \infty< \lim _{t\rightarrow \infty } M(t) < \infty$ hold with probability one.

Lemma 2

(See [8]). Let $(M(t))_{ t \ge 0}$ be a local martingale vanishing at time 0 and define:

$$\begin{aligned} \rho _M(t)=\int _0^t \frac{d \langle M,M\rangle (s)}{(1+s)^2}, \quad t \ge 0 \end{aligned}$$

where $\langle M,M\rangle (s)$ is Meyers angle bracket process. Then,

$\lim _{t\rightarrow \infty } \frac{M(t)}{t}=0$ a.s. provided that $\lim _{t\rightarrow \infty } \rho _M(t)< \infty$ a.s

Lemma 3

Let $f\in \mathcal {C}\left( [0,\infty )\times \varOmega ; (0,\infty ) \right)$. If there exist positive constants $\lambda _0, \; \lambda$ such that for all $t \ge 0$

$$\begin{aligned} \log f(t) \le \lambda t - \lambda _0 \int _0^t f(s)ds +F(t), \end{aligned}$$

where $F \in \mathcal {C}\left( [0,\infty )\times \varOmega , \mathbb {R}\right)$ verifies $\lim _{t\rightarrow \infty }\frac{F(t)}{t}=0 ~a.s.$ Then,

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{1}{t} \int _0^t f(s)ds \le \frac{\lambda }{\lambda _0} \quad a.s. \end{aligned}$$

Theorem 2

Assume that (s(t), u(t), q(t), c(t)) be a solution of the stochastic differential equation (2) along with initial value $(s(0),u(0),q(0),c(0))\in \mathbb {R}_{+}^{4}$, then

$$\begin{aligned} \limsup _{t\rightarrow \infty } (s(t)+u(t)+q(t)+c(t))<\infty \;\text {a.s}. \end{aligned}$$

(12)

Moreover,

$$\begin{aligned} \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t s(z)dB_1(z)=0, \quad \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t u(z)dB_2(z)=0 \;\text {a.s}. \nonumber \\ \quad \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t q(z)dB_3(z)=0, \quad \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t c(z)dB_4(z)=0 \;\text {a.s}. \end{aligned}$$

(13)

Proof

Using equations of (2), we can write

$$\begin{aligned} d(s+u+q+c)= & {} \left[ \varLambda -\mu _1 s(t)-( \mu _2+\lambda _1) u(t) - (\mu _3 +\lambda _2)q(t)- (\mu _4+\lambda _3) c(t) \right] dt\\&+ \sigma _1 s dB_1 (t)+ \sigma _2 u dB_2 (t)+ \sigma _3 q dB_3 (t)+ \sigma _4 c dB_4(t). \end{aligned}$$

Let $\mu = min\{ \mu _1,\; \mu _2+ \lambda _1,\; \mu _3 +\lambda _2,\; \mu _4+ \lambda _3 \},$ then,

$$\begin{aligned} d(s+u+q+c)\le & {} \left[ \varLambda -\mu ( s(t)+ u(t) + q(t)+ c(t)) \right] dt\\&+ \sigma _1 s dB_1 (t)+ \sigma _2 u dB_2 (t)+ \sigma _3 q dB_3 (t)+ \sigma _4 c dB_4(t). \end{aligned}$$

Now, let X(t) be the solution of the following differentiel equation:

$$\begin{aligned} {\left\{ \begin{array}{ll} dX(t) = \left[ \varLambda -\mu X(t) \right] dt + \sigma _1 s dB_1 (t)+ \sigma _2 u dB_2 (t)+ \sigma _3 q dB_3 (t)+ \sigma _4 c dB_4(t), \\ X(0) = s(0)- u(0) + q(0)- c(0). \end{array}\right. } \end{aligned}$$

On the one hand, by using stochastic comparaison theorem, we have:

$$s(t)+ u(t) + q(t)+ c(t) \le X(t).$$

On the other hand, X(t) verifies $X(t)= \frac{\varLambda }{\mu }- \left( X(0) - \frac{\varLambda }{\mu } \right) e^{-\mu t} + M(t),$ where

$$\begin{aligned} M(t)= & {} \sigma _1 \int _0^t s(z) e^{-\frac{\mu }{N} z} dB_1 (z)+ \sigma _2 \int _0^t u(z)e^{-\frac{\mu }{N} z} dB_2 (z)+ \sigma _3 \int _0^t q(z) dB_3 (z)\\&+ \sigma _4 \int _0^t c(z) e^{-\frac{\mu }{N} z} dB_4(z). \end{aligned}$$

Clearly, M(t) is a continuous local martingale with $M(0) = 0~a.s.$ Furthermore, we have

$$\begin{aligned} X(t)= X(0)+ A(t)-U(t)+M(t), \end{aligned}$$

where

$$\begin{aligned} A(t)=\frac{\varLambda }{\mu }\left( 1 - e^{-\frac{\mu }{N}t} \right) \quad \text{ and }\quad U(t)= X(0)(1-e^{-\mu t}) \;\text {for all } \; t \ge 0. \end{aligned}$$

It is quite easy to check that A(t) and U(t) are continuous adapted increasing progress on $t \ge 0$ with $A(0)=U(0)=0.$ By using lemma 1, we have $\lim _{t\rightarrow \infty } X(t) < \infty ~a.s.$

Hence, we deduce that $\limsup _{t\rightarrow \infty } (s(t)+u(t)+q(t)+c(t))< \infty \; ~a.s.$ This complete the proof of (12).

For convenience, we denote

$$\begin{aligned} M_1(t)= & {} \sigma _1 \int _0^t s(z) dB_1 (z), \quad M_2(t)= \sigma _2 \int _0^t u(z) dB_2 (z),\\ M_3(t)= & {} \sigma _3 \int _0^t Q(z) dB_3 (z), \quad M_4(t)=\sigma _4\int _0^t c(z) dB_4(z). \end{aligned}$$

We have $\langle M_1 , M_1\rangle (t)= \sigma _1^2 \int _0^t s^2(z) ds$ and by (12) because of the quadratic variation, we can write:

$$\begin{aligned} \lim _{t\rightarrow \infty } \rho _1(t)= \lim _{t\rightarrow \infty } \int _0^t \frac{\sigma _1^2 s^2(z)}{(1+z)^2} dz \le \sigma _1^2 \sup _{t \ge 0} \{ s^2(t) \} < \infty . \end{aligned}$$

Then, by lemma 2, we have $\lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t \sigma _1 s(z)dB_1(z)=0$.

Similary, we also get

$$\begin{aligned}&\lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t u(z)dB_2(z)=0, \quad \lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t q(z)dB_3(z)=0,\\&\lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t c(z)dB_4(z)=0 \; ~a.s. \end{aligned}$$

This draws an end to the proof. $\square$

The following theorem gives a a sufficient condition for the extinction of the disease expressed in terms of $\mathcal {R}_0^e.$

Theorem 3

For any given initial value, $(s(0),u(0),q(0),c(0))\in \mathbb {R}_{+}^{4}$, if $\mathcal {R}_0^e < 1$ . Then, the solution of the stochastic differential equation (2) obeys

$$\begin{aligned}& \lim _{t\rightarrow + \infty } \frac{1}{t} \int _0^t s(t) dt=\frac{\varLambda }{\mu _1} \quad a.s.\\& \lim _{t\rightarrow \infty } u(t)=\lim _{t\rightarrow \infty }q(t) =\lim _{t\rightarrow \infty } c(t)= 0 \quad a.s. \end{aligned}$$

Proof

Applying the Itô’s formula, we obtain:

$$\begin{aligned} d(\log (u(t))= & {} \left( \frac{g(s,u)}{u}-\gamma _1 - \mu _2 - ( 1-\gamma _1) \delta - \lambda _1 - \frac{\sigma _2^2}{2} \right) dt + \sigma _2 dB_2(t). \end{aligned}$$

Hence,

$$\begin{aligned} \frac{1}{t}\log (u(t))\le & {} \frac{\alpha }{t} \int _0^t s(x) dx -\left( \gamma _1 + \mu _2 + ( 1-\gamma _1) \delta + \lambda _1 + \frac{\sigma _2^2}{2} \right) \nonumber \\&+ \frac{\sigma _2}{t} B_2(t) + \frac{\log (u(0))}{t}. \end{aligned}$$

(14)

Denoting $\phi (t) = s(t)+ u(t),$ we have

$$\begin{aligned} d \phi (t)= & {} \Big ( \varLambda -\mu _1 s(t)-(\gamma _1 + \mu _2 + ( 1-\gamma _1) \delta + \lambda _1)u(t)\\&+ \frac{\sigma _2^2}{2} \Big )dt + \sigma _1 s B_1(t)+ \sigma _2 u dB_2(t). \end{aligned}$$

Intergrating the above relation along [0, t],  we obtain

$$\begin{aligned} \phi (t) - \phi (0) = \varLambda t -\mu _1 \int _0^t s(x) dx -(\gamma _1 + \mu _2 + ( 1-\gamma _1) \delta + \lambda _1) \int _0^t u(x) dx + N_1(t), \end{aligned}$$

(15)

where $N_1(t)= \sigma _1 \int _0^t s(x) d B_1(x)+ \sigma _2 \int _0^t u(x) dB_2(x).$ Combining (14) and (15), we deduce that

$$\begin{aligned} \log (u(t))\le & {} \left[ \frac{\alpha \varLambda }{ \mu _1} -\left( \gamma _1 + \mu _2 + ( 1-\gamma _1) \delta + \lambda _1+\frac{\sigma _2^2}{2} \right) \right] t \nonumber \\&- \frac{ \alpha (\gamma _1 + \mu _2 + ( 1-\gamma _1) \delta + \lambda _1) }{\mu _1 t} \int _0^t u(x) dx + N_2(t), \end{aligned}$$

(16)

where $N_2(t)= \frac{\alpha }{ \mu _1} N_1(t) - \frac{\alpha (\phi (t) - \phi (0))}{\mu _1 } + \sigma _2 B_2(t) + \log (u(0))$. Hence,

$$\begin{aligned} \log (u(t))\le & {} \left( \mu _2 + \gamma _1+\lambda _1 +(1 -\gamma _1) \delta \right) ( \mathcal {R}_0^e -1 )t \\&- \frac{\alpha ( \gamma _1 + \mu _2 + ( 1-\gamma _1) \delta +\lambda _1 ) }{\mu _1 t} \int _0^t u(x) dx + N_2(t). \end{aligned}$$

By the strong law of large numbers for martingales, we obtain $\lim _{t\rightarrow \infty }\frac{N_2(t)}{t}=0,$ and the lemma 3 gives that

$$\begin{aligned} \limsup _{t\rightarrow \infty }\frac{\log (u(t))}{t}\le & {} \left( \mu _2+\gamma _1 +\lambda _1+(1 -\gamma _1) \delta \right) ( \mathcal {R}_0^e -1 ) \; a.s. \end{aligned}$$

(17)

This means that whenever $\mathcal {R}_0^e < 1$, then

$$\begin{aligned} \lim _{t\rightarrow \infty } u(t)=0 \quad a.s. \end{aligned}$$

(18)

Next, we define $\varOmega _1=\{\omega \in \varOmega :\; \lim _{t\rightarrow \infty } u(t)=0 \}.$ Consequently, (18) implies that $\mathcal {P}(\varOmega _1)=1$. Moreover, we have for any $\epsilon > 0$ and $\omega \in \varOmega _1$, there exists a constant $T_1(\omega ;\epsilon ) > 0$ such that

$$\begin{aligned} u(\omega ;t) \le \epsilon ,\;\text {for all} \; t \ge T_1. \end{aligned}$$

(19)

Combining (19) and the third equation of the system (2), we obtain for all $(\omega ;t) \in \varOmega _1\times (T_1, \infty )$

$$\begin{aligned} dq(t)\le & {} \left( \gamma _1\epsilon - \lambda _2 q-( \mu _3 + \gamma _2 +(1 -\gamma _2) \sigma ) q \right) dt+ \sigma _3 q dB_3 (t). \end{aligned}$$

Integrating the above inequality from 0 to t,  dividing by t, and using the theorem 2, we obtain for all $(\omega ;t) \in \varOmega _1\times (T_1, \infty )$

$$\begin{aligned} q(t)\le & {} \frac{\gamma _1\epsilon }{\mu _3 + \lambda _2 + \gamma _2 +(1 -\gamma _2) \sigma } + q(T_1) e^{-( \mu _3 + \lambda _2 + \gamma _2 +(1 -\gamma _2) \sigma ) ( t-T_1 )} , \end{aligned}$$

Taking the limit superior of both sides, we deduce

$$\begin{aligned} \limsup _{t \rightarrow + \infty } q(t)\le \frac{\gamma _1 \epsilon }{\mu _3 + \lambda _2 + \gamma _2 +(1 -\gamma _2) \sigma } , \; a.s \end{aligned}$$

Since $\epsilon$ is arbitrary and $q(t) \ge 0,$ we arrive to

$$\begin{aligned} \lim _{t\rightarrow + \infty } q(t)=0 \quad a.s. \end{aligned}$$

(20)

Let $\varOmega _2=\{\omega \in \varOmega :\; \lim _{t\rightarrow \infty } u(t)=\lim _{t\rightarrow \infty } q(t)=0 \}$, by (19) and (20) we have $\mathcal {P}(\varOmega _2)=1$. Then, for all $\omega \in \varOmega _2$ and $\epsilon > 0$, there exists a constant $T_2(\omega ;\epsilon ) > 0$ such that

$$\begin{aligned} u(\omega ;t) \le \epsilon \ , \quad q(\omega ;t) \le \epsilon ,\quad \forall t\ge T_2. \end{aligned}$$

(21)

Substuting (21) into the fourth equation of the system (2), we have for all $(\omega ;t) \in \varOmega _2 \times (T_2, \infty )$

$$\begin{aligned} dc(t) \le \left( ( \gamma _2 +(1 -\gamma _2) \sigma +(1-\gamma _1)\delta ) \epsilon -(\mu _4+\lambda _3) c \right) dt + \sigma _4 c (t) dB_4(t). \end{aligned}$$

(22)

Using theorem 2, we obtain $\lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t c (t) dB_4 (t)=0.$

The Integration of the relation (22) from 0 to t and dividing it by t leads to

$$\begin{aligned} c(t)\le & {} \frac{\gamma _2 +(1 -\gamma _2) \sigma +(1-\gamma _1)\delta }{\mu _4+\lambda _3 }\epsilon +c(T_2) e^{-( \gamma _2 +(1 -\gamma _2) \sigma +(1-\gamma _1)\delta ) ( t-T_2 )} \nonumber \\&+ \frac{\sigma _4}{\mu _4+\lambda _3 } \frac{1}{t} \int _0^t c (t) dB_4 (t) , \;\text { for all } \; (\omega ;t) \in {\varOmega _2\times (T_1, \infty )}. \end{aligned}$$

(23)

Taking the limit superior of both sides we obtain

$$\begin{aligned} \limsup _{t\rightarrow + \infty }c(t) \le \frac{\gamma _2 +(1 -\gamma _2) \sigma +(1-\gamma _1)\delta }{\mu _4+\lambda _3 }\epsilon , \; a.s. \end{aligned}$$

By the positivity of the solution and the arbitrariness of $\epsilon$ we obtain

$$\begin{aligned} \lim _{t\rightarrow + \infty } c(t)=0 \quad a.s. \end{aligned}$$

Consequently, $\lim _{t\rightarrow + \infty } i(t)=0 \quad a.s.,$ where $i(t) = u(t)+q(t)+c(t)$ represents the number of individuals infected at the time t, which significate that when the value of $\mathcal {R}_0^e$ is below 1 will lead to the extinction of the disease.

Likewise, similar to the proof found in the study ran by [3], we have obtained the following result

$$\begin{aligned} \lim _{t\rightarrow + \infty } \frac{1}{t} \int _0^t s(t) dt=\frac{\varLambda }{\mu _1} \quad a.s., \end{aligned}$$

which proves the desired assertion and hence the theorem 3. $\square$

5 Persistence in mean

In epidemics modelling, persistence is an important property to investigate as it means that the disease continues to exist under some appropriate conditions. We define the number

$$\begin{aligned} \mathcal {R}_0 ^p = \mathcal {R}_0 - \frac{2 \alpha _1\varLambda + \mu _1\sigma _2^2}{ 2 \mu _1 (\gamma _1 + \lambda _1 + \mu _2 + ( 1-\gamma _1) \delta )}. \end{aligned}$$

In this section, we study the persistence in mean for the stochastic model (2). Firstly, we give the following definition and lemma.

Definition 1

System (2) is said to be persistent in the mean if

$$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t s(x)dx> 0 , \quad \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t i(x)dx > 0. \end{aligned}$$

Lemma 4

Let $f \in \mathcal {C}[[0;\infty )\times \varOmega ; (0;\infty ) ]$. If there exist positive constants $\lambda _0, \; \lambda$ such that

$$\begin{aligned} \log f(t) \ge \lambda t - \lambda _0 \int _0^t f(s)ds +F(t) \quad a.s. \end{aligned}$$

for all $t \ge 0$ where $F \in \mathcal {C}[[0;\infty )\times \varOmega ; \mathbb {R}]$ verifies $\lim _{t\rightarrow \infty }\frac{F(t)}{t}=0 \quad a.s.$.Then,

$$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t f(s)ds \ge \frac{\lambda }{\lambda _0} \quad a.s. \end{aligned}$$

We omit the proof of lemma 4 as it is similar to the one given in [5].

Theorem 4

For any given initial values $(s(0),u(0),q(0),c(0))\in \mathbb {R}_{+}^{4}$, if $\mathcal {R}_0 ^p > 1$ . Then, the solution of the stochastic differential equation (2) obeys

• (1) $\liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t s(x)dx \ge \frac{\varLambda }{\mu _1 + \alpha } \quad a.s.,$

• (2) $\liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t u(x)dx \ge a_1 ( \mathcal {R}_0 ^p -1 ) \quad a.s.,$

• (3) $\liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t q(x)dx \ge a_2 (\mathcal {R}_0 ^p -1 )\quad a.s.,$

• (4) $\liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t c(x)dx \ge a_3 (\mathcal {R}_0 ^p -1 )\quad a.s.$

For some positive constants, $a_i, \; i=1,\cdots ,3.$. That is the solution to the stochastic model (2) starting from any point in $\mathbb {R}_{+}^{4}$ are persistent in mean.

Proof

• (1) From the first equation of the system, (2) and the fact that $g(s,u) \le \alpha s,$ , we obtain

  $$\begin{aligned} ds \ge \left[ \varLambda -(\mu _1 +\alpha )s \right] dt +\sigma _1 s dB_1(t). \end{aligned}$$

  Integrating the above inequality and dividing both sides by t,  , we obtain

  $$\begin{aligned} \frac{1}{t} \int _0^t s(x)dx \ge \frac{\varLambda }{\mu _1 +\alpha } +\frac{\sigma _1}{\mu _1 +\alpha }\frac{1}{t} \int _0^t s(x) dB_1(x) - \frac{s(t)-s(0)}{(\mu _1 +\alpha )t} \end{aligned}$$

  From theorem 2, we have $\lim _{t\rightarrow \infty } \frac{1}{t} \int _0^t s (t) dB_1 (t)=0~a.s.$ Making use of (13) and the large numbers theorem for martingales, we obtain

  $$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t s(x)dx \ge \frac{\varLambda }{\mu _1 +\alpha }~a.s. \end{aligned}$$

• (2) Using the Itô’s formula, we obtain

  $$\begin{aligned} d\log u(t)= \left( \frac{g(s,u)}{u}-\gamma _1 - \mu _2 - \lambda _1 - ( 1-\gamma _1) \delta - \frac{\sigma _2^2}{2} \right) dt + \sigma _2 dB_2(t). \end{aligned}$$

  Hence,

  $$\begin{aligned} d\log u \ge \left[ (\alpha -\alpha _1 )s(t)-(\gamma _1 + \lambda _1+\mu _2 +(1-\gamma _1)\delta )- \frac{\sigma _2^2 }{2} \right] dt+\sigma _2 dB_2(t). \end{aligned}$$

  (24)

  Thus

  $$\begin{aligned} \log u(t)\ge & {} (\alpha -\alpha _1 ) \int _0^t s(x) dx -\left[ (\gamma _1 + \lambda _1+\mu _2 +(1-\gamma _1)\delta )+ \frac{\sigma _2^2 }{2} \right] t \nonumber \\&+\log (u(0))+ \sigma _2 dB_2(t). \end{aligned}$$

  (25)

  Combining the above inequality with (15), we obtain

  $$\begin{aligned} \log u(t)\ge & {} \left[ (\alpha -\alpha _1 )\frac{\varLambda }{\mu _1} - \left( \gamma _1 + \lambda _1+\mu _2 +(1-\gamma _1)\delta )+ \frac{\sigma _2^2 }{2} \right) \right] t \nonumber \\&-\frac{(\alpha -\alpha _1 )(\gamma _1 + \mu _2 + ( 1-\gamma _1) \delta + \lambda _1)}{\mu _1} \int _0^t u(x) dx + G(t), \end{aligned}$$

  (26)

  where

  $$\begin{aligned} G(t)= \frac{\alpha - \alpha _1}{ \mu _1 } N_1(t) - \frac{(\alpha - \alpha _1)( \phi (t) - \phi (0)) }{\mu _1 } + \sigma _2 dB_2(t) + \log (u(0)). \end{aligned}$$

  By virtue of the law of large numbers, we conclude that $\lim _{t\rightarrow \infty }\frac{G(t)}{t} = 0 .$ Hence, using lemma 4, one can obtain the following result:

  $$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t u(x) dx\ge & {} \frac{ \mu _1 }{\alpha - \alpha _1} \left[ \mathcal {R}_0 - \frac{2 \alpha _1\varLambda + \mu _1\sigma _2^2}{ 2 \mu _1 (\gamma _1 + \lambda _1 + \mu _2 + ( 1-\gamma _1) \delta )} -1 \right] , \end{aligned}$$

  (27)

  almost surely, which means that

  $$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t u(x)dx \ge a_1 ( \mathcal {R}_0 ^p -1 ) ~a.s., \end{aligned}$$

  (28)

  where $a_1= \dfrac{\mu _1 }{\alpha -\alpha _1} > 0.$

• (3) Integrating the third equation of system (2) and dividing by t we have

  $$\begin{aligned} \frac{1}{t} \int _0^t q(x)dx= & {} \left( \frac{\gamma _1}{\mu _3 +\lambda _2+\gamma _2+(1-\gamma _2)\sigma }\right) \frac{1}{t} \int _0^t u(x)dx \\&-\frac{q(t)-q(0)}{ \left( \mu _3 +\lambda _2+\gamma _2+(1-\gamma _2)\sigma \right) t} \\&+ \frac{\sigma _3}{ \mu _3 +\lambda _2+\gamma _2+(1-\gamma _2)\sigma } \frac{1}{t} \int _0^t q(x)dB_3 (x). \end{aligned}$$

  Using (28) and extending t to $\infty$, then applying theorem 2 and the law of large numbers, we obtain

  $$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t q(x)dx \ge \dfrac{\gamma _1}{\mu _3 +\lambda _2+\gamma _2+(1-\gamma _2)\sigma } a_1 ( \mathcal {R}_0^p -1 ) \quad a.s. \end{aligned}$$

  Hence

  $$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t q(x)dx \ge a_2 ( \mathcal {R}_0 ^p -1 ) \quad a.s., \end{aligned}$$

  (29)

  where $a_2= \dfrac{\gamma _1 a_1}{\mu _3 +\lambda _2+\gamma _2+(1-\gamma _2)\sigma } > 0.$

• (4) Integrating the fourth equation of system (2) and multiplying by $\frac{1}{t},$ we obtain

  $$\begin{aligned} \frac{1}{t} \int _0^t c(x)dx= & {} \left( \frac{\gamma _2+(1-\gamma _2)\sigma }{\mu _4+\lambda _3} \right) \frac{1}{t} \int _0^t q(x)dx -\frac{c(t)-c(0)}{ (\mu _4+\lambda _3) t}\\&+\left( \frac{(1-\gamma _1)\delta }{\mu _4+\lambda _3} \right) \frac{1}{t} \int _0^t u(x)dx + \frac{\sigma _4}{\mu _4+\lambda _3} \frac{1}{t} \int _0^t c(s)dB_4(s) . \end{aligned}$$

  Then,

  $$\begin{aligned} \frac{1}{t} \int _0^t c(x)dx\ge & {} \frac{min\{ \gamma _2+(1-\gamma _2)\sigma , (1-\gamma _1)\delta \}}{\mu _4+\lambda _3} \frac{1}{t} \int _0^t ( u(x)+q(x) )dx \\&-\frac{c(t)-c(0)}{(\mu _4+\lambda _3) t} + \frac{\sigma _4}{\mu _4+\lambda _3} \frac{1}{t} \int _0^t c(x)dB_4(x) . \end{aligned}$$

  Making use of the assertions (2) and (3), we come up with the following result:

  $$\begin{aligned} \frac{1}{t} \int _0^t c(x)dx \ge a_3 ( \mathcal {R}_0 ^p -1 ) -\frac{c(t)-c(0)}{(\mu _4+\lambda _3) t} + \frac{\sigma _4}{\mu _4+\lambda _3} \frac{1}{t} \int _0^t c(x)dB_4(x), \end{aligned}$$

  where $a_3= \frac{min\{ (\gamma _2+(1-\gamma _2)\sigma ) a_2, ((1-\gamma _1)\delta ) a_1 \}}{\mu _4+\lambda _3} > 0.$ Taking the inferior limit, and applying the theorem 2 and the law of large numbers, we obtain

  $$\begin{aligned} \liminf _{t\rightarrow \infty }\frac{1}{t} \int _0^t c(x)dx \ge a_3 ( \mathcal {R}_0 ^p -1 )~a.s. \end{aligned}$$

  It follows that $\mathcal {R}_0 ^p -1 > 0$ is a sufficient condition so that the disease would prevail and be persistent in mean. This completes the proof.

$\square$

6 Numerical simulations and discussion

To illustrate our analytical results, we show numerical simulations via Euler–Maruyama scheme [18] to approximate the solution of the SDE model (2). The parameter values presented in Table 2 remain inchanged throughout this section.

Table 2 Parameters values used in numerical simulations

To produce an extinction scenario, we choose $\alpha =0.35,\alpha _1=0.06$ with $f(u)=\frac{u}{1+u}.$ This corresponds to values $\mathcal {R}_0^e=0.95$ and $\mathcal {R}_0 =1.09.$ By theorem 3, the disease in the stochastic system (2) will go to zero with probability one even if it will be prevailing in the deterministic system (1) provided that $\mathcal {R}_0$ is greater than 1. Figure 1 illustrates these results.

Fig. 1

Trajectories of the solutions to systems (1) and (2) respectively, with parameters given in Table 2, $\sigma _1=\sigma _3=\sigma _4=0.2$ and $\sigma _2=0.3$

On the other hand, if we let $\alpha =1.13,\alpha _1=0.04,$ we obtain by computation $\mathcal {R}_0^p=3.5.$ By virtue of theorem 4, the disease will be persistent as long as $\mathcal {R}_0^p>1$. A simulation of this case is showed in Fig. 2.

Fig. 2

Paths solutions to the deterministic system (1) and stochastic system (2) showing the persistence of the disease under the condition $\mathcal {R}_0^p>1$

Now, let $f(u)=\frac{u}{10^{-3}+u}$ and using different values of $\alpha _1$ to generate trajectories of unquarantined infectives and new infected cases respectively. These paths are plotted in Fig. 3. Thus, high values of $\alpha _1$ representing media efforts significantly reduce the number of unquaranted infected individuals and minimize the number of new infectives. This means that intense media efforts play a key role in reducing the infective population size.

Fig. 3

The influence of media coverage on the unquarantined population size (left) and the new infected cases (right) for $\alpha =1.3$ according to different situations characterizing media alert. Blue line $\alpha _1=0,$ red line $\alpha _1=0.7,$ green line $\alpha _1=1.06$ (color figure online)

To sum up, due to its massive global outbreak, the 2019-nCoV virus has proven to be one of the wordlwide deadliest diseases over history. It has posed a potential threat to human health attracting worldwide attention after the (SARS) 2003 and the (MERS) 2012 and up to this very moment, there is no entirely proper treatment of it. Instead, preventive measures should be strictly implemented such as social distancing and other infection control measures to prevent the spread of SARSCoV-2 via human-to-human transmission. The compartmental model (Susceptible, Un-quarantined infected, Quarantined infected, Confirmed infected) proposed in the present study of the spread of COVID-19 has taken into account the particularities of this infectious disease where some of them are still not well-known. As well, we have used parameters and variables pertaining to the effects of quarantine and confirmation methods. In an attempt to render our model more realistic, we have included stochastic perturbations. Given that media awareness is one of the most useful tools that contributes to the control of epidemic spreading [11], we have tried to investigate the effects of media coverage on the transmission dynamics. By having recourse to the stochastic theory and the compartmental mathematical model keeping in view the characteristics of the novel COVID-19, our study seeks to study the spread and the transmission dynamics. We initially adopted the idea of stochastic Lyapunov functions theory to prove the existence and positivity of the solution. Then, the extinction has been further discussed to pave the way for the conditions that put an end to the disease. Sufficient condition to the persistence of the disease is also obtained. More significantly, numerical simulations are presented to show these results as well as the impact of media coverage on the size of the infected class. Overall, it is worth noting that there is a great influence of noise intensity on the COVID-19 transmission. Equally important, media efforts could be helpful to reduce the number of infectives and offer more time to authorities to react to the global pandemic.