From perturbative methods to machine learning techniques in space science

Abstract

Perturbation theory is a very useful tool to investigate the dynamics of models in space science. We start by presenting some results obtained implementing classical perturbation theory to investigate the motion of space debris, which are objects that populate the sky around the Earth after a satellite break-up event. When dealing with two or more break-up events, a clusterization of the fragments can be computed using machine learning techniques. We also present the celebrated KAM theory for symplectic and conformally symplectic systems. We recall several computer-assisted results in Celestial Mechanics in conservative and dissipative settings. Finally, we consider the spin-orbit problem and we show how machine learning methods can be conveniently used to classify regular and chaotic motions.

1 Introduction

Perturbative methods have greatly helped astronomers and mathematicians to understand the dynamics of the celestial bodies in the Solar system. It suffices to mention the discovery of the planet Neptune, whose existence was predicted by pen and paper by U. Leverrier to explain the discrepancies between the observations and the theoretical prediction of the motion of Uranus, the last planet known in the XIX century. Since its first statement, perturbation theory has been applied to a wide variety of problems in space, including the orbital and rotational motion of planets and satellites, the trajectories of spacecraft, the design of space missions.

Further developments of perturbation theory are represented by the Kolmogorov–Arnold–Moser (hereafter KAM) theory ([2, 31, 36]) and Nekhoroshev’s theorem ([38]). Briefly speaking, KAM theory allows to obtain results on the stability of the motion for infinite times and to explicitely construct invariant manifolds. Nekhoroshev’s theorem provides stability of an open set of initial data for exponentially long times.

In this work we consider some applications of perturbation theory and KAM theory to problems of Celestial Mechanics and Astrodynamics. In Sect. 2 we consider the dynamics of space debris around the Earth, which are the outcome of break-up events, either an explosion of an artificial satellite or a collision between two satellites. We consider satellites and space debris above 2000 km of altitude from the surface of the Earth, so that we can neglect the dissipative effect due to the atmosphere and write the model using the Hamiltonian formulation. The dynamics of the resulting fragments can be conveniently studied using the so-called proper elements. These quantities are quasi-integrals of motion, which are obtained implementing perturbation theory, taking into account the different time scales over which the coordinates of the problem vary. Proper elements have been successfully used in the space debris problem to investigate the dynamics of the fragments along their evolution over time, as well as to reconnect the fragments to their parent body (see, e.g., [14, 18,19,20, 40]). In order to interpret the results, the interplay with machine learning methods has been proved to be extremely useful. In fact, clusterization algorithms can be used to distinguish the fragments generated by multiple break-up events. We shortly provide some results in this direction, which appears to be very promising.

Section 3 provides a brief introduction to KAM theory for symplectic and conformally symplectic systems, the latter ones being dissipative systems with the property that they transform the symplectic form into a multiple of itself. KAM theory has the remarkable property that it gives constructive algorithms to compute estimates on the parameters, ensuring the existence of invariant tori. Once these algorithms are built on a computer, one can obtain rigorous results by implementing the so-called interval arithmetic, which allows to get a computer-assisted proof. Alternatively to the implementation of interval arithmetic, one can proceed to make a computer implementation of KAM theory with long precision (namely a high number of digits), so to have a computer-assisted validation of the results. KAM theory has been implemented in a number of problems of Celestial Mechanics, either conservative or dissipative. We review some model problems and provide a summary of the computer-assisted proofs/validations. For some models, machine learning methods can be used to investigate the dynamics, for example by predicting the occurrence of regular or chaotic motions, as we illustrate using different classification algorithms for a simple problem, namely the spin-orbit model ([8, 9]) describing the rotational motion of a satellite around a central planet (see also [16]).

These few examples of applications of machine learning techniques to complement results obtained with perturbative approaches might serve as a motivation to discover further potentialities and synergies between the two methods.

2 Perturbation theory and space debris

In this section we present an application of classical perturbation theory to a compelling problem of space science: the dynamics of the space debris around the Earth. The space debris problem is introduced in Sect. 2.1, a short review of perturbation theory is given in Sect. 2.2, an application of perturbation theory to the space debris problem is illustrated in Sect. 2.3, elementary results based on machine learning clusterization are given in Sect. 2.4.

2.1 The space debris dynamics

Space debris are remnants of satellites, which are left in space during or after their operative life. The number of space debris increases dramatically after a break-up event, either an explosion or a collision between two satellites. Using the ESA’s Meteoroid And Space debris Terrestrial Environment Reference (MASTER-8) model, it is estimated that the space surrounding the Earth is populated by about 36,500 space debris objects greater than 10 cm, about 1 million objects between 1 cm and 10 cm, 130 millions objects between 1 mm and 1 cm. Even if the fragments are small, their high velocity impact might provoke serious consequences to operational spacecraft. Understanding their dynamics is therefore of paramount importance.

In this work we concentrate on space debris whose orbits around the Earth lie at an altitude above 2000 km, which is the limit at which we can disregard the dissipative effect of the atmosphere. The model that we are going to use is given by the sum of the following effects:

(i):

the effect of the Earth, represented by its gravitational field expanded in spherical harmonics;

(ii):

the attraction exerted by Moon and Sun;

(iii):

the Solar radiation pressure.

For short, we denote by ${{\mathcal {H}}}$ the sum of all contributions, say

$$\begin{aligned} {{\mathcal {H}}}={{\mathcal {H}}}({\underline{J}}_d,{{\underline{\varphi }}}_d,{\underline{J}}_M,{{\underline{\varphi }}}_M, {\underline{J}}_S,{{\underline{\varphi }}}_S,\theta ), \end{aligned}$$

(2.1)

where $({\underline{J}},{{\underline{\varphi }}})$ denote action-angle coordinates referring to the debris (suffix d), Moon (suffix M), Sun (suffix S), while $\theta$ is the sidereal time accounting for the rotation of the Earth. The actions ${\underline{J}}$ are related to the orbital elements (a, e, i), where a is the semimajor axis, e the eccentricity, i the inclination. The angles ${{\underline{\varphi }}}$ are related to the orbital elements $(\ell ,g,h)$, where $\ell$ is the mean anomaly, g the argument of perigee and h the longitude of the ascending node.

It is important to stress that the Hamiltonian (2.1) depends on several angular variables pertaining to the debris, Sun and Moon, and that such variables vary on different time scales. Precisely, we can distinguish between the following angles:

(a):

fast angles, namely the mean anomaly of the debris and the sidereal time, varying with periods of days and describing, respectively, the motion of the debris and the rotation of the Earth;

(b):

semi-fast angles, namely the mean anomalies of Moon and Sun with periods, respectively, of 1 month and 1 year;

(c):

slow angles, namely the arguments of perigee and the longitudes of the ascending nodes of the debris, Moon and Sun, which vary with periods of several years.

Any application of perturbative methods must take into account the above hierarchy of angles. Since the Hamiltonian in (2.1) contains terms characterized by different orders of smallness, it is useful to introduce a book–keeping parameter $\varepsilon$, which will be set to one at the end of the procedure, and write (2.1) in the form

$$\begin{aligned} {{\mathcal {H}}}={{\mathcal {H}}}_0+\varepsilon {{\mathcal {H}}}_1+\cdots +\varepsilon ^N {{\mathcal {H}}}_N \end{aligned}$$

for a suitable integer N and suitable functions ${{\mathcal {H}}}_0$, ${{\mathcal {H}}}_1$,...,${{\mathcal {H}}}_N$.

2.2 Perturbative methods

We briefly recall below the basic results of perturbation theory for non-resonant Hamiltonian systems, according to the following definition.

Definition 1

Consider the Hamiltonian

$$\begin{aligned} {{\mathcal {H}}}={{\mathcal {H}}}_0({\underline{J}})+\varepsilon R({\underline{J}},{{\underline{\varphi }}}) \end{aligned}$$

(2.2)

for $({\underline{J}},{{\underline{\varphi }}})\in {{\mathbb {R}}}^n\times {{\mathbb {T}}}^n$ with n denoting the number of degrees of freedom, ${{\mathcal {H}}}_0$ being the integrable part and R being the perturbing function. We define the frequency vector ${{\underline{\omega }}}\in {{\mathbb {R}}}^n$ as

$$\begin{aligned} {{\underline{\omega }}}({\underline{J}})={{\partial {{\mathcal {H}}}_0({\underline{J}})}\over {\partial {\underline{J}}}}. \end{aligned}$$

We say that for ${\underline{J}}={\underline{J}}_0$ the frequency vector is non-resonant up to the order K if

$$\begin{aligned} |{{\underline{\omega }}}({\underline{J}}_0)\cdot {\underline{k}}|>0\ for\ all\ 0<|{\underline{k}}|\le K. \end{aligned}$$

(2.3)

Next, we introduce the definition of the domain $S_\rho ({\underline{J}}_0)$ for $\rho >0$ as

$$\begin{aligned} S_\rho ({\underline{J}}_0)=\{{\underline{J}}\in {{\mathbb {R}}}^n:\ |{\underline{J}}-{\underline{J}}_0|\le \rho \}. \end{aligned}$$

Then, we can state the main theorem of perturbation theory as follows.

Theorem 2

Consider the Hamiltonian function (2.2) defined for $({\underline{J}},{{\underline{\varphi }}})\in V\times {{\mathbb {T}}}^n$ with $V\subset {{\mathbb {R}}}^n$ open. Assume that R is analytic on $V\times {{\mathbb {T}}}^n$ and trigonometric with Fourier harmonics of total degree not greater than K. Assume that the frequency vector satisfies the non-resonance condition (2.3) up to order K. Then, there exist parameters $\rho _0>0$, $\varepsilon _0>0$ and for $|\varepsilon |<\varepsilon _0$ there exists a canonical transformation $({\underline{J}},{{\underline{\varphi }}}) \rightarrow ({\underline{J}}',{{\underline{\varphi }}}')$ defined in $S_{\rho _0\over 2}({\underline{J}}_0)\times {{\mathbb {T}}}^n\subset V\times {{\mathbb {T}}}^n$ and with values in $S_{\rho _0}({\underline{J}}_0)\times {{\mathbb {T}}}^n$, which transforms (2.2) into

$$\begin{aligned} {{\mathcal {H}}}'({\underline{J}}',{{\underline{\varphi }}}')\ =\ {{\mathcal {H}}}_0'({\underline{J}}')+\varepsilon ^2 R'({\underline{J}}',{{\underline{\varphi }}}') \end{aligned}$$

(2.4)

for suitable functions ${{\mathcal {H}}}_0'$, $R'$.

We remark that an iterative application of Theorem 2 can lead, under the condition that the generating function of the canonical transformation is convergent, to remove the perturbation to higher orders, say ${{\mathcal {H}}}''={{\mathcal {H}}}_0''+{\varepsilon ^3} R''$, ${{\mathcal {H}}}'''={{\mathcal {H}}}_0'''+{\varepsilon ^4} R'''$, etc.

Neglecting $O(\varepsilon ^2)$ in (2.4), we obtain that the actions are integrals for the new unperturbed Hamiltonian ${{\mathcal {H}}}'({\underline{J}}',{{\underline{\varphi }}}')={{\mathcal {H}}}_0'({\underline{J}}')$, since it results that

$$\begin{aligned} {{d{\underline{J}}'}\over {dt}}={{\partial {{\mathcal {H}}}_0'({\underline{J}}')}\over {\partial {{\underline{\varphi }}}'}}={\underline{0}}. \end{aligned}$$

Hence, the quantities ${\underline{J}}'$ are quasi-integrals for the full Hamiltonian. Back-transforming to the original set of variables through the generating function, we obtain the so-called proper elements that will be used in Sect. 2.3 to characterize the dynamics of a space science example, namely the space debris problem. We remark that proper elements have been introduced and used more than a century ago in the context of asteroid families (compare with [27], see also [4, 29, 32, 35]), well beyond their application to the space debris problem.

Let us conclude by saying that in the following we will compare the proper elements to the mean elements, which are obtained integrating the Hamiltonian (2.1) averaged with respect to the fast angles, namely the mean anomaly of the debris and the sidereal time.

2.3 Proper elements and breakup events

To simulate a break-up event, we used the program SIMPRO, which has been developed in [1] on the basis of the NASA break-up model EVOLVE 4.0 ([28]). SIMPRO provides simulations for explosions or collisions, taking as input the type and the orbital elements of the parent bodies, the minimum size of the generated fragments, the mass of the parent body and the projectile, the collision velocity, while it gives as output the evolution of each fragment, allowing to propagate them over time, and providing statistical data analysis of the orbital elements.

Using SIMPRO, we simulated in [19] two explosions taking place at the same values of the orbital elements, except for the inclination which is taken with 1 degree of difference ($i=20^\circ$ and $i=21^\circ$, see Fig. 1). The mean orbital elements have been computed for each fragment at two different times: at the break-up instant and after 150 ys. Next, we implemented perturbation theory to compute the proper elements of each fragment at the initial time and after the propagation. Precisely, we averaged the Hamiltonian over the fast and semi-fast angles; then, we expanded the Hamiltonian up to the third order around reference values $e_0$ and $i_0$ for the eccentricity and the inclination; afterwards, a normal form procedure has been implemented to remove the remainder to higher orders and finally we back-transformed the canonical transformations in terms of the original variables to obtain the proper elements. Figure 1, referring to the simulation of two nearby events, clearly shows that the mean elements might undergo strong variations over time, making difficult to identify the presence of two distinct groups of fragments, while the proper elements, which are an outcome of perturbation theory, keep a configuration similar to that at the break-up time. This feature can be successfully used to characterize the dynamical properties of different groups of fragments (compare with [18]).

Fig. 1

Fragments generated by two nearby explosions (blue and yellow) differing only in the inclination values ($i=20^\circ$ and $i=21^\circ$); the other elements are $a=24,600$ km, $e=0.02$, $g=110^\circ$, $h=120^\circ$. The left column shows the fragments in the plane (a, i) and the right column in the plane (i, e). The upper row gives the elements at break-up, the middle row shows the mean elements after 150 ys and the lower row shows the proper elements after 150 ys (reproduced with permission from [19], copyright by the authors)

2.4 Clustering space debris

When dealing with multiple nearby breakup events, an important task in practical applications is the assignment of the fragments to the clusters associated to the body that generated the fragmentation. This goal can be achieved by implementing machine learning clusterization algorithms ([14, 20, 40]), that we apply here in an elementary form, that allows us to make a few observations. We assume to have two explosions occurring with different orbital elements and each one generating a number of fragments. An important goal is to analyze the fragments after the break-up events, and assign them to the satellite that originated them by using a clusterization algorithm. This task is complex and requires a careful investigation; here, we limit to report some remarks that might be useful for a future research. A first remark comes from the fact that the fragments evolve in time and therefore it is useful to implement the clusterization algorithm at the break-up time and after a given evolution time. An example is shown in Fig. 2 (upper panels), where the clusters are determined at the initial time and after 50 years. The clusters are determined using Wolfram Kmeans, which is a centroid-based method working when the clusters have similar size and are isotropically distributed. The informations at different times can be combined to properly label the fragments within the respective clusters.

Fig. 2

Fragments generated by nearby explosions of two Molniya-type satellites with orbital elements $a=15\,000$ km, $e=0.1$, $i=10^\circ$, $\ell =30^\circ$, $g=12^\circ$, $h=22^\circ$ for the first group and $a=30,000$ km, $e=0.12$, $i=22^\circ$, $\ell =2^\circ$, $g=50^\circ$, $h=15^\circ$ for the second group. The minimum size of the fragments is 2 cm. Comparison of the clusterization at the break-up time (upper left) and after 50 years (upper right). Comparison between different clusterization methods at the break-up time: DBSCAN (lower left), GaussianMixture (lower right). The two original groups of fragments are denoted with small dots (red and blue); the groups determined through the clusterization method are denoted with larger dots (orange and light blue). If the clusterization method identifies three groups, the third cluster is denoted with green larger dots

We also remark that it is important to use different methods and to cross-check the results obtained with alternative techniques. Beside Kmeans, Fig. 2 (lower panels) shows the results obtained using DBSCAN, a density-based clustering method, and GaussianMixture, which reconstructs the probability density function using combined multivariate normal distributions. Due to the geometric properties of the groups of fragments, in this example Kmeans performs better than the other methods.

A final remark is that it is important to combine the results obtained using different orbital elements as shown in Fig. 3, which provides the outputs obtained through Kmeans in the planes (a, i), (e, i), (a, e).

These few examples show the potential of combining the dynamics of the space debris with machine learning methods, a methodology that, of course, can be extended to many other model problems and physical situations in space science.

Fig. 3

Fragments generated by nearby explosions of two Molniya-type satellites with orbital elements $a=20,000$ km, $e=0.05$, $i=5^\circ$, $\ell =30^\circ$, $g=12^\circ$, $h=22^\circ$ for the first group and $a=25,000$ km, $e=0.005$, $i=14^\circ$, $\ell =28^\circ$, $g=30^\circ$, $h=46^\circ$ for the second group. The minimum size of the fragments is 2 cm. Comparison between different projections of the clusterization at the break-up time in the planes: (a, i) (left), (e, i) (middle), (a, e) (right). The color code is the same as in Fig. 2

3 KAM theory in Celestial mechanics

In this Section we shortly recall the content of KAM theory (Sect. 3.1), we provide the basic definitions and statements for symplectic and conformally symplectic systems (Sect. 3.2), we review computer-assisted KAM estimates in model problems of Celestial Mechanics (Sect. 3.3), and we provide a simple implementation of machine learning methods to analyze the regular or chaotic behaviour of the dynamics (Sect. 3.4).

3.1 KAM theory

The theory developed in [2, 31, 36], and known as KAM theory, investigates the existence of quasi-periodic motions in non-integrable dynamical systems and, in particular, the persistence of invariant tori in nearly-integrable Hamiltonian and dissipative systems.

We are interested to study maximal quasi-periodic solutions, namely quasi-periodic solutions with a rationally independent frequency vector $\underline{\omega }=(\omega _1,\ldots ,\omega _n)$, which means that $\underline{\omega }\cdot \underline{k}\not =0$ for any $\underline{k}\in {{\mathbb {Z}}}^n$. A KAM theory for general (including dissipative) systems was developed in [37], see also [3]. An efficient KAM theory for a special class of dissipative systems, called conformally symplectic systems, was developed in [5]. It is important to stress that adding a dissipation to a Hamiltonian system is a very singular perturbation: while in the Hamiltonian case we can have many (co-existing) quasi-periodic solutions, in the dissipative case we can have at most one quasi-periodic attractor (co-existing with periodic orbit attractors) and we need to include drift parameters to compensate the loss of energy.

KAM theory is based on the construction of a sequence of approximate solutions, which are quadratically convergent to the true solution. We also remark that KAM theory can be developed under two main assumptions, that we briefly summarize as follows:

(i):

a Diophantine condition on the frequency, which is needed to control the small divisors appearing in the equations that give approximate solutions,

(ii):

a non–degeneracy condition on coordinates and parameters, which is needed to ensure the existence of a solution of the cohomological equations providing the approximate solutions.

It is worth mentioning that the main problems of Celestial Mechanics are typically modeled by nearly–integrable Hamiltonian systems depending on a perturbing parameter, say $\varepsilon$, or rather by a nearly Hamiltonian system, which includes a dissipation whose size is usually smaller than the conservative counterpart. In both cases KAM theory can be applied under conditions (i) and (ii), and it provides a constructive algorithm to give an estimate on the perturbing parameter $\varepsilon$, such that a quasi-periodic torus with fixed frequency $\underline{\omega }$ exists for $\varepsilon$ sufficiently small, say $\varepsilon \le \varepsilon _{KAM}(\underline{\omega })$, where $\varepsilon _{KAM}(\underline{\omega })$ is given explicitly by the theorem. Since the very first works on explicit KAM estimates in Celestial Mechanics, a crucial point has been to obtain good theoretical estimates on the perturbing parameter $\varepsilon _{KAM}(\underline{\omega })$. This means that the parameter should be as close as possible to the astronomical values (in case of astronomical models) or rather close to the experimental values obtained implementing numerical techniques (in case of theoretical models). The first KAM implementation with explicit estimates was given in [26] in the context of the restricted 3-body problem, but the results were far from a realistic value of the perturbing parameter, which, in this model, coincides with the mass-ratio of the primaries. The development of alternative KAM techniques (see [21, 22]) and the implementation of computer-assisted proofs led to results which, in simple model problems, are fully consistent with the astronomical and numerical values. Before reviewing KAM applications to Celestial Mechanics (see Sect. 3.3), we briefly recall the basic notions and the statement of the theorem in the case of symplectic and conformally symplectic systems (see Sect. 3.2).

3.2 KAM theory for symplectic and conformally symplectic systems

Realistic KAM estimates have been obtained using the a-posteriori approach developed in [21, 22] for symplectic systems and extended in [5] for conformally symplectic systems. The existence of invariant tori is obtained finding solutions of a suitable functional equation, namely the invariance equation for the torus; starting from an approximate solution of such equation satisfying some non-degeneracy conditions, then one can prove that near the approximately invariant torus, there is a true invariant torus. This method makes use of the automatic reducibility, so that in the neighborhood of an invariant torus one can find a change of coordinates that transforms the linearization of the invariance equation into a constant coefficient equation. The method developed in [21, 22] does not need that the Hamiltonian is nearly-integrable and that it is expressed in action-angle variables; besides, it gives an explicit algorithm that can be efficiently implemented on a computer, since all steps of the algorithm just involve diagonal operations in the Fourier space and/or diagonal operations in the real space.

In order to state the theorem, we need to introduce the following definitions, that we give for simplicity for mapping systems, although all definitions and statements can be extended to flows.

Definition 3

Let ${{\mathcal {M}}}\subseteq {{\mathbb {R}}}^n\times {{\mathbb {T}}}^n$ be a symplectic manifold with symplectic form $\Omega$. A diffeomorphism $f:{\mathcal {M}}\rightarrow {{\mathcal {M}}}$ is symplectic, if

$$\begin{aligned} f^* \Omega = \Omega \end{aligned}$$

(where $f^*$ denotes the pull-back by f). A family of maps $f_{\underline{\mu }}$ is conformally symplectic, if there exists a function $\lambda : {{\mathcal {M}}}\rightarrow {{\mathbb {R}}}$ such that

$$\begin{aligned} f_{\underline{\mu }}^* \Omega = \lambda \Omega . \end{aligned}$$

We remark that for $n=1$ any diffeomorphism is conformally symplectic with $\lambda (x)=\pm det(Df_{\underline{\mu }}(x))$, while for $n\ge 2$, then $\lambda$ is constant.

Definition 4

We say that the frequency vector $\underline{\omega }\in {{\mathbb {R}}}^n$ satisfies the Diophantine condition, if the following inequality is satisfied:

$$\begin{aligned} \left| {{\underline{\omega }}\over {2\pi }}\cdot {\underline{q}}-p\right| ^{-1}\ \le \ C |{\underline{q}}|^{\tau }\,\qquad p\in {{\mathbb {Z}}}\,\quad {\underline{q}}\in {{\mathbb {Z}}}^n\backslash \{0\}\quad C>0\,\quad \tau >0. \end{aligned}$$

We remark that for $\tau >n-1$ the set of Diophantine vectors ${{\mathcal {D}}}(C,\tau )$ has full Lebesgue measure in ${{\mathbb {R}}}^n$.

Definition 5

Given a symplectic map $f:{{\mathcal {M}}}\rightarrow {{\mathcal {M}}}$, a KAM torus with frequency vector $\underline{\omega }\in {{\mathcal {D}}}(C,\tau )$ is an n–dimensional invariant torus described parametrically by an embedding $K:{{\mathbb {T}}}^n \rightarrow {{\mathcal {M}}}$, which is the solution of the invariance equation:

$$\begin{aligned} f\circ K(\underline{\theta })=K(\underline{\theta }+\underline{\omega }). \end{aligned}$$

(3.1)

Given a family $f_{{\underline{\mu }}}:{{\mathcal {M}}}\rightarrow {{\mathcal {M}}}$ of conformally symplectic maps, a KAM torus with frequency $\underline{\omega }\in {{\mathcal {D}}}(C,\tau )$ is an n–dimensional invariant torus described parametrically by an embedding $K:{{\mathbb {T}}}^n \rightarrow \mathcal {M}$ and a drift ${\underline{\mu }}$ which solve the invariance equation:

$$\begin{aligned} f_{\underline{\mu }}\circ K(\underline{\theta })=K(\underline{\theta }+\underline{\omega }). \end{aligned}$$

Finally, to make quantitative estimates, we introduce the analytic norm as follows.

Definition 6

Given a parameter $\rho >0$ and having defined the extended torus ${{\mathbb {T}}}_\rho ^n = \{ {{\underline{\theta }}}\in {\mathbb C}^n/(2\pi {{\mathbb {Z}}})^n:\ \textrm{Re}({{\underline{\theta }}})\in {{\mathbb {T}}}^n,\ |\textrm{Im}(\theta _j)| \le \rho \ ,\ \ j=1,\ldots ,n \}$, the analytic norm of a function $f:{{\mathcal {M}}}\rightarrow {{\mathcal {M}}}$ is defined as

$$\begin{aligned} \Vert f\Vert _{\rho } = \sup _{{{\underline{\theta }}}\in {{\mathbb {T}}}_\rho ^n}\Vert f({{\underline{\theta }}})|. \end{aligned}$$

We provide now a simplified statement of the KAM theorem in the general case of a conformally symplectic map, referring to [5] for full details and to [21, 22] for the original formulation in the symplectic case.

Theorem 7

Let $f_{{{\underline{\mu }}}}$ be a family of conformally symplectic maps, let ${{\underline{\omega }}}\in {{\mathcal {D}}}(C,\tau )$ and let $\rho$ be a positive parameter.

Assume that $(K_0,{{\underline{\mu }}}_0)$ is an approximate solution of the invariance equation up to an error function $E_0=E_0({{\underline{\theta }}})$:

$$\begin{aligned} f_{{\underline{\mu }}_0}\circ K_0({{\underline{\theta }}})-K_0({{\underline{\theta }}}+{\underline{\omega }})=E_0({{\underline{\theta }}}) \end{aligned}$$

with $\Vert E_0\Vert _\rho$ small, say

$$\begin{aligned} \Vert E_0\Vert _\rho \le C_0 C^{-4}\delta ^{4\tau } \end{aligned}$$

for some positive constant $C_0$ and for $0<\delta <\rho /2$. Assume a suitable non–degeneracy condition on coordinates and parameters.¹

Then, there exists an exact solution of the invariance equation, say $(K_*,{\underline{\mu }}_*)$, such that

$$\begin{aligned} {f_{{\underline{\mu }}_*}\circ K_*({{\underline{\theta }}})-K_*({{\underline{\theta }}}+{\underline{\omega }})=0}. \end{aligned}$$

Moreover, for $0<\delta <{\rho \over 2}$, one has

$$\begin{aligned} \Vert K_*-K_0\Vert _{\rho -2\delta }\le C_1\ C^2\ \delta ^{-2\tau }\ \Vert E_0\Vert _\rho \,\quad |{\underline{\mu }}_*-{\underline{\mu }}_0|\le C_2\ \Vert E_0\Vert _\rho \end{aligned}$$

for suitable constants $C_1$, $C_2>0$.

For a symplectic map F, one just needs to find the embedding $K_0$ as the solution of (3.1); besides, the non–degeneracy condition concerns only the coordinates and, in the perturbative case, it coincides with the so-called twist condition.

3.3 Computer-assisted results in Celestial mechanics

Effective KAM results with explicit estimates on the parameters typically require very long computations, which are needed to find the approximate solution and to check the estimates providing the convergence to the true solution. These computations can be performed through a computer, hence the need to control the rounding-off and propagation errors introduced by the machine.

A rigorous control of the computer errors can be obtained through interval arithmetic; in short, one needs to reduce all computations to a sequence of elementary operations (sum, subtraction, multiplication and division). Then, one replaces any real number by an interval containing the number and afterwards one performs the elementary computations within intervals. This procedure, which was introduced e.g. in [30, 33], ensures a rigorous result providing a computer-assisted proof, hereafter CAP.

The implementation of interval arithmetics might result in a lengthy extension of the computer program. If one renounces to have a rigorous control on the numerical error, one can make a computer implementation with long precision, namely with many digits, provided that the estimate of the error function associated to the sequence of the approximate solutions decreases to zero; we refer to this result as a computer-assisted validation, hereafter CAV.

Explicit estimates in Celestial Mechanics have been found for several model problems, whose results are summarized in Table 1. For completeness, we include also the standard map, in its conservative and dissipative formulation, which is closely related to the Poincaré map of the spin-orbit problem. This map is described by the equations

$$\begin{aligned} y'= & {} \lambda y+\mu +\varepsilon \sin x\nonumber \\ x'= & {} x+y'\,\qquad \qquad \qquad y\in {{\mathbb {R}}},\ x\in {{\mathbb {T}}}, \end{aligned}$$

where $\lambda ,\mu ,\varepsilon \in {{\mathbb {R}}}$ are, respectively, the dissipative parameter, the drift term, the perturbing parameter. In the conservative case one has $\lambda =1$ and $\mu =0$.

The other model problems for which explicit KAM estimates have been found are the following:

(a):

the conservative spin-orbit problem,

(b):

the dissipative spin-orbit problem,

(c):

the planar, circular, restricted 3-body problem (hereafter PCR3BP),

(d):

the secular planetary problem,

(e):

the triangular Lagrangian points.

We briefly describe these model problems in the following sub-sections, providing a few details, and their relation with KAM theory and invariant tori.

3.3.1 Conservative spin-orbit problem

The spin-orbit problem describes the motion of a triaxial rigid satellite ${\mathcal {S}}$ (of mass m) moving around a central planet ${\mathcal {P}}$ (of mass M) along a Keplerian ellipse with semimajor axis a and eccentricity e; the position of the satellite on the orbit is given by the radius r and the true anomaly f (see Fig. 4). Furthermore, it is assumed that the spin–axis is perpendicular to the orbit plane and coincides with the direction of the shortest physical axis. We denote by x the rotation angle formed by the longest axis of the ellipsoid and the periapsis line. Denoting by $I_1<I_2<I_3$ the principal moments of inertia, the 1–dim, time–dependent Hamiltonian describing the model takes the form

$$\begin{aligned} {{\mathcal {H}}}(y,x,t)={y^2\over 2}-{\varepsilon \over 2} \left( {a\over r(t)}\right) ^3\ \cos (2x-2f(t)), \end{aligned}$$

(3.2)

where the perturbing parameter is given by $\varepsilon ={3\over 2}{{I_2-I_1}\over I_3}$, hence it represents the equatorial oblateness of the satellite; the astronomical value for the Moon amounts to $\varepsilon _{Moon}=3.45\cdot 10^{-4}$.

Fig. 4

The spin-orbit problem describing a rotating triaxial satellite ${\mathcal {S}}$ orbiting on a Keplerian ellipse around a planet ${\mathcal {P}}$; (r, f) are the polar coordinates of the barycenter of the satellite, while x is the rotation angle

We remark that the Hamiltonian (3.2) is an integrable system for $\varepsilon =0$ or for $e=0$. For $\varepsilon =0$, the unperturbed Hamiltonian is given by the function $h(y)={y^2\over 2}$, which satisfies Kolmogorov’s non-degeneracy condition:

$$\begin{aligned} {{\partial ^2 h(y)}\over {\partial y^2}}\not =0. \end{aligned}$$

Hence, KAM theory applies and since the phase space is 3D, the 2D invariant tori provide a topological confinement in the phase space, as shown in Fig. 5 (see, e.g., [9]).

Fig. 5

Two invariant tori for the spin-orbit problem for $\varepsilon =0.01$, $e=0.01$, whose existence ensures the stability for all initial conditions within the two tori

3.3.2 Dissipative spin-orbit problem

The dissipative spin-orbit problem is obtained from the conservative problem, assuming that the satellite is non-rigid and, hence, subject to a tidal torque that, according to [39], can be modeled by a linear function of the velocity:

$$\begin{aligned} {\ddot{x}+\varepsilon \left( {a\over r(t)}\right) ^3\ \sin (2x-2f(t))= - \eta \ \left( \frac{a}{r(t)}\right) ^6\ (\dot{x} - \dot{f}(t) )}, \end{aligned}$$

(3.3)

where $\eta$ is the dissipative factor, depending on the structure parameters of the satellite (rigidity, density, etc.). With reference to (3.3), we can write the dissipative parameter as $\lambda =\eta \ \big (\frac{a}{r(t)}\big )^6$ and the drift term as $\mu =\dot{f}(t)$, where r and f are known functions of time (since the orbit is a Keplerian ellipse), depending on the orbital eccentricity. Taking the average of the tidal torque over an orbital period, one obtains the equation of motion

$$\begin{aligned} {\ddot{x}+\varepsilon \left( {a\over r(t)}\right) ^3\ \sin (2x-2f(t))= - {\bar{\lambda }}\ (\dot{x} - {\bar{\mu }})}, \end{aligned}$$

(3.4)

where

$$\begin{aligned} {\bar{\lambda }}= & {} \eta {1\over {(1-e^2)^{9\over 2}}} \left( 1+3e^2+{3\over 8}e^4\right) \,\nonumber \\ {\bar{\mu }}= & {} {1\over {(1-e^2)^{3\over 2}}} {{1+{{15}\over 2}e^2+{{45}\over 8}e^4+{{5}\over {16}} e^6}\over {1+3e^2+{3\over 8}e^4}}. \end{aligned}$$

It can be shown that the model described by (3.3) or (3.4) is conformally symplectic. Hence, a KAM theory for conformally symplectic systems can be applied to ensure the existence of quasi-periodic attractors with preassigned frequency (see, e.g., [7]).

3.3.3 Planar, circular, restricted 3-body problem

The PCR3BP describes the motion of a massless particle, say ${\mathcal {S}}$, in the gravitational field of two primaries, say ${\mathcal {P}}_1$ and ${\mathcal {P}}_2$ with masses, respectively, $m_1$ and $m_2$. The primaries are supposed to move on a circular orbit around their common barycenter and ${\mathcal {S}}$ moves on the same plane of the primaries. The Hamiltonian describing the PCR3BP has 2 degrees of freedom in terms of the so-called action-angle Delaunay variables defined as follows: the actions are (in normalized units) $L=\sqrt{a}$ and $G=L\sqrt{1-e^2}$ with a the semimajor axis and e the eccentricity, while the angles are $\ell$ which is the mean-anomaly and $g=g_0-\psi$, with $g_0$ the argument of perihelion and $\psi$ the longitude of $P_2$. The Hamiltonian can then be written as

$$\begin{aligned} {{\mathcal {H}}}(L,G,\ell ,g)=-{1\over {2L^2}}-G+ \varepsilon R(L,G,\ell ,g), \end{aligned}$$

where the perturbing parameter $\varepsilon$ represents the primaries’ mass ratio, say $\varepsilon =m_2/m_1$, the integrable part $h(L,G)=-{1\over {2L^2}}-G$ represents the Keplerian interaction with ${\mathcal {P}}_1$, R is the perturbing function due to the gravitational interaction with ${\mathcal {P}}_2$. We remark that the unperturbed Hamiltonian does not satisfy Kolmogorov’s non-degeneracy condition, requiring that the determinant of the Hessian matrix is different from zero. However, it satisfies the iso-energetic non-degeneracy condition, requiring that

$$\begin{aligned} \det \left( \begin{array}{cc} h''(L,G) &{} h'(L,G) \\ h'(L,G)^T &{} 0 \\ \end{array} \right) \not =0. \end{aligned}$$

This condition allows to prove the existence of invariant tori on a preassigned energy level. Given that the phase space is 4D, fixing the energy level one obtains a 3D space in which the 2D invariant tori provide a topological confinement (see, e.g., [12, 13]).

3.3.4 Secular planetary problem

One considers two planets, say ${\mathcal {P}}_1$, ${\mathcal {P}}_2$ with masses $m_1$, $m_2$, orbiting around a star ${\mathcal {P}}_0$ with mass $m_0$. Due to the conservation of the linear momentum and the total angular momentum, the model has 4 degrees of freedom. It can be conveniently described using the following variables for the dynamics of the two planets:

$$\begin{aligned} \Gamma _j= & {} {{m_0m_j}\over {m_0+m_j}}\ \sqrt{{{\mathcal {G}}}(m_0+m_j)a_j}\,\qquad \gamma _j=\ell _j+g_j\,\quad j=1,2\nonumber \\ \xi _j= & {} \sqrt{2\Gamma _j}\ \sqrt{1-\sqrt{1-e_j^2}}\cos g_j\,\qquad \eta _j=-\sqrt{2\Gamma _j}\ \sqrt{1-\sqrt{1-e_j^2}}\sin g_j, \end{aligned}$$

where the variables $(\Gamma _j,\gamma _j)$ describe the fast motion, while the variables $(\xi _j,\eta _j)$ are associated to the slow dynamics. The Hamiltonian can then be written as

$$\begin{aligned} {{\mathcal {H}}}(\Gamma _1,\Gamma _2,\gamma _1,\gamma _2,\xi _1,\xi _2,\eta _1,\eta _2)=h(\Gamma _1,\Gamma _2)+\varepsilon R(\Gamma _1,\Gamma _2,\gamma _1,\gamma _2,\xi _1,\xi _2,\eta _1,\eta _2), \end{aligned}$$

where the function h represents the Keplerian part, the parameter $\varepsilon$ is defined as $\varepsilon =\max \{{m_1\over m_0},{m_2\over m_0}\}$, the function R is a homogeneous polynomial in the variables $\Gamma _1$, $\Gamma _2$, $\xi _1$, $\xi _2$, $\eta _1$, $\eta _2$ and a trigonometric polynomial in $\gamma _1$, $\gamma _2$. The system is further reduced by averaging with respect to the fast angles $\gamma _1,\ \gamma _2\,$. Given that the phase space is 4D, the 2D invariant tori provide a confinement of the motions on the 3D constant energy space (see, e.g., [34]).

3.3.5 Triangular Lagrangian points

The PCR3BP admits equilibrium solutions in the synodic frame, namely the frame rotating with the angular velocity of the primaries. Two equilibrium solutions form an equilateral triangle with the primaries; such solutions are stable for small enough values of the mass ratios ([10]). Denoting by (x, y) the coordinates in the synodic frame of the massless particle in the plane of the orbit and by $(p_x,p_y)$ the corresponding momenta, the Hamiltonian is given by

$$\begin{aligned} {{\mathcal {H}}}(p_x,p_y,x,y)={1\over 2}(p_x^2+p_y^2)+yp_x-xp_y-{{1-\varepsilon }\over \sqrt{(x-\varepsilon )^2+y^2}}-{\varepsilon \over \sqrt{(x-\varepsilon +1)^2+y^2}}\, \end{aligned}$$

where $\varepsilon$ represents the primaries’ mass ratio. The equilateral triangle equilibrium positions have coordinates $({1\over 2}-\varepsilon ,\pm {\sqrt{3}\over 2})$. The phase space is 4D, hence the 2D tori confine the dynamics on each 3D constant energy space (see, e.g., [25]; we refer to [15, 17] for applications of Nekhoroshev’s theorem).

3.3.6 Computer-assisted KAM estimates

Table 1 summarizes the main results obtained implementing computer-assisted KAM estimates for the model problems introduced in Sects. 3.3.1–3.3.5. The results are in conservative and dissipative models. We have included also the standard map, which represents a bench test for more complex problems of interest in Celestial Mechanics. The results are either computer-assisted proofs (CAP) or rather computer-assisted validations (CAV). Table 1 provides also the agreement (expressed in percentage) with the experimental (Exp) or the astronomical (Astr) break-down values of each model. We notice that, apart from the first estimates on the conservative standard maps (dating back to the years ’90 s of the last century), the KAM estimates (either proofs or validations) for all other models are in full agreement with the experimental or astronomical values, thus showing the full potential of KAM theory.

Table 1 KAM estimates in model problems of Celestial Mechanics

3.4 Regular and chaotic dynamics through machine learning methods

In this Section, we show that machine learning techniques can be used in the conservative spin-orbit problem with the aim, for example, to classify the dynamics.

Consider the equations of motion associated to the Hamiltonian (3.2), namely

$$\begin{aligned} \dot{x}= & {} y\nonumber \\ \dot{y}= & {} -\varepsilon \big ({a\over r(t)}\big )^3\ \sin (2x-2f(t))\, \end{aligned}$$

supplemented by the equations

$$\begin{aligned} r= & {} {{a(1-e^2)}\over {1+e\cos f}}\nonumber \\ \dot{f}= & {} {{\sqrt{{{\mathcal {G}}}M m a}\ \sqrt{1-e^2}}\over r^2}, \end{aligned}$$

where ${{\mathcal {G}}}$ is the gravitational constant (we recall that, as in Sect. 3.3.1, M denotes the mass of the planet and m is the mass of the satellite). As a test sample, we fix $\varepsilon =0.05$ and we select 10 values of the eccentricity: 0.001, 0.01, 0.03, 0.04, 0.05, 0.06, 0.07, 0.08. 0.1, 0.2. We consider the initial conditions over a grid with x taking the values $x=0$, $\pi /2$, $\pi$ and y taking ten values: $y=1$, 1.1, 1.2,...,1.9. For each eccentricity and for each initial condition we compute the Poincaré section taking the time modulus $2\pi$, each section being composed by 1000 points. For each eccentricity we obtain 30 orbits, see Fig. 6, hence in total we have 300 orbits.

Fig. 6

Poincaré map of the conservative spin-orbit problem in the x-y plane (with $y=\dot{x}$) for $\varepsilon =0.025$ and $e=0.01$ (left), $e=0.05$ (middle), $e=0.1$ (right)

We start by taking 90 orbits (which amounts to $30\%$ of the total number of orbits) to train the machine by classifying the orbits as regular (i.e., librational tori, periodic orbits, rotational tori) and chaotic. Then, we use Wolfram statement Classify, which generates a function attempting to predict the class regular or chaotic of the remaining orbits from the training samples. The results in Table 2 provide the rate of successful predictions for each eccentricity, using the method “RandomForest” (many other methods can be used with the function Classify, but the results with “RandomForest” seem to be quite stable for variations of the training set).

In total, the rate of failure with $30\%$ of datasets used for training is about $15\%$; this rate increases taking a larger dataset for the training. It must be noted that the higher is the number of datasets for the training, the more stable are the results when varying the data of the training. This is a very simple example of the implementation of a machine learning algorithm, that allows us to have information on the phase space and, therefore, to focus on specific regions in order to find regular trajectories.

Table 2 Conservative spin-orbit problem

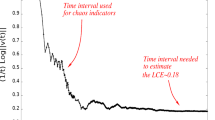
A more refined classification method was presented in [16]. Precisely, starting from time series and without knowing the underlying dynamics, chaos indicators have been used in [16] to distinguish between chaotic, rotational, librational motions. Then, a convolutional neural network was trained on the dynamic model to predict the character of the motion. The architecture used in [16] was InceptionTime, which is a convolutional neural network in which at each of its 5 layers, it applies a set of convolution operations to the time series, which creates a transformation of the input data, so that the series becomes easier to be classified.

The chaos indicators implemented in [16] are the Fast Lyapunov Indicators (FLI) and the Frequency Map Analysis (FMA). Precisely, given an initial condition, a finite number of time series have been generated as the solution at different time intervals with fixed step size. Then, for each time series, the FLI or FMA have been computed and assigned a label as follows: chaotic $\mapsto$ 0, librational $\mapsto$ 1, rotational $\mapsto$ 2. InceptionTime is finally used to train $80\%$ of the dataset, while $20\%$ of the dataset was used for validation, achieving an accuracy of $97\%$. This result provides a further example of how machine learning methods can be used to explore the dynamics of interesting problems in Celestial Mechanics.