Old perturbative methods for a new problem in Celestial Mechanics: the space debris dynamics

Abstract

Perturbative methods have been developed and widely used in the XVIII and XIX century to study the behavior of N-body problems in Celestial Mechanics. Such methods apply to nearly-integrable Hamiltonian systems and they have the remarkable property to be constructive. A well-known application of perturbative techniques is represented by the construction of the so-called proper elements, which are quasi-invariants of the dynamics, obtained by removing the perturbing function to higher orders. They have been used to identify families of asteroids; more recently, they have been used in the context of space debris, which is the main core of this work. We describe the dynamics of space debris, considering a model including the Earth’s gravitational attraction, the influence of Sun and Moon, and the Solar radiation pressure. We construct a Lie series normalization procedure and we compute the proper elements associated to the orbital elements. To provide a concrete example, we analyze three different break-up events with nearby initial orbital elements. We use the information coming from proper elements to successfully group the fragments; the clusterization is supported by statistical data analysis and by machine learning methods. These results show that perturbative methods still play an important role in the study of the dynamics of space objects.

1 Introduction

The study of problems in Celestial Mechanics often needs a complex interplay between three different aspects: modeling, scientific methods and applications. Models are needed to investigate the orbital and rotational dynamics of celestial bodies and they should have the following requisites: being simple enough to allow the implementation of mathematical theories, being accurate enough to provide a reliable description of natural and artificial celestial body dynamics. Models of Celestial Mechanics range from low to high dimensional, can be either conservative or dissipative, and they often present degeneracies. The aim of the scientific methods will be, among the others, to investigate the occurrence of regular or chaotic motions, periodic, resonant and quasi-periodic orbits, their stability and the long-term evolution of the celestial bodies. We can distinguish between analytical, numerical, semi-analytical methods. Among the analytical methods we quote perturbation theory, KAM theory, exponential estimates, variational methods, bifurcation theory, optimal control. Numerical methods include computer implementations for the integrations of the equations of motion, the determination of chaos indicators, the detection of periodic orbits. Semi-analytical methods are a combination of analytical and numerical methods.

In this work, we present some results concerning a timely problem, the dynamics of space debris, whose study will need to introduce a suitable model and to implement an appropriate version of perturbation theory, with the aim to give meaningful applications in simulated and real data.

It is well known that the sky around our planet is full of space debris, which are remnants of space missions, like rocket stages, fragments from disintegrations, lost equipment during space walks. At the time of writing this paper it is estimated that there are 36 500 objects whose size is greater than 10 cm, 1 million objects from 1 to 10 cm, about 130 million objects from 1 mm to 1 cm. Even the smaller objects can provoke big damages, due to their high impact velocities.

We will consider objects above 2 000 km of altitude from the surface of the Earth, so that the dissipative effect due to the atmospheric drag can be neglected. In this case, we have a conservative dynamical system, which can be described in terms of a Hamiltonian function. Modeling the space debris dynamics requires that one considers the attraction of the Earth, not just as a point mass (namely the Keplerian part of the Hamiltonian), but rather with its shape described in terms of a geopotential, which can be expanded in terms of spherical harmonic coefficients.

We denote by ${\mathcal {H}}_{Kep}$ the Keplerian part and by ${\mathcal {H}}_{geo}$ the geopotential, expanded in spherical harmonics that we truncate to a suitable order. We also consider the gravitational influence of Moon and Sun, and the Solar radiation pressure, whose contributions to the Hamiltonian are denoted as ${\mathcal {H}}_{Moon}$, ${\mathcal {H}}_{Sun}$ and ${\mathcal {H}}_{SRP}$, respectively. In summary, the Hamiltonian function will be of the form

$$\begin{aligned} {\mathcal {H}}= & {} {\mathcal {H}}_{Kep}(a)+{\mathcal {H}}_{geo}(a,e,i,M,\omega ,\Omega ,\theta ) \nonumber \\&+{\mathcal {H}}_{Moon}(a,e,i,M,\omega ,\Omega ,a_M,e_M,i_M,M_M,\omega _M,\Omega _M)\nonumber \\&+{\mathcal {H}}_{Sun}(a,e,i,M,\omega ,\Omega ,a_S,e_S,i_S,M_S,\omega _S,\Omega _S)\nonumber \\&+{\mathcal {H}}_{SRP}(a,e,i,M,\omega ,\Omega ,a_S,e_S,i_S,M_S,\omega _S,\Omega _S) , \end{aligned}$$

(1)

where $\theta$ is the sidereal time accounting for the rotation of the Earth, $(a,e,i,M,\omega ,\Omega )$ are the orbital elements of the space debris (respectively, semi-major axis, eccentricity, inclination, mean anomaly, argument of perigee, longitude of the ascending node) and the suffix M or S denotes that the orbital elements are referred to Moon or Sun. We can write the Fourier expansion of ${\mathcal {H}}_{geo}$, ${\mathcal {H}}_{Moon}$, ${\mathcal {H}}_{Sun}$, ${\mathcal {H}}_{SRP}$ as

$$\begin{aligned}&{\mathcal {A}}^{geo}_{k_1 k_2 k_3 k_4} (a, e, i) \cos (k_1 M + k_2 \theta + k_3 \omega +k_4 \Omega )\ ,\nonumber \\&{\mathcal {A}}^{Moon}_{k_1 k_2 k_3 k_4 k_5 k_6} (a, e, i, a_M, e_M, i_M) \cos (k_1 M + k_2 M_M + k_3 \omega +k_4 \omega _M+k_5 \Omega +k_6 \Omega _M)\ ,\nonumber \\&{\mathcal {A}}^{Sun/SRP}_{k_1 k_2 k_3 k_4 k_5 k_6} (a, e, i, a_S, e_S, i_S) \cos (k_1 M + k_2 M_S + k_3 \omega +k_4 \omega _S+k_5 \Omega +k_6 \Omega _S), \end{aligned}$$

(2)

with $k_j$ integers and with suitable functions ${\mathcal {A}}$ of the orbital elements. Hence, we obtain that the Fourier expansion of the Hamiltonian contains fast angles, namely M and $\theta$ with periods of days, semi-fast angles, namely $M_M$ and $M_S$ with periods of 1 month and 1 year, slow angles, namely $\omega$, $\Omega$, $\omega _M$, $\Omega _M$, $\omega _S$, $\Omega _S$ with periods of years. Correspondingly, we have short periodic terms, involving the fast angles (M, $\theta$) with ${\dot{M}}$ and ${\dot{\theta }}$ not commensurable; resonant terms, involving the fast angles (M, $\theta$) with a commensurability relation between ${\dot{M}}$ and ${\dot{\theta }}$; semi–secular terms, dependent on the semi-fast angles $M_M$, $M_S$; secular terms, depending on the remaining slow angles.

Given such classification of the different terms, we adopt a theoretical approach which consists in a hierarchical implementation of perturbation theory. Using Lie series transformations, we make an explicit construction of a normal form, which allows us to determine the proper elements according to the procedure that we briefly summarize as follows:

(i):

we first average over the fast angles and obtain that the semi-major axis becomes the first proper element; the elements which appear in the averaged Hamiltonian, and whose evolution can be obtained integrating the averaged Hamiltonian, are called mean elements;

(ii):

we implement the computation for a normal form of the averaged secular Hamiltonian obtained in (i) around some reference values for eccentricity and inclination, thus obtaining the proper elements for e and i.

As an application, we consider a sample of simulated space debris obtained through a break-up program (see [2]), based on the model EVOLVE 4.0 given in [32] (real cases have been studied in [18]). We consider three break-up events which are characterized to have, at initial time, nearby orbital elements. We generate the fragments of each event and compute the corresponding mean and proper elements at different time intervals. The results are then analyzed using statistical data analysis and machine learning techniques for clusterization of data sets. Our tests lead to conclude that the perturbative method to compute proper elements is an effective tool to group space debris with similar dynamical features and it might have interesting applications in real space problems.

Our work is organized as follows. In Sect. 2 we give a short introduction to some historical results obtained implementing perturbation theory, as a motivation for the successive implementation of perturbative methods to the space debris problem. The normal form method is reviewed in Sect. 3 and Appendix A. The model for the study of space debris is presented in Sect. 4, while the computation of the proper elements is given in Sect. 5, which includes statistical data analysis (Sect. 5.4) and machine learning clusterization results (Sect. 5.5).

2 Some celebrated historical applications of perturbation theory

One of the most striking results obtained by implementing perturbation theory was the discovery of a planet with pen and paper. At the middle of the XIX century, the last known planet was Uranus. However, scientists noticed a discrepancy between the astronomical observations of Uranus and its theoretically predicted position. Almost at the same time, Urbain Le Verrier and John Couch Adams conjectured the existence of a planet beyond Uranus, which could have justified the discrepancy between theory and observations. Implementing perturbation theory, it was possible to give a good estimate of the position of the extra planet. Le Verrier sent his mathematical prediction (see [54]) to the astronomer Johann Gottfried Galle, who discovered a new planet in the night 23–24 September 1846. In this way, the planet Neptune was discovered through perturbation theory.

The implementation of perturbation theory to determine an accurate prediction of the ephemerides of the Moon is far less known than the discovery of Neptune. Nowadays one uses the combination of numerical and analytical methods to determine the position of the Moon. The most accurate analytical method was developed in the XIX century by Charles Delaunay; he spent 20 years of his life to make the literal computations contained in the two volumes [21]. Lunar theory consists in the study of the 3-body problem Earth–Moon–Sun with the Sun moving on a Keplerian ellipse around the Earth–Moon barycenter. A perturbative method is then implemented to remove the dependence to high orders of the Hamiltonian on the monthly and annual terms. About one century later, the computations made by Delaunay were checked and found correct (with the exception of one term) in [23, 24], using a computer program and the method of Lie transforms. As remarked in [22], the advantage of using Lie transforms is that the transformation of variables is given in an explicit form; the transformation from original to new variables, as well as the inverse transformation consists of an iterative procedure involving only Poisson brackets.

In the rest of this work, we will consider a 4-body problem formed by Earth–Moon–Sun and a space debris (or a satellite), and we will implement perturbation theory using Lie series to determine the proper elements.

3 A review of the normal form procedure

In this section, we review a version of perturbation theory using the method of Lie series. In Sect. 3.1, we recall the statement and proof of the non-resonant case, while in Sect. 3.2 we briefly discuss the resonant normal form.

3.1 A non-resonant normal form

The aim of the theorem stated below is to build a canonical transformation, such that in the transformed Hamiltonian the perturbation is pushed to higher orders in $\varepsilon$.

Theorem 1

Let

$$\begin{aligned} {\mathcal H}({{\underline{I}}},{\underline{\varphi }})={\mathcal {Z}}({{\underline{I}}})+\varepsilon {\mathcal {R}}({{\underline{I}}},{{\underline{\varphi }}}) \end{aligned}$$

(3)

with $({{\underline{I}}},{{\underline{\varphi }}})\in V\times {\mathbb T}^n$ for $V\subset {\mathbb R}^n$ open.

Assume that ${\mathcal {R}}$ is an analytic function on $V\times {\mathbb T}^n$ and assume that it is a trigonometric function with N Fourier coefficients, $N\in {\mathbb N}$.

Assume that the frequency ${{\underline{\omega }}}$ is non-resonant in V, namely for any ${{\underline{I}}}_0\in V$ there exists $a\in {\mathbb R}_+$ such that

$$\begin{aligned} |{{\underline{\omega }}}({{\underline{I}}}_0)\cdot {{\underline{k}}}|\ge a>0\quad {for\ all}\ \ 0<|{{\underline{k}}}|\le N, \end{aligned}$$

(4)

where ${{\underline{\omega }}}({{\underline{I}}}_0) = \frac{\partial {\mathcal {Z}}}{\partial {{\underline{I}}}}({{\underline{I}}}_0)$. Then, there exists $\rho _0>0$, $\varepsilon _0>0$ and for $|\varepsilon |<\varepsilon _0$ there exists a canonical transformation $({{\underline{I}}},{{\underline{\varphi }}}) \rightarrow ({{\underline{I}}}',{{\underline{\varphi }}}')$ defined¹ in $B_{\rho _0\over 2}({\underline{I}}_0)\times {\mathbb T}^n\subset V\times {\mathbb T}^n$ and with values in $B_{\rho _0}({{\underline{I}}}_0)\times {\mathbb T}^n$, which transforms $\mathcal H$ into

$$\begin{aligned} {\mathcal H}'({{\underline{I}}}',{{\underline{\varphi }}}')\ =\ {\mathcal {Z}}'({{\underline{I}}}')+\varepsilon ^2 {\mathcal {R}}'({{\underline{I}}}',{{\underline{\varphi }}}')\ . \end{aligned}$$

(5)

We remark that the proof is constructive and it allows one to build explicitly the canonical transformation as well as the transformed Hamiltonian; we also remark that the procedure outlined in the proof of Theorem 1 can be iterated to get better approximate solutions. Indeed, the iteration can be performed up to an optimal order, after which the norm of the remainder starts to grow and diverges.

Although the proof of Theorem 1 is rather standard and can be found in several textbooks, we feel worthwhile to give some details in Appendix A, since the proof provides the constructive algorithm to determine an approximate Hamiltonian that will be used to compute the proper elements as shown in Sect. 5.

3.2 Resonant normal form

A resonance occurs when there exists an integer vector $\underline{{\widetilde{k}}}$, such that $\underline{\omega }({\underline{I}})\cdot \underline{\widetilde{k}}=0$. This term will generate zero divisors; however, a resonant perturbation theory can still be implemented to eliminate the non–resonant terms.

Precisely, one can construct a change of variables ${\mathcal C}:({{\underline{I}}},{{\underline{\varphi }}})\rightarrow ({\underline{I}}',{{\underline{\varphi }}}')$, such that the new Hamiltonian takes the form

$$\begin{aligned} {\mathcal H}'({{\underline{I}}}', {\underline{\varphi }}')={\mathcal {Z}}'({{\underline{I}}}', {{\underline{\varphi }}}' \cdot \underline{{\widetilde{k}}})+\varepsilon ^2 {\mathcal {R}}'({{\underline{I}}}', {{\underline{\varphi }}}')\ , \end{aligned}$$

where ${\mathcal {Z}}'$ depends on the angles ${\underline{\varphi }}'$, but only through the resonant combinations ${\underline{\varphi }}'\cdot \underline{{\widetilde{k}}}$.

Notice that the combinations ${{\underline{\varphi }}}\cdot \underline{{\widetilde{k}}}$ are slow, since

$$\begin{aligned} {d\over {dt}} ({{\underline{\varphi }}}\cdot \underline{{\widetilde{k}}})= {{\underline{\omega }}} \cdot \underline{{\widetilde{k}}}=0\ . \end{aligned}$$

Remark 2

We add here a note on the book-keeping (see [25] for further details). We start with a Hamiltonian that contains terms with different orders of smallness and it might contain also small parameters. We use a system to assign an arbitrary order of smallness to any term in our Hamiltonian. We use a symbol $\lambda$, called book-keeping, whose powers $\lambda ,\lambda ^2,\lambda ^3,\ldots$ appear as factors in front of particular groups of terms to show that these terms are considered of first, second, third, $\ldots$ order of smallness. Then, the Hamiltonian looks like:

$$\begin{aligned} {\mathcal H}({\underline{I}},\underline{\varphi })={\mathcal H}_0 + \lambda {\mathcal H}_1 + \lambda ^2 {\mathcal H}_2 + \cdots \end{aligned}$$

with ${\mathcal H}_0=\underline{\omega }\cdot {\underline{I}}$. At the end of the procedure we set $\lambda =1$, since the parameter $\lambda$ was used just as a label for ordering terms with different smallness.

4 The model

In satellite and space debris dynamics, it is usually convenient to distinguish between three main regions of the space surrounding the Earth, according to the following terminology:

• Low-Earth-Orbits (LEO) for the region up to 2000 km of altitude;

• Medium-Earth-Orbits (MEO) for the region between 2000 and 30,000 km of altitude;

• Geosynchronous Earth’s Orbits (GEO) above 30,000 km of altitude.

In all three regions, one needs to consider the attraction by the Earth, including the the fact that the Earth is non spherical. In LEO it is mandatory to consider the effect of the atmospheric drag, while in MEO and GEO a relevant role is played by the attractions of Moon, Sun and by the Solar radiation pressure (see, e.g., [12,13,14, 17, 29, 42, 50, 53]). In what follows, we will consider only objects in MEO and GEO, which are ruled by a conservative model.

For our purposes, it is convenient to consider a Hamiltonian function composed by different contributions: the Keplerian part ${\mathcal {H}}_{Kep}$ (accounting for the Earth’s attraction as if the Earth was a point mass), the geopotential ${\mathcal {H}}_{geo}$ (accounting for the influence of the Earth with a non-spherical shape), the gravitational attraction of Moon ${\mathcal {H}}_{Moon}$ and Sun ${\mathcal {H}}_{Sun}$, and the Solar radiation pressure ${\mathcal {H}}_{SRP}$:

$$\begin{aligned} {\mathcal {H}}= & {} {\mathcal {H}}_{Kep}(a)+{\mathcal {H}}_{geo}(a,e,i,M,\omega ,\Omega ,\theta ) \nonumber \\&+{\mathcal {H}}_{Moon}(a,e,i,M,\omega ,\Omega ,a_M,e_M,i_M,M_M,\omega _M,\Omega _M)\nonumber \\&+{\mathcal {H}}_{Sun}(a,e,i,M,\omega ,\Omega ,a_S,e_S,i_S,M_S,\omega _S,\Omega _S)\nonumber \\&+{\mathcal {H}}_{SRP}(a,e,i,M,\omega ,\Omega ,a_S,e_S,i_S,M_S,\omega _S,\Omega _S)\ , \end{aligned}$$

where we recall that $\theta$ is the sidereal time, $(a,e,i,M,\omega ,\Omega )$ are the orbital elements of the space debris and the suffix M or S denotes that the orbital elements are referred to Moon or Sun. We can write the Keplerian Hamiltonian as ${\mathcal {H}}_{Kep}=-{\mu _E\over {2a}}$ with $\mu _E={\mathcal {G}} m_E$, ${\mathcal {G}}$ the gravitational constant and $m_E$ the mass of the Earth.

We notice that the Fourier expansions of ${\mathcal {H}}_{geo}$, ${\mathcal {H}}_{Moon}$, ${\mathcal {H}}_{Sun}$, and ${\mathcal {H}}_{SRP}$, contain an infinite number of terms of the form (2); the angles appearing in the trigonometric terms of (2) may be classified as fast (M, $\theta$), semi–fast ($M_M$, $M_S$), slow angles ($\omega$, $\Omega$, $\omega _M$, $\Omega _M$, $\omega _S$, $\Omega _S$).

This leads us to the following hierarchical classification of the different terms in the expansions (2):

• short periodic terms, involving the fast angles M, $\theta$, but with not commensurable rates ${\dot{M}}$ and ${\dot{\theta }}$;

• resonant (tesseral) terms, involving the fast angles M, $\theta$ with a commensurability relation between ${\dot{M}}$ and ${\dot{\theta }}$, say $k_1\dot{M}+k_2{{\dot{\theta }}}=0$ for some $k_1,k_2\in {\mathbb Z}$;

• semi–secular terms, which depend on the semi-fast angles $M_M$, $M_S$;

• secular terms, which depend on the slow angles ${\dot{\omega }}$, ${\dot{\Omega }}$, ${\dot{\omega }}_{M}$, ${\dot{\Omega }}_{M}$, ${\dot{\omega }}_{S}$, ${\dot{\Omega }}_{S}$.

We notice that the semi–secular terms occur mostly in the LEO region, and that the secular terms might provoke long-term variations of e and i over tens or hundreds of years.

When implementing perturbation theory, the Hamiltonian (1) is conveniently represented in terms of the action-angle Delaunay variables, that we briefly recall as follows. The actions are denoted as L, G, H and they are related to the orbital elements a, e, i by the expressions:

$$\begin{aligned} L=\sqrt{\mu _E a}\ , \qquad G=L \sqrt{1-e^2}\ , \qquad H=G \cos i\ ; \end{aligned}$$

(6)

the conjugated angles are M, $\omega$, $\Omega$, namely the mean anomaly, the argument of perigee, and the longitude of the ascending node. In terms of the Delaunay variables the Keplerian part in (1) becomes

$$\begin{aligned} {\mathcal {H}}_{Kep}(L)=-{\mu _E^2\over {2L^2}}\ , \end{aligned}$$

while the geopotential expanded in spherical harmonics, limited to the most relevant terms with spherical harmonic coefficients $J_2$, $J_3$, and finally averaged over the fast variables (i.e., the mean anomaly and the sidereal time) is given by

$$\begin{aligned} {\mathcal {H}}_{geo}= & {} \mu _E {R_E^2\over a^3} J_2 \Bigg ({3\over 4} \left( 1-{H^2\over G^2}\right) -{1\over 2}\Bigg ) \left( {G^2\over L^2}\right) ^{-{3\over 2}}\\&+\mu _E {R_E^3\over a^4} J_3 \sqrt{1-{H^2\over G^2}} \Bigg ({{15}\over {8}} \left( 1-{H^2\over G^2}\right) -{3\over 2}\Bigg ) \sqrt{1-{G^2\over L^2}} \sin \omega \ \left( 1-{H^2\over G^2}\right) ^{-{5\over 2}}\ , \end{aligned}$$

where $R_E$ is the Earth’s radius, which is equal to about 6378.1363 km. The Hamiltonian functions for the Moon, the Sun, and the Solar radiation pressure have more complicated forms and we refer to [19] for their full expressions (see also [16]).

5 Proper elements

Let us consider the transformed Hamiltonian in (5) and let us discard the remainder ${\mathcal {R}}'$, so to reduce the Hamiltonian just to the normal form term, say ${\mathcal H}_{NF}'$ with

$$\begin{aligned} {\mathcal H}_{NF}'({{\underline{I}}}',{{\underline{\varphi }}}')\ =\ {\mathcal {Z}}'({{\underline{I}}}')\ . \end{aligned}$$

(7)

From (7) we conclude that the actions ${{\underline{I}}}'$ stay constant; once transformed back to the original elements, we obtain the proper elements. More in general, we can give the following definition.

Definition 3

Consider a nearly-integrable Hamiltonian function

$$\begin{aligned} {\mathcal H}({{\underline{I}}},{{\underline{\varphi }}})= {\mathcal {Z}}({{\underline{I}}})+\varepsilon {\mathcal {R}}({{\underline{I}}},{{\underline{\varphi }}}) \end{aligned}$$

defined on $V\times {\mathbb T}^n$ with V an open set and $\mathbb {T}^n$ the n-dimensional torus. Let ${\mathcal H}^{(k)}$ be the Hamiltonian transformed under Theorem 1 up to the order k, i.e.

$$\begin{aligned} {\mathcal H}^{(k)}({{\underline{I}}}^{(k)},{\underline{\varphi }}^{(k)})= {\mathcal {Z}}^{(k)}({\underline{I}}^{(k)})+\varepsilon ^{k+1} {\mathcal {R}}^{(k)}({\underline{I}}^{(k)},{{\underline{\varphi }}}^{(k)})\ , \end{aligned}$$

where $({{\underline{I}}}^{(k)},{{\underline{\varphi }}}^{(k)})$ denote the new variables, obtained through a Lie series transformation as $({{\underline{I}}}^{(k-1)},{\underline{\varphi }}^{(k-1)})=(e^{L_{\chi ^{(k)}}}{\underline{I}}^{(k)},e^{L_{\chi ^{(k)}}}{{\underline{\varphi }}}^{(k)})$. Let ${{\underline{I}}}^{(k)}_{NF}$ be the solution of Hamilton’s equations associated to ${\mathcal H}^{(k)}$ with ${\mathcal {R}}^{(k)}=0$. Then, we define the proper elements of ${\mathcal H}$ as the quantities

$$\begin{aligned} {{\underline{I}}}_{NF}=e^{L_{\chi ^{(1)}}}\cdots e^{L_{\chi ^{(k)}}}\ {{\underline{I}}}^{(k)}_{NF}\ . \end{aligned}$$

The definition of proper elements was extensively used in connection to the classification of asteroids into families, as briefly reviewed in Sect. 5.1. The computation of the proper elements is presented in Sect. 5.2 and is implemented in Sect. 5.3 for a sample case of the space debris problem.

5.1 Proper elements in the Solar system

The first computations of proper elements in the context of the dynamics of objects in the Solar system were performed on asteroids in the main belt. The aim was to group asteroids in families, by assuming that asteroids with nearby values of the proper elements might have been close in the past, thus belonging to the same family. This assumption was motivated by the fact that proper elements retain the same features of the original family, since they are nearly constant over time.

The first paper on groups of asteroids appeared in 1918 by Hirayama ([30]), which presented a study on the similarities of the elements obtained after using a linear theory of secular perturbations. The term proper elements appeared for the first time in [31]. Some decades later, Brouwer ([7]) determined the proper elements using a linear theory of secular perturbations for a more realistic model of planetary motion. The analysis of the asteroids with high inclination and eccentricity was firstly approached in [55] and in [38], using the theory developed by Yuasa in [58] (see also [41, 46]). Further progress was made in [4, 51, 52], especially within the context of resonant elements, associated to the Hildas and Trojans groups (compare with [45]).

The synthetic computation of proper elements relies on a purely numerical method, which is detailed in [8, 35,36,37, 39]. The synthetic theory significantly increased the accuracy of the computation of proper elements at the expenses of requiring a longer computational time.

The extension of Yuasa theory was deeply studied by Knežević and Milani (see, e.g., [34, 43, 44], see also [33, 40]), who developed an efficient method for the computation of proper elements for asteroids with low and medium eccentricity and inclination (see also [26]).

Methods from artificial intelligence have been recently used in [9,10,11] (see also [47]) to analyze a large dataset of asteroids using a machine learning classification algorithm.

As far as proper elements for space debris are concerned, the first attempts were done, e.g., in [15, 27], who analyzed objects in GEO. A synthetic theory was presented in [48, 49, 57], which provide a numerical computation of the proper elements, starting from the evolution of the osculating elements.

5.2 Procedure for computing proper elements of space debris

The computation of the proper elements for space debris needs a dedicated procedure at the light of the hierarchical classification of the terms appearing in the expansion of the Hamiltonian (1). Precisely, we compute the following different sets of proper elements, which are briefly described as follows:

• 1. Consider the Hamiltonian (1) including the effects of Earth, Moon, Sun and SRP. We first average with respect to the mean anomaly M and the sidereal time $\theta$; hence, the semi-major axis is constant (being conjugated to the mean anomaly) and it becomes the first proper element.

• 2. Since the longitude of the ascending node of the Moon and mean anomaly of the Sun depend on time (through the expression of SRP), $\Omega _M=\Omega _M(t)$, $M_S=M_S(t)$, the Hamiltonian in step 1 depends on the variables $(e,i,\omega ,\Omega ,\Omega _M,M_S)$, equivalently $(G,H,\omega ,\Omega ,\Omega _M,M_S)$, say ${\mathcal H}_2={\mathcal H}_2(G,H,\omega ,\Omega ,\Omega _M,M_S)$. We remark that ${\mathcal H}_2$ depends on time through $\Omega _M$ and $M_S$ with two different frequencies. Hence, we introduce the Hamiltonian in the extended phase space with the addition of two variables conjugated to $\Omega _M$, say $H_M$, and $M_S$, say $L_S$:

  $$\begin{aligned} {\mathcal H}_{ext}={\mathcal H}_{ext}(G,H,H_M,L_S,\omega ,\Omega ,\Omega _M,M_S)\ . \end{aligned}$$

• 3. Fix reference values for the eccentricity and inclination, say $e_0$ and $i_0$, and perform a linear change of coordinates to shift the corresponding variables G and H to the reference values $G_0$ and $H_0$ (which are associated to $e_0$ and $i_0$).

• 4. Introduce the displacements $\eta$ and $\iota$ as $e=e_0+\eta$, $i=i_0+\iota$; equivalently, introduce the variables $P=G-G_0$, $Q=H-H_0$; let p, q be the conjugated angles, $q_M=\Omega _{M}$, $r_{S}=M_S$, and let $Q_M$, $R_S$ be the associated action variables.

• 5. Expand the Hamiltonian ${\mathcal H}_{ext}$ around $P=0$, $Q=0$ up to order 4. Then, split the resulting Hamiltonian into its linear part and a remainder:

  $$\begin{aligned} {\mathcal {H}}_{exp}(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} {\mathcal {Z}}_0(P,Q,Q_M,R_S)\nonumber \\&+{\mathcal {R}}_0(P,Q,Q_M,R_S,p,q,q_M,r_S)\ , \end{aligned}$$

  (8)

  where ${\mathcal {Z}}_0$ is the linear part with frequencies $\omega _P$, $\omega _Q$, $\omega _{Q_M}$, $\omega _{R_S}$:

  $$\begin{aligned} {\mathcal {Z}}_0(P,Q, Q_M, R_S)=\omega _P\, P+\omega _Q\, Q+\omega _{Q_M}\, {Q_M}+\omega _{R_S}\, {R_S} \end{aligned}$$

  and ${\mathcal {R}}_0$ is the perturbing function.

• 6. Introduce a book-keeping parameter $\lambda$ by writing (8) as

  $$\begin{aligned} {\mathcal H}_{exp}(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} {\mathcal {Z}}_0(P,Q,Q_M,R_S)\\&+\lambda \ {\mathcal {R}}_0(P,Q,Q_M,R_S,p,q,q_M,r_S)\ . \end{aligned}$$

  Split ${\mathcal {R}}_0$ as its average $\overline{{\mathcal {R}}_0}$ and non-average part $\widetilde{{\mathcal {R}}_0}$;

  $$\begin{aligned} {\mathcal {R}}_0(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} \overline{{\mathcal {R}}_0}(P,Q,Q_M,R_S)\\&+\widetilde{{\mathcal {R}}_0}(P,Q,Q_M,R_S,p,q,q_M,r_S)\ . \end{aligned}$$

• 7. Implement a normal form up to second order by looking for a generating function $\chi ^{(1)}$ such that the transformation of variables given by $(P,Q,Q_M,R_S,p,q,q_M,r_S)=S_{\chi ^{(1)}}^\lambda (P^1,Q^1,Q_M^2,R_S^1,p^1,q^1,q_M^1,r_S^1)$, transforms the Hamiltonian (8) into

  $$\begin{aligned} {\mathcal {H}}^{(1)}(P^1,Q^1,Q_M^1,R_S^1,p^1,q^1,q_M^1,r_S^1)= & {} {\mathcal {Z}}_0(P^1,Q^1,Q_M^1,R_S^1)+\lambda \overline{{\mathcal {R}}_0}(P^1,Q^1,Q_M^1,R_S^1)\nonumber \\&+ \lambda ^2 {\mathcal {R}}_1(P^1,Q^1,Q_M^1,R_S^1,p^1,q^1,q_M^1,r_S^1)\ , \end{aligned}$$

  where ${\mathcal {R}}_1$ denotes the new perturbing function.

• 8. Once obtained the new Hamiltonian, disregard the remainder by considering the normal form Hamiltonian:

  $$\begin{aligned} {\mathcal H}^{(NF)}(P^1,Q^1,Q_M^1,R_S^1)={\mathcal {Z}}_0(P^1,Q^1,Q_M^1,R_S^1)+\lambda \overline{{\mathcal {R}}_0}(P^1,Q^1,Q_M^1,R_S^1)\ , \end{aligned}$$

  so that the two actions $P^1$ and $Q^1$ (corresponding to eccentricity and inclination) become constants of motion.

• 9. The initial values of the new constants of motion, which are the two additional proper elements at the initial time, are obtained back-transforming the canonical transformations in terms of the original variables, namely in terms of the initial data. This is a crucial point, that we detail as follows. Since the normal form depends only on the action variables, denoting by $(P^1_0,Q^1_0,Q^1_{M,0},R^1_{S,0},p^1_0,q^1_0,q^1_{M,0},r^1_{S,0})$ the initial condition at time $t=0$, then we have:

  $$\begin{aligned} P^1(t)= & {} P^1_0, \nonumber \\ Q^1(t)= & {} Q^1_0, \nonumber \\ Q^1_M(t)= & {} Q^1_{M,0}, \nonumber \\ R^1_S(t)= & {} R^1_{S,0}, \nonumber \\ p^1(t)= & {} p^1_0 + \dfrac{\partial {\mathcal H}^{(NF)}}{\partial P^1}(P^1_0,Q^1_0,Q^1_{M,0},R^1_{S,0}) t ,\nonumber \\ q^1(t)= & {} q^1_0+ \dfrac{\partial {\mathcal H}^{(NF)}}{\partial Q^1}(P^1_0,Q^1_0,Q^1_{M,0},R^1_{S,0}) t , \nonumber \\ q^1_M(t)= & {} q^1_{M,0}+ \dfrac{\partial {\mathcal H}^{(NF)}}{\partial Q^1_M}(P^1_0,Q^1_0,Q^1_{M,0},R^1_{S,0}) t , \nonumber \\ r^1_S(t)= & {} r^1_{S,0}+ \dfrac{\partial {\mathcal H}^{(NF)}}{\partial R^1_S}(P^1_0,Q^1_0,Q^1_{M,0},R^1_{S,0}) t\ . \end{aligned}$$

  To determine the values $(P^1_0,Q^1_0,Q^1_{M,0},R^1_{S,0},p^1_0,q^1_0,q^1_{M,0},r^1_{S,0})$, we need to express them in terms of the initial conditions in the original Hamiltonian system; this relation is given through the generating function $\chi ^{(1)}$ as

  $$\begin{aligned} P^1(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}} )^{-1}P, \nonumber \\ Q^1(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}})^{-1} Q, \nonumber \\ Q^1_M(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}})^{-1} Q_M, \nonumber \\ R^1_S(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}})^{-1} R_S, \nonumber \\ p^1(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}})^{-1} p, \nonumber \\ q^1(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}})^{-1} q, \nonumber \\ q^1_M(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}})^{-1} q_M, \nonumber \\ r^1_S(P,Q,Q_M,R_S,p,q,q_M,r_S)= & {} (S^{\lambda }_{\chi ^{(1)}})^{-1} r_S, \end{aligned}$$

  (9)

  where $S^{\lambda }_{\chi } =\sum _{k=0}^\infty \frac{\lambda ^k}{k!}L_\chi ^k$ is the Lie derivative (or Lie series operator). Then, we obtain the initial conditions in the transformed variables as

  $$\begin{aligned} P^1_0= & {} P^1(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \nonumber \\ Q^1_0= & {} Q^1(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \nonumber \\ Q^1_{M,0}= & {} Q^1_M(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \nonumber \\ R^1_{S,0}= & {} R^1_S(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \nonumber \\ p^1_0= & {} p^1(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \nonumber \\ q^1_0= & {} q^1(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \nonumber \\ q^1_{M,0}= & {} q^1_M(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \nonumber \\ r^1_{S,0}= & {} R^1_S(P_0,Q_0,Q_{M,0},R_{S,0},p_0,q_0,q_{M,0},r_{S,0}), \end{aligned}$$

which are the proper values at the initial time. Moreover, we end by noticing that we can compute the proper values $P^1_{\tau },Q^1_{\tau }$ at any time $\tau$ by using the transformation (9) according to

$$\begin{aligned} P^1_{\tau }= & {} P^1(P_{\tau },Q_{\tau },Q_{M,{\tau }},R_{S,{\tau }},p_{\tau },q_{\tau },q_{M,{\tau }},r_{S,{\tau }}), \nonumber \\ Q^1_{\tau }= & {} Q^1(P_{\tau },Q_{\tau },Q_{M,{\tau }},R_{S,{\tau }},p_{\tau },q_{\tau },q_{M,{\tau }},r_{S,{\tau }}), \end{aligned}$$

where $(P_{\tau },Q_{\tau },Q_{M,{\tau }},R_{S,{\tau }},p_{\tau },q_{\tau },q_{M,{\tau }},r_{S,{\tau }})$ are the values of the mean elements (in the transformed variables) obtained after a numerical integration.

The variables $(P^1_{\tau },Q^1_{\tau })$ are finally used to compute the proper eccentricity and inclination, by using the inverse transformation from the coordinates (P, Q, p, q) to the orbital elements $(e,i,\omega ,\Omega )$. To this end, we first shift back the actions to obtain the proper Delaunay’s actions $G_{\tau } = P_{\tau } + G_0$ and $H_{\tau } = Q_{\tau } + H_0$. Then, we can compute the proper eccentricity $e_{\tau }$ and proper inclination $i_{\tau }$ by using the formulae (6). A practical implementation of the above procedure is given in Sect. 5.3.

5.3 Proper elements of a sample case

In this section we describe the computation of the proper elements for a sample case of space debris. Some applications to real test cases can be found in [18]. Here, we provide an application to a sample case, which has been synthetically constructed. The simulation of an explosion of one or more satellites is done through the break-up simulator SIMPRO developed in [2] on the basis of the NASA model EVOLVE 4.0 (see [1, 32]). Such program allows one to obtain the elements associated to a collision or an explosion of different kinds of satellites, providing as inputs the position and mass of the parent body; in the case of collisions, also the mass of the projectile body and the impact velocity are needed. The program returns the position of the fragments, the relative velocity distribution with respect to the parent body, the size distribution and the area-to-mass-ratio. Such data suffice to compute the mean and proper elements of the fragments.

We proceed to analyze a break-up event, starting from the orbital elements of each generated fragment at the initial time and applying the following procedure:

(a):

we compute mean and proper elements of all fragments at the initial time $T_0$, namely at the instant at which the break-up event takes place;

(b):

starting from the mean elements at initial time $T_0$, and using Hamilton’s equations for the system described by (1), we propagate the fragments for a period of time $T_f$ (up to, e.g., $T_f=200$ years) and we record the mean elements, say every 6 months;

(c):

we use the generating function obtained after the normalization procedure to compute the canonical transformation from the mean elements to the proper elements for each fragment, every 6 months from $T_0$ to $T_f$;

(d):

we record the data obtained at item (c) and repeat the first three steps for each break-up event;

(e):

we analyze the differences in the evolution of mean and proper elements for each fragment of every group by using appropriate statistical and graphical methods.

Fig. 1

The comparison between the variation of the mean elements (group 1—light green, group 2—light orange, group 3—light pink) and proper elements (group 1—blue, group 2—magenta, group 3—brown) over 200 years, with the dots plotted every 10 years (color figure online)

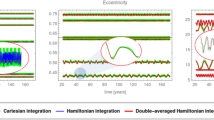
Figure 1 shows the result of the break-ups² of three different bodies located nearby, that have the following orbital elements at the break-up time:

$$\begin{aligned} \{a,e,i,M,\omega ,\Omega \}= & {} \{39600\, km,0.05,42^{\circ },110.54^{\circ },40.44^{\circ },80.34^{\circ }\}, \\ \{a,e,i,M,\omega ,\Omega \}= & {} \{36600\, km,0.1,35^{\circ },120.25^{\circ },10.71^{\circ },60.95^{\circ }\}, \\ \{a,e,i,M,\omega ,\Omega \}= & {} \{34600\, km,0.15,30^{\circ },10.13^{\circ },110.69^{\circ },10.11^{\circ }\}. \end{aligned}$$

The visual comparison of the plots corresponding to mean and proper elements variation over a period of 200 years makes already clear that only the proper elements remain almost constant and allow us to distinguish the three different groups, at the initial as well as at the final time. On the contrary, the mean elements of all three groups spread over time and, without appropriate colors, it would result impossible to distinguish between the three break-up events. Such conclusion will be supported by a statistical data analysis ([5], see Sect. 5.4) and by machine learning techniques ([3], see Sect. 5.5). Indeed, this line of research of combining artificial intelligence (AI) techniques with methods of Celestial Mechanics and Astrodynamics is very promising. In particular, AI methods have already been used in several works, among which [20] for the classification of regular and chaotic motions in the spin-orbit problem, [6] for the solution of the 3-body problem using deep neural networks, [11] for the identification of new asteroid families.

5.4 Statistical data analysis

In this section, the evolution of the distribution of the mean inclination is compared with the evolution of the distribution of the proper inclination. Figure 2 shows the probability density functions (PDF) of the mean and proper elements distributions at every 5 years up to 200 years. The PDF is computed assuming that the form of the desired distribution is known apriori³ and by using a maximum likelihood method [5] to estimate the parameters of the distribution w.r.t. a given dataset. In our case, we are looking for a mixture of three normal distributions.⁴

In the case of proper inclination (blue lines), we notice an almost perfect overlapping of the PDFs, that keep the same shape over time, while the distributions in mean elements change at every time step, so that the initial configuration totally disappears after a short time.

Fig. 2

The probability density functions computed every 5 years, over 200 years, for the mean (purple lines) and proper (blue lines) inclination of the fragments generated by three nearby break-up events as in Fig. 1 (color figure online)

More precisely, the initial distribution of the mean inclination is a Gaussian mixture of three normal distributions with the following parameters.

$$\begin{aligned} 0.41\ {\mathcal {N}}(29.8,0.87)+0.31\ {\mathcal {N}}(34.9,1.09)+0.27\ {\mathcal {N}}(41.3,1.98)\ , \end{aligned}$$

(10)

and the initial distribution of the proper inclination is as well a mixture of three normal distributions with the following parameters:

$$\begin{aligned} 0.42\ {\mathcal {N}}(25.7,1.91)+0.31\ {\mathcal {N}}(33.4,1.06)+0.25\ {\mathcal {N}}(41.4,1.75)\ . \end{aligned}$$

(11)

Hence, the mean and proper distributions (10) and (11) are similar at the initial time. However, when time goes on, the variation of the parameters (weights of the mixture, and means and variances of each normal distribution) relative to the proper inclination distribution is of order of $10^{-6}$ (compare with Fig. 2). On the contrary, the distribution of the mean inclination totally changes after 25 years and it becomes a mixture of two (instead of three) normal distributions. The physical meaning of the variation of the distribution with time is due to the overlapping of two groups over the three original groups, an effect that is corroborated by the results in Sect. 5.5.

5.5 Machine learning clusterization

In this section, we analyze the sample case shown in Fig. 1, using KMeans from Mathematica^©, which is a supervised machine learning clusterization method.

Fig. 3

The evolution of the fragments generated by three nearby break-up events as in Fig. 1 (group 1—yellow dots, group 2—green dots, group 3—blue dots) in the mean elements (left plots) and proper elements (right plots) at times 0, 50, 100, 150, 200 years (from top to bottom), and the wrongly classified fragments (red dots) at each time, following the procedure explained in the text (color figure online)

According to [56], KMeans is a centroid-based clustering, which works when the different clusters are similar in size, and they are locally and isotropically distributed around their centroid. In particular, KMeans minimizes the within-cluster variance for a fixed number of clusters, by computing the mean squared Euclidean distance from the clusters’ center [3]. The procedure that implements such computer-assisted classification is based on the following steps:

• 1. we separate the groups, both in the initial mean elements and initial proper elements at time $T_0$, and record the results;

• 2. at every intermediate time $T_i$, we use KMeans to classify the data in 3 groups and compare the original groups at time $T_0$ with the groups obtained at time $T_i$. More precisely, the output of KMeans assigns a number from 1 to 3 to each point (the predicted group of a fragment at time $T_i$). Having a similar list with numbers for time $T_0$, we can compare them and say which fragments changed group over the time;

• 3. we plot with red dots the wrongly classified objects, namely the points for which the number (group) obtained at time $T_i$ does not coincide with the number (group) obtained at the beginning, time $T_0$.

In Fig. 3 we show the results of the clusterization algorithm, comparing the results obtained for the classification of the fragments using the mean elements (left plots) with the classification of the fragments using the proper elements (right plots).

We notice that the number of red dots in Fig. 3 is increasing with time in the case of the mean elements evolution (due to the overlapping of the groups), while the configuration of the proper elements is almost constant over a period of 200 years of evolution.

Appendix A: Proof of the normal form theorem

We give below the proof of Theorem 1.

Let $L_{\chi }\equiv \{\cdot ,\chi \}$ with $\{\cdot ,\cdot \}$ the Poisson bracket operator; we can expand the exponential of $L_{\chi }$ as $e^{L_{\chi }}=\sum _{k=0}^\infty \frac{1}{k!}L_\chi ^k$. Let us split the perturbation ${\mathcal {R}}$ as ${\mathcal {R}}={\overline{{\mathcal {R}}}}+\widetilde{{\mathcal {R}}}$, where ${\overline{{\mathcal {R}}}}$ denotes the average of ${\mathcal {R}}$ and $\widetilde{{\mathcal {R}}}$ the non average part.

We look for a canonical transformation

$$\begin{aligned} ({\underline{I}},\underline{\varphi })= (e^{L_{\chi }}\ {\underline{I}}',e^{L_{\chi }}\ \underline{\varphi }')\ , \end{aligned}$$

which transforms (3) in

$$\begin{aligned} {\mathcal H}'({\underline{I}}',\underline{\varphi }')={\mathcal {Z}}({\underline{I}}')+ \varepsilon {\overline{{\mathcal {R}}}}({\underline{I}}')+\varepsilon ^{2} {\mathcal {R}}'({\underline{I}}',\underline{\varphi }')\ . \end{aligned}$$

The function ${\mathcal {Z}}'={\mathcal {Z}}+\varepsilon {\overline{{\mathcal {R}}}}$ is called the normal form Hamiltonian.

The transformed Hamiltonian is given by

$$\begin{aligned} {\mathcal H}'= & {} e^{L_{\chi }}{\mathcal H}={\mathcal H}+L_{\chi }{\mathcal H}+{1\over 2}L^2_{\chi }{\mathcal H}+\cdots \nonumber \\= & {} {\mathcal {Z}}+\varepsilon R+\{{\mathcal H},\chi \}+{1\over 2}L^2_{\chi }{\mathcal H}+\cdots \nonumber \\= & {} {\mathcal {Z}}+\varepsilon {\mathcal {R}}+\{{\mathcal {Z}},\chi \}+\varepsilon \{{\mathcal {R}},\chi \}+\cdots \nonumber \\= & {} {\mathcal {Z}}+\varepsilon {\overline{{\mathcal {R}}}}+\varepsilon \widetilde{{\mathcal {R}}}+\{{\mathcal {Z}},\chi \}+\varepsilon \{{\overline{{\mathcal {R}}}},\chi \}+ \varepsilon \{\widetilde{{\mathcal {R}}},\chi +\cdots \} \end{aligned}$$

To get (5), we require that the generating function $\chi$ satisfies the following normal form equation:

$$\begin{aligned} \varepsilon \widetilde{{\mathcal {R}}}+ \{{\mathcal {Z}},\chi \}=0\ . \end{aligned}$$

By definition of the Poisson bracket, we obtain that

$$\begin{aligned} \{{\mathcal {Z}},\chi \}= {{\partial {\mathcal {Z}}}\over {\partial \underline{\varphi }}} {{\partial \chi }\over {\partial {\underline{I}}}}- {{\partial {\mathcal {Z}}}\over {\partial {\underline{I}}}}{{\partial \chi }\over {\partial \underline{\varphi }}} =-{{\partial {\mathcal {Z}}}\over {\partial {\underline{I}}}}{{\partial \chi }\over {\partial \underline{\varphi }}}= -\underline{\omega }({\underline{I}})\ {{\partial \chi }\over {\partial \underline{\varphi }}} \end{aligned}$$

and therefore we are led to the equation

$$\begin{aligned} \underline{\omega }({\underline{I}})\ {{\partial \chi }\over {\partial \underline{\varphi }}}=\varepsilon \widetilde{{\mathcal {R}}}\ . \end{aligned}$$

(12)

To solve (12), we start to expand $\widetilde{{\mathcal {R}}}$ and $\chi$ in Fourier series as $\widetilde{{\mathcal {R}}}({\underline{I}}',\underline{\varphi }')= \sum _{{\underline{k}}\not ={\underline{0}}} \widehat{ {\mathcal {R}}_{{\underline{k}}}}({\underline{I}}') e^{i{\underline{k}}\cdot \underline{\varphi }'}$ and $\chi ({\underline{I}}',\underline{\varphi }')= \sum _{{\underline{k}}} {\widehat{\chi }}_{{\underline{k}}}({\underline{I}}') e^{i{\underline{k}}\cdot \underline{\varphi }'}$. Inserting such expansions in (12), we obtain

$$\begin{aligned} -i\sum _{{\underline{k}}} \underline{\omega }({\underline{I}}')\cdot {\underline{k}}\ \ {\widehat{\chi }}_{{\underline{k}}}({\underline{I}}') e^{i{\underline{k}}\cdot \underline{\varphi }'}= -\varepsilon \sum _{{\underline{k}}\not ={\underline{0}},\ |{\underline{k}}|\le N}\widehat{{\mathcal {R}}}_{{\underline{k}}}({\underline{I}}') e^{i{\underline{k}}\cdot \underline{\varphi }'}\ , \end{aligned}$$

which gives the solution for the Fourier coefficients of $\chi$ as

$$\begin{aligned} {\widehat{\chi }}_{{\underline{k}}}({\underline{I}}')=\varepsilon \ {{\widehat{{\mathcal {R}}}_{{\underline{k}}}({\underline{I}}')}\over {i\underline{\omega }({\underline{I}}')\cdot {\underline{k}}}}\ . \end{aligned}$$

Notice that ${\underline{I}}'=e^{-L_{\chi }}\ {\underline{I}}$ and, to first order, ${\underline{I}}'={\underline{I}}-\{{\underline{I}},\chi \}={\underline{I}}+{{\partial \chi }\over {\partial \underline{\varphi }}}$. Let M be an upper bound on ${{\partial \chi }\over {\partial \underline{\varphi }}}$ for $\underline{\varphi }\in {\mathbb T}^n$ and ${\underline{I}}\in B_{\rho _0}({\underline{I}}_0)$. Then, one has

$$\begin{aligned} |{\underline{I}}'-{\underline{I}}_0|\le \varepsilon _0 M+\rho _0\ . \end{aligned}$$

The small divisors $\underline{\omega }({\underline{I}}')\cdot {\underline{k}}$ are well defined in a suitable neighborhood of ${{\underline{I}}}_0$ by using (4) and the following inequalities:

$$\begin{aligned} |\underline{\omega }({\underline{I}}')\cdot {\underline{k}}|= & {} |\underline{\omega }({\underline{I}}_0)\cdot {\underline{k}}+ (\underline{\omega }({\underline{I}}')-\underline{\omega }({\underline{I}}_0))\cdot {\underline{k}}|\nonumber \\\ge & {} |\underline{\omega }({\underline{I}}_0)\cdot {\underline{k}}|- |{{\partial \underline{\omega }({\underline{I}}_0)}\over {\partial {\underline{I}}}}|\ |{\underline{I}}'-{\underline{I}}_0|\ |{\underline{k}}|\nonumber \\\ge & {} a - |{{\partial \underline{\omega }({\underline{I}}_0)}\over {\partial {\underline{I}}}}|\ |{\underline{I}}'-{\underline{I}}_0|\ N\nonumber \\\ge & {} a - |{{\partial \underline{\omega }({\underline{I}}_0)}\over {\partial {\underline{I}}}}|\ N\ (\varepsilon _0 M+\rho _0) >0 \end{aligned}$$

for a suitable choice of $\varepsilon _0$ and $\rho _0$. Finally, the generating function is given by the expression:

$$\begin{aligned} \chi ({\underline{I}}',\underline{\varphi }')=\varepsilon \sum _{{\underline{k}}\not ={\underline{0}},\ |{\underline{k}}|\le N} {{\widehat{{\mathcal {R}}}_{{\underline{k}}}({\underline{I}}')}\over {i\underline{\omega }({\underline{I}}')\cdot {\underline{k}}}}\ e^{i{\underline{k}}\cdot \underline{\varphi }'}\ . \end{aligned}$$

(13)

It should be mentioned that, provided $\varepsilon$ is sufficiently small, the Lie series transformations provide a function $\chi$ which is analytic in a suitable domain; this implies that the Fourier series expansion (13) is absolutely convergent. We refer to [28] for more details. This concludes the proof of Theorem 1.