Introduction

Ultrafast laser radiation enables highly efficient material processing, especially in laser micromachining with minimal thermal stress [1]. As a result, a large number of materials can be processed with minimal lateral damage and a very small heat-affected zone [2, 3]. Due to the extremely short pulse duration, the pulse energy is deposited into the electron system within the pulse duration time of a few hundreds of femtoseconds, and is transferred to the phonon system within the electron-phonon relaxation time, being in the range of a few picoseconds. If the amount of absorbed energy exceeds a material-dependent threshold, the material is ablated. Additionally, during the interaction between the laser radiation and the material, a diffusion of energy within the electron system occurs, which increases the energy density below the surface, and thus, may cause ablation up to an effective penetration depth. The effective penetration depth depends on the pulse duration and the fluence of the laser radiation. Therefore, by knowing the resulting penetration depth as a function of the pulse duration and fluence, the ablation depth, and thus, the ablation rate can be controlled. The ablation rate is important for industrial applications, such as laser micro-structuring, laser engraving or laser cutting, particularly for stainless steel.

The ultrafast excitation of metals is often described by the two-temperature model [4]. It is assumed that the excitation of the electrons by the laser radiation is followed by a rapid local thermalization of the electrons, and followed by the subsequent thermalization between the electrons and the phonons. This thermal process is described by two different temperature distributions, one for the electron system and one for the phonon system. The two temperature distributions depend on space and time, and their evolution is defined by two coupled differential equations describing the energy transfer between the two systems and the heat diffusion within each system. Due to the energy transfer, the phonon system may be heated up sufficiently so that ablation can occur. Due to the lack of knowledge of the temperature-dependent parameters, such as the reflectivity of the laser radiation, the absorption coefficient, or the electron-phonon coupling factor, the temperature dependency of the parameters was approximated by simple relations and assumed to be temperature-independent like in previous simulations of the interaction of ultrashort pulses with steel (or iron) which were already performed using the two temperature model [5,6,7]. Another possibility to calculate the ablation rate of steel or iron using ultrashort pulses is the molecular dynamic simulation technique [8, 9]. However, this simulation method requires a very high computing effort and also the knowledge of functional relationships between material-specific parameters and the electron temperature.

Experimental ablation studies on steel have demonstrated, that the effective penetration depth of ultrafast laser radiation can be much larger than the optical penetration depth [10,11,12,13,14]. In the current state of the art, the effective penetration depth is derived from the ablation depth or the ablated volume of a cavity produced by a single pulse or multiple pulses [10,11,12,13,14]. Nevertheless, large errors are obtained by measuring the ablation depth or the ablated volume induced by a single pulse. Another possibility to determine the effective penetration depth with a simultaneous reduction of the errors is given by the measurement of the ablation depth or the ablated volume of a cavity produced by multiple pulses. On the other hand, for multiple irradiations, the measurement of the required depths or volumes are more accurate, but the effective penetration depth differs from the values obtained from single-pulse experiments due to the incubation effect [15,16,17] induced by multiple irradiations.

To verify the experimental data and to obtain more accurate predictions, the ablation depth is simulated in this work by a relatively simple numerical approach of the two coupled equations of the two-temperature model, and an associated effective penetration depth is calculated. In contrast to the present state of the art, the temperature dependence of material-specific parameters such as the reflectance of the laser radiation, the thermal conductivity and the volumetric heat capacity is taken into account. This simulation model is intended to improve the precision of the ablation process for industrial applications of laser micro-structuring in a simple and fast way.

Theoretical Background

Two-Temperature Model

To calculate the heat propagation in the material, the two-temperature model is used [4, 18,19,20,21], in which the evolution of the electron temperature Te is described by

$$ C_{\text{e}}\partial_{t}T_{\text{e}}=\nabla\cdot(\lambda_{\text{e}}(T_{\text{e}})\nabla T_{\text{e}})-G(T_{\text{e}}-T_{\text{ph}})+S, $$
(1)

and the phonon temperature Tph is given by

$$ C_{\text{ph}}\partial_{t} T_{\text{ph}}=\nabla\cdot(\lambda_{\text{ph}}\nabla T_{\text{ph}})+G(T_{\text{e}}-T_{\text{ph}}). $$
(2)

In the two equations, connected through the coupling term G, Ce(Te) and Cph represent the volumetric heat capacities and the parameters λe(Te) and λph define the thermal conductivity of the electron and phonon system. The heat source (laser radiation) is characterized by the variable S. The phase state is considered with the volumetric heat capacity of the phonons

$$ C_{\text{ph}}=\rho \left[c_{\text{p0}} +\frac{\Delta {H_{\text{M}}}}{\Delta {T \sqrt 2 \pi}} \exp \left( -0.5\left( \frac{T_{\text{ph}}-T_{\text{M}}}{\Delta {T}} \right)^{2} \right)\right] $$
(3)

with the latent heat of fusion [22] ΔHM. The volumetric heat capacity of the electron system

$$ \begin{array}{@{}rcl@{}} C_{\text{e}}(T_{\text{e}})&=&\left[2.677\times 10^{6} \exp\left( 8.937\times 10^{-6} T_{\text{e}}/\text{K}\right)\right.\\ &&\left.-2.987\times 10^{6} \exp\left( -0.0003787 T_{\text{e}}/\text{K}\right)\right] \text{JK}^{-1}\text{m}^{-3} \end{array} $$
(4)

and the coupling factor

$$ \begin{array}{@{}rcl@{}} G&=&\left[2.837\times 10^{18} \exp\left( -\left( \frac{T_{\text{e}}/\text{K}-3077}{1.166\times 10^{4}}\right)^{2}\right) \right.\\ &&\left. +2.993\times 10^{18} \exp\left( -\left( \frac{T_{\text{e}}/\text{K}-2.988\times 10^{4}}{8.147\times 10^{4}}\right)^{2}\right)\right] \text{WK}^{-1}\text{m}^{-3} \end{array} $$

are fitted according to the theoretical results of the density-functional-theory (DFT)-calculations [23] (Figs. 1 and 2). The dependence of the thermal conductivity [23] of the electrons λe on the electron temperature is given by

$$ \lambda_{\text{e}}(T_{\text{e}})=\left [\left (0.535\times 10^{-4} {T}_{\text{e}}/\text{K} -0.004 \right )\times 10^{3}\right] \text{WK}^{-1}\text{m}^{-1} $$
(5)

and is visualized in Fig. 3. The thermal conductivity of the phonon system [24] (\(\lambda _{\text {ph}}=23 \text {W} \text {m}^{-1}\text {K}^{-1}\)) is neglected as the condition λe >> λph is fulfilled for Te > T0.

Fig. 1
figure 1

Volumetric heat capacity of the electrons Ce as a function of the electron temperature Te for stainless steel. The solid line represents the fitted function and the open circles the values of the DFT-calculations [23]

Full size image
Fig. 2
figure 2

Coupling factor G as a function of the electron temperature Te for stainless steel. The solid line represents the fitted function and the open circles the values of the DFT-calculations [23]

Full size image
Fig. 3
figure 3

Numerically determined thermal conductivity λe as a function of the electron temperature Te for stainless steel [23]. The solid line represents the fitted function

Full size image

The heat source S can be described as

$$ S=(1-R(T_{\text{e}}))\alpha (z) I(t) I(x,y,z) $$
(6)

with a gaussian-shaped temporal intensity distribution

$$ I(t)=I_{0} \exp\left[-4\text{ln2} \frac{(t-t_{0})^{2}}{\tau_{\text{H}}^{2}} \right] $$
(7)

with the laser peak intensity

$$ I_{0}=\sqrt{\frac{4\text{ln2}}{\pi}} \frac{H_{0}}{\tau_{\text{H}}}, $$
(8)

where H0 represents the laser peak fluence and τH the pulse duration. The peak intensity I0 is given at t0 = 2τH. In order to simplify the simulations, the spatial intensity distribution in the surface plane Ix,y is not taken into account and only one-dimensional simulations with the peak intensity I0 at x = y = 0 are considered. The spatial intensity distribution in the depth z is derived by Beer’s law

$$ I(z)=I_{0} \exp\left( -{\int}_{z_{0}}^{z}\alpha(z) \text{d} z\right), $$
(9)

where I represents the laser intensity, z the material depth, z0 the position of the surface and \(\alpha =\frac {4 \pi \kappa (T_{\text {e}})}{\lambda }\) the linear absorption coefficient. By integrating Eq. 9 under the assumption of an effective value \(\alpha =\frac {1}{\delta _{\text {opt}}}\), the so called reciprocal optical penetration depth averaged over space and time an approximation of the fluence H follows

$$ H(z)=H_{0} \exp \left( -\alpha z\right).\\ $$
(10)

In [25] the calculated temperature dependent optical properties for Fe, Cr and Ni were presented. By weighting the major elements of 316L (Fe70Cr17Ni13) the reflectance R and the extinction index κ as a function of the electron temperature is

$$ R(T_{\text{e}})=\left[11 \exp(-0.00013 {T}_{\text{e}}/\text{K})+ 59.2\right] \text{<percent>}. $$
(11)

and

$$ \kappa(T_{\text{e}})=1.4 \exp(-0.00015 {T}_{\text{e}}/\text{K})+ 3.75 $$
(12)

(Figs. 4 and 5). The results of the DFT simulations presented in [23] and in [25] were performed up to an electron temperature of 25 × 103K. Based on Eqs. 4, 5, 11 and 12, the material-specific and optical properties at higher electron temperatures are extrapolated in this study. The other required material-specific parameters for solving Eqs. 1 and 2 for stainless steel are given in Table 1. For the case that no data are available for stainless steel, the data for iron is used instead.

Fig. 4
figure 4

Reflectance R as a function of the electron temperature Te for pure iron, chromium, nickel and a weighting of the major elements of 316L (Fe70Cr17Ni13) at a wavelength λ = 1030 nm [25]. The solid line represents the fitted function Eq. 11

Full size image
Fig. 5
figure 5

Extinction coefficient κ as a function of the electron temperature Te for pure iron, chromium, nickel and a weighting of the major elements of 316L (Fe70Cr17Ni13) at a wavelength λ = 1030 nm [25]. The solid line represents the fitted function Eq. 12

Full size image
Table 1 Material-specific parameters for steel and iron
Full size table

By irradiating a material using ultrafast laser radiation the temperature of the phonon system increases within the heating time τheat, being defined by \(\tau _{\text {heat}}=\max \limits \{\tau _{\text {e-ph}};\tau _{\text {H}}\}\), wherein \(\tau _{\text {e-ph}}=\bigg (\frac {1}{C_{\text {e}}}+\frac {1}{C_{\text {ph}}}\bigg )^{-1} G^{-1}\) [26, 27] represents the electron-phonon relaxation time or also called electron-phonon coupling time in the absence of ablation, and τH the pulse duration. By increasing the temperature of the phonon system, thermal stress is induced, which usually induces a thermal expansion of the material in the case of slow heating, and therefore unloading and reduction of the induced thermal stress. The time scale needed for the reduction of the thermal stress is called acoustic relaxation time τac = Lth/cs [28] and is determined by the thermal diffusion length Lth and the speed of sound cs. In the case of irradiating a metal with ultrafast laser radiation, the condition τheat < τac is fulfilled, being called stress confinement [28, 29]. Within τheat the thermal expansion is neglectable and nearly isochoric heating of the material in conjunction with a large increase of the pressure as well as a phase change from solid to liquid is obtained (white to purple trajectories in Fig. 6). The induced pressure decays into two shock waves propagating in opposite directions, whereby one shock wave propagates into the material, and the other shock wave propagates towards the surface. The shock wave propagating towards the surfaces is reflected at the surfaces according to the wave impedance at the interface, and the shock wave is transformed into a rarefaction wave [23, 28,29,30]. Consequently, a pair of shock and rarefaction waves propagate into the material. The emission of the shock waves also enables the thermal expansion of the material, and heat transfer to surrounding material occurs during this relaxation process, resulting in a decrease of the density and the temperature (Fig. 6). The tensile stress of the rarefaction wave transforms the stable liquid into a metastable liquid, in which the binodal is crossed, and cavitation below the surface is induced if the time under negative pressure exceeds the time for forming a stable bubble. As a result, the spallation of layers of liquid material occurs. For higher fluences, and thus, higher temperatures of the material, the relaxation of the material results further in the crossing of the spinodal, why a fast-expanding liquid-vapor mixture is formed. This process is called phase explosion, explosive boiling, or spinodal decomposition, whereby in most cases, phase explosion is used. In contrast to spallation, representing a thermo-mechanical process, phase explosion represents mainly a thermodynamic process if only the ablated material is considered and the induced shock wave due to the recoil pressure of the ablated material is neglected. As a general rule based on the trajectories in the phase diagram (Fig. 6), spallation occurs if the maximum temperature is smaller than 90 % of the thermodynamic critical temperature Tc [31], and phase explosion occurs if the maximum temperature is larger than Tc,0.9. The result of Tc,0.9 based on the mentioned hydrodynamic descriptions is consistent with pure thermodynamic descriptions [32].

Fig. 6
figure 6

Schematic temperature-density-pressure and phase diagram according to [33,34,35,36,37,38,39] including four typical trajectories of a point slightly below the surface for spallation: white and light purple, and for phase explosion: purple and dark purple. The darker the color of the trajectory, the higher the fluence of the laser radiation. Different colors in the phase diagram correspond to different phase states (g, l+g, l, s+l, void), wherein metastable phases are indicated by brackets ((s), (s+l), (l), (g)). The dot represents the critical point CP with the critical temperature Tc, the critical density ρc as well as the critical pressure pc, bn the binodal, and sp the spinodal, respectively

Full size image

The phase explosion and the material removal of metals have been studied extensively [13, 17, 21, 40, 41]. However, most studies examined the thermal ablation within a low-fluence regime or within a high-fluence regime, in which the two regimes differ primarily in the ablation rate. The threshold fluence for stainless steel of the low fluence regime Hthr,low and the threshold fluence of the high fluence regime Hthr,high are presented in Table 1.

As the intention of the article is given by presenting a simple model, all hydrodynamic processes in conjunction with an equation of state [33,34,35] are neglected, and only the evolution of the electron and the phonon temperature is considered. The ablation criterion is defined to be Tc,0.9 [42,43,44], representing phase explosion. Therefore, spallation, occurring for fluences slightly above the ablation threshold of the low fluence regime, and representing the dominant ablation mechanism for temperatures up to Tc,0.9, is not taken into account. Thus, the applied model is only applicable for fluences well above the ablation threshold of the low fluence regime.

Due to the fast isochoric laser-induced heating up to Tc,0.9, no phase change from liquid to vapor, and thus, no evaporation occurs (Fig. 6). Therefore, the enthalpy of evaporation is neglected in the simulations. This assumption is supported by the fact, that the enthalpy of evaporation decreases for temperatures larger than the boiling temperature at normal conditions [45], and no enthalpy of evaporation exists for T > Tc. Concluding, and also defined in Eq. 3, only the enthalpy of fusion has to be considered. Furthermore, the density of the material is assumed constant in the simulations.

In the case of ablation of material, the ablated particles feature an average velocity of about 100 m/s [46]. Furthermore, the material surface is heated up to Tc,0.9 within a few picoseconds due to the fast energy transfer from the electron to the phonon system, and thus, ablation starts already within this time. Nevertheless, the ablated particles propagate only a few angstroms away from the surface during this time of a few picoseconds. Thus, an interaction of the free electrons from the ablation cloud with the non-ablated material is still probable. Therefore, in the simulations, only the temperature of the phonon system is limited to a maximum of Tc,0.9 and the ablation of material is only related to the phonon system. The electron system can reach much higher temperatures and is excluded from the ablation. The electrons can therefore heat the phonons up to the thermodynamic equilibrium between the two systems even if ablation has already occurred. The time to reach thermodynamic equilibrium is defined in this work as the electron-phonon coupling time τe-ph. The material thickness is regarded as infinite, so that a geometrically induced heat accumulation is prevented. The initial temperatures are set to be 300 K. The Eqs. 1 and 2 are solved numerically by applying the finite differences method for the spatial derivatives and the Euler method for the time integration.

For a quantitative statement about the ablation process, a 1D simulation during the interaction is sufficient as thermal diffusion can be neglected during the time scale of a few 10 ps due to the large aspect ratio d0/Lth ≈ 169 of the laser spot size d0 = 30μm and the thermal diffusion length \(L_{\text {th}}=\sqrt {\pi \lambda _{\text {e}}/C_{\text {e}}} t \approx 177 \text {nm} (\lambda _{\text {e}} \approx 1.5\times 10^{3} \text {W/(m K)}, C_{\text {e}} \approx 30\times 10^{5} J/(\text {m}^{3} K), t= 20 ps)\) [47].

The Effective Penetration Depth

Many studies in the recent years have demonstrated a much deeper transport of the absorbed energy into the material, compared to the optical penetration depth by absorption of the laser radiation, due to the effect of ballistic motion and the diffusion of hot electrons [43, 53,54,55,56]. The increased absorption depth has to be considered by an effective absorption coefficient in the source term in Eq. 6 including the optical and ballistic penetration depth [47]. In the simulations, the ballistic penetration depth is not considered as this value is not known. Nevertheless, the experimental determination of an effective penetration depths differs from a numerical one, as the experimental penetration depth includes further the thermal diffusion length. Thus, the experimental effective absorption coefficient αeff is defined by

$$ \alpha_{\text{eff}}(T_{\text{e}})=\frac{1}{\delta_{\text{opt}}(T_{\text{e}})+\delta_{\text{ball}}(T_{\text{e}})+\delta_{\text{diff}}(T_{\text{e}})}=\frac{1}{\delta_{\text{eff}}(T_{\text{e}})}, $$
(13)

including the reciprocal sum of the optical penetration depth δopt(Te), the depth of the ballistic electrons δball(Te), and the thermal diffusion length of the hot electrons δdiff(Te), with δeff as the effective penetration depth.

In order to calculate the effective penetration depth in accordance to the experimental methods in the low fluence regime [57,58,59,60], the threshold fluence Hth,low is substituted in Eq. 10 and zabl for z, resulting in

$$ H_{\text{th,low}}=H_{0} \exp \left( -\frac{1}{\delta_{\text{eff}}} z_{\text{abl}}\right). $$
(14)

Thus, by knowing the fluence H0, the threshold fluence Hth,low, and the ablation depth zabl, the effective penetration depth

$$ \delta_{\text{eff}}(T_{\text{e}})=\frac{z_{\text{abl}}}{\ln \left( \frac{H_{0}}{H_{\text{th,low}}}\right)} $$
(15)

can be determined.

For the calculation of the effective penetration depth in the high fluence regime an analytical method was presented, which was derived from the two temperature model [61]. The model assumes a constant coupling factor G, a constant reflectance R, and the constant volumetric heat capacity Ce. Consequently, the effective penetration depth is independent of the electron temperature, and thus also independent of the pulse duration. Another method [10] to calculate the effective penetration depth in the high fluence regime is given by

$$ \delta_{\text{eff}}(T_{\text{e}})=\frac{z_{\text{abl}}}{\sqrt{\ln \left( \frac{H_{0}}{H_{\text{th,low}}}\right)}}, $$
(16)

which represents an approximation of the fluence-dependent ablation depth in the thermal diffusion model [62].

Experimental Details

A solid-state laser (Pharos, Light Conversion) with a variable pulse duration in the range of 200 fs up to 10 ps and an emitting wavelength of 1030 nm is used for the experiments. The spatial intensity distributions nearly equals an ideal spatial gaussian profile (M2 < 1.1). A spherical lens with a focal length of 167 mm is used for focusing the laser radiation to a beam waist radius of 15 μm on the material surface.

Stainless steel (316L) with a thickness of 0.5 cm is used as the target material for the laser ablation. The ablation structures in the form of a micro blind hole are created with single-pulsed laser radiation with a fluence of 0.75 J/cm2 in the low fluence regime, and with a fluence of 3.0 J/cm2 as a representative for the high fluence regime, all for a pulse duration of 200 fs up to 10 ps. The ablation depth of the ablation structures are measured by confocal microscopy (Fig. 7).

Fig. 7
figure 7

Measured topology of the ablation structure using confocal microscopy for A: a fluence of 3.0J/cm2 and a pulse duration of 200 fs, B: 3.0J/cm2 and a pulse duration of 10 ps, C: 0.75J/cm2 and a pulse duration of 200 fs, D: 0.75J/cm2 and a pulse duration of 10 ps of the laser radiation. The green line in the left image represents the position of the cross-section on the right. The black dashed line in the right represents the moving average of the cross-section

Full size image

Results and Discussion

Simulation Results

In order to investigate the dependence of the ablation depth on the pulse duration, the pulse duration is varied in a range between 200 fs and 10 ps. Furthermore, the ablation threshold tends to be independent on the pulse duration in this range [10]. Furthermore, all other laser parameters of the experiments were used, namely the wavelength of 1030 nm, a peak fluence of H0 of 0.75J/cm2 in the low fluence regime and 3.0J/cm2 in the high fluence regime [5, 10, 63]. In the following, the evolution of the temperature distribution on the material surface and in the material depth z is discussed using a pulse duration of 200 fs and 10 ps exemplary. The temperature distribution as a function of time is presented in Fig. 8 for 200 fs and in Fig. 9 for 10 ps.

Fig. 8
figure 8

Calculated temperature distribution at the irradiated material surface with a pulse duration of 200 fs and a fluence of left: 3.0J/cm2 and right: 0.75J/cm2. The blue line represents the electron temperature and the red line represents the phonon temperature. (The temporal distribution of the intensity is plotted schematically as a black line)

Full size image
Fig. 9
figure 9

Calculated temperature distribution at the irradiated material surface with a pulse duration of 10 ps and a fluence of left: 3.0J/cm2 and right: 0.75J/cm2. The blue line represents the electron temperature and the red line represents the phonon temperature. (The temporal distribution of the intensity is plotted schematically as a black line)

Full size image

The comparison of the temperatures for the two pulse durations at the same fluence demonstrates that a much higher electron temperature is obtained at 200 fs. With longer pulse durations, the intensity of the pulse decreases according to Eq. 8, while the fluence remains constant. As a result, the lower electron temperature is observed for pulse durations in the picosecond regime compared to the pulse durations in the femtosecond regime and the reflectance is still comparatively high (Fig. 4). Furthermore, the time for diffusion and coupling between electrons and the phonon system is much longer for pulses in the picosecond regime than for pulses in the femtosecond regime. Consequently, at a constant fluence, the electron-phonon coupling time τe-ph is shorter for pulses in the femtosecond regime than in the picosecond regime. Using the pulse duration of 200 fs as an example, the coupling time at 0.75J/cm2 equals 3.3 ps and at 3.0J/cm2 6.2 ps (Fig. 8). The phonon temperature can only increase up to Tc,0.9 in the simulation, whereas the electron temperature also increases up to values much higher than Tc,0.9. Additionally, the coupling factor is nearly independent on the electron temperature for high electron temperatures (Fig. 2), and more energy is absorbed by the material applying high fluences compared to a low fluence of the laser radiation. Thus, the coupling time increases for high fluences as the energy transfer from the electron to the phonon system and the phonon temperature are constant, whereas the electron temperature features much higher values.

The electron-phonon coupling time is also the time at which the coupling of the term G(Te − Tph) becomes zero and thus no further energy is transferred from the electron system to the phonon system. After the coupling time, the phonon temperature decreases below 90 % of the thermodynamic critical temperature Tc,0.9 due to heat conduction within the electron system into the material. In conclusion, no material will be ablated after the electron-phonon coupling time in this purely thermodynamic simulation.

Comparison Between the Simulated and the Calculated Ablation Depths

Based on the performed numerical calculations, the ablation depths are extracted from the simulations by determining the deepest position of Tc,0.9 along the z-axis for all time steps. The results are visualized in Fig. 10 and demonstrate, that at shorter pulse durations of the laser radiation, much deeper ablation depths are obtained. The calculated ablation depths in the low fluence regime are in good agreement with the experimentally determined values in this and other studies [5, 10, 13, 52, 63]. However, Fig. 10 illustrates that the experimentally determined ablation depths in the high fluence regime at 3.0 J/cm2 are slightly lower than those of the simulations. The reflectance as a function of the electron temperature was approximated to the values of [25] with a regression function. Since the values of the DFT analysis were only performed up to an electron temperature of 25 × 103K, the regression function can become slightly inaccurate at higher temperature, occurring in the high fluence regime. Furthermore, the reflectance might increase again with increasing electron temperature. Additionally, a strong shock wave is induced in the high fluence regime, which also might influence the ablation depths presented in [10] which were obtained with a wavelength of 515 nm and are slightly higher than those obtained from the performed simulations. Since the reflectance decreases more for smaller wavelengths than for larger wavelengths at high electron temperatures (Fig. 11), more energy is absorbed for λ = 515 nm than for λ = 1030 nm, and thus, a lower ablation threshold is obtained for λ = 515 nm. Another possible explanation for the relatively high difference at 3.0J/cm2 between the experimental and calculated ablation depths is that the shielding of the laser radiation by a possible early plasma formation is not considered.

Fig. 10
figure 10

Calculated ablation depth as a function of the pulse duration at a fluence of 0.75J/cm2 and 3.0J/cm2 compared to experimentally determined ablation depths. The black circles and diamonds are the experimentally determined ablation depths from this study

Full size image
Fig. 11
figure 11

Reflectance R as a function of the electron temperature Te for iron at a wavelength λ = 1030 nm and λ = 400 nm based on [25]

Full size image

Effective Penetration Depths

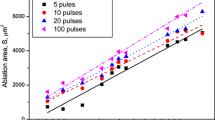
According to the calculated ablation depths from the simulations (Fig. 10), the effective penetration depths for both fluence regimes are calculated using Eqs. 15 and 16, respectively. Analogously to the ablation depth in Fig. 10, ablation of stainless steel using shorter pulse durations of the laser radiation results in a larger effective penetration depth. Furthermore, the effective penetration depth increases with increasing fluence as higher electron temperatures are observed resulting in an increased coupling time (e. g. the observed coupling times in Fig. 8 between 3.0J/cm2 and 0.75J/cm2) as well as in the increased thermal conductivity (Fig. 3). However, as can be seen in Fig. 12, the calculated values fit well to the determined experimental values from this study for 3J/cm2 in the high fluence regime, for 0.75J/cm2 in the low fluence regime, and are comparable to [10, 64].

Fig. 12
figure 12

Calculated effective penetration depth as a function of the pulse duration in comparison to experimental values from this study (black dots) and [10, 64]

Full size image

Conclusions

The evolution of the temperature distribution of the electron- and phonon system of stainless steel heated by ultrafast laser radiation in the femtosecond up to the picosecond regime, has been calculated using the two temperature model. The simulations were performed for a bulk material with a linear absorption of the laser radiation, and temperature-dependent thermophysical parameters, like the coupling factor, the thermal conductivity and the volumetric heat capacity. Furthermore, no laser-induced compressive stresses were taken into account. The ablation criterium was defined as 90 % of the thermodynamic critical temperature of the phonon system, which can be assumed as the phase explosion. With this condition, the ablation depth was extracted from the simulations as a function of the fluence as well as of the pulse duration.

Ablation of stainless steel with pulse durations in the femtosecond regime results in larger ablation depths compared to pulse durations in the picosecond regime, in which the calculated ablation depths fit very well to the experimentally determined ones. Analogously to the calculated ablation depth, a significantly larger effective penetration depth was observed for pulse durations in the femtosecond regime, compared to the picosecond regime, which fits very well with the experimentally determined effective penetration depths.

Finally, a simplified model was presented, which considers no hydrodynamic processes and interaction of the ablated material with the laser radiation, but uses temperature dependent parameters. On the one hand, the simple model enables a calculation in a very short time and is therefore very relevant for industrial applications. On the other hand, the simple model describes the experimental values very well. Therefore, ablation results can be predicted very well without calculating more complex processes like hydrodynamics or thermal stress.