1 Introduction

The interaction of ultra-short pulse lasers in industrial applications has led to the progressive development of high power laser systems in terms of their economy and acceptance in the field of metal processing [1,2,3]. For reasons of efficiency and productivity or for high throughput, high-frequency laser pulses are emitted with time delays of a couple of hundred picoseconds to a few nanoseconds [4,5,6]. In contrast to time delays in the microsecond range or longer, where an unaffected interaction of the individual laser pulses with the metal surface is given [7,8,9,10], the ablation with subsequent laser pulses at time delays in the pico- and nano-second range is affected by the laser-matter interaction of the previous laser pulses.

In general, considering of a stress confinement, the ablation of metals can be separated into two regimes depending on the fluence: thermo-mechanical spallation of a single or multiple layers and explosive disintegration of a superheated surface layer (phase explosion) [11, 12]. The processes of spallation and phase explosion occur on a comparable time scale and are closely related. At fluences close to the ablation threshold, ablation takes place in the spallation regime, leading to a reduction in the size of the melt zone and a sharp drop in the duration of the melting and solidification cycle [13]. At higher fluences, a transition from the spallation to the phase explosion regime occurs, associated with the ablation of a mixture of vapor phase atoms, small clusters, and droplets [13]. This regime also leads to a significant increase in the duration of the melting process and to hydrodynamic motions in the interaction zone [14]. Irrespective of the ablation regime taking place, a melt layer forms on the metal surface and persists up to the nanosecond range [15,16,17,18].

The ablation creates a plasma and an ablation cloud above the interaction zone. In a variety of theoretical and experimental investigations, interaction of subsequent laser pulses with an existing plasma or an ablation cloud has been demonstrated using multiple laser pulses and time delays of up to a few nanoseconds [15, 16, 19,20,21,22,23,24]. This interaction leads to a shielding of the laser radiation of subsequent laser pulses, with the result that only a part of the energy interacts with the metal surface and contributes to the ablation process. The excitation of the formed plasma or ablation cloud by subsequent laser pulses induces an interaction between the plasma and the metal surface as well as a re-deposition of ablated particles. Consequently, the shielding of subsequent laser pulses causes a reduction of ablated material.

During ablation with ultra-short laser pulses, a portion of the absorbed optical energy remains in the irradiated metal, is converted to heat, and dissipates into the metal within a few hundred nanoseconds to a few microseconds [7, 25, 26]. The use of shorter time delays causes subsequent laser pulses to interact with the heated metal surface, resulting in heat accumulation [27]. Studies demonstrate that heat accumulation using multiple laser pulses with time intervals in the nanosecond range increases the amount of material removed [17, 28,29,30,31,32,33].

However, quantitative characterization or differentiation of the presented particle-pulse and plasma-pulse interactions as well as heat accumulation is only feasible by means of complex hydrodynamic or molecular dynamic simulations, whose limitations primarily related to a one-dimensional consideration. An empirical characterization is difficult, due to the simultaneous occurrence of the mechanisms, which influence each other. Therefore, the ablated material and the resulting structures can only be used to determine the ablation characteristics ex situ and to draw conclusions about the dominant mechanism.

In this work, empirical findings for the ablation of stainless steel by means of multiple ultra-short laser pulses with time delays in the pico- and nano-second range are established. The characterization of the ablation is based on ablation structures generated by double and quadruple pulses as a function of the time delay and fluence per laser pulse, which are compared with those generated by single pulses.

2 Experimental setup

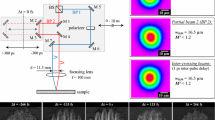
The experiments were performed with a laser system (Fuego®, Time-Bandwidth Products) emitting ultra-short laser pulses with a pulse duration \(\tau _\mathrm{{H}}\) of 10 ps at a wavelength \(\lambda\) of 1064 nm. The pulse energy Q of a laser pulse was split equally into two and four individual laser pulses, using two consecutive Michelson interferometers consisting of silver-coated deflection mirrors, quarter-wave plates and polarization-dependent beam splitters, respectively. A time delay dt of up to 1.2 ns between the laser pulses was obtained using a fixed and a variable optical path length. Verification of the spatial overlap of the laser pulses and the measurement of the beam waist radius \(w_0\) = 14.5  \(\upmu\)m (M\(^2\) < 1.3) of the spatial Gaussian profile was performed using a Primes MicroSpot monitor according to ISO 11146. The irradiation was conducted on a polished stainless steel sample (AISI 304) using geometrically separated single to quadruple pulses with fluences \(H_\textrm{0}\) in the range of up to 8.0 J/cm\(^2\) (single and double pulses) or 4.0 J/cm\(^2\) (quadruple pulses) per pulse. The ablated volume V was measured using laser scanning microscopy (Olympus Lext 3D OLS4100), and the generated ablation structures were imaged using scanning electron microscopy (SEM, Jeol JSM-6512V).

3 Results and discussion

3.1 Single pulse ablation

The results presented in this section for single pulse ablation are intended as a reference and basis for the discussion of the results of double and quadruple pulse ablation in the following sections. The ablated volumes \(V_\mathrm{{SP}}\) presented in Fig. 1 indicate the characteristic increase as a function of the fluence, as already reported in other studies [34,35,36,37,38,39,40,41], and can be categorized into three regimes with respect to the SEM images of the generated structures, shown in Fig. 2.

Fig. 1
figure 1

Ablated volume \(V_\textrm{SP}\) using single pulses as a function of the fluence \(H_\textrm{0}\). The dashed line is used to guide the eye

Full size image
Fig. 2
figure 2

SEM images of the generated structures using single pulses at different fluences \(H_\textrm{0}\)

Full size image

In the investigated parameter range, material was ablated in the spallation regime up to a fluence of 1.0 \({\mathrm{J/cm}}^{2}\), characterized by homogeneous ablation without hydrodynamic motion of the melt and precisely identifiable ablation diameters. Starting from a fluence of 1.5 \({\mathrm{J/cm}}^{2}\), initial inhomogeneities are identifiable in the center of the generated structures as a result of hydrodynamic motion. Due to the spatial Gaussian distribution of the laser radiation, a transition from the spallation to the phase explosion regime in the center of the interaction zone occurred at 1.5 \({\mathrm{J/cm}}^{2}\). In the outer region of the interaction zone, however, spallation remained dominant, as indicated by a homogeneous ablation structure without hydrodynamic motion and a pronounced ablation diameter. This fluence range can therefore be assigned to a mixed ablation regime. Starting from a fluence of 4.0 \({\mathrm{J/cm}}^{2}\), the hydrodynamic motion within the generated structure propagated towards the ablation diameter. The re-solidified melt caused a pronounced inhomogeneity of the resulting topography. Thus, the ablation of one or more layers characteristic for spallation and thus a precise determination of the ablation diameter is no longer possible. In summary, material was ablated by phase explosion starting at 4.0 \({\mathrm{J/cm}}^{2}\). In contrast to this work, where a mixed ablation regime was identified by measuring the ablated volume and performing a lateral analysis of the generated structures, a sharp transition from spallation to phase explosion has been demonstrated in most of experimental studies by measuring the ablation depth in the center of the generated structure [34,35,36] or by rather one-dimensional simulations [12, 37, 42].

A relevant parameter for the industrial application of ultra-short laser pulses is the ablation efficiency \(\eta\), given by

$$\begin{aligned} \eta = \frac{V}{Q}, \end{aligned}$$
(1)

the pulse energy Q

$$\begin{aligned} Q = \frac{H_\textrm{0}\,\pi \,w_\textrm{0}^{\,2}}{2}, \end{aligned}$$
(2)

and the ablated volume V. From the single pulse ablation efficiencies as a function of the fluence \(\eta _\textrm{SP}\), shown in Fig. 3, the highest values were determined to 1.0 \(\upmu {\textrm{m}}^{2}/ \upmu {\textrm{J}}\) at a fluence of 1.0 \({\mathrm{J/cm}}^{2}\) in the spallation regime.

Fig. 3
figure 3

Ablation efficiency \(\eta _\textrm{SP}\) using single pulses as a function of the fluence \(H_\textrm{0}\). The dashed line is used to guide the eye

Full size image

According to an ideal spatial Gaussian distribution, the optimal fluence for maximum ablation efficiency is given by

$$\begin{aligned} H_\textrm{opt} = e^2\,H_\textrm{thr}, \end{aligned}$$
(3)

and scaled with the material-specific ablation threshold \(H_\textrm{thr}\) [43]. For a single pulse ablation threshold of stainless steel in the range of 0.20–0.34 \({\mathrm{J/cm}}^{2}\) [44,45,46], Eq. 3 yields an optimal fluence between 1.5 and 2.5 J/cm\(^2\). The optimal fluence of 1.0 \({\mathrm{J/cm}}^{2}\) determined in this study is slightly lower than the state of the art, and is attributed to different material compositions and surface roughnesses resulting in different absorption properties. Similarly, the values presented in Fig. 3 indicate that the transition from spallation to phase explosion leads to a reduction in the ablation efficiency.

3.2 Double pulse ablation

According to the results of single pulse ablation presented in Sect. 3.1, the range of parameters was extended to double pulses with identical fluences per laser pulse and time delays between the laser pulses of 0.4 ns, 0.6 ns, and 1.2 ns. The discussion and interpretation of the results refer mainly to the ablated volume of the second laser pulse. Therefore, the difference between the total ablated volume of a double pulse \(V_\textrm{DP}\) (Fig. 4) and the ablated volume of a single pulse \(V_\textrm{SP}\) (see Sect. 3.1, Fig. 1) was determined by

$$\begin{aligned} {V_\textrm{2}} = {V_\textrm{DP}} - {V_\textrm{SP}}, \end{aligned}$$
(4)

that, as a result, represents with \(V_2\) the volume ablated by the second laser pulse (Fig. 5).

Fig. 4
figure 4

Ablated volume \(V_\textrm{DP}\) using double pulses as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image
Fig. 5
figure 5

Ablated volume by the second laser pulse \(V_\textrm{2}\) using double pulses as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image

Subsequently, the ratio of \(V_2\) to \(V_1\) (Fig. 6) was calculated, offering the possibility to compare the difference between \(V_2\) and \(V_1\).

Fig. 6
figure 6

Ratio of \(V_\textrm{2}\) to \(V_\textrm{SP}\) as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image

A significant reduction of the ablated volume was determined for \(V_\mathrm{{2}}\) compared to \(V_\mathrm{{1}}\) at a time delay of 0.4 ns. The maximum fluence of 8.0 \({\mathrm{J/cm}}^{2}\) leads to a reduction of almost 100 %, indicating that the second laser pulse ablated almost no volume (Fig. 6). This can be attributed on the one hand to a strong laser pulse-plasma interaction combined with a high shielding of the second laser pulse [47,48,49,50]. As a result, most of the pulse energy of the second laser pulse could not interact with the material surface, but instead transferred its energy to the plasma and leading to a strong plasma excitation [51]. The excited highly-dynamic plasma interacts with the partially melted surface being heated by the first laser pulse. On the other hand, an interaction of the second laser pulse with the ablation cloud generated by the first laser pulse can lead to a re-deposition of ablated particles [19, 52,53,54,55], combined with a momentum transfer [56] to the material surface. Due to these interaction mechanisms, a modified topography can be seen in the SEM images of the double pulse ablations at a time delay of 0.4 ns (Fig. 7, bottom row) compared to a time delay of 10 ms (Fig. 7, top row), where such interactions do not occur. In the case of a time delay of 0.4 ns, a very smooth and homogeneous surface is formed in the center of the interaction zone, and a two-ring structure is observed in the outer area. A possible explanation is hereby that the excitation of the existing plasma or the momentum transfer of re-deposited particles by the second laser pulse induced a pressure wave, causing the molten material to be rotationally symmetrically pushed outward, and the inner ring is a representation of the border of ejected melt. However, the outer ring, as illustrated in the SEM images, may be caused by the interaction of the second laser pulse itself with the material surface that was excited or melted by the first laser pulse, combined with heat accumulation.

Fig. 7
figure 7

SEM images of the generated structures using double pulses with different fluences \(H_\textrm{0}\) and time delays dt between the laser pulses

Full size image

The ablated volume of the second laser pulse increases with increasing time delay between the laser pulses in the investigated fluence range, which can be attributed to a reduction of the plasma shielding due to a temporally decreasing plasma density or to a reduced re-deposition of ablated particles due to the ongoing propagation. Consequently, the dimensions of the inner ring decreased at 0.6 ns and 1.2 ns compared to 0.4 ns, which is particularly noticeable at a fluence of 0.5 \({\mathrm{J/cm}}^{2}\) (Fig. 7). Furthermore, at higher fluences, the reduced plasma pressure or momentum transfer at larger time delays is no longer sufficient to smooth the molten material in the center of the generated structures, resulting in a fluctuating topography of re-solidified melt in the center of the interaction zone.

In the fluence range of 0.5 – 2.0 \({\mathrm{J/cm}}^{2}\) and a time delay of 1.2 ns or 1.0 – 1.5 \({\mathrm{J/cm}}^{2}\) and 0.6 ns, more material was removed by the second laser pulse compared to the single pulse (Fig. 6). The increase of \(V_\mathrm{{2}}\) can be attributed to an accumulation of heat [57], or to altered thermophysical and optical properties during the interaction of the second laser pulse with excited or molten material. This counteracts the reduction of the ablated volume due to the described interaction process with the plasma or the ablation cloud of the second laser pulse.

Analogous to the single pulse ablation efficiency \(\eta _\textrm{SP}\), the double pulse ablation efficiency \(\eta _\textrm{DP}\) was determined by

$$\begin{aligned} \eta _\mathrm{{DP}}=\frac{V_\mathrm{{DP}}}{2\,Q}, \end{aligned}$$
(5)

and visualized in Fig. 8.

Fig. 8
figure 8

Ablation efficiency \(\eta _\textrm{DP}\) using double pulses as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image

Whereas in the range of high fluences from 3.0 \({\mathrm{J/cm}}^{2}\) or at a time delay of 0.4 ns the ablation efficiency with double pulses decreased compared to ablation with single pulses, the ablation efficiency increased at 0.6 ns to 1.2 ns and 0.75 \({\mathrm{J/cm}}^{2}\) as well as 1.5 \({\mathrm{J/cm}}^{2}\).

The highest ablation efficiencies of 1.15 \(\upmu {\textrm{m}}^{2}/ \upmu {\textrm{J}}\) were obtained using double pulses at a fluence of 1.0 \({\mathrm{J/cm}}^{2}\) and a time delay of 0.6 ns and 1.2 ns, which is approximately 15 % higher than the maximum ablation efficiency using single pulses.

3.3 Quadruple pulse ablation

Based on the results of single and double pulse ablation, the parameter range was extended to quadruple pulses with the same time delays, but limiting the fluence to a maximum of 4.0 \({\mathrm{J/cm}}^{2}\) per laser pulse. The volume \(V_\mathrm{3+4}\) (Fig. 10), given by

$$\begin{aligned} {V_\mathrm{3+4}} = {V_\textrm{QP}} - {V_\textrm{DP}}, \end{aligned}$$
(6)

describes the amount of ablated volume of the third and fourth laser pulse, resulting from the difference of the total ablated volume of the quadruple pulses \(V_\textrm{QP}\) (Fig. 9) and the double pulses \(V_\textrm{DP}\) (Fig. 4). The following discussions and interpretations of the effects already mentioned in section 3.2, and the associated increase or decrease of the ablated volume in comparison to an unaffected ablation were performed using the ratio of \(V_\mathrm{3+4}\) to \(2\,V_\textrm{SP}\), as visualized in Fig. 11.

Fig. 9
figure 9

Ablated volume \(V_\textrm{QP}\) using quadruple pulses as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image
Fig. 10
figure 10

Ablated volume by the third and fourth laser pulse \(V_\mathrm{3+4}\) using quadruple pulses as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image
Fig. 11
figure 11

Ratio of \(V_\mathrm{3+4}\) to \(2\,V_\textrm{SP}\) as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image

The comparison of the ratios of \(V_\mathrm{3+4}\,/\,2\,V_\textrm{SP}\) (Fig. 11) with \(V_\textrm{2}\,/\,V_{\text {SP}}\) (Fig. 6 in Sect. 3.2) at a time delay of 0.4 ns demonstrates that the significant reduction of the ablated volume using double pulses due to shielding mechanisms is not found in the measurement results of the ablated volumes of the third and fourth laser pulses. Comparably low values were only determined at a fluence of 0.5 \({\mathrm{J/cm}}^{2}\). At higher fluences, the third and fourth laser pulses generally ablated the same volume as two separate laser pulses. Compared to \(2\,V_\textrm{SP}\), at time delays of 0.6 ns and 1.2 ns, an increased amount of ablated volume was determined for \(V_\mathrm{3+4}\), especially at low fluences, which decreased slightly at higher fluences. The interaction of quadruple pulses, in particular the mechanisms of the third and fourth laser pulse with an existing plasma, an ablation cloud or heated material, has not yet been fundamentally investigated. The interpretations in this study, based on the values visualized in Fig. 11, are primarily related to the state of the art for double pulse ablation:

  • In general, with time delays in the picosecond range, the interaction of a subsequent laser pulse with the plasma generated by the first laser pulse, can significantly extend the plasma lifetime [50, 58, 59] and thus lead to plasma shielding of the third laser pulse, resulting in a reduction of the ablated volume.

  • The second laser pulse reduces the density of the ablation cloud generated by the first laser pulse, due to the re-deposition of ablated particles, which reduces the particle shielding effect in addition to the re-deposition of particles of the third laser pulse. Compared to the second laser pulse, more material can be ablated.

  • Due to the heat accumulation, the third laser pulse could additionally use the remaining energy of the previous laser pulses for ablation of the material surface, thus increasing the ablated volume.

  • The increased ablation from the third laser pulse again induces a plasma and an ablation cloud, leading to a high shielding effect of the fourth laser pulse.

  • The absorption of the first three laser pulses results in a high accumulation of heat or deposited energy in the interaction zone, which leads to a significant increase in the ablated volume by the fourth pulse. Thus counteracts the reduction due to the shielding effects.

In the case of a time delay of 0.4 ns, \(V_\mathrm{3+4}\) is almost identical to \(2\,V_\textrm{SP}\), which leads to the conclusion that the reduction due to shielding or re-deposition, and the increase of the ablated volume due to heat accumulation compensate each other in the investigated fluence range. For the time intervals of 0.6 ns and 1.2 ns, the significant increase of \(V_\mathrm{3+4}\) to \(2\,V_\textrm{SP}\) at low fluences can be explained by the assumption that, compared to 0.4 ns, the longer time between the individual laser pulses leads to a considerable reduction of the density of the plasma or the ablation cloud, thus also reducing the shielding effects and mainly inducing an increased ablation by absorption and following heat accumulation. The use of higher fluences causes a denser plasma and a denser ablation cloud, therefore the shielding effect increases at 0.6 ns and 1.2 ns and consequently \(V_\mathrm{3+4}\) decreases again.

The topographies of the structures generated by quadruple pulses, as visualized in Fig. 12, illustrates an increased re-solidified amount of molten material, due to a higher hydrodynamic movement, compared to those of double pulses. This supports the assumption that the use of quadruple pulses results in a significantly higher heat accumulation compared to double pulses, which in turn leads to a further heating of the material surface and thus to an increase in the melt pool volume. Especially at low fluences, an increased number of ring structures can be identified. Since in this study the area of the rings corresponds to the amount of melt expulsion, and the number of rings equals to the number of laser pulses, the higher number of ring structures compared to double pulses can be interpreted as evidence of further plasma pressure waves or momentum transfer by re-deposition of ablated particles by the third and fourth laser pulse.

Fig. 12
figure 12

SEM images of the generated structures using quadruple pulses with different fluences \(H_\textrm{0}\) and time delays dt between the laser pulses

Full size image

In comparison to using single pulses (Fig. 3) and double pulses (Fig. 8), the increased ablated volume of the third and fourth laser pulse results in a higher ablation efficiency quadruple pulses \(\eta _\textrm{QP}\) (Fig. 13), given by

$$\begin{aligned} \eta _\textrm{QP}=\frac{V_\textrm{QP}}{4\,Q}. \end{aligned}$$
(7)

The highest efficiency of this study was achieved with 1.66 \(\upmu {\textrm{m}}^{2}/ \upmu {\textrm{J}}\) at a fluence of 0.5 \({\mathrm{J/cm}}^{2}\) and a time delay of 1.2 ns. This corresponds to an increase of 70% compared to single pulses and 48% to double pulses.

Fig. 13
figure 13

Ablation efficiency \(\eta _\textrm{QP}\) using quadruple pulses as a function of the fluence \(H_\textrm{0}\) for different time delays dt between the laser pulses. The dashed lines are used to guide the eye

Full size image

4 Summary and outlook

The dependence of the ablated volume and the ablation efficiency on the fluence per laser pulse and on the time delay between each laser pulse was investigated by ablating stainless steel (AISI 304) using ultra-short single, double and quadruple pulses with a pulse duration of 10 ps and an emitting wavelength of 1064 nm.

Compared to single pulse ablation, where the ablation volume increased continuously with increasing fluence per laser pulse, a significant change in the obtainable ablation volume as a function of fluence was determined in combination with the time delay of the laser pulses using double pulses. The shortest investigated time delay, 0.4 ns, resulted in less to nearly zero ablation of material in the investigated fluence range of up to 8.0 J/cm\(^2\) by the second laser pulse compared to the first laser pulse due to shielding mechanisms. In the fluence range of 1.0 J/cm\(^2\) to approximately 2.0 J/cm\(^2\), increasing the time delay to 0.6 ns and 1.2 ns caused the second laser pulse to ablate more material than a single pulse. Therefore, in this parameter range, it was suggested that the increase in the ablation volume due to heat accumulation was more pronounced than the decrease in the ablation volume due to shielding mechanisms. In general, based on a qualitative analysis of the solidified melt in the investigated parameter range, double pulse ablation demonstrated significantly higher melt dynamics compared to single pulse ablation, resulting in ring-shaped structures at the edges and, for a time range of 0.4 ns and 0.6 ns, a very smooth surface in the center of the generated structures. The physical mechanism for the expulsion of the melt and the smoothing of the material surface was assumed to be the interaction of the second laser pulse with an existing ablation cloud or plasma and the subsequent momentum transfer of redeposited particles or plasma pressure, since the expulsion of the melt and the smoothing decrease with a further increase of the time interval to 1.2 ns.

The discussion of the results using quadruple pulses was mainly based on the measured volume ablated by the third and fourth laser pulses compared to two single pulses. A differentiation in the interaction of the third and fourth laser pulses and a separate interpretation could not be realized. Compared to the results for double pulses, more material was ablated at a time interval of 0.4 ns with the third and fourth laser pulses compared to the second laser pulse. The reduced influence of shielding mechanisms was interpreted with a higher heat accumulation using four laser pulses. This correlation between heat accumulation and shielding is particularly evident at the 0.6 ns and 1.2 ns time delays, where the third and fourth laser pulses ablate significantly more material in the investigated fluence range of up to 4.0 J/cm\(^2\) compared to two individual pulses. Overall, the maximum obtainable ablation efficiency in the investigated parameter range was increased by up to 70 % using quadruple pulses compared to single pulses. Based on the topography of the generated structures, a significantly higher hydrodynamic motion was observed compared to double pulses, possibly due to a more pronounced heat accumulation followed by a higher amount of melt.

Based on the ex-situ investigations and the associated findings, parameter variations were identified where physical processes, such as heat accumulation or the shielding from the pulse energy of subsequent laser pulses are particularly pronounced. However, fundamental explanations for the influence of the individual physical processes on the ablation process were, however, only suggested in initial approaches. Drawing on the findings of this work, subsequent studies will focus on two fundamental topics. The laser-matter interaction of an ultra-short laser pulse with stainless steel, the interaction of subsequent laser pulses with an existing ablation cloud, and the melt dynamics during and after the interaction time will be investigated by means of hydrodynamic simulations, where the lateral resolution corresponds to the entire interaction zone. Similarly, pump/probe experiments are expected to provide insights into the density and geometric as well as temporal propagation of ablated particles as a function of the parameter variations induced in this work.