1 Introduction

Energy consumption, production, and supply have attracted the attention of governments, researchers, and companies because of their critical roles in livelihoods, urbanization, technological progress, and global economic development [1,2,3]. Due to environmental and economic considerations, there has been an increasing tendency to integrate sustainable energy sources into electricity grids [4]. However, using wind turbines (WTs) and photovoltaics (PVs) leads to unpredictable fluctuations in power output and voltage levels in distribution systems. As a result, more regulatory measures must be implemented to address these issues [5, 6]. By integrating inverters into the control devices of power system operators, an expedient and efficient control method can be achieved, which complements the conventional control devices [7]. This is possible because inverters could mitigate switching losses and uphold a balanced voltage profile within the distribution system [8, 9].

Multilevel inverters (MLIs) have gained significant popularity as power electronics devices in high-power applications and mid-voltage, surpassing traditional two-level inverters. Their widespread adoption can be attributed to several advantages they offer over their counterparts. MLIs provide improved voltage waveforms with reduced harmonic distortion, enhancing power quality and efficiency [10].

Based on their respective topologies, MLIs can be segregated into three unique categories: cascaded H-bridge inverters, flying capacitors, and diode clamped [11]. MLIs comprise several circuit elements, including DC power sources, semiconductors, and switches, primarily designed to produce an AC voltage. The utility of MLIs extends beyond PV and WT systems, encompassing various other applications. A detailed overview of the different MLI techniques that are well-suited for electric vehicles is presented by Poorfakhraei et al. [12]. Another application domain where MLIs find relevance is in uninterruptible power supply (UPS) systems [13]. MLIs have been extensively employed in various power system applications, particularly high-voltage direct-current (HVDC) techniques [14, 15]. Additionally, MLIs are widely utilized in power quality devices, including flexible AC transmission systems (FACTS) that play a crucial role in improving the stability, controllability, and reliability of power transmission systems [16, 17], static compensators (STATCOMs) [18, 19], dynamic voltage restorers (DVRs) [20, 21], and active filters (Afs) [22, 23].

However, this technology faces a challenge in the form of harmonic problems, which can have detrimental effects on the power system. The presence of harmonics is primarily responsible for the malfunction, amplification of loss, and voltage ripple. Additionally, the manifestation of harmonics has a discernible effect on the overall power quality [24].

Various switching methodologies are employed to effectively manage the output voltage and frequency of MLIs. These techniques are crucial in ensuring precise control and efficient operation of the inverters. Some commonly used switching methodologies include pulse width modulation (PWM), selective harmonic elimination (SHE), and space vector modulation (SVM) [25]. Twenty-two metaheuristic algorithms, each drawing inspiration from different sources, were employed to address the SHE problem across various MLIs. Initially, these algorithms were tested on an 11-level MLI circuit, and after extensive performance analysis, six approaches were identified as the most promising solutions [26].

Achieving the optimal calculation of the switching angle in MLIs aids in minimizing the overall THD. The methods for addressing this problem can be classified into two categories: analytical methods and numerical approaches. The numerical approach, specifically the Newton–Raphson (NR) method, has been employed in various applications related to MLIs. This includes minimizing harmonics in cascade MLIs [27] and solving SHE for a recently designed flying capacitor MLI [28]. Despite the presence of alternative controls and modulation techniques, it is noteworthy that the SHE technique serves as the principal modulation approach that resolves the previously mentioned issues [29]. An asymmetric MLI topology designed for PV applications, requiring fewer DC sources and switches, was introduced by Kumar et al. [30]. The inverter’s control is based on selective harmonic elimination-based pulse width modulation (SHEPWM), aimed at eliminating the predominant lower-order harmonics. The nonlinear equations generated by SHEPWM are resolved to determine the proposed inverter’s switching angles using the NR and PSO methods across various MI. The THD achieved with the NR method stands at 7.3%, while the PSO method results in a THD of 4.23% at an MI of 0.9.

Metaheuristic methods are frequently used in the literature to solve many problems [31, 32]. In metaheuristic techniques, solving SHE equations is a common task performed by applying optimization algorithms inspired by natural phenomena. These algorithms, include the GA [33, 34], PSO [35,36,37], whale optimization technique (WOA) [38, 39], enhanced krill herd (EKH) [40], the moth flame optimization [41] algorithm was implemented in [42], and salp swarm optimization algorithm [43], were also employed to solve the problem of harmonic elimination of MLIs [44].

[45] employed ant colony optimization (ACO) to determine the results of an optimization strategy to achieve a precise harmonic reduction within cascaded MLIs. To compare the performance of this approach, assessed it against various other optimization algorithms, including the recently introduced universe-influenced algorithm (CBO), as well as GA, harmonic search algorithm (HS), artificially developed bee colony algorithm (ABC), PSO, imperialized competitive algorithm (ICA), and ACO. To effectively differentiate between these methods, the impact of the optimal DC method was considered while considering 3-level, 7-level, and 15-level inverters.

Sajid et al. [46] employed the Runge–Kutta (RUN) metaheuristic optimization algorithm to illustrate the SHE-PWM technique in MLIs, specifically focusing on 5-level and 7-level modified H-bridge (MHB) topologies and a 9-level asymmetric cascaded H-bridge (CHB) inverter topology. To establish the superiority of the RUN algorithm, a comparative analysis was conducted against well-established metaheuristic algorithms like differential evolution (DE), GA, and Grey Wolf Optimizer (GWO). The results from simulations and experiments indicated that the proposed RUN method outperforms the other algorithms in terms of objective function values, algorithm robustness, fundamental harmonic magnitude, and THD values. Furthermore, the outcomes demonstrated the effective elimination of the fifth harmonic in 5-level MLIs, the fifth and seventh harmonics in 7-level MLIs, and the fifth, seventh, and ninth harmonics in 9-level MLIs.

Researchers are turning to newly developed optimization algorithms to find faster and more suitable solutions to solve the SHE-PWM problem. The recently developed algorithms GRO [47] and DO [48] were examined in this context. DO algorithm has demonstrated significant performance when compared to other algorithms. Moreover, it has been observed that the algorithm operates within acceptable limits [48]. Twenty-nine benchmarking problems were utilized to evaluate the GRO algorithm. The proposed algorithm was compared against twelve popular metaheuristic algorithms: SMA, KMA, WOA, WCA, SSA, SCA, PSO, IGWO, GSA, DE, FA, and GA. The results revealed that the proposed algorithm could generate high-quality solutions comparable to those obtained by other algorithms. It demonstrated the capability to overcome local optima and achieve global optima with a higher convergence rate than most algorithms examined [47].

In this study, the performance of traditional methods frequently used in the literature, such as PSO and GA, and current optimization methods, such as GRO and DO, were compared to solve the SHE-PWM problem. The fact that these optimization algorithms have not been used for SHE-PWM equations before and that the optimization algorithms presented by the authors proved more efficient than other algorithms in standard test functions were effective in choosing these two new algorithms. This paper improves on recent attempts to solve SHE problems more precisely and

  • Recommends current and effective optimization algorithm models that aim to eliminate harmonics and THD. DO and GRO are two new optimization algorithms developed recently and were applied for the first time in solving SHE-PWM equations.

  • The present study employs a contemporary GRO and DO, encompassing a disordered mapping function for the control parameter (θ) and an adaptable reset mechanism with a localized exploration technique. The performance of GRO and DO are compared with standard PSO, GA to solve SHE problems. GRO and DO are more effective in solving the problem.

  • Compares the simulation results of 11-level MLIs with different modulation indexes (MI) in terms of numerical accuracy.

  • In multilevel inverters, it determines the optimal switching angles for SHE-PWM and utilizes GA, PSO, DO, and GRO algorithms to achieve the optimum THD value. Forecasting performances of GA, PSO, DO, and GRO were demonstrated with various numerical data.

The paper's structure is outlined as follows: The following section explains cascaded H-bridge multilevel inverters. Section 3 gives details about the heuristic optimization technique. Section 4 shows the test and results of optimization techniques and MATLAB/Simulink results. Section 5 presents some information about the conclusion and future work.

2 Cascaded H-bridge Multilevel Inverters

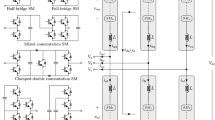
Figure 1a shows the general structure of an L-level cascade H-bridge multilevel inverter (CHB-MLI). An equal-value DC power supply is connected to each bridge. It transmits three different voltage levels (+ Vdc, 0, and − Vdc) to the output with different combinations of S11, S12, S13, and S14 switches on each h-bridge. The L-level CHB-MLI step output waveform is given in Fig. 1b.

Fig. 1
figure 1

Single-phase L-level CHB-MLI a circuit structure b output voltage waveform

Full size image

To represent the number of sources s, L = 2xs − 1 step waveforms can be obtained. The Fourier transform of the step waveform is given in Eq. (1).

$$V(\omega t) = \frac{{4V_{{{\text{dc}}}} }}{\pi }\mathop \sum \limits_{n} \left[ {\cos \left( {n\theta_{1} } \right) + \cos \left( {n\theta_{2} } \right) + \cdots + \cos \left( {n\theta_{s} } \right)} \right]\sin \left( {\frac{n\omega t}{n}} \right),\quad n = 1,3,5,7, \cdots$$
(1)

Here, ω and VDC respectively represent angular velocity and the amplitude of the DC input voltage source. θ1, θ2, …, θs represent the switching angles. Due to quarter-wave symmetry, switching angles 0 ≤ θ1 < θ2 < ,… < θs-1 < θs ≤ π/2 must satisfy the restriction condition. Equation (1) can be expressed more simply as follows.

$$V(n) = \frac{4}{n\pi }\mathop \sum \limits_{n} \left[ {\cos \left( {n\theta_{1} } \right) + \cos \left( {n\theta_{2} } \right) + \cdots + \cos \left( {n\theta_{{{\text{s}} - 1}} } \right) + \cos \left( {n\theta_{{\text{s}}} } \right)} \right], \, n = 1,3,5,7, \cdots$$
(2)

THD can be calculated as the ratio of the sum of the squares of the harmonics to the fundamental harmonic as given in Eq. (3).

$$\% {\text{THD}} = \frac{{\sqrt {\sum\nolimits_{n = 3,5,7,...}^{n = 49} {V_{n}^{2} } } }}{{\left| {V_{1} } \right|}}$$
(3)

The %THD value includes low-order harmonics but does not explain how much they affect. Therefore, the THD value is defined as the ratio of the square root of the sum of the amplitudes of the selected harmonics to the amplitude of the fundamental harmonic. The limit value is the selected maximum harmonic value. Third and multiples of three harmonics are not present in the system. Therefore, the THDe value for 11-level three-phase CHB-MLI can be calculated as given in Eq. (4), without considering the third and multiples of three harmonics.

$$\% {\text{THD}}_{e} = \frac{{\sqrt {V_{5}^{2} + V_{7}^{2} + V_{11}^{2} + V_{13}^{2} } }}{{\left| {V_{1} } \right|}}$$
(4)

The optimization aims to find the switching angles that will eliminate the selected low-order harmonics and keep the fundamental harmonic at the desired value. For an 11-level inverter, five switching angles need to be determined. The harmonic equations for the 11-level step waveform are given in Eq. (5).

$$\begin{aligned} V(1) & = \cos \left( {\theta_{1} } \right) + \cos \left( {\theta_{2} } \right) + \cos \left( {\theta_{3} } \right) + \, \cos \left( {\theta_{4} } \right) + \cos \left( {\theta_{5} } \right) = 5Mk{\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0pt} 4} \\ V(5) & = \cos \left( {5\theta_{1} } \right) + \cos \left( {5\theta_{2} } \right) + \cos \left( {5\theta_{3} } \right) + \cos \left( {5\theta_{4} } \right) + \cos \left( {5\theta_{5} } \right) \\ V(7) & = \cos \left( {7\theta_{1} } \right) + \cos \left( {7\theta_{2} } \right) + \cos \left( {7\theta_{3} } \right) + \cos \left( {7\theta_{4} } \right) + \cos \left( {7\theta_{5} } \right) \\ V(11) & = \cos \left( {11\theta_{1} } \right) + \cos \left( {11\theta_{2} } \right) + \cos \left( {11\theta_{3} } \right) + \cos \left( {11\theta_{4} } \right) + \cos \left( {11\theta_{5} } \right) \\ V(13) & = \cos \left( {13\theta_{1} } \right) + \cos \left( {13\theta_{2} } \right) + \cos \left( {13\theta_{3} } \right) + \cos \left( {13\theta_{4} } \right) + \cos \left( {13\theta_{5} } \right) \\ \end{aligned}$$
(5)

The first of the harmonic equations given in Eq. (5) is used to control the fundamental harmonic. Other remaining harmonics are used to eliminate the selected harmonics or to keep them minimal. The M given in the equation represents the MI. M, V1p is calculated as the ratio of the peak value of the desired base voltage to the total DC source value as given in Eq. (6).

$$M = \frac{{V_{{\text{1(peak)}}} }}{{sV_{{{\text{DC}}}} }}$$
(6)

Optimization problems are evaluated according to the fitness function (FF). The FF for SHE-PWM is given in Eq. (7).

$$FF = \mathop {\min }\limits_{{\theta_{i} }} \left\{ {\left| {V_{ref} - V_{1p} } \right| + \left( {V_{5} } \right)^{2} + \left( {V_{7} } \right)^{2} + \left( {V_{11} } \right)^{2} + \left( {V_{13} } \right)^{2} } \right\} = 0$$
(7)

3 Metaheuristic Techniques

This section explains the heuristics used for the SHE optimization problem. The DO and GRO algorithms are briefly described in the first subsection, and their step-by-step application to the SHE optimization problem is detailed. Following this, the GA and PSO techniques are elaborated upon in the subsequent sections. The SHE minimization problem is examined by implementing these techniques, where algorithms and flowcharts are provided to facilitate a comprehensive comprehension.

3.1 Dandelion Optimizer Algorithm

Heuristics methods are behaviours from natural processes. DO is a next-generation nature-inspired optimization algorithm that uses swarm intelligence to tackle continuous optimization problems. DO was developed with inspiration from the wind-blown behaviour of the dandelion plant. Seeds travel in three stages: ascending, descending, and settling in a random location during the landing stage. As shown in Fig. 2a, the pieces that break off from the plant start to fly, and they spin and fly away, as shown in Fig. 2b. The DO algorithm represents these three stages with mathematical models and seeks optimal solutions by mimicking these behaviours. This algorithm has been validated and tested according to CEC2017 international standard benchmark functions [48].

Fig. 2
figure 2

Spreading behaviour of the dandelion plant

Full size image

The mathematical steps of the DO algorithm are briefly as follows:

  1. 1.

    Initial Population A population of random starting points is created.

    $${\text{Population}} = \left[ {\begin{array}{*{20}c} {D_{1}^{1} } & \ldots & {D_{1}^{{\text{Dim }}} } \\ \vdots & \ddots & \vdots \\ {D_{{\text{pop }}}^{1} } & \ldots & {D_{{\text{pop }}}^{{\text{Dim }}} } \\ \end{array} } \right]$$
    (8)

    Here, pop denotes the population size and Dim the size of the variable. Each candidate solution is randomly generated between the upper limit (UB) and the lower limit (LB) of the given problem. The i individual Di is expressed as follows. The expression "rand" represents a function whose values are randomly distributed among [0, 1].

    $$D_{i} = {\text{rand}} \times \left( {U_{B} - L_{B} } \right) + L_{B}$$
    (9)
  2. 2.

    Calculation of Fitness Values The fitness function values of the problem to be optimized for each individual are calculated. The individual with the best fitness value is considered elite. The initial elite candidate solution can be mathematically expressed as:

    $$D_{{{\text{elite}}}} = D\left( {{\text{find}}\left( {f_{{{\text{best}}}} = f\left( {D_{i} } \right)} \right)} \right)$$
    (10)
  3. 3.

    Ascension Stage The new positions of individuals are determined using the fitness function values and moved upwards. With the effect of parameters such as wind speed and air humidity, chamomile seeds rise to different heights. Here, the weather is divided into the following two states.

Case 1 On a clear day, wind speeds can be assumed to be lognormal distribution lnY ∼ N(μ, σ2). The new position of the seeds is calculated as given in Eq. (11).

$$D_{(t + 1)} = D_{t} + \delta \times v_{x} \times v_{y} \times \ln Y \times \left( {D_{s} - D_{t} } \right)$$
(11)

Here Dt represents the position of the dandelion seed in the t th iteration. Ds represents the randomly chosen location in the search area in the t th iteration, vx and vy represent the lift component coefficients due to the separate hose motion of the dandelion. δ is a coefficient between 0 and 1 that decreases nonlinearly and approaches zero.

The lognormal distribution given in Eq. (11) is defined as µ = 0 and σ2 = 1 and can be expressed by the following equation [48]:

$$\ln Y = \left\{ {\begin{array}{*{20}c} {\frac{1}{{y\sqrt {2\pi } }}\exp \left[ { - \frac{1}{{2\sigma^{2} }}(\ln y)^{2} } \right]} & {y \ge 0} \\ 0 & {y < 0} \\ \end{array} } \right.$$
(12)

In the DO algorithm, the y value is chosen in the range (0, 1) according to the standard normal distribution. At each iteration of the algorithm, an adaptive factor 'γ' is used to control the length of the search process over the total number of iterations T. γ is defined as:

$$\gamma = {\text{rand}} * \left( {\frac{1}{{T^{2} }}t^{2} - \frac{2}{T}t + 1} \right)$$
(13)

Case 2 During a day marked by rainfall, the rise of dandelion seeds is hindered by air resistance, humidity, and a range of other factors. As a result, these seeds tend to stay close to their original location, and their behaviour can be precisely described using a mathematical equation:

$$D_{(t + 1)} = D_{t} \times (1 - {\text{rand}} \times p)$$
(14)

p is a parameter used to regulate the local search area of dandelion and is calculated as given in Eq. (15). Its value is updated at each iteration, depending on the maximum iteration and the number of iterations available.

$$p = \left( {\frac{{t^{2} - 2t + 1}}{{T^{2} - 2T + 1}} + 1} \right)$$
(15)

Here, t represents the value of the number of iterations available, and T represents the maximum number of iterations.

  1. 4.

    Descent Phase: Individuals fall at the height determined during the Ascension phase, and their position is updated.

    $$D_{t + 1} = D_{t} - \alpha \times \beta_{t} \times \left( {D_{{{\text{mean\_t}}}} - \alpha \times \beta_{t} \times D_{t} } \right)$$
    (16)

    Here, βt represents the Brownian motion and a random number drawn from the standard normal distribution [49]. Dmean_t represents the mean position of the population in the i th iteration.

  2. 5.

    Landing Location Determination Seeds settle in a random location because of wind and weather conditions in their new location. With the evolution of the population, the global best solution is expressed by Eq. (17).

    $$D_{t + 1} = D_{{\text{elite }}} + {\text{levy}}(\lambda ) \times \alpha \times \left( {D_{{\text{elite }}} - D_{t} \times \sigma } \right)$$
    (17)

    Here, Delite is the best (optimal) position of the dandelion seed during the ith iteration. levy(λ) represents the function of Levy flight and is calculated by the following equation [50]:

    $${\text{levy}}(\lambda ) = s \times \frac{w \times \sigma }{{|t|^{\frac{1}{B}} }}$$
    (18)

    where B is randomly defined in [0, 2]. S is a constant equal to 0.01. It is randomly chosen between ω and t [0, 1]. σ is calculated as [50]:

    $$\sigma = \left( {\frac{{{\Gamma }(1 + B) \times \sin \left( {\frac{\pi B}{2}} \right)}}{{{\Gamma }\left( {\frac{1 + B}{2}} \right) \times B \times 2^{{\left( {\frac{B + 1}{2}} \right)}} }}} \right)$$
    (19)
  3. 6.

    Repopulation A new population is created with the recent locations obtained.

  4. 7.

    Stopping Criteria Steps 2–7 are repeated until the stopping criterion is reached.

  5. 8.

    Best value The point with the best fitness value is considered the optimal solution.

3.2 Implementation of DO to MLI SHE-PWM Optimization Problem

To apply the DO approach to the 11-level CHB-MLI SHE-PWM optimization problem, the following procedure should be applied:

  1. 1.

    First, an initial population of size Ns is created. A random position, represented by five switching angles, is then assigned to each dandelion seed. Switching angles 0 ≤ θ1 < θ2 < ,…, < θs ≤ π/2 must satisfy the constraint.

  2. 2.

    Each dandelion seed is evaluated according to the fitness function given in Eq. (7). The population is then ranked according to the numerical results of their evaluation.

  3. 3.

    The best individual is assigned as Delite.

  4. 4.

    The ascension procedure is applied according to the determined weather conditions. (Eq. 11 or Eq. 14).

  5. 5.

    The landing procedure is performed, and the location of the Delite best dandelion seed is updated.

  6. 6.

    The global best position is the landing position (Eq. 17).

  7. 7.

    Repeat steps 2–7 until the stopping condition is satisfied (maximum iteration).

  8. 8.

    The best D(i+1) found represents the dandelion seed with the best fitness value and solves the problem.

The flowchart of the application of the DO algorithm to the optimization problem in 11-level 3-phase CHB-MLI is given in Fig. 3.

Fig. 3
figure 3

DO flowchart for SHE-PWM

Full size image

3.3 Gold Rush Optimizer Algorithm

GRO is a metaheuristic optimization algorithm inspired by the movements of natural gold prospectors. This algorithm solves various optimization problems based on their exploration and prospecting capabilities by mimicking the movements of gold prospectors. The GRO algorithm is based on five primary stages: The movements of gold prospectors: Exploration, Core Formation, Main Core, Dispersion, and Final Decision Stage. Each step generates new solution candidates by combining existing solutions with research and discovery capabilities and tries to find the best solution among these candidates. The GRO algorithm can successfully solve various engineering problems [47].

The mathematical steps of the GRO algorithm are briefly as follows:

3.3.1 Gold Prospectors Modelling

The GRO algorithm mimics gold rush fundamental events. In the GRO metaheuristic approach, the function of the seekers is analogous to that of the population in the GA and the particles in the PSO. The location of the gold prospectors is stored in a matrix called GGP, expressed in Eq. (20). In this equation, Gij represents the position of the ith seeker in the jth dimension. d represents dimension, and n represents gold prospector [47].

$$G_{GP} = \left[ {\begin{array}{*{20}c} {G_{11} } & {G_{12} } & \ldots & {G_{1d} } \\ {G_{21} } & {G_{22} } & \ldots & {G_{2d} } \\ \vdots & \vdots & \ddots & \vdots \\ {G_{n1} } & {G_{n2} } & \ldots & {G_{nd} } \\ \end{array} } \right]$$
(20)

An objective function is required to evaluate the gold prospectors and the results of the evaluation of the fitness function of the gold prospectors are recorded in the FGP matrix given in Eq. (21). Gij represents the position of the i-th seeker in the j-th dimension. While d represents the dimension, n represents the gold prospector, and f represents the fitness function [47].

$$F_{{{\text{GP}}}} = \left[ {\begin{array}{*{20}c} {f\left( {G_{11} } \right.} & {G_{12} } & \ldots & {\left. {G_{1d} } \right)} \\ {f\left( {G_{21} } \right.} & {G_{22} } & \ldots & {\left. {G_{2d} } \right)} \\ \vdots & \vdots & \ddots & \vdots \\ {f\left( {G_{n1} } \right.} & {G_{n2} } & \ldots & {\left. {G_{{{\text{nd}}}} } \right)} \\ \end{array} } \right]$$
(21)

3.3.2 Migration of Prospectors

Upon discovering a gold mine, individuals keen on gold prospecting relocate to the area to extract gold. During the execution of the metaheuristic algorithm, the optimal point within the search space is determined to represent the location of the most profitable gold mine. As the exact location of this mine remains unknown, the position of the most successful gold prospector is utilized as an approximation for the optimal mine location, as depicted in Fig. 4. The migration of a gold prospector towards the gold mine is simulated using Eqs. (22) and (23) [47].

$$\vec{D}_{1} = \vec{C}_{1} \cdot \vec{X}^{ * } (t) - \vec{X}_{i} (t)$$
(22)
$$\overrightarrow {{X{\text{ new }}_{i} }} (t + 1) = \vec{X}_{i} (t) + \vec{A}_{1} \cdot \vec{D}_{1}$$
(23)
Fig. 4
figure 4

Schematic view of Eq. (22) in two dimensions

Full size image

\(\vec{X}^{ * } (t)\), \(\vec{X}_{i} (t)\) and t, represent the position of the best gold mine, respectively, the position of the i-th gold prospector, and t the current iteration. \(\overrightarrow {{X{\text{ new }}_{i} }}\), where i is the new gold prospector position and \(\vec{A}_{1}\) the vector coefficients are calculated as given in Eqs. (24) and (25).

$$\vec{A}_{1} = 1 + l_{1} \left( {\vec{r}_{1} - \frac{1}{2}} \right)$$
(24)
$$\vec{C}_{1} = 2\vec{r}_{2}$$
(25)

\(\vec{A}_{1}\) and \(\vec{C}_{1}\), are random vectors whose values are in the range [0,1]. l1, is the convergence component defined by Eq. (26); if e is equal to 1, it decreases linearly from 2 to \(\frac{1}{{\max_{{{\text{iter}}}} }}\) value and nonlinearly decreases for values greater than 1.

$$l_{e} = \left( {\frac{{\max_{{{\text{iter}}}} - {\text{ iter }}}}{{\max_{{{\text{iter}}}} - 1}}} \right)^{e} \left( {2 - \frac{1}{{\max_{{{\text{iter}}}} }}} \right) + \frac{1}{{\max_{{{\text{iter}}}} }}$$
(26)

3.3.3 Gold Mining (Gold Panning)

For mathematical modelling of the gold prospecting situation, the location of each gold prospector is considered the approximate location of a gold mine. Relevant mathematical relationships of gold mining are given in Eqs. (27) and (28) [47].

$$\vec{D}_{2} = \vec{X}_{i} (t) - \vec{X}_{r} (t)$$
(27)
$$\overrightarrow {{X{\text{new}}_{i} }} (t + 1) = \vec{X}_{r} (t) + \vec{A}_{2} \cdot \vec{D}_{2}$$
(28)

\(\vec{X}_{r} (t)\), \(\vec{X}_{i} (t)\), t and \(\overrightarrow {{X{\text{ new }}_{i} }}\), represent the randomly chosen gold finder, the position of the i-th gold digger, t the current iteration, and the new position of the i-th gold finder, respectively. A2 is the vector coefficient calculated by Eq. (29).

$$\vec{A}_{2} = 2l_{2} \overrightarrow {{r_{1} }} - l_{2}$$
(29)

In this equation, parameter l2 is used instead of parameter l1 to increase the exploitation capability of the mining method.

3.3.4 Collaboration Between Prospectors

The collaborative nature of gold prospecting has led to the implementation of mathematical Eqs. (30) and (31) to shed light on the cooperation between prospectors. Here, g1 and g2 are two randomly chosen gold prospectors. In this case, three-person collaboration is performed between i, gl, and g2, and \(\vec{D}_{3}\) is the cooperation vector [47].

$$\vec{D}_{3} = \vec{X}_{{g_{2} }} (t) - \vec{X}_{{g_{1} }} (t)$$
(30)
$$\overrightarrow {{X{\text{new}}_{i} }} (t + 1) = \vec{X}_{i} (t) + \vec{r}_{1} \cdot \vec{D}_{3}$$
(31)

4 Prospectors Relocation

Gold prospectors can change places over time. During the gold mining process, gold prospectors can change their current location to explore new territories or find more gold. This process is mathematically modelled as given in Eq. (32).

$$\vec{X}_{i} (t + 1) = \overrightarrow {{X{\text{new}}_{i} }} (t + 1){\text{ if }}f\left( {\overrightarrow {{X{\text{new}}_{i} }} (t + 1)} \right) < f\left( {\vec{X}_{i} (t)} \right)$$
(32)

4.1 Domain Control

Building upon the preceding theoretical frameworks, the GRO algorithm proposes the definition of a novel position, Xnewi, in dimension d, which will be considered when the dimension d of the location lies between its lower and upper bounds; otherwise, Xi, the previous position of dimension d, remains unchanged. The GRO algorithm commences by initializing a starting population of gold prospectors, each positioned randomly within the search space. The most optimal solution acquired during the research process is designated as the prime location for the gold mine (global optimum). In each iteration, every gold prospector shifts to a fresh position, employing one of three strategies: migration, gold mining, or collaboration. Should the quantity of gold in the new position (measured by the objective function's value) surpass that of the current position (resulting in a decrease for optimization or an increase for maximization of the objective function), the gold prospector relocates to the new site. This progression persists until the iteration cycle concludes. The best solution achieved thus far is recognized as the outcome of the algorithm. The GRO algorithm is a powerful method for finding optimal or approximately optimal solutions in gold mining scenarios. Using the behaviour and interactions of gold prospectors, he effectively explores the search space and finds the richest gold mine [47].

4.2 Implementation of GRO to MLI SHE-PWM Optimization Problem

To apply the GRO algorithm to the 11-level CHB-MLI SHE-PWM optimization problem, the following procedure should be followed:

  1. 1.

    Defining the Objective Function For the MLI SHE-PWM optimization problem, an objective function represents the solution's performance or quality.

  2. 2.

    Initialize the Population Create an initial population of randomly placed gold prospectors in the search space. Every gold prospector represents a potential solution to the MLI SHE-PWM problem.

  3. 3.

    Calculating the Objective Function Evaluate the objective function given in Eq. (7) for each gold prospector and determine their suitability as a solution.

  4. 4.

    Identifying the Best Solution Identify the best gold prospector (solution) with the highest objective function value. This gold prospector represents the current position of the best gold mine (overall optimum).

  5. 5.

    Migration, Gold Mining, and Cooperation In each iteration, each gold prospector takes a new position using one of the migration methods, gold mining or collaboration, as defined in the GRO algorithm. Based on their new location, it reevaluates the objective function of each gold prospector.

  6. 6.

    Update Best Solution Follow the best gold prospector (solution) found throughout the search process, representing the current best solution to the MLI SHE-PWM optimization problem.

  7. 7.

    Termination The algorithm iterates until a termination criterion is met. This criterion may be the maximum number of iterations or reaching a desired level of convergence.

  8. 8.

    Final Solution The best solution (the best gold prospector) is the final solution to the MLI SHE-PWM optimization problem.

Adapting the GRO algorithm for the MLI SHE-PWM optimization problem is necessary for specific goals and constraints. In addition, the application may include specific details and objectives, including adjusting algorithm parameters (L1, L2, A1, A2, etc.) and defining the search space boundaries appropriate to the problem requirements.

The pseudocode of the algorithm is given in Fig. 5.

Fig. 5
figure 5

GRO algorithm pseudocode

Full size image

5 Test and Results

5.1 Comparison of DO and GRO with Other Algorithms

Tests have been performed for eleven-level and MLIs. Numerical calculations are done on a laptop with a 2.40 GHz quad-core processor and 16.00 GB of RAM. As mentioned above, DO, GRO, PSO, and GA are used for simulation. PSO, GA, DO, and GRO MATLAB source codes are modified to solve MLI optimization problems. The number of individuals for all algorithms is 50, and the maximum number of iterations is 100. Each optimization was run ten times for each MI value, and the best results were stored in the tables.

Figures 6, 7, and 8 show the convergence rate of the DO, GRO, PSO, and GA cost function for 11-level MLIs for iterations ranging from 100 to 500. In all cases, GRO showed the best performance, DO showed the second-best performance, and the GA algorithm showed the lowest.

Fig. 6
figure 6

Convergence speed graph in 100 iterations

Full size image
Fig. 7
figure 7

Convergence speed graph in 250 iterations

Full size image
Fig. 8
figure 8

Convergence speed graph in 500 iterations

Full size image

The switching angles calculated with GA are given in Table 1. These switching angles are applied to the inverter, and the simulation results are presented in the same table. Similarly, the switching angles calculated with the PSO algorithm, and the simulation results are given in Table 2. Tables 3 and 4 show the switching angles calculated with DO and GRO and the corresponding harmonic analysis values.

Table 1 Switching angles and harmonic analysis calculated with GA
Full size table
Table 2 Switching angles and harmonic analysis calculated with PSO
Full size table
Table 3 Switching angles and harmonic analysis calculated with DO
Full size table
Table 4 Switching angles and harmonic analysis calculated with GRO
Full size table

As the tables show, all algorithms have found suitable solutions within the MI range of 0.1 to 1.0. However, the algorithms that control the fundamental voltage with the least error are, respectively, the GRO and DO algorithms. While the PSO algorithm performs better than GA, it performs less than GRO and DO. In the MI range of 0.4 to 1.0, the GRO algorithm successfully controls the fundamental voltage with an error of less than 0.08%, eliminating the selected harmonics. The control error of the fundamental voltage for the DO algorithm is below 0.45%, whereas for GA, the maximum error is 2.5%, and for PSO, it is 0.45%.

Determining the best and worst values, as well as calculating the standard deviation values regarding the optimization results, is a crucial source of information concerning the efficiency and reliability of the solution. To assess the efficacy of the algorithms, a series of statistical analyses were conducted, entailing the examination of the optimal and suboptimal values as well as the standard deviation values of the fitness outcomes of ten diverse study outcomes for each MI. These values are given in Table 5 for GA, Table 6 for PSO, Table 7 for DO, and Table 8 for GRO. As seen in the tables, the GRO optimization with the lowest worst value, lowest best value, and lowest standard deviation provided the best performance.

Table 5 GA statistical analysis
Full size table
Table 6 PSO statistical analysis
Full size table
Table 7 DO statistical analysis
Full size table
Table 8 GRO statistical analysis
Full size table

5.2 MATLAB/Simulink Results

To enhance the credibility of the simulation results, an eleven-level MLI is created using MATLAB/Simulink, as depicted in Fig. 9. Harmonic analyses were performed for three different cases using the switching angles found by all algorithms for 0.3 low MI, 0.6 medium MI, and 1.0 high MI.

Fig. 9
figure 9

Simulink model for eleven-level cascaded H-bridge MLI

Full size image

In Fig. 10, the switching angles calculated with the four optimizations for the MI of 0.3, 0.6, and 1.0 show the output waveforms when the inverter is applied. Figure 7a shows the output waveform for GA, while Figs. 10b–d show the output waveform for PSO, DO, and GRO, respectively.

Fig. 10
figure 10

Load Voltage Waveform Comparison of Optimization Algorithms a GA, b PSO, c DO, and d GRO

Full size image

The harmonic analyses of the waveforms given in Fig. 10 for an MI of 0.3 are shown in Fig. 11 for THD and Fig. 12 for THDe. For the 0.3 MI, the THD value obtained with GA was 26.39%, the THD value obtained with PSO was 19.44%, the THD value obtained with DO was 20.64%, and the THD value obtained with GRO was 21.07%.

Fig. 11
figure 11

THD harmonic spectrums (M = 0.3) a GA, b PSO, c DO, and d GRO

Full size image
Fig. 12
figure 12

THDe harmonic spectrums (M = 0.3) a GA, b PSO, c DO, and d GRO

Full size image

As seen in Fig. 12, the measured harmonic values for THD were 12.35% for GA, 8.17% for PSO, 8.0% for DO, and 7.81% for GRO. Although PSO seems more performant for M = 0.3, since SHE optimization is the focus, the GRO algorithm is the most successful for this MI.

The harmonic analyses of the waveforms given in Fig. 10 for an MI of 0.6 are shown in Fig. 13 for THD. For the 0.6 MI, the THD value obtained with GA was 6.96%, the THD value obtained with PSO was 7.47%, the THD value obtained with DO was 6.85%, and the value obtained with GRO was 6.91%.

Fig. 13
figure 13

THD harmonic spectrums (M = 0.6) a GA, b PSO, c DO, and d GRO

Full size image

As seen in Fig. 14, the measured harmonic values for THDe were 1.54% for GA, 0.8% for PSO, 0.07% for DO, and 0.06% for GRO. Although GA seems more performant for M = 0.6, since SHE optimization is the focus, the GRO algorithm is the most successful for this MI.

Fig. 14
figure 14

THDe harmonic spectrums (M = 0.6) a GA, b PSO, c DO, and d GRO

Full size image

The harmonic analyses of the waveforms given in Fig. 10 for the MI 1.0 are shown in Fig. 16 for THDe and Fig. 15 for THD. For the 1.0 MI, the THD value obtained with GA was 7.20%, the THD value obtained with PSO was 5.05%, the THD value obtained with DO was 4.89%, and the THD value obtained with GRO was 4.80%.

Fig. 15
figure 15

THD harmonic spectrums (M = 1.0) a GA, b PSO, c DO, and d GRO

Full size image

As seen in Fig. 16, the measured harmonic values for THDe were 5.0% for GA, 0.59% for PSO, 0.03% for DO, and 0.04% for GRO. At the M = 1.0 index, the DO algorithm is more successful than other algorithms in suppressing the selected harmonics. However, the algorithm that controls the base voltage more accurately is the GRO algorithm.

Fig. 16
figure 16

THDe harmonic spectrums (M = 1.0) a GA, b PSO, c DO, and d GRO

Full size image

5.3 Testing of DO and Well-known Mathematical Functions

This section evaluates GA, PSO, DO, and GRO algorithms in 13 criterion functions (30 dimensions). Many researchers use these classical functions [51]. These test functions were chosen to compare the results with the results of existing metaheuristic algorithms. These standard functions are shown in Tables 9, 10; where ‘Dim’ represents the function dimensions, ‘Range’ is the boundary of the function's search space, and ‘fmin’ is the optimal value.

Table 9 Unimodal benchmark functions
Full size table
Table 10 Multimodal benchmark functions
Full size table

The algorithm was applied to 13 test functions with 30 dimensions. Of these 13 functions, the first 7 are single-mode, and the second 6 are multi-mode. Unimodal functions are suitable for measuring the usage of algorithms. Table 11 (F1–F7) shows that DO and GRO algorithms gave better results than GA and PSO algorithms in all 7 functions. This shows that these algorithms have been used successfully in the search space. Multimodal functions were used to demonstrate the success of the algorithms in the discovery phase. The statistical results of the specified algorithms for these functions are shown in Table 11 (F8–F13). DO and GRO algorithms perform better than GA and PSO algorithms in F9-F13 test functions. These results indicate that DO and GRO algorithms can explore the search space. GRO was the most successful algorithm in both single and multi-mode test functions, while the second-best algorithm was the DO algorithm. The most unsuccessful algorithm was the GA algorithm.

Table 11 Results for the Unimodal and Multimodal benchmark functions with 30 Dimension and 10,000 NFE
Full size table

6 Conclusion and Future Work

In this paper, the issues of harmonic elimination and THD minimization in cascade H-bridge MLI are examined through the implementation of four distinct intelligent optimization algorithms. Among these algorithms, two are novel optimization techniques, namely DO and GRO, which have been recently developed and are being used for the first time in resolving SHE-PWM equations. PSO and GA have been applied to the SHE-PWM problem by many researchers. Numerical simulations were performed on eleven-level CHB-MLI. All methods calculate and show optimum switched angles for cases with modulation indices ranging from 0.1 to 1.0. In addition, THD and THDe values are also calculated and displayed. The performance of the algorithms in controlling the fundamental voltage is also evaluated. Numerical simulations have illustrated that when tackling the issue of harmonic elimination, the DO and GRO algorithms are more effective than the PSO and GA methods.

Furthermore, the GRO algorithm has exhibited more consistent numerical simulation outcomes and has displayed a lower standard deviation than DO. An eleven-level cascade H-bridge MLI was modelled to validate the simulation results using MATLAB/Simulink. The voltages and harmonic analyses were presented using optimal switching angles for MI values of 0.3, 0.6, and 1.0. The FFT analysis tool was employed to calculate the THD values for these scenarios. The numerical values derived from the simulation scenarios and the MATLAB/Simulink model showcase consistent findings. In forthcoming research, this study will extend its scope to encompass MLIs with unequal DC sources to mimic photovoltaic systems with varying outputs. Additionally, a hybrid approach of optimization methods will be implemented to enhance performance refinement further.