Optimal Extensions of Conformal Mappings from the Unit Disk to Cardioid-Type Domains

Abstract

The conformal mapping $f(z)=(z+1)^2$ from ${\mathbb {D}}$ onto the standard cardioid has a homeomorphic extension of finite distortion to entire ${\mathbb {R}}^2 .$ We study the optimal regularity of such extensions, in terms of the integrability degree of the distortion and of the derivatives, and these for the inverse. We generalize all outcomes to the case of conformal mappings from ${\mathbb {D}}$ onto cardioid-type domains.

1 Introduction

The standard cardioid domain

$$\begin{aligned} \Delta = \{(x,y) \in {\mathbb {R}}^2 : (x^2 +y^2)^2 -4x (x^2 +y^2) -4y^2 <0\} \end{aligned}$$

(1.0.1)

is the image of the unit disk ${\mathbb {D}}$ under the conformal mapping $g(z)=(z+1)^2 .$ Since the origin is an inner-cusp point of $\partial \Delta ,$ the Ahlfors’ three-point property fails, and hence $\partial \Delta$ is not a quasicircle. Therefore the preceding conformal mapping does not possess a quasiconformal extension to the entire plane. However, there is a homeomorphic extension $f : {{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2$ by the Schoenflies theorem, see [10, Theorem 10.4]. Recall that homeomorphisms of finite distortion form a much larger class of homeomorphisms than quasiconformal mappings. A natural question arises: can we extend g as a homeomorphism of finite distortion? If we can, how good an extension can we find? Our first result gives a rather complete answer.

Theorem 1.1

Let ${\mathcal {F}}$ be the collection of homeomorphisms $f : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ of finite distortion such that $f(z)=(z+1)^2$ for all $z \in {\mathbb {D}} .$ Then ${\mathcal {F}} \ne \emptyset .$ Moreover

$$\begin{aligned}&\sup \{p \in [1, +\infty ): f \in {\mathcal {F}} \cap W^{1,p} _{\text {loc}} ({{\mathbb {R}}}^2 ,{{\mathbb {R}}}^2)\} =+\infty , \end{aligned}$$

(1.0.2)

$$\begin{aligned}&\sup \{q \in (0,+\infty ): f \in {\mathcal {F}},\ K_f \in L^q _{\text {loc}} ({\mathbb {R}}^2)\} = 2 , \end{aligned}$$

(1.0.3)

$$\begin{aligned}&\sup \{q \in (0,+\infty ): f \in {\mathcal {F}} \cap W^{1,p} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2) \text{ for } \text{ a } \text{ fixed } p>1 \text{ and } K_f \in L^q _{\text {loc}} ({\mathbb {R}}^2)\} \nonumber \\&\quad = 1 , \end{aligned}$$

(1.0.4)

$$\begin{aligned}&\sup \{p \in [1,+\infty ): f \in {\mathcal {F}},\ f^{-1} \in W^{1,p} _{\text {loc}}({\mathbb {R}}^2 , {{\mathbb {R}}}^2 ) \} = \frac{5}{2} \end{aligned}$$

(1.0.5)

and

$$\begin{aligned} \sup \{q \in (0,+\infty ): f \in {\mathcal {F}},\ K_{f^{-1}} \in L^q _{\text {loc}} ({\mathbb {R}}^2)\} = 5 . \end{aligned}$$

(1.0.6)

The cardioid curve $\partial \Delta$ contains an inner-cusp point of asymptotic polynomial degree 3/2. Motivated by this, we introduce a family of cardioid-type domains $\Delta _s$ with degree $s >1 ,$ see (2.3.2). Our second result is an analog of Theorem 1.1.

Theorem 1.2

Let g be a conformal map from ${\mathbb {D}}$ onto $\Delta _s ,$ where $\Delta _s$ is defined in (2.3.2) and $s >1 .$ Suppose that ${\mathcal {F}}_s (g)$ is the collection of homeomorphisms $f : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ of finite distortion such that $f|_{{\mathbb {D}}} =g .$ Then ${\mathcal {F}}_s (g)\ne \emptyset .$ Moreover

$$\begin{aligned}&\sup \{p \in [1, +\infty ): f \in {\mathcal {F}}_s (g) \cap W^{1,p} _{\text {loc}} ({{\mathbb {R}}}^2 ,{{\mathbb {R}}}^2)\} =+\infty , \end{aligned}$$

(1.0.7)

$$\begin{aligned}&\sup \{q \in (0,+\infty ): f \in {\mathcal {F}}_s (g),\ K_f \in L^q _{\text {loc}} ({\mathbb {R}}^2)\} = \max \left\{ \frac{1}{s-1},1 \right\} , \end{aligned}$$

(1.0.8)

$$\begin{aligned}&\sup \{q \in (0, +\infty ): f \in {\mathcal {F}}_s (g) \cap W^{1,p} _{\text {loc}} ({\mathbb {R}}^2, {{\mathbb {R}}}^2) \text{ for } \text{ a } \text{ fixed } p>1 \text{ and } K_f \in L^q _{\text {loc}} ({\mathbb {R}}^2)\} \nonumber \\&\quad = \max \left\{ \frac{1}{s-1}, \frac{3p}{(2s-1)p+4-2s} \right\} , \end{aligned}$$

(1.0.9)

$$\begin{aligned}&\sup \{p \in [1,+\infty ): f \in {\mathcal {F}}_s (g),\ f^{-1} \in W^{1,p} _{\text {loc}}({\mathbb {R}}^2 , {{\mathbb {R}}}^2) \} = \frac{2(s+1)}{2s-1} \end{aligned}$$

(1.0.10)

and

$$\begin{aligned} \sup \{q \in (0,+\infty ): f \in {\mathcal {F}}_s (g) ,\ K_{f^{-1}} \in L^q _{\text {loc}} ({\mathbb {R}}^2)\} = \frac{s+1}{s-1} . \end{aligned}$$

(1.0.11)

Let us recall previous extension results. In [3, 4], sufficient conditions on $\Omega$ are introduced to guarantee that a conformal mapping $g : {{\mathbb {D}}}\rightarrow \Omega$ has a homeomorphic extension of locally exponentially integrable distortion to the whole plane. Specially, when $\Omega$ is a Jordan domain with an outer-cusp point on its boundary, the authors from [8] established the optimal exponential regularity of distortion of homeomorphic extensions.

In Sect. 2, we recall some basic definitions and facts. We also introduce auxiliary mappings and domains. In Sect. 3, we give upper bounds for integrability degrees of potential extensions. Section 4 is devoted to the proof of Theorem 1.2. In Sect. 5 we prove Theorem 1.1.

2 Preliminaries

2.1 Notation

By $s \gg 1$ and $t \ll 1$ we mean that s is sufficiently large and t is sufficiently small, respectively. By $f \lesssim g$ we mean that there exists a constant $M > 0$ such that $f(x) \le Mg(x)$ for every x. We write $f \approx g$ if both $f \lesssim g$ and $g \lesssim f$ hold. By ${\mathcal {L}}^2$ (respectively ${\mathcal {L}}^1$) we mean the 2-dimensional (1-dimensional) Lebesgue measure. Furthermore we refer to the disk with center P and radius r by B(P, r) ,  and $S(P,r) = \partial B(P,r) .$ For a set $E \subset {\mathbb {R}}^2$ we denote by ${\overline{E}}$ the closure of E. If $A \in {\mathbb {R}}^{2 \times 2}$ is a matrix, adjA is the adjoint matrix of A.

2.2 Basic Definitions and Facts

Definition 2.1

Let $\Omega \subset {\mathbb {R}}^2$ and $\Omega ' \subset {\mathbb {R}}^2$ be domains. A homeomorphism $f : \Omega \rightarrow \Omega '$ is called K-quasiconformal if $f \in W^{1,2} _{\text {loc}} (\Omega , \Omega ')$ and if there is a constant $K \ge 1$ such that

$$\begin{aligned} |Df(z)|^2 \le K J_f (z) \end{aligned}$$

holds for ${\mathcal {L}}^2\hbox {-a.e. }z \in \Omega .$

Definition 2.2

Let $\Omega \subset {\mathbb {R}}^2$ be a domain. We say that a mapping $f: \Omega \rightarrow {\mathbb {R}}^2$ has finite distortion if $f \in W^{1,1} _{\text {loc}} (\Omega , {\mathbb {R}}^2),$ $J_f \in L^1 _{\text {loc}} (\Omega )$ and

$$\begin{aligned} |Df (z)|^2 \le K_f(z) J_f (z) \qquad {{\mathcal {L}}}^2 \text{-a.e. } z \in \Omega , \end{aligned}$$

(2.2.1)

where

$$\begin{aligned} K_f (z) = {\left\{ \begin{array}{ll} \frac{|Df(z)|^2}{J_f (z)} &{} \text{ for } \text{ all } z \in \{J_f >0 \}, \\ 1&{} \text{ for } \text{ all } z \in \{J_f =0 \}. \end{array}\right. } \end{aligned}$$

Note that a necessary condition in Definition 2.2 is that $J_f (z) \ge 0$ for ${{\mathcal {L}}}^2 \text{-a.e. } z \in \Omega .$ When $J_f (z) \le 0$ for ${{\mathcal {L}}}^2 \text{-a.e. } z \in \Omega ,$ we also define mappings of finite distortion. Modification on (2.2.1) is that $|Df (z)|^2 \le -K_f(z) J_f (z) \text{ for } {{\mathcal {L}}}^2 \text{-a.e. } z \in \Omega$ with

$$\begin{aligned} K_f (z) = {\left\{ \begin{array}{ll} \frac{|Df(z)|^2}{-J_f (z)} &{} \text{ for } \text{ all } z \in \{J_f <0 \}, \\ 1&{} \text{ for } \text{ all } z \in \{J_f =0 \}. \end{array}\right. } \end{aligned}$$

Analogous explanation is applied to Definition 2.1.

Definition 2.3

Given $A \subset {\mathbb {R}}^2 ,$ a map $f : A \rightarrow {\mathbb {R}}^2$ is called an (l, L)-bi-Lipschitz mapping if $0<l \le L <\infty$ and

$$\begin{aligned} l |x-y| \le |f(x) -f(y)| \le L|x-y| \end{aligned}$$

for all $x, y \in A .$

If $\Omega \subset {{\mathbb {R}}}^2$ is a domain and $f: \Omega \rightarrow {{\mathbb {R}}}^2$ is an orientation-preserving bi-Lipschitz mapping, then f is quasiconformal.

Definition 2.4

Given a function $\varphi$ defined on set $A \subset {\mathbb {R}}^2,$ its modulus of continuity is defined as

$$\begin{aligned} \omega (\delta ) \equiv \omega (\delta , \varphi , A) = \sup \{|\varphi (z_1) -\varphi (z_2)|: z_1 ,z_2 \in A,\ |z_1 -z_2| \le \delta \} \end{aligned}$$

for $\delta \ge 0.$ Then $\varphi$ is called Dini-continuous if

$$\begin{aligned} \int _{0} ^{\pi } \frac{\omega (t)}{t}\, dt < \infty , \end{aligned}$$

where the integration bound $\pi$ can be replaced by any positive constant.

We say that a curve C is $Dini$-$smooth$ if it has a parametrization $\alpha (t)$ for $t \in [0,2\pi ]$ so that $\alpha '(t) \ne 0$ for all $t \in [0,2\pi ]$ and $\alpha '$ is Dini-continuous.

Definition 2.5

Let $\Omega \subset {\mathbb {R}}^2$ be open and $f: \Omega \rightarrow {\mathbb {R}}^2$ be a mapping. We say that f satisfies the Lusin (N) condition if ${\mathcal {L}}^2 (f(E))=0$ for any $E \subset \Omega$ with ${\mathcal {L}}^2 (E)=0 .$ Similarly, f satisfies the Lusin ($N^{-1}$) condition if ${\mathcal {L}}^2 (f^{-1}(E))=0$ for any $E \subset f(\Omega )$ with ${\mathcal {L}}^2 (E)=0 .$

Lemma 2.1

([6, Theorem A.35]) Let $\Omega \subset {\mathbb {R}}^2$ be open and $f \in W^{1,1} _{\text {loc}} (\Omega , {\mathbb {R}}^2).$ Suppose that $\eta$ is a nonnegative Borel measurable function on ${\mathbb {R}}^2 .$ Then

$$\begin{aligned} \int _{\Omega } \eta (f(x)) |J_f (x)|\, \mathrm{{d}}x \le \int _{f(\Omega )} \eta (y) N(f,\Omega ,y)\, \mathrm{{d}}y, \end{aligned}$$

(2.2.2)

where the multiplicity function $N(f,\Omega ,y)$ of f is defined as the number of preimages of y under f in $\Omega .$ Moreover (2.2.2) is an equality if we assume in addition that f satisfies the Lusin (N) condition.

Let $\Omega \subset {{\mathbb {R}}}^2$ be open. Via Lemma 2.1, we have that

$$\begin{aligned} \text{ if } f \text{ is } \text{ a } W^{1,1}_{\text {loc}} (\Omega ,{{\mathbb {R}}}^2) \text{ homeomorphism, } \text{ then } J_f \in L^1 _{\text {loc}} (\Omega ). \end{aligned}$$

(2.2.3)

Lemma 2.2

( [6, Lemma A.28]) Suppose that $f: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ is a homeomorphism which belongs to $W^{1,1} _{\text {loc}} ({\mathbb {R}}^2 , {\mathbb {R}}^2).$ Then f is differentiable ${\mathcal {L}}^2\hbox {-a.e.}$ on ${\mathbb {R}}^2$.

Lemma 2.2 and a simple computation show that

$$\begin{aligned} \max _{\theta \in [0,2\pi ]}|\partial _{\theta } f (z)| =K_f (z) \min _{\theta \in [0,2\pi ]}|\partial _{\theta } f (z)| \qquad {{\mathcal {L}}}^2 \text{-a.e. } z \in {{\mathbb {R}}}^2 \end{aligned}$$

(2.2.4)

when $f: {{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2$ is a homeomorphism of finite distortion. Here $\partial _{\theta } f (z)= \cos ( \theta ) f_x (z) + \sin (\theta ) f_y (z)$ for $\theta \in [0, 2\pi ] .$

Lemma 2.3

([5, Theorem 1.2], [6, Theorem 1.6]) Let $\Omega \subset {\mathbb {R}}^2$ be a domain and $f: \Omega \rightarrow {{\mathbb {R}}}^2$ be a homeomorphism of finite distortion. Then $f^{-1}: f(\Omega ) \rightarrow \Omega$ is also a homeomorphism of finite distortion. Moreover

$$\begin{aligned} |Df^{-1} (y)|^2 \le K_{f^{-1}} (y) J_{f^{-1}} (y) \qquad {{\mathcal {L}}}^2 \text{-a.e. } y \in f(\Omega ). \end{aligned}$$

(2.2.5)

Lemma 2.4

([14, Theorem 2.1.11]) Let all $\Omega \subset {\mathbb {R}}^2, \ \Omega _1 \subset {\mathbb {R}}^2$ and $\Omega _2 \subset {\mathbb {R}}^2$ be open, and $T \in Lip (\Omega _1 , \Omega _2).$ Suppose that both $f \in W^{1,p} _{\text {loc}} (\Omega , \Omega _1)$ and $T \circ f \in L^{p} _{\text {loc}} (\Omega ,\Omega _2)$ hold for some p with $1 \le p \le \infty .$ Then $T \circ f \in W^{1,p} _{\text {loc}} (\Omega , \Omega _2 )$ and

$$\begin{aligned} D(T \circ f)(z) = DT(f(z)) Df(z) \qquad {\mathcal {L}}^2\text{-a.e. } z \in \Omega . \end{aligned}$$

Definition 2.6

A rectifiable Jordan curve $\Gamma$ in the plane is a chord-arc curve if there is a constant $C>0$ such that

$$\begin{aligned} \ell _{\Gamma } (z_1 ,z_2) \le C |z_1 -z_2| \end{aligned}$$

for all $z_1 , z_2 \in \Gamma ,$ where $\ell _{\Gamma } (z_1 ,z_2)$ is the length of the shorter arc of $\Gamma$ joining $z_1$ and $z_2 .$

It is a well-known fact that a chord-arc curve is the image of the unit circle under a bi-Lipschitz mappings of the plane, see [7]. Thus chord-arc curves form a special class of quasicircles. The connections between chord-arc curves and quasiconformal theory can be found in [1, 12].

2.3 Definition of Cardioid-Type Domains

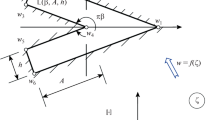
Let $s >1 .$ We introduce a class of cardioid-type domains $\Delta _s$ whose boundaries contain internal polynomial cusps of order s, see Fig. 1. For technical reasons we do this in the following manner. Denote

$$\begin{aligned} \ell _1 (s) = \{(u,v)\in {\mathbb {R}}^2 : u \in [-1, 0] ,\ v=(-u)^s\} \end{aligned}$$

and

$$\begin{aligned} \ell _2 (s) = \{(u,v) \in {\mathbb {R}}^2 : u \in [-1, 0] ,\ v=-(-u)^s\}. \end{aligned}$$

Write $\ell _1 (s)$ and $\ell _2 (s)$ in the polar coordinate system as

$$\begin{aligned}&\ell _1(s) = \{ R e^{i \Theta }:\ R= (-u) (1+(-u)^{2(s-1)})^{\frac{1}{2}} \\&\quad \text{ and } \Theta =\pi - \arctan ((-u)^{s-1}) \text{ for } u \in [-1, 0]\} \end{aligned}$$

and

$$\begin{aligned}&\ell _2 (s)= \{ R e^{i \Theta }:\ R= (-u) (1+(-u)^{2(s-1)})^{\frac{1}{2}} \\&\quad \text{ and } \Theta =-\pi + \arctan ((-u)^{s-1}) \text{ for } u \in [-1, 0]\}. \end{aligned}$$

Take the branch of complex-valued function $z = w^{1/2}$ with $1^{1/2} =1.$ Denote by $\ell ^m _1 (s)$ and $\ell ^m _2 (s)$ the images of $\ell _1 (s)$ and $\ell _2 (s)$ under the preceding $z=w^{1/2},$ respectively. Then we can write $\ell ^m _1 (s)$ and $\ell ^m _2 (s)$ in the polar coordinate system as

$$\begin{aligned}&\ell ^m _1 (s)=\{re^{i \theta }:\ r= \sqrt{-u} (1+(-u)^{2(s-1)})^{\frac{1}{4}} \nonumber \\&\quad \text{ and } \theta = \frac{\pi - \arctan ((-u)^{s-1})}{2} \text{ for } u \in [-1, 0]\} \end{aligned}$$

(2.3.1)

and

$$\begin{aligned}&\ell ^m _2 (s)=\{re^{i \theta }:\ r= \sqrt{-u} (1+(-u)^{2(s-1)})^{\frac{1}{4}} \\&\quad \text{ and } \theta = \frac{-\pi + \arctan ((-u)^{s-1})}{2} \text{ for } u \in [-1, 0]\}. \end{aligned}$$

Denote by $z_1$ and $z_2$ the end points of $\ell ^m _1 (s)\cup \ell ^m _2 (s).$ Notice that there is a unique circle sharing both the tangent of $\ell ^m _1 (s)$ at $z_1$ and the one of $\ell ^m _2 (s)$ at $z_2.$ This circle is divided into two arcs by $z_1$ and $z_2.$ Concatenating $\ell ^m _1 (s) \cup \ell ^m _2 (s)$ with the arc located on the right-hand side of the line through $z_1$ and $z_2$, we then obtain a Jordan curve $\ell ^m (s).$ Denote by $\ell (s)$ the image of $\ell ^m (s)$ under $z^2.$ Let

$$\begin{aligned} M_s \text{ and } \Delta _s \text{ be } \text{ the } \text{ interior } \text{ domains } \text{ of } \ell ^m (s) \text{ and } \ell (s),\ \text{ respectively. } \end{aligned}$$

(2.3.2)

Then $\Delta _s$ is the desired cardioid-type domain with degree s. Moreover $\ell ^m (s),\ \ell (s) ,\ M_s$ and $\Delta _s$ are symmetric with respect to the real axis.

Fig. 1

$M_s$ and $\Delta _s$

By the Riemann mapping theorem, there is a conformal mapping from ${\mathbb {D}} \cap {\mathbb {R}}^2 _+$ onto $M_s \cap {\mathbb {R}}^2 _+$ such that ${\mathbb {D}} \cap {\mathbb {R}}$ is mapped onto $M_s \cap {\mathbb {R}}.$ It follows from the Schwarz reflection principle that there is a conformal mapping

$$\begin{aligned} g_s : {\mathbb {D}} \rightarrow M_s. \end{aligned}$$

(2.3.3)

such that $g_s ({\bar{z}}) = \overline{g_s (z)}$ for all $z \in {{\mathbb {D}}}.$ Moreover by the Osgood–Carathéodory theorem $g_s$ has a homeomorphic extension from $\overline{{\mathbb {D}}}$ onto $\overline{M_s},$ still denoted $g_s .$

Lemma 2.5

Let $M_s$ and $g_s$ be as in (2.3.2) and (2.3.3) with $s >1 .$ Then $g_s$ is a bi-Lipschitz mapping on $\overline{{\mathbb {D}}} .$

Proof

If $\partial M_s$ were a Dini-smooth Jordan curve, from [11, Theorem 3.3.5] it would follow that $g' _s$ is continuous on $\overline{{\mathbb {D}}}$ and $g' _s (z) \ne 0$ for all $z \in \overline{{\mathbb {D}}}.$ Since $M_s$ is convex, the mean value theorem would then yield that $g_s$ is a bi-Lipschitz map from $\overline{{\mathbb {D}}}$ onto $\overline{M_s}.$

In order to prove that $\partial M_s$ is a Dini-smooth Jordan curve, we first analyze $\partial M_s$ in a neighborhood of the origin. For any point in $\ell ^m _1$ with Euclidean coordinate (x, y),  we have

$$\begin{aligned} x= r \cos \theta \text{ and } y= r \sin \theta . \end{aligned}$$

(2.3.4)

where both r and $\theta$ share the expression in (2.3.1). We then obtain that

$$\begin{aligned} r \approx \sqrt{-u},\ \theta \approx \frac{\pi }{2},\ \frac{\partial r}{\partial u} \approx \frac{-1}{\sqrt{-u}} \text{ and } \frac{\partial \theta }{\partial u} \approx (-u)^{s-2} \end{aligned}$$

(2.3.5)

whenever $|u| \ll 1.$ Therefore from (2.3.4) and (2.3.5), it follows that

$$\begin{aligned} x \approx (-u)^{s- \frac{1}{2}},\ y \approx (-u)^{\frac{1}{2}},\ \frac{\partial x}{\partial u} \approx - (-u)^{s- \frac{3}{2}} \text{ and } \frac{\partial y}{\partial u} \approx -(-u)^{-\frac{1}{2}}. \end{aligned}$$

Together with symmetry of $\partial M_s ,$ we conclude that $\frac{\partial x}{\partial y} \approx |y|^{2(s-1)}$ whenever $|y| \ll 1.$ Next, notice that the part of $\partial M_s$ away from the origin is piecewise smooth. By parametrizing $\partial M_s$ as $\alpha (y)=(x(y),y),$ we then obtain that the modulus of continuity of $\alpha '$ satisfies

$$\begin{aligned} \omega (\delta ,\alpha ',\partial M_s) \le \max \{\delta ^{2(s-1)}, \delta \} \qquad \forall \delta \ll 1. \end{aligned}$$

Consequently $\alpha '$ is Dini-continuous. Therefore $\partial M_s$ is a Dini-smooth Jordan curve. $\square$

Remark 2.1

Since $g_s : {\mathbb {S}}^1 \rightarrow \partial M_s$ is a bi-Lipschitz map by Lemma 2.5, via [13, Theorem A] there is a bi-Lipschitz mapping $g^c _s : {\mathbb {D}}^c \rightarrow M_s ^c$ such that $g^c _s |_{{\mathbb {S}}^1} =g_s .$ Let

$$\begin{aligned} G_s (z)= {\left\{ \begin{array}{ll} g_s (z) &{}\forall z \in \overline{{\mathbb {D}}}, \\ g^c _s (z) &{}\forall z \in {\mathbb {D}}^c . \end{array}\right. } \end{aligned}$$

(2.3.6)

Then $G_s$ is an orientation-preserving bi-Lipschitz mapping.

Lemma 2.6

Let $h_1 : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ be a homeomorphism of finite distortion, and $h_2 : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ be an (l, L)-bi-Lipschitz, orientation-preserving mapping. Then $h_1 \circ h_2$ is a homeomorphism of finite distortion.

Proof

Since $h_2$ is an orientation-preserving bi-Lipschitz mapping, we have that $h_2$ is quasiconformal. From [2, Corollary 3.7.6] it then follows that

$$\begin{aligned}&h_2 \text{ satisfies } \text{ Lusin } (N) \text{ and } (N^{-1}) \text{ condition, } \end{aligned}$$

(2.3.7)

$$\begin{aligned}&J_{h_2} >0 \quad {\mathcal {L}}^2 \text{-a.e. } \text{ on } {\mathbb {R}}^2. \end{aligned}$$

(2.3.8)

By Lemma 2.2 we have

$$\begin{aligned} \text{ both } h_1 \text{ and } h_2 \text{ are } \text{ differentiable } {\mathcal {L}}^2 \text{-a.e. } \text{ on } {\mathbb {R}}^2 . \end{aligned}$$

(2.3.9)

From (2.3.9) and (2.3.7) it therefore follows that $h_1 \circ h_2$ is differentiable ${\mathcal {L}}^2\hbox {-a.e.}$ on ${\mathbb {R}}^2,$ and

$$\begin{aligned} D(h_1 \circ h_2) (z) =Dh_1 (h_2 (z)) D h_2 (z) \qquad {\mathcal {L}}^2 \text{-a.e. } z \in {\mathbb {R}}^2 . \end{aligned}$$

(2.3.10)

From (2.3.10) and the distortion inequalities for $h_1$ and $h_2$ it follows that

$$\begin{aligned} |D(h_1 \circ h_2) (z)|^2 \le&|Dh_1 (h_2 (z))|^2 |Dh_2 (z)|^2 \le K_{h_1} (h_2 (z)) K_{h_2} (z) J_{h_1} (h_2 (z)) J_{h_2} (z) \nonumber \\ =&K_{h_1} (h_2 (z)) K_{h_2} (z) J_{h_1 \circ h_2} (z) \end{aligned}$$

(2.3.11)

for ${\mathcal {L}}^2\hbox {-a.e. }z \in {\mathbb {R}}^2 .$

To prove that $h_1 \circ h_2$ is a homeomorphism of finite distortion, via (2.2.3) and (2.3.11) it is sufficient to prove that $h_1 \circ h_2 \in W^{1,1} _{\text {loc}} ({{\mathbb {R}}}^2 ,{{\mathbb {R}}}^2).$ Since $h_2$ is an (l, L)-bi-Lipschitz orientation-preserving mapping, by (2.3.9) and (2.2.4) we then have that

$$\begin{aligned} l \le |Dh_2 (z)| \le L \text{ and } 1 \le K_{h_2} (z) \le \frac{L}{l} \qquad {\mathcal {L}}^2 \text{-a.e. } z \in {\mathbb {R}}^2 . \end{aligned}$$

(2.3.12)

From(2.3.8), (2.3.12), and (2.2.1) it then follows that

$$\begin{aligned} \frac{l^3}{L} \le J_{h_2} (z) \le L^2\qquad {\mathcal {L}}^2 \text{-a.e. } z \in {\mathbb {R}}^2 . \end{aligned}$$

(2.3.13)

By (2.3.10), (2.3.12), (2.3.13), and Lemma 2.1, we therefore have

$$\begin{aligned} \int _{M} |D(h_1 \circ h_2) (z)|\, \mathrm{{d}}z \le&\int _{M} |Dh_1 (h_2 (z))| \frac{|Dh_2 (z)| }{J_{h_2} (z)} J_{h_2} (z)\, \mathrm{{d}}z \\ \approx&\int _{M} |Dh_1 (h_2 (z))| J_{h_2} (z) \, \mathrm{{d}}z \\ =&\int _{h_2(M)} |Dh_1 (w)|\, \mathrm{{d}}w <\infty \end{aligned}$$

for any compact set $M \subset {\mathbb {R}}^2 ,$ where the last inequality is from $h_1 \in W^{1,1} _{\text {loc}} ({{\mathbb {R}}}^2 ,{{\mathbb {R}}}^2).$ $\square$

3 Bounds for Integrability Degrees

For a given $s>1 ,$ let $M_s$ as in (2.3.2). Define

$$\begin{aligned}&{\mathcal {E}}_s = \{f : \ f: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2 \text{ is } \text{ a } \text{ homeomorphism } \text{ of } \text{ finite } \text{ distortion } \nonumber \\&\quad \text{ and } f(z)=z^2 \text{ for } \text{ all } z \in \overline{M_s} \}. \end{aligned}$$

(3.0.1)

Lemma 3.1

Let ${\mathcal {E}}_s$ be as in (3.0.1) with $s > 1 ,$ and $f \in {\mathcal {E}}_s .$ Suppose that $f^{-1} \in W^{1,p}_{\text {loc}} ({\mathbb {R}}^2, {{\mathbb {R}}}^2)$ for some $p \ge 1.$ Then necessarily $p < 2(s+1)/(2s-1).$

Proof

Given $x \in (-1 ,0),$ denote by $I_x$ the line segment connecting the points $(x,|x|^{s})$ and $(x,-|x|^{s}).$ Since $f^{-1} \in W^{1,p}_{\text {loc}}$ for some $p \ge 1,$ by the ACL-property of Sobolev functions it follows that

$$\begin{aligned} \text{ osc }_{I_x} f^{-1} \le \int _{I_x} \big |D f^{-1}(x,y)\big |\, \mathrm{{d}}y \end{aligned}$$

(3.0.2)

holds for ${\mathcal {L}}^1\hbox {-a.e. }x \in (-1 ,0).$ Applying Jensen’s inequality to (3.0.2), we have

$$\begin{aligned} \frac{(\text{ osc }_{I_x} f^{-1})^p}{(-x)^{s(p-1)}} \le \int _{I_x} \big |D f^{-1} (x,y)\big |^p \, \mathrm{{d}}y. \end{aligned}$$

(3.0.3)

Since $f(z) =z^2$ for all $z \in \partial M_s ,$ we have

$$\begin{aligned} (-x)^{1/2} \lesssim \text{ osc }_{I_x} f^{-1} \qquad \forall x \in (-1 ,0). \end{aligned}$$

(3.0.4)

Combining (3.0.3) with (3.0.4), we hence obtain

$$\begin{aligned} (-x)^{\frac{p}{2} -s(p-1)} \lesssim \int _{I_x} \big |D f^{-1} (x,y)\big |^p \, \mathrm{{d}}y \qquad {\mathcal {L}}^1 \text{-a.e. } x \in (-1 ,0). \end{aligned}$$

(3.0.5)

Integrating (3.0.5) with respect to $x \in (-1 ,0)$ therefore implies

$$\begin{aligned} \int _{-1} ^{0}(-x)^{\frac{p}{2} -s(p-1)}\, \mathrm{{d}}x \lesssim \int _{B(0,\sqrt{2})} \big |D f^{-1} (x,y)\big |^p \, \mathrm{{d}}x \, \mathrm{{d}}y. \end{aligned}$$

(3.0.6)

Since $f^{-1} \in W^{1,p}_{\text {loc}} ,$ from (3.0.6) we necessarily obtain $\frac{p}{2}-s(p-1) >-1,$ which is equivalent to $p < 2(s+1)/(2s-1).$ $\square$

Our next proof borrows some ideas from [9, Theorem 1].

Lemma 3.2

Let ${\mathcal {E}}_s$ be as in (3.0.1) with $s > 1 .$ Let $f \in {\mathcal {E}}_s$ and suppose that $K_{f^{-1}} \in L^q _{loc} ({\mathbb {R}}^2)$ for a given $q \ge 1.$ Then $q < (s+1)/(s-1).$

Proof

For a given $t \ll 1,$ we denote

$$\begin{aligned} E_t = \{(x,y) \in {\mathbb {R}}^2 : x \in (-t^2 , -(\frac{t}{2})^2 ) \text{ and } y=-|x|^s\} \end{aligned}$$

and

$$\begin{aligned} F_t = \{(x,y)\in {\mathbb {R}}^2 : x \in (-t^2 , -(\frac{t}{2})^2 ) \text{ and } y=|x|^s\}. \end{aligned}$$

Let ${\tilde{E}}_t = f^{-1} (E_t) \text{ and } {\tilde{F}}_t = f^{-1} (F_t) .$ Set

$$\begin{aligned} L^1 _t= & {} \min \{|z| : z \in {\tilde{F}}_t\},\ L^2 _t = \max \{|z|: z \in {\tilde{F}}_t\}, \\ L_t= & {} \text {dist}({\tilde{E}}_t,{\tilde{F}}_t),\ L_0 = \max \{|f^{-1} (z)|: \text {Re}z=-1, \text {Im}z \in [-1,1] \}. \end{aligned}$$

Since $f(z)=z^2$ for all $z \in \partial M_s ,$ we have $L^1 _t \approx t/2,\ L^2 _t \approx t$ and $L_t \approx t$ whenever $t \ll 1 .$ Given $w \in A_t :=\{w \in {\mathbb {R}}^2 : L^1 _t \le |w| \le L^2 _t \} ,$ set $\rho (w) = L^2 _t /(L_t |w|).$ Define

$$\begin{aligned} v(z) = {\left\{ \begin{array}{ll} 1 &{} \text{ for } \text{ all } z \in B(0,L_0) \setminus A_t, \\ \inf _{\gamma _z} \int _{\gamma _z} \rho \, ds &{} \text{ for } \text{ all } z \in A_t, \end{array}\right. } \end{aligned}$$

(3.0.7)

where the infimum is taken over all curves $\gamma _z \subset A_t$ joining z and ${\tilde{E}}_t.$ From (3.0.7) it follows that for any $z_1,\ z_2 \in A_t$ and any curve $\gamma _{z_1 z_2} \subset A_t$ connecting $z_1$ and $z_2$ we have

$$\begin{aligned} |v(z_1) -v(z_2)|\le \int _{\gamma _{z_1 z_2}} \rho \, \mathrm{{d}}s . \end{aligned}$$

(3.0.8)

Therefore v is a Lipschitz function on $A_t .$ By Rademacher’s theorem, v is differentiable ${\mathcal {L}}^2\hbox {-a.e.}$ on $A_t.$ Hence (3.0.8) together with the continuity of $\rho$ gives

$$\begin{aligned} |Dv(z)| \le \rho (z) \qquad {\mathcal {L}}^2 \text{-a.e. } z \in A_t . \end{aligned}$$

(3.0.9)

Integrating (3.0.9) over ${\tilde{Q}} _t = A_t \setminus M_s$ then yields

$$\begin{aligned} \int _{{\tilde{Q}} _t} |Dv|^2 \le \int _{{\tilde{Q}} _t} \rho ^2 \approx \int _{L^1 _t} ^{L^2 _t} \frac{1}{r}\, \mathrm{{d}}r \approx \log 2 . \end{aligned}$$

(3.0.10)

By Lemma 2.3 we have $f^{-1} \in W^{1,1} _{\text {loc}} .$ Let $u =v \circ f^{-1} .$ From Lemma 2.4 we then have $u \in W^{1,1} _{\text {loc}} (f (B(0,L_0)))$ and

$$\begin{aligned} |Du(z)| \le |Dv(f^{-1} (z))| |Df^{-1}(z)| \qquad {\mathcal {L}}^2 \text{-a.e. } \text{ in } f (A_t) . \end{aligned}$$

(3.0.11)

By (3.0.7), $v(z) =0$ for all $z \in {\tilde{E}}_t .$ Hence $u (z) =0$ for all $z \in E_t .$ Whenever $z \in {\tilde{F}}_t,$ we have ${{\mathcal {L}}}^1 (\gamma _z ) \ge L_t$ for any curve $\gamma _z \subset A_t$ joining z and ${\tilde{E}}_t .$ Therefore $v(z) \ge 1$ for all $z \in {\tilde{F}}_t .$ Hence $u(z)\ge 1$ for all $z \in F_t .$ By the ACL-property of Sobolev functions and Hölder’s inequality, we therefore have that

$$\begin{aligned} 1 \le \int _{-x^s} ^{x^s} |Du(x,y)| \, \mathrm{{d}}y \le \left( \int _{-x^s} ^{x^s} |Du(x,y)|^p \, \mathrm{{d}}y \right) ^{\frac{1}{p}} (2 x^s)^{\frac{p-1}{p}} \end{aligned}$$

(3.0.12)

for any $p > 1$ and ${{\mathcal {L}}}^1\hbox {-a.e. }x \in [-t^2 ,-(t/2)^2].$ Define

$$\begin{aligned} R_t = \{(x,y)\in {\mathbb {R}}^2 : x \in (-t^2, -(t/2)^2) ,\ y \in (-|x|^s, |x|^s)\}. \end{aligned}$$

Fubini’s theorem and (3.0.12) then give

$$\begin{aligned} \int _{R_t} |Du(x,y)|^p \, \mathrm{{d}}x \, \mathrm{{d}}y =&\int _{-t^2} ^{-(t/2)^2} \int _{-x^s} ^{x^s} |Du(x,y)|^p \, \mathrm{{d}}y \, \mathrm{{d}}x \nonumber \\ \gtrsim&\int _{-t^2} ^{-(t/2)^2} x^{s(1-p)} \, \mathrm{{d}}x \approx t^{2(1+s(1-p))}. \end{aligned}$$

(3.0.13)

Set $Q_t = f({\tilde{Q}}_t).$ Then for any $z \in R_t \setminus Q_t$ there is an open disk $B_z \subset R_t \setminus Q_t$ such that $z \in B_z$ and $u|_{B_z} \equiv 1 .$ Therefore

$$\begin{aligned} \int _{Q_t} |Du|^p \ge \int _{Q_t \cap R_t} |Du|^p = \int _{R_t} |Du|^p . \end{aligned}$$

(3.0.14)

Combining (3.0.13) with (3.0.14) gives that

$$\begin{aligned} t^{2(1+s(1-p))} \lesssim \int _{Q_t} |Du|^p \end{aligned}$$

(3.0.15)

for all $p \ge 1.$

For any $p \in (0,2),$ by (3.0.11), (2.2.5), and Hölder’s inequality, we have

$$\begin{aligned} \int _{Q_t} |D u|^p \le&\int _{Q_t}\Big |D v \circ f^{-1}\Big |^p \Big |D f^{-1}\Big |^p \nonumber \\ \le&\int _{Q_t}\Big |D v \circ f^{-1}\Big |^p J^{\frac{p}{2}}_{f^{-1}} K^{\frac{p}{2}}_{f^{-1}} \nonumber \\ \le&\left( \int _{Q_t} \Big |D v \circ f^{-1}\Big |^2 J_{f^{-1}} \right) ^{\frac{p}{2}} \left( \int _{Q_t} K^{\frac{p}{2-p}}_{f^{-1}} \right) ^{\frac{2-p}{2}} \nonumber \\ \le&\left( \int _{{\tilde{Q}} _t} \Big |D v \Big |^2 \right) ^{\frac{p}{2}} \left( \int _{Q_t} K^{\frac{p}{2-p}}_{f^{-1}} \right) ^{\frac{2-p}{2}} \end{aligned}$$

(3.0.16)

where the last inequality comes from Lemma 2.1. Let $q = p/(2-p) .$ Via (3.0.10) and (3.0.15), we conclude from (3.0.16) that

$$\begin{aligned} t^{2(1+q +s(1-q))} \lesssim \int _{Q_t} K^q _{f^{-1}} \end{aligned}$$

(3.0.17)

for all $q \ge 1.$ We now consider the set $Q_t$ for $t =2^{-j}$ with $j \ge j_0$ for a fixed large $j_0 .$ Since

$$\begin{aligned} \sum _{j =j_0} ^{\infty } \chi _{Q_{2^{-j}}} (x) \le 2 \chi _{{\mathbb {D}}} (x) \qquad \forall x \in {{\mathbb {R}}}^2 , \end{aligned}$$

by (3.0.17) we have that

$$\begin{aligned} \sum _{j=j_0} ^{+\infty } 2^{j2(s(q-1)-q-1)} \lesssim \sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} K^q _{f^{-1}} \le 2\int _{{\mathbb {D}}} K^q _{f^{-1}}. \end{aligned}$$

(3.0.18)

The series in (3.0.18) diverges when $q \ge \frac{s+1}{s-1}$ and hence $K_{f^{-1}} \in L^q _{\text {loc}} ({\mathbb {R}}^2)$ can only hold when $q < (s+1)/(s-1) .$ $\square$

We continue with properties of our homeomorphism f. The following lemma is a version of [4, Theorem 4.4].

Lemma 3.3

Let ${\mathcal {E}}_s$ be as in (3.0.1) with $s > 1 .$ If $f \in {\mathcal {E}}_s$ and $K_f \in L^q _{loc} ({\mathbb {R}}^2)$ for some $q \ge 1,$ then $q < \max \{1, 1/(s-1)\}.$

Proof

Denote

$$\begin{aligned} \Omega = \{(x_1,x_2)\in {\mathbb {R}}^2 : x_1 \in (-1, 0),\ x_2 \in (-|x_1|^s, |x_1|^s) \} . \end{aligned}$$

For a given $t \ll 1,$ set

$$\begin{aligned} \Omega ^1 _t= & {} \{(x_1,x_2)\in \Omega : x_1 \in (-1, -t^2) \}, \\ {\tilde{Q}} _t= & {} \{(x_1,x_2)\in \Omega : x_1 \in [-t^2, -(\frac{t}{2})^2] \} \text{ and } \Omega ^2 _t =\Omega \setminus (\Omega ^1 _t \cup {\tilde{Q}} _t). \end{aligned}$$

Define

$$\begin{aligned} v(x_1,x_2)= {\left\{ \begin{array}{ll} 1 &{} \forall (x_1,x_2) \in \Omega ^1 _t ,\\ 1- \left( \int _{-t^2} ^{- (t/2)^2 } \frac{\mathrm{{d}}x}{(-x)^{s}} \right) ^{-1} \int _{-t^2} ^{x_1} \frac{\mathrm{{d}}x}{(-x)^{s}} &{} \forall (x_1,x_2) \in {\tilde{Q}} _t ,\\ 0 &{} \forall (x_1, x_2) \in \Omega ^2 _t. \end{array}\right. } \end{aligned}$$

(3.0.19)

Then v is a Lipschitz function on $\Omega .$ Let $u=v \circ f.$ By Lemma 2.4, we have $u \in W^{1,1} _{\text {loc}} (f^{-1} (\Omega ))$ and

$$\begin{aligned} Du(z) = Dv (f(z)) Df(z) \qquad {\mathcal {L}}^2 \text{-a.e. } z \in f^{-1} (\Omega ). \end{aligned}$$

(3.0.20)

Let $P_1 = f^{-1} ((-t^2,t^{2s})),\ P_2 = f^{-1} ((- (t /2)^2 , (t/2)^{2s}))$, and O be the origin. Denote by $L^1 _t$ and $L^2 _t$ the length of line segment $P_1 P_2$ and of $P_1 O ,$ respectively. Then $L^1 _t < L^2 _t .$ Since $f(z)=z^2$ for all $z \in \partial M_s ,$ we have

$$\begin{aligned} L^1 _t \approx \frac{t}{2} \text{ and } L^2 _t \approx t \qquad \text{ whenever } t \ll 1. \end{aligned}$$

(3.0.21)

Let ${\hat{S}}(P_1 , r) = S(P_1 , r) \cap f^{-1} (\Omega ) .$ From the ACL-property of Sobolev functions and Hölder’s inequality, we have that

$$\begin{aligned} \text {osc}_{{\hat{S}}(P_1 , r)} u \le \int _{{\hat{S}}(P_1 , r)} |D u| \, \mathrm{{d}} s \le (2 \pi r)^{\frac{p-1}{p}} \left( \int _{{\hat{S}}(P_1 , r)} |D u|^p \, \mathrm{{d}}s \right) ^{\frac{1}{p}} \end{aligned}$$

(3.0.22)

for any $p > 1$ and ${\mathcal {L}}^1\hbox {-a.e. }r \in (L^1 _t ,L^2 _t) .$ Since $\text {osc}_{{\hat{S}}(P_1 , r)} u = 1$ for all $r \in (L^1 _t , L^2 _t),$ we conclude from (3.0.22) that

$$\begin{aligned} \int _{{\hat{S}}(P_1 , r)} |D u|^p \, \mathrm{{d}}s \gtrsim r^{1-p} \qquad {\mathcal {L}}^1 \text{-a.e. } r \in (L^1 _t ,L^2 _t). \end{aligned}$$

(3.0.23)

Let $A_t = f^{-1} (\Omega )\cap B(P_1 , L^2 _t) \setminus \overline{B(P_1 , L^1 _t)} .$ By Fubini’s theorem and (3.0.21), we deduce from (3.0.23) that

$$\begin{aligned} \int _{A_t} |D u|^p = \int _{L^1 _t} ^{L^2 _t} \int _{{\hat{S}}(P_1 , r)} |D u|^p \, \mathrm{{d}}s \, \mathrm{{d}}r \gtrsim \int _{L^1 _t} ^{L^2 _t} r ^{1-p}\, \mathrm{{d}}r \approx t^{2-p}. \end{aligned}$$

(3.0.24)

Let $Q_t = f^{-1} ({\tilde{Q}} _t) .$ From (3.0.19), we have $|Du(z)|=0$ for all $z \in A_t \setminus Q _t .$ We hence conclude from (3.0.24) that

$$\begin{aligned} \int _{Q_t} |D u|^p \ge \int _{Q_t \cap A_t} |D u|^p = \int _{A_t} |D u|^p \gtrsim t^{2-p} \end{aligned}$$

(3.0.25)

for any $p \ge 1.$

From (3.0.20), (2.2.1), and Hölder’s inequality, it follows that for any $p \in (0,2)$

$$\begin{aligned} \int _{Q_t} |D u|^p \le&\int _{Q_t}\big |D v \circ f\big |^p \big |D f\big |^p \le \int _{Q_t}\big |D v \circ f\big |^p J^{\frac{p}{2}}_f K^{\frac{p}{2}}_f \nonumber \\ \le&\left( \int _{Q_t} \big |D v \circ f\big |^2 J_f \right) ^{\frac{p}{2}} \left( \int _{Q_t} K^{\frac{p}{2-p}}_f \right) ^{\frac{2-p}{2}} \nonumber \\ \le&\left( \int _{{\tilde{Q}} _t} \big |D v \big |^2 \right) ^{\frac{p}{2}} \left( \int _{Q_t} K^{\frac{p}{2-p}}_f \right) ^{\frac{2-p}{2}}, \end{aligned}$$

(3.0.26)

where the last inequality is from Lemma 2.1. From (3.0.19), we have that

$$\begin{aligned} \int _{{\tilde{Q}} _t } \big |D v (x_1, x_2)\big |^2 \, \mathrm{{d}}x_1 \, \mathrm{{d}}x_2= & {} \left( \int _{-t^2} ^{- (t/2)^2 } \frac{\mathrm{{d}}x}{(-x)^{s}} \right) ^{-2} \int _{-t^2} ^{- (t/2)^2 } \int _{-|x _1|^s} ^{|x _1|^s} \frac{1}{(-x _1)^{2s}} \, \mathrm{{d}}x_2 \, \mathrm{{d}}x_1 \nonumber \\\approx & {} \left( \int _{-t^2} ^{- (t/2)^2 } \frac{\mathrm{{d}}x}{(-x)^{s}} \right) ^{-1} \approx t^{2(s-1)}. \end{aligned}$$

(3.0.27)

Let $q =p/(2-p).$ Then $q \in [1,+\infty )$ whenever $p \in [1,2).$ Combining (3.0.27), (3.0.25) with (3.0.26) yields

$$\begin{aligned} t^{2+2(1-s) q} \lesssim \int _{Q_t} K^q_f \end{aligned}$$

(3.0.28)

for all $q \ge 1.$ We now consider the set $Q_t$ for $t =2^{-j}$ with $j \ge j_0$ for a fixed large $j_0 .$ Analogously to (3.0.18), it follows from (3.0.28) that

$$\begin{aligned} \sum _{j=j_0} ^{+\infty } 2^{2j((s-1)q-1)} \lesssim \sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} K^q _{f} \le 2\int _{B(0,1)} K^q _{f}. \end{aligned}$$

(3.0.29)

Whenever $s \ge 2,$ the sum in (3.0.29) diverges if $q \ge 1 .$ Whenever $s \in (1,2),$ the sum in (3.0.29) also diverges if $q \ge 1/(s-1).$ Hence $K_f \in L^q _{loc} ({\mathbb {R}}^2)$ is possible only when $q < \max \{1, 1/(s-1)\}.$ $\square$

In Lemma 3.3, we obtained an estimate for those q for which $K_f \in L^q _{\text {loc}} .$ We continue with the additional assumption that $f \in W^{1,p} _{\text {loc}}$ for some $p > 1 .$

Lemma 3.4

Let ${\mathcal {E}}_s$ be as in (3.0.1) with $s > 2 .$ If $f \in {\mathcal {E}}_s$, $f \in W^{1,p} _{\text {loc}} ({{\mathbb {R}}}^2 , {{\mathbb {R}}}^2)$ for some $p>1$ and $K_f \in L^q _{\text {loc}} ({{\mathbb {R}}}^2)$ for some $q \in (0,1),$ then $q < 3p/((2s-1)p+4-2s) .$

Proof

Let f be a homeomorphism with the above properties. By [5, Theorem 4.1] we have $f^{-1} \in W^{1,r} _{\text {loc}} ({\mathbb {R}}^2)$ where

$$\begin{aligned} r = \frac{(q+1)p -2q}{p-q}. \end{aligned}$$

Moreover

$$\begin{aligned} r< \frac{2(s+1)}{2s-1} \Leftrightarrow q < \frac{3p}{(2s-1)p+4-2s}. \end{aligned}$$

Hence the claim follows from Lemma 3.1. $\square$

Remark 3.1

Notice that in the proof of Lemma 3.3 we only care about the property of f in a small neighborhood of the origin. Let $t \ll 1.$ By modifying $\partial M_s \cap B(0,t),$ we may generalize Lemma 3.3. For example, we modify $\partial M_{3/2} \cap B(0,t)$ such that its image under $f(z)=z^2$ is

$$\begin{aligned} \{(x,y) \in {{\mathbb {R}}}^2 : x \in [-2^{-j_0} ,0],\ y^2=c |x|^3\} \end{aligned}$$

where c is a positive constant. If $K_f \in L^q _{\text {loc}} ({{\mathbb {R}}}^2)$ for some $q \ge 1,$ by the analogous arguments as for Lemma 3.3 we have $q <2 .$ Similarly, one may extend Lemmas 3.1, 3.2 and 3.4 to the above setting.

Lemma 3.5

Let $\Delta _s$ be as in (2.3.2) with $s >1 .$ Suppose that $f :{\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ is a homeomorphism of finite distortion such that f maps ${\mathbb {D}}$ conformally onto $\Delta _s .$ We have that

• (1) if $f^{-1} \in W^{1,p} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ for some $p \ge 1$ then $p < 2(s+1)/(2s-1) ,$

• (2) if $K_{f^{-1}} \in L^q _{loc} ({\mathbb {R}}^2 )$ for some $q \ge 1$ then $q < (s+1)/(s-1),$

• (3) if $K_f \in L^q _{loc} ({\mathbb {R}}^2)$ for some $q \ge 1$ then $q < \max \{1, 1/(s-1)\} ,$

• (4) if $s>2$, $f \in W^{1,p} _{\text {loc}} ({{\mathbb {R}}}^2 , {{\mathbb {R}}}^2)$ for some $p>1$ and $K_f \in L^q _{\text {loc}}$ for some $q \in (0,1),$ then $q < 3p/((2s-1)p+4-2s) .$

Proof

Let $g_s$ be as in (2.3.3), and $h_s = z^2 \circ g_s .$ Since $h_s : {\mathbb {D}} \rightarrow \Delta _s$ is conformal, there is a Möbius transformation

$$\begin{aligned} m_s (z) = e^{i \theta } \frac{z-a}{1-{\bar{a}} z}\qquad \text{ where } \theta \in [0, 2\pi ] \text{ and } |a|<1 \end{aligned}$$

such that $f(z)= h_s \circ m_s (z)$ for all $z \in {{\mathbb {D}}}.$ Since $m_s : {{\mathbb {S}}}^1 \rightarrow {{\mathbb {S}}}^1$ is a bi-Lipschitz mapping, by [13, Theorem A] there is a bi-Lipschitz mapping $m^c _s : {\mathbb {D}}^c \rightarrow \Delta ^c _s$ such that $m^c _s |_{{\mathbb {S}}^1} =m_s .$ Define

$$\begin{aligned} {\mathfrak {M}}_s (z) = {\left\{ \begin{array}{ll} m_s (z) &{} z \in \overline{{\mathbb {D}}} , \\ m^c _s (z) &{} z \in {\mathbb {D}}^c . \end{array}\right. } \end{aligned}$$

(3.0.30)

Then ${\mathfrak {M}}_s :{\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ is a bi-Lipschitz, orientation-preserving mapping. Let $G_s$ be as in (2.3.6). Define

$$\begin{aligned} E= f \circ {\mathfrak {M}}^{-1} _s \circ G^{-1} _s : {{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2 . \end{aligned}$$

Lemma 2.6 implies that $E \in {\mathcal {E}}_s ,$ where ${\mathcal {E}}_s$ is from (3.0.1). From Lemmas  2.2 and  2.3, it follows that

$$\begin{aligned} \text{ both } f^{-1} \text{ and } E^{-1} \text{ are } \text{ differentiable } {\mathcal {L}}^2 \text{-a.e. } \text{ on } {\mathbb {R}}^2 . \end{aligned}$$

(3.0.31)

Since

$$\begin{aligned} \frac{\Big |f^{-1} (z_1) - f^{-1} (z_2)\Big |}{\Big |z_1 -z_2\Big |} =&\frac{\Big |E^{-1} (z_1 ) - E^{-1} (z_2 )\Big |}{\Big |z_1- z_2 \Big |} \frac{\Big |(G^{-1} _s (E^{-1} (z_1))-(G^{-1} _s (E^{-1} (z_2)) \Big |}{\Big |E^{-1} (z_1 ) - E^{-1} (z_2 )\Big |} \times \\&\times \frac{\Big |{\mathfrak {M}}^{-1}_s (G^{-1} _s \circ E^{-1} (z_1)) - {\mathfrak {M}}^{-1}_s (G^{-1} _s \circ E^{-1} (z_2))\Big |}{\Big |G^{-1} _s \circ E^{-1} (z_1) - G^{-1} _s \circ E^{-1} (z_2) \Big |} \end{aligned}$$

for all $z_1, z_2 \in {\mathbb {R}}^2$ with $z_1 \ne z_2 ,$ by (3.0.31) and the bi-Lipschitz properties of $G^{-1} _s$ and ${\mathfrak {M}}^{-1} _s$ we have that

$$\begin{aligned} \Big |Df^{-1} (z)\Big |\approx & {} \Big |DE^{-1} (z)\Big |, \end{aligned}$$

(3.0.32)

$$\begin{aligned} \max _{\theta \in [0,2\pi ]} \Big |\partial _{\theta } f^{-1} (z)\Big |\approx & {} \max _{\theta \in [0,2\pi ]} \Big |\partial _{\theta } E^{-1} (z)\Big |,\nonumber \\ \min _{\theta \in [0,2\pi ]} \Big |\partial _{\theta } f^{-1} (z)\Big |\approx & {} \min _{\theta \in [0,2\pi ]} \Big |\partial _{\theta } E^{-1} (z)\Big | \end{aligned}$$

(3.0.33)

for ${\mathcal {L}}^2\hbox {-a.e. }z \in {\mathbb {R}}^2 .$ If $f^{-1} \in W^{1,p}_{\text {loc}}$ for some $p \ge 1 ,$ Lemma 3.2 together with (3.0.34) gives $p < 2(s+1)/(2s-1).$ By (3.0.33) and (2.2.4) we have that

$$\begin{aligned} K_{f^{-1}} (z) \approx K_{E^{-1}} (z) \qquad {\mathcal {L}}^2 \text{-a.e. } z \in {\mathbb {R}}^2 . \end{aligned}$$

(3.0.34)

If $K_{f^{-1}} \in L^q _{loc} ({\mathbb {R}}^2)$ for some $q \ge 1 ,$ combining (3.0.32) and Lemma 3.1 then yields $q < (s+1)/(s-1).$

By Lemma 2.2 and  2.6, we have that

$$\begin{aligned} \text{ both } f \text{ and } E \text{ are } \text{ differentiable } {\mathcal {L}}^2 \text{-a.e. } \text{ on } {\mathbb {R}}^2 . \end{aligned}$$

(3.0.35)

From [2, Corollary 3.7.6], $G_s \circ {\mathfrak {M}}_s$ satisfies Lusin (N) and $(N^{-1})$ conditions. Since

$$\begin{aligned} \frac{\Big |f(z_1 ) -f(z_2)\Big |}{\Big |z_1 -z_2\Big |} =&\frac{\Big |E (G_s \circ {\mathfrak {M}}_s (z_1)) -E (G_s \circ {\mathfrak {M}}_s (z_2))\Big |}{\Big |G_s \circ {\mathfrak {M}}_s (z_1) -G_s \circ {\mathfrak {M}}_s (z_2)\Big |} \frac{|G_s ({\mathfrak {M}}_s (z_1)) -G_s ({\mathfrak {M}}_s (z_2))\Big |}{\Big |{\mathfrak {M}}_s (z_1) -{\mathfrak {M}}_s (z_2)\Big |} \times \\&\times \frac{\Big |{\mathfrak {M}}_s (z_1) -{\mathfrak {M}}_s (z_2)\Big |}{\Big |z_1 -z_2\Big |} \end{aligned}$$

for all $z_1 , z_2 \in {\mathbb {R}}^2$ with $z_1 \ne z_2,$ from (3.0.35) and the bi-Lipschitz properties of $G_s$ and ${\mathfrak {M}}_s$ we have that

$$\begin{aligned} |Df(z)|\approx & {} |DE (G_s \circ {\mathfrak {M}}_s (z))|, \end{aligned}$$

(3.0.36)

$$\begin{aligned} \max _{\theta \in [0,2\pi ]} |\partial _{\theta } f (z)|\approx & {} \max _{\theta \in [0,2\pi ]} |\partial _{\theta } E (G_s \circ {\mathfrak {M}}_s (z))|, \end{aligned}$$

(3.0.37)

$$\begin{aligned} \min _{\theta \in [0,2\pi ]} |\partial _{\theta } f (z)|\approx & {} \min _{\theta \in [0,2\pi ]} |\partial _{\theta } E (G_s \circ {\mathfrak {M}}_s (z))| \end{aligned}$$

(3.0.38)

for ${\mathcal {L}}^2\hbox {-a.e. }z \in {\mathbb {R}}^2 .$ By (2.2.4), (3.0.37), and (3.0.38), we have that

$$\begin{aligned} K_{f} (z) \approx K_E (G_s \circ {\mathfrak {M}}_s (z))\qquad {\mathcal {L}}^2 \text{-a.e. } z \in {\mathbb {R}}^2 . \end{aligned}$$

(3.0.39)

Via the same reasons as for (2.3.13), we have that

$$\begin{aligned} J_{G_s \circ {\mathfrak {M}}_s}(z) \approx 1 \qquad {\mathcal {L}}^2 \text{-a.e. } z \in {\mathbb {R}}^2 . \end{aligned}$$

(3.0.40)

By (3.0.40) and Lemma 2.1, we derive from (3.0.39) that

$$\begin{aligned} \int _{A} K^q _{f} (z)\, \mathrm{{d}}z =&\int _{A} K^q _{E} (G_s \circ {\mathfrak {M}}_s(z)) \frac{J_{G_s \circ {\mathfrak {M}}_s}(z)}{J_{G_s \circ {\mathfrak {M}}_s(z)}} \, \mathrm{{d}}z \nonumber \\ \approx&\int _{A} K^q _{E} (G_s \circ {\mathfrak {M}}_s(z)) J_{G_s \circ {\mathfrak {M}}_s} (z)\, \mathrm{{d}}z = \int _{G_s \circ {\mathfrak {M}}_s (A)} K^q _{E} (w)\, \mathrm{{d}}w \end{aligned}$$

(3.0.41)

for any $q \ge 0$ and any compact set $A \subset {\mathbb {R}}^2 .$ By (3.0.36) and Lemma 2.1, we obtain that

$$\begin{aligned} \int _{A} |Df(z)|^p =&\int _{A} |D E (G_s \circ {\mathfrak {M}}_s(z))|^p \frac{J_{G_s \circ {\mathfrak {M}}_s}(z)}{J_{G_s \circ {\mathfrak {M}}_s } (z)} \, \mathrm{{d}}z \nonumber \\ \approx&\int _{A} |D E (G_s \circ {\mathfrak {M}}_s(z))|^p J_{G_s \circ {\mathfrak {M}}_s} (z) \, \mathrm{{d}}z = \int _{G_s \circ {\mathfrak {M}}_s (A)} |D E|^p (w) \, \mathrm{{d}}w \end{aligned}$$

(3.0.42)

for any $p \ge 0 .$ If $K_f \in L^q _{loc} ({\mathbb {R}}^2)$ for some $q \ge 1 ,$ Lemma 3.3 together with (3.0.41) gives that $q < \max \{1, 1/(s-1)\} .$ If $f \in W^{1,p} _{\text {loc}}$ and $K_f \in L^q _{\text {loc}}$ for some $p>1$ and some $q \in (0,1) ,$ combining Lemma 3.4 with (3.0.42) then implies $q < 3p/((2s-1)p+4-2s) .$ $\square$

Under a more general assumption that f in Lemma 3.5 is K-quasiconformal from ${{\mathbb {D}}}$ onto $\Delta _s ,$ authors from [4, Theorem 4.4] showed a result analogous to Lemma 3.5 (3).

4 Proof of Theorem 1.2

4.1 Prove that the Class ${\mathcal {F}}_s (g)$ from Theorem 1.2 is Nonempty

Proof

Let g be as in Theorem 1.2. The beginning of proof for Lemma 3.4 shows that

$$\begin{aligned} g= z^2 \circ g_s \circ m_s , \end{aligned}$$

where $m_s :{{\mathbb {D}}}\rightarrow {{\mathbb {D}}}$ is a Möbius transformation and $g_s : {{\mathbb {D}}}\rightarrow M_s$ from (2.3.3) is a conformal mapping. Recall that $m_s$ (or $g_s$) has a bi-Lipschitz extension ${\mathfrak {M}}_s : {{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2$ (or $G_s : {{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2$) as in (3.0.30) (or (2.3.6)). Via Lemma 2.6, it suffices to prove that $z^2 : M_s \rightarrow \Delta _s$ has a homeomorphic extension $E :{{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2$ of finite distortion. Then

$$\begin{aligned} f:= E \circ G_s \circ {\mathfrak {M}}_s \in {\mathcal {F}}_s (g). \end{aligned}$$

(4.1.1)

We divide the construction of E into two steps.

Step 1: we construct $E_1$ in a neighborhood of the cusp point, see Fig. 2. To be precise, we define $f_1,...,f_4$ and let $E_1$ be the sum of compositions of $f_1,...f_4 .$

Fig. 2

The construction $f^{-1} _3 \circ f^{-1} _4 \circ f_2 \circ f^{-1} _1 :Q_t \rightarrow {\tilde{Q}}_t$

Aim 1: to define $f_1$ and $f _2$. Fix $s >1,$ and define

$$\begin{aligned} \eta (x) =\sqrt{x} (1+x^{2(s-1)})^{\frac{1}{4}}\qquad \text{ for } \text{ all } x>0 . \end{aligned}$$

(4.1.2)

Then

$$\begin{aligned} \eta ' (x) = \frac{(1+x^{2(s-1)})^{\frac{1}{4}}}{2 \sqrt{x}} \left( 1+ \frac{(s-1) x^{2s-2}}{1+x^{2(s-1)}}\right) . \end{aligned}$$

(4.1.3)

For a given $t \ll 1,$ let

$$\begin{aligned} L^1 _t = \eta ( ( t/2 )^2) ,\ L^2 _t = \eta (t^2), \text{ and } \sigma _t =L^2 _t -L^1 _t. \end{aligned}$$

(4.1.4)

Then $L^1 _t \approx t/2,\ L^2 _t \approx t$ and $\sigma _t \approx t/2$ whenever $t \ll 1.$ Set

$$\begin{aligned} Q_t = \overline{B(0,L^2 _t)} \setminus ( B(0,L^1 _t) \cup M_s) \text{, } \text{ and } f_1 (x, y)=x e^{i y} \quad \forall x \ge 0 \text{ and } y \in [0,2\pi ].\nonumber \\ \end{aligned}$$

(4.1.5)

Let $\ell (r)$ be the length of $f^{-1}_1 (Q_t) \cap \{(x,y)\in {\mathbb {R}}^2 : x=r\}.$ Define

$$\begin{aligned} f_2 (r, \theta ) = \left( r, \frac{\sigma _t }{\ell (r)} (\pi -\theta ) \right) \qquad \forall (r, \theta ) \in f^{-1}_1 (Q_t). \end{aligned}$$

(4.1.6)

Since $\partial M_s$ is mapped onto $\partial \Delta _s$ by $z^2,$ we have that

$$\begin{aligned} \ell (r) = \pi + \arctan \tau ^{2(s-1)} \text{ and } r= \eta (\tau ^2) \end{aligned}$$

(4.1.7)

for all $\tau \in (t/2 ,t).$ Then $\ell (r) \approx \pi$ and $r \approx \tau$ whenever $\tau \ll 1.$ From (4.1.3), it follows that $\frac{\partial r}{\partial \tau } \approx 1 .$ Together with $\frac{\partial \ell }{\partial \tau } \approx \tau ^{2s-3},$ we have that

$$\begin{aligned} \frac{\partial \ell (r)}{\partial r} \approx r^{2s-3} \qquad \text{ for } \text{ all } r \ll 1. \end{aligned}$$

(4.1.8)

Denote $R_t = f_2 \circ f^{-1} _{1} (Q_t).$ Then $R_t = [L^1 _t ,L^2 _t] \times [-\sigma _t /2 , \sigma _t /2] .$ Combining (4.1.5) with (4.1.6) implies

$$\begin{aligned} f_1 \circ f^{-1} _2 (x,y) = \left( -x \cos \frac{\ell (x) y}{\sigma _t } , x \sin \frac{\ell (x) y}{\sigma _t } \right) \quad \forall (x,y) \in R_t . \end{aligned}$$

Therefore

$$\begin{aligned} D f_1 \circ f^{-1} _2 (x,y)= \begin{bmatrix} -\cos \frac{\ell (x) y}{\sigma _t } + \frac{xy \ell '(x) }{\sigma _t } \sin \frac{\ell (x) y}{\sigma _t } &{} \frac{x \ell (x) }{\sigma _t } \sin \frac{\ell (x) y}{\sigma _t } \\ \sin \frac{\ell (x) y}{\sigma _t } + \frac{xy \ell '(x) }{\sigma _t } \cos \frac{\ell (x) y}{\sigma _t } &{} \frac{x \ell (x) }{\sigma _t } \cos \frac{\ell (x) y}{\sigma _t } \end{bmatrix}. \end{aligned}$$

(4.1.9)

By (4.1.4), (4.1.7), and (4.1.8), we deduce from (4.1.9) that

$$\begin{aligned} |D f_1 \circ f^{-1} _2 (x,y)| \lesssim 1 \text{ and } J_{f_1 \circ f^{-1} _2 }(x,y) = -\frac{x \ell (x) }{\sigma } \approx -1 \end{aligned}$$

(4.1.10)

for all $t \ll 1$ and each $(x,y) \in R_t .$ Since $K_{f_1 \circ f^{-1} _2} \ge 1,$ from (4.1.10) we have

$$\begin{aligned} K_{f_1 \circ f^{-1} _2} \approx 1 . \end{aligned}$$

(4.1.11)

By (4.1.10) again we have that

$$\begin{aligned} |D f_2 \circ f^{-1} _1| =\frac{|adj D f_1 \circ f^{-1} _2|}{|J_{f_1 \circ f^{-1} _2 }|} \approx |D f_1 \circ f^{-1} _2 | \lesssim 1 \text{ and } J_{f_2 \circ f^{-1} _1} = \frac{1}{J_{f_1 \circ f^{-1} _2 }} \approx -1.\nonumber \\ \end{aligned}$$

(4.1.12)

Analogously to (4.1.11), we have that

$$\begin{aligned} K_{f_2 \circ f^{-1} _1} (x,y) \approx 1 \qquad \forall t \ll 1 \text{ and } \forall (x,y) \in Q_t . \end{aligned}$$

(4.1.13)

Aim 2: to define $f_3 : {\tilde{Q}}_t \rightarrow {\tilde{R}}_t$. Let

$$\begin{aligned} {\tilde{Q}}_t = \{(x,y)\in {\mathbb {R}}^2 : x \in [-t^2, -(t/2)^2] ,\ |y| \le |x|^s\} . \end{aligned}$$

Define

$$\begin{aligned} f_3 (u,v) = \left( -u, \frac{t^{2s}}{(-u)^s} v \right) \qquad \forall (u,v) \in {\tilde{Q}}_t. \end{aligned}$$

Then $f_3$ is diffeomorphic and

$$\begin{aligned} Df_3(u,v)= \begin{bmatrix} -1 &{} 0 \\ \frac{s t^{2s}}{(-u)^{s+1}} v &{} \frac{t^{2s}}{(-u)^s} \end{bmatrix}. \end{aligned}$$

(4.1.14)

From (4.1.14) we have that

$$\begin{aligned} |Df_3| \lesssim 1 \text{ and } J_{f_3} \approx -1 \qquad \forall (u,v) \in {\tilde{Q}}_t. \end{aligned}$$

(4.1.15)

Analogously to (4.1.11), we have that

$$\begin{aligned} K_{f_3}(u,v) \approx 1 \qquad \forall t \ll 1 \text{ and } \forall (u,v) \in {\tilde{Q}}_t . \end{aligned}$$

(4.1.16)

Let ${\tilde{R}}_t = f_3 ({\tilde{Q}}_t).$ Then ${\tilde{R}}_t = [(t/2)^2 , t^2] \times [-t^{2s} ,t^{2s}].$ The same reasons as for (4.1.12) and (4.1.13) imply that

$$\begin{aligned} |Df^{-1} _3 (x,y)| \lesssim 1,\ J_{f^{-1} _3} (x,y)\approx -1 \text{ and } K_{f^{-1} _3} (x,y)\approx 1 \end{aligned}$$

(4.1.17)

for all $t \ll 1$ and $(x,y) \in {\tilde{R}}_t .$

Aim 3: to define $f_4 : {\tilde{R}}_t \rightarrow R_t$. Denote by $P_1, P_2, P_3, P_4$ and ${\tilde{P}}_1 , {\tilde{P}}_2, {\tilde{P}}_3 ,{\tilde{P}}_4$ the four vertices of ${\tilde{R}}_t$ and $R_t ,$ respectively. Then

$$\begin{aligned} P_1 =\left( L^1 _t , \frac{\sigma _t }{2}\right) ,\ P_2 =\left( L^2 _t , \frac{\sigma _t}{2}\right) ,\ P_3 =\left( L^2 _t , -\frac{\sigma _t }{2}\right) ,\ P_4 =\left( L^1 _t , -\frac{\sigma _t }{2}\right) \end{aligned}$$

and

$$\begin{aligned} {\tilde{P}}_1 = \left( (t/2)^2 , t^{2s}\right) ,\ {\tilde{P}}_2 = (t^2 , t^{2s}),\ {\tilde{P}}_3 = (t^2 , -t^{2s}),\ {\tilde{P}}_4 = ((t/2)^2 , -t^{2s}). \end{aligned}$$

Since $\partial M_s$ is mapped onto $\partial \Delta _s$ by $z^2 ,$ the line segment ${\tilde{P}}_1 {\tilde{P}}_2$ is mapped onto $P_1 P_2$ by

$$\begin{aligned} (u,t^{2s}) \mapsto \left( \eta (u),\frac{\sigma _t}{2} \right) \qquad \forall u \in [(t/2)^2 ,t^2], \end{aligned}$$

and the line segment ${\tilde{P}}_4 {\tilde{P}}_3$ is mapped onto $P_4 P_3$ by

$$\begin{aligned} (u,-t^{2s}) \mapsto \left( \eta (u), -\frac{\sigma _t }{2} \right) \qquad \forall u \in [(t/2)^2 ,t^2]. \end{aligned}$$

Define

$$\begin{aligned} f_4 (u,v) = \left( \eta (u), \frac{\sigma _t }{2 t^{2s}}v \right) \qquad \forall (u,v) \in {\tilde{R}}_t. \end{aligned}$$

(4.1.18)

Then $f_4$ is a diffeomorphism from ${\tilde{R}}_t$ onto $R_t$ and

$$\begin{aligned} D f_4 (u,v)= \begin{bmatrix} \eta ' (u) &{} 0 \\ 0 &{} \frac{\sigma _t }{2 t^{2s}} \end{bmatrix}. \end{aligned}$$

(4.1.19)

By (4.1.3) and (4.1.4) we have that $\eta ' (u) \approx t^{-1}$ and $\frac{\sigma _t }{2 t^{2s}} \approx t^{1-2s}$ whenever $t \ll 1$ and $(u,v) \in {\tilde{R}}_t .$ It follows from (4.1.19) that

$$\begin{aligned} |Df_4 (u,v)| \approx t^{1-2s} \text{ and } J_{f_4} (u,v) \approx t^{-2s} \end{aligned}$$

(4.1.20)

for all $t \ll 1$ and all $(u,v) \in {\tilde{R}}_t .$ Then

$$\begin{aligned} K_{f_4} (u,v)= \frac{|Df_4 (u,v)|^2}{J_{f_4} (u,v)} \approx t^{2-2s} \qquad \forall t \ll 1 \text{ and } (u,v) \in {\tilde{R}}_t . \end{aligned}$$

(4.1.21)

The same reasons as for (4.1.12) and (4.1.13) imply that

$$\begin{aligned} \big |Df^{-1} _4 (x,y)\big | \approx t,\ J_{f^{-1} _4} (x,y) \approx t^{2s} \text{ and } K_{f^{-1} _4} (x,y) \approx t^{2-2s} \end{aligned}$$

(4.1.22)

for all $t \ll 1$ and all $(x,y) \in R_t .$

Aim 4: to define $E_1$. Set

$$\begin{aligned} F_t=f^{-1} _3 \circ f^{-1}_4 \circ f_2 \circ f^{-1} _{1} . \end{aligned}$$

Then $F_t$ is a diffeomorphism from $Q_t$ onto ${\tilde{Q}}_t .$ Therefore

$$\begin{aligned} DF_t (z)= Df^{-1} _3 (f^{-1}_4 \circ f_2 \circ f^{-1} _{1} (z)) Df^{-1}_4 ( f_2 \circ f^{-1} _{1} (z)) D (f_2 \circ f^{-1} _{1}) (z) \end{aligned}$$

for all $z \in Q_t .$ From (4.1.17), (4.1.22), and (4.1.12) it then follows that

$$\begin{aligned} \int _{Q_t} |DF_t |^p \, \mathrm{{d}}z\le&\int _{Q_t} \Big |D f^{-1} _3 (f^{-1} _4 \circ f_2 \circ f^{-1} _1) \Big |^p \Big |Df^{-1} _4 (f_2 \circ f^{-1} _1 )\Big |^p \Big |D f_2 \circ f^{-1} _1 \Big |^p \, \mathrm{{d}}z\nonumber \\ \lesssim&t^{p} {\mathcal {L}}^2(Q_t) \approx t^{2+p} \end{aligned}$$

(4.1.23)

for all $p \ge 0.$ For a fixed large $j_0,$ we now consider the set $Q_t$ with $t=2^{-j}$ for all $j \ge j_0 .$ Define

$$\begin{aligned} E_1 = \sum _{j=j_0} ^{+\infty } F_{2^{-j}} \chi _{Q_{2^{-j}}}. \end{aligned}$$

(4.1.24)

Denote $\Omega _1 = \cup _{j=j_0} ^{+\infty } Q_{2^{-j}} \text{ and } {\tilde{\Omega }}_1 = \cup _{j=j_0} ^{+\infty } {\tilde{Q}}_{2^{-j}}.$ Then $E_1$ is a homeomorphism from $\Omega _1$ onto ${\tilde{\Omega }}_1 ,$ and satisfies (2.2.1) for $E_1$ on ${\mathcal {L}}^2\hbox {-a.e. }\Omega _1 .$ In order to prove that $E_1$ has finite distortion on $\Omega _1 ,$ via (2.2.3) it thus suffices to prove that $E_1 \in W^{1,1} _{\text {loc}} (\Omega _1 , {\tilde{\Omega }}_1) .$ Actually, from (4.1.23) we have that

$$\begin{aligned} \int _{\Omega _1} |D E_1|^p =\sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} |DF_{2^{-j}} (z)|^p \, \mathrm{{d}}z \lesssim \sum _{j=j_0} ^{+\infty } 2^{-j(2+p)} <\infty \end{aligned}$$

(4.1.25)

for all $p \ge 1 .$

Step 2: we construct $E_2$ on the domain away from the cusp point. Denote

$$\begin{aligned} \Omega _2 = M_s ^c \setminus \Omega _1 \text{ and } {\tilde{\Omega }}_2 = \Delta _s ^c \setminus {\tilde{\Omega }}_1 . \end{aligned}$$

Notice that both $\partial \Omega _2$ and $\partial {\tilde{\Omega }}_2$ are piecewise smooth Jordan curves with nonzero angles at the two corners. Therefore both $\partial \Omega _2$ and $\partial {\tilde{\Omega }}_2$ are chord-arc curves. By [7] there are bi-Lipschitz mappings

$$\begin{aligned} H_1 : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2 \text{ and } H_2 : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2 \end{aligned}$$

(4.1.26)

such that $H_1 ({\mathbb {S}}^1) = \partial \Omega _2$ and $H_2 ({\mathbb {S}}^1) = \partial {\tilde{\Omega }}_2 .$ Define

$$\begin{aligned} h(z)= {\left\{ \begin{array}{ll} E_1 (z) &{} \forall z \in \partial \Omega _2 \cap \partial \Omega _1 ,\\ z^2 &{} \forall z \in \partial \Omega _2 \cap \partial M_s. \end{array}\right. } \end{aligned}$$

Then h is a bi-Lipschitz mapping in terms of the arc lengths. By the chord-arc properties of both $\partial \Omega _2$ and $\partial {\tilde{\Omega }}_2 ,$ we have that h is also a bi-Lipschitz mapping with respect to the Euclidean distances. Taking (4.1.26) into account, we conclude that $H^{-1} _2 \circ h \circ H_1 : {\mathbb {S}}^1 \rightarrow {\mathbb {S}}^1$ is a bi-Lipschitz mapping. By [13, Theorem A] there is then a bi-Lipschitz mapping

$$\begin{aligned} H : {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2 \end{aligned}$$

(4.1.27)

such that $H |_{{\mathbb {S}}^1} = H^{-1} _2 \circ h \circ H_1 .$ Define

$$\begin{aligned} E_2 = H _2 \circ H \circ H^{-1} _1 . \end{aligned}$$

(4.1.28)

By (4.1.26) and (4.1.27), we have that $E_2$ is a bi-Lipschitz extension of h. Furthermore since $\deg _{M_s} (h, w) =1 ,$ we obtain that $E_2$ is orientation-preserving. Hence $E_2$ is a quasiconformal mapping. The same reasons as for (2.3.12) and (2.3.13) imply

$$\begin{aligned} |DE_2 (z)|,\ K_{E_2} (z), \text{ and } J_{E_2} (z) \text{ are } \text{ bounded } \text{ from } \text{ both } \text{ above } \text{ and } \text{ below }\nonumber \\ \end{aligned}$$

(4.1.29)

for ${\mathcal {L}}^2\hbox {-a.e. }z \in {\mathbb {R}}^2,$ and

$$\begin{aligned} \Big |DE^{-1} _2 (w)\Big |,\ K^{-1} _{E_2} (w) \text{ and } J^{-1} _{E_2} (w) \text{ are } \text{ bounded } \text{ from } \text{ both } \text{ above } \text{ and } \text{ below }\nonumber \\ \end{aligned}$$

(4.1.30)

for ${\mathcal {L}}^2\hbox {-a.e. }w \in {\mathbb {R}}^2 .$

Via (4.1.24) and (4.1.28), we set

$$\begin{aligned} E(x,y)= {\left\{ \begin{array}{ll} E_1 (x,y)&{} \text{ for } \text{ all } (x,y) \in \Omega _1, \\ E_2 (x,y)&{} \text{ for } \text{ all } (x,y) \in \Omega _2 ,\\ (x^2 -y^2 , 2xy) &{} \text{ for } \text{ all } (x,y) \in \overline{M_s}. \end{array}\right. } \end{aligned}$$

(4.1.31)

By the properties of $E_1$ and $E_2,$ we conclude that $E \in {\mathcal {E}}_s .$ $\square$

4.2 Proof of (1.0.7), (1.0.10), and (1.0.11) in Theorem 1.2

Proof of(1.0.7) Let g be as in Theorem 1.2. It suffices to check that there is $f \in {\mathcal {F}}_s (g)$ satisfying that $f \in W^{1,p} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ for all $p \ge 1 .$ Let f be as in (4.1.1) and E be as in (4.1.31). By (4.1.25), (4.1.29), and the fact that $E(z)=z^2$ for all $z \in M_s,$ we obtain that $E \in W^{1,p} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ for all $p \ge 1 .$ By (3.0.42) $f \in W^{1,p} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ for all $p \ge 1 .$ $\square$

Proof of (1.0.10) Let g be as in Theorem 1.2. By Lemma 3.5 (1) it suffices to construct a $f \in {\mathcal {F}}_s (g)$ satisfying that $f^{-1} \in W^{1,p}_{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ for all $p < 2(s+1) /(2s-1).$ Let f be as in (4.1.1) and E be as in (4.1.31). Via (3.0.32) it suffices to check that $E^{-1} \in W^{1,p}_{\text {loc}} ({\mathbb {R}}^2 ,{{\mathbb {R}}}^2)$ for all $p < 2(s+1) /(2s-1).$

By (4.1.15), (4.1.20), and (4.1.10), we have that

$$\begin{aligned} \Big |DF^{-1} _{2^{-j}} (w)\Big | \le \Big |D f_1 \circ f^{-1}_2 (f_4 \circ f_3 (w))\Big | \Big |Df_4 (f_3 (w))\Big |\Big |Df_3 (w)\Big | \lesssim 2^{j(2s-1)} \end{aligned}$$

for all $j \ge j_0$ and ${\mathcal {L}}^2\hbox {-a.e. }w \in {\tilde{Q}}_{2^{-j}} .$ Together with ${\mathcal {L}}^2({\tilde{Q}}_{2^{-j}} )\approx 2^{-2j(s+1)},$ we hence obtain that

$$\begin{aligned} \int _{{\tilde{\Omega }}_1} \Big |DE^{-1}_1\Big |^p = \sum _{j =j_0} ^{+\infty } \int _{{\tilde{Q}}_{2^{-j}}} \Big |DF^{-1} _{2^{-j}}\Big |^p \lesssim \sum _{j =j_0} ^{+\infty } 2^{-j(2(s+1)+p(1-2s))} <\infty \qquad \end{aligned}$$

(4.2.1)

for all $p < 2(s+1)/(2s-1).$ Since

$$\begin{aligned} \Big |DE^{-1} (u,v)\Big | \lesssim (u^2 +v^2)^{-1/4} \qquad \forall (u,v) \in \Delta _s , \end{aligned}$$

(4.2.2)

by a change of variables we have that

$$\begin{aligned} \int _{\Delta _s} \Big |DE^{-1} (w)\Big |^p \, \mathrm{{d}}w \lesssim \int _{0} ^{2 \pi } \int _{0} ^{1} r^{1-\frac{p}{2}} \, \mathrm{{d}}r \, \mathrm{{d}}\theta \approx \int _{0} ^{1} r^{1-\frac{p}{2}} \, \mathrm{{d}}r <\infty \end{aligned}$$

(4.2.3)

for all $p < 2(s+1)/(2s-1) .$ By (4.1.30), (4.2.1), and (4.2.3), we conclude that $E^{-1} \in W^{1,p}_{\text {loc}} ({\mathbb {R}}^2 ,{{\mathbb {R}}}^2)$ for all $p < 2(s+1) /(2s-1).$ $\square$

Proof of (1.0.11) Let E be as in (4.1.31). Analogously to the proof of (1.0.10), it suffices to check that $K_{E^{-1}} \in L^{q}_{\text {loc}} ({\mathbb {R}}^2)$ for all $q < (s+1) /(s-1).$ Note that Lemma 3.5 (2) and (3.0.34) play game now. From (4.1.11), (4.1.21), and (4.1.16), we have that

$$\begin{aligned} K_{F^{-1} _{2^{-j}}} (w) = K_{f_1 \circ f^{-1} _2} (f_4 \circ f_3 (w)) K_{f_4} (f_3 (w)) K_{f_3} (w) \approx 2^{j(2s-2)} \end{aligned}$$

for all $j \ge j_0$ and ${\mathcal {L}}^2\hbox {-a.e. } w \in {\tilde{Q}}_{2^{-j}} .$ Together with ${\mathcal {L}}^2({\tilde{Q}}_{2^{-j}} )\approx 2^{-j2(s+1)},$ we then obtain that

$$\begin{aligned} \int _{{\tilde{\Omega }}_1} K^q _{E^{-1}}= \sum _{j =j_0} ^{+\infty } \int _{{\tilde{Q}}_{2^{-j}}} K^q _{F^{-1} _{2^{-j}}} \lesssim \sum _{j =j_0} ^{+\infty } 2^{2j[(s-1)q -(s+1)]} <\infty \end{aligned}$$

(4.2.4)

for all $q < (s+1) /(s-1).$ By (4.1.30), (4.2.4), and the fact that E is conformal on $M_s ,$ we conclude that $K_{E^{-1}} \in L^{q}_{\text {loc}} ({\mathbb {R}}^2)$ for all $q < (s+1) /(s-1) .$ $\square$

4.3 Proof of (1.0.8) in Theorem 1.2

Proof

Analogously to the proof of (1.0.10) in Sect. 4.2, via Lemma 3.5 (3) and (3.0.41) it suffices to construct a $E \in {\mathcal {E}}_s$ satisfying that $K_{E} \in L^q _{\text {loc}}$ for all $q < \max \{1, 1/(s-1)\} .$ The construction is divided into two cases.

Case 1: $\varvec{s \in (1,2)}.$ Let E be as in (4.1.31). From (4.1.17), (4.1.22), and (4.1.13), it follows that

$$\begin{aligned} K_{F_{2^{-j}}} (z) = K_{f^{-1} _3} (f^{-1} _4 \circ f_2 \circ f^{-1} _{1} (z)) K_{f^{-1} _4} (f_2 \circ f^{-1} _{1} (z)) K_{f_2 \circ f^{-1} _{1}} (z) \approx 2^{2j(s-1)} \end{aligned}$$

for all $j \ge j_0$ and ${\mathcal {L}}^2\hbox {-a.e. }z \in Q_{2^{-j}}.$ Together with ${\mathcal {L}}^2(Q_{2^{-j}}) \approx 2^{-2j}$ we then have that

$$\begin{aligned} \int _{\Omega _1} K^q _{E} = \sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} K^q _{F_{2^{-j}}} \approx \sum _{j=j_0} ^{+\infty } 2^{2j(q(s-1) -1)} <\infty \end{aligned}$$

(4.3.1)

for all $q < 1/(s-1) .$ By (4.3.1), (4.1.29), and the fact that E is conformal on $M_s ,$ we conclude that $K_E \in L^q _{\text {loc}} ({\mathbb {R}}^2)$ for all $q < 1/(s-1) .$ Therefore we have proved (1.0.8) whenever $s \in .(1,2).$

Case 2: $\varvec{s \in [2,\infty )}.$ Except for redefining $f^{-1} _4 : R_t \rightarrow {\tilde{R}}_t$ as in (4.1.18), we follow all processes in Sect. 4.1 to define a new E,  see Fig. 3. To redefine $f^{-1} _4 ,$ we should define mappings $A,\ B,\ C .$

We begin with notation. Let $\alpha _t$ and $\beta _t$ be the length of sides of ${\tilde{R}}_t,$ and $\gamma _t$ be the length of a side of $R_t.$ Whenever $t \ll 1,$ we have that

$$\begin{aligned} \alpha _t = t^2 -(t/2)^2 \approx t^2,\ \beta _t =2t^{2s} \text{ and } \gamma _t =\eta (t^2) -\eta ((t/2)^2) \approx t. \end{aligned}$$

(4.3.2)

Let ${\tilde{T}}_0 ={\tilde{Q}}_1 {\tilde{Q}}_2 {\tilde{Q}}_3 {\tilde{Q}}_4$ be the concentric square of ${\tilde{R}}_t$ with side length $\beta _t /2 .$ Set

$$\begin{aligned} \delta _t =\exp (- t^{-1}) \qquad \text{ for } t >0 \end{aligned}$$

(4.3.3)

and let $T_0 = Q_1 Q_2 Q_3 Q_4$ be the concentric square of $R_t$ with side length $\gamma _t (1-2 \delta _t).$ We divide $R_t \setminus T_0$ into four isosceles trapezoids $T_1,\ T_2,\ T_3$, and $T_4 .$ Similarly, we obtain isosceles trapezoids ${\tilde{T}}_1,\ {\tilde{T}}_2,\ {\tilde{T}}_3,\ {\tilde{T}}_4$ from ${\tilde{R}}_t \setminus {\tilde{T}}_0 ,$ see Fig. 3.

Fig. 3

The redefined $f^{-1} _4 :R_t \rightarrow {\tilde{R}}_t$

Aim 1: define $A: T_1 \rightarrow {\tilde{T}}_1$. Set

$$\begin{aligned} A_2 (x,y) = \frac{\beta _t}{4 \delta _t \gamma _t} \left( y-\gamma _t \big (\frac{1}{2} -\delta _t \big ) \right) +\frac{\beta _t}{4} \qquad \forall (x,y) \in T_1 . \end{aligned}$$

(4.3.4)

For a given $(x,y) \in T_1 ,$ let $(x_p, y) = P_1 Q_1 \cap \{(X,Y) \in {\mathbb {R}}^2 : Y=y\}$, $({\tilde{x}}_p , A_2 ) = {\tilde{P}}_1 {\tilde{Q}}_1 \cap \{(X,Y)\in {\mathbb {R}}^2 : Y= A_2 (x,y) \}$, $\ell (y)$ be the length of $T_1 \cap \{(X,Y): Y= y\},$ and ${\tilde{\ell }} (y)$ be the length of ${\tilde{T}}_1 \cap \{(X,Y): Y= A_2\}.$ Denote $(P_1)_1$ by the first coordinate of $P_1 .$ Then

$$\begin{aligned} x_p= & {} -y + \frac{\gamma _t}{2} + (P_1)_1 \text{ and } {\tilde{x}}_p = \frac{2\alpha _t -\beta _t}{\beta _t} \left( \frac{\beta _t}{2} -A_2 \right) +({\tilde{P}}_1)_1 , \end{aligned}$$

(4.3.5)

$$\begin{aligned} \ell (y)= & {} 2y \approx \gamma _t \text{ and } {\tilde{\ell }} (y) = \frac{4 \alpha _t -2 \beta _t}{\beta _t} A_2 (x,y) + \beta _t -\alpha _t \ge \frac{\beta _t}{2}. \end{aligned}$$

(4.3.6)

Let $u=\frac{\gamma _t}{\ell (y)} (x-x_p) + (P_1)_1$ for $(x,y) \in T_1 ,$ and $\eta$ be as in (4.1.2). Define

$$\begin{aligned} A_1 (x,y) = \frac{{\tilde{\ell }} (y)}{\alpha _t} \left( \eta ^{-1} (u) -({\tilde{P}}_1)_1 \right) + {\tilde{x}}_p \qquad \forall (x,y) \in T_1 . \end{aligned}$$

(4.3.7)

By (4.3.7) and (4.3.4), we have that

$$\begin{aligned} A= (A_1 , A_2 ) \end{aligned}$$

(4.3.8)

is a diffeomorphism from $T_1$ onto ${\tilde{T}}_1 .$ We next give some estimates for A. By (4.3.2) we have that

$$\begin{aligned} \frac{\partial A_2 (x,y)}{\partial y} = \frac{\beta _t}{4 \delta _t \gamma _t} \approx \frac{t^{2s-1}}{\delta _t} \qquad \forall (x,y) \in T_1. \end{aligned}$$

(4.3.9)

From (4.1.3), (4.3.6), and (4.3.2) it follows that

$$\begin{aligned} \frac{\partial A_1 (x,y)}{\partial x} = \frac{{\tilde{\ell }} (y)}{\alpha _t} (\eta ^{-1})' (u) \frac{\partial u}{\partial x} \approx \frac{{\tilde{\ell }} (y)}{t} \qquad \forall (x,y) \in T_1. \end{aligned}$$

(4.3.10)

Moreover, by (4.3.5) and (4.3.6) we have that

$$\begin{aligned} \frac{\partial x_p}{\partial y} =-1,\ \frac{\partial {\tilde{x}}_p}{\partial y} =\frac{\beta _t -2\alpha _t}{\beta _t} \frac{\partial A_2}{\partial y} ,\ \frac{\partial \ell (y)}{\partial y} =2 \text{ and } \frac{\partial {\tilde{\ell }}(y)}{\partial y} = \frac{4 \alpha _t -2 \beta _t}{\beta _t} \frac{\partial A_2}{\partial y}.\nonumber \\ \end{aligned}$$

(4.3.11)

It follows from (4.3.11) that

$$\begin{aligned} \frac{\partial A_1}{\partial y} =&\frac{\partial {\tilde{x}}_p}{\partial y} + \frac{\partial {\tilde{\ell }} (y)}{\alpha _t \partial y} \left( \eta ^{-1} (u) - ({\tilde{P}}_1 )_1 \right) + \frac{{\tilde{\ell }}(y)}{\alpha _t} (\eta ^{-1})' (u) \frac{\partial u}{\partial y} \nonumber \\ =&\frac{2\alpha _t -\beta _t}{\beta _t} \frac{\partial A_2}{\partial y} \left[ -1+\frac{2}{\alpha _t} (\eta ^{-1} (u) -({\tilde{P}}_1)_1)\right] \nonumber \\&+ \frac{\gamma _t {\tilde{\ell }}(y)}{\alpha _t \ell (y)} (\eta ^{-1})' (u) \left[ 1- \frac{2}{\ell (y)} (x-x_p)\right] . \end{aligned}$$

(4.3.12)

Notice that $0 \le \eta ^{-1} (u) -({\tilde{P}}_1)_1 \le \alpha _t$ and $0 \le x-x_p \le \ell (y)$ for all $(x,y) \in T_1 .$ Therefore (4.3.12) together with (4.3.2) and (4.3.9) implies

$$\begin{aligned} \left| \frac{\partial A_1 (x,y)}{\partial y} \right| \lesssim \frac{2\alpha _t -\beta _t}{\beta _t} \frac{\partial A_2 (x,y)}{\partial y} \approx \frac{t}{\delta _t} \qquad \forall (x,y) \in T_1 . \end{aligned}$$

(4.3.13)

We conclude from (4.3.9), (4.3.10), and (4.3.13) that

$$\begin{aligned} |DA(x,y)| \lesssim \max \left\{ \left| \frac{\partial A_1}{\partial x} \right| ,\ \left| \frac{\partial A_1}{\partial y}\right| ,\ \left| \frac{\partial A_2}{\partial x}\right| ,\ \left| \frac{\partial A_2}{\partial y} \right| \right\} \lesssim \frac{t}{\delta _t} \end{aligned}$$

(4.3.14)

and

$$\begin{aligned} J_A (x,y) = \frac{\partial A_1}{\partial x} \frac{\partial A_2}{\partial y} \approx \frac{t^{2s-2} {\tilde{\ell }}(y)}{\delta _t} \end{aligned}$$

(4.3.15)

for all $t\ll 1$ and all $(x,y) \in T_1 .$ Moreover by (4.3.14), (4.3.15), and (4.3.6) we have that

$$\begin{aligned} K_A (x,y)= \frac{|DA(x,y)|^2}{J_A (x,y)} \lesssim \frac{t^{4-2s}}{\delta _t {\tilde{\ell }}(y)} \lesssim \frac{t^{4(1-s)}}{\delta _t} \end{aligned}$$

(4.3.16)

holds for all $t\ll 1$ and all $(x,y) \in T_1 .$

Aim 2: define $B: T_2 \rightarrow {\tilde{T}}_2$. Denote by $P_c$ and ${\tilde{P}}_c$ be the center of $R_t$ and ${\tilde{R}}_t ,$ respectively. Given $(x,y) \in T_2,$ we define

$$\begin{aligned} B_1 (x,y)= & {} \frac{2 \alpha _t -\beta _t}{4 \delta _t \gamma _t} \left( x- (P_c)_1 - \frac{\gamma _t}{2} \right) + ({\tilde{P}}_c)_1 + \frac{\alpha _t}{2} ,\ B_2 (x,y)\\= & {} y \frac{a(x-(P_c)_1) +b}{c( x-(P_c)_1)+d}, \end{aligned}$$

where $a,\ b,\ c,\ d$ satisfy

$$\begin{aligned} a \gamma _t \left( \frac{1}{2} -\delta _t\right) +b= & {} \frac{\beta _t}{4} ,\ a \frac{\gamma _t}{2} +b = \frac{\beta _t}{2},\ c \gamma _t \left( \frac{1}{2} -\delta _t\right) +d \nonumber \\= & {} \gamma _t \left( \frac{1}{2} -\delta _t\right) ,\ c \frac{\gamma _t}{2} +d = \frac{\gamma _t}{2}. \end{aligned}$$

(4.3.17)

Then

$$\begin{aligned} B=(B_1 , B_2) \end{aligned}$$

(4.3.18)

is a diffeomorphism from $T_2$ onto ${\tilde{T}}_2.$ By (4.3.2) we have that

$$\begin{aligned} \frac{\partial B_1 (x,y)}{\partial x} = \frac{2\alpha _t -\beta _t}{4 \delta _t \gamma _t} \approx \frac{t}{\delta _t} \qquad \forall (x,y) \in T_2. \end{aligned}$$

(4.3.19)

Moreover, from (4.3.17) and (4.3.2) we have that

$$\begin{aligned} \frac{\partial B_2 (x,y)}{\partial y} = \frac{a(x-(P_c)_1) +b}{c( x-(P_c)_1)+d} \approx \frac{\beta _t}{\gamma _t} \approx t^{2s-1} \end{aligned}$$

(4.3.20)

and

$$\begin{aligned} \left| \frac{\partial B_2 (x,y)}{\partial x} \right| = \frac{|y (ad-bc)|}{[c( x-(P_c)_1)+d]^2} \lesssim \frac{\gamma _t b}{\gamma ^2 _t} \approx t^{2s-1} \end{aligned}$$

(4.3.21)

for all $(x,y) \in T_2.$ We then conclude from (4.3.19), (4.3.20) and (4.3.21) that

$$\begin{aligned} |DB (x,y)| \lesssim \max \left\{ \left| \frac{\partial B_1}{\partial x} \right| ,\ \left| \frac{\partial B_1}{\partial y}\right| ,\ \left| \frac{\partial B_2}{\partial x}\right| ,\ \left| \frac{\partial B_2}{\partial y} \right| \right\} \lesssim \frac{t}{\delta _t} \end{aligned}$$

(4.3.22)

and

$$\begin{aligned} J_B (x,y) = \frac{\partial B_1}{\partial x} \frac{\partial B_2}{\partial y} \approx \frac{t^{2s}}{\delta _t}. \end{aligned}$$

(4.3.23)

for all $t \ll 1$ and all $(x,y) \in T_2 .$ Moreover by (4.3.22) and (4.3.23) we have that

$$\begin{aligned} K_B (x,y) = \frac{|DB(x,y)|^2}{J_B (x,y)} \lesssim \frac{t^{2(1-s)}}{\delta _t} \end{aligned}$$

(4.3.24)

for all $t \ll 1$ and all $(x,y) \in T_2 .$

Aim 3: define $C : T_0 \rightarrow {\tilde{T}}_0$. By (4.3.8) and (4.3.18) we have that $Q_1 Q_2$ is mapped onto ${\tilde{Q}}_1 {\tilde{Q}}_2$ by $A_1 (\cdot , \gamma _t(1/2 -\delta _t),$ and $Q_2 Q_3$ is mapped onto ${\tilde{Q}}_2 {\tilde{Q}}_3$ by $B_2 ((P_c)_1 + \gamma _t(1/2 -\delta _t) , \cdot ).$ For a given $(x,y) \in T_0 ,$ define

$$\begin{aligned} C(x,y)= \left( A_1 \big (x, \gamma _t(\frac{1}{2} -\delta _t) \big ), B_2 \big ( (P_c)_1 + \gamma _t(\frac{1}{2} -\delta _t) , y \big ) \right) . \end{aligned}$$

(4.3.25)

Then $C : T_0 \rightarrow {\tilde{T}}_0$ is diffeomorphic. By (4.3.10) and (4.3.20), we have that

$$\begin{aligned} \frac{\partial }{\partial x} A_1 \left( x, \gamma _t(1/2 -\delta _t) \approx t^{2s -1},\ \frac{\partial }{y} B_2 ((P_c)_1 + \gamma _t(1/2 -\delta _t) , y\right) \approx t^{2s -1} \end{aligned}$$

for all $(x,y) \in T_0 .$ Therefore

$$\begin{aligned} |DC(x,y)| \lesssim t^{2s-1} \text{ and } K_C (x,y) \approx 1 \end{aligned}$$

(4.3.26)

for all $t \ll 1$ and all $(x,y) \in T_0 .$

Aim 4: redefine $f^{-1} _4$ and E. Via (4.3.8), (4.3.18), and (4.3.25), we set $f^{-1} _4: R_t \rightarrow {\tilde{R}}_t$ in (4.1.18) as

$$\begin{aligned} f^{-1} _4 (x,y) = {\left\{ \begin{array}{ll} A(x,y) &{}\forall (x,y) \in T_1 , \\ B(x,y) &{} \forall (x,y) \in T_2 ,\\ \left( A_1 (x,-y) ,-A_2 (x,-y) \right) , &{} \forall (x,y) \in T_3 ,\\ (2 ({\tilde{P}}_c)_1 -B_1 (2 (P_c)_1 -x,y), B_2 (2 (P_c)_1 -x,y)) &{} \forall (x,y) \in T_4 ,\\ C(x,y)&{} \forall (x,y) \in T_0 . \end{array}\right. }\nonumber \\ \end{aligned}$$

(4.3.27)

Like in Sect. 4.1, by taking a fixed $j_0 \gg 1$ we then define $F_{2^{-j}} :Q_{2^{-j}} \rightarrow {\tilde{Q}}_{2^{-j}}$ for all $j \ge j_0$, $E_1 :\Omega _1 \rightarrow {\tilde{\Omega }}_1$, $E_2 :\Omega _2 \rightarrow {\tilde{\Omega }}_2$, and $E :{{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2 .$ It is not difficult to see that the new-defined E is a homeomorphism such that $E(z) =z^2$ for all $z \in \overline{M_s}$ and satisfies (2.2.1) for E on ${\mathcal {L}}^2\hbox {-a.e. }{\mathbb {R}}^2 .$ To show that $E \in {\mathcal {E}}_s ,$ via (2.2.3) it is then enough to prove that $E \in W^{1,1} _{\text {loc}} ({{\mathbb {R}}}^2 , {{\mathbb {R}}}^2) .$ By (4.1.12), (4.1.17), (4.3.14), (4.3.22), and (4.3.26), we have that

$$\begin{aligned} DF_{2^{-j}} (z) =&Df^{-1} _3 (f^{-1} _4 \circ f_2 \circ f^{-1} _1 (z)) D f^{-1} _4 ( f_2 \circ f^{-1} _1 (z)) D (f_2 \circ f^{-1} _1) (z) \nonumber \\ \lesssim&{\left\{ \begin{array}{ll} \frac{2^{-j}}{\delta _{2^{-j}}} &{} {\mathcal {L}}^2 \text{-a.e. } z \in f_1 \circ f^{-1} _2 (\cup _{k=1} ^{4} T_k) , \\ 2^{j(1-2s)} &{} {\mathcal {L}}^2 \text{-a.e. } z \in f_1 \circ f^{-1} _2 (T_0) , \end{array}\right. } \end{aligned}$$

(4.3.28)

for all $j \ge j_0.$ Notice that

$$\begin{aligned} {\mathcal {L}}^2 (T_0 ) = (\gamma _{2^{-j}} (1-2\delta _{2^{-j}}))^2 \approx 2^{-2j} ,\ {\mathcal {L}}^2 (T_k) = \delta _{2^{-j}} \gamma ^2 _{2^{-j}} (1-\delta _{2^{-j}}) \approx \delta _{2^{-j}} 2^{-2j} \end{aligned}$$

for all $k=1,2,3,4$ and all $j \ge j_0 .$ It hence follows from (4.1.10) that

$$\begin{aligned} {\mathcal {L}}^2 (f_1 \circ f^{-1} _2 (T_0)) \approx 2^{-2j} ,\ {\mathcal {L}}^2 (f_1 \circ f^{-1} _2 (T_k)) \approx \delta _{2^{-j}} 2^{-2j} \quad \text{ for } \text{ all } k=1,2,3,4.\nonumber \\ \end{aligned}$$

(4.3.29)

By (4.3.28) and (4.3.29) we then have that

$$\begin{aligned} \int _{Q_{2^{-j}}} \big |DF_{2^{-j}}\big | = \sum _{k=0} ^{4} \int _{f_1 \circ f^{-1} _2 (T_k)} \big |DF_{2^{-j}}\big | \lesssim 2^{-3j} + 2^{-j(2s+1)} \lesssim 2^{-3j} \qquad \forall j \ge j_0 . \end{aligned}$$

Therefore

$$\begin{aligned} \int _{\Omega _1} |DE_1| = \sum _{j=j_0} ^{\infty } \int _{Q_{2^{-j}}} \big |DF_{2^{-j}}\big | \lesssim \sum _{j=j_0} ^{\infty } 2^{-3j} <\infty . \end{aligned}$$

(4.3.30)

By (4.1.29), (4.3.30), and the fact that $E(z)=z^2$ for all $z \in M_s ,$ we have that $E \in W^{1,1} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2) .$

We next show $K_{E} \in L^q _{\text {loc}} ({\mathbb {R}}^2)$ for all $q < 1.$ By (4.1.13), (4.1.17), (4.3.16), (4.3.24), and (4.3.26), we have that

$$\begin{aligned} K_{F_{2^{-j}}} (z)\lesssim {\left\{ \begin{array}{ll} \frac{2^{4j(s-1)}}{\delta _{2^{-j}}} &{} \forall \ z \in f_1 \circ f^{-1} _2 (T_1 \cup T_3),\\ \frac{2^{2j(s-1)}}{\delta _{2^{-j}}} &{}\forall \ z \in f_1 \circ f^{-1} _2 (T_2 \cup T_4), \\ 1 &{}\forall \ z \in f_1 \circ f^{-1} _2 (T_0). \end{array}\right. } \end{aligned}$$

(4.3.31)

for all $j \ge j_0 .$ For any $q \ge 0,$ via (4.3.29) and (4.3.31) we obtain that

$$\begin{aligned} \int _{Q_{2^{-j}}} K^q _{F_{2^{-j}}} = \sum _{k=0} ^{4} \int _{f_1 \circ f^{-1} _2 (T_k)} K^q _{F_{2^{-j}}} \lesssim \delta ^{1-q} _{2^{-j}} 2^{j(4q (s-1) -2)} \big (1+2^{2qj(1-s)}\big ) +2^{-2j} \end{aligned}$$

for all $j \ge j_0 .$ Therefore

$$\begin{aligned} \int _{\Omega _1} K^q_{E} =&\sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} K^q _{F_{2^{-j}}} \nonumber \\ \lesssim&\sum _{j=j_0} ^{+\infty } \exp \big ((q-1)2^j\big ) 2^{j(4q (s-1) -2)} \big (1+2^{j2q (1-s)}\big ) +\sum _{j=j_0} ^{+\infty } 2^{-2j} <+\infty \end{aligned}$$

(4.3.32)

for all $q \in (0,1)$ and each $s > 1.$ By (4.1.29), (4.3.32), and the fact that E is conformal on $M_s ,$ we conclude that $K_E \in L^q _{\text {loc}} ({{\mathbb {R}}}^2)$ for all $q \in (0,1) .$ $\square$

4.4 Proof of (1.0.9) in Theorem 1.2

Proof

Analogously to the proof of (1.0.10) in Sect. 4.2, via Lemma 3.5 (4), (3.0.41), and (3.0.42) it suffices to construct $E \in {\mathcal {E}}_s$ satisfying that $E \in W^{1,p} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ for some $p>1$ and $K_{E} \in L^q _{\text {loc}}$ for all $q < \max \{1/(s-1), M(p,s)\}.$ Here we denote $M(p,s) = 3p/((2s-1)p+4-2s)$ with $p>1 .$ The construction is divided into two cases.

Case 1: $\varvec{s \in (1,2)}.$ Let E be as in (4.1.31). Then $E \in {\mathcal {E}}_s .$ By (4.1.25), (4.1.29), and the fact that $E(z)=z^2$ for all $z \in M_s,$ we obtain that $E \in W^{1,p} _{\text {loc}} ({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ for all $p \ge 1 .$ From (4.1.17), (4.1.22), and (4.1.13), it follows that

$$\begin{aligned} K_{F_{2^{-j}}} (z) = K_{f^{-1} _3} (f^{-1} _4 \circ f_2 \circ f^{-1} _1 (z)) K_{f^{-1} _4} (f_2 \circ f^{-1} _1 (z)) K_{f_2 \circ f^{-1} _1} (z) \approx 2^{(2s-2)j} \end{aligned}$$

for all $j \ge j_0$ and ${\mathcal {L}}^2\hbox {-a.e. }z \in Q_{2^{-j}} .$ Together with ${\mathcal {L}}^2(Q_{2^{-j}})\approx 2^{-2j},$ we then obtain

$$\begin{aligned} \int _{\Omega _1} K^q _E = \sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} K^q _{F_{2^{-j}}} \approx \sum _{j=j_0} ^{+\infty } 2^{-j2(1+q(1-s))} <\infty \end{aligned}$$

(4.4.1)

for all $q < 1/(s-1).$ By (4.4.1), (4.1.29), and the fact that E is conformal on $M_s,$ we have that $K_E \in L^q _{\text {loc}} ({\mathbb {R}}^2)$ for all $q <1/(s-1) .$

Case 2: $\varvec{s \in [2,\infty )}.$ Redefining $\delta _t$ in (4.3.3) as

$$\begin{aligned} \delta _t=t^{\frac{p+2}{p-1}} \log ^{\frac{p}{p-1}} (t^{-1}). \end{aligned}$$

We follow the methods in Sect. 4.3 to define a new $f^{-1} _4 .$ Set $j_0 \gg 1.$ There are then new $F_{2^{-j}} :Q_{2^{-j}} \rightarrow {\tilde{Q}}_{2^{-j}}$ for all $j \ge j_0$, $E_1 :\Omega _1 \rightarrow {\tilde{\Omega }}_1$, $E_2 : \Omega _2 \rightarrow {\tilde{\Omega }}_2$, and $E :{{\mathbb {R}}}^2 \rightarrow {{\mathbb {R}}}^2 .$ It is not difficult to see that the new E is homeomorphic and satisfies (2.2.1) for E on ${\mathcal {L}}^2\hbox {-a.e. } {\mathbb {R}}^2 .$ To show that E satisfies all requirements, it is enough to check that $E \in W^{1,p} _{\text {loc}}({\mathbb {R}}^2 , {{\mathbb {R}}}^2)$ and $K_E \in L^{q} _{\text {loc}}({\mathbb {R}}^2)$ for all $q \in (0,M(p,s)) .$

From (4.1.12), (4.1.17), (4.3.14), (4.3.22), and (4.3.26), we have that

$$\begin{aligned} |DF_{2^{-j}} (z)| \lesssim {\left\{ \begin{array}{ll} \frac{2^{-j}}{\delta _{2^{-j}}} &{}\forall z \in f_1 \circ f^{-1} _2 (\cup _{k=1} ^{4} T_k) ,\\ 2^{j(1-2s)} &{} \forall z \in f_1 \circ f^{-1} _2 (T_0) , \end{array}\right. } \end{aligned}$$

(4.4.2)

for all $j \ge j_0 .$ It follows from (4.4.2) and (4.3.29) that

$$\begin{aligned} \int _{Q_{2^{-j}}} \big |DF_{2^{-j}}\big |^p = \sum _{k=0} ^{4} \int _{f_1 \circ f^{-1} _2 (T_k)} \big |DF_{2^{-j}}\big |^p \lesssim \delta ^{1-p} _{2^{-j}} 2^{-j(2+p)} +2^{j(p(1-2s) -2)} . \end{aligned}$$

Therefore

$$\begin{aligned} \int _{\Omega _1} |DE|^p = \sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} \big |DF_{2^{-j}}\big |^p \lesssim \sum _{j=j_0} ^{+\infty } \frac{1}{j^p } + \sum _{j=j_0} ^{+\infty } 2^{-j(p(2s-1) +2)} <\infty .\nonumber \\ \end{aligned}$$

(4.4.3)

By (4.4.3), (4.1.29), and the fact that $E(z)=z^2$ for all $z \in M_s ,$ we conclude that $E \in W^{1,p} _{\text {loc}}({\mathbb {R}}^2 , {{\mathbb {R}}}^2) .$ By (4.1.12), (4.1.13), Lemma 2.1, and (4.1.17), we have

$$\begin{aligned} \int _{f_1 \circ f^{-1} _2 (T_1)} K^q _{F_{2^{-j}}} \approx&\int _{f_1 \circ f^{-1} _2 (T_1)} K^q _{f^{-1} _3} (f^{-1} _4 \circ f_2 \circ f^{-1} _1) K^q _{f^{-1} _4} (f_2 \circ f^{-1} _1) K^q _{f_2 \circ f^{-1} _1} \big |J_{f_2 \circ f^{-1} _1} \big | \nonumber \\ \le&\int _{T_1} K^q _{f^{-1} _3} (f^{-1} _{4} ) K^q _{f^{-1} _{4}} \nonumber \\ \lesssim&\int _{T_1} K^q _{f^{-1} _{4}} \end{aligned}$$

(4.4.4)

for all $q \ge 0$ and all $j \ge j_0 .$ Notice ${\tilde{\ell }}(\gamma _{2^{-j}}/2) =\alpha _{2^{-j}}$ and ${\tilde{\ell }}(\gamma _{2^{-j}}(\frac{1}{2} -\delta _{2^{-j}})) =\beta _{2^{-j}}/2$ for all $j \ge 1.$ By Fubini’s theorem, (4.3.16), (4.3.6), and (4.3.2), we then have

$$\begin{aligned} \int _{T_1} K^q _{f^{-1} _{4}} \lesssim&\int _{\gamma _{2^{-j}}(\frac{1}{2} -\delta _{2^{-j}})} ^{\frac{\gamma _{2^{-j}}}{2}}\int _{x_p} ^{x_p +\ell (y)} \left( \frac{2^{j(2s-4)}}{\delta _{2^{-j}} {\tilde{\ell }} (y)} \right) ^q \, \mathrm{{d}}x \, \mathrm{{d}}y \nonumber \\ \approx&\frac{ 2^{jq(2s-4)} \gamma _{2^{-j}}}{\delta ^q _{2^{-j}}} \int _{\gamma _{2^{-j}}(\frac{1}{2} -\delta _{2^{-j}})} ^{\frac{\gamma _{2^{-j}}}{2}} \frac{1}{{\tilde{\ell }}^q (y)}\, \mathrm{{d}}y \nonumber \\ =&\frac{ 2^{jq(2s-4)} \gamma _{2^{-j}}}{(1-q)\delta ^q _{2^{-j}}} \frac{2 \delta _{2^{-j}} \gamma _{2^{-j}}}{2\alpha _{2^{-j}}-\beta _{2^{-j}}} \left( {\tilde{\ell }}^{1-q} (\frac{\gamma _{2^{-j}}}{2}) - {\tilde{\ell }}^{1-q}(\gamma _{2^{-j}}(\frac{1}{2} -\delta _{2^{-j}})) \right) \nonumber \\ \lesssim&\frac{\delta ^{1-q} _{2^{-j}} 2^{-2j[1+q(1-s)]}}{1-M(p,s)} \end{aligned}$$

(4.4.5)

for any fixed $q \in (0,M(p,s)).$ Combining (4.4.4) with (4.4.5) implies that

$$\begin{aligned} \int _{f_1 \circ f^{-1} _2 (T_1)} K^q _{F_{2^{-j}}} \lesssim \delta ^{1-q} _{2^{-j}} 2^{-2j[1+q(1-s)]} \qquad \forall j \ge j_0. \end{aligned}$$

(4.4.6)

By symmetry of $f^{-1} _4$ between $T_1$ and $T_3,$ it follows from (4.4.6) that

$$\begin{aligned} \int _{f_1 \circ f^{-1} _2 (T_3)} K^q _{F_{2^{-j}}} = \int _{f_1 \circ f^{-1} _2 (T_1)} K^q _{F_{2^{-j}}} \lesssim \delta ^{1-q} _{2^{-j}} 2^{-2j[1+q(1-s)]} \end{aligned}$$

(4.4.7)

for all $j \ge j_0 .$ By (4.3.31) and (4.3.29), we have that

$$\begin{aligned} \int _{f_1 \circ f^{-1} _2 (T_0)} K^q _{F_{2^{-j}}} \lesssim 2^{-2j} \end{aligned}$$

(4.4.8)

and

$$\begin{aligned} \int _{f_1 \circ f^{-1} _2 (T_2 \cup T_4)} K^q _{F_{2^{-j}}} \lesssim \delta _{2^{-j}} 2^{-2j} \left( \frac{2^{2j(s-1)}}{\delta _{2^{-j}}} \right) ^q = \delta ^{1-q} _{2^{-j}} 2^{2j[q(s-1)-1]} \end{aligned}$$

(4.4.9)

for all $j \ge j_0 .$ From (4.4.6), (4.4.7), (4.4.8), and (4.4.9), we conclude that

$$\begin{aligned} \int _{\Omega _1} K^q _{E} =&\sum _{j=j_0} ^{+\infty } \int _{Q_{2^{-j}}} K^q _{F_{2^{-j}}} = \sum _{j=j_0} ^{+\infty } \sum _{k=0} ^{4} \int _{f_1 \circ f^{-1} _2 (T_k)} K^q _{F_{2^{-j}}} \nonumber \\ \lesssim&\sum _{j=j_0} ^{+\infty } 2^{-2j} + 2^{-j \left( \frac{(p+2)(1-q)}{p-1} +2[1+q(1-s)]\right) } \log ^{\frac{p(1-q)}{p-1}} \left( 2^j\right) . \end{aligned}$$

(4.4.10)

Note that

$$\begin{aligned} \frac{(p+2)(1-q)}{p-1} +2[1+q(1-s)] > 0 \Leftrightarrow q < M(p,s). \end{aligned}$$

It from (4.4.10) follows that $\int _{\Omega _1} K^q _{E} < \infty$ for all $q \in (0, M(p,s) ) .$ Together with (4.1.29) and the fact that E is conformal on $M_s ,$ we conclude that $K_E \in L^{q} _{\text {loc}}({\mathbb {R}}^2)$ for all $q \in (0,M(p,s)) .$ $\square$

5 Proof of Theorem 1.1

Proof

Let $\Delta$ be as in (1.0.1). The representation of $\partial \Delta$ in Cartesian coordinates is

$$\begin{aligned} (x^2 +y^2)^2 -4x (x^2 +y^2) -4y^2 =0 . \end{aligned}$$

Hence we can parametrize $\partial \Delta$ in a neighborhood of the origin as

$$\begin{aligned} {\tilde{\Gamma }}_0 =\{(x,y)\in {\mathbb {R}}^2 : x \in [-2^{-j_0},0] , y^2 =d(x)\}, \end{aligned}$$

where $j_0 \gg 1$ and $\mathrm{{d}}(x) =\frac{- x^3 (4-x)}{2-x^2 +2x + \sqrt{1+2x}} .$ Since $\mathrm{{d}}(x) \approx |x|^3$ for all $|x| \ll 1 ,$ there are $c_1>0,\ c_2 >0$ such that

$$\begin{aligned} -c _1 x^3 \le \mathrm{{d}}(x) \le -c _2 x^3 \qquad \forall x \in [-2^{-j_0},0] . \end{aligned}$$

Denote

$$\begin{aligned} {\tilde{\Gamma }}_1= & {} \{(x,y)\in {\mathbb {R}}^2 :x \in [-2^{-j_0},0] , y^2 = -c _1 x^3\}, \\ {\tilde{\Gamma }}_2= & {} \{(x,y)\in {\mathbb {R}}^2 :x \in [-2^{-j_0},0] , y^2 = -c _2 x^3\}, \\ {\tilde{\Gamma }}_3= & {} \{(x,y)\in {\mathbb {R}}^2 : x= -2^{-j_0}, y^2 \in [c _1 (2^{-j_0})^3 , d(-2^{-j_0}) \} , \\ {\tilde{\Gamma }}_4= & {} \{(x,y)\in {\mathbb {R}}^2 : x= -2^{-j_0}, y^2 \in [d(-2^{-j_0}) , c _2 (2^{-j_0})^3] \} . \end{aligned}$$

Let ${\tilde{\Omega }}_u$ and ${\tilde{\Omega }}_d$ be the domains bounded by ${\tilde{\Gamma }}_0 \cup {\tilde{\Gamma }}_2 \cup {\tilde{\Gamma }}_4$ and ${\tilde{\Gamma }}_0 \cup {\tilde{\Gamma }}_1 \cup {\tilde{\Gamma }}_3 ,$ respectively. Denote by $\Omega _u , \Omega _d$ and $\Gamma _k$ for $k=0,...,4$ the images of ${\tilde{\Omega }}_u , {\tilde{\Omega }}_d$ and ${\tilde{\Gamma }}_k$ under the branch of complex-valued function $z^{1/2}$ with $1^{1/2} =1 ,$ respectively.

We first prove the existence of an extension, see Fig. 4.

Fig. 4

The existence of an extension

Let $r= (2^{-2j_0} +c _1 2^{-3 j_0})^{1/4} .$ Denote

$$\begin{aligned} M= & {} \{(x+1,y)\in {\mathbb {R}}^2 : (x,y) \in {\mathbb {D}}\} , \\ \Omega _1= & {} \overline{B(0, r)} \setminus (M \cup \Omega _d) ,\ \Omega _2 = {\mathbb {R}}^2 \setminus (\Omega _1 \cup \Omega _d \cup M), \\ {\tilde{\Omega }}_1= & {} \{(x,y)\in {\mathbb {R}}^2 : x \in [-2^{-j_0} ,0], y^2 \le c _1 |x|^3 \} \text{ and } {\tilde{\Omega }}_2 = {\mathbb {R}}^2 \setminus ({\tilde{\Omega }}_1 \cup {\tilde{\Omega }}_d \cup \Delta ) . \end{aligned}$$

Analogously to the arguments in Sect. 4.1, we define $E_1 : \Omega _1 \rightarrow {\tilde{\Omega }}_1$ and $E_2: \Omega _2 \rightarrow {\tilde{\Omega }}_2 .$ Here $\eta (x) = \sqrt{x} (1+c _1 x)^{1/4}$ and $s=3/2 .$ Define

$$\begin{aligned} E(x,y)= {\left\{ \begin{array}{ll} E_1 (x,y) &{}\forall \ (x,y) \in \Omega _1 ,\\ E_2 (x,y) &{}\forall \ (x,y) \in \Omega _2 ,\\ (x^2 -y^2 ,2xy) &{}\forall \ (x,y) \in M \cup \Omega _d , \end{array}\right. } \end{aligned}$$

(5.0.1)

and $f_0 (x,y) =E(x+1 ,y).$ By the analogous arguments as in Sect. 4.1, we have that $f_0 \in {\mathcal {F}}.$

We next prove (1.0.3). Suppose $f \in {\mathcal {F}} .$ Then ${\hat{f}} (u,v)=f(u-1,v)$ is a homeomorphism of finite distortion on ${\mathbb {R}}^2$ and ${\hat{f}} ( M \setminus \Omega _u) = \Delta \setminus {\tilde{\Omega }}_u.$ By Remark 3.1, we have that if $K_{{\hat{f}}} \in L^q _{\text {loc}} ({\mathbb {R}}^2 )$ then $q < 2 .$ Therefore if $K_f \in L^q _{\text {loc}} ({\mathbb {R}}^2 )$ then $q < 2 .$ In order to prove (1.0.3), it then suffices to construct a mapping $f_0 \in {\mathcal {F}}$ such that $K_{f_0} \in L^q _{\text {loc}} ({\mathbb {R}}^2)$ for all $q <2 .$ Let E be as in (5.0.1) and $f_0 (x,y)=E(x+1 ,y) .$ Then $f_0 \in {\mathcal {F}} .$ The same arguments as for the case $s \in (1,2)$ in Sect. 4.3 show that $K_{E} \in L^{q} _{\text {loc}} ({\mathbb {R}}^2)$ for all $q <2 .$ Therefore $K_{f_0} \in L^{q} _{\text {loc}} ({\mathbb {R}}^2)$ for all $q <2 .$

The strategies to prove (1.0.2), (1.0.4), (1.0.5), and (1.0.6) are same as the one to prove (1.0.3). We leave the details to the interested reader. $\square$