Skip to main content
SpringerLink
Log in

Conformal Mapping of an L-Shaped Domain in Analytical Form

  • GENERAL NUMERICAL METHODS
  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

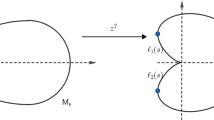
The problem of finding parameters of the Schwarz–Christoffel integral for a conformal mapping \(f\) of a canonical domain onto an L-shaped one is solved analytically for arbitrary geometric parameters of the domain. The unknown preimage is represented in the form of a series in powers of a small parameter with coefficients written in closed form, and an estimate for the moduli of the coefficients is obtained. We find asymptotics for the crowding effect (crowding of preimages), which is especially pronounced for elongated domains. are computing The mapping \(f\) and its inverse \({{f}^{{ - 1}}}\) are computed using series with closed-form coefficients, whose domains of convergence collectively cover the entire (closed) mapped domain. Combining \(f\) with linear fractional mappings and the elliptic sine function yields mappings of the half-plane, disk, and rectangle onto an L-shaped domain. Numerical implementations of the constructed mappings demonstrate the high efficiency of the applied methods.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.
Fig. 12.
Fig. 13.

Similar content being viewed by others

REFERENCES

  1. A. Weinstein, “Der Kontinuitätsbeweis des Abbildungssatzes für Polygone,” Math. Z. 19, 72–84 (1924).

    Article  MATH  Google Scholar 

  2. L. V. Kantorovich and V. I. Krylov, Approximate Methods of Higher Analysis (Fizmatgiz, Moscow, 1962; Wiley, New York, 1964).

  3. W. Koppenfels and F. Stallmann, Praxis der konformen Abbildung (Springer-Verlag, Berlin, 1959).

    Book  MATH  Google Scholar 

  4. D. Gaier, Konstructive Methoden der konformen Abbildung (Springer-Verlag, Berlin, 1964).

    Book  MATH  Google Scholar 

  5. Numerical Conformal Mapping, Ed. by L. N. Trefethen (North-Holland, Amsterdam, 1986).

    MATH  Google Scholar 

  6. P. Henrici, Applied and Computational Complex Analysis (Wiley, New York, 1991), Vol. 3.

    MATH  Google Scholar 

  7. T. A. Driscoll and L. N. Trefethen, Schwarz–Christoffel Mapping (Cambridge Univ. Press, Cambridge, 2002).

    Book  MATH  Google Scholar 

  8. R. Wegmann, “Methods for numerical conformal mapping,” in Handbook of Complex Analysis: Geometric Function Theory, Ed. by R. Kühnau (Elsevier, Amsterdam, 2005), Vol. 2, pp. 351–477.

    Google Scholar 

  9. Higher Transcendental Functions (Bateman Manuscript Project), Ed. by A. Erdélyi (McGraw-Hill, New York, 1953), Vol. 1.

    Google Scholar 

  10. E. T. Whittaker and G. N. Watson, A Course of Modern Analysis, 4th ed. (Cambridge Univ. Press, Cambridge, 1996).

    Book  MATH  Google Scholar 

  11. S. I. Bezrodnykh, “The Lauricella hypergeometric function \(F_{D}^{{(N)}}\), the Riemann–Hilbert problem, and some applications,” Russ. Math. Surv. 73 (6), 941–1031 (2018).

    Article  MathSciNet  MATH  Google Scholar 

  12. V. I. Vlasov, “Variation in a mapping function under domain deformation,” Dokl. Akad. Nauk SSSR 275 (6), 1299–1302 (1984).

    MathSciNet  Google Scholar 

  13. V. I. Vlasov, Boundary Value Problems in Domains with Curved Boundaries (Vychisl. Tsentr Akad. Nauk SSSR, Moscow, 1987) [in Russian].

    Google Scholar 

  14. F. Bowman, Introduction to Elliptic Functions with Applications (Dover, New York, 1961).

    MATH  Google Scholar 

  15. L. N. Trefethen, “Numerical computation of the Schwarz–Christoffel transformation,” SIAM J. Sci. Stat. Comput. 1, 82–102 (1980).

    Article  MathSciNet  MATH  Google Scholar 

  16. T. A. Driscoll, “A MATLAB toolbox for Schwarz–Christoffel mapping,” ACM Trans. Math. Soft. 22, 168–186 (1996).

    Article  MATH  Google Scholar 

  17. P. P. Kufarev, “A method for numerical determination of parameters in the Schwarz–Christoffel integral,” Dokl. Akad. Nauk SSSR 57 (6), 535–537 (1947).

    MathSciNet  MATH  Google Scholar 

  18. I. A. Aleksandrov, Parametric Extensions in the Theory of Univalent Functions (Nauka, Moscow, 1976) [in Russian].

    Google Scholar 

  19. N. N. Nakipov and S. R. Nasyrov, “Parametric method for finding accessory parameters in generalized Schwarz–Christoffel integrals,” Uch. Zap. Kazan. Univ. Ser. Fiz.-mat. Nauki 158 (2), 201–220 (2016).

    Google Scholar 

  20. D. Gaier, “Ermittlung des konformen Moduls von Vierecken mit Differenzenmethoden,” Numer. Math. 19, 179–194 (1972).

    Article  MathSciNet  MATH  Google Scholar 

  21. R. Wegmann, “An estimate for crowding in conformal mapping to elongated regions,” Complex Variables 18, 193–199 (1992).

    MathSciNet  MATH  Google Scholar 

  22. T. K. DeLillo, “The accuracy of numerical conformal mapping methods: A survey of examples and results,” SIAM J. Numer. Anal. 31 (2), 788–812 (1994).

    Article  MathSciNet  MATH  Google Scholar 

  23. S. I. Bezrodnykh and V. I. Vlasov, “The Riemann–Hilbert problem in a complicated domain for a model of magnetic reconnection in a plasma,” Comput. Math. Math. Phys. 42 (3), 263–298 (2002).

    MathSciNet  MATH  Google Scholar 

  24. S. Bezrodnykh, A. Bogatyrev, S. Goreinov, O. Grigor’ev, H. Hakula, and M. Vuorinen, “On capacity computation for symmetric polygonal condensers,” J. Comput. Appl. Math. 631, 272–282 (2019).

    MathSciNet  MATH  Google Scholar 

  25. S. I. Bezrodnykh and V. I. Vlasov, “Asymptotics of the Riemann–Hilbert problem for the Somov magnetic reconnection model for long shock waves,” Math. Notes 110 (5–6), 1702–1717 (2021).

    Article  MATH  Google Scholar 

  26. V. I. Vlasov and S. L. Skorokhodov, “Analytical solution of the Dirichlet problem for the Poisson equation in a class of polygonal domains,” Reports on Applied Mathematics (Vychisl. Tsentr Akad. Nauk SSSR, Moscow, 1988) [in Russian].

  27. V. I. Vlasov and S. L. Skorokhodov, “Development of the Trefftz method,” Dokl. Akad. Nauk 337 (6), 713–717 (1994).

    Google Scholar 

  28. V. I. Vlasov and S. L. Skorokhodov, “A generalization and development of the Trefftz method,” Z. Angew. Math. Mech. 76, suppl. 1, 547–548 (1996).

    MATH  Google Scholar 

  29. E. Trefftz, “Über die Torsion prismatiacher Stäbe von polygonalen Querschnitt,” Math. Ann. 82 (1–2), 97–112 (1921).

    Article  MathSciNet  Google Scholar 

  30. P. Frank and R. von Mises, Die Differential- und Integralgleichungen der Mechanik und Physik, 2nd ed. (Vieweg, Brunswick, 1930, 1935), Vols. 1, 2.

  31. L. N. Trefethen and R. J. Williams, “Conformal mapping solution of Laplace’s equation on a polygon with oblique derivative boundary condition,” J. Comput. Appl. Math. 14, 227–249 (1986).

    Article  MathSciNet  MATH  Google Scholar 

  32. R. Schinzinger and P. A. A. Layra, Conformal Mapping: Methods and Applications (Dover, New York, 1991).

  33. D. Gaier, “Conformal modules and their computation,” in Computational Methods and Function Theory 1994 (Peneng) (World Scientific, River Edge, N.J., 1995), pp. 159–171.

    Google Scholar 

  34. Z. C. Li and T. T. Lu, “Singularities and treatment of elliptic boundary value problems,” Math. Comput. Model. 31, 97–145 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  35. N. Papamichael and N. S. Stylianopoulos, Numerical Conformal Mapping: Domain Decomposition and the Mapping of Quadrilaterals (World Scientific, Singapore, 2010).

    Book  MATH  Google Scholar 

  36. S. D. Algazin, “Numerical experiments in the eigenvalue problem for the Laplace operator in a polygonal domain,” Mat. Model. 23 (7), 88–96 (2011).

    MathSciNet  MATH  Google Scholar 

  37. M. A. Lavrent’ev and B. V. Shabat, Methods of the Theory of Functions of a Complex Variable (Nauka, Moscow, 1965) [in Russian].

    Google Scholar 

  38. G. M. Goluzin, Geometric Theory of Functions of a Complex Variable (Nauka, Moscow, 1966; Am. Math. Soc., Providence, R.I., 1969).

  39. V. V. Golubev, Lectures on Analytic Theory of Differential Equations (Gostekhizdat, Moscow, 1950) [in Russian].

    MATH  Google Scholar 

  40. H. A. Schwarz, “Über die jenigen Falle, in welchen die Gaussische hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt,” J. Reine Angew. Math. 75, 292–335 (1873).

    MathSciNet  Google Scholar 

  41. A. I. Markushevich, Theory of Functions of a Complex Variable (Prentice Hall, Englewood Cliffs, N.J., 1965).

    MATH  Google Scholar 

  42. N. A. Lebedev, Area Principle in the Theory of Univalent Functions (Nauka, Moscow, 1975) [in Russian].

    MATH  Google Scholar 

  43. J. Dieudonne, “Sur les fonctions univalentes,” Compt. Rend. Acad. Sci. (Paris) 192, 1148–1150 (1931).

    MATH  Google Scholar 

  44. W. W. Rogosinski, “Über positive harmonische Entwicklungen und typisch-reelle Potenzreihen,” Math. Z. 32 (1), 93–121 (1932).

    Article  MATH  Google Scholar 

  45. I. I. Privalov, Introduction to the Theory of Functions of a Complex Variable (Nauka, Moscow, 1938) [in Russian].

    Google Scholar 

  46. I. M. Milin, Univalent Functions and Orthonormal Systems (Nauka, Moscow, 1971) [in Russian].

    MATH  Google Scholar 

  47. L. de Branges, “A proof of the Bieberbach conjecture,” Acta Math. 154 (1), 137–152 (1985).

    Article  MathSciNet  MATH  Google Scholar 

  48. C. Carathéodory, “Über die gegenseitige Bezeihung der Ränder bei der Konformer Abbildung des Innern einer Jordanschen Kurve auf einer Kreis,” Math. Ann. 73 (1), 137–152 (1913).

    Article  Google Scholar 

  49. J. Riordan, An Introduction to Combinatorial Analysis (Wiley, New York, 1958).

    MATH  Google Scholar 

  50. G. I. Arkhipov, V. A. Sadovnichii, and V. N. Chubarikov, Lectures on Calculus (Drofa, Moscow, 2004) [in Russian].

    MATH  Google Scholar 

Download references

Funding

This work was supported by the Ministry of Science and Higher Education of the Russian Federation as part of the program of the Moscow Center for Fundamental and Applied Mathematics, agreement no. 075-15-2022-284.

Author information

Authors and Affiliations

  1. Federal Research Center “Computer Science and Control,” Russian Academy of Sciences, 119333, Moscow, Russia

    V. I. Vlasov & S. L. Skorokhodov

  2. Lomonosov Moscow State University, Moscow Center for Fundamental and Applied Mathematics, 119991, Moscow, Russia

    V. I. Vlasov

Authors
  1. V. I. Vlasov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. L. Skorokhodov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to V. I. Vlasov or S. L. Skorokhodov.

Ethics declarations

The authors declare that they have no conflicts of interest.

Additional information

Translated by I. Ruzanova

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Vlasov, V.I., Skorokhodov, S.L. Conformal Mapping of an L-Shaped Domain in Analytical Form. Comput. Math. and Math. Phys. 62, 1971–2007 (2022). https://doi.org/10.1134/S0965542522120132

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542522120132

Keywords:

Search

Navigation