An efficient numerical method for a singularly perturbed Fredholm integro-differential equation with integral boundary condition

Abstract

In this paper, a linear singularly perturbed Fredholm integro-differential initial value problem with integral condition is being considered. On a Shishkin-type mesh, a fitted finite difference approach is applied using a composite trapezoidal rule in both; in the integral part of equation and in the initial condition. The proposed technique acquires a uniform second-order convergence in respect to perturbation parameter. Further provided the numerical results to support the theoretical estimates.

1 Introduction

Singularly perturbed differential equations are described by a small parameter $\varepsilon$ multiplying all or some of the differential equation’s highest order terms, as boundary layers are generally present in their solutions. These equations are crucial for sophisticated scientific computations in the twenty-first century. Singularly perturbed problems (SPPs) are used to express a variety of mathematical models, ranging from chemical reactions to problems in mathematical engineering, fluid dynamics, electrical networks, control theory, aerodynamics, biology and neuroscience. Further information on SPPs may be found in the works [18, 26, 27, 29] and their references. Numerical analysis of SPPs has always been difficult because of the solution’s boundary layer behavior. Within some thin layers at the inside or boundary of the problem domain, such a problem exhibits fast changes [26, 29]. Standard numerical techniques for resolving such problems are widely recognized for being unstable and failing to produce exact results when the perturbation parameter is small. On account of this, it is critical to design numerical methods for solving problems whose accuracy is independent on parameter value. The references [18, 22, 26, 33, 35, 40] cover a variety of techniques for numerically solving this type differential equations.

Differential equations with integral boundary conditions have also been utilized to describe a variety of processes in the applied sciences, such as subsurface water flow, chemical engineering and heat conduction [11, 21, 28]. Therefore, many authors have studied boundary value problems with integral boundary conditions. Researchers have considered the singularly perturbed cases of these problems. The authors in [9, 10, 25, 36] investigated first-order convergent finite difference schemes on non-uniform meshes for various problems with integral boundary conditions.

Integro-differential equations have emerged in most engineering applications and several fields of sciences. Plasma physics, financial mathematics, epidemic models, population dynamics, biology, artificial neural networks, fluid mechanics, electromagnetic theory, financial mathematics, oceanography and physical processes are among these (see, e.g., [8, 39]). For instance, in [23], the integro-differential equation used to modelling infectious diseases in optimal control strategies for policy decisions and applications in COVID-19 has been expressed as follows:

$$\begin{aligned}&\partial _t S\left( t,p\right) =\frac{\mathcal {R}_0}{\mathcal {N}_0}S\left( t,p\right) \int \limits _{t-\delta _{IP}-\delta _{CO}}^{t-\delta _{IP}}\int \limits _{\mathcal {P}}\int \limits _{\mathcal {K}}\hat{\gamma }_I\left( t,p,\tilde{p},\kappa ,t-\tau \right) \mu \left( \tilde{p},\kappa \right) \partial _\tau S\left( \tau ,\tilde{p}\right) d_\kappa d_{\tilde{p}}d_{\tau }, \\&S\left( \tau ,p\right) =S_0\left( \tau ,p\right) , \end{aligned}$$

where

• $\mathcal {P}\subset \mathbb {R}^n,n\in \mathbb {N}$ is the set of features characterizing dissimilar styles of populations (e.g. sex, age),

• $\mathcal {N}_0\in \mathbb {N}_{\ge 1}$ the aggregate number of people aforethought,

• $\mathcal {K}\subset \mathbb {R}^n, n\in \mathbb {N}$ represent a parametrization of different courses of diseases and $\mu :\mathcal {P}\times \mathbb {R}_{\ge 0}$ the probability of a person with property $\tilde{p}\in \mathcal {P}$ suffering from disease $\left( t,p,\tilde{p},\tau \right) \in \mathbb {R}_{>0}\times \mathcal {P}^2\times \mathbb {R}_{>0}$.

• $\mathcal {R}_0$ the basic breeding number, i.e. the number of people infected by a single infectious individual in a completely responsive population.

• $\hat{\gamma }_I:\mathbb {R}_{>0}\times \mathcal {P}^2\times \mathcal {K}\times \mathbb {R}\rightarrow \mathcal {R}_{\ge 0}$, with $\left\| \gamma _I\left( t,p,\tilde{p},.\right) \right\| _{L^1\left( 0,\infty \right) }=1 \, \forall \left( t,p,\tilde{p}\right) \in \mathbb {R}_{\ge 0}\times \mathcal {P}^2$,   $\tau \rightarrow \gamma _I\left( t,p,\tilde{p},t-\tau \right)$ the probability of an infection event between a person with property $\tilde{p}$ infected at time $\tau$ infecting a person with property p at time t.

• $S:\left[ -\delta _{IP}-\delta _{CO},0\right] \times \mathcal {P}\rightarrow \mathbb {R},\,\, \left( t,p,\tau \right) \in \left[ 0,T\right] \times \mathcal {P}\times \left( -\delta _{IP}-\delta _{CO},0\right]$ and $S_0$ is the initial datum. Further, the Incubation Period has been defined by $\delta _{IP}\in \mathbb {R}_{>0}$, and the infectious (COntagious) period by $\delta _{CO}\in \mathbb {R}_{>0}$.

That’s why, many researchers have been pondering the Fredholm integro-differential equations (FIDEs) for a long time. An overview of existence and uniqueness results for the solution of FIDEs can be found in some references such as [1, 19] (see also references therein). Furthermore, researchers employed fitted analytical approaches because of the difficulty of obtaining accurate solutions to these types of problems. Some of these methods are reproducing kernel Hilbert space method [7], Nyström method [38], Touchard polynomials method [2], Tau method [20, 32], Collocation and Kantorovich methods [37], Galerkin method [12, 41, 43], Boole collocation method [14], parameterization method [17], Legendre collocation matrix method[44], variational iteration technique [19]. The increasing interest in recent years is not limited to only FIDEs, but also the numerical solutions of linear and nonlinear Volterra or Volterra-Fredholm integro-differential equations are increasing in popularity. Recently, Turkyilmazoglu presented an effective technique for solving the linear FIDEs and nonlinear Volterra-Fredholm-Hammerstein integro-differential equations based on the Galerkin method [41, 42] (see also references therein).

We consider a singularly perturbed Fredholm integro-differential equation (SPFIDE) with integral boundary condition as follows:

$$\begin{aligned}&Lu:=\varepsilon u^{\prime }\left( x\right) +a(x)u\left( x\right) +\lambda \int \limits _{0}^{l}K(x,s)u(s)ds=f(x),\quad x \in \Omega , \end{aligned}$$

(1)

$$\begin{aligned}&u(0)= \mu u\left( l\right) +\int \limits _{0}^{l}c(s)u(s)ds+A, \end{aligned}$$

(2)

where $\Omega =\left( 0,l\right] \left( \bar{\Omega }=\Omega \cup \lbrace x=0\rbrace \right)$. $0<\varepsilon \le 1$ is a perturbation parameter. $\lambda$, A and $\mu \le 0$ are given constants. We assume that $a(x)\ge \alpha >0$, $c\left( x\right) \le 0$, f(x) and K(x, s) are the sufficiently smooth functions satisfying certain regularity conditions to be specified. Under these conditions, the solution u(x) of the problem (1)-(2) has in general initial layer at $x=0$ for small values of $\varepsilon$. This means that the derivatives of the solution become unbounded for small values of perturbation parameter near $x=0$.

The above-mentioned papers, related to FIDEs, were dealt mainly with the regular cases (i.e., when the boundary layers are absent). Scientists have also given numerical approaches to singular perturbation situations of FIDEs in recent years. Amiraliyev et al. [3, 5] proposed an exponentially fitted difference method on a uniform mesh for solving first and second-order linear SPFIDEs, demonstrating that the approach is first-order convergent uniformly in $\varepsilon$. Difference schemes of the fitted homogeneous type with an accuracy of $O(N^{-2}\ln N)$ on a piecewise uniform mesh for this type of problems are given in [4, 15]. It should also be noted that in [30, 31], for the numerical solution of singularly perturbed Volterra integro-differential equations, first-order difference schemes on a piecewise uniform mesh are given, followed by Richardson extrapolation to obtain the second order of accuracy.

The aim of this work is to present a homogeneous (non-hybrid) type difference scheme for the numerical solution of SPFIDE with an integral condition. A special technique is necessary to establish the appropriate difference scheme and investigate the error analysis for the numerical solution of such problems. The scheme is built using the integral identity method and suitable quadrature rules, with the remainder terms in integral form. The goal is to develop an $\varepsilon$-uniformly second-order homogeneous finite difference method that produces uniform convergent numerical approximations in order to solve problem (1)-(2).

The content is arranged as follows: Some properties of the solution of (1)-(2) are given in Sect. 2. A finite difference scheme and a special piecewise uniform mesh are presented in Sect. 3. The stability and convergence analysis of this scheme are shown in Sect. 4. The numerical results of two examples to verify the theoretical estimates are presented in Sect. 5. Finally, the work ends with a summary of the conclusions in Sect. 6.

2 Properties of the exact solution

We now present some properties of the solution of (1)-(2), which are needed in later sections for the analysis of the appropriate numerical solution. Here, we will use the following notations:

$$\begin{aligned} \left\| g\right\| _\infty \equiv \left\| g\right\| _{\infty ,\bar{\Omega }}=\displaystyle \max _{0\le x\le l}\left| g\left( x\right) \right| , \quad \left\| g\right\| _1 \equiv \left\| g\right\| _{1,\Omega }=\int \limits _{0}^{l}\left| g\left( x\right) \right| dx. \end{aligned}$$

Lemma 1

Assume that $a,f\in C^2[0,l]$ and $\frac{\partial ^m{K}}{\partial {x}^m}\in C[0,l]^2$, $(m=0,1,2).$ Moreover

$$\begin{aligned} \left| \lambda \right| <\frac{\alpha }{\left( \left| \mu \right| +\left\| c\right\| _1+1\right) \displaystyle \max _{0\le x\le l}\int \nolimits _{0}^{l}\left| K\left( x,s\right) \right| ds}. \end{aligned}$$

(3)

Then the solution u(x) of the problem (1)-(2) satisfies the bounds

$$\begin{aligned} \left| u^{(k)}(x)\right| \le C\left\{ 1+\frac{1}{\varepsilon ^k}e^{-\frac{\alpha x}{\varepsilon }}\right\} , \quad x\in [0,l], \quad k=0,1,2. \end{aligned}$$

(4)

Proof

From (1) we have the following relation for $u\left( x\right)$:

$$\begin{aligned} u\left( x\right)= & {} u\left( 0\right) e^{-\frac{1}{\varepsilon }\int \limits _{0}^{x}a\left( \tau \right) d\tau }+\frac{1}{\varepsilon }\int \limits _{0}^{x}f\left( \xi \right) e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{x}a\left( \tau \right) d\tau }d\xi \\&-\frac{\lambda }{\varepsilon }\int \limits _{0}^{x}e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{x}a\left( \tau \right) d\tau }\left( \int \limits _{0}^{l}K\left( \xi ,s\right) u\left( s\right) ds\right) d\xi . \end{aligned}$$

By using the boundary condition (2) we get

$$\begin{aligned} u\left( 0\right)= & {} \frac{\frac{\mu }{\varepsilon }\int \limits _{0}^{l}f\left( \xi \right) e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{l}a\left( \tau \right) d\tau }d\xi +\frac{1}{\varepsilon }\int \limits _{0}^{l}c\left( x\right) \left[ \int \limits _{0}^{x}f\left( \xi \right) e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{x}a\left( \tau \right) d\tau }d\xi \right] dx+A}{1-\mu e^{-\frac{1}{\varepsilon }\int \limits _{0}^{l}a\left( \tau \right) d\tau }-\int \limits _{0}^{l}c\left( x\right) e^{-\frac{1}{\varepsilon }\int \limits _{0}^{x}a\left( \tau \right) d\tau }dx} \nonumber \\&-\frac{\frac{\mu \lambda }{\varepsilon }\int \limits _{0}^{l}e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{l}a\left( \tau \right) d\tau }\left( \int \limits _{0}^{l}K\left( \xi ,s\right) u\left( s\right) ds\right) d\xi }{1-\mu e^{-\frac{1}{\varepsilon }\int \limits _{0}^{l}a\left( \tau \right) d\tau }-\int \limits _{0}^{l}c\left( x\right) e^{-\frac{1}{\varepsilon }\int \limits _{0}^{x}a\left( \tau \right) d\tau }dx} \nonumber \\&-\frac{\frac{\lambda }{\varepsilon }\int \limits _{0}^{l}c\left( x\right) \left[ \int \limits _{0}^{x}e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{x}a\left( \tau \right) d\tau }\left( \int \limits _{0}^{l}K\left( \xi ,s\right) u\left( s\right) ds\right) d\xi \right] dx}{1-\mu e^{-\frac{1}{\varepsilon }\int \limits _{0}^{l}a\left( \tau \right) d\tau }-\int \limits _{0}^{l}c\left( x\right) e^{-\frac{1}{\varepsilon }\int \limits _{0}^{x}a\left( \tau \right) d\tau }dx}. \end{aligned}$$

(5)

Since $\mu \le 0$ and $c\left( x\right) \le 0$, the denominator is bounded below by one.

Also, we can write the numerator of (5) as

$$\begin{aligned}&\left| \frac{\mu }{\varepsilon }\int \limits _{0}^{l}f\left( \xi \right) e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{l}a\left( \tau \right) d\tau }d\xi +\frac{1}{\varepsilon }\int \limits _{0}^{l}c\left( x\right) \left[ \int \limits _{0}^{x}f\left( \xi \right) e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{x}a\left( \tau \right) d\tau }d\xi \right] dx\right| \nonumber \\&\qquad +\left| \frac{\mu \lambda }{\varepsilon }\int \limits _{0}^{l}e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{l}a\left( \tau \right) d\tau }\left( \int \limits _{0}^{l}K\left( \xi ,s\right) u\left( s\right) ds\right) d\xi \right| \nonumber \\&\qquad +\left| A-\frac{\lambda }{\varepsilon }\int \limits _{0}^{l}c\left( x\right) \left[ \int \limits _{0}^{x}e^{-\frac{1}{\varepsilon }\int \limits _{\xi }^{x}a\left( \tau \right) d\tau }\left( \int \limits _{0}^{l}K\left( \xi ,s\right) u\left( s\right) ds\right) d\xi \right] dx\right| \nonumber \\&\quad \le \left| A\right| +\left| \mu \right| \alpha ^{-1}\left\| f\right\| _\infty \left( 1-e^{-\frac{\alpha l}{\varepsilon }}\right) +\alpha ^{-1}\left\| f\right\| _\infty \int \limits _{0}^{l}\left| c\left( x\right) \right| \left( 1-e^{-\frac{\alpha x}{\varepsilon }}\right) dx \nonumber \\&\qquad +\left| \mu \right| \left| \lambda \right| \alpha ^{-1}\left\| u\right\| _\infty \left( 1-e^{-\frac{\alpha l}{\varepsilon }}\right) \displaystyle \max _{0\le \xi \le l}\int \limits _{0}^{l}\left| K\left( \xi ,s\right) \right| ds \nonumber \\&\qquad +\left| \lambda \right| \alpha ^{-1}\left\| u\right\| _\infty \int \limits _{0}^{l}\left| c\left( x\right) \right| \left( 1-e^{-\frac{\alpha l}{\varepsilon }}\right) dx \displaystyle \max _{0\le \xi \le l}\int \limits _{0}^{l}\left| K\left( \xi ,s\right) \right| ds. \end{aligned}$$

(6)

Considering (5) and (6) together, we obtain

$$\begin{aligned} \left| u\left( 0\right) \right|\le & {} \left| A\right| +\left( \left| \mu \right| +\left\| c\right\| _1\right) \alpha ^{-1}\left\| f\right\| _\infty \nonumber \\&+\left( \left| \mu \right| +\left\| c\right\| _1\right) \left| \lambda \right| \alpha ^{-1}\left\| u\right\| _\infty \displaystyle \max _{0\le \xi \le l}\int \limits _{0}^{l}\left| K\left( \xi ,s\right) \right| ds. \end{aligned}$$

(7)

Later on, according to the maximum principle for $L_1u=\varepsilon u^\prime \left( x\right) +a\left( x\right) u\left( x\right)$ from (1), we have

$$\begin{aligned} \left\| u\right\| _\infty \le \left| u\left( 0\right) \right| +\alpha ^{-1}\left\| f\right\| _\infty +\alpha ^{-1}\left| \lambda \right| \left\| u\right\| _\infty \displaystyle \max _{0\le x\le l}\int \limits _{0}^{l}\left| K\left( x,s\right) \right| ds. \end{aligned}$$

Now, considering the estimate of (7) instead of $u\left( 0\right)$ in the above inequality by virtue of (3), we acquire

$$\begin{aligned} \left\| u\right\| _\infty\le & {} \frac{\left| A\right| +\left( \left| \mu \right| +\left\| c\right\| _1+1\right) \alpha ^{-1}\left\| f\right\| _\infty }{1-\left( \left| \mu \right| +\left\| c\right\| _1+1\right) \left| \lambda \right| \alpha ^{-1}\displaystyle \max _{0\le x\le l}\int \limits _{0}^{l}\left| K\left( x,s\right) \right| ds}, \end{aligned}$$

which implies the validity of (4) for $k=0$. The proof of (4) for $k=1,2$ can be proved in a similar way as in [3, 4]. $\square$

3 Designing of the numerical method

Let $\omega _N$ be any non-uniform mesh on [0, l] : 

$$\begin{aligned} \omega _N=\left\{ 0<x_1<...<x_N=l,\,\,\,h_i=x_i-x_{i-1}\right\} \end{aligned}$$

and

$$\begin{aligned} \overline{\omega }_N=\omega _N\cup \left\{ x_0=0\right\} , \quad \hbar _i=\frac{h_i +h_{i+1}}{2}. \end{aligned}$$

Prior to describing our numerical technique, we present certain notations for the mesh functions. To any mesh function v(x) described on $\overline{\omega }_N$, we utilize

$$\begin{aligned} v_i=v(x_i), \quad v_{_{\overset{\_}{x},i}}=\frac{v_i-v_{i-1}}{h_i}, \quad \left\| v\right\| _1\equiv \left\| v \right\| _{1,\omega _N}=\sum _{i=1}^{N}\hbar _i\left| v_i\right| . \end{aligned}$$

(8)

We construct the numerical method using the identity

$$\begin{aligned} \chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}Lu\varphi _i(x)dx=\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}f(x)\varphi _i(x)dx, \qquad 1\le i \le N, \end{aligned}$$

(9)

with the basis functions

$$\begin{aligned} \varphi _i(x)=e^{-\frac{a_{i}(x_i-x)}{\varepsilon }} \end{aligned}$$

and

$$\begin{aligned} \chi _{i}=h_i^{-1}\int \limits ^{x_i}_{x_{i-1}}\varphi _i(x)dx=\frac{1-e^{-a_i\rho _i}}{a_i\rho _i}, \qquad \rho _i=\frac{h_i}{\varepsilon }. \end{aligned}$$

We note that the function $\varphi _i(x)$ is the solution of the problem

$$\begin{aligned} -\varepsilon \varphi ^{\prime }(x)+a_i\varphi (x)=0,\quad \varphi (x_i)=1, \qquad x_{i-1}< x < x_i. \end{aligned}$$

Using the method of exact difference schemes [6, 13, 24, 45] (see also [34], pp. 207-214), for the differential part from (9), we obtain

$$\begin{aligned}&\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}\left[ \varepsilon u^{\prime }(x)+a(x)u(x)\right] \varphi _i(x)dx=\varepsilon \theta _i u_{_{\overset{\_}{x},i}}+a_iu_i \nonumber \\&\quad +\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}\left[ a(x)-a(x_i)\right] u(x)\varphi _i(x)dx \end{aligned}$$

(10)

with

$$\begin{aligned} \theta _i=\frac{a_i\rho _i}{1-e^{-a_i\rho _i}}e^{-a_i\rho _i}. \end{aligned}$$

(11)

By Newton interpolation formula with respect to mesh point $\left( x_{i-1},x_i\right)$ we have

$$\begin{aligned} \ a(x)-a(x_i)=(x-x_i)a_{_{\overset{\_}{x},i}} +\frac{a^{\prime \prime }\big (\xi _i(x)\big )}{2}(x-x_{i-1})(x-x_i). \end{aligned}$$

Therefore we get

$$\begin{aligned}&\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}\left[ a(x)-a(x_i)\right] u(x)\varphi _i(x)dx=a_{_{\overset{\_}{x},i}}\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}(x-x_i)u(x)\varphi _i(x)dx \nonumber \\&\quad +\frac{1}{2}\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}a^{\prime \prime }\big (\xi _i(x)\big )(x-x_{i-1})(x-x_i)u(x)\varphi _i(x)dx. \end{aligned}$$

(12)

Also using

$$\begin{aligned} u(x)=u(x_i)-\int \limits ^{x_i}_{x}u^\prime (s)ds \end{aligned}$$

in the first term at the right side of (12), we have

$$\begin{aligned} \chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}\left[ a(x)-a(x_i)\right] u(x)\varphi _i(x)dx =&\left( a_{_{\overset{\_}{x},i}}\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}(x-x_i)\varphi _i(x)dx\right) u_i \\&+R_i^{(1)}, \end{aligned}$$

where

$$\begin{aligned} R_i^{(1)}&=\frac{1}{2}\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}a^{\prime \prime }\big (\xi _i(x)\big )(x-x_{i-1})(x-x_i)u(x)\varphi _i(x)dx \nonumber \\&-a_{_{\overset{\_}{x},i}}\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}(x-x_i)\varphi _i(x)\bigg (\int \limits ^{x_i}_{x}u^\prime (s)ds\bigg )dx. \end{aligned}$$

(13)

Simple calculation gives

$$\begin{aligned} \chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}(x-x_i)\varphi _i(x)dx=h_i\delta _i, \end{aligned}$$

with

$$\begin{aligned} \delta _i=\frac{e^{-{a_i\rho }}}{1-e^{-{a_i\rho }}}-\frac{1}{a_i\rho }. \end{aligned}$$

(14)

It is easy to see that $-1\le \delta _i\le 0.$ So, the identity (10) degrades to

$$\begin{aligned} \chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}\left[ \varepsilon u^{\prime }(x)+a(x)u(x)\right] \varphi _i(x)dx=\varepsilon \theta _i u_{_{\overset{\_}{x},i}}+\bar{a}_iu_i+R_i^{(1)}, \end{aligned}$$

(15)

where

$$\begin{aligned} \bar{a}_i=a_i+a_{_{\overset{\_}{x},i}}h_i\delta _i \end{aligned}$$

(16)

and $\delta _i$ is given by (14). Analogously we derive

$$\begin{aligned} \chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}f(x)\varphi _i(x)dx=\bar{f}_i+R_i^{(2)}, \end{aligned}$$

(17)

where

$$\begin{aligned} \bar{f}_i= & {} f_i+f_{_{\overset{\_}{x},i}}h_i\delta _i, \end{aligned}$$

(18)

$$\begin{aligned} R_i^{(2)}= & {} \frac{1}{2}\chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}f^{\prime \prime }\big (\eta _i(x)\big )(x-x_{i-1})(x-x_i)\varphi _i(x)dx. \end{aligned}$$

(19)

It remains to obtain an approximation for integral term from (1). Using the Taylor expansion

$$\begin{aligned} K(x,s)=K(x_i,s)+(x-x_i)\frac{\partial }{\partial {x}}K(x_i,s)+ \frac{(x-x_i)^2}{2}\frac{\partial ^2}{\partial {x}^2}K\big (\xi _i(x),s\big ), \end{aligned}$$

we get

$$\begin{aligned} \chi _{i}^{-1}h_{i}^{-1}\lambda \int \limits ^{x_i}_{x_{i-1}}\varphi _i(x)\left( \int \limits ^{l}_{0}K(x,s)u(s)ds\right)&dx=\lambda \int \limits ^{l}_{0}K(x_i,s)u(s)ds \nonumber \\&+h_i\delta _i\lambda \int \limits ^{l}_{0}\frac{\partial }{\partial {x}}K(x_i,s)u(s)ds+R_i^{(3)} \nonumber \\&\equiv \lambda \int \limits ^{l}_{0}\mathcal {K}(x_i,s)u(s)ds+R_i^{(3)}, \end{aligned}$$

(20)

where

$$\begin{aligned} \mathcal {K}(x_i,s)= & {} K(x_i,s)+h_i\delta _i\frac{\partial }{\partial {x}}K(x_i,s), \end{aligned}$$

(21)

$$\begin{aligned} R_i^{(3)}= & {} \frac{1}{2}\lambda \chi _{i}^{-1}h_{i}^{-1}\int \limits ^{x_i}_{x_{i-1}}(x-x_i)^2\varphi _i(x)\left( \int \limits ^{l}_{0}\frac{\partial ^2}{\partial {x}^2}K\big (\xi _i(x),s\big )u(s)ds\right) dx. \qquad \end{aligned}$$

(22)

Next, if the first term at the right side of (20) is operated by applying the composite trapezoidal integration rule with the remainder term in the integral form [4], we get

$$\begin{aligned} \lambda \int \limits ^{l}_{0}\mathcal {K}(x_i,s)u(s)ds=\lambda \sum _{j=0}^{N}\hbar _j\mathcal {K}_{ij}u_j+R_i^{(4)}, \end{aligned}$$

(23)

where

$$\begin{aligned} R_i^{(4)}=\frac{1}{2}\lambda \sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(x_{j-1}-\xi )\frac{d^2}{d\xi ^2}\big (\mathcal {K}(x_i,\xi )u(\xi )\big )d\xi \end{aligned}$$

(24)

and

$$\begin{aligned}&\hbar _i=\frac{h_i + h_{i+1}}{2}, \quad \left( 1\le i \le N-1\right) , \quad \hbar _0=\frac{h_1}{2}, \quad \hbar _N=\frac{h_N}{2}. \end{aligned}$$

To approximate the boundary condition (2), using again the composite trapezoidal integration rule, we have

$$\begin{aligned} u_0=\mu u_N+\sum _{j=0}^{N}\hbar _jc_ju_j+A+r_i, \end{aligned}$$

(25)

where

$$\begin{aligned} r_i=\frac{1}{2}\sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(x_{j-1}-\xi )\frac{d^2}{d\xi ^2}\big (c(\xi )u(\xi )\big )d\xi . \end{aligned}$$

(26)

After taking into consideration (15), (17), (20) and (23) in (9) we obtain the following discrete identity for u(x):

$$\begin{aligned}&\varepsilon \theta _i u_{_{\overset{\_}{x},i}}+\bar{a}_iu_i+\lambda \sum _{j=0}^{N}\hbar _j\mathcal {K}_{ij}u_j+R_i=\bar{f_i} \end{aligned}$$

(27)

with remainder term

$$\begin{aligned} R_i=R_i^{(1)}-R_i^{(2)} + R_i^{(3)} + R_i^{(4)}, \end{aligned}$$

(28)

where $R_i^{(1)}, R_i^{(2)}, R_i^{(3)}, R_i^{(4)}$ and $r_i$ are defined by (13), (19), (22), (24) and (26) respectively.

Based on (27) we propose the following difference scheme for approximating (1)-(2):

$$\begin{aligned}&L_Ny_i:=\varepsilon \theta _i y_{_{\overset{\_}{x},i}}+\bar{a}_iy_i+\lambda \sum _{j=0}^{N}\hbar _j\mathcal {K}_{ij}y_j=\bar{f_i}, \qquad 1\le i\le N, \end{aligned}$$

(29)

$$\begin{aligned}&y_0=\mu y_N+\sum _{j=0}^{N}\hbar _jc_jy_j+A, \end{aligned}$$

(30)

where $\theta _i,\bar{a}_i,\bar{f}_i$ and $\mathcal {K}_{ij}$ are given by (11), (16), (18) and (21) respectively.

To discretize the interval [0, l],  we will use the piecewise-uniform Shishkin type mesh. As the problem (1)-(2) has an exponential initial layer in the neighborhood at $x=0$, we divide [0, l] into two subinterval $\left[ 0,\sigma \right]$ and $\left[ \sigma ,l\right] .$ For an even N,  a uniform mesh with N/2 intervals is placed on each subinterval, where the transition point $\sigma ,$ which separates the fine and coarse portions of $\omega _N$, that is defined as

$$\begin{aligned} \sigma =\min \left\{ \frac{l}{2},\alpha ^{-1}\varepsilon \ln N\right\} . \end{aligned}$$

Hence, if we denote by $h^{(1)}$ and $h^{(2)}$ the stepsizes in $[0,\sigma ]$ and $[\sigma ,l]$ respectively, our piecewise-uniform mesh can be expressed as

$$\begin{aligned} \overline{\omega }_N = \left\{ \begin{array}{lr} x_i=ih^{(1)},\qquad \qquad \qquad \quad \, i=0,1,...,\frac{N}{2};\qquad \quad \, h^{(1)}=\frac{2\sigma }{N}; &{} \\ x_i=\sigma +\left( i-\frac{N}{2}\right) h^{(2)},\qquad i=\frac{N}{2}+1,...,N; \qquad h^{(2)}=\frac{2(l-\sigma )}{N}.&{} \end{array} \right. \end{aligned}$$

4 The convergence

We proceed to estimate the error of the approximate solution $z_i=y_i-u_i$, $\left( 0\le i\le N\right) .$ From (27) and (29) we have

$$\begin{aligned}&L_Nz_i:=\varepsilon \theta _i z_{_{\overset{\_}{x},i}}+\bar{a}_iz_i+\lambda \sum _{j=0}^{N}\hbar _j\mathcal {K}_{ij}z_j=R_i, \qquad 1\le i\le N, \end{aligned}$$

(31)

$$\begin{aligned}&z_0=\mu z_N+\sum _{j=0}^{N}\hbar _jc_jz_j-r_i, \end{aligned}$$

(32)

where the truncation error functions $r_i$ and $R_i$ is given by (26) and (28).

It should be noted that since $a\in C^2 [0,l]$ and $\left| \delta _i \right| \le 1,$ then exist a number $\bar{\alpha }$ such that for sufficiently large values of N will be $\bar{a}_i\ge \bar{\alpha }>0$ ($\delta _i$ is defined by (14)).

Lemma 2

Assume that $a,f,c\in C^2[0,l]$ and $\frac{\partial ^m{K}}{\partial {x}^m},\frac{\partial ^{m+1}{K}}{\partial {x}\partial {s}^m}\in C^2[0,l]^2, (m=0,1,2).$ Then the truncation error functions $R_i$ and $r_i$ satisfy the estimates

$$\begin{aligned}&\left\| R \right\| _{\infty ,\overline{\omega }_N}\le CN^{-2}\ln N, \end{aligned}$$

(33)

$$\begin{aligned}&\left| r \right| \le CN^{-2}\ln N. \end{aligned}$$

(34)

Proof

First, we estimate the remainder term $r_i$. From the explicit expression (26), under the condition of Lemma 1, we obtain

$$\begin{aligned} \left| r_i\right|&\le C\sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})(1+\left| u^{\prime }(\xi )\right| +\left| u^{\prime \prime }(\xi )\right| )d\xi \nonumber \\&\le C\left( \sum _{j=1}^{N}h_j^3+\sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon }e^{-\frac{\alpha \xi }{\varepsilon }}\right) d\xi \nonumber \\&+C\sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{-\frac{\alpha \xi }{\varepsilon }}d\xi \nonumber \\&\le C\left( \sum _{j=1}^{N}h_j^3+\sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{-\frac{\alpha \xi }{\varepsilon }}\right) d\xi . \end{aligned}$$

(35)

Now we find a convergence error estimate for the first term in the right-side of (35) in our special piecewise-uniform mesh

$$\begin{aligned} \sum _{j=1}^{N}h_j^3=\frac{N}{2}\left| h^{(1)}\right| ^3+\frac{N}{2}\left| h^{(2)}\right| ^3&=4\sigma ^3N^{-2}+4(l-\sigma )^3N^{-2} \nonumber \\&\le CN^{-2}. \end{aligned}$$

(36)

Note that the above estimate is valid for values both $\sigma =\frac{l}{2}$ and $\sigma =\alpha ^{-1}\varepsilon \ln N$.

For the second two term in the right-side of (35), we find the estimate for the case $\sigma =\frac{l}{2}.$ Then it has the form $\frac{l}{2}<\alpha ^{-1}\varepsilon \ln N$ and $h^{(1)}=h^{(2)}=lN^{-1}$. Thus we get

$$\begin{aligned} \sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi&\le \frac{\left| h^{(1)}\right| ^2}{\varepsilon ^2}\int \limits ^{l}_{0}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi \nonumber \\&\le \frac{\left| h^{(1)}\right| ^2}{\varepsilon }\alpha ^{-1}\bigg (1-e^\frac{-\alpha l}{\varepsilon }\bigg ) \nonumber \\&\le 2\alpha ^{-2}lN^{-2}\ln N \nonumber \\&\le CN^{-2}\ln N, \qquad 1\le i\le N. \end{aligned}$$

(37)

For two term in the right-side of (35), we find the estimate for the case $\sigma =\alpha ^{-1}\varepsilon \ln N<\frac{l}{2}$. From this inequality, we can write

$$\begin{aligned}&\sum _{j=1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi =\sum _{j=1}^{N/2}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi \nonumber \\&\quad +\sum _{j=\frac{N}{2}+1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi . \end{aligned}$$

(38)

For the first term in the right-side of (38), we have

$$\begin{aligned} \sum _{j=1}^{N/2}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi&=\left| h^{(1)}\right| ^2\int \limits ^{\sigma }_{0}\frac{1}{\varepsilon ^2}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi \nonumber \\&\le \frac{\left| h^{(1)}\right| ^2}{\varepsilon }\alpha ^{-1} \nonumber \\&\le 2l\alpha ^{-2}N^{-2}\ln N \nonumber \\&\le CN^{-2}\ln N. \end{aligned}$$

(39)

For the second term in the right-side of (38), we obtain

$$\begin{aligned} \sum _{j=\frac{N}{2}+1}^{N}\int \limits ^{x_j}_{x_{j-1}}(x_j-\xi )(\xi -x_{j-1})\frac{1}{\varepsilon ^2}e^{\frac{-\alpha \xi }{\varepsilon }}d\xi&=2\alpha ^{-1}\sum _{j=\frac{N}{2}+1}^{N}\int \limits ^{x_j}_{x_{j-1}}\left( x_j-x-\frac{h^{(2)}}{2}\right) \frac{1}{\varepsilon }e^{\frac{-\alpha x}{\varepsilon }}dx \nonumber \\&\le 2\alpha ^{-1}h^{(2)}\int \limits ^{l}_{\sigma }\frac{1}{\varepsilon }e^{\frac{-\alpha x}{\varepsilon }}dx \nonumber \\&=2\alpha ^{-2}h^{(2)}\left( e^{\frac{-\alpha \sigma }{\varepsilon }}-e^{\frac{-\alpha l}{\varepsilon }}\right) \nonumber \\&\le 2\alpha ^{-2}h^{(2)}N^{-1} \nonumber \\&\le CN^{-2}. \end{aligned}$$

(40)

Therefore, the estimates (36), (37), (39) and (40) along with (35) yield (34).

Further, to confirm (33), we will estimate the remainder terms $R_i^{(1)}, R_i^{(2)}, R_i^{(3)}$ and $R_i^{(4)}$ separately. For $R_i^{(4)}$, taking into account the boundedness of $\frac{\partial ^2 K}{\partial x^2}$, from (24) similar to above, we get

$$\begin{aligned} \left| R_i^{(4)}\right| \le CN^{-2}\ln N. \end{aligned}$$

(41)

Next, we will estimate $R_i^{(1)}.$ Since $a\in C^2[0,l]$, $\left| x-x_{i-1}\right| \le h_i$ and $\left| x-x_i\right| \le h_i,$ by using Lemma 1, it follows that

$$\begin{aligned} \left| R_i^{(1)}\right|&\le Ch_i^2+\left| a_{{\overline{x}},i}\delta _i\right| h_i\int \limits ^{x_i}_{x_{i-1}}\left| u^{\prime }(x)\right| dx \nonumber \\&\le Ch_i^2+Ch_i\int \limits ^{x_i}_{x_{i-1}}\left| u^{\prime }(x)\right| dx \nonumber \\&\le C\left( h_i^2 + h_i\int \limits ^{x_i}_{x_{i-1}}\frac{1}{\varepsilon }e^{\frac{-\alpha x}{\varepsilon }}dx\right) . \end{aligned}$$

(42)

We find the estimate for the case $\sigma =\frac{l}{2}.$ Then $\frac{l}{2}<\alpha ^{-1}\varepsilon \ln N$ and $h^{(1)}=h^{(2)}=lN^{-1}.$ Hence we have

$$\begin{aligned} h_i\int \limits ^{x_i}_{x_{i-1}}\frac{1}{\varepsilon }e^{\frac{-\alpha x}{\varepsilon }}dx&\le \frac{\left| h^{(1)}\right| ^2}{\varepsilon } \nonumber \\&\le CN^{-2}, \qquad 1\le i\le N. \end{aligned}$$

(43)

We now consider the case $\sigma =\alpha ^{-1}\varepsilon \ln N<\frac{l}{2}$ in (42) on $\omega _N.$ The inequalities

$$\begin{aligned} h_i\int \limits ^{x_i}_{x_{i-1}}\frac{1}{\varepsilon }e^{\frac{-\alpha x}{\varepsilon }}dx&\le \frac{\left| h^{(1)}\right| ^2}{\varepsilon }=\left( \frac{2\sigma }{N}\right) ^2\frac{1}{\varepsilon }=\bigg (\frac{2\alpha ^{-1}\varepsilon \ln N}{N}\bigg )^2\frac{1}{\varepsilon }=4\alpha ^{-2}\varepsilon N^{-2}\ln ^{2}N \\&\le \frac{l}{2}4\alpha ^{-1}N^{-2}\ln N \\&\le CN^{-2}\ln N, \qquad 1\le i\le \frac{N}{2},\\ h_i\int \limits ^{x_i}_{x_{i-1}}\frac{1}{\varepsilon }e^{\frac{-\alpha x}{\varepsilon }}dx&\le h^{(2)}\alpha ^{-1}\bigg (e^{\frac{-\alpha x_{i-1}}{\varepsilon }}-e^{\frac{-\alpha x_i}{\varepsilon }}\bigg )=h^{(2)}\alpha ^{-1}e^{\frac{-\alpha x_{i-1}}{\varepsilon }}\bigg (1-e^{\frac{-\alpha h^{(2)}}{\varepsilon }}\bigg )\\&\le h^{(2)}\alpha ^{-1}e^{\frac{-\alpha x_{i-1}}{\varepsilon }}\\&\le h^{(2)}\alpha ^{-1}N^{-1}\\&\le CN^{-2}, \qquad \frac{N}{2}+1\le i\le N \end{aligned}$$

imply that

$$\begin{aligned} h_i\int \limits ^{x_i}_{x_{i-1}}\frac{1}{\varepsilon }e^{\frac{-\alpha x}{\varepsilon }}dx\le CN^{-2}\ln N, \qquad 1\le i\le N. \end{aligned}$$

(44)

Therefore, from (43) and (44), we deduce that

$$\begin{aligned} \left| R_i^{(1)}\right| \le CN^{-2}\ln N, \qquad 1\le i\le N. \end{aligned}$$

(45)

Third, we will estimate $R_i^{(2)}.$ Since $f\in C^2[0,l]$, $\left| x-x_{i-1}\right| \le h_i$ and $\left| x-x_i\right| \le h_i,$ by using Lemma 1, it follows that

$$\begin{aligned} \left| R_i^{(2)}\right|&=\frac{1}{2}\chi _{i}^{-1}h_{i}^{-1}\left| \int \limits ^{x_i}_{x_{i-1}}f^{\prime \prime }\big (\eta _i(x)\big )(x-x_{i-1})(x-x_i)\varphi _i(x)dx\right| \nonumber \\&\le Ch_i^2 \nonumber \\&\le CN^{-2}. \end{aligned}$$

(46)

Note that the above estimate is valid for values both $\sigma =\frac{l}{2}$ and $\sigma =\alpha ^{-1}\varepsilon \ln N$. Fourth, we will estimate $R_i^{(3)}$. By taking into account the boundedness of $\frac{\partial ^2K}{\partial x^2}$, from (22) it follows that

$$\begin{aligned} \left| R_i^{(3)}\right|&\le \frac{1}{2}\chi _{i}^{-1}h_{i}^{-1}\left| \int \limits ^{x_i}_{x_{i-1}}(x-x_i)^2\varphi _i(x)\left( \int \limits ^{l}_{0}\frac{\partial ^2}{\partial {x}^2}K\big (\xi _i(x),s\big )u(s)ds\right) dx\right| \nonumber \\&\le Ch_i^2 \nonumber \\&\le CN^{-2}. \end{aligned}$$

(47)

Note that the above estimate is valid for values both $\sigma =\frac{l}{2}$ and $\sigma =\alpha ^{-1}\varepsilon \ln N$. The inequalities (41), (45), (46) and (47) finish the proof of (33).$\square$

Theorem 1

Let a, c and K satisfy the assumptions from Lemma 2. Moreover

$$\begin{aligned} \left| \lambda \right| <\frac{\bar{\alpha }}{\left( \left| \mu \right| +\left\| c\right\| _1+1\right) \displaystyle \max _{0\le i\le N}\sum _{j=1}^{N}\hbar _j\left| \mathcal {K}_{i,j}\right| }. \end{aligned}$$

(48)

Then for the solution z of the difference problem (31)-(32) holds the estimate

$$\begin{aligned} \left\| z\right\| _{\infty ,\overline{\omega }_N}\le CN^{-2}\ln N. \end{aligned}$$

Proof

Equation (31) may be rewritten as

$$\begin{aligned} \varepsilon \theta _i z_{\bar{x},i}+\bar{a}_iz_i=F_i, \quad 1\le i \le N-1, \end{aligned}$$

(49)

where

$$\begin{aligned} F_i=R_i-\left| \lambda \right| \sum _{j=0}^{N}\hbar _j\mathcal {K}_{ij}z_j. \end{aligned}$$

From (49) we get

$$\begin{aligned} z_i=\frac{\varepsilon \theta _i}{\varepsilon \theta _i+\bar{a}_ih_i}z_{i-1}+\frac{h_iF_i}{\varepsilon \theta _i+\bar{a}_ih_i}. \end{aligned}$$

The solution to the above first-order difference equation will be as follows:

$$\begin{aligned} z_i=z_0Q_i+\sum _{k=1}^{i}\phi _kQ_{i-k}, \end{aligned}$$

(50)

where

$$\begin{aligned} Q_{i-k}=\left\{ \begin{array}{lr} 1, \qquad \qquad \qquad \quad k=i, \\ \prod \limits _{l=k+1}^{i}\frac{\varepsilon \theta _l}{\varepsilon \theta _l+\bar{a}_lh_l}, \quad 0\le k \le i-1, \end{array} \right. \qquad \phi _k=\frac{h_iF_i}{\varepsilon \theta _i+\bar{a}_ih_i}. \end{aligned}$$

Then, from (32) and (50), we obtain

$$\begin{aligned} z_0=\frac{\mu \sum \limits _{k=1}^{N}\frac{h_kF_k}{\varepsilon \theta _k+\bar{a}_kh_k}Q_{N-k}+\sum \limits _{i=1}^{N}\hbar _ic_i\left( \sum \limits _{k=1}^{i}\frac{h_kF_k}{\varepsilon \theta _k+\bar{a}_kh_k}Q_{i-k}\right) -r}{1-\mu Q_N-\sum \limits _{k=1}^{N}\hbar _kc_kQ_k}. \end{aligned}$$

(51)

Since, the denominator is bounded below by one and the equality (51) reduces to

$$\begin{aligned}&\left| \mu \sum \limits _{k=1}^{N}\frac{h_kF_k}{\varepsilon \theta _k+\bar{a}_kh_k}Q_{N-k}+\sum \limits _{i=1}^{N}\hbar _ic_i\left( \sum \limits _{k=1}^{i}\frac{h_kF_k}{\varepsilon \theta _k+\bar{a}_kh_k}Q_{i-k}\right) -r\right| \nonumber \\&\quad \le C\left( \left| \mu \right| \left\| F\right\| _{\infty ,\omega _N}+\left\| c\right\| _1\left\| F\right\| _{\infty ,\omega _N}+\left| r\right| \right) . \end{aligned}$$

(52)

Considering (51) and (52) together, we have

$$\begin{aligned} \left| z\left( 0\right) \right|\le & {} C\left( \left| \mu \right| +\left\| c\right\| _1\right) \left\| R\right\| _{\infty ,\omega _N} \nonumber \\&+C\left( \left( \left| \mu \right| +\left\| c\right\| _1\right) \bar{\alpha }^{-1}\left| \lambda \right| \displaystyle \max _{1\le i \le N}\sum _{j=1}^{N}\hbar _j\left| \mathcal {K}_{ij}\right| \left\| z\right\| _{\infty ,\omega _N}+\left| r\right| \right) . \end{aligned}$$

(53)

Now, applying discrete maximum principle for (49), we get

$$\begin{aligned} \left\| z \right\| _{\infty ,\bar{\omega }_N}\le & {} \left| z\left( 0\right) \right| +\bar{\alpha }^{-1}\left\| R\right\| _{\infty ,\omega _N}+\left| \lambda \right| \alpha ^{-1}\displaystyle \max _{1\le i\le N}\sum \limits _{j=1}^{N}\hbar _j\left| \mathcal {K}_{ij}\right| \left\| z \right\| _{\infty ,\bar{\omega }_N}. \end{aligned}$$

Finally, instead of $z\left( 0\right)$ in the above inequality, considering the estimate of (53), we get

$$\begin{aligned} \left\| z\right\| _\infty\le & {} \frac{C\left( \left| \mu \right| +\left\| c\right\| _1+1\right) \alpha ^{-1}\left\| R\right\| _{\infty ,\omega _N}+ C\left| r\right| }{1-\left( \left| \mu \right| +\left\| c\right\| _1+1\right) \left| \lambda \right| \alpha ^{-1}\displaystyle \max _{1\le i\le N}\sum \limits _{j=1}^{N}\hbar _j\left| \mathcal {K}_{ij}\right| }. \end{aligned}$$

Therefore

$$\begin{aligned} \left\| z\right\| _\infty \le C\left( \left\| R\right\| _{\infty ,\omega _N}+\left| r\right| \right) . \end{aligned}$$

This inequality together with (33) and (34) produces the desired result.$\square$

5 Numerical results

Here, we have considered two specific problems to demonstrate the feasibility of the proposed approach. The following iterative technique will be used.

$$\begin{aligned} y_i^{(n)}= & {} \frac{\bar{f}_i+\frac{\varepsilon \theta _i}{h_i}y_{i-1}^{(n)}-\lambda \sum \limits _{j=0}^{i-1}\hbar _j\mathcal {K}_{ij}y_j^{(n)}-\lambda \sum \limits _{j=i+1}^{N}\hbar _j\mathcal {K}_{ij}y_j^{(n-1)}}{\frac{\varepsilon \theta _i}{h_i}+\bar{a}_i+\lambda \hbar _i\mathcal {K}_{ii}}, \quad i=1,2,...,N, \\ y_0^{(n)}= & {} \mu y_N^{(n-1)}+\sum \limits _{j=0}^{N}\hbar _j c_jy_j^{(n-1)}+A, \quad n=1,2,..., \end{aligned}$$

where $y_1^{(0)}, y_2^{(0)},...,y_N^{(0)}$ are the given initial iterations.

Example 1

We consider the test problem

$$\begin{aligned} \varepsilon u^\prime \left( x\right) +u\left( x\right) +\frac{1}{20}\int \limits _{0}^{1}xu\left( s\right) ds= & {} -\frac{\varepsilon }{\left( 1+x\right) ^2}+\frac{1}{1+x}+x\varepsilon \left( 1-e^{-\frac{x}{\varepsilon }}\right) \\&+x\ln \left( 1+x\right) -\frac{19}{20}x\left[ \varepsilon \left( 1-e^{-\frac{x}{\varepsilon }}\right) +\ln \left( 1+x\right) \right] \\&+\frac{1}{20}x\left[ \varepsilon \left( e^{-\frac{x}{\varepsilon }}-e^{-\frac{1}{\varepsilon }}\right) +\ln \left( \frac{2}{1+x}\right) \right] , \quad 0<x\le 1, \\ u\left( 0\right) +2u\left( 1\right) +\int \limits _{0}^{1}su\left( s\right) ds= & {} 4+\varepsilon ^2+\left( 2-\varepsilon \left( 1+\varepsilon \right) \right) e^{-\frac{1}{\varepsilon }}-\ln 2. \end{aligned}$$

The exact solution of test problem is given by

$$\begin{aligned} u\left( x\right) =e^{-\frac{x}{\varepsilon }}+\frac{1}{1+x}. \end{aligned}$$

We define the exact errors as follows:

$$\begin{aligned} e_\varepsilon ^{N}=\left\| y-u \right\| _{\infty ,\bar{\omega }_N}. \end{aligned}$$

The results of the problem obtained by using different $\varepsilon$ and N values for both the present method and solving exact of SPFIDE are given in the following tables 1-6. In addition, in tables, exact errors are shown according to the exact solutions and approximate solutions.

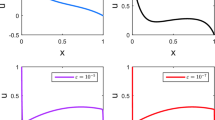
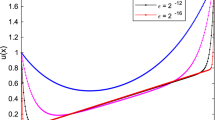
Figs. 1 and 2 represent the solution plots for different values of $\varepsilon$ and N in Example 1, according to the table values. The figures clearly show that the exact solution and the approximated solution for Example 1 overlap, thereby showing the aptness of the proposed techniques.

Table 1 The numerical results of Example 1 for $\varepsilon =2^{-4}$ and $N=64$

Table 2 The numerical results of Example 1 for $\varepsilon =2^{-4}$ and $N=128$

Table 3 The numerical results of Example 1 for $\varepsilon =2^{-4}$ and $N=256$

Table 4 The numerical results of Example 1 for $\varepsilon =2^{-8}$ and $N=128$

Table 5 The numerical results of Example 1 for $\varepsilon =2^{-8}$ and $N=256$

Table 6 The numerical results of Example 1 for $\varepsilon =2^{-8}$ and $N=512$

Fig. 1

Numerical results of Example 1 for $\epsilon =2^{-4}$ and $N=64,128,256$

Fig. 2

Numerical results of Example 1 for $\epsilon =2^{-8}$ and $N=128,256,512$

Example 2

Consider the other problem:

$$\begin{aligned}&\varepsilon u^\prime \left( x\right) +\frac{4}{1+x^2}u\left( x\right) +\frac{1}{10}\int \limits _{0}^{1}e^{1-xs}u\left( s\right) ds=2x+1, \quad 0<x\le 1,\\&u\left( 0\right) +2u\left( 1\right) +\int \limits _{0}^{1}\sin \left( \frac{\pi s}{2}\right) u\left( s\right) ds=-2. \end{aligned}$$

The exact solution to this problem is unknown. For this reason, we estimate errors and calculate solutions using the double-mesh method, which compares the obtained solution to a solution computed on a mesh that is twice as fine. We introduce the maximum point-wise errors and the computed as

$$\begin{aligned} e_\varepsilon ^N=\displaystyle \max _{i}\vert y_i^{\varepsilon ,N}-\tilde{y}_{2i}^{\varepsilon ,2N}\vert _{\infty ,\overline{\omega }_N}, \quad e^N=\displaystyle \max _{\varepsilon }e_\varepsilon ^N, \end{aligned}$$

where $\tilde{y}_i^{\varepsilon ,2N}$ is the approximate solution of the respective method on the mesh

$$\begin{aligned} \tilde{\omega }_{2N}=\lbrace x_{i/2} : i=0,1,...,2N \rbrace \end{aligned}$$

with

$$\begin{aligned} x_{{i+1}/2}=\frac{x_i+x_{i+1}}{2} \qquad \textsf {for} \qquad i=0,1,...,N-1. \end{aligned}$$

We also describe the rates of convergence and computed $\varepsilon$-uniform rate of convergence of the form

$$\begin{aligned} p_\varepsilon ^N=\frac{\ln \left( e_\varepsilon ^N /e_\varepsilon ^{2N}\right) }{\ln 2}, \quad p^N=\frac{\ln \left( e^N /e^{2N}\right) }{\ln 2}. \end{aligned}$$

Table 7 Maximum point-wise errors and the rates of convergence for different vales of $\varepsilon$ and N

The values of $\varepsilon$ and N for which we resolve the Example 2 are $\varepsilon = 2^{0}, 2^{-4}, 2^{-8}, 2^{-12}, 2^{-16}$ and $N = 64, 128, 256, 512, 1024$. From Table 7, we observe that the $\varepsilon$-uniform rate of convergence $p^N$ is monotonically increasing towards two, therefore in agreement with the theoretical rate given by Theorem 1.

6 Conclusion

This article comprises a numerical method employed to solve a linear SPFIDE of the form (1)-(2). On a special piecewise uniform mesh, the differential equation is discretized by using a fitted finite difference operator. The composite trapezoidal integration rule with the remainder term in integral form has been used for the integral part in (1) and initial condition (2), yielding uniform second-order convergence. Specific test problems have been performed to assess and test the performance of the numerical scheme. The obtained results can be presented to more complicated FIDEs.