1 Introduction

Additive manufacturing (AM) has been the focus of many studies over the past two decades. The layerwise manufacturing of components has disrupted the field of conventional manufacturing processes as it allows greater freedom in component shape and complexity.[1] The AM process laser powder bed fusion (LPBF) uses a laser beam as a thermal source to locally melt the metal powder and subsequently enables the manufacturing of a part in a layer-by-layer fashion. One of the major drawbacks of this process is the formation of large residual stress (RS).[2] The mechanisms leading to the formation of RS can be summarized by the influence of the structure, the process, and the material, as well as their interactions, e.g., thermal input and associated material behavior.[3] The formation of the RS in LPBF can be described by the interaction of the thermal gradient mechanism (TGM) and the cool-down phase model as proposed in Reference 4. In essence, the TGM describes how steep thermal gradients induced during LPBF lead to the subsequent heterogeneous expansion and contraction of the material. This effect is highly localized, leading to heterogeneous plastic deformation of the heat region due to the constraint of the cooler surroundings. Therefore, the generated misfit strains give rise to RS. The TGM is a solid-state mechanisms and does not require the material to be molten compared to the cool-down phase model.[4,5] In the cool-down phase model, the contraction of the solidifying material is constrained by the surrounding solidified material, leading to misfit and, therefore, acting as source for the formation of RS. Both these mechanisms tend to generate tensile RS at the top deposited region, balanced by surrounding compressive RS (beneath or adjacent). The effects of TGM and cool-down model (referred to as solidification shrinkage) were further investigated in Reference 6 to understand their individual contribution to the formation of RS. The extremely fast scanning speeds combined with a highly localized melting of the metal powder, and the layerwise manufacturing of the component leads to very complex RS distributions,[2,7] which are challenging to simulate and, therefore, benefit from experimental validation. The formation of the RS appears inherent to the LPBF process and independent of the processed material, since high residual RS is reported for many alloys such as Ti–6Al–4V,[8] Inconel 718,[4,9] Waspaloy,[10] AlSi10Mg,[11] and stainless steel 316L.[4,6] The focus of the present work is on the widely used austenitic stainless steel 316L.

Studies relating to RS in LPBF 316L report the presence of high tensile RS reaching values close to the material’s yield strength at the surface and compression RS in the bulk.[4,12,13,14] Process parameters such as the scanning strategy,[4,6,13,15,16] energy density,[17] base plate heating,[4] build location,[18] and the part geometry have a major influence on the magnitudes of the RS.[13] The influence of such parameters is also well studied for other materials (see References 8,19,20,21).

RS can have a detrimental effect on the material’s property and in-service life.[22] The geometrical accuracy of a part will be compromised if the relaxation of the RS induces distortion.[13,14] Therefore, it is important to understand the stress relaxation that can be achieved by post-processing heat treatments (HT). A few studies have analyzed the influence of various HT temperatures on RS in LPBF 316L. A summary of results on the RS relaxation in LPBF 316L reported in the literature is given in Table I. The XRD results are broadly in good agreement with each other. HTs at 400 °C, 650 °C, and 1100 °C are reported to yield a relaxation about 25, 65, and 90 pct.[23,24] Applying 950 °C as a HT temperature is reported to reduce the RS by about 95 pct.[25] For 650 °C, a relaxation of about 38 ± 12 pct was reported in Reference 26, depending on whether the relaxation was calculated using the RS at the surface or subsurface. This is also the case for the ND (bulk RS) and XRD measurements after a HT at 700 °C reported in Reference 27. Furthermore, the relaxation of the RS reported in Reference 27 depended heavily on the initial RS magnitudes.

Table I Reported Findings in the Literature on the Relaxation of RS in LPBF, Welded, and Shot-Peened Austenitic Steels Resulting from Different Heat Treatments
Full size table

In most cases, stress-relieve treatments tend to be avoided for welded austenitic steels,[28] as the low conductivity and the large coefficient of expansion can result in a non-homogenous heat distribution and distortion of the part. However, depending on the application environment, a stress-relieve HT might be necessary to avoid stress corrosion cracking.[29] According to ASM International, low-carbon austenitic steels such as 316L (welded) need to be heat treated at temperatures above 870 °C to obtain significant RS relaxation.[29,30]

The results on the relaxation of RS in LPBF in References 23,24,25,26,27, thus, follow broadly the indications given for stress-relieving welded austenitic steels.[29,30] However, especially the data on RS relaxation obtained at lower HT temperatures are scattered. In fact, the relaxation of an applied tensile load on the alloy 316 (solution treatment at 1100 °C and water quenched) at HT temperatures of 550 °C to 650 °C is in the order of 10 to 20 pct.[31] These values are well below the relaxation in LPBF 316L as reported in References 23,24,26,27. Also, the analysis of RS in shot-peened 316L revealed that applying 900 °C leads to a much lower relaxation of 40 pct,[32] when compared to the indications given in ASM International. The discrepancy between the thermal stress relaxations of RS in LPBF, conventional (welded, shot peened, applied stress) 316/316L shows that additional testing effort is required to understand the LPBF processed material. Further studies on LPBF 316L in the literature analyze the impact of the HT on fatigue properties,[33,34,35] or hardness[36,37] of 316L and claim to correlate the observed changes in material properties with the stress-relieving HT. However, the corresponding changes in RS remain undetermined.

In particular, results on the relaxation of RS obtained at temperatures above 700 °C and below the recrystallization temperature > 1050 °C[38,39] are scarce. One study[40] reports values of the RS relaxation in the temperature range of interest (800 °C and 5 hours); however, no clear baseline is mentioned. This temperature range is nevertheless of particular interest. Findings reported in References 36,37,41 reveal that the subgrain solidification cellular structure, now widely accepted as one of the sources for the better static properties of LPBF 316L compared to wrought counterparts, is dissolving in this temperature range. Furthermore, according to ASM International, excessive Cr carbide precipitation in the temperature range of 480 °C to 815 °C results in reduced corrosion resistance due to Cr depletion of the matrix.[29] Based on this information and the scarcity of published RS relaxation data for LPBF 316L between 700 °C and 1050 °C, the following study was conducted.

The design of an optimum HT cycle which balances the favorable tensile properties, reduces the RS state, and maintains sufficient corrosion resistance, is a challenge for the AM and wider engineering community. This paper investigates the lower and upper bounds of stress-relieving temperatures for 316L, while maintaining a non-recrystallized microstructure to retain aspects of the LPBF microstructure and associated mechanical properties. The investigation is carried out on single-edge notch beam (SENB) specimens. The temperatures 450 °C, 800 °C, and 900 °C are chosen to avoid increased sensitization to corrosion. As seen from the summary given in Table I, the temperatures investigated in this study close the gap between RS relaxation results over a temperature range of 700 °C and 1100 °C. Their effect on the microstructure is analyzed using electron backscattered diffraction (EBSD) and scanning electron microscopy (SEM). The RS distribution is determined in the bulk using ND to avoid any influence of the surface (e.g., variations in surface roughness, altered microstructures, and RS in machined surfaces). The relaxation of the triaxial bulk RS is non-destructively monitored within the same specimens, avoiding sample to sample variation. Moreover, the analysis of the diffraction peaks, i.e., full-width at half-maximum is performed to correlate the observed microstructural and RS changes. By using the non-destructive potential of ND, the SENB specimens can subsequently be used for crack propagation testing. The interaction of a propagating crack through the determined bulk RS is subject of a companion publication.

2 Methods

2.1 Specimen Manufacturing

The specimens were manufactured by LPBF on an SLM Solutions 280HL (SLM Solutions Group AG, Germany) machine using commercial 316L powder with spherical particle morphology. The chemical composition of the powder is shown in Table II. The powder had the following particle size distribution provided by the supplier: D10 = 18.22 μm, D50 = 30.50 μm, and D90 = 55.87 μm.

Table II Manufacturer Chemical Composition in Weight Pct of the 316L Powder
Full size table

The as-built specimens dimensions were 114.5 × 20 × 13 mm3 (see Figure 1(a)). The meander stripe scanning strategy with a 90 deg rotation between each layer was used. The scanning vector hereby remained parallel with the geometrical axes of the specimen. The manufacturing parameters were 50 µm layer thickness, 700 mm/s scanning velocity, 275 W laser power, and 0.12 mm hatch distance. The interlayer time was approximately 65 seconds.[42] An initial stress-relieving HT of 450 °C for 4 hours was performed before removing the specimen blanks from the baseplate to prevent excessive distortion resulting from the relaxation of RS.

Fig. 1
figure 1

(a) As-built specimen blank and meander stripe scanning strategy, and (b) SENB specimen and ND measurement plane A–A′

Full size image

The specimen blanks were subsequently removed from the build plate and machined to SENB specimens (see Figure 1(b)). The SENB specimens had almost the full length of the as-built geometry in the build direction (BD) but their cross section was machined to 19 × 6 mm2. Furthermore, the SENB geometry included a notch manufactured by wire electrical discharge machining (WEDM) as the final step of the specimen manufacturing. The SENB specimens were produced in two different build jobs but using identical manufacturing parameters.

The SENB specimens received additional HTs following the characterization of the RS after the HT of 450 °C for 4 hours to study their influence on the relaxation of the RS. The additional stress-relieve heat treatments of 800 °C (HT2) and 900 °C (HT3) for 1 hour were performed (after HT1). All HTs were performed under argon atmosphere or vacuum. A summary of the investigated HT strategies and specimen IDs is shown in Table III.

Table III Investigated Heat Treatment Strategies and Associated Heating and Cooling Rates
Full size table

2.2 Microstructural Investigations

For the investigation of microstructural features and crystallographic texture, scanning electron microscopy (SEM) in backscattered electron mode (BSE) and electron backscatter diffraction (EBSD) were used. The cross sections for the investigation were extracted at approximately 10 mm from the fracture surface of the tested SENB specimens, parallel to the XZ plane (see Figure 1). At the cross sections, the EBSD measurements were conducted approximately at the center of the samples. The cross-sectional samples were prepared using the following metallographic route: grinding with emery papers of 180, 320, 600, and 1200 grits followed by clothes with 3 and 1 µm diamond suspensions. The final polishing step was performed with MasterMet-2 non-crystallizing colloidal silica suspension (0.02 μm).

For the investigation of subgrain solidification cellular structures, the sections were subsequently etched with Bloech & Wedl II method (50 mL H2O, 50 mL HCl, 0.6 g K2S2O5).[43] The subgrain solidification cellular structures will be referred to as cellular structures henceforth for the sake of brevity.

A SEM Leo Gemini 1530 VP (Carl Zeiss Microscopy GmbH, Germany) equipped with a high-resolution EBSD detector e−FlashHR+ (Bruker Corporation) was used. The software package ESPRIT 1.94 (Bruker Corporation) was used for acquisition, indexing, and post-processing. An acceleration voltage of 20 kV was used. The settings for the EBSD measurements were set to 70 deg cross-sectional tilt, 2 µm pixel size, approximately 10 nA beam current (max. current set by manufacturer servicing), and a pattern size of 160 × 120 pixels. A smoothing algorithm was applied to the EBSD data in the software MTEX[44,45] to replace the non-indexed measurement points. The high-angle grain boundary was set to 15 deg to differentiate between grains and, thus, to calculate the grain area.

2.3 Neutron Diffraction Basic Principles and Measurement Set-Up

The use of ND permits the non-destructive determination of triaxial RS in the bulk of metallic parts of several millimeter thickness.[22,46] This method is based on the use of Bragg’s Law, in which the lattice spacing of a crystallographic plane family dhkl is related via the diffraction angle θhkl of a propagating wave of suitably penetrating radiation with wavelength λ from

$$ n\lambda = 2d_{hkl} \sin \left( \theta \right). $$
(1)

A shift of the lattice spacing dhkl with respect to a suitable stress-free lattice spacing is used to calculate the residual strain and subsequently the RS. In this sense, the lattice is used in a similar way to a strain gage. The 311 reflection is commonly used for RS analysis with angle-dispersive ND experiments on austenitic steels. Findings in the literature show that it does not accumulate intergranular strain[47,48,49] and, thus, is a good representation of the bulk elastic material behavior.

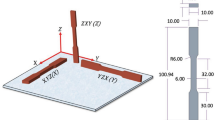
The ND measurement directions and the investigated points inside the SENB specimens are shown in Figure 2(a). The measurement directions were chosen based on the specimen geometry. The RS determined in these directions was assumed to be principal, as they are coincident with the scan direction and thermal gradients generated during the LPBF process. This assumption is commonly made when using ND[50] and means that the determined RS is representative of the maximum stress range at the measurement positions. The measurements were performed at eight positions with a step size of 2.8 mm along the X-direction. The distance between points in the Y-direction was 3 mm. To avoid spurious strains (also called pseudo-strain in the literature[51]) arising from partially immersed gage volumes, a distance of 0.2 mm between the gage volume edges and each surface was used.

Fig. 2
figure 2

(a) ND measurement locations of the determination of RS in the measurement plane A–A′, (b) E3 diffractometer set-up

Full size image

The angle-dispersive measurements were carried out at the monochromatic instrument E3 at the BER II neutron reactor of the Helmholtz Zentrum Berlin, Germany. The set-up is shown in Figure 2(b). The lattice spacing was calculated by measuring the diffraction angle for a fixed wavelength of 0.13734 nm. The position-sensitive detector used to measure the 311 reflection was set to a central angle of 2θ at 86 deg. The diffraction data were acquired using a sampling gage volume of 2 × 2 × 2 mm3 defined by the incident beam slit optics and a receiving radial collimator. The diffraction pattern was fitted using a linear background and a gaussian distribution (implemented in the software StressTextureCalculator[52]).

The strain ε was determined in three orthogonal orientations and calculated from

$$ \varepsilon_{311 } = \frac{{d_{311 } - d_{311}^{0} }}{{d_{311}^{0} }}. $$
(2)

The triaxial RS was then calculated according to Hooke’s law as follows:

$$ \sigma_{i} = \frac{{E_{311 } }}{{\left( {1 + \nu_{311} } \right)\left( {1 - 2\nu_{311} } \right)}}_{ } \left[ { \left( {1 - \nu_{311} } \right)\varepsilon_{i} + \nu_{311} \left( {\varepsilon_{j} + \varepsilon_{m} } \right)} \right]\quad i,j,m = {\text{XX, YY, ZZ}}. $$
(3)

Hereby, σ denotes the stress, E311, the Young’s modulus, and v311, the Poisson ratio associated with the (311) lattice plane, and ε, the strain in the measurement directions X, Y, and Z (see Figure 2(a)). It is to be noted that Eq. [3] is valid also if the principal stress directions are not known and only carries the approximation of quasi-isotropy of the diffraction elastic constants.[53] A Young’s modulus and Poisson’s ratio corresponding to the (311) lattice plane of 184 GPa and 0.294 were used.[48] The calculation of the associated error is detailed in References 9,49 and is resulting from the propagation of the fitting uncertainty.

2.4 Stress-Free Reference

A stress-free reference (SFR), \(d_{311}^{0}\) is required to calculate the strain in [2]. Different approaches are used to obtain a SFR, as described in the standard ISO 21432.[49] They are mostly based on the fundamental idea that macroscopic residual stress needs to balance over the component size (by definition). When small cubes are extracted from the specimen to be investigated, a substantial relaxation should be achieved. Moreover, since the cube dimensions are chosen according to the sampling length of the gage volume, the macroscopic RS should balance and give a good estimate of the stress-free state.[46,54] In this study, 3 × 3 × 3 mm3 cubes were extracted from twin specimens from the same build job for each specimen. The cubes were extracted using WEDM to prevent additional machining stresses to be induced. Stresses generated by WEDM are reported to be limited to a depth of approximately 50 µm[55] and were herein assumed to not affect the SFR. It was assumed that the cubes represented the local chemistry/phase distribution of the investigated material. The diffraction data were acquired along with the three orthogonal directions of the cubes and were averaged for the subsequent stress calculation. As it was not possible to perform additional heat treatments on the cubes, the SFR to determine the RS after HT2 and HT3 were calculated from Formula [3] by assuming that the through-thickness RS of the SENB specimens is zero.[10,49] The calculated SFR was subsequently used to determine the RS in the specimens after HT2 and HT3.

3 Results

The microstructure of the investigated cross sections (Figure 3) displays two typical grain shapes: elongated grains, usually traversing many layers and located at the middle of melt pools, and “cup”-shaped grains, usually situated between two adjacent melt pools of each layer. The observed microstructure has often been found in the literature for the meander stripe scanning strategy. The grain area mean values were determined as 1200, 1250, and 1660 µm2 for HT1, HT2, and HT3, respectively. While the mean grain areas of HT1 and HT2 are almost the same, the mean grain area of HT3 is higher. In the BD, a preferred \(\left\langle {110} \right\rangle\) texture is observed, whereas a \(\left\langle {100} \right\rangle\) texture in the directions of the scan vector is present in the cross section. This has also been observed in Reference 39. The crystallographic texture of HT3 specimen (Figure 3(f)) was found to be slightly stronger compared to the HT1 and HT2 specimens (Figures 3(b) and (d)).

Fig. 3
figure 3

EBSD Y-maps of the LPBF 316L in (a) after HT1, (c) after HT2, and (e) after HT3 and associated pole figures in (b), (d), and (f). The color code and coordinate system in (a) apply to all figures (Color figure online)

Full size image

3.1 Residual Stresses in the SENB Specimens

The magnitudes and distributions of the RS in the building direction, i.e., σZZ of the specimens A and B are shown in Figures 4(a) and (b), respectively. The RS are plotted against the distance from the notch in the SENB geometry. The stress ranges (maximum to minimum RS) are approximately 480 MPa for specimen A and 430 MPa for specimen B. The RS values reach approximately − 290 MPa in compression near the center and 220 MPa (tension) towards the rear surface of the specimens (in the X-direction). Differences in the σZZ values, especially close to the notch, between the two measurement lines can be observed (140 and 100 MPa difference for specimen A and B respectively) indicating a slight through-thickness gradient. The through-thickness variation between line 1 and line 2 appears large closer to the notch compared to the rear surface of the specimen (at X = 14 mm). Closer to the notch, the stresses are either compressive tending towards zero (line 2) or tensile in nature (line 1). The distribution of the σXX follows a similar trend for both specimens Figure 4(c) and (d). The differences in RS values between the two measurement lines are significantly less pronounced than for σZZ and are mostly within the error bar. Tensile σXX values in the vicinity of the notch slowly decrease towards the back surface of the specimens, where they tend to zero. The calculated stress field satisfies the free surface boundary condition, thereby, casting confidence on the choice of the SFR.

Fig. 4
figure 4

(a) and (b) σZZ, (c) and (d) σXX and (e)-(f) σYY in the measurement plane A–A′ of specimen A and B; – stress error < 22 MPa

Full size image

The distribution and magnitude (nearly zero) of σYY shown in Figures 4(e) and (f) indicate that the RS in the SENB geometry can be described as a plane stress field in the X–Z plane. Since no significant RS gradient is visible, it can be assumed that the macroscopic RS is almost fully relaxed in the through-thickness direction. A similar observation has been made on LMD 316L specimens with an as-built thickness of 1.5 and 5 mm in References 48,54. In reference,[10] the SFR has been determined by assuming vanishing through-thickness stresses in the thin part (in that case 5 mm). The σYY displayed in Figures 4(e) and (f) are calculated using a cube as SFR. As the RS ranges are very low (around 60 MPa), the determination of the SFR from the assumption of vanishing through-thickness RS is also considered applicable to the SENB geometry (thickness of 6 mm). The measurement positions were set far enough from the surfaces to avoid sampling the material layers undergoing machining, which could influence the SFR values. The calculated SFR (i.e., assuming that the through-thickness RS are zero) for the two specimens were found to be similar and within the error bar of the averaged SFR from the cubes.

3.2 Impact of HT2 and HT3 on the RS in Specimen A and B

The RS profiles after HT1, HT2, and HT3 are superposed for comparison purposes in Figure 5. The influence of HT2 on σZZ in specimen A is shown in Figure 5(a). The RS values are lower in HT2 compared to those found after HT1. However, a weak RS gradient is still present, indicating that the RS does not fully relax after this heat treatment variant. The difference in stress values along the two measurement lines is still present and is approximately 50 MPa (constant along the cross section). The general trends observed for HT2 are continued for HT3, whereby further relaxation of the RS is observed. The σXX profiles follow the general trend observed for the σZZ in both specimen A (Figure 5(c)) and specimen B (d). The peak σXX near the notch in specimen A and specimen B decreases, and comparable values along the ligament are observed after the additional heat treatments (HT2, HT3). A degree of stress relaxation is observed in HT2 but a gradient is still visible for this direction. This gradient is almost fully flattened after HT3. The σYY profiles in specimen A and specimen B are shown in Figure 5(e) and (f). The RS profiles before and after HT2 and HT3 overlay each other and are within the error bars.

Fig. 5
figure 5

(a) and (b) σZZ, (c) and (d) σXX, and (e) and (f) σYY in in the measurement plane A–A′ of specimen A-HT2 and B-HT3; stress error < 15 MPa

Full size image

The relaxation Ri of the RS following HT2 and HT3, compared to HT1, was calculated using the stress ranges, i.e., difference between maximum and minimum stresses for each measurement line from

$$ R_{i} = 100\, \times \,\left( {1 - \frac{{{\text{Stress}}\,{\text{range}}_{i} }}{{{\text{Stress}} \,{\text{range}}_{HT1} }}} \right)\quad i = HT2, HT3. $$
(4)

The RS ranges are used as they are unaffected by the choice of SFR. The stress ranges for the calculation of the relaxation are shown in Figure 6.

Fig. 6
figure 6

(a) Stress ranges in specimen A and A-HT2, (b) in specimen B and B-HT3

Full size image

The relaxation achieved from the various HT is summarized for each stress direction in Table IV. The σZZ decreases by 86 pct when applying HT3, which is 11 pct more compared to the relaxation obtained by HT2. This effect is not seen in the X-direction; this will be discussed later. The stress in the Y-direction is initially very low and stays small after all HT. Being associated to relative differences, error bars become much larger.

Table IV Relaxation After HT2 and HT3 for Each Stress Direction
Full size table

4 Discussion

4.1 Residual Stress Magnitudes and Distributions After HT1

As mentioned above, the RS shows typical distributions observed for LPBF, i.e., compressive RS at the center and tensile RS towards the surfaces. The σXX and σZZ are still of reasonably high magnitudes, despite a stress relief HT at a temperature of 450 °C for 4 hours and the mechanical release of RS during the machining of the SENB geometry. There is a notable redistribution of σXX observed towards the specimen center in the SENB specimen geometry. The σXX is tensile approaching the notch tip. At approximately 7 mm from the surface in the X-direction, compressive RS would have been expected as seen in References 6,13. In fact, it is well known that the introduction of a notch by WEDM leads to the relaxation and redistribution of the RS as observed in Reference 56. For an asymmetric clamping set-up during WEDM, as it was used for the SENB manufacturing, the magnitude and peak RS can be altered in their magnitude and position.[57] Also, the difference in σZZ along the two measurement lines and lower magnitudes compared to the rear surface (X = 12.4 mm) depicted in Figures 4(a) and (b) is assumed to be closely linked to the redistribution of RS during the manufacturing of the specimens.

Variations of the RS values depending on the position of the part on the baseplate have been reported in References 11,20. In this study, the manufacturing position of specimen A was close to the baseplate center whereas specimen B was manufactured close to the edge of the baseplate. While we would expect the SENB specimens to behave similarly, we observe a relative σZZ difference of about 10 pct. Thus, the stress difference is probably a result from the different build positions on the build plate and build-to-build variation, as the process and post-process parameters were identical for the two specimens. Thereby, the influence of the build position is preponderant compared to the build-to-build variation according to the findings in Reference [8]. This highlights the importance to monitor the influence of heat treatments within a single specimen as permitted by non-destructive RS analysis with ND.

4.2 Relaxation of Residual Stress from HT2 and HT3

There is a consistent trend in the degree of relaxation obtained from applying HT2 and HT3 subsequent to HT1. The process of stress relaxation can be described as the transformation of elastic residual strain to permanent inelastic strain.[58] The inelastic strain rate, i.e., rate of relaxation strongly depends on the velocity of dislocations, which in turn depends on the magnitudes of the RS. Lower RS, thus, reduces the relaxation rate.[58] This would explain the higher relaxation in the Z-direction compared to the X-direction in specimen B (see Table IV). For crack propagation testing, it is important to reduce the RS in the Z-direction (mode I crack opening). In this sense, using a temperature of 900 °C seems to be the right choice as not only the stress range is minimized but also the stress profiles shown in Figure 5(a) become flat. This is per definition an indication for fully relieved type I RS.

According to the deformation mechanism maps of stainless steel 316, the main relaxation mechanism at this temperature and magnitudes of RS is driven by dislocation motion.[59] However, it is possible that high near surface tensile RS exceeds locally the temperature-dependent yield strength. The yield strength of LPBF 316L at temperatures of 777 °C and 877 °C is reported to be about 180 and 120 MPa, respectively.[60] These values lie well below the tensile RS in specimen A and B. Since the RS values determined by ND are averaged over the size of the gage volume, near surface tensile stress maxima are not captured in the measurements. In the build direction, the RS in LPBF processed alloys tends to have a V- or U-shaped profile.[13,27,61] We, therefore, average partially the very steep gradients close to the surface and, thus, do not capture the maximum RS values which may be sufficient to cause local yielding during the heat treatment. However, this effect cannot be decoupled from diffusion-driven processes with the present data, since the relaxation is not followed in-situ in a time-resolved way.

To compare the different HT strategies used in this study with those available in the literature, their impact on the stress relaxation is calculated using the Larson–Miller equation.[62] The time-temperature effect on the stress relaxation was calculated using a so-called thermal effect TE, representing a figure of merit of the HT to be appropriate to relieving RS from

$$ T_{E} = T \times \left( {\log \left( t \right) + C} \right) \times 10^{ - 3} $$
(5)

using the temperature T (Kelvin), time t (hours), and the material constant C (values close to 20[29,63]). The values of the RS relaxation after different HTs as a function of the TE, obtained this study and reported in literature, are plotted in Figure 7. The relaxation is calculated according to formula [4]. The marker corresponding to HT1 indicates the reference for the calculation. The relaxation obtained via HT2 and HT3 agrees to some extent with the trend described by the results reported for LPBF 316L[23,24] and corresponds to HT indications for welded austenitic steels given in References 29,30. Heat-treating-welded austenitic steels in a range of 845 °C to 900 °C (TE = 22.4 to 23.5) yields a relaxation of 85 pct as reported in Reference 30. Unfortunately, the relaxation values reported for LPBF 316L in the literature determined by XRD are scattered, and it is not clear what stress relaxation can be obtained for a TE between 14 and 21 (see Figure 7). Horizontally built specimens are prone to the same mechanisms of RS formation as vertical specimens. However, the magnitudes of the RS and their orientation with respect to the geometrical axes are different and can often result in the distortion of the specimen upon release from the build plate[27] and, thus, alter the degree of stress relaxation. This, in turn, makes a comparison of the RS and their relaxation very difficult in different geometries. Based on this study, a heat treatment performed at 800 °C for 1 hour can reduce the RS by a maximum of 75 pct against the baseline of 450 °C for 4 hours. Applying 900 °C for 1 hour will result in a maximum stress relaxation of 86 pct, which corresponds to a TE of 23.5.

Fig. 7
figure 7

The relaxation of σZZ as a function of the TE calculated using the averaged RS in specimen A and B as reference and comparison to findings reported in the literature; hollow and full symbols define stress relaxation determined using XRD and ND respectively; H (horizontally built specimen) and V (vertically built specimen)

Full size image

Results for welded 347 stainless steel show that when heat treating below 650 °C, the maximum relaxation is about 40 pct.[29] The analysis of stress relaxation in shot-peened 316 Almen strips reported in Reference 32 shows that a relaxation of about 38 pct is resulting from a heat treatment at 900 °C. This result does not coincide with either our results or the indications and results given for welded stainless steels in References 29,30. The long-term stress relaxation of applied tensile stresses in 316 plates (solution treatment at 1100 °C and water quenched) was analyzed in Reference 31. For holding times of up to 2 hours, a relaxation of about 10 to 20 pct is obtained at temperatures of 550 °C and 650 °C, respectively. This is in contradiction with the results for LPBF 316L reported in References 23,24,26.

In fact, the scatter in Figure 7 is most probably a convolution of different aspects. The authors in Reference 64 analyzed the relaxation of RS induced by various sources, e.g., grinding, shot peening, and milling in different alloys. They observed that the relaxation behavior depended heavily on the origin of the RS and at which location, i.e., surface and subsurface, the RS was determined. It was observed in Reference 64 that the surface relaxation was more pronounced than in the subsurface layers. This corresponds well with the RS relaxation reported for LPBF 316L in Reference 26. Each manufacturing process (e.g., AM, forging, casting, welding) and mechanical post-process (e.g., machining, peening) introduces a different microstructure and RS. Thereby, the resulting arrangement of dislocations, defects, and the material properties all contribute to the mechanisms of relaxation that will be dominant for the relaxation in a given temperature range. It is, therefore, difficult to directly compare relaxation values between LPBF and conventional processes. Some of the relaxation values reported for the conventional 316[31,32] are much lower compared to our results and the findings reported in the literature. To also include another AM process, the relaxation of RS in direct energy-deposited 316L determined by synchrotron XRD (SXRD) was reported to be between 36 and 73 pct for a TE between 23 and 27.[65] Again, these values are much lower compared to our results. The smaller relaxation is, thereby, possibly due to the lower initial RS in the material. This explanation was also mentioned for the large scatter between the relaxation in horizontally (distorted upon removal from the base plate) and vertically manufactured LPBF 316L in Reference 27. Furthermore, it is noted that the relaxation values reported based on laboratory XRD in References 23,24 and SXRD[65] do not account for possible RS variations between different specimens. This might be another source for the scatter in relaxation at lower TE in Figure 7.

As mentioned in Reference 64, probing different areas within the material also yields different results and emphasizes the benefit to monitor RS changes using ND. In fact, based on our ND data, we can calculate the relaxation based on the RS close to the surface and in the center of the specimen as well as comparing to the total RS ranges reported herein. Using just the determined peak tensile and compression σZZ in the SENB to calculate the σZZ relaxation yields 84 to 87 pct for HT2 and 78 to 89 pct for HT3. Differences between the calculation using the RS ranges (see Table IV) or location-specific values, i.e., peak tensile or compression RS can, thereby, result from erroneous \(d_{311}^{0}\) and the difference in initial RS. The values are nonetheless in good agreement with the relaxation calculated from the RS ranges in Table IV. This reinforces the advantages of ND as we do not solely capture the location-specific relaxation of RS.

It is noted that since the baseline for our calculations is the material in the HT1 state, the relaxation from HT1 is not taken into account for the relaxation obtained by HT2 and HT3. However, it seems a stress relaxation plateau is reached at a TE around 24 (see Figure 7). In fact, the methods used to determine the relaxation of the RS are probably not sensitive enough to capture smaller degrees of relaxation < 10 pct. This is a consequence of the measurement error. Therefore, while there may be a small gradient in relaxation between a TE of 24-26, it is not captured, and thus, it appears that a plateau in relaxation is reached. Nonetheless, we can deduce that HT1 barely affected the relaxation as it would only shift the relaxation of HT2 and HT3 by ~ 5 pct. The relaxation of about 10 pct in wrought 316 for temperatures of 550 °C reported in Reference 31 further indicates that the relaxation after HT1 should be very low (lower than 10 pct). This is in accordance with the very stable hardness and yield strength up to 600 °C reported in References 36,39,66.

Both HT2 and HT3 are suited to reduce the RS by at least 75 pct, while maintaining a high yield strength when comparing to wrought 316L (about 170 MPa for hot-finished and annealed bars[30]). HT2 (800 °C for 1 hour) and HT3 (900 °C for 1 hour) are reported to reduce the hardness by approximately 8 pct and 12 pct[36] and the yield strength by 8 to 17 pct[39,67] and 13 to 25 pct,[67] respectively. Therefore, depending on the application and hence acceptable level of RS targeted in an LPBF 316L part, we suggest using HT temperatures between 800 °C and 900 °C with short holding times and gas quenching to reduce the RS to low values. The short holding duration and gas quench of HT2 and HT3, thereby, reduce the risk of sensitization, i.e., formation of M23C6 carbides.[68]

The present results show that peak tensile RS between 200 and 90 MPa still remains in LPBF 316L when heat treated at temperatures between 450 and 800 °C, respectively. Therefore, care has to be taken when evaluating the mechanical properties of LPBF 316L that have been heat treated at temperatures in this range.

4.3 Microstructure and Associated RS Changes

The grain size and texture of LPBF 316L are observed to be broadly stable up to 800 °C, but changes can be seen when applying a heat treatment temperature of 900 °C (see Figure 3) for HT3. HT3 appears to onset minor grain growth as observed in Reference 69. In addition, notable changes can be observed on the length scale of the cellular subgrain structures in Figure 8. The cellular structures,[36,67,70,71] melt pool, and grain boundaries (yellow arrows and green arrows, respectively) after HT1 are shown in Figure 8(a). The cellular structures, thereby, either appear as fine-elongated structures (inset (1) in Figure 8(a)) or polygons (inset (2) in Figure 8(a)). The appearance depends on the orientation of the grain with respect to the cut surface. The cellular structures are still seen after applying HT2 in Figure 8(c)) but are almost not observable following HT3 as shown in Figure 8(e)). From findings reported in the literature, we know that cellular structures are linked to the solidification mechanisms occurring during the LPBF process.[39] The formation of the cellular structure is both process and material specific. In LPBF 316L, the cell walls are areas of Cr and Mo segregation and accumulation of precipitates that are decorated with forests of dislocations.[39,70] This structure prevails up to temperatures of 800 °C[36] and gradually vanishes at higher temperatures.[36,72] Therefore, our microstructural observation agrees well with reported literature. Around 75 pct relaxation of the RS is obtained by applying HT2, where the cellular structure is still visible (see Figure 8(c)). It is interesting that the RS relaxation does not correlate with the reported relatively stable hardness[39,67] and yield strength (only slightly decreasing by about 10 to 15 pct[39,67]) up to temperatures of 800 °C. The diffusion of Cr and Mo starts at a temperature of 600 °C as shown by simulations performed in Reference 39. After applying a temperature of 800 °C for 1 hour (HT2), the presence of the two elements in the wall matrix is heavily reduced. It appears that the increased motion of dislocations, annihilation of dislocations, and diffusion of Cr and Mo in the temperature range 600 °C to 800 °C reduce the ability of the cellular structure to pin dislocations.[39,70,73] The mobility of dislocations through mechanisms of recovery and creep, in addition to the instantaneous relaxation upon reaching the temperature-dependent yield strength, is presumed to lead to the observed relaxation after HT2.

Fig. 8
figure 8

Cellular structure in LPBF 316L after HT1, HT2, and HT3 in (a), (c), and (e) and highlighted in insets (1)-(4). Grain and melt pool boundaries are highlighted by green and yellow arrows, respectively. The evolution of the RS in line 1 in (b) and of the FWHM after HT2 and HT3 in (d) and (f) (Color figure online)

Full size image

The Full-Width Half-Maximum (FWHM) of the diffraction peaks used to calculate the stresses gives indirect information on the microstructure (through crystallite size and mosaicity) and the microstrains (type 2 and 3). The FWHM profiles are shown in Figure 8(d) and (f). The FWHM decreases with HT2 and even more with HT3 (the spatial profile becomes flat). Since the grain growth in HT3 is minor (see Figure 3(c)), we can safely assume that it does not influence the variation of the FWHM. Therefore, we predicate that the observed evolution of the FWHM describes the loss of mosaicity and the relaxation of microstrains (mainly of Type III) as the cellular structure dissolves. Since the dislocation forests at subgrain boundaries (and tangles within the grains) are linked to intragranular stress fields, the dissolution of such sub-structures releases microstrains and yields a decrease of the spread of the local strain values, i.e., a decrease of the FWHM of diffraction peaks. In addition, the cellular sub-structures are linked to slight subgrain orientation differences. Such differences are within the FWHM of the diffraction peaks (~ 0.5 to 0.8 deg), i.e., they cannot be observed by EBSD. The dissolution of the cellular sub-structures yields again a homogenization of the subgrain orientations, i.e., a decrease of the FWHM. The fact that in HT2, the FWHM decreases in a non-uniform manner implies that the cellular sub-structures are non-uniformly dissolved. Indeed, the cellular structure is still visible in Figure 8(c). It is reported that the diffusion of entrapped elements and dislocation motion and annihilation occur at a temperature of 800 °C.[67,73] The mechanisms that drive the additional 11 pct RS relaxation resulting from HT3 could be related to the further decrease in the amount of Cr and Mo, dislocation density, and precipitates.[39] The corresponding FWHM profile, shown in Figure 8(f), is flat and fully agrees with the observed disappearance of the cellular substructure.

While the individual contributions of mosaicity and intragranular stress relaxation cannot be decoupled from our data, it is clear that the origin of our observations is the dissolution of the cellular structure.

5 Conclusion

The RS was determined using neutron diffraction in LPBF 316L SENB specimens having received different HT cycles. The chosen HT temperatures 450 °C, 800 °C, and 900 °C were below the recrystallization temperature. The original columnar microstructure of the LPBF process was thereby broadly retained, while the cellular structure was almost fully dissolved at the highest HT temperature. Furthermore, the temperatures 450 °C and 900 °C encompassed the lower and upper bounds of stress-relieving temperatures applied to conventional 316L. The following observations were made:

  1. 1.

    The SENB specimens exhibited almost a biaxial RS state in the plane of the two largest dimensions (X–Z). This permitted us to infer the stress-free reference for the RS determination by assuming plane stress.

  2. 2.

    High tensile and compressive RS values were still present after a heat treatment at 450 °C for 4 hours. A comparison with results on RS relaxation found in the literature showed that the relaxation obtained by this heat treatment is minor and lies within the specimen-to-specimen scatter.

  3. 3.

    Applying a subsequent heat treatment for 1 hour at 800 °C reduced the RS range by a maximum of 75 pct compared to the baseline of 450 °C for 4 hours. Peak RS of 90 MPa was still present in the material. Heat treating at 900 °C for 1 hour reduced the RS range by a maximum of 86 pct.

  4. 4.

    The degree of stress relaxation for a heat treatment at 900 °C for 1 hour corresponded with suggestions on stress-relieve heat treatments for conventionally processed 316L.

  5. 5.

    The use of ND permitted to calculate the location-specific and global (using RS ranges) relaxation. The two approaches were in good agreement and emphasize the advantages of using ND.

  6. 6.

    The relaxation of the RS appeared to be closely linked to the gradual dissolution of the cellular structure as shown by the scanning electron microscopy images and indicated by the flattening of the full-width-half-maximum profile.