Introduction

Magnetic surveying is a crucial subsurface imaging tool. The tool is routinely used to image subsurface geological structures (An and Di 2016; Araffa and Bedair 2021; Ugbor et al. 2021; Essa et al. 2022), and in support of hydrocarbon exploration (Saunders et al. 1991; Abubakar et al. 2015; Ivakhnenkoa et al. 2015; Innocent et al. 2019; Abdullahi and Kumar 2020), mineral exploration and mining (Mandal et al. 2015; Ghanati el al. 2017; Akinlalu et al. 2018; Biswas 2018; Essa and Elhussein 2019; Melo et al. 2020; Mehanee et al. 2021; Essa and Diab 2022a), geothermal energy (Abraham et al. 2014; Shirani et al. 2020; Hosseini et al. 2021), archeological studies (Scollar et al. 1986; Tsokas and Papazachos 1992; Gerard-Little et al. 2012; Linford et al. 2019), the detection of sinkholes (Balkaya et al. 2012), and other environmental and engineering investigations (Reynolds 2011; Niederleithinger et al. 2012; Liu et al. 2021).

Magnetic inversion is a significant geophysical approach that provides beneficial insights into the subsurface in many kinds of fields. It entails analyzing magnetic field data for the purpose of figuring out fault parameters, identifying geological structures, and outlining subsurface features. Magnetic inversion improves in gaining an understanding of fault systems, their geometries, and orientations in geology and tectonics. Researchers can acquire insights into the behavior and potential seismic risks connected with faults by precisely predicting fault characteristics such as dip angles, depths, and slip rates. This data is critical for determining the stability of geological formations, forecasting earthquakes, and planning infrastructure development in seismically active areas.

Multiple inversion methods were developed to model magnetic data. Each method employs a slightly different approach. The methods include the graphical technique, which is based upon a few distinct locations on the magnetic anomaly profile (Gay 1963; Subrahmanyam and Prakasa Rao 2009), the characteristic curve technique (Hutchison 1958; Grant and Martin 1966; Abdelrahman and Essa 2005), the least-square approach (Abdelrahman et al. 2007; Tlas and Asfahani 2011), the Euler deconvolution technique (Li 2003; Dewangan et al. 2007), the Werner deconvolution approach (Stagg et al. 1989; Hansen 2005; Usman et al. 2014), the gradient technique (Abdelrahman et al. 2003; Essa and Elhussein 2017), the analytical-signal technique (Nabighian 1972; Salem 2005; Aydin 2008), the tilt angle approach (Miller and Singh 1994; Essa et al. 2018; Pham et al. 2019; Elhussein and Shokry 2020), and the Fourier-transform technique (Gudmundsson 1966; Gupta 1988; Olurin et al. 2017). The disadvantages of these listed approaches are that they are sensitive to noise and dependent on prior information.

More recently, new artificial intelligence-based methods have been developed to model magnetic data. These methods are based on approaches including particle swarm optimizer (Liu et al. 2017; Essa and Elhussein 2020; Pace et al. 2021; Essa et al. 2023), the genetic algorithm technique (Currenti et al. 2007; Montesinos et al. 2016; Kaftan 2017), the simulated annealing approach (Biswas 2016, 2018; Biswas and Acharya 2016), the neural network approach (Hajian et al. 2012; Deng et al. 2022), Bat algorithm (Essa and Diab 2022b), the ant colony technique (Kushwaha et al. 2018), and the barnacle mating (Ai et al. 2022).

This work develops a method for modeling magnetic data acquired across faults. The approach employed is as follows. Initially, the second horizontal derivative helps confiscate the influence of regional background. The particle swarm optimizer scheme is then exploited to derivative anomalies to gauge the different fault structure parameters (amplitude coefficient (\({A}_{c}\)), fault angle (θ), effective magnetization vector dip angle (α), depths to the upper side of the fault (\({h}_{1}\)) and the lower side of the fault (\({h}_{2}\)), and the fault origin (\(w\))). Three synthetic models and three real field cases were examined from India, Australia, and Egypt to verify this method’s efficacy.

There are numerous merits when utilizing PSO for determining fault parameters. For starters, PSO is a global search algorithm, which implies it can identify the objective function’s global minimum regardless of whether the objective function contains several local minima. Second, PSO is simple to establish and requires few parameters. Third, PSO is being noticed to be useful in a range of applications, including the estimation of fault parameters. PSO can be sluggish to converge, especially when dealing with complex issues. Using horizontal derivatives of magnetic data to boost PSO convergence is one method. Horizontal derivatives can be utilized to lessen the effect of the regional magnetic field, allowing PSO to identify the global minimum more easily.

The paper is divided into four sections. The methodology and the corresponding algorithm are first detailed. The second section illustrates the utilization of three synthetic models. The third section illustrates the use of three real data. Finally, the paper ends with conclusions.

The methodology

Ideally, magnetic field data acquired across a feature of interest is comprised of the regional magnetic field (background) and the superposed residual anomaly (target anomaly) (Pawlowski 1994; Essa 2021). The following formula can give this magnetic field:

$$M\left( {x_{i} } \right) = M_{res} \left( {x_{i} } \right) + Z\left( {x_{i} } \right) .$$
(1)

Equation (1) shows the total measured magnetic field represented by \(M\left( {x_{i} } \right)\), \(M_{{{\text{res}}}} \left( {x_{i} } \right)\) is a residual anomaly, \(Z\left( {x_{i} } \right)\) is a regional magnetic field (background), and \(x_{i}\) is the observation data point.

In this study, the residual anomalies are generated by a vertical or dipping fault. The particle swarm optimizer technique examined residual anomalies, detached from the total magnetic anomaly utilizing the second horizontal derivative approach.

Forward modeling of fault structure and a second horizontal derivative scheme

The magnetic anomaly measured across arbitrarily dipping magnetized fault at any point (\({x}_{i}\)) is given by (Murthy et al. 2001; Ekinci et al. 2019). (Fig. 1):

$$M_{{{\text{res}}}} \left( {x_{i} } \right) \,=\, 2 A_{c} \sin \theta \left\{ {\cos \left( {\theta + \alpha^{\prime}} \right)\left( {\theta_{2} - \theta_{1} } \right) + \sin \left( {\theta + \alpha^{\prime}} \right) \ln \left( {\sqrt {\frac{{\left( {\left( {x_{i} - w} \right) + \left( {h_{2} - h_{1} } \right)\cot \left( \theta \right)} \right)^{2} + h_{2}^{2} }}{{\left( {x_{i} - w} \right)^{2} + h_{1}^{2} }}} } \right)} \right\}, \quad i = 0, 1, 2, 3, ...,P,$$
(2)

where P is the data numbers; \({A}_{\mathrm{c}}\) is the amplitude coefficient (nT) and is given by:

$$A_{{\text{c}}} = J \cdot \sqrt {1 - \left( {\left( {\cos \left( \beta \right)} \right)^{2} \cdot \left( {\cos \left( \gamma \right)} \right)^{2} } \right)} ,$$
Fig. 1
figure 1

A sketch diagram displays the dipping fault’s geometric structure and parameters

Full size image

J signifies the effective magnetization intensity (nT); and \(\beta\) is the strike of the 2-D fault structure measured east or west from the magnetic north (0° ≤ \(\beta\)  ≤ 90°). \(\gamma\) is the direction of measurements (which equals zero in the case of the horizontal component, \(\pi /2\) in the vertical component, and I (inclination angle) in the case of the total field). \(\theta\) is the fault angle (degree). \(\alpha ^{\prime}\) is given by: \(\alpha ^{\prime}= \alpha -{\mathrm{tan}}^{-1}\left(\mathrm{sin}\left(\beta \right)\cdot \mathrm{cot}\left(\gamma \right)\right)\). \(\alpha\) is the effective magnetization vector dip angle (degree). w is the fault origin (km). \({h}_{2}\) denotes the depth to the lower side of the fault (km). \({h}_{1}\) represents the depth to the upper side of the fault (km); \({\theta }_{2}\) is given by: \({\theta }_{2}=\frac{\pi }{2}+{\mathrm{tan}}^{-1}\left(\frac{\left({x}_{i}-w\right)+\left({h}_{2}-{h}_{1}\right) cot \theta }{{h}_{2}}\right)\), and \({\theta }_{1}\) is given by:

\(\theta_{1} = \left\{ {\begin{array}{*{20}l} {\frac{\pi }{2} + \tan^{ - 1} \left( {\frac{{x_{i} - w }}{{h_{1} }}} \right),} \hfill & {{\text{in}}\,{\text{case}}\,\, h_{1} \ne 0} \hfill \\ {\frac{\pi }{2}\left( {1 + \frac{{x_{i} - w}}{{\left| {x_{i} - w} \right|}}} \right), } \hfill & {{\text{in }}\,{\text{case}}\,\,h_{1} = 0, x_{i} \ne 0} \hfill \\ {\frac{\pi }{2},} \hfill & {{\text{in}}\,{\text{case}}\,\, h_{1} = 0, x_{i} = 0}. \hfill \\ \end{array} } \right.\).

For vertical faults (\(\theta ={90}^{o}\)), the magnetic anomaly (Eq. 2) can be given by the following formula:

$$M_{{{\text{res}}}} \left( {x_{i} } \right) \,=\, 2 A_{c} \left\{ { - \sin \left( {\alpha^{\prime}} \right)\left( {\theta_{2} - \theta_{1} } \right) + \cos \left( {\alpha^{\prime}} \right) \ln \left( {\sqrt {\frac{{\left( {x_{i} - w} \right)^{2} + h_{2}^{2} }}{{\left( {x_{i} - w} \right)^{2} + h_{1}^{2} }}} } \right)} \right\},\quad i = 0, 1, 2, 3, ...,P.$$
(3)

To remove the regional background\(Z\left({x}_{i}\right)\), the second horizontal derivative operator was applied to Eq. 1; for three observation points along the magnetic profile (xi – 2s, xi, xi + 2s), the second horizontal derivative (\({M}_{xx} \left({x}_{i }, s\right)\)) can be given by (Essa and Elhussein 2017):

$$M_{xx} \left( {x_{i } , s} \right) = \frac{{M \left( {x_{i } + 2s} \right) - 2M \left( {x_{i } } \right) + M \left( {x_{i } - 2s } \right)}}{{4 s^{2} }} ,$$
(4)

where s = 1, 2, 3, …, N separation units are graticule spacings, and xi is the observation data point.

Inversion approach

The proposed method is based on the particle swarm optimizer scheme. This algorithm was recognized primarily by Eberhart and Kennedy (1995). The particle swarm optimizer scheme is applied nowadays to different geophysical applications (Srivastava and Agarwal 2010; Xiong and Zhang 2015; Ekinci et al. 2019; Essa and Géraud 2020; Essa et al. 2021; Elhussein 2021). The particle swarm optimizer approach is stochastic. In this application, the approach can be explained metaphorically by considering a group of birds searching for food. Models can represent the birds; for each model, there is a velocity vector and a location vector collectively representing the parameter’s value. The inversion is initiated by giving random models for the swarm utilizing the possible ranges of the different variables. The velocity and position of the different models are iteratively updated using the following formulas:

$$V_{i}^{k + 1} = c_{3} V_{i}^{k} + c_{1} {\text{rand}}1\left( {K_{{{\text{best}}}} - X_{i}^{k + 1} } \right) + c_{2} {\text{rand}}2\left( {L_{{{\text{best}}}} - X_{i}^{k + 1} } \right),$$
(5)
$$X_{i}^{k + 1} = X_{i}^{k} + V_{i}^{k + 1} .$$
(6)

Equation (6) shows \({X}_{i}^{k}\) and \({V}_{i}^{k}\) that represent the place and velocity of the particle i, respectively, at iteration k; rand1 and rand2 represent two randomized numbers in the range [0,1]; c1 and c2 are cognitive and social coefficients that are usually equal to 2 represented by Eq. (5) (Singh and Biswas 2016; Essa and Elhussein 2018; Pace et al. 2021); c3 is the inertial coefficient that controls the model’s velocity and takes on a value of less than one; and Kbest is the best location which got by an individual model, while Lbest is the best global location reached by any model in the swarm. Afterward, the best solution (Kbest) and the global best solution (Lbest) are stored in memory. The model’s velocity and position are updated during an iterative process that ends when the convergence occurs (Venter and Sobieski 2002). The convergence is reached by optimizing the following objective function (Ψobj):

$$\Psi_{{{\text{obj}}}} = \frac{1}{P}\mathop \sum \limits_{i = 1}^{P} \left[ {M_{{{\text{res }}\,i}}^{{\text{O}}} \left( {x_{i} } \right) - M_{{{\text{res }}\,i}}^{{\text{c}}} \left( {x_{i} } \right)} \right]^{2} ,$$
(7)

P are the data points numbers, \({M}_{\mathrm{res} i}^{\mathrm{O}}\) are the observed magnetic anomaly, and \({M}_{\mathrm{res} i}^{\mathrm{c}}\) are the calculated magnetic anomaly at the different data points xi.

The fault structure parameters (\({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\)) are inverted by minimizing (Eq. 7) for the several graticule spacings (s values) applied in the separation of residual anomaly through applying the second horizontal derivative (Eq. 4); the solution of the different parameters is reached by taking the average value (Ѡ) of the inverted parameters for numerous s values. The RMS error (root mean square) is deliberated by using the following equation:

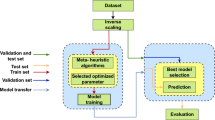
$${\text{RMS}} = \sqrt {\frac{1}{P}\mathop \sum \limits_{i = 1}^{P} \left[ {M_{{{\text{res}}\,i}}^{{\text{O}}} \left( {x_{i} } \right) - M_{{{\text{res}}\,i}}^{{\text{c}}} \left( {x_{i} } \right)} \right]^{2} } .$$
(8)

Figure 2 shows the flowchart, which explains the estimation of the different parameters using the employed approach.

Fig. 2
figure 2

Flowchart showing the complete steps for predicting the fault’s parameters using the proposed approach

Full size image

Synthetic models

Three theoretical models were generated to assess and verify the method’s applicability, accuracy, and efficacy.

Model I: Simple dipping fault magnetic anomaly without and with noise

A 120 km magnetic anomaly profile was generated without noise by dipping fault using \({A}_{c}\) = 300 nT, \(\theta\) = 70°, \(\alpha\) = 40°, \({h}_{1}\) = 4 km, \({h}_{2}\) = 10 km, and \(w\) = 60 km (Fig. 3a). The profile was filtered by applying the second horizontal derivative technique utilizing different graticule spacings (s = 2, 3, 4, 5, 6, 7, 8, and 9 km) (Fig. 3b). For estimating the different fault parameters, the particle swarm optimizer scheme was engaged to the calculated derivative anomalies using various ranges for the different parameters (Table 1). Table 1 explains the accuracy of the offered methodology through the errors (RMS) of valued parameters (\({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\)) which are 0%, and the RMS is 0 nT. The judgment between the predicted and the pure (noise-free) anomaly is revealed in Fig. 3a.

Fig. 3
figure 3

a A synthetic noise-free magnetic anomaly produced by dipping fault model with \({A}_{c}\) = 300 nT, \(\theta\) = 70°, \(\alpha\) = 40°, \({h}_{1}\) = 4 km, \({h}_{2}\) = 10 km, \(w\) = 60 km, and profile length = 120 km. The model structure and the predicted anomaly are also displayed. b Second horizontal derivative anomalies are calculated from the anomaly in Fig. 3a

Full size image
Table 1 Results of the global particle swarm optimization approach applied to second horizontal derivative anomalies for the magnetic anomaly profile (120 km) due to the dipping fault model (\({A}_{c}\) = 300 nT, \(\theta\) = 70°, \(\alpha\) = 40°, \({h}_{1}\) = 4 km, \({h}_{2}\) = 10 km, and \(w\) = 60 km), without and with 15% and 20% noise
Full size table

The efficacy of this approach in the presence of noise was assessed using the previous model infected with different Gaussian noise levels (15% and 20%).

Firstly, for a 15% noise anomaly (Fig. 4a), the noisy magnetic profile was subject to the second horizontal derivative technique, applying the same previous graticule spacings (Fig. 4b); the parameters were predicted by applying the particle swarm optimizer scheme (Table 1). Table 1 shows the predicted parameters (\({A}_{c}\) = 303.88 ± 10.40 nT, \(\theta\) = 69.36 ± 2.20°, \(\alpha\) = 40.34 ± 2°, \({h}_{1}\) = 3.94 ± 0.23 km, \({h}_{2}\) = 10.06 ± 0.38 km, and \(w\) = 60.19 ± 0.35 km), where the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 1.29%, 0.91%, 0.85%, 1.5%, 0.6%, and 0.32%, respectively, while the RMS error is 8.91 nT. Figure 4a reveals the judgment among the predicted and noisy anomalies.

Fig. 4
figure 4

a The magnetic anomaly mentioned in Fig. 3a is tainted with a 15% Gaussian noise and the predicted anomaly. b Second horizontal derivative anomalies are calculated from the noisy magnetic anomaly in Fig. 4a

Full size image

Secondly, for a 20% noise anomaly (Fig. 5a), the second horizontal derivative filter was exploited to the noisy anomaly profile with the previous graticule spacings (Fig. 5b). The particle swarm optimizer approach was employed for the derivative anomalies to predict the dipping fault parameters in case of a 20% noisy anomaly (Table 1). Table 1 presents the expected parameters (\({A}_{c}\) = 309.82 ± 13.57 nT, \(\theta\) = 70.78 ± 3.94°, \(\alpha\) = 41.6 ± 2.3°, \({h}_{1}\) = 3.74 ± 0.19 km, \({h}_{2}\) = 10.33 ± 0.15 km, and \(w\) = 59.87 ± 0.68 km), where the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 3.27%, 1.11%, 4%, 6.5%, 3.3%, and 0.22%, respectively, while the RMS error is 21.71 nT. Figure 5a clarifies the contrast between the predicted and noisy anomalies.

Fig. 5
figure 5

a The magnetic anomaly in Fig. 3a is contaminated with a 20% Gaussian noise and the predicted anomaly. b Second horizontal derivative anomalies are calculated from the noisy magnetic anomaly in Fig. 5a

Full size image

Model II: Effect of regional background

A 120 km composite magnetic anomaly profile was produced. The profile was generated by a dipping fault (\({A}_{c}\) = 450 nT, \(\theta\) = 100°, \(\alpha\) = 50°, \({h}_{1}\) = 5 km, \({h}_{2}\) = 16 km, and \(w\) = 75 km) superposed on a first-order regional background (2xi – 15) (Fig. 6a).

Fig. 6
figure 6

a A composite magnetic anomaly of dipping fault (\({A}_{c}\) = 450 nT, \(\theta\) = 100°, \(\alpha\) = 50°, \({h}_{1}\) = 5 km, \({h}_{2}\) = 16 km, \(w\) = 75 km, and profile length 120 km) and first-order regional anomaly (2xi – 15). The model structure and the predicted anomaly are also displayed. b Second horizontal derivative anomalies are calculated from the anomaly in Fig. 6a

Full size image

The profile was filtered by applying the second horizontal derivative technique utilizing different graticule spacings (s = 2, 3, 4, 5, 6, 7, 8, and 9 km) (Fig. 6b). For appraising the different fault structure parameters, the global particle swarm optimizer was engaged with the calculated derivative anomalies applying various ranges for the parameters (Table 2). Table 2 indicates the predicted parameters (\({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\)) where the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 0%, and the RMS is 0 nT. The mismatch among the predicted and pure (noise-free) composite anomalies is mentioned in Fig. 6a.

Table 2 Results of the global particle swarm optimization approach applied to second horizontal derivative anomalies for the magnetic anomaly profile (120 km) due to the composite anomaly of the dipping fault model (\({A}_{c}\) = 450 nT, \(\theta\) = 100°, \(\alpha\) = 50°, \({h}_{1}\) = 5 km, \({h}_{2}\) = 16 km, and \(w\) = 75 km) and first-order regional anomaly (2xi – 15), without and with 20% noise
Full size table

The aforementioned model was tainted with 20% Gaussian noise (Fig. 7a). The second horizontal derivative scheme was utilized to this noisy data (Fig. 7b), and the parameters were predicted by applying the particle swarm optimizer procedure (Table 2). Table 2 indicates the predicted parameters (\({A}_{c}\) = 460.52 ± 6.27 nT, \(\theta\) = 102.46 ± 2.44°, \(\alpha\) = 49.85 ± 2.35°, \({h}_{1}\) = 4.83 ± 0.33 km, \({h}_{2}\) = 16.11 ± 0.38 km, and \(w\) = 74.74 ± 0.44 km), where the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 2.34%, 2.46%, 0.3%, 3.4%, 0.69%, and 0.35%, respectively, while the RMS error is 21.04 nT. Figure 7a indicates the misfit among the predicted and noisy anomaly.

Fig. 7
figure 7

a The magnetic anomaly mentioned in Fig. 6a is contaminated with a 20% Gaussian noise and the predicted anomaly. b Second horizontal derivative anomalies are calculated from the noisy magnetic anomaly in Fig. 7a

Full size image

Model III: Multi-source

A composite magnetic profile of 140 km was produced. This profile was comprised of anomalies generated by two dipping faults (\({A}_{c}\) = 350 nT, \(\theta\) = 50°, \(\alpha\) = 70°, \({h}_{1}\) = 7 km, \({h}_{2}\) = 17 km, and \(w\) = 50 km) and (\({A}_{c}\) = 250 nT, \(\theta\) = 75°, \(\alpha\) = 70°, \({h}_{1}\) = 2 km, \({h}_{2}\) = 7 km, and \(w\) = 100 km) (Fig. 8a).

Fig. 8
figure 8

a A composite magnetic anomaly of dipping fault (\({A}_{c}\) = 350 nT, \(\theta\) = 50°, \(\alpha\) = 70°, \({h}_{1}\) = 7 km, \({h}_{2}\) = 17 km, \(w\) = 50 km, and profile length 140 km) and another dipping fault model (\({A}_{c}\) = 250 nT, \(\theta\) = 75°, \(\alpha\) = 70°, \({h}_{1}\) = 2 km, \({h}_{2}\) = 7 km, \(w\) = 100 km, and profile length 140 km). The model structure and the predicted anomaly are also displayed. b Second horizontal derivative anomalies are calculated from the anomaly in Fig. 8a

Full size image

The composite anomaly profile was filtered by applying a second horizontal derivative technique utilizing different graticule spacings (s = 2, 3, 4, 5, 6, 7, 8, and 9 km) (Fig. 8b). The different fault parameters were predicted by a particle swarm optimizer scheme, which was applied to the calculated derivative anomalies utilizing various ranges for various parameters (Table 3). Table 3 reveals the predicted parameters: \({A}_{c}\) = 354.48 ± 3.48 nT, \(\theta\) = 50.47 ± 0.94°, \(\alpha\) = 70.56 ± 0.89°, \({h}_{1}\) = 7.04 ± 0.14 km, \({h}_{2}\) = 16.96 ± 0.19 km, and \(w\) = 49.69 ± 0.79 km and the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 1.28%, 0.94%, 0.8%, 0.57%, 0.24%, and 0.62%, respectively, for the first fault, \({A}_{c}\) = 252.60 ± 4.08 nT, \(\theta\) = 75.13 ± 1.03°, \(\alpha\) = 69.60 ± 0.80°, \({h}_{1}\) = 2.00 ± 0.11 km, \({h}_{2}\) = 7.01 ± 0.16 km, and \(w\) = 99.59 ± 0.58 km and the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 1.04%, 0.17%, 0.57%, 0%, 0.14%, and 0.46%, correspondingly, for the second fault and the RMS error of the multi-source model is 10.56 nT. The judgment between the predicted and pure (noise-free) composite anomalies is mentioned in Fig. 8a.

Table 3 Results of the global particle swarm optimization approach applied to second horizontal derivative anomalies for the magnetic anomaly profile (140 km) due to composite anomaly of dipping fault model (\({A}_{c}\) = 350 nT, \(\theta\) = 50°, \(\alpha\) = 70°, \({h}_{1}\) = 7 km, \({h}_{2}\) = 17 km, and \(w\) = 50 km) and another dipping fault model (\({A}_{c}\) = 250 nT, \(\theta\) = 75°, \(\alpha\) = 70°, \({h}_{1}\) = 2 km, \({h}_{2}\) = 7 km, and \(w\) = 100 km), without and with 20% noise
Full size table

The former model was tainted with 20% Gaussian noise to assess the method’s efficacy (Fig. 9a). The noisy magnetic profile was exposed to the second horizontal derivative technique employing similar graticule spacings (Fig. 9b). The different parameters for the two faults in the case of a noisy data were predicted by employing the particle swarm optimizer approach for derivative anomalies (Table 3). Table 3 indicates the predicted parameters in case of a noisy data: \({A}_{c}\) = 359.24 ± 4.60 nT, \(\theta\) = 50.95 ± 2.44°, \(\alpha\) = 71.45 ± 2.73°, \({h}_{1}\) = 7.1 ± 0.31 km, \({h}_{2}\) = 17.16 ± 0.28 km, and \(w\) = 49.93 ± 0.98 km and the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 2.64%, 1.9%, 2.07%, 1.43%, 0.94%, and 0.14%, respectively, for the first fault. \({A}_{c}\) = 260.05 ± 3.45 nT, \(\theta\) = 75.57 ± 1.49°, \(\alpha\) = 71.21 ± 1.96°, \({h}_{1}\) = 1.9 ± 0.19 km, \({h}_{2}\) = 7.11 ± 0.27 km, and \(w\) = 99.77 ± 0.83 km and the errors of \({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\) are 4.02%, 0.76%, 1.73%, 5%, 1.57%, and 0.26%, respectively, for the second fault and the RMS error of the multi-source noisy composite anomaly is 18.49 nT. The mismatch among the predicted and noisy composite anomalies is indicated in Fig. 9a.

Fig. 9
figure 9

a The magnetic anomaly in Fig. 8a is contaminated with a 20% Gaussian noise and the predicted anomaly. b Second horizontal derivative anomalies are calculated from the noisy magnetic anomaly in Fig. 9a

Full size image

Real datasets investigation

The efficacy and robustness of the proposed approach when employed with actual data from India, Australia, and Egypt were examined below as follows:

Magnetic anomaly from Dehri, Bihar Area, India

The geology of the Bihar area, India, is composed of different units which are (from recent to Archean) (Karan 1953; Prasad 1961); Quaternary alluvium deposits, which include various grades of clay, silt, sand, and gravel; Laterite, which is rich in aluminum and iron; a Tertiary unit, which includes sandstones and claystones; the Mesozoic layered volcanic unit named the Rajmahal Traps; the Paleozoic Vindhyans Supergroup which is comprised of limestone, sandstone, and shale; the Archaean lavas and basic igneous intrusive rocks; the Archean schists which include an iron ore series; and the gneiss basement complex (Prasad 1961) (Fig. 10a).

Fig. 10
figure 10figure 10

a Geologic map of the Bihar area, India (modified after Prasad 1961); red rectangle indicates the study area (not to scale). b Observed and predicted magnetic anomaly profile for the East–West striking fault, Southwest of Dehri, Bihar zone, India. c Second horizontal derivative anomalies deliberated from the observed anomaly in Fig. 10b. d Convergence rate

Full size image

The magnetic anomaly profile data were acquired southwest of Dehri, Bihar zone, India. This anomaly was generated by an east–west striking fault (Rama Rao et al. 1987; Murthy et al. 2001). The magnetic profile length equal to 50 km was digitized at 0.64 km (Fig. 10b). The second horizontal derivative technique processed the profile using different graticule spacings (s = 1.28, 1.92, 2.56, 3.2, 3.84, 4.48, 5.12, and 5.76 km) (Fig. 10c). To estimate the different fault parameters (\({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\)), the particle swarm optimizer algorithm was engaged to derivative anomalies using various ranges (Table 4), the predicted parameters are: \({A}_{c}\) = 150.98 ± 3.93 nT, \(\theta\) = 90.71 ± 1.14°, \(\alpha\) = − 98.24 ± 3.22°, \({h}_{1}\) = 7.23 ± 0.22 km, \({h}_{2}\) = 32.30 ± 0.28 km, and \(w\) = 34.04 ± 0.13, and the RMS error is 7.47 nT. The comparison among observed and predicted anomalies is displayed in Fig. 10a. Moreover, the convergence rate is indicated in Fig. 10d. Table 5 shows the correlation between the parameters estimated by the suggested process and those estimated by other methods published in the literature.

Table 4 Results of the global particle swarm optimization approach applied to second horizontal derivative anomalies for the magnetic anomaly profile of Dehri, Bihar area, India
Full size table
Table 5 A comparison between numerical solutions resulted from different methods for the magnetic anomaly profile of Dehri, Bihar area, India
Full size table

Magnetic anomaly from Perth Basin, Australia

Perth Basin was initiated by the intercontinental rift on the eastern side of Gondwana and advanced, through the separation of Greater India from Australia, into an inactive edge alongside southwestern Australia (Harris 1994; Ali and Aitchison 2014; Olierook et al. 2015). The basin is subdivided into at least fifteen sub-basins, filled with sedimentary layers ranging in age from the Permian to the Recent. The sediment rocks are mainly fluviatile and trivial marine intrusions (Olierook et al. 2015). The basin’s eastern edge is noticeably designed by a Darling Fault, which isolates it from the Precambrian rock bearing Yilgarn Craton; the northern and southern edges are bordered by the Northampton block and the Leeuwin block, respectively. Both blocks are Precambrian in age (Qureshi and Nalaye 1978; Olierook et al. 2015).

A magnetic anomaly profile was acquired across the western edge of Perth Basin. This residual anomaly is generated by a deeper north–south striking fault (Qureshi and Nalaye 1978; Murthy et al. 2001; Ekinci et al. 2019). The magnetic profile length was 41 km and digitized at 0.25 km (Fig. 11a). The profile was filtered using the second horizontal derivative technique using different graticule spacings (s = 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2, and 2.25 km) (Fig. 11b). To estimate the different fault parameters (\({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\)), the particle swarm optimizer scheme was engaged with derivative anomalies utilizing various ranges (Table 6). The predicted parameters are: \({A}_{c}\) = 82.33 ± 3.43 nT, \(\theta\) = 127.94 ± 2.39°, \(\alpha\) = − 17.03 ± 1.53°, \({h}_{1}\) = 5.63 ± 0.36 km, \({h}_{2}\) = 14.1 ± 0.25 km, and \(w\) = 16.64 ± 0.08, and the RMS error is 2.10 nT. Furthermore, the convergence rate is represented in Fig. 11c. The close relationship between observed and predicted anomalies is displayed in Fig. 11a. Table 7 shows the correlation between the parameters estimated by this method and those estimated by other published methods, and the depths to the top and the bottom of this fault are estimated by Qureshi and Nalaye (1978) using master curves and analytical methods. (Murthy et al. 2001) by using a damped least-square inversion method estimated the depths to the top and the bottom of this fault, the fault angle, and the effective magnetization vector dip angle. (Ekinci et al. 2019) estimated the depths to the top and the bottom of this fault, the fault angle, and the effective magnetization vector dip angle.

Fig. 11
figure 11figure 11

a Observed and predicted magnetic anomaly profile for the north–south striking fault, Western edge of Perth basin, Australia. b Second horizontal derivative anomalies deliberated from the observed anomaly in Fig. 11a. c Convergence rate

Full size image
Table 6 Results of the global particle swarm optimization approach applied to second horizontal derivative anomalies for the magnetic anomaly profile of Perth Basin, Australia
Full size table
Table 7 A comparison between numerical solutions resulted from different methods for the magnetic anomaly profile of Perth Basin, Australia
Full size table

Magnetic anomaly from the Central Eastern Desert, Egypt

Figure 12a shows the study area “Central Eastern Desert,” which is in the middle part of Eastern Desert, Egypt, and characterized by a dominant NW–SE sinistral shear zone of the Najd Fault System that represents one of the larger Neoproterozoic shear zones on the Earth (Stern 1985). The area is characterized by dome structures, which are fabricated from medium to high grade gneisses–migmatites (core) and the upper part of volcanogenic metagraywackes, metamudstones, and ophiolitic (Pan-African Nappe complex) (Fowler et al. 2007; Hamimi et al. 2019).

Fig. 12
figure 12figure 12

a Geological map of the central Eastern Desert, Egypt (modified after Conoco and Egyptian General Petroleum Corporation 1987; Rabeh 2009), showing the location of the magnetic profile, A–Á. b The observed and the predicted magnetic anomaly profile f A–Á, Central Eastern Desert, Egypt. c Second horizontal derivative anomalies deliberated from the observed anomaly in Fig. 12a. d Convergence rate

Full size image

Figure 12b shows a profile A–Á for the land magnetic data acquired across the study area and was digitized with intervals of 0.5 km (taken from Rabeh 2009; Fig. 12). This magnetic profile was filtered applying the second horizontal derivative technique using different graticule spacings (s = 1.0, 1.5, 2.0, 2.5, 3.0, 3.5, 4.0, and 4.5 km) (Fig. 12c). The fault parameters (\({A}_{c}\), \(\theta\), \(\alpha\), \({h}_{1}\), \({h}_{2}\), and \(w\)) were calculated by applying particle swarm optimization algorithm to the calculated gradient anomalies (Table 8). Table 8 shows the predicted parameters, which are \({A}_{c}\) = −9.84 ± 0.62 nT, \(\theta\) = 42.92 ± 1.14°, \(\alpha\) = 30.85 ± 0.62°, \({h}_{1}\) = 0.78 ± 0.02 km, \({h}_{2}\) = 1.76 ± 0.03 km, and \(w\) = 35.64 ± 0.02, and the RMS error is 0.43 nT. Moreover, the convergence rate is exposed in Fig. 12d. The match among observed and predicted anomalies is displayed in Fig. 12b. These results show a satisfactory correlation with the geologic cross section after said (1990), the 2.5D magnetic model along the aeromagnetic profile (Rabeh 2009; Fig. 12).

Table 8 Results of the global particle swarm optimization approach applied to second horizontal derivative anomalies for the magnetic anomaly profile A–Á of the Central Eastern Desert, Egypt
Full size table

From the above three field examples, we can conclude that the method can be used effectively for different types of faults as in the first field example (Dehri, Bihar Area, India), and the fault is vertical (\(\theta\) = 90.71 ± 1.14°), while the faults in the second (Perth Basin, Australia) and the third (Central Eastern Desert, Egypt) field examples are dipping as \(\theta\) = 127.94 ± 2.39° and \(\theta\) = 42.92 ± 1.14° for the second and third field example, respectively. The third field example represents the shallowest fault as the depth is 0.78 ± 0.02 km, while in the second field example, the depth is 5.63 ± 0.36 km, and in the first one the depth is 7.23 ± 0.22 km; also, the length of the fault in the third field example is the shortest which is about 0.98 km, while in the second field example, the length is about 8.47 km, and in the first one which represents the longest is about 25.07 km.

Conclusions

An extended combination of applying the particle swarm optimizer and second horizontal derivative schemes to interpret and investigate the magnetic data generated by dipping and vertical faults was presented. This method can be effectively applied to geophysical exploration data (e.g., mining), and fault characterization data. Besides, it can estimate the multiple fault parameters (amplitude coefficient (\({A}_{c}\)), fault angle (\(\theta\)), effective magnetization vector dip angle (\(\alpha\)), depth to the upper side of the fault (\({h}_{1}\)), depth to the lower side of the fault (\({h}_{2}\)), and the fault origin (\(w\))). Moreover, it completely removes the regional magnetic background. The suggested approach’s applicability and efficacy were verified utilizing six different data sets, three synthetic and three real examples (from India, Australia, and Egypt, respectively). The models generated for the actual data sets correlated well with the faults described in published literature.