Noether symmetries, group analysis and soliton solutions of a (3+1)-dimensional generalized fifth-order Zakharov–Kuznetsov model with power, dual power laws and dispersed perturbation terms with real-world applications

Abstract

Highly important is a three-dimensional nonlinear partial differential equation because for many physical systems, one can, subject to suitable idealizations, formulate a differential equation that describes how the system changes in time. Thus, this article comprehensively reveals the investigation carried out on a (3+1)-dimensional generalized fifth-order Zakharov–Kuznetsov equation with power-law as well as dual power-law nonlinearities analytically, where the fifth-order term involved is regarded as a dispersion perturbation term. We utilize the well-celebrated Noether’s theorem to comprehensively construct conserved currents of the underlying equation. A detailed Lie group analysis of the understudied model consisting of power-law nonlinearities is further performed. This involves performing reductions of the underlying models using their Lie point symmetries. In consequence, various invariants are found. In addition, the equation reduces to diverse ordinary differential equations using its point symmetries and consequently diverse solutions of interest were achieved. Moreover, we derive some solitary wave solutions by invoking the newly introduced logistic function technique for some particular cases of the equation under consideration. In consequence, we achieve some exponential function solutions. In addition, the physical meaning of the results is put on the front burner by revealing the wave dynamics of these solutions via graphical depictions. Finally, the significance of the robust and detailed findings in the work are further corroborated with various real-world applications.

1 Introduction

The examination of solitary wave solutions in exact structure to nonlinear partial differential equations (NLNPDEQ) plays an active and highly pivotal role in investigating nonlinear physical occurrences (phenomena). These equations (i.e. NLNPDEQs) remain the subject of much research. This is due to their unquestionable role in attempting to model natural and man-made relationships between physical quantities. In recent times, significant inroads have been made in coming up with algorithms for handling NLNPDEQs, with much credit due to the advancement of computers and their computational power. Nevertheless, great minds have had to lay the theoretical foundations upon which these technologies are built.

Lately, many researchers, who have a keen interest in the nonlinear physical phenomena, delve into examining exact solutions of NLNPDEQ’s due to their relevance in analyzing the outcome of any given model. Therefore, it is germane that research into closed-form solutions to NLNPDEQ’s serves a very crucial purpose in observing certain physical circumstances. Besides, the diversity of solutions of NLNPDEQ’s occupies an essential position in a variety of areas of sciences inclusive of optical fibers, chemical physics, geochemistry, biology, hydrodynamics, chemical kinematics, meteorology, heat flow, plasma physics, together with electromagnetic theory. Given the aforementioned and for emphasis, having realized that sizeable scientists have contemplated nonlinear science as the most outstanding borderline for fundamental cognition of nature, we present some pertinent models that include a 3D generalized nonlinear potential Yu-Toda-Sasa-Fukuyama equation in Physics alongside Engineering, recently investigated by the authors in Adeyemo et al. (2023). Moreover, the authors in Adeyemo et al. (2022) examined another generalized NLNPDEQs called advection–diffusion equation with power law nonlinearity in fluid mechanics. This generalized equation characterized buoyancy-propelled plume movement embedded in a medium that is bent on nature. Further to that, a generalized structure of Korteweg-de Vries-Zakharov–Kuznetsov model in the paper (Khalique and Adeyemo 2020) was investigated. The dilution of warm isentropic fluid alongside cold static framework species together with hot isothermal, applicable in fluid dynamics, was recounted via the use of the model. Besides, an investigation in Du et al. (2020) was carried out on the modified as well as generalized Zakharov–Kuznetsov model, delineating the ion-acoustic meandering solitary waves resident in a magneto-plasma and possessive of electron-positron-ion observable in an autochthonous universe. This model was utilized in representing waves in the structure of dust-magneto, ion, together with dust-ion acoustics in laboratory dusty plasmas. Additionally, the vector bright solitons, alongside their various interaction attributes related to the coupled Fokas-Lenells system (Zhang et al. 2020) were studied in the given reference. The femto-second optical pulses embedded in a double-refractive optical fiber, modeled into an NLNPDEQs, were further investigated. Furthermore, the Boussinesq-Burgers-type system recounting shallow water waves and also emerging near ocean beaches and lakes was given attention in the paper (Gao et al. 2020). We can continue with the list but we mention a few. See more in Adeyemo et al. (2022), Adeyemo and Khalique (2023a), Adeyemo and Khalique (2023b), Al Khawajaa et al. (2019), Adeyemo et al. (2022), Wazwaz (2017), Adeyemo and Khalique (2023), Ablowitz and Clarkson (1991), Adeyemo (2024), Jarad et al. (2022), Khater et al. (2021), Márquez et al. (2023), Raza et al. (2024), Khalique et al. (2024), Adeyemo et al. (2024), Pillay and Mason (2023), Mubai and Mason (2022), Kopcasız et al. (2022), Kopcasız and Yasar (2023), Zahran et al. (2024) and Rabie et al. (2024).

Now, having established the fact that no general technique in achieving various exact travelling wave results of NLNPDEQs has been found, mathematicians and physicists came up with some sound, effective, and efficient techniques lately so that the seemingly nagging problem could be nipped in the bud. Take, for example, Sophus Lie (1842–1899) with his quintessential work on Lie Algebras (Ovsiannikov 1982; Olver 1993), which is essentially a unified approach for the treatment of a wide class of differential equations (DEs). More recent methods of solving DEs include Hirota’s bilinear method (Li et al. 2019), power series solution method (Feng et al. 2017), simplest equation method (Yu et al. 2016), Darboux transformation (Zhang et al. 2020), Kudryashov’s technique (Kudryashov and Loguinova 2008), just to mention a few. Some others include bifurcation technique (Zhang and Khalique 2018), Painlevé expansion (Weiss et al. 1985), homotopy perturbation technique (Chun and Sakthivel 2010), tanh-coth approach (Wazwaz 2007), extended homoclinic test approach (Darvishi and Najafi 2011), Cole–Hopf transformation technique (Salas and Gomez 2010), Adomian decomposition approach (Wazwaz 2002), Bäcklund transformation (Gu 1990), Lie symmetry analysis (Ovsiannikov 1982; Olver 1993), F-expansion technique (Zhou et al. 2003), rational expansion technique (Zeng and Wang 2009), tan-cot technique (Jawad et al. 2014), extended simplest equation approach (Kudryashov and Loguinova 2008), Kudryashov’s technique (Kudryashov 2005), Hirota technique (Hirota 2004), Darboux transformation (Matveev and Salle 1991), tanh-function technique (Wazwaz 2005), the $\left( \frac{G'}{G}\right)$-expansion technique (Wang et al. 2005), sine-Gordon equation expansion technique (Chen and Yan 2005), generalized unified technique (Osman 2019), exponential function technique (He and Wu 2006), the list continues. Since the inception of Kadomtsev and Petviashvili’s hierarchy of equations a little more than half a century ago, dozens of research papers have emerged, each exploring an aspect of this rich domain of equations, see for example, Kuo and Ma (2020); Wazwaz (2012); Date et al. (1981); Ma and Fan (2011); Ma (2015); Zhao and Han (2017); Simbanefayi and Khalique (2020).

The usual basic Zakharov–Kuznetsov (ZK) model, furnished as Zakharov and Kuznetsov (1974),

$$\begin{aligned} \phi _t + \phi \phi _x + \nabla ^{2}\phi _x = 0, \end{aligned}$$

(1.1)

where variable $\phi = \phi (t,x)$ instituted by Kuznetsov and his counterpart Zakharov, came to light in the first place. The model (1.1) delineates the forward movement of the decrepitly nonlinear plasma-containing-acoustic-ion waves possessing hot plutonic electrons as well as cold ions with the attendant involvement of a dissimilar magnetic field tending towards x-direction. Underlying model (1.1) also surfaced in areas like optical fibre, geochemistry, alongside physics in solid states Yan and Liu (2006). In Shivamoggi (1989), the author outlined a discourse with regard to the analytical characteristics of ZK model (1.1). Besides, in Nawaz et al. (2013), the authors instituted significant solutions to a version referred to as ZK(3, 3, 3) equation presented as

$$\begin{aligned} \phi _t + (\phi ^3)_x + 2 (\phi ^3)_{xxx} + 2 (\phi ^3)_{xyy} = 0, \end{aligned}$$

(1.2)

where there is an attendance of dispersion property that are fully nonlinear from the homotopy analytical viewpoint.

Moreover, another model, 3-D ZK equation presented as Moleleki et al. (2017)

$$\begin{aligned} \phi _t + p_1\phi \phi _x + p_2\phi _{xxx} + p_3\phi _{xyy} + p_4\phi _{xzz}=0, \end{aligned}$$

(1.3)

contains the nonzero constant parameters $p_1$, $p_2$, $p_3$ and $p_4$. Equation (1.3) has been investigated in the literature by a handful of researchers. For example, the authors in Moleleki et al. (2017) achieve some analytic results to (1.3) via the application of the Jacobi elliptic function (JEF) together with Kudryashov’s techniques. They went a step further to construct various forms of low-order conserved vectors for the model by invoking the multiplier technique. In addition, in Kumar and Kumar (2019), the authors gained a group of closed-form solutions to the 3-D ZK model (1.3) which in their own case, called the model an extended version of ZK. The solutions they found include kink wave, lump-type soliton, explicit Weierstrass Zeta function, travelling wave, quasi-periodic-soliton, single soliton, alongside solitary wave solutions through the engagement of the invariance of (1.3). On the exploration of Lie symmetry transformations, they also produced various invariant solutions to the model (1.3). Moreover, in Magalakwe and Khalique (2019), diverse conserved current of 3-D ZK (1.3) were derived by the authors via the application of the classical Noether theorem.

Further to the above, the authors in Islam et al. (2014) considered a modified version (MZKeQ) of (1.3) that reads

$$\begin{aligned} \phi _t+ q_{1}\phi ^2\phi _x+q_{2}\phi _{xxx}+ q_{3}(\phi _{xzz}+\phi _{xyy})=0, \end{aligned}$$

(1.4)

where $q_{1}$, $q_{2}$, $q_{3}$ serve as real constants. A large number of exact travelling wave outcomes of the model were computed. These results consist of solitary waves occasioned by enhanced $\left( \frac{G'}{G}\right)$-expansion technique. Not only that, in Tariq and Seadawy (2019), Tariq and Seadway examined the MZKeQ (1.4) with the authors invoking the auxiliary equation technique, thereby securing analytical outcomes of the model under consideration. Besides, in Seadawy (2016), the author affirmed the problem derivation of copious ion-acoustic waves that are frailly nonlinear embedded in plasma-induced magnetic electron-positron comprising equal hot-cool components present in the MZKeQ (1.4). Not only that, implementation of the extended direct algebraic (EDA) as well as fractional direct algebraic (FDA) technique were taken into account by him to find solutions to (1.4). This consequently affords him the space to gain outcomes that are of solitary wave in nature to the model. Moreover, in Lu et al. (2017), Lu et al. sought solutions to (1.4), formatted as elliptic function and new exact solitary wave. These were made possible by the researchers via the involvement of modified extended EDA technique, thereby occasioning various kinds of solitons, namely; anti-bell soliton, periodic bell soliton, bright as well as dark solitons. In addition to that, solitary wave that is of bright-dark structure of periodic shape was attained. The secured solutions possess a variety of significant applications which can largely be found in physics as well as other areas of applied science.

Now, in Elwakil et al. (2011), Elwakil et al. introduced a fifth-order dispersion perturbation term to the (1.3) which reads

$$\begin{aligned} u_t + a_1 uu_x + \frac{a_2}{2} u_{xxx} + \frac{a_3}{2}\left( u_{xyy} + u_{xzz}\right) + \varepsilon u_{xxxxx}=0, \end{aligned}$$

(1.5)

which is a fifth-order three-dimensional ZK equation (3D-FoZKeQ) with $a_1,\dots ,a_3$ representing real constants and $\varepsilon$ a small parameter. We notice that if the parameter $\varepsilon = 0$, with $p_1 = a_1$, $p_2 = a_2/2$ and $p_3 = p_4 = a_3/2$, we recover (1.3). The authors in their research engaged the reductive perturbation technique to derive (1.5). They investigated how consequential the frequency of cold electron cyclotron, outer magnetic field, the obliqueness as well as the energetic demographic characteristics could be on solitary waves which are higher-ordered, that brought about some changes in both the roughly-calculated electric field and soliton energy of the electrostatic format for a system of a plasma that is collisionlessly magnetized which comprises a non-thermal hot electrons as well as cold electron fluid. These obey stationary ions along with a non-thermal distribution. Moreover, it was revealed that solitons possessive of both positive as well as negative density perturbations could surface. In Kumar and Kumar (2020), some solutions of (1.5) were gained using Lie symmetries. Moreover, the authors in Ali et al. (2019) achieved nonlocal conservation laws and six Lie symmetries of (1.5). Instead of utilizing "group-invariant solution," they engaged wave transformation in lessening 3D-FoZKeQ (1.5) into nonlinear ordinary differential equations (NLNODEs). The authors generated analytic results via the application of modified Kudryashov alongside the sine-cosine techniques. Akin to that, multiplier together with the new conservation theorem given by Ibragimov (Ibragimov 2007) were used for computing the local-conservation laws related to the 3D-FoZKeQ (1.5).

In our research work, we investigate a more generalized structure of (1.5) given as the (3+1)-dimensional fifth-order generalized Zakharov–Kuznetsov (3D-gnFoZKe) equations with power-law and dual power-law nonlinearities presented as

$$\begin{aligned} u_t + a u^nu_x + b u_{xxx} + c u_{xyy} + d u_{xzz} + e u_{xxxxx} = 0, \end{aligned}$$

(1.6)

$$\begin{aligned} u_t + a (hu^n + ku^{2n})u_x + b u_{xxx} + c u_{xyy} + d u_{xzz} + e u_{xxxxx} = 0, \end{aligned}$$

(1.7)

where parameters a, b, c, d, e, k and h, nonzero real valued constants with $n>0$. We state categorically here for the purpose of emphasis and to preserve the novelty of the research work that (1.5) is just a particular case of (1.6), that is when $n = 1$, and so we are considering a more generalized version and as such more generalized results as can be observed subsequently. Besides, for the first time we obtain various nonlocal and local conservation laws of the equation with n-power and 2n-power laws with nonlinearities using the classical Noether’s theorem. This research fills the gap in the literature regarding the work done on the model so far.

In this study, explicit solutions of the 3D-gnFoZKe (1.6) and (1.7) were abundantly provided. The paper is outlined in the following structure: Sect. 1 introduces the topic while Sect. 2 focuses on constructing diverse conserved currents of the equations using the well-known Noether’s theorem. Section 3 explains the procedural steps involved in performing the Lie group analysis of 3D-gnFoZKe (1.6) and (1.7) along with their symmetry reductions. In Sect. 4, we utilize Kudryashov’s logistic function approach to derive closed-form results of the equations for specific cases. Additionally, Sect. 5 presents the solutions graphically to comprehend the dynamics and physical implications of the results. Finally, concluding remarks are given.

2 Conserved currents of 3D-gnFoZKe (1.6) and (1.7)

This section exhibits conserved currents’ computations for 3D-gnFoZKe (1.6) and (1.7). The focal point is Lagrangian construction, first, for the equations by invoking the Noether theorem (Noether 1918) to secure their conserved vectors. We explicate a brief outline of this technique and some other essential definitions.

2.1 Preliminary information

We observe $\mathcal {G}th$-order of system $\mathcal {Q}\ge 1$ partial differential equations (PDEQs) presented as

$$\begin{aligned} \Theta =\left\{ \Theta (t,x,\Psi ,\partial \Psi ,\ldots ,\partial ^\mathcal {G}\Psi ),\ldots ,\Theta ^\mathcal {Q}(t,x,\Psi ,\partial \Psi ,\ldots ,\partial ^\mathcal {G}\Psi )\right\} =0, \end{aligned}$$

(2.8)

where variables $x=(x^1,\ldots ,x^n)$ alongside t, connote the independent variables, $n\ge 1$ together-with $\Psi =(\Psi ^1,\ldots ,\Psi ^m)$ standing in for the dependent variables in the case where $m\ge 1$. In addition, $\partial \Psi =(\Psi _t,\Psi _{x^1}\ldots ,\Psi _{x^n})$ appears for the partial derivatives of $\Psi$ regarding the presented t, x, whereas $\partial ^k\Psi , k\ge 2$ appears for the kth-order partial derivatives. Not only that, an observation is made to the space of all locally smooth outcomes related to $\Psi (t, x)$ of the system represented as $\Xi$.

Conservation law A local conservation law of related to any furnished system of PDEQ (2.8) is explicated as a local continuity relation

$$\begin{aligned} \left( D_x\cdot C^{x}+D_tC^t\right) \Big |_{ \Xi }=0, \end{aligned}$$

(2.9)

holding for the system on the entire domain of solution space $\Xi$ with differential operators $(D_t,D_x)$, on t and x denoting the total derivatives of involved variables accordingly and Div=$D_x\cdot$, the spatial divergence connoting the vector dot product. Moreover, $C^t(t,x,\Psi ,\partial \Psi ,\ldots ,\partial ^r\Psi )$ stands for the conserved density whereas $C^x=\left\{ C^1(t,x,\Psi ,\partial \Psi ,\ldots ,\partial ^r\Psi ),\ldots ,C^n(t,x,\Psi ,\partial \Psi ,\ldots ,\partial ^r\Psi )\right\}$ denotes the spatial flux. Therefore, the relation $\Phi ^*=(C^t,C^x)$, with components $C^t$ and $C^x$, refers to the conserved current.

Lagrangian A PDEQ system explicated in (2.8) is said to be locally variational if one could express it via the Euler-Lagrange relations

$$\begin{aligned} E_\Psi (L)^t=0=\Theta , \end{aligned}$$

(2.10)

where t connoting for some differential function explicated as $\mathcal {L}(t,x,\Psi ,\partial \Psi ,\ldots ,\partial ^k\Psi )$, the transpose, referred to as a Lagrangian. Thus, $E_\Psi$ is explicated as

$$\begin{aligned} E_\Psi =\frac{\delta }{\delta _\Psi }= {{\partial }\over {\partial \Psi }}-D_t \frac{\partial }{\partial \Psi _t}-D_x \frac{\partial }{\partial \Psi _x}+ D_tD_x \frac{\partial }{\partial \Psi _{tx}} +\cdots . \end{aligned}$$

(2.11)

Next, let us observe a Lemma;

Lemma 2.1

$\Theta =E_\Psi (L)^t$ holds for some defined Lagrangian $\mathcal {L}(t,x,\Psi ,\partial \Psi ,\ldots ,\partial ^k\Psi )$ iff

$$\begin{aligned} \delta _v\Theta ^{t}=\delta _v^*\Theta ^t \end{aligned}$$

(2.12)

for all differential functions v(t, x) also holds.

One could regain a Lagrangian from defined system $\Theta =(\Theta ^1,\ldots ,\Theta ^\mathcal {Q})$ through the general homotopy integral relation explicated as

$$\begin{aligned} \mathcal {L}=\int _{0}^{1}\partial _{\lambda }\Psi _{(\lambda )}\Theta ^t\bigg |_{\Psi =\Psi _{(\lambda )}}d\lambda . \end{aligned}$$

(2.13)

Remark 2.1

One could add a complete divergence to Lagrangian $\mathcal {L}$ in (2.13) in a bid to achieve an equivalent Lagrangian that attains the lowest possible differential order, and that is, $\mathcal {G}/2$.

A variational symmetry also called divergence symmetry, for a local variational principle explicated in (2.10), is a generator with its prolongation fulfilling the invariance criterion

$$\begin{aligned} \text {Pr}\textbf{V}(\mathcal {L})=\xi ^1D_t\mathcal {L}+\xi ^i\cdot D_x\mathcal {L}+D_t\varPsi ^t+D_x\cdot \varPsi ^x \end{aligned}$$

(2.14)

where $i=2,3,4$, (with $\textbf{V}=\xi ^1\partial /\partial t+\xi ^i\partial /\partial x$) for some differential vector function $\varPsi ^x$ along-side differential scalar function $\varPsi ^t$.

2.2 Conservation laws’ construction using the Noether theorem

We thoroughly explain the Noether theorem (Noether 1918) to derive the conserved currents of 3D-gnFoZKe (1.6) with both n-power and 2n-power-law nonlinearities. In the first instance, the observation that (1.6) admits no Lagrangian in its current state is made. Nonetheless, invoking the transformation $u=v_x$ could interestingly yield a six-order structure of Eq. (1.6) which readily has a Lagrangian. Thus, in the light of this, (1.6) becomes:

$$\begin{aligned} v_{tx}+ a v^{n}_{x}v_{xx}+ b v_{xxxx}+c v_{xxyy}+dv_{xxzz}+ev_{xxxxxx}=0. \end{aligned}$$

(2.15)

Therefore, the 3D-gnFoZKe (1.6) is variational locally under the previously mentioned transformation. Having been sure of the fact that a Lagrangian $(\mathcal {L})$ is repossessed for (2.15), equivalent differential order in a minimal format for $\mathcal {L}$ thus explicates as

$$\begin{aligned} \mathcal {L}&=-\frac{1}{2}\, v_t v_x -{ \frac{a\, v_x^{n+2}}{ (n+1) (n+2) }} +\frac{1}{2}\,b\, v_{xx}^{2} +\frac{1}{2}\,c\,v_{xx} v_{yy}+\frac{1}{2}\,d\,v_{xx}v_{zz}-\frac{1}{2}\,e\, v_{xxx}^{2}, \end{aligned}$$

(2.16)

we give a Lemma.

Lemma 2.2

The 3D-gnFoZKe (1.6) admits a functional for the Euler-Lagrange equation demonstrated as

$$\begin{aligned} J(v)=\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty }\int _{0}^{\infty }\mathcal {L}(t,x,y,z,v_t,v_x,v_{xx},v_{xxx},v_{yy},v_{zz})dtdxdydz \end{aligned}$$

(2.17)

with Lagrange’s conforming function enucleated as

$$\begin{aligned} \mathcal {L}&=-\frac{1}{2}\, v_t v_x -{ \frac{a\, v_x^{n+2}}{ (n+1) (n+2) }} +\frac{1}{2}\,b\, v_{xx}^{2} +\frac{1}{2}\,c\,v_{xx} v_{yy}+\frac{1}{2}\,d\,v_{xx}v_{zz}-\frac{1}{2}\,e\, v_{xxx}^{2}. \end{aligned}$$

(2.18)

We emphasize clearly here that one can verify that Lagrangian (2.16) satisfies the Euler–Lagrange equation (2.11). We establish variational symmetry $\textbf{V}$ by invoking the symmetry invariance criterion as delineated, that is

$$\begin{aligned} \text{ Pr}^{(2)}\textbf{V}\mathcal {L}+\mathcal {L}[D_t(\xi ^1)+D_x(\xi ^2)+D_y(\xi ^3)+D_z(\xi ^4)]=D_t(B^{t})+D_x(B^{x})+D_y(B^{y})+D_z(B^{z}), \end{aligned}$$

(2.19)

where the second extension of $\Omega$, Pr$^{(2)}\Omega$ of $\Omega$, can be repossessed via (2.14) with functions (gauge) $B^t$, $B^x$, $B^y$, together with $B^z$ dependent on (t, x, y, z, u). Monomials’ separation in the expanded structure of (2.19) purveys sixty-one systems of linear PDEQs, viz;

$$\begin{aligned}&\xi ^{1}_{v}=0,\,\,\, \xi ^{1}_{x}=0,\,\,\,\xi ^{1}_{y}=0,\,\,\, \xi ^{1}_{z}=0, \,\,\, \xi ^{1}_{vv}=0, \,\,\, \xi ^{1}_{vy}=0, \,\,\, \xi ^{1}_{vz}=0, \,\,\, \xi ^{2}_{v}=0, \nonumber \\&\xi ^{1}_{xx}=0, \,\,\, \xi ^{3}_{v}=0, \,\,\, \xi ^{3}_{x}=0, \,\,\, \xi ^{3}_{vv}=0, \,\,\, \xi ^{3}_{vx}=0, \,\,\, \eta _{xx}=0, \,\,\, \xi ^{4}_{v}=0, \,\,\, \xi ^{4}_{vv}=0,\nonumber \\&\eta _{x}=0, \,\,\, \xi ^{1}_{vx}=0, \,\,\, \xi ^{3}_{xx}=0, \,\,\, \xi ^{4}_x=0, \,\,\, \xi ^{3}_t=0, \,\,\, \xi ^{4}_{t}=0, \,\,\, \xi ^{4}_{vx}=0, \,\,\, \xi ^{4}_{xx}=0, \nonumber \\&\xi ^2_{t}=0, \,\,\, B^y_{v}=0, \,\,\, B^z_{v}=0, \,\,\, \xi ^1_{xxx}=0, \,\,\, \xi ^2_{vvv}=0, \,\,\, \xi ^3_{vvv}=0, \,\,\, \xi ^3_{xxx}=0, \nonumber \\&\xi ^4_{vvv}=0, \,\,\, \xi ^4_{xxx}=0, \,\,\, \eta _{xxx}=0, \,\,\, \xi ^1_{vvx}=0, \,\,\, \xi ^1_{vxx}=0, \,\,\, \xi ^3_{vvx}=0, \,\,\, \xi ^3_{vxx}=0, \nonumber \\&\xi ^{1}_{v}+B^t_v=0, \,\,\, 2b \xi ^3_x+c \xi ^2_y=0, \,\,\, 2b \xi ^4_x+d \xi ^2_z=0, \,\,\, \eta _{t}+2B_v^x=0, \,\,\, \xi ^1_{vvv}=0,\nonumber \\&\eta _{vv}-2\xi ^{2}_{vx}=0, \,\,\, \eta _{vv}-2\xi ^{3}_{vy}=0, \,\,\, 2\eta _{vx}-\xi ^{2}_{xx}=0, \,\,\, \eta _{vv}-3\xi ^{2}_{vx}=0, \nonumber \\&\eta _{vv}-2\xi ^{4}_{vz}=0, \,\,\, 2b \xi ^4_{vx}+d \xi ^2_{vz}=0, \,\,\, 2b \xi ^3_{vx}+c \xi ^2_{vy}=0, \,\,\, \xi ^4_{vvx}=0,\nonumber \\&\xi ^2_{xxx}-3\eta _{vxx}=0, \,\,\, c\xi ^{4}_{vy}+d\xi ^{3}_{vz}=0,\,\,\, (n+1)\xi ^{1}_{v}+B^t_v=0, \,\,\, \xi ^4_{vxx}=0, \nonumber \\&\eta _{vvx}-\xi _{vxx}, \,\,\, B^t_t-\eta _{v}-\xi ^3_y-\xi ^4_z=0, \,\,\, 2b \eta _{xx}+c\eta _{yy}+d\eta _{zz}=0, \nonumber \\&2b \xi ^1_{xx}+c \xi ^1_{yy}+d\xi ^1_{zz}=0, \,\,\, 2\eta _{vy}- (\xi ^3_{yy}+\xi ^3_{zz})=0, \,\,\, B^x_x+B^y_y+B^z_z=0,\nonumber \\&2d\eta _{vz}-2b \xi ^4_{xx}-c\xi _{yy}^4-d\xi _{zz}^4=0, \,\,\, 2\eta _v-3\xi ^2_{x}+\xi ^1_{t}+\xi ^3_{y}+\xi ^4_{z}-B^t_{t}=0, \nonumber \\&\xi ^2_{x}+\xi ^4_{z}-\xi ^1_{t}-\xi ^3_{y}-2\eta _v+B^t_{t}=0, \,\,\, \xi ^2_{x}+\xi ^3_{y}-\xi ^1_{t}-\xi ^4_{z}-2\eta _v+B^t_{t}=0,\nonumber \\&\xi ^4_{z}+\xi ^1_{t}+\xi ^3_{y}-5\xi ^2_{x}+2\eta _v-B^t_{t}=0, \,\,\, 4b \eta _{vx}-2b\xi ^2_{xx}-c\xi _{yy}^2-d\xi _{zz}^2=0,\nonumber \\&(n+1)\xi _x^2-(n+2)\eta _{v}-\xi _t^1-\xi ^3_y-\xi ^4_z+B_t^t=0, \,\,\, \xi ^{2}_{vv}=0,\nonumber \\&2c \eta _{vy}-2b\xi ^3_{xx}-c\xi _{yy}^3-d\xi _{zz}^3=0. \end{aligned}$$

Solving the above systems of PDEQs, one gains the results explicated as

$$\begin{aligned}&\xi ^{1}=C_1, \,\,\, \xi ^{2}=C_5, \,\,\, \xi ^{3}=C_2z+C_3, \,\,\, \xi ^{4}=-\frac{d}{c}C_2y+C_4, \,\,\, \eta =F(t),\\&B^x=-\int (F^2_y+F^3_z)dx-\frac{1}{2}F'(t)v+F^4(t,y,z), \,\,\, B^y=F^2(t,x,y,z),\\&B^t=F^1(x,y,z), \,\,\, B^z=F^3(t,x,y,z). \end{aligned}$$

Aftermath of the computation finally gives the following six Noether symmetries together with their associate gauge functions, that is,

$$\begin{aligned} \textbf{V}_{1}&= \frac{\partial }{\partial t}, \,\,\, B^{t}=0, \,\,\, B^{x}=0, \,\,\, B^{y}=0, \,\,\, B^{z}=0,\nonumber \\ \textbf{V}_{2}&=\frac{\partial }{\partial x}, \,\,\, B^{t}=0, \,\,\, B^{x}=0, \,\,\, B^{y}=0, \,\,\, B^{z}=0,\nonumber \\ \textbf{V}_{3}&=\frac{\partial }{\partial y}, \,\,\, B^{t}=0, \,\,\, B^{x}=0, \,\,\, B^{y}=0, \,\,\, B^{z}=0, \nonumber \\ \textbf{V}_{4}&=\frac{\partial }{\partial z}, \,\,\, B^{t}=0, \,\,\, B^{x}=0, \,\,\, B^{y}=0, \,\,\, B^{z}=0, \nonumber \\ \textbf{V}_{5}&=cz\frac{\partial }{\partial y}-dy\frac{\partial }{\partial z}, \,\,\, B^{t}=0, \,\,\, B^{x}=0, \,\,\, B^{y}=0, \,\,\, B^{z}=0, \nonumber \\ \textbf{V}_F&= F(t)\frac{\partial }{\partial v} \,\,\, B^{t}=0, \,\,\, B^{x}=-\frac{1}{2}F'(t)v, \,\,\, B^{y}=0, \,\,\, {B^{z}=0,} \end{aligned}$$

(2.20)

where arbitrary function F(t) satisfies $F'(t)=0$. Using the relation (Sarlet 2010)

$$\begin{aligned} \begin{aligned} C^{k} =\,{\mathcal {L}}\tau ^{k}+(\xi ^{\alpha }-\psi ^{\alpha }_{x^{j}}\tau ^{j})\Bigg (\frac{\partial {\mathcal {L}}}{\partial \psi ^{\alpha }_{x^{k}}}-\sum _{l=1}^{k}D_{x^{l}}\Big (\frac{\partial {\mathcal {L}}}{\partial \psi ^{\alpha }_{x^{l}x^{k}}}\Big )\Bigg ) +\sum _{l=k}^{n}(\eta ^{\alpha }_{l}-\psi ^{\alpha }_{x^{l}x^{j}}\tau ^{j})\frac{\partial {\mathcal {L}}}{\partial \psi ^{\alpha }_{x^{k}x^{l}}}, \end{aligned} \end{aligned}$$

thus, conserved vectors corresponding to the six Noether symmetries are respectively calculated as

$$\begin{aligned} C_1^{t}&=\frac{1}{2} b v_{xx}^2-\frac{a}{(n+1) (n+2)} v_{x}^{n+2}+\frac{1}{2} c v_{xx} v_{yy}+\frac{1}{2} d v_{xx} v_{zz}-\frac{1}{2} e v_{xxx}^2, \\ C_1^{x}&=\frac{a}{n+1} v_{t} v_{x}^{n+1} + \frac{b }{n+1}v_{t} v_{xxx}+\frac{b n}{n+1} v_{t} v_{xxx} - b v_{xx} v_{tx}+\frac{c }{2 (n+1)}v_{t} v_{xyy} \\&\quad +\frac{c n }{2 (n+1)}v_{t} v_{xyy}-\frac{1}{2} c v_{yy} v_{tx}+\frac{d }{2 (n+1)}v_{t} v_{xzz}+\frac{d n}{2 (n+1)} v_{t} v_{xzz}+\frac{1}{2}v_{t}^2 \\&\quad - \frac{1}{2} d v_{zz} v_{tx}+\frac{e}{n+1} v_{t} v_{xxxxx} + \frac{e n }{n+1}v_{t} v_{xxxxx}-e v_{xxxx} v_{tx}+e v_{xxx} v_{txx}, \\ C_1^{y}&=\frac{1}{2} c v_{t} v_{xxy}-\frac{1}{2} c v_{xx} v_{ty}, \\ C_1^{z}&=\frac{1}{2} d v_{t} v_{xxz}-\frac{1}{2} d v_{xx} v_{tz}; \\ C_2^{t}&=\frac{1}{2}v_{x}^2, \\ C_2^{x}&=\frac{a }{n+1}v_{x}^{n+2}-\frac{a}{(n+1) (n+2)} v_{x}^{n+2}+\frac{b }{n+1}v_{xxx} v_{x}+\frac{b n }{n+1}v_{xxx} v_{x}-\frac{1}{2} b v_{xx}^2 \\&\quad +\frac{c}{2 (n+1)} v_{x} v_{xyy}+\frac{c n }{2 (n+1)}v_{x} v_{xyy}+\frac{d}{2 (n+1)} v_{x} v_{xzz}+\frac{d n }{2 (n+1)}v_{x} v_{xzz} \\&\quad +\frac{e }{n+1}v_{xxxxx} v_{x}+\frac{e n }{n+1}v_{xxxxx} v_{x}+\frac{1}{2} e v_{xxx}^2-e v_{xx} v_{xxxx}+\frac{n}{2 (n+1)} v_{t} v_{x} \\&\quad +\frac{1}{2 (n+1)}v_{t} v_{x}-\frac{1}{2} v_{t} v_{x}, \\ C_2^{y}&=\frac{1}{2} c v_{x} v_{xxy}-\frac{1}{2} c v_{xx} v_{xy}, \\ C_2^{z}&=\frac{1}{2} d v_{x} v_{xxz}-\frac{1}{2} d v_{xx} v_{xz}; \\ C_3^{t}&=\frac{1}{2} v_{x} v_{y}, \\ C_3^{x}&=\frac{a}{n+1} v_{y} v_{x}^{n+1}+\frac{b }{n+1}v_{xxx} v_{y}+\frac{b n }{n+1}v_{xxx} v_{y}-b v_{xx} v_{xy}+\frac{c }{2 (n+1)}v_{y} v_{xyy} \\&\quad +\frac{c n }{2 (n+1)}v_{y} v_{xyy}-\frac{1}{2} c v_{yy} v_{xy}+\frac{d }{2 (n+1)}v_{y} v_{xzz}+\frac{d n }{2 (n+1)}v_{y} v_{xzz} \\&\quad -\frac{1}{2} d v_{zz} v_{xy}+\frac{e}{n+1} v_{xxxxx} v_{y}+\frac{e n }{n+1}v_{xxxxx} v_{y}+e v_{xxx} v_{xxy} \\&\quad -e v_{xxxx} v_{xy}+\frac{n }{2 (n+1)}v_{t} v_{y}+\frac{1}{2 (n+1)}v_{t} v_{y}, \\ C_3^{y}&=\frac{1}{2} b v_{xx}^2-\frac{a }{(n+1) (n+2)}v_{x}^{n+2}+\frac{1}{2} c v_{y} v_{xxy}+\frac{1}{2} d v_{xx} v_{zz}-\frac{1}{2} e v_{xxx}^2 \\&\quad -\frac{1}{2} v_{t} v_{x}, \end{aligned}$$

$$ \begin{aligned} C_3^{z}&=\frac{1}{2} d v_{y} v_{xxz}-\frac{1}{2} d v_{xx} v_{yz}; \\ C_4^{t}&= \frac{1}{2} v_{x} v_{z}, \\ C_4^{x}&=\frac{a}{n+1} v_{z} v_{x}^{n+1}+\frac{b }{n+1}v_{xxx} v_{z}+\frac{b n }{n+1}v_{xxx} v_{z}-b v_{xx} v_{xz}+\frac{c }{2 (n+1)}v_{z} v_{xyy} \\&\quad +\frac{c n }{2 (n+1)}v_{z} v_{xyy}-\frac{1}{2} c v_{yy} v_{xz}+\frac{d}{2 (n+1)} v_{z} v_{xzz}+\frac{d n }{2 (n+1)}v_{z} v_{xzz} \\&\quad -\frac{1}{2} d v_{zz} v_{xz}+\frac{e}{n+1} v_{xxxxx} v_{z}+\frac{e n }{n+1}v_{xxxxx} v_{z}+e v_{xxx} v_{xxz}-e v_{xxxx} v_{xz} \\&\quad +\frac{n }{2 (n+1)}v_{t} v_{z}+\frac{1}{2 (n+1)}v_{t} v_{z}, \\ C_4^{y}&=\frac{1}{2} c v_{z} v_{xxy}-\frac{1}{2} c v_{xx} v_{yz}, \\ C_4^{z}&=-\frac{a}{(n+1) (n+2)} v_{x}^{n+2}+\frac{1}{2} b v_{xx}^2+\frac{1}{2} c v_{xx} v_{yy}+\frac{1}{2} d v_{z} v_{xxz}-\frac{1}{2} e v_{xxx}^2-\frac{1}{2} v_{t} v_{x}; \\ C_5^{t}&=\frac{1}{2} c z v_{y} v_{x}-\frac{1}{2} d y v_{z} v_{x}, \\ C_5^{x}&=\frac{a c }{n+1}z v_{y} v_{x}^{n+1}-\frac{a d }{n+1}y v_{z} v_{x}^{n+1}+\frac{1}{2} d^2 y v_{zz} v_{xz}+\frac{1}{2} c d y v_{yy} v_{xz} \\ &\quad -\frac{d^2 }{2 (n+1)}y v_{z} v_{xzz}-\frac{d^2 n}{2 (n+1)} y v_{z} v_{xzz}+\frac{c d }{2 (n+1)}z v_{y} v_{xzz}+\frac{c d n }{2 (n+1)}z v_{y} v_{xzz} \\ &\quad -\frac{1}{2} c d z v_{zz} v_{xy}-\frac{1}{2} c^2 z v_{yy} v_{xy}-\frac{c d }{2 (n+1)}y v_{z} v_{xyy}-\frac{c d n }{2 (n+1)}y v_{z} v_{xyy}\end{aligned} $$

$$ \begin{aligned} &\quad +\frac{c^2}{2 (n+1)} z v_{y} v_{xyy}+\frac{c^2 n }{2 (n+1)}z v_{y} v_{xyy}+b d y v_{xz} v_{xx}-\frac{b d }{n+1}y v_{z} v_{xxx} \\ &\quad-\frac{b d n}{n+1} y v_{z} v_{xxx}+\frac{b c}{n+1} z v_{y} v_{xxx}+\frac{b c n }{n+1}z v_{y} v_{xxx}-d e y v_{xxz} v_{xxx}+c e z v_{xxy} v_{xxx} \\ &\quad+d e y v_{xz} v_{xxxx}-b c z v_{xy} v_{xx}-c e z v_{xy} v_{xxxx}-\frac{d e }{n+1}y v_{z} v_{xxxxx}-\frac{d e n }{n+1}y v_{z} v_{xxxxx} \\ &\quad+\frac{c e }{n+1}z v_{y} v_{xxxxx}+\frac{c e n}{n+1} z v_{y} v_{xxxxx}-\frac{d }{2 (n+1)}y v_{z} v_{t}-\frac{d n }{2 (n+1)}y v_{z} v_{t} \\ &\quad+\frac{c}{2 (n+1)} z v_{y} v_{t}+\frac{c n}{2 (n+1)} z v_{y} v_{t}, \\ C_5^{y}&=-\frac{a c}{(n+1) (n+2)} z v_{x}^{n+2}-\frac{1}{2} c z v_{t} v_{x}+\frac{1}{2} b c z v_{xx}^2-\frac{1}{2} c e z v_{xxx}^2+\frac{1}{2} c d v_{z} v_{xx} \\ &\quad+\frac{1}{2} c d z v_{zz} v_{xx}+\frac{1}{2} c d y v_{yz} v_{xx}-\frac{1}{2} c d y v_{z} v_{xxy}+\frac{1}{2} c^2 z v_{y} v_{xxy}, \\ C_5^{z}&=\frac{a d }{(n+1) (n+2)}y v_{x}^{n+2}+\frac{1}{2} d y v_{t} v_{x}-\frac{1}{2} b d y v_{xx}^2+\frac{1}{2} d e y v_{xxx}^2-\frac{1}{2} c d v_{y} v_{xx} \\ &\quad-\frac{1}{2} c d z v_{yz} v_{xx}-\frac{1}{2} c d y v_{yy} v_{xx}-\frac{1}{2} d^2 y v_{z} v_{xxz}+\frac{1}{2} c d z v_{y} v_{xxz}; \\ C_F^{t}&=-\frac{1}{2} F(t) v_{x}, \\ C_F^{t}&=-\frac{a F(t)}{n+1} v_{x}^{n+1}-\frac{b}{n+1} F(t) v_{xxx}-\frac{b n}{n+1} F(t) v_{xxx}-\frac{c}{2 (n+1)} F(t) v_{xyy} \\ &\quad-\frac{c n }{2 (n+1)}F(t) v_{xyy}-\frac{d }{2 (n+1)}F(t) v_{xzz}-\frac{d n}{2 (n+1)} F(t) v_{xzz}-\frac{e }{n+1}F(t) v_{xxxxx} \\ &\quad -\frac{e n }{n+1}F(t) v_{xxxxx}-\frac{n }{2 (n+1)}F(t) v_{t}-\frac{1}{2 (n+1)}F(t) v_{t}, \\ C_F^{t}&=-\frac{1}{2} c F(t) v_{xxy}, \\ C_F^{t}&=-\frac{1}{2} d F(t) v_{xxz}. \end{aligned} $$

Hence, retrograding to the original variables, we have the conserved currents accordingly as

$$\begin{aligned} C_1^{t}&= \frac{1}{2}b u^{2}_x+\frac{1}{2}c u_x\int u_{yy}dx+\frac{1}{2}du_x\int u_{zz}dx-\frac{a}{(n+1)(n+2)}u^{n+2} \\&\quad -\frac{1}{2}e u^{2}_{xx}, \\ C_1^{x}&= \left( \frac{a}{n+1}u^{n+1}+ \frac{d}{2(n+1)}u^{n+1}u_{zz}+\frac{nd}{2(n+1)}u_{zz}\right) \int u_tdx \\&\quad +\left( \frac{nc}{2(n+1)}u_{yy}+\frac{c}{2(n+1)}u_{yy}+\frac{b}{n+1}u_{xx}+\frac{nb}{n+1}u_{xx}\right) \int u_tdx \\&\quad +\left( \frac{e}{n+1}u_{xxxx}+\frac{ne}{n+1}u_{xxxx}+\frac{1}{2(n+1)}\int u_tdx\right) \int u_tdx \\&\quad +\frac{n}{2(n+1)}\left( \int u_tdx\right) ^{2}-\frac{1}{2}du_t \int u_{zz}dx -\frac{1}{2}cu_t \int u_{yy}dx \\&\quad -bu_tu_x-eu_tu_{xxx}, \\ C_1^{y}&=\frac{1}{2}cu_{xy} \int u_{t}dx-\frac{1}{2}cu_x \int u_{ty}dx, \\ C_1^{z}&=\frac{1}{2}du_{xz} \int u_{t}dx-\frac{1}{2}du_x \int u_{tz}dx; \\ C_2^{t}&=\frac{1}{2}u^2, \\ C_2^{x}&= \frac{a}{n+1}u^{n+2}- \frac{a}{(n+1)(n+2)}u^{n+2}+\frac{d}{2(n+1)}uu_{zz} \\&\quad +\frac{c}{2(n+1)}uu_{yy}+\frac{nc}{2(n+1)}uu_{yy}-\frac{1}{2}bu^2_{x}+\frac{b}{n+1}uu_{xx} \\&\quad +\frac{nb}{n+1}uu_{xx}+\frac{nd}{2(n+1)}uu_{zz}+\frac{1}{2}eu^{2}_{xx}-u_{x}u_{xxx}+\frac{e}{n+1}uu_{xxxx} \\&\quad +\frac{ne}{n+1}uu_{xxxx}+\frac{1}{2(n+1)}u\int u_tdx+\frac{n}{2(n+1)}u\int u_tdx \\&\quad -\frac{1}{2}u\int u_t dx, \\ C_2^{y}&=\frac{1}{2}cuu_{xy}-\frac{1}{2}c u_xu_y, \\ C_2^{z}&=\frac{1}{2}duu_{xz}-\frac{1}{2}d u_xu_z; \\ C_3^{t}&=\frac{1}{2}u\int u_ydx, \\ C_3^{x}&=\frac{a}{n+1}u^{n+1}\int u_ydx+\frac{d}{2(n+1)}u_{zz}\int u_ydx+\frac{nd}{2(n+1)}u_{zz}\int u_ydx \\&\quad -\frac{1}{2}du_{y}\int u_{zz}dx-\frac{1}{2}cu_{y}\int u_{yy}dx-\frac{c}{2(n+1)}u_{yy}\int u_{y}dx \\&\quad +\frac{cn}{2(n+1)}u_{yy}\int u_{y}dx-bu_xu_y+\frac{b}{n+1}u_{xx}\int u_{y}dx \\&\quad +\frac{nb}{n+1}u_{xx}\int u_{y}dx+eu_{xx}u_{xy}-eu_{xxx}u_{y}+\frac{e}{n+1}u_{xxxx}\int u_{y}dx \\&\quad +\frac{en}{n+1}u_{xxxx}\int u_{y}dx+\frac{1}{2(n+1)}\int u_{t}dx\int u_{y}dx \\&\quad +\frac{n}{2(n+1)}\int u_{t}dx\int u_{y}dx, \\ C_3^{y}&= \frac{1}{2}du_x\int u_{zz}dx-\frac{a}{(n+1)(n+2)}u^{n+2}+\frac{1}{2}cu_{xy}\int u_{y}dx \\&\quad +\frac{1}{2}bu_x^2-\frac{1}{2}eu_{xx}^2-\frac{1}{2}u\int u_tdx, \\ C_3^{z}&=\frac{1}{2}du_{xz}\int u_ydx-\frac{1}{2}d u_x\int u_{yz}dx; \\ C_4^{t}&=\frac{1}{2}u\int u_zdx,\end{aligned}$$

$$\begin{aligned} C_4^{x}&=\frac{a}{n+1}u^{n+1}\int u_zdx-\frac{1}{2}du_{z}\int u_{zz}dx-\frac{1}{2}cu_{z}\int u_{yy}dx \\&\quad +\frac{d}{2(n+1)}u_{zz}\int u_{z}dx+\frac{nd}{2(n+1)}u_{zz}\int u_{z}dx \\&\quad +\frac{c}{2(n+1)}u_{yy}\int u_{z}dx+\frac{nc}{2(n+1)}u_{yy}\int u_{z}dx-bu_xu_z \\&\quad +\frac{b}{n+1}u_{xx}\int u_{z}dx+\frac{bn}{n+1}u_{xx}\int u_{z}dx+eu_{xx}u_{xz}-eu_zu_{xxx} \\&\quad +\frac{en}{n+1}u_{xxxx}\int u_{z}dx+\frac{1}{2(n+1)}\int u_{t}dx\int u_{z}dx \\&\quad +\frac{e}{n+1}u_{xxxx}\int u_{z}dx+\frac{n}{2(n+1)}\int u_{t}dx\int u_{z}dx, \\ C_4^{y}&=\frac{1}{2}cu_{xy}\int u_zdx-\frac{1}{2}c u_x\int u_{yz}dx, \\ C_4^{z}&=\frac{1}{2}bu_x^2-\frac{a}{(n+1)(n+2)}u^{n+2}+\frac{1}{2}du_{xz}\int u_{z}dx+\frac{1}{2}c u_x\int u_{yy}dx \\&\quad -\frac{1}{2}eu_{xx}^2-\frac{1}{2}u\int u_tdx; \\ C_5^{t}&=\frac{1}{2}c zu\int u_ydx-\frac{1}{2}d uy\int u_zdx, \\ C_5^{x}&=\frac{ac}{n+1}zu^{n+1}\int u_ydx-\frac{ad}{n+1}yu^{n+1}\int u_zdx+\frac{1}{2}d^2yu_z\int u_{zz}dx \\&\quad +\frac{1}{2}cdyu_z\int u_{yy}dx - \frac{d^2}{2(n+1)}yu_{zz}\int u_zdx- \frac{nd^2}{2(n+1)}yu_{zz}\int u_zdx \\&\quad + \frac{cd}{2(n+1)}zu_{zz}\int u_ydx + \frac{ncd}{2(n+1)}zu_{zz}\int u_ydx - \frac{1}{2}cdzu_{y}\int u_{zz}dx \\&\quad - \frac{1}{2}c^2zu_{y}\int u_{yy}dx - \frac{cd}{2(n+1)}yu_{yy}\int u_zdx - \frac{ncd}{2(n+1)}yu_{yy}\int u_zdx \\&\quad + \frac{c^2}{2(n+1)}zu_{yy}\int u_ydx + \frac{nc^2}{2(n+1)}zu_{yy}\int u_ydx + bd y u_xu_z \\&\quad -bczu_xu_y - \frac{bd}{n+1}yu_{xx}\int u_zdx - \frac{nbd}{n+1}yu_{xx}\int u_zdx \\&\quad + \frac{bc}{n+1}zu_{xx}\int u_ydx+ \frac{nbc}{n+1}zu_{xx}\int u_ydx-deyu_{xx}u_{xz} \\&\quad +cezu_{xx}u_{xy}+ deyu_{xxx}u_z-cezu_yu_{xxx}- \frac{de}{n+1}yu_{xxxx}\int u_zdx \\&\quad - \frac{ned}{n+1}yu_{xxxx}\int u_zdx+ \frac{ec}{n+1}zu_{xxxx}\int u_ydx+ \frac{nec}{n+1}zu_{xxxx}\int u_ydx \\&\quad - \frac{d}{2(n+1)}y\int u_{t}\int u_zdx- \frac{nd}{2(n+1)}y\int u_{t}\int u_zdx \\&\quad + \frac{c}{2(n+1)}z\int u_{t}\int u_ydx+ \frac{nc}{2(n+1)}z\int u_{t}\int u_ydx; \\ C_5^{y}&=\frac{1}{2}cdu_{x}\int u_zdx -\frac{ac}{(n+1)(n+2)}zu^{n+2} + \frac{1}{2}cdzu_{x}\int u_{zz}dx \\&\quad + \frac{1}{2}cdyu_{x}\int u_{yz}dx + \frac{1}{2}bczu_x^2 - \frac{1}{2}cdyu_{xy}\int u_{z}dx + \frac{1}{2}c^2zu_{xy}\int u_{y}dx \\&\quad -\frac{1}{2}cezu^2_{xx} + \frac{1}{2}czu\int u_{t}dx, \\ C_5^{z}&=\frac{ad}{(n+1)(n+2)}yu^{n+2}-\frac{1}{2}cdu_{x}\int u_ydx - \frac{1}{2}cdzu_{x}\int u_{yz}dx \\&\quad - \frac{1}{2}cdyu_{x}\int u_{yy}dx - \frac{1}{2}bdyu_x^2 - \frac{1}{2}d^2yu_{xz}\int u_{z}dx + \frac{1}{2}cdzu_{xz}\int u_{y}dx \\&\quad + \frac{1}{2}deyu^2_{xx} + \frac{1}{2}dyu\int u_{t}dx; \\ C_F^{t}&= -\frac{1}{2}uF(t), \\ C_F^{x}&= -\frac{a}{n+1}u^{n+1}F(t) - \frac{d}{2(n+1)}u_{zz}F(t) - \frac{nd}{2(n+1)}u_{zz}F(t) \\&\quad - \frac{c}{2(n+1)}u_{yy}F(t)- \frac{nc}{2(n+1)}u_{yy}F(t)- \frac{b}{n+1}u_{xx}F(t) \\&\quad - \frac{nb}{n+1}u_{xx}F(t)- \frac{e}{n+1}u_{xxxx}F(t)- \frac{ne}{n+1}u_{xxxx}F(t) \\&\quad - \frac{1}{2(n+1)}F(t)\int u_tdx- \frac{n}{2(n+1)}F(t)\int u_tdx, \\ C_F^{y}&=-\frac{1}{2}c u_{xy}F(t), \\ C_F^{z}&=-\frac{1}{2}d u_{xz}F(t).\end{aligned}$$

Construction of the conserved currents of (1.7)

Computations of the conserved vectors related to (1.7) is enunciated here. Thus, following the procedural steps earlier-adopted, that is, invoking the transformation $u=v_x$, one has

$$\begin{aligned} v_{tx}+ a(hv^{n}_{x}+kv^{2n}_{x})v_{xx}+ b v_{xxxx}+c v_{xxyy}+dv_{xxzz}+ev_{xxxxxx}=0. \end{aligned}$$

(2.21)

In consequence, the 3D-gnFoZKe (1.7) is consequently variational and owns a Lagrangian $(\mathcal {L})$ which commensurate with the minimal differential order given as

$$\begin{aligned} \mathcal {L}&=-\frac{1}{2}\, v_t v_x -{ \frac{ah\, v_x^{n+2}}{ (n+1) (n+2) }} -{ \frac{ak\, v_x^{2n+2}}{ (2n+1) (2n+2) }}+\frac{1}{2}\,b\, v_{xx}^{2} +\frac{1}{2}\,c\,v_{xx} v_{yy}\nonumber \\&\quad +\frac{1}{2}\,d\,v_{xx}v_{zz}-\frac{1}{2}\,e\, v_{xxx}^{2}. \end{aligned}$$

(2.22)

Just as previously engendered, one achieves six Noether symmetries (2.20) here also, and we get different conserved currents analogous to the gained-symmetries as

$$\begin{aligned} C_1^{t}&= \frac{1}{2}b u^{2}_x+\frac{1}{2}c u_x\int u_{yy}dx+\frac{1}{2}du_x\int u_{zz}dx-\frac{ah}{(n+1)(n+2)}u^{n+2} \\&\quad -\frac{ak}{(2n+1)(2n+2)}u^{2n+2}-\frac{1}{2}e u^{2}_{xx}, \\ C_1^{x}&= \frac{ah}{n+1}u^{n+1}\int u_tdx+ \frac{ak}{2n+1}u^{2n+1}\int u_tdx+\frac{1}{2}du_{zz} \int u_tdx \\&\quad + \frac{1}{2}cu_{yy}\int u_tdx+bu_{xx}\int u_tdx+eu_{xxxx}\int u_tdx \\&\quad +\frac{1}{2}\left( \int u_tdx\right) ^{2}-\frac{1}{2}du_t \int u_{zz}dx -\frac{1}{2}cu_t \int u_{yy}dx \\&\quad -bu_tu_x-eu_tu_{xxx}+ e u_{tx}u_{xx}, \\ C_1^{y}&=\frac{1}{2}cu_{xy} \int u_{t}dx-\frac{1}{2}cu_x \int u_{ty}dx, \\ C_1^{z}&=\frac{1}{2}du_{xz} \int u_{t}dx-\frac{1}{2}du_x \int u_{tz}dx; \\ C_2^{t}&=\frac{1}{2}u^2, \\ C_2^{x}&= \frac{ah}{n+1}u^{n+2}- \frac{ah}{(n+1)(n+2)}u^{n+2}- \frac{ak}{(2n+1)(2n+2)}u^{2n+2} \\&\quad + \frac{ak}{2n+1}u^{2n+2}+\frac{1}{2}duu_{zz}+\frac{1}{2}cuu_{yy}-\frac{1}{2}bu^2_{x}+buu_{xx} \\&\quad +\frac{1}{2}eu^{2}_{xx}-eu_{x}u_{xxx}+e uu_{xxxx}, \\ C_2^{y}&=\frac{1}{2}cuu_{xy}-\frac{1}{2}c u_xu_y, \\ C_2^{z}&=\frac{1}{2}duu_{xz}-\frac{1}{2}d u_xu_z; \\ C_3^{t}&=\frac{1}{2}u\int u_ydx, \\ C_3^{x}&=\frac{ah}{n+1}u^{n+1}\int u_ydx+\frac{ak}{2n+1}u^{2n+1}\int u_ydx+\frac{1}{2}du_{zz}\int u_ydx \\&\quad -\frac{1}{2}du_{y}\int u_{zz}dx-\frac{1}{2}cu_{y}\int u_{yy}dx+\frac{1}{2}cu_{yy}\int u_{y}dx \\&\quad +bu_{xx}\int u_{y}dx+eu_{xx}u_{xy}-eu_{xxx}u_{y}-bu_xu_y \\&\quad +eu_{xxxx}\int u_{y}dx+\frac{1}{2}\int u_{t}dx\int u_{y}dx, \\ C_3^{y}&= \frac{1}{2}du_x\int u_{zz}dx-\frac{ah}{(n+1)(n+2)}u^{n+2}+\frac{1}{2}cu_{xy}\int u_{y}dx \\&\quad -\frac{ak}{(2n+1)(2n+2)}u^{2n+2}+\frac{1}{2}bu_x^2-\frac{1}{2}eu_{xx}^2-\frac{1}{2}u\int u_tdx, \\ C_3^{z}&=\frac{1}{2}du_{xz}\int u_ydx-\frac{1}{2}d u_x\int u_{yz}dx; \\ C_4^{t}&=\frac{1}{2}u\int u_zdx, \end{aligned}$$

$$\begin{aligned} C_4^{x}&=\frac{ah}{n+1}u^{n+1}\int u_zdx+\frac{ak}{2n+1}u^{2n+1}\int u_zdx-\frac{1}{2}du_{z}\int u_{zz}dx \\&\quad -\frac{1}{2}cu_{z}\int u_{yy}dx+\frac{1}{2}du_{zz}\int u_{z}dx+\frac{1}{2}cu_{yy}\int u_{z}dx \\&\quad +bu_{xx}\int u_{z}dx+eu_{xx}u_{xz}-eu_zu_{xxx}-bu_xu_z \\&\quad +eu_{xxxx}\int u_{z}dx+\frac{1}{2}\int u_{t}dx\int u_{z}dx, \\ C_4^{y}&=\frac{1}{2}cu_{xy}\int u_zdx-\frac{1}{2}c u_x\int u_{yz}dx, \\ C_4^{z}&=\frac{1}{2}bu_x^2-\frac{ah}{(n+1)(n+2)}u^{n+2}+\frac{1}{2}du_{xz}\int u_{z}dx+\frac{1}{2}c u_x\int u_{yy}dx \\&\quad -\frac{ak}{(2n+1)(2n+2)}u^{2n+2}-\frac{1}{2}eu_{xx}^2-\frac{1}{2}u\int u_tdx; \\ C_5^{t}&=\frac{1}{2}c zu\int u_ydx-\frac{1}{2}d uy\int u_zdx, \\ C_5^{x}&=\frac{ach}{n+1}zu^{n+1}\int u_ydx-\frac{adh}{n+1}yu^{n+1}\int u_zdx+\frac{1}{2}d^2yu_z\int u_{zz}dx \\&\quad +\frac{1}{2}cdyu_z\int u_{yy}dx +\frac{ach}{2n+1}zu^{2n+1}\int u_ydx-\frac{adh}{2n+1}yu^{2n+1}\int u_zdx \\&\quad + \frac{1}{2}cdzu_{zz}\int u_ydx - \frac{1}{2}d^2yu_{zz}\int u_zdx - \frac{1}{2}cdzu_{y}\int u_{zz}dx \\&\quad - \frac{1}{2}c^2zu_{y}\int u_{yy}dx - \frac{1}{2}cdyu_{yy}\int u_zdx+ \frac{1}{2}c^2zu_{yy}\int u_ydx \\&\quad + bd y u_xu_z-bczu_xu_y - bdyu_{xx}\int u_zdx+ bczu_{xx}\int u_ydx \\&\quad -deyu_{xx}u_{xz}+cezu_{xx}u_{xy}+ deyu_{xxx}u_z- edyu_{xxxx}\int u_zdx \\&\quad + eczu_{xxxx}\int u_ydx-cezu_yu_{xxx}- \frac{1}{2}dy\int u_{t}\int u_zdx \\&\quad + \frac{1}{2}cz\int u_{t}\int u_ydx; \\ C_5^{y}&=\frac{1}{2}cdu_{x}\int u_zdx -\frac{ach}{(n+1)(n+2)}zu^{n+2} + \frac{1}{2}cdzu_{x}\int u_{zz}dx \\&\quad + \frac{1}{2}cdyu_{x}\int u_{yz}dx + \frac{1}{2}bczu_x^2 - \frac{1}{2}cdyu_{xy}\int u_{z}dx + \frac{1}{2}c^2zu_{xy}\int u_{y}dx \\&\quad -\frac{ack}{(2n+1)(2n+2)}zu^{2n+2}-\frac{1}{2}cezu^2_{xx} - \frac{1}{2}czu\int u_{t}dx, \\ C_5^{z}&=\frac{adh}{(n+1)(n+2)}yu^{n+2}-\frac{1}{2}cdu_{x}\int u_ydx - \frac{1}{2}cdzu_{x}\int u_{yz}dx \\&\quad - \frac{1}{2}cdyu_{x}\int u_{yy}dx - \frac{1}{2}bdyu_x^2 - \frac{1}{2}d^2yu_{xz}\int u_{z}dx + \frac{1}{2}cdzu_{xz}\int u_{y}dx \\&\quad +\frac{adk}{(2n+1)(2n+2)}yu^{2n+2}+ \frac{1}{2}deyu^2_{xx} + \frac{1}{2}dyu\int u_{t}dx; \\ C_F^{t}&= -\frac{1}{2}uF(t), \\ C_F^{x}&= -\frac{ah}{n+1}u^{n+1}F(t) - \frac{1}{2}du_{zz}F(t) - \frac{1}{2}cu_{yy}F(t) - bu_{xx}F(t) \\&\quad -eu_{xxxx}F(t) -\frac{ak}{2n+1}u^{2n+1}F(t) - \frac{1}{2}F(t)\int u_tdx, \\ C_F^{y}&=-\frac{1}{2}c u_{xy}F(t), \\ C_F^{z}&=-\frac{1}{2}d u_{xz}F(t). \end{aligned}$$

3 Determining equations via Lie group analysis

This part of the research, first reveals the computation of the related Lie point symmetries to models (1.6) and (1.7), which are thereafter, utilized to compute exact solutions to the models.

3.1 Computations of infinitesimal generators of (1.6)

Symmetry group of 3D-gnFoZKe (1.6) will be achieved via the vector field which is formatted as

$$\begin{aligned} W&= \xi ^1(t,x,y,z,u)\frac{\partial }{\partial x}+\xi ^2(t,x,y,z,u)\frac{\partial }{\partial y}+\xi ^3(t,x,y,z,u)\frac{\partial }{\partial z}+\xi ^4(t,x,y,z,u)\frac{\partial }{\partial t} \\&\quad + \eta (t,x,y,z,u)\frac{\partial }{\partial u}, \end{aligned}$$

where $\xi ^i,i=1,\cdots ,4$ and $\eta$ are coefficient-functions of t, x, y, z and u. W is a Lie point symmetry of model (1.6) if invariant criterion

$$\begin{aligned} \text{ Pr}^{(5)}W[ u_t+a u^nu_x+b u_{xxx}+ cu_{xyy}+du_{xzz}+eu_{xxxxx}]=0, \end{aligned}$$

(3.23)

whenever $u_t+a u^nu_x+b u_{xxx}+ cu_{xyy}+du_{xzz}+eu_{xxxxx}=0$. We express that Pr$^{(5)}W$ denotes fifth extension of W delineated as

$$\begin{aligned} \text{ Pr}^{(5)}=W+\zeta _{t}\partial _{u_t}+\zeta _{x}\partial _{u_x}+\zeta _{xxx}\partial _{u_{xxx}}+\zeta _{xyy}\partial _{u_{xyy}}+\zeta _{xzz}\partial _{u_{xzz}}++\zeta _{xyy}\partial _{u_{xyy}}+\zeta _{xxxxx}\partial _{u_{xxxxx}}, \end{aligned}$$

(3.24)

where the $\zeta '$s are defined as

$$\begin{aligned} \begin{aligned}&\zeta _{t}= D_{t}(\eta )-u_{x}D_{t}(\xi ^{1})-u_{y}D_{t}(\xi ^{2})-u_{z}D_{t}(\xi ^{3})-u_{t}D_{t}(\xi ^{4}), \\&\zeta _{x}= D_{x}(\eta )-u_{x}D_{x}(\xi ^{1})-u_{y}D_{x}(\xi ^{2})-u_{z}D_{x}(\xi ^{3})-u_{t}D_{x}(\xi ^{4}), \\&\zeta _{xxx}=D_{x}(\zeta _{xx})-u_{xxx}D_{x}(\xi ^{1})-u_{xxy}D_{x}(\xi ^{2})-u_{xxz}D_{x}(\xi ^{3})-u_{xxt}D_{x}(\xi ^{4}), \\&\zeta _{xyy}=D_{x}(\zeta _{yy} )-u_{xyy}D_{x}(\xi ^{1})-u_{yyy}D_{x}(\xi ^{2})-u_{zyy}D_{x}(\xi ^{3})-u_{yyt}D_{x}(\xi ^{4}), \\&\zeta _{xzz}=D_{x}(\zeta _{zz})-u_{xzz}D_{x}(\xi ^{1})-u_{zzy}D_{x}(\xi ^{2})-u_{zzz}D_{x}(\xi ^{3})-u_{zzt}D_{x}(\xi ^{4}) \\&{\zeta _{xxxxx}=D_{x}(\zeta _{xxxx})-u_{xxxxx}D_{x}(\xi ^{1})-u_{xxxxy}D_{x}(\xi ^{2})-u_{xxxxz}D_{x}(\xi ^{3})-u_{xxxxt}D_{x}(\xi ^{4}),} \\ \end{aligned} \end{aligned}$$

(3.25)

where the total differential operators are given as

$$\begin{aligned}&D_{t}=\, \partial _{t}+u_{t}\partial _{u}+u_{tt}\partial _{u_{t}}+u_{xt}\partial _{u_{x}}+\cdots ,\nonumber \\&D_{x}=\, \partial _{x}+u_{x}\partial _{u}+u_{xx}\partial _{u_{x}}+u_{xt}\partial _{u_{t}}+\cdots . \end{aligned}$$

(3.26)

Expanding equation (3.23) and splitting same over the various derivatives of u, we procure twenty-one overdetermined system of linear PDEQs

$$\begin{aligned}&\xi ^{1}_{t}=0, \quad \xi ^{1}_{u}=0, \quad \xi ^{1}_{x}=0, \quad \xi ^{1}_{y}=0, \quad \xi ^{1}_{z}=0, \\&\xi ^{4}_{t}=0,\quad \xi ^{4}_{u}=0,\quad \xi ^{4}_{x}=0, \quad \xi ^{4}_{y}=0,\quad \xi ^{4}_{z}=0, \\&\xi ^{2}_{t}=0, \quad \xi ^{2}_{u}=0, \quad \xi ^{2}_{x}=0, \quad \xi ^{2}_{y}=0, \quad \xi ^{2}_{zz}=0, \quad \xi ^{3}_{t}=0, \\&\xi ^{3}_{u}=0, \quad \xi ^{3}_{x}=0, \quad c\xi ^{3}_{y}+d\xi ^{2}_{z}=0, \quad \xi ^{3}_{z}=0, \quad \eta =0. \end{aligned}$$

Six Lie point symmetries that are secured from the solution of the system are

$$\begin{aligned}&W_{1}=\frac{\partial }{\partial x}, \,\,\, W_{2}=\frac{\partial }{\partial y}, \,\,\, W_{3}=\frac{\partial }{\partial z}, \,\,\, W_{4}=\frac{\partial }{\partial t}, \nonumber \\&W_{5}={c}z\frac{\partial }{\partial y}-{d}y\frac{\partial }{\partial z}. \end{aligned}$$

(3.27)

Therefore 3D-gnFoZKe equation (1.6) admits a five-dimensional Lie algebra spanned by the above vectors $W_1,\dots ,W_5$. In the same vein, following the earlier-given procedure, we achieve the same set of symmetries for (1.7).

Next, we utilize the obtained Lie point symmetries to reduce equations (1.6) and (1.7) with a view to achieving possible exact solutions. Thus, we consider the theorem:

Theorem 3.1

Symmetry reductions and invariant solutions to 3D-gnFoZKe (1.6) and (1.7) are achieved using symmetries given as: $W_5$, $W_{1}+W_{2}$, $W_{1} + e_0 W_{3} + e_1 W_{4}$, $W_{1} + c_0 W_{3} + c_1 W_{4}$ and $\beta W_{1} + W_2 + W_{3} + W_{4}$, for arbitrary constants $\beta , c_i, e_i, i= 0,1$.

3.1.1 Reductions of (1.6) using symmetry generator $W_1 = W_{1}+W_{2}$

The characteristic equations associated to symmetry $W_1 = \partial /\partial t + \partial /\partial x$ are

$$\begin{aligned} \frac{dt}{1} = \frac{dx}{1} = \frac{dy}{0} = \frac{dz}{0} = \frac{du}{0}. \end{aligned}$$

(3.28)

This system of equations solves to give the invariants attained as

$$\begin{aligned} X = x - t, \, \, Y = y, \, \, \text {and} \, \, Z = z, \, \, \text {where} \, \, \textbf{R}(X,Y,Z) = u(t,x,y,z). \end{aligned}$$

Using these obtained invariants transform equation (1.6) to the NLNPDE

$$\begin{aligned} \textbf{R}_{X} - a \textbf{R}^n\textbf{R}_{X} - b \textbf{R}_{XXX} - c \textbf{R}_{XYY} - d\textbf{R}_{XZZ} - e \textbf{R}_{XXXXX} = 0. \end{aligned}$$

(3.29)

On solving equation (3.29) for $n = 1$, one obtains a solution of (1.6) as

$$\begin{aligned} u(t,x,y,z)&= \frac{1}{a}\left\{ 3360 A_2^4 e \tanh ^2\bigg (A_1 - \frac{1}{d} \sqrt{-d\left( 52A_2^4 e + A_2^2 b + A_3^2 c \right) } z \right. \nonumber \\&\left. + A_2 \big [x - t\big ] + A_3 y\bigg )- 1680 A_2^4 e \tanh ^4\bigg ( A_2 \big [x - t\big ] + A_3 y \right. \nonumber \\&\left. - \frac{1}{d} \sqrt{-d\left( 52A_2^4 e + A_2^2 b + A_3^2 c \right) } z + A_1\bigg ) \right. \nonumber \\&\left. - \frac{1}{a} \left( 1104 A_2^4 - 1\right) \right\} , \end{aligned}$$

(3.30)

where $A_1$, $A_2$ and $A_3$ are integration constants. Also, when $n = 2$, we have

$$\begin{aligned} u(t,x,y,z)&= \frac{1}{a}\left\{ - 6 \sqrt{-10ae} B_2^2 \tanh ^2\bigg (B_1 - \frac{1}{d} \sqrt{-\left( b B_2^2 d + B_3^2 cd + \Omega _0 \right) } z \right. \nonumber \\&\quad \left. + B_2 \big [x - t\big ] + B_3 y\bigg ) \right\} + \frac{1}{\sqrt{-10ae} B_2^2} \bigg [ b B_2^2 + B_3^2 c - 40 e B_2^4 \nonumber \\&\quad - \frac{1}{d} \left( b B_2^2 d + B_3^2 c d + \Omega _0 \right) \bigg ] \end{aligned}$$

(3.31)

with $\Omega _0 = \sqrt{-240 B_2^8 d^2 e^2 - 10 B_2^4 d^2 e}$, and integration constants $B_1$, $B_2$ and $B_3$. Further study on (3.29) reveals that Lie point symmetries furnished as

$$\begin{aligned} M_1 = \frac{\partial }{\partial X}, \, \, \, M_2 = \frac{\partial }{\partial Y}, \, \, \, M_3 = \frac{\partial }{\partial Z}, \, \, \, M_4 = c Z \frac{\partial }{\partial Y} - d Y \frac{\partial }{\partial Z} \end{aligned}$$

are admitted by the equation. Exploring $M_1$, one observes that it produces a trivial solution and so on engaging $M_2$, one discovers that it purveys invariant $\Theta (r,s) = \textbf{R}(X,Y,Z)$, where $r = X$, $s = Z$. Insertion of the achieved result in (3.29), attains a reduction of the equation explicated as

$$\begin{aligned} \Theta _{r} - a \Theta ^n\Theta _{r} - b \Theta _{rrr} - d\Theta _{rss} - e \Theta _{rrrrr} = 0. \end{aligned}$$

(3.32)

A particular case of (3.32) for $n = 1$ gives the result purveyed as

$$\begin{aligned} u(t,x,y,z)&= \frac{1}{a} \bigg \{ 3360 C_2^4 e \tanh ^2\left( C_2 x - \frac{1}{d}\sqrt{-d\left( 52 C_2^2 e + b \right) } C_2 z + C_1 \right) \nonumber \\&\quad - 1680 C_2^4 e \tanh ^4\left( C_2 x - \frac{1}{d}\sqrt{-d\left( 52 C_2^2 e + b \right) } C_2 z + C_1 \right) \nonumber \\&\quad - 1104 C_2^4 e - 1 \bigg \}, \end{aligned}$$

(3.33)

where $C_i, i = 1,2,3$ are arbitrary constants. In the same vein when $n = 2$, we secure

$$\begin{aligned} u(t,x,y,z)&= \frac{1}{a} \bigg \{- \sqrt{-360 a e} C_2^2 \tanh ^2\left( C_2 x - \frac{1}{d}\sqrt{-bd - \Omega _3 } C_2 z + C_1 \right) \bigg \} \nonumber \\&\quad + \frac{1}{\sqrt{-10 a e}}\left[ b - 40 e C_2^2 - \frac{1}{d} \left( bd + \Omega _3 \right) \right] , \end{aligned}$$

(3.34)

where $\Omega _3 = \sqrt{-240 C_2^4 d^2 e^2 - 10 d^2 e}$. Further exploration of (3.32) gives symmetries $N_1 = \partial /\partial r$ and $N_2 = \partial /\partial s$, which we linearly combine as $N = b_0 N_1 + b_1 N_2$, where real constants $b_0 = b_1 \ne 0$ and furnishes invariant $G (w) = \Theta (r,s)$ where $w = s - b_1/b_0 r$. Substituting the result further reduces 3D-gnFoZKe (1.6) to a nonlinear ordinary differential equation (NONLDE)

$$\begin{aligned} b_0^4 G' (w) - a b_0^4 G^n (w) G' (w) - b b_0^2b_1^2 G''' (w) - b_0^4 dG''' (w) - b_1^4e G''''' (w) = 0. \end{aligned}$$

(3.35)

Examining $M_3$, gives $\Theta (r,s) = \textbf{R}(X,Y,Z)$, $r = X$, $s = Y$, which reduces (3.29) to

$$\begin{aligned} \Theta _{r} - a \Theta ^n\Theta _{r} - b \Theta _{rrr} - c\Theta _{rss} - e \Theta _{rrrrr} = 0. \end{aligned}$$

(3.36)

Again, a particular scenario of (3.32) for $n = 1$ gives the result purveyed as

$$\begin{aligned} u(t,x,y,z)&= \frac{1}{a} \bigg \{ 3360 C_2^4 e \tanh ^2\left( C_2 x - \frac{1}{c}\sqrt{-c\left( 52 C_2^2 e + b \right) } C_2 y + C_1 \right) \nonumber \\&\quad - 1680 C_2^4 e \tanh ^4\left( C_2 x - \frac{1}{c}\sqrt{-c\left( 52 C_2^2 e + b \right) } C_2 y + C_1 \right) \nonumber \\&\quad - 1104 C_2^4 e - 1 \bigg \}, \end{aligned}$$

(3.37)

where $C_i, i = 1,2,3$ are arbitrary constants. In the same vein when $n = 2$, we secure

$$\begin{aligned} u(t,x,y,z)&= \frac{1}{a} \bigg \{- \sqrt{-360 a e} C_2^2 \tanh ^2\left( C_2 x - \frac{1}{c}\sqrt{-bc - \Omega _3 } C_2 y + C_1 \right) \bigg \} \nonumber \\&\quad + \frac{1}{\sqrt{-10 a e}}\left[ b - 40 e C_2^2 - \frac{1}{c} \left( bc + \Omega _3 \right) \right] , \end{aligned}$$

(3.38)

where $\Omega _3 = \sqrt{-240 C_2^4 c^2 e^2 - 10 c^2 e}$. Next, we investigate $M = M_1 + M_2 + M_3$ and this gives $\Theta (r,s) = \textbf{R}(X,Y,Z)$, for $r = Y - X$, as well as $s = Z - X$, thus transforming (3.29) to

$$\begin{aligned}&\Theta _{r} + \Theta _{s} - a \Theta ^n\Theta _{r} - a \Theta ^n\Theta _{s} - b \Theta _{rrr} - c \Theta _{rrr} - 3 b \Theta _{rss} - d \Theta _{rss} - 3 b \Theta _{rrs} - c \Theta _{rrs} \nonumber \\&\quad - b \Theta _{sss} - d \Theta _{sss} - e \Theta _{rrrrr} - 5 e \Theta _{rrrrs} - 10 e \Theta _{ssrrr} - 10 e \Theta _{sssrr} - 5 e \Theta _{ssssr} \nonumber \\&\quad - e \Theta _{sssss} = 0. \end{aligned}$$

(3.39)

Solving the equation produces a solution of 3D-gnFoZKe (1.6) as

$$\begin{aligned} u(t,x,y,z)&= A_2 + A_4 \tanh ^2\left( A_1 \left[ t - x + y\right] - A_1 \left[ t + z - x\right] + A_0\right) \nonumber \\&\quad + A_3 \tanh \left( A_1 \left[ t - x + y \right] - A_1 \left[ t + z - x \right] + A_0\right) \end{aligned}$$

(3.40)

with arbitrary constants $A_i, i = 0,1,\dots ,4$. Furthermore, equation (3.39) admits translation symmetries combined as $\partial /\partial r + a_0 \partial /\partial s$, with real constant $a_0 \ne 0$. This eventually gives invariant $G (w) = \Theta (r,s)$ where $w = s - a_0 r$. The use of the invariant further reduces (1.6) to the NONLDE

$$\begin{aligned}&G' (w) - a_0 G' (w) - a G^n (w) G' (w) + a a_0 G^n (w) G' (w) + a_0^3 b G''' (w) + a_0^3 c G''' (w) \nonumber \\&\quad - 3 a_0^2 b G''' (w) + a_0 d G''' (w) + 3 a_0 b G''' (w) - a_0^2 c G''' (w) - b G''' (w) - d G''' (w) \nonumber \\&\quad + a_0^5 e G''''' (w) - 5 a_0^4 e G''''' (w) + 10 a_0^3 e G''''' (w) - 10 a_0^2 e G''''' (w) + 5 a_0 e G''''' (w) \nonumber \\&\quad - e G''''' (w) = 0. \end{aligned}$$

(3.41)

Now, we consider the use of $M_4$ which gives $\Theta (r,s) = \textbf{R}(X,Y,Z)$, where $r = X$, and $s = Z^2 + d/c Y^2$. Now, introducing the new invariant, (3.29) under $M_4$ reduces to

$$\begin{aligned} \Theta _{r} - a \Theta ^n\Theta _{r} - 4 d \Theta _{rs} - b \Theta _{rrr} - 4 d s \Theta _{rss} - e \Theta _{rrrrr} = 0 \end{aligned}$$

(3.42)

from which no solution of importance could be found.

3.1.2 Reductions of (1.6) via symmetry generator $W_3 = W_{1} + e_0 W_{3} + e_1 W_{4}$

In this part of the reduction process, we engage symmetry $W_3 = \partial /\partial t + e_0 \partial /\partial y + e_1 \partial /\partial z$. Therefore, the corresponding invariants to the symmetry are given as

$$\begin{aligned} X = x, \, \, \, Y = y - e_0 t, \, \, \, \, Z = z - e_1 t, \, \, \, \textbf{R}\left( X,Y,Z\right) = u(t,x,y,z). \end{aligned}$$

(3.43)

Application of the obtained-outcome (3.43) provides a reduced form of (1.6) as

$$\begin{aligned} e_0\textbf{R}_{Y} + e_1\textbf{R}_{Z} - a \textbf{R}^n\textbf{R}_{X} - b \textbf{R}_{XXX} - c \textbf{R}_{XYY} - d \textbf{R}_{XZZ} - e \textbf{R}_{XXXXX} = 0. \end{aligned}$$

(3.44)

Solving equation (3.29) for $n = 1$, one achieves a solution of (1.6) as

$$\begin{aligned} u(t,x,y,z)&= \, \frac{1}{a}\left\{ 3360 B_2^4 e \tanh ^2\bigg (B_1 - \frac{1}{d} \sqrt{-d\left( 52B_2^4 e + B_2^2 b + B_3^2 c \right) }\left( z - e_1 t \right) \right. \nonumber \\&\left. + B_2 x + B_3 \big [y - e_0 t\big ]\bigg )- 1680 B_2^4 e \tanh ^4\bigg ( B_2 x + B_3 \big [y - e_0 t\big ] \right. \nonumber \\&\left. - \frac{1}{d} \sqrt{-d\left( 52B_2^4 e + B_2^2 b + B_3^2 c \right) }\left( z - e_1 t \right) + B_1\bigg ) \right. \nonumber \\&\left. + \frac{1}{B_2 } \left[ \left( B_3 e_0 - 1104 B_2^5 e - \frac{e_1}{d} \sqrt{-d\left( 52B_2^4 e + B_2^2 b + B_3^2 c \right) }\right) \right] \right\} , \end{aligned}$$

(3.45)

where $B_1$, $B_2$ and $B_3$ are integration constants. However, for $n = 2$, no solution of interest could be attained. Now, invoking the Lie group analysis, we observe that (3.44) admits translation symmetries: $M_1 = \partial /\partial X$, $M_2 = \partial /\partial Y$ and $M_3 = \partial /\partial Z$. As usual, we engage $M_1$ yields $\Theta (r,s) = \textbf{R}(X,Y,Z)$, where $r = Y$ and $s = Z$. Invoking the invariant in (3.44), one gets $e_0 \Theta _r + e_1 \Theta _s = 0$, which solves to give

$$\begin{aligned} u(t,x,y,z) = f\left\{ \left( z - e_1 t \right) - \dfrac{e_1}{e_0} \left( y - e_0 t \right) \right\} , \end{aligned}$$

(3.46)

where arbitrary f is a function depending on its argument. In the case of $M_3$, we attain the invariant $\Theta (r,s) = \textbf{R}(X,Y,Z)$, where $r = X$ and $s = Z$. Substituting the new relation in (3.44) produces NLNPDE

$$\begin{aligned} e_1\Theta _{s} - a \Theta ^n\Theta _{r} - b \Theta _{rrr} - d \Theta _{rss} - e \Theta _{rrrrr} = 0. \end{aligned}$$

(3.47)

Solving (3.47) for $n=1$ gives no new result and for $n=2$, no interesting solution could be achieved. Furthermore, symmetries $N_1 = \partial /\partial r$ and $N_2 = \partial /\partial s$, linearly combine as $N = N_1 - a_0 N_2$, where real constants $a_0 \ne 0$ and furnishes invariant $G (w) = \Theta (r,s)$ where $w = s + a_0 r$, and this further reduces 3D-gnFoZKe (1.6) to

$$\begin{aligned} e_1 G' (w) - a a_0 G^n (w) G' (w) - b a_0^3 G''' (w) - a_0 dG''' (w) - a_0^5e G''''' (w) = 0. \end{aligned}$$

(3.48)

Examining $M_3$, one gets $\Theta (r,s) = \textbf{R}(X,Y,Z)$, $r = X$, $s = Y$, reducing (3.44) to

$$\begin{aligned} e_0\Theta _{s} - a \Theta ^n\Theta _{r} - b \Theta _{rrr} - c \Theta _{rss} - e \Theta _{rrrrr} = 0, \end{aligned}$$

(3.49)

which purveys no new solutions of importance but admits symmetries combined linearly as $\partial /\partial r + \theta \partial /\partial s$, $\theta \ne 0$. This gives invariant $G (w) = \Theta (r,s)$ where $w = s - \theta r$ which when it is substituted in (3.49) produces the fifth-order NONLDE

$$\begin{aligned} e_0 G' (w) - a \theta G^n (w) G' (w) - b \theta ^3 G''' (w) - \theta dG''' (w) - \theta ^5e G''''' (w) = 0. \end{aligned}$$

(3.50)

Finally, we consider $\partial /\partial X + \partial /\partial Y + \partial /\partial Z$, furnishing $\Theta (r,s) = \textbf{R}(X,Y,Z)$, $r = Y - X$, $s = Z - X$. This function eventually further transforms (1.6) to

$$\begin{aligned}&e_0 \Theta _{r} + e_1 \Theta _{s} + a \Theta ^n\Theta _{r} + a \Theta ^n\Theta _{s} + b \Theta _{rrr} + c \Theta _{rrr} + 3 b \Theta _{rss} + d \Theta _{rss} + 3 b \Theta _{rrs} + c \Theta _{rrs} \nonumber \\&\quad + b \Theta _{sss} + d \Theta _{sss} + e \Theta _{rrrrr} + 5 e \Theta _{rrrrs} + 10 e \Theta _{ssrrr} + 10 e \Theta _{sssrr} + 5 e \Theta _{ssssr} \nonumber \\&\quad + e \Theta _{sssss} = 0. \end{aligned}$$

(3.51)

Just as experienced earlier, we linearly combine the admitted symmetries of (3.51) as $\partial /\partial r + \vartheta \partial /\partial s$, with real constant $\vartheta \ne 0$. This eventually gives invariant $G (w) = \Theta (r,s)$ where $w = s - \vartheta r$. The use of the invariant further reduces (1.6) to

$$\begin{aligned}&e_1 G' (w) - \vartheta e_0 G' (w) - a G^n (w) G' (w) + a \vartheta G^n (w) G' (w) + \vartheta ^3 b G''' (w) + \vartheta ^3 c G''' (w) \nonumber \\&\quad - 3 \vartheta ^2 b G''' (w) + \vartheta d G''' (w) + 3 \vartheta b G''' (w) - \vartheta ^2 c G''' (w) - b G''' (w) - d G''' (w) \nonumber \\&\quad + \vartheta ^5 e G''''' (w) - 5 \vartheta ^4 e G''''' (w) + 10 \vartheta ^3 e G''''' (w) - 10 \vartheta ^2 e G''''' (w) + 5 \vartheta e G''''' (w) \nonumber \\&\quad - e G''''' (w) = 0. \end{aligned}$$

(3.52)

Next, in this research work, we reduce the dual power-law 3D-gnFoZKe (1.7) via the attained symmetries and obtain some exact solutions of the equation.

3.1.3 Reductions of (1.7) using symmetry generator $W_1 = W_{1}+W_{2}$

Reducing (1.7) using symmetry $W_1 = \partial /\partial t + \partial /\partial x$, the related Lagrangian system solve to give the invariants attained as

$$\begin{aligned} X = x - t, \, \, Y = y, \, \, \text {and} \, \, Z = z, \, \, \text {with} \, \, \textbf{R}(X,Y,Z) = u(t,x,y,z). \end{aligned}$$

Applying these obtained invariants transform equation (1.7) to the NLNPDE

$$\begin{aligned} \textbf{R}_{X} - a h \textbf{R}^n\textbf{R}_{X} - a k \textbf{R}^{2n}\textbf{R}_{X} - b \textbf{R}_{XXX} - c \textbf{R}_{XYY} - d\textbf{R}_{XZZ} - e \textbf{R}_{XXXXX} = 0. \end{aligned}$$

(3.53)

In this case, we have for $n = 1$, a group-invariant solution of 3D-gnFoZKe (1.7) as

$$\begin{aligned} u(t,x,y,z)&= \, \Bigg \{\left[ -\frac{1}{2}\Omega _5 +2\sqrt{10} C_2^2 d\left( eC_2^2 k - \frac{\sqrt{-10ake}}{40} h \right) \right] \nonumber \\&\times \cosh ^2 \Bigg (\frac{1}{2d}\Bigg [\sqrt{\frac{1}{k}\left[ -2\sqrt{10}\Omega _5 - 4 d k \left( C_2^2 b + C_3^2 c\right) \right] }z - 2 d \left[ C_2 \left( x - t \right) \right. \nonumber \\&\left. + C_3 y + C_1 \right] \Bigg ]\Bigg ) - 3 e C_2^4 d k \Bigg \} \left\{ kdC_2^2\sqrt{-ake}\cosh ^2 \Bigg (\frac{1}{2d}\Bigg [ - 2 d \left[ C_2 \left( x - t \right) \right. \right. \nonumber \\&{\left. \left. + C_3 y + C_1 \right] +\sqrt{\frac{1}{k}\left[ -2\sqrt{10}\Omega _5 - 4 d k \left( C_2^2 b + C_3^2 c\right) \right] }z \Bigg ]\Bigg )\right\} ^{-1},} \end{aligned}$$

(3.54)

where $\Omega _5 = \sqrt{-ekC_2^4 d^2\left( k\left[ 96C_2^4 e + 4\right] + a h^2 \right) }$ with arbitrary constants $C_1$, $C_2$ as well as $C_3$. In addition, for $n = 2$, one obtains the tan-hyperbolic complexion solution

$$\begin{aligned} u(t,x,y,z)&= \, \sqrt{-\frac{1}{6akh}\left( 5 a h^2 - \Omega _6\right) } \tanh \left\{ \left( \frac{\sqrt{2}}{12}\left[ -\frac{1}{ke}\left( 3\Omega _6 - 15 a h^2 - 54k \right) \right] ^{1/4} \right. \right. \nonumber \\&\left. \left. + \frac{\sqrt{2}}{12}i\left[ -\frac{1}{ke}\left( 3\Omega _6 - 15 a h^2 - 54k \right) \right] ^{1/4} \right) \left[ x - t\right] + C_2 y + C_1 \right. \nonumber \\&{\left. + \sqrt{-\frac{1}{108dk}\left( 3bk i \sqrt{-\frac{1}{ke}\left( 3\Omega _6 - 15 a h^2 - 54k \right) } + 180 c k C_2^2 + \Omega _7 \right) }z\right\} ,} \end{aligned}$$

(3.55)

where $\Omega _6 = \sqrt{25 a^2\,h^4 + 180 a k h^2}$, $\Omega _7 = 10 a h^2 - 2\Omega _6 + 90k$. Further to that, Eq. (3.53) produces four symmetries; $M_1 = \partial /\partial X$, $M_2 = \partial /\partial Y$, $M_3 = \partial /\partial Z$, $M_4 = c Z\partial /\partial Y - d Y \partial /\partial Z$. Studies show that $M_1$ gives a trivial solution whereas $M _2$ and $M_3$ do not give new solutions of interest. However, we try to examine the combination of the three, linearly, and so we have $\partial /\partial X + \partial /\partial Y + \partial /\partial Z$, which yields $\Theta (r,s) = \textbf{R}(X,Y,Z)$, $r = Y - X$, $s = Z - X$. Therefore, using the result reduces (3.53) to

$$\begin{aligned}&\Theta _{r} + \Theta _{s} - a h \Theta ^n\Theta _{r} - a h \Theta ^n\Theta _{s} - a k \Theta ^{2n}\Theta _{r} - a k \Theta ^{2n}\Theta _{s} - b \Theta _{rrr} - c \Theta _{rrr} - 3 b \Theta _{rss} \nonumber \\&\quad - d \Theta _{rss} - 3 b \Theta _{rrs} - c \Theta _{rrs} - b \Theta _{sss} - d \Theta _{sss} - e \Theta _{rrrrr} - 5 e \Theta _{rrrrs} - 10 e \Theta _{ssrrr} \nonumber \\&\quad - 10 e \Theta _{sssrr} - 5 e \Theta _{ssssr} - e \Theta _{sssss} = 0. \end{aligned}$$

(3.56)

Solving (3.56) produces an outcome fulfilling 3D-gnFoZKe (1.7) as

$$\begin{aligned} u(t,x,y,z)&= \, C_2 + C_4 \tanh ^2\left( C_1 \left[ y + t - x\right] - C_1 \left[ z + t - x\right] + C_0\right) \nonumber \\&\quad + C_3 \tanh \left( C_1 \left[ y + t - x \right] - C_1 \left[ z + t - x \right] + C_0\right) \end{aligned}$$

(3.57)

with $C_i, i = 0,1,\dots ,4$ as arbitrary constants. We linearly combine translation symmetries of (3.51) as $e_0 \partial /\partial r + e_1 \partial /\partial s$, with real constant $e_0 = e_1 \ne 0$. This eventually gives invariant $G (w) = \Theta (r,s)$ where $w = s - e_0/e_1 r$. On using the invariant, one further reduces (1.7) to

$$\begin{aligned}&a k e_0^5 G^{2n} (w) G' (w) - a k e_1 e_0^4 G^{2n} (w) G' (w) + a h e_0^5 G^{n} (w) G' (w) - a h e_1 e_0^4 G^{n} (w) G' (w) \nonumber \\&\quad - c e_1^3 e_0^2 G''' (w) + 3 b e_1^2 e_0^3 G''' (w) + d e_0^5 G''' (w) - b e_1^3 e_0^2 G''' (w) - d e_1 e_0^4 G''' (w) \nonumber \\&\quad + 10 e e_1^2 e_0^3 G''''' (w) - 10 e e_1^3 e_0^2 G''''' (w) - 5 e e_1 e_0^4 G''''' (w) + e e_0^5 G''''' (w) +b e_0^5 G''' (w) \nonumber \\&\quad + c e_1^2 e_0^3 G''' (w) - 3 b e_1 e_0^4 G''' (w) + 5 e e_1^4 e_0 G''''' (w) - e e_1^5 G''''' (w) = 0. \end{aligned}$$

(3.58)

Next, we examine symmetry $M_4$ which gives us $\textbf{R}(X,Y,Z) = \Theta (r,s)$, with $r = X$ as well as $s = Z^2 + d/c Y^2$. Inserting the outcome in (3.53) gives a reduction of (1.7) as

$$\begin{aligned} \Theta _{r} - a h \Theta ^n \Theta _{r} - a k \Theta ^{2n} \Theta _{r} - 4 d \Theta _{rs}- b \Theta _{rrr} - 4 d s \Theta _{rss} - e \Theta _{rrrrr} = 0. \end{aligned}$$

(3.59)

Further investigation of NLNPDEQ (3.53) produces no solution of significance.

3.1.4 Reductions of (1.7) via symmetry generator $W_3 = W_{1} + c_0 W_{3} + c_1 W_{4}$

Lie symmetry application using $W_3 = \partial /\partial t + c_0 \partial /\partial y + c_1 \partial /\partial z$ gives invariants

$$\begin{aligned} X = x, \, \, \, Y = y - c_0 t, \, \, \, \, Z = z - c_1 t, \, \, \, \textbf{R}\left( X,Y,Z\right) = u(t,x,y,z), \end{aligned}$$

(3.60)

which in turn transform the 3D-gnFoZKe (1.7) with dual power-law to

$$\begin{aligned}&c_0 \textbf{R}_{Y} + c_1 \textbf{R}_{Z} - a h \textbf{R}^n\textbf{R}_{X} - a k \textbf{R}^{2n}\textbf{R}_{X} - b \textbf{R}_{XXX} - c \textbf{R}_{XYY} \nonumber \\&\quad - d\textbf{R}_{XZZ} - e \textbf{R}_{XXXXX} = 0. \end{aligned}$$

(3.61)

Equation (3.61) admits three translation symmetries which are $M_1 = \partial /\partial X$, $M_2 = \partial /\partial Y$, and $M_3 = \partial /\partial Z$. On examining $M_1$, we obtain $\Theta (r,s) = \textbf{R}(X,Y,Z)$, $r = Y$, $s = Z$. Using the invariant in (3.44), one gets $c_0 \Theta _r + c_1 \Theta _s = 0$, which solves to give

$$\begin{aligned} u(t,x,y,z) = f\left\{ \left( z - c_1 t \right) - \dfrac{c_1}{c_0} \left( y - c_0 t \right) \right\} \end{aligned}$$

(3.62)

with the prevalence of arbitrary f as a function depending on its argument. Studying $M_2$, and $M_3$ individually, one sees that none of them produce any new results so we contemplate linear combination of the achieved three symmetries leading to invariant $\Theta (r,s) = \textbf{R}(X,Y,Z)$, $r = Y - X$, $s = Z - X$. Applying the result in (3.61), yields

$$\begin{aligned}&c_0 \Theta _{r} + c_1 \Theta _{s} + a h \Theta ^n\Theta _{r} + a h \Theta ^n\Theta _{s} + a k \Theta ^{2n}\Theta _{r} + a k \Theta ^{2n}\Theta _{s} + b \Theta _{rrr} + c \Theta _{rrr} \nonumber \\&\quad + d \Theta _{rss} + 3 b \Theta _{rrs} + c \Theta _{rrs} + b \Theta _{sss} + d \Theta _{sss} + e \Theta _{rrrrr} + 5 e \Theta _{rrrrs} + 10 e \Theta _{ssrrr} \nonumber \\&\quad + 3 b \Theta _{rss} + 10 e \Theta _{sssrr} + 5 e \Theta _{ssssr} + e \Theta _{sssss} = 0. \end{aligned}$$

(3.63)

We note that equation (3.63) admits symmetries combined linearly as; $N = e_0 \partial /\partial r + e_1 \partial /\partial s$, with real constant $e_0 = e_1 \ne 0$. This eventually gives invariant $G (w) = \Theta (r,s)$ where $w = s - e_0/e_1 r$. Application of the invariant, one transforms (3.63) to

$$\begin{aligned}&c_0 e_0^3 e_1 G' (w) - c_1 e_0^5 G' (w) + a k e_1 e_0^4 G^{2n} (w) G' (w) - a k e_0^5 G^{2n} (w) G' (w) - a h e_0^5 G^{n} (w) G' (w) \nonumber \\&\quad + a h e_1 e_0^4 G^{n} (w) G' (w) + c e_1^3 e_0^2 G''' (w) + 3 b e_1^2 e_0^3 G''' (w) + d e_0^5 G''' (w) - b e_1^3 e_0^2 G''' (w) \nonumber \\&\quad - d e_1 e_0^4 G''' (w) + 10 e e_1^2 e_0^3 G''''' (w) - 10 e e_1^3 e_0^2 G''''' (w) - 5 e e_1 e_0^4 G''''' (w) + e e_0^5 G''''' (w) \nonumber \\&\quad +b e_0^5 G''' (w) - c e_1^2 e_0^3 G''' (w) - 3 b e_1 e_0^4 G''' (w) + 5 e e_1^4 e_0 G''''' (w) - e e_1^5 G''''' (w) = 0. \end{aligned}$$

(3.64)

Next, we utilize the combination of all the four symmetries which are $W_1$, $W_2$, $W_3$, and $W_4$ to reduce equations (1.6) and (1.7) concurrently. This will give us a more general case than any of the other cases earlier considered.

3.1.5 Reductions using symmetry generator $W = \beta W_{1}+W_{2}+W_{3}+ W_{4}$

In this segment, we involve symmetry $W=\beta W_{1}+W_{2}+W_{3}+ W_{4}$ with constant value $\beta \ne 0$ to reduce the 3D-gnFoZKe (1.6) alongside (1.7) to a PDEQ in three independent variables. Thus, solving the related Lagrangian systems for symmetry W, one secures four invariants:

$$\begin{aligned} z-y = f, \quad x-\beta y = g, \quad t-y = w, \quad u(t,x,y,z) = \theta (f,g,w). \end{aligned}$$

(3.65)

We treat $\theta$ as new dependent variables and g, f and w as new variables that are independent, 3D-gnFoZKe (1.6) and (1.7) then transforms respectively to

$$\begin{aligned}&\theta _{w}+a \theta ^{n}\theta _{g}+b \theta _{ggg}+c(\beta ^{2}\theta _{ggg}+2\beta \theta _{ggw}+2\beta \theta _{ggf}+\theta _{gww}+2\theta _{gfw} \nonumber \\&\quad +\theta _{gff}) +d\theta _{gff}+e \theta _{ggggg}=0,\end{aligned}$$

(3.66a)

$$\begin{aligned}&\theta _{w} + a h \theta ^{n}\theta _{g} + a k \theta ^{2n}\theta _{g} +b \theta _{ggg}+c(\beta ^{2}\theta _{ggg}+2\beta \theta _{ggw} +2\beta \theta _{ggf}\nonumber \\&\quad +\theta _{gww}+2\theta _{gfw}+\theta _{gff}) +d\theta _{gff}+e \theta _{ggggg}=0, \end{aligned}$$

(3.66b)

which is a NLNPDEQ in three independent variables. Investigating (3.66) further, we managed to find a solution of (3.66a) appropriately for $n = 1$ as

$$\begin{aligned} u(t,x,y,z)&= \, \frac{1}{a} \Bigg \{ 3360 B_3^4 e \tanh ^2\bigg \{B_2 \left( z - y\right) + B_3 \left( x - \beta y\right) + B_1 \nonumber \\&\quad +\left[ -1104 B_3^5 e + \frac{1}{c}\left( 1104 B_3^5 ce - \beta c B_3 - c B_2 - \Omega _8\right) \right] \left( t - y \right) \bigg \} \nonumber \\&\quad - 1680 B_3^4 e \tanh ^4\bigg \{B_2 \left( z - y\right) + B_3 \left( x - \beta y\right) + B_1 \nonumber \\&\quad +\left[ -1104 B_3^5 e + \frac{1}{c}\left( 1104 B_3^5 ce - \beta c B_3 - c B_2 - \Omega _8\right) \right] \left( t - y \right) \bigg \} \nonumber \\&\quad + \frac{1}{B_3 c} \left( 1104 B_3^5 ce - \beta c B_3 - c B_2 - \Omega _8\right) \Bigg \}, \end{aligned}$$

(3.67)

where $\Omega _8 = \sqrt{-c\left( 52 B_3^4 e + B_2^2 d + B_3^2 b \right) }$, with constants $B_i, i = 1,2,3$ arbitrary.

Now utilization of Lie point symmetries of (3.66) is done in transforming the PDEQ to a NLNPDEQ in two independent variables. Thus, equations (3.66a) together with (3.66b) then yield the following three translation symmetries, viz.,

$$\begin{aligned} \Upsilon _{1}=\frac{\partial }{\partial f}, \quad \Upsilon _{2}=\frac{\partial }{\partial g}, \quad \Upsilon _{3}=\frac{\partial }{\partial w}. \end{aligned}$$

Utilizing the linear combination $\Upsilon =\Upsilon _1+\alpha \Upsilon _2+\Upsilon _3$, of the generators $\Upsilon _1$, $\Upsilon _2$ and $\Upsilon _3$, with arbitrary constant $\alpha \ne 0$, we reduce (3.66). Solving the related Lagrangian system for $\Upsilon$, we have the following three invariants, viz.,

$$\begin{aligned} r=g - \alpha f, \quad s=w - f, \quad \theta =\phi . \end{aligned}$$

(3.68)

Now handling $\phi$ as the new dependent variable with new independent variables r and s, then 3D-gnFoZKe (1.6) as well as (1.7) are further reduced accordingly to

$$\begin{aligned}&\phi _{s}+ a \phi ^{n}\phi _{r}+b \phi _{rrr}+c(\beta ^2\phi _{rrr}-2\alpha \beta \phi _{rrr}+\alpha ^2\phi _{rrr})+d (\alpha ^2\phi _{rrr} \nonumber \\&\quad +2\alpha \phi _{rrs}+\phi _{rss})+e\phi _{rrrrr}=0, \end{aligned}$$

(3.69a)

$$\begin{aligned}&\phi _{s} + a h \phi ^{n}\phi _{r} + a k \phi ^{2n}\phi _{r} +b \phi _{rrr}+c(\beta ^2\phi _{rrr}-2\alpha \beta \phi _{rrr}+\alpha ^2\phi _{rrr}) \nonumber \\&\quad +d (\alpha ^2\phi _{rrr}+2\alpha \phi _{rrs}+\phi _{rss})+e\phi _{rrrrr}=0, \end{aligned}$$

(3.69b)

which are also NLNPDEQs in two independent variables. Now, invoking Lie point symmetries of (3.69), we then make a transformation to an ordinary differential equation (ODEQ). Thus equations (3.69) give the following two translation symmetries, namely

$$\begin{aligned} \Omega _{1}=\frac{\partial }{\partial r}\quad \text{ and } \quad \Omega _{2}=\frac{\partial }{\partial s}. \end{aligned}$$

(3.70)

Combined form of secured translation symmetries gives $\Omega =\gamma \Omega _{1}+ \Omega _{2}$, where $\omega$ is a constant, thus producing invariants

$$\begin{aligned} p=r-\gamma s\quad \text{ and } \quad \phi =G, \end{aligned}$$

(3.71)

thus yielding a group invariant solution $\phi =G(p)$. Consequently, applying these invariants, PDEQ (3.69a) is transformed into the fifth-order NONLDE

$$\begin{aligned} eG^{(5)}(p)+a G^{n}(p)G'(p)+(b+c\beta ^2-2\alpha \beta c+\alpha ^2 c+ \alpha ^2 d-2d\alpha \gamma +\gamma ^2d)G'''(p)-\gamma G'(p)=0. \end{aligned}$$

(3.72)

In the same vein, the dual-powerlaw nonlinearity (1.7) becomes also

$$\begin{aligned}&eG^{(5)}(p)+a (hG^{n}(p)+kG^{2n}(p))G'(p)+\left( b+c\beta ^2-2\alpha \beta c+\alpha ^2 c \right. \nonumber \\&\left. +\alpha ^2d - 2d\alpha \gamma +\gamma ^2d\right) G'''(p)-\gamma G'(p)=0 \end{aligned}$$

(3.73)

with $p=x+(\alpha -\beta )y+(\gamma -\alpha )z-\gamma t$.

Next, in additions to the earlier gained solution under symmetry W, we utilize a standard technique to achieve some solitary wave solutions of both (3.72) and (3.73) for some particular cases of n in the equations.

4 Solitary wave solutions of (1.6) and (1.7)

This section focuses on securing the solitary wave solutions of 3D-gnFoZKe for both the power-law (1.6) and dual power-law (1.7) for some particular cases of the equations via Kudryashov’s logistic function technique.

4.1 Kudryashov’s logistic function technique

In our approach, we shall utilize the logistic function Q(p) introduced in Kudryashov (2020); Dan et al. (2020) and based on the function R(p) defined by

$$\begin{aligned} R(p) = [a\, \text {exp}\, (\alpha p) + q\, \text {exp}\, (-\alpha p)]^{-1} \end{aligned}$$

(4.74)

to find solutions to (1.6) and (1.7). In (4.74), a, q as well as $\alpha$ are parameters related to function R(p). Kudryashov’s function R(p) has the property that it satisfies

$$\begin{aligned} {R_{p}^{2} = \alpha R^2(p)(1-\chi R^2(p)),} \end{aligned}$$

(4.75)

where $\chi =4aq$ and this can be proved by inserting R(p) given by

$$\begin{aligned} R(p) = 4a[4a^2\, \text {exp}\, (\alpha p) + \chi \, \text {exp}\, (-\alpha p)]^{-1} \end{aligned}$$

(4.76)

into equation (4.75). Furthermore, (4.75) possesses the property that its even higher-ordered derivatives can be expressed in terms of the polynomials of R. However, its odd higher-order derivatives are polynomials of R as well as $R_p$. The main difference between the logistic function Q and R lies in the fact that the former fulfills either $Q_p = Q^2 - 1$ or $Q_p = Q^2 - Q$ and therefore all the higher-order derivatives of logistic function Q are necessarily polynomials only of Q. Now, we hypothesize a finite series term solution of the form

$$\begin{aligned} G(p) = \sum _{j=0}^{M}A_jR^j(p), \end{aligned}$$

(4.77)

where the constant parameter $A_j, j = 0,\dots ,M$ needs to be determined. Furthermore, we note that without loss of generality, we assume $\alpha = 1$ to simplify our calculations.

Fig. 1

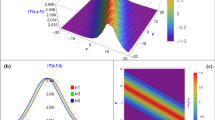
Solitary wave profile of solution (3.40) at $t=2$ and $x=4$

Fig. 2

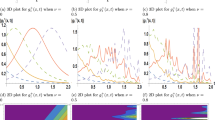
Soliton wave interaction depiction of solution (3.46)

4.1.1 Solutions of (1.6) via Kudryashov’s logistic function technique

We consider some particular cases of the power-law equation (1.6) for $n=1$ and $n=2$ to obtain some soliton solutions using the logistic function technique.

Case 1

We first secure the solutions of NONLDE (3.72) when $n=1$ and the balancing term $M=4$. Consequently, (4.77) assumes the structure

$$\begin{aligned} G(p)= A_0 + A_1 R(p)+ A_2 R^2(p)+ A_3 R^3(p)+ A_4 R^4(p). \end{aligned}$$

(4.78)

Reckoning (4.78) in (3.72) in conjunction with (4.75) we get the system of equations

$$\begin{aligned}&1680\,{\chi }^{3}eA_{{4}}+\,a\chi \,A_{{4}}^{2}=0,\\&2520\,{\chi }^{3}eA_{{3}}+7\,a\chi \,A_{{3}}A_{4}=0,\\&\alpha \,{c}^{2}dA_{{1}}-2\,\alpha \,\beta \,cA_{{1}}+\alpha \,{c}^{2}A_{{ 1}} -2\,\alpha \,d\gamma \,A_{{1}}+{\beta }^{2}cA_{{1}}+d{\gamma }^{2}A_{{1 }} \\&\quad +aA_{{0}}A_{{1}}+bA_{{1}}+eA_{{1}}-\gamma \,A_{{1}}=0, \\&8\,\alpha \,{c}^{2}dA_{{2}}-16\,\alpha \,\beta \,cA_{{2}}+8\,\alpha \,{c}^ {2}A_{{2}}-16\,\alpha \,d\gamma \,A_{{2}}+8\,{\beta }^{2}cA_{{2}}+8\,d{ \gamma }^{2}A_{{2}}\\&\quad +2\,aA_{{0}}A_{{2}}+aA_{{1}}^{2}+8\,bA_{{2}}+32\,e A_{{2}}-2\,\gamma \,A_{{2}}=0, \\&120\,\alpha \,{c}^{2}\chi ^{2}dA_{{4}}-240\,\alpha \,\beta \,c{\chi }^{2} A_{{4}}+120\,\alpha \,{c}^{2}{\chi }^{2}A_{{4}}-240\,\alpha \,{\chi }^{2}d \gamma \,A_{{4}}\\&\quad +120\,{\beta }^{2}c{\chi }^{2}A_{{4}}+120\,{\chi }^{2}d{ \gamma }^{2}A_{{4}}-720\,{\chi }^{3}eA_{{2}}-6\,a\chi \,A_{{2}}A_{{4}}-3 \,a\chi \,A_{{3}}^{2}\\&\quad +120\,b{\chi }^{2}A_{{4}}+12960\,{\chi }^{2}eA_{{4 }}+4\,aA_{{4}}^{2}=0, \\&60\,\alpha \,{c}^{2}{\chi }^{2}dA_{{3}}-120\,\alpha \,\beta \,c{\chi }^{2}A _{{3}}+60\,\alpha \,{c}^{2}{\chi }^{2}A_{{3}}-120\,\alpha \,{\chi }^{2}d \gamma \,A_{{3}}\\&\quad +60\,{\beta }^{2}c{\chi }^{2}A_{{3}}+60\,{\chi }^{2}d{ \gamma }^{2}A_{{3}}-120\,{\chi }^{3}eA_{{1}}-5\,a\chi \,A_{{1}}A_{{4}}-5 \,a\chi \,A_{{2}}A_{{3}}\\&\quad +60\,b{\chi }^{2}A_{{3}}+4560\,{\chi }^{2}eA_{{3} }+7\,aA_{{3}}A_{{4}}=0, \\&14\,\alpha \,\beta \,c\chi \,A_{{1}}-7 \,\alpha \,{c}^{2}\chi \,A_{{1}}+27\,\alpha \,{c}^{2}dA_{{3}}+14\,\alpha \,\chi \,d\gamma \,A_{{1}}-7\,{\beta }^{2}c\chi \,A_{{1}}\\&\quad -7\,\chi \,d{\gamma }^{2}A_{{1}}-a\chi \,A_{{0}}A_{{1}}-54\,\alpha \,\beta \,cA_{{3}}+ 27\,\alpha \,{c}^{2}A_{{3}}-54\,\alpha \,d\gamma \,A_{{3}}\\&\quad +27\,{\beta }^{2 }cA_{{3}}+27\,d{\gamma }^{2}A_{{3}}+3\,aA_{{0}}A_{{3}}+3\,aA_{{1}}A_{{2 }}-7\,b\chi \,A_{{1}}-61\,\chi \,eA_{{1}}\\&\quad +\chi \,\gamma \,A_{{1}}+27\,bA_{ {3}}+243\,eA_{{3}}-3\,\gamma \,A_{{3}}-7\,\alpha \,{c}^{2}\chi \,dA_{{1}}=0, \\&\quad -32\,\alpha \,{c}^{2}\chi \,dA_{{2}}+64\,\alpha \,\beta \,c\chi \,A_{{2}}- 32\,\alpha \,{c}^{2}\chi \,A_{{2}}+64\,\alpha \,{c}^{2}dA_{{4}}+64\, \alpha \,\chi \,d\gamma \,A_{{2}}\\&\quad -32\,{\beta }^{2}c\chi \,A_{{2}}-32\,\chi \,d{\gamma }^{2}A_{{2}}-2\,a\chi \,A_{{0}}A_{{2}}-a\chi \,A_{{1}}^{2}- 128\,\alpha \,\beta \,cA_{{4}}+64\,\alpha \,{c}^{2}A_{{4}} \\&\quad +64\,{\beta }^{2}cA_{{4}}+64\,d{\gamma }^{2}A_{{4}}+4\,aA _{{0}}A_{{4}}+4\,aA_{{1}}A_{{3}}+2\,aA_{{2}}^{2}-32\,b\chi \,A_{{2}}- 512\,\chi \,eA_{{2}} \\&\quad +2\,\chi \,\gamma \,A_{{2}}+64\,bA_{{4}}+1024\,eA_{{4 }}-4\,\gamma \,A_{{4}}-128\,\alpha \,d \gamma \,A_{{4}}=0, \\&6\,\alpha \,{c}^{2}{\chi }^{2}dA_{{1}}-12\,\alpha \,{\chi }^{2}d\gamma \,A_{{1}}-12\,\alpha \,\beta \,c{\chi }^{2}A_{ {1}}+6\,\alpha \,{c}^{2}{\chi }^{2}A_{{1}}-87\,\alpha \,{c}^{2}\chi \,dA_{ {3}}\\&\quad +6\,{\beta }^{2}c{\chi }^{2}A _{{1}}+6\,{\chi }^{2}d{\gamma }^{2}A_{{1}}+174\,\alpha \,\beta \,c\chi \,A_ {{3}}-87\,\alpha \,{c}^{2}\chi \,A_{{3}}+174\,\alpha \,\chi \,d\gamma \,A_{ {3}}\\&\quad -87\,{\beta }^{2}c\chi \,A_{{3}}-87\,\chi \,d{\gamma }^{2}A_{{3}}-3\,a \chi \,A_{{0}}A_{{3}}-3\,a\chi \,A_{{1}}A_{{2}}+6\,b{\chi }^{2}A_{{1}}+ 180\,{\chi }^{2}eA_{{1}}\\&\quad +5\,aA_{{1}}A_{{4}}+5\,aA_{{2}}A_{{3}}-87\,b \chi \,A_{{3}}-2283\,\chi \,eA_{{3}}+3\,\chi \,\gamma \,A_{{3}}=0, \\&24\,\alpha \,{c}^{2}{\chi }^{2}dA_{{2}}-48\,\alpha \,\beta \,c{\chi }^{2}A_ {{2}}+24\,\alpha \,{c}^{2}{\chi }^{2}A_{{2}}-184\,\alpha \,{c}^{2}\chi \,d A_{{4}}\\&\quad -48\,\alpha \,{\chi }^{2}d\gamma \,A_{{2}}+24\,{\beta }^{2}c{\chi }^ {2}A_{{2}}+24\,{\chi }^{2}d{\gamma }^{2}A_{{2}}+368\,\alpha \,\beta \,c \chi \,A_{{4}}-184\,\alpha \,{c}^{2}\chi \,A_{{4}}\\&\quad +368\,\alpha \,\chi \,d \gamma \,A_{{4}}-184\,{\beta }^{2}c\chi \,A_{{4}}-184\,\chi \,d{\gamma }^{2 }A_{{4}}-4\,a\chi \,A_{{0}}A_{{4}}-4\,a\chi \,A_{{1}}A_{{3}}\\&\quad +24\,b{\chi }^{2}A_{{2}}+1200\,{\chi }^{2}eA_{{2}}+6\,aA_{{2 }}A_{{4}}+3\,aA_{{3}}^{2}-184\,b\chi \,A_{{4}}-7264\,\chi \,eA_{{4}} \\&\quad -2\,a\chi \,{ A_{{2}}}^{2}+4\,\chi \,\gamma \,A_{{4}}=0. \end{aligned}$$

Employing a computer software package to secure the solutions of the ten given system of equation, one achieves the solution

$$\begin{aligned}&A_{{0}}=\frac{1}{13a} \left\{ \left[ \left( -144\,d-144 \right) {c}^{2} +288(\beta \,c+d\gamma ) \right] \alpha -144({\beta }^{2}c+d{\gamma }^{2}+b)+13\,\gamma \right\} ,\nonumber \\&A_{{1}}= A_{{2}}= A_{{3}}=0, \,\, A_{{4}}=\frac{1}{13a}\left\{ 420\,{\chi }^{2} \left[ \left\{ \left( d+1 \right) {c} ^{2}-2\beta \,c-2d\gamma \right\} \alpha +{\beta }^{2}c+d{\gamma }^{2}+ b \right] \right\} ,\nonumber \\&e=-\frac{1}{52}\left\{ \left[ \left\{ \left( d+1 \right) {c} ^{2}-2\,\beta \,c-2\,d\gamma \right\} \alpha +{\beta }^{2}c+d{\gamma }^{2}+ b \right] \right\} . \end{aligned}$$

(4.79)

Thus, we have a corresponding general solution to the results in (4.79) as

$$\begin{aligned} u(t,x,y,z)= A_0 + A_4\,\left[ \frac{4a}{4a^2\,\text {exp}\,{(p)}+\chi \,\text {exp}\,{(-p)} }\right] ^{4}\text {exp}\,{(p)}, \end{aligned}$$

(4.80)

where $p=x+(\alpha -\beta )y+(\gamma -\alpha )z-\gamma t$.

Fig. 3

Soliton wave interaction depiction of solution (3.46)

Fig. 4

Soliton wave interaction depiction of solution (3.62)

Case 2

Now we contemplate the solution of (3.72) when $n=2$ and the balancing term is $M=2$. Thus, (4.77) assumes the structure

$$\begin{aligned} G(p)= A_0 + A_1 R(p)+ A_2 R^2(p). \end{aligned}$$

(4.81)

Invoking the expression of G(p) from (4.81) in NONLDE (3.72) in consonance with (4.75), we gain eight system of equations which solves to give the solution

$$\begin{aligned}&A_{{0}}=\frac{1}{a}\sqrt{a \left( \gamma -16\,e+4\,\sqrt{-240\,{e}^{2}- 10\,e\gamma } \right) }, \,\, A_{{1}}=0,\nonumber \\&{A_{{2}}=\frac{3\chi \, \left( -80\,e+4\,\sqrt{-240\,{e}^{2}-10\,e\gamma } \right) }{2\sqrt{a \left( \gamma -16\,e+4\,\sqrt{-240\,{e}^{2}-10\,e \gamma } \right) }},}\nonumber \\&b=\frac{1}{12\,\sqrt{-24e^2-e\gamma } \, \Theta _0} \left\{ - 768 \left( \Theta _1 e-\Theta _2 \right) \sqrt{-24\,{e}^{2}-e\gamma }\sqrt{10}+\Theta _3 {e}^{2}\right. \nonumber \\&{\left. -496 \left( \alpha \, \left( d+1 \right) {c}^{2}+\beta \, \left( \beta -2\,\alpha \right) c-2\,d\alpha \,\gamma +d{\gamma }^{2}-{\frac{5\, \gamma }{31}} \right) \gamma \,e+{\gamma }^{2} \Theta _4 \right\} ,} \nonumber \\&\Theta _2={\frac{1}{64}}\left\{ \gamma \, \left( \alpha \, \left( d+1 \right) {c}^{2}+\beta \, \left( \beta -2\,\alpha \right) c-2 \,d\alpha \,\gamma +d{\gamma }^{2}-\gamma /12 \right) \right\} , \end{aligned}$$

(4.82)

where $\Theta _0=\left( 64\,e-\gamma \right) \sqrt{10}+5120\,{e}^{2}+496\,e\gamma -{\gamma }^{2}$, $\Theta _1= \alpha \, \left( d+1 \right) {c}^{2}+\beta \, \left( \beta -2\,\alpha \right) c-2\,d\alpha \,\gamma +d{\gamma }^{2}-{ \frac{11\,\gamma }{48}}$, $\Theta _3= -5120\,\alpha \, \left( d+1 \right) {c}^{2}-5120\,\beta \, \left( \beta -2\,\alpha \right) c+ 10240\,d\alpha \,\gamma -5120\,d{\gamma }^{2}+320\,\gamma$, $\Theta _4= \alpha \, \left( d+1 \right) {c}^{2}+\beta \, \left( \beta -2\,\alpha \right) c-2\,d\gamma \, \left( \alpha -\gamma /2 \right)$. Therefore, we have the associated general solution to (4.82) as

$$\begin{aligned} u(t,x,y,z)= A_0 + A_2\,\left[ \frac{4a}{4a^2\,\text {exp}\,{(p)}+\chi \,\text {exp}\,{(-p)} }\right] ^{2}\text {exp}\,{(p)} \end{aligned}$$

(4.83)

with $p=x+(\alpha -\beta )y+(\gamma -\alpha )z-\gamma t$.

Fig. 5

Soliton wave interaction depiction of solution (3.62)

Fig. 6

Bright soliton wave profile of solution (4.80) at $t=3$ and $x=2$

4.1.2 Solutions of (1.7) via Kudryashov’s logistic function technique

In this part of the study, we consider some particular cases of dual power-law equation (1.7) for $n=1$ and $n=2$ to achieve some soliton solutions via the logistic function technique.

Case A

Next, we achieve the solutions of NONLDE (3.73) when $n=1$ and then we use the balancing term $M=2$. Consequently, (4.77) assumes the form

$$\begin{aligned} G(p)= A_0 + A_1 R(p)+ A_2 R^2(p). \end{aligned}$$

(4.84)

Substituting the expression of G(p) from (4.84) into NONLDE (3.73) and using (4.75), we gain seven system of equations which solves to give the solutions

$$\begin{aligned} A_{{0}}&=\frac{1}{2ak\chi } \left( \Theta _5-4\,ak\sqrt{-{\frac{{10\chi }^{2}e}{ak}}}-a\chi \,h \right) , \,\, A_{{1}}=0, \,\, A_{{2}}=6\,\sqrt{-10\,{\frac{{\chi }^{2}e}{ak}}},\nonumber \\ b&=\frac{1}{2\chi \, \left( \Theta _5 -a\chi \,h \right) } \left\{ -a \left[ \left\{ -a{h}^{2}-4\,k \left( \gamma +24\,e \right) \right\} \chi +\Theta _5h \right] \sqrt{-{\frac{{10\chi }^{2}e}{a k}}}\right. \nonumber \\&\left. -2\,\chi \, \left( \Theta _5 -a\chi \,h \right) \left[ {\gamma }^{2} d-2\,\alpha \,d\gamma + \left\{ \left( cd-2\,\beta +c \right) \alpha +{ \beta }^{2} \right\} c \right] \right\} , \end{aligned}$$

(4.85)

$$\begin{aligned} A_{{0}}&=\frac{1}{ah}\left\{ \left[ \left( -4\,d-4 \right) {c}^{2}+8\,\beta \,c+8 \,\gamma \,d \right] \alpha -4(\,c{\beta }^{2}+{\gamma }^{2}d+b) \right\} , \,\, A_{{1}}=0,\nonumber \\ A_{{2}}&=\frac{1}{ah}\left\{ 12\left[ \left\{ \left( d+1 \right) {c}^{2}-2\, \beta \,c-2\,\gamma \,d \right\} \alpha +c{\beta }^{2}+{\gamma }^{2}d+b \right] \chi \right\} , \nonumber \\ k&={\frac{5\,\gamma \,a{h}^{2}}{48\, \left\{ \left[ \left( d+1 \right) {c}^{2}-2\,\beta \,c-2\,\gamma \,d \right] \alpha +c{\beta }^{2}+ {\gamma }^{2}d+b \right\} ^{2}}}, \end{aligned}$$

(4.86)

where $\Theta _5=\sqrt{a{\chi }^{2} \left( a{h}^{2}+96\, \left( e+\gamma /24 \right) k \right) }$. Hence, we have the related general solution to the results in (4.85) as well as (4.86), being given accordingly as

$$\begin{aligned} u(t,x,y,z)= A_0 + A_2\,\left[ \frac{4a}{4a^2\,\text {exp}\,{(p)}+\chi \,\text {exp}\,{(-p)} }\right] ^{2}\text {exp}\,{(p)}, \end{aligned}$$

(4.87)

$$\begin{aligned} u(t,x,y,z)= A_0 + A_2\,\left[ \frac{4a}{4a^2\,\text {exp}\,{(p)}+\chi \,\text {exp}\,{(-p)} }\right] ^{2}\text {exp}\,{(p)}, \end{aligned}$$

(4.88)

where $p=x+(\alpha -\beta )y+(\gamma -\alpha )z-\gamma t$.

Fig. 7

Bright soliton wave profile of solution (4.80) at $y=1$ and $z=1$

Fig. 8

Bright soliton wave profile of solution (4.87) at $t=-2$ and $x=0.2$

Case B

Finally, we find the solution of NONLDE (3.73) when $n=2$ and then we use the balancing term $M=1$. Consequently, (4.77) assumes G(p) as

$$\begin{aligned} G(p)= A_0 + A_1 R(p). \end{aligned}$$

(4.89)

Reckoning (4.89) in NONLDE (3.73) in conjunction with (4.75), we get a system of equation whose solution gives

$$\begin{aligned}&A_{{0}}=0, \,\, A_{{1}}=\mp \sqrt{\frac{54\,\chi \,e+6\,\chi \,\gamma }{ha}}\gamma , \,\, k=\frac{-10ea{h}^{2}}{3\left( \gamma +9\,e \right) ^{2}} , \nonumber \\&b=2\,\beta \,\alpha \,c-d\alpha \,{c}^{2}-\alpha \,{c}^{2}+2\,d\alpha \, \gamma -c{\beta }^{2}-{\gamma }^{2}d-e+\gamma . \end{aligned}$$

(4.90)

Thus, we have the general solution

$$\begin{aligned} u(t,x,y,z)= A_1\,\left[ \frac{4a}{4a^2\,\text {exp}\,{(p)}+\chi \,\text {exp}\,{(-p)} }\right] \text {exp}\,{(p)}, \end{aligned}$$

(4.91)

where $p=x+(\alpha -\beta )y+(\gamma -\alpha )z-\gamma t$.

Next, we reduce both (1.6) as well as (1.7) side-by-side using symmetry $W_5$.

4.1.3 Reductions of (1.6) and (1.7) using symmetry generator $W_{5}$

The Lagrangian system related to $W_{5}$ is given as

$$\begin{aligned} \frac{dt}{0}=\frac{dx}{0}=\frac{dy}{cz}=\frac{dz}{-dy}=\frac{du}{0}, \end{aligned}$$

(4.92)

thus producing invariants $f=t$, $g=x$ and $w=cz^2+dy^2$. So we have a group-invariant

$$\begin{aligned} u=\theta (f,g,w), \end{aligned}$$

(4.93)

where $\theta$ stands for an arbitrary function. Utilizing (4.93), PDEQs (1.6) and (1.7) transform to

$$\begin{aligned}&\theta _{f} + a \theta ^{n}\theta _{g}+b \theta _{ggg}+4 c d w \theta _{gww}+ 4 c d \theta _{gw} + e \theta _{ggggg}=0, \end{aligned}$$

(4.94a)

$$\begin{aligned}&\theta _{f} + a h \theta ^{n}\theta _{g} + a k \theta ^{2n}\theta _{g} +b \theta _{ggg}+4 c d w \theta _{gww}+ 4 c d \theta _{gw} + e \theta _{ggggg}=0, \end{aligned}$$

(4.94b)

which yield the translational symmetries $Y_1=\partial /\partial f$, and $Y_2=\partial /\partial g$.

Fig. 9

Bright soliton wave profile of solution (4.87) at $t=-3$ and $x=1.2$

Fig. 10

Bright soliton wave profile of solution (4.87) at $t=-3$ and $x=1.2$

Subcase a

So we contemplate using $Y_1=\partial /\partial f$ thus transforming (1.6) further to

$$\begin{aligned}&a \phi ^n \phi _{r}+b \phi _{rrr}+ 4 c d s \phi _{rss} + 4 cd \phi _{rs}+e \phi _{rrrrr}=0, \end{aligned}$$

(4.95a)

$$\begin{aligned}&a h \phi ^n \phi _{r} + a k \phi ^{2n} \phi _{r} + b \phi _{rrr}+ 4 c d s \phi _{rss} + 4 cd \phi _{rs}+e \phi _{rrrrr}=0. \end{aligned}$$

(4.95b)

The usual Lie symmetry process when applied to (4.95) gives $Q_1=\partial /\partial r$ which obviously gives a trivial solution.

Fig. 11

Bright soliton wave profile of solution (4.88) at $y=-3.2$ and $z=1$

Fig. 12

Bright soliton wave profile of solution (4.88) at $t=-0.2$ and $x=1.2$

Subcase b

Considering $Y_2=\partial /\partial g$ and taking the usual steps earlier highlighted yields $\phi _{r}(r,s)=0$, whose solution in the case of (1.6) as well as the dual power-law (1.7) gives

$$\begin{aligned} u(t,x,y,z)=H(cz^2+dy^2), \end{aligned}$$

(4.96)

where arbitrary function H is depending on its argument.

Fig. 13

Bright soliton wave profile of solution (4.88) at $y=-1$ and $z=1.02$

Fig. 14

Kink shaped soliton wave profile of solution (4.91) at $y=10$ and $z=0.2$

5 Graphical depiction of solutions and discussion

This section provides the diagrammatic representation of the obtained results. The dynamics of the solitary wave solutions are provided by choosing appropriate parameters in the solutions, using computer software. Additionally, the solution obtained under symmetry $W_5$ contains an arbitrary function that can take on various mathematical functions to represent the wave motions. Thus, we plot the solitary wave profile of the hyperbolic function solution (3.40) in Fig. 1 with different parameter values $A_0 = 10$, $A_1 = 2$, $A_2 = 10$, $A_3 = 5$, $A_4 = 10$, within the range of $-10 \le y, z \le 10$ where variables $t=2$ and $x=4$. Next, we examine solution (3.46) with assumption that $f = f_1 (\Delta _0) + f_2 (\Delta _1)$, where $\Delta _0 = z - e_1 t$ and $y - e_0 t$. Letting $f_1$ take a $\sin$ function and $f_2$ assuming a sech function with parameter value $e_0 = e_1 = 1$, as well as $z = 10$ in the intervals $-10 \le t, y \le 10$, we plot Fig. 2. This furnishes a wave interaction between 1-soliton and periodic soliton. Moreover, we further examine the dynamics of the solution using the assumed mathematical functions assignments with a slight difference where $e_0 = 0.5$ and $e_1 = 1$ in the same interval as earlier given. This consequently yields Fig. 3. Now, we consider solution (3.62) with the plotting of Fig. 4, allocating $\sin$ function to $f_3$ and $\cos$ function for $f_4$ in $f = f_3 (\Delta _2) + f_4 (\Delta _3)$, where $\Delta _2 = z - c_1 t$ and $y - c_0 t$ with the parameter values $c_0 = c_1 = 1$, together with $z = 10$ in the intervals $-10 \le t, y \le 10$. Furthermore, the wave motion of (3.62) is examined with the same trigonometric functions and intervals but for $c_0 = 0.5$ and $c_1 = 1$. Thus, Fig. 5 is plotted. These wave interactions showcase the interesting aspect of obtaining algebraic solutions with arbitrary functions. Now, we turn our attention to solution (4.80) in Fig. 6 with the adequate selection of the involved parameters as: $\alpha = 2$, $\gamma = 2$, $\beta = 1$, $a = 50$, $b = 1$, $c = 10$, $d = 0.5$, $\chi = 3$, using the interval of $-3 \le y, z \le 3$ with variables $t=3$ and $x=2$. Moreover, for Fig. 7, we assign the values $\alpha = 0.2$, $\gamma = 1.2$, $\beta = 0.3$, $a = 10$, $b = 1$, $c = 40$, $d = 0.5$, $\chi = 30$, in the interval of $-3.3 \le t, x \le 3.3$ for $y=z=1$. In the case of the solitary wave solution (4.87) allocation of values to parameters in plotting Fig. 8 is done as $k = 2$, $h = 2$, $\Theta _5 = 0$, $\alpha = 2$, $\gamma = 1.1$, $\beta = 3.6$, $a = 2$, $b = 20$, $c = 10$, $d = 0.5$, $e = -1$, $\chi = 3000$, using the interval of $-3.2 \le y, z \le 3.2$ with variables $t=-2$ and $x=0.2$. Figure 9 is diagrammatically depicted by using the same value allocation with $-5 \le y, z \le 5$ with $t=-3$ and $x=1.2$. Moreover, we plot Fig. 10 by using the assigned values $k = 2$, $h = 2$, $\Theta _5 = 0$, $\alpha = 2$, $\gamma = 1.1$, $\beta = 2.6$, $a = 2$, $b = 20$, $c = 10$, $d = 0.5$, $e = -1$, $\chi = 3000$, using the interval of $-5 \le y, z \le 5$ with $t=-3$ and $x=1.2$. Meanwhile, solitary wave solution (4.88) is dynamically revealed via Fig. 11 by letting $k = 4$, $h = 0.2$, $\Theta _5 = 0$, $\alpha = 2$, $\gamma = 1.1$, $\beta = 3.6$, $a = 2$, $b = 20$, $c = 10$, $d = 0.5$, $e = -1$, $\chi = 3000$, where $-4 \le t, x \le 4$ with $y=-3.2$ and $z=1$. We experience a change in the behaviour of the solution in Fig. 12 by using the same value-allocation with the slight change $k = h = 2$, with $-4 \le y, z \le 4$ for $t=-0.2$ and $x=1.2$. In the case of Fig. 13 representing solution (4.88), we do the selection $k = 2$, $h = 1.2$, $\Theta _5 = 0$, $\alpha = 2$, $\gamma = 1.1$, $\beta = 3.6$, $a = 2$, $b = 20$, $c = 10$, $d = 0.5$, $e = -1$, $\chi = 2000$, where $-5 \le t, x \le 5$ with $y=-1$ and $z=1.02$. Next, we examine the wave behaviour of solitary wave solution (4.91) by plotting Fig. 14 using the parameter assignment $k = 2$, $h = 0.5$, $e = 1$, $A_0 = 10.2$, $\alpha = 2$, $\gamma = 10.1$, $\beta = 3.6$, $a = 0.1$, $b = 0$, $c = 10$, $d = -0.5$, $\chi = 300$, whereas $-5 \le t, x \le 5$ with $y=10$ and $z=0.2$. Regarding Fig. 15, we do the Figure using the same parametric values with $-3 \le t, x \le 3$ with $y=2$ and $z=2.2$.

Fig. 15

Kink shaped soliton wave profile of solution (4.91) at $y=2$ and $z=2.2$

Fig. 16

Soliton wave interaction profile of solution (4.96) at $t=0$ and $x=0$

Fig. 17

Soliton wave interaction profile of solution (4.96) at $t=0$ and $x=0$

Furthermore, we study the wave dynamics of algebraic solution (4.96) in Fig. 16 by taking arbitrary H as the sum of the square of trigonometric functions $\sin (y)$ and $\cos (z)$ with $c = d = 1$ and $t=x=0$ in the interval $-3 \le y, z \le 3$. The soliton interaction experienced in Fig. 17 is come-by using trigonometric functions $\sin (\Omega )$ and $\cos (\Omega )$, summed up where $\Omega$ is the sum of the square of the involved variables, with the usual $c = d = 1$ alongside $t=x=0$. Furthermore, we repeat the same thing for (4.96) in Fig. 18 with $\sin (\Omega ) = \text {sech}(\Omega )$ in the interval $-4 \le y, z \le 4$ where $c = d = 1$ and $t=x=0$. In the case of Fig. 19, with some constant coefficients, we implore together with $\cos (\Omega )$ and $\text {sech}(\Omega )$, the tangent-hyperbolic function, in the interval $-2 \le y, z \le 2$ where $c = d = 1$ and $t=x=0$. Finally, we plot Fig. 20 to depict (4.96) using the explicated trigonometric and hyperbolic functions with some slightly changed constant coefficients. We notice that various wave interaction of interest are come by using the dissimilar assignments of functions.

Fig. 18

Soliton wave interaction profile of solution (4.96) at $t=0$ and $x=0$

Fig. 19

Soliton wave interaction profile of solution (4.96) at $t=0$ and $x=0$

Fig. 20

Soliton wave interaction profile of solution (4.96) at $t=0$ and $x=0$

5.1 Real-world application of the obtained results

In this section, we aim to showcase practical examples of how the results obtained can be applied in real-world scenarios. We have discovered a range of hyperbolic function solutions and algebraic solutions with flexible functions that can encompass trigonometric and other important mathematical functions to solve the models under study. It is important to highlight several intriguing cases where these solutions prove to be beneficial.

A practical application of hyperbolic functions is seen in the behavior of hanging cables. When a cable of uniform density is suspended between two supports with only its own weight as a load, it forms a curve known as a catenary (see Fig. 21). Cables such as high-voltage power lines (see the illustrative diagram in Fig. 22), chains between posts, and even strands of a spider’s web all take on the shape of a catenary. The illustration below displays chains hanging from a line of posts (https://courses.lumenlearning.com/calculus1/chapter/applications-of-hyperbolic-functions/).

Trigonometry plays a crucial role in navigation, helping determine the direction to orient a compass for a straight path. By utilizing a compass and trigonometric functions during navigation, it becomes simpler to pinpoint a location, calculate distances, and identify the horizon. Additionally, in the field of criminology, trigonometry proves to be valuable for analyzing crime scenes. Trigonometric functions are

Fig. 21

Diagrammatic representation of a typical catenary. https://courses.lumenlearning.com/calculus1/chapter/applications-of-hyperbolic-functions/

instrumental in calculating projectile trajectories and determining factors contributing to car accidents. They are also utilized to assess the trajectory of falling objects and the angle at which a gun is fired (https://byjus.com/maths/applications-of-trigonometry).

Trigonometry is a versatile mathematical tool that can be utilized to determine the heights of towering mountains and structures, as well as to measure the distances between celestial bodies such as stars and planets. This mathematical concept finds application in various fields including physics, architecture, and GPS navigation systems (https://www.vedantu.com/maths/application-of-trigonometry) (see Fig. 23 to view the design of the working mechanism of the GPS system). The GPS known as Global Positioning System, is a system that relies on satellites in space to transmit signals for navigation purposes. This network includes a group of satellites that broadcast these signals, as well as ground stations and satellite control stations that are used for monitoring and managing the system.

Fig. 22

Pictorial representation of a typical high voltage power transmission system. http://dx.doi.org/10.13140/RG.2.2.34578.76484

In architecture, right angles play a crucial role in designing structures, while manufacturing processes rely on trigonometric calculations for precise measurements. Construction projects often involve the use of right triangles to ensure accurate positioning of components. Furthermore, trigonometry is essential in Engineers frequently rely on trigonometric principles to determine angles. In particular, civil and mechanical engineers apply trigonometry to compute torque (see Fig. 24 for the diagram of a typical torque in a car) and forces acting on various structures, like bridges and building beams.

Fig. 23

Diagrammatic representation of the working mechanisms of a typical Global Positioning System. https://www.sciencedirect.com/topics/biochemistry-genetics-and-molecular-biology/global-positioning-system

Architects utilize trigonometry in their work to accurately calculate the structural loads, angles, and material lengths necessary for constructing safe and visually appealing buildings. In the field of engineering, trigonometry plays a crucial role in designing mechanical components, analyzing forces, and solving problems related to waves and oscillations. Moreover, trigonometry is also widely used in the development of video games and computer graphics. It aids in creating lifelike animations, simulating physical movements, and rendering scenes in three-dimensional environments (https://www.geeksforgeeks.org/what-are-some-real-life-applications-of-trigonometry/).

Fig. 24

Pictorial representation of a typical engine torque in cars. https://www.dubizzle.com/blog/cars/engine-torque/

In the same vein, various conservation laws found here furnish important conserved quantities which are highly significant in physical sciences. These include, conservation of energy and momenta (Adeyemo and Khalique 2023). For more detail understanding of these, see the recent work established in reference (Adeyemo and Khalique 2023).

6 Concluding remarks

In this article, an exhibition of the research carried out on the (3+1)-dimensional generalized fifth-order Zakharov–Kuznetsov model with power-law and dual power-law nonlinearities (1.6) and (1.7) is analytically presented. For the very first time, a detailed Lie group analysis of the models with power-law nonlinearities was investigated with the purpose of attaining various exact solutions. Thus, we gained exact solutions for the fallout models using Lie symmetry reductions, direct integration in conjunction with the logistic function technique, and achieved solitary wave solutions for understudied models for some particular cases of n (engendered from the fallout of the original model), appearing in the form of exponential functions. Besides, we depicted the streaming figures of the various outcomes by invoking suitable representations pictorially. Furthermore, we derived conserved currents of (1.6) and (1.7) by employing Noether’s theorem. Consequently, these conserved currents contain both nonlocal and local conserved vectors of first integrals. In the end, the pertinence of the comprehensive work explicated in this work was further supported with various real-world applications in science and engineering fields using adequate diagrams and references. This implies that the results obtained in this investigation could be of particular interest to researchers in fields such as architecture, building, and structural engineering, electrical, and mechanical engineering.