Abstract
Higher-dimensional nonlinear integrable partial differential equations are significant as they often describe diverse phenomena in nonlinear systems like laser radiations in a plasma, optical pulses in the glass fibres, fluid mechanics, radio waves in the ion sphere, condensed matter and electromagnetics. This article shows an analytical investigation of a (3+1)-dimensional fifth-order nonlinear model with KdV forming its main part. Lie group analysis of the model is performed through which its infinitesimal generators are obtained. These generators are engaged in the construction of an optimal system of Lie subalgebra in one dimension. Moreover, members of the system secured are utilized in reducing the underlying model to ordinary differential equations (ODEs) for possible exact solutions. In consequence, we achieve various functions, ranging from trigonometric, logarithmic, rational, to hyperbolic. In addition, the results found constitute diverse solitonic solutions such as complex, topological kink and anti-kink, trigonometric and bright. We utilize the power series technique to obtain a series solution of the most complicated ordinary differential equation with forty-four terms. In addition, we reveal the dynamics of these solutions via graphical depictions. In the end, we constructed conserved currents of the underlying equation through the use of the multiplier technique. Further, we utilize the optimal system of the underlying model to derive more conserved vectors using Ibragimov’s theorem for conservation laws.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In the context of higher-order nonlinear evolution equations, investigations are proliferating as a result of the fact that real characteristics and hallmarks covering diverse areas of science together with technology and engineering are being described through these equations. Moreover, studies that bother on gaining soliton solutions to the nonlinear equations within a variety of fields have attracted a huge number of works. Towards this goal, powerful methods in their varieties for constructing multiple soliton solutions have been established in diverse fields of mathematical physics, other nonlinear sciences and engineering [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20].
In recent studies, physicists, engineers, as well as mathematicians mostly focus their studies on (1+1)-dimensional alongside (2+1)-dimensional integrable models. In other words, investigations of various solitary waves in these dimensions have extensively been studied both in theoretical as well as experimental aspects [3, 6,7,8].
However, for higher dimensions, the situation seems much fuzzy. Nevertheless, the physical space–time models which are in the structure of (3+1)-dimension are considered to be realistic. In consequence, this has encouraged the investment of more energy and tenacity on the part of physicists and mathematicians in looking for ways to introduce more higher-dimensional models [1,2,3,4]. Some avenues have been adopted to develop (3+1)-dimensional integrable models such as using powerful techniques like the symmetry method which emerges from the Lie group theory.
Lie group theory, a robust and highly efficient technique was established by Marius Sophus Lie in the nineteenth century [21, 22]. The impact of this technique is profound on diverse fields like differential geometry, algebraic topology, bifurcation theory, invariant theory, control theory, special functions, quantum mechanics, continuum mechanics and so on. In the area of applied mathematics, the method affords one the chance of transforming solutions of a system of differential equations into other solutions. Lie groups comprise geometric transformations on the space of dependent as well as independent variables for the system and also act on solutions by transforming their graph. We consider one of the existing nonlinear evolution equations. This technique is highly useful in the sense that it is universal and can be applied to secure various closed-form solutions of the diverse complicated or sophisticated nonlinear partial differential equations just as it is demonstrated in this research work.
A (3+1)-dimensional integrable nonlinear evolution equation presented as [23, 24]
where the inverse operator \( \partial _x^{-1} \) defined as
preserved under the decaying condition at infinity, has been explored by a number of researchers. It is to be observed that the inverse operator defined in (1.2) has the property \( \partial _x \partial _x^{-1} = \partial _x^{-1} \partial _x = 1\). The equation which was originally introduced by Geng [23] was established in the course of investigating algebraic-geometrical solutions to mathematical problems. Wazwaz [24] reveals that the relationship between the (3+1)-dimensional integrable nonlinear equation (1.1) and the well-recognized Korteweg-de Vries equation is highly remarkable [25]. This is as a result of the fact that equation (1.1) possesses Korteweg-de Vries equation
by reason of the presence of main term \( 2 w_t - 2 w w_x + w_{xxx} \) in the high-dimensional evolution equation under the transformation expressed in the form
In consequence of the aforementioned, equation (1.1) may be utilized in the investigation of shallow-water waves as well as short waves in a dispersive model that is nonlinear. The authors in [23] with the aid of the (1+1)-dimensional AKNS equation, decomposed (3+1)-dimensional nonlinear evolution equation (1.1) into systems of solvable ordinary differential equations (ODEs). The decomposition was done into the nonlinear Schrödinger (NLS) equation, Lakshmanan–Porsezian–Daniel (LPD) equation and the complex modified KdV (cmKdV) equation which as a result justifies the physical application asserted by Geng. Moreover, Wronskian determinant of solutions, as well as perturbation technique, were engaged in determining the N-soliton solutions for the reduced equation in [26]. Besides, simplified Hirota’s technique was considered in [27, 28] to secure multiple soliton solutions alongside multiple singular soliton solutions to (1.1). Wazwaz [27], in particular, secured multiple-soliton solutions as well as multiple singular soliton solutions for (1.1) via Hirota’s bilinear technique. Recently, Wang et al. [29] examined rational solutions of equation (1.1) which was revealed to exhibit doubly localized lumps along with line rogue waves on a finite background through the Darboux transformation technique.
Furthermore, the generalized version of (1.1) structured as [30]
with non-zero real constants parameters \( h_i, i = 1,2,\dots ,5\) was studied lately. The authors derived the bilinear structure of the equation. Semi-rational solutions were achieved through Kadomtsev–Petviashvili hierarchy reduction. In addition, they present the analysis of interactions existing between the lumps and solitons. They also found out that for the first-order semi-rational solutions, the lump, as well as the soliton, agglutinate into the soliton. Secondly, the lump that arose from the soliton separates again from the soliton. In the third instance, the first-order semi-rational solutions on the \( y-z \) plane have a line profile whereas the change in wave shape varies concerning t. The authors discovered that for the multi-semi-rational solutions, the two lumps amalgamate into the two solitons on the \( x-y \) plane. Besides, the two lumps emerge on and then split from the two solitons on the \( x-z \) and \( y-z \) planes. In the case of the higher-order semi-rational solutions, they observed the existence of three kinds of interaction phenomena, in the first place, the two lumps merge into the soliton; secondly, the two lumps which propagate towards each other amalgamate into one lump with the outcome thereafter splitting into two other lumps and finally the two lumps arise from the soliton and then separate again from it. In addition, they also reveal the influences of the coefficients in the original equation on the semi-rational solutions.
Wazwaz [31] on the bases of nonlinear evolution equation (1.1) and the explanations earlier given proposed a (3+1)-dimensional model I expressed in the form
which exhibits integrable properties and also gives multiple-soliton solutions [31]. In a bid to remove the integral term in the equation, he introduced the potential \( w(t,x,y,z) = u_x(t,x,y,z) \) and in consequence secured the (3+1)-dimensional fifth-order nonlinear model I
In [31] multiple soliton solutions for equation (1.7) were found using the simplified form of the Hirota’s method. In this work we use Lie’s theory, which is a universal method, to obtain exact solutions of (1.7). The solutions obtained are more general than the ones given in [31].
The study of exact solitary wave solutions to nonlinear partial differential equations (NLPDEs) is significant in examining nonlinear physical phenomena. Besides, these NLPDEs continue to play a vital role in today’s world as they are used as models that describe natural phenomena in fluids, plasmas, solid-state materials, continuum mechanics, meteorology and climate, astronomy, oceanography, system theory and control, operations research, just to mention a few. Some of these models include the modified and generalized Zakharov–Kuznetsov model [1, 2], which recounts the ion-acoustic drift solitary waves existing in a magnetoplasma with electron–positron–ion which are found in the primordial universe. A generalized system of three-dimensional variable-coefficient modified Kadomtsev–Petviashvili–Burgers-type equation in [3] was studied. This equation was used to model ion-acoustic, dust-magneto-acoustic, quantum-dust-ion-acoustic and/or dust-ion-acoustic waves in one of the cosmic or laboratory dusty plasmas. Moreover, in [4] the vector bright solitons, as well as their interaction characteristics of the coupled Fokas–Lenells system, which models the femtosecond optical pulses in a birefringent optical fibre, were investigated. In addition, the Boussinesq–Burgers-type system of equations which delineates shallow water waves appearing close to lakes or ocean beaches was studied in [5], the list continues, see also [5–10]. However, there had been in general no methodical theories that can be infused into NLPDEs so that their closed-form solutions can be found.
Nonetheless, lately, scientists have advanced in developing effective techniques so as to procure viable closed-form solutions to NLPDEs. Besides the Lie symmetry technique earlier mentioned, others include extended homoclinic test approach [12], tanh-coth approach [13], generalized unified technique [14], bifurcation technique [15], Adomian decomposition approach [16], homotopy perturbation technique [17], mapping and extended mapping technique [18], ansatz technique [19], exp\( (-\Phi (\eta )) \)-expansion technique [20], Painlevé expansion [32], Cole–Hopf transformation approach [33], Bäcklund transformation [34], rational expansion method [35], F-expansion technique [36], tan–cot method [37], extended simplest equation method [38], Hirota technique [39], the \((G'/G)-\)expansion method [40], Darboux transformation [41], sine-Gordon equation expansion technique [42], the list continues.
In our research work, we investigate the (3+1)-dimensional fifth-order nonlinear model I (4D-NLMe) (1.7) expressed in the structure
In this study, we explicitly investigate solutions of 4D-NLMe (1.8) via the Lie group theoretic approach. The outline of the paper is as follows: Section 1 is devoted to the introduction while Section 2 reveals the outline of the step-by-step procedure engaged in carrying out Lie group analysis of 4D-NLMe (1.8). We further obtain the optimal system of Lie subalgebra of the equation via its Lie point symmetries. These symmetries are used to perform reductions of the equation. Moreover, the power series method is adopted to secure possible solutions to the most complicated nonlinear ODE with forty-four terms. In Section 3, the various solitonic and power series results are depicted diagrammatically. Moreover, Section 4 is dedicated to the construction of the conserved currents of the underlying model via the multiplier technique. Besides, members of the optimal system obtained are engaged to gain more conserved vectors for the model through Ibragimov’s theorem. Finally, the concluding remarks are given.
2 Lie Symmetry Analysis of 4D-NLMe
In this section, we first compute the Lie point symmetries of (1.8) and thereafter use them to construct an optimal system of Lie subalgebra through which reductions of the equation is performed for the possible achievement of exact solutions.
2.1 Succinct Overview of Lie Point Symmetries of (1.8)
Theorem 2.1
[22] A connected transformation group G is referred to as symmetry group of a differential equation taken as \(\Delta = 0\) if and only if the classical infinitesimal symmetry criteria
holds for every infinitesimal generator \(Y \in \mathfrak {g}\) (Lie algebra) of G with Y representing the vector field of the infinitesimal generators defined as
where \(\xi ^i,i=1,\cdots ,m\) with \(m=4\) and \(\eta \) are functions dependent on t, x, y, z, u.
As it is usually done, an attempt shall be made to perform the fundamental similarity reductions for the fifth-order 4D-NLMe (1.8) via the infinitesimal criterion approach[22]. Next, we present another important theorem:
Theorem 2.2
Suppose Y is an infinitesimal generator of classical Lie point symmetry group for governing equation (1.8) as defined in (2.2), then we obtain the variable coefficients \(\xi ^1(t,x,y,z,u)\), \(\xi ^2(t,x,y,z,u)\), \(\xi ^3(t,x,y,z,u)\), \(\xi ^4(t,x,y,z,u)\) and \(\phi (t,x,y,z,u)\) as
where \(\textbf{c}_i, i = 1,2,\dots ,4\) are arbitrary constants with functions \( \mathcal {G}(t,z) \), \( \mathcal {H}(t,z) \), \( \mathcal {F}_1(z) \) as well as \( \mathcal {F}_2(t,z) \) arbitrary and dependent on their various arguments.
Proof
We apply the invariance criteria (2.1) and consequently achieve
with \(Y^{(5)}\) denoting the fifth prolongation of Y and is given in the structure
where the \(\eta ^{t}\), \(\eta ^{x}\), \(\eta ^{y}\), \(\eta ^{tx}\), \(\eta ^{xx}\), \(\eta ^{xy}\), \(\eta ^{xz}\), \(\eta ^{txy}\), \(\eta ^{xxx}\), \(\eta ^{xxy}\), \(\eta ^{xxz}\), \(\eta ^{xxxxy}\), can be completely expounded, (see [21, 22, 43]) via the general relations given by
representing the coefficient functions in \(Y^{(5)}\) and the total derivatives \(D_i\) in (2.6) given too in general form as
which can also be used for \(D_j\). For instance
Inserting the relations expounded in (2.6) into equation (2.5), expanding and splitting the outcome over the various derivatives of u, one achieves the twenty-four overdetermined system of linear partial differential equations LIPDEs
Solving the secured system of LIPDEs, we achieve the solution presented in (2.3). Hence, the proof of the theorem is concluded. Furthermore, suppose we take arbitrary functions \(\mathcal {F}_1 (z) = \frac{1}{2}\textbf{c}_5\), \(\mathcal {F}_2 (t,z) = \textbf{c}_6\), \( \mathcal {G}(t,z) = 0 \), and \(\mathcal {H} (t,z) = \frac{1}{6}\textbf{c}_7\) in solution (2.3), then, we obtain seven classical Lie point symmetries. Hence, we present a corollary:
Corollary 2.1
In essence, the Lie algebra \(\mathfrak {g}\) of infinitesimal projectable symmetries of 4D-NLMe (1.8) is spanned by seven vector fields together with their respective names as subsequently given:
Remark 2.1
In order to secure the group transformation which are generated by the infinitesimal generators of 4D-NLMe (1.8) as presented in (2.9), one is obliged to compute the associated integral curves.
2.2 Lie Group Transformation of (1.8) via \(\mathfrak {g}\)
In this subsection, we furnish the transformation group of 4D-NLMe (1.8) using \(\mathfrak {g}\). The Lie group of transformation is defined as
Therefore, by adopting the approach expounded in [22], we deduce the theorem:
Theorem 2.3
If group \(G_{\epsilon }^i(t,x,y,z,u), i = 1,2,3,\dots , 7\) is defined as one parameter group generated by vectors \(Y_1,Y_2,Y_3\dots ,Y_7\) in (2.9), then, for each of the vectors, we have respectively
In general, corresponding to each one parameter subgroups of full symmetry group of any system, there exist a family of solution.
Theorem 2.4
If \(u(t,x,y,z)=P(t,x,y,z)\) is a solution of the 4D-NLMe (1.8), so are the functions given in the structure
where \(u^i(t,x,y,z) = G_i^{\epsilon } \cdot P(t,x,y,z), i = 1,2,\dots ,7\) where \(\epsilon<<1\) is taken as any positive real number.
2.3 Optimal Classification of 1-D Subalgebras
In a bid to perform symmetry reductions of a given PDE problem in a systematic way so as to gain its group invariant solutions, it is needful for us to secure the classification of subalgebras of the symmetry algebra into various conjugate classes under the adjoint action of the symmetry group. Moreover, the problem of classifying orbits of the adjoint representation is identical to the task associated with the classification of one subalgebras [22]. It is imperative to decide on conjugacy classes of 1-D subalgebras together with conjugacy classes in their normalizers for the reduction process to be done. In addition, subsequently preceded by classes of the corresponding normalizer is the first reduction by subalgebras in an optimal system of 1-D subalgebras. Furthermore, we achieve an optimal set of subalgebras by choosing just one representative from any class of equivalent subalgebras. Engaging a general member of Lie algebra and simplifying the same through sundry adjoint transformations, one can solve the bottleneck involved in orbit classifications.
2.3.1 1-D subalgebras optimal system of 4D-NLMe (1.8)
Therefore, we carry out the detailed computation of 1-D subalgebras optimal system of 4D-NLMe (1.8) in the subsequent part of this subsection using the algorithm highlighted in [44] and later do the comprehensive symmetry reductions.
Now, for the \(7-\)dimensional symmetry algebra \(\mathfrak {g}\), we first compute commutation relation existing between \(Y_i\) and \(Y_j\) which can be revealed in Table 1 with row i alongside column j portraying \([Y_i,Y_j] = Y_iY_j - Y_jY_i\).
2.3.2 Basic invariants of 4D-NLMe (1.8)
Definition
The symmetric bilinear structure \( \Phi \) on the space of Lie algebra \( \mathcal {L} \), that is the mapping \( \Phi : \mathcal {L} \times \mathcal {L} \mapsto \mathbb {R}\) is referred to as “invariant" if for any inner automorphism \( \mathcal {A} \in Int\, \mathcal {L}\) (group of inner automorphisms) and also for any points \( x,y \in \mathcal {L} \) we have relation
In other words, a real-valued function depicted as \( \Phi \) which is defined on Lie algebra \( \mathcal {L} \) is referred to as an invariant under adjoint action (Ad) , in this study, if \( \Phi (x) = \Phi (Ad_{g}(x)) \) for all x in \( \mathcal {L} \) as well as g in the Lie group designated as G generated by \( \mathcal {L} \). In this instance, \( Ad_{g} \) is referred to as the adjoint representation of G on the given Lie algebra \( \mathcal {L} \).
Now, by taking any subgroup \(s = e^{v}\left( v = \sum _{j=1}^{7}\beta _jY_j \right) \) so that it can act on Y, we then achieve [44]
with function \(\Theta _i\equiv \Theta _i(\alpha _1,\dots ,\alpha _7, \, \beta _1,\dots ,\beta _7)\) easily computable from the commutator Table 1.
Thus, we calculate the values of \(\Theta _i, i = 1,2,\dots ,7\) by imploring Table 1 as
It is required that for any real number \(\beta _i, i = 1,2,\dots ,7\), we have the relation
Computing all the coefficients of \(\beta _1,\beta _2,\dots ,\beta 7\) in equation (2.13), we gain seven differential equations with regards to \(\Phi (\alpha _1,\alpha _2,\alpha _3,\alpha _4,\alpha _5,\alpha _6,\alpha _7)\) as
Calculation of \(\Phi \) in the system of equations secured in (2.14) gives
with Q denoting an arbitrary function dependent on \(\alpha _6\) and \(\alpha _7\). This implies that 4D-NLMe (1.8) possesses two basic invariants \(\alpha _6\) and \(\alpha _7\).
2.3.3 Adjoint transformation matrix of 4D-NLMe (1.8)
Now, we calculate the adjoint transformation matrix of 4D-NLMe (1.8) which is the product of the different matrices of the separate adjoint actions \(J^{\epsilon _{1}}_1,J^{\epsilon _{2}}_2,\dots ,J^{\epsilon _{7}}_7\). The reader is directed to [22, 44] for more details. Consequently, we adopt the same approach in constructing \(AdJ^{\epsilon }\) which is the global adjoint matrix, with the help of Table 2 that reveals the adjoint representation of (1.8) calculated using \(Ad_{\exp (\epsilon Y_i)(Y_j)}\).
Having giving the adjoint representation table of (1.8) in Table 2, we apply the adjoint action of \(Y_1\) to the relation
Thus, by engaging the adjoint action of \(Y_1\) to \(Y = \sum _{i = 1}^{7} \alpha _i Y_i\) with the aid of adjoint representation table (Table 2), we achieve the connection
whereby we have \(J^{\epsilon _{1}}_1\) to be
Therefore, in the same manner, one can secure adjoint matrices \(J^{\epsilon _{2}}_2\), \(J^{\epsilon _{3}}_3\), \(J^{\epsilon _{4}}_4\), \(J^{\epsilon _{5}}_5\), \(J^{\epsilon _{6}}_6\), \(J^{\epsilon _{7}}_7\), as \( J^{\epsilon _{2}}_2 = \left( \begin{array}{ccccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} -\epsilon _{2} &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} -\epsilon _{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) , \qquad J^{\epsilon _{3}}_3 = \left( \begin{array}{ccccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} \epsilon _{3} &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} \epsilon _{3} &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) , \)
\( J^{\epsilon _{4}}_4 = \left( \begin{array}{ccccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 2 \epsilon _{4} &{} 0 &{} 0 &{} 1 \\ \end{array} \right) , \qquad J^{\epsilon _{5}}_5 = \left( \begin{array}{ccccccc} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} -2 \epsilon _{5} &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) , \)
\( J^{\epsilon _{6}}_6 = \left( \begin{array}{ccccccc} e^{3 \epsilon _{6} } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{\epsilon _{6} } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} e^{-\epsilon _{6} } &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} e^{2 \epsilon _{6} } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) , \qquad J^{\epsilon _{7}}_7 = \left( \begin{array}{ccccccc} e^{3 \epsilon _{7} } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{\epsilon _{7} } &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} e^{-\epsilon _{7} } &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} e^{-2 \epsilon _{7} } &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) . \)
In consequence, we achieve the general adjoint transformation matrix \(AdJ^{\epsilon } \) as
\( AdJ^{\epsilon } = \left( \begin{array}{ccccccc} e^{3 \epsilon _6+3 \epsilon _7} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} e^{\epsilon _6+\epsilon _7} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} e^{-\epsilon _6-\epsilon _7} &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} e^{-2 \epsilon _7} &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} e^{2 \epsilon _6} &{} 0 &{} 0 \\ -3 e^{3 \epsilon _6+3 \epsilon _7} \epsilon _1 &{} -e^{\epsilon _6+\epsilon _7} \epsilon _2 &{} e^{-\epsilon _6-\epsilon _7} \epsilon _3 &{} 0 &{} -2 e^{2 \epsilon _6} \epsilon _5 &{} 1 &{} 0 \\ -3 e^{3 \epsilon _6+3 \epsilon _7} \epsilon _1 &{} -e^{\epsilon _6+\epsilon _7} \epsilon _2 &{} e^{-\epsilon _6-\epsilon _7} \epsilon _3 &{} 2 e^{-2 \epsilon _7} \epsilon _4 &{} 0 &{} 0 &{} 1 \\ \end{array} \right) . \)
Hence, this implies that exploring the most general adjoint action
to Y, one can consequently have a relation expressed as
Conversely, it is possible to admit that the equivalence of \(Y = \sum _{i = 1}^{7} \alpha _i Y_i\) and \(\mathcal {Q} = \sum _{i = 1}^{7} \tilde{\alpha }_i Y_i\) can be shown with respect to parameters \(\epsilon _{1},\epsilon _{2}, \dots , \epsilon _{7}\) via the connection
This important connection expressed in (2.18) is referred to as the adjoint transformation equation which plays a crucial role in the computations of optimal system of one dimensional subalgebra using the approach[44] in this study.
2.4 Calculation of 1-D Subalgebra Optimal System of (1.8)
Now, we engage the results and information given earlier to obtain the optimal system for 4D-NLMe (1.8) by first utilizing the invariants \(\alpha _6 \) and \(\alpha _7\). We first of all contemplate two main cases whereby \(\alpha _6 =1 \), \(\alpha _7=1\) and \(\alpha _6 \alpha _7 = 0\).
Case 1. \(\alpha _6 = 1\), \(\alpha _7 = 1\),
We scale the invariant and select the optimal representative element \(\mathcal {Q} = Y_6 + Y_7\). Therefore by inserting the parametric values \(\tilde{\alpha }_i = 0, i = 1,2,\dots ,5 \) as well as \( \tilde{\alpha }_i = 1, i = 6,7 \) into adjoint system (2.18), we achieve the solution
Case 2. \(\alpha _6 \alpha _7 = 0\),
In this instance, we further scale down the invariant by contemplating three subcases:
Case 2.1. \(\alpha _6 = 0\), \(\alpha _7 = 1\),
We choose the optimal representative element \(\mathcal {Q} = Y_7\). Then by substituting the parameter \(\tilde{\alpha }_i = 0, i = 1,2,\dots ,6 \) alongside \( \tilde{\alpha }_i = 1, i = 7 \) into adjoint system (2.18), we gain the outcome
Case 2.2. \(\alpha _6 = 1\), \(\alpha _7 = 0\),
Further, we select the optimal representative element \(\mathcal {Q} = Y_6\). We invoke, the parametric values \(\tilde{\alpha }_i = 0, i = 1,2,\dots ,5,7 \) together with \( \tilde{\alpha }_i = 1, i = 6 \) into system (2.18) which gives us the result presented as
Case 2.3. \(\alpha _6 = 0\), \(\alpha _7 = 0\),
In this occasion, we substitute \(\alpha _6 = 0\), \(\alpha _7 = 0\) in the system of partial differential equations (2.14). As a result, we obtain the value of function \(\Phi (\alpha _1,\alpha _2, \alpha _3,\alpha _4, \alpha _5)\) as
Consequently, we put into consideration, some possible cases that we can infer from the new invariant and so we have the cases highlighted in detail hereafter.
Case 2.3.1. \(\frac{\alpha _2}{\root 3 \of {\alpha _1}} = 1\), \(\alpha _3 \root 3 \of {\alpha _1} = 1\), \(\frac{\alpha _5}{\alpha _4\root 3 \of {\alpha _1^2}}=1\),
Here, for \( \frac{\alpha _2}{\root 3 \of {\alpha _1}} = 1 \), we have \(\alpha _2^{3} = \alpha _1 \). The second invariant is \({\alpha _1}\alpha _3^{3} = 1\) and for the third invariant, we have \( \alpha _5^{3} = \alpha _4^{3}{\alpha _1^2} \). So, for this case, by inserting parameters \(\tilde{\alpha }_i = 0, i = 6,7 \) alongside \( \tilde{\alpha }_i = 1, i = 1,2,\dots ,5 \) into adjoint system (2.18), we achieve
Thus, we have a unique setting because for the three invariants, each of them can produce a representative. In consequence and without loss of generality, we choose representative elements \(\mathcal {Q} = Y_1 + Y_2\), \(\mathcal {Q} = Y_1 + Y_3\) as well as \(\mathcal {Q} = Y_1 + Y_4 + Y_5\).
Case 2.3.2. \(\frac{\alpha _2}{\root 3 \of {\alpha _1}} = - 1\), \(\alpha _3 \root 3 \of {\alpha _1} = - 1\), \(\frac{\alpha _5}{\alpha _4\root 3 \of {\alpha _1^2}} = -1\),
In this case, we contemplate \( \alpha _1 > 0, \alpha _2<0, \alpha _3 <0 \), while \(\alpha _4 >0 \) and \( \alpha _5 <0 \). Therefore, by invoking the appropriate values of parameters \( \tilde{\alpha }_i, i = 1,2,\dots , 7\) into adjoint system presented in (2.18), we achieve a logarithmic solution expressed as
As a result, we select in this regard representative elements \(\mathcal {Q} = Y_1 - Y_2\), \(\mathcal {Q} = Y_1 - Y_3\) as well as \(\mathcal {Q} = Y_1 + Y_4 - Y_5\). Next, we consider other various possible cases of F.
Case 2.3.3. \(\frac{\alpha _2}{\root 3 \of {\alpha _1}} = 0\), \(\alpha _3 \root 3 \of {\alpha _1} = 1\), \(\frac{\alpha _5}{\alpha _4\root 3 \of {\alpha _1^2}}=1\),
For \(\frac{\alpha _2}{\root 3 \of {\alpha _1}} = 0\) with \( \alpha _1 \ne 0 \), \( \alpha _2 \) must be zero. Hence, we select representative element \(\mathcal {Q} = Y_1\). On substituting parametric values \(\tilde{\alpha }_i = 0, i = 2, 6,7 \) with \( \tilde{\alpha }_i = 1, i = 1,3,\dots ,5 \) into adjoint system (2.18), one gets
Remark 2.2
We observe that for \(\alpha _1 \ne 0\) in Case 2.3.3., we have the possibilities \(\mathcal {Q} = \pm Y_1\), but we disregarded \(\mathcal {Q} = - Y_1\) since ± does not have any impact on a single vector. Besides, a list of vectors can be reduced by the admittance of discrete symmetry \((t,x,y,z,u) \mapsto (-t,-x,-y,-z,u)\) that are not in the connected component of the identity of the full symmetry group [22]. Moreover, other possible representatives have been obtained earlier thereby contributing no additional subalgebra to the optimal system under consideration.
Case 2.3.4. \(\frac{\alpha _2}{\root 3 \of {\alpha _1}} = 1\), \(\alpha _3 \root 3 \of {\alpha _1} = 0\), \(\frac{\alpha _5}{\alpha _4\root 3 \of {\alpha _1^2}}=1\),
This case presents two scenarios whereby \( \alpha _1 =0 \), \(\alpha _3 \ne 0\) and \( \alpha _1 \ne 0 \), \(\alpha _3 = 0\) but by virtue of remark (2.2), we give consideration to the first scenario. Therefore, we select optimal representative element \(\mathcal {Q} = Y_3\). Imploring the substitution of parameters \(\tilde{\alpha }_i = 0, i = 1,6,7 \) alongside \( \tilde{\alpha }_i = 1, i = 2,3,\dots ,5 \) into adjoint system (2.18), we gain the outcome
Case 2.3.5. \(\frac{\alpha _2}{\root 3 \of {\alpha _1}} = 1\), \(\alpha _3 \root 3 \of {\alpha _1} = 1\), \(\frac{\alpha _5}{\alpha _4\root 3 \of {\alpha _1^2}}=0\),
Here, \(\frac{\alpha _5}{\alpha _4\root 3 \of {\alpha _1^2}}=0\) if and only if \( \alpha _5 = 0\) with \( \alpha _1 = \alpha _4 \ne 0\). Thus, we choose the representative element \(\mathcal {Q} = Y_1 + Y_4 \). Invoking parametric values \(\tilde{\alpha }_i = 0, i = 5,6,7 \) together with \( \tilde{\alpha }_i = 1, i = 1,2,\dots ,4 \) into adjoint system (2.18) gives us the result
However, we also select the representative element \(\mathcal {Q} = Y_1 - Y_4 \) and by inserting \(\tilde{\alpha }_i = 0, i = 5,6,7 \) together with \( \tilde{\alpha }_i = 1, i = 1,2,\dots ,3, -4 \) into system (2.18), we get
In order to reduce the number of inequivalent subalgebras, we use remark (2.2) whereby we map subalgebra \( Y_1 - Y_2 \) to \(Y_1 + Y_2 \), \( Y_1 - Y_3 \) to \(Y_1 + Y_3 \) as well as \( Y_1 - Y_4 \) to \(Y_1 + Y_4 \). In consequence, we secure ten members of optimal system of 1-D subalgebras for 4D-NLMe (1.8) as: \(Y_6 + Y_7 \); \(Y_1\); \(Y_6\); \(Y_1 + Y_3 \); \(Y_1 + Y_4 +Y_5\); \(Y_3\); \(Y_1 + Y_2\); \(Y_7\); \(Y_1 + Y_4 \); \(Y_1 + Y_4 - Y_5\).
2.5 Similarity Solution of Optimal Lie Subalgebras of (1.8)
This subsection utilizes the obtained Lie subalgebras to reduce 4D-NLMe (1.8) to nonlinear ordinary differential equations (NODEs) and thereafter get some non-trivial closed-form solutions of the equation by solving their respective NODEs.
2.5.1 Optimal Subalgebra \( \mathcal {Q}_1 = Y_6 + Y_7 \)
We engage Lie subalgebra \( Y_6 + Y_7 \) whose related Lie characteristic equations are
System (2.29) gives us a group-invariant which is calculated in this regard as
Using the obtained similarity solutions in equation (1.8), we achieve a reduced form
Remark 2.3
We observe that Lie symmetry analysis of the obtained nonlinear partial differential equation gives no outcome of interest.
2.5.2 Optimal Subalgebra \( \mathcal {Q}_2 = Y_6 \)
We obtain a reduced form of equation (1.8) using generator \( Y_6 \) and that is
We achieve (2.32) by imploring group-invariant solution of \( Y_6 \) calculated as
Subsequently, on performing Lie symmetry analysis on equation (2.32), we obtain
On engaging Lie point symmetry \( V_1 \) with \( F_1(Z) = 0 \) and \( F_2(Z) = 1 \), we obtain \( W(X,Y,Z) = G(r,w) + Y \) where \( r = X \), \( w = Z \). This, reduces NLPDE (2.32) to
Solving the linear partial differential equation (2.34), we secure the result
Thus, on reverting to the basic variables, we achieve a solution of (1.8) as
with arbitrary functions \( f_1 \), \( f_2 \) and \( f_3 \) depending on their various arguments. Further, we contemplate a combination of \( Q_1 = \partial /\partial r \) together with \(Q_2 = \partial /\partial w \) which are two basic symmetries of (2.36) as \( Q = a \partial /\partial r + b \partial /\partial w \). We derive the solution of Q as \( G (r,w) = U(\xi ) \) with \( \xi = a w - b r \). In consequence, we reduce (2.34) further to the linear ODE \( U'''(\xi ) = 0 \), giving a solution of 4D-NLMe (1.8) in this regard as
with constants of integration \( A_1, A_2\) and \( A_3 \). Moreover, we discover that on performing Lie symmetry reduction of \( V_2 \), no solution of interest could be obtained.
2.5.3 Optimal Subalgebra \( \mathcal {Q}_3 = Y_1 \)
Optimal Lie subalgebra \( \mathcal {Q}_1 = \partial /\partial t\) possesses Lagrangian system expressed as
Solving system (2.38), we obtain a function with respect to X, Y and Z as
In consequence, we insert the obtained function in (1.8) and then reduce it to
The solution of equation (2.40) with regards to X, Y and Z is presented as
where arbitrary constants \( A_0 \), \( A_1 \), \( A_2 \) as well as \( A_3 \) are present in the solution. Therefore, on retrograding to the basic variables, we achieve a solution of (1.8) as
which is a steady-state topological kink soliton solution of 4D-NLMe (1.8). We further explore equation (2.40) using Lie theoretic approach and so we gain generators
Similarity solution associated to generator \( V_1 \) yields \( W(X,Y,Z) = G (r,w) + X\), where \( r = Y - X \), \( w = Z - X \). On utilizing the function, we further reduce (1.8) to
Hence, the outcome of (2.43) which gives a solution of equation (1.8) is obtained as
which is another steady-state kink soliton solution of (1.8) with constants \( A_i, i=0,1,2,3 \) arbitrary. Further study on (2.43) reveals that it admits Lie symmetries
We discover that upon investigation, \( Q_1 \) gives a trivial solution. On turning attention to generator \( Q_2 \), we obtain solution \( G (r,w) = U(\xi ) + 5r/2\), where \( \xi = w \). Thus, using the expression of G(r, w) in (2.43) gains ordinary differential equation (ODE)
Integration of (2.45) three times, one can consequently obtain a solution of (1.8) as
where \( A_0 \), \( A_1 \) and \( A_2 \) are integration constants. We proceed to explore \( Q_3 \) and then, we have the solution \( G (r,w) = r^{-1}U(\xi ) + 3r/2\) with \( \xi = w/r \) which reduces (1.8) to
Further, on engaging \( V_2 \), no solution of interest could be found. Next, we move to \( V_3 \) and on solving its characteristic equations, we get \( W(X,Y,Z) = X^{-1}G (r,w)\) with \( r = Y \) alongside \( w = Z / X^2 \). Inserting W(X, Y, Z) in (2.40), we transform (1.8) to
Equation (2.48) then gives four Lie point symmetries which are presented as
Now, we take a linear combination \(Q = Q_1 + Q_3 \) and so, Q furnishes the solution \( G (r,w) = U(\xi ) - r/\sqrt{w}\) with \( \xi = w \). On using the function, we reduce (1.8) to ODE
On solving the nonlinear ordinary differential equation (NODE) (2.49), we have
which is a steady-state algebraic solution of (1.8) with constants of integration \( A_1 \), \( A_2 \) and \( A_3 \). Moreover, in the same vein, we combine \( Q_1\) and \(Q_2 \) which yields function \( G (r,w) = U(\xi ) - 2/\sqrt{w}\) with \( \xi = w/r \). Utilizing the function reduces (1.8) to NODE
We observe upon study that generator \( Q_4 \) yields no solution of importance.
2.5.4 Optimal Subalgebra \( \mathcal {Q}_4 = Y_1 + Y_3 \)
Solution to the Lagrangian system corresponding to optimal Lie subalgebra \( \mathcal {Q}_4 \) gives
On inserting (2.52) in 4D-NLMe (1.8), we obtain a fifth order NLPDE given as
Further, we achieve a solution of equation (2.53) in terms of X, Y and Z as
where constants \( A_i, i = 0,1,2,3 \) are arbitrary. Therefore, solution of (1.8) gives
which is a complex bright soliton solution. Moreover, (2.53) gives three symmetries
We engage \( V_1 \) which produces function \( W(X,Y,Z) = G(r,w) + X \) where \( r = Y - X \), \( w = Z - X \). We insert the achieved function in equation (2.53) and so obtain
Solving the equation and retrograding to basic variables gains a solution of (1.8) as
where \( A_1,\dots ,A_4 \) are arbitrary constants. Further study on (2.56) secures generators
On exploring \( Q_1 \), we obtain a trivial solution of (1.8) and then from \( Q_2 \) we get solution \( G (r,w) = U(\xi ) + 5r/2\), where \( \xi = w \). Thus, using the expression of G(r, w) in (2.43), we gain linear ODE \( U'''(\xi ) = 0 \), which solves to give a solution of (1.8) as
where \( A_0 \), \( A_1 \) and \( A_2 \) are integration constants. Investigation of generator \( Q_3 \) reveals no results of interest. In addition, the same reason applies to symmetries \( V_2 \) and \( V_3 \).
2.5.5 Optimal Subalgebra \( \mathcal {Q}_5 = Y_1 + Y_4 + Y_5 \)
Similarity solution associated to \( \mathcal {Q}_5 = \partial /\partial t + \partial /\partial y + \partial /\partial z \) reduces (1.8) to equation
The similarity solution used in the transformation gives the function with variables
On solving equation (2.59), one secures an outcome structured as
with arbitrary constants \( A_1,A_2,A_3 \). Thus, returning to variables (t, x, y, z) , we have
which is a complex tan-hyperbolic solution of 4D-NLMe (1.8). Besides, (2.59) admits
On exploring \( V_1 \), we gain group-invariant \( W(X,Y,Z) = G(r,w) + X \) where \( r = Y \), \( w = Z - X \). Reckoning equation (2.59), we invoke the group-invariant and obtain
Therefore, (2.63) gives a solution which on reverting to the basic variables yields
where \( A_1 \), \( A_2 \) as well as \( A_3 \) are arbitrary constants. Moreover, equation (2.59) admits
Contemplating linear combination of \( Q_1 \), \( Q_2 \) and \( Q_3 \) as \( Q = \alpha _0 Q_1 +\alpha _1 Q_2 + \alpha _2 Q_3\). Thus, the solution to Q gives \( G (r,w) = U(\xi ) + \alpha _2r/\alpha _0\), where \( \xi = \alpha _0 w - \alpha _1 r \). Subsequently, on utilizing the function, equation (1.8) further reduces to the form
In addition, by using \( Q_4 \), we have the solution \( G (r,w) = r ^{-1/3} U(\xi ) + 3 r/2 + 7w/6\), where \( \xi = w / r ^{1/3} \). Therefore, using the function G(r, w) , (1.8) transforms to NODE
Next, we consider symmetry \( V_2 \) and by solving its related characteristic equations, one gains \( W(X,Y,Z) = G(r,w) + X \), \( r = Y - X\), \( w = Z \). Thus, we reduce (1.8) to
In consequence, we solve (2.65) and on returning to basic variables, we obtain
which is a logarithmic-tan hyperbolic solution of 4D-NLMe (1.8) with arbitrary constants \( A_0 \), \( A_1 \), \( A_2 \) as well as function f dependent on t and z. Further studies on Lie point symmetries \( V_2 \) and \( V_3 \) give no outcome of interest.
2.5.6 Optimal Subalgebra \( \mathcal {Q}_6 = Y_1 + Y_2\)
Having realized that Lagrangian system related to \( \mathcal {Q}_6 \) can be expressed as
we solve the system and secure the corresponding invariants presented as
These invariants alongside their group-invariant when utilized transform (1.8) to
On solving the NLPDE, we obtain a solution which is presented in the structure
with arbitrary constants \( A_0,A_1,A_2, A_3 \). Therefore, back-substitution in this regard, achieves sin hyperbolic function solution which satisfies 4D-NLMe (1.8) as
This solution is a singular soliton of (1.8). Application of Lie symmetry analysis on equation (2.69) further reveals that it admits three Lie point symmetries given as
On exploring \( V_1 \), we have similarity solution \( W(X,Y,Z) = G(r,w) + X \) where \( r = Y - X\), \( w = Z - X \). Inserting the obtained function in (2.69) reduces it to
The solution of (1.8) with regards to (2.72) gives the topological kink soliton
where \( A_0, A_1 \), \( A_2 \) are arbitrary constants. Further studies reveal that (2.72) admits
We find from generator \( Q_1 \), solution \( G (r,w) = U(\xi ) + 3r/2\), where \( \xi = w - r \), which solves (2.72) to give a trivial solution. Moreover, group-invariant associated to \( Q_2 \) gives \( G (r,w) = U(\xi ) + 5r/2\), where we have \( \xi = w \). Thus, equation (2.72) becomes \( U'''(\xi ) =0 \). Solving the linear ordinary differential equation (LORDE) gives us
where \( C_0 \), \( C_1 \) as well as \( C_2 \) are arbitrary constants of integration. We observe from investigation that no result of importance could be found via \( Q_3 \) with \( V_2 \) and \( V_3 \).
2.5.7 Optimal Subalgebra \( \mathcal {Q}_7 = Y_7\)
Optimal Lie subalgebra \( \mathcal {Q}_7 = 3 t \partial /\partial t + x \partial /\partial x - 2 y \partial /\partial y - u \partial /\partial u\) solves to give
The obtained function, when utilized appropriately transforms equation (1.8) to
In this case, further investigation of NLPDE (2.76) shows that remark (2.3) applies.
2.5.8 Optimal Subalgebra \( \mathcal {Q}_8 = Y_1 + Y_4\)
Using subalgebra \( \mathcal {Q}_8 \), we transform (1.8) to a NLPDE, which is expressed as
The group-invariant related to \( \mathcal {Q}_8 \) used in the transformation process is obtained as
On solving the found NLPDE, we secure a solution of 4D-NLMe (1.8) and that is
which is a complex trigonometric soliton solution of (1.8) where constants \( A_0 \), \( A_1 \), \( A_2 \) and \( A_3 \) are arbitrary. Further, equation (2.78) admits two symmetries namely
We engage Lie point symmetry \( V_1 \) in the reduction of (1.8) by using function \( W(X,Y,Z) = G(r,w) + X \) where \( r = Y - X\), \( w = Z - X \) and so (1.8) becomes
Solving (2.79), we obtain a hyperbolic solution of (1.8) in this case as
with \( C_0, C_1 \), \( C_2 \), \( C_3 \) arbitrary constants. Further studies show that (2.79) admits
Utilizing the generators \( Q_1 \), \( Q_2 \) and \( Q_3 \) combined linearly, no valuable outcome could be obtained. The same reason applies to \( Q_4 \). Next, we turn attention to \( V_2 \) from which we gain function \( W(X,Y,Z) = X^{-1}G(r,w) \) where \( r = Y / X^3\), \( w = Z / X^5 \). On invoking W(X, Y, Z) in equation (2.78), we obtained a reduced structure of it as
Applying Lie theoretic approach to (2.81), we secure three Lie point symmetries, viz
We know that invariant of \( Q_1 \) does not exist and so for \( Q_2 \) we secure group-invariant \( G (r,w) = U(\xi ) - 3 r/10 w \), where \( \xi = w \). On inserting G(r, w) in (2.81), we have
Solving NODE (2.82) and returning to basic variables, we gain a solution of (1.8) as
where \( A_0 \), \( A_1 \) and \( A_2 \) are arbitrary constants of integration. Exploring \( Q_3 \), we find \( G (r,w) = r^{-1/3} U(\xi ) + 3 r/10 w \), \( \xi = w/r^{5/3} \), which gives a trivial solution of (2.81).
2.5.9 Optimal Subalgebra \( \mathcal {Q}_9 = Y_1 + Y_4 - Y_5 \)
Group-invariant solution associated to optimal Lie subalgebra \( \mathcal {Q}_9 \) is computed as
Applying the achieved solution to 4D-NLMe (1.8) transforms it to equation
Solving (2.85) gives solution in terms of X, Y, Z and back-substitution to (t, x, y, z) ,
with constants \( B_0, B_1 \) and \( B_2 \) arbitrary. Lie symmetry analysis shows (2.85) admits
On utilizing \( V_1 \), we obtain function \( W(X,Y,Z) = G(r,w) + X \) with \( r = Y \), \( w = Z - X \). On invoking the function in equation (2.85), one secures a reduced NLPDE
Consequently, (2.87) gives a solution where back-substitution to basic variables gains
with arbitrary constants \( B_3 \), \( B_4 \) along with \( B_5 \). Moreover, equation (2.59) admits
Considering linear combination of \( Q_1 \), \( Q_2 \) and \( Q_3 \), we obtain no result(s) of importance and same situation applies to generator \( Q_4 \). Now, symmetry reduction is done via \( V_2 \) where from its related Lagrangian system, one gains \( W(X,Y,Z) = G(r,w) + X \), \( r = Y - X\), \( w = Z \). The function then transforms (1.8) further to
Hence, by solving NLPDE (2.89) and reverting to fundamental variables, we obtain
where constants \( c_0 \), \( c_1 \), \( c_2 \) are arbitrary and function f depends on t and z. Finally, we contemplate \( V_3 \). On following the usual process, we have similarity solution \( W(X,Y,Z) = X^{-1} G(r,w) + 1/2 X \), \( r = Z / X^3\), \( w = \left( Y + Z\right) / X \) reducing (1.8) to
Further investigation on NLPDE (2.91) reveals that remark (2.3) is applicable here.
2.5.10 Steady-State Power Series Solution of (1.8) in Explicit Form
We adopt power series technique[45,46,47] to secure a solution of the complicated NODE (2.47) having forty-four terms which involves a quite lengthy calculations. We begin this process by assuming a series solution of a formal structure
Finally, by computing the power series solution of (2.47) explicitly in terms of arbitrary constants \( g_0, g_1, g_2 \) and \( g_3 \) (See the appendix for a detailed calculation of the steady-state power series solution), we achieve a steady-state power series solution of 4D-NLMe (1.8) as
Remark 2.4
We discovered that using a computer software, that is Mathematica to validate our result, the approximate of (2.93) which is the partial sum up to the tenth term \( T_0,\dots ,T_9 \) (see [59]) of the series solution (that is solution (2.93) excluding the recursion relation part) satisfies 4D-NLMe (1.8). Thus, the approximate series solution (2.93) is a solution of the model under study. Moreover, having demonstrated that the power series solution of the most difficult NODE with the highest number of terms (forty-four) can be obtained, one can equally achieve series solutions of other seemingly non-solvable NODEs in this study in a similar manner. Hence, the power series technique is very viable and ideal for achieving solutions to complicated nonlinear differential equations of any number of terms.
2.6 Graphical Depictions and Discussion of Solutions
Great importance is attached to explanations and discussions of mathematical formulations acquired as invariant solutions while investigating solitons and closed-form solutions of NLPDEs. In consequence, physical interpretations are provided graphically for the study of various novel solitary wave structures which have been established for exact-soliton solutions of 4D-NLMe (1.8) in this subsection. Diverse novel closed-form invariant solutions such as (2.36), (2.37), (2.42), (2.44), (2.50), (2.55), (2.57), (2.58), (2.62), (2.78), (2.90), ranging from algebraic, hyperbolic, complex, trigonometric to logarithmic types of solutions are achieved in the study. Thus, we try to understand the dynamical behaviour of some of the various kinds of solitons/solitary solutions (since some functions are repeatedly obtained) found and then analyze them graphically. In the first place, assigning suitable mathematical functions to arbitrary functions in a solution allows one to investigate the behaviour of soliton interactions which is of interest. Therefore, we demonstrate the dynamics of various soliton interactions for (2.36), in Figs. 1, 2, 3, 4, 5 in the form of two and three dimensions together with density plot.
Thus, on utilizing Mathematica 11.3 to numerically simulate our results, we start by assuming that with \( x = 0 \) and \( t = 1 \), the solution furnishes a function of y and z, hence, we say \( u = g_0 (y) + g_1 (z) + g_2 (2z) \) where \( - 10 \le y,z \le 10 \). Soliton interaction is demonstrated in Fig. 1 by letting \( g_0 (y) = \text {coversin}(y)\), \( g_1 (z) = \text {vercosin}(z)\) and \( g_2 (z) = \text {sinc}(2z)\). Consequently, we observe the propagated waves, moving in the same direction with uniform frequency. We portray the soliton interaction in Fig. 2 via the use of representations: \( g_0 (y) = \text {covercosin}(y)\), \( g_1 (z) = \text {versin}(z)\) and \( g_2 (z) = \text {sinc}(2z)\). Thus, we notice waves propagating at different amplitudes and frequencies. Moreover, on engaging \( g_0 (y) = \text {sech}^2(y)\), \( g_1 (z) = \text {sech}(z)\) and \( g_2 (z) = \text {sinc}(2z)\) in Fig. 3, we observe waves interacting and moving at variant amplitudes and frequency with respect to time. In Fig. 4, we invoke \( g_0 (y) = \text {sech}^2(y)\), \( g_1 (z) = -\text {sech}(2z)\) and \( g_2 (z) = 5\, \text {sinc}(2z)\), and these occasion waves travelling at different amplitudes and frequencies. In the same vein, Fig. 5 demonstrates propagation of waves at variant speed and amplitudes in relation to time by assuming \( g_0 (y) = \text {sech}^2(y) - 5\, \text {sinc}(y)\), \( g_1 (z) = -2\,\text {sech}(2z)\) and \( g_2 (z) = 5\, \text {sinc}(2z)\).
Furthermore, Fig. 6 gives the graphical exhibition of interaction between double-parabolic waves in opposite directions for algebraic solution (2.36) under optimal subalgebra \( Y_6 \) via 3D, contour and 2D plots. The dynamical behaviour of the solution is achieved via numerical simulations that involve interacting periodic solitons and doubly-periodic soliton \( f_1(\theta _{1}) = \text {sech}\,(\theta _{1}) \), \( f_2(\theta _{1}) =\cosh (\theta _{1}) \) and \( f_3(\theta _{1}, \theta _{2}) = \text {cn}\,(2\theta _{1},3\theta _{2}) \), where \( \theta _{1} = \frac{z}{\root 3 \of {t^2}}\), \( \theta _{2} = \frac{x}{\root 3 \of {t}}\) with variables \( t = 0.1 \), \( y = 10 \) and \( -2 \le x,z \le 2 \). Moreover, various soliton wave structures of the solution from multi-peak to a single-peak are achieved in Figs. 7, 8, 9, 10, 11 in 3D plot, density as well as 2D plots. In Fig. 7, we demonstrate the interaction between solitons \( f_1 \) alongside \( f_2 \) as earlier given and periodic \( f_3(\theta _{1}, \theta _{2}) = \cos (2\theta _{1}-3\theta _{2}) \) with \( t = 0.01 \), \( z = 0 \) alongside \( -1.1 \le x,y \le 1.1 \). Multi-waves structures which gradually transform to a single-wave structure as perceived in Figs. 8, 9, 10, 11 are achieved through soliton interactions between periodic and doubly-periodic solitons when we assume \( x = 0 \) along with \( t = 0.1\), \( t = 0.2 \), and \( t = 0.4 \). Thus, the annihilation of a multi-soliton is observed for Eq. (2.36) with an increase in time. Besides, the multi-soliton structures reduce to a stable wave profile after \( t = 0.2 \). In the course of wave propagation, we notice that the velocity, the amplitude as well as the shape of the soliton all remain invariant. Finally, under the optimal subalgebra, we depict the wave motion related to algebraic solution (2.37) using 3D plot, 2D plot and density plot in Fig. 12 with dissimilar parametric values \( a = 20 \), \( b = 0 \), \( A_1 = - 0.1 \), \( A_2 = 10 \), \( A_3 = 100 \) such that \( t = 0.00001\), \( y = 10 \) and \( -5 \le x,z \le 5 \). Next, we represent the dynamical behaviour of steady-state topological kink-soliton solution (2.44) in Fig. 13 via 3D, contour and 2D plots with unalike parameters \( A_0 = 0.1 \), \( A_1 = 0.1 \), \( A_2 = 10 \), \( A_3 = 100 \), where we have \( t = 0 \), \( x = 3 \) and \( -35 \le y,z \le 35 \). In addition, we depict
Soliton interaction depiction of (2.36) with the propagated wave travelling towards the same direction with uniform frequency
Soliton interaction portrayal of (2.36) with wave propagating at different amplitudes and frequencies
Soliton collision depicting (2.36) with waves moving at variant amplitudes, frequencies and in different directions, relative to time
Soliton interaction depiction of (2.36) with waves travelling at different amplitudes and frequencies
Soliton collision depicting (2.36) with waves propagating at variant speeds and amplitudes in relation to time
Wave profile depiction of algebraic solution (2.36) at \(t=0.1\) and \( y = 10 \)
Wave profile depiction of algebraic solution (2.36) at \(t=0.01\) and \( z = 0 \)
Wave profile depiction of algebraic solution (2.36) at \(t=0.1\) and \( y = 10 \)
Wave profile depiction of algebraic solution (2.36) at \(t=0.1\) and \( y = 10 \)
Wave profile depiction of algebraic solution (2.36) at \(t=0.2\) and \( y = 1 0 \)
Wave profile depiction of algebraic solution (2.36) at \(t=0.4\) and \( y = 10 \)
Wave depiction of algebraic solution (2.37) at \(t=0.00001\) and \( y = 10 \)
Wave profile depiction of hyperbolic solution (2.44) at \(t=0\) and \( x = 3 \)
Wave profile depiction of algebraic solution (2.50) at \(t=0\) and \( z = 1 \)
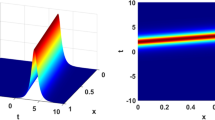
Wave profile depiction of complex solution (2.55) at \(t=2\) and \( z = -0.2 \)
Wave profile depiction of complex solution (2.62) at \(t=2\) and \( x = 0.2 \)
Wave profile depiction of complex solution (2.62) at \(t=2\) and \( x = 0.2 \)
waves of the steady-state algebraic solution (2.50) which is given in similar structure as we have in Fig. 14 with varying parametric values \( A_1 = -100 \), \( A_2 = 80 \), \( A_3 = -120 \) with \( t = 0 \), \( z = 1 \) as well as \( -2 \le x,y \le 2 \). We reveal the wave motion of complex secant hyperbolic solution (2.55) in Fig. 15 with 3D plot as well as contour and 2D plots by numerically simulating its real part where we take \( A_0 = 30 \), \( A_1 = 10 \), \( A_2 = 1 \), \( A_3 = 100 \), \( \pi = 3 \) and \( t = 2 \), \( z = -0.2 \), \( -10 \le x,y \le 10 \). Further, complex tangent hyperbolic solution (2.62) is depicted via 3D, contour and 2D plots in Fig. 16 with consideration first, to the real part of the solution using parameter values \( A_1 = 10 \), \( A_2 = 1 \), \( A_3 = 100 \) along with \( t = 2 \), \( x = 0.2 \) and \( -5 \le y,z \le 5 \). Now, we display the wave character for imaginary part of the solution in Fig. 17 in the same format where parameters \( A_1 = 10 \), \( A_2 = 1 \), \( A_3 = 100 \) with \( t = 2 \), \( x = 0.2 \), \( -7 \le y,z \le 7 \). We observe that both parts of the solution give combo-type multi-soliton waves which are rich localized wave structures. Finally, we depict the various dynamics of steady-sate power series solution of (1.8) presented in Eq. (2.93). On assigning constant values \( g_0 = 0.5\), \( g_1 = 1\), \( g_2 = 1\), \( g_3 = 1\), whereas \( t = 0 \), \( x = 0 \), \( 0 \le z \le 1 \) and \( -1 \le y \le 1 \) in the solution, we have 3D, 2D and contour plots in Fig. 18. Besides, assigning \( g_0 = 1.2\), \( g_1 = 1\), \( g_2 = 1\), \( g_3 = 1\) with \( t = 0 \), \( x = 0.02 \), \( -1000 \le z \le 1000 \) and \( -50 \le y \le 50 \), we achieve Fig. 19. We take steps further to explore the motion of the series solution and for dissimilar values \( g_0 = 1\), \( g_1 = 1\), \( g_2 = 1\), \( g_3 = 1\), whereas \( t = 0 \), \( x = 0 \), \( 0 \le z \le 1000 \) and \( -5 \le y \le 5 \), we plot Fig. 20. In addition, 3D, 2D and contour plot for (2.93) in Fig. 21 is achieved with constant values \( g_0 = 1\), \( g_1 = 1\), \( g_2 = 4\), \( g_3 = 1\), whereas \( t = 0 \), \( x = 0.1 \), \( 0 \le z \le 10 \) and \( -5 \le y \le 5 \). Lastly, we plot the graphs of the solution in Fig. 22 with \( g_0 = 1\), \( g_1 = 1\), \( g_2 = 1\), \( g_3 = 2\) where \( t = 0 \), \( x = 0 \), \( -1 \le z \le 1 \) and \( -5 \le y \le 5 \). We notice that there is a constant time factor \( (t = 0) \) throughout which does not affect the deflection of the wave as it is exhibited in Figs. 18, 19, 20, 21, 22. It implies that the wave can still deflect irrespective of the non-availability of time t and this attests to the fact that the solution can still exist independent of time.
Steady-state series solution (2.93) wave depiction at \(t=0\) and \( x = 0 \)
Steady-state series solution (2.93) wave depiction at \(t=0\) and \( x = 0.02 \)
Steady-state series solution (2.93) wave depiction at \(t=0\) and \( x = 0 \)
Steady-state series solution (2.93) wave depiction at \(t=0\) and \( x = 0.1 \)
Steady-state series solution (2.93) wave depiction at \(t=0\) and \( x = 0 \)
2.7 Steady-State Soliton/Solitary Wave Solutions and their Application in Various Fields of Science and Engineering
This section presents the explicit significance of the previously computed results in various fields of study, including economics, chemical sciences, medical sciences, pharmacy and engineering. A steady-state in systems theory refers to a process or system whose variables, commonly called state variables which define the behaviour of the processor system do not change with time[48]. Consequently, a steady-state solution of a system is a condition of the system which does not change over time and so it is time-independent. In other words, steady-state soliton/solitary wave solutions depict solitary wave solutions that are unchanging with time. In mathematical dynamics regarding continuous-time also, the rate of change of the system or process (say q) with respect to time is zero, i.e \( \partial q/\partial t = 0 \) and in discrete time, \( q_t-q_{t-1} = 0 \). In addition, from an asymptotic point of view, an unstable system diverges from the steady state, so the stability of such a system is important. Thus, if a system is found to be in a steady-state, then one can guarantee that the recently observed behaviour of such a system will continue into the future. This is an interesting fact about a steady-state of a process. Therefore, the concept steady-state is highly pertinent in many fields of study, in particular economics, thermodynamics and engineering and so are the solitary wave solutions associated with it.
Typical electric power system single-line diagram [49]
In electronics, periodic steady-state solutions (steady-state solitary wave solutions) is a prerequisite for small signal dynamic modelling. Besides, many design specifications of electronic systems (see Figs. 23, 24) are presented with regards to the steady-state properties. Hence, steady-state analysis is an indispensable component of the design process. In chemistry, thermodynamics, and other chemical engineering, a steady state is a scenario whereby all state variables are constant in spite of ongoing processes that strive to alter them.
There must be a flow through a system if the entire system is at a steady-state for all state variables of a system to be constant. A steady-state flow process requires conditions at all points in an apparatus and remain constant as time changes. Furthermore, no accumulation of mass or energy over the period of interest must be involved. The same mass flow rate through each element of the system will remain constant in the flow path [50]. Thermodynamic properties may differ from point to point, but they will remain unaltered at any given point[51].
Diagrammatic representation of an evolutionary electric power system infrastructure [52]
In electrical engineering, sinusoidal steady-state analysis is a technique used in analyzing alternating current circuits which is also used in solving DC circuits[48]. (See Figs. 25, 26). The potential of a power system or an electrical machine to regain its previous or original state is referred to as steady-state stability. Power is generated when synchronous generators are made to operate in synchrony with the rest of the system. A generator is synchronized with a bus when both of them possess the same voltage, frequency and phase sequence. One can therefore define the power system stability as the ability of the system to return to a steady-state without losing synchronicity. Often, power system stability is categorized into steady-state, transient and dynamic stability. In mechanical engineering, when a periodic force is applied to a mechanical system, it will typically reach a steady-state after going through some transient behaviour. This is usually observed in vibrating systems, such as a clock pendulum, but it can also occur in any dynamic system which is either stable or semi-stable.
Transformer-less Power Supply Circuit (A) Half-Wave Rectified; (B) Full-Wave Rectified. [53]
In pharmacy, steady-state is a dynamic equilibrium existing in the body where drug concentrations persistently stay within a therapeutic limit over time. In chemical science, a steady-state is a more general situation than dynamic equilibrium where the latter refers to two or more reversible processes occurring at the same time, definitely, one can say that such a system is in a steady state. A system that exists in a steady-state may not necessarily be in a state of dynamic equilibrium due to the fact that some of the processes included are not reversible. In stochastic systems, probabilities that various states will be repeated will remain constant and so the situation is in a steady state. In economics, a steady-state economy is that whose stable size is characterized by a stable population and stable consumption that remain either at or below carrying capacity.
Research in recent times has revealed some significant steady-state solutions in diverse processes. Mathematical models for realistic ice sheets have been found generally to be unsolvable by analytical approaches due to the nonlinearity of the equations. However, lately, steady-state solutions with realistic margins together with vanishing ice flux and shear stress were numerically observed for ice sheets with Weertman-type sliding [54]. Nonzero steady-state solutions for a nonlinear mathematical model of inverted pendulum with stochastic perturbations and nonclassical technique of stabilization was considered. In consequence, criteria by which stable, unstable and one-sided stable equilibrium points exist were achieved [55]. Multiple steady-state solutions are known to occur in situations involving fluid-flow problems, chemical reaction systems, elasticity theory, along with biological models, as mentioned by Jepson and Spence (1985). However, until the last few decades, multiple solutions had not been observed in separation systems. Recently, four steady-state solutions have been discovered when the purities of three product streams and bottoms total flow rate are specified in Petlyuk separation system over a range of reflux ratios [56]. Only two various steady-state solutions were found for each of two other interlinked systems comprising a single pair of interlinking streams. In [57], resonant dynamics of a two-degree-of-freedom (DOF) dissipative forced strongly nonlinear system was investigated. The periodic (soliton/solitary wave) steady-state solutions of the underlying Hamiltonian system was first examined and then the forced and damped configuration was done. Specifically, analysis of the steady periodic responses of the two DOF systems involving a grounded strongly nonlinear oscillator with harmonic excitation coupled to a light linear attachment under the condition of resonance was carried out. It was discovered that varying the forcing amplitude revealed that the phenomena of interest can be enhanced greatly when optimal forcing levels and excitation frequencies are applied. Further, the authors note that this type of localization in the dynamics of the system may have practical implications. An example of such an application could include imploring the variation in the forcing amplitude to introduce essential and controllable changes in the frequency spectrum of a nonlinear structure with a lightweight attachment.
Pictorial representation of different types of DC Circuit Breakers [58]
3 Conserved Currents of 4D-NLMe (1.8)
This Section furnishes the derivation of conserved quantities of 4D-NLMe (1.8) via the engagement of the multiplier approach as highlighted in [59]. In addition, we construct more conserved vectors of the underlying equation via Ibragimov’s conserved vectors’ theorem [59, 60] using the obtained optimal system of Lie subalgebras.
3.1 Conserved Currents Utilizing the Multiplier Technique
The multiplier approach is known over the years for its capability in handling the conserved quantities of differential equations with or without variational principles [1, 22, 59, 61]. On constructing conserved currents of (1.8), we consider a theorem:
Theorem 3.1
The zeroth-order multiplier associated with 4D-NLMe (1.8) reads
where \( \Omega = \Omega (t,x,y,z,u) \). Therefore, we have four conserved quantities secured via the multiplier presented in (3.1), which are consequently furnished basically by arbitrary functions e(t, y, z) , h(t, z) , f(t) as well as p(t) that are given in (3.1).
Proof
Given that the Euler operator related to 4D-NLMe (1.8) in this case is expressed as
In seeking the zeroth order multiplier of (1.8) represented by \(\Omega (t,x,y,z,u)\), we consider the governing equation [1]
On contemplating (3.3) and following the steps analogous to the common algorithm involved in Lie symmetry analysis, we obtain forty-five determining equations which simplifies to the seven presented as
On solving the seven system of linear partial differential equations, we achieve
where functions e(t, y, z) , h(t, z) , f(t) as well as p(t) are arbitrary. Conserved quantities required are now found via the divergence identity expressed as
where \( C^t\) represent conserved density and \(( C^x, C^y, C^z)\), spatial fluxes [61]. Hence after some computations, one secures four local conserved vectors of (1.8) given as
Hence, the proof of theorem (3.1) is concluded.
3.2 Conserved Currents of (1.8) via Ibragimov’s Technique
It is known that Ibragimov’s theorem for conserved quantity recommends that for every Lie point symmetry of a differential equation, one can achieve a distinctive conservation law of the differential equation. Here, we invoke the members of the optimal system of Lie subalgebra of (1.8) in Section 2 for the construction of new conserved currents via the theorem of Ibragimov[59, 60, 62]. Thus, we give a theorem
Theorem 3.2
Given the Euler operator \( \delta /\delta u \) as defined in (3.2), the adjoint equation of 4D-NLMe (1.8) [60] can be expressed through the relation
Further expansion of (3.5) secures
The formal Lagrangian of 4D-NLMe (1.8) together with its adjoint presented in (3.6) is expressed in the format
Hence, one constructs the associated conserved vectors \( T^i, i=(t,x,y,z) \) for the expressed Lagrangian by utilizing the relation purveyed as [60]
for \(\alpha =1,2\) and \(j=1,2,3,4\), the Lie characteristic function \(W^{\alpha }\) is \(W^{\alpha }=\eta ^{\alpha }-\xi ^{j}u_j^{\alpha }\).
Having established in Section 2 that optimal system of Lie subalgebra of 4D-NLMe (1.8) contains ten members, we reckon the conserved vectors [59, 63] for (1.8) using theorem (3.2) alongside information provided in the references. Thus, we have
Remark 3.1
We observe that conserved quantities obtained via the multiplier approach contain arbitrary functions whereas none of the ten found using Ibragimov’s technique contains any function. However, having said that, we noticed the prevalence of variable v which is a newly introduced variable required in computations of that of the latter. We want to state here categorically that both perform the same function in the sense that, their availability in the conserved vectors symbolizes the fact that 4D-NLMe (1.8) possesses infinitely many conserved quantities. Besides, having known that these quantities have various applications in physical systems (such as in establishing existence and uniqueness of solutions, investigation of integrability and linearization mappings, stability analysis and global behaviour of solutions and so on), we have among them depicting momentum as well as energy thereby making them very useful in studying physical systems.
4 Conclusions
We have studied explicit solutions of (3+1)-dimensional fifth-order nonlinear model I (1.8). Consideration has been given to securing the solution of the underlying equation using Lie group analysis. Thus, we obtained the optimal system of the Lie subalgebras of the equation. Further, these subalgebras are engaged in successfully reducing the equation under investigation to diverse nonlinear ordinary differential equations of various orders. Consequently, this occasion the gaining of various kinds of exact solutions for the equations comprising hyperbolic, trigonometric, complex, algebraic and rational. In addition to that, the functions constitute the availability of diverse steady and non-steady state solitonic/solitary wave solutions which appear in the form of kink, complex, bright, singular and nonsingular. Besides, we depicted the streaming pattern of the results by using suitable pictorial representations. We took a step further to derive the conserved currents of (1.8) using the multiplier technique. Ibragimov’s theorem of conserved quantities enabled us to secure more conserved vectors of the underlying equation via its optimal system of Lie subalgebras. A thing of note in the research is the utilization of the power series technique to gain a steady-state series solution of (1.8) from the most complicated nonlinear differential equation with forty-four terms emerging during our reduction process. Moreover, the significance and pertinence of steady-state solutions are pointed out, which reveal their importance in various fields of science and engineering ranging from chemical, statistical, nursing and pharmaceutical sciences to electronics, mechanical, electrical and chemical engineering. Having said that, it is noteworthy to mention that the solutions found in this study will be a thing of interest to scientists and engineers for analysis in their various fields of research.
Data Availability
Not applicable.
Abbreviations
- ODEs:
-
Ordinary differential equations
- NODEs:
-
Nonlinear ordinary differential equations
- PDEs:
-
Partial differential equations
- NLPDEs:
-
Nonlinear partial differential equations
- LIPDEs:
-
Linear partial differential equations
- KdV:
-
Korteweg-de Vries
- cmKdV:
-
Complex modified Kortweg-de Vries
- AKNS:
-
Ablowitz–Kaup–Newell–Segur
- LPD:
-
Lakshmanan–Porsezian–Daniel
- 4D-NLMe:
-
(3+1)-Dimensional Nonlinear Model
- NLS:
-
Nonlinear Schrödinger equation
- 1-D:
-
One-dimensional
- DC:
-
Direct current
- DOF:
-
Degree-of-freedom
References
Khalique, C.M., Adeyemo, O.D.: A study of (3+1)-dimensional generalized Korteweg-de Vries-Zakharov-Kuznetsov equation via Lie symmetry approach. Results Phys. 2, 103197 (2020)
Du, X.X., Tian, B., Qu, Q.X., Yuan, Y.Q., Zhao, X.H.: Lie group analysis, solitons, self-adjointness and conservation laws of the modified Zakharov-Kuznetsov equation in an electron-positron-ion magnetoplasma. Chaos Solitons Fract. 134, 109709 (2020)
Gao, X.Y.: Mathematical view with observational/experimental consideration on certain (2+1)-dimensional waves in the cosmic/laboratory dusty plasmas. Appl. Math. Lett. 91, 165–172 (2019)
Zhang, C.R., Tian, B., Qu, Q.X., Liu, L., Tian, H.Y.: Vector bright solitons and their interactions of the couple Fokas-Lenells system in a birefringent optical fiber. Z. Angew. Math. Phys. 71, 1–19 (2020)
Gao, X.Y., Guo, Y.J., Shan, W.R.: Water-wave symbolic computation for the Earth, Enceladus and Titan: The higher-order Boussinesq-Burgers system, auto-and non-auto-Bäcklund transformations. Appl. Math. Lett. 104, 106170 (2020)
Benoudina, N., Zhang, Y., Khalique, C.M.: Lie symmetry analysis, optimal system, new solitary wave solutions and conservation laws of the Pavlov equation. Commun. Nonlinear Sci. Numer. Simulat. 94, 105560 (2021)
Khalique, C.M., Abdallah, S.A.: Coupled Burgers equations governing polydispersive sedimentation; a Lie symmetry approach. Results Phys. 16, 102967 (2020)
Gandarias, M.L., Duran, M.R., Khalique, C.M.: Conservation laws and travelling wave solutions for double dispersion equations in (1+1) and (2+1) dimensions. Symmetry 12, 950 (2020). https://doi.org/10.3390/sym12060950
Shafiq, A., Rasool, G., Khalique, C.M.: Significance of thermal slip and convective boundary conditions in three dimensional rotating Darcy-Forchheimer nanofluid flow. Symmetry 12, 741 (2020). https://doi.org/10.3390/sym12050741
Shafiq, A., Rasool, G., Khalique, C.M., Aslam, S.: Second grade bioconvective nanofluid flow with buoyancy effect and chemical reaction. Symmetry 12, 621 (2020). https://doi.org/10.3390/sym12040621
Wazwaz, A.M.: Exact soliton and kink solutions for new (3+1)-dimensional nonlinear modified equations of wave propagation. Open Eng. 7, 169–174 (2017)
Darvishi, M.T., Najafi, M.: A modification of extended homoclinic test approach to solve the (3+1)-dimensional potential-YTSF equation. Chin. Phys. Lett. 28, 040202 (2011)
Wazwaz, A.M.: Traveling wave solution to (2+1)-dimensional nonlinear evolution equations. J. Nat. Sci. Math. 1, 1–13 (2007)
Osman, M.S.: One-soliton shaping and inelastic collision between double solitons in the fifth-order variable-coefficient Sawada-Kotera equation. Nonlinear Dynam. 96, 1491–1496 (2019)
Zhang, L., Khalique, C.M.: Classification and bifurcation of a class of second-order ODEs and its application to nonlinear PDEs. Discr. Continuous Dyn. Syst. Ser. S 11(4), 777–790 (2018)
Wazwaz, A.M.: Partial Differential Equations. CRC Press, Boca Raton (2002)
Chun, C., Sakthivel, R.: Homotopy perturbation technique for solving two point boundary value problems-comparison with other methods. Comput. Phys. Commun. 181, 1021–1024 (2010)
Zheng, C.L., Fang, J.P.: New exact solutions and fractional patterns of generalized Broer-Kaup system via a mapping approach. Chaos Soliton Fract. 27, 1321–1327 (2006)
Biswas, A., Jawad, A.J.M., Manrakhan, W.N.: Optical solitons and complexitons of the Schrödinger-Hirota equation. Opt. Laser Technol. 44, 2265–2269 (2012)
Akbar, M.A., Ali, N.H.M.: Solitary wave solutions of the fourth-order Boussinesq equation through the exp\( (-\Phi (\eta )) \)-expansion method. Springerplus 3, 344 (2014)
Ovsiannikov, L.V.: Group Analysis of Differential Equations. Academic Press, New York (1982)
Olver, P.J.: Applications of Lie Groups to Differential Equations, 2nd edn. Springer-Verlag, Berlin (1993)
Geng, X.: Algebraic-geometrical solutions of some multidimensional nonlinear evolution equations. J. Phys. A: Math. Gen. 36, 2289–2303 (2003)
Wazwaz, A.M.: New (3+1)-dimensional nonlinear evolution equation: multiple soliton solutions. Cent. Eur. J. Eng. 4, 352–356 (2014)
Zhaqilao, Rogue waves and rational solutions of a (3+1)-dimensional nonlinear evolution equation, Phys. Lett. A, 377 (2013) 3021–3026
Geng, X., Ma, Y.: \( N- \)soliton solution and its Wronskian form of a (3+1)-dimensional nonlinear evolution equation. Phys. Lett. A 369, 285–289 (2007)
Wazwaz, A.M.: A (3+1)-dimensional nonlinear evolution equation with multiple soliton solutions and multiple singular soliton solutions. Appl. Math. Comput. 215, 1548–1552 (2009)
Wazwaz, A.M.: A variety of distinct kinds of multiple soliton solutions for a (3+1)-dimensional nonlinear evolution equations. Math. Methods Appl. Sci. 36, 349–357 (2013)
Wang, X., Wei, J., Geng, X.G.: Rational solutions for a (3+1)-dimensional nonlinear evolution equation. Commun. Nonlinear. Sci. Numer. Simulat. 83, 105116 (2020)
Feng, Y.J., Gao, Y.T., Li, L.Q., Jia, T.T.: Bilinear form and solutions of a (3+1)-dimensional generalized nonlinear evolution equation for the shallow-water waves. Appl. Anal. 100, 1544–1556 (2021)
Wazwaz, A.M.: New (3+1)-dimensional nonlinear equations with KdV equation constituting its main part: multiple soliton solutions. Math. Methods Appl. Sci. 39, 886–891 (2016)
Weiss, J., Tabor, M., Carnevale, G.: The Painlévé property and a partial differential equations with an essential singularity. Phys. Lett. A 109, 205–208 (1985)
Salas, A.H., Gomez, C.A.: Application of the Cole-Hopf transformation for finding exact solutions to several forms of the seventh-order KdV equation, Math. Probl. Eng., (2010) 2010
Gu, C.H.: Soliton Theory and Its Application. Zhejiang Science and Technology Press, Zhejiang (1990)
Zeng, X., Wang, D.S.: A generalized extended rational expansion method and its application to (1+1)-dimensional dispersive long wave equation. Appl. Math. Comput. 212, 296–304 (2009)
Zhou, Y., Wang, M., Wang, Y.: Periodic wave solutions to a coupled KdV equations with variable coefficients. Phys. Lett. A 308, 31–36 (2003)
Jawad, A.J.M., Mirzazadeh, M., Biswas, A.: Solitary wave solutions to nonlinear evolution equations in mathematical physics. Pramana 83, 457–471 (2014)
Kudryashov, N.A., Loguinova, N.B.: Extended simplest equation method for nonlinear differential equations. Appl. Math. Comput. 205, 396–402 (2008)
Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)
Wang, M., Li, X., Zhang, J.: The \( (G^{\prime }/G)-\) expansion method and travelling wave solutions for linear evolution equations in mathematical physics. Phys. Lett. A 24, 1257–1268 (2005)
Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer, New York (1991)
Chen, Y., Yan, Z.: New exact solutions of (2+1)-dimensional Gardner equation via the new sine-Gordon equation expansion method. Chaos Solitons Fract. 26, 399–406 (2005)
Khalique, C.M., Adeyemo, O.D.: Soliton solutions, travelling wave solutions and conserved quantities for a three-dimensional soliton equation in plasma physics. Commun. Theor. Phys. 73, 125003 (2021)
Hu, X., Li, Y., Chen, Y.: A direct algorithm of one-dimensional optimal system for the group invariant solutions. J. Math. Phys. 56, 053504 (2015)
Simbanefayi, I., Khalique, C.M.: An optimal system of group-invariant solutions and conserved quantities of a nonlinear fifth-order integrable equation, Open. Physics 18, 829–841 (2020)
Khalique, C.M., Simbanefayi, I.: Conservation laws, classical symmetries and exact solutions of a (1+1)-dimensional fifth-order integrable equation, Int. J. Geom. Methods Mod., (2021) 2150137
Khalique, C.M., Simbanefayi, I.: Conserved quantities, optimal system and explicit solutions of a (1+1)-dimensional generalised coupled mKdV-type system. J. Adv. Res. 29, 159–166 (2021)
Gagniuc, P.A.: Markov Chains: from Theory to Implementation and Experimentation. John Wiley & Sons, New Jersey, USA (2017)
Keller, J. , Kroposki, B.: Understanding fault characteristics of inverter-based distributed energy resources. No. NREL/TP-550-46698. National Renewable Energy Lab.(NREL), Golden, United States, 2010
Smith, J.M.: Introduction to Chemical Engineering Thermodynamics, 2nd edn. American Chemical Society, USA (1950)
Zemansky, M.W., Abbott, M.M., Van Ness, H.C.: Basic engineering thermodynamics. McGraw-Hill Companies, New York (1975)
Basso, T.S.: System impacts from interconnection of distributed resources: current status and identification of needs for further development. No. NREL/TP-550-44727. National Renewable Energy Lab.(NREL), Golden, United States, 2009
Hamuro, “Types of AC/DC Power Supply Adapter Circuits and How to Use Them". [Online]. Available: https://www.deeptronic.com/electronic-circuit-design/types-of-power-supply-circuits-how-to-design-the-right-ac-dc-adapter/. [Accessed 14 April 2022]
Jouvet, G., Rappaz, J., Bueler, E., Blatter, H.: Existence and stability of steady-state solutions of the shallow-ice-sheet equation by an energy-minimization approach. J. Glaciol. 57, 345–354 (2011)
Borne, P., Kolmanovskiı, V.B., Shaıkhet, L.E.: Steady-state solutions of nonlinear model of inverted pendulum: Proceedings of the 3rd Ukrainian–Scandinavian Conference in Probability Theory and Mathematical Statistics, 1999
Chavez, R.C., Seader, J.D., Wayburn, T.L.: Multiple steady-state solutions for interlinked separation systems. Ind. Eng. Chem. Fundam. 25, 566–576 (1986)
Kurt, M., Slavkin, I., Eriten, M., McFarland, D.M.: Effect of 1:3 resonance on the steady-state dynamics of a forced strongly nonlinear oscillator with a linear light attachment. Arch. Appl. Mech. 84, 1189–1203 (2014)
Elserougi, A., Ahmed, S., Massoud, A.: Half-bridge modular multilevel-based HVDC converters with external pre-charged capacitors for dc fault current suppression capability, Conference paper (2016): https://doi.org/10.1049/cp.2016.0186.
Khalique, C.M., Adeyemo, O.D.: Closed-form solutions and conserved vectors of a generalized (3+1)-dimensional breaking soliton equation of engineering and nonlinear science. Mathematics 8, 1692 (2020)
Ibragimov, N.H.: A new conservation theorem. J. Math. Anal. Appl. 333, 311–328 (2007)
Anco, S.C.: Generalization of Noether’s Theorem in Modern Form to Non-variational Partial Differential Equations. In Recent progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science; Melnik, R., Makarov, R., Belair, J., Eds.; Fields Institute Communications, Springer: New York, NY, 2017
Ibragimov, N.H.: Integrating factors, adjoint equations and Lagrangians. J. Math. Anal. Appl. 318, 742–757 (2006)
Khalique, C.M., Moleleki, L.D.: A (3+1)-dimensional generalized BKP-Boussinesq equation: Lie group approach. Results Phys. 13, 2211–3797 (2019)
Acknowledgements
The authors thank the North-West University, Mafikeng campus for its continued support.
Funding
Open access funding provided by North-West University. Not applicable.
Author information
Authors and Affiliations
Contributions
The authors, ODA and CMK, equally contributed to the paper and have approved the submitted version.
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Authors declare the consent for manuscript publication.
Appendix—Detailed Computations of the Steady-State Power Series Solution to Equation (2.47)
Appendix—Detailed Computations of the Steady-State Power Series Solution to Equation (2.47)
On inserting the expression of \( U (\xi )\) from (2.92) into equation (2.47), we have
Moreover, from the extended equation (4.1), we contemplate the partial sum to the fifth term (that is the sum of the first five terms \( T_0,\dots , T_4 \)) for each of the terms in the equation which involves some lengthy calculations and by expanding the result, we have a more simplified structure given as (see[45,46,47])
Next, we compare the various coefficients of \( \xi \) that appear in equation (4.2). Meanwhile, generally for \( m \ge 5 \), we secure the recurrence relation presented as
Therefore, by comparing the coefficients of \( \xi \) relative to (4.2), we achieve solution for \( g_4, g_5, \dots , g_9 \) in terms of arbitrary \( g_0, g_1, g_2 \) and \( g_3 \) through some lengthy computation and expansion as
Moreover, on invoking the recursion formula, other successive terms like \( g_{p}, p = 10,11,12,\dots ,\infty \) can be secured. Thus, we have the series solution in the structure
which is better presented in relation (2.93) as the power series solution to (1.8).
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Adeyemo, O.D., Khalique, C.M. An optimal System of Lie Subalgebras and Group-Invariant Solutions with Conserved Currents of a (3+1)-D Fifth-Order Nonlinear Model I with Applications in Electrical Electronics, Chemical Engineering and Pharmacy. J Nonlinear Math Phys 30, 843–916 (2023). https://doi.org/10.1007/s44198-022-00101-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s44198-022-00101-5