1 Introduction

Since the explanation of the nonlinear evolution equations (NLEEs) for certain nonlinear phenomena appearing in fluid dynamics, plasma astrophysics, optics, and various other fields, analytic solutions of the NLEEs have been the subjects of extensive investigations, recently yielding many significant and compelling results in the literature [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. In this context, various nonlinear models, such as the extended Kadomtsev-Petviashvili (KP) equations in different dimensions [1, 2], the extended (3+1)-dimensional Ito equations [3, 4], the KdV–Calogero–Bogoyavlenskii–Schiff (KdV-CBS) and negative-order KdV-CBS models developed within the framework of (3+1)-dimensional equations [5], as well as a fifth-order nonlinear integrable equation [6], the time-dependent two members of the KP hierarchy [7], and various Boussinesq equations [8], were investigated to explore their integrability characteristics and to recover multiple-soliton solutions and other solutions. Using Hirota’s bilinear form, an examination and exploration were conducted to investigate lump solutions and collisions between lump and soliton solutions within the framework of the (3+1)-dimensional extended KP equation [9]. The Hirota–Satsuma–Ito equation underwent scrutiny employing the Hirota direct method, resulting in the discovery of multi-wave, breather wave, and interaction solutions for the model [10]. Localized solutions for the (2+1)-dimensional BKP equation were obtained [11]. The study of the (2+1)-dimensional complex mKdV equation revealed the emergence of rogue waves, along with a discussion on modulation instability [12]. The examination of interaction solutions for the extended Jimbo–Miwa equation in (3+1) dimensions was conducted [13]. Lump solutions for a (3+1)-dimensional Boussinesq-type equation were revealed through the utilization of the long-wave limit approach, and simultaneously, interaction solutions were systematically formulated [14]. Hirota’s bilinear method was applied to investigate the generalized water wave equation, leading to the construction of lump and lump-type solutions for the examined model [15]. The investigation of a generalized Whitham–Broer–Kaup–Boussinesq–Kupershmidt system revealed that the system passed the Painlevé test, and both bilinear forms and N-soliton solutions of the system were obtained [16]. Two families of hetero-Bäcklund transformations, along with a family of similarity reductions, were developed for an extended coupled (2+1)-dimensional Burgers system [17]. The auto-Bäcklund transformations of an enlarged three-coupled KdV system were sought and yielded some solitons to the governing system [18]. By constructing a set of the similarity reductions, a (3+1)-dimensional generalized Yu-Toda-Sasa-Fukuyama system for certain interfacial waves in a two-layer liquid or elastic waves in a lattice was researched [19]. An investigation was carried out on a generalized Darboux transformation and solitons of the Ablowitz-Ladik equation [20]. The N-fold Darboux transformation (DT), N-fold generalized DT, and multi-pole soliton solutions of the system were reported as a result of the study conducted on a system for ultra-short pulses in an inhomogeneous multi-component nonlinear optical medium [21]. The exploration of auto-Bäcklund transformations was conducted for a (3+1)-dimensional Korteweg-de Vries-Calogero-Bogoyavlenskii-Schif equation in a fluid, uncovering soliton solutions to the model as well [22]. A (2+1)-dimensional generalized variable-coefficient Boiti–Leon–Pempinelli system was discussed, presenting two branches of the similarity reductions [23].

Solitons have been essentially described as the exceptional solutions of a particular class of the NLEEs, which may have variable or constant coefficients [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. Several well-known NLEEs, such as nonlinear Schrödinger’s equation (NLSE), complex Ginzburg-Landau equation (CGLE), Sasa-Satsuma equation (SSE), Radhakrishnan-Kundu-Lakshmanan (RKL) equation, Lakshmanan-Porsezian-Daniel (LPD) model, and others, describe the propagation of solitons through intercontinental optical fibers. The concatenation model, which combines the well-known NLSE with the LPD model and SSE, is a recent and interesting equation that was proposed in 2014 [24, 25]. The model underwent extensive research following its introduction and then for the model, optical solitons [26,27,28, 30, 32,33,34], Painlevé analysis [26], conservation laws [28], bifurcation analysis [29, 32], as well as chaotic behavior [29], quiescent optical solitons [31], implicit quiescent optical solitons [35], and dark solitary pulses and moving fronts [36] have been reported. Afterwards, the model was examined in birefringent fibers, and optical solitons [37,38,39], complexitons [39], and quiescent optical solitons [40] have also been discovered in that case. The presentation of the concatenation model having multiplicative white noise and the reporting of its soliton solutions have occurred very recently [41]. The aim of this research is to examine how multiplicative white noise affects the concatenation model. Several analytic solutions for the governing concatenation model are derived with the assistance of direct test functions and the Cole–Hopf transformation, and the associated constraint conditions for their existence are also provided. In particular, the results presented below demonstrate the richness of an optical fiber medium described by concatenation model, which is measured by the diversity of structures that it can support. This may have potential application for the further experiments and research in nonlinear optics. Following a brief presentation of the model, the details are enlisted in the subsequent sections of the paper.

1.1 Governing model

The stochastic concatenation model with the inclusion of perturbation terms is formulated as follows [41]:

$$\begin{aligned}&i q_{t}+aq_{xx} +bq_{xt} + c|q|^2q \nonumber \\&\quad + d_1 \Bigg [\rho _1 q_{xxxx}+ \rho _2 \left( q_{x}\right) ^{2}q^{*}+ \rho _3 |q_{x}|^2q \nonumber \\&\quad + \rho _4 |q|^2q_{xx} +\rho _5 q^{2}q^{*}_{xx}+ \rho _6 |q|^4 q \Bigg ] \nonumber \\&\quad + i d_2 \left[ \rho _7 q_{xxx}+ \rho _8 |q|^2 q_{x} + \rho _9 q^2 q^{*}_{x} \right] \nonumber \\&\quad +\sigma \left( q-ibq_x\right) \frac{dW(t)}{dt} \nonumber \\&= i \left[ \alpha q_{x}+ \lambda \left( |q|^2 q \right) _x + \mu \left( |q|^2 \right) _x q \right] . \end{aligned}$$
(1)

Here the dependent variable q(x, t), which characterizes the wave profile, is a complex-valued function, where x and t respectively stand for the spatial and temporal coordinates as two independent variables, while \(i=\sqrt{-1}\). The linear temporal evolution is governed by the initial term, while the terms a, b, and c are the coefficients of chromatic dispersion (CD), spatio-temporal dispersion (STD), and the Kerr law of self-phase modulation (SPM), respectively. Next, the coefficient of \(d_1\) is associated with the LPD model, and the coefficient of \(d_2\) is sourced from the SSE. The role of \(\sigma \) is to signify the coefficient of noise strength, while W(t) corresponds to the standard Wiener process, and dW(t)/dt expresses the white noise. The parameters \(\alpha \), \(\lambda \), and \(\mu \) play a significant role as the coefficients of inter-modal dispersion, self-steepening effect, and self-frequency shift, respectively. It should also be noted here that in the case of \(d_1 = d_2 = 0\), the governing model simplifies to the perturbed stochastic NLSE; however, if either \(d_1 = 0\) or \(d_2 = 0\), it corresponds to the perturbed stochastic SSE or the perturbed stochastic LPD model, respectively. Thus, Eq. (1), which combines the perturbed stochastic versions of the NLSE, LPD model, and SSE, is referred to as the concatenation model.

As to the novelty of this study, it is recognized that multi-wave, two solitary wave, breather, periodic cross kink, Peregrine-like rational, and three-wave solutions for the perturbed stochastic concatenation model given by Eq. (1) have not been reported. As a result and hereby, it will make sense for us to explore multi-wave, two solitary wave, breather, periodic cross kink, Peregrine-like rational, and three-wave solutions to the governing equation (1). Therefore, the findings presented in the study are novel and reported here for the first time.

The content of this paper is as follows: In Sect. 2, Eq. (1) will be transformed into the desired form with the help of an assumption based on amplitude-phase format. Next, the Cole–Hopf transformation and three-wave hypothesis will be utilized to obtain multi-wave solutions in Sect. 3. In Sect. 4, interactional solutions will be investigated under the influence of the double exponential function assumption. The homoclinic breather approach will be employed to investigate breather wave solutions in Sect. 5. From Sect. 6–8, periodic cross kink, Peregrine-like rational, and three-wave solutions will be derived by the implementation of various direct test functions. Finally, in Sect. 9, the results of the research will be outlined.

2 Mathematical setup

To carry out the integration of the governing equation (1), the employed hypothesis is

$$\begin{aligned} q(x,t)=P(\xi ) {e^{i\phi (x,t)}} \end{aligned}$$
(2)

where the wave variable is given by

$$\begin{aligned} \xi = x - v t . \end{aligned}$$
(3)

The amplitude part is represented by the function P(x, t) and the soliton velocity is symbolized as v, according to the aforementioned hypothesis. Next, the phase component is presented with the structure

$$\begin{aligned} \phi = - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta . \end{aligned}$$
(4)

Here \(\kappa \) stands for the frequency and \(\omega \) signifies the wave number, while \(\sigma \) corresponds to the noise coefficient and \(\theta \) denotes the phase constant. Substituting (2) into (1), one obtains the real part

$$\begin{aligned}&-\Bigg [\alpha \kappa + a \kappa ^2+(b \kappa -1) \left( \sigma ^2-\omega \right) \nonumber \\&\quad +\kappa ^3 \left( d_2 \rho _7-d_1 \kappa \rho _1\right) \Bigg ] P \nonumber \\&\quad + \Bigg [c-\kappa \lambda -d_1\kappa ^2 \left( \rho _2-\rho _3+\rho _4+\rho _5\right) \nonumber \\ {}&\quad +d_2 \kappa \left( \rho _8-\rho _9\right) \Bigg ] P ^3 \nonumber \\&\quad +d_1 \rho _6 P ^5 +d_1 \left( \rho _2+\rho _3\right) P \left( P' \right) ^2 \nonumber \\&\quad + \left( a-b v-6 d_1 \kappa ^2 \rho _1+3 d_2 \kappa \rho _7\right) P ''\nonumber \\&\quad +d_1 \left( \rho _4+\rho _5\right) P ^2 P '' +d_1 \rho _1 P ^{({4})} =0 \end{aligned}$$
(5)

and the imaginary portion

$$\begin{aligned}&\Bigg (v+\alpha + 2 a \kappa -b v \kappa +b \sigma ^2-b \omega -4 d_1 \kappa ^3 \rho _1\nonumber \\ {}&\quad +3 d_2 \kappa ^2 \rho _7\Bigg ) P ' \nonumber \\&\quad + \Bigg [3 \lambda +2\mu + 2 d_1 \kappa \left( \rho _2+\rho _4-\rho _5\right) \nonumber \\ {}&\quad -d_2 \left( \rho _8+\rho _9\right) \Bigg ] P ^2 P ' \nonumber \\&\quad + \left( 4 d_1 \kappa \rho _1-d_2 \rho _7\right) P ^{(3)} =0. \end{aligned}$$
(6)

From the imaginary equation given by (6), the velocity can be computed as

$$\begin{aligned} v= \frac{\alpha + 2 a \kappa +b \sigma ^2-b \omega -4 d_1 \kappa ^3 \rho _1+3 d_2 \kappa ^2 \rho _7}{b \kappa -1} \end{aligned}$$
(7)

with constraints

$$\begin{aligned} 3 \lambda +2 \mu + 2 d_1 \kappa \left( \rho _2+\rho _4-\rho _5\right) -d_2 \left( \rho _8+\rho _9\right) =0 \end{aligned}$$
(8)

and

$$\begin{aligned} 4 d_1 \kappa \rho _1-d_2 \rho _7=0 . \end{aligned}$$
(9)

Utilizing some abbreviations, Eq. (5) can be reformulated as follows:

$$\begin{aligned}&M _1 P +M _2 P^3 +M _3 P^5 +M _4 P \left( P'\right) ^2 \nonumber \\&\quad +M _5 P'' +M _6 P^2 P'' +P^{(4)} =0 \end{aligned}$$
(10)

where

$$\begin{aligned} \begin{array}{l} \displaystyle M_1=-\frac{\alpha \kappa +a \kappa ^2+(b \kappa -1) \left( \sigma ^2-\omega \right) +\kappa ^3 \left( d_2 \rho _7-d_1 \kappa \rho _1\right) }{d_1 \rho _1}, \\ \\ \displaystyle M_2=\frac{c-\kappa \lambda -d_1 \kappa ^2 \left( \rho _2-\rho _3+\rho _4+\rho _5\right) +d_2 \kappa \left( \rho _8-\rho _9\right) }{d_1 \rho _1}, \\ \\ \displaystyle M_3=\frac{\rho _6}{\rho _1}, \quad M_4=\frac{\rho _2+\rho _3}{\rho _1}, \\ \displaystyle M_5=\frac{a-b v-6 d_1 \kappa ^2 \rho _1+3 d_2 \kappa \rho _7}{d_1 \rho _1}, \quad M_6=\frac{\rho _4+\rho _5}{\rho _1}. \end{array} \end{aligned}$$
(11)

Eq. (10) will now be examined to derive a variety of analytical solutions to the governing model.

3 Multi-wave solutions

By means of the transformation

$$\begin{aligned} P=2 \left( \ln \psi \right) _\xi \end{aligned}$$
(12)

one converts Eq. (10) into

$$\begin{aligned}&M_1 \psi ^4 \psi ' +2 \left( 2 M_2+M_5\right) \psi ^2 \left( \psi ' \right) ^3 \nonumber \\&\quad +4 \left( 4 M_3+M_4+2 M_6+6\right) \left( \psi ' \right) ^5 -3 M_5 \psi ^3 \psi ' \psi '' \nonumber \\&\quad -4 \left( 2 M_4+3\left( M_6+5\right) \right) \psi \left( \psi '\right) ^3 \psi '' \nonumber \\&\quad +2 \left( 2 M_4+15\right) \psi ^2 \psi ' \left( \psi ''\right) ^2 +M_5 \psi ^4 \psi ^{(3)} \nonumber \\&\quad +4 \left( M_6+5\right) \psi ^2 \left( \psi '\right) ^2 \psi ^{(3)} -10\psi ^3 \psi '' \psi ^{(3)}\nonumber \\&\quad -5 \psi ^3 \psi ' \psi ^{(4)} +\psi ^4 \psi ^{(5)} =0 . \end{aligned}$$
(13)

The chosen assumption for deriving multi-wave solutions to the model is [42,43,44,45,46]:

$$\begin{aligned} \psi&= \varrho _1 \cosh \left( \chi _1 \xi +\chi _2\right) +\varrho _2 \cos \left( \chi _3 \xi +\chi _4\right) \nonumber \\&\quad \;\; +\varrho _3 \cosh \left( \chi _5 \xi +\chi _6\right) \end{aligned}$$
(14)

where \(\chi _j\) for \(1\le j \le 6\) are constants. Substituting (14) into (13), collecting the coefficients of \(\sinh \left( \chi _1 \xi +\chi _2\right) \), \(\cosh \left( \chi _1 \xi +\chi _2\right) \), \(\sin \left( \chi _3 \xi +\chi _4\right) \), \(\cos \left( \chi _3 \xi +\chi _4\right) \), \(\sinh \left( \chi _5 \xi +\chi _6\right) \), \(\cosh \left( \chi _5 \xi +\chi _6\right) \), and then working with the resulting system, one can uncover various sets of solutions.

  1. (i)

    The first solution set is

    $$\begin{aligned} \displaystyle M_3&= -\frac{M_1+4 M_2 \chi _1^2}{16 \chi _1^4} ,\quad \nonumber \\ M_5&= \frac{M_1 + 4 \left( M_4+4\right) \chi _1^4}{2 \chi _1^2} ,\quad M_6\nonumber \\&\quad = \frac{1}{8} \left( \frac{M_1}{\chi _1^4}+\frac{4 M_2}{\chi _1^2}-4 \left( M_4+6\right) \right) ,\nonumber \\&\quad \chi _3= i \epsilon \chi _1 ,\quad \varrho _3= 0 . \end{aligned}$$
    (15)

    The obtained results are inserted into (14), and the hypothesis (2) along with the transformation (12) are taken into account. Then, this process leads to deriving the rational multi-wave solution to the model (1) as

    $$\begin{aligned}&q(x, t) \nonumber \\ {}&= \frac{2 \chi _1 \!\left[ \varrho _1 \sinh \left( \chi _1 \xi \!+\!\chi _2\right) \! +\epsilon \! \varrho _2 \sinh \left( \epsilon \chi _1 \xi -i \chi _4\right) \right] }{\varrho _1 \cosh \left( \chi _1 \xi +\chi _2\right) +\varrho _2 \cosh \left( \epsilon \chi _1 \xi -i \chi _4\right) } \nonumber \\&\quad \;\; \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
    (16)

    This solution exists for \(\chi _4=i \beta _1\), \(\beta _1 \in {\mathbb {R}}.\)

  2. (ii)

    The second solution set is

    $$\begin{aligned}&\displaystyle M_3= -\frac{M_1 + 4 M_2 \chi _1^2}{16 \chi _1^4},\nonumber \\ {}&M_5= \frac{M_1 + 4 \left( M_4+4\right) \chi _1^4}{2 \chi _1^2}, \nonumber \\&M_6 = \frac{1}{8} \left( \frac{M_1}{\chi _1^4}+\frac{4 M_2}{\chi _1^2}-4 \left( M_4+6\right) \right) ,\nonumber \\ {}&\quad \chi _5= \epsilon \chi _1 ,\quad \varrho _2= 0 . \end{aligned}$$
    (17)

    These outcomes lead to the recovery of

    $$\begin{aligned}&q(x, t)\nonumber \\ {}&= \frac{2 \chi _1 \left[ \varrho _1 \sinh \!\left( \chi _1 \xi \!+\!\chi _2\right) \!+\!\epsilon \varrho _3\! \sinh \left( \epsilon \chi _1 \xi \!+ \chi _6 \right) \right] }{\varrho _1 \cosh \left( \chi _1 \xi +\chi _2\right) +\varrho _3 \cosh \left( \epsilon \chi _1 \xi + \chi _6 \right) } \nonumber \\&\quad \;\; \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
    (18)
  3. (iii)

    The third solution set is

    $$\begin{aligned} \displaystyle M_3&= -\frac{M_1-4 M_2 \chi _3^2}{16 \chi _3^4} ,\quad \nonumber \\ {}&M_5= -\frac{M_1 + 4 \left( M_4+4\right) \chi _3^4}{2 \chi _3^2} ,\quad M_6\nonumber \\&= \frac{1}{8} \left( \frac{M_1}{\chi _3^4}-\frac{4 M_2}{\chi _3^2}-4 \left( M_4+6\right) \right) ,\nonumber \\ {}&\quad \chi _5= i \epsilon \chi _3 ,\quad \varrho _1= 0 . \end{aligned}$$
    (19)

    Considering these results, the subsequent solution to the governing equation is formulated as

    $$\begin{aligned}&q(x, t) \nonumber \\ {}&= -\frac{2 \chi _3 \left[ \varrho _2 \sin \!\left( \chi _3 \xi \!+\!\chi _4\right) \!+\!\epsilon \varrho _3 \!\sin \left( \epsilon \chi _3 \xi -i \chi _6\right) \right] }{\varrho _2 \cos \left( \chi _3 \xi +\chi _4\right) +\varrho _3 \cos \left( \epsilon \chi _3 \xi -i \chi _6\right) }\nonumber \\&\qquad \qquad \;\;\; \exp \left[ i \left( - \kappa x \!+\! \omega t \!+\! \sigma W(t) -\sigma ^2 t\! +\! \theta \right) \right] . \end{aligned}$$
    (20)

    The existence condition for this solution is \(\chi _6=i \beta _2\), \(\beta _2 \in {\mathbb {R}}.\)

  4. (iv)

    The fourth solution set is

    $$\begin{aligned} \displaystyle&M_3= -\frac{M_1 + 4 M_2 \chi _5^2}{16 \chi _5^4},\nonumber \\&M_5= \frac{M_1 + 4 \left( M_4+4\right) \chi _5^4}{2 \chi _5^2}, \nonumber \\&M_6= \frac{1}{8} \left( \frac{M_1}{\chi _5^4}+\frac{4 M_2}{\chi _5^2}-4 \left( M_4+6\right) \right) ,\nonumber \\ {}&\quad \chi _1= \chi _5 ,\quad \chi _3= i \epsilon \chi _5 . \end{aligned}$$
    (21)

    Under this circumstance, the rational multi-wave solution takes form as

    $$\begin{aligned}&q(x, t) = \frac{2 \chi _5 \left[ \varrho _1 \sinh \!\left( \chi _5 \xi \!+\!\chi _2\right) \!+\! \epsilon \varrho _2 \!\sinh \left( \epsilon \chi _5 \xi - i \chi _4 \right) +\varrho _3 \sinh \left( \chi _5 \xi +\chi _6\right) \right] }{\varrho _1 \cosh \left( \chi _5 \xi +\chi _2\right) +\varrho _2 \cosh \left( \epsilon \chi _5 \xi - i \chi _4 \right) +\varrho _3 \cosh \left( \chi _5 \xi +\chi _6\right) } \nonumber \\&\qquad \qquad \quad \; \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] \end{aligned}$$
    (22)

    which introduces the constraint \(\chi _4=i \beta _1\), \(\beta _1 \in {\mathbb {R}}.\) Also, it should be pointed out that \(\epsilon \) equals \(\pm 1\) in all solution sets.

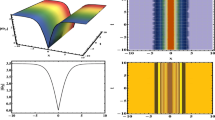
Figure 1 illustrates the dynamical properties of rational multi-waves solution (22). In the (x, t)-plane, Fig. 1a, b, and c depict the 3D graphs, while Fig. 1d, e, and f enumerate the corresponding contour diagrams of Fig. 1a, b, and c. The chosen parameter values are \( v = 3.4,\ \epsilon = -1,\ \theta = 5,\ \kappa = 1.5,\ \varrho _1= 5,\ \varrho _2= 2,\ \varrho _3= 7,\ \chi _2= 9,\ \chi _4= 12 i,\ \chi _6= 3,\ W(t)= \frac{\sigma }{2} t \) when \( \sigma = 0,\ \chi _5= 2.6,\ \omega = 0.5 \) in (a) and (d), \( \sigma = 3,\ \chi _5= 0.2,\ \omega = 2.5 \) in (b) and (e), \( \sigma = 10,\ \chi _5=-0.1,\ \omega =5.8 \) in (c) and (f). The graphical presentation of the multi-wave solution given by Eq. (22) is depicted in Fig. 1. The influence of the noise effect \(\sigma \) and the parameters \(\chi _5\) and \(\omega \) on the behavior of the solution is examined, as can be seen from the chosen parameter values. It should be noted that Fig. 1a and d are simulated in the case of \((\sigma =0)\), while Fig. 1b, c, e, and f are depicted in the case of \(\sigma \ne 0\). Also, the examination range for these graphics is set as \(-5 \le x \le 5\) and \(-5 \le t \le 5\).

Fig. 1
figure 1

Dynamical behavior of solution (22)

Full size image

4 Exponential form

When recovering interactional solutions, the double exponential function is picked as follows [44,45,46]:

$$\begin{aligned} \psi = \varrho _1 \exp \left( \chi _1 \xi +\chi _2 \right) +\varrho _2 \exp \left( \chi _3 \xi +\chi _4 \right) \end{aligned}$$
(23)

where \(\chi _j\) with \(1\le j \le 4\) are constants. Putting (23) into (13) and subsequently setting the coefficients of \(\exp \left( \chi _1 \xi +\chi _2\right) \), \(\exp \left( \chi _3 \xi +\chi _4\right) \), and other terms to zero, the following sets of solutions are identified by overcoming the resulting system of equations:

Set-1.

$$\begin{aligned}&\displaystyle M_1= 2 \chi _1^2 \left[ M_5 \!+\! 4 \left( 2 M_3+M_6+1\right) \chi _1^2\right] ,\quad \nonumber \\&\quad \;\; M_2= -\frac{M_5}{2} -2 \left( 4 M_3+M_6+1\right) \chi _1^2 , \nonumber \\&\quad M_4= -2 \left( 2 M_3+M_6+3\right) ,\quad \chi _3= -\chi _1. \end{aligned}$$
(24)

Utilizing these parameter values within (23), and considering (2) along with (12), the multi-wave interactional solution is revealed as follows:

$$\begin{aligned}&q(x, t) = \frac{2 \chi _1 \left[ \varrho _1 \exp (\chi _1 \xi \! +\chi _2) \!-\! \varrho _2 \exp (\chi _4\!-\! \chi _1 \xi )\right] }{\varrho _1 \exp (\chi _1 \xi \!+\chi _2) \!+\varrho _2 \exp (\chi _4- \chi _1 \xi )}\nonumber \\&\qquad \qquad \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(25)

Set-2.

$$\begin{aligned} \displaystyle M_1&= \frac{16}{9} M_3 \chi _1^4 \Bigg [32 M_3 \left( 4 M_3-3\right) +9 \nonumber \\ {}&\quad + 8 \left( 3-8 M_3\right) \sqrt{M_3 \left( 4 M_3-3\right) }\Bigg ], \nonumber \\ \displaystyle M_2&= -\frac{8}{9} M_3 \left( 8 M_3-3\right) \chi _1^2\nonumber \\&\quad \left[ 8 M_3-3 -4 \sqrt{M_3 \left( 4 M_3-3\right) }\right] , \nonumber \\ \displaystyle M_4&= 12 \left( M_3-1\right) ,\quad M_5= -\frac{4}{9} \left( 4 M_3-9\right) \chi _1^2 \nonumber \\ {}&\quad \left[ 8 M_3-3 -4 \sqrt{M_3 \left( 4 M_3-3\right) }\right] , \nonumber \\ \displaystyle M_6&= 3-8 M_3 ,\quad \chi _3= \frac{1}{3} \chi _1\nonumber \\&\quad \left[ 3-8 M_3 +4 \sqrt{M_3 \left( 4 M_3-3\right) }\right] . \end{aligned}$$
(26)

The solution derived from the second set of parameters for the model in question is

$$\begin{aligned} q(x, t) =&\frac{2 \chi _1 \left[ 3\varrho _1 \exp (\chi _1 \xi \!+\!\chi _2) \!+\! \varrho _2 \left( 3-8 M_3\!+\!4 \sqrt{M_3 \left( 4 M_3\!-\!3\right) }\right) \! \exp \left( \frac{1}{3} \left[ 3-8 M_3\!+\!4 \sqrt{M_3 \left( 4 M_3\!-3\right) }\right] \chi _1 \xi \!+\!\chi _4\right) \right] }{3 \left[ \varrho _1 \exp [\chi _1 \xi \!+\chi _2] \!+\! \varrho _2 \exp \left( \frac{1}{3} \left[ 3-8 M_3+4 \sqrt{M_3 \left( 4 M_3-3\right) }\right] \chi _1 \xi +\chi _4\right) \right] } \nonumber \\&\times \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(27)

This solitary wave solution will exist provided \(M_3 \left( 4 M_3-3\right) >0\) holds.

The dynamic behaviors of Solution (27) are displayed in Fig. 2. In the (x, t)-plane, Fig. 2a, b, and c demonstrate the 3D graphs, while Fig. 2d, e, and f are the corresponding contour diagrams of Fig. 2a, b, and c. The picked parameter values are \( v= 0.7,\ \theta = 1,\ \kappa = 1.5,\ \varrho _1= 2,\ \varrho _2= 5,\ \chi _2= 3,\ \chi _4= -4,\ M_3= 1.4,\ W(t)= \frac{\sigma }{2} t \) when \( \sigma = 0,\ \chi _1= -1.5,\ \omega = 9 \) in (a) and (d), \( \sigma = 4,\ \chi _1= -0.9,\ \omega = 6 \) in (b) and (e), \( \sigma = 10,\ \chi _1= -3.5,\ \omega = 25 \) in (c) and (f). The interaction phenomenon of two solitary waves, as depicted by Fig. 2, is discussed along with the influence of the noise effect \(\sigma \) and the parameters \(\chi _1\) and \(\omega \) on the behavior of the solution. Also, the examination range is set as \(-5 \le x \le 5\) and \(-5 \le t \le 5\).

Fig. 2
figure 2

Dynamical behavior of solution (27)

Full size image

5 Homoclinic breather approach

Breather wave hypothesis is represented by [42,43,44]

$$\begin{aligned} \psi&= \exp \left[ -\varpi \left( \chi _1 \xi +\chi _2\right) \right] +\varrho _1 \exp \left[ \varpi \left( \chi _3 \xi +\chi _4\right) \right] \nonumber \\&\quad \;+\varrho _2 \cos \left[ \varpi _1 \left( \chi _5 \xi +\chi _6\right) \right] \end{aligned}$$
(28)

or equivalently

$$\begin{aligned}&\psi = \sinh \left[ -\varpi \left( \chi _1 \xi +\chi _2\right) \right] + \cosh \left[ -\varpi \left( \chi _1 \xi +\chi _2\right) \right] \nonumber \\ {}&\quad \quad +\varrho _1 \sinh \left[ \varpi \left( \chi _3 \xi +\chi _4\right) \right] \nonumber \\&\quad \quad +\varrho _1 \cosh \left[ \varpi \left( \chi _3 \xi +\chi _4\right) \right] \nonumber \\&\quad \quad +\varrho _2 \cos \left[ \varpi _1 \left( \chi _5 \xi +\chi _6\right) \right] \end{aligned}$$
(29)

where \(\chi _j\) \((1\le j \le 6)\) are constants. Inserting (29) into (13), collecting the coefficients of each power of \(\sinh \left[ \varpi \left( \chi _1 \xi +\chi _2\right) \right] \), \(\cosh \left[ \varpi \left( \chi _1 \xi +\chi _2\right) \right] \), \(\sinh \left[ \varpi \left( \chi _3 \xi +\chi _4\right) \right] \), \(\cosh \left[ \varpi \left( \chi _3 \xi +\chi _4\right) \right] \), \(\sin \left[ \varpi _1 \left( \chi _5 \xi +\chi _6\right) \right] \), \(\cos \left[ \varpi _1 \left( \chi _5 \xi +\chi _6\right) \right] \), as well as other terms, and solving the system of coefficients yields the following:

  1. (i)

    The first set is

    $$\begin{aligned} \begin{array}{l} \displaystyle M_2= \left( M_4+2 M_6+6\right) \chi _1^2 \varpi ^2-\frac{M_1}{4 \chi _1^2 \varpi ^2} ,\\ M_3= -\frac{1}{4} \left[ M_4+2 \left( M_6+3\right) \right] , \\ \\ \displaystyle M_5= \frac{M_1 + 4 \left( M_4+4\right) \chi _1^4 \varpi ^4}{2 \chi _1^2 \varpi ^2} ,\\ \varrho _1= 0 ,\quad \chi _5= \frac{i \epsilon \chi _1 \varpi }{\varpi _1}. \end{array} \end{aligned}$$
    (30)

    By substituting (30) into (29), and employing (2) along with (12), the breather solution emerges as

    $$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \varpi \left[ \epsilon \varrho _2 \exp [\varpi \left( \chi _1 \xi +\chi _2\right) ] \sinh \left( \epsilon \chi _1 \varpi \xi -i \chi _6 \varpi _1\right) -1 \right] }{\varrho _2 \exp [\varpi \left( \chi _1 \xi +\chi _2\right) ] \cosh \left( \epsilon \chi _1 \varpi \xi -i \chi _6 \varpi _1\right) + 1}\nonumber \\&\quad \quad \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
    (31)
  2. (ii)

    The second set is

    $$\begin{aligned}&\displaystyle M_2= -\frac{13 M_1+280 \chi _1^4 \varpi ^4}{66 \chi _1^2 \varpi ^2} ,\nonumber \\&M_3= \frac{7}{528} \left( 80-\frac{M_1}{\chi _1^4 \varpi ^4}\right) ,\nonumber \\&M_4= \frac{8}{3}-\frac{7 M_1}{12 \chi _1^4 \varpi ^4} , \nonumber \\&\displaystyle M_5= \frac{2 \left( 20 \chi _1^4 \varpi ^4-M_1\right) }{3 \chi _1^2 \varpi ^2} ,\nonumber \\ {}&M_6= \frac{7 M_1}{22 \chi _1^4 \varpi ^4}-\frac{71}{11} ,\nonumber \\ {}&\chi _3= \chi _1 ,\quad \chi _5= \frac{i \epsilon \chi _1 \varpi }{\varpi _1}. \end{aligned}$$
    (32)

    Continuing in the same manner, the following solution is established:

    $$\begin{aligned} q(x, t) =&\frac{2 \chi _1 \varpi \left[ -\exp [-\varpi \left( \chi _1 \xi +\chi _2\right) ] +\varrho _1 \exp [\varpi \left( \chi _1 \xi +\chi _4\right) ] +\epsilon \varrho _2 \sinh \left( \epsilon \chi _1 \varpi \xi -i\chi _6 \varpi _1\right) \right] }{\exp [-\varpi \left( \chi _1 \xi +\chi _2\right) ] +\varrho _1 \exp [\varpi \left( \chi _1 \xi +\chi _4\right) ] +\varrho _2 \cosh \left( \epsilon \chi _1 \varpi \xi -i \chi _6 \varpi _1\right) } \nonumber \\&\; \times \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
    (33)

    Here, in all sets of solutions, \(\epsilon = \pm 1\). It should also be emphasized that the solutions provided by Eqs. (31) and (33) are valid for \(\chi _6=i \beta \), \(\beta \in {\mathbb {R}}.\)

Figure 3 presents the physical structure of breather solution (33). In the (x, t)-plane, Fig. 3a, b, and c show the 3D graphs, while Fig. 3a, e, and f list the corresponding contour diagrams of Fig. 3a, b, and c. The chosen parameter values are \( v= 1.5,\ \epsilon = -1,\ \theta = 1,\ \kappa = 2,\ \varpi = 2.4,\ \varpi _1= 3,\ \varrho _1= 3,\ \varrho _2= -7,\ \chi _2= 9,\ \chi _4= 2,\ \chi _6= 5 i,\ W(t)= \frac{\sigma }{2} t \) when \( \sigma = 0,\ \chi _1= -0.7,\ \omega = 1.2 \) in (a) and (d), \( \sigma = 5,\ \chi _1= -0.9,\ \omega = 3.6 \) in (b) and (e), \( \sigma = 10,\ \chi _1= 1.7,\ \omega = 6.3 \) in (c) and (f). The dynamical behavior of breather waves provided by Eq. (33) is displayed in Fig. 3. Considering the same examination range in Sects. 3 and 4, the graphical presentations for the case \(\sigma =0\) are demonstrated in Fig. 3a and d, while Figs. 3b, c, e, and f stand for the case \(\sigma \ne 0\). The influence of the parameters \(\chi _1\) and \(\omega \) on the behavior of the solution is also investigated.

6 Periodic cross kink solution

The derivation of a periodic cross kink solution to the concatenation model with multiplicative white noise is enabled by the following assumption [47, 48]:

$$\begin{aligned} \psi&= \exp \left( \chi _1 \xi +\chi _2 \right) + \varrho _1 \exp \left[ - (\chi _1 \xi +\chi _2) \right] \nonumber \\ {}&\quad \; +\varrho _2 \cos \left( \chi _3 \xi +\chi _4\right) \nonumber \\&\quad \; +\varrho _3 \cosh \left( \chi _5 \xi +\chi _6\right) + \varrho _4 \end{aligned}$$
(34)
Fig. 3
figure 3

Dynamical behavior of solution (33)

Full size image

where \(\chi _j\) for \(1\le j \le 6\) are constants. Plugging (34) into (13), collecting the coefficients of \(\exp \left( \chi _1 \xi +\chi _2 \right) \), \(\exp \left[ - (\chi _1 \xi +\chi _2) \right] \), \(\cos \left( \chi _3 \xi +\chi _4\right) \), \(\sin \left( \chi _3 \xi +\chi _4\right) \), \(\cosh \left( \chi _5 \xi +\chi _6\right) \), \(\sinh \left( \chi _5 \xi +\chi _6\right) \), and other terms, setting them equal to zero, and solving the resulting system leads to:

Case-1.

$$\begin{aligned} \displaystyle&M_2= -\frac{M_1+ 16 M_3 \chi _1^4}{4 \chi _1^2} ,\quad \nonumber \\&M_5= \frac{M_1+4 \left( M_4+4\right) \chi _1^4}{2 \chi _1^2} ,\nonumber \\&M_6= -2 M_3-\frac{M_4}{2}-3 ,\nonumber \\ {}&\varrho _1=\varrho _2=\varrho _4= 0 ,\quad \chi _5= \epsilon \chi _1 . \end{aligned}$$
(35)

Based on these outcomes, one secures the solution

$$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \left[ \exp (\chi _1 \xi +\chi _2) \!+\!\epsilon \varrho _3 \sinh \left( \epsilon \chi _1 \xi \!+\! \chi _6 \right) \right] }{\exp (\chi _1 \xi \!+\!\chi _2) \!+\varrho _3 \cosh \left( \epsilon \chi _1 \xi + \chi _6 \right) } \nonumber \\&\quad \quad \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(36)

Case-2.

$$\begin{aligned} \displaystyle&M_2= -\frac{M_1 + 16 M_3 \chi _1^4}{4 \chi _1^2},\nonumber \\ {}&M_5= \frac{M_1\! +\! 4 \left( M_4+4\right) \chi _1^4}{2 \chi _1^2} ,\quad \nonumber \\&M_6= -2 M_3-\frac{M_4}{2}-3 ,\quad \varrho _2=\varrho _4= 0 ,\nonumber \\ {}&\quad \chi _5= \epsilon \chi _1 . \end{aligned}$$
(37)

In this case, the solution is expressed as

$$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \left[ \exp (\chi _1 \xi +\chi _2) \left[ \exp (\chi _1 \xi +\chi _2) +\epsilon \varrho _3 \sinh \left( \epsilon \chi _1 \xi + \chi _6\right) \right] -\varrho _1\right] }{\exp ( \chi _1 \xi +\chi _2) \left[ \exp (\chi _1 \xi +\chi _2) +\varrho _3 \cosh \left( \epsilon \chi _1 \xi + \chi _6 \right) \right] +\varrho _1} \nonumber \\&\quad \quad \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(38)

Case-3.

$$\begin{aligned}{} & {} \displaystyle M_2= -\frac{ M_1 + 16 M_3 \chi _1^4}{4 \chi _1^2} ,\quad \nonumber \\{} & {} M_5= \frac{M_1 + 4 \left( M_4+4\right) \chi _1^4}{2 \chi _1^2} ,\quad \nonumber \\ {}{} & {} M_6= -2 M_3-\frac{M_4}{2}-3 , \nonumber \\{} & {} \displaystyle \varrho _1=\varrho _4= 0 ,\quad \chi _3= i \chi _1 ,\quad \chi _5= \epsilon \chi _1 . \end{aligned}$$
(39)

This in turn gives rise to

$$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \left[ \exp (\chi _1 \xi +\chi _2) +\varrho _2 \sinh \left( \chi _1 \xi -i \chi _4\right) +\epsilon \varrho _3 \sinh \left( \epsilon \chi _1 \xi + \chi _6 \right) \right] }{\exp (\chi _1 \xi +\chi _2) +\varrho _2 \cosh \left( \chi _1 \xi -i \chi _4\right) +\varrho _3 \cosh \left( \epsilon \chi _1 \xi + \chi _6 \right) } \nonumber \\&\quad \quad \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(40)

Case-4.

$$\begin{aligned} \displaystyle M_2= & {} {-}\frac{M_1+ 16 M_3 \chi _1^4}{4 \chi _1^2} ,\quad M_5{=} \frac{M_1 {+} 4 \left( M_4+4\right) \chi _1^4}{2 \chi _1^2} ,\nonumber \\ M_6= & {} -2 M_3-\frac{M_4}{2}-3 ,\quad \varrho _4= 0 ,\quad \chi _3= i \chi _1 , \nonumber \\ \chi _5= & {} \epsilon \chi _1 . \end{aligned}$$
(41)

By the help of this set of parameters, it is discovered that

$$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \left[ \exp (\chi _1 \xi +\chi _2) \left[ \exp (\chi _1 \xi +\chi _2) +\varrho _2 \sinh \left( \chi _1 \xi -i \chi _4\right) +\epsilon \varrho _3 \sinh \left( \epsilon \chi _1 \xi + \chi _6 \right) \right] -\varrho _1 \right] }{ \exp (\chi _1 \xi +\chi _2) \left[ \exp (\chi _1 \xi +\chi _2) +\varrho _2 \cosh \left( \chi _1 \xi -i \chi _4\right) +\varrho _3 \cosh \left( \epsilon \chi _1 \xi + \chi _6 \right) \right] + \varrho _1} \nonumber \\&\quad \quad \times \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(42)

In all solution sets presented here, \(\epsilon \) equals \(\pm 1\). Also, it is important to highlight that the solutions (40) and (42) will exist as long as the considered equation satisfies the condition \(\chi _4=i \beta \ (\beta \in {\mathbb {R}})\), which stands as the requisite condition for the existence of solutions.

The propagation characteristics of Solution (42) are illustrated in Fig. 4. In the (x, t)-plane, Fig. 4a, b, and c demonstrate the 3D graphs, while Fig. 4d, e, and f are the corresponding contour diagrams of Fig. 4a, b, and c. The parameter values that are taken in this case are \( v= 0.8,\ \epsilon = -1,\ \theta = 1,\ \kappa = 0.5,\ \varrho _1= -7.5,\ \varrho _2= 3.9,\ \varrho _3= -25.8,\ \chi _2= 6,\ \chi _4= 17 i,\ \chi _6= 5,\ W(t)= \frac{\sigma }{2} t \) when \( \sigma = 0,\ \chi _1= 2.6,\ \omega = 3.7 \) in (a) and (d), \( \sigma = 4,\ \chi _1= 5.2,\ \omega = 43 \) in (b) and (e), \( \sigma = 10,\ \chi _1= -1.9,\ \omega = 41 \) in (c) and (f). The dynamic behaviors of the periodic cross kink solution (42) are analyzed for various values of the parameters \(\sigma \), \(\chi _1\), and \(\omega \).

Fig. 4
figure 4

Dynamical behavior of solution (42)

Full size image

7 Peregrine-like rational solitons

The adopted assumption for this solution form is [45, 49]

$$\begin{aligned} \psi =\left( \chi _1 \xi +\chi _2\right) ^2+\left( \chi _3 \xi +\chi _4\right) ^2+\chi _5 \end{aligned}$$
(43)

where \(\chi _j\) with \(1\le j \le 5\) are constants. Inserting (43) into (13) yields the following results:

  1. (i)
    $$\begin{aligned}{} & {} \displaystyle M_1= 0 ,\quad M_3= -\frac{1}{32} \left( 2 M_4+4 M_6+3\right) ,\quad \nonumber \\{} & {} M_5= -8 M_2 , \nonumber \\{} & {} \chi _5 = -\frac{\left( \chi _2 \chi _3-\chi _1 \chi _4\right) ^2}{\chi _1^2+\chi _3^2} . \end{aligned}$$
    (44)

    Using these results in (43), and considering (2) along with (12) brings about the solution

    $$\begin{aligned} q(x, t)&= \frac{4 \left( \chi _1^2+\chi _3^2\right) }{\chi _1^2 \xi +\chi _3 \left( \chi _3 \xi +\chi _4\right) + \chi _1 \chi _2 }\nonumber \\&\quad \;\; \exp \left[ i \left( {-} \kappa x {+} \omega t {+} \sigma W(t) {-}\sigma ^2 t {+} \theta \right) \right] . \end{aligned}$$
    (45)
  2. (ii)
    $$\begin{aligned}{} & {} \displaystyle M_1= 0 ,\quad M_3= -\frac{1}{32} \left( 2 M_4+4 M_6+3\right) ,\quad M_5\nonumber \\{} & {} \quad \;\; = -8 M_2 ,\quad \chi _2= -\frac{\chi _3 \chi _4}{\chi _1} ,\quad \nonumber \\{} & {} \chi _5= -\frac{\left( \chi _1^2+\chi _3^2\right) \chi _4^2}{\chi _1^2}. \end{aligned}$$
    (46)

    From these results, one explores

    $$\begin{aligned} q(x, t) {=} \frac{4}{\xi } \exp \left[ i \left( {-} \kappa x {+} \omega t {+} \sigma W(t) {-}\sigma ^2 t {+} \theta \right) \right] .\nonumber \\ \end{aligned}$$
    (47)
  3. (iii)
    $$\begin{aligned}{} & {} \displaystyle M_1= 0 ,\quad \nonumber \\{} & {} M_3= \frac{1}{8} \left[ 3 - M_2 \left( \frac{2 \chi _4^2}{\chi _1^2}+\frac{2 \chi _5}{\chi _1^2+\chi _3^2}\right) \right] ,\quad \nonumber \\{} & {} M_4= -\frac{15}{2} - M_2 \left( \frac{3 \chi _4^2}{\chi _1^2}+\frac{3 \chi _5}{\chi _1^2+\chi _3^2}\right) , \nonumber \\ \nonumber \\{} & {} \displaystyle M_5{=} {-}8 M_2 ,\quad M_6{=} 2 M_2 \left( \frac{\chi _4^2}{\chi _1^2}+\frac{\chi _5}{\chi _1^2+\chi _3^2}\right) ,\quad \nonumber \\{} & {} \chi _2= -\frac{\chi _3 \chi _4}{\chi _1}. \end{aligned}$$
    (48)

    This results in the following solution:

    $$\begin{aligned} q(x, t){} & {} = \frac{4 \chi _1^2 \left( \chi _1^2+\chi _3^2\right) \xi }{\left( \chi _1^2+\chi _3^2\right) \left( \chi _1^2 \xi ^2 +\chi _4^2\right) + \chi _1^2 \chi _5 } \nonumber \\{} & {} \quad \;\; \exp \left[ i \left( - \kappa x + \omega t \right. \right. \nonumber \\{} & {} \quad \left. \left. + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
    (49)
  4. (iv)
    $$\begin{aligned}{} & {} \displaystyle M_1= 0 ,\quad M_3= \frac{3 \chi _1^4+4 M_2 \chi _1 \chi _2 \chi _3 \chi _4 +\chi _3^2 \left[ 3 \chi _3^2-2 M_2 \left( \chi _2^2+\chi _5\right) \right] -2 \chi _1^2 \left[ M_2 \left( \chi _4^2+\chi _5\right) -3 \chi _3^2\right] }{8 \left( \chi _1^2+\chi _3^2\right) ^2}, \nonumber \\ \nonumber \\{} & {} \displaystyle M_4= -\frac{3 \left( 5 \chi _1^4 -4M_2 \chi _1 \chi _2 \chi _3 \chi _4 +\chi _3^2 \left[ 5\chi _3^2 + 2 M_2 \left( \chi _2^2+\chi _5\right) \right] + 2 \chi _1^2 \left[ 5 \chi _3^2 + M_2 \left( \chi _4^2+\chi _5\right) \right] \right) }{2 \left( \chi _1^2+\chi _3^2\right) ^2} , \nonumber \\ \nonumber \\{} & {} \displaystyle M_5= -8 M_2 ,\quad M_6= \frac{2 M_2 \left[ \left( \chi _2 \chi _3-\chi _1 \chi _4\right) ^2+\left( \chi _1^2+\chi _3^2\right) \chi _5\right] }{\left( \chi _1^2+\chi _3^2\right) ^2} . \end{aligned}$$
    (50)

Taking these results into consideration, the governing equation possesses the solution

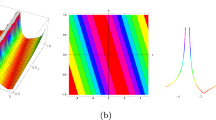
$$\begin{aligned} q(x, t)&= \frac{4 \left[ \chi _1 \left( \chi _1 \xi +\chi _2\right) + \chi _3 \left( \chi _3 \xi +\chi _4\right) \right] }{\left( \chi _1 \xi +\chi _2\right) ^2+\left( \chi _3 \xi +\chi _4\right) ^2+\chi _5}\nonumber \\&\quad \;\; \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(51)

Figure 5 provides the dynamical behavior of Peregrine-like rational solution (51). In the (x, t)-plane, Fig. 5a, b, and c exhibit the 3D graphs, while Fig. 5d, e, and f enumerate the corresponding contour diagrams of Fig. 5a, b, and c. In this case, the values of the parameters are \( v= 1.1,\ \theta = 3,\ \kappa = 0.7,\ \chi _2= 3,\ \chi _4= 7,\ W(t)= \frac{\sigma }{2} t \) when \( \sigma = 0,\ \chi _1= 4.2,\ \chi _3= 3.4,\ \chi _5= -125,\ \omega = 4 \) in (a) and (d), \( \sigma = 2,\ \chi _1= 2.4,\ \chi _3= -6.5,\ \chi _5= 7,\ \omega = 1.5 \) in (b) and (e), \( \sigma = 10,\ \chi _1= 4.7,\ \chi _3= 16.4,\ \chi _5= 75,\ \omega = 53 \) in (c) and (f).

Fig. 5
figure 5

Dynamical behavior of solution (51)

Full size image

From Fig. 5d, e, and f, one can clearly see that the pulse profile remains unchanged during evolution. This is one of the important properties of soliton, which is highly desired in practical applications.

8 Three-wave solutions

Based on the three-wave approach, the solution is structured as [50]

$$\begin{aligned} \psi&= \varrho _1 \exp \left( \chi _1 \xi +\chi _2 \right) + \exp \left[ - (\chi _1 \xi +\chi _2) \right] \nonumber \\&\quad \; +\varrho _2 \cos \left( \chi _3 \xi +\chi _4\right) +\varrho _3 \sin \left( \chi _5 \xi +\chi _6\right) \end{aligned}$$
(52)

where \(\chi _j\) \((1\le j \le 6)\) are constants. Inserting (52) into (13) and collecting the coefficients of \(\exp \left( \chi _1 \xi +\chi _2 \right) \), \(\exp \left[ - (\chi _1 \xi +\chi _2) \right] \), \(\cos \left( \chi _3 \xi +\chi _4\right) \), \(\sin \left( \chi _3 \xi +\chi _4\right) \), \(\cos \left( \chi _5 \xi +\chi _6\right) \), \(\sin \left( \chi _5 \xi +\chi _6\right) \), and other terms, and solving the resulting system, the following results are acquired:

Set-1.

$$\begin{aligned}{} & {} \displaystyle M_3= -\frac{M_1 + 4 M_2 \chi _1^2}{16 \chi _1^4} ,\quad \nonumber \\{} & {} M_4= \frac{M_1}{4 \chi _1^4}+\frac{M_2}{\chi _1^2}-2 M_6-6 ,\quad \nonumber \\{} & {} M_5= -4 \left( M_6+1\right) \chi _1^2+\frac{M_1}{\chi _1^2}+2 M_2 , \nonumber \\ \nonumber \\{} & {} \displaystyle \varrho _1=\varrho _2= 0 ,\quad \chi _5= i \epsilon \chi _1 . \end{aligned}$$
(53)

Putting these parameter values into (52), and utilizing (2) along with (12), one gets the solution given by

$$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \left[ \epsilon \varrho _3 \exp (\chi _1 \xi +\chi _2) \cosh \left( \epsilon \chi _1 \xi -i \chi _6\right) +i\right] }{\varrho _3 \exp (\chi _1 \xi +\chi _2) \sinh \left( \epsilon \chi _1 \xi -i \chi _6\right) -i} \nonumber \\&\quad \quad \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] .\nonumber \\ \end{aligned}$$
(54)

Set-2.

$$\begin{aligned} \displaystyle M_3&= -\frac{M_1 + 4 M_2 \chi _1^2}{16 \chi _1^4} ,\quad M_4= \frac{M_1}{4 \chi _1^4}+\frac{M_2}{\chi _1^2}\nonumber \\&\quad -2 M_6-6 ,\quad M_5= -4 \left( M_6+1\right) \chi _1^2+\frac{M_1}{\chi _1^2}\nonumber \\&\quad +2 M_2 ,\quad \varrho _2\nonumber \\&= 0 ,\quad \chi _5= i \epsilon \chi _1. \end{aligned}$$
(55)

From the solution set, it is procured that

$$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \left[ \varrho _1 \exp [2 \left( \chi _1 \xi +\chi _2\right) ] +i \epsilon \varrho _3 \exp (\chi _1 \xi +\chi _2) \cosh \left( \epsilon \chi _1 \xi -i \chi _6\right) -1\right] }{\varrho _1\exp [2 \left( \chi _1 \xi +\chi _2\right) ] +i \varrho _3 \exp (\chi _1 \xi +\chi _2) \sinh \left( \epsilon \chi _1 \xi -i \chi _6\right) +1} \nonumber \\&\quad \;\; \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(56)

From (54) and (56), it appears that these solutions remain valid as long as the constraint relations \(\varrho _3=i \beta _1\) and \(\chi _6=i \beta _2\) (\(\beta _1, \ \beta _2 \in {\mathbb {R}}\)) hold.

Set-3.

$$\begin{aligned} M_3{} & {} = -\frac{M_1+ 4 M_2 \chi _1^2}{16 \chi _1^4} ,\quad \nonumber \\ M_4{} & {} = \frac{M_1}{4 \chi _1^4}+\frac{M_2}{\chi _1^2}-2 M_6-6 ,\quad \nonumber \\ M_5{} & {} = -4 \left( M_6+1\right) \chi _1^2+\frac{M_1}{\chi _1^2}+2 M_2 , \nonumber \\{} & {} \varrho _1= 0 ,\quad \chi _3= i \chi _1 ,\quad \chi _5= i \epsilon \chi _1 . \end{aligned}$$
(57)

Then, the solution falls out as

$$\begin{aligned} q(x, t)&= \frac{2 \chi _1 \left[ \exp (\chi _1 \xi +\chi _2) \left[ \varrho _2 \sinh \left( \chi _1 \xi -i \chi _4\right) +i \epsilon \varrho _3 \cosh \left( \epsilon \chi _1 \xi -i \chi _6\right) \right] -1 \right] }{\exp (\chi _1 \xi +\chi _2) \left[ \varrho _2 \cosh \left( \chi _1 \xi -i\chi _4\right) +i \varrho _3 \sinh \left( \epsilon \chi _1 \xi -i \chi _6\right) \right] + 1} \nonumber \\&\quad \;\; \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(58)

Set-4.

$$\begin{aligned} \displaystyle M_3&= -\frac{ M_1+ 4 M_2 \chi _1^2}{16 \chi _1^4} ,\quad \nonumber \\ M_4&= \frac{M_1}{4 \chi _1^4}+\frac{M_2}{\chi _1^2}-2 M_6-6 ,\quad \nonumber \\ M_5&= -4 \left( M_6+1\right) \chi _1^2+\frac{M_1}{\chi _1^2}+2 M_2 ,\quad \chi _3= i \chi _1 ,\quad \nonumber \\ \chi _5&= i \epsilon \chi _1. \end{aligned}$$
(59)

Finally, these outcomes yield the following three-wave solution:

$$\begin{aligned} q(x, t) =&\frac{2 \chi _1 \left[ \exp (\chi _1 \xi +\chi _2) \left[ \varrho _1 \exp (\chi _1 \xi +\chi _2) +\varrho _2 \sinh \left( \chi _1 \xi -i \chi _4\right) +i\epsilon \varrho _3 \cosh \left( \epsilon \chi _1 \xi -i \chi _6\right) \right] -1 \right] }{\exp (\chi _1 \xi +\chi _2) \left[ \varrho _1 \exp (\chi _1 \xi +\chi _2) +\varrho _2 \cosh \left( \chi _1 \xi -i \chi _4\right) +i \varrho _3 \sinh \left( \epsilon \chi _1 \xi -i \chi _6\right) \right] +1} \nonumber \\&\times \exp \left[ i \left( - \kappa x + \omega t + \sigma W(t) -\sigma ^2 t + \theta \right) \right] . \end{aligned}$$
(60)

In all solution sets given here, \(\epsilon = \pm 1\). Also, it needs to be mentioned that the solutions (58) and (60) remain valid under the conditions \(\varrho _3=i \beta _1\), \(\chi _6=i \beta _2\), and \(\chi _4=i \beta _3\), where \(\beta _j (j=1, 2, 3) \in {\mathbb {R}}\).

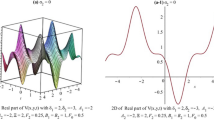
The solution provided by Eq. (60) is depicted graphically in Fig. 6. In the (x, t)-plane, Fig. 6a, b, and c show the 3D graphs, while Fig. 6a, e, and f are the corresponding contour diagrams of Fig. 6a, b, and c. In Fig. 6, the parameter values are \( v= 1.8,\ \epsilon = -1,\ \theta = 4,\ \kappa = 1,\ \varrho _1= 3,\ \varrho _2= 7,\ \varrho _3= 2 i,\ \chi _2= 5,\ \chi _4= 9 i,\ \chi _6= 11 i,\ W(t)= \frac{\sigma }{2} t \) when \( \sigma = 2,\ \chi _1= 0.3,\ \omega = 72 \) in (a) and (d), \( \sigma = 4,\ \chi _1= 1,\ \omega = 7.77 \) in (b) and (e), \( \sigma = 0,\ \chi _1= -0.53,\ \omega = 3.9 \) in (c) and (f). For various values of the parameters \(\sigma \), \(\chi _1\), and \(\omega \), the propagation characteristics of the three-wave solution provided by Eq. (60) are displayed in Fig. 6, along with the examination range \(-5 \le x \le 5\) and \(-5 \le t \le 5\).

Fig. 6
figure 6

Dynamical behavior of solution (60)

Full size image

Before arriving at a conclusion, let us compare the obtained analytical solutions with the experimental results of nonlinear waves found in optical contexts. Here, we compare for example the obtained Peregrine-like rational soliton (51) with the Peregrine soliton that is experimentally observed in optical fibers by Kibler et al. [51]. Different from the Peregrine soliton obtained within the framework of the cubic NLSE [51], the Peregrine-like rational solution presented here possess a nontrivial phase structure which depends crucially on the noise coefficient \(\sigma \) and includes the time-dependent function W(t). This special form of the phase may lead to chirped pulses when the function W(t) do not exhibit a linear variation in time. There are a number of real-world applications for this interesting frequency-chirping property, including effective pulse amplification or compression. It should be noted that only the two fundamental effects, namely group velocity dispersion and self-phase modulation nonlinearity, may be balanced for the Peregrine soliton to form in a pure Kerr optical medium. This is different from the findings of the current study, which show that for them to exist in the optical fiber, a balance between higher-order effects of different nature is necessary.

9 Conclusions

The present research discussed the effect of multiplicative white noise in the Itô sense on the analytic solutions of the concatenation model, which is the conjunction of the NLSE, LPD model, and SSE, along with the Kerr law nonlinear form of SPM and STD, in addition to perturbation terms of the Hamiltonian type. To achieve this, the direct test functions, which comprise a combination of exponential, trigonometric, hyperbolic, and quadratic functions, were implemented along with the Cole–Hopf transformation. The procedure continued with the extraction of multi-wave, two solitary wave, breather, periodic cross kink, Peregrine-like rational, and three-wave solutions for the perturbed stochastic concatenation model. The restrictions on the parameters essential for the existence of such solutions were also introduced. The interaction phenomenon of the recovered solutions is illustrated through 3D and contour graphics by assigning specific values to the parameters.

This study illustrates the potentially rich set of localized pulses and periodic waves in optical fiber media governed by the concatenation model. These results may be advantageous for further understanding of the nonlinear phenomena and dynamical processes arising in optical fibers and may be useful for experimental realization of undistorted transmission of nonlinear waves in optical waveguiding systems.