Abstract
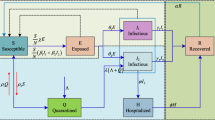
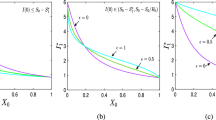
Two different approaches to incorporate environmental perturbations in stochastic systems are compared analytically and computationally. Then we present a stochastic model for COVID-19 that considers susceptible, exposed, infected, and recovered individuals, in which the contact rate between susceptible and infected individuals is governed by the Ornstein–Uhlenbeck process. We establish criteria for the existence of a stationary distribution of the system by constructing a suitable Lyapunov function. Next, we derive the analytical expression of the probability density function of the model near the quasi-equilibrium. Additionally, we establish sufficient conditions for the extinction of disease. Finally, we analyze the effect of the Ornstein–Uhlenbeck process on the dynamic behavior of the stochastic model in the numerical simulation section. Overall, our findings shed light on the underlying mechanisms of COVID-19 dynamics and the influence of environmental factors on the spread of the disease, which can inform policy decisions and public health interventions.





Similar content being viewed by others
Data availability
Data sharing is not applicable to this article as no new data are created or analyzed in this study.
References
World Health Organization, Coronavirus disease (COVID-19). https://www.who.int/health-topics/coronavirus
Annas, S., Pratama, M.I., Rifandi, M., Sanusi, W., Side, S.: Stability analysis and numerical simulation of SEIR model for pandemic COVID-19 spread in Indonesia. Chaos Solitons Fract. 39, 110072 (2020). https://doi.org/10.1016/j.chaos.2020.110072
Liang, K.: Mathematical model of infection kinetics and its analysis for COVID-19, SARS and MERS. Infect. Genet. Evol. 82, 104306 (2020). https://doi.org/10.1016/j.meegid.2020.104306
Almocera, A.E.S., Quiroz, G., Hernandez-Vargas, E.A.: Stability analysis in COVID-19 within-host model with immune response. Commun. Nonlinear Sci. Numer. Simul. 95, 105584 (2021). https://doi.org/10.1016/j.cnsns.2020.105584
Enrique Amaro, J., Dudouet, J., Nicolás Orce, J.: Global analysis of the COVID-19 pandemic using simple epidemiological models. Appl. Math. Model. 90, 995–1008 (2021). https://doi.org/10.1016/j.apm.2020.10.019
Ndaïrou, F., Area, I., Nieto, J.J., Torres, D.F.: Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fract. 135, 109846 (2020). https://doi.org/10.1016/j.chaos.2020.109846
Biswas, S.K., Ghosh, J.K., Sarkar, S., Ghosh, U.: COVID-19 pandemic in India: a mathematical model study. Nonlinear Dyn. 102(1), 537–553 (2020). https://doi.org/10.1007/s11071-020-05958-z
Khan, M.A., Atangana, A.: Mathematical modeling and analysis of COVID-19: a study of new variant Omicron. Physica A 599, 127452 (2022). https://doi.org/10.1016/j.physa.2022.127452
Raza, A., Rafiq, M., Awrejcewicz, J., Ahmed, N., Mohsin, M.: Dynamical analysis of coronavirus disease with crowding effect, and vaccination: a study of third strain. Nonlinear Dyn. 107(4), 3963–3982 (2022). https://doi.org/10.1007/s11071-021-07108-5
Yu, Z., Sohail, A., Arif, R., Nutini, A., Nofal, T.A., Tunc, S.: Modeling the crossover behavior of the bacterial infection with the COVID-19 epidemics. Results Phys. 39, 105774 (2022). https://doi.org/10.1016/j.rinp.2022.105774
Ahmed, N., Elsonbaty, A., Raza, A., Rafiq, M., Adel, W.: Numerical simulation and stability analysis of a novel reaction–diffusion COVID-19 model. Nonlinear Dyn. 106(2), 1293–1310 (2021). https://doi.org/10.1007/s11071-021-06623-9
Tilahun, G.T., Alemneh, H.T.: Mathematical modeling and optimal control analysis of COVID-19 in Ethiopia. J. Interdiscip. Math. 24(8), 2101–2120 (2021). https://doi.org/10.1080/09720502.2021.1874086
Smirnova, A., deCamp, L., Chowell, G.: Forecasting epidemics through nonparametric estimation of time-dependent transmission rates using the SEIR Model. Bull. Math. Biol. 81(11), 4343–4365 (2019). https://doi.org/10.1007/s11538-017-0284-3
Raza, A., Arif, M.S., Rafiq, M.: A reliable numerical analysis for stochastic gonorrhea epidemic model with treatment effect. Int. J. Biomath. 12(06), 1950072 (2019). https://doi.org/10.1142/S1793524519500724
Raza, A., Awrejcewicz, J., Rafiq, M., Mohsin, M.: Breakdown of a nonlinear stochastic nipah virus epidemic models through efficient numerical methods. Entropy 23(12), 1588 (2021). https://doi.org/10.3390/e23121588
Hamam, H., Raza, A., Alqarni, M.M., Awrejcewicz, J., Rafiq, M., Ahmed, N., Mahmoud, E.E., Pawłowski, W., Mohsin, M.: Stochastic modelling of Lassa fever epidemic disease. Mathematics 10(16), 2919 (2022). https://doi.org/10.3390/math10162919
Raza, A., Awrejcewicz, J., Rafiq, M., Ahmed, N., Mohsin, M.: Stochastic analysis of nonlinear cancer disease model through virotherapy and computational methods. Mathematics 10(3), 368 (2022). https://doi.org/10.3390/math10030368
Feng, T., Qiu, Z., Meng, X.: Analysis of a stochastic recovery-relapse epidemic model with periodic parameters and media coverage. J. Appl. Anal. Comput. 9(3), 1007–1021 (2019). https://doi.org/10.11948/2156-907X.20180231
Din, A., Li, Y.: Stationary distribution extinction and optimal control for the stochastic hepatitis B epidemic model with partial immunity. Phys. Scr. 96(7), 074005 (2021). https://doi.org/10.1088/1402-4896/abfacc
Shi, Z.: A stochastic SEIRS rabies model with population dispersal: stationary distribution and probability density function. Appl. Math. Comput. 23, 127189 (2022)
Nipa, K.F., Allen, L.J.S.: Disease emergence in multi-patch stochastic epidemic models with demographic and seasonal variability. Bull. Math. Biol. 82(12), 152 (2020). https://doi.org/10.1007/s11538-020-00831-x
May, R.M.: Stability and Complexity in Model Ecosystems. Princeton Landmarks in Biology, 1st edn. Princeton University Press, Princeton (2001)
Gao, N., Song, Y., Wang, X., Liu, J.: Dynamics of a stochastic SIS epidemic model with nonlinear incidence rates. Adv. Differ. Equ. 2019(1), 41 (2019). https://doi.org/10.1186/s13662-019-1980-0
Wang, W., Cai, Y., Ding, Z., Gui, Z.: A stochastic differential equation SIS epidemic model incorporating Ornstein–Uhlenbeck process. Physica A 509, 921–936 (2018). https://doi.org/10.1016/j.physa.2018.06.099
Zhang, X., Yuan, R.: A stochastic chemostat model with mean-reverting Ornstein–Uhlenbeck process and Monod-Haldane response function. Appl. Math. Comput. 394, 125833 (2021). https://doi.org/10.1016/j.amc.2020.125833
Cai, Y., Jiao, J., Gui, Z., Liu, Y., Wang, W.: Environmental variability in a stochastic epidemic model. Appl. Math. Comput. 329, 210–226 (2018). https://doi.org/10.1016/j.amc.2018.02.009
Mamis, K., Farazmand, M.: Stochastic compartmental models of COVID-19 pandemic must have temporally correlated uncertainties. Proc. R. Soc. A: Math. Phys. Eng. Sci. 479(2269), 20220568 (2023). https://doi.org/10.1098/rspa.2022.0568
Allen, E.: Environmental variability and mean-reverting processes. Discrete Contin. Dyn. Syst. Ser. B 21(7), 2073–2089 (2016). https://doi.org/10.3934/dcdsb.2016037
Du, N.H., Nguyen, D.H., Yin, G.G.: Conditions for permanence and ergodicity of certain stochastic predator–prey models. J. Appl. Probab. 53(1), 187–202 (2016). https://doi.org/10.1017/jpr.2015.18
Meyn, S.P., Tweedie, R.L.: Stability of Markovian processes III: Foster–Lyapunov criteria for continuous-time processes. Adv. Appl. Probab. 25(3), 518–548 (1993). https://doi.org/10.2307/1427522
Dieu, N.T.: Asymptotic properties of a stochastic SIR epidemic model with Beddington–DeAngelis incidence rate. J. Dyn. Differ. Equ. 30(1), 93–106 (2018). https://doi.org/10.1007/s10884-016-9532-8
Zhou, B., Jiang, D., Dai, Y., Hayat, T.: Threshold dynamics and probability density function of a stochastic avian influenza epidemic model with nonlinear incidence rate and psychological effect. J. Nonlinear Sci. 33(2), 29 (2023). https://doi.org/10.1007/s00332-022-09885-8
Yang, Q., Zhang, X., Jiang, D.: Dynamical behaviors of a stochastic food chain system with Ornstein–Uhlenbeck process. J. Nonlinear Sci. 32(3), 34 (2022). https://doi.org/10.1007/s00332-022-09796-8
Zhou, B., Han, B., Jiang, D., Hayat, T., Alsaedi, A.: Stationary distribution, extinction and probability density function of a stochastic vegetation-water model in arid ecosystems. J. Nonlinear Sci. 32(3), 30 (2022). https://doi.org/10.1007/s00332-022-09789-7
Shi, Z., Jiang, D.: Environmental variability in a stochastic HIV infection model. Commun. Nonlinear Sci. Numer. Simul. 120, 107201 (2023). https://doi.org/10.1016/j.cnsns.2023.107201
Higham, D.J.: An algorithmic introduction to numerical simulation of stochastic differential equations. SIAM Rev. 43(3), 525–546 (2001). https://doi.org/10.1137/S0036144500378302
Kifle, Z.S., Obsu, L.L.: Mathematical modeling for COVID-19 transmission dynamics: a case study in Ethiopia. Results Phys. 34, 105191 (2022). https://doi.org/10.1016/j.rinp.2022.105191
Funding
We are grateful to anonymous reviewers and Dr. Suli Liu for their effort reviewing our paper and positive feedback. This work is supported by the Natural Science Foundation of Shandong Province (No. ZR2019MA010) and Central University Basic Research Fund of China (No. 22CX03030A).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix (Local asymptotic stability of endemic equilibrium in the deterministic model (1.1))
Appendix (Local asymptotic stability of endemic equilibrium in the deterministic model (1.1))
For the deterministic model (1.1), we rewrite it by letting \(N(t)=S(t)+E(t)+I(t)+R(t)\) to obtain the following equivalent model:
It is not difficult to obtain that there exists a unique endemic equilibrium for model (A.1) as follows:
such that the following equations hold
where \(S^*=N^*-E^*-I^*-R^*\).
Lemma A.1
If \(R_0 > 1\), then the endemic equilibrium \( (N^*,E^*,I^*,R^*)\) of the system (A.1) is locally asymptotically stable..
Proof
Consider
In view of (A.2), we obtain
Note that
Thus we have
Since
Denote
Then we have
Next define
Combining (A.3) and (A.4), we have
Note that
Then we have
In addition, we get
Define
with
Combining (A.5), (A.6) and (A.7), we have
Then from
We have
Then define
with
Combining (A.8) and (A.9), we have
In view of (A.10), one can obtain that there are positive constants \(q_1\), \(q_2\) and \(q_3\) such that
and
Hence we have
which implies that the endemic equilibrium \((N^*,E^*, \)\( I^*,R^*) \) of system (A.1) is exponentially stable and hence the endemic equilibrium is locally asymptotically stable. This completes the proof. \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shi, Z., Jiang, D. Dynamics and density function of a stochastic COVID-19 epidemic model with Ornstein–Uhlenbeck process. Nonlinear Dyn 111, 18559–18584 (2023). https://doi.org/10.1007/s11071-023-08790-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-023-08790-3