Forecasting Epidemics Through Nonparametric Estimation of Time-Dependent Transmission Rates Using the SEIR Model

Abstract

Deterministic and stochastic methods relying on early case incidence data for forecasting epidemic outbreaks have received increasing attention during the last few years. In mathematical terms, epidemic forecasting is an ill-posed problem due to instability of parameter identification and limited available data. While previous studies have largely estimated the time-dependent transmission rate by assuming specific functional forms (e.g., exponential decay) that depend on a few parameters, here we introduce a novel approach for the reconstruction of nonparametric time-dependent transmission rates by projecting onto a finite subspace spanned by Legendre polynomials. This approach enables us to effectively forecast future incidence cases, the clear advantage over recovering the transmission rate at finitely many grid points within the interval where the data are currently available. In our approach, we compare three regularization algorithms: variational (Tikhonov’s) regularization, truncated singular value decomposition (TSVD), and modified TSVD in order to determine the stabilizing strategy that is most effective in terms of reliability of forecasting from limited data. We illustrate our methodology using simulated data as well as case incidence data for various epidemics including the 1918 influenza pandemic in San Francisco and the 2014–2015 Ebola epidemic in West Africa.

1 Introduction

Real-time reconstruction of disease parameters for an emerging outbreak provides crucial information to government agencies working to design and implement public health intervention measures and policies. Despite tremendous progress in both deterministic and stochastic algorithms for solving parameter estimation problems in epidemiology, there is still a long way to go before our understanding of disease transmission is sufficient for accurate control and forecasting.

In various compartmental models, the transmission rate parameter is defined as the effective contact rate, that is, the probability of infection given contact between an infectious and susceptible individual multiplied by the average rate of contacts between these groups. It is the defining rate in disease progression and one of the two components in the basic reproduction number, $R_0$, by which the continued growth or decline is decided. When $R_0 = \beta /\gamma =$ transmission rate/recovery rate $<1$, an outbreak dies off; otherwise, the outbreak continues to expand. The transmission rate of a disease may vary in time (take measles and influenza, for example), and models may incorporate seasonality characteristics to capture this behavior. The transmission rate may also be directly affected by social response and public health policy by which this effective contact rate is reduced to the point that the reproductive rate falls under 1, and the disease dies off. Public policies and control measures have their greatest impact on the transmission rate of a disease. Having the tools needed to recover a time-dependent transmission rate allows for the real-time analysis of the effectiveness of control measures, for the ability to determine the most powerful response and, finally, for the conceivably more accurate forecasting of the outbreak. Whereas other system parameters, i.e. recovery rates, are less dependent on intervention measures, the reproductive capacity of an outbreak and the underlying transmission rate are directly related to the efficiency of control and prevention.

There are a number of common approaches to investigating transmission rates of diseases in the literature, based on system design with deterministic (Lipsitch et al. 2003; Rivers et al. 2014; Chowell et al. 2016; Pollicott et al. 2012; Lange 2016), stochastic (Lekone and Finkenst 2006; Bjørnstad et al. 2002; Taylor et al. 2016; Ponciano and Capistrán 2011), and network (Newman 2002; Kiskowski 2014; Xia 2004) models being most prevalent and in many cases in combination. In these models, the common practice is to either assume a constant transmission rate (although considering transmission from various settings: hospital, funeral, community) (Xia 2004; Cauchemez et al. 2008; Lewnard et al. 2014; Chretien et al. 2015; Merler et al. 2015; Taylor et al. 2016; Meltzer et al. 2016), or to assume that transmission rate behaves as some pre-set periodic, exponential, or other function with a finite number of parameters (Bjørnstad et al. 2002; Chowell et al. 2016; Szusz et al. 2010; Finkenstädt and Grenfell 2000; Ponciano and Capistrán 2011; Capistrán et al. 2009). In recovering these parameter values, the most common methods are least squares data fitting or optimization and statistical approaches (Finkenstädt and Grenfell 2000; Cauchemez et al. 2008; Dureau et al. 2013; Biggerstaff et al. 2016).

Pollicott et al. (2012) reconstructed a time-dependent transmission rate, $\beta (t)$, by reformulating the SIR model. However, their approach requires the knowledge of $\beta _0$, not easily determined, and the use of prevalence data. There are additional limitations on changes in the infected class. Hadeler (2011) modified this approach so that S(0), the initial number of susceptible individuals, is assumed to be given and, though it uses incidence data, the formulation requires prevalence data at one point. Cauchemez et al. (2008) use a stochastic framework and MCMC to recover time-dependent transmission rate as well as other disease model parameters. The challenge here included limitations on parameter relationships and the discrete form of the recovered transmission rate. Camacho et al. (2015) model the time-varying transmission parameter, $\beta (t)$, by a Wiener process (also known as standard Brownian motion) with positivity constraints using a stochastic SEIR framework. To estimate future cases in real time, 5000 stochastic trajectories are simulated by sampling a set of parameters and states from the joint posterior distribution for the last fitted data point.

Regardless of the type of a transmission rate, fitting model predictions for an invading pathogen to a short-term incidence series results in an ill-posed problem due to instability and lack of data. For classical compartmental models, parameter identification is generally cast as an ODE constrained nonlinear optimization problem, where a numerical method has to be coupled with an appropriate regularization strategy in order to balance accuracy and stability in the reconstruction process. A reliable tool for uncertainty quantification is equally important. Even if a computational algorithm is carefully regularized, an iterative scheme for the nonlinear optimization would usually consist of solving a sequence of ill-conditioned linear equations. With noise propagation at every step, the accuracy of the recovered transmission parameters turns out to be low, especially in case of limited data for an emerging outbreak.

To partially overcome this difficulty, we propose an alternative problem-oriented approach, where the original nonlinear problem is reduced to a linear Volterra-type operator equation of the first kind. The variable transmission rate is reconstructed by fitting to both incidence and cumulative time series. Rather than pre-setting a specific shape of the unknown function by using a solution space with a small number of parameters, we discretize the time-dependent transmission rate by projecting onto a finite subspace spanned by Legendre polynomials. We further show that recovering the transmission rate as a linear combination of Legendre polynomials enables us to effectively forecast future incidence cases, the clear advantage over recovering the transmission rate at finitely many grid points within the interval where the data are currently available. To incorporate stability into the linear equation, we employ three regularization algorithms: variational (Tikhonov’s) regularization, truncated singular value decomposition (TSVD), and modified TSVD (MTSVD) (Bakushinsky et al. 2015). The goal is to determine, which stabilizing strategy is the most effective in terms of reliability of forecasting from limited data.

In Sect. 6, both short-term and long-term forecasts of disease incidence relying on case incidence data of the early epidemic growth phase are carried out. In all our experiments, “the early epidemic growth phase”, i.e., the minimum length of the early growth phase that is required to initiate forecasting, is about 5–6 weeks of incidence data. Further forecasting results as well as theoretical analysis of MTSVD regularization procedure are given in “Appendix”.

In our numerical study, case incidence data describing the trajectory of the 1918 influenza pandemic in San Francisco, California (daily incidence data) (Chowell et al. 2007), and the 2013–2015 Ebola epidemic in West Africa (weekly reported data) (World Health Organization 2016) are used. Specifically, we investigate national Ebola epidemic curves for Liberia and Sierra Leone and sub-national Ebola epidemic curves for Montserrado in Liberia and Western Area Urban/Rural in Sierra Leone.

2 Problem Formulation

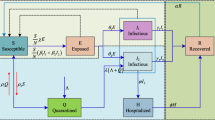
Consider a general SEIR transmission process (Chowell et al. 2004), where the population is divided in four categories: susceptible (S), exposed (E), symptomatic and infectious (I) and removed (R) individuals. The total population size, N, is assumed constant and initially completely susceptible to an emerging viral infection. We also assume that the population is well-mixed. That is, each individual has the same probability of having contact with any other individual in the population.

Susceptible individuals infected with a virus enter the latent period (category E) at the rate $\beta (t) S(t) I(t)/N$, where $\beta (t)$ is the mean transmission rate per day (week). Latent individuals progress to the infectious class, I, at the rate k (1 / k is the mean latent period). Infectious individuals recover or die at the rate $\gamma$, where the mean infectious period is $1/\gamma$. Removed , R, are assumed to be fully protected for the duration of the outbreak. The deterministic equations of this compartmental model are given by:

$$\begin{aligned} \frac{\hbox {d}S}{\hbox {d}t}&=\,-\beta (t) S(t)\frac{I(t)}{N} \end{aligned}$$

(1)

$$\begin{aligned} \frac{\hbox {d}E}{\hbox {d}t}&=\,\beta (t) S(t)\frac{I(t)}{N}-k E(t) \end{aligned}$$

(2)

$$\begin{aligned} \frac{\hbox {d}I}{\hbox {d}t}&=\,k E(t)-\gamma I(t) \end{aligned}$$

(3)

$$\begin{aligned} \frac{\hbox {d}R}{\hbox {d}t}&=\,\gamma I(t). \end{aligned}$$

(4)

System parameters are either pre-estimated or fitted to the incidence data, $\frac{\hbox {d}C}{\hbox {d}t}$, where

$$\begin{aligned} \frac{\hbox {d}C}{\hbox {d}t}&=\,k E(t). \end{aligned}$$

(5)

As it follows from (1)–(5),

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}t}(S(t)+E(t)+C(t))=0,\quad S(t)+E(t)+C(t)=S(t_1)+E(t_1)+C(t_1). \end{aligned}$$

From the above, one concludes

$$\begin{aligned} S(t)= & {} -\frac{kE(t)}{k}-C(t)+S(t_1)+E(t_1)+C(t_1)\\= & {} -\frac{1}{k}\frac{\hbox {d}C}{\hbox {d}t}(t)-C(t)+S(t_1)+E(t_1)+C(t_1). \end{aligned}$$

Substitute this expression into the equation

$$\begin{aligned} \frac{\hbox {d}S}{S}=-\beta (t) \frac{I(t)}{N}\,\hbox {d}t,\quad \text{ then } \quad \ln \frac{S(t)}{S(t_1)}=-\int _{t_1}^t\beta (\lambda )\frac{I(\lambda )}{N}\,\hbox {d}\lambda . \end{aligned}$$

(6)

To find I(t), use the equation

$$\begin{aligned} \frac{\hbox {d}I}{\hbox {d}t}+\gamma I(t)=\frac{\hbox {d}C}{\hbox {d}t}, \end{aligned}$$

which gives

$$\begin{aligned} I(t)=I(t_1)\exp (-\gamma (t-t_1))+\int _{t_1}^t\exp (-\gamma (t-\lambda )) \frac{\hbox {d}C}{\hbox {d}\lambda }(\lambda )\,\hbox {d}\lambda . \end{aligned}$$

(7)

Combining (6) and (7), one derives

$$\begin{aligned}&-N \ln \left[ \frac{-\frac{1}{k}\frac{\hbox {d}C}{\hbox {d}t}(t)-C(t) +E(t_1)+C(t_1)}{S(t_1)}+1\right] \nonumber \\&\quad =\int _{t_1}^t\beta (\tau )\left\{ I(t_1)\exp (-\gamma (\tau -t_1))+\int _{t_1}^\tau \exp (-\gamma (\tau -\lambda ))\frac{\hbox {d}C}{\hbox {d}\lambda }(\lambda )\hbox {d}\lambda \right\} \,\hbox {d}\tau ,\nonumber \\ \end{aligned}$$

(8)

which is a linear Volterra-type integral equation of the first kind with the unknown transmission rate, $\beta (t)$, to be recovered from limited cumulative and incidence time series, C(t) and $\frac{\hbox {d}C}{\hbox {d}t}$, respectively.

3 Regularization Strategies and Discrete Approximation

As it has been established in the previous section, the reconstruction of $\beta (t)$ can be reformulated as a linear equation of the first kind with noise added to the response vector and to the operator itself

$$\begin{aligned} A\beta = f,\quad \mathcal {X} \rightarrow \mathbb {R}^n, \end{aligned}$$

(9)

where A is given by its h-approximation, $||A-A_h||\le h$, and f is given by its $\sigma$-approximation, $||f-f_\sigma ||\le \sigma$. Noise enters the operator through incidence data under the kernel:

$$\begin{aligned} A_h\beta (t):=\int _{t_1}^t\beta (\tau )\left\{ I(t_1)\exp (-\gamma (\tau -t_1))+\int _{t_1}^\tau \exp (-\gamma (\tau -\lambda ))\frac{\hbox {d}C}{{\hbox {d}\lambda }}(\lambda ){\hbox {d}\lambda }\right\} \,{\hbox {d}\tau }, \end{aligned}$$

and it enters the right-hand side through its dependence on both incidence and cumulative data as shown in (8):

$$\begin{aligned} f_\sigma :=-N \ln \left[ \frac{-\frac{1}{k}\frac{\hbox {d}C}{\hbox {d}t}(t)-C(t)+E(t_1)+C(t_1)}{S(t_1)}+1\right] . \end{aligned}$$

The true solution, $\beta (t)$, in (9) lies in a Hilbert space $\mathcal {X}$, the noise-contaminated operator, $A_h$, maps $\mathcal {X}$ into $\mathbb {R}^n$, and $f_\sigma$ is a vector in the finite-dimensional data space, $\mathbb {R}^n$. Due to the nature of our application, $\mathcal {X}$ is infinite dimensional and, upon discretization, its dimensionality is much larger than n. This results in an ill-posed problem that needs to be regularized prior to its inversion.

To introduce the proposed regularization strategies, we consider a singular system of the operator $A_h$, $\{u_i, \lambda _i, v_i\}_{i=1}^n$, with singular values

$$\begin{aligned} \lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _n > 0. \end{aligned}$$

Here $v_i\in \mathcal {X}$ and $u_i\in \mathbb {R}^n$ are such that $(v_i, v_j)_\mathcal {X}=\delta _{ij}$ and $(u_i, u_j)_{\mathbb {R}^n}=u_i^T u_j=\delta _{ij}$, and $\delta _{ij}$ denotes the Kronecker delta, equal to 1 if $i=j$ and to 0 otherwise. If a regularized solution, $\beta _\alpha$, is obtained by filtering the noisy data

$$\begin{aligned} \beta _\alpha : = \sum _{i=1}^n \omega _\alpha (\lambda _i)\frac{(u_i,f_\sigma )}{\lambda _i}v_i :=R_{\alpha ,h} f_\sigma , \end{aligned}$$

(10)

then the choice of $\omega _\alpha$ defines a particular type of a regularization strategy $R_\alpha : \mathbb {R}^n \rightarrow \mathcal {X}$, and $\alpha$ is a stabilizing parameter, which regulates the extent of filtering and depends on the level of noise in $A_h$ and $f_\sigma$. To reconstruct time-dependent transmission rate, $\beta (t)$, we use three admissible filters, which ensure convergence of the regularized solution as the noise level tends to zero, Engl et al. (1996):

• 1) $\omega _\alpha (\lambda )=\frac{\lambda ^2}{\lambda ^2+\alpha } \quad (\hbox {Tikhonov's regularization}),$

• 2) $\omega _\alpha (\lambda )=\left\{ \begin{array}{ll} 1, &{} \lambda \ge \sqrt{\alpha } \\ 0, &{} \lambda <\sqrt{\alpha } \\ \end{array} \right. \quad (\text{ Truncated } \text{ SVD }),$

• 3) $\omega _\alpha (\lambda )=\left\{ \begin{array}{ll} 1, &{} \lambda \ge \sqrt{\alpha } \\ \frac{\lambda }{\sqrt{\alpha }}, &{} \lambda <\sqrt{\alpha } \\ \end{array} \right. \quad (\text{ Modified } \text{ Truncated } \text{ SVD }).$

The first two filters are probably the most known and the most used. The third filter (MTSVD) was recently studied in Bakushinsky et al. (2015) for the case of a noise-free operator. It has a remarkable optimal property: among all filters with the same level of stability, it provides the highest accuracy of the algorithm. In “Appendix,” we will verify this property for the case of noise present both in the operator and in the right-hand side. In our numerical experiments, discussed in the next sections, all three filters give consistent results. However, MTSVD tends to do slightly better in terms of forecasting from limited data.

As we discretize the unknown transmission rate, $\beta (t)$, our goal is not to incorporate any specific behavior of this function in Eq. (9). Instead, we attempt to recover that behavior in addition to recovering numerical values for all entries of the solution vector. This aspect is extremely important since our experiments show that the shape of $\beta (t)$ can be drastically different for different outbreaks. What all transmission rates have in common is that eventually the values of $\beta (t)$ would go down. However, the nature of that decay is never the same, and it is impacted by a large number of factors, such as the severity of the outbreak spread over the period of its initial detection, the timing and the efficiency of proper intervention and control measures, the intensity of transmission pathways within various risk groups, etc.

For some outbreaks with an aggressive initial spread, $\beta (t)$ may start off growing, or it can remain near-constant through the first phase of the disease progression. At the same time, if the government agencies act quickly or the population changes behavior quickly, the transmission rate would decrease almost from the beginning. In case of the most successful intervention measures, $\beta (t)$ can decrease very fast before the outbreak reaches its pick and then $\beta (t)$ would remain essentially unchanged for the second half of the outbreak. When intervention measures are less effective, the transmission rate may oscillate a lot as it goes down, and the timing of its descent may be substantially delayed. Capturing a unique behavior of a particular transmission rate is paramount for the accurate forecasting of future incident cases as shown in Sects. 5 and 6 with additional results presented in Appendix.

To recover the shape of $\beta (t)$, we project this function onto a finite subset spanned by the shifted Legendre polynomials of degree $0,1,\ldots ,m$ defined recursively as follows

$$\begin{aligned}&x=\frac{2t-a-b}{b-a},\quad P_0(x)=1,\quad P_1(x)=x,\quad t\in [a,b],\\&(m+1)P_{m+1}(x)=(2m+1)xP_m(x)-mP_{m-1}(x). \end{aligned}$$

These functions are orthogonal on the interval [a, b], the duration of the outbreak, with respect to the $L_2$ inner product

$$\begin{aligned} \langle P_m,P_k\rangle \,= \,\frac{b-a}{2m+1}\,\delta _{mk}. \end{aligned}$$

The discretization of the original operator equation by projection onto a finite subspace spanned by Legendre polynomials results in solving (in the sense of least squares) a linear system of n equations with $m+1$ unknowns for the coefficients $C_i$, $i=0,1,\ldots ,m,$ in the Legendre polynomial expansion and then computing $\beta _\alpha (t)$ as

$$\begin{aligned} \beta _\alpha (t) = \sum _{i=0}^{m} C_iP_i(t),\quad t\in [a,b]. \end{aligned}$$

For all three regularization algorithms, the value of $\alpha$ is chosen from the goodness of fit of the incidence data, generated by $\beta _\alpha$, to the real data used for the inversion (discrepancy principle).

Fig. 1

(Color figure online) Recovery of $\beta _\alpha (t)$ by MTSVD, TSVD and Tikhonov’s stabilizing algorithms from full synthetic incidence data set and quantification of uncertainty in $\beta _\alpha (t)$ . a Comparison of the original $\beta (t)$ used to solve the forward problem to the approximate functions $\beta _\alpha (t)$ recovered by the regularization methods. b Comparison of incidence data generated by the original function $\beta (t)$ to the incidence data resulting from the recovered values of $\beta _\alpha (t)$. c The incidence curve $C'(t)$ generated by the original $\beta (t)$ together with 2000 noisy incidence curves obtained by adding Poisson noise to $C'(t)$. d Mean values of $\beta _\alpha (t)$ along with 95% confidence intervals recovered with MTSVD, TSVD and Tikhonov’s stabilizing algorithms

4 Numerical Experiments with Simulated Data

First, we test the above regularization methods using a simulated set of data. The experiment is conducted as follows. We discretize the infinite-dimensional Hilbert space, $\mathcal {X}=L_2[a,b]$, by projecting onto a subspace spanned by a large number of Legendre polynomials (250) to get an accurate approximation of the original $\beta (t)$. Given this $\beta (t)$, we generate incidence data by solving the forward problem (See Fig. 1). Once the incidence data, $\frac{\hbox {d}C}{\hbox {d}t}$, have been computed, we solve the inverse problem by TSVD, MTSVD, and Tikhonov’s regularization algorithms. To examine both regularization and discretization errors, while solving the inverse problem we discretize $\mathcal {X}$ with a smaller number of Legendre polynomials (100). Figure 1 illustrates how the original $\beta (t)$ compares to $\beta _\alpha (t)$ recovered by each regularization scheme.

In (8), we choose the total population size, N, and the initial number of cumulative cases, C(0), to be $1.5\times 10^6$ and 3, respectively. Mimicking an 8 day latent period and a 6 day infectious period, we take $\kappa = 7/8$ and $\gamma = 7/6$ and assume that $[a,b] = [1,50]$, i.e., the outbreak is over in 50 weeks. Due to ill-posedness of the inverse problem, all three regularization methods are semi-convergent in a sense that the discrepancy initially goes down as $\alpha$ decreases, but then it begins to grow after $\alpha$ reaches a certain admissible level. We choose $\alpha$ right before it happens. For that $\alpha$, the discrepancy is about the same as the amount of noise in the incidence data. The values of the regularization parameter, $\alpha$, as selected by the discrepancy principle (Morozov 1984), are $1.26\times 10^{-7}$, $3.00\times 10^{-8}$, and $1.50\times 10^{-8}$ for MTSVD, TSVD and Tikhonov regularization methods.

To quantify uncertainty in $\beta _\alpha (t)$ for the three methods, we take the simulated incidence curve (shown in black in Fig. 1), add Poisson noise to this curve to generate 2000 boot-strap curves, and reconstruct the mean value of $\beta _\alpha (t)$ and the associated $95\%$ confidence intervals. The Poisson curves and the resulting uncertainty in each $\beta _\alpha (t)$ are presented in Fig. 1, which highlights a slightly higher uncertainty for TSVD regularization procedure as compared to Tikhonov’s and MTSVD.

5 Approximation of Time-Dependent Transmission Rate and Quantification of Uncertainty for Real Data

In this section, we use real data for the most recent outbreak of Ebola Virus Disease (EVD) in West Africa, predominately affecting Guinea, Liberia, and Sierra Leone, in order to examine regularizing properties of the proposed algorithms. This EVD outbreak, which began in early 2014, has received wide attention due to its scale, scope, location and alarming potential. The World Health Organization (WHO) declared the latest Ebola outbreak a public health emergency on August 8, 2014 (World Health Organization 2014). By the 21st of that month, the case count exceeded the total of all other previous outbreaks combined—2387 cases. As of the most recent WHO situation report (March 30, 2016) , there have been 28,646 Ebola cases with 11,323 fatalities (World Health Organization 2016), and these numbers are widely believed to be underreported.

In the beginning of our numerical analysis, we take full data set for the 2014 EVD outbreak in Sierra Leone and apply Tikhonov’s, TSVD, and MTSVD regularization schemes to pre-estimate $\beta _\alpha (t)$ in each case. To quantify the uncertainty in the recovered $\beta _\alpha (t)$, we add Poisson noise (2000 iterations for the results given, see Fig. 2) to the incidence curve and reconstruct the corresponding $\beta _\alpha (t)$ via the respective methods. This yields 95% confidence intervals for the approximate $\beta _\alpha (t)$ as well as the mean values of the recovered function. The reconstructed values of $\beta _\alpha (t)$ and the corresponding forecasting curves for TSVD and Tikhonov’s regularization schemes are very difficult to tell apart. Therefore, TSVD results are not included in Fig. 2. Tikhonov’s and MTSVD approximations of $\beta _\alpha (t)$are slightly different (see Fig. 2). The forecasting curves for partial data sets obtained with MTSVD $\beta _\alpha (t)$ are the most accurate and the least uncertain as illustrated in Figs. 5 and 7 below.

Figure 3 demonstrates the parameter selection process for this experiment. The first plot in Fig. 2 shows the dependence of relative discrepancy on $\alpha$ in the interval $[0,10^{-6}]$. For each method, the corresponding graph gives the lower bound of $\alpha$ that cannot be crossed. If $\alpha$ moves below this value, the discrepancy goes up almost vertically, and the relative error on the generated data quickly reaches 100%. The TSVD curve illustrates the discrete nature of TSVD regularization: for all values of $\alpha$ between two consecutive singular values, $\lambda _k$ and $\lambda _{k+1}$, the filtering function, $\omega _\alpha$, remains the same, and therefore the regularized solution, $\beta _\alpha (t)$, and the resulting discrepancy do not change either. After the initial preview of a big picture, we magnify the area where the discrepancy reaches its minimum, $[0,10^{-9}]$, and for each method we select the smallest value of $\alpha$ where this minimum is attained.

Fig. 2

(Color figure online) Noisy data used to quantify uncertainty in the transmission rate $\beta _\alpha (t)$ together with 95% confidence intervals and mean values of $\beta _\alpha (t)$ reconstructed from full incidence data set for Ebola epidemic in Sierra Leone. a Real EVD incidence data $C'(t)$ along with 2000 noisy incidence curves obtained by adding Poisson noise to the values of $C'(t)$. b Mean values of $\beta _\alpha (t)$ along with 95% confidence intervals recovered by MTSVD and Tikhonov’s regularization methods

Fig. 3

(Color figure online) Selection of regularization parameter, $\alpha$, for the reconstruction of $\beta _\alpha (t)$ from real incidence data on Ebola epidemic in Sierra Leone—full data set. a Relative discrepancy between actual and recovered incident case values as a function of $\alpha$ for MTSVD, TSVD and Tikhonov’s stabilizing algorithms, $\alpha \in [0,10^{-6}]$. b The magnified view of relative discrepancy as a function of the regularization parameter, $\alpha$, for MTSVD, TSVD and Tikhonov’s stabilizing algorithms, $\alpha \in [0,10^{-9}]$

The reproduction number, $R_0$, of an outbreak gives the number of cases one case generates on average over the course of its infectious period during the early epidemic growth phase in a completely susceptible population. When $R_0<1$, we expect the outbreak to die out; with $R_0>1$, the infection can spread and with higher values of $R_0$, it can become harder to control the outbreak. In the model given, $R_0(t)=\beta (t)/\gamma$ and therefore reconstruction of time-dependent $\beta (t)$ has direct ties to $R_0(t)$. Since $R_0 \propto \beta$, qualitatively the behaviors are the same. The transmission rate and the corresponding $R_0(t)$ curve, recovered from Sierra Leone data, evidence sporadic decline (Fig. 2). Some of this behavior may be attributed to noise in the data, but for the most part we see it as the result of less than effective implementation of control measures. When we apply the MTSVD regularization method to Liberia’s data from the 2014 EVD outbreak using the full data set, we see a marked drop in the transmission rate (Fig. 4) and a more smooth transition to an outbreak die off level. The application of MTSVD enables us to capture differing behaviors of the transmission rate that may be correlated to the efficiency of control measures or other intervention tools impacting the transmission rate. The early lack of fit of the model to the Ebola epidemic in Liberia highlights that regularization algorithms prevent over-fitting in the reconstruction of $\beta _\alpha (t)$ to account for the presence of noise in the incident case data.

Fig. 4

(Color figure online) Noisy data used to quantify uncertainty in the transmission rate $\beta _\alpha (t)$ together with 95% confidence intervals and mean values of $\beta _\alpha (t)$ reconstructed from full incidence data set for Ebola epidemic in Liberia. a Real EVD incidence data $C'(t)$ along with 2000 noisy incidence curves generated by adding Poisson noise to the values of $C'(t)$. b Mean values of $\beta _\alpha (t)$ along with 95% confidence intervals recovered by MTSVD regularization method

6 Forecasting from Limited Data for Emerging Outbreaks

Since our algorithm produces coefficients in the Legendre polynomial expansion, we can use $\beta _\alpha (t)$ recovered from early data to forecast the remaining part of the outbreak. In order to determine the forecasting curves, data are taken for the first n weeks and the regularization parameter, $\alpha _n$, is estimated by the discrepancy principle (Morozov 1984) as in the previous sections. At the next step, $\beta _\alpha (t)$ is recovered based on n weeks of data. It is then used to generate an incidence curve for the entire duration of the outbreak.

Table 1 Regularization parameters chosen by discrepancy principle in combination with MTSVD, TSVD and Tikhonov’s stabilizing algorithms applied to real incidence data on Ebola epidemic in Sierra Leone

In the first forecasting experiment, we employ all three, TSVD, Tikhonov’s, and MTSVD regularization methods on limited data sets for 2014 EVD outbreak in Sierra Leone. Table 1 gives the respective chosen regularization parameters for each method and the associated relative discrepancy (RD). For Sierra Leone, MTSVD does a better job forecasting from 6 and 26 weeks of incidence data (Fig.  5). The results from using Tikhonov’s method tend to overstate the forecasted incidence until after the outbreak’s peak (Fig. 5). The results obtained by TSVD algorithm, unlike Tikhonov’s scheme, tend to underestimate future incidence cases.

Fig. 5

(Color figure online) Comparison of forecasting curves generated from early incidence data for Ebola epidemic in Sierra Leone by MTSVD, TSVD and Tikhonov’s algorithms. a Forecasting incidence curves generated by MTSVD method from 6, 11, 16, 21 and 26 weeks of data, respectively, as compared to actual incidence data. b Forecasting incidence curves generated by Tikhonov’s method from 6, 11, 16, 21 and 26 weeks of data, respectively, as compared to actual incidence data. c Forecasting incidence curves generated by TSVD method from 6, 11, 16, 21 and 26 weeks of data, respectively, as compared to actual incidence data. d Forecasting incidence curves generated by MTSVD, TSVD and Tikhonov’s methods from 16 weeks of data as compared to actual incidence data

Fig. 6

(Color figure online) Comparison of forecasting curves generated from early incidence data for Ebola epidemic in Liberia by MTSVD regularization scheme using time-dependent and constant transmission rates. a Forecasting incidence curves generated with variable $\beta (t)$ from 13, 15, 17 and 19 weeks of data, respectively, as compared to actual incidence data. b Forecasting incidence curves generated with constant $\beta$ from 13, 15, 17 and 19 weeks of data, respectively, as compared to actual incidence data

While MTSVD does a better job at forecasting with time-dependent $\beta (t)$, all three methods are a vast improvement over forecasting that results from the use of constant $\beta$. We compare them in Fig. 6. The forecasting curves for Liberia (with a time-dependent $\beta (t)$) at week 13 indicate a potentially much larger outbreak; the largest recovered reproductive number was observed at week 12. This is not surprising if one takes into consideration that $\beta (t)$ is growing for the first 12 weeks, when the outbreak is on its rise. However, between weeks 12 and 13, $\beta (t)$ declines very fast. The forecasting curve captures that decline, and, despite of overestimating future cases, it shows a clear turning point (that is not far from the actual turning point), and a rapid decrease afterward.

The subsequent forecasting curves with a time-dependent $\beta (t)$ do an excellent job in approximating future incidence levels. The forecasting curves with a constant $\beta$ show a growing number of incidence cases suggesting the growth will continue until the population runs out of susceptible individuals. Forecasting curves for various districts for the EVD outbreak are given in “Appendix.”

Table 2 illustrates the forecasting performance of MTSVD regularization method with time-dependent transmission rate, $\beta (t)$, at 4, 5, and 6 weeks ahead as compared to the null model where $\beta$ is constant. The lower part of the table gives the corresponding forecasting errors. Table 2 quantitatively shows that forecasting with variable $\beta (t)$ outperforms the one with constant $\beta$. Figure 6 provides visual evidence of this conclusion.

The next experiment shows that one can use early data, before incidence peaks, to forecast in short forward time the projected incident cases with confidence intervals. In this application, we utilize n weeks of data and recover $\beta _\alpha (t)$. Given this $\beta _\alpha (t)$, we generate the initial n week incidence data curve and add Poisson noise to this curve (2000 iterations for the results given). For each noisy curve, $\beta _\alpha (t)$ is recovered employing a data-specific regularization parameter, $\alpha$. Each recovered $\beta _\alpha (t)$ is then used to project forward $n+5$ weeks for Sierra Leone and $n+2$ weeks for Liberia, and confidence intervals are determined from the forecasts at each week. We repeat this process every 5 and 2 weeks, respectively, until the incidence peak is reached, and present the results for Sierra Leone and Liberia in Fig. 7.

Forecasting for Sierra Leone begins at week 11 and does an excellent job capturing future epidemic behavior. For Liberia, where we begin forecasting at week 13, there tends to be an overestimate of incidence cases. This can be explained when we consider the behavior of $\beta _\alpha (t)$ in Fig. 5. We note that the peak of $\beta _\alpha (t)$ occurs at week 12, and the transmission rate makes a sharp drop continuing to epidemic peak at week 19, and this is the period of forecasting. The overestimate in this method is considerably less significant when compared to either a constant $\beta$ forecast or to forecasting with Tikhonov’s and TSVD regularization methods.

The impact of intervention and control on a disease transmission rate can also be seen when the algorithm is applied to outbreaks other than EVD. The recovered transmission rate may then be used to forecast future incidence cases. Prior to the implementation of vaccination for measles (1948–1964), outbreaks of the disease were common. The 1948 outbreak in London produced $28{,}000+$ cases in 40 weeks. The model parameters are $\kappa = 7/8$ and $\gamma = 7/6$ indicating an 8-day latent period and a 6-day infectious period. London’s population in 1948 was 8,200,000.

Another example is the pandemic influenza outbreak in 1918, which affected many cities. San Francisco experienced 28,310 cases in 63 days. For this disease, the latent and infectious periods are given as 2 and 4 days, respectively; the population of San Francisco at that time was 550,000. The last two plots in Fig. 7 demonstrate forecasting results for the 1948 measles outbreak in London and for the 1918 pandemic influenza outbreak in San Francisco obtained with MTSVD regularization method. In Appendix, we include numerical experiments for various districts affected by the EVD outbreak of 2014-2016.

Table 2 Comparison of MTSVD-regularized predicted and actual incidence cases for time-dependent and constant transmission rates given limited incidence data for Ebola epidemic in Liberia

Fig. 7

(Color figure online) Short-term forecasting curves with confidence intervals generated by MTSVD regularization algorithm with time-dependent transmission rate and data-specific regularization parameter, $\alpha$. a Short-term forecasting curves with confidence intervals for Ebola epidemic in Sierra Leone generated from 11,16, 21 and 26 weeks of data used to project 5 weeks forward. b Short-term forecasting curves with confidence intervals for Ebola epidemic in Liberia generated from 13, 15, 17 and 19 weeks of data used to project 2 weeks forward. c Short-term forecasting curves with confidence intervals for Measles Outbreak in London generated from 10, 12, 14 and 16 weeks of data used to project 2 weeks forward. d Short-term forecasting curves with confidence intervals for Influenza in San Francisco generated from 18, 22, 26 and 30 days of data used to project 4 days forward

7 Discussion and Concluding Remarks

Static SEIR epidemic models that assume constant transmission rates tend to overestimate epidemic impact owing to the assumption of early exponential epidemic growth. Yet, disease transmission is not a static process, and a number of factors affect the transmission dynamics during an epidemic including the effects of reactive behavior changes, control interventions (e.g., school closures, market closures), and spatial heterogeneity that can dampen or amplify disease transmission rates. Indeed, several studies have reported sub-exponential growth patterns in case incidence even during the first few generations of disease transmission across a range of infectious disease outbreaks including HIV/AIDS (Colgate et al. 1989; Szendroi and Csnyi 2004; Viboud et al. 2016), Ebola (Viboud et al. 2016; Chowell et al. 2015), and foot-and-mouth disease (Viboud et al. 2016). In a recent study (Viboud et al. 2016), the authors investigated this early ascending phase for 20 infectious disease outbreaks using a generalized growth model, in which a “deceleration of growth” parameter modulates the early epidemic phase. Findings revealed significant diversity in the early dynamics of epidemic growth across infectious disease outbreaks, highlighting the presence of sub-exponential growth, which contrasts with the traditional assumption of early exponential epidemic spread (Viboud et al. 2016).

Slower than exponential epidemic growth could be derived by models that incorporate transmission rates that decline over time (Chowell et al. 2016). Incorporating time-dependent transmission rates in epidemic models is crucial to reliably forecast disease spread in a population. For this purpose, in this paper we introduced a novel approach for estimating the transmission rate of an epidemic in near real time for SEIR-type epidemics in order to generate informative forecasts of epidemic impact. We demonstrate the practical utility of our methodology using synthetic and real outbreak data for influenza and Ebola in various settings.

In summary, we have introduced a novel nonparametric methodology to estimate the time-dependent changes in the transmission rate during epidemics that can be modeled using the standard SEIR transmission processes. We show that this method is able to provide reasonable forecasts of epidemic impact using different regularization techniques and varying the length of the early epidemic growth phase. Our methodology is designed to help with forecasting of emerging and re-emerging infectious diseases, and it could be adapted to incorporate other additional epidemiological (e.g., varying levels of infectiousness) and transmission (e.g., environmental vs. close contact transmission) mechanisms.

Appendix

1.1 Theoretical Analysis

In what follows, we show that gentle regularization

$$\begin{aligned} \beta _\alpha :=\sum _{i=1}^{n}\omega _\alpha (\lambda _i)\frac{(u_i,f_\sigma )}{\lambda _i}v_i:=R_{\alpha ,h}f_\sigma \quad \text{ with }\quad \omega _\alpha (\lambda )=\left\{ \begin{array}{ll} 1, &{} \lambda \ge \sqrt{\alpha } \\ \frac{\lambda }{\sqrt{\alpha }}, &{} \lambda <\sqrt{\alpha } \\ \end{array} \right. \end{aligned}$$

(11)

has a certain optimal property, which may be the reason for some computational advantage it has over other regularization algorithms. Let $\hat{\beta }$ be the exact solution to $A\beta =f$. From (11), one concludes

$$\begin{aligned} \hat{\beta }-\beta _\alpha = \hat{\beta }- R_{\alpha , h}A_h\hat{\beta }+ R_{\alpha ,h}[(A_h-A)\hat{\beta }+f-f_\sigma ], \end{aligned}$$

and therefore

$$\begin{aligned} ||\hat{\beta }-\beta _\alpha || \le ||\hat{\beta }- R_{\alpha , h}A_h\hat{\beta }|| + ||R_{\alpha ,h}||\,||A||\left[ \frac{||A_h-A||\,||\hat{\beta }||}{||A||}+\frac{||f-f_\sigma ||}{||A||}\right] . \end{aligned}$$

Taking into consideration the obvious estimate $||f||\le ||A||\,||\hat{\beta }||,$ i.e., $\frac{1}{||A||}\le \frac{||\hat{\beta }||}{||f||},$ one obtains

$$\begin{aligned} \frac{||\hat{\beta }-\beta _\alpha ||}{||\hat{\beta }||} \le \frac{||\hat{\beta }- R_{\alpha , h}A_h\hat{\beta }||}{||\hat{\beta }||}+ \underbrace{||R_{\alpha ,h}||\,||A||}_{\mathrm{cond}_{R_{\alpha ,h}}(A)}\left[ \frac{||A_h-A||}{||A||}+\frac{||f-f_\sigma ||}{||f||}\right] . \end{aligned}$$

(12)

In case of a noise-free operator, the first term in (12) measures the loss of accuracy due to a numerical algorithm, and if one passes to the limit in (12) as $\alpha \rightarrow 0^+$, one gets the classical estimate

$$\begin{aligned} \frac{||\hat{\beta }-\beta _\sigma ||}{||\hat{\beta }||} \le \underbrace{||A^{-1}||\,||A||}_{\mathrm{cond}(A)}\frac{||f-f_\sigma ||}{||f||} \end{aligned}$$

(13)

known for un-regularized problems. Hence, the product $||R_{\alpha ,h}||\,||A||$ may be understood as the generalized condition number.

Now assuming that both the operator, A, and the right-hand side, f, are noise-contaminated, i.e., $||A_h-A||\le h$ and $||f_\sigma -f||\le \sigma$, we formulate the problem: among all regularizing strategies with the same$cond_{R_{\alpha ,h}}(A)=||R_{\alpha ,h}||\,||A||$, find a strategy that minimizes the error of the computational algorithm, $||\hat{\beta }- R_{\alpha , h}A_h\hat{\beta }||/||\hat{\beta }||$.

Let $\mathcal {N}$ be the fixed value of the generalized condition number $cond_{R_{\alpha ,h}}(A)$. It appears that gentle truncation (11) solves the above problem provided that the regularization parameter, $\hat{\alpha }$, is selected as $\hat{\alpha }= \frac{||A||^2}{\mathcal {N}^2}.$ In other words,

$$\begin{aligned} \beta _{opt}:=\sum _{i=1}^{n}\hat{\omega }_{\hat{\alpha }}(\lambda _i)\frac{(u_i,f_\sigma )}{\lambda _i}v_i:=\hat{R}_{\hat{\alpha },h}f_\sigma , \end{aligned}$$

(14)

where

$$\begin{aligned} \hat{\omega }_{\hat{\alpha }}(\lambda )=\left\{ \begin{array}{l@{\quad }l} 1, &{} \lambda \ge ||A||/\mathcal {N} \\ \mathcal {N}\lambda /||A||, &{} \lambda <||A||/\mathcal {N}.\\ \end{array} \right. \end{aligned}$$

(15)

Indeed, assume the converse. From (11) and (12), one has

$$\begin{aligned} ||\hat{\beta }-R_{\alpha ,h}A_h\hat{\beta }||=\left\| \hat{\beta }-\sum _{i=1}^{n}\omega _\alpha (\lambda _i)\frac{(u_i,A_h\hat{\beta })}{\lambda _i}v_i\right\| . \end{aligned}$$

(16)

Notice that

$$\begin{aligned} (u_i,A_h\hat{\beta }) = (A^*_hu_i,\hat{\beta }) = \lambda _i(v_i,\hat{\beta }). \end{aligned}$$

(17)

According to (16) and (17), one concludes

$$\begin{aligned} ||\hat{\beta }-R_{\alpha ,h}A_h\hat{\beta }||^2=\left\| \hat{\beta }-\sum _{i=1}^n\omega _\alpha (\lambda _i)(v_i,\hat{\beta })v_i\right\| ^2 =\sum _{i=1}^n(1-\omega _\alpha (\lambda _i))^2|(v_i,\hat{\beta })|^2. \end{aligned}$$

Let $\bar{R}_{\bar{\alpha },h}:=\sum _{i=1}^{n}\bar{\omega }_{\bar{\alpha }}(\lambda _i)\frac{(u_i,\,\cdot \,)}{\lambda _i}v_i$ be some other strategy with $cond_{R_{\alpha ,h}}(A)=\mathcal {N}$ that results in a higher accuracy of the algorithm as compared to $\hat{R}_{\hat{\alpha },h}$. Then, there exists $\lambda _j$, $\,0<\lambda _j\le ||A_h||$, such that

$$\begin{aligned} (1-\bar{\omega }_{\bar{\alpha }}(\lambda _j))^2<(1-\hat{\omega }_{\hat{\alpha }}(\lambda _j))^2. \end{aligned}$$

(18)

Since $0\le \omega _\alpha (\lambda )\le 1$ for all $\alpha >0$ and $0<\lambda \le ||A_h||$, (15) and (18) imply

$$\begin{aligned} 1-\bar{\omega }_{\bar{\alpha }}(\lambda _j)<\left\{ \begin{array}{l@{\quad }l} 0, &{} \lambda _j\ge ||A||/\mathcal {N} \\ 1-\mathcal {N}\lambda _j/||A||, &{} \lambda _j<||A||/\mathcal {N}.\\ \end{array} \right. \end{aligned}$$

The first case is not possible. The second case yields $\bar{\omega }_{\bar{\alpha }}(\lambda _j)>\mathcal {N}\lambda _j/||A||$. Hence

$$\begin{aligned} ||\bar{R}_{\bar{\alpha },h}u_j||^2= & {} \left\| \sum _{i=1}^n\bar{\omega }_{\bar{\alpha }}(\lambda _i)\frac{(u_i,u_j)v_i}{\lambda _i}v_i\right\| ^2 =\left[ \frac{\bar{\omega }_{\bar{\alpha }}(\lambda _j)}{\lambda _j}\right] ^2\,| (u_j,u_j)|^2>\frac{\mathcal {N}^2}{||A||^2}||u_j||^2\\= & {} \frac{\mathcal {N}^2}{||A||^2}, \end{aligned}$$

which proves that $cond_{\bar{R}_{\bar{\alpha },h}}(A) = ||\bar{R}_{\bar{\alpha },h}||\,||A||>\mathcal {N}.$ Thus, we arrive at a contradiction, and the choice of $\hat{R}_{\hat{\alpha },h}$ by (14)–(15) is, in fact, optimal.

Fig. 8

(Color figure online) Noisy data used to quantify uncertainty in the transmission rate $\beta _\alpha (t)$ together with 95% confidence intervals and mean values of $\beta _\alpha (t)$ reconstructed from full incidence data set for EVD in Sierra Leone—Western Areas Urban and Rural. a Real EVD incidence data $C'(t)$ along with 2000 noisy incidence curves obtained by adding Poisson noise to the values of $C'(t)$—Western Area Urban. b Mean values of time-dependent $\beta _\alpha (t)$ along with 95% confidence intervals recovered by MTSVD regularization procedure—Western Area Urban. c Real EVD incidence data $C'(t)$ along with 2000 noisy incidence curves obtained by adding Poisson noise to the values of $C'(t)$—Western Area Rural. d Mean values of time-dependent $\beta _\alpha (t)$ along with 95% confidence intervals recovered by MTSVD regularization procedure—Western Area Rural

Fig. 9

(Color figure online) Comparison of forecasting curves generated from early incidence data for Ebola epidemic in Sierra Leone by MTSVD regularization algorithm—Western Areas Urban and Rural. a Forecasting incidence curves generated by MTSVD method from 6, 11, 16, 21 and 26 weeks of data, respectively, as compared to actual incidence data—Western Area Urban (Sierra Leone). b Forecasting incidence curves generated by MTSVD method from 7, 12, 17 and 22 weeks of data, respectively, as compared to actual incidence data—Western Area Rural (Sierra Leone)

Fig. 10

(Color figure online) Noisy data used to quantify uncertainty in the transmission rate $\beta _\alpha (t)$ together with 95% confidence intervals and mean values of $\beta _\alpha (t)$ reconstructed from full incidence data set for EVD in Liberia—Montserrado and Gueckedou Districts. a Real EVD incidence data $C'(t)$ along with 2000 noisy incidence curves obtained by adding Poisson noise to the values of $C'(t)$—Montserrado District. b Mean values of time-dependent $\beta _\alpha (t)$ along with 95% confidence intervals recovered by MTSVD regularization procedure—Montserrado District. c Real EVD incidence data $C'(t)$ along with 2000 noisy incidence curves obtained by adding Poisson noise to the values of $C'(t)$—Gueckedou District. d Mean values of time-dependent $\beta _\alpha (t)$ along with 95% confidence intervals recovered by MTSVD regularization procedure—Gueckedou District

Fig. 11

(Color figure online) Comparison of forecasting curves generated from early incidence data for Ebola epidemic in Liberia by MTSVD regularization algorithm—Montserrado and Gueckedou Districts. a Forecasting incidence curves generated by MTSVD method from 6, 10, 14 and 18 weeks of data, respectively, as compared to actual incidence data—Montserrado District (Liberia). b Forecasting incidence curves generated by MTSVD method from 6, 12, 18 and 24 weeks of data, respectively, as compared to actual incidence data—Gueckedou District (Liberia)

1.2 Additional Numerical Results

The districts Western Area Urban and Western Area Rural are 2nd of 14th districts in Sierra Leone. Freetown, the capital and the largest city in Sierra Leone, is located in Western Area Urban. Population for the two districts are 1.1 million and 500 thousand, respectively, and these two districts were primary hotspots of the 2014 EVD outbreak. Utilizing weekly data sets from these two regions, we approximate $\beta _\alpha (t)$ by MTSVD regularization method. Figure 8 gives these results. We use 1000 noisy data sets to quantify the uncertainty. It appears that the transmission rate was effectively reduced in the urban district, but that this reduction was more erratic in the rural area. In the rural area, the decline in speed and behavior more closely matches the country-wide result. The forecasting curves for both districts are given in Fig. 9.

The 2014 outbreak in Liberia consisted of 10,678 cases and 4810 deaths. The experiments are conducted with the country-wide data for the outbreak as well as for two of the country’s districts: Montserrado and Gueckedou. Montserrado district is home to Monrovia, the capital of Liberia, and two of its infected individuals were responsible for the outbreak in Nigeria and for the cases in the USA. Gueckedou is the site of the index case for the 2014 outbreak and is located in the vicinity of the conflux of borders between Liberia, Sierra Leone and Guinea.

Figure 10 gives the uncertainty quantification for 2000 noisy curves. Figure 11 illustrates the forecasting results. For these Liberia districts, we see similarity in the behavior of $\beta _\alpha (t)$ for the urban district of Montserrado as compared to the country as a whole. The rural district exhibits a slower decline in the transmission rate.