Nonlinear phenomena of contact in multibody systems dynamics: a review

Abstract

In the present work, an introduction to the contact phenomena in multibody systems is made. The different existing approaches are described, together with their most distinctive features. Then, the term of coefficient of restitution is emphasized as a tool to characterize impact events and the algorithm for calculating the relative indentation between two convex-shaped bodies is developed. Subsequently, the main penalty contact models developed in the last decades are presented and developed, analysing their advantages and drawbacks, as well as their respective applications. Furthermore, some models with specific peculiarities that could be useful to the reader are included. The aim of this work is to provide a resource to the novice researcher in the field to facilitate the choice of the appropriate contact model for their work.

1 Introduction

Multibody system dynamics, often denoted as MSD, has its origins in the work made on the field of dynamics by Lagrange, thanks to previous studies of big names such as Galileo, Kepler, Brahe or Newton. In his Mécanique Analytique, Lagrange laid the foundations for the formulation and resolution of complex mechanical systems [1]. At the end of the twentieth century, the technological development of computers took this methodology to a new level, with figures such as Shabana, Pfeiffer, Nikravesh or Lankarani, who started the modern MSD [2,3,4,5,6,7]. Nowadays, its applications are countless: robotics [8, 9], mechanical components analysis [10, 11], vehicle dynamics [12,13,14], biomechanical studies [15,16,17], among others [18,19,20].

In brief, a multibody system is defined as a set of bodies whose relative motion can be restricted by kinematic joints and that is subjected to the action of external forces [21]. Bodies, considered as groups of material points, can be rigid or deformable. They are said to be rigid when it is assumed that their deformations are small enough and they do not affect the global motion produced by the body. On the other hand, a flexible body is elastic: that is, it undergoes reversible deformations that disappear when the external force that produces them ceases. Bodies usually are assumed to be completely rigid, so their modelling process is easier [5]. Kinematic joints secure the connection between two or more bodies, constraining the relative motion between them. The kind of joint defines the type of motion between the links, the most typical being the revolute and the translational joints [22]. The forces applied on the different components of the system have their origin in phenomena such as gravity or inertia. They can be punctual or state functions of the bodies of the system.

Contact–impact phenomena, which are present in almost all branches of engineering [23,24,25], are included in the latter. Contact forces and, specifically, impact events are responsible for the appearance of harmful phenomena in mechanical elements such as vibrations [26], wave propagation [27], fatigue [28], wear [29], crack [30], etc. Sudden changes take place during impact processes, in which the conditions of the mechanical system vary in short times. This implies the appearance of great magnitude forces, energy dissipation and discontinuities of velocities and accelerations, among other issues. They are complex events, difficult to model, that pose a challenge for the engineers due to the large number of variables that must be taken into account: geometry of the contacting surfaces, material properties, inclusion of friction phenomena and, specially, how to characterize the contact itself [5, 6, 31].

The remaining of the paper is organized as follows. In Sect. 2, some considerations about the contact process are presented. Later, the main approaches taken when modelling the contact event are introduced and described in Sect. 3. Subsequently, the main algorithm to calculate the relative indentation between bodies in penalty models is developed in Sect. 4. Then, contact models are presented in Sect. 5, starting with the fully elastic approaches and introducing later those that consider damping phenomena, then comparing their main differences. Finally, the main conclusions are drawn in Sect. 4, proposing some starting points for future works.

2 Considerations about the contact phenomena

The problem of contact is a research field with a long history, being a topic of interest to researchers in the last decades, with the development of commercial software [32, 33] and the publication of numerous books about this subject [34,35,36,37]. In Antiquity, Aristotle already proposed the use of levers to increase the impact force [38]. Later, different figures such as Galileo, Descartes or Euler made some works about the contact phenomenon [39, 40]. According to Kozlov and Treschëv [41], the first detailed study about impact events dates from 1668, this being proposed by the Royal Society. Wallis, Wren and Huygens presented their respective works about the subject [42], where they exposed their theories about the collision between bodies, based on the principle of conservation of momentum. Newton later used Wren’s experimental results in his Philosophiæ Naturalis Principia Mathematica [43], which was published in 1687, and defined the concept of coefficient of restitution to explain the energy losses that take place during the impact event. This element simplified enormously all the phenomena that occur around the contact process, explaining the success of Newton’s work, which is the basis of classical mechanics. This approach to the study of the impact event, from the point of view of contact mechanics, poses the contact region as a spring–damper pair, allowing to model the contact process as a continuous function, which represents more faithfully a process that is dynamic itself [44]. The mathematical relation that associates the stresses (forces) experienced by the material with the deformations suffered throughout the process is called material constitutive law [45]. Dynamic analysis of multibody systems requires models that provide reliable and accurate results of the contact forces [8, 46]. Thus, the study of the force–indentation relation and the determination of the exact value of the coefficient restitution are two key tasks.

Gilardi and Sharf proposed four types of impacts and then added up another one defined by Wang and Mason [47]: central or collinear, eccentric, direct, oblique and tangential (see Fig. 1). A central impact is that in which the mass centres of the two bodies are in the impact line, whereas an eccentric contact takes place when at least one of the mass centres is not on the impact line. On the other hand, an impact is direct if the initial velocities of both bodies are along the impact line, or oblique if at least one of these velocities is not along said line. Finally, a tangential impact is that in which both bodies have no component of their velocities along the line of impact.

Fig. 1

Different types of impact, according to the classification defined by Gilardi and Sharf [48]: a central, b eccentric, c direct, d oblique, e tangential

If the energy dissipation is defined as the criteria to classify the contact event, a distinction is made between elastic impacts (all energy is conserved), inelastic collisions (part of the energy is dissipated) or plastic contacts (all energy is transmitted from one body to the other) [37, 48].

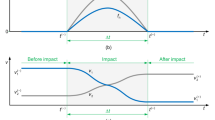
Two main phases are identified in a contact process: the compression, approximation or load stage and the restitution, separation or unload phase [47, 49]. The compression stage starts when two bodies get into contact and ends when the maximum indentation is reached, that is, when the relative normal velocity is null. If a fully elastic impact is considered, the highest force values take place in this instant. In this time, the restitution phase starts, in which the two bodies start to separate. This second stage ends when deformations in both bodies cease. Throughout these two phases, initial kinetic energy of the two bodies has transformed into elastic deformation energy during the compression phase and then turned into kinetic energy again. If the collision is not considered as fully elastic, part of this energy is dissipated in the form of vibratory waves that propagates through the contacting bodies (actually, bodies do not deform uniformly, it is a process that starts on the impact region and then spreads to the rest of the body). Another part of the energy is dissipated in the form of plastic, permanent deformations and material self-damping (usually in the form of heat), among other phenomena [48].

As it has been stated above, the proper definition of the values of the variables is critical if consistent results are to be sought. In particular, the coefficient of restitution is one of the most important magnitudes. Usually denoted by $e$ [48] or $c_{r}$ [31, 50], it takes values between 0 and 1, being 0 associated with a perfectly plastic impact and 1 related to a fully elastic impact. This magnitude is a function of different parameters of the contacting bodies (geometry, material properties, etc.) and the boundary conditions of the system (initial velocities of the bodies, inclusion of friction phenomena, etc.). Several models of coefficient of restitution are identified [48]:

• Poisson’s model: defined as the ratio of the impulse during the restitution phase to the one produced in the compression stage [47, 51]

$$ c_{r} = \frac{{P_{\text{r}} }}{{P_{\text{c}} }} $$

(2.1)

where $P_{\text{r}}$ is the impulse of the restitution phase and $P_{\text{c}}$ denotes the compression impulse.

• Newton’s approach is the most used one, being defined as the quotient of the relative velocities after and before the impact [43, 52]

$$ c_{r} = - \frac{{C_{f} }}{{C_{0} }} $$

(2.2)

$C_{f}$ denotes the relative velocity between two bodies after the collision, whereas $C_{0}$ accounts for the relative velocity before the impact. Although the masses of the contacting bodies do not appear explicitly in the definition of $c_{r}$, final velocities are related to these through the hypothesis of conservation of momentum [43].

• Stronge defined, in terms of energy, a relation between the square of the velocity and the ratio of the elastic deformation energy released during restitution to the work produced by the normal force throughout the compression phase [53]

$$ c_{r}^{2} = \frac{{W_{\text{r}} }}{{ - W_{\text{c}} }} $$

(2.3)

where $W_{\text{r}}$ is the work done by the normal force during the restitution phase and $W_{\text{c}}$ denotes the compression phase work. Later, Stronge introduced an energy loss term associated with the wave propagation phenomena during the deformation process [54].

• Hedrih (Stevanović) proposed, in the context of the dynamical analysis of central collision of two balls rolling along a curvilinear circle trace, a definition of the coefficient of restitution based on the ratio of the relative angular velocities after and before the impact [55,56,57]

$$ c_{r} = - \frac{{\omega_{2}^{\left( + \right)} - \omega_{1}^{\left( + \right)} }}{{\omega_{2}^{\left( - \right)} - \omega_{1}^{\left( - \right)} }} $$

(2.4)

being $\omega_{1}^{\left( + \right)}$ and $\omega_{2}^{\left( + \right)}$ the angular velocities of bodies 1 and 2 after the impact, respectively, and $\omega_{1}^{\left( - \right)}$ and $\omega_{2}^{\left( - \right)}$ the angular velocities before at the when contact event starts.

3 Contact modelling approaches

There are two main approaches when modelling the contact event: the nonsmooth approach and the models based on contact forces [58,59,60]. Three main factors differentiate these two methods: the location of the contact points, the relative indentation between the bodies and the definitions of the contact forces [50]. The main features of each methodology will be presented and developed in the following pages.

3.1 Nonsmooth methods

Nonsmooth models, also known as piecewise methods [61], rigid approaches [62] or momentum-based methods [63], assume two features: the deformations experienced by the bodies involved in the process are small compared to their geometry, so they can be considered as rigid solids, and that the contact process is almost instantaneous [62]. Thus, the potential energy of the system does not change, and the rest of external forces can be neglected. The dynamic analysis is divided into two intervals (before and after the impact), to which secondary phases are added (stick-slip, inverse motion, etc.) [48]. Two coefficients are used to model the phenomena of energy transfer and energy dissipation: the coefficient of restitution and the impulse ratio [64]. To deal with this kind of models, two methods are usually utilized: the linear complementarity problem (LCP, [6, 65, 66]) and the differential variational inequality (DVI, [67,68,69]).

The LCP uses unilateral constraints when proposing the dynamic analysis to calculate the contact forces, under the principle of preventing relative indentation between bodies from happening. Only a minimum value of penetration is allowed to take place in order to detect the initial time of contact, and it is not then utilized in the calculation of the impulse magnitude. This approach uses an explicit formulation of the unilateral constraints between the bodies, in which the contact points coincide [70]. The idea of complementarity applied to the contact event in MSD is expressed in two ways: the velocities or the impulses are null, and the product of these two magnitudes must be always zero [70,71,72]. On the other hand, it is assumed that the impulsive forces cannot be negative: that is, bodies are not attracted to each other, so, when contact is not active (before or after the impact), these forces are not active. This leads to an efficient modelling of the contact, from a computational point of view. However, different strategies must be considered to apply when dealing with specific situations, such as a permanent contact or an intermittent one [6]. This makes it difficult to develop a generic LCP-based program for MSD [73]. Furthermore, the inclusion of friction phenomena in an LCP-modelled contact event can lead to multiple or no solutions [74], as well as to a violation of the principle of conservation of energy [75].

Instead, the DVI is considered as a suitable tool for working with systems in which multiple contacts happen simultaneously, showing an acceptable behaviour when dealing with friction phenomena [31]. This methodology does not use time differentials as small as those utilized by models based on contact forces, thus allowing the use of simple integration schemes for the dynamic analysis [67]. However, the algorithmic procedures of this DVI approach are highly complex [68, 76].

One of the first works based on the nonsmooth approach was developed by Signorini, who introduced the impenetrability condition through a LCP [77]. Later, Moreau [78] and Panagiotopoulos [79] applied the concept of complementarity to the dynamic analysis of systems based on a nonsmooth approach. Yigit et al. [80, 81] developed, in a two-part paper, a dynamic, computational model of a rotating beam subjected to multiple impact events, then being the obtained results compared with those from experimental tests. Pfeiffer and Glocker [6] took the previous work of these authors a step further, using it on the study of multibody systems with unilateral contacts. The reader interested in studies based on a nonsmooth approach is referred to the works by Flores [82, 83], Ebrahimi [84] and Khulief [85, 86].

3.2 Penalty methods

In contrast to nonsmooth methods, approaches based on contact forces are proposed. They are also known as penalty [87], compliant [88] or regularized [89] models. Regularized makes reference to the process of reformulating a problem, trying to get a solvable representation of it [90]. Applied to the study of contact forces, it can be said that a model of this kind can approximate the contact phenomenon in such a way it can be properly modelled. Penalty methods are characterized by their simplicity, computational efficiency and implementation easiness [31, 91], allowing them to deal with specific events such as repeated impacts properly [8, 92]. These approaches are widely used in nowadays commercial FEM and MBD software [93,94,95,96]. Penalty models define contact forces as continuous functions of the relative penetration (and its temporal derivative) of the contacting bodies [87, 97], which are supposed to be deformable (hence, the adjective compliant, as the surfaces of both bodies couple) [98]. The contact regions of each body are modelled as a set of spring–damper elements scattered over their surfaces (see Fig. 2). Most of the models based on this approach consist of two terms: one associated with the elastic component (the spring) and another related to energy dissipation (the damper). These terms are calculated on the basis of the relative indentation, its time derivative, the material properties of the contacting bodies and the geometry of their surfaces [31]. These forces prevent penetration between the bodies from occurring, making it unnecessary to define unilateral restrictions. However, this approach also presents some drawbacks. The main handicap is the proper choice of the parameters associated with the definitions of the forces such as, for example, the equivalent stiffness or the degree of nonlinearity of the indentation. This is critical in systems with complex geometries and nonmetallic materials [99, 100]. Another disadvantage is the inclusion of high frequencies in the system due to the definition of excessively stiff springs. This forces to increase the discretization of the dynamic analysis, making the computing time to skyrocket. In these models, the proper detection of the initial instant of contact is critical [88, 101,102,103].

Fig. 2

Spring–damper model that characterizes the contact process between a foot and the ground. Two sets are displayed, one for each contact direction (normal and tangential)

One of the first works based on this approach was developed by Hertz [104], who only considered the elastic component. Later, Kelvin and Voigt [34] introduced the damping term, which was subsequently optimized by Hunt and Crossley [105]. In the last decades, several authors have developed new models based on the work of Hunt and Crossley, some of them being applicable to certain types of impacts [106, 107] and others being generalizable to the entire range of the coefficient of restitution [89, 108, 109]. Again, some works based on these methods are left to the interested reader [8, 19, 24, 110].

The present work aims to be a continuation and an upgrade of the content developed in previous reviews focused on contact force models based on penalty approaches [50, 98, 111], including the most recent advances on this subject.

4 Contact formulation in penalty models

In this section, the general algorithm for calculating the indentation between two bodies is described, for its implementation in contact models based on penalty approaches. Following the system proposed in Figure (a), the absolute velocities of each body, $\dot{r}_{i}$ and $\dot{r}_{j}$, are defined. The potential points of contact are denoted by $P_{i}$ and $P_{j}$. The contact evaluation at each moment of the dynamic analysis time involves the calculation of three variables [98]: the position of the potential points of contact in each body, their Euclidean distance (vector $d$ in Fig. 3) and the relative normal velocity. Positive values of $d$ indicate that there is no contact, whereas negative values mean that there is indentation between the bodies. The change in sign indicates the transition from separation stage to contact phase and vice versa [101]. On the other hand, positive values of the relative normal velocity indicate that bodies are getting closer to each other, whereas negative values mean a separation of the bodies.

Fig. 3: a

Two potentially contacting bodies, with their respective potential points, located with respect the global reference system, in a state of separation; b the same two bodies, now contacting

The nomenclature defined by Flores and Machado in [31] and [98], respectively, will be used to define the variables. The vector between the potential points of contact or distance vector $\vec{d}$ is defined by the following expression

$$ \vec{d} = \overrightarrow {{r_{j}^{P} }} - \overrightarrow {{r_{i}^{P} }} $$

(4.1)

where $\overrightarrow {{r_{i}^{P} }}$ and $\overrightarrow {{r_{i}^{P} }}$ are described with respect to the global reference system [3]

$$ \overrightarrow {{r_{k}^{P} }} = \overrightarrow {{r_{k} }} + \overrightarrow {{s_{k}^{P} }} = \overrightarrow {{r_{k} }} + A_{k} \cdot \overrightarrow {{s_{k}^{\prime P} }} \quad \left( {k = i,j} \right) $$

(4.2)

where $\overrightarrow {{s_{k}^{P} }}$ is the position vector of the contact point with respect to the local reference system, in global system coordinates, $A_{k}$ is the rotational transformation matrix that describes the orientation of the local system of the body $k$ with respect to the global one and $\overrightarrow {{s_{k}^{\prime P} }}$ is the position vector of the contact point with respect to the local system, in local system coordinates [3]. In two-dimensional spaces, $A$ is given by

$$ A_{i} = \left[ {\begin{array}{*{20}c} {a_{11} } & {a_{12} } \\ {a_{21} } & {a_{22} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \psi_{k} } & { - \sin \psi_{k} } \\ {\sin \psi_{k} } & {\cos \psi_{k} } \\ \end{array} } \right]\quad \left( {k = i,j} \right) $$

(4.3)

where $\psi_{k}$ is the rotation angle of the local system with respect to the global one.

On the other hand, the normal unit vector, $\vec{n}$, is defined in the direction normal to the contact plane [98], being the vector product of this magnitude and vector $\vec{d}$ the minimum distance condition between the bodies. However, this is not enough to define univocally the potential points of contact, these defined as the points where the maximum indentation takes place [31]. Two additional conditions must be established: $\vec{d}$ must be collinear with $\overrightarrow {{n_{i} }}$ (vector normal to the contact plane, associated with body i) and $\overrightarrow {{n_{j} }}$ (vector normal to the contact plane, associated with body j) must be collinear with $\overrightarrow {{n_{i} }}$, that is, with the normal direction $\vec{d}$ [31]. These three conditions form a system of nonlinear equations that must be solved iteratively. Once the potential points of contact are defined, the value of indentation is obtained

$$ \delta = \sqrt {\vec{d} \cdot \vec{d}} $$

(4.4)

Likewise, the relative normal velocity is obtained as a projection of the contact velocity onto the direction normal to the contact plane

$$ \overrightarrow {{v_{N} }} = \vec{\delta } = \vec{n}\cdot\left( {\overrightarrow {{\dot{r}_{j}^{P} }} - \overrightarrow {{\dot{r}_{i}^{P} }} } \right) $$

(4.5)

where $\overrightarrow {{\dot{r}_{i}^{P} }}$ and $\overrightarrow {{\dot{r}_{j}^{P} }}$ are the time derivatives of the position vectors, in global coordinates, of the potential points of contact. This definition is only applicable to contact events between convex rigid solids, in which the contact area is reduced to a single point. This approach will be valid as long as a single contact plane is defined [98].

5 Definition and comparison of several penalty contact models

In this section, different constitutive laws used to model contact-impact events in multibody systems will be presented and described. Both elastic and inelastic approaches will be introduced, following a chronological order to show the evolution of this subject of study. The mathematical expressions of all models are listed in Table 1.

Table 1 Contact models developed in Chapter 5

The first model and also the simplest is the one described by Hooke in 1661 [112], which is defined as [31, 113]

$$ F_{N} = k \cdot \delta $$

(5.1)

where $k$ is the spring stiffness used to model the contact and $\delta$ represents the indentation given by Eq. (4.4). The value of $k$ can be obtained by different analytical expressions, depending on the case study, by simulations based on the Finite Element Method (FEM) or by experimental tests [114,115,116]. The main weakness associated with this model is the accurate quantification of the value of $k$, since it is a function of the geometries and materials of the contacting bodies. Likewise, the assumption of a linear relation between indentation and contact force is excessively rough, since other features must be considered when defining the contact event, such as the shape of the contacting surfaces or the materials of the bodies, among other factors. Furthermore, Hooke’s model does not consider the energy dissipation phenomena that take place during contact-impact events.

The next model described is the one proposed by Heinrich Hertz in 1881 [104], which was introduced previously. While he was investigating on Newton’s optical interface fringes, Hertz observed that the contact area between a glass sphere placed on top of a lens was elliptical [34, 104, 117]. The Hertzian contact law defines contact force as a function of the indentation through a nonlinear relation [118]

$$ F_{N} = K \cdot \delta^{n} $$

(5.2)

where $K$ is the contact stiffness parameter and $n$ is an exponent that quantifies the degree of nonlinearity of the force–indentation relation. The value of the stiffness can be calculated numerically [119], obtained by experimental tests [120] or defined theoretically as a function of the geometries of the contacting bodies, when working with simple geometries. For a contact between two spheres, $i$ and $j$, with radii $R_{i}$ and $R_{j}$, respectively [34]

$$ K = \frac{4}{{3\left( {\sigma_{i} + \sigma_{j} } \right)}} \cdot \sqrt {R_{\text{eff}} } \quad R_{\text{eff}} = \frac{{R_{i} \cdot R_{j} }}{{R_{i} + R_{j} }} $$

(5.3)

where $R_{\text{eff}}$ is the equivalent radius. $R_{i}$ and $R_{j}$ have the same ± sign if the contact is external (convex surfaces) and opposite if it is an internal one (one of the surfaces is concave—the sphere with the largest radius—, with a negative radius value, whereas the other sphere is convex and its radius is positive) [121]. $\sigma_{i}$ and $\sigma_{j}$ are material parameters given by

$$ \sigma_{l} = \frac{{1 - v_{l}^{2} }}{{E_{l} }}\quad \left( {l = i,j} \right) $$

(5.4)

being $v_{l}$ and $E_{l}$ the Poisson’s ratio and the Young’s modulus of each sphere, showing the influence of the material properties in the contact event.

On the other hand, the expression below is used when defining the contact process between a sphere $i$ and a planar surface $j$ [34, 100]

$$ K = \frac{4}{{3\left( {\sigma_{i} + \sigma_{j} } \right)}} \cdot \sqrt {R_{i} } $$

(5.5)

Last, the following expression is used to characterize the parameter $K$ in an interaction between two square-shaped planar surfaces $i$ and $j$, the length of their sides being $2a$ [122]

$$ K = \frac{a}{{0.475\left( {\sigma_{i} + \sigma_{j} } \right)}} $$

(5.6)

On the other hand, the nonlinearity exponent $n$ takes a value of 3/2, according to the work by Hertz [118], who assumed a parabolic distribution of the stresses in the contact area. Expressions in the same way ($f(x) = A \cdot x^{n}$) based on experimental results or numerical calculations use the value $n = 1.5$ for metallic materials, changing it when working with other materials such as glass or different polymers [101, 123, 124]. This must not be confused with the Hertzian model just described. Other works hold that this exponent is dependent on the materials of the contacting bodies and the local geometry of the contact area [111].

The model developed by Hertz represented a great advance in relation to the one proposed by Hooke, since it considered several factors that play a central role for the value of the contact force, such as the materials of the bodies and their geometries, as well as the pressure distribution in the contact area, giving physical meaning to the expression of the force. However, this model, like Hooke’s, is based on the theory of elasticity, so it does not consider energy dissipation phenomena, which are present in contact/impact events that take place usually. This makes it applicable only when modelling contacts between perfectly elastic (very rigid) solids with frictionless surfaces and low impact velocities [31, 34, 48]. Another drawback of this approach is the difficulty in obtaining the values of the stiffness parameter when contact is not punctual, but linear or even superficial [100, 121]. For example, in rectangular contact areas that are generated when two cylindrical bodies with parallel axis touch, the physical meaning of $K$ is not so straightforward and it cannot be estimated using the Hertzian theory. Brändlein et al. proposed an alternative model in the same way as Hertz’s, but modifying the value of $n$ and decoupling $K$ from the radii of the cylinders and making it a function of the duration of the contact event [125]. Also, Hertz’s model assumes a little contact area, compared to the curvature of the contacting surfaces. This is good when surfaces are nonconformable, but it is ineffective when working with conformable ones [117].

To solve the energy dissipation problem and make Hertz’s model applicable to contact events with soft materials and/or higher impact velocities [126, 127], Goldsmith considered plastic deformation and strain rate effects and proposed a modified Hertzian model to characterize the contact event between two spheres [34, 128].

$$ F_{N} = F_{\hbox{max} } \cdot \left( {\frac{{\delta - \delta_{P} }}{{\delta_{\hbox{max} } - \delta_{P} }}} \right)^{n} $$

(5.7)

where $F_{\hbox{max} }$ and $\delta_{\hbox{max} }$ are the maximum values of contact force and indentation (they occur simultaneously [48, 128]), respectively, while $\delta_{p}$ denotes the permanent indentation that remains, being a measure of the dissipated energy throughout the process. The interested reader can find in [128] the development of the different parameters.

Although the model proposed by Goldsmith quantifies in some way the energy dissipation process that takes place in the contact event, it is based on the work by Hertz, focused on impacts of elastic solids in which the energy is conserved throughout the process. When a body experiences cyclic loads, the energy loss associated with internal damping gives rise to a hysteresis loop that can observed in the force–indentation graph [129].

Before the model proposed by Goldsmith [130], Meyer had already defined in 1874 the mathematical foundations in the form of a differential equation of a model that considered the so-called internal friction of the material [131]. However, the independent works by Kelvin [132] and Voigt [133] were what gave name to a contact model that characterizes the contact/impact event between two bodies as a system that consists of a linear spring in parallel with a linear damper, being its expression [34]

$$ F_{N} = k\cdot\delta + D\cdot\dot{\delta } $$

(5.8)

where the first term corresponds to the elastic component associated with the spring (as in Hooke’s model) and the second term accounts for the energy dissipation carried out by the damper during the process. Again, $k$ and $\delta$ represent the stiffness parameter and the indentation, respectively; $D$ is the damping coefficient of the damper and $\dot{\delta }$ refers to the relative normal contact velocity [48]. This model can be found in a wide variety of studies due to its simplicity [134,135,136,137]. For example, Roger and Andrews used K–V’s model to perform a dynamic analysis of planar mechanisms where impacts took place in revolution joints with clearance [138], while Khulief and Shabana applied this model to analyse multibody systems with flexible solids [139]. More recently, Eberle and his co-authors used this model to characterize the contact interaction between the skis and the snow in the context of a study of the vibrations produced during the exercise of alpine skiing [140]. The general consensus is that, although this model stands out for its reliability and simplicity, the response in dynamic systems is not optimal, as it does not consider the nonlinear nature of the impact event. Furthermore, K–V’s model is not recommended when working with high impact velocities, when internal damping is not the main mechanism of energy dissipation [98, 141]. A work by Dubowsky et al. proposed the use of nonlinear relations between the elastic and dissipative components of the contact force and indentation and impact velocity, respectively [142]. In addition, Kelvin–Voigt’s model has some physical inconsistencies. For example, the contact force is not null at the beginning of the contact, when indentation is zero, due to the dissipative component [101]. Likewise, at the end of the end of the restitution phase, penetration is null, and the relative contact velocity is negative, as bodies are separating. Consequently, the contact force is negative, that is, bodies are attracting each other. Finally, considering the damping coefficient to be constant throughout the contact process is not completely consistent from a physical point view [48, 143].

Aiming at reflecting the nonlinear nature of the energy conversion during the contact process, Hunt and Crossley used Hertz’s elastic component term instead of Hooke’s, combined with a nonlinear viscoelastic element [105]

$$ F_{N} = K \cdot \delta^{n} + D \cdot \dot{\delta } $$

(5.9)

where $K$ is again the generalized stiffness parameter, $\delta$ denotes the penetration, $n$ defines the nonlinear exponent factor, $D$ refers to the damping coefficient and $\dot{\delta }$ is the relative normal contact velocity. To ensure that the damping term meets the boundary conditions at the beginning and at the end of the contact event, $D$ is defined so that the dissipative force is in phase with the penetration velocity and is, at the same time, proportional to the indentation [122]

$$ D = \chi \cdot \delta^{n} $$

(5.10)

where $\chi$ is the hysteresis factor associated with the damping phenomenon. Its expression, for this model, is given by [46]

$$ \chi = \frac{{3 \cdot \left( {1 - c_{r} } \right)}}{2} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.11)

where $K$ is the stiffness parameter, $\dot{\delta }^{\left( - \right)}$ denotes the relative contact velocity at the initial instant of the contact event and $c_{r}$ refers to the coefficient of restitution. After substituting Eqs. (5.11) and (5.10) into (5.9) and manipulating them, the following expression is obtained

$$ F_{N} = K \cdot \delta^{n} \cdot \left[ {1 + \frac{{3 \cdot \left( {1 - c_{r} } \right)}}{2} \cdot \frac{{\dot{\delta }}}{{\dot{\delta }^{\left( - \right)} }}} \right] $$

(5.12)

This model relates the energy losses produced throughout the contact process to the internal damping of the materials, which dissipate energy in the form of heat [31]. This damping is a function of the indentation, which is reasonable from a physical point of view, and does not give rise to any physical inconsistency. This model has been used in many different works due to its simplicity and straightforward implementation [144,145,146,147]. Guess and his co-authors carried out an optimization process of the values of $K$ and $D$ to obtain results similar to those obtained in a FEM model [16]. Recently, Jacobs and Waldron used a genetic algorithm to obtain the optimal values of the different parameters from the results of five experiments conducted previously [148]. Almost all authors agree that Hunt and Crossley model is appropriated for contact cases in which the value of the coefficient of restitution is close to unity, when energy dissipation is not excessively significant [89, 149, 150].

From H-C’s model, a wide range of models opens up, developed by different authors to fill its gaps, most of them being focused on determining, through different methods, the expression or the value of the hysteresis factor or the damping coefficient that provides the most consistent results, for all kinds of impact, that its, for the whole range of the coefficient of restitution. Safaeifar and Farshidianfar classified all these models into four different categories, according to the method used to define $\chi$ [151]. The first category groups those models in which the hysteresis factor is obtained from experimental tests. In the second group, an exact equation for determining $\chi$ is proposed, that is, a nonlinear function that relates the hysteresis factor to the physical parameters of the system. The third category considers those models that, from considering a simple assumption, provide an explicit expression of $\chi$ (this group includes Hunt and Crossley’s model). In the fourth group, researchers considered an expression to relate the indentation and its temporal derivative, obtaining an explicit expression of the coefficient of restitution and the hysteresis damping factor. In addition, it has been decided to add a fifth group, in which those models with alternative/innovative approaches that cannot be classified in any of the previously described groups are presented. This classification is shown in Table 1.

5.1 Models based on experimental tests

The first model of this group of experimental approaches is the one developed by Ristow [152], which was applied to the simulation of a granular flow between two chambers with a rectangular profile, both communicated through a rectangular hole. This model considered the flow as a set of spheres with different diameters that can move freely

$$ F_{N} = K \cdot \delta^{3/2} + \chi \cdot m_{\text{eff}} \cdot \dot{\delta } $$

(5.13)

where $m_{\text{eff}}$ is the equivalent mass of the two bodies, defined as

$$ m_{\text{eff}} = \frac{{m_{1} \cdot m_{2} }}{{m_{1} + m_{2} }} $$

(5.14)

being $m_{1}$ and $m_{2}$ the masses of bodies 1 and 2, respectively. The value of $\chi$ was obtained by comparing the output values with the experimental results, in order to get the highest possible consistency. This model was used by Corral and his co-authors to define the contact interaction between a passive robot and the ground [8]. A similar approach to the one presented by Ristow was defined by Lee and Hermann [153]. It was also designed to be used in the simulation of granular flows, in this case a rectangular box from which one side is removed. Schäfer et al. [154] based on Ristow’s to propose a similar expression, also applied to the modelling of impacts between spheres of granular flows, comparing the results obtained with those provided by other approaches.

Later, Falcon et al. [155] proposed a model in which they included the indentation term in the calculation of the dissipative component of the contact force

$$ F_{N} = K \cdot \delta^{3/2} + \chi \cdot \left| {\delta^{\gamma } } \right| \cdot \dot{\delta } $$

(5.15)

where $\gamma$ is a real number that characterizes the nature of the dissipative term, which can be linear ($\gamma = 0$) or nonlinear ($\gamma \ne 0$). For each value of $\gamma$, a corresponding $\chi$ is chosen, so it provides the best adjustment with the experimental results. This model was applied to the experimental study of an inelastic sphere that bounces repeatedly off a flat horizontal surface. When the time between two successive bounces reaches a value in the order of the impact duration, the ball does not no longer bounces, but oscillates on the elastically deformed surface before coming to rest. Falcon and his co-authors showed that, if impact velocity is high enough to neglect the effects of gravity, then $c_{r}$ does not depend on the initial impact velocity, being $\gamma = {\raise.5ex\hbox{$\scriptstyle 1$}\kern-.1em/ \kern-.15em\lower.25ex\hbox{$\scriptstyle 4$} }$. However, if gravity is not negligible, the value of $\gamma$ would have to be defined numerically, in order to get the highest possible degree of consistency with the experimental results [155].

Bordbar and Hyppänen presented another model following the path of Falcon et al. [156]

$$ F_{N} = K \cdot \delta^{3/2} + \chi \cdot \delta^{0.65} \cdot \dot{\delta } $$

(5.16)

The results provided by this model were compared with those provided by FEM simulations, getting a reasonable degree of conformity. Bordbar and Hyppänen obtained the value of the exponent of the indentation included in the dissipative component from the experimental results of a research on the impact between ice particles of Saturn’s rings, being this value 0.65.

Finally, Alizadeh et al. [157] presented a nonlinear contact model between two spheres of a granular flow based on the sum of an Hertzian elastic term and a damper filled with a non-Newtonian fluid

$$ F_{N} = K \cdot \delta^{3/2} + 4 \cdot \pi \cdot \mu \cdot \delta \cdot \dot{\delta }^{{n_{l} }} $$

(5.17)

The values of $\mu$ and $n_{l}$ must be defined experimentally for each material and each type of collision (sphere-sphere or sphere-plane). Unlike previous models, the variable exponent was set on the impact velocity instead of the indentation.

As can be seen, most of the models described in this section have very specific applications, being mostly focused on the field of the discrete element method (DEM), which is out of the scope of this work.

5.2 Models that propose an exact equation for determining $\chi$

This section contains those models that define an exact expression to obtain the hysteresis damping factor from physical parameters of the contact process. This equation does not have an exact solution, but it can be solved numerically [151].

The first model of this group was developed by Herbert and McWhannell [158], who carried out a research on the impact of a mass between two thick plates. It started from the previous work by Hunt and Crossley, defining the same expression for the contact force and proposing a new one for the hysteresis factor:

$$ F_{N} = K \cdot \delta^{3/2} + \chi \cdot \delta^{3/2} \cdot \dot{\delta } $$

(5.18)

$$ \chi = \frac{{6 \cdot \left( {1 - c_{r} } \right)}}{{\left[ {\left( {2 \cdot c_{r} - 1} \right)^{2} + 3} \right]}} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.19)

The difference between the hysteresis loops in the force–indentation graphs of both models is minimal. As Hunt and Crossley’s model, this approach is only applicable to impacts where the value of $c_{r}$ is close to unity. This model has been used by several authors on works on gears or related to underactuated robots [159,160,161].

Later, Goyal et al. [162, 163] did, in a two-part paper, an analysis on the phenomenon of contact, identifying two key aspects: the contact detection and the calculation of the value of the contact force. They proposed the following expressions to calculate the damping coefficient

$$ D = \frac{\xi }{{2 \cdot m_{\text{eff}} \cdot w_{n} }} $$

(5.20)

$$ w_{n} = \sqrt {\frac{K}{{m_{\text{eff}} }}} $$

(5.21)

where $\xi$ is a term related to the coefficient of restitution through

$$ c_{r} = e^{{ - \frac{4 \cdot \xi }{{\sqrt {1 - \xi^{2} } }} \cdot \tan^{ - 1} \left( {\frac{{\sqrt {1 - \xi^{2} } }}{\xi }} \right)}} $$

(5.22)

The contact force is calculated through Eq. (5.8). This model was used, for example, to calculate the forces experienced by a hopping rotochute when it came into contact with the ground. This device was designed to explore interior spaces with rough terrains, leaping over any possible obstacles [164].

The following approach of this group was proposed by Gonthier et al. [89]. It is applicable to nonconformal contacts, in which the contact area is larger and, therefore, cannot be assumed as punctual. The equation of motion was integrated for the whole contact process, obtaining the expression

$$ \frac{{1 + d/c_{r} }}{{\left( {1 - d} \right)}} = e^{{d \cdot \left( {1 + \frac{1}{{c_{r} }}} \right)}} $$

(5.23)

where $d$ is a dimensionless factor defined as

$$ d = a \cdot c_{r} \cdot \dot{\delta }^{\left( - \right)} $$

(5.24)

being $a$ a damping factor given by

$$ \chi = a \cdot K $$

(5.25)

Gonthier and his co-authors approximated $d \approx \left( {1 - c_{r}^{2} } \right)$ in Eq. (5.23), obtaining the following expression for the hysteresis damping factor

$$ \chi = \frac{d}{{c_{r} }} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} = \frac{{\left( {1 - c_{r}^{2} } \right)}}{{c_{r} }} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.26)

The contact force is calculated with the expression defined in Eq. (5.18). This model can be applied to the entire range of values of the coefficient of restitution, without restrictions regarding the initial impact velocity. When $c_{r} = 1$, the hysteresis damping factor is null, so the dissipative component is zero, whereas if $c_{r} = 0$, the dissipative term reaches an infinite value. This is logical from a physical point of view and is in contrast to the rest of models described above. For high values of the coefficient of restitution, the hysteresis loop tends to be symmetrical around the elastic line, whereas for low values, most of the energy is dissipated on the compression phase. This model is often explicitly expressed as a function of the volume of interference and the contact volumetric stiffness, being force per unit volume [98].

Simultaneously and independently, Zhang and Sharf [165] got to the same expression defined in Eq. (5.23), but they did not approximate $d \approx \left( {1 - c_{r}^{2} } \right)$. Both models considered a linear relation between the coefficient of restitution and the initial impact velocity $c_{r} = 1 - \alpha \cdot \dot{\delta }^{\left( - \right)}$, for materials working in the elastic range [34]. Luo and Nahon [166] proposed the same expression described in Eq. (5.23) to define the hysteresis factor of the dissipative term of the contact force, but they defined the contact stiffness in an alternative way

$$ F_{{N,{\text{el\'a stica}}}} = \gamma \cdot \pi \cdot E^{*} \cdot \frac{{A^{\prime } }}{{\tau_{\hbox{max} }^{\prime } }} \cdot \delta_{\hbox{max} } $$

(5.27)

where $\gamma$ is a case-coefficient that depends on the particular contact case and that considers the pressure distribution on the contact surface and the difference between contact geometry and interference geometry. $E^{*}$ is the equivalent Young’s modulus of the contact, considering both bodies [166]

$$ E^{*} = \frac{{E_{1} \cdot E_{2} }}{{E_{1} \cdot \left( {1 - v_{2}^{2} } \right) + E_{2} \cdot \left( {1 - v_{1}^{2} } \right)}} $$

(5.28)

$A^{\prime }$ is the contact area of the interference geometry, $\tau_{\hbox{max} }^{\prime }$ is the shape coefficient of the interference geometry, dependent on the size and shape of the contact polygon, and $\delta_{\hbox{max} }$ is the maximum normal surface deformation. The dissipative component is equal to the elastic one, multiplied by the hysteresis factor, being its definition [166]

$$ \chi^{\prime } = \frac{\chi }{K} $$

(5.29)

where $K$ is the Hertzian stiffness parameter described above. Thus, the value of the contact force is calculated as [166]

$$ F_{N} = \left( {\chi^{\prime } \cdot \dot{\delta } + 1} \right) \cdot \gamma \cdot \pi \cdot E^{*} \cdot \frac{{A^{\prime } }}{{\tau_{\hbox{max} }^{\prime } }} \cdot \delta_{\hbox{max} } $$

(5.30)

Subsequently, Khatiwada et al. developed a model to characterize the pounding damage produced in bridges and buildings due to earthquakes, which range from minor aesthetic effects up to structural collapse. They obtained an expression similar to Eq. (5.23) in absolute terms, preventing the appearance of negative values that destabilize the computations. In addition, they did not consider a linear relation between $c_{r}$ and $\dot{\delta }^{\left( - \right)}$ [167]

$$ \left( {1 + c_{r} } \right) = \frac{K}{{\chi \cdot \dot{\delta }^{\left( - \right)} }} \cdot \ln \left| {\frac{{\frac{K}{{\chi \cdot \dot{\delta }^{\left( - \right)} }} + 1}}{{\frac{K}{{\chi \cdot \dot{\delta }^{\left( - \right)} }} - c_{r} }}} \right| $$

(5.31)

More recently, Yu et al. [168] proposed a model that can be applied to the entire range of $c_{r}$ and that considered the effects of plastic deformation. Starting from Eq. (5.23) aims to reduce the obtained error

$$ \begin{aligned} y_{1} & = \left| {\frac{{1 + \frac{d}{{c_{r} }}}}{1 - d} - e^{{d \cdot \left( {1 + \frac{1}{{c_{r} }}} \right)}} } \right| \\ y_{2} & = \ln y_{1} \\ \end{aligned} $$

(5.32)

Due to the broad range of values of $y_{1}$ for the entire range of the coefficient of restitution, $y_{2}$ is defined. For low values of $c_{r}$, $y_{2}$ skyrockets. Equation (5.23) cannot be solved for low values of coefficient of restitution under the condition $- c_{r} \le d \le 1$. This means that, when plastic deformations are large, Eq. (5.23) is not valid to calculate $\chi$. Yu and his co-authors considered that, for values of $c_{r}$ greater than 0.25, permanent deformation could be ignored, as numerical errors are minimal ($y_{1} \le 6 \cdot 10^{ - 5}$). They presented then an explicit expression of the hysteresis factor based on $d$ and $c_{r}$ [168]

$$ \chi = \frac{d}{{c_{r} }} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.33)

where $d$ is a piecewise function that minimizes the errors in each interval of values of $c_{r}$

$$ d = \left\{ {\begin{array}{*{20}l} 1 \hfill & { c_{r} \in \left[ {0,0.25} \right]} \hfill \\ {2.1663 \cdot c_{r}^{3} - 3.7216 \cdot c_{r}^{2} + 0.8724 \cdot c_{r} + 0.9409} \hfill & {c_{r} \in \left( {0.25, 0.4} \right]} \hfill \\ {1.1664 \cdot c_{r}^{3} - 2.4893 \cdot c_{r}^{2} + 0.3625 \cdot c_{r} + 1.0117} \hfill & {c_{r} \in \left( {0.4, 0.6} \right]} \hfill \\ {0.5048 \cdot c_{r}^{3} - 1.3255 \cdot c_{r}^{2} - 0.3236 \cdot c_{r} + 1.1472} \hfill & {c_{r} \in \left( {0.6, 0.8} \right]} \hfill \\ {0.2256 \cdot c_{r}^{3} - 0.6663 \cdot c_{r}^{2} - 0.8437 \cdot c_{r} + 1.2844} \hfill & {c_{r} \in \left( {0.8, 1} \right]} \hfill \\ \end{array} } \right. $$

(5.34)

This model is valid for any value of $c_{r}$, showing a high degree of consistency between the values of $c_{r}$ defined as an input variable when calculating the value of the force and the results obtained as the ratio of the velocities after and before the contact event. The contact force is calculated using Eq. (5.18).

As can be seen, most of the models described in this section can be applied to any type of impact and provide reasonably accurate results, unlike the models of the first group, designed to meet specific applications.

5.3 Simplified explicit hysteresis factor models

In this section, those models that assume certain relations or conditions of the contact process to define an explicit expression of $\chi$ are presented. This expression is a function of the properties of the contacting bodies and the variables of the contact event. In this group, the model proposed by Hunt and Crossley, described above, is included.

Lee and Wang [169] defined a hysteresis factor similar to that presented by Hunt and Crossley, aiming at satisfying the boundary conditions of the hysteresis loop: null contact force when there is no indentation or this is maximal

$$ \chi = \frac{{3 \cdot \left( {1 - c_{r} } \right)}}{4} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.35)

This model was designed to carry out dynamic analyses of mechanisms with clearances and intermittent motion, although it has not been used much afterwards [98]. In the same way as the approach defined by Hunt and Crossley, this model is only applicable to contact events with a high value of $c_{r}$, being the force calculated with Eq. (5.18).

Kuwabara and Kono [170] based on the theory of elasticity, define a function of the $c_{r}$ from the elastic and geometric properties of two contacting viscoelastic spheres, as well as the impact velocities, comparing the results obtained with another model that considered the plasticity of the contacting solids. The expression that defined the contact force is given by

$$ F_{N} = K \cdot \delta^{3/2} + \chi \cdot \delta^{1/2} \cdot \dot{\delta } $$

(5.36)

where the hysteresis factor is defined as

$$ \chi = 2 \cdot \frac{{\sqrt {R_{\text{eff}} } }}{{D^{\prime } }} $$

(5.37)

where factor $D^{\prime }$ considers the so-called internal friction of the materials of the contacting bodies

$$ D^{\prime } = \frac{{4 \cdot \left( {3 \cdot \xi_{1} + \eta_{1} } \right)^{2} - 9\left( {\xi_{1} - \eta_{1} } \right)^{2} }}{{36 \cdot \left( {3 \cdot \xi_{1} + \eta_{1} } \right) \cdot \xi_{1} \cdot \eta_{1} }} + \frac{{4 \cdot \left( {3 \cdot \xi_{2} + \eta_{2} } \right)^{2} - 9\left( {\xi_{2} - \eta_{2} } \right)^{2} }}{{36 \cdot \left( {3 \cdot \xi_{2} + \eta_{2} } \right) \cdot \xi_{2} \cdot \eta_{2} }} $$

(5.38)

being $\eta$ and $\xi$ the viscosities related to the shear and bulk phenomena, respectively, for each material involved in the contact event. It is assumed that materials are isotropic and that there are no plastic deformations [170]. This model was used by James and his co-authors to develop a method for simulating multiple impacts in granular mediums [171].

Anagnostopoulos developed a contact model to study the pounding between adjacent buildings and between parts of the same building due to strong earthquakes. He modelized each building as a single-degree-of-freedom system, simulating the pounding through impact elements (springs and dampers). Working with the equations of motion, he obtained the following expression of the damping coefficient [172]

$$ D = 2 \cdot \xi_{i} \cdot \sqrt {K \cdot m_{\text{eff}} } $$

(5.39)

where $\xi_{i}$ is the damping ratio, defined as

$$ \xi_{i} = \frac{{ - \ln c_{r} }}{{\sqrt {\pi^{2} + \left( {\ln c_{r} } \right)^{2} } }} $$

(5.40)

The contact force is calculated using Eq. (5.8). Results presented by Anagnostopoulos showed that exterior structures experienced amplified responses, whereas interior structures can experience amplified or reduced responses depending on the ratio of their natural periods to the natural periods of the adjacent structures [172].

One of the most widespread and used models is the one proposed by Lankarani and Nikravesh [106], in which they assumed that the energy dissipated throughout the impact process is much lower than that absorbed by the bodies through elastic deformation. This means that the model can be applied only to contacts in which the value of $c_{r}$ is close to unity. On the one hand, they quantified the kinetic energy losses due to internal damping of the bodies, evaluated as a function of the coefficient of restitution and the initial impact velocity [106]

$$ \Delta T = \frac{1}{2} \cdot m_{\text{eff}} \cdot \dot{\delta }^{\left( - \right)2} \cdot \left( {1 - c_{r}^{2} } \right) $$

(5.41)

On the other hand, they evaluated the kinetic energy losses by integrating the contact force around the hysteresis loop, considering that the damping deformation characteristics during both phases of the contact are nearly the same [106]

$$ \Delta T = \oint {D \cdot \dot{\delta } \cdot {\text{d}}\delta = \frac{2}{3} \cdot \frac{\chi }{K} \cdot m_{\text{eff}} \cdot \dot{\delta }^{\left( - \right)3} } $$

(5.42)

By equalling both expressions, they obtained the following definition of the hysteresis factor

$$ \chi = \frac{{3 \cdot \left( {1 - c_{r}^{2} } \right)}}{4} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.43)

The contact force is calculated through Eq. (5.18). The applications of this model are multiple [19, 24, 91, 173,174,175]. However, this model has another limitation: it is applicable only when initial relative normal velocity is lower than the propagation velocity of elastic waves across both bodies [128, 176]

$$ \dot{\delta }^{\left( - \right)} \le 10^{ - 5} \cdot \sqrt {\frac{E}{\rho }} $$

(5.44)

where $E$ and $\rho$ are the Young’s modulus and the mass density of the material, respectively. Shivaswamy proved, both theoretically and experimentally, that, for low impact velocities, the internal damping of the material is the prime factor for energy dissipation [141]. Impacts at velocities higher than the wave propagation velocity have an energy dissipation mechanism not considered in this model, mainly in the form of permanent deformation. In [128], Lankarani and Nikravesh described an alternative approach that does consider permanent indentation of the contacting bodies.

Later, Tsuji et al. [177] carried out a numerical simulation of a granular flow consisting of elastic, spherical particles in a horizontal duct, defining the damping coefficient as

$$ D = \alpha \cdot \sqrt {m_{\text{eff}} \cdot K} \cdot \delta^{1/4} $$

(5.45)

They considered that the damping coefficients in the tangential and normal directions were of the same value, for oblique impacts, so $D$ can be applied to both directions. $\alpha$ is an empirical constant related to the coefficient of restitution, obtained from a curve defined through heuristic techniques [177]. The contact force is calculated using the following expression

$$ F_{N} = K \cdot \delta^{3/2} + \alpha \cdot \sqrt {m_{\text{eff}} \cdot K} \cdot \delta^{1/4} \cdot \dot{\delta } $$

(5.46)

In line with the approach proposed by Kuwabara and Kono, Brilliantov et al. [178] developed a model to characterize the inelastic collision of spherical particles of granular materials calculating $c_{r}$ as a function of the impact velocities and considering the materials to be viscoelastic. The contact force is obtained through Eq. (5.36), while the hysteresis damping factor is given by

$$ \chi = \frac{3}{2} \cdot K \cdot A $$

(5.47)

where $A$ is a material constant whose expression is [178]

$$ A = \frac{1}{3} \cdot \frac{{(3 \cdot \xi - \eta )^{2} }}{(3 \cdot \xi + 2\eta )} \cdot \frac{{(1 - v^{2} ) \cdot (1 - 2 \cdot v)}}{{E \cdot v^{2} }} $$

(5.48)

Zheng et al. [179] corrected the derivation of $A$ made by Brilliantov and his co-authors, defining instead

$$ A = \frac{{\left( {1 - 2 \cdot v} \right) \cdot \left( {1 + v} \right)}}{E} \cdot \left( {2 \cdot \xi + \frac{\eta }{3}} \right) $$

(5.49)

They used the following expression of the hysteresis factor

$$ \chi = 2 \cdot A \cdot \frac{E}{{(1 - v^{2} )}} \cdot \sqrt {R_{\text{eff}} } $$

(5.50)

Brilliantov et al. [180] subsequently presented an upgrade of his model, correcting the inconsistencies of the first version and generalizing it, making it applicable to a wide range of material parameters

$$ A = \frac{1}{E} \cdot \frac{1 + v}{1 - v} \cdot \left[ {\frac{4}{3} \cdot \eta \cdot \left( {1 - v + v^{2} } \right) + \xi \cdot \left( {1 - 2 \cdot v} \right)^{2} } \right] $$

(5.51)

This model was used by Merkel et al. to carry out a dynamic analysis of an elastic structure composed of a cylindrical rod in contact with a bead at one extremity, studying the wave propagation within the elements [181].

On the other hand, Marhefka and Orin [149] demonstrated that the model defined by Hunt and Crossley is only applicable to contact events in which the coefficient of restitution is close to unity, implementing it in the simulation of robotic systems and considering a linear relation between $c_{r}$ and the initial impact velocity $c_{r} = 1 - \alpha \cdot \dot{\delta }^{\left( - \right)}$, as described above [34].

Jankowski [182] based on the model presented by Kelvin and Voigt to define a viscoelastic, nonlinear approach designed to simulate the structural pounding between adjacent structures during earthquakes. He proposed an improvement in Anagnostopoulos’ model, with separate expressions of the contact force according to the event phase (compression and restitution)

$$ F_{N} = \left\{ {\begin{array}{*{20}l} {K \cdot \delta^{3/2} + \chi \cdot \delta^{1/4} \cdot \dot{\delta }} \hfill & {\dot{\delta } > 0} \hfill \\ {K \cdot \delta^{3/2} } \hfill & {\dot{\delta } \le 0} \hfill \\ \end{array} } \right. $$

(5.52)

The hysteresis damping factor is defined as

$$ \chi = 2 \cdot \bar{\xi } \cdot \sqrt {K \cdot m_{\text{eff}} } $$

(5.53)

where the value of $\bar{\xi }$ is obtained from a function related to the coefficient of restitution. In a later work, Jankowski provided two expressions for this function, being the second more precise with respect to the numerical results than the first one [183]

$$ \bar{\xi } = \sqrt 5 \cdot \frac{{1 - c_{r}^{2} }}{{2 \cdot \pi \cdot c_{r} }} $$

(5.54)

$$ \bar{\xi } = \frac{9 \cdot \sqrt 5 }{2} \cdot \frac{{\left( {1 - c_{r}^{2} } \right)}}{{c_{r} \cdot \left[ {c_{r} \cdot \left( {9 \cdot \pi - 16} \right) + 16} \right]}} $$

(5.55)

Zhiying and Qishao [184] proposed a model that defined the hysteresis factor as a function of $c_{r}$, the contact parameters and the energy dissipated throughout the contact event. Their work, published in Chinese language, presented a contact force calculated using Eq. (5.18) and the hysteresis factor given by

$$ \chi = \frac{{3 \cdot \left( {1 - c_{r}^{2} } \right) \cdot e^{{2 \cdot \left( {1 - c_{r} } \right)}} }}{4} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.56)

The comparative study carried out by Alves and her co-authors showed that the model developed by Zhiying and Qishao provided good results in terms of energy dissipation, for low and medium values of the coefficient of restitution, compared to other models such as those proposed by Lee and Wang or Lankarani and Nikravesh’s [50].

Gharib and Hurmuzlu presented a set of correlations between the $c_{r}$ of nonsmooth models and the stiffness parameter of smooth ones, showing that, under certain conditions, both approaches provide similar results. Considering that deformations only happened in the elastic range of the material and low impact velocities, as well as Newton’s definition of the coefficient of restitution, they defined the hysteresis factor as [107]

$$ \chi = \frac{1}{{c_{r} }} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.57)

This model provides consistent results in the spectrum of low values of $c_{r}$ [50], since it is rooted in an inelastic approach [107]. Contact force is calculated through Eq. (5.18).

Wang et al. [185] recently proposed, in a Chinese-language work, a contact model that related $c_{r}$ to material parameters of the contacting bodies

$$ c_{r}^{*} = 1 - 0.26 \cdot K^{*} \cdot \dot{\delta }^{\left( - \right)1/3} $$

(5.58)

where $K^{*}$ is defined as a relation of the yield strengths of the materials of the bodies, which are denoted by 1 and 2, having three different cases

$$ K^{*} = \left\{ {\begin{array}{*{20}l} {\frac{{\sigma_{1} }}{{\sigma_{1} - \sigma_{2} }},} \hfill & {\sigma_{1} \ge 2\sigma_{2} } \hfill \\ {\frac{{\sigma_{1} }}{{\sigma_{2} }},} \hfill & {\sigma_{2} \simeq \sigma_{1} } \hfill \\ {\frac{{\sigma_{1} }}{{\sigma_{1} + \sigma_{2} }},} \hfill & {\text{rest of cases}} \hfill \\ \end{array} } \right. $$

(5.59)

The hysteresis damping factor is defined as follows, being similar to the expression presented by Zhiying and Qishao

$$ \chi = \frac{{3 \cdot \left( {1 - c_{r}^{*2} } \right) \cdot e^{{\left( {2 \cdot \left( {1 - c_{r}^{*} } \right)} \right)}} }}{4} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.60)

Contact force is calculated using the expression described in Eq. (5.18).

As can be seen, models of this third group cover a wide range of conditions and applications. Some of them consider viscous parameters of the materials, and others are restricted to a specific range of values of the coefficient of restitution, etc. Models such as those proposed by Lankarani and Nikravesh, Hunt and Crossley or Brilliantov et al. are among the most widely used approaches to simulate impact events in multibody systems.

5.4 Explicit hysteresis factor models that consider an expression to relate the indentation and its temporal derivative

In this section, those models that can be applied to the entire range of values of the coefficient of restitution are presented. These define expressions of the hysteresis damping factor as functions of the deformation and its time derivative.

The first approach of this group was developed by Ye et al., who considered a nonlinear damping to define a contact model designed to simulate the contact events between adjacent buildings induced due to earthquake-induced pounding, as previously done by Anagnostopoulos, Jankowski and other authors. Starting from the model defined by Lankarani and Nikravesh, they proposed a new expression of the hysteresis damping factor [108]

$$ \chi = \frac{{8 \cdot \left( {1 - c_{r} } \right)}}{{5 \cdot c_{r} }} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.61)

Flores et al. [59] obtained the same expression, considering three issues in their derivation: the relation between the energy dissipated in the contact process and the coefficient of restitution through the kinetic energy balance and the principle of conservation of momentum, the elastic strain energy stored due to the work produced by the normal force throughout the process and the energy dissipated due to internal damping. Contact force is calculated using Eq. (5.18). Both authors proposed the same relation between the indentation and its time derivative [59, 108]

$$ \dot{\delta } = \dot{\delta }^{\left( \pm \right)} \cdot \sqrt {1 - \left( {\frac{\delta }{{\delta_{m} }}} \right)^{\beta } } $$

(5.62)

where $\dot{\delta }^{\left( - \right)}$ represents the relative contact velocity at the initial instant of contact, in the compression phase, whereas $\dot{\delta }^{\left( + \right)}$ is the initial relative velocity in the restitution stage, with a negative value. Exponent $\beta$ takes a value $\beta = 2$. This model was used, for example, to model the contact interaction between mechanical elements in revolute joints with clearance [186].

Hu and Guo [109] proposed a new expression for the hysteresis damping factor considering deformation and its temporal derivative

$$ \chi = \frac{{3 \cdot \left( {1 - c_{r} } \right)}}{{2 \cdot c_{r} }} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.63)

Their model was designed to characterize contact events between soft materials, with low or medium values of the coefficient of restitution, such as biomechanical systems or bearings. The results obtained proved the validity of the model for any value of $c_{r}$. The relation between indentation and contact velocity is the same as defined in Eq. (5.62), with $\beta$ being determined numerically rather than analytically, as done in the previous works by Ye et al. and Flores and his co-authors. Hu and Guo obtained a value of $\beta = 5/2$, similar to that used in the work by Lankarani and Nikravesh [106, 109]. The value of the contact force is calculated using Eq. (5.18).

Recently, Zhang et al. presented a contact model applicable to both regular and irregular contacting surfaces. They worked with different values of $\beta$ to define a model that provides more accurate results, compared to the models described above, under the same conditions of analysis, especially when dealing with low values of the coefficient of restitution. Contact force is given by Eq. (5.18) and hysteresis factor is defined as [187]

$$ \chi = \frac{{249 \cdot \left( {1 - c_{r} } \right)}}{{\left( {6 + 160 \cdot c_{r} } \right)}} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.64)

Safaeifar and Farshidianfar started from Eq. (5.23), which was defined by Zhang and Sharf in [165], and proposed a new expression to relate indentation and its velocity [151]

$$ \dot{\delta } = \dot{\delta }^{\left( - \right)} \cdot \left( {1 - \left( {\frac{\delta }{{\delta_{m} }}} \right)^{\beta } } \right)^{{\frac{1}{\gamma }}} $$

(5.65)

They obtained, by calculating the root-mean-square (RMS) of the hysteresis damping ratio with respect to the numerical model, the optimal values of $\beta$ and $\gamma$, being these $\beta = 1.5$ and $\gamma = 5.5$. Contact force is defined through Eq. (5.18), and the hysteresis damping factor is given by [151]

$$ \chi = \frac{{5 \cdot \left( {1 - c_{r} } \right)}}{{4 \cdot c_{r} }} \cdot \frac{K}{{\dot{\delta }^{\left( - \right)} }} $$

(5.66)

In this fourth group, five contact force models with similar fundamentals and minimal differences have been described. These approaches are applicable to any type of impact and provide consistent results.

5.5 Alternative/innovative approaches

This section presents those models that represent an innovation or an alternative approach with respect to the models described in the previous groups, this making them to be classified apart.

The first model of this group was developed by Thornton, who proposed a contact model between two elastic–perfectly plastic spheres. The expression that defined the contact force depends on the tensile state of the material [188]

$$ F_{N} = \left\{ {\begin{array}{*{20}l} {K_{L} \cdot \delta^{3/2} } \hfill & {0 \le \delta \le \delta_{y} } \hfill \\ {P_{y} + \pi \cdot \sigma_{y} \cdot R_{\text{eff}} \cdot \left( {\delta - \delta_{y} } \right)} \hfill & {\delta_{y} \le \delta \le \delta_{m} } \hfill \\ {K_{H} \cdot \left( {\delta - \delta_{P} } \right)^{3/2} } \hfill & {\text{elastic recovery}} \hfill \\ \end{array} } \right. $$

(5.67)

where $K_{L}$ and $K_{H}$ are the stiffness parameters during compression and restitution phases, respectively

$$ K_{L} = \frac{4}{3} \cdot E^{*} \cdot \sqrt {R_{\text{eff}} } \quad K_{H} = \frac{4}{3} \cdot E^{*} \cdot \sqrt {R_{{{\text{eff}},P}} } $$

(5.68)

where $R_{{{\text{eff}},P}}$ is the equivalent radius of the system after yield [188]

$$ R_{{{\text{eff}},P}} = \frac{4}{3} \cdot \frac{{E^{*} }}{{P^{*} }}\left( {\frac{{2P^{*} + P_{y} }}{{2 \cdot \pi \cdot \sigma_{y} }}} \right)^{{\frac{3}{2}}} $$

(5.69)

Being $P^{*}$ the maximum value of the contact force. $\sigma_{y}$ is the yield strength of the material, and $P_{y}$ represents the value of the contact force at yield [188]

$$ \sigma_{y} = \frac{{3 \cdot P_{y} }}{{2 \cdot \pi \cdot a_{y}^{2} }} $$

(5.70)

$$ P_{y} = K_{L} \cdot \delta_{y}^{3/2} $$

(5.71)

where $a_{y}$ and $\delta_{y}$ are the contact radius and the penetration at yield, respectively. $\delta_{P}$ is the permanent deformation that remains after elastic recovery. Thornton demonstrated in his work the dependence of the coefficient of restitution on the initial impact velocity.

The second model of this group was proposed by Choi et al., who developed an algorithm to calculate indentation for complex geometries, designed to identify and separate multiple contact regions simultaneously by modelling surfaces as sets of triangles. Based on the work developed by Lankarani and Nikravesh, they proposed the following expression for the contact force [88]

$$ F_{N} = \hbox{max} \left( {K \cdot \delta^{{m_{s} }} + \chi \cdot \delta^{{m_{i} }} \cdot \dot{\delta }, F_{N,\hbox{min} } } \right) $$

(5.72)

where the hysteresis factor is given by

$$ \chi = D \cdot \frac{{\left| {\dot{\delta }} \right|^{{m_{d} }} }}{{\left| {\dot{\delta }} \right|}} $$

(5.73)

and $F_{N,\hbox{min} }$ is the minimum possible value of the contact force in order to avoid attractive forces between bodies during restitution phase [88]

$$ F_{N,\hbox{min} } = R_{c} \cdot K \cdot \delta^{{m_{s} }} $$

(5.74)

where $R_{c}$ is the rebound normal force coefficient, which takes values between 0 and 1. Exponents $m_{s}$, $m_{d}$ and $m_{i}$ are related to the spring, the damper and the indentation of the contact, respectively.

Later, Yigit et al. [189] presented a viscoelastic model to characterize the impact process between a compact body and a composite element, considering plastic deformations and viscous dissipation. In this case, the contact event is divided into three phases: an elastic compression, followed by an elastoplastic compression and, finally, an elastic unloading. The contact force is given by

$$ F_{N} = \left\{ {\begin{array}{*{20}l} {K \cdot \delta^{3/2} } \hfill & {0 \le \delta \le \delta_{y} } \hfill \\ {K \cdot \delta_{y}^{3/2} + K_{y} \left( {\delta - \delta_{y} } \right)} \hfill & {\delta_{y} \le \delta \le \delta_{m} } \hfill \\ {K \cdot \left( {\delta^{3/2} - \delta_{m}^{3/2} + \delta_{y}^{3/2} } \right) + K_{y} \left( {\delta_{m} - \delta_{y} } \right)} \hfill & {\text{unloading}} \hfill \\ \end{array} } \right. $$

(5.75)

where $K_{y}$ is the stiffness parameter during the elastoplastic phase, defined as

$$ K_{y} = 1.5 \cdot K \cdot \sqrt {\delta_{y} } $$

(5.76)

$\delta_{y}$ is the indentation at yield and $\delta_{m}$ represents the maximum value of indentation reached during the process. In the same work, Yigit et al. proposed a linearization of this model, simplifying it [189]

$$ F_{N} = \left\{ {\begin{array}{*{20}l} {K_{y} \cdot \delta } \hfill & {\text{carga}} \hfill \\ {\frac{{K_{y} }}{{\gamma^{2} }} \cdot \left( {\delta - \delta_{f} } \right)} \hfill & {\text{descarga}} \hfill \\ \end{array} } \right. $$

(5.77)

where $\delta_{f}$ is the permanent deformation experienced by the spring of the contact

$$ \delta_{f} = \delta_{m} \cdot \left( {1 - \frac{{K_{y} }}{{K \cdot \sqrt {\delta_{m} } }}} \right)^{2/3} $$

(5.78)

And $\gamma$ is the plastic loss factor, defined in [190], given by

$$ \gamma = 1 - \frac{{\delta_{f} }}{{\delta_{m} }} $$

(5.79)

This model provides results consistent with the numerical values for low and medium impact velocities [189].

Roy and Carretero [191] based on the work by Gonthier and his co-authors developed an alternative damping model based on the material properties of the contacting bodies. The contact force is defined as a function of the volumetric interference and its time derivative. Its expression is derived using principles of the mechanics of materials

$$ F_{N} = \frac{{E_{1} \cdot E_{2} }}{{R_{2} \cdot E_{1} + R_{1} \cdot E_{2} }} \cdot V + \frac{{D_{1} \cdot D_{2} }}{{R_{2} \cdot E_{1} + R_{1} \cdot E_{2} }} \cdot \dot{V} $$

(5.80)

The values of the damping parameters are considered constant regardless of the impact velocity. Roy and Carretero compared the results obtained to those provided by other contact models such as the approach of Gonthier et al. and the model of Hunt and Crossley, for a central impact between two equal spheres, obtaining similar results [191].

Xiong et al. [192] presented an analysis on the contact phenomenon in which they identified three principles that characterize the force–indentation relation: the continuity of the value of the contact force throughout the process, that this force has the shape of a Hertzian curve and that indentation has a nonzero value when contact force is null. K–V’s model does not comply with the second principle, while the approach defined by Hunt and Crossley does not meet the third one. Xiong et al. defined the contact force through a differential algebraic inclusion (DAI) [192]

$$ \begin{aligned} 0 & \in a + \left( {\frac{1}{\gamma } + \beta_{1} + \beta_{2} \cdot a} \right) \cdot \dot{a} - {\text{dio}}\left( {\gamma \left( {a - p\left| p \right|^{\lambda - 1} } \right) + \dot{a}} \right) \\ F_{N} & = K \cdot a + K \cdot \left( {\frac{1}{\gamma } + \beta_{1} + \beta_{2} \cdot a} \right) \cdot \dot{a} \\ \end{aligned} $$

(5.81)

where $p$ represents the penetration, $a$ is a state variable, $\beta_{1} \ge 0$ and $\beta_{2} \ge 0$ are parameters related to damping, $\lambda \ge 1$ is referred to a constant that determines the degree of nonlinearity of the force–indentation relation and $\gamma \ge 0$ is an appropriate constant that makes it possible to rewrite the DAI into an ordinary differential equation (ODE) [192]

$$ \begin{aligned} \dot{a} & = \hbox{max} \left( { - \frac{\gamma \cdot a}{{1 + \gamma \left( {\beta_{1} + \beta_{2} \cdot a} \right)}},\gamma \cdot \left( {p\left| p \right|^{\lambda - 1} - a} \right)} \right) \\ F_{N} & = - K \cdot \hbox{max} \left( {0,p\left| p \right|^{\lambda - 1} + \gamma \cdot \left( {\beta_{1} + \beta_{2} a} \right)\left( {p\left| p \right|^{\lambda - 1} - a} \right)} \right) \\ \end{aligned} $$

(5.82)

The behaviour of variable $a$ is defined by the first expression of Eq. (5.82), while the value of the contact force is calculated using the second formula. Xiong and his co-authors analysed the effects of the different parameters on the force–indentation curve and the coefficient of restitution:

• $\beta_{1}$ determines the residual indentation and the rate-of-change of the contact force at the beginning of the contact process.

• $\beta_{2}$ affects the roundedness of the force–indentation curves.

• $\gamma$ influences the overall shape of the force–indentation curves.

• $\beta_{1}$ and $\beta_{2}$ affect the value of $c_{r}$. If these values increase, the coefficient of restitution decreases, since damping is greater.

• For a fixed value of the initial contact velocity, $c_{r}$ decreases if $\gamma$ is increased, until a certain value from which the coefficient of restitution becomes insensitive to $\gamma$.

Recently, Jian et al. proposed a contact model to simulate the impact between viscoelastic spheres of the same material, based on the theory of viscoelasticity [193]. They defined the following expression for the elastic and dissipative components of the contact force

$$ F_{{N,{\text{elastic}}}} = \frac{{4 \cdot G_{e} \cdot \sqrt {R_{\text{eff}} } }}{{3 \cdot \left( {1 - v} \right)}} \cdot \delta^{3/2} \left( t \right) $$

(5.83)

$$ F_{{N,{\text{dissipative}}}} = \frac{2 \cdot \eta }{1 - v} \cdot \left( {1 - e^{{ - \frac{t}{T}}} } \right) \cdot \sqrt {R_{\text{eff}} \cdot \delta \left( t \right)} \cdot \dot{\delta }\left( t \right) $$

(5.84)

where $G_{e}$ represents the elastic term, constant in time, of the shear relaxation modulus of the material. This module is defined as the sum of an equilibrium shear term and a decaying function such that, for large time frames, it becomes null, reflecting the viscoelastic behaviour of the material

$$ G\left( t \right) = G_{e} + \hat{G}\left( t \right) $$

(5.85)

The bulk modulus is also a time-dependent magnitude [193]

$$ K_{\text{bulk}} \left( t \right) = \frac{2}{3} \cdot \frac{1 + v}{1 - 2 \cdot v} \cdot G\left( t \right) $$

(5.86)

$\eta$ is the viscosity of the contact damper and $T$ is the relaxation time of the material

$$ T = \frac{\eta }{{G^{\prime } }} $$

(5.87)

where $G^{\prime }$ is defined as

$$ \hat{G}\left( t \right) = G^{\prime } \cdot e^{{ - \frac{t}{T}}} $$

(5.88)

Jian and his co-authors demonstrated that, after a certain time $\tau$ since the contact started, the viscoelastic material goes into a zone called “rubbery region”, where $G\left( t \right)$ reduces to a value near $G_{e}$, until it reaches the point $t = t_{m}$, when the maximum indentation takes place.

According to the Hertzian contact theory, the relative displacement of two elastic spheres in a collinear impact tends to be a sinusoidal function with respect to time. This displacement is given by [193]

$$ \delta \left( t \right) = \delta_{m} \cdot \sin \left( {\frac{\pi }{{2 \cdot t_{m} }} \cdot t} \right) $$

(5.89)

where $\delta_{m}$ represents the maximum indentation, which happens at $t = t_{m}$. The expressions of the elastic and dissipative components of the force are defined as

$$ F_{{N,{\text{elastic}}}} = \frac{{4 \cdot G_{e} \cdot \sqrt {R_{\text{eff}} } }}{{3 \cdot \left( {1 - v} \right)}} \cdot \left[ {\delta_{m} \cdot \sin \left( {\frac{\pi }{{2 \cdot t_{m} }} \cdot t} \right)} \right]^{3/2} $$

(5.90)

$$ F_{{N,{\text{dissipative}}}} = \frac{\pi \cdot \eta }{{t_{m} \cdot \left( {1 - v} \right)}} \cdot \left( {1 - e^{{ - \frac{t}{T}}} } \right) \cdot \sqrt {R_{\text{eff}} } \cdot \delta_{m}^{3/2} \cdot \sqrt {\sin \left( {\frac{\pi }{{2 \cdot t_{m} }} \cdot t} \right)} \cdot \cos \left( {\frac{\pi }{{2 \cdot t_{m} }} \cdot t} \right) $$

(5.91)

In their work, Jian and his co-authors stated that $\tau$ is little compared to $t_{m}$. The lower the ratio $\tau /t_{m}$, the higher the precision of Eq. (5.84) [193].

In this section, some alternative approaches have been described. These models, due to their uniqueness, have not been able to be assigned to any of the groups described previously. The reader interested in contact phenomena research can find relevant information in the references [194,195,196,197,198,199,200,201,202,203].

6 Concluding remarks

In the present work, the history and the fundamentals of the contact phenomenon in multibody system dynamics have been presented, drawing a distinction between nonsmooth approaches and penalty models and focusing the attention on the latter. The concept of coefficient of restitution has been emphasized, and the algorithm of calculation between two contacting bodies has been described.

Later, multiple contact force models have been introduced and described, highlighting their respective advantages and drawbacks, as well as their applications. There are models that can be implemented in a wide range of applications, such as those developed by Gonthier et al., Zhiying and Qishao, Flores and his co-authors or Hu and Guo, whereas there are others restricted to certain types of impacts, such as the models developed by Lankarani and Nikravesh, Anagnostopoulos or Lee and Wang.

As can be seen, the study of the phenomenon of contact is a research field under permanent development, with almost constant innovations.