Robustness analysis of exponential stability of fuzzy inertial neural networks through the estimation of upper limits of perturbations

Abstract

This paper characterizes the robustness of exponential stability of fuzzy inertial neural network which contains time delays or stochastic disturbance through the estimation of upper limits of perturbations. By utilizing Gronwall-Bellman lemma, stochastic analysis, Cauchy inequality, the mean value theorem of integrals, as well as the properties of integrations, the limits of both time delays and stochastic disturbances are derived in this paper which can make the disturbed system keep exponential stability. The constraints between the two types of disturbances are provided in this paper. Examples are offered to validate our results.

1 Introduction

Neural networks (NNs) have attracted an increasing amount of attention over the last decade, due to their widespread applications of neural networks in image encryption technology [1], signal processing [2], control theory [3, 4] and other fields [5,6,7]. With the deepening of research on neural networks, many classic neural network models have been proposed, such as Hopfiled neural network (HNN) [8], cellular neural network (CNN) [9, 10], recurrent neural network [11], etc. These models mentioned above are all represented by linear or nonlinear differential equations with first order derivatives. However, due to the biological and physical application of second-order derivative terms, they can not be ignored while analyzing the dynamic behaviors of system. The second derivative term is also called inertia term, which is considered to be an effective method to generate chaos, bifurcation and other complex dynamic behaviors. Moreover, inertial terms can also be used for unordered searches of memory. In addition, the inertia term can also be used to describe the relationship between flux and current in physics [12]. Hence, in [13], Babcock and Westervelt considered the inertia in connections of neurons for the first time, and described the embryonic form of inertial neural networks (INNs) as a class of second-order differential equations. Due to the existence of inertia terms, the analysis of properties, like stability, bifurcation, passivity, dissipativity, and so on, are more complex than other kinds of NNs. Many scholars have utilized the reduced order method (ROM) to reduce the complexity of INNs and obtained some significant results [14,15,16,17,18].

Among the properties of INNs, stability is the prerequisite for the applications. However, in the actual circuit simulation process, due to the limited conversion speed of amplifiers and the random fluctuations during the operation of electronic equipment, time delays and stochastic disturbances are inevitable which may destroy the stability of NNs. Different time delays can also lead to different dynamic behaviors of INN. Different working mechanisms of electronic devices can lead to different time delays, for example, time-varying delays [19], distributed delays [20], constant delays [21] and so on. In addition, stochastic disturbance is a class of complex and irregular perturbation, which is completely different from traditional processes. It can cause uncertain oscillations during system operation to make the system can not reach the designed performance. Some stability criteria of INNs disturbed by those two disturbances are obtained in recent years, for example, in [22], the problems of finite time stabilization and fixed time stabilization of stochastic INNs (SINNs) are explored by designing feedback control laws inputs as well as using the stochastic analysis theory. Huang et al. discussed the problem of global exponential stability by differential inequality analysis, and some novel assertions to ensure the global exponential stability of delayed INNs (DINNs) are obtained in [23]. In [24], Cui et al. obtained stability criteria for DINN with random pulses by using matrix measurement method as well as stochastic theory. Wang and Chen studied the mean-square exponential stability of delayed SINNs (DSINNs) by constructing Lyapunov–Krasovskii functionals in [25].

It is worth noting that the preceding works focuses on the stability of INNs perturbed by time delays or stochastic disturbances in the absence of fuzzy logic. In the process of handling practical problems by using NNs, there inevitably are some inconveniences, for example, the vagueness. Hence, fuzzy logic as a powerful tool to deal with the fuzziness are widely used to deal with the problem in [26,27,28,29]. Different with general NNs, fuzzy neural network (FNN) has not only sum and product operations but also fuzzy MAX and fuzzy MIN operation in their structures, this also greatly improves its ability of image recognition. In addition, neural network models with fuzzy logic operations are recognized as universal approximators. In order to ensure the designed FNNs without inertial terms meet the performance requirements, some conditions are obtained in recent years [30,31,32,33,34]. Besides, in [35], Chen and Kong combined the fuzzy logic and DINNs (FDINNs), and several delay-dependent conditions for exponential stability of FDINNs are obtained.

Noting that the literature mentioned above all explore the problem of stability, and there are few scholars to discuss the robustness of stability (RoS). Robustness refers to the ability of systems to maintain their properties within a certain range of parameters or structures changes. Besides, time delay and stochastic disturbances as two typical structural changes exist in neural networks extensively. And, for an exponential stable system with disturbance, its original decay coefficient and decay rate will be changed when certain intensities of disturbances are changed, it may destroy the stability of original system. So, it is worth exploring how much intensity of disturbances can make perturbed system maintain the original feature of stability of the original system. This is also a motivation for this article. At present, most researches on ROS only focuses on first-order neural networks [30, 31, 36,37,38,39,40] and none of the results have involved FINNs. However, in practical applications, due to the inherent special properties of electronic components, high-order neural network models are usually needed to more accurately describe their dynamic behaviors in reality. Hence, it is very necessary to study the RoS of FINN.

Therefore, based on the above discussions, the works and contributions of this paper are listed below.

• FDINN and SDFINN models are proposed in this paper, and those models are transformed into two coupled first-order FINNs by using ROM. Compared with [16, 17], the ROM used in this paper includes two positive variable parameters $\eta _i,\xi _i$, which further expands the ROM used in [16, 17] which is only contain one variable parameter.

• In addition, in this paper, we have removed the limitation on the derivative of time delay function $\varsigma (t)$ in [37,38,39,40, 43], which means that $\varsigma '(t)\le \delta < 1$ not satisfied in this paper.

• The upper limits of time delay and max intensity of noise are obtained respectively by applying Grownwall-Bellman lemma as well as inequality techniques to ensure the perturbed FINNs keep exponential stability. The constraint relationship between disturbances is given when two types of disturbances are active simultaneously.

Finally, the structure of this paper is given below. In Sect. 2, the model considered is given, and transform the second-order system into first-order system by using ROM, and some assumptions and definitions are given. In Sect. 3, the upper limits of time delay to make FDINNs keep exponential stability is derived by using Grownwall-Bellman lemma and other inequality techniques. Moreover, stochastic FDINN model (SFDINN) is discussed in Sect. 4, and limits of two types of perturbations are obtained, and the relationship between time delay and noise are highlighted. Several numerical instances are given in Sect. 5 to verify the results in this paper.

Notations $\mathbb {R}=(-\infty ,+\infty )$. $\mathbb {Z}^+$ represents the set which contains all positive integers. $\mathbb {R}^n$ and $\mathbb {R}^{n\times m}$ represent real valued n-dimensional vector and real valued $n\times m$ matrices, respectively. $\bigwedge$ and $\bigvee$ are fuzzy AND and fuzzy OR operations, respectively. $|\cdot |$ represent the Euclidean norm and $||x(t)||=\sum _{i=1}^n|x_i(t)|$. $(\hbar ,\mathfrak {F},\{\mathfrak {F}_t\}_{t\ge 0},\mathcal {P})$ is the complete probability space which embraces all $\mathcal {P}$-null sets, and filtration $\mathfrak {F}_{t\ge 0}$ is right continuous and satisfies the usual conditions. B(t) is a Brownian movement which is defined in $(\hbar ,\mathfrak {F},\{\mathfrak {F}_t\}_{t\ge 0},\mathcal {P})$. $\mathbb {E}$ is the operator of mathematical expectation. $L^2_{\mathfrak {F}_0}([-P,0];\mathbb {R}^n)$ is a set of all $C([-P,0];\mathbb {R}^n)$ valued stochastic variables $\hslash =\{\hslash (t):-P\le t\le 0\}$ which are $\mathfrak {F}_0$ measurable and $\sup _{-P\le t\le 0}\mathbb {E}||\hslash (t)||^2\le \infty$. $\varsigma (t)$ is time varying delay and $0\le \varsigma (t)\le P$.

2 Primaries

Consider the following FINN model.

$$\begin{aligned} \ddot{y}_i(t)=&-a_i\dot{y}_i(t)-b_{i}y_i(t)+\sum _{j}c_{ij}g_j(y_j)+\sum _{j}h_{ij}g_j(y(t))\nonumber \\&+\sum _{j}d_{ij}v_j+\bigwedge _{j}e_{ij}g_j(y_i(t))+\bigvee _{j}k_{ij}g_j(y_j(t))\nonumber \\&+\bigvee _{j}S_{ij}v_j+\bigwedge _{j}T_{ij}v_j+I_i, \end{aligned}$$

(1)

where $i\in \{1,\dots ,n\}$, n is the number of neurons. The second derivative is the inertial term of system (1). $y_i(t)\in \mathbb {R}$ is the state of ith neuron. $a_i$ and $b_i$ are two positive constants. $g_j$ is the jth activation function. $c_{ij},~h_{ij}$ are connection weights between ith and jth neuron. $e_{ij},~k_{ij},~S_{ij},~T_{ij}$ represent fuzzy feedback MIN template, fuzzy feedback MAX template, fuzzy feedforward MAX template and fuzzy feedforward MIN template, respectively. $I_i$ denotes the external input of ith neuron. In addition, $\sum _j=\sum _{j=1}^{n}$, $\bigwedge _j=\bigwedge _{j=1}^n$ and $\bigvee _j=\bigvee _{j=1}^n$.

Let $\bar{y}_i=\eta _i\frac{dy_i(t)}{dt}+\xi _{i}y_i(t),$, where $\eta _i$ and $\xi _i$ are positive constants and $\eta _i\ne 0$, then

$$\begin{aligned} \left\{ \begin{aligned}&\dot{y}_i(t)=\frac{1}{\eta _i}\bar{y}_i(t)-\frac{\xi _i}{\eta _i}y_i(t),\\&\dot{\bar{y}}_i(t)=\eta _i\ddot{y}_i(t)+\xi _i\dot{y}_i(t). \end{aligned} \right. \end{aligned}$$

(2)

Hence,

$$\begin{aligned} \left\{ \begin{aligned} \dot{y}_i(t)&=\frac{1}{\eta _i}\bar{y}_i(t)-\frac{\xi _i}{\eta _i}y_i(t),\\ \dot{\bar{y}}_i(t)&=(\frac{\xi _i}{\eta _i}-a_i)\bar{y}_i(t)+(a_i\xi _i-b_i\eta _i-\frac{\xi _i^2}{\eta _i})y_i(t)+\eta _i\biggl \{\sum _{j}c_{ij}g_j(y_j)\\&\quad +\sum _{j}h_{ij}g_j(y_j(t))+\bigwedge _{j}e_{ij}g_j(y_j(t))+\bigvee _{j}k_{ij}g_j(y_j(t))\\&\quad +\bigvee _{j}S_{ij}v_j+\bigwedge _{j}T_{ij}v_j+I_i\biggr \}.\\ \end{aligned} \right. \end{aligned}$$

(3)

Therefore, assume the $(y^*,\bar{y}^*)$ is the equilibrium point of system (1), let $\zeta _i(t)=y_i(t)-y_i^*$, $\varrho _j(\zeta _j(t))=g(y_j(t)-y_j^*)-g_j(y_j^*)$, then system (3) can be rewritten in the following form

$$\begin{aligned} \left\{ \begin{aligned} \dot{\zeta }_i(t)&=\frac{1}{\eta _i}\bar{\zeta }_i(t)-\frac{\xi _i}{\eta _i}\zeta _i(t),\\ \dot{\bar{\zeta }}_i(t)&=(\frac{\xi _i}{\eta _i}-a_i)\bar{\zeta }_i(t)+(a_i\xi _i-b_i\eta _i-\frac{\xi _i^2}{\eta _i})\zeta _i(t)+\eta _i\biggl \{\sum _{j}c_{ij}\varrho _j(\zeta _j(t))\\&\quad +\sum _{j}h_{ij}\varrho _j(\zeta _j(t))+\bigwedge _{j}e_{ij}\varrho _j(\zeta _j(t))+\bigvee _{j}k_{ij}\varrho _j(\zeta _j(t))\biggr \}. \end{aligned} \right. \end{aligned}$$

(4)

Before achieving our main results, the following assumptions, definitions and lemmas are needed.

Assumption 1

There exists a positive constant l such that

$$\begin{aligned} |\varrho _j(u)-\varrho _j(v)|\le l|u-v| \end{aligned}$$

(5)

holds, where u, $v\in \mathbb {R}$.

Remark 1

According to the definition of $\varrho _j(\cdot )$, we can obtain that $\varrho _j(0)=0$, which means that $\varrho _j(\cdot )$ satisfies the linear growth condition, i.e., $|\varrho _j(u)|\le l|u|$. Furthermore, from the definition of $||\cdot ||$, we can get that $||\varrho (u)-\varrho (v)||\le l||u-v||$, where $\varrho (\cdot )=(\varrho _1(\cdot ),\cdots ,\varrho _n(\cdot ))^T$.

Definition 1

[41] FINN (4) is said to be global exponential stable (GES), if there exist constants $\ell >0$ and $\wp >0$ such that

$$\begin{aligned} ||\zeta (t)||+||\bar{\zeta }(t)||\le \ell \exp (-\wp (t-t_0))\biggl (||\zeta (t_0)||+||\bar{\zeta }(t_0)||\biggr ) \end{aligned}$$

(6)

holds, where $\ell$ represents the decay coefficient, $\wp$ is decay rate.

In this paper, unless specified, assume that model (4) is exponential stable.

Lemma 1

Assume u and v are two states of model (4), then we have

$$\begin{aligned}&\biggl |\bigwedge _je_{ij}\varrho _j(u)-\bigwedge _je_{ij}\varrho _j(v)\biggr |\le \sum _j|e_{ij}|l|u-v|,\\&\biggl |\bigvee _jk_{ij}\varrho _j(u)-\bigvee _jk_{ij}\varrho _j(v)\biggr |\le \sum _j|k_{ij}|l|u-v|. \end{aligned}$$

3 The limit of time delay

In this section, we will explore the limit of time delays that make FDINN maintains exponential stability. Firstly, the form of FDINN model is in below.

$$\begin{aligned} \left\{ \begin{aligned} \dot{\varphi }_i(t)&=\frac{1}{\eta _i}\bar{\varphi }_i(t)-\frac{\xi _i}{\eta _i}\zeta _i(t),\\ \dot{\bar{\varphi }}_i(t)&=(\frac{\xi _i}{\eta _i}-a_i)\bar{\varphi }_i(t)+(a_i\xi _i-b_i\eta _i-\frac{\xi _i^2}{\eta _i})\varphi _i(t)\\&\quad +\eta _i\biggl \{\sum _{j}c_{ij}\varrho _j(\varphi _j(t))+\sum _{j}h_{ij}\varrho _j(\varphi _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{ij}\varrho _j(\varphi _j(t-\varsigma (t)))+\bigvee _{j}k_{ij}\varrho _j(\varphi _j(t-\varsigma (t)))\biggr \}, \end{aligned} \right. \end{aligned}$$

(7)

where $\varsigma (t)$ is time varying delay function.

Remark 2

Due to the existence of time delay, the definition of exponential stability of (7) is in the following form

$$\begin{aligned} ||\varphi (t)||+||\bar{\varphi }(t)||\le \ell \exp (-\wp (t-t_0))\sup _{s\in [t_0-P,t_0]}\biggl (||\varphi (s)||+||\bar{\varphi }(s)||\biggr ). \end{aligned}$$

Theorem 1

Let Assumption 1 holds, $\Delta >\ln {\ell }/\wp$, then, FDINN is said to be exponentially stable if $P\le \min \{\Delta /2,\bar{P}\}$, and $\bar{P}$ is the unique solution of the following transcendental equation

$$\begin{aligned} \Psi _1\exp (2\Psi _2\Delta )+\ell \exp (-\wp (\Delta -P))=1, \end{aligned}$$

(8)

where $\Psi _1=\ell /\wp \epsilon _5P\Lambda _2+2P^2\Lambda _2$, and $\Psi _2=\Lambda _1+\epsilon _5P\Lambda _2$.

Proof

For simplicity, denote $\varphi _i=\varphi _i(t)$, $\bar{\varphi }_i=\bar{\varphi }_i(t)$, $\varphi ^\varsigma _i=\varphi _i(t-\varsigma (t))$, $\zeta _i=\zeta _i(t)$, $\bar{\zeta }_i=\bar{\zeta }_i(t)$, $W_i=\varphi _i-\zeta _i,\bar{W}_i=\bar{\varphi }_i-\bar{\zeta }_i$, $\varphi =\{\varphi _1,\dots ,\varphi _n\}$ and $\bar{\varphi }=\{\bar{\varphi }_1,\dots ,\bar{\varphi }_n(t)\}$, hence, we can obtain

$$\begin{aligned} \left\{ \begin{aligned} \dot{W}_i&=\frac{1}{\eta _i}\bar{W}_i-\frac{\xi _i}{\eta _i}W_i,\\ \dot{\bar{W}}_i&=(\frac{\xi _i}{\eta _i}-a_i)\bar{W}_i+(a_i\xi _i-b_i\eta _i-\frac{\xi _i^2}{\eta _i})W_i+\eta _i\biggl \{\sum _{j}c_{ij}\biggl (\varrho _j(\varphi _j)-\varrho _j(\zeta _j)\biggr )\\&\quad +\sum _{j}h_{ij}\biggl (\varrho _j(\varphi _j^\varsigma )-\varrho _j(\zeta _j)\biggr )+\biggl [\bigwedge _{j}e_{ij}\varrho _j(\varphi _i^\varsigma )-\bigwedge _{j}e_{ij}\varrho _j(\zeta _j)\biggr ]\\&\quad +\biggl [\bigvee _{j}k_{ij}\varrho _j(\varphi _j^\varsigma )-\bigvee _{j}k_{ij}\varrho _j(\zeta _j)\biggr ]\biggr \}. \end{aligned} \right. \end{aligned}$$

(9)

Then, let $\epsilon _1=\max \limits _{i=1,\dots ,n}\{1/|\eta _i|\}$, $\epsilon _2=\max \limits _{i=1,\dots ,n}\{|\xi _i/\eta _i|\}$, $\epsilon _3=\max \limits _{i=1,\dots ,n}\{|\alpha _i|\}$, $\epsilon _4=\max \limits _{i=1,\dots ,n}\{|\beta _i|+l\sum _{j}[|\eta _j|(|c_{ji}|+|h_{ji}|+|e_{ji}|+|k_{ji}|)]\}$, $\epsilon _5=\max \limits _{i=1,\dots ,n}\{l\sum _{j}|\eta _j|(|h_{ji}|+|e_{ji}|+|k_{ji}|)\}$, we have

$$\begin{aligned} \left\{ \begin{aligned}|W_i|&\le \int _{t_0}^t\frac{1}{|\eta _i|}|\bar{W}_i|+\biggl |\frac{\xi _i}{\eta _i}\biggr ||W_i|ds,\\ |\bar{W}_i|&\le \int _{t_0}^t\biggl \{|\alpha _i||\bar{W}_i|+|\beta _i||W_i|+|\eta _i|\biggl [\sum _{j}|c_{ij}|l|W_i|\\&\quad +\sum _{j}|h_{ij}|l|\varphi _j^\varsigma -\zeta _j| +\sum _{j}|e_{ij}|l|\varphi ^\varsigma _i-\zeta _i|\\&\quad +\sum _{j}|k_{ij}|l|\varphi ^\varsigma _i-\zeta _i|\biggr ]\biggr \}ds,\\ \end{aligned} \right. \end{aligned}$$

(10)

and

$$\begin{aligned} \left\{ \begin{aligned} ||W||&\le \epsilon _1\int _{t_0}^t||\bar{W}||ds+\epsilon _2\int _{t_0}^t||W||ds,\\ ||\bar{W}||&\le \epsilon _3\int ||\bar{W}||ds+\epsilon _4\int _{t_0}^t||W||ds+\epsilon _5\int _{t_0}^t||\varphi ^\varsigma -\varphi ||ds. \end{aligned}\right. \end{aligned}$$

(11)

Thus,

$$\begin{aligned} ||W||+||\bar{W}|| \le \Lambda _1\int ||W||+||\bar{W}||ds+\epsilon _5\int _{t_0}^t||\varphi ^\varsigma -\varphi ||ds, \end{aligned}$$

(12)

where $\Lambda _1=\max \{\epsilon _1+\epsilon _3,\epsilon _2+\epsilon _4\}$.

Since

$$\begin{aligned} ||\varphi ^\varsigma -\varphi ||\le \int _{t-\varsigma }^t||\dot{\varphi }||ds\le \int _{t-\varsigma }^t\epsilon _1||\bar{\varphi }||+\epsilon _2||\varphi ||ds. \end{aligned}$$

Therefore,

$$\begin{aligned} \int _{t_0}^t||\varphi ^\varsigma -\varphi ||ds&=\int _{t_0}^{t_0+\varsigma }||\varphi ^\varsigma -\varphi ||ds+\int _{t_0+\varsigma }^t||\varphi ^\varsigma -\varphi ||ds\\&\le \int _{t_0}^{t_0+\varsigma }\int _{s-\varsigma }^s\epsilon _1||\bar{\varphi }||+\epsilon _2||\varphi ||dqds\\&\quad +\int _{t_0+\varsigma }^{t}\int _{s-\varsigma }^s\epsilon _1||\bar{\varphi }||+\epsilon _2||\varphi ||dqds. \end{aligned}$$

and

$$\begin{aligned} \int _{t_0+\varsigma }^t\int _{s-\varsigma }^s\epsilon _1||\bar{\varphi }||+\epsilon _2||\varphi ||dqds \le&\varsigma \int _{t_0}^t\epsilon _1||\bar{\varphi }||ds+\varsigma \int _{t_0}^t\epsilon _2||\varphi ||ds\\ \le&\varsigma \Lambda _2\int _{t_0}^t||\bar{\varphi }||+||\varphi ||ds, \end{aligned}$$

where $\Lambda _2=\max \{\epsilon _1,\epsilon _2\}$.

Similarly,

$$\begin{aligned} \int _{t_0}^{t_0+\varsigma }\int _{s-\varsigma }^s\epsilon _1||\bar{\varphi }||+\epsilon _2||\varphi ||dqds&\le \int _{t_0-\varsigma }^{t_0+\varsigma }\int _{q}^{q+\varsigma }\epsilon _1||\bar{\varphi }||+\epsilon _2||\varphi ||dsdq\\&\le 2\varsigma ^2\Lambda _2\sup _{s\in [t_0-\varsigma ,t_0+\varsigma ]}(||\bar{\varphi }||+||\varphi ||). \end{aligned}$$

Then, when $t>t_0+P$,

$$\begin{aligned} ||W||+||\bar{W}||&\le \Lambda _1\int _{t_0}^t||W||+||\bar{W}||ds+\epsilon _5\int _{t_0}^t||\varphi ^\varsigma -\varphi ||ds\nonumber \\&\le (\Lambda _1+\epsilon _5P\Lambda _2)\int _{t_0}^t||W||+||\bar{W}||ds+\epsilon _5P\Lambda _2\int _{t_0}^t||\bar{\zeta }||+||\zeta ||ds\nonumber \\&\quad +2\varsigma ^2\Lambda _2\sup _{s\in [t_0-P,t_0+P]}(||\bar{\varphi }||+||\varphi ||)\nonumber \\&\le (\Lambda _1+\epsilon _5P\Lambda _2)\int _{t_0}^t||W||+||\bar{W}||ds\nonumber \\&\quad +\biggl [\ell /\wp (\epsilon _5P\Lambda _2) +2P^2\Lambda _2\biggr ]\sup _{s\in [t_0-P,t_0+P]}(||\varphi ||+||\bar{\varphi }||). \end{aligned}$$

(13)

By utilizing Grownwall inequality, when $t_0+P\le t\le t_0+2\Delta$, we have

$$\begin{aligned}&||W||+||\bar{W}||\nonumber \\&\quad \le \Psi _1\exp (\Psi _2(t-t_0))\sup _{s\in [t_0-P,t_0+P]}(||\varphi ||+||\bar{\varphi }||)\nonumber \\&\quad \le \Psi _1\exp (2\Psi _2\Delta )\sup _{s\in [t_0-P,t_0+P]}(||\varphi ||+||\bar{\varphi }||), \end{aligned}$$

(14)

where $\Psi _1=\ell /\wp \epsilon _5P\Lambda _2+2P^2\Lambda _2$, and $\Psi _2=\Lambda _1+\epsilon _5P\Lambda _2$.

Note that $P\le \Delta /2$, hence, when $t_0-P+\Delta \le t\le t_0-P+2\Delta$,

$$\begin{aligned} ||\varphi ||+||\bar{\varphi }||&\le ||W||+||\bar{W}||+||\zeta ||+||\bar{\zeta }||\nonumber \\&\le \biggl (\Psi _1\exp (2\Psi _2\Delta )+\ell \exp (-\wp (\Delta -P))\biggr )\sup _{s\in [t_0-P,t_0+P]}(||\varphi ||+||\bar{\varphi }||), \end{aligned}$$

(15)

Select $\varTheta (P)=\Psi _1\exp (2\Psi _2\Delta )+\ell \exp (-\wp (\Delta -P))$. From the definition of $\vartheta$, we could find that $\varTheta (P)$ is strictly increasing with respect to P. In addition, since $\Delta >\frac{\ln l}{\wp }$, hence, $\varTheta (0)<1$. Therefore, there exists a constant $\bar{P}$ such that $\varTheta (\bar{P})=1$, i.e. for all $0<P\le \bar{P}$, $\varTheta (P)\le 1$ holds.

Let $\mho =-\ln \varTheta /\Delta$, hence, $\mho >0$, when $P\in [0,\bar{P}]$. Therefore, from (15), we have

$$\begin{aligned} \sup _{s\in [t_0-P+\Delta ,t_0-P+2\Delta ]}\biggl (||\varphi ||+||\bar{\varphi }||\biggr ) \le \exp (-\mho \Delta )\sup _{s\in [t_0-P,t_0-P+\Delta ]}\biggl (||\varphi ||+||\bar{\varphi }||\biggr ). \end{aligned}$$

(16)

Thus, by using mathematical induction and the existence and uniqueness of (4), a constant $\kappa \in \mathbb {N}^+$, such that

$$\begin{aligned}&\sup _{s\in [t_0-P+\kappa \Delta ,t_0-P+(\kappa +1)\Delta ]}\biggl (||\varphi ||+||\bar{\varphi }||\biggr )\nonumber \\&\quad \le \exp (-\mho \Delta )\sup _{s\in [t_0-P+(\kappa -1)\Delta ,t_0-P+\kappa \Delta ]}\biggl (||\varphi ||+||\bar{\varphi }||\biggr )\nonumber \\&\quad \le \dots \nonumber \\&\quad \le \exp (-\kappa \mho \Delta )\mathfrak {Z}, \end{aligned}$$

(17)

where $\mathfrak {Z}=\sup _{s\in [t_0-P,t_0-P+\Delta ]}\biggl (||\varphi ||+||\bar{\varphi }||\biggr )$.

And then, for all $t>t_0-P+\Delta$,

$$\begin{aligned} ||\varphi ||+||\bar{\varphi }|| \le \mathfrak {Z}\exp (\mho \Delta )\exp (-\mho (t-t_0)) \end{aligned}$$

(18)

holds.

Clearly, (18) also holds for $t_0\le t\le t_0-P+\Delta$. Thus, system (4) can maintain global exponential stable. $\square$

Remark 3

The time delay is common in the process of system operation, and the system will produce different dynamic behavior with different time delay. In the current studies [12, 15, 21], there is no upper bound on the time delay that the system can withstand to maintain exponential stability.

4 The limit of time delay and the intensity of stochastic disturbance

In this section, we consider the following system with two types of disturbances:

$$\begin{aligned} d{\gamma }'_{i}&=\biggl [-a_i{\gamma }'_i(t)-b_{i}\gamma _i(t)+\sum _{j}c_{ij}g_j(\gamma _j)+\sum _{j}h_{ij}g_j(\gamma _j(t-\varsigma (t)))\nonumber \\&\quad +\bigwedge _{j}e_{ij}g_j(\gamma _j(t-\varsigma (t)))+\bigvee _{j}k_{ij}g_j(\gamma _j(t-\varsigma (t)))\biggr ]dt\nonumber \\&\quad +\varpi _i \gamma _i(t)dB(t), \end{aligned}$$

(19)

where $\varsigma (t)$ is the time-varying delay function; B(t) is the Brownian movement defined in complete probability space; $\varpi _i$ is the intensity of Brownian movement.

Similarly, let $\bar{\gamma }_i=\eta _i\frac{d\gamma _i(t)}{dt}+\xi _{i}\gamma _i(t),\eta _i\ne 0$, we can obtain that

$$\begin{aligned} \left\{ \begin{aligned} d\gamma _i(t)&=\biggl [\frac{1}{\eta _i}\bar{\gamma }_i(t)-\frac{\xi _i}{\eta _i}\gamma _i(t)\biggr ]dt,\\ d\bar{\gamma }_i(t)&=\biggl \{(\frac{\xi _i}{\eta _i}-a_i)\bar{\gamma }_i(t)+(a_i\xi _i-b_i\eta _i-\frac{\xi _i^2}{\eta _i})\gamma _i(t)\\&\quad +\eta _i\biggl [\sum _{j}c_{ij}\varrho _j(\gamma _j(t))+\sum _{j}h_{ij}\varrho _j(\gamma _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{ij}\varrho _j(\gamma _j(t-\varsigma (t)))+\bigvee _{j}k_{ij}\varrho _j(\gamma _j(t-\varsigma (t)))\biggr ]\biggr \}dt\\&\quad +\varpi _i\gamma _i(t)dB(t). \end{aligned} \right. \end{aligned}$$

(20)

Then, we give the definition of exponential stability of SFDINN (20) in mean square.

Definition 2

[42] SFDINN (20) is said to be mean square exponentially stable if there are two constants $\ell>0,~\wp >0$ such that

$$\begin{aligned} \mathbb {E}\biggl [||\gamma (t)||^2+||\bar{\gamma }(t)||^2\biggr ]\le \ell \exp (-\wp (t-t_0)) \sup _{s\in [t_0-P,t_0]}\biggl (||\gamma (s)||^2+||\bar{\gamma }(s)||^2\biggr ) \end{aligned}$$

(21)

holds.

In order to maintain exponential stability of SFDINN in mean square, we have the following theorem.

Theorem 2

Let Assumption 1 holds, $\Delta >\ln {2\ell ^2}/2\wp$, then, SFDINN (20) is said to be exponential stability in mean square if $|\varpi |<\bar{\varpi }$ and $P<\min \{\Delta /2,\bar{P}\}$, $\bar{\varpi }$ and $\bar{P}$ satisfy the following two transcendental equations

$$\begin{aligned} 2\bar{\varpi }^2\ell ^2/\wp \exp (2\Delta \Lambda _3)+\ell ^2\exp (-2\wp \Delta )=1, \end{aligned}$$

(22)

and

$$\begin{aligned}&\ell ^2\exp (-2\wp (\Delta -\bar{P}))+\biggl \{24\Delta \Lambda _4[(2\ell ^2/\wp +1)\bar{P}^2]\nonumber \\&\quad +\bar{\varpi }^2\ell ^2/\wp \biggr \}\exp \{2\Delta [\bar{\Lambda }_3+48\Delta \epsilon _5^2\bar{P}^2\Lambda _4]\}=1, \end{aligned}$$

(23)

where

$$\begin{aligned} \bar{\Lambda }_3=\max \{4\Delta \epsilon _1^2+12\Delta \epsilon _3^2,4\Delta \epsilon _2^2+12\Delta \epsilon _4^2+2\bar{\varpi }^2\}. \end{aligned}$$

Proof

For simplify, denote $\gamma _i=\gamma _i(t)$, $\bar{\gamma }_i=\bar{\gamma }(t)$, $\gamma _i^\varsigma =\gamma _i(t-\varsigma (t))$, $\zeta _i=\zeta _i(t)$, $\bar{\zeta }_i=\bar{\zeta }_i(t)$, $\gamma =\{\gamma _1,\dots ,\gamma _n\}$, $\bar{\gamma }=\{\bar{\gamma }_1,\dots ,\bar{\gamma }_n\}$, $\zeta =\{\zeta _1,\dots ,\zeta _n\}$, $\bar{\zeta }=\{\bar{\zeta }_1,\dots ,\bar{\zeta }_n\}$, $\varGamma _i=\gamma _i-\zeta _i$ and $\bar{\varGamma }_i=\bar{\gamma }_i-\bar{\zeta }_i$ From SFDINN (20), we can obtain that

$$\begin{aligned} \left\{ \begin{aligned} d\varGamma _i&=\biggl [\frac{1}{\eta _i}\bar{\varGamma }_i-\frac{\xi _i}{\eta _i}\varGamma _i\biggr ]dt,\\ d\bar{\varGamma }_i&=\biggl \{(\frac{\xi _i}{\eta _i}-a_i)\bar{\varGamma }_i+(a_i\xi _i-b_i\eta _i-\frac{\xi _i^2}{\eta _i})\varGamma _i+\eta _i\biggl [\sum _{j}c_{ij}\biggl (\varrho _j(\gamma _j)-\varrho _j(\zeta _j)\biggr )\\&\quad +\sum _{j}h_{ij}\biggl (\varrho _j(\gamma _j^\varsigma )-\varrho _j(\zeta _j)\biggr )+\biggl (\bigwedge _{j}e_{ij}\varrho _j(\gamma _i^\varsigma )-\bigwedge _{j}e_{ij}\varrho _j(\zeta _j)\biggr )\\&\quad +\biggl (\bigvee _{j}k_{ij}\varrho _j(\gamma _j^\varsigma )-\bigvee _{j}k_{ij}\varrho _j(\zeta _j)\biggr )\biggr ]\biggr \}dt+\varpi _i\gamma _idB(t). \end{aligned} \right. \end{aligned}$$

(24)

Hence,

$$\begin{aligned} \left\{ \begin{aligned} |\varGamma _i|&\le \int _{t_0}^t\biggl [\frac{1}{|\eta _i|}|\bar{\varGamma }_i|+\biggl |\frac{\xi _i}{\eta _i}\biggr ||\varGamma _i|\biggr ]ds,\\ |\bar{\varGamma }_i|\le&\int _{t_0}^t\biggl \{|\alpha _i||\bar{\varGamma }_i|+|\beta _i||\varGamma _i|+|\eta _i|\biggl [\sum _{j}|c_{ij}|l|\gamma _j-\zeta _j|\\&\quad +\sum _{j}|h_{ij}|l|\gamma _j^\varsigma -\zeta _j|+\sum _j|e_{ij}|l|\gamma _i^\varsigma -\zeta _j|\\&\quad +\sum _j|k_{ij}|l|\gamma _j^\varsigma -\zeta _j|\biggr ]\biggr \}ds+\int _{t_0}^t|\varpi _i||\gamma _i|dB(s). \end{aligned} \right. \end{aligned}$$

(25)

Therefore, for $t<t_0+2\Delta$,

$$\begin{aligned} \left\{ \begin{aligned} \mathbb {E}||\varGamma ||^2&\le 4\Delta \epsilon _1^2\int _{t_0}^t \mathbb {E}||\bar{\varGamma }||^2ds+4\Delta \epsilon _2^2\int _{t_0}^t \mathbb {E}||\varGamma ||^2ds,\\ \mathbb {E}||\bar{\varGamma }||^2&\le 12\Delta \bigg \{\epsilon _3^2\int _{t_0}^t \mathbb {E}||\bar{\varGamma }||^2ds+\epsilon _4^2\int _{t_0}^t \mathbb {E}||\varGamma ||^2ds\\&\quad +\epsilon _5^2\int _{t_0}^t \mathbb {E}||\gamma ^\varsigma -\gamma ||^2ds\biggr \}+2\varpi ^2\int _{t_0}^t \mathbb {E}||\gamma (s)||^2ds, \end{aligned}\right. \end{aligned}$$

(26)

where $\varpi =\max \limits _{i=1,2,\dots ,n}|\varpi _i|$.

Thus,

$$\begin{aligned}&\mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )\nonumber \\&\quad \le \Lambda _3\int _{t_0}^t\mathbb {E}\biggl (||\bar{\varGamma }||^2+\mathbb {E}||\varGamma ||^2\biggr )ds+12\Delta \epsilon _5^2\int _{t_0}^t||\gamma ^\varsigma -\gamma ||^2ds\nonumber \\&\qquad +4\varpi ^2\int _{t_0}^t\mathbb {E}\biggl (||\zeta (s)||^2+||\bar{\zeta }(s)||^2\biggr )ds, \end{aligned}$$

(27)

where $\Lambda _3=\max \{4\Delta \epsilon _1^2+12\Delta \epsilon _3^2,4\Delta \epsilon _2^2+12\Delta \epsilon _4^2+4\varpi ^2\}$.

Since, when $t<t_0+2\Delta$,

$$\begin{aligned} \int _{t_0}^t \mathbb {E}||\gamma ^\varsigma -\gamma ||^2ds=\int _{t_0}^{t_0+\varsigma }\mathbb {E}||\gamma ^\varsigma -\gamma ||^2ds+\int _{t_0+\varsigma }^t\mathbb {E}||\gamma ^\varsigma -\gamma ||^2ds, \end{aligned}$$

(28)

and

$$\begin{aligned} \mathbb {E}||\gamma ^\varsigma -\gamma ||^2\le 2\varsigma \int _{t-\varsigma }^t\epsilon _1^2\mathbb {E}||\bar{\gamma }||^2+\epsilon _2^2\mathbb {E}||\gamma ||^2ds. \end{aligned}$$

(29)

Therefore,

$$\begin{aligned} \int _{t_0+\varsigma }^t\mathbb {E}||\gamma ^\varsigma -\gamma ||^2ds&\le 2\varsigma \int _{t_0+\varsigma }^t\int _{s-\varsigma }^{s}\Lambda _4\mathbb {E}(||\bar{\gamma }||^2+||\gamma ||^2)d\theta ds\nonumber \\&\le 2\varsigma ^2\int _{t_0}^t\Lambda _4\mathbb {E}(||\bar{\gamma }||^2+||\gamma ||^2)d\theta \nonumber \\&\le 4\varsigma ^2\Lambda _4\int _{t_0}^t \!\mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )d\theta \!+\!4\varsigma ^2\Lambda _4\int _{t_0}^t \!\mathbb {E}(||\zeta ||\!+\!||\bar{\zeta }||)^2d\theta \nonumber \\&\le 4P^2\Lambda _4\int _{t_0}^t \mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )d\theta \nonumber \\&\quad +4P^2\ell ^2/\wp \Lambda _4\sup _{s\in [t_0-P,t_0]}\mathbb {E}(||\zeta ||^2+||\bar{\zeta }||^2), \end{aligned}$$

(30)

and

$$\begin{aligned} \int _{t_0}^{t_0+\varsigma }\mathbb {E}||\gamma ^\varsigma -\gamma ||^2ds&\le 2\varsigma \int _{t_0}^{t_0+\varsigma }\int _{s-\varsigma }^{s}\Lambda _4\mathbb {E}(||\bar{\gamma }||^2+||\gamma ||^2)d\theta ds\nonumber \\&\le 2P^2\Lambda _4\sup _{s\in [t_0-P,t_0+P]}\mathbb {E}(||\bar{\gamma }||^2+||\gamma ||^2). \end{aligned}$$

(31)

Hence,

$$\begin{aligned}&\mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )\nonumber \\&\quad \le \Lambda _3\int _{t_0}^t\mathbb {E}\biggl (||\bar{\varGamma }||^2+||\varGamma ||^2\biggr )ds+12\Delta \epsilon _5^2\int _{t_0}^t\mathbb {E}||\gamma ^\varsigma -\gamma ||^2ds\nonumber \\&\qquad +4\varpi ^2\int _{t_0}^t\mathbb {E}\biggl (||\zeta ||^2+||\bar{\zeta }||^2\biggr )ds\nonumber \\&\le \Lambda _3\int _{t_0}^t \mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )ds\nonumber \\&\qquad +12\Delta \epsilon _5^2\biggl \{4P^2\Lambda _4\int _{t_0}^t \mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )d\theta \nonumber \\&\qquad +(4P^2\ell ^2/\wp \Lambda _4+2P^2\Lambda _4)\sup _{s\in [t_0-P,t_0+P]}\mathbb {E}(||\gamma ||^2+||\bar{\gamma }||^2)\biggr \}\nonumber \\&\qquad +4\varpi ^2\int _{t_0}^t\mathbb {E}\biggl (||\zeta ||^2+||\bar{\zeta }||^2\biggr )ds\nonumber \\ \le&(\Lambda _3+48\Delta \epsilon _5^2P^2\Lambda _4)\int _{t_0}^t \mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )ds\nonumber \\&\qquad +\biggl [24\Delta \Lambda _4(2P^2\ell ^2/\wp +P^2)+2\varpi ^2\ell ^2/\wp \biggr ]\nonumber \\&\qquad \times \sup _{s\in [t_0-P,t_0+P]}\mathbb {E}(||\gamma ||^2+||\bar{\gamma }||^2). \end{aligned}$$

(32)

So, when $t\le t_0+2\Delta$, from the Gronwall inequality, we can obtain

$$\begin{aligned} \mathbb {E}\biggl (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )\le \mathfrak {A}(\varpi ,P)\exp (2\mathfrak {B}(\varpi ,P)\Delta )\sup _{s\in [t_0-P,t_0+P]}\mathbb {E}(||\gamma ||^2+||\bar{\gamma }||^2), \end{aligned}$$

(33)

where $\mathfrak {A}(\varpi ,P)=24\Delta \Lambda _4(2P^2\ell ^2/\wp +P^2)+2\varpi ^2\ell ^2/\wp$, $\mathfrak {B}(\varpi ,P)=\Lambda _3+48\Delta \epsilon _5^2P^2\Lambda _4$.

Furthermore, when $t_0-P+\Delta \le t\le t_0-P+2\Delta$, noting that $P\le \Delta /2$, then

$$\begin{aligned}&\mathbb {E}\biggl (||\gamma ||^2+||\bar{\gamma }||^2\biggr )\nonumber \\&\quad \le 2\mathbb {E}\bigg (||\varGamma ||^2+||\bar{\varGamma }||^2\biggr )+2\mathbb {E}\biggl (||\zeta ||^2+||\bar{\zeta }||^2\biggr )\nonumber \\&\quad \le 2\biggl [\mathfrak {A}(\varpi ,P)\exp (2\mathfrak {B}(\varpi ,P)\Delta )+\ell ^2\exp (-2\wp (\Delta -P))\biggr ]\nonumber \\&\qquad \times \sup _{s\in [t_0-P,t_0-P+\Delta ]}\mathbb {E}(||\gamma ||^2+||\bar{\gamma }||^2)\nonumber \\&=:\mathbb {Q} (\varpi ,P)\sup _{s\in [t_0-P,t_0-P+\Delta ]}\mathbb {E}(||\gamma ||^2+||\bar{\gamma }||^2), \end{aligned}$$

(34)

where $\mathbb {Q} (\varpi ,P)=\mathfrak {A}(\varpi ,P)\exp (2\mathfrak {B}(\varpi ,P)\Delta )+\ell ^2\exp (-2\wp (\Delta -P))$.

From Assumption 1, we can obtain that $\mathbb {Q}(0,0)<1$ and $\mathbb {Q}(\infty ,0)>1$. Since, $\mathbb {Q}(\varpi ,0)$ is strictly increasing for $\varpi$, hence, there exists a $\bar{\varpi }>0$ such that $\mathbb {Q}(\bar{\varpi },0)=1$. Similarly, $\mathbb {Q}(\varpi ,P)$ is also increasing for P when $|\varpi |\le \bar{\varpi }$, thus, exist a $\bar{P}>0$ such that $\mathbb {Q}(\varpi /\sqrt{2},\bar{P})=1$ holds. That means SFDINN is exponential stable in mean square when $|\varpi |\le \bar{\varpi }$ and $P<\min \{\Delta /2,\bar{P}\}$.

Select $\varOmega =-\ln {\mathbb {Q}(\varpi ,P)}/\Delta$, then we have

$$\begin{aligned} \sup _{t_0-P+\Delta \le t\le t_0-P+2\Delta } \mathbb {E}\biggl (||\gamma ||^2+||\bar{\gamma }||^2\biggr ) \le \exp (-\varOmega \Delta ) \sup _{t_0-P\le t\le t_0-P+\Delta } \mathbb {E}\biggl (||\gamma ||^2+||\bar{\gamma }||^2\biggr ). \end{aligned}$$

(35)

The rest of the proof is similar with the Theorem 1, so it is omitted here. $\square$

Remark 4

The result in Theorem 2 in not a simple extension of the result of Theorem 1, there is a mutual constraint relationship between the magnitude of the intensity of two disturbance factors.

Remark 5

Table 1 provides a comparison of the existing literature with this paper. Elements to be compared are time delay (T-D), stochastic disturbances (S-D), RoS, inertial terms (I-T), fuzzy logic (F-L).

Table 1 A brief comparison between several existing literature and this paper

Remark 6

The Fig. 1 shows the detailed analysis steps of Theorems 1 and 2. In addition, due to random perturbations in SFDINN, $It\hat{o}$ formula is essential, which also leads to the fact that Theorem 1 is not a simple generalization of Theorem 2.

Fig. 1

The analysis steps of this paper

5 Examples

Example 1 Consider the following inertial neural network.

$$\begin{aligned} \left\{ \begin{aligned}\ddot{\varphi }_1(t)&=-a_1\dot{\varphi }_1(t)-b_1\varphi _1(t)+\sum _{j}c_{1j}\varrho _j(\varphi _j(t))+\sum _{j}h_{1j}\varrho _j(\varphi _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{1j}\varrho _j(\varphi _j(t-\varsigma (t)))+\bigvee _{j}k_{1j}\varrho _j(\varphi _j(t-\varsigma (t))),\\ \ddot{\varphi }_2(t)&=-a_2\dot{\varphi }_2(t)-b_2\varphi _2(t)+\sum _{j}c_{2j}\varrho _j(\varphi _j(t))+\sum _{j}h_{2j}\varrho _j(\varphi _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{2j}\varrho _j(\varphi _j(t-\varsigma (t)))+\bigvee _{j}k_{2j}\varrho _j(\varphi _j(t-\varsigma (t))),\\ \end{aligned} \right. \end{aligned}$$

(36)

where $a_1=a_2= 2$, $b_1=b_2=1$, $c=[0.2~-0.2;-0.1~-0.3]$, $h=[-0.3~0.1;-0.2~0.2]$, $e=[0.2~-0.1;-0.1~0.1]$, $k=[0.1~-0.1;-0.1~0.1]$.

Let $\eta _1=\eta _2=1$, $\xi _1=\xi _2=1$ and $\Delta =0.15$, (36) can be rewritten as the following form

$$\begin{aligned} \left\{ \begin{aligned} \dot{\varphi }_1(t)&=\frac{1}{\eta _1}\bar{\varphi }_1(t)-\frac{\xi _1}{\eta _1}\varphi _1(t),\\ \dot{\bar{\varphi }}_1(t)&=(\frac{\xi _1}{\eta _1}-a_1)\bar{\varphi }_1(t)+(a_1\xi _1-b_1\eta _1-\frac{\xi _1^2}{\eta _1})\varphi _1(t)\\&\quad +\eta _1\biggl \{\sum _{j}c_{1j}\varrho _j(\varphi _j(t))+\sum _{j}h_{1j}\varrho _j(\varphi _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{1j}\varrho _j(\varphi _j(t-\varsigma (t)))+\bigvee _{j}k_{1j}\varrho _j(\varphi _j(t-\varsigma (t)))\biggr \},\\ \dot{\varphi }_2(t)&=\frac{1}{\eta _2}\bar{\varphi }_2(t)-\frac{\xi _2}{\eta _2}\varphi _2(t),\\ \dot{\bar{\varphi }}_2(t)&=(\frac{\xi _2}{\eta _2}-a_2)\bar{\varphi }_2(t)+(a_2\xi _2-b_2\eta _2-\frac{\xi _2^2}{\eta _2})\varphi _1(t)\\&\quad +\eta _2\biggl \{\sum _{j}c_{2j}\varrho _j(\varphi _j(t))+\sum _{j}h_{2j}\varrho _j(\varphi _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{2j}\varrho _j(\varphi _j(t-\varsigma (t)))+\bigvee _{j}k_{2j}\varrho _j(\varphi _j(t-\varsigma (t)))\biggr \}. \end{aligned} \right. \end{aligned}$$

(37)

In addition, choose decay coefficient $\ell =1$ and decay rate $\wp =0.4$. Then $\epsilon _1=\epsilon _2=1$, $\epsilon _3=-1$, $\epsilon _4=1.3$, $\epsilon _5=1$, $\Lambda _1=2.3$ and $\Lambda _2=1$. Hence, from (15), we have

$$\begin{aligned} (\bar{P}+3\bar{P}^2)&\exp (0.3(2.3+\bar{P}))+\exp (\bar{P}-0.15)=1. \end{aligned}$$

(38)

Therefore, $\bar{P}=0.0107$, i.e., inertial neural network (36) is GES if $P\le \bar{P}$.

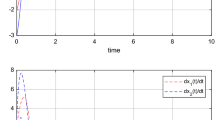
Figure 2 shows the states of FINN (37) in initial values $(-0.7,-0.1)$ and (0.1, 0.4) with $P=0.001<0.0107$. Hence, FDINN is GES. And, the value of $||\varphi (t)||+||\bar{\varphi }(t)||$ is shown in Fig. 3.

Example 2 Consider the following SFDINN.

$$\begin{aligned} \left\{ \begin{aligned}d{\gamma }'_1(t)&=\biggl [-a_1{\gamma }'_1(t)-b_1\gamma _1(t)+\sum _{j}c_{1j}\varrho _j(\gamma _j(t))+\sum _{j}h_{1j}\varrho _j(\gamma _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{1j}\varrho _j(\gamma _j(t-\varsigma (t)))+\bigvee _{j}k_{1j}\varrho _j(\gamma _j(t-\varsigma (t)))\biggr ]dt\\&\quad +\varpi _1\gamma _i(t)dB(t),\\ d{\gamma }'_2(t)&=\biggl [-a_2{\gamma }'_2(t)-b_2\gamma _2(t)+\sum _{j}c_{2j}\varrho _j(\gamma _j(t))+\sum _{j}h_{2j}\varrho _j(\gamma _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{2j}\varrho _j(\gamma _j(t-\varsigma (t)))+\bigvee _{j}k_{2j}\varrho _j(\gamma _j(t-\varsigma (t)))\biggr ]dt\\&\quad +\varpi _2\gamma _i(t)dB(t), \end{aligned} \right. \end{aligned}$$

(39)

where the parameters are the same as those in Example 1.

Fig. 2

The states of (37) with $P=0.001$ in initial value $(\varphi _1(t_0),\varphi _2(t_0))=(-0.7,-0.1)$ and $(\bar{\varphi }_1(t_0),\bar{\varphi }_2(t_0))=(0.1,0.4)$

Fig. 3

The value of $||\varphi (t)||+||\bar{\varphi }(t)||$

Similarly, take same $\eta _i$ and $\xi _i$ in Example 1., then SFDINN (39) can be rewritten in the following form,

$$\begin{aligned} \left\{ \begin{aligned} d\gamma _1(t)&=\biggl [\frac{1}{\eta _1}\bar{\gamma }_1(t)-\frac{\xi _1}{\eta _1}\gamma _1(t)\biggr ]dt,\\ d\bar{\gamma }_1(t)&=\biggl \{(\frac{\xi _1}{\eta _1}-a_1)\bar{\gamma }_1(t)+(a_1\xi _1-b_1\eta _1-\frac{\xi _1^2}{\eta _1})\gamma _1(t)\\&\quad +\eta _1\biggl [\sum _{j}c_{1j}\varrho _j(\gamma _j(t))+\sum _{j}h_{1j}\varrho _j(\gamma _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{1j}\varrho _j(\gamma _j(t-\varsigma (t)))+\bigvee _{j}k_{1j}\varrho _j(\gamma _j(t-\varsigma (t)))\biggr ]\biggr \}dt\\&\quad +\varpi _1\gamma _1(t)dB(t),\\ d\gamma _2(t)&=\biggl [\frac{1}{\eta _2}\bar{\gamma }_2(t)-\frac{\xi _2}{\eta _2}\gamma _2(t)\biggr ]dt,\\ d\bar{\gamma }_2(t)&=\biggl \{(\frac{\xi _2}{\eta _2}-a_2)\bar{\gamma }_2(t)+(a_2\xi _2-b_2\eta _2-\frac{\xi _2^2}{\eta _2})\gamma _2(t)\\&\quad +\eta _2\biggl [\sum _{j}c_{2j}\varrho _j(\gamma _j(t))+\sum _{j}h_{2j}\varrho _j(\gamma _j(t-\varsigma (t)))\\&\quad +\bigwedge _{j}e_{2j}\varrho _j(\gamma _j(t-\varsigma (t)))+\bigvee _{j}k_{2j}\varrho _j(\gamma _j(t-\varsigma (t)))\biggr ]\biggr \}dt\\&\quad +\varpi _2\gamma _2(t)dB(t). \end{aligned} \right. \end{aligned}$$

(40)

Then, from (22) and (23), we can obtain the following two transcendental Equations

$$\begin{aligned} 5\bar{\varpi }^2\exp (0.3\Lambda _3)+\exp (-0.24)=1, \end{aligned}$$

(41)

and

$$\begin{aligned} \exp (-0.8(0.15-\bar{P}))+\biggl \{21.6\bar{P}^2+2.5\bar{\varpi }^2\biggr \}\exp [2\Delta (\bar{\Lambda }_3+7.2\bar{P}^2)]=1. \end{aligned}$$

(42)

After calculations, we can obtain $\bar{\varpi }=0.0067$, and $\bar{P}=0.0021$, i.e. SFDINN (39) is MSES when $|\varpi |\le \bar{\varpi }/\sqrt{2}=0.0047$ and $P\le \min \{\Delta /2,\bar{P}\}=0.0021$.

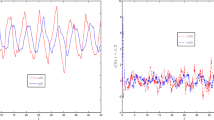
Choose $P=0.001<0.0021$ and $\varpi =0.003<0.0047$, then it can maintain exponential stability as shown in Fig. 4. Figure 5 shows the states of SFDINN (39) in the sense of mean square with $P=0.001<0.0021$ and $\varpi =0.003<0.0047$.

Figure 6 shows the state of system (39) when $P=0.001$ and $\varpi =2$. Since $\varpi$ is greater than the result derived from Theorem 2, the system cannot continue to maintain exponential stability, which is exactly what Fig. 7 shows. In Figs. 8 and 9, we take $P=4$ and $\varpi =4$. At this time, the intensities of both perturbations are greater than the upper bound derived from the Theorem 2, so the system is not exponentially stable. Therefore, it can be seen that only when both perturbations satisfy the conditions, the disturbed system can still maintain global exponential stability.

Fig. 4

The state of SFDINN (40) with $P=0.001$ and $\varpi =0.003$

Fig. 5

The value of $\mathbb {E}||\gamma (t)||^2+\mathbb {E}||\bar{\gamma }(t)||^2$ under $P=0.001$ and $\varpi =0.003$

Fig. 6

The state of SFDINN (40) with $P=0.001$ and $\varpi =2$

Fig. 7

The value of $\mathbb {E}||\gamma (t)||^2+\mathbb {E}||\bar{\gamma }(t)||^2$ under $P=0.001$ and $\varpi =2$

Fig. 8

The state of SFDINN (40) with $P=4$ and $\varpi =4$

Fig. 9

The value of $\mathbb {E}||\gamma (t)||^2+\mathbb {E}||\bar{\gamma }(t)||^2$ under $P=4$ and $\varpi =4$

Remark 7

By Examples 1 and 2, we can see that the system will continue to maintain exponential stability when both perturbations are in the range we have calculated. In addition, Fig. 10 gives a brief calculation process for numerical examples.

Fig. 10

A brief calculation process for numerical examples

Remark 8

The ROM used in this paper contains two variable parameters $\eta _i$ and $\xi _i$, which is different from the [16, 17]. The choice of variable parameters also affects the norm of the system, for example consider the following system model:

$$\begin{aligned} \ddot{y}(t)&=-0.0833\dot{y}(t)-14.8157y(t)-16.0714 \tanh (y(t)). \end{aligned}$$

(43)

Use the ROM for the above systems, take $z(t)=\eta \dot{y}(t)+\xi y(t)$, then, the system transforms to a high dimensional system below:

$$\begin{aligned} \left\{ \begin{aligned} \dot{y}(t)&=\frac{1}{\eta }z(t)-\frac{\xi }{\eta }y(t),\\ \dot{z}(t)&=\left( \frac{\xi }{\eta }-0.0833\right) z(t)+(0.0833\xi -14.8157\eta \\&\quad -\frac{\xi ^2}{\eta })y(t)-16.0714\eta \tanh (y(t)). \end{aligned} \right. \end{aligned}$$

(44)

It can be found that when either or both $\eta$ and $\xi$ are 1, the transformed system is a special case of system (44). Figure 11 shows the states of system (44) under different $\eta$ and $\xi$. As can be seen from the Fig. 11, different selection of transformation parameters will lead to changes in the state of z(t), which will also indirectly lead to changes in the norm of the whole system. Figure 12 illustrates this point. Therefore, according to the theorem in this paper, it can be seen that when the norm of the whole system changes, the upper bound of the perturbation it can withstand can be found to change accordingly. Hence, if only one or zero variable transformation coefficients are considered in this paper, the results are conservative and may not be applicable to all transformations.

Fig. 11

The states of system (44) under different coefficients selections

Fig. 12

The norm of system (44) under different coefficients selections

6 Conclusion

Through the calculations of upper limits of perturbations, this paper analyzes the RoS of FINNs. This paper derives upper limits of both time delays and stochastic disturbances using the Gronwall-Bellman lemma and various inequality techniques to make the disturbed FINN maintain exponential stability. Limitations between the two forms of disturbances are provided. Examples are provided to validate our findings. Those conclusions reached here provide a solid foundation for applications and designs of TSFCNN. Future study may focus on combining the famous methods like LMI method, Lyapunov theory etc. to reduce the conservative of this paper.