1 Introduction

Recently, Babcock and Westervelt [1, 2] have introduced the well-known inertial neural networks that take the following second-order delay differential equations:

$$\begin{aligned} x_{i}''(t) =&-a_{i}x_{i}'(t)-b_{i}x_{i}(t)+ \sum_{j=1}^{n}c_{ij}f_{j} \bigl(x_{j}(t)\bigr) \\ &{}+ \sum_{j=1}^{n}d_{ij}g_{j} \bigl(x_{j}(t-\tau _{j})\bigr)+I_{i}(t), \quad i \in J=\{1,2,\ldots,n\}, \end{aligned}$$
(1.1)

to discover the complicated dynamic behavior of electronic neural networks. Here the initial conditions are defined as

$$\begin{aligned}& \begin{aligned}&x_{i}(s)=\psi _{i}(s), \\ & x_{i}'(s)=\psi '_{i}(s),\quad -\tau \leq s \leq 0, \psi _{i}\in C^{1}\bigl([-\tau , 0], \mathbb{R}\bigr), i\in J,\tau = \max_{j\in J}\{\tau _{j} \}, \end{aligned} \end{aligned}$$
(1.2)

where \(x(t)=(x_{1}(t), x_{2}(t),\ldots , x_{n}(t))\) is the state vector, \(x_{i}''(t)\) is called the ith inertial term, the positive parameters \(a_{i}\), \(b_{i}\), the nonnegative parameters \(\tau _{j}\), and the other parameters \(c_{ij}\), \(d_{ij }\) are all constant, \(I_{i}(t)\) is the external input of ith neuron at time t and \(I=(I_{1}(t), I_{2}(t),\ldots , I_{n}(t))\in \ell _{\infty }\), where \(\ell _{\infty }\) denotes the family of essential bounded functions I from \([0,\infty )\) to \(\mathbb{R}^{n}\) with norm \(\|I\|_{\infty }=\operatorname{ess}\sup_{t\geq 0}\sqrt{\sum_{i=1}^{n}I_{i}^{2}(t)} \). The activation functions \(f_{j} \) and \(g_{j} \) satisfy \(f_{j}(0)=g_{j}(0)=0\) and Lipschitz conditions, i.e., there exist positive constants \(F_{j}\) and \(G_{j}\) such that

$$ \bigl\vert f_{j}(u )-f_{j}(v ) \bigr\vert \leq F_{j} \vert u -v \vert ,\qquad \bigl\vert g_{j}(u )-g_{j}(v ) \bigr\vert \leq G_{j} \vert u -v \vert \quad \text{for all } u , v \in \mathbb{ R}. $$
(1.3)

There are two main methods to study inertial neural network (1.1). One is the so-called reduced order method that has been adopted to study Hopf bifurcation [3–8], stability of equilibrium point [9–13] and periodicity [14–16], synchronization [17–21] and dissipativity [22, 23]. The other is the non-reduced order method that can overcome the great increase of dimension, and many researchers have used this approach to consider dynamic behaviors of (1.1) and its generalizations [22–36].

However, both reduced order and non-reduced order methods involve only deterministic inertial neural networks, do not incorporate stochastic inertial neural networks under the effect of environmental fluctuations. Remarkably, Haykin [37] has pointed out that synaptic transmission, caused by random fluctuations in neurotransmitter release and other probabilistic factors, is a noisy process in real nervous systems and in the implementation of artificial neural networks, hence one should take into consideration noise in modeling since it is unavoidable.

Assume that the parameter \(b_{i}\) (\(i\in J\)) is affected by environmental noise, with \(b_{i}\rightarrow b_{i}-\sigma _{i}\,dB_{i}(t)\), where \(B_{i}(t)\) is independent white noise (i.e., standard Brownian motion) with \(B_{i}(0) = 0\) defined on a complete probability space \((\Omega ,\{\mathcal{F}_{t}\}_{t\geq 0},\mathcal{P})\), \(\sigma _{i}^{2}\) denotes noise intensity. Then, corresponding to inertial neural network (1.1), we obtain the following stochastic system:

$$\begin{aligned} dx_{i}'(t) =&\Biggl[-a_{i}x_{i}'(t)-b_{i}x_{i}(t)+ \sum_{j=1}^{n}c_{ij}f_{j} \bigl(x_{j}(t)\bigr)+ \sum_{j=1}^{n}d_{ij}g_{j} \bigl(x_{j}(t-\tau _{j})\bigr)+I_{i}(t)\Biggr] \,dt \\ &{}+ \sigma _{i}x_{i}(t)\,dB_{i}(t),\quad i\in J. \end{aligned}$$
(1.4)

Obviously, the white noise disturbance term \(\sigma _{i}x_{i}(t)\,dB_{i}(t)\) will induce randomness such that the traditional deterministic inertial neural network (1.1) becomes stochastic system (1.4). One difficulty of this paper is to process white noise disturbances and the other is to introduce a suitable concept of stability to explain the dynamics of (1.4) precisely. The main aim of this paper is to investigate the mean-square exponential input-to-state stability of stochastic inertial neural network (1.4) with initial conditions (1.2). Input-to-state stability, different from the traditional stability such as asymptotical stability, almost sure stability, and exponential stability that means the system states will converge to an equilibrium point as time tends to infinity, can describe the system states varying within a certain region under external control. For more details about input-to-state stability, one can refer to [38–42]. However, as far as we know, almost no one has studied mean-square exponential input-to-state stability of stochastic inertial neural networks.

The remaining part of this paper includes four sections. In Sect. 2, we give the main result: several sufficient conditions that ensue the stochastic inertial neural network (1.4) is mean-square exponentially input-to-state stable. In Sect. 3, we provide numerical examples to check the effectiveness of the developed result. Finally, we summarize and evaluate our work in Sect. 4.

2 Mean-square exponential stability

Although Wang and Chen [43] have studied the mean-square exponential stability of stochastic inertial neural network (1.4) with two groups of different initial conditions (1.2), it is not appropriate to mean-square exponentially input-to-state stability. Fortunately, motivated by Zhu and Cao [38], who introduced the definition of the mean-square exponential input-to-state stability for stochastic delayed neural networks, together with the mean-square exponential stability (Wang and Chen [43]), we present the following definition.

Definition 2.1

Let \(x (t,\psi )=(x_{1}(t), x_{2}(t),\ldots , x_{n}(t))\) be a solution of (1.4) with initial conditions (1.2) \(\psi (s)=(\psi _{1}(s), \psi _{2}(s),\ldots , \psi _{n}(s))\). The stochastic inertial neural network (1.4) is said to be mean-square exponentially input-to-state stable if there exist positive constants λ, η, and K such that

$$ E\bigl( \bigl\Vert x(t,\psi ) \bigr\Vert ^{2}+ \bigl\Vert x'(t,\psi ) \bigr\Vert ^{2}\bigr)\leq Ke^{-\lambda t}+ \eta \Vert I \Vert ^{2}_{\infty } \quad \text{for all } t\geq 0, $$

where \(\|\bullet \|\) means square norm.

Theorem 2.1

Under assumptions (1.3), the stochastic inertial neural network (1.4) is mean-square exponentially input-to-state stable if there exist positive constants \(\beta _{i}\), \(\bar{\beta }_{i}\), and nonzero constants \(\alpha _{i}\), \(\gamma _{i}\), \(\bar{\alpha }_{i}\), \(\bar{\gamma }_{i}\), \(i\in J\) such that

$$ A_{i}< 0,\qquad B_{i}< 0,\qquad 4A_{i}B_{i}>C_{i}^{2} $$
(2.1)

and

$$ \bar{A}_{i}< 0,\qquad \bar{B}_{i}< 0,\qquad 4 \bar{A}_{i}\bar{B}_{i}>\bar{C}_{i}^{2}, $$
(2.2)

where

$$ \textstyle\begin{cases} A_{i}=-\alpha _{i}^{2}a_{i}+\alpha _{i}\gamma _{i}+\frac{1}{2}\alpha _{i}^{2} \sum_{j=1}^{n}( \vert c_{ij} \vert F_{j}+ \vert d_{ij} \vert G_{j}+1), \\ B_{i}=-\alpha _{i}\gamma _{i}b_{i}+\frac{1}{2}\alpha _{i}^{2}\sigma _{i}^{2}+ \frac{1}{2}\sum_{j=1}^{n}(\alpha _{j}^{2}+ \vert \alpha _{j} \gamma _{j} \vert )( \vert d_{ji} \vert G_{i}e^{\lambda \tau _{i}}+ \vert c_{ji} \vert F_{i}) \\ \hphantom{B_{i}=}{} +\frac{1}{2} \vert \alpha _{i}\gamma _{i} \vert (\sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1), \\ C_{i} =\beta _{i}+\gamma _{i}^{2}-\alpha _{i}^{2}b_{i}-\alpha _{i} \gamma _{i}a_{i}, \\ \bar{A}_{i}=-(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2})a_{i}+\bar{\alpha }_{i} \bar{\gamma }_{i}+\frac{1}{2}(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2})( \sum_{j=1}^{n} \vert c_{ij} \vert F_{j}+\sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1), \\ \bar{B}_{i}=\frac{1}{2}(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2})\sigma _{i}^{2}- \bar{\alpha }_{i}\bar{\gamma }_{i}b_{i}+\frac{1}{2}\sum_{j=1}^{n}( \bar{\beta }_{j}+\bar{\alpha }_{j}^{2}+ \vert \bar{\alpha }_{j}\bar{\gamma }_{j} \vert )( \vert d_{ji} \vert G_{i}+ \vert c_{ji} \vert F_{i}) \\ \hphantom{\bar{B}_{i}=}{} +\frac{1}{2} \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert (\sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1), \\ \bar{C}_{i}=-\bar{\beta }_{i}b_{i}-\bar{\alpha }_{i}^{2}b_{i}-\bar{ \alpha }_{i}\bar{\gamma }_{i}a_{i}+\bar{\gamma }^{2}_{i}. \end{cases} $$

Proof

Let \(x (t)=(x_{1}(t), x_{2}(t),\ldots , x_{n}(t))\) be a solution of stochastic system (1.4) with initial values (1.2) such that \(x_{i}(s)=\psi _{i}(s)\), \(x_{i}'(s) = \psi _{i}'(s)\), \(s\in [-\tau , 0]\), \(i\in J\). In view of (2.1) and (2.2), for \(i\in J\), we can find a sufficient little positive number λ such that

$$ A_{i}^{\lambda }< 0,\qquad B_{i}^{\lambda }< 0,\qquad 4A_{i}^{\lambda }B_{i}^{\lambda }> \bigl(C_{i}^{\lambda }\bigr)^{2} $$
(2.3)

and

$$ \bar{A}_{i}^{\lambda }< 0,\qquad \bar{B}_{i}^{\lambda }< 0, \qquad 4\bar{A}_{i}^{\lambda }\bar{B}_{i}^{\lambda }> \bigl(\bar{C}_{i}^{\lambda }\bigr)^{2}, $$
(2.4)

where

$$ \textstyle\begin{cases} A_{i}^{\lambda }=-\alpha _{i}^{2}(a_{i}-\frac{\lambda }{2})+\alpha _{i} \gamma _{i}+\frac{1}{2}\alpha _{i}^{2}(\sum_{j=1}^{n} \vert c_{ij} \vert F_{j}+ \sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1), \\ B_{i}^{\lambda }=-\alpha _{i}\gamma _{i}b_{i}+\frac{1}{2}\alpha _{i}^{2} \sigma _{i}^{2}+\frac{\lambda }{2}(\beta _{i}+\gamma _{i}^{2}) \\ \hphantom{B_{i}^{\lambda }=}{} +\frac{1}{2}\sum_{j=1}^{n}(\alpha _{j}^{2}+ \vert \alpha _{j} \gamma _{j} \vert )( \vert d_{ji} \vert G_{i}e^{\lambda \tau _{i}}+ \vert c_{ji} \vert F_{i})+ \frac{1}{2} \vert \alpha _{i}\gamma _{i} \vert (\sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1), \\ C_{i}^{\lambda }=\beta _{i}+\gamma _{i}^{2}-\alpha _{i}^{2}b_{i}- \alpha _{i}\gamma _{i}(a_{i}-\lambda ), \\ \bar{A}_{i}^{\lambda }=-(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2})(a_{i}- \frac{\lambda }{2})+\bar{\alpha }_{i}\bar{\gamma }_{i}+\frac{1}{2}(\bar{ \beta }_{i}+\bar{\alpha }_{i}^{2})(\sum_{j=1}^{n} \vert c_{ij} \vert F_{j}+ \sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1), \\ \bar{B}_{i}^{\lambda }=\frac{1}{2}\bar{\gamma }_{i}^{2}\lambda + \frac{1}{2}(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2})\sigma _{i}^{2}-\bar{ \alpha }_{i}\bar{\gamma }_{i}b_{i}, \\ \hphantom{\bar{B}_{i}^{\lambda }=}{} +\frac{1}{2}\sum_{j=1}^{n}(\bar{\beta }_{j}+\bar{ \alpha }_{j}^{2}+ \vert \bar{\alpha }_{j}\bar{\gamma }_{j} \vert )( \vert d_{ji} \vert G_{i}e^{ \lambda \tau _{i}}+ \vert c_{ji} \vert F_{i})+\frac{1}{2} \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert (\sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1), \\ \bar{C}_{i}^{\lambda }=-\bar{\beta }_{i}b_{i}-\bar{\alpha }_{i}^{2}b_{i}- \bar{\alpha }_{i}\bar{\gamma }_{i}(a_{i}-\lambda )+\bar{\gamma }^{2}_{i}. \end{cases} $$

Then we construct the following two Lyapunov–Krasovskii functionals:

$$\begin{aligned} U(t) =& \sum_{i=1}^{n}\beta _{i}x_{i}^{2}(t)e^{\lambda t}+ \sum _{i=1}^{n}\bigl(\alpha _{i} x _{i}'(t)+\gamma _{i}x_{i}(t) \bigr)^{2}e^{ \lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{\lambda \tau _{j}} \int _{t- \tau _{j}}^{t}x_{j}^{2}(s)e^{\lambda s} \,ds \end{aligned}$$

and

$$\begin{aligned} V(t) =& \sum_{i=1}^{n}\bar{\beta }_{i}\bigl(x'_{i}(t)\bigr)^{2}e^{ \lambda t} +\sum_{i=1}^{n}\bigl(\bar{\alpha }_{i} x _{i}'(t)+\bar{\gamma }_{i}x_{i}(t)\bigr)^{2}e^{ \lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+\bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{ \lambda \tau _{j}} \int _{t-\tau _{j}}^{t}x_{j}^{2}(s)e^{\lambda s} \,ds. \end{aligned}$$

Using Itô’s formula, we obtain the following stochastic differential:

$$ dU(t)=\mathcal{L}U(t)\,dt+\sum_{i=1}^{n}2 \bigl(\alpha _{i}^{2} \sigma _{i}x_{i}(t)x'_{i}(t)+ \alpha _{i}\gamma _{i}\sigma _{i}x_{i}^{2}(t) \bigr)e^{ \lambda t}\,dB_{i}(t) $$
(2.5)

and

$$ dV(t)=\mathcal{L}V(t)\,dt+\sum_{i=1}^{n}2 \bigl(\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2} \bigr)\sigma _{i}x_{i}(t)x'_{i}(t)+ \bar{\alpha }_{i} \bar{\gamma }_{i}\sigma _{i}x_{i}^{2}(t)\bigr)e^{\lambda t} \,dB_{i}(t), $$
(2.6)

where \(\mathcal{L}\) is the weak infinitesimal operator such that

$$\begin{aligned} \mathcal{L}U(t) =&2 \sum_{i=1}^{n}\biggl[ \bigl(\beta _{i}+\gamma _{i}^{2}- \alpha _{i}^{2}b_{i}-\alpha _{i}\gamma _{i}(a_{i}-\lambda )\bigr)x_{i}(t)x'_{i}(t) \\ &{}+ \biggl( \alpha _{i}\gamma _{i}-\alpha _{i}^{2} \biggl(a_{i}-\frac{\lambda }{2}\biggr)\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\biggl(\frac{1}{2}\alpha _{i}^{2}\sigma _{i}^{2}+\frac{\lambda }{2}\bigl( \beta _{i}+ \gamma _{i}^{2}\bigr)-\alpha _{i}\gamma _{i}b_{i}\biggr)x^{2}_{i}(t) \biggr]e^{ \lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{\lambda \tau _{j}}x_{j}^{2}(t)e^{ \lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t-\tau _{j})e^{ \lambda t} \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}x'_{i}(t)+ \alpha _{i}\gamma _{i}x_{i}(t) \bigr)e^{\lambda t}c_{ij}f_{j}\bigl(x_{j}(t) \bigr) \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}x'_{i}(t)+ \alpha _{i}\gamma _{i}x_{i}(t) \bigr)e^{\lambda t}d_{ij}g_{j}\bigl(x_{j}(t- \tau _{j})\bigr) \\ &{}+2\sum_{i=1}^{n}\bigl(\alpha _{i}^{2}x'_{i}(t)+\alpha _{i} \gamma _{i}x_{i}(t)\bigr)e^{\lambda t}I_{i}(t) \\ \leq &2\sum_{i=1}^{n}\biggl[\bigl(\beta _{i}+\gamma _{i}^{2}-\alpha _{i}^{2}b_{i}- \alpha _{i}\gamma _{i}(a_{i}-\lambda ) \bigr)x_{i}(t)x'_{i}(t) \\ &{}+\biggl(\alpha _{i} \gamma _{i}-\alpha _{i}^{2} \biggl(a_{i}-\frac{\lambda }{2}\biggr)\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\biggl(\frac{1}{2}\alpha _{i}^{2}\sigma _{i}^{2}+\frac{\lambda }{2}\bigl( \beta _{i}+ \gamma _{i}^{2}\bigr)-\alpha _{i}\gamma _{i}b_{i}\biggr)x^{2}_{i}(t) \biggr]e^{ \lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{\lambda \tau _{j}}x_{j}^{2}(t)e^{ \lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t-\tau _{j})e^{ \lambda t} \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert x'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \vert c_{ij} \vert \bigl\vert f_{j}\bigl(x_{j}(t)\bigr)-f_{j}(0) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert x'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \vert d_{ij} \vert \bigl\vert g_{j}\bigl(x_{j}(t- \tau _{j}) \bigr)-g_{j}(0) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert x'_{i}(t) \bigr\vert + \vert \alpha _{i} \gamma _{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \bigl\vert I_{i}(t) \bigr\vert \\ \leq &2\sum_{i=1}^{n}\biggl[\bigl(\beta _{i}+\gamma _{i}^{2}-\alpha _{i}^{2}b_{i}- \alpha _{i}\gamma _{i}(a_{i}-\lambda ) \bigr)x_{i}(t)x'_{i}(t) \\ &{}+\biggl(\alpha _{i} \gamma _{i}-\alpha _{i}^{2} \biggl(a_{i}-\frac{\lambda }{2}\biggr)\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\biggl(\frac{1}{2}\alpha _{i}^{2}\sigma _{i}^{2}+\frac{\lambda }{2}\bigl( \beta _{i}+ \gamma _{i}^{2}\bigr)-\alpha _{i}\gamma _{i}b_{i}\biggr)x^{2}_{i}(t) \biggr]e^{ \lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{\lambda \tau _{j}}x_{j}^{2}(t)e^{ \lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t-\tau _{j})e^{ \lambda t} \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert x'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \vert c_{ij} \vert F_{j} \bigl\vert x_{j}(t) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert x'_{i}(t) \bigr\vert + \vert \alpha _{i}\gamma _{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \vert d_{ij} \vert G_{j} \bigl\vert x_{j}(t- \tau _{j}) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\bigl(\alpha _{i}^{2} \bigl\vert x'_{i}(t) \bigr\vert + \vert \alpha _{i} \gamma _{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \bigl\vert I_{i}(t) \bigr\vert \\ \leq &2\sum_{i=1}^{n}\biggl[\bigl(\beta _{i}+\gamma _{i}^{2}-\alpha _{i}^{2}b_{i}- \alpha _{i}\gamma _{i}(a_{i}-\lambda ) \bigr)x_{i}(t)x'_{i}(t) \\ &{}+\biggl(\alpha _{i} \gamma _{i}-\alpha _{i}^{2} \biggl(a_{i}-\frac{\lambda }{2}\biggr)\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\biggl(\frac{1}{2}\alpha _{i}^{2}\sigma _{i}^{2}+\frac{\lambda }{2}\bigl( \beta _{i}+ \gamma _{i}^{2}\bigr)-\alpha _{i}\gamma _{i}b_{i}\biggr)x^{2}_{i}(t) \biggr]e^{ \lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{\lambda \tau _{j}}x_{j}^{2}(t)e^{ \lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t-\tau _{j})e^{ \lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl[(\alpha _{i}^{2} \bigl(\bigl(x'_{i}(t)\bigr)^{2}+x_{j}^{2}(t) \bigr)+ \vert \alpha _{i}\gamma _{i} \vert \bigl(x_{i}^{2}(t)+x_{j}^{2}(t)\bigr) \bigr]e^{\lambda t} \vert c_{ij} \vert F_{j} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl[\alpha _{i}^{2} \bigl(\bigl(x'_{i}(t)\bigr)^{2}+x_{j}^{2}(t- \tau _{j})\bigr)+ \vert \alpha _{i}\gamma _{i} \vert \bigl(x_{i}^{2}(t)+x_{j}^{2}(t- \tau _{j})\bigr)\bigr]e^{ \lambda t} \vert d_{ij} \vert G_{j} \\ &{}+\sum_{i=1}^{n}\bigl[\alpha _{i}^{2}\bigl(\bigl(x'_{i}(t) \bigr)^{2}+I_{i}^{2}(t)\bigr)+ \vert \alpha _{i}\gamma _{i} \vert \bigl(x_{i}^{2}(t)+I_{i}^{2}(t) \bigr)\bigr]e^{\lambda t} \\ =&\sum_{i=1}^{n}\Biggl[2\bigl(\beta _{i}+\gamma _{i}^{2}-\alpha _{i}^{2}b_{i}- \alpha _{i}\gamma _{i}a_{i}(a_{i}- \lambda )\bigr)x_{i}(t)x'_{i}(t) \\ &{}+\Biggl(-\alpha _{i}^{2}(2a_{i}-\lambda )+2 \alpha _{i}\gamma _{i}+\alpha _{i}^{2} \Biggl( \sum_{j=1}^{n} \vert c_{ij} \vert F_{j}+\sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1\Biggr)\Biggr) \bigl(x'_{i}(t)\bigr)^{2} \\ &{}+\Biggl(-2\alpha _{i}\gamma _{i}b_{i}+ \alpha _{i}^{2}\sigma _{i}^{2}+ \lambda \bigl(\beta _{i}+\gamma _{i}^{2}\bigr) \\ &{}+\sum _{j=1}^{n}\bigl(\alpha _{j}^{2}+ \vert \alpha _{j}\gamma _{j} \vert \bigr) \bigl( \vert d_{ji} \vert G_{i}e^{\lambda \tau _{i}}+ \vert c_{ji} \vert F_{i}\bigr) \\ &{}+ \vert \alpha _{i}\gamma _{i} \vert \Biggl(\sum _{j=1}^{n} \vert d_{ij} \vert G_{j}+1\Biggr)\Biggr)x^{2}_{i}(t) \Biggr]e^{ \lambda t}+\sum_{i=1}^{n}\bigl( \alpha _{i}^{2}+ \vert \alpha _{i} \gamma _{i} \vert \bigr)I_{i}^{2}(t)e^{\lambda t} \\ =&\sum_{i=1}^{n}\Biggl[2A_{i}^{\lambda } \biggl(x_{i}'(t)+ \frac{C_{i}^{\lambda }}{2A_{i}^{\lambda }}x_{i}(t) \biggr)^{2}+2\biggl(B_{i}^{\lambda }- \frac{(C_{i}^{\lambda })^{2}}{4A_{i}^{\lambda }} \biggr)x^{2}_{i}(t) \\ &{}+\sum_{i=1}^{n}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr)I_{i}^{2}(t) \Biggr]e^{ \lambda t} \\ \leq &\sum_{i=1}^{n}\biggl[2A_{i}^{\lambda } \biggl(x_{i}'(t)+ \frac{C_{i}^{\lambda }}{2A_{i}^{\lambda }}x_{i}(t) \biggr)^{2}+2\biggl(B_{i}^{\lambda }- \frac{(C_{i}^{\lambda })^{2}}{4A_{i}^{\lambda }} \biggr)x^{2}_{i}(t)\biggr]e^{\lambda t} \\ &{}+e^{\lambda t}\max_{i\in J}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i} \gamma _{i} \vert \bigr) \Vert I \Vert _{\infty }^{2} ( ) \end{aligned}$$
(2.7)

and

$$\begin{aligned} \mathcal{L}V(t) =& \sum_{i=1}^{n}\biggl[2 \bigl(-\bar{\beta }_{i}b_{i}- \bar{\alpha }_{i}^{2}b_{i}-\bar{\alpha }_{i}\bar{ \gamma }_{i}(a_{i}- \lambda )+\bar{\gamma }^{2}_{i}\bigr)x_{i}(t)x'_{i}(t) \\ &{}+2\biggl(-\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2} \bigr) \biggl(a_{i}-\frac{\lambda }{2}\biggr)+ \bar{\alpha }_{i}\bar{\gamma }_{i}\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\bigl(\bar{\gamma }_{i}^{2} \lambda + \bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \sigma _{i}^{2}-2\bar{ \alpha }_{i}\bar{\gamma }_{i}b_{i}\bigr)x^{2}_{i}(t) \biggr]e^{\lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{ \lambda \tau _{j}}x_{j}^{2}(t)e^{\lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t- \tau _{j})e^{\lambda t} \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr)x'_{i}(t)+ \bar{\alpha }_{i}\bar{\gamma }_{i}x_{i}(t) \bigr)c_{ij}f_{j}\bigl(x_{j}(t) \bigr)e^{ \lambda t} \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr)x'_{i}(t)+ \bar{\alpha }_{i}\bar{\gamma }_{i}x_{i}(t) \bigr)d_{ij}g_{j}\bigl(x_{j}(t- \tau _{j})\bigr)e^{\lambda t} \\ &{}+2\sum_{i=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr)x'_{i}(t)+ \bar{\alpha }_{i}\bar{\gamma }_{i}x_{i}(t) \bigr)I_{i}(t)e^{\lambda t} \\ \leq & \sum_{i=1}^{n}\biggl[2\bigl(-\bar{ \beta }_{i}b_{i}-\bar{\alpha }_{i}^{2}b_{i}- \bar{\alpha }_{i}\bar{\gamma }_{i}(a_{i}-\lambda )+\bar{\gamma }^{2}_{i}\bigr)x_{i}(t)x'_{i}(t) \\ &{}+2\biggl(-\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2} \bigr) \biggl(a_{i}-\frac{\lambda }{2}\biggr)+ \bar{\alpha }_{i}\bar{\gamma }_{i}\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\bigl(\bar{\gamma }_{i}^{2} \lambda + \bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \sigma _{i}^{2}-2\bar{ \alpha }_{i}\bar{\gamma }_{i}b_{i}\bigr)x^{2}_{i}(t) \biggr]e^{\lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{ \lambda \tau _{j}}x_{j}^{2}(t)e^{\lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t- \tau _{j})e^{\lambda t} \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr) \bigl\vert x'_{i}(t) \bigr\vert + \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{ \lambda t} \vert c_{ij} \vert \bigl\vert f_{j} \bigl(x_{j}(t)\bigr)-f_{j}(0) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr) \bigl\vert x'_{i}(t) \bigr\vert + \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{ \lambda t} \vert d_{ij} \vert \bigl\vert g_{j} \bigl(x_{j}(t-\tau _{j})\bigr)-g_{j}(0) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \bigl\vert x'_{i}(t) \bigr\vert + \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \bigl\vert I_{i}(t) \bigr\vert \\ \leq & \sum_{i=1}^{n}\biggl[2\bigl(-\bar{ \beta }_{i}b_{i}-\bar{\alpha }_{i}^{2}b_{i}- \bar{\alpha }_{i}\bar{\gamma }_{i}(a_{i}-\lambda )+\bar{\gamma }^{2}_{i}\bigr)x_{i}(t)x'_{i}(t) \\ &{}+2\biggl(-\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2} \bigr) \biggl(a_{i}-\frac{\lambda }{2}\biggr)+ \bar{\alpha }_{i}\bar{\gamma }_{i}\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\bigl(\bar{\gamma }_{i}^{2} \lambda + \bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \sigma _{i}^{2}-2\bar{ \alpha }_{i}\bar{\gamma }_{i}b_{i}\bigr)x^{2}_{i}(t) \biggr]e^{\lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{ \lambda \tau _{j}}x_{j}^{2}(t)e^{\lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t- \tau _{j})e^{\lambda t} \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr) \bigl\vert x'_{i}(t) \bigr\vert + \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{ \lambda t} \vert c_{ij} \vert F_{j} \bigl\vert x_{j}(t) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr) \bigl\vert x'_{i}(t) \bigr\vert + \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{ \lambda t} \vert d_{ij} \vert G_{j} \bigl\vert x_{j}(t- \tau _{j}) \bigr\vert \\ &{}+2\sum_{i=1}^{n}\bigl(\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \bigl\vert x'_{i}(t) \bigr\vert + \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigl\vert x_{i}(t) \bigr\vert \bigr)e^{\lambda t} \bigl\vert I_{i}(t) \bigr\vert \\ \leq & \sum_{i=1}^{n}\biggl[2\bigl(-\bar{ \beta }_{i}b_{i}-\bar{\alpha }_{i}^{2}b_{i}- \bar{\alpha }_{i}\bar{\gamma }_{i}(a_{i}-\lambda )+\bar{\gamma }^{2}_{i}\bigr)x_{i}(t)x'_{i}(t) \\ &{}+2\biggl(-\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2} \bigr) \biggl(a_{i}-\frac{\lambda }{2}\biggr)+ \bar{\alpha }_{i}\bar{\gamma }_{i}\biggr) \bigl(x'_{i}(t) \bigr)^{2} \\ &{}+\bigl(\bar{\gamma }_{i}^{2} \lambda + \bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \sigma _{i}^{2}-2\bar{ \alpha }_{i}\bar{\gamma }_{i}b_{i}\bigr)x^{2}_{i}(t) \biggr]e^{\lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}e^{ \lambda \tau _{j}}x_{j}^{2}(t)e^{\lambda t} \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl(\bar{\beta }_{i}+ \bar{ \alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{ \gamma }_{i} \vert \bigr) \vert d_{ij} \vert G_{j}x_{j}^{2}(t- \tau _{j})e^{\lambda t} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl[\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr) \bigl(\bigl(x'_{i}(t) \bigr)^{2}+x_{j}^{2}(t)\bigr)+ \vert \bar{\alpha }_{i} \bar{\gamma }_{i} \vert \bigl(x_{i}^{2}(t)+x_{j}^{2}(t) \bigr)\bigr]e^{\lambda t} \vert c_{ij} \vert F_{j} \\ &{}+\sum_{i=1}^{n}\sum _{j=1}^{n}\bigl[\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}\bigr) \bigl(\bigl(x'_{i}(t) \bigr)^{2}+x_{j}^{2}(t-\tau _{j})\bigr) \\ &{}+ \vert \bar{ \alpha }_{i}\bar{\gamma }_{i} \vert \bigl(x_{i}^{2}(t)+x_{j}^{2}(t-\tau _{j})\bigr)\bigr]e^{ \lambda t} \vert d_{ij} \vert G_{j} \\ &{}+\sum_{i=1}^{n}\bigl[\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \bigl( \bigl(x'_{i}(t)\bigr)^{2}+I_{i}^{2}(t) \bigr)+ \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigl(x_{i}^{2}(t)+I_{i}^{2}(t)\bigr) \bigr]e^{ \lambda t} \\ =& \sum_{i=1}^{n}\Biggl[2\bigl(-\bar{\beta }_{i}b_{i}-\bar{\alpha }_{i}^{2}b_{i}- \bar{\alpha }_{i}\bar{\gamma }_{i}(a_{i}-\lambda )+\bar{\gamma }^{2}_{i}\bigr)x_{i}(t)x'_{i}(t) \\ &{}+\Biggl(-\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2} \bigr) (2a_{i}-\lambda )+2\bar{ \alpha }_{i}\bar{\gamma }_{i} \\ &{}+\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \Biggl( \sum_{j=1}^{n} \vert c_{ij} \vert F_{j}+\sum _{j=1}^{n} \vert d_{ij} \vert G_{j}+1\Biggr)\Biggr) \bigl(x_{i}'(t) \bigr)^{2} \\ &{}+\Biggl(\bar{\gamma }_{i}^{2}\lambda +\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}\bigr) \sigma _{i}^{2}-2\bar{\alpha }_{i}\bar{\gamma }_{i}b_{i} \\ &{}+\sum_{j=1}^{n} \bigl( \bar{\beta }_{j}+\bar{\alpha }_{j}^{2}+ \vert \bar{\alpha }_{j}\bar{\gamma }_{j} \vert \bigr) \bigl( \vert d_{ji} \vert G_{i}e^{ \lambda \tau _{i}}+ \vert c_{ji} \vert F_{i}\bigr) \\ &{}+ \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \Biggl(\sum_{j=1}^{n} \vert d_{ij} \vert G_{j}+1\Biggr)\Biggr)x^{2}_{i}(t) \Biggr]e^{ \lambda t}+\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}+ \vert \bar{\alpha }_{i} \bar{\gamma }_{i} \vert \bigr)I^{2}_{i}(t)e^{\lambda t} \\ =& \sum_{i=1}^{n}\biggl[2 \bar{B}_{i}^{\lambda }\biggl(x_{i}(t)+ \frac{\bar{C}_{i}^{\lambda }}{2\bar{B}_{i}^{\lambda }}x'_{i}(t)\biggr) ^{2}+2\biggl( \bar{A}_{i}^{\lambda }-\frac{(\bar{C}_{i}^{\lambda })^{2}}{4\bar{B}_{i} ^{\lambda }}\biggr) \bigl(x'_{i}(t)\bigr)^{2} \\ &{}+\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigr)I^{2}_{i}(t)\biggr]e^{ \lambda t} \\ \leq & \sum_{i=1}^{n}\biggl[2 \bar{B}_{i}^{\lambda }\biggl(x_{i}(t)+ \frac{\bar{C}_{i}^{\lambda }}{2\bar{B}_{i}^{\lambda }}x'_{i}(t)\biggr)^{2}+2\biggl( \bar{A}_{i}^{\lambda }-\frac{(\bar{C}_{i}^{\lambda })^{2}}{4\bar{B}_{i}^{\lambda }}\biggr) \bigl(x'_{i}(t)\bigr)^{2}\biggr]e^{ \lambda t} \\ &{}+e^{\lambda t}\max_{i\in J}\bigl(\bar{\beta }_{i}+\bar{\alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigr) \Vert I \Vert _{\infty }^{2}. \end{aligned}$$
(2.8)

Integrating both sides of (2.5), (2.6) and taking the expectation operator, we obtain from (2.3), (2.4), (2.7), and (2.8) that

$$ EU(t)\leq U(0)+ \Vert I \Vert _{\infty }^{2}\max _{i\in J}\bigl(\alpha _{i}^{2}+ \vert \alpha _{i}\gamma _{i} \vert \bigr) \int _{0}^{t}e^{\lambda s}\,ds $$
(2.9)

and

$$ EV(t)\leq V(0)+ \Vert I \Vert _{\infty }^{2}\max _{i\in J}\bigl(\bar{\beta }_{i}+ \bar{\alpha }_{i}^{2}+ \vert \bar{\alpha }_{i}\bar{\gamma }_{i} \vert \bigr) \int _{0}^{t}e^{ \lambda s}\,ds. $$
(2.10)

Choosing \(\gamma =\max_{i\in J}\{\alpha _{i}^{2}+|\alpha _{i}\gamma _{i}|, \bar{\beta }_{i}+\bar{\alpha }_{i}^{2}+|\bar{\alpha }_{i}\bar{\gamma }_{i}| \} \) and \(\beta =\min_{i\in J}\{\beta _{i},\bar{\beta }_{i}\}\), we obtain from (2.9) and (2.10) that

$$ \beta e^{\lambda t} E\Biggl(\sum_{i=1}^{n}x^{2}_{i}(t) \Biggr)\leq EU(t) \leq U(0)+\frac{\gamma }{\lambda } \Vert I \Vert ^{2}_{\infty }\bigl(e^{\lambda t}-1\bigr) $$
(2.11)

and

$$ \beta e^{\lambda t} E\Biggl(\sum_{i=1}^{n} \bigl(x'_{i}(t)\bigr)^{2}\Biggr)\leq EV(t) \leq V(0)+\frac{\gamma }{\lambda } \Vert I \Vert ^{2}_{\infty } \bigl(e^{\lambda t}-1\bigr). $$
(2.12)

Combining (2.11) and (2.12), the following holds:

$$ E\bigl( \bigl\Vert x(t) \bigr\Vert ^{2}+ \bigl\Vert x'(t) \bigr\Vert ^{2}\bigr)\leq \frac{U(0)+V(0)}{\beta }e^{-\lambda t}+ \frac{2\gamma }{\beta \lambda } \Vert I \Vert ^{2}_{\infty }, $$

which, together with Definition 2.1, implies that the stochastic inertial neural network (1.4) is mean-square exponentially input-to-state stable. This completes the proof of Theorem 2.1. □

Remark 2.1

From Definition 2.1, it is obvious that if stochastic inertial neural networks are mean-square exponentially input-to-state stable, the second moments of states and their first-order derivatives will remain bounded, but not converge to the equilibrium point. This reveals that the external inputs influence the dynamics of the stochastic inertial neural networks, and when they are bounded, the second moments of states and their first-order derivatives remain bounded. In Theorem 2.1, we derive some sufficient conditions for stochastic inertial neural network (1.4) to ensure the mean-square exponential input-to-state stability. To the best of our knowledge, it is the first time to consider the mean-square exponential input-to-state stability for stochastic inertial neural networks. Since references [1–18] and [20–36] are concerned with the deterministic inertial neural networks, Prakash et al. [19] only consider synchronization of Markovian jumping inertial neural networks, and the authors of [38–42] only study input-to-state stability of non-inertial neural networks. Those results are invalid for mean-square exponential input-to-state stability of stochastic inertial neural network (1.4).

3 An illustrative example

In order to verify correctness and effectiveness of the theoretical results, we show an example with numerical simulations.

Example 3.1

$$ \textstyle\begin{cases} dx_{1}'(t)=[-3 x_{1}'(t) -8x_{1}(t)+ 1.2 f_{1}(x_{1}(t))+ 1.5 f_{2}(x_{2}(t)) \\ \hphantom{dx_{1}'(t)=}{}-0.8g_{1}(x_{1}(t-2))+1.9g_{2}(x_{2}(t-2))+6 \cos t]\,dt+x_{1}(t)\,dB_{1}(t) , \\ dx_{2}'(t)=[-4x_{2}'(t) -10x_{2}(t)- 0.9f_{1}(x_{1}(t))- 1.7f_{2}(x_{2}(t)) \\ \hphantom{dx_{2}'(t)=}{} -2.5g_{1}(x_{1}(t-2))+2.1g_{2}(x_{2}(t-2))+7 \sin t]\,dt+x_{2}(t)\,dB_{2}(t) , \end{cases} $$
(3.1)

where \(f_{i}(u) = g_{i}(u) = 0.25(|u + 1|-|u-1|)\), \(i=1,2 \).

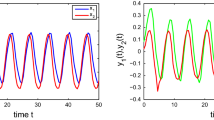
Choosing \(\alpha _{1}=\alpha _{2}=\gamma _{1}=\gamma _{2}=1\), \(\beta _{1}=8\), \(\beta _{2}=9\), \(\bar{\alpha }_{1}=\frac{1}{10}\), \(\bar{\alpha }_{2}=\frac{1}{4}\), \(\bar{ \gamma }_{1}=10\), \(\bar{\gamma }_{2}=4\), \(\bar{\beta }_{1}=1.1\), \(\bar{\beta }_{2}=1\), we obtain \(A_{1}=-0.65\), \(A_{2} =-1.2\), \(B_{1}=-2.95\), \(B_{2}=-3.6\), \(C_{1}=-2\), \(C_{2}=-4\), \(\bar{A}_{1}=-0.7715\), \(\bar{A}_{2} =-1.3375\), \(\bar{B}_{1}=-1.757\), \(\bar{B}_{2}=-4.2219\), \(\bar{C}_{1}=0.82\), \(\bar{C}_{2}=0.14\). Then (2.1) and (2.2) hold. Therefore, by Theorem 2.1, we see that the stochastic inertial neural network (3.1) is mean-square exponentially input-to-state stable. Furthermore, Fig. 1 shows this fact.

Figure 1
figure 1

The states and their first-order derivatives of (3.1) with initial values \((x_{1}(s),x_{2}(s),x'_{1}(s),x'_{2}(s))=(1,-3,0,0)\), \(s\in [-2,0]\)

Full size image

4 Concluding remarks

In this paper, we have studied the mean-square exponential input-to-state stability for a class of stochastic inertial neural networks. By applying non-reduced order method and Lyapunov–Krasovskii functional, we have obtained several sufficient conditions to guarantee the mean-square exponential input-to-state stability of the suggested stochastic system, which has been considered by few authors. An example and its numerical simulation have been presented to check the theoretical result well.