Bifurcation and vibration resonance in the time delay Duffing system with fractional internal and external damping

Abstract

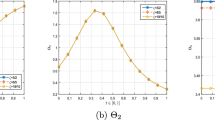
This paper is focused on investigating the bifurcation and vibration resonance problems of fractional double-damping Duffing time delay system driven by external excitation signal with two wildly different frequencies $\omega$ and $\Omega$. Firstly, the approximate expressions of the critical bifurcation point and response amplitude Q at low-frequency $\omega$ are obtained by means of the direct separation of the slow and fast motions. And then corresponding numerical simulation is made to show that it is a good agreement with the theoretical analysis. Next, the influence of system parameters, including internal damping order $\alpha$, external damping order $\lambda$, high-frequency amplitude F, and time delay size $\tau$, on the vibration resonance is discussed. Some significant results are obtained. If the fractional orders $\alpha$ and $\lambda$ are treated as a control parameter, then $\alpha$ and $\lambda$ can induce vibration resonance of the system in three different types when the response amplitude Q changes with the high-frequency amplitude F. If the high-frequency amplitude F is treated as a control parameter, then F can induce vibration resonance of the system as well at some particular points. If the time delay $\tau$ is treated as a control parameter, not only can $\tau$ induce three types of vibration resonance, but the response amplitude Q views periodically with $\tau$. In addition, the resonance behaviors of the considered system are more abundant than those in other similar systems since the internal damping order $\alpha$, external damping order $\lambda$, time delay $\tau$ and cubic term coefficient $\beta$ are introduced into the system which changes the shapes of the effective potential function.