1 Introduction

In economics, many processes depend on past events, so it is natural to use time-delay differential equations to model economic phenomena. Two main areas of applications are business cycle and economic growth theories. In recent decades, the analysis of the effect of investment delay has been the focus of extensive examination as a tool for endogenous cycles to explain business cycles and growth cycles. Differential equations with time delay (discrete or distributed) and their mathematical methods have been seen to be the most adequate tools to model the business cycle and growth in an economy where the investment delay plays a crucial role [1,2,3,4,5], as well as in physics, finance and biology [6,7,8,9].

The mechanism of the supercritical Hopf bifurcation leading to a stable limit cycle is a well-known route to the self-sustainable cyclic behavior. It can be employed for both ordinary differential equations and delay differential equations. Many examples of its use can be found in economics [10,11,12,13,14] and in other sciences [15,16,17].

One of the most influential models of business cycle with time delay is the Kaldor–Kalecki model [18], which is based on the Kaldor model, one of the earliest endogenous business cycle models [19,20,21]. The Kaldor is a prototype of a dynamical system with cyclic behavior in which nonlinearity plays a crucial role in generating endogenous cycles. The nonlinearities are a common feature used to model the complexity of economic systems [22]. In turn, the investment delay was assumed to be the average time of making investment as it was proposed by Kalecki [23].

The investment decisions are taken given the current state of economy. These past investment decisions lead to the change of capital stock in a present economy and may cause fluctuations in economic variables. This kind of time delay, i.e., the time required for building new capital, is an intrinsic (response) type of time delay, which could be also found in neuron due to the autapse connection [24]. Time-delay systems with both response and propagation time delay were studied in many domains of science [25].

The Kaldor–Kalecki business cycle model has been the topic of several studies as well as augmentations. One of these was to incorporate an exponential trend to describe growth of an economy [26]. This new Kaldor–Kalecki growth model was formulated in a similar manner; the Kaldor growth model was developed from the Kaldor business cycle model [27].

The Kaldor–Kalecki model has been extensively studied. While mostly the discrete delay was investigated, some Kaldor–Kalecki models with distributed delays were also proposed. The Kaldor–Kalecki models with fixed delay include both models with one delay and two delays [28,29,30,31,32].

In the existing literature, time delays can be modeled by assuming either fixed time lags or continuously distributed time lags (distributed delay henceforth). The former refers to economic circumstances where there is a set amount of time gap, institutionally or socially defined, for the agents concerned. The latter is suitable for economic situations where different lengths of delays are distributed across the various agents. A major difficulty is that time delays are not known exactly. On the other hand, distributed delays are based on the weighted average of all past data from time zero up to the current time period. Thus, distributed delays provide a more realistic description of economic systems with time delay. There is also some experimental evidence which indicates that they are more accurate than those with instantaneous time lags (see [33]). Cushing [34] introduced and used distributed delays in mathematical biology, while Invernizzi and Medio [35] presented distributed delays into mathematical economics. Some examples in context of economic growth are provided in [36] and [37].

In [38], we proposed an economic growth model where the average time of investment completion is replaced by a distributed time length of investment. The gamma distribution function for the investment delay is assumed. This allows to consider different time lengths of investment accomplishment. The resulting model is described by a dynamical system with a distributed time delay.

While the delay differential equation methods are developing rapidly, the mathematical methods for ordinary differential equations are superlative, especially when distributed delays are considered. Therefore, it is convenient to approximate systems with distributed delays with those of ordinary differential equations. One way to do it is provided by the so-called linear chain trick [39,40,41]. Consequently, an infinite-dimensional dynamical system is approximated by a finite-dimensional dynamical system, where the dimension of the system can be chosen. For an example of this method applied to delayed chemical reaction networks, see [42]. We note that another way to approximate a delay differential equation system with a ordinary differential equation system is via the Padé approximation [43, 44].

The main aim of this paper is to study the emergence of a bifurcation due to the change of the parameter values in the approximated Kaldor–Kalecki growth model. We consider two simplest cases of three- and four-dimensional dynamical systems obtained through the linear chain trick from the Kaldor–Kalecki growth model with the distributed delay, corresponding to the weak and strong kernels, respectively. For both models, we establish conditions for the existence of Hopf bifurcation with respect to the time-delay parameter and the rate of growth parameter. It is found that both parameters play role in a scenario leading to the Hopf bifurcation and arising cyclic behavior.

In the numerical part of this paper, we determine in detail the ranges of parameter values for which cyclical behavior is possible. In this analysis, we use the investment function obtained by Dana and Malgrange for the French economy [27]. As in the theoretical part of the paper, we choose the time-delay parameter and the rate of growth parameter, as well as the adjustment parameter, for the bifurcation investigations. It is shown how some combinations of these three-parameter values can trigger the cycles through the Hopf bifurcation mechanism. In the three-parameter space of the model, we were able to obtain the surface (a section of a paraboloid) separating the regions with stable and cyclic solutions.

2 Model

In Economic growth cycles driven by investment delay, Krawiec and Szydłowski [26] formulated the model based on the Kaldor business cycle model with two modifications: exponential growth introduced by Dana and Malgrange [27] and Kaleckian investment time delay [18]. This model of economic growth is described by the following system of differential equations with time delay \(\tau \ge 0\),

$$\begin{aligned} {\dot{y}}(t)&= \alpha [I(y(t),k(t))-\gamma y(t)+G_{0}]-gy(t), \end{aligned}$$
(1)
$$\begin{aligned} {\dot{k}}(t)&= I(y(t-\tau ),k(t))-(g+\delta )k(t), \end{aligned}$$
(2)

where \(I(y(t),k(t))=k(t)\Phi (y(t)/k(t))\) is the investment function depending on product y and capital stock k, with

$$\begin{aligned} \Phi (y/k)=c+\frac{d}{1+e^{-a\left( vy/k-1\right) }}, \end{aligned}$$

and \(\alpha \), \(\gamma \), g, \(\delta \), \(G_{0}\), g and a, c, d, v are positive constants.

It can be found that the system has a unique fixed point \((y^{*},k^{*})\) with positive coordinates, where

$$\begin{aligned} y^{*}=x^{*}k^{*}\quad \text {and}\quad k^{*}=\frac{\alpha G_{0}}{gx^{*}+\alpha \left[ sx^{*}-(g+\delta )\right] }, \end{aligned}$$

with \(x^{*}\) the unique solution of the equation

$$\begin{aligned} \Phi (x^{*})=g+\delta . \end{aligned}$$

Because of the S shape of function \(\Phi (x)\), we have that \(x^{*}\) always exists and the values of \(y^{*}\) and \(k^{*}\) depend only on \( x^{*}\). (In our case, \(c<g+\delta <c+d\).) Notice that, for economic considerations, the investment function I(y(t), k(t)) is such that

$$\begin{aligned} I_{y}^{*}=I_{y}(y^{*},k^{*})=\frac{adve^{-a(vx^{*}-1)}}{ [1+e^{-a(vx^{*}-1)}]^{2}}>0 \end{aligned}$$
(3)

and

$$\begin{aligned} I_{k}^{*}=I_{k}(y^{*},k^{*})=g+\delta -x^{*}I_{y}^{*}<0. \end{aligned}$$
(4)

In this paper, we generalize their model by replacing the time delay in Eq. (2) with a distributed delay as follows:

$$\begin{aligned} {\dot{y}}(t)&= \alpha [I(y(t),k(t))-\gamma y(t)+G_{0}]-gy(t), \end{aligned}$$
(5)
$$\begin{aligned} {\dot{k}}(t)&= I \left( \int \limits _{-\infty }^{t}y(r)\kappa (t-r)\mathrm{{d}}r,k(t)\right) -(g+\delta )k(t), \end{aligned}$$
(6)

where \(\kappa (\cdot )\) is a gamma distribution, i.e.,

$$\begin{aligned} \kappa (\xi )=\left( \frac{m}{T}\right) ^{m} \dfrac{\xi ^{m-1}e^{-\frac{m}{T}\xi }}{(m-1)!}, \end{aligned}$$

with m a positive integer that determines the shape of the weighting function. \(T\ge 0\) is a parameter associated with the mean time delay of the distribution. Notice that as \(T\rightarrow 0\) the distribution function approaches the Dirac distribution, and thus, one recovers the time-delay case.

The introduction of distributed delays leads to a form of the characteristic equation for which it is hard to derive general stability conditions. For this reason, in the literature dealing with these delays, researchers focus on some special cases with small values of m. For \(m=1\) (weak kernel), the quantity is assigned to current quantity density, while past density has (exponentially) decreasing influence. For \(m=2\) (strong kernel), the maximum weight is assigned to the quantity density at the time \(t-T\). For \(m>2\), the shape of the weighting function takes a unimodal form which becomes taller and thinner as m increases.

More precisely, the case \(m=2\) can be interpreted as the fact that the investment decisions are made based primarily on the values of the realized income (the product y) in a neighborhood of \(t-T\). The incomes more distant in time enter the decisions, but with a gradually decreasing weight. Economic agents are less and less influenced by the value of incomes that are distant over time. Instead, the income closest to t enters relatively unimportant as investment decisions require both processing times and the availability of information. Income too close to t may not be common knowledge across the manufacturing sector, i.e., their weight. For a more complete exposition of what these weights economically are and what they do, refer to references [35, 45, 46].

Henceforth, we will consider only the cases \(m=1\) (weak delay kernel) and \(m=2\) (strong delay kernel). According to the so-called linear chain trick technique, we set new variables so that the integro-differential equation (6) is replaced by a sequence of linear ordinary differential equations. (For a detailed explanation, see section 2a in [41, p. 13–15].) As a result, systems (5)–(6) are converted to a differential system without the delay. More precisely, defining the new variable

$$\begin{aligned} u(t)=\int \limits _{-\infty }^{t}y(r)\left( \frac{1}{T}\right) e^{-\frac{1}{T}(t-r)}\mathrm{{d}}r, \end{aligned}$$

one has the system (case \(m=1\))

$$\begin{aligned} {\dot{y}}(t)&= \alpha [I(y(t),k(t))-\gamma y(t)+G_{0}]-gy(t), \end{aligned}$$
(7)
$$\begin{aligned} {\dot{u}}(t)&= \dfrac{1}{T}\left[ y(t)-u(t)\right] , \end{aligned}$$
(8)
$$\begin{aligned} {\dot{k}}(t)&= I(u(t),k(t))-(g+\delta )k(t), \end{aligned}$$
(9)

while defining the new variables

$$\begin{aligned} p(t)=\int \limits _{-\infty }^{t}y(r)\left( \frac{2}{T}\right) ^{2}(t-r)e^{-\frac{2}{T}(t-r)}\mathrm{{d}}r \end{aligned}$$

and

$$\begin{aligned} w(t)=\int \limits _{-\infty }^{t}y(r)\left( \frac{2}{T}\right) e^{-\frac{2}{T}(t-r)}\mathrm{{d}}r, \end{aligned}$$

one obtains the system (case \(m=2\))

$$\begin{aligned} {\dot{y}}(t)&= \alpha [I(y(t),k(t))-\gamma y(t)+G_{0}]-gy(t), \end{aligned}$$
(10)
$$\begin{aligned} {\dot{p}}(t)&= \dfrac{2}{T}\left[ w(t)-p(t)\right] , \end{aligned}$$
(11)
$$\begin{aligned} {\dot{w}}(t)&= \dfrac{2}{T}\left[ y(t)-w(t\right] ), \end{aligned}$$
(12)
$$\begin{aligned} {\dot{k}}(t)&= I(p(t),k(t))-(g+\delta )k(t). \end{aligned}$$
(13)

We will now analyze the stability and Hopf bifurcation of systems (7)–(9) and (10)–(13) by determining eigenvalues of linearized systems around the critical point \((y^{*},y^{*},k^{*})\) and \((y^{*},y^{*},y^{*},k^{*})\), respectively.

3 The time-delay bifurcation analysis

4 Case \(m=1\)

The characteristic equation of the linearized systems (7)–(9) at the critical point \((y^{*},u^{*},k^{*})\), where \(u^{*}=y^{*}\), is given by

$$\begin{aligned} \left| \begin{array}{ccc} \alpha I_{y}^{*}-\alpha \gamma -g-\lambda \quad &{} \quad 0 &{} \quad \alpha I_{k}^{*}\\ \dfrac{1}{T} &{} \quad -\dfrac{1}{T}-\lambda &{} \quad 0 \\ 0 &{} \quad I_{y}^{*} &{} \quad I_{k}^{*}-(g+\delta )-\lambda \end{array} \right| =0, \nonumber \\ \end{aligned}$$
(14)

where \(\lambda \) denotes a characteristic root. A direct calculation implies that Eq. (14) leads to

$$\begin{aligned} \lambda ^{3}+a_{1}(T)\lambda ^{2}+a_{2}(T)\lambda +a_{3}(T)=0, \end{aligned}$$
(15)

where

$$\begin{aligned} a_{1}(T)= & {} \dfrac{1}{T}-A,\quad \quad a_{2}(T)=-\dfrac{A}{T}-B,\\ a_{3}(T)= & {} \frac{1}{T}\left( -B-\alpha I_{k}^{*}I_{y}^{*}\right) . \end{aligned}$$

with

$$\begin{aligned} A= & {} \alpha \left( I_{y}^{*}-\gamma \right) -g-x^{*}I_{y}^{*}\quad \text {and}\quad \\ B= & {} \left[ \alpha \left( I_{y}^{*}-\gamma \right) -g\right] x^{*}I_{y}^{*}. \end{aligned}$$

The necessary and sufficient condition for the local stability of the equilibrium point is that all characteristic roots of Eq. (15) have negative real parts, which, from the Routh–Hurwitz condition, is equivalent to \( a_{1}(T)>0,a_{3}(T)>0\) and \(a_{1}(T)a_{2}(T)>a_{3}(T)\). Then, \(a_{2}(T)>0\) is necessarily satisfied.

Let us examine whether these inequalities hold. First, we notice that \(A<0\). In fact, by contradiction, if \(A=0\), then \(a_{2}(T)=-\left[ x^{*}I_{y}^{*}\right] ^{2}<0\). On the other hand, if \(A>0\), then \(B>0\), and so \(a_{2}(T)<0\). The fact \(A<0\) implies that \(a_{1}(T)>0\) holds always true, while the inequality \(a_{3}(T)>0\) is valid if and only if \(B+\alpha I_{k}^{*}I_{y}^{*}<0\). Thus, \(a_{3}(T)>0\) is always satisfied when \( B\le 0\), and it is verified for \(g+\delta -(g+\alpha \gamma )x^{*}<0\) when \(B>0\). Finally, let us consider \(a_{1}(T)a_{2}(T)>a_{3}(T)\). Since

$$\begin{aligned} a_{1}(T)a_{2}(T)-a_{3}(T)=\frac{(AB)T^{2}+(A^{2}+\alpha I_{k}^{*}I_{y}^{*})T-A}{T^{2}}, \end{aligned}$$

the sign of \(a_{1}(T)a_{2}(T)-a_{3}(T)\) depends on the sign of \( (AB)T^{2}+(A^{2}+\alpha I_{k}^{*}I_{y}^{*})T-A\), which is a quadratic polynomial in T. We have now several cases.

  1. (i)

    If \(B=0\), then \(a_{1}(T)a_{2}(T)-a_{3}(T)>0\) holds true if \( A^{2}+\alpha I_{k}^{*}I_{y}^{*}\ge 0\) or if \(A^{2}+\alpha I_{k}^{*}I_{y}^{*}<0\) and \(T<A/(A^{2}+\alpha I_{k}^{*}I_{y}^{*})\). \(I)=T_{0}^{*}\).

  2. (ii)

    If \(B>0\), then \(AB<0\) and \(-A>0\). By Descartes’ rule of signs, we find that the polynomial \((AB)T^{2}+(A^{2}+\alpha I_{k}^{*}I_{y}^{*})T-A\) has exactly one positive root \(T=T_{1}^{*}\). Hence, \( a_{1}(T)a_{2}(T)-a_{3}(T)>0\) if \(0<T<T_{1}^{*}\).

  3. (iii)

    If \(B<0\), then \(AB>0\) and \(-A>0\). Applying again the Descartes’ rule of signs, we see that \((AB)T^{2}+(A^{2}+\alpha I_{k}^{*}I_{y}^{*})T-A\) has (two) sign changes only if \(A^{2}+\alpha I_{k}^{*}I_{y}^{*}<0\), meaning that this polynomial may have two positive roots \(T_{2}^{*}<T_{3}^{*}\). If this happens, then \(a_{1}(T)a_{2}(T)-a_{3}(T)>0\) if \( 0<T<T_{2}^{*}\) and \(T>T_{3}^{*}\).

Let \(T=T_{*}\) such that \(a_{1}(T_{*})a_{2}(T_{*})-a_{3}(T_{*})=0\), namely \(T_{*}=T_{j}^{*}\)\((j=0,1,2,3)\). The curve \(T=T_{*} \) divides the parameter space into stable and unstable parts. Choosing T as a bifurcation parameter, we apply the Hopf bifurcation theorem to establish the existence of a cyclical movement. This theorem asserts the existence of the closed orbit, if the characteristic equation (15) has a pair of pure imaginary roots and a nonzero real root, and if the real part of the imaginary roots is not stationary with respect to the changes of the parameter T. At the critical value \(T=T_{*}\), Eq. (15) factors as

$$\begin{aligned} \left[ \lambda +a_{1}(T_{*})\right] \left[ \lambda ^{2}+a_{2}(T_{*}) \right] =0, \end{aligned}$$

so we have the following three roots \(\lambda _{1,2}=\pm i\sqrt{ a_{2}(T_{*})}=\pm i\omega _{*}\) and \(\lambda _{3}=-a_{1}(T_{*})<0\). Next, let us investigate the sign of the real parts of this roots as T varies. A differentiation of (15) with respect to T yields

$$\begin{aligned}&\left[ 3\lambda ^{2}+2a_{1}(T)\lambda +a_{2}(T)\right] \frac{\mathrm{{d}}\lambda }{\mathrm{{d}}T}\nonumber \\&\quad =- \left[ a_{1}^{\prime }(T)\lambda ^{2}+a_{2}^{\prime }(T)\lambda +a_{3}^{\prime }(T)\right] , \end{aligned}$$
(16)

where

$$\begin{aligned} a_{1}^{\prime }(T)&= -\dfrac{1}{T^{2}}<0,\\ a_{2}^{\prime }(T)&= \dfrac{A}{T^{2}}<0, \\ a_{3}^{\prime }(T)&= -\frac{1}{T^{2}} \left( -B-\alpha I_{k}^{*}I_{y}^{*}\right) =-\frac{a_{3}(T)}{T}<0. \end{aligned}$$

Then, from (16), we get

$$\begin{aligned}&\text {Re} \left( \frac{\mathrm{{d}}\lambda }{\mathrm{{d}}T}\right) _{T=T_{*}}\\&\quad =\frac{ -a_{1}^{\prime }(T_{*})a_{2}(T_{*})-a_{1}(T_{*})a_{2}^{\prime }(T_{*})+a_{3}^{\prime }(T_{*})}{2\left[ a_{2}(T_{*})+a_{1}^{2}(T_{*})\right] }. \end{aligned}$$

Since

$$\begin{aligned}&-a_{1}^{\prime }(T_{*})a_{2}(T_{*})-a_{1}(T_{*})a_{2}^{\prime }(T_{*})+a_{3}^{\prime }(T_{*})\\&\quad =-\dfrac{A}{T_{*}^{3}}\left( BT_{*}^{2}+1\right) , \end{aligned}$$

we obtain

$$\begin{aligned} \mathop {\mathrm {sign}}\left[ \text {Re}\left( \frac{\mathrm{{d}}\lambda }{\mathrm{{d}}T}\right) _{T=T_{*}}\right] =\mathop {\mathrm {sign}}\left( BT_{*}^{2}+1\right) . \end{aligned}$$

If \(B\ge 0\), we observe that \(\text {Re}\left( \mathrm{{d}}\lambda /\mathrm{{d}}T\right) _{T=T_{*}}>0\) (with \(T_{*}=T_{0}^{*},T_{1}^{*})\) holds always true, whether if \(B<0\), then \(\text {Re}\left( \mathrm{{d}}\lambda /\mathrm{{d}}T\right) _{T=T^{*}}>0\) (with \(T_{*}=T_{2}^{*},T_{3}^{*})\) if \(0<T<1/ \sqrt{-B}\), and \(\text {Re}\left( \mathrm{{d}}\lambda /\mathrm{{d}}T\right) _{T=T^{*}}<0\) if \( T>1/\sqrt{-B}\).

The previous analysis leads to the following conclusions.

Theorem 1

Let \(A<0\), with A defined as in (15).

(1):

If \(B=0\) and \(A^{2}+\alpha I_{k}^{*}I_{y}^{*}<0\) or if \( B>0\) and \(B+\alpha I_{k}^{*}I_{y}^{*}<0\), then there exists \( T=T_{*}>0\) such that the equilibrium point \((y^{*},y^{*},k^{*})\) of (7)–(9) is locally asymptotically stable for all \(T<T_{*}\) and unstable for \(T>T_{*}\). Systems (7)–(9) undergo a Hopf bifurcation at \((y^{*},y^{*},k^{*})\) when \(T=T_{*}\).

(2):

If \(B<0\), then there exists \(0<T_{2}^{*}<T_{3}^{*}\) such that the equilibrium point \((y^{*},y^{*},k^{*})\) of (7)–(9) is locally asymptotically stable for all \(T<T_{2}^{*}\) and \( T<T_{3}^{*}\), and unstable for all \(T_{2}^{*}<T<T_{3}^{*}\). A comparison of \(1/\sqrt{-B}\) with \(T_{2}^{*}\) and \(T_{3}^{*}\) yields that systems (7)–(9) undergo a Hopf bifurcation at \((y^{*},y^{*},k^{*})\) when \(T=T_{2}^{*}\) or \(T=T_{3}^{*}\) or \(T=T_{2}^{*} \) and \(T=T_{3}^{*}\).

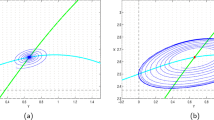
For systems (7)–(9), Fig. 1 presents the bifurcation diagram for the time-delay parameter T.

Fig. 1
figure 1

The bifurcation diagram for model for systems (7)–(9) \(m=1\) with investment function (25) for the delay parameter T. The solid line indicates a critical point with asymptotic stability, and the dot-dashed line corresponds to an unstable critical point with a limit cycle around it

Full size image

5 Case \(m=2\)

The characteristic equation of the linearized systems (10)–(13) at the critical point \((y^{*},p^{*},w^{*},k^{*})\), where \(p^{*}=w^{*}=y^{*}\), takes the form

$$\begin{aligned} \left| \begin{array}{cccc} \alpha I_{y}^{*}-\alpha \gamma -g-\lambda \quad &{} \quad 0\quad &{} \quad 0 &{} \quad \alpha I_{k}^{*} \\ 0\quad &{} -\dfrac{2}{T}-\lambda \quad &{} \quad \dfrac{2}{T} &{} \quad 0 \\ \dfrac{2}{T}\quad &{} \quad 0\quad &{} -\dfrac{2}{T}-\lambda &{} \quad 0 \\ 0\quad &{} \quad I_{y}^{*}\quad &{} \quad 0 &{} \quad I_{k}^{*}-(g+\delta )-\lambda \end{array} \right| , \nonumber \\ \end{aligned}$$
(17)

where \(I_{y}^{*}\) and \(I_{k}^{*}\) are defined as in (3) and (4), which leads to the following fourth-order algebraic equation in \(\lambda \)

$$\begin{aligned} \lambda ^{4}+a_{1}(T)\lambda ^{3}+a_{2}(T)\lambda ^{2}+a_{3}(T)\lambda +a_{4}(T)=0, \end{aligned}$$
(18)

where

$$\begin{aligned} a_{1}(T)= & {} \dfrac{4}{T}-(M+N) , \\ a_{2}(T)= & {} \dfrac{4}{T^{2}}-\dfrac{4(M+N)}{T}+MN, \end{aligned}$$

and

$$\begin{aligned} a_{3}(T)= & {} \dfrac{4}{T}\left[ MN-\dfrac{M+N}{T}\right] , \\ a_{4}(T)= & {} \dfrac{4(MN+P)}{T^{2}}, \end{aligned}$$

with

$$\begin{aligned} M= & {} \alpha \left( I_{y}^{*}-\gamma \right) -g,\quad \quad \quad N=I_{k}^{*}-(g+\delta )<0,\quad \quad \nonumber \\ P= & {} -\alpha I_{k}^{*}I_{y}^{*}>0. \end{aligned}$$
(19)

According to the Routh–Hurwitz conditions for stable roots, the equilibrium point \((y^{*},y^{*},y^{*},k^{*})\) of system (14) is locally asymptotically stable if \(a_{1}(T)>0,a_{3}(T)>0,a_{4}(T)>0\) and \( a_{1}(T)a_{2}(T)a_{3}(T)>a_{3}^{2}(T)+a_{1}^{2}(T)a_{4}(T)\), namely if

$$\begin{aligned}&\dfrac{4}{T}-(M+N)>0,\quad MN-\dfrac{M+N}{T}>0,\quad \nonumber \\&\quad MN+P>0 \end{aligned}$$
(20)

and

$$\begin{aligned}&\varphi (T)\\&\quad =\left[ (M+N)(MN)^{2}\right] T^{4}+[(M+N)^{2}(P-4MN)]T^{3} \\&\qquad +\left\{ 4(M+N)\left[ (M+N)^{2}+2MN-2P\right] \right\} T^{2} \\&\qquad +\left\{ 16\left[ P-(M+N)^{2}\right] \right\} T+16(M+N)<0. \end{aligned}$$

Taking in mind that \(N<0\) and \(P>0\), we derive that conditions (20) hold always true if \(M\le 0\). On the other hand, when \(M>0\), they are valid if \(M+N<0\), \(MN+P>0\) and \(T<(M+N)/(MN)\). The condition \(\varphi (T)<0\) is difficult to handle, unless \(M=0\). In fact, in this case,

$$\begin{aligned} \varphi (T)= & {} \left( N^{2}P\right) T^{3}+\left[ 4N\left( N^{2}-2P\right) \right] T^{2}\\&+\left[ 16\left( P-N^{2}\right) \right] T+16N \end{aligned}$$

is such that \(\varphi (0)<0\) and \(\varphi (+\infty )=+\infty \). Hence, there exists at least a positive value of T, say \(T_{0}^{*}\), such that \( \varphi (T)=0\). We need now to recall Descartes’ rule of signs and its corollary, which state “the number of positive roots of the polynomial \(\varphi (T)\) is either equal to the number of sign differences between consecutive nonzero coefficients, or less than it by an even number” and “the number of negative roots is the number of sign changes after multiplying the coefficients of odd-power terms by \(-1\), or fewer than it by an even number”, respectively. Applying these rules to the polynomial \(\varphi (T)\), we get that \(\varphi (T)\) has one positive zero and the number of negative zeros must be either 2 or 0. Therefore, \( \varphi (T)<0\) if \(T<T_{0}^{*}\). When \(M=0\), the equilibrium point \( (y^{*},y^{*},y^{*},k^{*})\) of (14) is locally asymptotically stable for \(T<T_{0}^{*}\).

Assume there exists \(T_{*}>0\) such that \(\varphi (T_{*})=0\), i.e.,

$$\begin{aligned} a_{1}(T_{*})a_{2}(T_{*})a_{3}(T_{*})-a_{3}^{2}(T_{*})-a_{1}^{2}(T_{*})a_{4}(T_{*})=0. \end{aligned}$$

In this case, we can rewrite the characteristic equation (18) as

$$\begin{aligned}&\left[ a_{1}(T_{*})\lambda ^{2}+a_{3}(T_{*})\right] \left[ a_{1}(T_{*})\lambda ^{2}+a_{1}^{2}(T_{*})\lambda \right. \nonumber \\&\qquad \left. +a_{1}(T_{*})a_{2}(T_{*})-a_{3}(T_{*})\right] =0. \end{aligned}$$

so that we have two purely imaginary roots

$$\begin{aligned} \lambda _{1,2}=\pm i\sqrt{\frac{a_{3}(T_{*})}{a_{1}(T_{*})}}=\pm i\omega _{*}, \end{aligned}$$

and two other roots,

$$\begin{aligned}&\lambda _{3,4}\\&\quad =\frac{-a_{1}^{2}(T_{*})\pm \sqrt{a_{1}^{4}(T_{*})-4a_{1}(T_{*})\left[ a_{1}(T_{*})a_{2}(T_{*})-a_{3}(T_{*}) \right] }}{2a_{1}(T_{*})}, \end{aligned}$$

which have real parts different from zero since

$$\begin{aligned} \lambda _{3}+\lambda _{4}=-a_{1}(T_{*})<0 \end{aligned}$$

and

$$\begin{aligned} \lambda _{3}\lambda _{4}=\left[ a_{1}(T_{*})a_{2}(T_{*})-a_{3}(T_{*})\right] /a_{1}(T_{*})>0. \end{aligned}$$

Differentiating the characteristic equation (18) with respect to T, we have

$$\begin{aligned}&\left[ 4\lambda ^{3}+3a_{1}(T)\lambda ^{2}+2a_{2}(T)\lambda +a_{3}(T)\right] \frac{\mathrm{{d}}\lambda }{\mathrm{{d}}T} \\&\quad =-\left[ a_{1}^{\prime }(T)\lambda ^{3}+a_{2}^{\prime }(T)\lambda ^{2}+a_{3}^{\prime }(T)\lambda +a_{4}^{\prime }(T)\right] , \end{aligned}$$

i.e.,

$$\begin{aligned} \frac{\mathrm{{d}}\lambda }{\mathrm{{d}}T}=-\frac{a_{1}^{\prime }(T)\lambda ^{3}+a_{2}^{\prime }(T)\lambda ^{2}+a_{3}^{\prime }(T)\lambda +a_{4}^{\prime }(T)}{4\lambda ^{3}+3a_{1}(T)\lambda ^{2}+2a_{2}(T)\lambda +a_{3}(T)}, \nonumber \\ \end{aligned}$$
(21)

where

$$\begin{aligned} a_{1}^{\prime }(T)=-\dfrac{4}{T^{2}},\qquad \quad a_{2}^{\prime }(T)=-\dfrac{8}{T^{3}}+\dfrac{4(M+N)}{T^{2}}, \end{aligned}$$

and

$$\begin{aligned} a_{3}^{\prime }(T)= & {} -\dfrac{4MN}{T^{2}}+\dfrac{8(M+N)}{T^{3}},\\ a_{4}^{\prime }(T)= & {} -\dfrac{8(MN+P)}{T^{3}}. \end{aligned}$$

Letting \(\lambda =i\omega _{*}\) in (21), a direct calculation yields

$$\begin{aligned}&\text {Re}\left( \frac{\mathrm{{d}}\lambda }{\mathrm{{d}}T}\right) _{T=T_{*}}\\&\quad =-\frac{ a_{1}(T_{*})\varphi ^{\prime }(T_{*})}{2\left\{ a_{1}^{3}(T_{*})a_{3}(T_{*})+\left[ a_{1}(T_{*})a_{2}(T_{*})-2a_{3}(T_{*}) \right] ^{2}\right\} }, \end{aligned}$$

where

$$\begin{aligned} \varphi ^{\prime }(T_{*})= & {} a_{1}^{\prime }(T_{*})a_{2}(T_{*})a_{3}(T_{*})\\&+a_{1}(T_{*})a_{2}^{\prime }(T_{*})a_{3}(T_{*})+a_{1}(T_{*})a_{2}(T_{*})a_{3}^{\prime }(T_{*}) \\&-2a_{3}(T_{*})a_{3}^{\prime }(T_{*})-2a_{1}(T_{*})a_{1}^{\prime }(T_{*})a_{4}(T_{*})\\&-a_{1}^{2}(T_{*})a_{4}^{\prime }(T_{*}). \end{aligned}$$

Let us notice that \(\mathop {\mathrm {sign}}\left[ \text {Re}\left( \mathrm{{d}}\lambda /\mathrm{{d}}T\right) _{T=T_{*}} \right] =\mathop {\mathrm {sign}}\left[ -\varphi ^{\prime }(T_{*})\right] \), as well as recall that \(\mathop {\mathrm {sign}}\left[ \text {Re}\left( \mathrm{{d}}\lambda /\mathrm{{d}}T\right) _{T=T_{*}}\right] >0\) and \(\mathop {\mathrm {sign}}\left[ \text {Re}\left( \mathrm{{d}}\lambda /\mathrm{{d}}T\right) _{T=T_{*}}\right] <0\) correspond to crossings of the imaginary axis from right to left and from left to right, respectively.

Summarizing all the previous analysis, we have the following results.

Theorem 2

Let M be defined as in (19).

(1):

Let \(M=0\). There exists \(T_{0}^{*}>0\) such that the equilibrium point \((y^{*},y^{*},y^{*},k^{*})\) of (14) is locally asymptotically stable for \(T<T_{0}^{*}\), unstable for \( T>T_{0}^{*}\), and bifurcates to a limit cycle through a Hopf bifurcation at the equilibrium point when \(T=T_{0}^{*}\).

(2):

Let \(M\ne 0\). The equilibrium point \((y^{*},y^{*},y^{*},k^{*})\) of (14) is locally asymptotically stable if \( M<0\) and \(\varphi (T)<0\) or if \(M>0,M+N<0\), \(MN+P>0,T<(M+N)/(MN)\) and \( \varphi (T)<0\). If there exists \(T=T_{*}\) such that \(\varphi (T_{*})=0\) and \(\varphi ^{\prime }(T_{*})\ne 0\), then a Hopf bifurcation may occur at the equilibrium point as T passes through \(T_{*}\).

6 The rate of growth bifurcation analysis

Let us consider the dynamics of systems (7)–(9) with respect to the change of the parameter g (the rate of economic growth).

Proposition 1

The critical point of systems (7)–(9) (and equivalently systems (1)–(2) always exists for the rate of growth parameter g in the interval \(c - \delta< g < c + d - \delta \).

It is shown earlier that systems (1)–(2) have a unique fixed point for \(c< g + \delta < c +d\). The economy with the investment function \(I(y,k)= k\Phi (y,k)\) has a fixed point or a limit cycle solution only for some rates of growth within the interval \((c - \delta , c + d - \delta )\). The parameters c and d of the investment function (and also the capital stock depreciation parameter) put some limit on minimal and maximal rates of growth.

Let us consider the characteristic equation of the linearized systems (10)–(13) at the critical point \((y^*, u^*, k^*)\), in the form

$$\begin{aligned} \left| \begin{array}{ccc} \alpha (I_y^*(g) - \gamma ) - g - \lambda &{} 0 &{} \alpha (g + \delta - x^*(g) I_y^*(g)) \\ \frac{1}{T} &{} - \frac{1}{T} - \lambda &{} 0 \\ 0 &{} I_y^* &{} - x^*(g) I_y^*(g) - \lambda \end{array} \right| = 0\nonumber \\ \end{aligned}$$
(22)

or

$$\begin{aligned} \lambda ^3 + a_1(g) \lambda ^2 + a_2(g) \lambda + a_3(g) = 0, \end{aligned}$$
(23)

where

$$\begin{aligned} a_1(g)&= \frac{1}{T} - \alpha (I_y^*(g) - \gamma ) + g + x^*(g) I_y^*(g), \\ a_2(g)&= -\frac{1}{T} [\alpha (I_y^*(g) - \gamma ) - g - x^*(g) I_y^*(g)]\\&\quad - [\alpha (I_y^*(g) - \gamma ) - g)x^*(g) I_y^*(g) \\ a_3(g)&= \frac{1}{T} [ -[\alpha (I_y^*(g) - \gamma ) - g]x^*(g) I_y^*(g), \\&\quad -\alpha I_k^*(g) I_y^*(g)], \end{aligned}$$

where \(\lambda \) is a root of the characteristic equation.

The discriminant of the characteristic equation is

$$\begin{aligned} \Delta = 18a_1 a_2 a_3 - 4a_2^3 a_3 + a_2^2 a_3^2 -4a_3^3 -27 a_3^2. \end{aligned}$$
(24)

Proposition 2

If expression (24) is positive, then the all eigenvalues are real, and if it is negative, there is one real, one pair of conjugate complex eigenvalues. For the zero value of expression (24), the critical point is non-hyperbolic.

For real eigenvalues, we have the following proposition

Proposition 3

In the interval \(c - \delta< g < c + d - \delta \), there are two subintervals with the positive values of the discriminant (24); these are two subintervals of the values of the rate of growth parameter g. In these subintervals, there are three negative real eigenvalues.

The subintervals of the parameter g with two negative and one positive eigenvalues are non-physical regions as the critical point (\(y^*, u^*, k^*\)) does not lie in a positive quadrant.

For complex eigenvalues, we have the following proposition

Proposition 4

In the interval, \(c - \delta< g < c + d - \delta \) and negative values of the discriminant (24) for the increasing value of the rate of growth parameter g there are two supercritical Hopf bifurcations. For the value \(g = g_{1,\text {Hopf}}\), the limit cycle is created, and for the value \(g=g_{2,\text {Hopf}}\), the limit cycle is destroyed (\(g_{1,\text {Hopf}}<g_{2,\text {Hopf}}\)).

Therefore, as the rate of growth parameter is increasing in the interval \(g_\text {min} = c - \delta< g < c + d - \delta = g_\text {max}\), the eigenvalues change as follows. In the first subinterval \((g_{\text {min}}; g_1)\), there are three real eigenvalues (two negative, one positive). In the second subinterval \((g_1; g_{1,\text {Hopf}})\), there are three real eigenvalues (three negative). In the third subinterval \(( g_{1,\text {Hopf}};g_{2,\text {Hopf}})\), there are one real eigenvalue (negative) and one conjugate complex eigenvalue (positive real parts). In the fourth subinterval \((g_{2,\text {Hopf}};g_2)\), there are three real eigenvalues (three negative). And finally, in the fifth subinterval \(g_2,(g_{\text {max}})\) there are three real eigenvalues (two negative, one positive).

For some example values of parameters, we can determine the values of the rate of growth parameter for which the eigenvalues change their character or sign. We assume the values of investment function parameters obtained by Dana and Malgrange, namely, \(c=0.01\), \(d=0.026\), \(a=9\), \(v=4.23\). We fix also the following model parameters \(\alpha =1\), \(\gamma =0.15\), \(\delta =0.007\), \(G_0=2\) and \(T=1\). The rate of growth parameter g is taken within the interval \(g_\text {min} = c - \delta< g < c + d - \delta = g_\text {max}\). The results are presented in Table 1.

Table 1 The intervals of values of rate of growth parameter g and respective signs of eigenvalues of the characteristic equation (22)
Full size table

For systems (7)–(9), Fig. 2 presents the bifurcation diagram for the rate of growth parameter g.

Fig. 2
figure 2

The bifurcation diagram for model for systems (7)–(9) \(m=1\) with investment function (25) for the rate of growth parameter g (the delay parameter \(T=1\)). The solid line indicates critical point with asymptotic stability, and the dot-dashed line corresponds to the unstable critical with a limit cycle around it

Full size image

7 Numerical analysis of the Hopf bifurcation

The original Kaldor model exhibited limit cycle behavior due to the Hopf bifurcation caused by the increase of the parameter \(\alpha \) value [20]. Later, it has been augmented by introducing both the investment lag T and exogenous growth trend g. The increase of the investment time-delay parameter value also generates the limit cycle [18]. However, the dependence the Hopf bifurcation on the rate of growth parameter has been not elaborated so far. Both Chang and Smyth in the Kaldor model [20] as well as Dana and Malgrange in the Kaldor model with exogenous growth trend investigated the parameter \(\alpha \) as the bifurcation parameter [27].

Fig. 3
figure 3

The phase portrait for systems (7)–(9) (\(m=1\)) with investment function (25) for the delay parameter \(T=1\), the rate of growth parameter \(g=0.016\) and the parameter \(\alpha =0.75\). The stable limit cycle is shown (black) and two arbitrary chosen trajectories (red and blue). (Color figure online)

Full size image

For numerical studies, we use the program XPPAUT [47] and conduct the numerical analysis of both models: \(m=1\) and \(m=2\). The investment function is assumed to have the following parameter values: \(c=0.01\), \(d=0.026\), \(a=9\) and \(v=4.23\) [27]

$$\begin{aligned} I(y,k) = k \Phi (y,k) = 0.01 + \frac{0.026}{1+e^{-9(4.23y/k -1)}}. \end{aligned}$$
(25)

Montgomery analyzed the averaged construction period in the US economy and found that the value-weighted average construction in 1961–1991 was 16.7 months with projects completed in the interval from 0 to 48+ months [48]. Therefore, we consider the delay parameter \(T \in (0,5)\). For bifurcation analysis, we also assume \(\alpha \in (0.5, 1.0)\) and \(g \in (0.005, 0.025)\). For the rest of parameters, we take \(\gamma =0.15\), \(\delta =0.007\), \(G_0=2\) [27].

8 Case \(m=1\)

In this case, we consider the three-dimensional model (7)–(9) for the state variables (y, u, k) and study numerically the stability of the critical point \((y^* = u^*, k^*)\) in order to find the values of parameter T for which the critical point loses the stability and the limit cycle is created through the Hopf bifurcation mechanism. In the phase portrait presented in Fig. 3, the limit cycle is shown with two arbitrary chosen trajectories attracted to it.

A detailed study will be conducted on the dependence of the bifurcation value of T from the model parameters \(\alpha \) and g as well as the dependence of the bifurcation value of g from the model parameters \(\alpha \) and T.

The bifurcation surface in the parameter space (a, g, T) is presented in Fig. 4. For each pair of fixed values of parameters a and T in the interval of (0.70, 0, 78) and (0.1, 1.5), respectively, the two bifurcation values of the parameter g have been obtained in the program XPPAUT [47]. The region below the surface corresponds to the asymptotic stability of the critical point \((y^*, u^*, k^*)\). The region inside instead corresponds to parameter values for which systems (7)–(9) have an unstable critical point with a limit cycle around it.

Fig. 4
figure 4

The Hopf bifurcation surface in the space of parameters \((\alpha , g, T)\) for systems (7)–(9) \(m=1\) and with investment function (25). Outside of the surface is the region of asymptotic stability, while inside of the surface is the region of parameters values for which a limit cycle solution exists

Full size image

To conduct a more detailed analysis, we now consider relations between two parameters with a third parameter fixed. First, the relation of T on \(\alpha \) for \(g=0.016\) is shown in Fig. 5. We find that the asymptotic stability region exist only if \(\alpha < 0.7644\) (with \(g=0.016\)). In the interval of \(\alpha \in (0.6, 0.764)\), we find the relation \(T_\text {bi}(\alpha )\) is

$$\begin{aligned} T_{\text {bi}} = -11.137983 + \frac{8.512805}{\alpha }. \end{aligned}$$
(26)
Fig. 5
figure 5

The plane of parameters \((\alpha ,T)\) for system \(m=1\) and \(g=0.016\) with investment function (25). Region I is the region of asymptotic stability, while region II is the region of parameters value for which a limit cycle solution exists

Full size image
Fig. 6
figure 6

The plane of parameters (g, T) for system \(m=1\) with investment function (25). Here, it is assumed that \(\alpha =0.6\) (left panel) and \(\alpha = 0.9\) (right panel). Region A is the region of asymptotic stability, and region B is the region of limit cycle solution, and they are separated by the bifurcation line \(T_{\text {bi}}(g)\)

Full size image

Second, we investigate the dependence of the parameter T on the parameter g with the fixed value of \(\alpha \). We take the three values of parameter \(\alpha \). The stability regions on the plane (g, T) are shown for \(\alpha = 0.6\) and \(\alpha = 0.9\) in Fig. 6. As the value of the parameter g increases, region B is growing.

The bifurcation line separating regions A and B is described by a quadratic equation

$$\begin{aligned} T_{\text {bi}} = a_2 g^2 + a_1 g + a_0. \end{aligned}$$
(27)

Finally, we analyze the time paths of the model for the economic variable y for different values of the time-delay parameter for the amplitude and period of cycles. In region I, there exists a stable equilibrium reached by trajectories in an oscillating manner. It is the region of asymptotic stability of the model. In Fig. 7, there are two cases for \(\alpha = 0.6, 0.9\) with three solutions y(t) obtained for given \(T = 0.5, 1.5, 3\) and the same initial function \(y(t)=1\), \(k(t)=100\) where \(t \in (-T,0)\). We can see that the dumping of oscillations is weaker as the time delay T increases.

Fig. 7
figure 7

Trajectories of model \(m=1\) with investment function (25) for the parameter \(g=0.016\) and \(\alpha = 0.6\) (left panel) and \(\alpha = 0.9\) (right panel)

Full size image

9 Case \(m=2\)

In this case, we consider the four-dimensional model (10)–(13) for the state variables (y, p, w, k). In this model, the critical point values of \((y^* = p^* = w^*, k^*)\) are the same as the critical point values of \((y^* = u^*, k^*)\) of three-dimensional model presented in the previous section.

In a similar way as in the previous section, we analyze the occurrence of the Hopf bifurcation for the parameter T depending on parameters \(\alpha \) and g. The relation of T on \(\alpha \) for \(g=0.016\) is shown in Fig. 8. The asymptotic stability region exists only if \(\alpha < 0.7644\) (with \(g=0.016\)). It is the same result as in the case of model \(m=1\).

Next, we study the cycle characteristics for some values of the parameter \(\alpha \) with different values of the delay parameter T. Figure 9 shows the solutions of y for two cases of \(\alpha = 0.6, 0.9\) and three values of the parameter \(T = 0.5, 1.5, 3.0\). The amplitude and period of cycles are decreasing as the parameter T increases for \(\alpha = 0.6\).

Fig. 8
figure 8

The plane of parameters \((\alpha ,T)\) for system \(m=2\) and parameter \(g=0.016\) with investment function (25). Region I is the region of asymptotic stability, while regions II and III are regions of parameter values for which a limit cycle solution exists

Full size image
Fig. 9
figure 9

Trajectories of model \(m=2\) with investment function (25) for parameter \(g=0.016\) and \(\alpha = 0.6\) (left panel) and \(\alpha = 0.9\) (right panel)

Full size image

10 Comparison of \(m=1\) and \(m=2\)

The models presented can be treated as the approximation of the delay Kaldor–Kalecki growth model. To find how good are the subsequent approximations, we compare the bifurcation values of the parameter T in models \(m=1\) and \(m=2\).

First, we consider the bifurcation diagram in the parameter plane \((\alpha , T)\) presented in Fig. 10. It occurs that for the given value of parameter \(\alpha \) the Hopf bifurcation value of the parameter \(T_{\text {bi}}\) is lower for the model \(m=2\). This difference is zero for \(T=0\) and then increases as the value \(T_{\text {bi}}\) increases for the fixed value of the parameter \(\alpha \). On the other hand, for the fixed value of the parameter T, the bifurcation value of the parameter \(\alpha _\text {bi}\) is greater in the model \(m=2\). For the parameter \(g=0.016\), the difference is close zero at \(\alpha = 0.7644\) and equals 0.04 at \(\alpha = 0.6\), while for the parameter \(g=0.011\), the difference is 0.234 at \(\alpha = 0.6\). It is demonstrated in Fig. 10 for \(g=0.016\) (left panel) and \(g=0.011\) (right panel).

Fig. 10
figure 10

The plane of parameters \((\alpha ,T)\) for systems (\(m=1\)) and (\(m=2\)) with investment function (25). Here, it is assumed that \(g=0.016\) (left panel) and \(g=0.011\) (right panel). The dashed line is for model \(m=1\), and the dotted line is for model \(m=2\). These bifurcation curves separate region I of asymptotic stability on the left side of curves and region II of limit cycle solution on the right side of curves

Full size image

We compare trajectories of y(t) for systems \(m=1\) and \(m=2\) with the same initial conditions. In Figs. 11 and 12, there are trajectories y(t) for assumed the parameter \(g=0.016\) and combinations of parameters \(\alpha \) and T. We find that for the same parameters \(\alpha \), g and T, the period of cycles is smaller for model \(m=2\) and amplitude is also smaller, although the difference is very small. For example, for \(\alpha = 0.9\), \(g=0.016\) and \(T=3\), the period of cycle in model \(m=1\) is 114.85 and in model \(m=2\) is 116.45, while amplitudes are 12.9555 and 12.966, respectively. Taking models with greater m, we should obtain the cycles with longer periods and amplitudes.

Fig. 11
figure 11

Trajectories of models \(m=1\) and \(m=2\) with investment function (25) for the same initial condition \((y=p=w=15, k=100)\) (left panel) for \(\alpha =0.6\) and \(g=0.016\). The left panel for \(T=0.5\) and the right panel for \(T=3\)

Full size image
Fig. 12
figure 12

Trajectories of models \(m=1\) and \(m=2\) with investment function (25) for the same initial condition \((y=p=w=15, k=100)\) (left panel) for \(\alpha = 0.9\) and \(g=0.016\). The left panel for \(T=0.5\) and right panel for \(T=3\)

Full size image

We can explore further approximations of the model and compare values of the bifurcation parameter g for successive m in Table 2.

Table 2 The Hopf bifurcation points \(g_\text {bi,1}\) and \(g_\text {bi,2}\) for subsequent approximations
Full size table

11 Conclusions

The Kaldor–Kalecki growth model with distributed delay is investigated. To simplify our analysis, the gamma distribution has been considered to have only weak and strong kernels. Using the linear chain trick, the delay differential equations describing our model are replaced by three-dimensional and four-dimensional dynamical systems, respectively.

The model is found to have an equilibrium only for some interval of values of the rate of growth parameter. This interval depends on the values of investment function which are chosen for analyzing the model.

The birth of a limit cycle (the Hopf bifurcation) is conducted due to the change of two parameters: the time delay T and the rate of growth g. Additionally, we take into consideration the speed of adjustment parameter \(\alpha \) which is the bifurcation parameter of the original Kaldor model. In order to have a better insight of the dynamics, the bifurcations are analyzed in the three-dimensional space of these parameters.

Considering the dynamics of the model under the change of the growth rate parameter, we discover numerically two bifurcation values of the rate of growth parameter when the Hopf bifurcations occur. Increasing the value of this rate of growth parameter, for a smaller value of this parameter the limit cycle emerges and then for a larger value of this parameter the limit cycle is destroyed to a stable focus through the Hopf bifurcations. Therefore, the cyclic behavior takes place in some interval of the rate of growth parameter values. Outside of this interval, the system through damping oscillation goes to a stable stationary solution. Similar dynamic behavior with two Hopf bifurcations separating stable, unstable and stable regions appeared in the macroeconomic model extending the Calvo and Obstfeld framework [49].

There are two oscillating regimes. For lower and higher rates of growth, the oscillations are damped and asymptotically stationary state is reached. For intermediate rates of growth, the self-sustained oscillations of constant amplitude are present. For some model parameters, this intermediate interval of rate of growth values is obtained to be (0.01011989, 0.0238466) for three-dimensional and four-dimensional systems. The range of this intermediate interval depends on the model parameters: \(\alpha \), \(\gamma \) and \(\delta \).

All numerical analyses have been done with Dana and Malgrange’s investment function for the French macroeconomic data [27].

  • The Kaldor–Kalecki model with distributed delay is reduced to the ordinary differential system using the linear chain trick technique.

  • Depending on the value of the parameter m of the \(\Gamma \) distribution function, the reduced system is \((m+2)\)-dimensional ordinary differential equation system.

  • For the increasing time-delay parameter, there is the supercritical Hopf bifurcation.

  • For the increasing rate of growth parameter, first the limit cycle emerges and then the limit cycle disappears. Therefore, there are two supercritical Hopf bifurcations with two bifurcation values of the rate of growth parameter.

  • For some values of parameters \(\alpha \) and T, in the allowed range of the rate of growth parameter values, for both lower and higher values of the rate growth parameter the model has the stable stationary point, while for the middle range of parameter values there is the limit cycle.

  • The period of cycle increases and decreases as the rate of growth parameter increases in the range of unstable solution.

  • Comparing the models with different m, the stable region in the parameter space is slightly diminished as m is greater.