Parameter identification in elastoplastic material models by Small Punch Tests and inverse analysis with model reduction

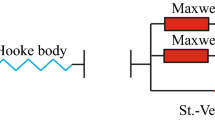
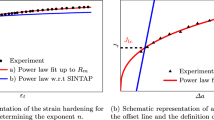
Abstract

Small Punch Tests (SPT) are, at present, frequently employed for diagnostic analyses of metallic structural components and are considered in codes of practice because the damage generated by miniature specimen extraction is small (“quasi-non-destructive” tests). This paper contains a description of the following contributions for improvement in the state-of-the-art of SPT practice: assessment of material parameters through inverse analysis, made faster and more economical by employing model reduction through a Proper Orthogonal Decomposition (POD) procedure. The methodology is developed to assess material parameters entering into diverse constitutive models, thus resulting in a more flexible identification framework, capable of addressing different kinds of material behaviour. Within the paper, real experimental data are used and comparisons of computed stress–strain curves with experimentally measured ones, through typical tensile tests, show an excellent agreement.

A: On Proper Orthogonal Decomposition (POD) and Radial Basis Functions (RBF) interpolation

Proper Orthogonal Decomposition (POD) procedure adopted here is rooted originally in mathematics oriented to economics. Details related to the present purposes can be found in a broad literature, particularly in [7, 8, 36, 41]. By assuming the parameters ${\varvec{p}}_i$ at each node of a grid generated on the search domain, a test simulation leads to the vector ${\varvec{u}}_i$ containing the pseudo-experimental data (“snapshot” corresponding to ${\varvec{p}}_i$) through direct analysis, usually, by FEM. Let a $M\times N$ matrix $\varvec{U}$ gather all such snapshots.

The responses ${\varvec{u}}_i$ of the tested system to the same given external actions, but with diverse parameters ${\varvec{p}}_i$ internal to the search domain, turn out to be correlated, namely “almost parallel” in their space. Such correlation is clearly physically motivated in the present context and can be easily checked in matrix ${\varvec{U}}$.

Within the M-dimensional space of the snapshots ${\varvec{u}}_i$ $\left( i=1\ldots N\right)$ a new reference axis is singled out by maximizing, with respect to all directions, an Euclidean norm of the projections on it of all N snapshots ${\varvec{u}}_i$. Then, another axis is found by similar maximization over the set of all directions orthogonal to the one above singled out. A sequence of such optimizations leads to a new reference system, or new basis, analytically described by an orthonormal matrix ${\varvec{\varPhi }}$ of order M such that:

$$\begin{aligned} {\varvec{\varPhi }}^{\mathrm {T}}{\varvec{\varPhi }}=\varvec{I}{\mathrm {,}}\qquad \varvec{U}={\varvec{\varPhi }}\varvec{A}{\mathrm {,}}\qquad \varvec{A}={\varvec{\varPhi }}^{\mathrm {T}}\varvec{U} \end{aligned}$$

(11)

where the $M\times N$ matrix ${\varvec{A}}$ gathers as columns the vectors (called “amplitudes” ${\varvec{a}}_i$ in the POD jargon) which describe the snapshots ${\varvec{u}}_i$ in the new basis.

The above mentioned correlation among test responses with different parameters within their search domain motivates large differences among amplitude components. Therefore a meaningful simplification is achieved by removal of axes with negligible components in the new basis. Operative details can be found in [14], while here only the main features are mentioned, namely: the above truncation is based on the computation of the eigenvalues $\lambda _i$ $\left( i=1\ldots N\right)$ of matrix $\varvec{D}=\varvec{U}^{\mathrm {T}}\varvec{U}$ (of order N, symmetric positive definite or semidefinite) and on preservation of the axes corresponding to the $\lambda _i$ larger by orders of magnitude than the smallest eigenvalues.

Thus a truncated basis (matrix $\hat{{\varvec{\varPhi }}}$ of order $M\times K$ with $K\ll M$) is generated for approximations of the test responses ${\varvec{u}}_i$ through their dependence on reduced amplitudes $\hat{\varvec{a}}_i$, namely:

$$\begin{aligned} {\varvec{u}}_i\cong \hat{{\varvec{\varPhi }}}\hat{\varvec{a}}_i\quad \left( i=1\ldots N\right) \quad {\mathrm {or}}\quad \varvec{U}\cong \hat{{\varvec{\varPhi }}}\hat{\varvec{A}} \end{aligned}$$

(12)

Approximation errors implied by the above truncation can be evaluated by comparing the sum of the eigenvalues $\lambda _i$ $\left( i=1\ldots K\right)$ related to the K preserved directions (or “modes”) to the sum of all the original ones $\lambda _i$ $\left( i=1\ldots N\right)$.

The truncated basis $\hat{{\varvec{\varPhi }}}$ exhibits the mathematical features of the original basis ${\varvec{\varPhi }}$ expressed by Eq. (11); therefore the reduced amplitude $\hat{\varvec{a}}_i$ of any snapshot ${\varvec{u}}_i$ can be computed with the approximation as in Eq. (12), namely:

$$\begin{aligned} \hat{\varvec{a}}_i\cong \hat{{\varvec{\varPhi }}}^{\mathrm {T}}{\varvec{u}}_i\quad \left( i=1\ldots N\right) \quad {\mathrm {or}}\quad \hat{\varvec{A}}\cong \hat{{\varvec{\varPhi }}}^{\mathrm {T}}{\varvec{U}} \end{aligned}$$

(13)

The “model reduction” procedure outlined in what precedes concerns the set of the N parameter vectors ${\varvec{p}}_i$ pre-selected as grid nodes in the search domain. Such reduction can be done once-for-all, in view of repeated practical applications of inverse analyses.

The minimization of the discrepancy function $\omega ({\varvec{p}})$, Eqs. (9) and (10) in Sect. 3, requires a high number of test simulations, as underlined earlier, both if a GA is employed or if an algorithm of mathematical programming, as TRA, is adopted. Such practical difficulty can be overcome by means of the computational provisions summarized in what follows.

For each parameter grid node ${\varvec{p}}_i$ $\left( i=1\ldots N\right)$ a Radial Basis Function (RBF) is considered, namely:

$$\begin{aligned} g_i({\varvec{p}})=\left[ \left( {\varvec{p}}-{\varvec{p}}_i\right) ^{\mathrm {T}}\left( {\varvec{p}}-{\varvec{p}}_i\right) +r^2\right] ^{\mathrm {-\frac{1}{2}}}\quad \left( i=1\ldots N\right) \end{aligned}$$

(14)

with the “smoothing coefficient” r to be calibrated, once-for-all (see e.g. [6]); to the present purposes r = 0.05 is assumed. Each component ${\hat{a}}^k_j$ $\left( k=1\ldots K{\mathrm {,}}\ j=1\ldots N\right)$ of the reduced amplitude vector $\hat{\varvec{a}}_j$ corresponding to node parameters ${\varvec{p}}_j$, defined by Eq. (13), is expressed as a linear combination of the values acquired there by the RBFs Eq. (14):

$$\begin{aligned} \hat{a}^k_j=\sum ^{N}_{i=1}b^k_ig_i({\varvec{p}}_j)\quad \left( k=1\ldots K{\mathrm {,}}\ j=1\ldots N\right) \quad {\mathrm {or}}\quad \hat{\varvec{A}}=\varvec{B}\varvec{G} \end{aligned}$$

(15)

The above Eq. (15) consists of $K\times N$ linear equations in $K\times N$ unknowns $b^k_i$, gathered in matrix ${\varvec{B}}$; matrix ${\varvec{G}}$ contains the known values $g_i({\varvec{p}}_j)$ of all functions RBF in all N parameter nodes ${\varvec{p}}_i$ of the grid over the search domain.

The simple solution of Eq. (15) provides the coefficients $b^k_i$ for the linear combination which leads from any new parameter vector ${\varvec{p}}$ out of the grid nodes to the relevant reduced amplitudes $\hat{\varvec{a}}$ of the snapshot ${\varvec{u}}$. This vector ${\varvec{u}}$ quantifies the pseudo-experimental data resulting from the test simulation based on the parameters contained in that vector ${\varvec{p}}$, namely:

$$\begin{aligned} {\varvec{u}}({\varvec{p}})=\hat{{\varvec{\varPhi }}}\hat{\varvec{a}}=\hat{{\varvec{\varPhi }}}\varvec{B}\varvec{g}({\varvec{p}}) \end{aligned}$$

(16)

In this final formula, vector ${\varvec{g}}$ gathers the N values of $g_i({\varvec{p}})$ $\left( i=1\ldots N\right)$ which are acquired by the RBF centred on ${\varvec{p}}$ in all grid nodes, Eq. (14). When matrix ${\varvec{B}}$ is available, since it was provided by the solution once-for-all of Eq. (15), any direct analysis (i.e. any test simulation leading to the measurable quantities), can be carried out by Eq. (16), rather than by FEM or by other methods. Consequently, the computing times become by various orders of magnitude shorter, at comparable accuracy. Clearly, the practical benefits for parameter identifications by means of either TRA or GA are significant. The above circumstance implies substantial computational advantages also when an ANN is adopted for fast inverse analyses, since the ANN input may consist of amplitude vector $\hat{\varvec{a}}$ which represents the snapshot ${\varvec{u}}$ with much lesser number of components.