Introduction

According to Web of Science, around six thousand papers have been published that indicated one or more popular isoconversional kinetic evaluation methods in their title, abstract or keywords [1]. These methods provide the activation energy, E, as a function of reacted fraction, α. See, e.g., Table 1 in the work of Cai et al. [2] for a concise overview. There are different aims for carrying out such calculations [3, 4], but the researchers publishing in this field usually find the obtained dependence of E on α important enough to show it in figures and/or tables. This appears to be the present situation, too. A test on recent literature is given in the next section in which 97% of the surveyed papers published such figures or tables.

Table 1 Results of the reliability tests on the evaluation of α(t) curves
Full size table

Accordingly, the reliability of the E–α relations published in the literature regularly is a subject well worth studying. The popular isoconversional methods assume a kinetic equation in the form

$${\text{d}}\alpha /{\text{d}}t = A\left( \alpha \right)f\left( \alpha \right){\text{exp}}\left( { - \frac{E\left( \alpha \right)}{{RT}}} \right)$$
(1)

See the list of symbols for the notations. Theoretically, the activation energy may be a function of both α and T [3, 4], but general E(α,T) functions are rarely determined from thermoanalytical experiments. Usually, the dependence of E on α is studied only. The present work also deals only with E(α) functions. Note that the thermal analysis experiments can hardly provide information for the separation of the A(α)f(α) term into A(α) and f(α): no matter what f(α) is assumed, a freely varying A(α) makes the corresponding A(α)f(α) product to be an arbitrary function. The A(α)f(α) notation is maintained here to express that this term should change several magnitudes as E(α) varies to keep the left-hand side of Eq. (1) at realistic values. The usual f(α) functions of the non-isothermal kinetics vary in a much narrower range, e.g., between 1 and 0.

Several papers discussed and criticized the methods and concepts of the isoconversional kinetic evaluations, among others the recent work of Šimon et al. [5]. The present study has different aims. We shall not deal here with the merits and drawbacks of the specific isoconversional evaluation techniques. The author accepts that special cases of Eq. (1) with variable E may serve as empirical models for processes which are too complicated for a detailed kinetic modelling. We shall examine here whether the thermoanalytical experiments themselves contain enough information for the reliable determination of such empirical models.

In a recent paper [6], the author showed that the information provided by the TG curves may not be sufficient for the trustworthy determination of E(α). For this purpose, a special case of Eq. (1) was used that contained adjustable parameters. Its numerical solutions could be compared with the original αobs(t) data. Examples were constructed showing that the numerical solutions of Eq. (1) at highly variable E(α) functions can approximate well the numerical solutions of Eq. (1) at constant E values [6].

In the present work, further aspects of the problem are examined. Many researchers prefer the least squares evaluation of the derivative thermoanalytical curves to other evaluation methods due to the higher information content of the derivative curves. This has been the preference of the present author since 1979 [7] for models built with partial reactions with non-varying E values. The groundbreaking work of Braun and Burnham also included a curve fitting procedure on the derivative experimental curves in 1987 [8]. Hence, the determination of E(α) functions from dα/dt curves is also studied in the present work. It is shown by examples that the least squares evaluation of the derivative curves can lead to better-defined results than a similar evaluation of the corresponding TG curves. Increasing and decreasing E(α) functions are studied alike.

The last section deals with the determination of the activation energy from single modulated experiments by a standard of ASTM International [9]. Though this standard is rarely used in practice, the information content of the modulated thermoanalytical experiments is a subject well worth studying because many apparatuses exist which are suitable for carrying out modulated experiments.

The present work is based on a least squares evaluation method that was proposed by the author in 2019 [10]. 85 TG experiments on 16 biomass samples were evaluated in that work. The results clearly showed that markedly different E(α) functions can result in acceptable fit qualities for a given set of experiments. However, the experiments treated there were conducted on rather complex chemical systems: They were taken from biomass pyrolysis studies. It was not clear whether these observations were due to some general problems, or they were specific to the studied reactions. That is why the present work and its predecessor one [6] were based on experiments simulated by assuming simpler reaction kinetics.

Most of the results of the present work can easily be reproduced by a relatively simple computer source code which is given as Supplementary Material. The code is written in C and can be compiled and run under Windows or Linux.

Methods, equations, and a check on the literature

A check on the recent literature

As outlined in Introduction, a test was carried out on the recent literature. Some of its results are used in the next section; hence, the method of this survey is described here. Such works were searched in Web of Science [1], which contained the following terms in their title, abstract or keywords:

  1. (i)

    The word kinetics or kinetic or kinetically; and

  2. (ii)

    At least one of the following terms: isoconversional; iso-conversional; model-free; Akahira-Sunose; Flynn-Ozawa; Friedman method; Kissinger-Akahira; Starink; Vyazovkin method.

The test was carried out for works that were indexed by Web of Science in a period of 62 days during the preparation of the present paper, from 20 August 20 till 20 October 2023. The search formula resulted in a few false hits (i.e., works in other fields) which were disregarded. Altogether 73 papers could be downloaded and examined. Only two of them did not present figures or tables on the variation of E with the advance of the processes studied. Around 80% of these works were published in journals with impact factors higher than three; the highest impact factor was near to 17 [11]. Roughly one tenth of the papers were published by Journal of Thermal Analysis and Calorimetry. In this latter subgroup, all but one works presented figures or tables on E(α) dependencies [12,13,14,15,16].

Simulated experimental

As in the preceding work of the author [6], experiments were simulated assuming first-order kinetics with E = 200 kJ mol−1 and A = 1016 s−1 at different heating rates for test evaluations. A general ODE solving procedure was used for the simulation which produced both the α(t) and the dα/dt curves with high precision, as outlined in the next section. Burnham emphasized that a wide range of heating rates is needed for a dependable kinetic evaluation and the heating rates should form a geometric progression [17]. His suggestions are followed in the present paper, too. The basic set of heating rates was chosen to be 2.5, 5, 10, 20 and 40 °C min−1, similarly to the work of Cai et al. [2]. In this set, the ratio between the highest and the lowest heating rates, βmax/βmin, is 16. Usually lower heating rate ratios are employed in the kinetic studies of thermal analysis. 92% of the papers employed lower βmax/βmin ratios in the literature test outlined above. Accordingly, the reliability of the experiments is also checked on narrower ranges of heating rates. Two sets were selected for this purpose: 5, 10, 20 and 40 °C/min (βmax/βmin = 8) and 5, 10, 15, 20 °C min−1 (βmax/βmin = 4). The latter set of heating rates is particularly popular; nearly every fifth of works in the literature check employed a β series of 5, 10, 15, 20 °C min−1.

Besides, modulated T(t) functions were also employed in the last section of this work where the reliability of an ASTM standard [9] on the kinetic evaluation of modulated experiments is tested. The corresponding temperature programs were taken from the ASTM standard and from sone related publications, as outlined there.

The simulated experimental curves were evaluated between the time values belonging to α ≅ 0.001 and α ≅ 0.999 at each heating rate or modulated heating program.

The employed E(α) functions and a version of Eq. (1) with optimizable parameters

In this work, such solutions of Eq. (1) were searched for which approximate well the same set of simulated experiments. A special case of Eq. (1) was used for this purpose. With some restrictions on the generality of Eq. (1), we can use a version of Eq. (1) which contain adjustable parameters [10]:

$${\text{d}}\alpha /{\text{d}}t = {\text{exp}}[p(\alpha ) - \frac{E\left( \alpha \right)}{{RT}}]\left( {{1} - \alpha } \right)$$
(2)

Equation (2) is a special case of Eq. (1); hence, all solutions of Eq. (2) are also a solution of Eq. (1). Here p(α) and E(α) are polynomials. Their coefficients can be found by the least squares method. Factor (1-α) in Eq. (2) ensures that dα/dt is zero at α = 1 for any set of polynomial coefficients. This behavior simplifies the least squares procedures based on Eq. (2) [6, 10]. Other expressions could also be employed in Eq. (2) to ensure that dα/dt would be zero at α = 1 [18]. If Eq. (2) is rearranged to the form of Eq. (1), we get

$$A\left( \alpha \right)f\left( \alpha \right)^{{}} = {\text{e}}^{{\text{p}(\upalpha )}{}} \left( {{1} - \alpha } \right)$$
(3)

Obviously, we cannot get exact solutions for Eq. (2); we use high-precision numerical solutions instead. A Runge--Kutta method was used for this purpose and a relative precision of 10–8 was required for the numerical solution. See section “Computational Methods” in Reference [10] for more details on the employed numerical methods.

Equation (2) can be regarded as an empirical model which is capable of describing complex thermal processes kinetically [10, 18, 19]. Recently, Nasfi et al. [20] introduced the name VAEM (variable activation energy model) for this method.

In the present work, p(α) was a fifth-order polynomial. Its coefficients were adjusted so that the solution of Eq. (2) would be close to the evaluated experiments. The method of least squares was used for this purpose as outlined in the next section. The convergence is safer and faster if α is transformed to an x variable that varies from − 1 to 1 and p(α) is expressed by Chebyshev polynomials of the first kind [10].

The order of the E(α) polynomials was between zero and two in the study. One or more parameters of the E(α) polynomials were altered from their true values, and it was checked how the rest of the model parameters could compensate for these changes with the smallest possible worsening of the fit between the calculated and the evaluated data. Four types of test evaluations were carried out:

  1. (i)

    Linear E(α) functions were constructed at various positive and negative b slopes:

    $$E(\alpha ) = a + b\alpha$$
    (4)

    In the corresponding test evaluations, slope b was kept at constant values while the rest of the parameters in Eq. (2) were determined by the method of least squares. In this way we got information on how Eq. (2) with a varying E(α) can approximate the data simulated with a constant E.

  2. (ii)

    In reference [6], a parabolic E(α) was extensively tested for checking the reliability of the integral isoconversional evaluation methods. In the present work, its use was extended to the DTG evaluations, too. The corresponding equation can be written as

    $$E(\alpha ) = a + bx + 2bx^{2}$$
    (5)

    where x = 2α-1 and b is a parameter. Figure 1 in reference [6] showed five examples for this type of parabolic E(α) functions which were denoted there by #4, #5, #6, #7 and #8.

  3. (iii)

    Eq. (2) was used with constant E. E was altered from its true value, 200 kJ mol−1, while all other kinetic parameters in Eq. (2) were determined by the method of least squares. In this way, it was estimated how a change of A(α)f(α) in Eq. (1) can compensate for a change of a constant E. The obtained range of E values with good fit qualities is given as a percent of the true E. Notation: (ΔE)A(α)f(α)/%, where the subscript indicates that the change of E was compensated by a suitable change of the A(α)f(α) term of Eq. (1). (Here A(α)f(α) is a general term that includes the product of a constant A and an f(α) function, too.)

  4. (iv)

    First-order kinetics was assumed. E was altered from its true value, 200 kJ mol−1, while the preexponential factor was determined by the method of least squares. This procedure measures the classical kinetic compensation effect between E and A on the given set of experiments. The obtained range of E values with good fit qualities is given as a percent of the true E. Notation: (ΔE)A/%, where the subscript indicates that the change of E is compensated by a suitable change of A.

Fig. 1
figure 1

Linear a and parabolic b E(α) functions that provided close approximations to the α(t)obs curves in heating rate domains βmax/βmin = 4 (dashed lines), βmax/βmin = 8 (dots) and βmax/βmin = 16 (solid lines)

Full size image

In test evaluations (i) and (ii), the b parameter of Eqs. (4) and (5) was varied systematically with a step size of 0.1 kJ mol−1 until a preset fit quality was reached. In test evaluations (iii) and (iv), the constant E was varied in a similar way.

The characterization of the fit quality and the method of the least squares

The fit quality of a single experiment was characterized by the normalized root-mean-square error, NRMSE [21]. The range of the observations, h, was used for normalization. h ≅ 1 for αobs curves and h ≅ max (dα/dt)obs for the derivative curves. Accordingly, we get for the jth αobs curve

$${\text{NRMSE}}_{{\text{j}}} = \left( {M_{{\text{j}}}^{ - 1} \sum\nolimits_{\text i = 1}^{{M_{\text j} }} {\left[ {\alpha_{{\text{j}}}^{{{\text{obs}}}} (t_{{\text{i}}} ) - \alpha_{{\text{j}}}^{{{\text{calc}}}} (t_{{\text{i}}} )} \right]}^{2} } \right)^{0.5}$$
(6)

where Mj is the number of the ti time values in experiment j. For the jth (dα/dt)obs curve, we obtain

$${\text{NRMSE}}_{\text{j}} = h_{\text{j}}^{ - 1} \left( {M_{\text{j}}^{ - 1} \sum\nolimits_{\text i = 1}^{{M_{\text{j}} }} {\left[ {({\text{d}}\alpha /{\text{d}}t)_{\text{j}}^{{{\text{obs}}}} (t_{\text{i}} ) - ({\text{d}}\alpha /{\text{d}}t)_{\text{j}}^{{{\text{calc}}}} (t_{\text{i}} )} \right]^{2} } } \right)^{0.5}$$
(7)

The fit quality for a series of N experiments was characterized by the root-mean-square of the corresponding NRMSEj values. This quantity was expressed as percent for a compatibility with the earlier works of the author and his coworkers since 1993 [22]:

$$reldev/\% = 100\left( {N^{ - 1} \sum\nolimits_{\text j = 1}^{N} {{\text{NRMSE}}_{\text{j}}^{2} } } \right)^{0.5}$$
(8)

The notation changed time by time in our works. Among others, the quantity defined by Eq. (8) was denoted by dev in the latest published work of the author [6].

The method of the least squares was used to achieve the best possible fit quality at a selected E(α) function. The objective function minimized is proportional to the square of reldev:

$${\text{of}} = N^{ - 1} \sum\nolimits_{\text j = 1}^{N} {{\text{NRMSE}}_{\text{j}}^{2} }$$
(9)

Such E(α) functions were selected for publication at which good fit quality could be achieved by the method of least squares, i.e., by the minimization of Eq. (9). The term “good fit quality” is explained in the next section.

Results and discussions

Tests on the evaluation of αobs data

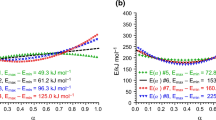
In the preceding work of the author [6], reldev = 0.83% was considered as a good fit quality. For compatibility, the same reldev = 0.83% value was used in the present work, too. The selection of this value was based on the author’s experience with least squares evaluations for decades. Visual inspection showed that the fit was nice when reldev was 0.83% for a given set of curves. See Eq. (8) above for the definition of reldev and see the figures on the fit quality in this paper as examples. It is possible that the actual reliability of the thermal analytical experiments is worse than that, especially when reactions with high reaction heats are studied. Figure 1 displays the E(α) functions at which a fit quality of reldev = 0.83% could be achieved for the three αobs datasets described in section “Simulated experiments.” In this paper, all but one E(α) plot was scaled to the same value, 302 kJ mol−1. The exception is Fig. 1b, where the highest E value is 413 kJ mol−1. (In the preceding work of the author the highest E value was a bit lower, 396 kJ mol−1 [6].) Fig. 2 illustrates the evaluations in more detail.

Fig. 2
figure 2

α(t) curves at E = 200 kJ mol−1 (○, ▽, ◻, ◇, △) and their counterparts simulated with linearly increasing E(α) functions (solid lines) in heating rate domains βmax/βmin = 4 a, and βmax/βmin = 16 b

Full size image

The evaluations with parabolic E(α) functions, i.e., the use of Eq. (5), gave results similar to the ones presented in reference [6]. The alteration of an E(α) function from a nonvarying E will be characterized by a way adopted from the work of Vyazovkin et al. [3]. Accordingly, the part of the E(α) functions in α domain [0.1,0.9] is used for the characterization. In this domain, the difference between the maximum and the minimum E is given as percent of the mean E. We shall use the Q[0.1,0.9] notation for this quantity:

$$Q_{{\left[ {0.{1},0.{9}} \right]}} /_{{}} \% \, = { 1}00(E_{{{\text{max}}}} {-}E_{{{\text{min}}}} )/E_{mean} , \;0.{1} \le \alpha \le 0.{9}$$
(10)

Table 1 lists Q[0.1,0.9] for the sets of heating rates and type E(α) functions used in the present study. The results of the tests on the determination of constant E values are also presented. (See section “The employed E(α) functions and a version of Eq. (1) with optimizable parameters” above for explanations about the related procedures and quantities.)

The obtained data support the conclusions of the preceding work of the author [6]: the determination of E(α) from TG data has considerable inherent uncertainties. Figure 1 indicates that small, hardly observable experimental errors may change the TG curves of a simple first-order kinetics into TG curves which belong to significantly non-constant E(α) functions. Especially at the set of heating rates of 5, 10, 15 and 20 °C min−1 (βmax/βmin = 4), where the highest Q[0.1,0.9], 82% was found. Emax and Emin of 168 and 341 kJ mol−1 were found at 0.1 ≤ α ≤ 0.9, while Emax went up to 413 kJ mol−1 until α = 1.

An observation of smaller importance is that the Q[0.1,0.9] values of the linearly decreasing E(α) functions are higher than that of their linearly increasing counterpart. It follows from the normalization by the mean value of E in Eq. (10). At linear functions the mean E is E(0.5). Figure 1 shows that the E(0.5) values are considerably lower at the decreasing functions.

Tests on the evaluation of the (dα/dt)obs data

The test evaluations of the previous section were also carried out with the dα/dt data for the reasons outlined in Introduction. The same fit quality, reldev = 0.83%, was requested here, too. Figure 3 displays the E(α) functions at which a fit quality of reldev = 0.83% could be achieved for the (dα/dt)obs datasets. Figure 4 displays details on the fit quality with linearly increasing E(α) functions. Here the scaling is different for the different heating rates for a better view. (At a common scaling, the curves belonging to the 2.5 and 5 °C min−1 heating rates would be too small in Fig. 4b.) An additional figure (Fig. S1) is given in the 1st Supplementary Information file about the fit quality with parabolic E(α). Table 2 displays the numerical characteristics of the evaluations.

Fig. 3
figure 3

Linear a and parabolic b E(α) functions that provided close approximations to the (dα/dt)obs curves in heating rate domains βmax/βmin = 4 (dashed lines), βmax/βmin = 8 (dots), and βmax/βmin = 16 (solid lines)

Full size image
Fig. 4
figure 4

dα/dt curves at E = 200 kJ mol−1 (○, ▽, ◻, ◇, △) and their counterparts obtained with linearly increasing E(α) functions (solid lines) in heating rate domains βmax/βmin = 4 a, and βmax/βmin = 16 b

Full size image
Table 2 Results of the reliability tests on the evaluation of dα/dt curves
Full size table

The figures and data indicate that the problems outlined in the previous section are much smaller at the evaluation of DTG curves. The Q[0.1,0.9] values at linear E(α) functions in Table 2 are roughly the third of the corresponding values in Table 1. The improvement is higher at parabolic E(α) functions. However, the ΔE values in the tests with constant E decreased only to roughly the half of the corresponding values of Table 1, as the comparison of the last two rows show in Tables 1–2.

Note that the Q[0.1,0.9] values found at βmax/βmin = 4 are still elevated. Vyazovkin et al. wrote [3]: “Then variation in Eα is insignificant if the difference between the maximum and minimum value of Eα is less than 10–20% of the average Eα value. … the constancy (or insignificant variability) are best judged by analyzing the values within the range α = 0.1–0.9.” According to these considerations, Q[0.1,0.9] values of 13–16% do not allow a clear distinction between processes with approximately constant E and more complex processes with varying E. It is better to use a wider range of heating rates for the experiments, as Burnham advised [17]. The Q[0.1,0.9] values found at βmax/βmin = 16 in the present work are safely below 10%.

Evaluations from modulated TG experiments

As mentioned in Introduction, ASTM International issued a standard method for the determination of kinetic parameters by modulated thermogravimetry [9]. The method is based on a “model-free” evaluation of the activation energy. Optionally the preexponential factor can also be determined by assuming first-order kinetics. In the corresponding experiments a sinusoidal modulation is added to a linear heating with 1 °C min−1 heating rate. The amplitude and the wavelength of the added sine function is ± 5 °C and 300 s, respectively. The user should select a failure criterion, i.e., a reacted fraction at which the tested material is supposed to fail. It is typically 5% mass loss for TG experiments [9]. The standard method includes an equation that allows the calculation of E as function of the reacted fraction. At the end of the calculations, the instructions are as follows: “Create a table of activation energy and logarithm of the pre-exponential factor versus conversion. Select the activation energy and logarithm of the pre-exponential factor nearest the failure criterion conversion level …” Accordingly, the present paper examines the uncertainty at α = 0.05, too. This uncertainty will be characterized as

$${\text{err}}_{{\upalpha = 0.0{5}}} /\% \, = { 1}00[E\left( {0.0{5}} \right) \, {-}E_{{{\text{true}}}} ]/E_{{{\text{true}}}}$$
(11)

where Etrue is the value used for the simulated experiments, 200 kJ mol−1.

The ASTM standard lists important works that contributed to developing and establishing the method [23,24,25,26,27]. Besides it is worth mentioning the related works of Ochoa et al. [28] and Budrugeac [29]. These studies developed and improved the evaluation methods and tested their reliability. The aims of the present work, however, are different, as outlined in the previous sections. We show by examples that markedly different E(α) functions may belong to dα/dt curves which are close to each other. Three modulated heating programs are employed for this purpose, as follows. The first is the one recommended by the ATMS standard: base heating rate, β is 1 °C min−1, wavelength, λ is 300 s, and the amplitude of the modulation is ± 5 °C. Generally lower wavelengths are used in the literature; hence λ = 200 s was selected for the second modulated T(t). In the literature the base heating rate is frequently higher than 1 °C min−1 for practical reasons, thus a higher β, β = 5 °C min−1 was selected for the third modulated T(t) with λ = 200 s. The amplitude of the modulation was the same in the three cases, ± 5 °C. Figure 5 displays the E(α) functions at which a fit quality of reldev = 0.83% could be achieved for the (dα/dt)obs datasets at the first and third modulated temperature programs. Figure 6 shows the corresponding fit qualities at linearly increasing E(α) functions. The numerical characteristics of the evaluations are presented in Table 3.

Fig. 5
figure 5

E(α) functions that provided close approximations to the modulated (dα/dt)obs curves at β = 1 °C min−1 and λ = 300 s a, and β = 5 °C min−1 and λ = 200 s b

Full size image
Fig. 6
figure 6

dα/dt curves at E = 200 kJ mol−1 (○) and their counterparts obtained with linearly increasing E(α) functions (thick solid lines) at β = 1 °C min−1 and λ = 300 s a, and β = 5 °C min−1 and λ = 200 s b

Full size image
Table 3 Results of the reliability tests on the evaluation of modulated dα/dt curves
Full size table

It might be worth observing that there are much fewer waves in Fig. 6b than in Fig. 6a because the reactions take place in shorter time intervals at a higher heating rate. In the present case, the ratio of the corresponding reaction times is about five. The decrease in the wavelength from Fig. 6a (300 s) to Fig. 6b (200 s) cannot compensate for it. This may explain why higher Q[0.1,0.9] and errα=0.05 values were found at 5 °C min−1 than at 1 °C min−1. On the other hand, a change from λ = 300 s to λ = 200 s at 1 °C min−1 resulted in practically the same values in Table 3. Nevertheless, the Q[0.1,0.9] values belonging to the first and second modulated T(t) are still much higher than the limits quoted above from the work of Vyazovkin et al. [3]. Accordingly, it is hard to distinguish between a simple process with constant E and a complex process with variable E by the kinetic evaluation of a modulated experiment. The observed E errors at α = 0.05 also appear to be substantial. These observations support Budrugeac’s conclusion: “modulated TG methods are not a viable alternative to multi-heating isoconversional methods” [29]. In the present work, however, we dealt mainly with the uniqueness of the solutions. In this way we can add to Budrugeac’s quoted conclusion that—from the aspects treated here—the evaluation of a modulated DTG curve at β = 1 °C min−1 with wavelength 200 or 300 s is still less problematic than the determination of E(α) from αobs data at usual linear T(t) programs. The highest Q[0.1,0.9] was 30% at β = 1 °C min−1 in Table 3. On the other hand, Q[0.1,0.9] values up to 82% were listed in Table 1. Even the highest |errα=0.05| at β = 1 °C min−1 was slightly lower than the corresponding value from the evaluations of the TG curves at βmax/βmin = 4 (18 vs. 20%). The highest E(0.05) was 236 and 239 kJ mol−1 in Figs. 5a and 1a, respectively.

The use of the isoconversional kinetics as empirical models

Mankind produces several billion tons of such materials yearly which can be studied by thermal analysis, but their thermal processes/reactions are too complex for physically—chemically meaningful models. Coals, various wastes, and other materials with complicated physical or chemical structure can be considered here as examples. If there is a need for a mathematical description of their thermal  behavior, it can be achieved only by empirical models. A useful empirical model is—obviously—expected to describe the experiments in domains of β, T, etc. as wide as possible. Further criteria may also arise for the assessment of their usefulness.

As outlined in Introduction and in section “A check on the recent literature,” the isoconversional studies results usually in sets of discrete E versus α and Af versus α data that are presented in tables and plots. Despite the frequently used name “model-free,” Eq. (1) with the obtained E(α) and A(α)f(α) values forms a model of the evaluated experiments [30]. One should decide whether it is a good model or not. For this purpose αobs or (dα/dt)obs data should be derived from the obtained model which can be compared with their experimental counterparts. This can be achieved if the obtained E(α) and A(α)f(α) data are approximated by continuous functions which can be used for the solution of Eq. (1) by a numerical ODE solving method. See the work of Berčič for an example [31]. Alternatively, the evaluation can be based on Eq. (2) and such parameter values can be searched for which minimize the difference between the experimental and the calculated data [10, 18]. Whichever way is chosen, the comparison of the experimental and calculated TG curves is not particularly informative because rather different E(α) functions can result in very similar α(t) functions, as the figures show in the present work and in reference [6]. The situation is better when dα/dt curves are compared as demonstrated in section “Tests on the evaluation of the (dα/dt)obs data.”

When a kinetic work is based on DTG data, it may be well worth checking the errors that are introduced by the differentiation of the TG curves. As a test, one can integrate the DTG data numerically in the domains of the kinetic evaluation and compare the integrated curves to the original TG data. The differences are usually much lower than the other uncertainties of the thermal analysis experiments. Obviously, the integration constant should be carefully selected for such a comparison. No need for this numerical integration when the DTG curve is determined by the differentiation of a smooth function that approximates the TG curves, e.g., by the differentiation of a smoothing spline [32]. The method of smoothing splines has been used in thermal analysis for at least 30 years for this purpose [33]. The root-mean-square error of the approximation by smoothing splines can be flexibly adjusted according to the noise level of the evaluated TG experiments [34]. Besides, obviously, the instrument itself should be checked whenever noisy TG curves are observed. For example, the deposits forming in the TG furnace can frequently cause high noises according to the experience of the author.

Obviously, (dα/dt)obs data can be obtained without a numerical differentiation from several experimental techniques, including DSC, which can also be suitable for isoconversional evaluations. Six papers with DSC-based kinetics appeared in the literature in the 62 days covered by the literature check of this work. In the present study we did not deal with the origin and physical meaning of the dα/dt curves; we employed a general treatment that can be valid for any dα/dt curves from any source.

Can varying activation energy be determined reliably from thermogravimetric experiments?

The answer for this question is probably “yes,” but particular care is needed. We can list some necessary conditions for that. The evaluation has to be based on a wide range of heating rates [17]. The obtained model should provide (dα/dt)calc curves which are close to the (dα/dt)obs curves for all evaluated experiments. If the (dα/dt)obs curves are determined from TG experiments then the determination of the DTG data from the TG curves also needs some care and caution, as outlined above. The most straightforward way to ensure the closeness of the (dα/dt)calc and (dα/dt)obs data is the method of least squares which can be carried out on a version of Eq. (1) that contains parameters to be adjusted for the closest possible fit. Equation (2) is a possibility for that purpose [10]. Its usage and advantages can be summarized as follows. The polynomials in Eq. (2) can be expressed by Chebyshev polynomials for improved numerical properties. The minimization of the least squares method can be carried out without domain restrictions because Eq. (3) is a smooth, continuous function with zero value at α = 1 at any values of the polynomial coefficients, as mentioned in the section “Methods.” The p(α) and the − E(α)/(RT) terms occur side by side in Eq. (2) which facilitate the use of parameter transformation to mitigate the interrelations (compensation effects) of the parameters during the minimization [10]. The use of Eq. (2) with variable E was tested on 85 TG experiments which had been measured earlier on 16 biomass samples. The resulting plots and data are shown in the Supporting Information of reference [10].

Is it worth using kinetics with E(α)?

All evaluations in reference [10] were carried out both with variable E and with non-variable E and the latter way also resulted in reasonable fit qualities. When E does not vary with α, Eq. (1) becomes simpler and is written usually as

$${\text{d}}\alpha /{\text{d}}t = A\;f\left( \alpha \right){\text{exp}}( - \frac{E}{RT})$$
(12)

The literature contains numerous f(α) functions which were deduced from theories assuming idealized cases. However, the materials, reactions and processes studied by thermal analysis are usually too complex for such an idealized treatment, as mentioned in the previous section. Accordingly, we regard Af(α) as an empirical function and approximate it by Eq. (3). This procedure led to reasonable descriptions of the processes in the 16 cases of biomass pyrolysis in reference [10]. Based on this experience, further 76 TG experiments on other 16 samples were taken from earlier publications and were reevaluated by Eq. (12) [19, 35, 36]. The experiments reevaluated in this way belonged to the combustion and CO2 gasification of biomasses and biomass chars. The evaluations were simpler, and the results were mathematically better defined than in the models with variable E. When E does not vary, f(α) alone describes the change of the reactivity with the advance of the reaction. The resulting Af(α) can be split to A and f(α) by a normalization of f(α), e.g., by requesting that the highest value of f(α) would be one.

Supplementary information

The source code of a relatively simple sample program is given in the Supplementary Information which can generate data for 36 curves of the present work. It serves as a check for the results of the present work. The data provided by this program can also be used for test evaluations by other methods. Besides, the source code is an example for the numerical solution of Eq. (2).Three files are given which are entitled as.

  1. 1.

    The description of a sample program, and additional figures for the paper

  2. 2.

    The source code of a sample program

  3. 3.

    Parameters for the sample program

Conclusions

TG and DTG data were simulated by first-order kinetics with E = 200 kJ mol−1 at different heating rates. They were approximated by the solutions of the isoconversional kinetic equation with various E(α) functions. Equation (2) was used for this purpose, which is a special case of the general isoconversional equation, Eq. (1). The results obtained in this way can be summarized as follows:

  1. 1.

    Highly different E(α) functions may belong to TG curves which are close to each other. Here the term “close” means small root-mean-square differences between the curves. This part of the work is a reinforcement of the earlier results of the author [6] by using other heating rates and other E(α) functions.

  2. 2.

    The same type of calculations gave more favorable results when dα/dt curves were examined. The uncertainties observed at the evaluation of the dα/dt curves were smaller by a factor of 1/3 than the ones at the evaluation of α(t) curves when linear E(α) functions were tested. The improvement was higher at nonlinear E(α) functions and smaller in the test evaluations with constant E values.

  3. 3.

    There are isoconversional procedures in the literature which are based on the evaluation of single modulated DTG curves. The results of the present work reinforced the conclusions of earlier works by other authors about the weaknesses of this procedure. It was found that the information content of a single modulated DTG curve is not enough for the reliable determination of an E(α) function. Nevertheless, smaller problems were observed with the evaluation of a single modulated DTG curve at the temperature program of the corresponding ASTM standard [9] than with the evaluation of several TG curves at frequently used heating rates.

  4. 4.

    The outcomes of the work suggest that the determination of an E(α) dependence should utilize the information content of the (dα/dt)obs curves in a wide range of heating rates. The method of least squares may help to find the parameter values at which the model approximates well the experimental dα/dt curves for each studied heating rate.

  5. 5.

    The present work together with the related earlier papers of Várhegyi et al. [10, 18, 19, 35, 36] suggests that an empirical kinetic model with non-varying E and may be more advantageous than with a varying E.