Introduction

Hundreds of papers are published yearly that determine the activation energy, E as function of the reacted fraction, α, by isoconversional evaluation methods [1]. Recently Muravyev and Vyazovkin performed a bibliometric study on the works dealing with pyrolysis kinetics [2]. They examined the best cited works published in 2021 and found that more than half of them used the Flynn-Ozawa-Wall method while only around every sixth paper used nonlinear least squares curve fitting.

The isoconversional (“model-free”) methods usually assume variable activation energy, E(α), and variable pre-exponential factor, A(α):

$$\text{d}\alpha /\text{d}t = A\left( \alpha \right)f\left( \alpha \right){\text{exp}}\left( { - \frac{E\left( \alpha \right)}{{RT}}} \right)$$
(1)

Here f(α) can be any continuous function with positive values below α < 1 and zero at α = 1. f(α) can be derived from a theory in idealistic cases [3]. However, the samples studied by thermal analysis are usually too complex for the idealized models. In such cases a kinetic evaluation can provide information on the A(α)f(α) product in Eq. (1) [3].

Equation (1) is a generalization of a simpler equation when E and A do not vary with α:

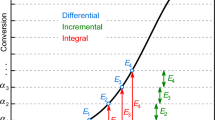
$$\text{d}\alpha /\text{d}t = Af\left( \alpha \right){\text{exp}}\left( { - \frac{E}{RT}} \right)$$
(2)

It is well known that there is a marked compensation effect between E and A in Eq. (2) [4] which may hinder the precise determination of E and A from thermal analysis experiments. Intuitively one can expect higher compensation effects in Eq. (1) when infinite numbers of function values in E(α) and A(α)f(α) can participate in the compensation. This will be the subject of the present work. For this purpose, a general definition of the compensation effect was selected from the literature which is not based on the linear relationship between E and ln A. According to Holstein et al. “…a given set of experimental data can be fitted equally well by several pairs of A and E values. This lack of uniqueness in the determination of kinetic parameters is called the compensation effect.” [5]. The above cited approach was adopted by other authors, too [6,7,8,9]. One can generalize this definition by replacing the term “pairs of A and E value” as follows: a given set of experimental data can be described equally well by different sets of model parameters. This appears to be a general problem in science; the question is the extent of this compensation effect. If this extent is large enough, then significantly different model parameters can produce nearly identical simulated curves and the experiments do not help deciding which of them should be accepted.

Using the above generalized definition, the present paper aims at showing by examples that the compensation effect in Eq. (1) can be much higher than in Eq. (2). It will be shown that significantly different E(α) functions may describe the same TGA experiments equally well. The basis will be the evaluation of a dataset simulated by Eq. (2) at f(α) = 1 − α. In this simple case the compensation effects can be studied easily and unambiguously without complicating factors. The non-isothermal kinetic studies are based almost always on experiments with constant heating rates. Accordingly, this way will be followed in the present work, too. Burnham emphasized that “Heating rates need to vary at least a tenfold to give accurate kinetic parameters” in the Highlights part of his paper in 2014 [10]. In his actual examples the ratio of the highest and the lowest heating rates was 16 [10]. Following Burnham’s recommendations, the ratio of the highest and the lowest heating rates will be 16 in the present work. However, less wide heating range domains are more frequent in the literature on non-isothermal kinetics accordingly the effect of narrower heating rate domains will also be examined.

The various evaluation methods used in the literature will not be discussed here because high quality reviews are available on this topics [3, 11]. Besides, the methods of the mathematical statistics will not be employed in the paper because the experimental errors in the thermal analysis are mainly non-statistical [12]. Among others the thermal lag; the self-heating effects of the exothermic reactions and the effect of a hindered diffusion are non-statistical. Usually, the kinetic equations can only approximate the complexity of the real processes and the differences between the reality and the models also add non-statistical error terms to the kinetic evaluations.

The present author has been supporting the view for decades that the experimental data should always be compared to their counterparts calculated from the given kinetic model [12, 13]. Such a comparison should be carried out for the case of a “model-free” evaluations, too [14,15,16,17,18]. Note that the term “model free” is misleading because Eq. (1) itself is a model [3]. The method of least squares is a practical tool to ensure that that the difference between the evaluated data and the solution of Eq. (1) would be as small as possible. The author proposed flexible empirical models for the least squares evaluations by Eq. (1) four years ago [14]. Since then further studies demonstrated the applicability of this method [15,16,17,18]. This approach will be used in the present work, too. Simple, slowly changing E(α) functions will be presented in the paper that provide good fit for the data generated at a constant E by Eq. (2).

The Supplementary Information contains the data, equations, and formulas for most kinetic evaluations of this work so that an interested user could check the results and extend them by further calculations.

Methods

In this section, we shall deal with the following topics: (i) the simulation of a series of experiments for this study; (ii) the construction of simple, slowly changing E(α) functions; (iii) a suitable measure for the closeness of the evaluated data and their counterparts calculated from Eqs. (1) or (2); (iv) and the kinds of compensation effects studied in the paper.

Simulated experiments

A first-order reaction was assumed with E = 200 kJ mol−1 and A = 1016 s−1. The heating rates were selected by recommendations found in the literatures: 3–5 runs at different heating rates are needed for the evaluation [3]; a wide range of heating rates is needed [10]; and the heating rates should follow a geometric progression [10, 11]. Accordingly TGA experiments were simulated by solving Eq. (2) at heating rates of 2, 4, 8, 16 and 32 °C min−1 with f(α) = 1−α. No solid residue was assumed hence the normalized sample mass, m equals 1−α. The data of the simulated TGA experiments will be denoted as (1−α)obs in the treatment. The evaluations of the (1−α)obs curves were carried out from 0.999 till 0.001 in around 1000 time points.

The E(α) functions used in the paper

As outlined in the Introduction, the present work aims at showing that markedly different E(α) functions can approximate equally well the simulated experiments described above. Mathematically an endless variety of E(α) functions may occur in Eq. (1). However, pikes and other sudden changes would be unrealistic for most samples studied by thermal analysis. Hence the treatment was restricted to slowly changing E(α) functions. Besides, an overall increasing tendency was also requested as α increases because the species with higher E usually inclined to decompose/react at higher α values. By the term “overall increasing tendency” we mean that a linear regression on any E(α) function would result in a correlation coefficient of 0.70 or higher and a markedly increasing straight line. As shown in the last section of the work, the increase in this straight line from α = 0 till α = 1 was between 64 and 100% of the Emax–Emin distances.

Mathematically the simplest slowly changing, nonlinear functions are the parabolas, hence the compensation effects in Eq. (1) are demonstrated by parabolic E(α) functions. As described in earlier publications and their Supporting/Supplementing materials, the employed method uses polynomials which are expressed by Chebyshev polynomials of the first kind to facilitate the numerical solutions [14,15,16,17,18]. Accordingly, the parabolic E(α) functions of the present study are also rearranged into the form:

$$E\left( \alpha \right) = c_{0} + c_{1} {\text{T}}_{1} \left( x \right) + c_{2} {\text{T}}_{2} \left( x \right)$$
(3)

here c0, c1, and c2 are coefficients, x is a variable that varies in domain [−1,1]

$$x = {2}\alpha {-}{ 1}$$
(4)

While T1 and T2 are Chebyshev polynomials of the first kind:

$${\text{T}}_{{1}} \left( x \right) = x$$
(5)
$${\text{T}}_{{2}} \left( x \right) = {2}x^{{2}} {-}{ 1}$$
(6)

Note that T1(x) and T2(x) have the same magnitude. They vary between −1 and 1 in the x domain [−1,1]. The overall increase in E(α), E(1)–E(0) is determined by c1 (due to the symmetry of the T2(x) parabola). The Emax–Emin difference is determined by c1 and c2 together. The overall increasing tendency of the E(α) functions was achieved by constrains

$$c_{1} {\text{ > }}0\;{\text{and}}\;\left| {c_{2} } \right| \le c_{1}$$
(7)

as shown in the last section of this work.

Characterization of the fit quality and the method of least squares

The root-mean-square deviation can be a suitable measure for the closeness of the experimental and calculated data. For compatibility with earlier works back to 1989 [13] we express it as percent of the highest observed value, which can be replaced by 1 in the present case. Keeping in mind that no solid residue was assumed (i.e., m = 1−α) we get

$${\text{dev}}/\% = { }100\left[ {\mathop \sum \limits_{{{\text{i}} = 1}}^{M} \left( {m_{{\text{i}}}^{\text{obs}} - m_{{\text{i}}}^{\text{calc}} } \right)^{2} /M} \right]^{0.5} { } = { }100{ }\left[ {\mathop \sum \limits_{{{\text{i}} = 1}}^{M} \left( {\alpha_{{\text{i}}}^{\text{obs}} - \alpha_{{\text{i}}}^{\text{calc}} } \right)^{2} /M} \right]^{0.5}$$
(8)

here M is the number of digitized points in the given experiment, and \(\alpha_{{\text{i}}}^{{{\text{calc}}}}\) is the ith value calculated from Eqs. (1) or (2) by the methods published earlier [14,15,16,17,18]. The fit quality of a series of N experiments can be characterized by the root mean square of the dev values calculated for each experiment, devN. In the present work N = 5, 4 or 3.

A good fit quality is searched for each E or E(α) tested in the work. For this purpose, the unknown parameters were determined so that devN would be as small as possible. This was achieved by carrying out the method of least squares with the objective function (devN)2.

The compensation effects studied, and the empirical models employed

Three types of compensation effects were studied. The first was the well-known kinetic compensation effect between E and A. In that case the model is Eq. (2) with f(α) = 1–α, and the best A values were determined by the method of least squares for a grid of fixed E values, as outlined in the treatment.

In the second case it was examined how a given change of E can be compensated by changes of the Af(α) product in Eq. (2). For this purpose a general model was used which can describe a wide variety of f(α) shapes [14,15,16,17,18]:

$$\text{d}\alpha /\text{d}t = {\text{exp}}\left[ {p(\alpha ) - \frac{E}{RT}} \right]\left( {{1} - \alpha } \right)$$
(9)

Here p(α) is a polynomial. The factor (1–α) ensures that dα/dt is zero at α = 1 for any polynomial coefficients hence the polynomial coefficients can be determined by the method of least squares without constraints on their domains. Equation (9) can be rearranged into the form of Eq. (2) yielding a formula for Af(α):

$$Af\left( \alpha \right) = {\text{e}}^{\text{p}(\alpha )} \left( {{1} - \alpha } \right)$$
(10)

In the third case of compensation effects a given change of function E(α) in Eq. (1) is compensated by changes in A(α) and f(α). Here again these factors form an A(α)f(α) product in Eq. (1) and the above-mentioned general model was used which can approximate a wide variety of A(α)f(α) functions [14,15,16,17,18]. The corresponding kinetic equation is

$$\text{d}\alpha /\text{d}t = {\text{exp}}\left[ {p(\alpha ) - \frac{E\left( \alpha \right)}{{RT}}} \right]\left( {{1} - \alpha } \right)$$
(11)

where E(α) is the parabolic function described above. The rearrangement of Eq. (11) into the format of Eq. (1) gives

$$A\left( \alpha \right)f\left( \alpha \right) = {\text{e}}^{\text{p}(\alpha )} \left( {{1} - \alpha } \right)$$
(12)

In the present work E(α) is defined by Eq. (3), as described above. The coefficients of the first-order and second-order terms in Eq. (3), c1 and c2 were predefined, fixed values during the calculations. All other parameters were determined by the method of least squares.

Fifth-order polynomials were used for p(α) in Eqs. (9) – (12). Though the employed numerical methods allows the use of higher-order polynomials, too [16, 18], the use of higher polynomial orders did not result in significantly better fit qualities in the present work.

Results and discussions

Different E(α) functions can describe well the five simulated experiments

In the first step of the work integer c1 and c2 values were selected for Eq. (3). Evaluations were carried out with the obtained E(α) functions and the resulting fit qualities were surveyed graphically. Around 130 E(α) functions were tried in this way. Their dev5 values scattered between 0.21 and 3.06%. By inspecting the figures of the obtained curve fitting results, the dev5 values around 0.83% appeared the highest ones that could be regarded as an indicator for a high–quality fit. Here the term “high–quality fit” was based on the kinetic studies carried out with the author’s contribution since 1989 [13] to the present [18]. Papers published by other authors in the literature were also taken into account; a selection is listed in References [19,20,21,22,23,24,25,26,27]. Nevertheless, the choice of other dev5 values was also tested. It turned out that the choice of a particular dev5 value only slightly affected the ratios of the compensation effects studied in this work. Note that the same dev5 values were used to estimate the compensation effects at constant E values and E(α) functions. The characteristics of the E(α) functions of this study depend on the ratio of the first-order and second-order terms in Eq. (3). Coefficient c1 was positive in all cases as described above at the conditions defined in Eq. (7). Four E(α) were selected for the first part of the work which are shown in Fig. 1a: a concave function with c2 = –c1 (E(α) #1), a linear function with c2 = 0 (E(α) #2), a moderately convex function with c2 = 0.5c1 (E(α) #3), and a markedly convex function with c2 = c1 (E(α) #4). Their c1 and c2 coefficients were slightly altered from the integer numbers found in the 1st stage of the work to change the dev5 values from dev5≈0.83% to dev5 = 0.83%. (Except #4 which gave dev5 = 0.83 with its original integer coefficients. The last section lists the employed c1 and c2 values.)

Fig. 1
figure 1

The E(α) functions employed in the study. (See the text for explanations.)

Full size image

Figure 2b displays further E(α) functions formed via the c1 = c2 equality that will be discussed later in the treatment. E(α) #5 and #6 served to test how the choice of dev5 values differing from 0.83% affect the ratios of the compensation effects studied. E(α) #7 and #8 served to test how the number of the evaluated experiments affect the results. They provided dev4 = 0.83% and dev3 = 0.83% during the evaluation of four and three experiments, respectively.

Fig. 2
figure 2

The fit qualities belonging to E(α) #1, #2, #4 and #5

Full size image

Figure 2 displays the fit qualities belonging to E(α) #1, #2, #4 and #5. It may be interesting to note how the shape of E(α) influences the differences between the observed and calculated values. E(α) #1 is a concave function, in this case the differences are more observable at the beginning of the plotted curves. The convex E(α) #4 and #5 result in higher differences near to the end of the curves.

Comparison of the compensation effects at five experiments

Let us start with the compensation effect between E and A in Eq. (2). Least squares evaluations by a grid of fixed E values showed that the five experiments can be described at dev5 = 0.83% with E = 192.4 kJ mol−1 and E = 208.1 kJ mol−1. The width of the interval, 15.7 kJ mol−1, is denoted by (ΔE)E,A where the subscript indicates the parameters compensating each other. Within this interval dev5 ≤ 0.83%.

Next follows the case when a change of E is compensated by a change of the Af(α) product in Eq. (2). Here again the evaluation was carried out on a grid of fixed E values. It was found that dev5 ≤ 0.83% between E = 190.4 and 210.6 kJ mol−1. The width of this interval, 20.2 kJ mol−1, is denoted by (ΔE)E,Af(α). As expected, (ΔE)E,Af(α) is higher than (ΔE)E,A. It is notable that the (ΔE)E,Af(α)/(ΔE)E,A ratio is the same value, 1.29 from E(α) #1 till E(α) #6. The explanation of this observation is not known yet; it is left for a later work.

The (ΔE)E,A and (ΔE)E,Af(α) values can also be compared to the Emax–Emin differences of the E(α) functions. In this way the compensation effect in Eq. (1) can be compared to the compensation effects of Eq. (2). Table 1 displays these ratios, too.

Table 1 The ratio of the various compensation effects at selected E(α) functions
Full size table

As mentioned in the previous section, E(α) #5 and #6 served to check how the value of dev5 affects the ratio of the compensation effects. For this purpose, such c2 = c1 values were searched at which the kinetic evaluation with E(α) #5 and #6 resulted in dev5 = 0.50% and dev5 = 1.00%, respectively. As expected, (ΔE)E,A and (ΔE)E,Af(α) decreased at E(α) #5 and increased at E(α) #6 in comparison with the corresponding values of E(α) #4. Nevertheless, the ratios indicated in Table 1 only changed slightly. (Emax–Emin)/(ΔE)E,A was around eight while (Emax–Emin)/(ΔE)E,Af(α) was around six for E(α) #4, #5 and #6. The (ΔE)E,Af(α)/(ΔE)E,A ratio did not depend at all on the dev5 value, as noted above.

Compensation effects in narrower ranges of heating rates

The ratio of the highest and lowest heating rates, βmax/βmin was 16 in the previous sections. However, most kinetic papers in the literature appear to have lower heating rate ratios. A comprehensive review on this topic was out of the scope of the present study. As a quick check, the works cited in the present paper were examined from this respect. βmax/βmin of 16 or higher were found in four of the cited works: [10, 11, 19, 25]. βmax/βmin values of 6, 8 or 10 were found in four of the cited works: [5, 19, 20, 22]. βmax/βmin of four or less were found in seven of the cited works: [6, 7, 21, 23, 24, 26, 27].

Accordingly, there is a need to study the compensation effects at lower βmax/βmin ratios, too. By omitting the first simulated experiment from the evaluated series, βmax/βmin decreased to 8. When the second simulated experiment was also omitted, βmax/βmin became 4. According to the recommendations of the ICTAC Kinetics Committee, 3–5 experiments are needed for the isoconversional methods [3], hence N = 4 and N = 3 are suitable values. E(α) functions were derived from E(α) #4 by increasing its c2 = c1 coefficients till dev4 = 0.83% was reached at N = 4 (E(α) #7) and dev3 = 0.83% was reached at N = 3 (E(α) #8). As Table 1 shows, their Emax–Emin, (ΔE)E,A and (ΔE)E,Af(α) values are considerably higher than those of E(α) #4 showing that the compensation effects are higher when the information content of the experimental series is lower.

As shown in Table 1, the (Emax–Emin)/(ΔE)E,A ratio went up to 9 at E(α) #8. The (ΔE)E,Af(α)/(ΔE)E,A ratio also increased a bit. However, the (Emax–Emin)/(ΔE)E,Af(α) ratio remained around 6 for all E(α) constructed with the c2 = c1 conditions, from E(α) #4 till E(α) #8. The cause of this observation was not investigated in the present work.

The fit qualities belonging to E(α) #7 and 8 are shown in Fig. 3. The corresponding E versus α plots are presented in Fig. 1b.

Fig. 3
figure 3

The fit qualities belonging to E(α) #7 and #8

Full size image

More details on the E(α) functions and the significance of the results

Eight E(α) functions were introduced and used in the previous sections. They are shown in Fig. 1. Herewith more data is given about their characteristics. Besides, the significance of the results is checked by recommendations published in the literature in 2020 [28].

As mentioned in the Introduction and in the section Methods, an increasing tendency of the E(α) functions was requested. For its visualization linear regression was carried out on each E(α). Table 2 lists additional characteristics of the E(α) functions. The data show that the overall increase, E(1)–E(0) is comparable to the Emax–Emin differences because their ratio is 0.64 or higher. The slopes given by the linear regression are equal to E(1)–E(0), accordingly the regression line also corresponds to an E(1)–E(0) change of E. This observation is related to the mathematical properties of Eq. (3). The correlation coefficient, r is 0.70 or higher. Figure 4 graphically shows the increasing tendency and the alteration from the linearity when r = 0.70 and (E(1)–E(0))/(Emax–Emin) = 0.64.

Fig. 4
figure 4

The features of E(α) #8 visualized by linear regression

Full size image
Table 2 Characteristics of the employed E(α) functions
Full size table

The data in Tables 1 and 2 indicate that the systematic experimental errors listed in the Introduction may highly alter the results of the evaluations. If they cause an alteration of devN≈0.83% from the theoretical TGA curves, then the best fitting E(α) may change from a constant 200 kJ mol−1 to an E(α) varying between 170.6 and 395.6 kJ mol−1 at the frequently used βmax/βmin = 4 ratio. The corresponding range is [178.3, 338.3] at βmax/βmin = 8 and [182.8, 307.8] at βmax/βmin = 16, as the data of E(α) #6 and #4 show. The significance of these alterations can be assessed by the recommendations of the ICTAC Kinetics Committee [28]:

“…variation in Eα is insignificant if the difference between the maximum and minimum value of Eα is less than 10–20 % of the average Eα value. When applying this criterion, one should keep in mind that the Eα values typically are subject to larger fluctuations at α<0.1 and α>0.9. Therefore, the constancy (or insignificant variability) are best judged by analyzing the values within the range α =0.1−0.9”

For this test, the Emin, Emax and Emean values were determined in the [0.1, 0.9] interval of α, too. These data are shown in Table 3. As the last column reveals, E(α) #2, #3, … #8 have (Emax–Emin)/Emean ratios between 0.23 and 0.75 in the [0.1, 0.9] interval of α. Noteworthy is that the linearly increasing E (E(α) #2) also proved to be significantly different from a constant E when it was used in an evaluation with βmax/βmin = 16.

Table 3 Some characteristics of the employed E(α) functions in the [0.1, 0.9] interval of α
Full size table

Conclusions

The compensation effects arising in Eqs. (1) and (2) were investigated by numerical examples. The work aimed at finding information on the extent of the compensation effects between (i) E and A; (ii) E and Af(α); and (iii) E(α) and A(α)f(α). For this purpose, a general definition of the compensation effect was adapted from the literature [5]. According to this definition, the term compensation effect means that a given set of experimental data can be fitted equally well by different sets of kinetic parameters. The root-mean-square deviation between the evaluated and the calculated data was used as a measure for the term “equally well.” A method recommended four years ago [14] was employed to get the best fit at a given set of kinetic parameters without assuming predefined models in Eqs. (1) and (2). It was shown that highly different E(α) functions can result in good descriptions for a series of 3–5 simulated experiments that were generated with a constant E. The extent of the compensation effect between E(α) and A(α)f(α) may be 8–11 times higher than that between E and A and six times higher than the compensation effect between E and Af(α). The treatment was restricted to E(α) functions which do not have sharp changes and have an increasing tendency. The latter condition can be visualized so that a linear regression of the studied E(α) functions would result in an increasing straight line with correlation coefficient 0.7 or higher. Accordingly, the treatment is not exhausting. The aim of the paper was to show by examples that the determination of an E(α) is far from being unique and this could be achieved in a restricted range of E(α) functions as well. The extent of the observed compensation effects depended on the ratio of the highest and lowest heating rates of the evaluated experiments, βmax/βmin. Higher βmax/βmin values resulted in lower compensation effects. Among others, an E(α) increasing linearly from 180.7 to 241.9 kJ mol−1 also described well the simulated experiments at the highest heating rate ratio of the study, βmax/βmin = 16. Higher effects were found with curved E(α) functions. The results indicate that relatively small experimental errors may highly change the determined E(α) functions even if the evaluation is based on a true least squares procedure and carried out in a wide range of heating rates.