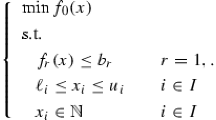1 Introduction and motivation

In optimization, the objective function of the underlying mathematical model represents a certain performance measure to be optimized. In many situations this performance is described as the ratio of two functions to accurately reflect the trade-off between two, sometimes competing, aspects of the system, like profit versus the number of employees or production versus consumption, mean value and variance, cost versus time or volume. Problems of this kind arise in many different activities such as financial planning (where the ratio of debt/equity must be considered), in production planning (inventory/sales or revenue/employee), health care (cost/patient), blending problems (income/quantity of raw material), in the domains of optics, engineering, or information retrieval, to name just a few. More application examples can be found in the first chapter of [25].

Sometimes the fractional relation is ignored for the sake of model simplicity and replaced by a parameterized linear function. An alternative approach introduces bounds on one of the functions as a constraint in the model. However, recent interest has focused on more realistic mathematical models, and increased research effort focuses on advanced methodologies to directly address the problem of ratio optimization, also known as fractional programming.

Consider the so called single-ratio fractional problem,

$$\begin{aligned} \min \limits _{{\mathsf {x}}\in \Omega } \, \frac{f({\mathsf {x}})}{g({\mathsf {x}})} \, , \end{aligned}$$
(1.1)

where \(\Omega \subseteq {\mathbb {R}}^n\) is a bounded convex set and it is assumed that \(g({\mathsf {x}})>0\) for \({\mathsf {x}}\in \Omega \). If f and g are affine functions and \(\Omega \) is a polyhedron, problem (1.1) is called a linear fractional optimization problem. If the functions f and g are quadratic (one of them can be affine) and \(\Omega \) is a polyhedron, we will call this problem as a quadratic fractional optimization problem on a polyhedron. If \(\Omega \) is not a polyhedron it will just be referred as a quadratic fractional optimization problem.

Fractional problems (1.1) are nonconvex in general. Under convexity and concavity assumptions for f and g respectively, and nonnegativity of f if g is not affine, (1.1) is termed a convex–concave fractional program [22], and the objective function is strictly quasi-convex. Any local solution to a convex–concave fractional program is also a global solution, as it happens for general convex programs, and in addition a solution of the Karush–Kuhn–Tucker optimality conditions is a global solution if the numerator and denominator functions are differentiable on an open set containing \(\Omega \). But the convexity and concavity assumptions are restrictive, and in many practical problems they are not valid.

As a generalization of (1.1) we can find the generalized fractional program or min–max fractional optimization problem

$$\begin{aligned} \min \limits _{{\mathsf {x}}\in \Omega } \max \limits _{{\mathsf {y}}\in U} \frac{f({\mathsf {x}},{\mathsf {y}})}{g({\mathsf {x}},{\mathsf {y}})}\, , \end{aligned}$$
(1.2)

and as a special case the discrete case, where we have a finite set \(I=\left\{ 1, \ldots , m\right\} \) instead of U:

$$\begin{aligned} \min \limits _{{\mathsf {x}}\in \Omega } \max \limits _{i \in I} \frac{f_i({\mathsf {x}})}{g_i({\mathsf {x}})} \, . \end{aligned}$$
(1.3)

In the sequel we will consider the discrete case and assume that:

$$\begin{aligned}&\bullet \Omega \subset {\mathbb {R}}^n \hbox { is compact;} \end{aligned}$$
(1.4)
$$\begin{aligned}&\bullet \hbox { for all } i\in I, f_i \hbox { and } g_i \hbox { are continuous on an open set } \tilde{\Omega } \subseteq {\mathbb {R}}^n \hbox { containing } \Omega \, ; \end{aligned}$$
(1.5)
$$\begin{aligned}&\bullet g_i({\mathsf {x}})> 0 \hbox { for all } {\mathsf {x}}\in \Omega \hbox { and all } i\in I\, ; \end{aligned}$$
(1.6)
$$\begin{aligned}&\bullet f_i({\mathsf {x}})> 0 \hbox { for all } {\mathsf {x}}\in \Omega \hbox { and all } i\in I\, . \end{aligned}$$
(1.7)

Note that condition (1.6) aims at ensuring that \(g_i({\mathsf {x}})\ne 0\) and so the problem is well-posed. The positivity condition is not restrictive because we can multiply both numerator and denominator by \((-1)\) ensuring this condition even if \(g_i({\mathsf {x}})<0\). We can assume (1.7) without loss of generality since we can always consider an equivalent problem adding L to \(\frac{f_i({\mathsf {x}})}{g_i({\mathsf {x}})}\) in the objective function for \(i\in I\) with \(L>0\) large enough such that the new numerator \(f_i({\mathsf {x}}) + Lg_i({\mathsf {x}})>0\) on \(\Omega \).

In this paper we are particularly interested in problems (1.3) since they are relevant for performing worst-case analysis as mentioned in [15, 20]. Indeed, suppose that the uncertainty set \(U\subset {\mathbb {R}}^p\) is a polytope with known (few) vertices \({\mathsf {v}}_1,\ldots {\mathsf {v}}_m\), so \(U=\hbox {conv }\left\{ {\mathsf {v}}_i : i\in I\right\} \), and further assume that the objective \(f({\mathsf {x}},{\mathsf {y}})/g({\mathsf {x}},{\mathsf {y}})\) depends in a quasiconvex way on \({\mathsf {y}}\) for any fixed \({\mathsf {x}}\in \Omega \). Now putting \(f_i ({\mathsf {x}}) = f({\mathsf {x}},{\mathsf {v}}_i)\) and \(g_i({\mathsf {x}}) = g({\mathsf {x}},{\mathsf {v}}_i)\), it is obvious that problems (1.2) and (1.3) are the same, so that the robust formulation can be phrased in terms of finitely many scenarios which do not affect the set \(\Omega \) representing precisely known (not uncertain, global) constraints. Closely related applications arise from goal programming and multicriteria optimization when Chebychev’s norm is used to evaluate the goals or criteria, leading to

$$\begin{aligned} \min _{{\mathsf {x}}\in \Omega }\max _{{\mathsf {w}}\in \Delta } \left\{ \sum _{i=1}^m w_i\frac{f_i({\mathsf {x}})}{g_i({\mathsf {x}})}\right\} \, , \end{aligned}$$
(1.8)

where \(\Delta = \left\{ {\mathsf {w}}\in {\mathbb {R}}^m_+ : \sum _{i=1}^m w_i = 1\right\} \) is the standard simplex in \({\mathbb {R}}^m\). The equivalence of (1.3) and (1.8) follows as above, or else directly from the fact that the maximum of m numbers is equal to the maximum of their convex combinations [8, 13]. Problem (1.8) is particularly interesting when pooling of the rival objective functions is considered, in which case the components \(w_i\) are the pooling weights. Then the min–max solution provides a robust pooling by suggesting a strategy that does not depend on the prevailing scenario.

The solution of (1.3) allows the decision maker to compute the best strategy under the worst-case scenario. In practical terms, solving the min–max problem ensures that the solution value will not deteriorate whichever scenario turns out to be the true one. The real solution evaluation will be at least as good as the min–max value. In this context the above mentioned applications of (1.1) can be directly extended to (1.3) in cases where there is some uncertainty related to outside factors. The maximum operator can be avoided by introducing another variable; indeed, problem (1.3) is equivalent to the following problem

$$\begin{aligned} \min _{{\mathsf {x}},v}\left\{ v: {\mathsf {x}}\in \Omega , \frac{f_i({\mathsf {x}})}{g_i({\mathsf {x}})} \le v , \; i \in I\right\} \, . \end{aligned}$$
(1.9)

We will investigate (1.3) in case of quadratic functions \(f_i\) and affine \(g_i\). Problems of this type have applications in maximal predictability portfolio [11], cluster analysis [19], transportation problems with several objective functions [24], and investment allocation problems [27], to name but a few.

This paper is organized in five sections. After this introduction, Sect. 2 presents a review on some methods for addressing general min–max problems. In Sect. 3 the conic reformulation and a tractable relaxation is constructed. This section also incorporates a discussion regarding the extension of these results to the quadratic over quadratic case. Sect. 4 reports computational experience, followed by concluding remarks in the last section.

2 Short review of some traditional methods

Before we proceed we will present in this section two traditional approaches for addressing the min–max problem. Both suffer from the same drawback, namely for general matrices the subproblems are nonconvex, so most of them cannot be solved quickly and the first approach does not even guarantee optimality. Throughout this section, we assume for simplicity of exposition that \(\Omega \) is compact and all involved functions are continuous.

2.1 The minimum-regret approach

We start by introducing a naive minimax strategy based on the regret concept [20]. First, an optimal solution (which generically is unique) for each individual objective function is obtained:

$$\begin{aligned} {\mathsf {x}}_k^*\in \arg \min _{{\mathsf {x}}\in \Omega } \frac{f_k({\mathsf {x}})}{g_k({\mathsf {x}})}\,. \end{aligned}$$
(2.1)

Next, the impact of solution \({\mathsf {x}}_k^*\), \(k\in I\), on the other objective functions is investigated, tantamount to the loss incurred by adopting \({\mathsf {x}}_k^*\) if a scenario different from k occurs:

$$\begin{aligned} \alpha _k:=\max _{i\in I{\setminus }\left\{ k\right\} } \left\{ \frac{f_i({\mathsf {x}}_k^*)}{g_i({\mathsf {x}}_k^*)}-\frac{f_i({\mathsf {x}}_i^*)}{g_i({\mathsf {x}}_i^*)} \right\} \, . \end{aligned}$$

The best strategy \({\mathsf {x}}^*\) will be the one corresponding to the solution that would be the least damaging if a different scenario replaces the one for which the solution is optimal, i.e., select \(i\in I\) such that \(\alpha _i = \min \nolimits _{k\in I} \alpha _k \) and put \({\mathsf {x}}^*={\mathsf {x}}_i^*\).

2.2 A generalization of the Dinkelbach approach

Denote by

$$\begin{aligned} \lambda ^* = \min _{{\mathsf {x}}\in \Omega } \max _{i\in I} \frac{f_i({\mathsf {x}})}{g_i({\mathsf {x}})} \, . \end{aligned}$$
(2.2)

In [9] a method for solving (1.3) based on the Dinkelbach approach for a single ratio is presented. considering a parameterized version of problem (2.2):

$$\begin{aligned} F(\lambda )= \min _{ {\mathsf {x}}\in \Omega }\left\{ \max _{i\in I} \left\{ f_i({\mathsf {x}})-\lambda g_i({\mathsf {x}}) \right\} \right\} , \end{aligned}$$
(2.3)

and a solution of the equation \(F(\lambda ) = 0\) is sought. It is known that \(F(\lambda )\) has some important properties, namely:

(a):

F is real-valued, decreasing and continuous;

(b):

(2.2) and (2.3) always have optimal solutions;

(c):

\(\lambda ^*\) is finite and \(F(\lambda ) = 0\) if and only if \(\lambda =\lambda ^*\).

Algorithm 1 describes the adaptation of the single ratio Dinkelbach method to multiple ratios. The difference consists mainly in the update of the parameter \(\lambda \) in each iteration, steps (1) and (2).

figure a

The convergence of this method is linear, in contrast to the superlinear convergence in case of the Dinkelbach method for a single ratio (which follows by analogy to the Newton method). A better convergence is obtained by modifying the update of \({\mathsf {x}}^k\) to

$$\begin{aligned}&{\mathsf {x}}^k\in \arg \min _{{\mathsf {x}}\in \Omega }\max _{i\in I} \frac{f_i({\mathsf {x}})-\lambda _k g_i({\mathsf {x}})}{g_i({\mathsf {x}}^{k-1})}&\end{aligned}$$

by approximating a Newton step, and thus increasing the convergence rate to superlinearity. This method is also equivalent to the partial linearization procedure in [3]. See [9].

3 A copositive approach

Let us recall the problem (1.3) under investigation

$$\begin{aligned} \min \limits _{{\mathsf {x}}\in \Omega } \max \limits _{i \in I} \frac{f_i({\mathsf {x}})}{g_i({\mathsf {x}})}. \end{aligned}$$

In this work we are considering

$$\begin{aligned} f_i({\mathsf {x}})= & {} {\mathsf {x}}^\top {\mathsf {Q}}_i{\mathsf {x}}+2{\mathsf {b}}_i^\top {\mathsf {x}}+c_i= \left[ \begin{array}{ll} 1&{\mathsf {x}}^\top \end{array} \right] \left[ \begin{array}{rr} c_i &{}\quad {\mathsf {b}}_i^\top \\ {\mathsf {b}}_i &{}\quad {\mathsf {Q}}_i \end{array} \right] \left[ \begin{array}{l} 1\\ {\mathsf {x}}\end{array} \right] \end{aligned}$$
(3.1)
$$\begin{aligned} g_i({\mathsf {x}})= & {} 2{\mathsf {r}}_i^\top {\mathsf {x}}+d_i= \left[ \begin{array}{rr} d_i&2{\mathsf {r}}_i^\top \end{array} \right] \left[ \begin{array}{l} 1\\ {\mathsf {x}}\end{array} \right] \end{aligned}$$
(3.2)

and

$$\begin{aligned} \Omega =\left\{ {\mathsf {x}}\in {\mathbb {R}}^n_+ : {\mathsf {A}}{\mathsf {x}}= {\mathsf {a}}\; , \;{\mathsf {x}}^\top {\mathsf {A}}_q {\mathsf {x}}+ 2{\mathsf {a}}_q^\top {\mathsf {x}}+\alpha _q \le 0\hbox { for all }q{ \in \! [{1}\! : \! {p}]}\right\} \end{aligned}$$
(3.3)

with \({\mathsf {A}}\) a \(k\times n\) matrix while \({\mathsf {a}}_q\in {\mathbb {R}}^n\) and \({\mathsf {A}}_q\in {\mathcal M}_n\) for all \(q{ \in \! [{1}\! : \! {p}]}\). We write \(2{\mathsf {r}}_i\) in the linear term later in (3.2), to keep the analogy with the numerator and to allow for a simpler notation when discussing extensions to the quadratic over quadratic case. Observe that we have implicitly introduced slack variables for the linear constraints but keep quadratic inequalities as constraints. No definiteness assumptions are made on \({\mathsf {A}}_q\). Likewise, in the sequel we will make no assumptions about matrices \({\mathsf {Q}}_i\) in (3.1), other than symmetry.

Our proposal is to use copositive optimization to construct good lower bounds that can be incorporated in a global optimization method for solving this class of min–max problems. Many solvers return a feasible solution at early stages of the branch and bound tree which turns out to be optimal after a following, in many cases long, sequence of iterations, incurring heavy computational burden for obtaining an optimality certificate. Good lower bounds are crucial at this stage. We will show how the lower bounds provided by the copositive relaxation can speed up BARON to obtain this optimality certificate earlier. But before that we briefly recapitulate some essential concepts about copositive optimization.

3.1 Quick facts about copositive optimization

A conic optimization problem in the space \({\mathcal {S}}_n\) of symmetric matrices of order n consists in optimizing a linear function with linear constraints over a cone \({\mathcal {K}}\subseteq {\mathcal {S}}_n\):

$$\begin{aligned} \gamma _{{\mathcal {K}}} :=\inf _{{\mathsf {X}}\in {\mathcal {K}} }\left\{ {\mathsf {C}}\bullet {\mathsf {X}}: {\mathsf {A}}_{i}\bullet {\mathsf {X}}\ge b_i\; , \; \quad i { \in \! [{1}\! : \! {m}]}\right\} \end{aligned}$$
(3.4)

where \({\mathsf {X}}\bullet {\mathsf {Y}}= \hbox {trace }({\mathsf {Y}}^\top {\mathsf {X}})=\sum _{i,j=1}^n X_{ij}Y_{ij}\). The dual of (3.4) is also a conic optimization problem of the form

$$\begin{aligned} \gamma _{{\mathcal {K}}^*} := \sup _{{\mathsf {u}}\in {\mathbb {R}}^m_+}\left\{ {\mathsf {b}}^\top {\mathsf {u}}: {\mathsf {S}}_{\mathsf {u}}:= {\mathsf {C}}- \sum _{i=1}^m u_i {\mathsf {A}}_i \in {\mathcal {K}}^*\right\} \end{aligned}$$
(3.5)

which involves the dual cone

$$\begin{aligned} {\mathcal {K}}^*:=\left\{ {\mathsf {Y}}\in {\mathcal {S}}_n : {\mathsf {X}}\bullet {\mathsf {Y}}\ge 0 \hbox { for all }{\mathsf {X}}\in {\mathcal {K}} \right\} \, . \end{aligned}$$
(3.6)

As usual, we drop sign constraints \(u_i\ge 0\) on the dual variables in case of linear equality constraints \({\mathsf {A}}_i\bullet {\mathsf {X}}= b_i\) on the primal side.

Well-investigated special matrix cones include the semidefinite cone \({\mathcal {S}}^+_n\subset {\mathcal {S}}_n \) of all positive-semidefinite symmetric \(n\times n\) matrices (i.e. those \({\mathsf {X}}\) with no negative eigenvalue, denoted by \({\mathsf {X}}\succeq {\mathsf {O}}\)), and the cone \({\mathcal {N}}_n\subset {\mathcal {S}}_n\) of symmetric \(n\times n\) matrices \({\mathsf {X}}\) with no negative entry (denoted by \({\mathsf {X}}\ge {\mathsf {O}}\)). These two cones are selfdual, \({\mathcal {S}}^+_n = {\mathcal {S}}^{+*}_n\) and \({\mathcal {N}}_n = {\mathcal {N}}_n^*\).

Combination of both properties leads to the cone of so-called doubly nonnegative matrices

$$\begin{aligned} {\mathcal {D}}_n={\mathcal {S}}^+_n\cap {\mathcal {N}}_n= \left\{ {\mathsf {X}}\in {\mathcal {S}}_n : {\mathsf {X}}\ge {\mathsf {O}}\hbox { and } {\mathsf {X}}\succeq {\mathsf {O}}\right\} \, . \end{aligned}$$
(3.7)

The dual cone \({\mathcal {D}}_n^* = {\mathcal {S}}^+_n + {\mathcal {N}}_n\), so \({\mathcal {D}}_n\) is no longer self-dual. While all of aforementioned cones are tractable in a certain sense, there is an important intractable subcone of \({{\mathcal {D}}}_n\), namely the cone of all completely positive symmetric \(n\times n\) matrices,

$$\begin{aligned} {\mathcal {CP}}_n=\hbox {conv }\left\{ {\mathsf {x}}{\mathsf {x}}^\top : {\mathsf {x}}\in {\mathbb {R}}^n_+ \right\} \, , \end{aligned}$$
(3.8)

with its dual cone, that of copositive matrices which are symmetric of order n:

$$\begin{aligned} {\mathcal {COP}}_n=\left\{ {\mathsf {X}}\in {\mathcal {S}}_n : {\mathsf {y}}^\top {\mathsf {X}}{\mathsf {y}}\ge 0 \hbox { for all }{\mathsf {y}}\in {\mathbb {R}}^n_+\right\} \, . \end{aligned}$$
(3.9)

We have \({\mathcal {CP}}_4 = {\mathcal {D}}_4\) but \({\mathcal {CP}}_n \subsetneqq {\mathcal {D}}_n\) for \(n\ge 5\).

A copositive optimization problem is a conic problem (3.4) with \({\mathcal {K}}={\mathcal {COP}}_n\), and most authors include in the definition of copositive optimization also the case \({\mathcal {K}}={\mathcal {CP}}_n\). This problem class has recognized merits since it admits reformulations of hard optimization problems, such as continuous nonconvex quadratic [4, 5, 18], mixed-integer quadratic [7], continuous [2] and mixed-integer [1] fractional quadratic problems. Basically, by lifting quadratic expressions, all constraints can be linearized, pushing the hardness entirely into the cone description. Indeed, checking that a matrix is in \({\mathcal {CP}}_n\) is NP-hard [10], and it is co-NP-complete to check whether a matrix is copositive [14]. Nevertheless it is an important feature of completely positive formulations that relaxations giving tight lower bounds can be obtained by replacing \({\mathcal {CP}}_n\) by \({\mathcal {D}}_n\), for instance. Even tighter relaxation bounds can be obtained by the so-called approximation hierarchies which replace \({\mathcal {CP}}_n\) by other tractable cones (polyhedral or expressible by linear matrix inequalities). These approximation hierarchies can be constructed using simplices [6, 23], sums-of-squares [16] or polynomials [4, 17].

3.2 Copositive reformulation

We now present a reformulation based on copositive optimization of problem (1.3) written now in a more descriptive way to facilitate further reading.

$$\begin{aligned} \lambda ^* = \min \limits _{{\mathsf {x}}\in \Omega } h({\mathsf {x}}) \quad \hbox {with}\quad h({\mathsf {x}})=\max \limits _{i \in I} \frac{ \left[ \begin{array}{ll} 1&{\mathsf {x}}^\top \end{array} \right] \left[ \begin{array}{rr} c_i &{}\quad {\mathsf {b}}_i^\top \\ {\mathsf {b}}_i &{}\quad {\mathsf {Q}}_i \end{array} \right] \left[ \begin{array}{l} 1\\ {\mathsf {x}}\end{array} \right] }{\left[ \begin{array}{rr} d_i&2{\mathsf {r}}_i^\top \end{array} \right] \left[ \begin{array}{l} 1\\ {\mathsf {x}}\end{array} \right] } \, . \end{aligned}$$
(3.10)

Using a Shor lifting and considering \({\mathsf {y}}^\top =\left[ 1 \; , \; {\mathsf {x}}^\top \right] \) we write \(h({\mathsf {x}})\) in (3.10) by

$$\begin{aligned} {\widehat{h}}({\mathsf {y}}) = \max _{i \in I}\frac{{\mathsf {y}}^\top {\widehat{{\mathsf {Q}}}}_i{\mathsf {y}}}{\widehat{{\mathsf {r}}}_i^\top {\mathsf {y}}} \quad \hbox {with}\quad {\widehat{{\mathsf {Q}}}}_i= \left[ \begin{array}{rr} c_i &{}\quad {\mathsf {b}}_i^\top \\ {\mathsf {b}}_i &{}\quad {\mathsf {Q}}_i \end{array} \right] \;\hbox { and }\; \widehat{{\mathsf {r}}}_i = \left[ \begin{array}{rr} d_i \\ 2{\mathsf {r}}_i \end{array} \right] \, . \end{aligned}$$

Next we square the homogenized linear constraints:

$$\begin{aligned} {\mathsf {A}}{\mathsf {x}}={\mathsf {a}}\quad \Longleftrightarrow \quad \Vert {\mathsf {A}}{\mathsf {x}}-{\mathsf {a}}\Vert ^2\le 0 \quad \Longleftrightarrow \quad {\mathsf {y}}^\top \widehat{{\mathsf {A}}_0} {\mathsf {y}}\le 0 \, , \end{aligned}$$
(3.11)

where

$$\begin{aligned} {\widehat{{\mathsf {A}}_0}}=\left[ \begin{array}{rr} {\mathsf {a}}^\top {\mathsf {a}}&{}\quad -{\mathsf {a}}^\top {\mathsf {A}}\\ -{\mathsf {A}}^\top {\mathsf {a}}&{}\quad {\mathsf {A}}^\top {\mathsf {A}}\end{array} \right] \,. \end{aligned}$$

Likewise, homogenize the quadratic constraints by introducing, for all \(q{ \in \! [{1}\! : \! {p}]}\),

$$\begin{aligned} {{\widehat{{\mathsf {A}}_q}}}= \left[ \begin{array}{rr} \alpha _q &{} {\mathsf {a}}_q^\top \\ {\mathsf {a}}_q &{} {\mathsf {A}}_q \end{array} \right] \, . \end{aligned}$$

So, denoting

$$\begin{aligned} \widehat{\Omega }= \left\{ {\mathsf {y}}\in {\mathbb {R}}^{n+1}_+: y_0=1, \, {\mathsf {y}}^\top {\widehat{{\mathsf {A}}_q}}{\mathsf {y}}\le 0 \hbox { for all }q{ \in \! [{0}\! : \! {p}]} \right\} , \end{aligned}$$

we arrive at

$$\begin{aligned} \lambda ^* = \min _{{\mathsf {y}}\in {\widehat{\Omega }}} {\widehat{h}}({\mathsf {y}}). \end{aligned}$$
(3.12)

The linear constraints (3.11) are homogenized as inequalities instead of equivalent equalities (given that \(\widehat{{\mathsf {A}}_0}\) is pd) to simplify notation, defining all the constraints, quadratic and linear, with the same structure.

Next, borrowing from (1.9), we introduce another variable \(v \in {\mathbb {R}}\) and using hypothesis (1.6), we obtain

$$\begin{aligned} \lambda ^*= & {} \min _{({\mathsf {y}},v)\in {\widehat{\Omega }}\times {\mathbb {R}}}\left\{ v : \frac{{\mathsf {y}}^\top {\widehat{{\mathsf {Q}}}}_i{\mathsf {y}}}{\widehat{{\mathsf {r}}}_i^\top {\mathsf {y}}} \le v\hbox { for all } i\in I \right\} \nonumber \\= & {} \min _{({\mathsf {y}},v)\in {\widehat{\Omega }}\times {\mathbb {R}}}\left\{ v : {\mathsf {y}}^\top {\widehat{{\mathsf {Q}}}}_i{\mathsf {y}}\le v \widehat{{\mathsf {r}}}_i^\top {\mathsf {y}}\hbox { for all }i\in I \right\} \, . \end{aligned}$$
(3.13)

Now considering \({\mathsf {z}}=[ {\mathsf {y}}^\top \; v ]^\top \) and

$$\begin{aligned} \breve{{\mathsf {Q}}}_i= & {} \left[ \begin{array}{rr} {\widehat{{\mathsf {Q}}}}_i &{}\quad {\mathsf {o}}\\ {\mathsf {o}}^\top &{}\quad 0 \end{array} \right] \quad \hbox { for } i \in I,\\ \breve{{\mathsf {R}}}_i= & {} \left[ \begin{array}{rr} {\mathsf {O}}&{}\quad \frac{1}{2}\widehat{{\mathsf {r}}}_i\\ \frac{1}{2}\widehat{{\mathsf {r}}}_i^\top &{}\quad 0\end{array} \right] \quad \hbox { for } i \in I,\\ \breve{{\mathsf {A}}}_q= & {} \left[ \begin{array}{rr} {\widehat{{\mathsf {A}}_q}} &{}\quad {\mathsf {o}}\\ {\mathsf {o}}^\top &{}\quad 0 \end{array} \right] \quad \hbox { for } q { \in \! [{0}\! : \! {m}]}, \end{aligned}$$

we obtain

$$\begin{aligned} \lambda ^* = \min _{{\mathsf {z}}\in {\mathbb {R}}^{n+1}_+} \left\{ z_{n+1} : z_0=1,\, {\mathsf {z}}^\top \breve{{\mathsf {Q}}}_i{\mathsf {z}}\le {\mathsf {z}}^\top \breve{{\mathsf {R}}}_i{\mathsf {z}}, \, i\in I, \, {\mathsf {z}}^\top \breve{{\mathsf {A}}}_q{\mathsf {z}}\le 0, \, q{ \in \! [{0}\! : \! {p}]}\right\} . \end{aligned}$$
(3.14)

Now for \({\mathsf {X}}={\mathsf {z}}{\mathsf {z}}^\top \), we obtain the following reformulation of (3.14), more precisely, of \((\lambda ^*)^2\), in view of \(z_{n+1}^*\ge 0\):

$$\begin{aligned} \gamma ^* = \min _{{\mathsf {X}}\in {\mathcal {CP}}^{\mathrm {rk}\,1}_{n+2}} \left\{ X_{n+1,n+1} : X_{00}=1\, , \, (\breve{{\mathsf {Q}}}_i-\breve{{\mathsf {R}}}_i)\bullet {\mathsf {X}}\le 0 \,,\, i \in I\, , \breve{{\mathsf {A}}}_q \bullet {\mathsf {X}}\le 0 \; ,\; q{ \in \! [{0}\! : \! {p}]} \right\} \, ,\nonumber \\ \end{aligned}$$
(3.15)

where \({\mathcal {CP}}_{n+2}^{\mathrm {rk}\,1}:= \left\{ {\mathsf {X}}\in {\mathcal {CP}}_{n+2} : \hbox {rank }{\mathsf {X}}=1\right\} \). Dropping the rank constraint leads to the completely positive relaxation

$$\begin{aligned} \gamma ^*_{CP} = \min _{{\mathsf {X}}\in {\mathcal {CP}}_{n+2}} \left\{ X_{n+1,n+1}: X_{00}=1\, , \, (\breve{{\mathsf {Q}}}_i-\breve{{\mathsf {R}}}_i)\bullet {\mathsf {X}}\le 0 \,,\, i \in I\, , \breve{{\mathsf {A}}}_q \bullet {\mathsf {X}}\le 0 \; ,\; q{ \in \! [{0}\! : \! {p}]} \right\} \, ,\nonumber \\ \end{aligned}$$
(3.16)

with its dual

$$\begin{aligned} \gamma ^*_{COP} = \sup _{{\mathsf {u}}\in {\mathbb {R}}^{m+p+2}_+} \left\{ u_0 : {\mathsf {E}}_{n+1} - u_0{\mathsf {E}}_0 -\sum _{i=1}^m u_i(\breve{{\mathsf {Q}}}_i-\breve{{\mathsf {R}}}_i)-\sum _{q=0}^{p} \mu _{q} \breve{{\mathsf {A}}}_q \in {\mathcal {COP}}_{n+2}\right\} \, ,\nonumber \\ \end{aligned}$$
(3.17)

where \({\mathsf {E}}_k\bullet {\mathsf {X}}= X_{kk}\). Weak duality and rank relaxation yield immediately the relations \(\gamma ^*_{COP}\le \gamma ^*_{CP} \le \gamma ^* = (\lambda ^*)^2\). If an optimal solution of (3.16) has rank one then we have \(\gamma ^*_{CP} = \gamma ^* \) and vice versa.

Further, tractable relaxations of above conic problems may use approximation hierarchies for \({\mathcal {CP}}_{n+2}\), for instance by replacing \({\mathcal {CP}}^{rk1}_{n+2}\) by \({\mathcal {D}}_{n+2}\), the cone of doubly nonnegative matrices. In this case we obtain the following problem:

$$\begin{aligned} \delta ^* = \min _{{\mathsf {X}}\in {\mathcal {D}}_{n+2}} \left\{ X_{n+1,n+1} : X_{00} = 1\;,(\breve{{\mathsf {Q}}}_i-\breve{{\mathsf {R}}}_i)\bullet {\mathsf {X}}\le 0 \;, i \in I\; ,\; \breve{{\mathsf {A}}}_q\bullet {\mathsf {X}}\le 0 \, , \, q{ \in \! [{0}\! : \! {p}]} \right\} \nonumber \\ \end{aligned}$$
(3.18)

for which \(\sqrt{\delta ^*}\le \sqrt{\gamma ^*_{CP}}\le \sqrt{\gamma ^*} = \lambda ^*\).

Fig. 1
figure 1

Nonconvex quadratic over affine: Example 3.1

Full size image

Example 3.1

Consider the following example:

$$\begin{aligned} \min _{{\mathsf {x}}\in {\mathbb {R}}^2_+}\max&\left\{ -\frac{{x_1}^2 - 4\, x_1\, x_2 + 2\, x_1 + {x_2}^2 - 4\, x_2 - 1}{2\, x_1 + 2\, x_2 + 1}, \frac{2\, {x_1}^2 - 2\, x_1\, x_2 + 4\, x_1 + 2\, {x_2}^2 - 4\, x_2 + 4}{4\, x_1 + 8\, x_2 + 3} \right\} \\ \hbox { s.t. }&x_1 + 2x_2=2 \\&-x_1^2+4x_2^2 \le 4 \end{aligned}$$

Upon \(0\le x_2=1-\frac{x_1}{2}\), the quadratic constraints reduces to \(x_1 \ge 0\) (which is redundant) and we obtain the following one-dimensional problem

$$\begin{aligned} \min _{x_1\in [0,2]} \max \left\{ \frac{ - 13\, {x_1}^2 + 4\, x_1 + 16}{4\, \left( x_1 + 3\right) }, \frac{7\, {x_1}^2}{22} + \frac{2\, x_1}{11} + \frac{2}{11} \right\} \, . \end{aligned}$$

Figure 1 shows both fractions and the nonconvex objective \(h({\mathsf {x}})\). The optimal solution \({\mathsf {x}}^* =[0.8898,0.5551]^\top \) is designated by a circle. The optimal value is 0.5955 as opposed to the copositive relaxation bound 0.5141 attained at an optimal solution with a rank exceeding one. Note that as we are in dimension four, problems (3.16) and (3.18) coincide.

The next example considers a convex instance where the objective \(h({\mathsf {x}})\) is smooth at the optimal solution.

Fig. 2
figure 2

Convex quadratic over affine: Example 3.2

Full size image

Example 3.2

Consider

$$\begin{aligned} \min _{{\mathsf {x}}\in {\mathbb {R}}_+^2}\max&\left\{ \frac{3\, {x_1}^2 - 2\, x_1\, x_2 + 2\, x_1 + 2\, {x_2}^2 - 4\, x_2 + 1}{2\, x_1 + 2\, x_2 + 1} \, , \, \frac{4\, {x_1}^2 - 2\, x_1\, x_2 + 4\, x_1 + 3\, {x_2}^2 - 4\, x_2 + 4}{4\, x_1 + 1} \right\} \\&\hbox { s.t. } 2x_1 + 5x_2=10 \end{aligned}$$

Upon \(x_2=(10-2x_1)/5\) we obtain the following one-dimensional problem

$$\begin{aligned} \min _{x_1\in [0,5]} \max \left\{ \frac{103\, {x_1}^2 - 90\, x_1 + 25}{30\, x_1 + 125} \, , \, \frac{132\, {x_1}^2 - 80\, x_1 + 200}{100\, x_1 + 25} \right\} \end{aligned}$$

Figure 2 shows a representation of the univariate problem, now the solution is obtained at a stationary point of one function corresponding to the optimal solution \(x_1^*= 1.0650\) and \(x_2^*= 1.5740\). The optimal value is \(\lambda ^*=2.0115\), the square of which coincides with the value \(\gamma ^*_{CP}\) at the optimal rank-one-solution \({\mathsf {z}}^*({\mathsf {z}}^*)^\top \) of the copositive relaxation (3.16) with \({\mathsf {z}}^* = [1,x_1^*,x_2^*,\lambda ^*]^\top \). Again we are in dimension four, so problems (3.16) and (3.18) coincide. Furthermore, there is neither a conic duality gap nor a relaxation gap, \(\sqrt{\delta ^*}= \sqrt{\gamma ^*_{COP}} = \sqrt{\gamma ^*_{CP}} = \sqrt{\gamma ^*} = \lambda ^*\), in this example. We will specify a more general condition for zero relaxation gap below.

Theorem 3.3

(a) For any \({\mathsf {u}}= [u_0,\ldots u_{m},\mu _0,\ldots \mu _p]^\top \in {\mathbb {R}}^{m+p+2}_+\) consider the following symmetric matrix of order \(n+2\):

$$\begin{aligned} {\mathsf {S}}_{\mathsf {u}}:= \left[ \begin{array}{ccc} \sigma _{\mathsf {u}}&{}\quad {\mathsf {s}}_{\mathsf {u}}^\top &{}\quad -\sum \limits _{i=1}^m u_i d_i/2 \\ {\mathsf {s}}_{\mathsf {u}}&{}\quad {\mathsf {P}}_{\mathsf {u}}&{}\quad -\sum \limits _{i=1}^m u_i{\mathsf {r}}_i \\ -\sum \limits _{i=1}^m u_i d_i/2 &{}\quad \left( -\sum \limits _{i=1}^m u_i{\mathsf {r}}_i\right) ^\top &{}\quad 1 \end{array} \right] , \end{aligned}$$
(3.19)

where

and

$$\begin{aligned} {\mathsf {P}}_{\mathsf {u}}:= \sum \limits _{i=1}^m u_i {\mathsf {Q}}_i + \sum \limits _{q=1}^p \mu _{q}{\mathsf {A}}_q + \mu _{0}{\mathsf {A}}^\top {\mathsf {A}}\, . \end{aligned}$$

If \({\mathsf {S}}_{\mathsf {u}}\) is copositive, then \(\sqrt{u_0} \le \lambda ^*\), so we get a valid lower bound for the problem (1.3) with affine-linear denominators \(g_i({\mathsf {x}})\).

(b) Now suppose that \({\mathsf {x}}^*\in \Omega \) and put \({\sqrt{u_0}}= h({\mathsf {x}}^*)\). If for this value of \(u_0\), above \({\mathsf {S}}_{\mathsf {u}}\) is copositive, then \({\mathsf {x}}^*\) solves the problem (1.3) with affine-linear denominators \(g_i({\mathsf {x}})\), and both the conic duality and relaxation gaps are zero:

$$\begin{aligned} \sqrt{\gamma ^*_{COP}} = \sqrt{\gamma ^*_{CP}} = \sqrt{\gamma ^*} = \lambda ^*= h({\mathsf {x}}^*)\, . \end{aligned}$$

Proof

(a) The matrix \({\mathsf {S}}_{\mathsf {u}}\) as defined in (3.19) coincides with the slack matrix of the dual problem (3.17), as one can easily verify. By assumption, this \({\mathsf {S}}_{\mathsf {u}}\) is feasible to (3.17), hence we obtain

$$\begin{aligned} {\sqrt{u_0}}\le \sqrt{\gamma ^*_{COP}} \le \sqrt{\gamma ^*_{CP}} \le \sqrt{\gamma ^*} = \lambda ^*\, . \end{aligned}$$

(b) Now put \({\sqrt{u_0}} =h({\mathsf {x}}^*)\). If \({\mathsf {S}}_{\mathsf {u}}\) is still feasible to (3.17), we now get \(h({\mathsf {x}}^*)={\sqrt{u_0}} \le \sqrt{\gamma ^*_{COP}} \le \sqrt{\gamma ^*_{CP}} \le \sqrt{\gamma ^*} = \lambda ^* \le h({\mathsf {x}}^*)\), and all assertions are established. \(\square \)

3.3 Some considerations about the constrained min–max quadratic over quadratic case

Before presenting the computational experience we discuss some limitations regarding extensions of the previous work, on a conic reformulation, to the quadratic over quadratic case, when:

$$\begin{aligned} f_i({\mathsf {x}})= & {} {\mathsf {x}}^\top {\mathsf {Q}}_i{\mathsf {x}}+2{\mathsf {b}}_i^\top {\mathsf {x}}+c_i= \left[ \begin{array}{ll} 1&{\mathsf {x}}^\top \end{array} \right] \left[ \begin{array}{rr} c_i &{}\quad {\mathsf {b}}_i^\top \\ {\mathsf {b}}_i &{}\quad {\mathsf {Q}}_i \end{array} \right] \left[ \begin{array}{l} 1\\ {\mathsf {x}}\end{array} \right] \end{aligned}$$
(3.20)
$$\begin{aligned} g_i({\mathsf {x}})= & {} {\mathsf {x}}^\top {\mathsf {T}}_i{\mathsf {x}}+2{\mathsf {r}}_i^\top {\mathsf {x}}+d_i= \left[ \begin{array}{ll} 1&{\mathsf {x}}^\top \end{array} \right] \left[ \begin{array}{rr} d_i &{}\quad {\mathsf {r}}_i^\top \\ {\mathsf {r}}_i &{}\quad {\mathsf {T}}_i \end{array} \right] \left[ \begin{array}{l} 1\\ {\mathsf {x}}\end{array} \right] \end{aligned}$$
(3.21)

The quadratic over affine case is obtained considering \({\mathsf {T}}_i = {\mathsf {O}}\) for \(i \in I\). Knowing that it is possible to replace a quadratic expression in the objective function by an additional variable introducing this relation as a constraint of the problem, we immediately looked for the possibility of applying the same conic reformulation to this more general case but we faced strong limitations regarding the conic relaxation.

First we show that that this case can be converted to a quadratic over affine problem, as (3.10) with the introduction of additional variables, \(x_{n+i}\) replacing the quadratic expressions \({\mathsf {x}}^\top {\mathsf {T}}_i{\mathsf {x}}\) in \({g}_i({\mathsf {x}})\) and adding the quadratic constraints \({\mathsf {x}}^\top {\mathsf {T}}_i{\mathsf {x}}\ge x_{n+i}\) for \(i\in I\). A problem with an affine denominator is obtained subject to \(m+p+1\) quadratic constraints plus (linear) sign constraints. It is worth noting that additional quadratic constraints should not pose further difficulties concerning the conic reformulation. An equivalent problem is obtained as follows:

$$\begin{aligned} {\lambda }^*= \min _{{\mathsf {x}}\in \overline{\Omega }} \overline{h}({\mathsf {x}}) \end{aligned}$$
(3.22)

where

$$\begin{aligned} \overline{\Omega } = \left\{ {\mathsf {x}}\in {\mathbb {R}}^{n+m}_+: \overline{{\mathsf {A}}}{\mathsf {x}}={\mathsf {a}}, {\mathsf {x}}^\top \overline{{\mathsf {T}}}_i{\mathsf {x}}\ge x_{n+i}\, ,\, i\in I \right\} \subset {\mathbb {R}}^{n+m}\, , \end{aligned}$$

denoting by \({\mathsf {O}}\) zero matrices of various but suitable size

$$\begin{aligned} \overline{{\mathsf {A}}} = \left[ \begin{array}{rr} {\mathsf {A}}&{\mathsf {O}}\end{array} \right] \quad \hbox {and}\quad \overline{{\mathsf {T}}}_i = \left[ \begin{array}{rr} {\mathsf {T}}_i &{}\quad {\mathsf {O}}\\ {\mathsf {O}}&{}\quad {\mathsf {O}}\end{array} \right] ,\, i\in I, \end{aligned}$$

and

$$\begin{aligned} \overline{h}({\mathsf {x}}) = \max \limits _{i \in I} \frac{\overline{f}_i({\mathsf {x}})}{\overline{{\mathsf {g}}}_i({\mathsf {x}})}\, , \quad \overline{f}_i({\mathsf {x}}) = {\mathsf {x}}^\top \overline{{\mathsf {Q}}}_i{\mathsf {x}}+2\overline{{\mathsf {b}}}_i^\top {\mathsf {x}}+c_i\, ,\quad \overline{g}_i({\mathsf {x}}) = 2\overline{{\mathsf {r}}}_i^\top {\mathsf {x}}+d_i \end{aligned}$$

where we abbreviated

$$\begin{aligned} \overline{{\mathsf {Q}}}_i = \left[ \begin{array}{rr} {\mathsf {Q}}_i &{}\quad {\mathsf {O}}\\ {\mathsf {O}}&{}\quad {\mathsf {O}}\end{array} \right] \, ,\quad \overline{{\mathsf {b}}}_i = \left[ \begin{array}{r} {\mathsf {b}}_i \\ {\mathsf {o}}\end{array} \right] ,\quad 2\overline{{\mathsf {r}}}_i = \left[ \begin{array}{r} 2{\mathsf {r}}_i \\ {\mathsf {e}}_i \end{array}\right] \end{aligned}$$

with \({\mathsf {e}}_i\) the \(i\hbox {th}\) column of the identity matrix \({\mathsf {I}}_m\) of order m.

Fig. 3
figure 3

Nonconvex quadratic over quadratic: Example 3.4

Full size image

Example 3.4

Consider the following example

$$\begin{aligned} \min _{{\mathsf {x}}\in \Omega }\max \left\{ -\frac{{x_1}^2 - 4\, x_1\, x_2 + 2\, x_1 + {x_2}^2 - 4\, x_2 - 1}{{x_1}^2 + 2\, x_1 + {x_2}^2 + 2\, x_2 + 1}, \frac{2\, {x_1}^2 - 2\, x_1\, x_2 + 4\, x_1 + 2\, {x_2}^2 - 4\, x_2 + 4}{3\, {x_1}^2 + 2\, x_1\, x_2 + 4\, x_1 + 3\, {x_2}^2 + 8\, x_2 + 3} \right\} \nonumber \\ \end{aligned}$$
(3.23)

with \(\Omega = \left\{ {\mathsf {x}}\in {\mathbb {R}}^2_+ : x_1 + 2x_2=2\right\} \). Upon replacing \(x_2=1-\frac{x_1}{2}\) we obtain the following one-dimensional problem

$$\begin{aligned} \min _{x_1\in [0,2]} \max \left\{ \frac{ - 13\, {x_1}^2 + 4\, x_1 + 16}{5\, {x_1}^2 + 16},\, \frac{14\, {x_1}^2 + 8\, x_1 + 8}{11\, {x_1}^2 - 4\, x_1 + 56}\right\} \, . \end{aligned}$$

Figure 3 shows both quadratic ratios, and the optimal value 0.4381 over [0, 2] attained at the optimal solution \({\mathsf {x}}^* =[0.9122,0.5439]^\top \) is designated by a circle. Applying above reasoning, problem (3.23) can be rewritten as

$$\begin{aligned} \min _{{\mathsf {x}}\in \overline{\Omega }}\max \left\{ -\frac{{x_1}^2 - 4\, x_1\, x_2 + 2\, x_1 + {x_2}^2 - 4\, x_2 - 1}{x_3+ 2\, x_1 + 2\, x_2 + 1}, \frac{2\, {x_1}^2 - 2\, x_1\, x_2 + 4\, x_1 + 2\, {x_2}^2 - 4\, x_2 + 4}{x_4+ 4\, x_1 + 8\, x_2 + 3} \right\} \end{aligned}$$

with

$$\begin{aligned} \overline{\Omega }= \left\{ {\mathsf {x}}\in {\mathbb {R}}^4_+ : x_1 + 2x_2=2\,, \, {x_1}^2 + {x_2}^2 \ge x_3 \, , \, 3\, {x_1}^2 + 2\, x_1\, x_2 + 3\, {x_2}^2 \ge x_4\right\} \, , \end{aligned}$$

with the same optimal value, now attained at \([0.9122,\;0.5439,\;1.1279, \;4.3759]^\top \) with objective value \(\lambda ^* =0.4381\). Solving problem (3.16) for this instance yields an optimal solution with a relaxation bound of \(\sqrt{\delta ^*}= 0.3713\). We note that this lower bound is not as tight as in the previous examples with a relative relaxation gap \(\frac{\lambda ^*- \sqrt{\delta ^*}}{\lambda ^*} \approx 15.25\%\) as opposed to \(13.67\%\) in Example 3.1 (and zero in Example 3.2).

When observing in detail the structure of the constraints of the conic optimization relaxation for the quadratic over quadratic case we have (abbreviating \({\mathsf {Z}}={\mathsf {X}}_{n+1:n+m,n+1:n+m}\))

(3.24)
(3.25)

and

(3.26)

The occurrence of a sub-matrix of zeros (in the framed box) in constraints (3.24)–(3.26) contributes to a severe deterioration of the quality of the lower bounds. Further research on this topic is left for future investigation.

4 Computational experience

The numerical experiments were performed on a PC, Intel(R) Core(TM) i7-2640M, 2.80 Ghz,400 GB RAM. The software Matlab 2013Ra was used to run the global optimization solver BARON [21] and SDPT3(4.0)/Octave [26], a Matlab package for solving convex optimization problems involving linear equations and inequalities, second-order cone constraints, and semidefinite constraints (linear matrix inequalities). The interface YALMIP [12] was used to call SDPT3.

To study the empirical quality of the lower bounds provided by the relaxation (3.18) we used the global optimization solver BARON to obtain, when possible, the optimal solution to define the gaps and to provide a lower bound for comparison. It would be useless to use the last lower bound provided by BARON since in most problems it would coincide with the optimal value and it is the result of a chain of different methods (which are unknown to the user). To compare with the first lower bound of BARON would be a fair choice, but even better is to compare the performance of BARON with itself when the lower bound of relaxation \(\delta ^*\) is provided to this solver.

The formulation defined for BARON input was the following:

$$\begin{aligned} \lambda ^* = \min \left\{ v : \frac{f_i({\mathsf {x}})}{g_i({\mathsf {x}})} \le v ,\,i\in I , {\mathsf {x}}^\top {\mathsf {A}}_q {\mathsf {x}}+ {\mathsf {a}}_q^\top {\mathsf {x}}+\alpha _q \le 0,\, q{ \in \! [{1}\! : \! {p}]},\, {\mathsf {A}}{\mathsf {x}}={\mathsf {a}},\, {\mathsf {x}}\ge {\mathsf {o}}, \, v_l \le v \le v_u\right\} \, . \end{aligned}$$

The software BARON does not accept, as input, an initial lower bound to start the search, but in this case, since the objective function is a single variable v and BARON accepts box bounds (lower and upper) for variables it was in fact possible to indirectly impose a lower bound by introducing the lower box bound \(v_l\) for v. This allowed to study the quality of the lower bound by solving (3.18), obtaining as optimal value \(X_{n+1,n+1}^*\) and running BARON twice, with \(v_l=-\infty \) and \(v_l=\sqrt{X_{n+1,n+1}^*}\).

The limit time ( in seconds) for the first run of BARON was set to \(\mathtt{MaxTime} = 250\) and the gap tolerance \(\mathtt{EpsA} = 10^{-4}\). On the second run of BARON, the time limit was set differently to each instance to 250 minus the run time of SDPT3 for that instance. The settings for SDPT3 were \(\mathtt{sdpt3.maxit}= 500\) for the maximal number of iterations and \({\texttt {sdpt3.gaptol}}=10^{-2}\) for the gap tolerance.

Ten test instances were randomly generated for up to ten ratios, i.e. \(m=\#I\in \{3, 5, 10\}\) in (3.18), and variable dimensions \(n\in \left\{ 5, 25, 50,75\right\} \). All experiments had one linear equality and one quadratic inequality constraint (\(k=p=1\)) with, again, randomly chosen coefficients.

4.1 Empirical study on the quality of lower bounds

Table 1 Results for \(m=5\), \(n\in \left\{ 5, 25, 50, 75\right\} \)
Full size table

In the analysis of the results we focus to answer the question whether the relaxation is more efficient than the battery of techniques used in BARON to generate lower bounds for this problem, using a first run of BARON with \(v \ge -\infty \) (RUN1) and a second run with \(v \ge \sqrt{X_{n+1,n+1}^*}\) (RUN2). We compare to the result of the SDPT3 solver for solving (3.18), designated by RUN0.

Table 1 presents results from RUN0, RUN1 and RUN2 where the columns represent:

  • Problem—Problem name ‘INSTaMbNc’ where ‘a’ is the instance number (0–9) for the same specifications: ‘b’ number of ratios and ‘c’ number of variables.

  • E1—Status of BARON RUN1 solution, ‘NorC’ means ‘textitNormal Completion’ and ‘MCPU’ stands for ‘Max. allowable CPU time exceeded’. The limit was set to 250 seconds.

  • Btime—the difference between the CPU time of RUN1 and RUN2 when the status of RUN1 was ‘Normal Completion’ or the time of RUN2 alone when RUN1 stopped because of ‘Max. allowable CPU time exceeded’. When E1 is ‘MCPU’ and Btime is 250,00 it means that also in the RUN2 the maximal CPU time was exceeded.

  • Biter—the difference between the number of iterations of RUN1 and RUN2 when the status of RUN1 was ‘Normal Completion’ or the time of RUN2 alone when RUN1 stopped because of ‘Max. allowable CPU time exceeded’.

  • BMN—the difference between the index of the best node (where the best upper bound was obtained) of RUN1 and RUN2 when the status of RUN1 was ‘textitNormal Completion’ or the best node for RUN2 alone when RUN1 stopped because of ‘Max. allowable CPU time exceeded’.

  • Baron LB—Lower Bound output for RUN1.

  • Baron UB—Upper Bound output for RUN1.

  • GAP1—\(100\frac{\mathtt{BARON}\hbox { UB}-\mathtt{BARON}\hbox { LB} }{\mathtt{BARON}\hbox { UB}}\) for RUN1

  • GAP2—\(100\frac{\mathtt{BARON}\hbox { UB}-\mathtt{BARON}\hbox { LB} }{\mathtt{BARON}\hbox { UB}}\) for RUN2

  • E2—Status of solution, 0 for ‘Successfully solved’, 3 for ‘Maximum iterations or time limit exceeded’, 4 for ‘Numerical problems’ and 5 for ‘textitLack of progress’.

  • YLB—SDPT3 RUN0 optimal value’s square root.

  • GAP0—\(100\frac{\mathtt{BARON}\hbox { UB}-\hbox {YLB} }{\mathtt{BARON}\hbox { UB}}\) for RUN0

  • Time—CPU time of RUN0

Looking at Table 1, merits of the lower bounds provided by (3.18) are clear and more pronounced for larger instances. First we should observe the resulting gaps and see that for the smaller problems the lower bound coincides with the optimal value in most instances. As the size increases, it is evident that the lower bound from (3.18) outperforms BARON’s lower bounding techniques. In some cases (INST8M5N25, INST8M5N50) only by providing the lower bound from (3.18) it was possible to obtain the optimal solution. The caveats occur for some numerical problems (\(\mathtt{E2}=4\)) encountered in some instances, and the lower bound cannot be trusted. In fact significantly negative gap values (\(<-10^{-2}\)) represent these cases while small negative gaps are just the result of error propagation. Figure 4 gives a graphical representation of these gaps. It is clear that the line for GAP1 is mostly above that of GAP2 and GAP0 due to usage of (3.18), and that the line of GAP2 lies close to that of GAP0, meaning that the proposed lower bound represents an important contribution. The decrease in each instance from GAP1 to GAP2 is the direct result of the a priori knowledge of this lower bound.

Fig. 4
figure 4

Relative gaps for the \(m=5\) instances

Full size image

The next observation is related to CPU time in columns BTime and Time. Most of the time the best upper bound is achieved at an early stage and so BARON puts considerably larger effort in improving the lower bound. So, even discounting the fact that BARON time is not only related to lower bound calculations, Table 1 shows that it clearly pays to have an initial lower bound calculated by (3.18).

In just a few cases (Btime \(<0\)) it seems that it does not compensate the a priori knowledge of the lower bound given by (3.18), even if the bound in the first node is really weak. We must bear in mind that it is not clear at which stage of the procedure (if at all) BARON interprets the lower bound box constraint for variable v also as a lower bound for the optimal value. Nevertheless the overall conclusion is that it is a benefit and sometimes even crucial to have the lower bound provided by (3.18).

5 Conclusion

In this paper we make a contribution to extend the class of hard optimization problems for which a conic reformulation, based on the cone of copositive or completely positive matrices, is known. We address min–max problems of fractional quadratic (not necessarily convex) over affine functions on a feasible set described by linear and (not necessarily convex) quadratic functions. Relaxations of copositive reformulations have proved to produce tight lower bounds and empirical evidence obtained by the computational experience on this problem corroborates this statement. Relaxation of the completely positive cone by the doubly nonnegative cone led to a tractable relaxation problem providing lower bounds with very small gaps, enabling us to globally solve a difficult optimization problem. It is known that in branch and bound methods, very good, sometimes even optimal, solutions are obtained at early stages of traversing the problem tree. The effort to prove optimality or to state a safe termination criterion for the search depends on closing the gap between the lower and upper bound, so the quality of the first are crucial. In this paper we present a lower bounding procedure that justifies once more the high reputation of relaxations gained from conic reformulations.