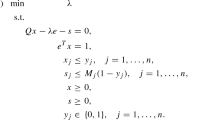Abstract
We study linear programming relaxations of nonconvex quadratic programs given by the reformulation–linearization technique (RLT), referred to as RLT relaxations. We investigate the relations between the polyhedral properties of the feasible regions of a quadratic program and its RLT relaxation. We establish various connections between recession directions, boundedness, and vertices of the two feasible regions. Using these properties, we present a complete description of the set of instances that admit an exact RLT relaxation. We then give a thorough discussion of how our results can be converted into simple algorithmic procedures to construct instances of quadratic programs with exact, inexact, or unbounded RLT relaxations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A quadratic program involves minimizing a (possibly nonconvex) quadratic function over a polyhedron:
where \(q: {\mathbb {R}}^n \rightarrow {\mathbb {R}}\) and \(F \subseteq {\mathbb {R}}^n\) are given by
Here, \(Q \in {\mathbb {R}}^{n \times n}\), \(c \in {\mathbb {R}}^n\), \(G \in {\mathbb {R}}^{n \times m}\), \(H \in {\mathbb {R}}^{n \times p}\), \(g \in {\mathbb {R}}^m\), and \(h \in {\mathbb {R}}^p\) constitute the parameters, and \(x \in {\mathbb {R}}^n\) denotes the decision variable. Without loss of generality, we assume that Q is a symmetric matrix. We denote the optimal value of (QP) by \(\ell ^* \in {\mathbb {R}}\cup \{-\infty \} \cup \{+\infty \}\), with the usual conventions for infeasible and unbounded problems.
Quadratic programs constitute an important class of problems in global optimization and they arise in a wide variety of applications, ranging from support vector machines and portfolio optimization to various combinatorial optimization problems such as the maximum stable set problem and the MAX-CUT problem. We refer the reader to [1] and the references therein. In addition, quadratic programs also appear as subproblems in sequential quadratic programming algorithms for solving more general classes of nonlinear optimization problems (see, e.g., [2]).
It is well-known that quadratic programs, in general, are NP-hard (see, e.g., [3, 4]). As such, global optimization algorithms for quadratic programs are generally based on spatial branch-and-bound methods. Convex relaxations play the crucial role of generating lower bounds in this framework.
In this paper, we focus on a linear programming relaxation of (QP) arising from the reformulation-and-linearization technique (RLT), henceforth referred to as the RLT relaxation [5]. The RLT relaxation is constructed in two stages. The reformulation stage consists of generating quadratic constraints that are implied by the linear constraints in F. Such quadratic constraints are obtained either by multiplying two linear inequality constraints, or by multiplying a linear equality constraint by a variable. In the linearization stage, the resulting implied quadratic constraints are linearized by introducing a new variable for each quadratic term. Finally, the substitution of quadratic terms in the objective function of (QP) with the new variables gives rise to the RLT relaxation, whose optimal value, denoted by \(\ell _R^*\), yields a lower bound on \(\ell ^*\). We say that the RLT relaxation is exact if \(\ell _R^* = \ell ^*\).
We investigate the relations between the polyhedral properties of the feasible region F of (QP) given by (2) and that of its RLT relaxation, denoted by \({{\mathcal {F}}}\). In particular, we focus on the relations between recession directions, boundedness, and vertices of the two feasible regions. As a byproduct of our analysis, we obtain a complete algebraic description of the set of instances of (QP) that admit an exact RLT relaxation. We also discuss how our results can be used to construct an instance of (QP) that admits an exact, inexact, or unbounded RLT relaxation. Our contributions are as follows:
-
1.
For a certain family of instances of (QP), we show that the RLT relaxation can be simplified by identifying a set of redundant RLT constraints.
-
2.
We show that various properties of F such as boundedness and existence of vertices directly translate to \({{\mathcal {F}}}\).
-
3.
We present simple procedures for constructing recession directions and vertices of \({{\mathcal {F}}}\) from their counterparts in F.
-
4.
For a certain subclass of quadratic programs, we obtain a complete description of the set of all vertices of \({{\mathcal {F}}}\). By observing that every quadratic program can be equivalently reformulated in this form, we discuss the implications of this observation on RLT relaxations of general quadratic programs.
-
5.
We present a complete description of the set of instances that admit an exact RLT relaxation.
-
6.
By using the aforementioned exactness characterization together with the optimality conditions of the RLT relaxation, we present simple algorithmic procedures to construct an instance of (QP) with an exact, inexact, or unbounded RLT relaxation.
We consider the polyhedron F in the general form given by (2) as opposed to a more convenient form such as the standard form for the following reasons. First, many classes of problems such as quadratic programs with box constraints and standard quadratic programs have an associated natural formulation, and converting it to another form generally requires the introduction of additional variables and/or constraints. Such a conversion increases the dimension of the corresponding RLT relaxation, which, in turn, increases the computational cost of solving the relaxation. Second, such a conversion may change the polyhedral structure of the feasible region of (QP). For instance, a nonempty polyhedron F given by (2) may not have any vertices but any nonempty polyhedron in standard form necessarily has at least one vertex. On the other hand, our goal in this paper is to identify the relations between the polyhedral properties of the original feasible region F and those of \({{\mathcal {F}}}\). Third, as we shall illustrate in Sect. 3.3.2, the RLT relaxations arising from two equivalent formulations may not necessarily be equivalent. As such, we adopt the general description given by (2).
This paper is organized as follows. We review the literature in Sect. 1.1 and define our notation in Sect. 1.2. We present basic results about polyhedra in Sect. 2. We introduce the RLT relaxation and discuss its polyhedral properties in Sect. 3. Section 4 is devoted to the discussion of duality and optimality conditions of the RLT relaxation. We introduce the convex underestimators induced by the RLT relaxation and present a complete description of the set of instances that admit an exact RLT relaxation in Sect. 5. We discuss how our results can be used to efficiently construct instances of (QP) with exact, inexact, or unbounded RLT relaxations in Sect. 6. Finally, Sect. 7 concludes the paper.
1.1 Literature review
In this section, we briefly review the relevant literature.
The ideas that led to the RLT relaxation were developed by several authors in a series of papers. To the best of our knowledge, the terminology first appears in [6], where the authors develop a branch-and-bound method based on RLT relaxations for solving bilinear quadratic programs, i.e., instances of (QP) for which all the diagonal entries of Q are equal to zero. In [7], this approach is extended to general quadratic programs and several properties of the RLT relaxation are established. The RLT relaxation has been extended to more general classes of discrete and nonconvex optimization problems (see, e.g., [5]).
RLT relaxations of quadratic programs can be further strengthened by adding a set of convex quadratic constraints [7] or by adding semidefinite constraints [8], referred to as the SDP-RLT relaxation. The latter relaxation usually provides much tighter bounds than the RLT relaxation at the expense of significantly higher computational effort. Furthermore, a continuum of linear programming relaxations between the RLT relaxation and the SDP-RLT relaxation can be obtained by viewing the semidefinite constraint as an infinite number of linear constraints and adding these linear cuts in a cutting plane framework [9]. Alternatively, by using another representation as an infinite number of second-order conic constraints, one can obtain a sequence of second-order conic relaxations that are provably tighter than their linear programming counterparts [10]. In terms of computational cost, second-order conic relaxations roughly lie between cheaper linear programming relaxations and more expensive semidefinite programming relaxations. Alternative convex relaxations can be obtained by relying on the observation that every quadratic program can be equivalently formulated as an instance of a copositive optimization problem [11], which is a convex but NP-hard problem. Nevertheless, the copositive cone can be approximated by various sequences of tractable convex cones, each of which gives rise to relaxation hierarchies that are exact in the limit. We refer the reader to [12] for a unified treatment of a rather large family of convex relaxations arising from the copositive formulation, and to [13,14,15] for comparisons of various convex relaxations.
Despite the fact that there exist many convex relaxations that are provably at least as tight as the RLT relaxation, the latter is used extensively in global optimization algorithms (see, e.g., [5, 16, 17]) due to the fact that state-of-the-art linear programming solvers can usually scale very well with the size of the problem. Furthermore, they are generally much more numerically stable than second-order conic programming and semidefinite programming solvers that are required for solving tighter relaxations. As such, RLT relaxations play a central role in global solution algorithms for nonconvex optimization problems, which motivates our focus on their polyhedral properties.
Recently, the authors of this paper studied RLT and SDP-RLT relaxations of quadratic programs with box constraints, which is a special case of (QP) [18]. They presented algebraic descriptions of instances that admit exact RLT relaxations as well as those that admit exact SDP-RLT relaxations. Using these descriptions, they proposed simple algorithmic procedures for constructing instances with exact or inexact RLT and SDP-RLT relaxations. Some of our results in this paper can be viewed as extensions of the corresponding results in [18] to general quadratic programs. In contrast with [18], where the focus is on the specific class of quadratic programs with box constraints, our main focus in this paper is on the relations between the polyhedral properties of general quadratic programs and their RLT relaxations as well as the interplay between such properties and the quality of the RLT relaxation.
1.2 Notation
We use \({\mathbb {R}}^n\), \({\mathbb {R}}^n_+\), \({\mathbb {R}}^{m \times n}\), \({{\mathcal {S}}}^n\), and \({{\mathcal {N}}}^n\) to denote the n-dimensional Euclidean space, the nonnegative orthant, the set of \(m \times n\) real matrices, the space of \(n \times n\) real symmetric matrices, and the cone of componentwise nonnegative \(n \times n\) real symmetric matrices, respectively. We use 0 to denote the real number 0, the vector of all zeroes, as well as the matrix of all zeroes, which should always be clear from the context. We denote by \(e \in {\mathbb {R}}^n\) the vector of all ones. All inequalities on vectors or matrices are componentwise. The rank of a matrix \(A \in {\mathbb {R}}^{m \times n}\) is denoted by \(\text {rank}(A)\). We use \(\text {conv}(\cdot )\), \(\text {cone}(\cdot )\), and \(\text {span}(\cdot )\) to denote the convex hull, conic hull, and the collection of all linear combinations of a set, respectively. For \(x \in {\mathbb {R}}^n\), \(B \in {\mathbb {R}}^{m \times n}\), and two index sets \({\textbf{J}} \subseteq \{1,\ldots ,m\}\) and \({\textbf{K}} \subseteq \{1,\ldots ,n\}\), we denote by \(x_{\textbf{K}} \in {\mathbb {R}}^{|{\textbf{K}}|}\) the subvector of x restricted to the indices in \({\textbf{K}}\) and by \(B_{{\textbf{J}}{\textbf{K}}} \in {\mathbb {R}}^{|{\textbf{J}}|\times |{\textbf{K}}|}\) the submatrix of B whose rows and columns are indexed by \({\textbf{J}}\) and \({\textbf{K}}\), respectively, where \(|\cdot |\) denotes the cardinality of a finite set. We use \(x_j\) and \(Q_{ij}\) for singleton index sets. For any \(U \in {\mathbb {R}}^{m \times n}\) and \(V \in {\mathbb {R}}^{m \times n}\), the trace inner product is denoted by
2 Preliminaries
In this section, we review basic facts about polyhedra. We refer the reader to [19] for proofs and further results.
Let \(F \subseteq {\mathbb {R}}^n\) be a nonempty polyhedron given by (2). The recession cone of F, denoted by \(F_\infty \subseteq {\mathbb {R}}^n\), is given by
Note that \(F_\infty \) is a polyhedral cone. By the Minkowski-Weyl Theorem, it is finitely generated, i.e., there exists \(d^j \in {\mathbb {R}}^n,~j = 1,\ldots ,t\) such that
Recall that a hyperplane \(\{x \in {\mathbb {R}}^n: a^T x = \alpha \}\), where \(a \in {\mathbb {R}}^n {\backslash \{0\}}\) and \(\alpha \in {\mathbb {R}}\), is a supporting hyperplane of F if \(\alpha = \min \{a^T x: x \in F\}\). A set \(F_0 \subseteq F\) is a nonempty face of F if \(F_0 = F\) or \(F_0\) is given by the intersection of F with a supporting hyperplane. In particular, \(F_0 \subseteq F\) is a face of F if and only if there exists a (possibly empty) submatrix \(G^0 \in {\mathbb {R}}^{n \times m_0}\) of G, where \(m_0 \le m\), such that
where \(g^0 \in {\mathbb {R}}^{m_0}\) denotes the corresponding subvector of g. In particular, \(F_0\) is a minimal face of F if and only if it is an affine subspace, i.e., if and only if there exists a submatrix \(G^0 \in {\mathbb {R}}^{n \times m_0}\) of G, where \(m_0 \le m\), and a corresponding subvector \(g^0 \in {\mathbb {R}}^{m_0}\) of g such that
Let
The dimension of each minimal face \(F_0 \subseteq F\) is equal to \(n - \rho \). Note that every polyhedron has a finite number of minimal faces. In particular, if \(\rho = n\), then each minimal face \(F_0 \subseteq F\) consists of a single point called a vertex. This gives rise to the following useful characterizations of vertices.
Lemma 1
Let \(F \subseteq {\mathbb {R}}^n\) be a nonempty polyhedron given by (2) and let \({\hat{x}} \in F\). Then, the following statements are equivalent:
-
(i)
\({\hat{x}}\) is a vertex of F.
-
(ii)
\({\hat{x}} - {\hat{d}} \in F\) and \({\hat{x}} + {\hat{d}} \in F\) if and only if \({\hat{d}} = 0\).
-
(iii)
There exists a partition of \(G = \begin{bmatrix} G^0&G^1\end{bmatrix}\) and a corresponding partition of \(g^T = \begin{bmatrix} (g^0)^T&(g^1)^T \end{bmatrix}\) such that \((G^0)^T {\hat{x}} = g^0\), \((G^1)^T {\hat{x}} < g^1\), and the matrix \(\begin{bmatrix} G^0&H \end{bmatrix}\) has full row rank.
-
(iv)
There exists \(a \in {\mathbb {R}}^n\) such that \({\hat{x}}\) is the unique optimal solution of \(\min \{a^T x: x \in F\}\).
Next, we collect several results concerning the recession cone \(F_\infty \) given by (3).
Lemma 2
Let \(F \subseteq {\mathbb {R}}^n\) be a nonempty polyhedron given by (2). Then, the following statements are equivalent:
-
(i)
F has no vertices.
-
(ii)
F contains a line.
-
(iii)
\(\rho < n\), where \(\rho \) is defined as in (7).
-
(iv)
There exists \({\hat{d}} \in {\mathbb {R}}^n \backslash \{0\}\) such that \({\hat{d}} \in F_\infty \) and \(-{\hat{d}} \in F_\infty \) (i.e., \(F_\infty \) contains a line).
-
(v)
\(F_\infty \) has no vertices.
Recall that F is a polytope if it is bounded. In this case, \(F_\infty = \{0\}\). We next state a useful characterization of polytopes.
Lemma 3
Let \(F \subseteq {\mathbb {R}}^n\) be a nonempty polyhedron given by (2). Then, F is bounded if and only if, for every \(z \in {\mathbb {R}}^n\), there exists \((u,v) \in {\mathbb {R}}^m \times {\mathbb {R}}^p\) such that
Proof
Since F is nonempty, the boundedness of F is equivalent to
Therefore, F is bounded if and only if, for every \(z \in {\mathbb {R}}^n\), the optimal value of the linear programming problem
is equal to zero. The assertion follows from linear programming duality. \(\square \)
Finally, we close this section with a useful decomposition result.
Lemma 4
Let \(F \subseteq {\mathbb {R}}^n\) be a nonempty polyhedron given by (2), and let \(F_i \subseteq F,~i = 1,\ldots ,s\) denote the set of minimal faces of F. Then,
where \(v^i \in F_i,~i = 1,\ldots ,s\), and \(F_\infty \) is given by (3).
3 Polyhedral properties of RLT relaxations
In this section, given an instance of (QP), we introduce the corresponding RLT (reformulation–linearization technique) relaxation and make some observations about the RLT procedure. We then focus on the relations between the polyhedral properties of the feasible region of (QP) and that of its RLT relaxation. We establish several connections between recession directions, boundedness, and vertices of the two feasible regions. For a specific class of quadratic programs, we give a complete characterization of the set of vertices of the feasible region of the RLT relaxation. We finally discuss the implications of this observation on RLT relaxations of general quadratic programs.
3.1 RLT relaxations
Recall that an instance of (QP) is completely specified by the objective function q(x) and the feasible region F given by (1) and (2), respectively. The RLT relaxation of (QP) is obtained by generating quadratic constraints implied by linear constraints. Such quadratic constraints are obtained by multiplying each pair of linear inequality constraints and by multiplying each linear equality constraint by a variable. The resulting quadratic constraints and the objective function are then linearized by substituting each quadratic term \(x_i x_j\) by a new variable \(X_{ij},~i = 1,\ldots ,n; j = 1,\ldots ,n\).
For a given instance of (QP), the RLT relaxation of (QP) is therefore given by
where
Note that (RLT) is a linear programming relaxation of (QP) since the objective function and all constraints are linear functions of \((x,X) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n\) and, for each \({\hat{x}} \in F\), we have \(({\hat{x}}, {\hat{x}} {\hat{x}}^T) \in {{\mathcal {F}}}\) with the same objective function value. Therefore,
We remark that every other quadratic constraint that can be generated by the pairwise multiplication of linear constraints in F is already implied by \({{\mathcal {F}}}\) (see also [7, Remark 1]). Indeed, consider the RLT constraints obtained by multiplying each pair of equality constraints given by \(H^T X H - H^T x h^T - h x^T H + h h^T = 0\) as well as those arising from the multiplication of each inequality and equality constraint given by \(h g^T - h x^T G - H^T x g^T + H^T X G = 0\). It is easy to see that both are implied by the constraints \(H^T x = h\) and \(H^T X = h x^T\).
An interesting question is whether all constraints in (10) are, in fact, necessary for the RLT relaxation. Our next result identifies a family of instances of (QP) for which \({{\mathcal {F}}}\) can be simplified without affecting the lower bound \(\ell ^*_R\).
Proposition 5
Suppose that F given by (2) is nonempty and that \(G \in {\mathbb {R}}^{n \times m}\) and \(H \in {\mathbb {R}}^{n \times p}\) can be permuted into the following block diagonal form:
where \(G^i \in {\mathbb {R}}^{n_i \times m_i}\) and \(H^i \in {\mathbb {R}}^{n_i \times p_i},~i = 1,\ldots ,k\). Suppose that \(Q \in {{\mathcal {S}}}^n\), \(g \in {\mathbb {R}}^m\), \(h \in {\mathbb {R}}^p\), and \(x \in {\mathbb {R}}^n\) are permuted accordingly so that
where \(Q^{ii} \in {{\mathcal {S}}}^{n_i}\), \(g^i \in {\mathbb {R}}^{m_i}\), \(h^i \in {\mathbb {R}}^{p_i}\), and \(x^i \in {\mathbb {R}}^{n_i}\) for each \(i = 1,\ldots ,k\), and \(Q^{ij} = (Q^{ji})^T \in {\mathbb {R}}^{n_i \times n_j}\) for each \(1 \le i < j \le k\). For \((x,X) \in {{\mathcal {F}}}\), suppose also that \(X^{ij}\) denotes the submatrix of X corresponding to \(Q^{ij},~i = 1,\ldots ,k;~j = 1,\ldots ,k\).
-
(i)
If \(Q^{ii} = 0\) for some \(i = 1,\ldots ,k\), then the RLT lower bound \(\ell ^*_R\) remains unchanged if the following RLT constraints are removed from \({{\mathcal {F}}}\):
$$\begin{aligned} (H^i)^T X^{ii}= & {} h^i (x^i)^T \\ (G^i)^T X^{ii} G^i - (G^i)^T x^i (g^i)^T - g^i (x^i)^T G^i + g^i (g^i)^T\ge & {} 0. \end{aligned}$$ -
(ii)
If \(Q^{ij} = 0\) for some \(1 \le i < j \le k\), then the RLT lower bound \(\ell ^*_R\) remains unchanged if the following RLT constraints are removed from \({{\mathcal {F}}}\):
$$\begin{aligned} (H^i)^T X^{ij}= & {} h^i (x^j)^T \\ (H^j)^T X^{ji}= & {} h^j (x^i)^T \\ (G^i)^T X^{ij} G^i - (G^i)^T x^i (g^j)^T - g^i (x^j)^T G^j + g^i (g^j)^T\ge & {} 0. \end{aligned}$$
Proof
We prove only (i) as the proof of (ii) is very similar. Let \({\bar{{{\mathcal {F}}}}} \subseteq {\mathbb {R}}^n \times {{\mathcal {S}}}^n\) denote the feasible region obtained from \({{\mathcal {F}}}\) by removing the two sets of constraints in (i) and let \({{\bar{\ell }}}\) denote the optimal value of the RLT relaxation over \({{\bar{{{\mathcal {F}}}}}}\). Clearly, \({{\bar{\ell }}} \le \ell ^*_R\) since \({{\mathcal {F}}}\subseteq {{\bar{{{\mathcal {F}}}}}}\). By (12) and the structure of the RLT constraints, note that \(X^{ii}\) is unrestricted in \({{\bar{{{\mathcal {F}}}}}}\). Therefore, for any \(({\bar{x}}, {\bar{X}}) \in {{\bar{{{\mathcal {F}}}}}}\), let us define \(x = {\bar{x}}\), \(X = {\bar{X}}\), and redefine \(X^{ii} = {\bar{x}}^i (\bar{x}^i)^T\). It is easy to verify that \((x,X) \in {{\mathcal {F}}}\) as it satisfies the two sets of constraints in (i). Furthermore, \(\textstyle \frac{1}{2}\langle Q, {\bar{X}} \rangle + c^T {\bar{x}} = \textstyle \frac{1}{2}\langle Q, X \rangle + c^T x\) since \(Q^{ii} = 0\). Therefore, for each feasible solution in \({{\bar{{{\mathcal {F}}}}}}\), there exists a corresponding feasible solution in \({{\mathcal {F}}}\) with the same objective function value. It follows that \({{\bar{\ell }}} = \ell ^*_R\), which completes the proof. \(\square \)
Under the assumptions of Proposition 5, one can compute the same RLT lower bound \(\ell ^*_R\) by instead solving a linear programming problem of a smaller dimension, which may considerably reduce the computational cost of solving (RLT). For instance, if \(F = \{x \in {\mathbb {R}}^n: 0 \le x_j \le 1, \quad j = 1,\ldots ,n\}\), it follows from Proposition 5 that one only needs to introduce the RLT constraints \(X_{ii} - x_i \le 0\), \(X_{ii} \ge 0\), and \(X_{ii} - 2 x_i + 1 \ge 0\) whenever \(Q_{ii} \ne 0,~i = 1,\ldots ,n\); and the RLT constraints \(X_{ij} - x_i \le 0\), \(X_{ij} - x_j \le 0\), \(X_{ij} \ge 0\), and \(X_{ij} - x_i - x_j + 1 \ge 0\) whenever \(Q_{ij} \ne 0,~1 \le i < j \le n\).
Henceforth, we assume that \(\mathcal{F}\) contains all the RLT constraints as given by (10) since Proposition 5 implies that the RLT lower bound is independent of the exclusion of unnecessary RLT constraints from \(\mathcal{F}\).
3.2 Recession cones and boundedness
In this section, we present several relations between the recession cones associated with the polyhedral feasible regions F and \({{\mathcal {F}}}\) of (QP) and (RLT), respectively. We also discuss the boundedness relation between F and \({{\mathcal {F}}}\).
Recall that the recession cone of F, denoted by \(F_\infty \), is given by (3). Similarly, we use \({{\mathcal {F}}}_\infty \) to denote the recession cone of \({{\mathcal {F}}}\), which is given by
Note that
Our next result gives a recipe for constructing recession directions of \({{\mathcal {F}}}\) from recession directions and elements of F.
Proposition 6
Let \(F \subseteq {\mathbb {R}}^n\) be a nonempty polyhedron given by (2) and let \(P = \begin{bmatrix} d^1&\cdots&d^t \end{bmatrix} \in {\mathbb {R}}^{n \times t}\), where \(d^1,\ldots ,d^t\) are defined as in (4). Then, for each \({\hat{d}} \in F_\infty \), each \({\hat{x}} \in F\), and each \({\hat{K}} \in {{\mathcal {N}}}^t\), we have \(({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \), where \({\hat{D}} = {\hat{x}} {\hat{d}}^T + {\hat{d}} {\hat{x}}^T + P {\hat{K}} P^T \in {{\mathcal {S}}}^n\).
Proof
Since \({\hat{d}} \in F_\infty \), we have \(G^T {\hat{d}} \le 0\) and \(H^T {\hat{d}} = 0\) by (3). Furthermore, we have
where we used \(H^T {\hat{x}} = h\), \(H^T {\hat{d}} = 0\), and \(H^T P = 0\). Finally,
where the last inequality follows from \(G^T {\hat{x}} \le g\), \(G^T {\hat{d}} \le 0\), \(G^T P \le 0\), and \({\hat{K}} \ge 0\). Therefore, \(({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \) by (13). \(\square \)
An interesting question is whether, for each \(({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \), there exist some \({\hat{x}} \in F\) and some \({\hat{K}} \in {{\mathcal {N}}}^t\) such that \({\hat{D}}\) can be expressed in the form given in Proposition 6. The following example illustrates that this is not the case.
Example 1
Let
i.e., \(n = 2\), \(m = 2\), \(p = 0\), and
Clearly,
Let \({\hat{d}} = 0 \in {\mathbb {R}}^2\) and
By (13), we have \(({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \) since \(G^T {\hat{D}} G = 0 \in {{\mathcal {S}}}^2\). On the other hand, for any \({\hat{x}} \in F\) and any \({\hat{K}} \in {{\mathcal {N}}}^2\), we obtain
which implies that \({\hat{D}}\) cannot be expressed in this form for any \({\hat{K}} \in {{\mathcal {N}}}^2\).
Next, we discuss the boundedness relation between F and \({{\mathcal {F}}}\).
Lemma 7
F is nonempty and bounded if and only if \({{\mathcal {F}}}\) is nonempty and bounded.
Proof
Suppose that F is nonempty and bounded. Then, \(F_\infty = \{0\}\). Clearly, \({{\mathcal {F}}}\) is nonempty since, for each \({\hat{x}} \in F\), we have \(({\hat{x}}, {\hat{x}} {\hat{x}}^T) \in {{\mathcal {F}}}\). Let \(({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \). By (14), we obtain \({\hat{d}} \in F_\infty \), which implies that \({\hat{d}} = 0\). By (13),
By Lemma 3, for every \(z^1 \in {\mathbb {R}}^n\) and \(z^2 \in {\mathbb {R}}^n\), there exist \(u^1 \in {\mathbb {R}}^m_+\), \(w^1 \in {\mathbb {R}}^p\), \(u^2 \in {\mathbb {R}}^m_+\), and \(w^2 \in {\mathbb {R}}^p\) such that \(G u^1 + H w^1 = z^1\) and \(G u^2 + H w^2 = z^2\). Therefore, for every \(z^1 \in {\mathbb {R}}^n\) and \(z^2 \in {\mathbb {R}}^n\),
where we used \(H^T {\hat{D}} = 0\), \(G^T {\hat{D}} G \ge 0\), \(u^1 \ge 0\), and \(u^2 \ge 0\). Since the inequality above holds for every \(z^1 \in {\mathbb {R}}^n\) and \(z^2 \in {\mathbb {R}}^n\), we obtain \({\hat{D}} = 0\). Therefore, \(({\hat{d}}, {\hat{D}}) = (0,0)\), which implies that \({{\mathcal {F}}}_\infty = \{(0,0)\}\). It follows that \({{\mathcal {F}}}\) is bounded.
Conversely, if \({{\mathcal {F}}}\) is nonempty and bounded, then F is nonempty and bounded since F is the projection of \({{\mathcal {F}}}\) onto the x-space. \(\square \)
3.3 Vertices
In this section, we focus on the relations between the vertices of F and those of \({{\mathcal {F}}}\). First, we consider the case in which F has no vertices.
Lemma 8
Suppose that F is nonempty. If F has no vertices, then \({{\mathcal {F}}}\) has no vertices.
Proof
By Lemma 2 (iv), there exists a nonzero \({\hat{d}} \in {\mathbb {R}}^n \backslash \{0\}\) such that \({\hat{d}} \in F_\infty \) and \(-{\hat{d}} \in F_\infty \). Let \({\hat{x}} \in F\) and define \({\hat{D}} = {\hat{x}} {\hat{d}}^T + {\hat{d}} {\hat{x}}^T\). By Proposition 6, we obtain \(({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \) and \(-({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \), which implies that \({{\mathcal {F}}}\) contains a line. By Lemma 2, \({{\mathcal {F}}}\) has no vertices. \(\square \)
Before we present the relations between the set of vertices of F and that of \({{\mathcal {F}}}\), we state a useful technical lemma that will be helpful in the remainder of this section.
Lemma 9
Let \(A \in {\mathbb {R}}^{n \times k}\) and \(Z \in {{\mathcal {S}}}^k\). Then, the system \(A^T W A = Z\) has a solution \(W \in {{\mathcal {S}}}^n\) if and only if the range space of Z is contained in the range space of \(A^T\). Furthermore, if A has full row rank, then the solution is unique.
Proof
If \(A^T W A = Z\) has a solution \(W \in {{\mathcal {S}}}^n\), then, for any \(y \in {\mathbb {R}}^k\), we have \(Z y = A^T (W A y)\), which implies that the range space of Z is contained in the range space of \(A^T\).
Conversely, let \(Z = \sum \nolimits _{j=1}^\kappa \lambda _j z^j (z^j)^T\) denote the eigenvalue decomposition of Z, where \(\kappa \le k\) denotes the rank of Z and \(z^j \in {\mathbb {R}}^k,~j = 1,\ldots ,\kappa \). By the hypothesis, the range space of Z, given by \(\text {span}\{z^1,\ldots ,z^\kappa \}\), is contained in the range space of \(A^T\). Therefore, for each \(j = 1,\ldots ,\kappa \), there exists \(u^j \in {\mathbb {R}}^n\) such that \(z^j = A^T u^j\). It follows that \(Z = A^T U \Lambda U^T A\), where \(U = \begin{bmatrix} u^1&\cdots&u^\kappa \end{bmatrix} \in {\mathbb {R}}^{n \times \kappa }\) and \(\Lambda \in {{\mathcal {S}}}^{\kappa }\) is a diagonal matrix whose entries are given by \(\lambda _1,\ldots ,\lambda _{\kappa }\). Therefore, \(W = U \Lambda U^T\) is a solution of \(A^T W A = Z\).
If A has full row rank, then the uniqueness of the solution \(W \in {{\mathcal {S}}}^n\) follows from the observation that the matrix U is uniquely determined. \(\square \)
We are now in a position to present the first relation between the set of vertices of F and that of \({{\mathcal {F}}}\).
Proposition 10
Suppose that F is nonempty. Let \({\hat{x}} \in F\) and \({\hat{X}} = {\hat{x}} {{\hat{x}}}^T \in {{\mathcal {S}}}^n\). Then, \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\) if and only if \({\hat{x}}\) is a vertex of F.
Proof
For each \({\hat{x}} \in F\), we clearly have \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\), where \({\hat{X}} = {\hat{x}} {{\hat{x}}}^T \in {{\mathcal {S}}}^n\).
First, suppose that \({\hat{x}} \in {\mathbb {R}}^n\) is a vertex of F. Let \(G^0 \in {\mathbb {R}}^{n \times m_0}\) and \(G^1 \in {\mathbb {R}}^{n \times m_1}\) denote the submatrices of G, where \(m_0 + m_1 = m\), and let \(g^0 \in {\mathbb {R}}^{m_0}\) and \(g^1 \in {\mathbb {R}}^{m_1}\) denote the corresponding subvectors of g such that
First, we identify the set of active constraints of (RLT) at \(({\hat{x}}, {\hat{X}})\):
where \(r^1 = g^1 - (G^1)^T {\hat{x}} > 0\). Therefore, \(r^1 (r^1)^T\) is componentwise strictly positive.
By Lemma 1 (iii), it suffices to show that the system
where \(({\hat{d}}, {\hat{D}}) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n\), has a unique solution \(({\hat{d}}, {\hat{D}}) = (0,0)\).
Since \({\hat{x}}\) is a vertex of F, the matrix \(\begin{bmatrix} G^0&H \end{bmatrix}\) has full row rank by Lemma 1 (iii). Therefore, we obtain \({\hat{d}} = 0\) from the first two equations. Substituting \({\hat{d}} = 0\) into the third and fourth equations, we obtain
where we used \(H^T {\hat{D}} = 0\) by the third equation. By Lemma 9, we obtain \({\hat{D}} = 0\), which implies that \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\).
Conversely, suppose that \({\hat{x}}\) is not a vertex of F. By Lemma 1 (ii), there exists a nonzero \({\hat{d}} \in {\mathbb {R}}^n\) such that each of \({\hat{d}}\) and \(-{\hat{d}}\) is a feasible direction at \({\hat{x}} \in F\). Using the same partition as in (15), we obtain
Let \({\hat{D}} = {\hat{d}} {\hat{x}}^T + {\hat{x}} {\hat{d}}^T \in {{\mathcal {S}}}^n\). We claim that each of \(({\hat{d}}, {\hat{D}})\) and \(-({\hat{d}}, {\hat{D}})\) is a feasible direction at \(({\hat{x}}, {\hat{X}})\). Indeed,
Furthermore, since \((G^1)^T {\hat{x}} < g^1\) and \((G^1)^T {\hat{X}} G^1 - (G^1)^T {\hat{x}} (g^1)^T - g^1 {\hat{x}}^T G^1 + g^1 (g^1)^T = r^1 (r^1)^T > 0\), where \(r^1 = g^1 - (G^1)^T {\hat{x}} > 0\), it follows that there exists a real number \(\epsilon > 0\) such that \(({\hat{x}}, {\hat{X}}) + \epsilon ({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}\) and \(({\hat{x}}, {\hat{X}}) - \epsilon ({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}\), which implies that \(({\hat{x}}, {\hat{X}})\) is not a vertex of \({{\mathcal {F}}}\) by Lemma 1 (ii). \(\square \)
By Proposition 10, for each vertex \({\hat{x}} \in F\), there is a corresponding vertex \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\), where \({\hat{X}} = {\hat{x}} {\hat{x}}^T\). We therefore obtain the following result.
Corollary 11
Suppose that F is nonempty. The set of vertices of F is nonempty if and only if the set of vertices of \({{\mathcal {F}}}\) is nonempty.
Proof
The result immediately follows from Lemma 8 and Proposition 10. \(\square \)
Next, we identify another connection between the set of vertices of \({{\mathcal {F}}}\) and the set of vertices of F.
Proposition 12
Let \(v^1 \in F\) and \(v^2 \in F\) be two vertices such that \(v^1 \ne v^2\). Let \({\hat{x}} = \textstyle \frac{1}{2}(v^1 + v^2)\) and \({\hat{X}} = \textstyle \frac{1}{2}\left( v^1 (v^2)^T + v^2 (v^1)^T\right) \). Then, \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\).
Proof
Let \(v^1 \in F\) and \(v^2 \in F\) be two vertices. Let \({\hat{x}} = \textstyle \frac{1}{2}(v^1 + v^2)\) and \({\hat{X}} = \textstyle \frac{1}{2}\left( v^1 (v^2)^T + v^2 (v^1)^T\right) \). First, we verify that \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\). Clearly, we have
Let us define
Then, we obtain
where we used (16). Therefore, \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\).
Next, we show that \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\). We define the following submatrices of G and the corresponding subvectors of g:
We remark that \(G^1\) and \(G^2\) are nonempty submatrices of G since \(v^1 \ne v^2\). By (16) and (17), we can identify the set of active constraints of (RLT) at \(({\hat{x}}, {\hat{X}})\):
where, in the last equation, we assume without loss of generality that \(G = \begin{bmatrix} G^0&G^1&G^2&G^3 \end{bmatrix}\) and g is partitioned accordingly, and \(+\) denotes a submatrix with strictly positive entries.
Therefore, by Lemma 1 (iii), it suffices to show that the system
where \(({\hat{d}}, {\hat{D}}) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n\), has a unique solution \(({\hat{d}}, {\hat{D}}) = (0,0)\).
Therefore, \(({\hat{d}}, {\hat{D}})\) should simultaneously solve the following two systems:
Substituting \((G^0)^T v^1 = g^0\) and \(H^T v^1 = h\) into the first equation, and \((G^0)^T v^2 = g^0\) and \(H^T v^2 = h\) into the second one, we obtain
Since \(v^1\) and \(v^2\) are vertices of F, Lemma 1 (iii) implies that each of the two matrices \(\begin{bmatrix} G^0&G^1&H \end{bmatrix} \) and \(\begin{bmatrix} G^0&G^2&H \end{bmatrix}\) has full row rank. By Lemma 9, we obtain
which implies that \((v^1 - v^2) {\hat{d}}^T + {\hat{d}} (v^1 - v^2)^T = 0\). Since \(v^1 \ne v^2\), we obtain \({\hat{d}} = 0\). Substituting this into the matrix equations above, we obtain \({\hat{D}} = 0\) by Lemma 9, which proves the assertion. \(\square \)
Propositions 10 and 12 identify two sets of vertices of \({{\mathcal {F}}}\) under the assumption that F contains at least one vertex. An interesting question is whether every vertex of \({{\mathcal {F}}}\) belongs to one of these two sets. The following example illustrates that this is not necessarily true even when F is a polytope.
Example 2
Let \(n = 2\) and
i.e., we have \(p = 0\), \(m = 4\), \(G = \begin{bmatrix} I&- I \end{bmatrix}\), and \(g^T = \begin{bmatrix} e^T&{0^T} \end{bmatrix}\), where \(e \in {\mathbb {R}}^2\), \(0 \in {\mathbb {R}}^2\), and \(I \in {{\mathcal {S}}}^2\) denotes the identity matrix. F has four vertices given by
The feasible region of the RLT relaxation is given by
By Proposition 10, there are four vertices of \({{\mathcal {F}}}\) in the form of \((v^j,v^j (v^j)^T),~j = 1,\ldots ,4\). Similarly, by Proposition 12, \({{\mathcal {F}}}\) has another set of six vertices in the form of
We now claim that \({{\mathcal {F}}}\) has at least one other vertex that does not belong to these two sets. Consider \(({\hat{x}}, {\hat{X}}) \in {\mathbb {R}}^2 \times {{\mathcal {S}}}^2\) given by
It is easy to verify that \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) and that \(({\hat{x}}, {\hat{X}})\) does not belong to either of the two sets of vertices identified by Proposition 10 and Proposition 12. It is an easy exercise to show that \(({\hat{x}}, {\hat{X}}) \pm ({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}\) if and only if \(({\hat{d}}, {\hat{D}}) = (0,0)\). Therefore, we conclude that \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\) by Lemma 1 (ii).
By Example 2, the two sets of vertices identified in Propositions 10 and 12 do not necessarily encompass all vertices of \({{\mathcal {F}}}\) in general even if F is a polytope. In the next section, we identify a subclass of quadratic programs for which all vertices of \({{\mathcal {F}}}\) are completely characterized by Propositions 10 and 12. We then discuss the implications of this observation on general quadratic programs.
3.3.1 A specific class of quadratic programs
In this section, we present a specific class of quadratic programs with the property that all vertices of the feasible region \({{\mathcal {F}}}\) of the RLT relaxation are precisely given by the union of the two sets identified in Propositions 10 and 12.
Consider the class of instances of (QP), where \(Q \in {{\mathcal {S}}}^n\), \(c \in {\mathbb {R}}^n\), and
Therefore, the feasible region is given by
Let us define the following index sets:
It is straightforward to verify that the set of vertices of F is
The feasible region \({{\mathcal {F}}}\) of the corresponding RLT relaxation is given by
We next present our main result in this section.
Proposition 13
Suppose that \({{\mathcal {F}}}\) is given by (25), where \(a \in {\mathbb {R}}^n_+ \backslash \{0\}\). Then, \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\) if and only if \(({\hat{x}}, {\hat{X}}) = (v,vv^T)\) for some \(v \in V\), where V is given by (24), or \(({\hat{x}}, {\hat{X}}) = \left( \textstyle \frac{1}{2}(v^1 + v^2), \textstyle \frac{1}{2}(v^1 (v^2)^T + v^{2} (v^1)^T)\right) \) for some \(v^1 \in V\), \(v^2 \in V\), and \(v^1 \ne v^2\).
Proof
By Propositions 10 and 12, it suffices to prove the forward implication.
Let us first define
where \({\textbf{P}}\) is given by (22). By (24) and Propositions 10 and 12, it follows that each of \((w^k,W^k),~k \in {\textbf{P}}\), and \((z^{ij},Z^{ij}),~i \in {\textbf{P}}, ~j \in {\textbf{P}}, ~i \ne j\), is a vertex of \({{\mathcal {F}}}\).
Let \(({\hat{x}}, {\hat{X}})\) be a vertex of \({{\mathcal {F}}}\). By (25) and (22), we obtain
First, we claim that \({\hat{x}}_{{\textbf{Z}}} = 0\), \({\hat{X}}_{{\textbf{P}}{\textbf{Z}}} = 0\), \({\hat{X}}_{{\textbf{Z}}{\textbf{P}}} = 0\), and \({\hat{X}}_{{\textbf{Z}}{\textbf{Z}}} = 0\). Indeed, by (30), if any of these conditions is not satisfied, it is easy to construct a nonzero \(({\hat{d}}, {\hat{D}}) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n\) such that \(({\hat{x}}, {\hat{X}}) \pm ({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}\), which would contradict that \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\) by Lemma 1 (ii). Therefore,
where \(\mu _k = {\hat{X}}_{kk} \, a_k^2 \ge 0,~k \in {\textbf{P}}\); \(\lambda _{ij} = {\hat{X}}_{ij} \, a_i a_j \ge 0,~i \in {\textbf{P}},~j \in {\textbf{P}},~i \ne j\); \(W^k\) and \(Z^{ij}\) are defined as in (27) and (29), respectively. By using \(W^k a = w^k,~k \in {\textbf{P}}\); \(Z^{ij} a = z^{ij},~i \in {\textbf{P}},~j \in {\textbf{P}},~i \ne j\); and (25), the previous equality implies that
By (30), we obtain
Therefore, \(({\hat{x}}, {\hat{X}})\) is given by a convex combination of \((w^k,W^k),~k \in {\textbf{P}}\), and \((z^{ij},Z^{ij}),~i \in {\textbf{P}}, ~j \in {\textbf{P}}, ~i \ne j\). By Propositions 10 and 12, we conclude that either \(({\hat{x}}, {\hat{X}}) = (w^k,W^k)\) for some \(k \in {\textbf{P}}\), or \(({\hat{x}}, {\hat{X}}) = (z^{ij},Z^{ij})\) for some \(i \in {\textbf{P}}, ~j \in {\textbf{P}}, ~i \ne j\). This completes the proof. \(\square \)
Our next result gives a closed-form expression of the lower bound \(\ell ^*_R\) for an instance of (QP) in this specific class.
Corollary 14
Consider an instance of (QP), where F is given by (21) and \(a \in {\mathbb {R}}^n_+ \backslash \{0\}\). If \(\ell ^*_R\) is finite, then
where V is given by (24).
Proof
If \(\ell ^*_R\) is finite, the relation (31) follows from Proposition 13 since (RLT) is a linear programming problem and the optimal value is attained at a vertex. \(\square \)
We close this section with a discussion of a well-studied class of quadratic programs that belong to the specific class of quadratic programs identified in this section. An instance of (QP) is referred to as a standard quadratic program (see, e.g., [20]) if
Therefore, the feasible region of a standard quadratic program is the unit simplex given by
Similarly, the feasible region of the RLT relaxation of a standard quadratic program is given by
Proposition 13 gives rise to the following result on standard quadratic programs.
Corollary 15
Consider an instance of a standard quadratic program and let \({{\mathcal {F}}}\) denote the feasible region of the RLT relaxation given by (34). Then, \(({\hat{x}}, {\hat{X}})\) is a vertex of \({{\mathcal {F}}}\) if and only if \(({\hat{x}}, {\hat{X}}) = (e^j,e^j (e^j)^T)\) for some \(j = 1,\ldots ,n\), or \(({\hat{x}}, {\hat{X}}) = \left( \textstyle \frac{1}{2}(e^i + e^j), \textstyle \frac{1}{2}\left( e^i (e^j)^T + e^j (e^i)^T\right) \right) \) for some \(1 \le i < j \le n\). Furthermore,
Proof
The first assertion follows from Proposition 13 and (24) by using \(a = e \in {\mathbb {R}}^n_+ \backslash \{0\}\), and the second one from Lemma 7 and Corollary 14 since F is bounded. \(\square \)
In [21], using an alternative copositive formulation of standard quadratic programs in [22], a hierarchy of linear programming relaxations arising from the sequence of polyhedral approximations of the copositive cone proposed by [23] was considered and the same lower bound given by Corollary 15 was established for the first level of the hierarchy. Therefore, it is worth noting that the relaxation arising from the copositive formulation turns out to be equivalent to the RLT relaxation arising from the usual formulation of standard quadratic programs as an instance of (QP).
3.3.2 Implications on general quadratic programs
In Sect. 3.3.1, we identified a specific class of quadratic programs with the property that Propositions 10 and 12 completely characterize the set of all vertices of the feasible region of the corresponding RLT relaxation. In this section, we first observe that every quadratic program can be equivalently formulated as an instance of (QP) in this class. We then discuss the implications of this observation on RLT relaxations of general quadratic programs.
Consider a general quadratic program, where F given by (2) is nonempty. By Lemma 4 and (4),
where \(v^i \in F_i,~i = 1,\ldots ,s\), and each \(F_i \subseteq F,~i = 1,\ldots ,s\), denotes a minimal face of F, and \(d^1,\ldots ,d^t\) are the generators of \(F_\infty \). Let us define
By (35) and (36), \({\hat{x}} \in F\) if and only if there exists \(y \in {\mathbb {R}}^s_+\) and \(z \in {\mathbb {R}}^{t}_+\) such that \(e^T y = 1\) and \({\hat{x}} = My + Pz\). Therefore, (QP) admits the following alternative formulation:
We conclude that every quadratic program admits an equivalent reformulation as an instance in the specific class identified in Sect. 3.3.1. However, we remark that this equivalence is mainly of theoretical interest since such a reformulation requires the enumeration of all minimal faces of F and all generators of \(F_\infty \), each of which may have an exponential size.
Nevertheless, in this section, we will discuss the relations between the RLT relaxation of (QP) and that of the alternative formulation (QPA) and draw some conclusions.
Let us introduce the following notations:
Therefore, (QPA) can be expressed by
where
Similarly, the RLT relaxation of (QPA) is given by
where
We now present the first relation between the RLT relaxations of (QP) and (QPA) given by (RLT) and (RLTA), respectively.
Proposition 16
Consider a general quadratic program, where F given by (2) is nonempty. Then, \(\ell ^*_R \le \ell ^*_{RA} \le \ell ^*\).
Proof
Let \(({\hat{x}}_A, {\hat{X}}_A) \in {{\mathcal {F}}}_A\) be an arbitrary feasible solution of (RLTA). We will construct a corresponding feasible solution \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) of (RLT) with the same objective function value. Let
where M and P are defined as in (36). By (35) and (40), we conclude that \({\hat{x}} \in F\), i.e., \(G^T {\hat{x}} \le g\) and \(H^T {\hat{x}} = h\).
Since \(G^T v^i \le g\) for each \(i = 1,\ldots ,s\), and \(G^T d^j \le 0\) for each \(j = 1,\ldots ,t\), we obtain
where we used (36) and (40). Since \({\hat{X}}_A \ge 0\), we have
where we used (43) and (44) in the second line.
Since \(H^T v^i = h\) for each \(i = 1,\ldots ,s\), and \(H^T d^j = 0\) for each \(j = 1,\ldots ,t\), we obtain
where we used (36) and (40). Therefore,
where we used (43) and (44) in the third line. Therefore, \(({\hat{x}}, {\hat{X}}) \in \mathcal {F}\). Furthermore,
where we used (44) in the first line, and (38) and (39) in the second line. Therefore, for each \(({\hat{x}}_A, {\hat{X}}_A) \in {{\mathcal {F}}}_A\), there exists a corresponding solution \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) with the same objective function value. We conclude that \(\ell ^*_R \le \ell ^*_{RA} \le \ell ^*\). \(\square \)
By Proposition 16, the RLT relaxation (RLTA) of the alternative formulation (QPA) is at least as tight as the RLT relaxation (RLT) of the original formulation (QP). An interesting question is whether the lower bounds arising from the two relaxations are in fact equal (i.e., \(\ell ^*_R = \ell ^*_{RA}\)). Our next example illustrates that this is, in general, not true.
Example 3
Consider the following instance of (QP) for \(n = 2\), where
and
i.e., we have \(p = 0\), \(m = 4\), \(G = \begin{bmatrix} I&- I \end{bmatrix}\), and \(g^T = \begin{bmatrix} e^T&{0^T} \end{bmatrix}\), where \(e \in {\mathbb {R}}^2\), \(0 \in {\mathbb {R}}^2\), and \(I \in {{\mathcal {S}}}^2\) denotes the identity matrix. For the RLT relaxation of the original formulation, we obtain \(\ell ^*_R = -\textstyle \frac{3}{2}\), and an optimal solution is given by (19). By (18), we have \(F = \text {conv}\left( \{v^1,\ldots ,v^4\}\right) \). Defining \(M = \begin{bmatrix} v^1 \cdots v^4 \end{bmatrix} \in {\mathbb {R}}^{2 \times 4}\) and using (38), (39), and (40), we obtain
Therefore, (QP) can be equivalently formulated as (QPA), which is an instance of a standard quadratic program. By Corollary 15, we have \(\ell ^*_{RA} = -1\) and an optimal solution is
Therefore, we obtain \(\ell ^*_R = -\textstyle \frac{3}{2} < -1 = \ell ^*_{RA}\). In fact, for this instance of (QP), we have \(\ell ^* = -1\), which is attained at \(x^* = \begin{bmatrix} 1&0 \end{bmatrix}^T\). Therefore, the RLT relaxation (RLTA) of the alternative formulation (QPA) is not only tighter than that of the original formulation but is, in fact, an exact relaxation.
As illustrated by Example 3, despite the fact that (QP) and (QPA) are equivalent formulations, (RLTA) may lead to a strictly tighter relaxation of (QP) than (RLT). Therefore, we conclude that the quality of the RLT relaxation may depend on the particular formulation. Recall, however, that the alternative formulation (QPA) may, in general, have an exponential size. We close this section with the following result on the RLT relaxation of the original formulation.
Corollary 17
Consider a general quadratic program, where F given by (2) is nonempty. Let \(v^i \in F_i,~i = 1,\ldots ,s\), where each \(F_i \subseteq F,~i = 1,\ldots ,s\), denotes a minimal face of F. Then,
Proof
If F contains at least one vertex, then the assertion follows from Propositions 10 and 12 since each \(v^i,~i = 1,\ldots ,s\), is a vertex. Otherwise, by (24), the vertices of \(F_A\) given by (42) are \(e^j \in {\mathbb {R}}^{n_A},~j = 1,\ldots ,s\). The assertion follows directly from Proposition 16 and Corollary 14 by observing that \((e^i)^T Q_A e^j = (v^i)^T Q v^j\) for each \(i = 1,\ldots ,s\) and each \(j = 1,\ldots ,s\) by (36) and (38). \(\square \)
4 Duality and optimality conditions
In this section, we focus on the dual problem of (RLT) and discuss optimality conditions.
By defining the dual variables \((u,w,R,S) \in {\mathbb {R}}^m \times {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n} \times {{\mathcal {S}}}^m\) corresponding to the four sets of constraints in (10), respectively, the dual of (RLT) is given by
Note that the variable \(S \in {{\mathcal {S}}}^m\) is scaled by a factor of \(\textstyle \frac{1}{2}\) in (RLT-D). We first review the optimality conditions.
Lemma 18
Suppose that (QP) has a nonempty feasible region. Then, \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) is an optimal solution of (RLT) if and only if there exists \(({\hat{u}}, {\hat{w}}, {\hat{R}}, {\hat{S}}) \in {\mathbb {R}}^m_+ \times {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n} \times {{\mathcal {N}}}^m\) such that
where \({\hat{r}} = g - G^T {\hat{x}} \in {\mathbb {R}}^m_+\).
Proof
Since \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\), we have
where we used \({\hat{r}} = g - G^T {\hat{x}}\). The claim now follows from the optimality conditions for (RLT) and (RLT-D). \(\square \)
We remark that Lemma 18 gives a recipe for constructing instances of (QP) with a known optimal solution of (RLT) and a finite RLT lower bound on the optimal value. We will discuss this further in Sect. 6.
By Lemma 7, if F is nonempty and bounded, then \({{\mathcal {F}}}\) is nonempty and bounded, which implies that (RLT) has a finite optimal value. By Lemma 18, we conclude that the (RLT-D) always has a nonempty feasible region under this assumption.
For the first set of vertices of \({{\mathcal {F}}}\) given by Proposition 10, we next establish necessary and sufficient optimality conditions.
Proposition 19
Suppose that \(v \in F\) is a vertex. Suppose that \(G = [G^0 \quad G^1]\) so that \((G^0)^T v = g^0\) and \((G^1)^T v < g^1\), where \(G^0 \in {\mathbb {R}}^{n \times m_0}\), \(G^1 \in {\mathbb {R}}^{n \times m_1}\), \(g^0 \in {\mathbb {R}}^{m_0}\), and \(g^1 \in {\mathbb {R}}^{m_1}\). Then, \((v,v v^T) \in {{\mathcal {F}}}\) is an optimal solution of (RLT) if and only if there exists \(({\hat{u}}, {\hat{w}}, {\hat{R}}, {\hat{S}}) \in {\mathbb {R}}^m \times {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n} \times {{\mathcal {S}}}^m\), where \({\hat{u}} \in {\mathbb {R}}^m\) and \({\hat{S}} \in {{\mathcal {S}}}^m\) can be accordingly partitioned as
where \({\hat{u}}^0 \in {\mathbb {R}}^{m_0}\), \({\hat{S}}^{00} \in {{\mathcal {S}}}^{m_0}\), and \({\hat{S}}^{01} \in {\mathbb {R}}^{m_0 \times m_1}\), such that (45) and (46) are satisfied. Furthermore, if \({\hat{S}}^{00} \in {{\mathcal {S}}}^{m_0}\) is strictly positive and \({\hat{u}}_0 \in {\mathbb {R}}^{m_0}\) is strictly positive, then \((v,vv^T) \in {{\mathcal {F}}}\) is the unique optimal solution of (RLT).
Proof
Suppose that \(v \in {\mathbb {R}}^n\) is a vertex of F. By Proposition 10, \((v, v v^T)\) is a vertex of \({{\mathcal {F}}}\). Following a similar argument as in the proof of Proposition 10, we obtain
where \(+\) denotes a submatrix with strictly positive entries. The first assertion now follows from Lemma 18.
For the second part, suppose further that \({\hat{S}}_{00} \in {{\mathcal {S}}}^{m_0}\) is strictly positive and \({\hat{u}}_0 \in {\mathbb {R}}^{m_0}\) is strictly positive. Let \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) be an arbitrary feasible solution of (RLT). Then, using the same partitions of G and g as before, we have
where \(r^0 \in {\mathbb {R}}^{m_0}_+\) and \(r^1 \in {\mathbb {R}}^{m_1}_+\). By Lemma 18, \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) is an optimal solution if and only if \(r^0 = 0\) and \((G^0)^T {\hat{X}} G^0 - g^0 (g^0)^T = 0\). Note that any \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) with this property should satisfy the following equation:
By Lemma 9, it follows that \({\hat{X}} = vv^T\) is the only solution to this system since \(\begin{bmatrix} G^0&H \end{bmatrix}\) has full row rank by Lemma 1 (iii). By Lemma 18, \((v,vv^T) \in {{\mathcal {F}}}\) is the unique optimal solution of (RLT). \(\square \)
Next, we present necessary and sufficient optimality conditions for the second set of vertices of \({{\mathcal {F}}}\) given by Proposition 12.
Proposition 20
Let \(v^1 \in F\) and \(v^2 \in F\) be two vertices such that \(v^1 \ne v^2\). Suppose that \(G = [G^0 \quad G^1 \quad G^2 \quad G^3]\) so that \((G^0)^T v^1 = (G^0)^T v^2 = g^0\); \((G^1)^T v^1 = g^1\) and \((G^1)^T v^2 < g^2\); \((G^2)^T v^1 < g^1\) and \((G^2)^T v^2 = g^2\); \((G^3)^T v^1 < g^3\) and \((G^3)^T v^2 < g^3\), where \(G^0 \in {\mathbb {R}}^{n \times m_0}\), \(G^1 \in {\mathbb {R}}^{n \times m_1}\), \(G^2 \in {\mathbb {R}}^{n \times m_2}\), \(G^3 \in {\mathbb {R}}^{n \times m_3}\), \(g^0 \in {\mathbb {R}}^{m_0}\), \(g^1 \in {\mathbb {R}}^{m_1}\), \(g^2 \in {\mathbb {R}}^{m_2}\), and \(g^3 \in {\mathbb {R}}^{m_3}\). Then, \((\frac{1}{2}(v^1 + v^2), \frac{1}{2} (v^1 (v^2)^T + v^2 (v^1)^T)) \in {{\mathcal {F}}}\) is an optimal solution of (RLT) if and only if there exists \(({\hat{u}}, {\hat{w}}, {\hat{R}}, {\hat{S}}) \in {\mathbb {R}}^m \times {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n} \times {{\mathcal {S}}}^m\), where \({\hat{u}} \in {\mathbb {R}}^m\) and \({\hat{S}} \in {{\mathcal {S}}}^m\) can be accordingly partitioned as
where \({\hat{u}}^0 \in {{\mathbb {R}}^{m_0}}\), \({\hat{S}}^{kk} \in {{\mathcal {S}}}^{m_k},~k = 0, 1, 2\), \({\hat{S}}^{0j} \in {\mathbb {R}}^{m_0 \times m_j},~j = 1, 2, 3\), such that (45) and (46) are satisfied. Furthermore, if each of \({\hat{S}}^{00} \in {{\mathcal {S}}}^{m_0}\), \({\hat{S}}^{01} \in {\mathbb {R}}^{m_0 \times m_1}\), \({\hat{S}}^{02} \in {\mathbb {R}}^{m_0 \times m_2}\), \({\hat{S}}^{11} \in {{\mathcal {S}}}^{m_1}\), \({\hat{S}}^{22} \in {{\mathcal {S}}}^{m_2}\), and \({\hat{u}}^0 \in {\mathbb {R}}^{m_0}\) is strictly positive, then \((\frac{1}{2}(v^1 + v^2), \frac{1}{2} (v^1 (v^2)^T + v^2 (v^1)^T)) \in {{\mathcal {F}}}\) is the unique optimal solution of (RLT).
Proof
By Proposition 12, \((\frac{1}{2}(v^1 + v^2), \frac{1}{2} (v^1 (v^2)^T + v^2 (v^1)^T))\) is a vertex of \({{\mathcal {F}}}\). The proof is similar to the proof of Proposition 19. By a similar argument as in the proof of Proposition 12, we have
where we assume that \(G = \begin{bmatrix} G^0&G^1&G^2&G^3 \end{bmatrix}\) and g is partitioned accordingly, and \(+\) denotes a submatrix with strictly positive entries. The first claim follows from Lemma 18.
For the second assertion, suppose further that each of \({\hat{S}}^{00} \in {{\mathcal {S}}}^{m_0}\), \({\hat{S}}^{01} \in {\mathbb {R}}^{m_0 \times m_1}\), \({\hat{S}}^{02} \in {\mathbb {R}}^{m_0 \times m_2}\), \({\hat{S}}^{11} \in {{\mathcal {S}}}^{m_1}\), \({\hat{S}}^{22} \in {{\mathcal {S}}}^{m_2}\), and \({\hat{u}}_0 \in {\mathbb {R}}^{m_0}\) is strictly positive. Let \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) be an arbitrary solution. Then, using the same partition of G and g, we have
where \(r^i \in {\mathbb {R}}^{m_i}_+,~i = 0,1,2,3\), and the last set of inequalities is componentwise. By Lemma 18, \(({\hat{x}}, {\hat{X}}) \in {{\mathcal {F}}}\) is an optimal solution if and only if
Note that \((\frac{1}{2}(v^1 + v^2), \frac{1}{2} (v^1 (v^2)^T + v^2 (v^1)^T)) \in {{\mathcal {F}}}\) with \(r^1 = g^1 - \frac{1}{2} (G^1)^T (v^1 + v^2)\) and \(r^2 = g^2 - \frac{1}{2} ({G^2})^T (v^1 + v^2)\) satisfies this system. Using a similar argument as in the proof of Proposition 12, one can show that this solution is unique. By Lemma 18, we conclude that \((\frac{1}{2}(v^1 + v^2), \frac{1}{2} (v^1 (v^2)^T + v^2 (v^1)^T)) \in {{\mathcal {F}}}\) is the unique optimal solution of (RLT). \(\square \)
5 Exact RLT relaxations
In this section, we present necessary and sufficient conditions in order for an instance of (QP) to admit an exact RLT relaxation.
First, following [12], we define the convex underestimator arising from RLT relaxations. To that end, let
We next define the following function:
By [12], \(\ell _R(\cdot )\) is a convex underestimator of \(q(\cdot )\) over F, i.e., \(\ell _R({\hat{x}}) \le q({\hat{x}})\) for each \({\hat{x}} \in F\), and
By (52),
where
Note that (RLT)\(({\hat{x}})\) has a nonempty feasible region for each \({\hat{x}} \in F\) since \({\hat{X}} = {\hat{x}} {\hat{x}}^T\) is a feasible solution. By defining the dual variables \((R,S) \in {\mathbb {R}}^{p \times n} \times {{\mathcal {S}}}^m\) corresponding to the first and second sets of constraints in (RLT)\(({\hat{x}})\), respectively, the dual of (RLT)\(({\hat{x}})\) is given by
We start with a useful result on the convex underestimator \(\ell _R(\cdot )\).
Lemma 21
Suppose that F is nonempty. If there exists \({\hat{x}} \in F\) such that \(\ell _R({\hat{x}}) = -\infty \), then \(\ell _R({{\tilde{x}}}) = -\infty \) for each \({{\tilde{x}}} \in F\). Therefore, \(\ell ^*_R = -\infty \).
Proof
Suppose that there exists \({\hat{x}} \in F\) such that \(\ell _R({\hat{x}}) = -\infty \). By linear programming duality, (RLT-D)\(({\hat{x}})\) is infeasible. Therefore, (RLT-D)\(({{\tilde{x}}})\) is infeasible for each \({{\tilde{x}}} \in F\) since the feasible region of (RLT-D)\(({\hat{x}})\) does not depend on \({\hat{x}} \in F\). Since (RLT)\(({{\tilde{x}}})\) has a nonempty feasible region for each \({{\tilde{x}}} \in F\), (RLT)\(({{\tilde{x}}})\) is unbounded below. By (54), \(\ell _R({{\tilde{x}}}) = -\infty \) for each \({{\tilde{x}}} \in F\). The last assertion simply follows from (53). \(\square \)
We next establish another property of \(\ell _R(\cdot )\).
Lemma 22
Suppose that F is nonempty and there exists \({\hat{x}} \in F\) such that \(\ell _R({\hat{x}}) > -\infty \). Then, \(\ell _R(\cdot )\) is a piecewise linear convex function.
Proof
Suppose that F is nonempty and there exists \({\hat{x}} \in F\) such that \(\ell _R({\hat{x}}) > -\infty \). By using a similar argument as in the proof of Lemma 21, we conclude that \(\ell _R({{\tilde{x}}}) > -\infty \) for each \({{\tilde{x}}} \in F\). By linear programming duality, for each \({\hat{x}} \in F\) the optimal value of (RLT-D)\(({\hat{x}})\) equals \(\ell ^0_R({\hat{x}})\). By Lemma 4, there exist feasible solutions \((R^i,S^i) \in {\mathbb {R}}^{p \times n} \times {{\mathcal {S}}}^m,~i = 1,\ldots ,s\), of (RLT-D)\(({\hat{x}})\) and a polyhedral cone \({{\mathcal {C}}}\subseteq {{\mathbb {R}}^{p \times n} \times {{\mathcal {S}}}^m}\) such that the feasible region of (RLT-D)\(({\hat{x}})\) is given by \(\text {conv}\{(R^i,S^i):i = 1,\ldots ,s\} + {{\mathcal {C}}}\). Since the optimal value of (RLT-D)\(({\hat{x}})\) is finite, it follows that
The assertion follows from (54). \(\square \)
We remark that a similar result was established in [18] for the convex underestimator \(\ell _R(\cdot )\) arising from the RLT relaxation of quadratic programs with box constraints. For this class of problems, the hypothesis of Lemma 22 is vacuous. Therefore, Lemma 22 extends this result to RLT relaxations of all quadratic programs under a mild assumption.
We next focus on the description of the set of instances of (QP) that admit an exact RLT relaxation. To that end, let us start with a simple observation.
Lemma 23
Suppose that F is nonempty and \(\ell ^*\) is finite. Then, the RLT relaxation given by (RLT) is exact, i.e., \(\ell ^*_R = \ell ^*\), if and only if there exists an optimal solution \(({\hat{x}}, {\hat{x}} {\hat{x}}^T) \in {{\mathcal {F}}}\) of (RLT). Furthermore, in this case, \({\hat{x}} \in F\) is an optimal solution of (QP).
Proof
Suppose that the RLT relaxation given by (RLT) is exact, i.e., \(\ell ^*_R = \ell ^* > -\infty \). Then, the set of optimal solutions of (QP) is nonempty by the Frank-Wolfe theorem [24]. Therefore, for any optimal solution \({\hat{x}} \in F\) of (QP), \(({\hat{x}}, {\hat{x}} {\hat{x}}^T) \in {{\mathcal {F}}}\) is an optimal solution of (RLT) since \(\ell ^* = q({{\hat{x}}}) = \textstyle \frac{1}{2}\langle Q, {\hat{x}} {\hat{x}}^T \rangle + c^T {\hat{x}} = \ell ^*_R\).
Conversely, if there exists an optimal solution \(({\hat{x}}, {\hat{x}} {\hat{x}}^T) \in {{\mathcal {F}}}\) of (RLT), then \(\ell ^*_R = \textstyle \frac{1}{2}\langle Q, {\hat{x}} {\hat{x}}^T \rangle + c^T {\hat{x}} = q({\hat{x}}) \ge \ell ^*\) since \({\hat{x}} \in F\). Then, \(\ell ^*_R = \ell ^*\) by (11). The last assertion follows from these arguments. This completes the proof. \(\square \)
Let F be nonempty and let \({\hat{x}} \in F\). Let us define the submatrices \(G^0\), \(G^1\), and the subvectors \(g^0\), \(g^1\) such that (15) holds. Consider \(({\hat{x}}, {\hat{x}} {\hat{x}}^T) \in {{\mathcal {F}}}\) and assume without loss of generality that \(G = \begin{bmatrix} G^0&G^1 \end{bmatrix}\). Therefore,
where \(r^1 = g^1 - (G^1)^T \hat{x} > 0\). By Lemma 18, \(({\hat{x}}, {\hat{x}} {\hat{x}}^T) \in {{\mathcal {F}}}\) is an optimal solution of (RLT) if and only if \((Q,c) \in {{\mathcal {E}}}({\hat{x}})\), where
where \({\hat{u}}^0 \in {\mathbb {R}}^{m_0}\), \({\hat{S}}^{00} \in {{\mathcal {S}}}^{m_0}\), and \({\hat{S}}^{01} \in {\mathbb {R}}^{m_0 \times m_1}\).
For each \({\hat{x}} \in F\), it is easy to see that \({{\mathcal {E}}}({\hat{x}})\) is a polyhedral cone in \({{\mathcal {S}}}^n \times {\mathbb {R}}^n\). By Lemma 23,
We next show that the description of instances of (QP) that admit an exact relaxation given by (56) can be considerably simplified.
Proposition 24
Suppose that F is nonempty and \(\ell ^*\) is finite. Let \(F_i \subseteq F,~i = 1,\ldots ,s\) denote the minimal faces of F and let \(v^i \in F_i,~i = 1,\ldots ,s\) be an arbitrary point on each minimal face. Then, the RLT relaxation given by (RLT) is exact, i.e., \(\ell ^*_R = \ell ^*\), if and only if
Furthermore, if \((Q,c) \in {{\mathcal {E}}}(v^i)\) for some \(i = 1,\ldots ,s\), then any \({\hat{x}} \in F_i\) is an optimal solution of (QP).
Proof
By (56), it suffices to show that
Clearly, the set on the left-hand side is a subset of the one on the right-hand side. For the reverse inclusion, let \((Q,c) \in {{\mathcal {E}}}({\hat{x}})\), where \({\hat{x}} \in F \backslash \left( \bigcup _{i \in \{1,\ldots ,s\}} F_i\right) \). Let us define the submatrices \(G^0\), \(G^1\) and the subvectors \(g^0\), \(g^1\) such that (15) holds and let \(F_0 \subseteq F\) denote the smallest face of F that contains \({\hat{x}}\). Then, there exists a minimal face \(F_i \subseteq F_0\). Let \(v = v^i \in F_i\). Assuming that \(G = \begin{bmatrix} G^0&G^1 \end{bmatrix}\), we therefore obtain
where \(r_v^1 = g^1 - (G^1)^T v \ge 0\) so that \(r_v^1 (r_v^1)^T \in {{\mathcal {N}}}^{m_1}\). By (55) and Lemma 18, it follows that \((v, v v^T) = (v^i,v^i (v^i)^T) \in {{\mathcal {F}}}\) is an optimal solution of (RLT). Therefore, \((Q,c) \in {{\mathcal {E}}}(v^i)\). The last assertion follows from the observation that the argument is independent of the choice of \(v \in F_i\) and Lemma 23. \(\square \)
Proposition 24 presents a complete description of the set of instances of (QP) that admit an exact RLT relaxation and reveals that this property holds if and only if (Q, c) lies in the union of a finite number of polyhedral cones. This result is a generalization of the corresponding result established for RLT relaxations of quadratic programs with box constraints [18]. If \(\ell ^*\) is finite, it is worth noticing that the exactness of the RLT relaxation implies that the set of optimal solutions of (QP) either contains a vertex of F or an entire minimal face of F if F has no vertices.
We close this section by establishing a necessary condition for having a finite lower bound from the RLT relaxation whenever F has no vertices.
Proposition 25
Suppose that F given by (2) is nonempty but contains no vertices. Let
denote the lineality space of F, where \(F_\infty \) is defined as in (3). Let \(B^1 \in {\mathbb {R}}^{n \times (n - \rho )}\) be a matrix whose columns form a basis for L (or, equivalently, the null space of \(\begin{bmatrix} G&H \end{bmatrix}^T\)), where \(\rho \) is defined as in (7), and let \(B^2 \in {\mathbb {R}}^{n \times \tau }\) be a matrix whose columns are the extreme directions of \(F_\infty \cap L^\perp \), where \(L^\perp \subset {\mathbb {R}}^n\) denotes the orthogonal complement of L. Let \(F_i \subseteq F,~i = 1,\ldots ,s\), denote the minimal faces of F and let \(v^i \in F_i,~i = 1,\ldots ,s\), be an arbitrary point on each minimal face. If \(\ell ^*_R > -\infty \), then
Furthermore,
where q(x) is defined as in (1).
Proof
Note that L is a nontrivial subspace since the dimension of L given by \(n - \rho > 0\) by Lemma 2 (iii). Furthermore, \(F_\infty \cap L^\perp \subseteq {\mathbb {R}}^n\) is a pointed polyhedral cone (possibly equal to \(\{0\}\)). Suppose that \(\ell ^*_R > -\infty \) and let \(({\hat{x}},{\hat{X}}) \in {{\mathcal {F}}}\) be an optimal solution of (RLT). By Lemma 18, there exists \(({\hat{u}}, {\hat{w}}, {\hat{R}}, {\hat{S}}) \in {\mathbb {R}}^m_+ \times {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n} \times {{\mathcal {N}}}^m\) such that (45)–(48) are satisfied. Let \(d^1 \in L\) and \(d^2 \in F_\infty \). Since \(G^T d^1 = 0\) and \(H^T d^1 = H^T d^2 = 0\), it follows from (46) that \((d^1)^T Q d^2 = 0\). Since \(F_\infty = L + (F_\infty \cap L^\perp )\), we conclude that \((B^1 \, b)^T Q (B^1 \, b^1 + B^2 \, b^2) = b^T (B^1)^T Q B^1 b^1 + b^T (B^1)^T Q B^2 b^2 = 0\) for each \(b \in {\mathbb {R}}^{n - \rho }, b^1 \in {\mathbb {R}}^{n - \rho }\), and \(b^2 \in {\mathbb {R}}^{\tau }_+\). We therefore obtain (58) and (59). Next, for each \(v^i,~i = 1,\ldots ,s\), and each \(d \in L\), we obtain \(d^T (Q v^i + c) = d^T {\hat{R}}^T h - d^T {\hat{R}}^T h = 0\) by (45) and (46). Therefore, \(Q v^i + c \in L^\perp \) for each \(i = 1,\ldots ,s\), which yields (60). Finally, let \(x \in F\) and \(d \in L\). By Lemma 4, there exist \(\lambda _i \ge 0,~i = 1,\ldots ,s\), and \(d^2 \in F_\infty \) such that \(\sum \nolimits _{i=1}^s \lambda _i = 1\) and \(x = \sum \nolimits _{i=1}^s \lambda _i v^i + d^2\). Therefore, \(d^T (Q x + c) = \sum \nolimits _{i=1}^s \lambda _i d^T \left( Q v^i + c\right) + d^T Q d^2 = 0\) since \(Q v^i + c \in L^\perp \) for each \(i = 1,\ldots ,s\) by (60) and \(d^T Q d^2 = 0\) by the first part of the proof. Therefore, by (58), we obtain \(q(x + \alpha d) = q(x) + \alpha d^T (Q x + c) + \textstyle \frac{1}{2}\alpha ^2 d^T Q d = q(x)\), which establishes the last assertion. This completes the proof. \(\square \)
Under the hypotheses of Proposition 25, the objective function of (QP) is constant along each line in F. Note, however, that the conditions (58), (59), and (60) are not sufficient for a finite RLT lower bound. For instance, if there exists \({\hat{d}} \in F_\infty \cap L^\perp \) such that \({\hat{d}}^T Q {\hat{d}} < 0\), then (QP) is unbounded along the ray \(x + \lambda {\hat{d}}\) for any \(x \in F\), where \(\lambda \ge 0\), which would imply that \(\ell ^* = \ell ^*_R = -\infty \).
In the next section, we discuss the implications of our results on the algorithmic construction of instances of (QP) with exact, inexact, or unbounded RLT relaxations.
6 Implications on algorithmic constructions of instances
In this section, we discuss how our results can be utilized to design algorithms for constructing an instance of (QP) such that the lower bound from the RLT relaxation and the optimal value of (QP) will have a predetermined relation. In particular, our discussions on instances with exact and inexact RLT relaxations in this section can be viewed as generalizations of the algorithmic constructions discussed in [18] for quadratic programs with box constraints.
To that end, we will assume that the nonempty feasible region F is fixed and given by (2). We will discuss how to construct an objective function in such a way that the resulting instance of (QP) will have an exact, inexact, or unbounded RLT relaxation.
6.1 Instances with an unbounded RLT relaxation
By Lemma 7, if F is nonempty and bounded, then the RLT relaxation cannot be unbounded. Therefore, a necessary condition to have an unbounded RLT relaxation is that F is unbounded. In this case, the recession cone \({{\mathcal {F}}}_\infty \) given by (13) contains a nonzero \(({\hat{d}}, {\hat{D}}) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n\) by Proposition 6. By linear programming duality, the RLT relaxation (RLT) is unbounded if and only if
Let \({\hat{x}} \in F\) and \({\hat{d}} \in F_\infty {\backslash \{0\}}\) be arbitrary. Let \({\hat{D}} = {\hat{x}} {\hat{d}}^T + {\hat{d}} {\hat{x}}^T \in {{\mathcal {S}}}^n\). By Proposition 6, \(({\hat{d}}, {\hat{D}}) \in {{\mathcal {F}}}_\infty \). By (62), it suffices to choose \((Q,c) \in {{\mathcal {S}}}^n \times {\mathbb {R}}^n\) such that
which would ensure that the RLT relaxation is unbounded.
While this simple procedure can be used to construct an instance of (QP) with an unbounded RLT relaxation, we remark that the resulting instance of (QP) itself may also be unbounded. In particular, if \({\hat{d}}^T Q {\hat{d}} \le 0\) in the aforementioned procedure, then (QP) will be unbounded along the ray \({\hat{x}} + \lambda {\hat{d}}\), where \(\lambda \ge 0\). One possible approach to construct an instance of (QP) with a finite optimal value but an unbounded RLT relaxation is to generate \((Q,c) \in {{\mathcal {S}}}^n \times {\mathbb {R}}^n\) in such a way that (62) holds while a tighter relaxation of (QP) such as the RLT relaxation strengthened by semidefinite constraints has a finite lower bound. This property can be satisfied by ensuring the feasibility of (Q, c) with respect to the dual problem of the tighter relaxation. Such an approach would require the solution of a semidefinite feasibility problem.
6.2 Instances with an exact RLT relaxation
By Proposition 24, the RLT relaxation is exact if and only if there exists \(v \in F\) that lies on a minimal face of F such that \((Q,c) \in {{\mathcal {E}}}(v)\), where \({{\mathcal {E}}}(v)\) is defined as in (55). This result can be used to easily construct an instance of (QP) with an exact RLT relaxation.
The first step requires the computation of a point \(v \in F\) that lies on a minimal face of F. Then, it suffices to choose \({\hat{u}} \in {\mathbb {R}}^m_+\) and \({\hat{S}} \in {{\mathcal {N}}}^n\) as in (55). Finally, choosing an arbitrary \(({\hat{w}}, {\hat{R}}) \in {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n}\) and defining Q and c using (55), we ensure that \((Q,c) \in {{\mathcal {E}}}(v)\). It follows from Proposition 24 that the RLT relaxation is exact and that \(v \in F\) is an optimal solution of (QP). We remark that this procedure not only ensures an exact RLT relaxation but also yields an instance of (QP) with a predetermined optimal solution \(v \in F\).
6.3 Instances with an inexact and finite RLT relaxation
First, we assume that F has at least two distinct vertices \(v^1 \in F\) and \(v^2 \in F\). In this case, one can choose \({\hat{u}} \in {\mathbb {R}}^m_+\) and \({\hat{S}} \in {{\mathcal {N}}}^m\) such that the assumptions of the second part of Proposition 20 are satisfied. Then, by choosing an arbitrary \(({\hat{w}}, {\hat{R}}) \in {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n}\) and defining Q and c using (46) and (45), respectively, we obtain that \((\frac{1}{2}(v^1 + v^2), \frac{1}{2} (v^1 (v^2)^T + v^2 (v^1)^T)) \in {{\mathcal {F}}}\) is the unique optimal solution of (RLT). Therefore, the RLT relaxation has a finite lower bound \(\ell _R^*\). By Lemma 23, we conclude that the RLT relaxation is inexact, i.e., \(-\infty< \ell ^*_R < \ell ^*\).
We next consider the case in which F has no vertices. In this case, \({{\mathcal {F}}}_\infty \) also has no vertices by Lemma 8. Therefore, the RLT relaxation can never have a unique optimal solution. However, our next result shows that we can extend the procedure above to construct an instance of (QP) with an inexact but finite RLT lower bound under a certain assumption on F.
Lemma 26
Suppose that F given by (2) has no vertices but it has two distinct minimal faces \(F_1 \subseteq F\) and \(F_2 \subseteq F\). Let \(v^1 \in F_1\) and \(v^2 \in F_2\). Suppose that \(G = [G^0 \quad G^1 \quad G^2 \quad G^3]\) is defined as in Proposition 20. Let \({\hat{u}} \in {\mathbb {R}}^m_+\) and \({\hat{S}} \in {{\mathcal {N}}}^m\) be such that the assumptions of the second part of Proposition 20 are satisfied. Let \(({\hat{w}}, {\hat{R}}) \in {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n}\) be arbitrary. If Q and c are defined by (46) and (45), respectively, then the RLT relaxation of the resulting instance of (QP) is inexact and satisfies \(-\infty< \ell ^*_R < \ell ^*\).
Proof
Arguing similarly to the first part of the proof of Proposition 20, we conclude that \((\frac{1}{2}(v^1 + v^2), \frac{1}{2} (v^1 (v^2)^T + v^2 (v^1)^T)) \in {{\mathcal {F}}}\) is an optimal solution of the RLT relaxation of the resulting instance of (QP). Therefore, \(-\infty < \ell ^*_R\).
Next, we argue that the RLT relaxation is inexact. First, since each of \(F_1\) and \(F_2\) are minimal faces, they are affine subspaces given by
Suppose, for a contradiction, that the RLT relaxation is exact. Then, by Proposition 24, there exists \(v \in F_0\), where \(F_0 \subseteq F\) is a minimal face of F, such that \((v,vv^T)\) is an optimal solution of (RLT). Let us define \(r = g - G^T v \ge 0\) and partition r accordingly as
where \(r^i \in {\mathbb {R}}^{m_i}_+,~i = 0,1,2,3\). By Lemma 18, \((v,vv^T)\) and \(({\hat{u}}, {\hat{w}}, {\hat{R}}, {\hat{S}}) \in {\mathbb {R}}^m \times {\mathbb {R}}^p \times {\mathbb {R}}^{p \times n} \times {{\mathcal {S}}}^m\) satisfy the optimality conditions (45)–(48). By (47) and \({\hat{u}}^0 > 0\), we conclude that \(r^0 = 0\). On the other hand,
By (48), we obtain \(r^1 = 0\) and \(r^2 = 0\) since \({\hat{S}}^{11} \in {{\mathcal {S}}}^{m_1}\) and \({\hat{S}}^{22} \in {{\mathcal {S}}}^{m_2}\) are strictly positive. It follows that \(v \in F_0\) satisfies
i.e., v lies on a face whose dimension is strictly smaller than each of \(F_1\) or \(F_2\). This contradicts our assumption that each of \(F_1\) and \(F_2\) is a minimal face of F. We therefore conclude that (RLT) cannot have an optimal solution of the form \((v,vv^T)\), where v lies on a minimal face of F, or equivalently \((Q,c) \not \in {{\mathcal {E}}}(v)\) for any v that lies on a minimal face of F, where \({{\mathcal {E}}}(v)\) is defined as in (55). By Proposition 24, we conclude that the RLT relaxation is inexact, i.e., \(-\infty< \ell ^*_R < \ell ^*\). \(\square \)
The next example illustrates the algorithmic construction of Lemma 26.
Example 4
Suppose that F is given as in Example 1. Note that F has no vertices since it contains the line \(\{x \in {\mathbb {R}}^2: x_1 + x_2 = 0\}\). F has two minimal faces given by
Therefore, F satisfies the assumptions of Lemma 26. Let us choose \(v^1 = [1 \quad 0]^T \in F_1\) and \(v_2 = [0 \quad -1]^T \in F_2\). We obtain
Since \(g - G^T {\hat{x}} > 0\), we choose \({\hat{u}} = 0 \in {\mathbb {R}}^2\). Using the partition given in Proposition 20, we obtain that \(G^0\) is an empty matrix, \(G^1 = [1 \quad 1]^T\), \(G^2 = [-1 \quad -1]^T\), and \(G^3\) is an empty matrix. By the second part of Proposition 20, we choose
Therefore, by (46) and (45), we obtain
By Proposition 20, \(\ell ^*_R = \textstyle \frac{1}{2}\langle Q, {\hat{X}} \rangle + c^T {\hat{x}} = -\textstyle \frac{3}{2}\). Note that \(L = F_\infty \) as given in Example 1. In view of Proposition 25, it is worth noticing that (58) and (60) are satisfied whereas (59) is vacuous in this example. Furthermore, for each \(x \in F\) such that \(x_1 + x_2 = \beta \), where \(\beta \in [-1,1]\), we have \(q(x) = \textstyle \frac{3}{2}\beta ^2 + \beta \). Therefore, the minimum value is attained at \(\beta ^* = -\textstyle \frac{1}{3}\). It follows that \(\ell ^* = -\textstyle \frac{1}{6}\) and the set of optimal solutions of (QP) is given by \(\left\{ x \in {\mathbb {R}}^2: x_1 + x_2 = -\textstyle \frac{1}{3}\right\} \). Therefore, \(-\infty< \ell ^*_R < \ell ^*\).
6.4 Implications of one minimal face
We finally consider the case in which F has exactly one minimal face. For any instance of (QP) with this property, we show that the RLT relaxation is either exact or unbounded below.
Lemma 27
Consider an instance of (QP), where F given by (2) is nonempty and has exactly one minimal face. Then, the RLT relaxation is either exact or unbounded below.
Proof
Suppose that F has one minimal face \(F_0 \subseteq F\) and let \(v \in F_0\). Suppose that \(G = [G^0 \quad G^1]\) so that \((G^0)^T v = g^0\) and \((G^1)^T v < g^1\), where \(G^0 \in {\mathbb {R}}^{n \times m_0}\), \(G^1 \in {\mathbb {R}}^{n \times m_1}\), \(g^0 \in {\mathbb {R}}^{m_0}\), and \(g^1 \in {\mathbb {R}}^{m_1}\). First, we claim that the set of inequalities \((G^1)^T x \le g^1\) is redundant for F. Let \({\hat{x}} \in F\) be arbitrary. By Lemma 4,
where \(F_\infty \) is given by (3). Therefore, there exists \({\hat{d}} \in F_\infty \) such that \({\hat{x}} = v + {\hat{d}}\). Therefore, \((G^1)^T {\hat{x}} = (G^1)^T v + (G^1)^T {\hat{d}} < g^1\) since \((G^1)^T v < g^1\) and \((G^1)^T {\hat{d}} \le 0\) by (3). Therefore, \((G^1)^T x \le g^1\) is implied by \((G^0)^T x \le g^0\) and \(H^T x = h\). By [7, Proposition 2], all of the RLT constraints obtained from \((G^1)^T x \le g^1\) are implied by the RLT constraints obtained from \((G^0)^T x \le g^0\) and \(H^T x = h\). Therefore, we have \(({\hat{x}},{\hat{X}}) \in {{\mathcal {F}}}\) if and only if \((G^0)^T {\hat{x}} \le g^0\), \(H^T {\hat{x}} = h\), \(H^T {\hat{X}} = h {\hat{x}}^T\), and
Note that all of the inequality constraints of \({{\mathcal {F}}}\) are active at \((v,vv^T)\) (or at any \((v^\prime ,v^\prime (v^\prime )^T)\), where \(v^\prime \in F_0\), if v is not a vertex of F). If the feasible region of the dual problem given by (RLT-D) is nonempty, then any \((v,vv^T) \in {{\mathcal {F}}}\), where \(v \in F_0\), satisfies the optimality conditions of Lemma 18 together with any feasible solution of (RLT-D). It follows that any such \((v,vv^T) \in {{\mathcal {F}}}\) is an optimal solution of (RLT). By Lemma 23, we conclude that the RLT relaxation is exact. On the other hand, if (RLT-D) is infeasible, then (RLT) is unbounded below by linear programming duality. The assertion follows. \(\square \)
We conclude this section with the following corollary.
Corollary 28
Suppose that F given by (2) has exactly one vertex \(v \in F\). Then, \({{\mathcal {F}}}\) given by (10) has exactly one vertex \((v,vv^T)\). Furthermore, if \(F = \{v\}\), then \({{\mathcal {F}}}= \{(v,vv^T)\}\).
Proof
Suppose that F has one vertex \(v \in F\). By Proposition 10, \((v,vv^T)\) is a vertex of \({{\mathcal {F}}}\). By Proposition 24 and Lemma 27, we either have \((Q,c) \in {{\mathcal {E}}}(v)\), where \({{\mathcal {E}}}(v)\) is defined as in (55), in which case, the RLT relaxation is exact and \((v,vv^T)\) is an optimal solution of (RLT), or \((Q,c) \not \in {{\mathcal {E}}}(v)\) and the RLT relaxation is unbounded below. By Lemma 1 (iv), we conclude that \((v,vv^T)\) is the unique vertex of \({{\mathcal {F}}}\). If \(F = \{v\}\), then \({{\mathcal {F}}}\) is bounded by Lemma 7 and contains a unique vertex \((v,vv^T)\) by the first part. Therefore, by Lemma 4, we conclude that \({{\mathcal {F}}}= \{(v,vv^T)\}\). \(\square \)
Corollary 28 reveals that the description of \({{\mathcal {F}}}\) is independent of the particular representation of F if F consists of a single point. We remark that, in general, this is not the case. For instance, let \(F_1 = \{x \in {\mathbb {R}}^n: e^T x = 1\}\), where \(e \in {\mathbb {R}}^n\) denotes the vector of all ones. Then, the RLT procedure yields \({{\mathcal {F}}}_1 = \{(x,X) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n: e^T x = 1, \quad X e = x\}\). On the other hand, consider \(F_2 = \{x \in {\mathbb {R}}^n: e^T x \le 1, \quad - e^T x \le -1\}\). Clearly, \(F_1 = F_2\). However, the feasible region of the RLT relaxation is now given by \({{\mathcal {F}}}_2 = \{(x,X) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n: e^T x = 1, 1 - 2 e^T x + e^T X e = 0 \} = \{(x,X) \in {\mathbb {R}}^n \times {{\mathcal {S}}}^n: e^T x = 1, \quad e^T X e = 1\}\). It is easy to see that \({{\mathcal {F}}}_1 \subset {{\mathcal {F}}}_2\) for each \(n \ge 2\).
7 Concluding remarks
In this paper, we studied various relations between the polyhedral properties of the feasible region of a quadratic program and its RLT relaxation. We presented a complete description of the set of instances of quadratic programs that admit exact RLT relaxations. We then discussed how our results can be used to construct quadratic programs with an exact, inexact, and unbounded RLT relaxation.
For RLT relaxations of general quadratic programs, we are able to establish a partial characterization of the set of vertices of the feasible region of the RLT relaxation. We intend to work on a complete characterization of this set in the near future. Such a characterization may have further algorithmic implications for constructing a larger set of instances with inexact but finite RLT relaxations.
Our results in this paper establish several properties of RLT relaxations of quadratic programs. Another interesting question is how the structural properties change for higher-level RLT relaxations.
Data availability
The manuscript has no associated data.
References
Furini, F., Traversi, E., Belotti, P., Frangioni, A., Gleixner, A.M., Gould, N., Liberti, L., Lodi, A., Misener, R., Mittelmann, H.D., Sahinidis, N.V., Vigerske, S., Wiegele, A.: QPLIB: A library of quadratic programming instances. Math. Program. Comput. 11(2), 237–265 (2019). https://doi.org/10.1007/s12532-018-0147-4
Nocedal, J., Wright, S.J.: Numerical Optimization, 2nd edn. Springer, New York (2006). https://doi.org/10.1007/978-0-387-40065-5
Sahni, S.: Computationally related problems. SIAM J. Comput. 3(4), 262–279 (1974). https://doi.org/10.1137/0203021
Pardalos, P.M., Vavasis, S.A.: Quadratic programming with one negative eigenvalue is NP-hard. J. Glob. Optim. 1, 15–22 (1991). https://doi.org/10.1007/BF00120662
Sherali, H.D., Adams, W.P.: A Reformulation-Linearization Technique for Solving Discrete and Continuous Nonconvex Problems, pp. 297–367. Springer, Boston (1999). https://doi.org/10.1007/978-1-4757-4388-3
Sherali, H.D., Alameddine, A.: A new reformulation-linearization technique for bilinear programming problems. J. Glob. Optim. 2(4), 379–410 (1992). https://doi.org/10.1007/BF00122429
Sherali, H.D., Tunçbilek, C.H.: A reformulation-convexification approach for solving nonconvex quadratic programming problems. J. Glob. Optim. 7(1), 1–31 (1995). https://doi.org/10.1007/BF01100203
Anstreicher, K.M.: Semidefinite programming versus the reformulation-linearization technique for nonconvex quadratically constrained quadratic programming. J. Glob. Optim. 43, 471–484 (2009). https://doi.org/10.1007/s10898-008-9372-0
Sherali, H.D., Fraticelli, B.M.P.: Enhancing RLT relaxations via a new class of semidefinite cuts. J. Glob. Optim. 22(1–4), 233–261 (2002). https://doi.org/10.1023/A:1013819515732
Kim, S., Kojima, M.: Exact solutions of some nonconvex quadratic optimization problems via SDP and SOCP relaxations. Comput. Optim. Appl. 26(2), 143–154 (2003). https://doi.org/10.1023/A:1025794313696
Burer, S.: On the copositive representation of binary and continuous nonconvex quadratic programs. Math. Program. 120(2), 479–495 (2009). https://doi.org/10.1007/s10107-008-0223-z
Yıldırım, E.A.: An alternative perspective on copositive and convex relaxations of nonconvex quadratic programs. J. Glob. Optim. 82(1), 1–20 (2022). https://doi.org/10.1007/s10898-021-01066-3
Bao, X., Sahinidis, N.V., Tawarmalani, M.: Semidefinite relaxations for quadratically constrained quadratic programming: a review and comparisons. Math. Program. 129(1), 129–157 (2011). https://doi.org/10.1007/s10107-011-0462-2
Anstreicher, K.M.: On convex relaxations for quadratically constrained quadratic programming. Math. Program. 136(2), 233–251 (2012). https://doi.org/10.1007/s10107-012-0602-3
Bomze, I.M.: Copositive relaxation beats Lagrangian dual bounds in quadratically and linearly constrained quadratic optimization problems. SIAM J. Optim. 25(3), 1249–1275 (2015). https://doi.org/10.1137/140987997
Audet, C., Hansen, P., Jaumard, B., Savard, G.: A branch and cut algorithm for nonconvex quadratically constrained quadratic programming. Math. Program. 87, 131–152 (2000). https://doi.org/10.1007/s101079900106
Tawarmalani, M., Sahinidis, N.V.: A polyhedral branch-and-cut approach to global optimization. Math. Program. 103(2), 225–249 (2005). https://doi.org/10.1007/s10107-005-0581-8
Qiu, Y., Yıldırım, E.A.: On exact and inexact RLT and SDP-RLT relaxations of quadratic programs with box constraints. Technical report, School of Mathematics, The University of Edinburgh, Edinburgh, United Kingdom (2023). arxiv:2303.06761
Schrijver, A.: Theory of Linear and Integer Programming. Wiley-Interscience series in discrete mathematics and optimization. Wiley, New York (1999)
Bomze, I.M.: On standard quadratic optimization problems. J. Glob. Optim. 13(4), 369–387 (1998). https://doi.org/10.1023/A:1008369322970
Sağol, G., Yıldırım, E.A.: Analysis of copositive optimization based linear programming bounds on standard quadratic optimization. J. Glob. Optim. 63(1), 37–59 (2015). https://doi.org/10.1007/s10898-015-0269-4
Bomze, I.M., Dür, M., de Klerk, E., Roos, C., Quist, A.J., Terlaky, T.: On copositive programming and standard quadratic optimization problems. J. Glob. Optim. 18(4), 301–320 (2000). https://doi.org/10.1023/A:1026583532263
de Klerk, E., Pasechnik, D.V.: Approximation of the stability number of a graph via copositive programming. SIAM J. Optim. 12(4), 875–892 (2002). https://doi.org/10.1137/S1052623401383248
Frank, M., Wolfe, P.: An algorithm for quadratic programming. Naval Res. Logist. Q. 3(1–2), 95–110 (1956). https://doi.org/10.1002/nav.3800030109
Acknowledgements
We gratefully acknowledge the insightful comments and suggestions of the Associate Editor and three anonymous reviewers, which considerably improved our manuscript and prompted the addition of several new results.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Qiu, Y., Yıldırım, E.A. Polyhedral properties of RLT relaxations of nonconvex quadratic programs and their implications on exact relaxations. Math. Program. (2024). https://doi.org/10.1007/s10107-024-02070-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10107-024-02070-7