Introduction

Motivation

Titanium-based alloys are subject to steadily increasing interest in both, a wide variety of applications, ranging from aerospace [1, 2] over additive manufacturing [3, 4] to biomedical implementations [5, 6] and as a subject of fundamental research [7, 8]. Commercially most relevant are α–β titanium alloys, i.e., alloys with minor additions that stabilize the low-temperature close-packed hexagonal α-phase of titanium as well as those which stabilize the bcc β-phase [9]. Aluminum is the most prominent α-stabilizing element, while vanadium is one of the most frequently used β-stabilizing elements [9]. Therefore, the Al-Ti-V system is of great significance, including many industrially used titanium alloys. Al6Ti90V4, often referred to as Ti64, is the most established example of these alloys, finding wide spread utilization as medical implant material [10], additive manufacturing feedstock [11], aerospace construction material [12] and many more.

With increasing industrial use, the interest in thermophysical properties of the Al-Ti-V system also rises. Therefore, recently different studies investigated the thermophysical properties of several selected Ti-based alloys of high industrial interest, such as the Ti64 [13] alloy or γ-TiAl-based alloys [14]. The liquid phase is hereby crucial. Precise knowledge of thermophysical properties of the liquid phase—such as density, viscosity and surface tension—are required for modeling and design of metallurgical processes [15] like casting or additive manufacturing processes [16] such as selective laser melting (SLM) and electron beam melting (EBM). Additionally, thermophysical properties are often the foundation of understanding the basic interaction mechanisms in multicomponent alloy systems. Thus, it is very surprising that, despite of the importance of the Al-Ti-V systems, only very few systematic data exist on the pure binary and ternary subsystems, except the results already produced in previous studies at DLR [17,18,19,20,21,22].

These previous investigations at our group focused on the Al-Ti system, its thermophysical properties, and its interactions with oxygen [17,18,19,20]. Recently, we expanded these works toward the liquid Ti-V system [21] in order to characterize and understand the complete Al-Ti-V ternary system by progressing its investigation by means of its binary margins.

Liquid Ti-V shows the behavior of an ideal solution regarding density and molar volume [21]. It is therefore interesting to examine if such an ideal behavior is also observed for other thermophysical properties, such as the surface tension.

Thus, the purpose of the present work is twofold. On the one hand, we aim to provide systematic and reliable surface tension data for the complete Ti-V liquid system in order to complete existing datasets for this system [21]. The second aim of the present work is to gather further insights into the general mixing behavior of this interesting and important class of alloys.

The high melting temperatures of titanium (1941 K) and vanadium (2183 K) [23] as well as their high chemical reactivity possess severe challenges for conventional container-based surface tension measurement techniques at elevated temperatures. Thus, electromagnetic levitation (EML) as a container-less method is applied in the present work in order to handle these challenges and to allow for a precise surface tension measurement over a broad temperature range without the risk of contamination from any container walls [24]. The measured data will be evaluated using the Butler equation [25] as thermodynamic model.

Butler equation

In the Butler model [25], surface and bulk are considered as two distinct thermodynamic phases, each having their own composition and chemical potential. The chemical potential of the surface phase has an additional term which depends on the surface tension γ. If the two phases are in equilibrium with each other, their chemical potentials are equal, resulting in the Butler equation. For an ideal solution, the latter can be written in following form [26, 27]

$$\gamma = \gamma_{{\text{i}}} \frac{{\omega_{{\text{i}}}^{0} }}{{\omega_{{\text{i}}} }} + \frac{RT}{{\omega_{{\text{i}}} }}ln\left( {\frac{{x_{{\text{i}}}^{S} }}{{x_{{\text{i}}}^{B} }}} \right)$$
(1)

In this equation, γi represents the surface tension of pure element i and xiS and xiB represent its mole fraction in the surface- and the bulk phase, respectively. R is the molar gas constant, R = 8.314 J/mol/k and ωi0 is the molar surface area of the pure, unmixed component i and ωi is the corresponding partial molar surface area of component i in the mixture. The latter has been identified by Kaptay as an immanent property [26]. It is defined as.

$$\omega_{{\text{i}}} \equiv \frac{{A_{{\text{i}}} }}{{n_{{\text{i}}} }},$$
(2)

if ni denotes the number of moles of species i in the surface area and Ai is the size of the surface covered by it under the condition that the total surface area is \(A = \mathop \sum \limits_{{\text{i}}} A_{{\text{i}}}\). ωi and ωi0 are related to the molar volume Vmol of the solution [26]. In the case of a binary alloy (i,j) this relation reads [27]:

$$\omega_{{\text{i}}} = \omega_{{\text{i}}}^{0} + \left( {x_{{\text{j}}}^{S} } \right)^{2} L_{\omega }$$
(3)

with

$$\omega_{{\text{i}}}^{0} = f \cdot N_{Av}^{\frac{1}{3}} \left( {V_{{\text{i}}}^{0} } \right)^{2/3}$$
$$L_{{\upomega }} = f \cdot N_{Av}^{\frac{1}{3}} \left( {L_{{\text{V}}} } \right)^{2/3}$$
(4)

whereas f = 1.0 is a geometrical factor, whose value is chosen in agreement with Ref. [28]. Nav is the Avogadro number and Vi0 is the molar volume of pure substance i. Lω is an interaction constant that is related via Eq. (4) to the interaction constant of the molar volume Lv that determines the excess volume \(V^{E} = x_{{\text{i}}} x_{{\text{j}}} L_{V}\). If the excess volume is zero or can be neglected, as is the case with liquid Ti-V [21], Eq. (3) turns into the following:

$$\omega_{{\text{i}}} = \omega_{{\text{i}}}^{0} = f \cdot N_{Av}^{\frac{1}{3}} \left( {V_{{\text{i}}}^{0} } \right)^{2/3}$$
(5)

Thus, for Ti-V, the Butler equation of the ideal solution can be simplified so that it attains the usual form:

$$\gamma = \gamma_{{{\text{Ti}}}} + \frac{RT}{{\omega_{{{\text{Ti}}}}^{0} }}ln\left( {\frac{{x_{{{\text{Ti}}}}^{S} }}{{x_{{{\text{Ti}}}}^{B} }}} \right) = \gamma_{V} + \frac{RT}{{\omega_{{\text{V}}}^{0} }}ln\left( {\frac{{1 - x_{{{\text{Ti}}}}^{S} }}{{1 - x_{{{\text{Ti}}}}^{B} }}} \right)$$
(6)

Under the condition that γTi, γV, V0Ti and V0V are known, Eq. (6) can be solved numerically for given xBTi and T using some standard algorithm. As result, γ and xSTi are obtained for a given temperature and bulk composition. When the calculation is carried out at various different temperatures, also the temperature coefficient γT can be obtained.

For a non-ideal system, where \({}_{{}}^{E} G \ne 0\), Eq. (6) expands to

$$\gamma = \gamma_{{{\text{Ti}}}} + \frac{RT}{{\omega_{{{\text{Ti}}}}^{0} }}ln\left( {\frac{{x_{Ti}^{S} }}{{x_{Ti}^{B} }}} \right) + \frac{1}{{\omega_{{{\text{Ti}}}}^{0} }}\left( {{}_{{}}^{E} G_{{{\text{Ti}}}}^{S} (T,x_{{{\text{Ti}}}}^{S} , x_{V}^{S} } \right) - {}_{{}}^{E} G_{{{\text{Ti}}}}^{B} \left( {T,x_{{{\text{Ti}}}}^{B} , x_{V}^{B} } \right))$$
(7)

with \({}_{{}}^{E} G_{{{\text{Ti}}}}^{S}\) and \({}_{{}}^{E} G_{{{\text{Ti}}}}^{B}\) being the excess free energies of titanium in the Ti-V system, for the surface and the bulk phase. While the excess free energies for the bulk phase can be determined using thermodynamic assessments, they are not so easily obtained for the surface. For our work we used a procedure described in more detail in [29], calculating the excess free energy of the surface from those of the bulk, as follows:

$${}_{{}}^{E} G_{Ti}^{S} (T,x_{Ti}^{S} , x_{V}^{S} ) \approx \xi {}_{{}}^{E} G_{Ti}^{B} (T,x_{Ti}^{S} , x_{V}^{S} )$$
(8)

Here \(\xi\) is a geometrical factor to incorporate the coordination of the surface phase atoms. Finally, the excess free energy was calculated following a Redlich–Kister polynomial of the form

$${}_{{}}^{E} G_{{{\text{Ti}}}}^{B} (T,x_{{{\text{Ti}}}}^{S} , x_{V}^{S} ) = x_{{{\text{Ti}}}}^{B} x_{V}^{B} \mathop \sum \limits_{v} {}_{{}}^{v} L_{{{\text{Ti}},V}} \left( T \right)*\left( {x_{{{\text{Ti}}}}^{B} - x_{V}^{B} } \right)^{v}$$
(9)

The parameters used are taken from Ref. [30] and listed in Table 1. A more detailed description for the Butler model of the regular solution can be found in [29, 31, 32].

Table 1 Redlich–Kister parameters for liquid Ti-V taken from Ref. [30]
Full size table

Experimental method

Electromagnetic levitation

Electromagnetic levitation (EML) is based on the principle that an alternating inhomogeneous magnetic field induces eddy currents inside the electrically conducting sample which, apart from an inductive heating and melting of the specimen, also leads to its stable positioning against gravity due to the action of Lorenz-forces. The method is described in detail in reference [24].

Experiments are performed in an inert He, Ar (99.9999 vol pct. purity) mixture atmosphere of 750 hPa and inside a vacuum chamber. The chamber has been evacuated prior to the actual experiment down to a pressure of at least 10−6 hPa in order to remove residual gas components such as H2O, O2, CO, CO2 and hydrocarbons. Thus, the contamination risk of the sample is further reduced. In the beginning of an experiment, the sample is located on a ceramic sample holder and introduced into the water-cooled levitation coil to which then an alternating current in the order of 200 A is applied with a frequency of approximately 250 kHz. As soon as the sample levitates, the sample holder is withdrawn.

The samples are nearly of spherical shapes with typical diameters of 7 mm. Depending on the material’s density, the masses of the sample vary between 0.9 to 1.3 g.

In electromagnetic levitation, heating and positioning are not decoupled. Thus, to adjust the temperature by counter-cooling of the sample, a variable flow of He- or Ar- gas is admitted to it through an alumina nozzle. In addition, the temperature can be adjusted within certain limits by cautiously reducing the generator power.

The droplet temperature is determined by use of a single-color pyrometer. Since the emissivity of the specimen is generally unknown, a correction of the pyrometer signal is necessary to obtain the actual temperature \(T\) of the sample. Assuming that the effective emissivity at constant wavelength does not significantly vary over the temperature range of the measurement, T can be approximated using the equation below, which is derived from Wiens’ law [33]:

$$\frac{1}{T} = \frac{1}{{T_{{\text{P}}} }} - \frac{1}{{T_{{\text{P,L}}} }} + \frac{1}{{T_{{\text{L}}} }}$$
(7)

Here, \(T_{{\text{P}}}\) is the uncorrected pyrometer signal, \(T_{{\text{L}}}\) is the true liquidus temperature and \(T_{{\text{L,P}}}\) denotes the liquidus temperature observed in the pyrometer signal.\(T_{{\text{L,P}}}\) manifests itself in the pyrometer signal as a kink at the end of the melting plateau where the melting process is concluded. \(T_{{\text{L}}}\) is usually taken from an independent measurement. In this work, it is read from the phase diagram reported in Reference [23]. The liquidus temperature for each composition, as well as the measurement temperature range from the minimum temperature \(T_{{{\text{min}}}}\) to the maximum temperature \(T_{{{\text{max}}}}\) are listed in Table 2.

Table 2 Liquidus temperature TL, minimum temperature Tmin and maximum measurement temperature Tmax for each investigated composition
Full size table

Oscillating drop method

The oscillating drop method has been applied in many previous works to accurately measure the surface tension of a molten droplet in levitation [17, 24, 31, 32, 34,35,36,37]. For this technique, a high-speed camera records a series of 6000 frames at a frequency of 400 fps of the sample from a top view position. Afterward the frames are analyzed by a custom software extracting the frequency spectra of two perpendicular radii \(r_{{\text{x}}} \left( \omega \right)\) and \(r_{{\text{y}}} \left( \omega \right)\), as well as three translational frequencies \(\omega_{{{\text{x}}, }} \omega_{{\text{y}}}\) and \(\omega_{{\text{z}}}\) of the sample center of mass.

In a force-free environment the surface tension \(\gamma\) of a spherical, non-rotating droplet can be correlated to the Rayleigh frequency \(\omega_{{\text{R}}}^{{}}\) via the following equation [24], if \(M\) is the mass of the droplet:

$$\omega_{{\text{R}}}^{2} = \frac{32\pi }{{3M}}\gamma$$
(8)

It can be shown, that the Rayleigh frequency corresponds to an l = 2 mode with fivefold degeneracy |m|≤ l under the condition of the spherical symmetry. However, on earth, the droplets are no longer force-free and in the electromagnetic levitation environment, the spherical symmetry needs to be replaced by a cylindrical symmetry. Therefore, the degeneracy is lifted and the Rayleigh frequency splits into a set of three distinct frequencies ω2,±2, ω2,±1, and ω2,0 where the m =  ± 2- and the m =  ± 1- modes are still twofold degenerate [38]. This degeneracy, however, is also removed, if the droplet rotates slightly, which is usually the case. It is important to note, that the frequency of these sample rotations needs to be very small compared to the Rayleigh-frequency (≤ 5 Hz) since sample rotations of frequencies in the order of the Rayleigh-frequency can greatly impair the measurement as will be explained in more detail later. As a result, five distinct frequencies, ωm are observed in the spectrum. The surface tension, γ, is calculated from these frequencies using the formula of Cummings and Blackburn [32] or one of its variants:

$$\gamma = \frac{3M}{{160\pi }}\left( {\mathop \sum \limits_{m = - 2}^{2} \omega_{m}^{2} - 9.5\Omega^{2} - 1.5\left( \frac{g}{a} \right)^{2} \Omega^{ - 2} } \right)$$
(9)

Here, M is the mass of the sample, a is its radius, and g is the gravitational acceleration. In Eq. (9), the parameter Ω corrects for the magnetic pressure. It is calculated from the three translational frequencies, ωX,Y,Z, corresponding to the horizontal and vertical movements of the sample: Ω2 = 1/3(ω2X + ω2Y + ω2Z). Depending on the mass of the sample, the frequencies of the translational movements are typically between 5 and 20 Hz, whereas as a rule of thumb, ωZ ≈ 2ωX ≈ 2ωY. The frequencies ωX and ωY are determined from the horizontal motion of the droplet center, while ωZ is extracted from the spectrum of the apparent droplet area, which changes with vertical movement of the sample due to the changing distance between the sample and the high-speed camera.

Sample material and preparation

In order to sufficiently map the Ti-V system, 10 different alloy compositions equally covering the whole compositional range, including the pure elements, were prepared. As raw materials, titanium from AlphaAesar with a purity of 99.999% as well as vanadium from Hauner GmbH with a purity of 99.99% were used. After cutting the desired weight for each element, the raw materials were alloyed together in an arc-furnace under a protective argon atmosphere. Before and after alloying the samples were cleaned in an isopropanol ultrasonic bath to remove any residual surface impurities. The resulting samples had a near spherical shape with a diameter of approximately 7 mm.

Different sources of quantified experimental errors and their potential impact on the surface tension measurement are given in Table 3. Mass loss due to sample evaporation during levitation was kept below 0.5% by measuring the mass of each sample before and after levitation and discarding all samples that showed a mass loss of \(\ge 0.3\%\). Sample contamination was minimized by the use of high purity raw materials and an inert protective atmosphere (He, Ar) during alloying and levitation. Special attention is hereby paid to the oxygen influence on the measurement, since already a small oxygen content can have a major impact on the surface measurement of a liquid metal. Previous research in our group [1] has shown, that the implementation of the mentioned purity conditions, such as the high purity raw material and the protective argon atmosphere during all sample preparation as well as measurement steps, keeps the oxygen content during the measurement neglectable small. In order to obtain an estimate on how much oxygen is introduced into the sample during the levitation, an oxygen analysis on pure vanadium was done before and after the levitation experiment. The measurements were carried out by the analytical services of the ‘Elektrowerk Weisweiler GmbH’. Two identical samples of pure vanadium were prepared. Afterward one of these samples was processed in the electromagnetic levitation furnace while the second sample was not. The oxygen content of both samples was subsequently analyzed. The ‘as prepared’ sample showed 0.08 at. − % oxygen, while the ‘processed’ sample showed 0.1 at. − %. A similar approach was taken for pure titanium in [20] and [39], where the oxygen content of pure titanium samples was analyzed for different processing durations. There, an increase from 0.079 at. − % for the ‘as prepared’ sample, to 0.23 at. − % for the sample processed for 90 min. was observed. In both cases a slight increase in oxygen content can be noted. Even for pure titanium the oxygen content after processing in the electromagnetic levitation furnace still lays well below the threshold of around 1 at. − % at which oxygen has a noticeable impact on the surface tension as shown by [20] and [39]. However, the influence of oxygen on thermophysical properties and surface tension in particular is far too complex to just be neglected. Therefore, consecutive investigations are currently carried out at our group, examining the influence of different oxygen contents on various Ti and V alloys and their thermophysical properties. First results indicate a similar behavior for pure liquid V and Ti. All this leads to the assumption, that even though there is a slight increase in oxygen content over the course of the measurement, it is not big enough to have a major impact on the surface tension.

Table 3 Error sources as well as their impact on the surface tension measurement for the oscillating drop method
Full size table

Additionally, sample rotations with a frequency in the same order of magnitude as the Rayleigh frequency can greatly impair the surface tension measurement, as they superimpose the frequency spectrum, usually with a much higher intensity than the surface oscillations. Strong rotations of the sample during levitation, make an identification of five distinct peaks corresponding to the Rayleigh Frequency impossible. Instead, only one major peak at the rotation frequency can be observed. The coil design must therefore be carefully adjusted in order to suppress any sample rotations during the levitation process. An estimation of the measurement error can be done by investigating the propagation of uncertainty of all parameters in Eqs. (8) and (9). The deviation in temperature was assumed to be ± 10 K, the maximum mass loss \(\ge 0.3\%\) and the error for the frequency reading ± 0.5 Hz. These assumptions lead to an estimated error in surface tension of \(\le 5\%\). An experimental validation for these assumptions can be found in [29].

Results and discussion

Pure elements

Surface tension data γ of pure liquid Ti and V are plotted versus temperature T in Figs. 1 and 2, respectively.

Figure 1
figure 1

Surface tension of liquid titanium versus temperature (symbols). The solid line represents the fit from Eq. (10). The dashed line represents data measured by Wessing [17] and the dash-dotted line represents data measured by Paradis [41] for comparison

Full size image
Figure 2
figure 2

Surface tension of liquid vanadium versus temperature (symbols). The solid line represents the fit from Eq. (10). The dashed line represents data measured by Okada [42] et al. for reference

Full size image

For liquid Ti (Fig. 1) data are measured over a temperature range from 1800 to 2300 K. This includes a maximum undercooling of 140 K below the liquidus temperature TL = 1941 K. Over this interval, the measured surface tensions range from 1.47 N/m at a temperature of 2305 K to 1.53 N/m at 1823 K. Within the error bars of ± 5%, the results are in good agreement with the displayed results from literature [17, 40], although they are by a little more than half a percent lower.

The surface tension follows a linear law with a negative slope. This is represented by the following equation, whereas γL denotes the surface tension at the liquidus temperature TL and γT denotes the temperature coefficient, i.e., the slope:

$$\gamma \left( T \right) = \gamma_{{\text{L}}} + \gamma_{{\text{T}}} \left( {T - T_{{\text{L}}} } \right)$$
(10)

Fitting Eq. (10) to the data in Fig. 1 yields γL = 1.52(± 0.01) N/m and γT =  − 1.8(± 0.3)·10−4 N·m−1 K−1, see Table 4.

Table 4 Parameters TL, γL, γT for pure elements titanium and vanadium with the corresponding uncertainties
Full size table

In the case of liquid V, Fig. 2, the temperature range extends from 1950 to 2300 K. Thus, a deep undercooling of the liquidus temperature, TL = 2183 K, by more than 200 K is evident. The measured surface tensions range from 1.92 N/m at 2290 K to 2.06 N/m at 1957 K. Within the error bars of ± 5% the results are in excellent agreement with those of Okada [42]. Again, γ linearly decays with temperature. Fitting of Eq. (10) yields γL = 1.94(± 0.07) N/m and γT =  − 3.3(± 0.07)·10−4 N·m−1 K−1, see Table 4.

Alloys

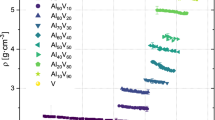
In the case of the binary Ti-V alloys, the temperature dependent surface tension data γ (T) are shown in Fig. 3. For the sake of completeness, the figure also shows the data of the pure elements. An overall temperature range from ≈1800 K to ≈2300 K is covered for all samples. Similar to the cases of the pure elements, γ is obtained as linear functions of T with negative slopes. The corresponding parameters γL and γT, obtained from fitting Eq. (10), are listed in Table 5. As a general trend, the surface tension decreases with increasing Ti bulk mole fraction xBTi. In order to further discuss this dependence on concentration, the surface tension at T = 2100 K is calculated using Eq. (10) and the parameters in Table 5. This temperature is marked in Fig. 3 by a vertical line. It was chosen because, for all alloys, it lies in the center of the investigated temperature intervals.

Figure 3
figure 3

Surface tension of liquid Ti, V and Ti-V binary alloys versus temperature. The solid lines represent the fits according to Eq. (10). The dashed line marks 2100 K, a reference point for the compositional dependence

Full size image
Table 5 Parameters TL, \(\gamma_{{\text{L}}}\), and \(\gamma_{{\text{T}}}\) for every composition examined in the Ti-V system
Full size table

The result γ (2100 K) is plotted in Fig. 4 versus xBTi. Obviously, there is a monotonous decrease of γ with xBTi following a moderately convex curve from 1.97 N/m corresponding to pure liquid V down to 1.46 N/m for pure liquid Ti. The non-linear shape of the curve indicates already, that the surface is slightly enriched in Ti, since pure Ti has the lower surface tension of the two components.

Figure 4
figure 4

Isothermal surface tension of liquid Ti-V at 2100 K as a function of the titanium bulk mole fraction xBTi. The red line represents the surface tension of an ideal solution calculated from Eq. (6). For comparison, the blue dashed line shows the surface tension calculated for a regular solution, using the Butler model analogous to Ref. [43]

Full size image

In Fig. 3, the steepness of the curves, i.e., the temperature coefficient γT, also varies with composition in a way, that the γ-T curves in Fig. 3 are steeper for the pure elements and flatter for the alloys. This is shown in detail in Fig. 5 where γT is plotted versus xBTi. Starting on the side of pure vanadium in the figure, γT steeply increases with xBTi from initially − 3.3·10−4 N·m−1 K−1 to − 9.8·10−5 N/m/K at xBTii = 5 at. − %, i.e., within the first few at. − % of Ti. The further increase is much slower and there appears to be a maximum of γT at xBTi = 37 at. − % where γT =  − 3.64·10−5 N·m−1 K−1. Upon further increase of xBTi the temperature coefficient γT is decreasing slowly but monotonously with respect to the margin of scatter until the value of pure Ti, − 1.80·10−4 N·m−1 K−1, is reached. This behavior indicates a smaller surface entropy of the alloys as compared to the pure elements which, interestingly, may be interpreted as that there is a higher degree of order.

Figure 5
figure 5

Temperature coefficient γT versus the titanium bulk mole fraction xBTi. The solid line represents the calculation utilizing the Butler model, Eq. (6), for the ideal solution. The dashed line represents the regular solution

Full size image

The results in Figs. 4 and 5 can be compared to the Butler equation, Eq. (6). For this purpose, the temperature dependent data of \(V_{{{\text{Ti}}}}^{0}\) and \(V_{{\text{V}}}^{0}\), needed in Eq. (5), are derived from the corresponding density data in our previous work on Ti-V [21]. They are listed in Table 6 together with corresponding volume expansion coefficients β. The latter are used in order to calculate the Butler equation at different temperatures. In addition, γ is calculated for T = 2090 K and for T = 2110 K, so that the temperature coefficient γT is obtained as γT = (γ(2110 K)- γ(2090 K))/20 K.

Table 6 Parameters for pure Ti and V used in order to calculate the Butler equation,
Full size table

Thus, Figs. 4 and 5 also show the calculations, Eq. (6), of γ at 2100 K and γT as functions of the Ti bulk mole fraction xBTi. Obviously, the agreement with the experimental data is excellent. In Fig. 4, the Butler equation exactly reproduces the data and it needs to be emphasized at this point, that Eq. (6) is purely predictive and that no kind of fitting or adjustment to the data is involved. For comparison, the surface tension calculated for the regular solution using the Butler equation is also included. The calculations for the regular solutions have been done analogous to Ref. [43]. Using the Redlich–Kister coefficients from [30], the calculated excess Gibbs energies are very small and thus the difference between the calculations for the ideal and regular solution are neglectable. This strengthens the findings of Ti-V showing near ideal behavior in regard to the surface tension. However, since the excess Gibbs energies are different from zero, the mixing behavior in the liquid phase is not exactly ideal in a strict sense, but they are extremely close to ideal, so that there is no difference from a practical point of view.

In Fig. 5, the values of γT are also nicely reproduced qualitatively, as well as quantitatively. The calculated curve highlights details in the experimental data, which would not have so easily become obvious without the calculation: For instance, it shows that the true position of the maximum is at xBTi = 20 at. − % rather than at 37 at. − % as indicated by the data and also, there seems to be an inflection point at around xBTi = 40 at. − % where the curvature of the graph changes from concave to convex.

In addition to the surface tension, the Butler equation can also predict the surface Ti mole fraction xSTi. This is shown in Figs. 6 and 7 for a constant temperature T = 2100 K. Figure 6 compares the segregation of three different titanium alloys, namely Al-Ti, Cu-Ti and Ti-V. For this comparison, the model that reproduces the measured surface tension data best was used to calculate the surface composition of the respective alloy. Subsequently the surface concentration of the segregating species was plotted against the bulk concentration of the segregating species. The diagram displays a convex curve for Ti-V with a moderately strong increase on the left hand side in the figure so that xSSeg ≈ 80 at. − % is already reached at xBSeg ≈ 50 at.-%. In the case of Ti-V, the segregating species is Ti (\(x_{{{\text{Seg}}.}}^{s} = x_{{{\text{Ti}}.}}^{s} )\), thus, in liquid Ti-V, the surface is enriched in Ti. This so called (surface-)segregation obviously takes place already if, as in the case of present study, the ideal solution model is considered. The phenomenon can be interpreted in terms of overall energy minimization. Thus, by segregation of the component with the smaller surface free energy, Ti in the case of Ti-V, the total energy of the system is minimized. Consequently, the effect is larger in systems with a positive excess free energy EG > 0, i.e., where there is a tendency to demix [29]. In contrast to this, attractively mixing systems where EG < 0 exhibit only weak segregation [29].

Figure 6
figure 6

Calculated mole fraction \(x_{{{\text{Seg}}.}}^{S}\) of the segregating species in the surface layer for different Ti-based alloys at 2100 K as a function of the bulk mole fraction \(x_{{{\text{Seg}}.}}^{B}\). For each composition the Butler model was chosen, that represents the respective measured data best. For Al-Ti and Cu-Ti this is the case for the Butler model of the regular solution. For Ti-V this is the case for the ideal solution Butler model

Full size image
Figure 7
figure 7

Calculated mole fraction \(x_{{{\text{Ti}}.}}^{S}\) of titanium in the surface layer for Ti-V compared to Al-Ti at 2100 K as a function of the bulk mole fraction \(x_{{{\text{Ti}}.}}^{B}\). For each alloy the Butler model for the ideal as well as the regular solution is displayed. The solid line represents the ideal solution, while the dashed line represents the regular solution

Full size image

In Fig. 7, the surface concentration of titanium is shown as a function of the bulk titanium concentration for both Ti-V and Al-Ti. Calculations using the Butler model for both, the ideal and the regular solution are shown for either system. Ti-V shows moderate segregation compared to the strong segregation of Al-Ti. Additionally, for the Ti-V system the surface is enriched in Ti, while the opposite is true for Al-Ti. However, in the case of Al-Ti, the experimentally measured data are not adequately reproduced by the Butler equation for the ideal solution. Instead the Butler model for the regular solution needs to be implemented, which shows a significantly weaker segregation effect, especially at mole fractions ≥ 0.5. For Ti-V the deviation between both models is neglectable small.

Discussion

The fact, that the surface tension of the Ti-V system can be well be reproduced by the Butler-equation for the ideal solution, see Figs. 4 and 5, is remarkable, because it agrees with our earlier observation that also the molar volume of liquid Ti-V obeys the ideal solution model [21]. In our investigations regarding the density and molar volume of the Ti-V system we suggested the similarities in electronic structure of Ti and V, both being d-transition metals, as a possible indicator for the lack of excess volume in the system. The same argument can be applied when considering the surface tension of liquid Ti-V. The proximity of Ti and V in the periodic table may imply, that the electronic structure does not change dramatically upon mixing, indicating an overall ideal behavior. The present work confirms this hypothesis for the surface tension, since no significant excess surface tension was evident.

Brillo [29] ordered several binary and ternary metallic systems in two groups regarding their behavior upon mixing, as well as their excess surface tension. Systems of the first group tend to demix, showing a positive excess free energy \({}_{{}}^{E} G > 0\), a negative excess surface tension and a strong segregation behavior while systems belonging to the second group tend to mix, showing negative excess free energy \({}_{{}}^{E} G < 0\), a positive excess surface tension. All titanium alloys investigated at our institute, much like most titanium alloys, show a negative excess free energy and therefore fit in the second group. Even though for Ti-V the excess free energy calculated from [43] almost zero, it is still negative. It can be seen, that Ti-V shows moderate segregation, similar to that of the other titanium alloys displayed.

In an effort to illustrate the ideality of the Ti-V system, the segregation of the Ti-V system was compared to that of the Al-Ti system in Fig. 7. Here two things become evident. Firstly, for Ti-V titanium is the segregating species, while for Al-Ti aluminum segregates to the surface. Secondly, there is a significant difference between the calculations of the Butler model for the ideal and the regular solution in case of Al-Ti while the difference is neglectable small for the Ti-V system. So, while the general magnitude of the segregation seems to be related to the excess free energy as classified in [29], the segregating species as well as the ideality of the surface composition seems to be highly dependent on the alloying element for Ti- alloys.

Another sign for liquid Ti-V being an ideal solution is the phase diagram [23] which is characterized by convex solidus- and liquidus lines close together become are tangent to each other in one point, namely the azeotropic point at high temperatures, as well as a miscibility gap at low temperatures. Phase diagrams of this form are exemplary for systems with an ideal behavior in the liquid phase and demixing solid phase [44]. A similar phase diagram, also with an azeotropic point, is exhibited by the Au-Cu system [45] which, similar to Ti-V is regarded as an ideal solution, just as Ag-Au, where the solidus and liquidus lines are lentil-shaped [46] indicating that mixing entropy dominates over the mixing enthalpy. Knowing that Ag-Au, Au-Cu and Ti-V all show almost no excess volume it would be highly interesting to investigate if Ag-Au and Au-Cu also show the same surface tension and segregation behavior as Ti-V.

As shown, existing thermophysical assessments suggest a neglectable small, negative excess free energy \({}_{{}}^{E} G\) [47] and excess enthalpy \({}_{{}}^{E} H\) [30] for the Ti-V system. These calculations, combined with the experimental findings of this and our previews work strongly indicate that the liquid Ti-V system overall follows the ideal solution model. Whether other thermophysical properties of the system also follow the ideal solution law should be subject of future studies.

Summary

The oscillating drop technique has been used in electromagnetic levitation in order to systematically investigate the surface tension of the liquid binary Ti-V system over a broad temperature range. A linear decrease of the surface tension with increasing temperature was found for all investigated compositions. Thereupon the isothermal compositional surface tension dependence was developed for the liquid Ti-V system. The experimental data show excellent agreement with the Butler model for an ideal solution. Accordingly, no excess surface tension was evident. The experimental surface tension temperature coefficient is also well represented by the Butler model for the ideal solution. Therefore, the same model was used in order to investigate the segregation behavior of the liquid Ti-V system. It was shown, that the segregation behavior of Ti-alloys strongly depends on the alloying element as well as the excess free energy. Alloys with a positive excess energy show strong segregation, alloys with negative excess energy show rather weak segregation, while the Ti-V system shows moderate segregation effects corresponding to the non-existent excess free energy. The assumption of the Ti-V system as an overall ideal solution was further fortified by the analysis of the surface tension.