Introduction

There is a wide range of titanium alloys in numerous technical applications of great variety, with vanadium being one of the most prominent alloying elements [1]. Vanadium acts as a \(\beta\) stabilizer and therefore plays a significant role in many \(\alpha +\beta\) titanium alloys [2]. These alloys show plenty of beneficial properties, such as low density, high mechanical strength and toughness as well as good corrosion resistance, making them prime candidates for construction materials used under extreme conditions as can be found in many aerospace applications with turbine blades being a prime example [3, 4]. Combining these favorable mechanical properties with a high biocompatibility, \(\alpha +\beta\) titanium alloys are of high interest for many medical industries [5].

The recent progress in additive manufacturing rouse a great interest for \(\alpha +\beta\) titanium alloys as feedstock for these processes [4, 6]. A great deal of research is done assessing these alloys—the most established being the Ti6Al4V alloy—regarding their processability in additive manufacturing processes [7, 8]. A majority of this research is focused on understanding and modeling the behavior of the melt during processes like selective laser melting (SLM) or electron beam melting (EBM). Reliable thermophysical property data of the liquid Ti–V system is as vital for these investigations as it is sparse.

Density and the molar volume are two of the most fundamental thermophysical properties, often used to calculate and model many other material properties. The rather high melting temperatures of titanium and vanadium of 1941 K (1668 °C) and 2183 K (1910 °C), respectively, greatly complicate their measurement using conventional container-based methods such as the sessile drop or bubble pressure methods. Due to the highly reactive nature of the liquid Ti–V system, a container-less measurement needs to be implemented in order to avoid any reactions of the investigated liquid with existing container walls. Many scientific works have already demonstrated the advantages of electromagnetic levitation for processing highly reactive metal melts [9, 10]. In this work the already established optical dilatometry method is used for the density determination [9, 11].

In view of the high industrial relevance and importance of the Al–Ti–V system, it is somewhat surprising that information on systematic thermophysical property data of the liquid phase is sparse or practically not available.

It is the overall goal of the present work to change this situation.

Some results, mostly gathered by ourselves, can already be found in literature [12,13,14,15,16] for the liquid binary Al–Ti system. These include data on density, molar volume and excess volume [13]. It is therefore the next logical step to also investigate the liquid binary Ti–V system, i.e., measuring its density in order to complement our previous investigations of Al–Ti [17].

So far, there is not yet any model or rule of thumb in order to predict the molar volume of any liquid alloy, its excess volume or even the sign of the latter [18]. Titanium alloys generally show a strongly non-ideal behavior with regard to their mixing properties. In particular, Al–Ti alloys exhibit a strongly negative excess volume [13], while the opposite is true for Cu–Ti alloys [19] although both systems exhibit a negative excess free energy corresponding to strong attractive interactions between unlike atoms.

On the other hand, it has been shown that liquid alloys consisting of elements with similar electronic configuration seem to exhibit almost ideal behavior with respect to the molar volume [18]. Prominent examples are Fe–Ni [20] and Co–Fe [21], where the constituents are 3d-transition metals. Other examples are Au–Cu [22], Ag–Au [23], as well as Ag–Cu [23] where the constituents are all semi-noble s-metals. Ti–V belongs to this class as well, as both elements are 3d-transition metals with incomplete d-shell. It is therefore especially interesting to investigate, how Ti–V behaves with respect to the molar volume, i.e., whether it will exhibit rather ideal behavior or highly non-ideal behavior as would generally be the case for Ti alloys.

In this work, the densities of several Ti–V alloys of varying compositions are measured, in order to obtain the compositional as well as the temperature dependence of the system. Thereupon, the molar volume of the Ti–V system is discussed in relation to existing trends predicting the excess volume of metallic alloys [18, 19].

Experimental method

Electromagnetic Levitation

High-purity titanium (99.999 pct.) and vanadium (99.995 pct.) are used for sample preparation. After cutting and subsequent grinding to the desired masses the metals are cleaned in an ultrasonic bath using iso-propanol, before alloying in an arc furnace. In order to avoid a change in composition due to evaporation, the weight is determined before and after arc-melting. Prior to inserting the samples into the levitation apparatus, another cleaning cycle was carried out. Typical sample masses are around 1 g; the diameters are typically around 7 mm.

Measurements are taken in an inert He, Ar (99.9999 vol pct. purity) mixture atmosphere of 750 mbar. The vacuum chamber is previously evacuated down to at least 10–6 mbar in order to avoid pollution from residual gas components such as H2O, O2, CO, CO2 and hydrocarbons. The sample is placed in the center of a water-cooled copper coil, resting on an alumina specimen holder. An alternating current of 200 A with a frequency of approximately 250 kHz then generates an inhomogeneous electromagnetic field surrounding the coil. The resulting eddy currents inside the sample lead to a stable levitation of the specimen. The ohmic losses that go along with the eddy currents continuously heat and eventually melt the sample. Thus, to control the temperature of the sample, He cooling gas has to be applied to the sample through an alumina nozzle in a laminar flow. Further information regarding the electromagnetic levitation technique used in this work can be found in reference [9].

The droplet temperature is observed via a single-color pyrometer. Since the emissivity of the alloy droplet is generally unknown, a correction of the pyrometer signal is necessary to obtain the actual temperature \(T\) of the sample. Assuming that the effective emissivity does not change over the temperature range of the measurement, T can be estimated using the equation below, which is derived from Wiens’ law [24]:

$$\frac{1}{T}-\frac{1}{{T}_{P}}=\frac{1}{{T}_{L}}-\frac{1}{{T}_{L,P}}$$
(1)

Here, \({T}_{P}\) is the uncorrected pyrometer signal, \({T}_{L}\) is the true liquidus temperature, and \({T}_{L,P}\) denotes the liquidus temperature observed in the pyrometer signal.\({T}_{L,P}\) manifests in the pyrometer signal as a kink, when the melting process is concluded. In this work \({T}_{L}\) is taken from the phase diagram reported in Reference [25]. The liquidus temperature for each composition, as well as the measurement temperature range \({T}_{min}\) to \({T}_{max}\), is listed in Table 1. More details regarding this correction procedure can be found in reference [24].

Table 1 Liquidus temperature, minimum measurement temperature Tmin and maximum measurement temperature Tmax for each investigated composition. The liquidus temperatures are read out of the phase diagram introduced in Ref. [25]
Full size table

Density Determination

The density of a sample in electromagnetic levitation is measured by determination of the sample volume. With the known sample mass the density can be calculated. For the volume determination in this work, the optical dilatometry method is used [9, 26]. This method utilizes an expanded laser to project a shadowgraph image of the levitating sample onto a CCD camera opposite to the laser. Figure 1 schematically illustrates the experimental setup of the optical dilatometry in electromagnetic levitation, and Fig. 2a shows a shadowgraph captured for pure titanium. The optical elements (polarizer, filter and pinhole) ensure that only non-scattered light directly from the laser reaches the camera. A more detailed description of the optical dilatometry can be found in [9, 18, 27].

Figure 1
figure 1

Schematic of the optical dilatometry setup used in this work. From the shadowgraph image, projected on the CCD sensor, the sample volume, and ultimately the density, is calculated

Full size image
Figure 2
figure 2

a Shadowgraph of a levitated, molten titanium sample, recorded with the used setup. b Edge curve fitted to the obtained shadow graph. The gray squares indicate where the software detected the edge area of the sample. The edge curve is depicted in pink

Full size image

For each captured image, an edge curve \(R(\varphi )\) of the shadowgraph is determined by an edge detection algorithm. Here, \(R\) is the radius from the droplet center as a function of the azimuthal angle \(\varphi\). The algorithm is described in more detail in [28]. For each measurement, the edge curve, averaged over 2500 frames, is fitted by Legendre polynomials of order ≤ 6 according to the following formula:

$$\langle R(\varphi )\rangle =\sum_{i=0}^{6}{a}_{i}{\Pi }_{i}(\mathrm{cos}\left(\varphi \right))$$
(2)

\({\Pi }_{i}\) is the ith Legendre polynomial, \({a}_{i}\) is the series coefficient, and \(\langle \dots \rangle\) marks time averaging carried out for each angle φ separately. Assuming rotational symmetry of the averaged sample image with respect to the vertical specimen axis the volume VP can be calculated from the following equation:

$${V}_{P}=\frac{2}{3}\pi {\int }_{0}^{\pi }{\langle R(\varphi )\rangle }^{3}\mathrm{sin}\left(\varphi \right)d\varphi$$
(3)

The expression yields the specimen volume VP in pixel3 units. Figure 2b shows the edge detection of a shadowgraph. The gray squares indicate the area where the algorithm detected the edge of the sample. The pink curve shows the edge detected by the algorithm. A calibration with metal balls of precisely known dimensions provides a scaling factor \(q\) to subsequently calculate the real sample volume \({V}^{S}\). More information about the calibration procedure can be found in [28]. The density ρ is then calculated as \(\rho ={m}_{S} {{(\mathrm{V}}^{S})}^{-1}\), where \({m}_{S}\) is the sample mass.

To measure the temperature dependency, the density measurements were taken in incremental steps from high to low temperature. Before each measurement the sample was given 40 s to reach thermal equilibrium. Two ways were used to reduce the sample temperature. For the first 100 K the generator power was stepwise reduced; therefore, reducing the heating power induced into the sample. This cooling method is limited since a reduction in heating power also results in a reduction of levitation force, subsequently resulting in a more turbulent levitation. Therefore, the reduction was limited to 10% of the generator power. Following the generator power reduction, the sample was cooled by gradually increasing the cooling gas flow. Throughout the measurement, the gas flow was kept low enough, so that no change in the levitation behavior of the sample could be observed.

The measurement error relates to errors in mass \(\Delta m\), calibration \(\Delta q\), volume \(\Delta {V}_{p}\) and temperature \(\Delta T\). Additionally, strong lateral and rotational sample movement can distort the sample shape, falsifying the volume calculation. Mass loss due to evaporation, the calibration error and sample rotation has the most severe impact on the measurement accuracy. To cushion the effect of mass loss, samples were weighted before and after the levitation and discarded if the loss in mass was \(\ge 0.3\%\). Following Ref. [23], the error in density \(\Delta \rho\) was estimated using the following expression:

$$\frac{{\Delta \rho }^{2}}{{\rho }^{2}}=\frac{{\Delta m}^{2}}{{m}^{2}}+\frac{{\Delta q}^{2}}{q}+\frac{\Delta {V}_{p}^{2}}{{V}_{p}^{2}}+{(\frac{\partial {V}_{p}}{\partial T})}^{2}\frac{{\Delta T}^{2}}{{V}_{p}^{2}}$$
(4)

In addition to the before-mentioned sources of errors special attention has to be paid to the axial symmetry of the sample as well as to the oxygen influence during the measurement. The latter has been carefully examined for titanium by Wessing [17]. The bottom line of this research is that although titanium has a high solubility of oxygen, only a high oxygen content of more than 1 at% has a noticeable impact on the thermodynamic properties of the melt. It was shown [17] that the inert high-purity argon atmosphere used during all sample preparation steps, as well as during the measurement itself ensures, that the samples stay well below that threshold content at all times. Nevertheless, research aimed at investigating the thermophysical properties of the Ti–V–O system is currently being carried out by our group.

Regarding the axial symmetry of the sample during the measurement, Brillo et al. [29] developed a method that allows the density determination for samples whose (time-)averaged shape deviates from the axial symmetry assumption during the levitation. The method utilizes a second camera that independently records the sample from a top point of view. The recorded frames are subsequently used to calculate the real sample volume if the assumption of axial symmetry is violated. This method was used as a spot check to assure the mean axial symmetry during the measurements. Figure 3 shows a comparison of our “conventional” measurement and a measurement using the 2nd camera method. It can be seen that the hollow squares which represent the density measured with the 2nd camera method lie well inside the error bars of the filled squares representing the conventional method under the assumption of a mean axial symmetry over the measurement period. Therefore, the validity of the condition of axial symmetry is evident. The inlay in Fig. 3 shows an image of the molten sample captured with the 2nd camera in top view.

The order of magnitude for every considered error source is listed in Table 2 together with the resulting impact on the density measurement. Trying to minimize all the influences mentioned above, the uncertainty in density was around \(\pm 1\) pct.

Table 2 Error sources for the optical dilatometry and their order of magnitude, as well as their impact on the density measurement. T denotes the Temperature, m the sample mass, Vp the sample volume in pixels and q the scaling factor for the real sample volume
Full size table

Pure Ti samples with a mass of around 1 g could be steadily levitated, while their circumference is fully visible in the shadowgraph images. Due to the higher melting point of vanadium compared to titanium, the sample mass has been slightly increased for the pure vanadium measurement. The increased sample size results in an expanded temperature range but also causes more intense sample motion, thus leading to a slightly increased scatter in the measurements for vanadium. The levitation behavior of the sample was carefully observed during the cooling. No change in shape or levitation behavior could be observed for neither the generator cooling nor the gas cooling. Combined with the low cooling gas flow and the large diameter of the cooling nozzle this leads to the assumption that the gas cooling has no influence on the sample shape, and thus the volume, of the levitated sample.

To ensure a steady levitation behavior the sample masses of the investigated liquid Ti–V alloys have been increased from the mass of the pure titanium sample to the pure vanadium sample mass with increasing vanadium content. Neither strong translational nor heavy rotational sample movement has been observed (Fig. 3).

Figure 3
figure 3

Comparison of density measurements of liquid titanium carried out with the conventional optical dilatometry (filled squares) and with the method introduced in [29] utilizing a second camera directed at the sample from the top. The inset shows an image of the molten sample captured with the 2nd camera. Both methods provide almost identical data

Full size image

Results

Pure elements

A reasonable density measurement could be carried out over a temperature range of \(\Delta T\approx 230\mathrm{K}\). In this temperature range no major evaporation was observed. The densities for the pure elements, \(\rho (T)\), are shown as functions of the temperature T in Figs. 4 and 5 for liquid Ti and V, respectively. For liquid Ti, the measured density decreases linearly from approximately \(\approx 4.22\mathrm{ g }{\mathrm{cm}}^{-3}\) at 2088 K (1815 °C) to about \(\approx 4.19\mathrm{ g }{\mathrm{cm}}^{-3}\) at 1858 K (1585 °C). Liquid V shows a steeper decline from \(\approx 5.71 \mathrm{g }{\mathrm{cm}}^{-3}\) at 2234 K (1961 °C) to \(\approx 5.50 \mathrm{g }{\mathrm{cm}}^{-3}\) at 1927 K (1654 °C). In both figures, the dashed lines represent results from the literature [30, 31] for comparison. In both cases the results of this work are a little higher, but still in reasonable agreement with the reported data, regarding the calculated error for both measurements.

Figure 4
figure 4

Density of liquid titanium versus temperature. The solid line represents the fit from Eq. (5). The dashed line shows data by Paradis et al. [31] for comparison

Full size image
Figure 5
figure 5

Density of liquid vanadium versus temperature. The solid line represents the fit from Eq. (5). The dashed line shows data measured in electrostatic levitation by Ishikawa et al. [30] for comparison

Full size image

The clear linear decline for both elements allows for a fit, following the equation:

$$\rho ={\rho }_{L}+{\rho }_{T}(T-{T}_{L})$$
(5)

Here \(T\) is the temperature, \({\rho }_{L}\) is the density at the liquidus temperature \({T}_{L}\), and \({\rho }_{T}=\frac{\partial \rho }{\partial T}\) is the constant temperature coefficient. The fits are shown for both elements as solid lines in Figs. 4 and 5, respectively. The obtained parameters \({\rho }_{T}\) and \({\rho }_{L}\), as well as their uncertainties calculated from Eq. (4), are compared with literature data for the corresponding element in Table 3.

Table 3 Parameters TL, ρL, ρT for pure elements titanium and vanadium with the corresponding uncertainties. Additionally, the isothermal densities for 2023 K are shown
Full size table

Alloys

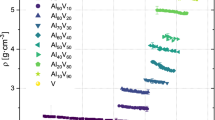
The density for each examined alloy is plotted against the temperature in Fig. 6. Pure titanium and vanadium are included for reference. Every binary alloy, as well as the pure elements, could be investigated over a temperature range of at least 300 K. The obtained fitting parameters following Eq. (4), as well as the calculated density at 2023 K can be found in Table 4. Different symbols of the same kind and color represent different measurements for the same alloy. The density for all samples in the liquid Ti–V system varies between the density of pure vanadium and the density of pure titanium, decreasing with increasing titanium content. All analyzed alloys show a linear decrease in density with increasing temperature. Linear fits, corresponding to Eq. (5), are included for every composition as solid lines.

Figure 6
figure 6

Density of liquid Ti, V, and Ti–V binary alloys versus the temperature. The solid lines represent the fits, according to Eq. (5) for each composition. The dashed line marks 2023 K (1750 °C), a reference point for the following analysis

Full size image
Table 4 Parameters TL, ρL, ρT for every sample examined in the Ti–V system. Additionally, the isothermal densities for 2023 K are shown
Full size table

Composition Dependence

To examine the compositional dependence of the density, ρ at 2023 K is calculated from the obtained fits for each composition. 2023 K was chosen for the isothermal density comparison because it lays well in the middle of all experimental temperature ranges. The resulting compositional dependency of the density is shown in Fig. 7 for increasing vanadium mole fraction xV. The density increases nearly linear with increasing vanadium content. The dashed line in Fig. 7 represents the compositional dependency of the density for an ideal solution of titanium and vanadium.

Figure 7
figure 7

Isothermal density of liquid Ti–V at 2023 K (1750 °C) as a function of the mole fraction \({\mathrm{x}}_{\mathrm{V}}\). The dashed line represents the density of an ideal solution calculation from the molar volume from Eq. (6)

Full size image

Under the assumption of an ideal solution, the density can be calculated utilizing the molar volume. For Ti–V the ideal molar volume Vid can be calculated as

$${V}^{id}={x}_{Ti}{V}_{Ti}+{x}_{V}{V}_{V}$$
(6)

where \({x}_{Ti}\) and \({x}_{V}\) denote the mole fractions of Ti and V with \({V}_{Ti}\) and \({V}_{V}\) representing the molar volume of pure liquid titanium and vanadium, respectively. Typically, the molar volume of liquid titanium alloys such as Ni–Ti and Al–Ti derives from the ideal behavior [13, 29]. The difference between the ideal molar volume Vid and the observed molar volume Vmol is the so-called excess volume \({V}^{E}\). Using the corresponding isothermal densities, the molar volume at 2023 K could be calculated for every analyzed composition. The result is shown in Fig. 8. An almost linear decline from 11.5 cm3mol−1 for liquid titanium to 8.9 cm3mol−1 for liquid vanadium can be observed. The molar volume for an ideal solution, following Eq. (6), was included as the dashed line.

Figure 8
figure 8

Isothermal molar volume at 2023 K (1750 °C) as a function of the V mole fraction \({\upchi }_{\mathrm{V}}\). The dashed line represents the molar volume of an ideal solution, calculated using Eq. (6)

Full size image

With the greatest deviation of the observed molar volume from the ideal molar volume being roughly 1.5 pct., it is reasonable to assume that the liquid Ti–V system shows no significant excess volume. The lack of an excess volume strongly indicates that the Ti–V system behaves like an ideal solution with regard to density and molar volume. This stands in contrast to other Ti-based alloys that show either negative excess volume like the Ti–Al [13] and Ti–Ni [29] systems or a positive excess volume like the Ti–Cu [19] system.

Temperature Dependence

Figure 9 shows the temperature coefficient \({\rho }_{T}\) as a function of the vanadium content. The temperature coefficient decreases with increasing vanadium content. Taking the negative sign into account this indicates a stronger temperature dependency for the density of alloys with higher vanadium content, since \({\rho }_{T}\) represents the differentiation of the density \(\rho \left(T\right)=M/V(T)\), utilizing Eq. (6) to describe V(T). Since the Ti–V system shows no excess volume \({V}^{E}\), \({\rho }_{T}\) can thus be calculated as [32]:

$${\rho }_{T}=M\frac{[{x}_{Ti}\frac{{M}_{Ti}{\rho }_{T,Ti}}{{\rho }_{Ti}^{2}}+{x}_{V}\frac{{M}_{V}{\rho }_{T,V}}{{\rho }_{V}^{2}}]}{{{(V}^{id})}^{2}}$$
(7)
Figure 9
figure 9

Temperature coefficient for the density calculation following Eq. (5), versus the V mole fraction \({\mathrm{x}}_{\mathrm{V}}\). The dashed line represents the temperature coefficient derived from the pure elements following Eq. (7)

Full size image

Here \({\rho }_{T,Ti}\) and \({\rho }_{T,V}\) are the temperature coefficients for the pure titanium and vanadium. \({M}_{Ti}\) and \({M}_{V}\) are the molar volumes of the pure elements. Note that the temperature coefficient can be calculated for every composition utilizing solely parameters of the pure elements. Figure 9 shows Eq. (7) as a dashed line. Within error bars of ≈1%, there is convincing agreement between this calculation and the experimental data. This confirms the assumption that, with respect to density and molar volume, Ti–V is an ideal system.

Discussion

Up to now, no clear rule or model to predict the excess volume of an alloy could be established [18]. In addition, for different titanium alloys widely different excess volumes have been observed [13, 19]. However, several general trends and dependencies have been proposed in recent works. Brillo et al. [33] classified various binary and ternary alloys into three different groups, proposing several basic trends for the sign of the excess volume for each group. Following these trends, the Ti–V system should display little to no excess volume, since titanium and vanadium show a similar electronic structure indicated by their proximity in the periodic table. This conforms with the findings in this work of an ideal behavior for the Ti–V system.

Other works suggest a link between the excess volume of a system and its excess free energy. Watanabe postulated a correlation between the excess volume and the excess free energy for Pt-X [34] and Fe–Ni [35] melts. This work has recently been extended for numerous other alloys, connecting the excess volume with the exhibited excess free energy [36]. Existing calculations [37] suggest a slightly positive excess free energy for the Ti–V system. Combining this calculated excess free energy with the correlation proposed by Watanabe, predicts no significant excess volume, which agrees with the results of the present work.

However, on the level of interatomic potential, molecular dynamics (MD) simulations by Amore et al. [38] lead to the conclusion that the excess volume yields no direct information about the mixing behavior of the system but rather results from the relation of repulsive and attractive interactions in chemical ordering, allowing for all possible combinations of the sign of the excess volume and the enthalpy of mixing. Taking these results into account, the Ti–V system showing no excess volume can be explained by a near equilibrium of attractive and repulsive interactions in chemical ordering. However, further investigations are required, e.g., MD simulations, to fully understand the mixing behavior of the Ti–V system.

Summary

The temperature and concentration dependency of the density was measured for the binary liquid Ti–V system, using the optical dilatometry method in electromagnetic levitation. A linear dependency was observed for temperature as well as for concentration. The obtained densities were analyzed concerning the molar volume. It was found that the liquid Ti–V system is a near-ideal system in reference to density, molar volume and temperature coefficient. No excess volume was observed for the liquid Ti–V system. The lack of excess volume allows for the application of simple formalisms in order to calculate the density for the liquid Ti–V system over the entire compositional range. With the Ti–Al system showing negative excess volume, the Ti–Cu system displaying a positive excess volume and this work finding no significant excess volume for the Ti–V system no clear trend for the excess volume in titanium containing alloys can be developed. In fact, the excess volume in titanium-based alloys is strongly dependent on the present alloying elements. However, the Ti–V system follows and fortifies several trends developed by previous research, predicting no excess volume for systems consisting of elements with similar electronic structure [33] and systems with a comparatively small positive excess free energy [34].