Categorical relations between Langlands dual quantum affine algebras: doubly laced types

Abstract

We prove that the Grothendieck rings of category $\mathcal {C}^{(t)}_Q$ over quantum affine algebras $U_q'(\mathfrak {g}^{(t)})$$(t=1,2)$ associated with each Dynkin quiver Q of finite type $A_{2n-1}$ (resp. $D_{n+1}$) are isomorphic to one of the categories $\mathcal {C}_{\mathscr {Q}}$ over the Langlands dual $U_q'({^L}\mathfrak {g}^{(2)})$ of $U_q'(\mathfrak {g}^{(2)})$ associated with any twisted adapted class $[\mathscr {Q}]$ of $A_{2n-1}$ (resp. $D_{n+1}$). This results provide simplicity-preserving correspondences on Langlands duality for finite-dimensional representation of quantum affine algebras, suggested by Frenkel–Hernandez.

1 Introduction

Let $U_q'(\mathfrak {g}^{(r)})$$(r=2,3)$ be the twisted quantum affine algebra ($\mathfrak {g}^{(r)}=A_{2n-1}^{(2)}$, $D_{n+1}^{(2)}$,$E_{6}^{(2)}$,$D_{4}^{(3)}$), and let $U_q'({^L}\mathfrak {g}^{(r)})$ be its untwisted Langlands dual (${}^L\mathfrak {g}^{(r)}=B_{n}^{(1)}$,$C_{n}^{(1)}$,$F_{4}^{(1)}$,$G_{2}^{(1)}$) whose generalized Cartan matrix is the transpose of that of $U_q'(\mathfrak {g}^{(r)})$. Let us denote by $\mathcal {W}_{q,t}({{\varvec{g}}})$ the (q, t)-deformed $\mathcal {W}({{\varvec{g}}})$-algebra associated with the simple Lie subalgebra ${{\varvec{g}}}$ of $^{L}\mathfrak {g}^{(r)}$, introduced by Frenkel and Reshetikhin in [8] (see also [27]). Then it is known that (i) the limit $q \rightarrow \mathrm{exp}(\pi i /r)$ of $\mathcal {W}_{q,t}({{\varvec{g}}})$ recovers the commutative Grothendieck ring of finite-dimensional integrable representations $\mathcal {C}_{\mathfrak {g}^{(r)}}$ over $U_q'(\mathfrak {g}^{(r)})$, and (ii) the limit $t \rightarrow 1$ of $\mathcal {W}_{q,t}({{\varvec{g}}})$ recovers the one of $\mathcal {C}_{{^L}\mathfrak {g}^{(r)}}$ over $U_q'({^L}\mathfrak {g}^{(r)})$ [7]:

(1.1)

Thus, $\mathcal {W}_{q,t}({{\varvec{g}}})$interpolates the Grothendieck rings of the categories $\mathcal {C}_{\mathfrak {g}^{(r)}}$ and $\mathcal {C}_{{^L}\mathfrak {g}^{(r)}}$. Since then, the duality between the representations over $U_q'(\mathfrak {g}^{(r)})$ and $U_q'({^L}\mathfrak {g}^{(r)})$ has been intensively studied (for example, see [9, 10]). We remark that this duality is related to the geometric Langlands correspondence (see [10, Introduction]).

On the other hand, Hernandez [12] proved that, for the untwisted quantum affine algebra $U_q'(\mathfrak {g}^{(1)})$ ($\mathfrak {g}^{(1)}=A_{2n-1}^{(1)}$,$D_{n+1}^{(1)}$,$E_{6}^{(1)}$,$D_{4}^{(1)}$) corresponding to $U_q'(\mathfrak {g}^{(r)})$, the commutative Grothendieck ring of $\mathcal {C}_{\mathfrak {g}^{(1)}}$ is isomorphic to the one of $\mathcal {C}_{\mathfrak {g}^{(r)}}$:

(1.2)

Hence, we can expect that the isomorphisms among the Grothendieck groups can be lifted to equivalences of categories:

(1.3)

However, there is no satisfactory answer for the reason why such dualities happen. The goal of paper is to provide new point of view for these dualities through the categorification theory of quantum groups.

The quiver Hecke algebras $R_\mathsf {g}$, introduced by Khovanov–Lauda [25, 26] and Rouquier [37] independently, categorify the negative part $U^-_q(\mathsf {g})$ of quantum groups $U_q(\mathsf {g})$ for all symmetrizable Kac–Moody algebras $\mathsf {g}$. The categorification for (dual) PBW-bases and global bases of the integral form $U_\mathbb {A}^-(\mathsf {g})$ of $U^-_q(\mathsf {g})$ were developed very actively since the introduction of quiver Hecke algebras. Among them, [3, 24, 29] give the categorification theory for (dual) PBW-bases of $U^-_\mathbb {A}(\mathsf {g})$ associated with finite simple Lie algebra $\mathsf {g}$ by using convex orders on the set of positive roots $\Phi ^+$.

On the other hand, Hernandez and Leclerc [14] defined a subcategory $\mathcal {C}^{(1)}_Q$ of $\mathcal {C}_{\mathfrak {g}^{(1)}}$ for quantum affine algebras $U_q'(\mathfrak {g}^{(1)})$ of untwisted affine type ADE, which depends on the Auslander–Reiten quiver $\Gamma _Q$ for each Dynkin quiver Q of finite type ADE. They proved that $\mathcal {C}^{(1)}_Q$ categorifies $U^-_\mathbb {A}(\mathsf {g})^\vee |_{q=1}$, where $\mathsf {g}$ is the finite simple Lie subalgebra of $\mathfrak {g}^{(1)}$. Furthermore, they provided the categorification theories for the upper global basis and for the dual PBW-basis associated with Q via certain sets of modules in $\mathcal {C}^{(1)}_Q$.

For a quantum affine algebra $U_q'(\mathfrak {g})$, the first-named author and his collaborators constructed the quantum affine Schur–Weyl duality functor $\mathcal {F}: \mathrm{Rep}(R^\Xi ) \rightarrow \mathcal {C}_\mathfrak {g}$ by observing denominator formulas$d_{V,W}(z)$ of the normalized R-matrices $R^{\mathrm{norm}}_{V,W}(z)$ between good modules $V,W \in \mathcal {C}_\mathfrak {g}$ [17, 18]. Here $R^\Xi$ is the quiver Hecke algebra determined by Schur–Weyl datum $\Xi$ which depends on the choice of good modules in $\mathcal {C}_\mathfrak {g}$ (see Sect. 5.3 for details), and we denote by $\mathrm{Rep}(R^\Xi )$ the category of finite-dimensional modules over $R^\Xi$. In [18], they construct an exact functor

$$\begin{aligned} \mathcal {F}^{(1)}_Q : \mathrm{Rep}(R_\mathsf {g}) \overset{\simeq }{\longrightarrow } \mathcal {C}^{(1)}_Q\text { sending simples to simples}, \end{aligned}$$

(1.4)

where $\mathsf {g}=A_n$ or $D_n$ is a finite simple Lie subalgebra of $A_n^{(1)}$ or $D_n^{(1)}$, and Q is of type $\mathsf {g}$, respectively. Furthermore, the authors and their collaborators [19] defined the subcategory $\mathcal {C}^{(2)}_{Q'}$ of $\mathcal {C}_{\mathfrak {g}^{(2)}}$ and constructed twisted analogues of (1.4): For any Dynkin quivers Q and $Q'$ of type $A_n$ or $D_n$, we have

(1.5)

Here $\mathsf {g}=\mathfrak {g}=A_n$ or $D_n$. The above result provides the categorification theoretical interpretation of the similarity between the modules over $\mathcal {C}_{\mathfrak {g}^{(1)}}$ and $\mathcal {C}_{\mathfrak {g}^{(2)}}$, described in (1.2).

In this paper, we define certain subcategory $\mathscr {C}_{\mathscr {Q}}$ of $\mathcal {C}_{B_n^{(1)}}$ and $\mathcal {C}_{C_n^{(1)}}$ for any twisted adapted class $[\mathscr {Q}]$ of finite type $A_{2n-1}$ and $D_{n+1}$, and prove that (1) Grothendieck rings $[\mathscr {C}_{\mathscr {Q}}]$ are isomorphic to $[\mathcal {C}^{(t)}_Q]$$(t=1,2)$ for each Dynkin quiver Q of finite type $A_{2n-1}$ and $D_{n+1}$, respectively, (2) there exists an exact functor between $\mathscr {C}_{\mathscr {Q}}$ and $\mathcal {C}^{(t)}_Q$$(t=1.2)$ sending simples to simples. To explain our main result, we need to introduce several notions and previous results.

Let Q be a Dynkin quiver of finite type ADE. By the Gabriel theorem [11], it is well known that Auslander–Reiten(AR) quiver $\Gamma _Q$ reflects the representation theory for the path algebra $\mathbb {C}Q$. Moreover, the vertices of $\Gamma _Q$ can be identified with $\Phi ^+$ and the convex partial order $\prec _Q$ of $\Phi ^+$ is represented by the paths in $\Gamma _Q$ (see [2, 11] for more detail). On the other hand, each commutation class $[{\widetilde{w}_0}]$ of reduced expressions for the longest element $w_0$ of a finite Weyl group determines the convex partial order $\prec _{[{\widetilde{w}_0}]}$ on $\Phi ^+$. In particular, each $\prec _Q$ coincides with the convex partial order induced from the commutation class [Q] consisting of all reduced expressions adapted to Q and has its unique Coxeter element $\phi _Q$. Interestingly, all commutation classes $\{ [Q] \}$ are reflection equivalent and hence can be grouped into one r-cluster point$\llbracket Q \rrbracket$. In [34], the second-named author and Suh introduced the combinatorial AR-quiver $\Upsilon _{[{\widetilde{w}_0}]}$ for every $[{\widetilde{w}_0}]$ of $w_0$ for any finite type to realize the convex partial order $\prec _{[{\widetilde{w}_0}]}$ and studied the combinatorial properties of $\Upsilon _{[{\widetilde{w}_0}]}$ of type A.

In the papers [30, 31, 33], the second-named author proved that important information on the representation theories for $U_q'(A^{(1)}_n)$ and $U_q'(D^{(1)}_n)$ is encoded in the AR-quiver $\Gamma _Q$ in the following sense:

• (1) In [30, 31], he proved that the conditions for

  $$\begin{aligned} \mathrm{Hom}(V(\varpi _i)_x\otimes V(\varpi _j)_y, V(\varpi _k)_z) \ne 0, \end{aligned}$$

  (1.6)

  can be interpreted as the coordinates of $(\alpha ,\beta ,\gamma )$ in some $\Gamma _Q$ where $\alpha +\beta =\gamma \in \Phi ^+$ and $\mathfrak {g}$ is of type $A^{(1)}_{n}$ and $D^{(1)}_{n}$. Here the conditions in (1.6) are referred as Dorey’s rule for quantum affine algebras of type $A^{(1)}_{n}$, $D^{(1)}_{n}$, $B^{(1)}_{n}$ and $C^{(1)}_{n}$ and studied by Chari–Pressley [5] by using Coxeter elements and twisted Coxeter elements.

• (2) By using the newly introduced notions on the sequences of positive roots in [33], he proved that we can read the denominator formulas $d_{k,l}(z)$ for $U_q'(A_n^{(1)})$ and $U_q'(D_n^{(1)})$ from any$\Gamma _Q$.

In [35, 36], to extend the previous results to quantum affine algebras of type $B^{(1)}_{n}$ and $C^{(1)}_{n}$, the second-named author and Suh developed the twisted analogues by using twisted Coxeter elements $\widetilde{\phi }$ of type $A_{2n-1}$ and $D_{n+1}$ associated with Dynkin diagram automorphisms

(1.7)

They characterized the r-cluster point $\llbracket \mathscr {Q}\rrbracket$arising from any twisted Coxeter element $\widetilde{\phi }$ in terms of Coxeter composition (see Definition 2.8 and [35, Observation 4.1]). We call the commutation classes $[\mathscr {Q}]$ in $\llbracket \mathscr {Q}\rrbracket$twisted adapted classes. (Hence the notation $\mathscr {Q}$ in this paper can be understood as the label of the combinatorial AR-quiver $\Upsilon _{[\mathscr {Q}]}$ for each $[\mathscr {Q}]$ in $\llbracket \mathscr {Q}\rrbracket$.) Moreover, by assigning coordinate system to $\Upsilon _{[\mathscr {Q}]}$ and folding $\Upsilon _{[\mathscr {Q}]}$, they proved that (1$'$) Dorey’s rule for quantum affine algebras of type $B^{(1)}_{n}$ and $C^{(1)}_{n}$ can be interpreted as the coordinates of $(\alpha ,\beta ,\gamma )$ in some folded AR-quiver$\widehat{\Upsilon }_{[\mathscr {Q}]}$ where $(\alpha ,\beta )$ is a $[\mathscr {Q}]$-minimal pair of $\gamma$, (2$'$) we can read the denominator formulas $d_{k,l}(z)$ for $U_q'(B_n^{(1)})$ and $U_q'(C_n^{(1)})$ from any$\widehat{\Upsilon }_{[\mathscr {Q}]}$.

With the previous results at hand, we first introduce the subcategory $\mathscr {C}_\mathscr {Q}$ for $U_q'(B_n^{(1)})$ and $U_q'(C_n^{(1)})$ by considering the coordinates of positive roots in $\widehat{\Upsilon }_{[\mathscr {Q}]}$, where $[\mathscr {Q}]$ is a twisted adapted class of type $A_{2n-1}$ and $D_{n+1}$ respectively (Definition 6.1). Note that $\mathscr {C}_\mathscr {Q}$ can be considered as the smallest tensor subcategory of the category $\mathscr {C}^-$ in [15] containing fundamental representations $V_{\mathscr {Q}}(\beta )$$(\beta \in \Phi ^+)$ in (4.8) (up to parameter shift). By considering the denominator formulas for $U_q'(B^{(1)}_{n})$ (resp. $U_q'(C^{(1)}_{n})$) and the coordinate system of $\widehat{\Upsilon }_{[\mathscr {Q}]}$, we can take the Schur–Weyl datum $\Xi$ for each twisted adapted class $[\mathscr {Q}]$ yielding the exact functor

$$\begin{aligned} \mathcal {F}_\mathscr {Q}: \mathrm{Rep}(R_\mathsf {g}) \longrightarrow \mathscr {C}_\mathscr {Q}\subset \mathscr {C}_\mathfrak {g}\end{aligned}$$

where $\mathsf {g}$ is the finite simple Lie algebra of type $A_{2n-1}$ and $D_{n+1}$, and $\mathfrak {g}=B^{(1)}_{n}$ and $C^{(1)}_{n}$, respectively (Theorem 6.2). Furthermore, by applying the correspondence between Dorey’s rule and $[\mathscr {Q}]$-minimal pair, we can prove that the functor $\mathcal {F}_\mathscr {Q}$sends simples to simples (Theorem 6.5). Thus, we have Langlands analogues of (1.5):

(1.8)

Hence we have

(1.9)

Our result is closely related to the conjecture of Frenkel–Hernandez in [9, Conjecture 2.2, Conjecture 2.4, Conjecture 3.10]: They conjectured that

• For a representation V in $\mathcal {C}_{\mathfrak {g}^{(2)}}$, it has a Langlands dual representation ${^L}V$ in $\mathcal {C}_{^{L}\mathfrak {g}^{(2)}}$ which satisfies the certain properties. In particular, if V is simple, so is ${}^LV$.

In the following sense, our results provide correspondences related to the conjecture:

• For a representation V in $\mathcal {C}^{(2)}_{Q}$, it corresponds to the representation $\widehat{V}$ in $\mathscr {C}_\mathscr {Q}$ via the induced functor $\mathcal {F}_\mathscr {Q}\circ {\mathcal {F}^{(2)}_Q}^{-1}$ for any [Q] and $[\mathscr {Q}]$. In particular if V is simple, so is $\widehat{V}$.

(see Remark 6.9 for more detail)

As an application, we can characterize the sets of modules in $\mathscr {C}_\mathscr {Q}$ categorifying the upper global basis and the dual PBW-basis associated with $[\mathscr {Q}]$ of $U_\mathbb {A}(\mathsf {g})^\vee |_{q=1}$ (Corollary 6.7). In Sect. 7, we continue the study of [33] about the intersection of the dual PBW-basis $P_{[{\widetilde{w}_0}]}$ associated with a commutation class $[{\widetilde{w}_0}]$ and the upper global basis $B(\infty )$. More precisely, in [33, Corollary 5.24], the second-named author proved that an element $\mathbf {b} \in P_{[Q]} \cap B(\infty )$ if and only if $\mathbf {b}$ corresponds to a [Q]-simple sequence $\underline{m}$, for any $[Q] \in \llbracket Q\rrbracket$. In this paper, we also prove that

• an element $\mathbf {b} \in P_{[\mathscr {Q}]} \cap B(\infty )$ if and only if $\mathbf {b}$ corresponds to a $[\mathscr {Q}]$-simple sequence $\underline{m}$, for any $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$ (Corollary 7.2).

Now we suggest the following conjecture:

Conjecture 1.1

An element $\mathbf {b} \in P_{[{\widetilde{w}_0}]} \cap B(\infty )$ if and only if $\mathbf {b}$ corresponds to a $[{\widetilde{w}_0}]$-simple sequence $\underline{m}$, for any $[{\widetilde{w}_0}]$ of $w_0$.

In “Appendix,” we propose several conjectures on the dualities among quantum affine algebras $U_q'(E^{(i)}_6)$$(i=1,2)$ and $U_q'(F^{(1)}_4)$ by applying the same framework of this paper.

2 Cluster points and their AR-quivers with coordinates

Let I be an index set. A symmetrizable Cartan datum is a quintuple $(\mathsf {A},\mathsf {P},\Pi ,\mathsf {P}^{\vee },\Pi ^{\vee })$ consisting of (a) a symmetrizable generalized Cartan matrix$\mathsf {A}=(a_{ij})_{i,j \in I}$, (b) a free abelian group $\mathsf {P}$, called the weight lattice, (c) $\Pi = \{ \alpha _i \in \mathsf {P}\mid \ i \in I \}$, called the set of simple roots, (d) $\mathsf {P}^{\vee }\mathbin {:=}\mathrm{Hom}(\mathsf {P}, \mathbb {Z})$, called the coweight lattice, (e) $\Pi ^{\vee }= \{ h_i \ | \ i \in I \}\subset P^{\vee }$, called the set of simple coroots. It satisfies certain conditions$:$$\langle h_i,\alpha _j\rangle =a_{ij}$, etc (see [20, §1.1] for precise definition).

The free abelian group $\mathsf {Q}\mathbin {:=}\oplus _{i \in I} \mathbb {Z}\alpha _i$ is called the root lattice. Set $\mathsf {Q}^{+}= \sum _{i \in I} \mathbb {Z}_{\ge 0} \alpha _i$. For $\mathsf {b}=\sum _{i\in I}m_i\alpha _i\in \mathsf {Q}^+$, we set $\mathrm{ht}(\mathsf {b})=\sum _{i\in I}m_i$.

We denote by $U_q(\mathsf {g})$ the quantum group associated with a symmetrizable Cartan datum which is generated by $e_i,f_i$$(i \in I)$ and $q^{h}$$(h \in \mathsf {P}^\vee )$.

2.1 Foldable r-cluster points

Let us consider the Dynkin diagrams $\Delta$ of finite simply laced type, labeled by an index set I, and their automorphisms $\vee$. By the Dynkin diagram automorphisms $\vee$, we can obtain the Dynkin diagrams of finite type BCFG as orbits of $\vee :$

(2.1a)

(2.1b)

(2.1c)

(2.1d)

Let $\mathsf {W}_0$ be the Weyl group, generated by simple reflections $( s_i \ | \ i \in I)$ corresponding to $\Delta$, and $w_0$ the longest element of $\mathsf {W}_0$. We denote by $^*$, the involution on I defined by

$$\begin{aligned}&w_0(\alpha _i)=-\alpha _{i^*}. \end{aligned}$$

(2.2)

We also denote by $\Phi$ the set of all roots and by $\Phi ^+$ the set of all positive roots.

Definition 2.1

We say that two reduced expressions $\widetilde{w}=s_{i_1}s_{i_2}\cdots s_{i_{\ell }}$ and $\widetilde{w}'=s_{j_1}s_{j_2}\cdots s_{j_{\ell }}$ of $w \in \mathsf {W}_0$ are commutation equivalent, denoted by $\widetilde{w} \sim \widetilde{w}'$, if $s_{j_1}s_{j_2}\cdots s_{j_{\ell }}$ is obtained from $s_{i_1}s_{i_2}\cdots s_{i_{\ell }}$ by applying the commutation relations $s_{k}s_{l} =s_{l}s_{k}$ ($\langle h_k,\alpha _l\rangle =0$). We denote by $[\widetilde{w}]$ the commutation equivalence class of $\widetilde{w}$.

For each $[{\widetilde{w}_0}]$, there exists a convex partial order $\prec _{[{\widetilde{w}_0}]}$ on $\Phi ^+$, the set of positive roots, satisfying the following property (see [33] for details): For $\alpha ,\beta \in \Phi ^+$ with $\alpha +\beta \in \Phi ^+$, we have either

$$\begin{aligned} \alpha \prec _{[{\widetilde{w}_0}]} \alpha +\beta \prec _{[{\widetilde{w}_0}]} \beta \quad \text { or } \quad \beta \prec _{[{\widetilde{w}_0}]} \alpha +\beta \prec _{[{\widetilde{w}_0}]} \alpha . \end{aligned}$$

Definition 2.2

Fix a Dynkin diagram $\Delta$ of finite type. For an equivalence class $[{\widetilde{w}_0}]$ of reduced expression ${\widetilde{w}_0}$, we say that $i\in I$ is a sink (resp. source) of $[{\widetilde{w}_0}]$ if there is a reduced expression ${\widetilde{w}_0}'\in [{\widetilde{w}_0}]$ of w starting with $s_i$ (resp. ending with $s_i$).

The following proposition is well known (for example, see [24, 34]):

Proposition 2.3

For ${\widetilde{w}_0}=s_{i_1}s_{i_2}\cdots s_{i_{\mathsf {N}-1}}s_{i_\mathsf {N}}$, ${\widetilde{w}_0}'=s_{i_\mathsf {N}^*}s_{i_1}s_{i_2}\cdots s_{i_{\mathsf {N}-1}}$ is a reduced expression of $w_0$ and $[{\widetilde{w}_0}'] \ne [{\widetilde{w}_0}]$. Similarly, ${\widetilde{w}_0}''=s_{i_2}\cdots s_{i_{\mathsf {N}-1}}s_{i_\mathsf {N}}s_{i^*_1}$ is a reduced expression of $w_0$ and $[{\widetilde{w}_0}''] \ne [{\widetilde{w}_0}]$.

Definition 2.4

The right action of the reflection functor $r_i$ on $[{\widetilde{w}_0}]$ is defined by

$$\begin{aligned}{}[{\widetilde{w}_0}]\, r_i = {\left\{ \begin{array}{ll} [(s_{i_2},\cdots , s_{i_N}, s_{i^*})] &{} \text {if there is } {\widetilde{w}_0}'=(s_{i}, s_{i_2}, \cdots , s_{i_N})\in [{\widetilde{w}_0}],\\ \ [{\widetilde{w}_0}] &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

On the other hand, the left right action of the reflection functor $r_i$ on $[{\widetilde{w}_0}]$ is defined by

$$\begin{aligned} r_i \, [{\widetilde{w}_0}]= {\left\{ \begin{array}{ll} [(s_{i^*},s_{i_1}\cdots , s_{i_{N-1}})] &{} \text {if there is } {\widetilde{w}_0}'=(s_{i_1}, \cdots , s_{i_{N-1}}, s_i)\in [{\widetilde{w}_0}],\\ \, [{\widetilde{w}_0}] &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Definition 2.5

[34] Let $[{\widetilde{w}_0}]$ and $[{\widetilde{w}_0}']$ be two commutation classes. We say $[{\widetilde{w}_0}]$ and $[{\widetilde{w}_0}']$ are reflection equivalent and write $[{\widetilde{w}_0}]\overset{r}{\sim } [{\widetilde{w}_0}']$ if $[{\widetilde{w}_0}']$ can be obtained from $[{\widetilde{w}_0}]$ by a sequence of reflection maps. The equivalence class $\llbracket {\widetilde{w}_0}\rrbracket \mathbin {:=}\{\, [{\widetilde{w}_0}]\, |\, [{\widetilde{w}_0}]\overset{r}{\sim }[{\widetilde{w}_0}']\, \}$ with respect to the reflection equivalence relation is called an r-cluster point.

Definition 2.6

[35, Definition 1.8] Fix a Dynkin diagram automorphism $\vee$ in (2.1). Let $\widehat{I} \mathbin {:=}\{ \widehat{i} \ | \ i \in I \}$ be the orbit classes of I induced by $\vee$. For an r-cluster point $\llbracket {\widetilde{w}_0}\rrbracket = \llbracket s_{i_1} \cdots s_{i_{\mathsf {N}}} \rrbracket$ of $w_0$ and $\widehat{k}\in \widehat{I}$, define

$$\begin{aligned} \mathsf {C}^\vee _{\llbracket {\widetilde{w}_0}\rrbracket }(\widehat{k}) = |\{ i_s \ | \ i_s \in \widehat{k}, \ 1 \le s \le \mathsf {N} \} | \quad (\mathsf {N}=\ell (w_0)). \end{aligned}$$

We call the composition $\mathsf {C}^{\vee }_{\llbracket {\widetilde{w}_0}\rrbracket }=\big (\mathsf {C}^\vee _{\llbracket {\widetilde{w}_0}\rrbracket }(\widehat{1}),\ldots , \mathsf {C}^{\vee }_{\llbracket {\widetilde{w}_0}\rrbracket } ( |\widehat{I}|) \big )$, the $\vee$-Coxeter composition of $\llbracket {\widetilde{w}_0}\rrbracket$.

Example 2.7

For ${\widetilde{w}_0}=s_1s_2s_3s_5s_4s_3s_1s_2s_3s_5s_4s_3s_1s_2s_3$ of type $A_5$, we have

$$\begin{aligned} \mathsf {C}^{\vee }_{\llbracket {\widetilde{w}_0}\rrbracket }=(5,5,5). \end{aligned}$$

Definition 2.8

[35, Definition 1.10] For an automorphism $\vee$ and an cluster $\llbracket {\widetilde{w}_0}\rrbracket$ of type ADE, we say that an r-cluster point $\llbracket {\widetilde{w}_0}\rrbracket$ is $\vee$-foldable if

$$\begin{aligned} \mathsf {C}^{\vee }_{\llbracket {\widetilde{w}_0}\rrbracket }(\widehat{k}) = \mathsf {C}^{\vee }_{\llbracket {\widetilde{w}_0}\rrbracket }(\widehat{l}) \qquad \text { for any } \widehat{k},\widehat{l}\in \widehat{I}. \end{aligned}$$

In [35, 36], the existence for a $\vee$-foldable r-cluster point is proved, but we do not know whether it is unique or not:

Proposition 2.9

[35, 36]    

• (a) A $\vee$-foldable r-cluster point exists and is denoted by $\llbracket \mathscr {Q}\rrbracket$.

• (b) The number of commutation classes in each $\llbracket \mathscr {Q}\rrbracket$ is equal to $2^{|I|-|\vee |} \times |\vee |$, where $|\vee |$ denotes the order of $\vee$.

The r-cluster point $\llbracket \mathscr {Q}\rrbracket$ is called a twisted adapted cluster point, and a class $[\mathscr {Q}]$ in $\llbracket \mathscr {Q}\rrbracket$ is called a twisted adapted class.

Let $\sigma \in GL(\mathbb {C}\Phi )$ be a linear transformation of finite order which preserves $\Pi$. Hence, $\sigma$ preserves $\Phi$ itself and normalizes $\mathsf {W}_0$ and so $\mathsf {W}_0$ acts by conjugation on the coset $\mathsf {W}_0\sigma$.

Definition 2.10

   

• (1) Let $\{ \Pi _{i_1}, \ldots ,\Pi _{i_k} \}$ be the all orbits of $\Pi$ in $\Phi$ with respect to $\sigma$. For each $r\in \{1, \cdots , k \}$, choose $\alpha _{i_r} \in \Pi _{i_r}$ arbitrarily, and let $s_{i_r} \in \mathsf {W}_0$ denote the corresponding reflection. Let w be the product of $s_{i_1}, \ldots , s_{i_k}$ in any order. The element $w\sigma \in \mathsf {W}_0\sigma$ of $w\in \mathsf {W}_0$ thus obtained is called a $\sigma$-Coxeter element.

• (2) If $\sigma$ in (1) is $\vee$ in (2.1a), (2.1b), (2.1c), then $\sigma$-Coxeter element is also called a twisted Coxeter element.

Remark 2.11

   

• (i) For types $A_{2n-1}$, $D_{n+1}$ and $E_6$, $\llbracket \mathscr {Q}\rrbracket$ are given as follows:

  

  where

  • $s_{j_1}s_{j_2}s_{j_3}\cdots s_{j_n}$ is an arbitrary twisted Coxeter element of type $A_{2n-1}$ [resp. $D_{n+1}$ and $E_6$],

  • $\vee$ is given in (2.1a) (resp. (2.1b) and (2.1c)),

  • $(s_{j_1} \cdots s_{j_n})^\vee \mathbin {:=}s_{j^\vee _1} \cdots s_{j^\vee _n}$ and $(s_{j_1} \cdots s_{j_n})^{k \vee } \mathbin {:=}(\cdots ((s_{j_1} \cdots s_{j_n} \underbrace{ )^\vee )^\vee \cdots )^\vee }_{k\text { -times}}$.

  Note that $s_1s_2s_3\cdots s_{n}$ is a twisted Coxeter element of type $A_{2n-1}$, $D_{n+1}$ and $E_6$.

• (ii) For types $D_{4}$, $\llbracket \mathscr {Q}\rrbracket$ with respect to (2.1d) is given as follows:

  

Example 2.12

   

• (i) For $\vee$ in (2.1a), the Coxeter composition of a foldable cluster is

  $$\begin{aligned} \mathsf {C}^{\vee }_{\llbracket \mathscr {Q}\rrbracket }=( \underbrace{2n-1, \ldots ,2n-1}_{ n\text {-times}} ). \end{aligned}$$

• (ii) For $\vee$ in (2.1b), the Coxeter composition of a foldable cluster is

  $$\begin{aligned} \mathsf {C}^{\vee }_{\llbracket \mathscr {Q}\rrbracket }=( \underbrace{n+1, \ldots ,n+1}_{ n\text {-times}} ). \end{aligned}$$

• (iii) For $\vee$ in (2.1c), the Coxeter composition of a foldable cluster is $\mathsf {C}^{\vee }_{\llbracket \mathscr {Q}\rrbracket }=(9,9,9,9)$.

• (iv) For $\vee$ in (2.1d), the Coxeter composition of a foldable cluster is $\mathsf {C}^{\vee }_{\llbracket \mathscr {Q}\rrbracket }=(6,6)$.

2.2 Adapted cluster point and Auslander–Reiten quiver

Let Q be a Dynkin quiver by orienting edges of a Dynkin diagram $\Delta$ of type ADE. We say that a vertex i in Q is a source (resp. sink) if and only if there are only exiting arrows out of it (resp. entering arrows into it). For a source (resp. sink) i, if i is a sink or source, $s_iQ$ denotes the quiver obtained by Q by reversing the arrows incident with i. We say that a reduced expression ${\widetilde{w}}=s_{i_1}s_{i_2}\cdots s_{i_{\ell (w)}}$ of $w \in \mathsf {W}_0$ is adapted toQ if $i_k$ is a sink of the quiver $s_{i_{k-1}} \cdots s_{i_2}s_{i_1}Q$ for all $1 \le k \le \ell (w)$.

The followings are well known:

Theorem 2.13

   

• (1) Any reduced word ${\widetilde{w}_0}$ of $w_0$ is adapted to at most one Dynkin quiver Q.

• (2) For each Dynkin quiver Q, there is a reduced word ${\widetilde{w}_0}$ of $w_0$ adapted to Q. Moreover, any reduced word ${\widetilde{w}_0}'$ in $[{\widetilde{w}_0}]$ is adapted to Q, and the commutation equivalence class $[{\widetilde{w}_0}]$ is uniquely determined by Q. We denote by [Q] of the commutation equivalence class $[{\widetilde{w}_0}]$.

• (3) For every commutation class [Q], there exists a unique Coxeter element $\phi _Q$ which is a product of all simple reflections and adapted to Q.

• (4) For every Coxeter element $\phi$, there exists a unique Dynkin quiver Q such that $\phi =\phi _Q$.

• (5) All commutation classes $\{ [Q] \}$ are reflection equivalent and form the r-cluster point $\llbracket Q \rrbracket$, called the adapted cluster point. The number of commutation classes in $\llbracket Q \rrbracket$ is $2^{|I|-1}$.

Remark 2.14

For the Dynkin diagram automorphism of $A_{2n-1}$ in (2.1a), of $D_{n+1}$ in (2.1b) and of $E_6$ in (2.1c), the number of commutation classes of each $\llbracket Q \rrbracket$ and the one of each $\llbracket \mathscr {Q}\rrbracket$ are the same and are equal to $2^{2n-2}$, $2^n$ and $2^5$, respectively.

Let $\Phi (\phi _Q)$ be the subset of $\Phi ^+$ determined by $\phi _Q=s_{i_1}s_{i_2}\cdots s_{i_n}$ with $|I|=n$:

$$\begin{aligned} \Phi (\phi _Q)= \left\{ \beta ^{\phi _Q}_1=\alpha _{i_1}, \beta ^{\phi _Q}_2=s_{i_1}(\alpha _{i_2}), \ldots ,\beta ^{\phi _Q}_n =s_{i_1}\cdots s_{i_{n-1}}(\alpha _{i_n}) \right\} . \end{aligned}$$

The height function$\xi$ on Q is an integer-valued map $\xi :Q \rightarrow \mathbb {Z}$ satisfying $\xi (j)=\xi (i)+1$ when $i \rightarrow j$ in Q.

The Auslander–Reiten quiver (AR-quiver) $\Gamma _Q$ associated with Q is a quiver with coordinates in $I \times \mathbb {Z}$ defined as follows [14, §2.2]: Construct an injective map $\Omega _Q: \Phi ^+\rightarrow I \times \mathbb {Z}$ in an inductive way

• (i) $\Omega _Q(\beta _k^{\phi _Q}) \mathbin {:=}(i_k,\xi (i_k))$.

• (ii) If $\Omega _Q(\beta )$ is already assigned as (i, p) and $\phi _Q(\beta ) \in \Phi ^+$, then $\Omega _Q(\phi _Q(\beta ))=(i,p-2)$.

The AR-quiver $\Gamma _Q$ is a quiver whose vertices consist of $\mathrm{Im}(\Omega _Q)$ ($\simeq \Phi ^+$) and arrows $(i,p) \rightarrow (j,q)$ are assigned when i and j are adjacent in $\Delta$ and $p-q=-1$.

Example 2.15

The AR-quiver $\Gamma _Q$ associated with of type $A_4$ with the height function such that $\xi (1)=0$ is given as follows:

Here [a, b] $(1 \le a,b \le 4)$ stands for the positive root $\sum _{k=a}^b \alpha _k$ of $\Phi ^+_{A_4}$.

Interestingly, $\Gamma _Q$ can be understood as a visualization of $\prec _{Q} \mathbin {:=}\prec _{[Q]}$ and is closely related to the commutation class [Q]:

Theorem 2.16

[2, 34]

• (1) $\alpha \prec _Q \beta$ if and only if there exists a path from $\beta$ to $\alpha$ inside of $\Gamma _Q$.

• (2) By reading the residues (i.e., i for (i, p)) of vertices in a way compatible with arrows, we can obtain all reduced expressions ${\widetilde{w}_0}\in [Q]$.

In Example 2.15, we can get a reduced expression ${\widetilde{w}_0}$ in [Q] as follows:

$$\begin{aligned} {\widetilde{w}_0}=s_4s_1s_3s_2s_4s_1s_3s_2s_4s_3 \end{aligned}$$

2.3 Relationship between $\llbracket \mathscr {Q}\rrbracket$ and $\llbracket Q \rrbracket$

In this subsection, we briefly recall the relationship between $\llbracket \mathscr {Q}\rrbracket$ and $\llbracket Q \rrbracket$ studied in [35, 36]. We shall first consider a Dynkin quiver Q of type A and ${\widetilde{w}_0}= s_{i_1}s_{i_2} \cdots s_{i_\mathsf {N}}$ in [Q].

Theorem 2.17

[35] For ${\widetilde{w}_0}=s_{i_1}s_{i_2} \cdots s_{i_\mathsf {N}} \in [Q]$ of type $A_{2n-2}$, we can obtain two distinct twisted adapted classes $[\mathscr {Q}^>], [\mathscr {Q}^<] \in \llbracket \mathscr {Q}\rrbracket$ of type $A_{2n-1}$ as follows:

• (1) For each pair $(i_k,i_l)$ such that $\{ i_k ,i_l \} = \{ n-1, n \}$ and $i_j \not \in \{ n-1, n \}$ for any j with $k< j <l$, we replace subexpression $s_{i_k}s_{i_{k+1}} \cdots s_{i_l}$ with $s_{i^+_k}s_{n}s_{i^+_{k+1}} \cdots s_{i^+_l}$ where $i^+=i+1$ if $i > n-1$ and $i^+=i$ otherwise.

• (2) For the smallest index (resp. the largest index) $i_t$ with $i_t \in \{ n-1,n \}$, we replace $s_{i_t}$ with $s_{n}s_{i^+_t}$ (resp. $s_{i^+_t}s_{n})$.

Then the resulted reduced expression ${\widetilde{w}_0}^>$ (resp. ${\widetilde{w}_0}^<)$ is a reduced expression whose commutation class $[\mathscr {Q}^>]$ (resp. $[\mathscr {Q}^<])$ is well defined and twisted adapted. Conversely, each commutation class in $\llbracket \mathscr {Q}\rrbracket$ can be obtained in this way and $[\mathscr {Q}] \ne [\mathscr {Q'}]$ if $Q \ne Q'$.

By the work of [34], the combinatorial AR-quivers $\Upsilon _{[\mathscr {Q}^>]}$ and $\Upsilon _{[\mathscr {Q}^<]}$ of Q in Example 2.15 can be understood as realization of the convex partial orders $\prec _{[\mathscr {Q}^>]}$ and $\prec _{[\mathscr {Q}^<]}$:

(2.3)

For each new vertex, denoted by $\bigstar$ above, we can assign its coordinate in $I \times \mathbb {Z}/2$ in a canonical way. By [34], we can obtain all reduced expressions ${\widetilde{w}_0}\in [\mathscr {Q}^>]$ (resp. $[\mathscr {Q}^<]$) by reading it in a compatible way with arrows: For instances, we have

• $s_5s_3s_1s_4s_3s_2s_5s_3s_1s_4s_3s_2s_5s_3s_4\in [\mathscr {Q}^>]$.

• $s_5s_4s_1s_3s_2s_3s_5s_4s_1s_3s_2s_3s_5s_4s_3 \in [\mathscr {Q}^<]$.

In $D_{n+1}$ case, we can get two distinct commutation classes $[\mathscr {Q}^{\leftarrow n}]$ and $[\mathscr {Q}^{\leftarrow n+1}] \in \llbracket \mathscr {Q}\rrbracket$ from $\Gamma _Q$ of type $A_n$:

Theorem 2.18

[36]

• (1) For a given $\Gamma _Q$, consider the copy $\Gamma ^{\updownarrow }_Q$ of $\Gamma _Q$ by turning upside down.

• (2) By putting $\Gamma ^{\updownarrow }_Q$ to the left of $\Gamma _Q$, we have new quiver inside of $I \times \mathbb {Z}$ by assigning arrows to vertices (i, p) and $(j,q) \in \Gamma ^{\updownarrow }_Q \sqcup \Gamma _Q$, $(i,p)\rightarrow (j,q)$ such that i, j are adjacent in Q and $q-p=1$.

• (3) For vertices whose residues are n, we change their residues as $n,n+1,n,n+1...$ (resp. $n+1,n,n+1,n...)$ from the right-most one.

Then the resulted quiver coincides with the combinatorial quiver $\Upsilon _{[\mathscr {Q}^{\leftarrow n}]}$ (resp. $\Upsilon _{[\mathscr {Q}^{\leftarrow n+1}]})$ of type $D_{n+1}$ introduced in [34, 36]. Thus, we can obtain all reduced expressions ${\widetilde{w}_0}\in [\mathscr {Q}^{\leftarrow n}]$ (resp. $[\mathscr {Q}^{\leftarrow n+1}])$ by reading it. Conversely, each commutation class in $\llbracket \mathscr {Q}\rrbracket$ can be obtained in this way and $[\mathscr {Q}] \ne [\mathscr {Q'}]$ if $Q \ne Q'$.

Example 2.19

For better explanation of the above theorem, we now give examples by using $\Gamma _Q$ in Example 2.15: For the $\Gamma _Q$, $\Gamma ^{\updownarrow }_Q$ can be described as follows:

By putting $\Gamma ^{\updownarrow }_Q$ to the left of $\Gamma _Q$, we have new quiver as follows:

Now we can get $\Upsilon _{[\mathscr {Q}^{\leftarrow n}]}$ and $\Upsilon _{[\mathscr {Q}^{\leftarrow n+1}]}$ as follows:

One can easily notice that we can assign a coordinate to each vertex in a canonical way.

2.4 Folded AR-quivers

Now we can define a foldedAR-quiver$\widehat{\Upsilon }_{[\mathscr {Q}]}$ associated with the commutation class $[\mathscr {Q}]$ in $\llbracket \mathscr {Q}\rrbracket$ of type $A_{2n-1}$ and $D_{n+1}$ by folding $\Upsilon _{[\mathscr {Q}]}$ [35, 36]:

• (i) ($[\mathscr {Q}]$ of type $A_{2n-1}$) By replacing coordinate $\Omega _Q(\beta )=(i,p/2)$ of $\beta$ in $\Upsilon _{[\mathscr {Q}]}$ with $\widehat{\Omega }_{[\mathscr {Q}]}(\beta )=(\widehat{i},p) \in \widehat{I} \times \mathbb {Z}$, we have new quiver $\widehat{\Upsilon }_{[\mathscr {Q}]}$ with folded coordinates, which is isomorphic to $\Upsilon _{[\mathscr {Q}]}$ as quivers.

• (ii) ($[\mathscr {Q}]$ of type $D_{n+1}$) By replacing coordinate $\Omega (\beta )=(i,p)$ of $\beta$ in $\Upsilon _{[\mathscr {Q}]}$ with $\widehat{\Omega }_{[\mathscr {Q}]}(\beta )=(\widehat{i},p) \in \widehat{I} \times \mathbb {Z}$, we have new quiver $\widehat{\Upsilon }_{[\mathscr {Q}]}$ with folded coordinates.

We call $\widehat{\Upsilon }_{[\mathscr {Q}]}$ the folded AR-quiver associated with $[\mathscr {Q}]$ and $\widehat{\Omega }_{[\mathscr {Q}]}(\beta )=(\widehat{i},p)$ the folded coordinate of $\beta$ with respect to $[\mathscr {Q}]$.

Example 2.20

From (2.3) and Example 2.19, we can obtain folded AR-quivers $\widehat{\Upsilon }_{[\mathscr {Q}]}$ as follows:

• (1) $[\mathscr {Q}]$ of type $A_{5}$ cases:

  

• (2) $[\mathscr {Q}]$ of type $D_{5}$ cases:

  

3 Positive root systems

In this section, we recall main results of [33, 35, 36], which investigated the positive root systems by using newly introduced notions and (combinatorial) AR-quivers. The results will be used in later sections.

3.1 Notions

For a reduced expression ${\widetilde{w}_0}=s_{i_1}s_{i_2}\cdots s_{i_\mathsf {N}}$ of $w_0$, there exists the convex total order $<_{{\widetilde{w}_0}}$ on $\Phi ^+$ defined as follows:

$$\begin{aligned} \beta ^{{\widetilde{w}_0}}_{k}<_{{\widetilde{w}_0}} \beta ^{{\widetilde{w}_0}}_{l} \quad \text {if and only if }k <l, \end{aligned}$$

where $\beta ^{{\widetilde{w}_0}}_{k} \mathbin {:=}s_{i_1}\cdots s_{i_{k-1}}(\alpha _{i_k})$.

With the convex total order $<_{{\widetilde{w}_0}}$, we identify $\underline{m}=(\underline{m}_1,\underline{m}_2,\ldots ,\underline{m}_\mathsf {N}) \in \mathbb {Z}_{\ge 0}^{\mathsf {N}}$ with

$$\begin{aligned} \underline{m}_{{\widetilde{w}_0}}\in \ (\mathbb {Z}_{\ge 0})^{|\Phi ^+|}, \end{aligned}$$

whose coordinate at $\beta ^{{\widetilde{w}_0}}_{k}$ is $m_k$. For a sequence $\underline{m}$, we set $\mathrm{wt}(\underline{m})=\sum _{i=1}^\mathsf {N}\underline{m}_i\beta ^{{\widetilde{w}_0}}_i\in \mathsf {Q}^+$.

Definition 3.1

[29, 33] We define the partial orders $<^\mathtt {b}_{{\widetilde{w}_0}}$ and $\prec ^\mathtt {b}_{[{\widetilde{w}_0}]}$ on $\mathbb {Z}_{\ge 0}^{\mathsf {N}}$ as follows:

• (i) $<^\mathtt {b}_{{\widetilde{w}_0}}$ is the bi-lexicographical partial order induced by $<_{{\widetilde{w}_0}}$. Namely, $\underline{m}<^\mathtt {b}_{{\widetilde{w}_0}}\underline{m}'$ if there exist j and k ($1\le j\le k\le \mathsf {N}$) such that $\underline{m}_s=\underline{m}'_s$ for $1\le s<j$, $\underline{m}_j<\underline{m}'_j$ and $\underline{m}_{s}=\underline{m}'_{s}$ for $k<s\le \mathsf {N}$, $\underline{m}_k<\underline{m}'_k$.

• (ii) For sequences $\underline{m}$ and $\underline{m}'$, $\underline{m}\prec ^\mathtt {b}_{[{\widetilde{w}_0}]} \underline{m}'$ if and only if $\mathrm{wt}(\underline{m})=\mathrm{wt}(\underline{m}')$ and $\underline{n}<^\mathtt {b}_{{\widetilde{w}_0}'} \underline{n}'$ for all ${\widetilde{w}_0}' \in [{\widetilde{w}_0}]$, where $\underline{n}$ and $\underline{n}'$ are sequences such that $\underline{n}_{{\widetilde{w}_0}'}=\underline{m}_{{\widetilde{w}_0}}$ and $\underline{n}'_{{\widetilde{w}_0}'}=\underline{m}_{{\widetilde{w}_0}}$.

We call a sequence $\underline{m}$ a pair if $|\underline{m}|\mathbin {:=}\sum _{i=1}^\mathsf {N}m_i=2$ and $m_i \le 1$ for $1\le i\le \mathsf {N}$. We mainly use the notation $\underline{p}$ for a pair. We also write $\underline{p}$ as $(\beta ^{{\widetilde{w}_0}}_{i_1},\beta ^{{\widetilde{w}_0}}_{i_2})$ or $(i_1,i_2)$ where $\underline{p}_{i_1}=\underline{p}_{i_2}=1$ and $i_1 \le i_2$.

Definition 3.2

[33]

• (i) A pair $\underline{p}$ is called $[{\widetilde{w}_0}]$-simple if there exists no sequence $\underline{m}\in \mathbb {Z}^{\mathsf {N}}_{\ge 0}$ satisfying $\underline{m}\prec ^\mathtt {b}_{[{\widetilde{w}_0}]} \underline{p}$.

• (ii) A sequence $\underline{m}=(\underline{m}_1,\underline{m}_2,\ldots ,\underline{m}_{\mathsf {N}}) \in \mathbb {Z}^{\mathsf {N}}_{\ge 0}$ is called $[{\widetilde{w}_0}]$-simple if $\underline{m}=(\underline{m}_k \beta ^{\widetilde{w}_0}_k)$ for some $1\le k \le \mathsf {N}$ or any pair $({i_1},{i_2})$ such that $\underline{m}_{i_1},\underline{m}_{i_2} >0$ is a $[{\widetilde{w}_0}]$-simple pair.

Definition 3.3

[29, 33] For a given $[{\widetilde{w}_0}]$-simple sequence $\underline{s}=(s_1,\ldots ,s_{\mathsf {N}}) \in \mathbb {Z}^{\mathsf {N}}_{\ge 0}$, we say that a sequence $\underline{m}\in \mathbb {Z}^{\mathsf {N}}_{\ge 0}$ is called a $[{\widetilde{w}_0}]$-minimal sequence of$\underline{s}$ if $\underline{m}$ satisfies the following properties:

$$\begin{aligned} \underline{s}\prec ^\mathtt {b}_{{\widetilde{w}_0}} \underline{m}\text { and there exists no sequence } \underline{m}'\in \mathbb {Z}^{\mathsf {N}}_{\ge 0}\text { such that }\underline{s}\prec ^\mathtt {b}_{[{\widetilde{w}_0}]} \underline{m}' \prec ^\mathtt {b}_{[{\widetilde{w}_0}]} \underline{m}. \end{aligned}$$

Definition 3.4

[33] The $[{\widetilde{w}_0}]$-distance of a sequence $\underline{m}$, denoted by $\mathrm{dist}_{[{\widetilde{w}_0}]}(\underline{m})$, is the largest integer $k\ge 0$ such that there exists a family of sequences $\{\underline{m}^{(i)}\}_{0\le i\le k}$ satisfying

$$\begin{aligned} \underline{m}^{(0)} \prec ^\mathtt {b}_{[{\widetilde{w}_0}]} \cdots \prec ^\mathtt {b}_{[{\widetilde{w}_0}]} \underline{m}^{(k)}=\underline{m}. \end{aligned}$$

Note that $\underline{m}^{(0)}$ should be $[{\widetilde{w}_0}]$-simple.

Definition 3.5

[33] For a pair $\underline{p}$, the $[{\widetilde{w}_0}]$-socle of $\underline{p}$, denoted by ${{\text {soc}}}_{[{\widetilde{w}_0}]}(\underline{p})$, is a $[{\widetilde{w}_0}]$-simple sequence $\underline{s}$ satisfying $\underline{s}\preceq ^\mathtt {b}_{[{\widetilde{w}_0}]} \underline{p}$ if such an $\underline{s}$ exists uniquely.

3.2 Socles, minimal pairs and folded distance polynomial

Proposition 3.6

[3, Lemma 2.6] For $\gamma \in \Phi ^+\setminus \Pi$ and any ${\widetilde{w}_0}$ of $w_0$, a $[{\widetilde{w}_0}]$-minimal sequence of $\gamma$ is indeed a pair $(\alpha ,\beta )$ for some $\alpha ,\beta \in \Phi ^+$ such that $\alpha +\beta = \gamma$.

Theorem 3.7

[35, 36] For any $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$ and any pair $\underline{p}$, we have the followings$:$

• (1) ${{\text {soc}}}_{[\mathscr {Q}]}(\underline{p})$ is well defined.

• (2) $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p}) \le 2$. In particular, if $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p})=2$, there exist a unique $\underline{m}$ and a unique chain of length 3 such that

  $$\begin{aligned} {{\text {soc}}}_{[\mathscr {Q}]}(\underline{p}) \prec ^{\mathtt {b}}_{[\mathscr {Q}]} \underline{m}\prec ^{\mathtt {b}}_{[\mathscr {Q}]} \underline{p}. \end{aligned}$$

• (3) If $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p}) =1$, then $\underline{p}$ is a $[\mathscr {Q}]$-minimal pair of ${{\text {soc}}}_{[\mathscr {Q}]}(\underline{p})$.

For the involutions $\vee$ in (2.1a) and (2.1b), we can identify $\widehat{I}$, the orbit space of $\vee$, with $\{ 1,2,\ldots ,n\}$ and the order of $\vee$ is equal to $\widehat{\mathsf {d}}\mathbin {:=}2$. The following propositions tell the characterization of the positions of minimal pairs for $\gamma \in \Phi ^+$ inside of $\widehat{\Upsilon }_{[\mathscr {Q}]}$.

Proposition 3.8

[35, Proposition 7.8] Let us fix $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$ of finite type $A_{2n-1}$. For $\alpha ,\beta ,\gamma \in \Phi ^+$ with $\widehat{\Omega }_{[\mathscr {Q}]}(\alpha )=(i,p)$, $\widehat{\Omega }_{[\mathscr {Q}]}(\beta )=(j,q)$$\widehat{\Omega }_{[\mathscr {Q}]}(\gamma )=(k,r)$ and $\alpha +\beta =\gamma$, $(\alpha ,\beta )$ is a $[\mathscr {Q}]$-minimal pair of $\gamma$ if and only if one of the following conditions holds$:$

(3.1)

Proposition 3.9

[36, Corollary 8.26] Let us fix $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$ of finite type $D_{n+1}$. For $\alpha ,\beta ,\gamma \in \Phi ^+$ with $\widehat{\Omega }_{[\mathscr {Q}]}(\alpha )=(i,p)$, $\widehat{\Omega }_{[\mathscr {Q}]}(\beta )=(j,q)$$\widehat{\Omega }_{[\mathscr {Q}]}(\gamma )=(k,r)$ and $\alpha +\beta =\gamma$, $(\alpha ,\beta )$ is a $[\mathscr {Q}]$-minimal pair of $\gamma$ if and only if one of the following conditions holds$:$

(3.2)

Definition 3.10

[35, Definition 8.7] For a folded AR-quiver $\widehat{\Upsilon }_{[\mathscr {Q}]}$, indices $\widehat{k},\widehat{l} \in \widehat{I}$ and an integer $t \in \mathbb {Z}_{\ge 1}$, we define the subset $\Phi _{[\mathscr {Q}]}(\widehat{k},\widehat{l})[t]$ of $\Phi ^+\times \Phi ^+$ as follows:

A pair $(\alpha ,\beta )$ is contained in $\Phi _{[\mathscr {Q}]}(\widehat{k},\widehat{l})[t]$ if $\alpha \prec _{[\mathscr {Q}]} \beta$ or $\beta \prec _{[\mathscr {Q}]} \alpha$ and

$$\begin{aligned} \{\widehat{\Omega }_{[\mathscr {Q}]}(\alpha ),\widehat{\Omega }_{[\mathscr {Q}]}(\beta )\}=\{(\widehat{k},a), (\widehat{l},b)\} \quad \text { such that } \quad |a-b|=t. \end{aligned}$$

Proposition 3.11

[35, 36] For any $(\alpha ^{(1)},\beta ^{(1)}), \ (\alpha ^{(2)},\beta ^{(2)}) \in \Phi _{[\mathscr {Q}]}(\widehat{k},\widehat{l})[t]$, we have

$$\begin{aligned} \mathrm{dist}_{[\mathscr {Q}]}(\alpha ^{(1)},\beta ^{(1)})=\mathrm{dist}_{[\mathscr {Q}]}(\alpha ^{(2)},\beta ^{(2)}). \end{aligned}$$

Thus, the notion

$$\begin{aligned} o^{[\mathscr {Q}]}_t(\widehat{k},\widehat{l}) \mathbin {:=}\mathrm{dist}_{[\mathscr {Q}]}(\alpha ,\beta ) \quad \text { for any } (\alpha ,\beta ) \in \Phi _{[\mathscr {Q}]}(\widehat{k},\widehat{l})[t] \end{aligned}$$

is well defined.

Definition 3.12

[35, Definition 8.9] For $\widehat{k},\widehat{l} \in \widehat{I}$ and a folded AR-quiver $\widehat{\Upsilon }_{[\mathscr {Q}]}$, we define a polynomial $\widehat{D}^{[\mathscr {Q}]}_{\widehat{k},\widehat{l}}(z) \in \mathbf {k}[z]$ as follows: Let q be an indeterminate, $q_s^{\widehat{\mathsf {d}}}=q_s^2=q$ and $\mathtt {o}^{[\mathscr {Q}]}_t(\widehat{k},\widehat{l}) \mathbin {:=}\lceil o^{[\mathscr {Q}]}_t(\widehat{k},\widehat{l}) / \widehat{\mathsf {d}} \rceil$.

• (i) When $[\mathscr {Q}]$ is of type $A_{2n-1}$, $\widehat{D}^{[\mathscr {Q}]}_{\widehat{k},\widehat{l}}(z) \mathbin {:=}\prod _{ t \in \mathbb {Z}_{\ge 0} } (z- (-1)^{\widehat{k}+\widehat{l}}(q_s)^{t})^{\mathtt {o}^{[\mathscr {Q}]}_t(\widehat{k},\widehat{l})}.$

• (ii) When $[\mathscr {Q}]$ is of type $D_{n+1}$, $\widehat{D}^{[\mathscr {Q}]}_{\widehat{k},\widehat{l}}(z) \mathbin {:=}\prod _{ t \in \mathbb {Z}_{\ge 0} } (z- (-q_s)^{t})^{\mathtt {o}^{[\mathscr {Q}]}_t(\widehat{k},\widehat{l})}.$

Proposition 3.13

[35, 36] For $\widehat{k},\widehat{l} \in \widehat{I}$ and any twisted adapted classes $[\mathscr {Q}]$ and $[\mathscr {Q}']$ in $\llbracket \mathscr {Q}\rrbracket$, we have

$$\begin{aligned} \widehat{D}^{[\mathscr {Q}]}_{\widehat{k},\widehat{l}}(z)=\widehat{D}^{[\mathscr {Q}']}_{\widehat{k},\widehat{l}}(z). \end{aligned}$$

From the above proposition, we can define $\widehat{D}_{\widehat{k},\widehat{l}}(z)$ for $\llbracket \mathscr {Q}\rrbracket$ in a natural way and call it the folded distance polynomial at $\widehat{k}$ and $\widehat{l}$.

4 Quantum affine algebras, denominator formulas and Dorey’s rule

4.1 Quantum affine algebras

Let $\mathsf {A}$ be a generalized Cartan matrix of affine type, i.e., $\mathsf {A}$ is positive semi-definite of corank 1. We choose $0 \in I\mathbin {:=}\{ 0,1,\ldots ,n\}$ as the leftmost vertices in the tables in [16, pages 54, 55] except $A^{(2)}_{2n}$-case in which we take the longest simple root as $\alpha _0$. We set $I_0 \mathbin {:=}I \setminus \{ 0 \}$. We denote by $\delta \mathbin {:=}\sum _{i \in I} d_i \alpha _i$ the imaginary root and by $c=\sum _{i \in I} c_ih_i$ the center. We have $d_0=1$.

For an affine Cartan datum $(\mathsf {A},\mathsf {P},\Pi ,\mathsf {P}^{\vee },\Pi ^{\vee })$, we denote by $\mathfrak {g}$ the affine Kac–Moody algebra, $\mathfrak {g}_0$ the subalgebra generated by $\{ e_i,f_i,h_i \ | \ i \in I_0\}$, by $U_q(\mathfrak {g})$ and $U_q(\mathfrak {g}_0)$ the corresponding quantum groups. We denote by $U_q'(\mathfrak {g})$ the subalgebra of $U_q(\mathfrak {g})$ generated by $\{ e_i, f_i, q^{\pm h_i} \ | \ i \in I\}$. We mainly deal with $U_q'(\mathfrak {g})$ which is called the quantum affine algebra.

We say that a $U_q'(\mathfrak {g})$-module M is integrable if

• (i) it is $\mathsf {P}/ \mathbb {Z}\delta$-graded,

  $$\begin{aligned} M = \mathop {\bigoplus }\limits _{\lambda \in \mathsf {P}/ \mathbb {Z}\delta } M_\lambda \ \ \text { where } M_\lambda =\{ u \in M \ | \ q^{h_i} u =q^{\langle h_i,\lambda \rangle } u \ \text { for all } i \in I \}, \end{aligned}$$

• (ii) for all $i \in I$, $e_i$ and $f_i$ act on M locally nilpotently.

We denote by $\mathcal {C}_\mathfrak {g}$ the category of finite-dimensional integrable $U_q'(\mathfrak {g})$-modules. For the rest of this paper, we take the algebraic closure of $\mathbb {C}(q)$ in $\displaystyle \cup _{m >0} \mathbb {C}((q^{1/m}))$ as the base field $\mathbf {k}$ of $U_q'(\mathfrak {g})$-modules. A simple module M in $\mathcal {C}_\mathfrak {g}$ contains a nonzero vector u of weight $\lambda \in \mathsf {P}_\mathrm{cl}\mathbin {:=}\mathsf {P}/\mathbb {Z}\delta$ such that

• $\langle c,\lambda \rangle =0$ and $\langle h_i,\lambda \rangle \ge 0$ for all $i \in I_0$,

• all the weights of M are contained in $\lambda - \sum _{i \in I_0} \mathbb {Z}_{\ge 0} \mathrm{cl}(\alpha _i)$,

where $\mathrm{cl}:\mathsf {P}\rightarrow \mathsf {P}_\mathrm{cl}$. Such a $\lambda$ is unique, and u is unique up to a constant multiple. We call $\lambda$ the dominant extremal weight of M and u the dominant extremal weight vector of M.

For $M \in \mathcal {C}_\mathfrak {g}$ and $x\in \mathbf {k}^\times$, let $M_x$ be the $U_q'(\mathfrak {g})$-module with the actions of $e_i$, $f_i$ replaced with $x^{\delta _{i0}}e_i$, $x^{-\delta _{i0}}f_i$, respectively.

For each $i \in I_0$, we set

$$\begin{aligned} \varpi _i \mathbin {:=}\mathrm{gcd}(c_0,c_i)^{-1}\mathrm{cl}(c_0\Lambda _i-c_i \Lambda _0) \in \mathsf {P}_\mathrm{cl}. \end{aligned}$$

Then there exists a unique simple $U_q'(\mathfrak {g})$-module $V(\varpi _i)$ in $\mathcal {C}_\mathfrak {g}$ with its dominant extremal weight $\varpi _i$ and its dominant extremal weight vector $u_{\varpi _i}$, called the fundamental representation of weight$\varpi _i$, satisfying certain conditions (see [1, §1.3] for more detail). Moreover, there exist the left dual $V(\varpi _i)^*$ and the right dual ${}^*V(\varpi _i)$ of $V(\varpi _i)$ with the following $U_q'(\mathfrak {g})$-homomorphisms

$$\begin{aligned} V(\varpi _i)^* \otimes V(\varpi _i) \overset{\mathrm{tr}}{\longrightarrow } \mathbf {k}\quad \text { and } \quad V(\varpi _i) \otimes {}^*V(\varpi _i) \overset{\mathrm{tr}}{\longrightarrow } \mathbf {k}. \end{aligned}$$

(4.1)

We have

$$\begin{aligned} V(\varpi _i)^*\simeq V(\varpi _{i^*})_{(p^*)^{-1}}, \ {}^*V(\varpi _i)\simeq V(\varpi _{i^*})_{p^*} \ \ \text { with } \ \ p^* \mathbin {:=}(-1)^{\langle \rho ^\vee ,\delta \rangle } q^{\langle c,\rho \rangle }. \end{aligned}$$

(4.2)

Here $\rho$ is defined by $\langle h_i,\rho \rangle =1$, $\rho ^\vee$ is defined by $\langle \rho ^\vee ,\alpha _i \rangle =1$ and $i^*$ is the involution of $I_0$ defined in (2.2).

For $k \in \mathbb {Z}$ and $V(\varpi _i)_x$, we denote by

$$\begin{aligned} V(\varpi _i)^{k*}_x&\mathbin {:=}&{\left\{ \begin{array}{ll} V(\varpi _i)_x &{}\text {if }k=0,\\ ( \cdots ((V(\varpi _i)_x \underbrace{ )^*)^* \cdots )^{*}}_{k\text {-times}} &{}\text {if }k>0,\\ \underbrace{{}^*( \cdots {}^*({}^*(}_{-k\text {-times}}V(\varpi _i)_x)) \cdots ) &{}\text {if }k<0. \end{array}\right. } \end{aligned}$$

We say that a $U_q'(\mathfrak {g})$-module M is good if it has a bar involution, a crystal basis with simple crystal graph, and a global basis (see [23] for the precise definition). For instance, $V(\varpi _i)$ is a good module for every $i \in I$.

4.2 Denominator formulas and folded distance polynomials

For a good module M and N, there exists a $U_q'(\mathfrak {g})$-homomorphism

$$\begin{aligned} R^{\mathrm{norm}}_{M,N}: M_{z_M} \otimes M_{z_N} \rightarrow \mathbf {k}(z_M,z_N) \otimes _{\mathbf {k}[z_M^{\pm 1},z_N^{\pm 1}]} N_{z_N} \otimes M_{z_M} \end{aligned}$$

such that

$$\begin{aligned} R^{\mathrm{norm}}_{M,N} \circ z_M = z_M \circ R^{\mathrm{norm}}_{M,N}, \ R^{\mathrm{norm}}_{M,N} \circ z_N = z_N \circ R^{\mathrm{norm}}_{M,N} \text { and } R^{\mathrm{norm}}_{M,N} (u_M \otimes u_N) = u_N \otimes u_M, \end{aligned}$$

where $u_M$ (resp. $u_N$) is the dominant extremal weight vector of M (resp. N).

The denominator$d_{M,N}$ of $R^{\mathrm{norm}}_{M,N}$ is the unique nonzero monic polynomial $d(u) \in \mathbf {k}[u]$ of the smallest degree such that

$$\begin{aligned} d_{M,N}(z_N/z_M)R^{\mathrm{norm}}_{M,N}(M_{z_M} \otimes N_{z_N}) \subset N_{z_N} \otimes M_{z_M}. \end{aligned}$$

(4.3)

Theorem 4.1

[1, 4, 23]

• (1) For good modules $M_1$ and $M_2$, the zeroes of $d_{M_1,M_2}(z)$ belong to $\mathbb {C}[[q^{1/m}]]\;q^{1/m}$ for some $m\in \mathbb {Z}_{>0}$.

• (2) $V(\varpi _i)_{a_i} \otimes V(\varpi _j)_{a_j}$ is simple if and only if

  $$\begin{aligned} d_{i,j}(z)\mathbin {:=}d_{V(\varpi _i),V(\varpi _j)}(z) \end{aligned}$$

  does not vanish at $z=a_i/a_j$ nor $a_j/a_i$.

• (3) Let M be a finite-dimensional simple integrable $U'_q(\mathfrak {g})$-module M. Then, there exists a finite sequence

  $$\begin{aligned} \left( (i_1,a_1),\ldots , (i_l,a_l)\right) \text { in } (I_0\times \mathbf {k}^\times )^l \end{aligned}$$

  such that $d_{i_k,i_{k'}}(a_{k'}/a_k) \not =0$ for $1\le k<k'\le l$ and M is isomorphic to the head of $\bigotimes _{i=1}^{l}V(\varpi _{i_k})_{a_k}$. Moreover, such a sequence $\left( (i_1,a_1),\ldots , (i_l,a_l)\right)$ is unique up to permutation.

• (4) $d_{k,l}(z)=d_{l,k}(z)=d_{k^*,l^*}(z)=d_{l^*,k^*}(z)$ for $k,l \in I_0$.

The denominator formulas between fundamental representations are calculated in [1, 6, 18, 32] for all classical quantum affine algebras (see [32, Appendix A]). In this paper, we will focus on the denominator formulas for $U'_q(B_n^{(1)})$ and $U'_q(C_n^{(1)})$:

Proposition 4.2

[1, 32]

$$\begin{aligned} d^{B_{n}^{(1)}}_{k,l}(z)&= {\left\{ \begin{array}{ll} \displaystyle \prod _{s=1}^{\min (k,l)} \big (z-(-q)^{|k-l|+2s}\big )\big (z+(-q)^{2n-k-l-1+2s}\big ) &{} 1 \le k,l \le n-1, \\ \displaystyle \prod _{s=1}^{k}\big (z-(-1)^{n+k}q_s^{2n-2k-1+4s}\big ) &{} 1 \le k \le n-1, \ l=n, \\ \displaystyle \prod _{s=1}^{n} \big (z-(q_s)^{4s-2}\big ) &{} k=l=n. \end{array}\right. } \end{aligned}$$

(4.4a)

$$\begin{aligned} d^{C_{n}^{(1)}}_{k,l}(z)&= \displaystyle \prod _{s=1}^{ \min (k,l,n-k,n-l)} \big (z-(-q_s)^{|k-l|+2s}\big )\prod _{i=1}^{ \min (k,l)} \big (z-(-q_s)^{2n+2-k-l+2s}\big ) \end{aligned}$$

(4.4b)

The following theorem tells that we can read $d^{B_{n}^{(1)}}_{k,l}(z)$ from any $\widehat{\Upsilon }_{[\mathscr {Q}]}$ of type $A_{2n-1}$ and $d^{C_{n}^{(1)}}_{k,l}(z)$ from any $\widehat{\Upsilon }_{[\mathscr {Q}]}$ of type $D_{n+1}$:

Theorem 4.3

[35, 36] For any $k,l \in \widehat{I}$, we have

$$\begin{aligned}&d^{B_{n}^{(1)}}_{k,l}(z)= \widehat{D}_{k,l}(z) \times (z-q^{2n-1})^{\delta _{k,l}}&\text { where }\llbracket \mathscr {Q}\rrbracket \text { is of type }A_{2n-1}, \end{aligned}$$

(4.5a)

$$\begin{aligned}&d^{C_{n}^{(1)}}_{k,l}(z)= \widehat{D}_{k,l}(z) \times (z-q^{n+1})^{\delta _{k,l}}&\text { where }\llbracket \mathscr {Q}\rrbracket \text { is of type }D_{n+1}. \end{aligned}$$

(4.5b)

4.3 Dorey’s rule and minimal pairs

The morphisms in

$$\begin{aligned} \mathrm{Hom}_{U_q'(\mathfrak {g})}\big ( V(\varpi _i)_a \otimes V(\varpi _j)_b, V(\varpi _k)_c \big ) \quad \text { for } i,j,k\in I_0 \quad \text {and}\quad a,b,c \in \mathbf {k}^\times \end{aligned}$$

are studied by [5, 18, 32, 39] and called Dorey’s type morphisms. In [30, 31], the condition of non-vanishing of the above Hom space are interpreted the positions of $\alpha ,\beta ,\gamma \in \Phi ^+$ in $\Gamma _Q$ where $(\alpha ,\beta )$ is a pair for $\gamma$ and $\mathfrak {g}$ is of type $A^{(1)}_{n}$ or $D^{(1)}_{n}$.

Theorem 4.4

[5, Theorem 8.1, Theorem 8.2] For $\mathfrak {g}^{(1)}=B^{(1)}_{n}$ or $C^{(1)}_{n}$, let (i, x), (j, y), $(k,z) \in I_0 \times \mathbf {k}^\times$. Then

$$\begin{aligned} \mathrm{Hom}_{U'_q(\mathfrak {g}^{(1)})}\big ( V(\varpi _{j})_y \otimes V(\varpi _{i})_x , V(\varpi _{k})_z \big ) \ne 0 \end{aligned}$$

if and only if one of the following conditions holds$:$

• (1) When $\mathfrak {g}^{(1)}=B^{(1)}_{n}$, the conditions are given as follows$:$

  

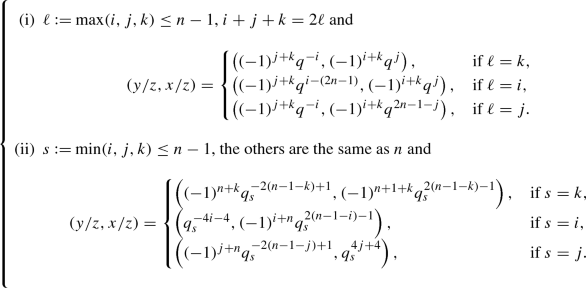  (4.6)

• (2) When $\mathfrak {g}^{(1)}=C^{(1)}_{n}$, the conditions are given as follows$:$

  

  (4.7)

Definition 4.5

[35, 36] For any $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$ and any positive root $\beta \in \Phi ^+$ of type $A_{2n-1}$ or $D_{n+1}$, we set the $U_q'(\mathfrak {g}^{(1)})$-module ($\mathfrak {g}^{(1)}=B_n^{(1)}$ or $C_n^{(1)}$) $V_{\mathscr {Q}}(\beta )$ defined as follows$:$ For $\widehat{\Omega }_{\mathscr {Q}}(\beta )=(i,p)$, we define

$$\begin{aligned} V_{\mathscr {Q}}(\beta ) \mathbin {:=}{\left\{ \begin{array}{ll} V(\varpi _{i})_{(-1)^i(q_s)^{p}} &{} \text { if } \mathfrak {g}^{(1)}=B_n^{(1)}, \\ V(\varpi _{i})_{(-q_s)^{p}} &{} \text { if } \mathfrak {g}^{(1)}=C_n^{(1)}. \end{array}\right. } \end{aligned}$$

(4.8)

By Proposition 3.8, Proposition 3.8 and Theorem 4.4, we have the following:

Theorem 4.6

[35, 36] Let (i, x), (j, y), $(k,z) \in I_0 \times \mathbf {k}^\times$. Then

$$\begin{aligned} \mathrm{Hom}_{U_q'(\mathfrak {g}^{(1)})}\big ( V(\varpi _{j})_y \otimes V(\varpi _{i})_x , V(\varpi _{k})_z \big ) \ne 0 \quad \text { for } \mathfrak {g}^{(1)}=B^{(1)}_{n} \ ( \text { resp.}\ C^{(1)}_{n}) \end{aligned}$$

if and only if there exists a twisted adapted class $[\mathscr {Q}]$ of type $A_{2n-1}$ (resp. $D_{n+1})$ and $\alpha ,\beta ,\gamma \in \Phi _{A_{2n-1}}^+$ (resp. $\Phi _{D_{n+1}}^+)$ such that

• (1) $(\alpha ,\beta )$ is a $[\mathscr {Q}]$-minimal pair of $\gamma$,

• (2) $V(\varpi _{j})_y = V_{\mathscr {Q}}(\beta )_a, \ V(\varpi _{i})_x = V_{\mathscr {Q}}(\alpha )_a, \ V(\varpi _{k})_z = V_{\mathscr {Q}}(\gamma )_a$ for some $a \in \mathbf {k}^\times$.

5 Categorifications and Schur–Weyl dualities

In this section, we review the categorifications of quantum groups via quiver Hecke algebras and quantum affine Hecke algebras and the generalized quantum affine Schur–Weyl dualities between them introduced in [17].

5.1 Categorifications via modules over quiver Hecke algebras

For a given symmetrizable Cartan datum $(\mathsf {A},\mathsf {P},\Pi ,\mathsf {P}^\vee ,\Pi ^\vee )$, we choose a polynomial $\mathcal {Q}_{ij}(u,v) \in \mathbf {k}[u,v]$ for $i,j \in I$ which is of the form

$$\begin{aligned} \mathcal {Q}_{ij}(u,v) = \delta (i \ne j)\sum \limits _{ \begin{array}{c} (p,q)\in \mathbb {Z}^2_{\ge 0} \\ p(\alpha _i | \alpha _i) + q(\alpha _j | \alpha _j)=-2(\alpha _i|\alpha _j) \end{array}} t_{i,j;p,q} u^p v^q \end{aligned}$$

(5.1)

with the condition on $t_{i,j;p,q}\in \mathbf {k}$ as follows:

$$\begin{aligned} t_{i,j;p,q}=t_{j,i;q,p} \quad \text {and} \quad t_{i,j:-a_{ij},0} \in \mathbf {k}^{\times }. \end{aligned}$$

Thus, we have $\mathcal {Q}_{i,j}(u,v)=\mathcal {Q}_{j,i}(v,u)$.

For $n \in \mathbb {Z}_{\ge 0}$ and $\mathsf {b} \in \mathsf {Q}^+$ such that $\mathrm{ht}(\mathsf {b}) = n$, we set

$$\begin{aligned} I^{\mathsf {b}} = \left\{ \nu = (\nu _1, \ldots , \nu _n) \in I^{n} \ | \ \alpha _{\nu _1} + \cdots + \alpha _{\nu _n} = \beta \right\} . \end{aligned}$$

For $\mathsf {b} \in \mathsf {Q}^+$, we denote by $R(\mathsf {b})$ the quiver Hecke algebra at $\mathsf {b}$ associated with $(\mathsf {A},\mathsf {P},\Pi ,\mathsf {P}^\vee ,\Pi ^\vee )$ and $(\mathcal {Q}_{i,j})_{i,j \in I}$. It is a $\mathbb {Z}$-graded $\mathbf {k}$-algebra generated by the generators $\{ e(\nu ) \}_{\nu \in I^{\mathsf {b}}}$, $\{x_k \}_{1 \le k \le \mathrm{ht}(\mathsf {b})}$, $\{ \tau _m \}_{1 \le m < \mathrm{ht}(\mathsf {b})}$ with the certain defining relations (see [30, Definition 2.7] for the relations).

Let $\mathrm{Rep}(R(\mathsf {b}))$ be the category consisting of finite-dimensional graded $R(\mathsf {b})$-modules and $[\mathrm{Rep}(R(\mathsf {b}))]$ be the Grothendieck group of $\mathrm{Rep}(R(\mathsf {b}))$. Then $[\mathrm{Rep}(R(\mathsf {b}))]$ has a natural $\mathbb {Z}[q^{\pm 1}]$-module structure induced by the grading shift. In this paper, we often ignore grading shifts.

For $M \in \mathrm{Rep}(R(\mathsf {a}))$ and $N \in \mathrm{Rep}(R(\mathsf {b}))$, we denote by $M \circ N$ the convolution product of M and N. Then $\mathrm{Rep}(R)\mathbin {:=}\mathop {\bigoplus }\limits _{\mathsf {b} \in \mathsf {Q}^+} \mathrm{Rep}(R(\mathsf {b}))$ has a monoidal category structure by the convolution product and its Grothendieck group $[\mathrm{Rep}(R)]$ has a natural $\mathbb {Z}[q^{\pm 1}]$-algebra structure induced by the convolution product $\circ$ and the grading shift functor q.

For $M \in \mathrm{Rep}(\mathsf {b})$ and $M_k \in \mathrm{Rep}(\mathsf {b}_k)$$(1 \le k \le n)$, we denote by

$$\begin{aligned} M^{\circ 0} \mathbin {:=}\mathbf {k}, \quad M^{\circ r} = \overbrace{ M \circ \cdots \circ M }^r, \quad \overset{n}{\underset{k=1}{\circ }} M_k = M_1 \circ \cdots \circ M_n. \end{aligned}$$

The quiver Hecke algebras, a vast generalization of affine Hecke algebras of type A, were introduced independently by Khovanov and Lauda [25], and Rouquier [37] to provide a categorification of quantum groups:

Theorem 5.1

[25, 37] For a given symmetrizable Cartan datum, let $U^-_{\mathbb {A}}(\mathsf {g})^\vee$$(\mathbb {A}=\mathbb {Z}[q^{\pm 1}])$ the dual of the integral form of the negative part of quantum groups $U_q(\mathsf {g})$ and let R be the quiver Hecke algebra related to the datum. Then we have

$$\begin{aligned} U^-_{\mathbb {A}}(\mathsf {g})^{\vee } \simeq [\mathrm{Rep}(R)]. \end{aligned}$$

(5.2)

Definition 5.2

We say that the quiver Hecke algebra R is symmetric if $\mathsf {A}$ is symmetric and $\mathcal {Q}_{ij}(u,v)$ is a polynomial in $u-v$ for all $i,j\in I$.

Theorem 5.3

 [38, 40] Assume that the quiver Hecke algebra R is symmetric and the base field $\mathbf {k}$ is of characteristic zero. Then under the isomorphism (5.2) in Theorem 5.1, the upper global basis of $U^-_{\mathbb {A}}(\mathsf {g})^{\vee }$ corresponds to the set of the isomorphism classes of self-dual simple R-modules.

Theorem 5.4

[24, 29, 33] For a finite-dimensional simple Lie algebra $\mathsf {g}$, the dual PBW-basis of $U^-_\mathbb {A}(\mathsf {g})^\vee$ associated with $[{\widetilde{w}_0}]$ is categorified in the following sense: for each $\beta \in \Phi ^+$, there exists a simple $R(\beta )$-module $S_{[{\widetilde{w}_0}]}(\beta )$ such that

• (1) $S_{[{\widetilde{w}_0}]}(\beta )^{\circ r}$ is simple for any $r \in \mathbb {Z}_{\ge 0}$,

• (2) for each $\underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}$, set $S_{[{\widetilde{w}_0}]}(\underline{m})\mathbin {:=}S_{[{\widetilde{w}_0}]}(\beta _1)^{\circ m_1}\circ \cdots \circ S_{[{\widetilde{w}_0}]}(\beta _\mathsf {N})^{\circ m_\mathsf {N}}$. Then the set $\{ S_{[{\widetilde{w}_0}]}(\underline{m})\ | \ \underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}\}$ corresponds to the dual PBW-basis under the isomorphism in (5.2) (up to a grading shifts),

• (3) for each simple module $M \in \mathrm{Rep}(R)$, there exists a unique $\underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}$ such that ${{\text {hd}}}(S_{[{\widetilde{w}_0}]}(\underline{m})) \simeq M$ and ${{\text {hd}}}(S_{[{\widetilde{w}_0}]}(\underline{m})) \simeq {{\text {hd}}}(S_{[{\widetilde{w}_0}]}(\underline{m}'))$ if and only if $\underline{m}=\underline{m}'$.

5.2 Categorifications via modules over untwisted quantum affine algebras

Definition 5.5

[13, 14, 21] Fix any $[Q] \in \llbracket Q \rrbracket$ of finite type $A_n$ or $D_n$, and any positive root $\beta \in \Phi ^+$ with $\Omega _{Q}(\beta )=(i,p)$.

• (i) We set the $U_q'(\mathfrak {g}^{(1)})$-module ($\mathfrak {g}^{(1)}=A_n^{(1)}$ , $D_n^{(1)}$) $V^{(1)}_{Q}(\beta )$ defined as follows$:$

  $$\begin{aligned} V^{(1)}_{Q}(\beta ) \mathbin {:=}V(\varpi _{i})_{(-q)^{p}}. \end{aligned}$$

• (ii) We set the $U_q'(\mathfrak {g}^{(2)})$-module ($\mathfrak {g}^{(2)}=A_n^{(2)}$, $D_n^{(2)}$) $V^{(2)}_{Q}(\beta )$ defined as follows$:$

  $$\begin{aligned} V^{(2)}_{Q}(\beta ) \mathbin {:=}V(\varpi _{i^\star })_{((-q)^{p})^\star }, \end{aligned}$$

  where

  $$\begin{aligned} (i^\star ,((-q)^{p})^\star ) \mathbin {:=}{\left\{ \begin{array}{ll} (i,(-q)^{p}) &{} \text { if } \mathfrak {g}^{(2)}=A^{(2)}_n \text { and } 1 \le i \le \left\lfloor \dfrac{n+1}{2} \right\rfloor , \\ (n+1-i,(-1)^n(-q)^{p}) &{} \text { if } \mathfrak {g}^{(2)}=A^{(2)}_n \text { and } \left\lfloor \dfrac{n+1}{2} \right\rfloor \le i \le n , \\ (i,(\sqrt{-1})^{n-i}(-q)^{p}) &{} \text { if } \mathfrak {g}^{(2)}=D^{(2)}_n \text { and } 1 \le i \le n-2, \\ (n-1,(-1)^i(-q)^{p})&{} \text { if } \mathfrak {g}^{(2)}=D^{(2)}_n \text { and } n-1 \le i \le n. \end{array}\right. } \end{aligned}$$

  (5.3)

• (1) We define the smallest abelian full subcategory $\mathcal {C}^{({t})}_Q$$({t}=1,2)$ of $\mathcal {C}_{\mathfrak {g}^{({t})}}$ such that

  • (a) it is stable by taking subquotient, tensor product and extension,

  • (b) it contains $V^{({t})}_Q(\beta )$ for all $\beta \in \Phi ^+$.

• (2) We define the smallest abelian full subcategory $\mathcal {C}^{({t})}_\mathbb {Z}$$({t}=1,2)$ of $\mathcal {C}_{\mathfrak {g}^{({t})}}$ such that

  • (a) it is stable by taking subquotient, tensor product and extension,

  • (b) it contains $V^{({t})}_Q(\beta )^{k*}$ for all $\beta \in \Phi ^+$ and all $k \in \mathbb {Z}$.

Note that the definition $\mathcal {C}^{({t})}_{\mathbb {Z}}$ does not depend on the choice of Q and its height function.

Theorem 5.6

[14, 21] We have a ring isomorphism given as follows$:$ For any Q and $Q'$,

$$\begin{aligned} \left[ \mathcal {C}^{(1)}_Q \right] \simeq U^-_{\mathbb {A}}(\mathsf {g})^{\vee }|_{q=1} \simeq \left[ \mathcal {C}^{(2)}_{Q'} \right] , \end{aligned}$$

(5.4)

where $\left[ \mathcal {C}^{({t})}_Q \right]$ denotes the Grothendieck ring of $\mathcal {C}^{({t})}_Q$$({t}=1,2)$.

Theorem 5.7

[14, 21] Let Q be a Dynkin quiver of finite type $A_n$, $D_n$$(t = 1,2)$ and $E_n$$(t=1)$. Then the dual PBW-basis associated with [Q] and the upper global basis of $U^-_{\mathbb {A}}(\mathsf {g})^{\vee }$ are categorified by the modules over $U_q'(\mathfrak {g}^{(t)})$ in the following sense $:$

• (1) The set of all simple modules in $\mathcal {C}^{({t})}_Q$ corresponds to the upper global basis of $U^-_{\mathbb {A}}(\mathsf {g})^{\vee }|_{q=1}$.

• (2) For each $\underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}$, define the $U_q'(\mathfrak {g})$-module $V^{({t})}_{Q}(\underline{m})$ by $V_{Q}^{({t})}(\beta _1)^{\otimes m_1}\otimes \cdots \otimes V_{Q}^{({t})}(\beta _\mathsf {N})^{\otimes m_\mathsf {N}}$. Then the set $\{ V^{({t})}_{Q}(\underline{m})\ | \ \underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}\}$ corresponds to the dual PBW-basis under the isomorphism in (5.4).

• (3) For each simple module $M \in \mathcal {C}_Q^{(t)}$, there exists a unique $\underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}$ such that ${{\text {hd}}}(V_Q^{(t)}(\underline{m})) \simeq M$ and ${{\text {hd}}}(V_Q^{(t)}(\underline{m})) \simeq {{\text {hd}}}(V_Q^{(t)}(\underline{m}'))$ if and only if $\underline{m}=\underline{m}'$.

5.3 Generalized quantum affine Schur–Weyl dualities

In this subsection, we briefly review the generalized quantum affine Schur–Weyl duality which was studied in [17, 18, 20, 21].

Let $\mathcal {S}$ be an index set. A Schur–Weyl datum $\Xi$ is a quintuple

$$\begin{aligned} (U_q'(\mathfrak {g}),J,X,s,\{V_s\}_{s \in \mathcal {S}}) \end{aligned}$$

consisting of (a) a quantum affine algebra $U_q'(\mathfrak {g})$, (b) an index set J, (c) two maps $X:J \rightarrow \mathbf {k}^\times , \ s: J \rightarrow \mathcal {S}$, (d) a family of good $U'_q(\mathfrak {g})$-modules $\{V_s\}$ indexed by $\mathcal {S}$.

For a given $\Xi$, we define a quiver $\Gamma ^{\Xi }=(\Gamma ^{\Xi }_0,\Gamma ^{\Xi }_1)$ in the following way$:$ (i) $\Gamma ^{\Xi }_0= J$, (ii) for $i,j \in J$, we assign $\mathtt {d}_{ij}$ many arrows from i to j, where $\mathtt {d}_{ij}$ is the order of the zero of $d_{V_{s(i)},V_{s(j)}}(z_2/z_1)$ at X(j) / X(i). We call $\Gamma ^{\Xi }$ the Schur–Weyl quiver associated with $\Xi$.

For a Schur–Weyl quiver $\Gamma ^{\Xi }$, we have

• a symmetric Cartan matrix $\mathsf {A}^{\Xi }=(a^{\Xi }_{ij})_{i,j \in J}$ by

  $$\begin{aligned} a^{\Xi }_{ij} = 2 \quad \text { if } i =j, \quad a^{\Xi }_{ij} = -\mathtt {d}_{ij}-\mathtt {d}_{ji} \quad \text { if } i \ne j, \end{aligned}$$

  (5.5)

• the set of polynomials $(\mathcal {Q}^{\Xi }_{i,j}(u,v))_{i,j \in J}$

  $$\begin{aligned} \mathcal {Q}^{\Xi }_{i,j}(u,v) =(u-v)^{\mathtt {d}_{ij}}(v-u)^{\mathtt {d}_{ji}} \quad \text { if } i \ne j. \end{aligned}$$

We denote by $R^{\Xi }$ the symmetric quiver Hecke algebra associated with $(\mathcal {Q}^{\Xi }_{i,j}(u,v))$.

Theorem 5.8

[17] For a given ${\Xi }$, there exists a functor

$$\begin{aligned} \mathcal {F}: \mathrm{Rep}(R^{\Xi }) \rightarrow \mathcal {C}_\mathfrak {g}. \end{aligned}$$

Moreover, $\mathcal {F}$ satisfies the following properties$:$

• (1) $\mathcal {F}$ is a tensor functor; that is, there exist $U_q'(\mathfrak {g})$-module isomorphisms

  $$\begin{aligned} \mathcal {F}(R^{\Xi }(0)) \simeq \mathbf {k}\quad \text { and } \quad \mathcal {F}(M_1 \circ M_2) \simeq \mathcal {F}(M_1) \otimes \mathcal {F}(M_2) \end{aligned}$$

  for any $M_1, M_2 \in \mathrm{Rep}(R^{\Xi })$.

• (2) If the underlying graph of $\Gamma ^{\Xi }$ is a Dynkin diagram of finite type ADE, then $\mathcal {F}$ is exact and $R^{\Xi }$ is isomorphic to the quiver Hecke algebra associated with $\mathsf {g}$ of finite type ADE.

We call the functor $\mathcal {F}$ the generalized quantum affine Schur–Weyl duality functor.

Theorem 5.9

[18, 21] Let $U_q'(\mathfrak {g}^{(t)})$ be a quantum affine algebra of type $A^{(t)}_{n}$ (resp. $D^{({t})}_{n})$ and let Q be a Dynkin quiver of finite type $A_n$ (resp. $D_n)$ for ${t}=1,2$. Take J and $\mathcal {S}$ as the set of simple roots $\Pi$ associated with Q. We define two maps

$$\begin{aligned} s: \Pi \rightarrow \{ V(\varpi _i) \ | \ i \in I_0 \} \quad \text { and } \quad X: \Pi \rightarrow \mathbf {k}^\times \end{aligned}$$

as follows$:$ for $\alpha \in \Pi$ with $\Omega _Q(\alpha )=(i,p)$, we define

$$\begin{aligned} s(\alpha )={\left\{ \begin{array}{ll} V(\varpi _i) &{} \text {if }\mathfrak {g}^{(1)}=A^{(1)}_{n}\text { or }D^{(1)}_{n}, \\ V(\varpi _{i^\star }) &{} \text {if }\mathfrak {g}^{(2)}=A^{(2)}_{n}\text { or }D^{(2)}_{n}, \end{array}\right. } \qquad X(\alpha )= {\left\{ \begin{array}{ll} (-q)^p &{} \text {if }\mathfrak {g}^{(1)}=A^{(1)}_{n}\hbox { or }D^{(1)}_{n}, \\ ((-q)^p)^\star &{} \text {if }\mathfrak {g}^{(2)}=A^{(2)}_{n}\hbox { or }D^{(2)}_{n}. \end{array}\right. } \end{aligned}$$

Then we have the followings$:$

• (1) The underlying graph of $\Gamma ^{\Xi }$ coincides with the one of Q. Hence, the functor

  $$\begin{aligned} \mathcal {F}^{({t})}_Q: \mathrm{Rep}(R^{\Xi }) \rightarrow \mathcal {C}^{({t})}_Q \quad ({t}=1,2) \end{aligned}$$

  in Theorem 5.8 is exact.

• (2) The functor $\mathcal {F}^{({t})}_Q$ induces a bijection from the set of the isomorphism classes of simple objects of $\mathrm{Rep}(R^{\Xi })$ to that of $\mathcal {C}^{({t})}_Q$. In particular, $\mathcal {F}^{({t})}_Q$ sends $S_Q(\beta ) \mathbin {:=}S_{[Q]}(\beta )$ to $V^{({t})}_Q(\beta )$. Moreover, the induced bijection between the set of the isomorphism classes of simple objects of $\mathcal {C}^{(1)}_Q$ and that of $\mathcal {C}^{(2)}_Q$ preserves the dimensions.

• (3) The functors $\mathcal {F}^{(1)}_Q$ and $\mathcal {F}^{(2)}_Q$ induce the ring isomorphisms in (5.4).

6 Isomorphism between Grothendieck rings

In this section, we first introduce subcategories $\mathscr {C}_{\mathscr {Q}}$ and $\mathscr {C}_\mathbb {Z}$ of $\mathcal {C}_{B^{(1)}_{n}}$ or $\mathcal {C}_{C^{(1)}_{n}}$.

Definition 6.1

[15, 35, 36] (see also [21, Section 4.1])

• (i) Let us define $\mathscr {C}_\mathscr {Q}^{B^{(1)}_{n}}$ (resp. $\mathscr {C}_\mathscr {Q}^{C^{(1)}_{n}}$) as the smallest abelian full subcategory of $\mathcal {C}_{B^{(1)}_{n}}$ (resp. $\mathcal {C}_{C^{(1)}_{n}}$) such that

  • (a) it is stable by taking subquotient, tensor product and extension,

  • (b) it contains $V_\mathscr {Q}(\beta )$ for all $\beta \in \Phi ^+_{A_{2n-1}}$ (resp. $\Phi ^+_{D_{n+1}})$.

• (ii) Let us define $\mathscr {C}_\mathbb {Z}^{B^{(1)}_{n}}$ (resp. $\mathscr {C}_\mathbb {Z}^{C^{(1)}_{n}}$) as the smallest abelian full subcategory of $\mathcal {C}_{B^{(1)}_{n}}$ (resp. $\mathcal {C}_{C^{(1)}_{n}})$) such that

  • (a) it is stable by taking subquotient, tensor product and extension,

  • (b) it contains $V_\mathscr {Q}(\beta )^{k*}$ for all $k\in \mathbb {Z}$ and all $\beta \in \Phi ^+_{A_{2n-1}}$ (resp. $\Phi ^+_{D_{n+1}})$.

We sometimes omit the superscript ${B^{(1)}_{n}}$ or $C^{(1)}_{n}$ if there is no risk of confusion.

Note that the definition $\mathscr {C}_\mathbb {Z}$ does not depend on the choice of $[\mathscr {Q}]$ in $\llbracket \mathscr {Q}\rrbracket$.

Theorem 6.2

   

• (1) There exists an exact functor $\mathcal {F}_\mathscr {Q}:\mathrm{Rep}(R_{A_{2n-1}})\rightarrow \mathscr {C}_\mathscr {Q}\subset \mathcal {C}_{B^{(1)}_{n}}$ for any $[\mathscr {Q}]$ of type $A_{2n-1}$.

• (2) There exists an exact functor $\mathcal {F}_\mathscr {Q}:\mathrm{Rep}(R_{D_{n+1}})\rightarrow \mathscr {C}_\mathscr {Q}\subset \mathcal {C}_{C^{(1)}_{n}}$ for any $[\mathscr {Q}]$ of type $D_{n+1}$.

Proof

(1) For the construction of a functor, we need to take a Schur–Weyl datum $\Xi$. (i) Take J and $\mathcal {S}$ as the set of simple roots $\Pi$ of $\Phi ^+_{A_{2n-1}}$. (ii) Define two maps

$$\begin{aligned} s: \Pi \rightarrow \{ V(\varpi _i) \ | \ i \in I_0 \} \quad \text { and } \quad X: \Pi \rightarrow \mathbf {k}^\times \end{aligned}$$

as follows$:$ For $\alpha \in \Pi$ with $\widehat{\Omega }(\alpha )=(i,p)$, we define

$$\begin{aligned} s(\alpha )= V(\varpi _i) \ \text { and } \ X(\alpha )= (-1)^iq_s^p. \end{aligned}$$

Then we can conclude that the underlying graph of Schur–Weyl quiver $\Gamma ^{\Xi }$ coincides with the Dynkin diagram $\Delta$ of $A_{2n-1}$, since

• $\mathrm{dist}_{[\mathscr {Q}]}(\alpha _{i},\alpha _{j}) ={\left\{ \begin{array}{ll} 1 &{} \text { if } i\hbox { and }j\hbox { are adjacent in } \Delta , \\ 0 &{} \text { otherwise}, \end{array}\right. }$

• $d^{B_{n}^{(1)}}_{k,l}(z)= \widehat{D}_{k,l}(z) \times (z-q^{2n-1})^{\delta _{k,l}}$ (Theorem 4.3),

• $d^{B_{n}^{(1)}}_{k,l}(z)$ has only roots of order 1.

Thus, our assertion follows from (2) of Theorem 5.8.

(2) The assertion can be proved by the same argument of (1) with the two maps s and X given as follows$:$ For $\alpha \in \Pi$ with $\widehat{\Omega }(\alpha )=(i,p)$, we define

$$\begin{aligned} s(\alpha )= V(\varpi _i) \ \text { and } \ X(\alpha )= (-q_s)^p. \end{aligned}$$

$\square$

Theorem 6.3

For any $[\mathscr {Q}]$ of $\llbracket \mathscr {Q}\rrbracket$ and $\gamma \in \Phi ^+_{A_{2n-1}}$ (resp. $\gamma \in \Phi ^+_{D_{n+1}})$, we have

$$\begin{aligned} \mathcal {F}_\mathscr {Q}(S_\mathscr {Q}(\gamma )) \simeq V_\mathscr {Q}(\gamma ). \end{aligned}$$

Proof

We shall prove our assertion by an induction on $\mathrm{ht}(\gamma )$. For $\gamma$ with $\mathrm{ht}(\gamma )=1$, our assertion follows from [17, Proposition 3.2.2]. Now we assume that $\mathrm{ht}(\gamma ) \ge 2$. Note that there exists a minimal pair $(\alpha ,\beta )$ of $\gamma$. By [29, Theorem 3.1], we have a six-term exact sequence of $R(\gamma )$-modules

Applying the functor $\mathcal {F}_\mathscr {Q}$, we have an exact sequence of $U_q'(\mathfrak {g})$-modules by the induction hypothesis

On the other hand, Theorem 4.6 tells that $V_{\mathscr {Q}}(\beta ) \otimes V_{\mathscr {Q}}(\alpha )$ is not simple.

We have then $\mathcal {F}_\mathscr {Q}(S_{\mathscr {Q}}(\gamma )) \ne 0$. Indeed, if it vanished, we would have

$$\begin{aligned} V_{\mathscr {Q}}(\alpha ) \otimes V_{\mathscr {Q}}(\beta ) \simeq V_{\mathscr {Q}}(\beta ) \otimes V_\mathscr {Q}(\alpha ), \end{aligned}$$

which implies that $V_\mathscr {Q}(\alpha ) \otimes V_{\mathscr {Q}}(\beta )$ is simple by [19, Corollary 3.16].

Hence, $\mathcal {F}_\mathscr {Q}(S_{\mathscr {Q}}(\gamma ))$ is the image of a nonzero homomorphism

$$\begin{aligned} \mathcal {F}_\mathscr {Q}(t \circ s):V_\mathscr {Q}(\beta ) \otimes V_\mathscr {Q}(\alpha )\rightarrow V_\mathscr {Q}(\alpha ) \otimes V_\mathscr {Q}(\beta ). \end{aligned}$$

Thus, [19] and the quantum affine version of  [22, Proposition 3.2.9] imply that $\mathcal {F}_\mathscr {Q}(S_{\mathscr {Q}}(\beta ))$ is the simple head of $V_\mathscr {Q}(\beta ) \otimes V_\mathscr {Q}(\alpha )$ which coincides with $V_\mathscr {Q}(\gamma )$. $\square$

Lemma 6.4

Let $\beta ,\gamma \in \Phi ^+$. If $R^{\mathrm{norm}}_{V_\mathscr {Q}(\alpha ),V_\mathscr {Q}(\beta )}(z)$ has a pole at $z=1$, then $\beta \prec _{[\mathscr {Q}]} \alpha$.

Proof

We shall prove this for $[\mathscr {Q}]$ of type $A_{2n-1}$, since the remained case can be proved in a similar way. Set $\widehat{\Omega }_{[\mathscr {Q}]}(\alpha )=(i,a)$ and $\widehat{\Omega }_{[\mathscr {Q}]}(\beta )=(j,b)$, where $i,j \in \widehat{I}$. By Theorem 4.1, $a>b$ and $(-1)^{i-j}q_s^{a-b}$ is a root of $d^{B_n^{(1)}}_{i,j}(z)$. Then our assertion follows from the facts that $d^{B_n^{(1)}}_{i,j}(z)$ has only roots of order 1 [see (4.4a)] and (4.5a).

Theorem 6.5

The functor $\mathcal {F}_\mathscr {Q}$ sends a simple module to a simple module. Moreover, the functor $\mathcal {F}_\mathscr {Q}$ induces a bijection from the set of simple modules in $\mathrm{Rep}(R)$ to the set of simple modules in $\mathscr {C}_\mathscr {Q}$.

Proof

By [29, Theorem 3.1], every simple module M in $\mathrm{Rep}(R)$ is isomorphic to the image of the homomorphism

$$\begin{aligned} {\mathbf {r}}_{\underline{m}} :S_{\mathscr {Q}}(\underline{m}) \rightarrow S_\mathscr {Q}( \overset{\leftarrow }{\underline{m}}) \mathbin {:=}\overset{\mathsf {N}}{\underset{k=1}{\circ }} S_{\mathscr {Q}}(\beta _{r-k+1})^{\circ m_{r-k+1}} \end{aligned}$$

(6.1)

for a unique $\underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}$. Here $S_{\mathscr {Q}}(\beta ) \mathbin {:=}S_{[\mathscr {Q}]}(\beta )$. Moreover, we have (see also [33])

$$\begin{aligned}{}[S_{\mathscr {Q}}(\underline{m})] \in [\mathrm{Im}({\mathbf {r}}_{\underline{m}})] + \sum _{\underline{m}' \prec ^\mathtt {b}_{\mathscr {Q}} \underline{m}} \mathbb {Z}_{\ge 0} [\mathrm{Im}({\mathbf {r}}_{\underline{m}'})]. \end{aligned}$$

(6.2)

Applying the functor $\mathcal {F}_\mathscr {Q}$ on (6.1), we have

Now we shall prove that $\mathrm{Im}\big (\mathcal {F}_\mathscr {Q}({\mathbf {r}}_{\underline{m}})\big ) \simeq \mathcal {F}_\mathscr {Q}\big ( \mathrm{Im}({\mathbf {r}}_{\underline{m}})\big )$ is simple and isomorphic to $\mathrm{hd}(V_\mathscr {Q}(\underline{m}))$.

If $\underline{m}$ is a unit vector, then our claim follows from Theorem 6.3. Assume that $\underline{m}$ is not a unit vector. By Lemma 6.4, [17, Theorem 2.2.1 (ii)] tells that $V_\mathscr {Q}(\underline{m})$ has a simple head which is equal to the image of any nonzero map from $V_Q(\underline{m})$ to $V_\mathscr {Q}( \overset{\leftarrow }{\underline{m}})$. Thus, it is enough to show that $\mathcal {F}_\mathscr {Q}({\mathbf {r}}_{\underline{m}})$ is nonzero.

By the induction hypothesis on $\prec ^\mathtt {b}_\mathscr {Q}$, every composition factor of $\mathrm{Ker}\big (\mathcal {F}_\mathscr {Q}({\mathbf {r}}_{\underline{m}})\big )$ is of the form $\mathrm{hd}(V_\mathscr {Q}(\underline{m}'))$ for some $\underline{m}' \prec ^\mathtt {b}_\mathscr {Q}\underline{m}$. By [17, Theorem 2.2.1 (iii)], $\mathrm{hd}(V_\mathscr {Q}(\underline{m}))$ is isomorphic to $\mathrm{hd}(V_\mathscr {Q}(\underline{m}'))$ if and only if $\underline{m}' = \underline{m}$. Thus, we conclude that $\mathrm{hd}(V_\mathscr {Q}(\underline{m}))$ cannot appear as a composition factor of $\mathrm{Ker}\big (\mathcal {F}_\mathscr {Q}({\mathbf {r}}_{\underline{m}})\big )$, which yields that $\mathcal {F}_\mathscr {Q}({\mathbf {r}}_{\underline{m}})$ is nonzero. $\square$

Thus, for any [Q], $[Q']$ and $[\mathscr {Q}]$, we have the following diagrams$:$

(6.3)

Corollary 6.6

Let $\mathsf {g}=A_{2n-1}$ or $D_{n+1}$. For any $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$, there exists an isomorphism between $[\mathscr {C}_\mathscr {Q}]$ and $U^-_\mathbb {A}(\mathsf {g})^\vee |_{q=1}$ induced by $\mathcal {F}_\mathscr {Q}:$

$$\begin{aligned}{}[\mathcal {F}_\mathscr {Q}] : [\mathscr {C}_\mathscr {Q}] \simeq U^-_\mathbb {A}(\mathsf {g})^\vee |_{q=1}. \end{aligned}$$

(6.4)

Hence, we have isomorphisms which extend (5.4)$:$

(6.5)

Now we have a $[\mathscr {Q}]$-analogue of Theorem 5.7:

Corollary 6.7

A dual PBW-basis associated with $[\mathscr {Q}]$ and the upper global basis of $U^-_{\mathbb {A}}(\mathsf {g})^{\vee }$ are categorified by the modules over $U_q'(\mathfrak {g})$ in the following sense$:$

• (1) The set of all simple modules in $\mathscr {C}_\mathscr {Q}$ corresponds to the upper global basis of $U^-_{\mathbb {A}}(\mathsf {g})^{\vee }|_{q=1}$ and hence the set of all simple modules in $\mathrm{Rep}(R_\mathsf {g})$.

• (2) The set $\{ V_{\mathscr {Q}}(\underline{m})\ | \ \underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}\}$ corresponds to the dual PBW-basis under the isomorphism in (6.4).

• (3) For each simple module $M \in \mathscr {C}_\mathscr {Q}$, there exists a unique $\underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}$ such that ${{\text {hd}}}(V_\mathscr {Q}(\underline{m})) \simeq M$ and ${{\text {hd}}}(V_\mathscr {Q}(\underline{m})) \simeq {{\text {hd}}}(V_\mathscr {Q}(\underline{m}'))$ if and only if $\underline{m}=\underline{m}'$.

Corollary 6.8

For any [Q] and $[\mathscr {Q}]$ of type $A_{2n-1}$ (resp. $D_{n+1})$, the ring isomorphism

sends simples to simples, bijectively.

Remark 6.9

In [9], Frenkel and Hernandez conjectured that, for a module V in $\mathcal {C}_{\mathfrak {g}^{(r)}}$$(r=2,3)$, there exists a Langlands dual${}^LV$ in $\mathcal {C}_{{}^L\mathfrak {g}^{(r)}}$ whose characters satisfy certain properties. Here $U_q'({}^L\mathfrak {g}^{(r)})$ denotes the quantum affine algebra whose generalized Cartan matrix is a transpose the one of $U_q'(\mathfrak {g}^{(r)})$. They proved the conjecture when V is a Kirillov-Reshetikhin module. On the other hand, Corollary 6.8 tells that, for any module V in $\mathcal {C}_Q$, there exists the corresponding $\widehat{V}$ in $\mathscr {C}_\mathscr {Q}$ via $\mathcal {F}_\mathscr {Q}\circ {\mathcal {F}^{(2)}_Q}^{-1}$, which depends on the choice of $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$. Here, $\mathfrak {g}^{(r)}$ is of type $A_{2n-1}^{(2)}$ or $D_{n+1}^{(2)}$. Moreover, each $\widehat{V}$ is simple when V is simple, which is also related to the conjecture on preserving simplicity.

Corollary 6.10

For any [Q] and $[\mathscr {Q}]$ of type $A_{2n-1}$ (resp. $D_{n+1})$, the ring isomorphism $\phi ^{({t})}_{Q,\mathscr {Q}}$ sends $[V^{(t)}_{Q}(\alpha _i)]$ to $[V_{\mathscr {Q}}(\alpha _i)]$ for each simple root $\alpha _i$.

Proof

For any $i \in I$, the 1-dimensional module L(i) is the unique simple module over $R(\alpha _i)$. Thus, our assertion follows from [17, Proposition 3.2.2]. $\square$

Now we have a conjecture which can be understood as a Langlands analogue of [21, Conjecture 5.7]$:$

Conjecture 6.11

The functor $\mathcal {F}_{\mathscr {Q}} :\mathrm{Rep}(R) \rightarrow \mathscr {C}_\mathscr {Q}$ is an equivalence of categories.

7 Simple head and socle

In this section, we study the simple head and socle of $S_\mathscr {Q}(\alpha ) \circ S_\mathscr {Q}(\beta )$ and $V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )$ which has been studied in many context (see [19, 28, 33]). Since the Dorey’s rule can be interpreted as the conditions that a fundamental representation appears as the simple head of tensor product of two fundamental representations, the results in this section can be considered as a generalization of Dorey’s rule and its application.

Theorem 7.1

A pair $\underline{p}=(\alpha ,\beta )$ is $[{\widetilde{w}_0}]$-simple if and only if $S_\mathscr {Q}(\alpha ) \circ S_\mathscr {Q}(\beta )$ and $V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )$ are simple.

Proof

Only if part is an immediate consequence of [33, Theorem 5.10] (see also [29, Theorem 3.1]). Assume that $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p})>0$. Then there exists $\underline{m}$ such that $\underline{m}\prec ^\mathtt {b}_{[\mathscr {Q}]} \underline{p}$ and there exists no $\underline{m}'$ such that

$$\begin{aligned} \underline{m}\prec ^\mathtt {b}_{[\mathscr {Q}]} \underline{m}' \prec ^\mathtt {b}_{[\mathscr {Q}]} \underline{p}. \end{aligned}$$

Furthermore, by [35, Theorem 6.16] and [36, Theorem 8.12], $\underline{m}$ satisfies one of the following conditions$:$

• (1) if $\underline{m}=\alpha +\beta$, $\underline{p}$ is a minimal pair of $\alpha +\beta$.

• (2) if (a) $\alpha +\beta \not \in \Phi ^+$, (b) $\mathrm{dist}_{[\mathscr {Q}]}(\alpha ,\beta )=2$ and (c) $[\mathscr {Q}]$ is of type $A_{2n-1}$, $\underline{m}$ is a triple $(\mu ,\nu ,\eta )$ such that

  • (i) $\mu +\nu \in \Phi ^+$, $(\mu ,\nu )$ is a $[\mathscr {Q}]$-minimal pair of $\mu +\nu$ and $\alpha -\mu ,\beta -\nu \in \Phi ^+$,

  • (ii) $\eta$ is not comparable to $\mu$ and $\nu$ with respect to $\prec _{[\mathscr {Q}]}$,

  • (iii) $\eta =(\alpha -\mu )+(\beta -\nu )$ and $((\alpha -\mu ),(\beta -\nu ))$ is a $[\mathscr {Q}]$-minimal pair for $\eta$,

  • (iv) $(\alpha -\mu ,\mu )$, $(\nu ,\beta -\nu )$ are $[\mathscr {Q}]$-minimal pairs for $\alpha$ and $\beta$ respectively,

• (3) if $\alpha +\beta \not \in \Phi ^+$ and it does not satisfy one of (b) and (c) in (2), then $\underline{m}$ is a pair $(\alpha ',\beta ')$ and either (i) $\alpha '-\alpha , \beta -\beta ' \in \Phi ^+$ or (ii) $\alpha -\alpha ', \beta '-\beta \in \Phi ^+$ such that (i$^*$) $(\alpha '-\alpha ,\alpha )$ is a minimal pair for $\alpha$ or (ii$^*$) $(\beta '-\beta ,\beta )$ is a minimal pair for $\beta$.

(see [35, Remark 6.23] and [36, Remark 8.19] also). Thus, our assertion for $\underline{m}=\alpha +\beta$ holds by [29, Theorem 3.1]. For the case when $\underline{m}$ is a pair, we have a nonzero composition of homomorphisms

• (i) $S_\mathscr {Q}(\alpha ')\circ S_\mathscr {Q}(\beta ') \rightarrowtail S_\mathscr {Q}(\alpha )\circ S_\mathscr {Q}(\alpha '-\alpha ) \circ S_\mathscr {Q}(\beta ') \twoheadrightarrow S_\mathscr {Q}(\alpha )\circ S_\mathscr {Q}(\beta )$ or

• (ii) $S_\mathscr {Q}(\alpha ')\circ S_\mathscr {Q}(\beta ') \rightarrowtail S_\mathscr {Q}(\alpha ')\circ S_\mathscr {Q}(\beta '-\beta ) \circ S_\mathscr {Q}(\beta ) \twoheadrightarrow S_\mathscr {Q}(\alpha )\circ S_\mathscr {Q}(\beta )$,

by [19, Corollary 3.11]. For the case when $\underline{m}$ is a triple, we have a nonzero composition

$$\begin{aligned}&S_\mathscr {Q}(\mu ) \circ S_\mathscr {Q}(\nu ) \circ S_\mathscr {Q}(\eta ) \simeq S_\mathscr {Q}(\mu ) \circ S_\mathscr {Q}(\eta ) \circ S_\mathscr {Q}(\nu ) \\&\quad \rightarrowtail S_\mathscr {Q}(\mu ) \circ S_\mathscr {Q}(\alpha -\mu ) \circ S_\mathscr {Q}(\beta -\nu ) \circ S_\mathscr {Q}(\nu ) \twoheadrightarrow S_\mathscr {Q}(\mu ) \circ S_\mathscr {Q}(\alpha -\mu ) \circ S_\mathscr {Q}(\beta ). \end{aligned}$$

and hence a desired nonzero composition

$$\begin{aligned}&S_\mathscr {Q}(\mu ) \circ S_\mathscr {Q}(\nu ) \circ S_\mathscr {Q}(\eta ) \rightarrow S_\mathscr {Q}(\mu ) \circ S_\mathscr {Q}(\alpha -\mu ) \circ S_\mathscr {Q}(\beta ) \twoheadrightarrow S_\mathscr {Q}(\alpha ) \circ S_\mathscr {Q}(\beta ) \end{aligned}$$

by [19, Corollary 3.11]. Hence, our assertion follows from the fact that the heads of $S_\mathscr {Q}(\underline{m})$ and $S_\mathscr {Q}(\alpha )\circ S_\mathscr {Q}(\beta )$ are distinct. Our assertion for $V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )$ can be obtained by applying the functor $\mathcal {F}_\mathscr {Q}$. $\square$

Corollary 7.2

For $\underline{m}\in \mathbb {Z}_{\ge 0}^\mathsf {N}$,

$$\begin{aligned} S_{\mathscr {Q}}(\underline{m}) \text { and } V_{\mathscr {Q}}(\underline{m}) \text { are simple if and only if }\underline{m}\hbox { is }[\mathscr {Q}]\hbox {-simple.} \end{aligned}$$

Proof

It is an immediate consequence of Theorem 7.1.

Lemma 7.3

Let $U_q'(\mathfrak {g})$ be a quantum affine algebra and let V and W be good $U_q'(\mathfrak {g})$-modules. If the normalized R-matrix $R^{\mathrm{norm}}_{V,W}(z)$ has a simple pole at $z=a$ for some $a \in \mathbf {k}^\times$, then we have

$$\begin{aligned} \mathrm{Im} \big ( (z-a) R^{\mathrm{norm}}_{V,W} |_{z=a} \big ) = \mathrm{Ker} \big ( R^{\mathrm{norm}}_{W,V} |_{z=a} \big ). \end{aligned}$$

Moreover, the tensor product $V \otimes W_a$ is of length 2.

Proof

The first assertion follows from the fact$:$

• Let A(z) and B(z) be $n\times n$-matrices with entries in rational functions in z. Assume that A(z) and B(z) have no poles at $z=a$. If $A(z)B(z) =(z-a)\mathrm{id}$, then we have $\mathrm{Im} A(a) =\mathrm{Ker} B(a)$.

Recall that $\mathrm{Ker} \big ( R^{\mathrm{norm}}_{W,V} |_{z=a} \big )$ is simple. By [19, Theorem 3.2], $\mathrm{Im} \big ( (z-a) R^{\mathrm{norm}}_{V,W} |_{z=a} \big )$ is also simple. Hence, we conclude that $V \otimes W_a$ is of composition length 2 by the first assertion. $\square$

Theorem 7.4

For a pair $\underline{p}=(\alpha ,\beta )$ with $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p}) >0$, the composition length of $V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )$ is 2 and the composition series of $V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )$ consists of its distinct head and socle. In particular,

• (1) if $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p})=1$, ${{\text {soc}}}(V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )) \simeq V_{\mathscr {Q}}({{\text {soc}}}_{[\mathscr {Q}]}(\alpha ,\beta ))$,

• (2) if $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p})=2$, ${{\text {soc}}}(V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )) \simeq {{\text {hd}}}(V_\mathscr {Q}(\underline{m}))$ where $\underline{m}$ is a unique sequence such that

  $$\begin{aligned} {{\text {soc}}}_{[\mathscr {Q}]}(\underline{p}) \prec ^\mathtt {b}_{[\mathscr {Q}]} \underline{m}\prec ^\mathtt {b}_{[\mathscr {Q}]} \underline{p}. \end{aligned}$$

The same assertions for $S_\mathscr {Q}(\alpha ) \circ S_\mathscr {Q}(\beta )$ hold.

Proof

By Theorem 7.1, Lemma 7.3 and the fact that $d^{B_n^{(1)}}_{k,l}(z)$ and $d^{C_n^{(1)}}_{k,l}(z)$ have only roots of order 1, $V_\mathscr {Q}(\alpha ) \circ V_\mathscr {Q}(\beta )$ has composition length 2 if $\mathrm{dist}_{\mathscr {Q}}(\alpha ,\beta ) \ne 0$. If $\mathrm{dist}_{[\mathscr {Q}]}(\underline{p})=1$, then ${{\text {soc}}}_\mathscr {Q}(\underline{p})$ is a unique sequence such that ${{\text {soc}}}_\mathscr {Q}(\underline{p}) \prec _{[\mathscr {Q}]}^\mathtt {b}\underline{p}$ and $V_\mathscr {Q}({{\text {soc}}}_\mathscr {Q}(\underline{p}))$ is simple. Thus, by the previous proof, there exists a nonzero homomorphism

$$\begin{aligned} V_\mathscr {Q}({{\text {soc}}}_\mathscr {Q}(\underline{p})) \longrightarrow V_\mathscr {Q}(\underline{p}). \end{aligned}$$

Hence, $V_\mathscr {Q}({{\text {soc}}}_\mathscr {Q}(\underline{p}))\simeq {{\text {soc}}}(V_\mathscr {Q}(\underline{p}))$ by [19, Theorem 3.2]. For $\mathrm{dist}_{\mathscr {Q}}(\underline{p})=2$, we have a nonzero homomorphism

$$\begin{aligned} V_\mathscr {Q}(\underline{m}) \longrightarrow V_\mathscr {Q}(\underline{p}) \end{aligned}$$

where $\underline{m}$ is the unique sequence such that ${{\text {soc}}}_\mathscr {Q}(\underline{p}) \prec _{[\mathscr {Q}]}^\mathtt {b}\underline{m}\prec _{[\mathscr {Q}]}^\mathtt {b}\underline{p}$. Thus, our last assertion follows since

• $V_\mathscr {Q}(\underline{p})$ has composition length 2,

• $V_\mathscr {Q}(\underline{p})$ and $V_\mathscr {Q}(\underline{m})$ have distinct heads.

Our assertions for $S_\mathscr {Q}(\underline{p})$ can be obtained by applying the functor $\mathcal {F}_\mathscr {Q}$. $\square$

Appendix: Exceptional doubly laced type

In this appendix, we discuss the exceptional doubly laced type analogue of our main results and give several conjectures on it. We first recall the $\vee$-foldable cluster point $\llbracket \mathscr {Q}\rrbracket$ of $E_6$ associated with $\vee$ in (2.1c) and the twisted Coxeter element $s_1s_2s_6s_3$ [35, Appendix]$:$

$$\begin{aligned} \llbracket \mathscr {Q}\rrbracket = \llbracket {\widetilde{w}_0}\rrbracket \qquad \text { where } \quad {\widetilde{w}_0}= \prod _{k=0}^{8} (s_1s_2s_6s_3)^{k\vee }. \end{aligned}$$

Here,

$$\begin{aligned}&(s_{j_1} \cdots s_{j_n})^\vee \mathbin {:=}s_{j^\vee _1} \cdots s_{j^\vee _n} \text { and } (s_{j_1} \cdots s_{j_n})^{k \vee } \mathbin {:=}( \cdots ((s_{j_1} \cdots s_{j_n} \underbrace{ )^\vee )^\vee \cdots )^\vee }_{ k\text { -times} }. \end{aligned}$$

(7.1)

Note that the number of distinct commutation classes in $\llbracket \mathscr {Q}\rrbracket$ is 32 [35, Appendix].

Now, we assign the coordinates of $\Upsilon _{[{\widetilde{w}_0}]}$ in the following way (see also [33, Appendix])$:$

. Then the quiver $\Upsilon _{[{\widetilde{w}_0}]}$ is foldable in the sense that there exists no (i, p) and $(j,q) \in \Upsilon _{[{\widetilde{w}_0}]}$ such that $i^\vee =j$ and $p=q$. Hence, we can fold in a canonical way$:$

Thus, $\widehat{\Upsilon }_{[{\widetilde{w}_0}]}$ is well defined.

Furthermore, the action of reflection maps on $\llbracket \mathscr {Q}\rrbracket$ is well described by the datum of $F_4$ in the following sense (see also [35, Algorithm 7.6], [36, Algorithm 7.15])$:$

(In [15, §6.7], they took that $\alpha _1$ and $\alpha _2$ are short simple roots which is reversed to our convention.)

Let us denote by (i) $\mathsf {D}=\mathrm{diag}(d_{i} \ | \ 1 \le i \le 4 )$ the diagonal matrix which diagonalizes the Cartan matrix $\mathsf {A}$ of type $F_{4}$, (ii) $\widehat{\mathsf {d}}=\mathrm{lcm}(d_{i} \ | \ 1 \le i \le 4)=2$, (iii) $\alpha _i$ a sink of $\widehat{\Upsilon }_{[{\widetilde{w}_0}]}$ and (iv) $\mathsf {h}^\vee =9$ the dual Coxeter number of type $F_4$. Now the algorithm obtaining $\widehat{\Upsilon }_{[{\widetilde{w}_0}]r_i}$ from $\widehat{\Upsilon }_{[{\widetilde{w}_0}]}$ can be described as follows$:$

• (A1) Remove the vertex (i, p) corresponding $(\alpha _i)$ and arrows entering into (i, p) in $\widehat{\Upsilon }_{[{\widetilde{w}_0}]}$.

• (A2) Add the vertex $(i,p-\widehat{\mathsf {d}} \times \mathsf {h}^\vee )$ and arrows to all vertices whose coordinates are $(j, p-\widehat{\mathsf {d}} \times \mathsf {h}^\vee +\min (d_{i},d_{j})) \in \widehat{\Upsilon }_{[{\widetilde{w}_0}]}$, where j is adjacent to i in $\Delta$.

• (A3) Label the vertex $(i,p-\widehat{\mathsf {d}} \times \mathsf {h}^\vee )$ with $\alpha _i$ and change the labels $\beta$ to $s_i(\beta )$ for all $\beta \in \widehat{\Upsilon }_{[{\widetilde{w}_0}]} \setminus \{\alpha _i\}$.

For example $\widehat{\Upsilon }_{[{\widetilde{w}_0}]r_1}$ can be depicted as follows$:$

By applying the results in [35, 36], one can check that the folded distance polynomials $D_{k,l}(z)$ are well defined on $\llbracket \mathscr {Q}\rrbracket$ and have natural conjectural formulas for $d^{F^{(1)}_4}_{k,l}(z)$ as follows$:$ Set $q^2_s=q$.

$$\begin{aligned} d^{F^{(1)}_4}_{1,1}(z)&=\left( z-q_s^{4}\right) \left( z-q_s^{10}\right) \left( z-q_s^{12}\right) \left( z-q_s^{18}\right) , \\ d^{F^{(1)}_4}_{1,2}(z)&=\left( z+q_s^{6}\right) \left( z+q_s^{8} \right) \left( z+q_s^{10}\right) \left( z+q_s^{12}\right) \left( z+q_s^{14}\right) \left( z+q_s^{16}\right) , \\ d^{F^{(1)}_4}_{1,3}(z)&=\left( z-q_s^{7}\right) \left( z-q_s^{9} \right) \left( z-q_s^{13}\right) \left( z-q_s^{15}\right) , \\ d^{F^{(1)}_4}_{1,4}(z)&=\left( z+q_s^{8}\right) \left( z+q_s^{14}\right) , \\ d^{F^{(1)}_4}_{2,2}(z)&=\left( z-q_s^{4}\right) \left( z-q_s^{6} \right) \left( z-q_s^{8} \right) ^2\left( z-q_s^{10}\right) ^2\left( z-q_s^{12}\right) ^{2} \left( z-q_s^{14}\right) ^2\left( z-q_s^{16}\right) \left( z-q_s^{18}\right) , \\ d^{F^{(1)}_4}_{2,3}(z)&=\left( z+q_s^{5}\right) \left( z+q_s^{7} \right) \left( z+q_s^{9} \right) \left( z+q_s^{11} \right) ^2\left( z+q_s^{13}\right) \left( z+q_s^{15}\right) \left( z+q_s^{17}\right) , \\ d^{F^{(1)}_4}_{2,4}(z)&=\left( z-q_s^{6}\right) \left( z-q_s^{10}\right) \left( z-q_s^{12}\right) \left( z-q_s^{16} \right) , \\ d^{F^{(1)}_4}_{3,3}(z)&=\left( z-q_s^{2}\right) \left( z-q_s^{6} \right) \left( z-q_s^{8} \right) \left( z-q_s^{10} \right) \left( z-q_s^{12}\right) \left( z-q_s^{16}\right) \left( z-q_s^{18}\right) , \\ d^{F^{(1)}_4}_{3,4}(z)&=\left( z+q_s^{3}\right) \left( z+q_s^{7} \right) \left( z+q_s^{11}\right) \left( z+q_s^{13} \right) \left( z+q_s^{17}\right) , \\ d^{F^{(1)}_4}_{4,4}(z)&=\left( z-q_s^{2}\right) \left( z-q_s^{8} \right) \left( z-q_s^{12}\right) \left( z-q_s^{18} \right) . \end{aligned}$$

Now we can define $V_{\mathscr {Q}}(\beta )$, for each $\beta \in \Phi ^+_{E_6}$ and $[\mathscr {Q}] \in \llbracket \mathscr {Q}\rrbracket$ naturally.

Definition 7.5

   

• (1) We define the smallest abelian full subcategory $\mathscr {C}_\mathscr {Q}$ inside $\mathcal {C}_{F^{(1)}_{4}}$ such that

  • (a) it is stable by taking subquotient, tensor product and extension,

  • (b) it contains $V_\mathscr {Q}(\beta )$ for all $\beta \in \Phi ^+_{E_{6}}$.

• (2) We define the smallest abelian full subcategory $\mathscr {C}_\mathbb {Z}$ inside $\mathcal {C}_{F^{(1)}_{4}}$ such that

  • (a) it is stable by taking subquotient, tensor product and extension,

  • (b) it contains $V_\mathscr {Q}(\beta )^{k*}$ for all $k\in \mathbb {Z}$ and all $\beta \in \Phi ^+_{E_{6}}$.

Recall the subcategories $\mathcal {C}^{(1)}_Q$ of $\mathcal {C}_{E^{(1)}_{6}}$ in [14], $\mathcal {C}^{(2)}_Q$ of $\mathcal {C}_{E^{(2)}_{6}}$ in [33, Arxiv version 1]. Now we can naturally expect that all results in this paper can be extended to $\mathcal {C}^{({t})}_Q$$({t}=1,2)$, $\mathscr {C}_\mathscr {Q}$, $U^-_\mathbb {A}(E_6)^\vee$ and $V_\mathscr {Q}(\underline{m})$, etc.