Derivatives on the downstream side of a moving, curved shock

Abstract

Novel relations are developed for the tangential and normal derivatives of the pressure, density, and velocity components just downstream of a regular point on a curved shock wave. The perfect gas flow is three dimensional with a nonuniform freestream and the flow may be unsteady. The analysis starts with data in a fixed, laboratory-frame Cartesian coordinate system. By means of an orthogonal transformation, a coordinate system is introduced via a solid-body translation and two solid-body rotations. This Cartesian system is shock based and limits the analysis to a selected shock point at a given instant of time when the flow is unsteady. The analysis is a local one in that Taylor series expansions are utilized for the configuration of the shock and the upstream gradients of the velocity, pressure, and density. The coefficients in the last three expansions must satisfy Euler equation constraints. These expansions are performed in both Cartesian systems, with occasional preference given to the laboratory-frame expansions where there are known data. The derivatives are in terms of a third coordinate system that is shock based and utilizes the flow plane at the selected shock point. Exact, explicit results are provided for the tangential and normal derivatives in as simple a form as possible. In the Taylor series expansion version for the tangential derivatives, the relative importance of various factors can be assessed. These are the upstream velocity, pressure, and density gradients, curvatures, and shock-shape terms not associated with curvatures. A different type of discussion is provided for the more involved normal derivatives.

Appendices

Appendix A

1.1 Taylor series expansions

$$\begin{aligned} F= & {} c_1 x_1 +c_2 x_2 +c_3 x_3 +\frac{1}{2}\left( {c_{11} x_1^2 +c_{22} x_2^2 +c_{33} x_3^2 } \right) + c_{12} x_1 x_2 +c_{13} x_1 x_3 +c_{23} x_2 x_3 =0, \end{aligned}$$

(61)

$$\begin{aligned} c_{ij}= & {} c_{ji} ,\quad c_3 =0, \end{aligned}$$

(62)

$$\begin{aligned} {\vec V_1}= & {} \sum {\upsilon _{1,i}}{{\hat{|}}_i}, \end{aligned}$$

(63)

$$\begin{aligned} \upsilon _{1,1}= & {} V_{1o} +\sum e_{1j} x_j ,\quad \upsilon _{1,2} =\sum e_{2j} x_j ,\quad \upsilon _{1,3} =\sum e_{3j} x_j, \end{aligned}$$

(64)

$$\begin{aligned} e_{ij}= & {} \left( {\frac{\partial \upsilon _{1,i} }{\partial x_j }} \right) _o =\,\upsilon _{1,ix_j o}, \end{aligned}$$

(65)

$$\begin{aligned} p_1= & {} p_{1o} +\sum f_j x_j ,\quad \rho _1 =\rho _{1o} +\sum g_j x_j, \end{aligned}$$

(66)

$$\begin{aligned} f_j= & {} \left( {\frac{\partial p_1 }{\partial x_j }} \right) _o =p_{1x_j o} ,\quad g_j =\left( {\frac{\partial \rho _1 }{\partial x_j }} \right) _o =\rho _{1x_j o}. \end{aligned}$$

(67)

1.2 Euler equations constraints

The foregoing expansions must be consistent with the Euler equations at state 1. These equations are written as

$$\begin{aligned} \frac{\partial \rho }{\partial t}+\rho \nabla \cdot \vec {V}+ \vec {V}\cdot \nabla \rho =0, \end{aligned}$$

(68a)

$$\begin{aligned} \frac{{\partial \vec V}}{{\partial t}} + \vec V\cdot \left( {\nabla {{\tilde{V}}} } \right) + \frac{1}{\rho }\nabla p = 0, \end{aligned}$$

(68b)

$$\begin{aligned} \frac{1}{p}\,\frac{\mathrm{D}p}{\mathrm{D}t}-\frac{\gamma }{\rho }\,\frac{\mathrm{D}\rho }{\mathrm{D}t}=0, \end{aligned}$$

(68c)

where the last relation is for isentropic flow. The continuity equation becomes

$$\begin{aligned} \frac{\partial \rho _1 }{\partial t}+\rho _1 \left( {\frac{\partial \upsilon _{1,1} }{\partial x_1 }+\frac{\partial \upsilon _{1,2} }{\partial x_2 }+\frac{\partial \upsilon _{1,3} }{\partial x_3 }} \right) +V_1 {\hat{|}}_1 \cdot \left( {\frac{\partial \rho _1 }{\partial x_1 }{\hat{|}}_1 +\frac{\partial \rho _1 }{\partial x_2 }{\hat{|}}_2 +\frac{\partial \rho _1 }{\partial x_3 }{\hat{|}}_3 } \right) =0 \end{aligned}$$

or

$$\begin{aligned}&\frac{\mathrm{d}\rho _{1o} }{\mathrm{d}t}+\rho _{1o} e_{11} +\rho _{1o} e_{22} +\rho _{1o} e_{33} +V_{1o} g_1 =0, \quad \quad g_1 =-\frac{\rho _{1o} }{V_{1o} }\sum e_{jj} -\frac{1}{V_{1o} }\rho _{1ot}, \end{aligned}$$

(69a)

where

$$\begin{aligned} \rho _{1ot} =\frac{\mathrm{d}\rho _{1o} }{\mathrm{d}t}. \end{aligned}$$

There is no constraint on $g_2$ or $g_3$.

In the momentum equation, the various terms are

$$\begin{aligned} {\left( {\frac{{\partial \vec V}}{{\partial t}}} \right) _{1o}}= & {} \sum {\left( {\frac{{\mathrm{d}{\upsilon _{1,i}}}}{{\mathrm{d}t}}} \right) _o}{{\hat{|}}_i} = \frac{{\mathrm{d}{V_{1o}}}}{{\mathrm{d}t}} {{\hat{|}}_1} = {V_{{ 1ot}}}{{\hat{|}}_1},\\ {{\vec {V}}_{{ 1o}}}\cdot {\left( {\nabla {{\vec V}_1}} \right) _o}= & {} {V_{1o}}\sum {e_{j1}}{{\hat{|}}_j},\\ \frac{1}{p_{1o} }\left( {\nabla p_{1o} } \right)= & {} \frac{f_1 }{p_{1o} }, \end{aligned}$$

with the result

$$\begin{aligned} V_{1ot} +V_{1o} e_{11} +\frac{f_1 }{\rho _{1o} }= & {} 0,\\ V_{1o} e_{21} +\frac{f_2 }{\rho _{1o} }= & {} 0, \\ V_{1o} e_{31} +\frac{f_3 }{\rho _{1o} }= & {} 0 \end{aligned}$$

or

$$\begin{aligned} f_1 =-\rho _{1o} V_{1o} e_{11} -\rho _{1o} V_{1ot} ,\quad f_j =-\rho _{1o} V_{1o} e_{j1} ,\quad j=2,3. \end{aligned}$$

(69b)

The substantial derivative in the isentropic relation is

$$\begin{aligned} \frac{\mathrm{D}}{\mathrm{D}t}=\frac{\partial }{\partial t}+V_{1o} \frac{\partial }{\partial x_1 } \end{aligned}$$

and, therefore,

$$\begin{aligned} \frac{1}{p_{1o} }\left( {\frac{\mathrm{d}p}{\mathrm{d}t}} \right) _{1o} +\frac{V_{1o} }{p_{1o} }p_{1\,x_{1o} } -\frac{\gamma }{\rho _{1o} }\left( {\frac{\mathrm{d}\rho }{\mathrm{d}t}} \right) _{1o} -\frac{\gamma V_{1o} }{\rho _{1o} }\rho _{1\,x_{1o} } =0 \end{aligned}$$

or

$$\begin{aligned} \frac{1}{p_{1o} }\,p_{1ot} +\frac{V_{1o} }{p_{1o} }f_1 -\frac{\gamma }{\rho _{1o} }\,\rho _{1ot} -\frac{\gamma V_{1o} }{\rho _{1o} }g_1 =0. \end{aligned}$$

Replace $g_1$ and $f_1$ with Eqs. (69a, 69b), to obtain

$$\begin{aligned} \left( {M_{1o}^2 -1} \right) e_{11} -e_{22} -e_{33} =\frac{p_{1ot} }{\gamma p_{1o} }-\frac{M_{1o}^2 }{V_{1o} }V_{1ot}. \end{aligned}$$

(69c)

Equations (69) are the constraints for a steady or unsteady flow.

Appendix B

1.1 The $c_i ,c_{ij}$ coefficients in $F=0$

$$\begin{aligned} F_{x_1^*}^*= & {} c_1^*+c_{11}^*x_{1o}^*+c_{12}^*x_{2o}^*+c_{13}^*x_{3o}^*, \end{aligned}$$

(70a)

$$\begin{aligned} F_{x_2^*}^*= & {} c_2^*+c_{12}^*x_{1o}^*+c_{22}^*x_{2o}^*+c_{23}^*x_{3o}^*, \end{aligned}$$

(70b)

$$\begin{aligned} F_{x_3^*}^*= & {} c_3^*+c_{13}^*x_{1o}^*+c_{23}^*x_{2o}^*+c_{33}^*x_{3o}^*, \end{aligned}$$

(70c)

$$\begin{aligned} c_i= & {} \sum F_{x_j^*}^*a_{ji}, \end{aligned}$$

(71)

$$\begin{aligned} c_{11}= & {} \frac{1}{2}\left( {c_{11}^*a_{11}^2 +c_{22}^*a_{21}^2 +c_{33}^*a_{31}^2 } \right) + c_{12}^*a_{11} a_{21} +c_{13}^*a_{11} a_{31} +c_{23}^*a_{21} a_{31}, \end{aligned}$$

(72a)

$$\begin{aligned} c_{22}= & {} \frac{1}{2}\left( {c_{11}^*a_{12}^2 +c_{22}^*a_{22}^2 +c_{33}^*a_{32}^2 } \right) + c_{12}^*a_{12} a_{22} +c_{13}^*a_{12} a_{32} +c_{23}^*a_{22} a_{32}, \end{aligned}$$

(72b)

$$\begin{aligned} c_{33}= & {} \frac{1}{2}\left( {c_{11}^*a_{13}^2 +c_{22}^*a_{23}^2 +c_{33}^*a_{33}^2 } \right) + c_{12}^*a_{13} a_{23} +c_{13}^*a_{13} a_{33} +c_{23}^*a_{23} a_{33}, \end{aligned}$$

(72c)

$$\begin{aligned} c_{12}= & {} c_{11}^*a_{11} a_{12} +c_{22}^*a_{21} a_{22} +c_{33}^*a_{31} a_{32} +c_{12}^*a_{11} a_{22} \nonumber \\&+\, c_{12}^*a_{12} a_{21} +c_{13}^*a_{11} a_{32} +c_{13}^*a_{12} a_{31} +c_{23}^*a_{21} a_{32} +c_{23}^*a_{22} a_{31}, \end{aligned}$$

(73a)

$$\begin{aligned} c_{13}= & {} c_{11}^*a_{11} a_{13} +c_{22}^*a_{21} a_{23} +c_{33}^*a_{31} a_{33} +c_{12}^*a_{11} a_{23} \nonumber \\&+\,c_{12}^*a_{13} a_{21} +c_{13}^*a_{11} a_{33} +c_{13}^*a_{13} a_{31} +c_{23}^*a_{21} a_{33} +c_{23}^*a_{23} a_{31}, \end{aligned}$$

(73b)

$$\begin{aligned} c_{23}= & {} c_{11}^*a_{12} a_{13} +c_{22}^*a_{22} a_{23} +c_{33}^*a_{32} a_{33} +c_{12}^*a_{12} a_{23} \nonumber \\&+\,c_{12}^*a_{13} a_{22} +c_{13}^*a_{12} a_{33} +c_{13}^*a_{13} a_{32} +c_{23}^*a_{22} a_{33} +c_{23}^*a_{23} a_{32}. \end{aligned}$$

(73c)

1.2 The $a_{ij}$ coefficients

$$\begin{aligned} a_{i1}= & {} {\hat{|}}_i^{*} \cdot {\hat{|}}_1 =\frac{\beta _i }{V_1 }, \end{aligned}$$

(74)

$$\begin{aligned} a_{i2}= & {} {\hat{|}}_i^{*} \cdot {\hat{|}}_2 =\frac{1}{c_2 }\left( {F_{x_i^*}^*-\frac{c_1 }{V_1 }\beta _i } \right) , \end{aligned}$$

(75)

$$\begin{aligned} a_{13}= & {} {\hat{|}}_1^*\cdot {\hat{|}}_3 =\frac{1}{c_2 V_1 }\left( {\upsilon _{1,2}^*F_{x_3^*}^*-\upsilon _{1,3}^*F_{x_2^*}^*} \right) , \end{aligned}$$

(76a)

$$\begin{aligned} a_{23}= & {} {\hat{|}}_2^*\cdot {\hat{|}}_3 =\frac{1}{c_2 V_1 }\left( {\upsilon _{1,3}^*F_{x_1^*}^*-\upsilon _{1,1}^*F_{x_3^*}^*} \right) , \end{aligned}$$

(76b)

$$\begin{aligned} a_{33}= & {} {\hat{|}}_3^*\cdot {\hat{|}}_3 =\frac{1}{c_2 V_1 }\left( {\upsilon _{1,1}^*F_{x_2^*}^*-\upsilon _{1,2}^*F_{x_1^*}^*} \right) . \end{aligned}$$

(76c)

Appendix C: Common parameters

All parameter values are evaluated at a regular shock point, where $x_{io} =0$, and

$$\begin{aligned} F_{x_j }= & {} c_j ,\quad F_{x_3 } =c_3 =0,\quad F_{x_i x_j } =c_{ij} =c_{ji}, \end{aligned}$$

(77a)

$$\begin{aligned} \nabla F= & {} c_1 {\hat{|}}_1 +c_2 {\hat{|}}_2 ,\quad \left| {\nabla F} \right| =\left( {c_1^2 +c_2^2 } \right) ^{1/2}. \end{aligned}$$

(77b)

The following parameters stem from [16, Sect. 10.2]

$$\begin{aligned} \hbox {sin}\,\theta= & {} \frac{\sum \upsilon _{1,j} F_{x_j } }{V_1 \left| {\nabla F} \right| }=\frac{c_1 }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}},\,\,\hbox {cos}\,\theta =\pm \left( {1-\hbox {sin}^{\mathrm {2}}\theta } \right) ^{1/2} = -\frac{c_2 }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}},\,\,\hbox {cot}\,\theta =-\frac{c_2 }{c_1 }. \end{aligned}$$

(78)

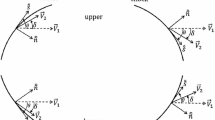
The minus sign is for an upper convex shock, where $c_1 >0,\,c_2 <0$.

$$\begin{aligned} M_1^2= & {} \frac{\rho _1 V_1^2 }{\gamma p_1 }, \end{aligned}$$

(79a)

$$\begin{aligned} m= & {} M_1^2 \,\hbox {sin}^{\mathrm {2}}\theta =M_{1o}^2 \frac{c_1^2 }{c_1^2 +c_2^2 }, \end{aligned}$$

(79b)

$$\begin{aligned} X=1+\frac{\gamma -1}{2}m,\quad Y=\gamma m-\frac{\gamma -1}{2},\quad Z=m-1. \end{aligned}$$

(80)

The frequently encountered m parameter is the square of the Mach number component normal to the shock. It is bounded

$$\begin{aligned} 1\le m\le M_1^2, \end{aligned}$$

(79c)

where the left bound represents a Mach wave and the right bound represents a normal shock. The acute angle, $\delta$, shown in Fig. 1, is between $\vec {V}_1$ and $\vec {V}_2$

$$\begin{aligned} \hbox {tan}\,\delta= & {} \frac{1}{\hbox {tan}\,\theta }\,\frac{M_1^2\, \hbox {sin}^{{2}}\theta -1}{\left( {\frac{\gamma +1}{2}} \right) M_1^2 -M_1^2\, \hbox {sin}^{{2}}\theta +1}=-\frac{c_2 }{c_1 }\,\frac{m-1}{\left( {\frac{\gamma +1}{2}} \right) M_{1o}^2 -m+1}. \end{aligned}$$

(81)

$$\begin{aligned} K_1= & {} \upsilon _{1,3} F_{x_2 } -\upsilon _{1,2} F_{x_3 } =0, \end{aligned}$$

(82a)

$$\begin{aligned} K_2= & {} \upsilon _{1,1} F_{x_3 } -\upsilon _{1,3} F_{x_1 } =0, \end{aligned}$$

(82b)

$$\begin{aligned} K_3= & {} \upsilon _{1,2} F_{x_1 } -\upsilon _{1,1} F_{x_2 } =-c_2 V_{1o}, \end{aligned}$$

(82c)

$$\begin{aligned} L_1= & {} F_{x_3 } K_2 -F_{x_2 } K_3 =c_2^2 V_{1o}, \end{aligned}$$

(83a)

$$\begin{aligned} L_2= & {} F_{x_1 } K_3 -F_{x_3 } K_1 =-c_1 c_2 V_{1o}, \end{aligned}$$

(83b)

$$\begin{aligned} L_3= & {} F_{x_2 } K_1 -F_{x_1 } K_2 =0, \end{aligned}$$

(83c)

$$\begin{aligned} \chi= & {} \frac{1}{V_1 \left| {\nabla F} \right| \hbox {cos}\,\theta }=\frac{1}{\left( {\sum K_j^2 } \right) ^{1/2}}=-\frac{1}{c_2 V_{1o}}, \end{aligned}$$

(84)

$$\begin{aligned} \frac{M_{1x_i } }{M_1 }= & {} \frac{1}{V_1^2 }\sum \upsilon _{1,j} \upsilon _{1,jx_i } -\frac{p_{1x_i } }{2p_1 }+\frac{\rho _{1x_i } }{2\rho _1 }=\frac{e_{1i} }{V_{1o} }-\frac{f_i }{2p_{1o} }+\frac{g_i }{2\rho _{1o} }, \end{aligned}$$

(85)

$$\begin{aligned} \theta _{x_i }= & {} \frac{\chi }{V_1^2 \left| {\nabla F} \right| ^{2}}\left\{ {\left| {\nabla F} \right| ^{2}\left[ {V_1^2 \sum \upsilon _{1,jx_i } F_{x_j } -\left( {\sum \upsilon _{1,j} F_{x_j } } \right) \sum \upsilon _{1,j} \upsilon _{1,j\,x_i } } \right] } \right. \nonumber \\&\left. {+V_1^2 \left[ {\left| {\nabla F} \right| ^{2}\sum \upsilon _{1,j} F_{x_i x_j } -\left( {\sum \upsilon _{1,j} F_{x_j } } \right) \sum F_{x_j } F_{x_i x_j } } \right] } \right\} \end{aligned}$$

(86a)

$$\begin{aligned}= & {} -\frac{e_{2i} }{V_{1o} }+\frac{c_1 c_{2i} -c_2 c_{1i} }{c_1^2 +c_2^2 }. \end{aligned}$$

(86b)

$$\begin{aligned} \sum L_j \left[ {\frac{M_{1x_j } }{M_1 }+\left( {\hbox {cot}\,\theta } \right) \theta _{x_j } } \right]= & {} c_2 V_{1o} \left[ {-\left( {\frac{c_1 e_{12} -c_2 e_{11} }{V_{1o} }} \right) -\frac{c_2 }{c_1 }} \right. \left( {\frac{c_1 e_{22} -c_2 e_{21} }{V_{1o} }} \right) \nonumber \\&+\frac{c_2 }{c_1 }\,\frac{C}{c_1^2 +c_2^2 }+\frac{1}{2}\left. {\left( {\frac{c_1 f_2 -c_2 f_1 }{p_{1o} }} \right) -\frac{1}{2}\left( {\frac{c_1 g_2 -c_2 g_1 }{\rho _{1o} }} \right) } \right] , \end{aligned}$$

(87)

$$\begin{aligned} \sum K_j \left[ {\frac{M_{1x_j } }{M_1 }+\left( {\hbox {cot}\,\theta } \right) \theta _{x_j } } \right]= & {} -c_2 V_{1o} \left[ {\frac{1}{c_1 }\left( {\frac{c_1 e_{13} +c_2 e_{23} }{V_{1o} }} \right) } -\frac{c_2 }{c_1 }\left( {\frac{c_1 c_{23} -c_2 c_{13} }{c_1^2 +c_2^2 }} \right) {-\frac{1}{2}\,\frac{f_3 }{p_{1o} }+\frac{1}{2}\frac{g_3 }{\rho _{1o} }} \right] . \end{aligned}$$

(88)

Appendix D

1.1 Summation evaluations

$\sum L_i L_j F_{x_i x_j },\,\sum K_i K_j F_{x_i x_j }$ , and C are given by (33),

$$\begin{aligned} \sum \upsilon _{1,j} \upsilon _{1,jx_i }= & {} V_{1o} e_{1i}, \end{aligned}$$

(89)

$$\begin{aligned} \sum \upsilon _{1,j} F_{x_j }= & {} c_1 V_{1o}, \end{aligned}$$

(90)

$$\begin{aligned} \sum \upsilon _{1,jx_i } F_{x_j }= & {} c_1 e_{1i} +c_2 e_{2i}, \end{aligned}$$

(91)

$$\begin{aligned} \sum \upsilon _{1,j} F_{x_i x_j }= & {} c_{1i} V_{1o}, \end{aligned}$$

(92)

$$\begin{aligned} \sum F_{x_j } F_{x_i x_j }= & {} c_1 c_{1i} +c_2 c_{2i}, \end{aligned}$$

(93)

$$\begin{aligned} \sum \upsilon _{1,j} L_i \upsilon _{1,j\,x_i }= & {} -c_2 V_{1o}^2 \left( {c_1 e_{12} -c_2 e_{11} } \right) , \end{aligned}$$

(94)

$$\begin{aligned} \sum \upsilon _{1,j} K_i \upsilon _{1,j\,x_i }= & {} -c_2 V_{1o}^2 e_{13}, \end{aligned}$$

(95)

$$\begin{aligned} \sum L_j \theta _{x_j }= & {} c_2 V_{1o} \left[ {\left( {\frac{c_1 e_{22} -c_2 e_{21} }{V_{1o} }} \right) -\frac{C}{c_1^2 +c_2^2 }} \right] , \end{aligned}$$

(96)

$$\begin{aligned} \sum K_j \theta _{x_j }= & {} c_2 V_{1o} \left( {\frac{e_{23} }{V_{1o} }-\frac{c_1 c_{23} -c_2 c_{13} }{c_1^2 +c_2^2 }} \right) , \end{aligned}$$

(97)

$$\begin{aligned} \sum L_j \frac{M_{1x_j } }{M_1 }= & {} c_2 V_{1o} \left[ {-\left( {\frac{c_1 e_{12} -c_2 e_{11} }{V_{1o} }} \right) +\left( {\frac{c_1 f_2 -c_2 f_1 }{2p_{1o} }} \right) -\left( {\frac{c_1 g_2 -c_2 g_1 }{2\rho _{1o} }} \right) } \right] , \end{aligned}$$

(98)

$$\begin{aligned} \sum K_j \frac{M_{1x_j } }{M_1 }= & {} c_2 V_{1o} \left( {-\frac{e_{13} }{V_{1o} }+\frac{f_3 }{2p_{1o} }-\frac{g_3 }{2\rho _{1o} }} \right) , \end{aligned}$$

(99)

$$\begin{aligned} \sum L_j \frac{p_{1x_j } }{p_1 }= & {} -c_2 V_{1o} \left( {\frac{c_1 f_2 -c_2 f_1 }{p_{1o} }} \right) , \end{aligned}$$

(100)

$$\begin{aligned} \sum K_j \frac{p_{1x_j } }{p_1 }= & {} -c_2 V_{1o} \frac{f_3 }{p_{1o} }, \end{aligned}$$

(101)

$$\begin{aligned} \sum L_j \frac{\rho _{1x_j } }{\rho _1 }= & {} -c_2 V_{1o} \left( {\frac{c_1 g_2 -c_2 g_1 }{\rho _{1o} }} \right) , \end{aligned}$$

(102)

$$\begin{aligned} \sum K_j \frac{\rho _{1x_j } }{\rho _1 }= & {} -c_2 V_{1o} \frac{g_3 }{\rho _{1o} }, \end{aligned}$$

(103)

$$\begin{aligned} \sum F_{x_i } L_j F_{x_i x_j }= & {} F_{x_1 } L_1 F_{x_1 x_1 } +F_{x_1 } L_2 F_{x_1 x_2 } +F_{x_2 } L_1 F_{x_1 x_2 } +F_{x_2 } L_2 F_{x_2 x_2}\nonumber \\= & {} c_2 V_{1o} \left[ {c_1 c_2 c_{11} -\left( {c_1^2 -c_2^2 } \right) c_{12} -c_1 c_2 c_{22} } \right] , \end{aligned}$$

(104)

$$\begin{aligned} \sum K_i L_j F_{x_i x_j }= & {} c_2^2 V_{1o}^2 \left( {c_1 c_{23} -c_2 c_{13} } \right) , \end{aligned}$$

(105)

$$\begin{aligned} \sum K_i L_j \upsilon _{1,i\,x_j }= & {} c_2^2 V_{1o}^2 \left( {c_1 e_{32} -c_2 e_{31} } \right) , \end{aligned}$$

(106)

$$\begin{aligned} \sum F_{x_i } K_j F_{x_i x_j }= & {} -c_2 V_{1o} \left( {c_1 c_{13} -c_2 c_{23} } \right) , \end{aligned}$$

(107)

$$\begin{aligned} \sum K_i K_j \upsilon _{1,i\,x_j }= & {} c_2^2 V_{1o}^2 e_{33}. \end{aligned}$$

(108)

1.2 Tangential derivatives

$$\begin{aligned} \frac{\partial p}{\partial {{\tilde{s}}} }= & {} \frac{2}{\gamma +1}\,\frac{p_1 \chi }{\left| {\nabla F} \right| }\left[ {Y\sum L_j \frac{p_{1x_j } }{p_1 }} {+\,2\gamma m\sum L_j \frac{M_{1x_j } }{M_1 }+2\gamma m\left( {\hbox {cot}\,\theta } \right) \sum L_j \theta _{x_j } } \right] \nonumber \\= & {} -\frac{2}{\gamma +1}\,\frac{p_{1o} }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}\left\{ {-2\gamma m\left[ {\left( {\frac{c_1 e_{12} -c_2 e_{11} }{V_{1o} }} \right) } \right. } \right. +\frac{c_2 }{c_1 }\left( {\frac{c_1 e_{22} -c_2 e_{21} }{V_{1o} }} \right) \end{aligned}$$

(109a)

$$\begin{aligned}&\left. {\left. {+\frac{1}{2}\left( {\frac{c_1 g_2 -c_2 g_1 }{\rho _{1o} }} \right) -\frac{c_2 }{c_1 }\left( {\frac{C}{c_1^2 +c_2^2 }} \right) } \right] +\frac{\gamma -1}{2}\left( {\frac{c_1 f_2 -c_2 f_1 }{p_{1o} }} \right) } \right\} , \end{aligned}$$

(109b)

$$\begin{aligned} \frac{\partial p}{\partial {{\tilde{b}}} }= & {} -\frac{2}{\gamma +1}p_1 \chi \left[ {Y\sum K_j \frac{p_{1x_j } }{p_1 }+2\gamma m\sum K_j } \frac{M_{1x_j } }{M_1 } {+\,2\gamma m\left( {\hbox {cot}\theta } \right) \sum K_j \theta _{x_j } } \right] \end{aligned}$$

(110a)

$$\begin{aligned}= & {} -\frac{2}{\gamma +1}p_{1o} \left\{ {\frac{2\gamma m}{c_1 }\left[ {\left( {\frac{c_1 e_{13} +c_2 e_{23} }{V_{1o} }} \right) +\frac{c_1 g_3 }{2\rho _{1o} }} {-c_2 \left( {\frac{c_1 c_{23} -c_2 c_{13} }{c_1^2 +c_2^2 }} \right) } \right] -\frac{\gamma -1}{2}\,\frac{f_3 }{p_{1o} }} \right\} , \end{aligned}$$

(110b)

$$\begin{aligned} \frac{\partial \rho }{\partial {{\tilde{s}}} }= & {} \frac{\gamma +1}{2}\,\frac{\rho _1 m\chi }{\left| {\nabla F} \right| X^{2}}\left[ {X\sum L_j } \frac{\rho _{1x_j } }{\rho _1 } {+\,2\sum L_j \frac{M_{1x_j } }{M_1 }+2\left( {\hbox {cot}\,\theta } \right) \sum L_j \theta _{x_j } } \right] \end{aligned}$$

(111a)

$$\begin{aligned}= & {} -\frac{\gamma +1}{2}\,\frac{\rho _{1o} m}{\left( {c_1^2 +c_2^2 } \right) ^{1/2}X^{2}}\left\{ {-2\left[ {\left( {\frac{c_1 e_{12} -c_2 e_{11} }{V_{1o} }} \right) } \right. } + {\frac{c_2 }{c_1 }\left( {\frac{c_1 e_{22} -c_2 e_{21} }{V_{1o} }} \right) } \right] +\left( {\frac{c_1 f_2 -c_2 f_1 }{p_{1o} }} \right) \nonumber \\&\left. {-\left( {2+\frac{\gamma -1}{2}m} \right) \left( {\frac{c_1 g_2 -c_2 g_1 }{\rho _{1o} }} \right) +\frac{2c_2 }{c_1 }\left( {\frac{C}{c_1^2 +c_2^2 }} \right) } \right\} , \end{aligned}$$

(111b)

$$\begin{aligned} \frac{\partial \rho }{\partial {{\tilde{b}}} }= & {} -\frac{\gamma +1}{2}\,\frac{\rho _1 m\chi }{X^{2}}\left[ {X\sum K_j \frac{\rho _{1x_j } }{\rho _1 }+2\sum K_j \frac{M_{1x_j } }{M_1 }} {+\,2\left( {\hbox {cot}\,\theta } \right) \sum K_j \theta _{x_j } } \right] \end{aligned}$$

(112a)

$$\begin{aligned}= & {} \frac{\gamma +1}{2}\,\frac{\rho _{1o} m}{X^{2}}\left[ {-\frac{2}{c_1 }\left( {\frac{c_1 e_{13} +c_2 e_{23} }{V_{1o} }} \right) +\frac{f_3 }{p_{1o} }} {-\left( {2+\frac{\gamma -1}{2}m} \right) \frac{g_3 }{\rho _{1o} }+2\frac{c_2 }{c_1 }\left( {\frac{c_1 c_{23} -c_2 c_{13} }{c_1^2 +c_2^2 }} \right) } \right] , \end{aligned}$$

(112b)

$$\begin{aligned} \frac{\partial {{\tilde{u}}} }{\partial {{\tilde{s}}} }= & {} \frac{V_1 \chi }{\left| {\nabla F} \right| }\left( {\frac{\hbox {cos}\,\theta }{V_1^2 }\sum \upsilon _{1,j} L_i \upsilon _{1,j\,x_i } -\left( {\hbox {sin}\,\theta } \right) \sum L_j \theta _{x_j } } \right) \end{aligned}$$

(113a)

$$\begin{aligned}= & {} \frac{V_{1o} }{\left( {c_1^2 +c_2^2 } \right) }\left\{ {-c_2 \left( {\frac{c_1 e_{12} -c_2 e_{11} }{V_{1o} }} \right) +c_1 } \right. \left[ {\left( {\frac{c_1 e_{22} -c_2 e_{21} }{V_{1o} }} \right) } \right. \left. {\left. {-\left( {\frac{C}{c_1^2 +c_2^2 }} \right) } \right] } \right\} , \end{aligned}$$

(113b)

$$\begin{aligned} \frac{\partial {{\tilde{u}}} }{\partial {{\tilde{b}}} }= & {} -\chi \left( {\frac{\hbox {cos}\,\theta }{V_1^2 }\sum \upsilon _{1,j} K_i \upsilon _{1,j\,x_i } -\left( {\hbox {sin}\,\theta } \right) \sum K_j \theta _{x_j } } \right) \end{aligned}$$

(114a)

$$\begin{aligned}= & {} \frac{V_{1o} }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}\left[ {-\left( {\frac{c_1 e_{23} -c_2 e_{13} }{V_{1o} }} \right) +c_1 \left( {\frac{c_1 c_{23} -c_2 c_{13} }{c_1^2 +c_2^2 }} \right) } \right] , \end{aligned}$$

(114b)

$$\begin{aligned} \frac{\partial {{\tilde{\upsilon }}} }{\partial {{\tilde{s}}} }= & {} \frac{2}{\gamma +1}\,\frac{V_1 \chi }{m\left| {\nabla F} \right| }\left[ {\frac{X\hbox {sin}\,\theta }{V_1^2 }\sum \upsilon _{1,j} L_i \upsilon _{1,j\,x_i } } {-2\left( {\hbox {sin}\,\theta } \right) \sum L_j \frac{M_{1x_j } }{M_1 }-\left( {1-\frac{\gamma -1}{2}m} \right) \left( {\hbox {cos}\,\theta } \right) \sum L_j \theta _{x_j } } \right] \nonumber \\\end{aligned}$$

(115a)

$$\begin{aligned}= & {} -\frac{2}{\gamma +1}\,\frac{V_{1o} }{m\left( {c_1^2 +c_2^2 } \right) }\left\{ {\left( {1-\frac{\gamma -1}{2}m} \right) \left[ {c_1 \left( {\frac{c_1 e_{12} -c_2 e_{11} }{V_{1o} }} \right) } \right. \,} +c_2 \left( {\frac{c_1 e_{22} -c_2 e_{21} }{V_{1o} }} \right) -c_2 {\left( {\frac{C}{c_1^2 +c_2^2 }} \right) } \right] \nonumber \\&-\left. {c_1 \left( {\frac{c_1 f_2 -c_2 f_1 }{p_{1o} }} \right) +c_1 \left( {\frac{c_1 g_2 -c_2 g_1 }{\rho _{1o} }} \right) } \right\} , \end{aligned}$$

(115b)

$$\begin{aligned} \frac{\partial {{\tilde{\upsilon }}} }{\partial {{\tilde{b}}} }= & {} -\frac{2}{\gamma +1}\,\frac{V_1 \chi }{m}\left[ {\frac{X\,\hbox {sin}\,\theta }{V_1^2 }\sum \upsilon _{1,j} K_i \upsilon _{1,j\,x_i } } {-2\left( {\hbox {sin}\,\theta } \right) \sum K_j \frac{M_{1x_j } }{M_1 }-\left( {1-\frac{\gamma -1}{2}m} \right) \left( {\hbox {cos}\,\theta } \right) \sum K_j \theta _{x_j } } \right] \nonumber \\\end{aligned}$$

(116a)

$$\begin{aligned}= & {} \frac{2}{\gamma +1}\,\frac{V_{1o} }{m}\,\frac{1}{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}\,\left\{ {\left( {1-\frac{\gamma -1}{2}m} \right) } \right. \left[ {\left( {\frac{c_1 e_{13} +c_2 e_{23} }{V_{1o} }} \right) } {\left. {-c_2 \left( {\frac{c_1 c_{23} -c_2 c_{13} }{c_1^2 +c_2^2 }} \right) } \right] -c_1 \frac{f_3 }{p_{1o} }+c_1 \frac{g_3 }{\rho _{1o} }} \right\} .\nonumber \\ \end{aligned}$$

(116b)

Appendix E: Shock-based derivative parameter summary

The $J_i$ evaluation requires transforming state 2 shock-based derivatives into Cartesian coordinate derivatives [16, Appendix G]

$$\begin{aligned} \frac{\partial }{\partial {{\tilde{s}}} }= & {} \sum \frac{\partial x_j }{\partial {{\tilde{s}}} }\,\frac{\partial }{\partial x_j }=\frac{\chi }{\left| {\nabla F} \right| }\sum L_j \frac{\partial }{\partial x_j }, \end{aligned}$$

(117a)

$$\begin{aligned} \frac{\partial }{\partial {{\tilde{n}}} }= & {} \sum \frac{\partial x_j }{\partial {{\tilde{n}}} }\,\frac{\partial }{\partial x_j }=\frac{1}{\left| {\nabla F} \right| }\sum F_{x_j } \frac{\partial }{\partial x_j }, \end{aligned}$$

(117b)

$$\begin{aligned} \frac{\partial }{\partial {{\tilde{b}}} }= & {} \sum \frac{\partial x_j }{\partial {{\tilde{b}}} }\,\frac{\partial }{\partial x_j }=-\chi \sum K_j \frac{\partial }{\partial x_j }. \end{aligned}$$

(117c)

In addition, the following identities simplify results [16, Eqs. (10.17)]:

$$\begin{aligned} \sum F_{x_j } K_j =\sum F_{x_j } L_j =\sum K_j L_j =\sum \upsilon _{1,j} K_j =0,\,\,\,\sum K_j^2 =\frac{1}{\chi ^{2}},\,\,\,\sum L_j^2 =\frac{\left| {\nabla F} \right| ^{2}}{\chi ^{2}}. \end{aligned}$$

(118)

For instance,

$$\begin{aligned} \sum F_{x_j } K_j =0 \end{aligned}$$

(119)

results in the replacement of the derivative term on the left

$$\begin{aligned} \sum \nolimits _j F_{x_j } K_{jx_i } =-\sum \nolimits _j K_j F_{x_j x_i }. \end{aligned}$$

(120)

with the simpler result on the right.

The method is illustrated by deriving $J_3$ in both its general and expansion coefficient forms. From [16, Sect. 10.2], the ${\hat{{\tilde{s}}}}$ and ${\hat{{\tilde{b}}}}$ vectors are

$$\begin{aligned} {\hat{{\tilde{s}}}} =\frac{\chi }{\left| {\nabla F} \right| }\sum L_i {\hat{|}}_i ,\quad {\hat{{\tilde{b}}}} =-\chi \sum K_i {\hat{|}}_i. \end{aligned}$$

(121)

The ${\hat{{\tilde{b}}}}$ differential is

$$\begin{aligned} \frac{\partial {\hat{{\tilde{b}}}} }{\partial x_j }=-\chi _{x_j } \sum K_i {\hat{|}}_i -\chi \sum K_{i\,x_j } {\hat{|}}_i. \end{aligned}$$

Equation (117a) transforms this to an ${{\tilde{s}}}$ derivative

$$\begin{aligned} \frac{\partial {\hat{{\tilde{b}}}} }{\partial {{\tilde{s}}} }= & {} \frac{\chi }{\left| {\nabla F} \right| }\sum L_j \frac{\partial {\hat{{\tilde{b}}}} }{\partial x_j }=\frac{\chi }{\left| {\nabla F} \right| }\sum L_j \left( {-\chi _{x_j } \sum K_i {\hat{|}}_i -\chi \sum K_{i\,x_j } {\hat{|}}_i } \right) \\= & {} -\frac{\chi }{\left| {\nabla F} \right| }\left[ {\left( {\sum L_j \chi _{x_j } } \right) \sum K_i {\hat{|}}_i +\chi \sum L_j K_{i x_j } {\hat{|}}_i } \right] . \end{aligned}$$

Hence, $J_3$ is

$$\begin{aligned} J_3= & {} -{\hat{{\tilde{s}}}} \cdot \frac{\partial {\hat{{\tilde{b}}}} }{\partial {{\tilde{s}}} }=\frac{\chi ^{2}}{|\nabla F|^{2}}\sum L_k {\hat{|}}_k \cdot \left[ {\left( {\sum L_j \chi _{x_j } } \right) \sum K_i {\hat{|}}_i +\chi \sum L_j K_{ix_j } {\hat{|}}_i } \right] \\= & {} \frac{\chi ^{2}}{|\nabla F|^{2}}\left[ {\left( {\sum L_j \chi _{x_j } } \right) \sum L_k K_i \delta _{ki} +\chi \sum L_k L_j K_{i\,x_j } \delta _{ki} } \right] \\= & {} \frac{\chi ^{2}}{|\nabla F|^{2}}\left[ {\left( {\sum L_j \chi _{x_j } } \right) \left( {\sum L_i K_i } \right) +\chi \sum L_i L_j K_{i x_j } } \right] . \end{aligned}$$

With the aid of (118), this simplifies to (124a).

Appendix C is used for the expansion coefficient values of $\chi$, $\left| {\nabla F} \right|$, and $L_i$. The $K_{i\,x_j }$ values require differentiating (82), with the $K_1$ result

$$\begin{aligned} K_{1x_1 }= & {} \upsilon _{1,3\,x_1 } F_{x_2 } +\upsilon _{1,3} F_{x_1 x_2 } -\upsilon _{1,2\,x_1 } F_{x_3 } -\upsilon _{1,2} F_{x_1 x_3 }, \\ K_{1x_2 }= & {} \upsilon _{1,3\,x_2 } F_{x_2 } +\upsilon _{1,3} F_{x_2 x_2 } -\upsilon _{1,2\,x_2 } F_{x_3 } -\upsilon _{1,2} F_{x_2 x_3 }, \\ K_{1x_3 }= & {} \upsilon _{1,3\,x_3 } F_{x_2 } +\upsilon _{1,3} F_{x_2 x_3 } -\upsilon _{1,2\,x_3 } F_{x_3 } -\upsilon _{1,2} F_{x_3 x_3 }, \end{aligned}$$

with similar relations for $K_2$ and $K_3$. These are simplified by utilizing

$$\begin{aligned} \upsilon _{1,1} =V_{1o} ,\quad \upsilon _{1,2} =\upsilon _{1,3} =0,\quad F_{x_3 } =c_3 =0,\quad \upsilon _{1,i\,x_j } =e_{ij} \end{aligned}$$

so that, e.g.,

$$\begin{aligned} K_{1x_1 } =c_2 e_{31} ,\quad K_{2x_1 } =V_{1o} c_{13} -c_1 e_{31} ,\quad \,K_{3x_1 } =c_1 e_{21} -c_2 e_{11} -V_{1o} c_{12} \end{aligned}$$

with similar results for the other K derivatives. The foregoing then yields (124b).

$J_i$ parameters

$$\begin{aligned} J_1= & {} {\hat{{\tilde{s}}}} \cdot \frac{\partial {\hat{{\tilde{n}}}} }{\partial {{\tilde{s}}} }=-{\hat{{\tilde{n}}}} \cdot \frac{\partial {\hat{{\tilde{s}}}} }{\partial {{\tilde{s}}} }=\frac{\chi ^{2}}{\left| {\nabla F} \right| ^{3}}\sum L_i L_j F_{x_i x_j } \end{aligned}$$

(122a)

$$\begin{aligned}= & {} \frac{c_1^2 c_{22} -2c_1 c_2 c_{12} +c_2^2 c_{11} }{\left( {c_1^2 +c_2^2 } \right) ^{3/2}}=-S_\mathrm{a}, \end{aligned}$$

(122b)

$$\begin{aligned} J_2= & {} {\hat{{\tilde{s}}}} \cdot \frac{\partial {\hat{{\tilde{n}}}} }{\partial {{\tilde{n}}} }=-{\hat{{\tilde{n}}}} \cdot \frac{\partial {\hat{{\tilde{s}}}} }{\partial {{\tilde{n}}} }=\frac{\chi }{\left| {\nabla F} \right| ^{3}}\sum F_{x_i } L_j F_{x_i x_j } \end{aligned}$$

(123a)

$$\begin{aligned}= & {} \frac{-c_1 c_2 c_{11} +\left( {c_1^2 -c_2^2 } \right) c_{12} +c_1 c_2 c_{22} }{\left( {c_1^2 +c_2^2 } \right) ^{3/2}}=-S_\mathrm{n}, \end{aligned}$$

(123b)

$$\begin{aligned} J_3= & {} {\hat{{\tilde{b}}}} \cdot \frac{\partial {\hat{{\tilde{s}}}} }{\partial {{\tilde{s}}} }=-{\hat{{\tilde{s}}}} \cdot \frac{\partial {\hat{{\tilde{b}}}} }{\partial {{\tilde{s}}} }=\frac{\chi ^{3}}{\left| {\nabla F} \right| ^{2}}\sum L_i L_j K_{i\,x_j } \end{aligned}$$

(124a)

$$\begin{aligned}= & {} \frac{1}{c_2 }\left( {\frac{c_1 e_{32} -c_2 e_{31} }{V_{1o} }} \right) -\frac{c_1 }{c_2 }\left( {\frac{c_1 c_{23} -c_2 c_{13} }{c_1^2 +c_2^2 }} \right) , \end{aligned}$$

(124b)

$$\begin{aligned} J_4= & {} -{\hat{{\tilde{s}}}} \cdot \frac{\partial {\hat{{\tilde{b}}}} }{\partial {{\tilde{b}}} }={\hat{{\tilde{b}}}} \cdot \frac{\partial {\hat{{\tilde{s}}}} }{\partial {{\tilde{b}}} }=-\frac{\chi ^{3}}{\left| {\nabla F} \right| }\sum K_i L_j K_{j\,x_i } \end{aligned}$$

(125a)

$$\begin{aligned}= & {} \frac{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}{c_2 }\,\frac{e_{33} }{V_{1o} }, \end{aligned}$$

(125b)

$$\begin{aligned} J_5= & {} {\hat{{\tilde{b}}}} \cdot \frac{\partial {\hat{{\tilde{n}}}} }{\partial {{\tilde{n}}} }=-{\hat{{\tilde{n}}}} \cdot \frac{\partial {\hat{{\tilde{b}}}} }{\partial {{\tilde{n}}} }=-\frac{\chi }{\left| {\nabla F} \right| ^{2}}\sum F_{x_i } F_{x_j } K_{i\,x_j } \end{aligned}$$

(126a)

$$\begin{aligned}= & {} \left( {\frac{c_1 c_{13} +c_2 c_{23} }{c_1^2 +c_2^2 }} \right) , \end{aligned}$$

(126b)

$$\begin{aligned} J_6 ={\hat{{\tilde{b}}}} \cdot \frac{\partial {\hat{{\tilde{n}}}} }{\partial {{\tilde{b}}} }=-{\hat{{\tilde{n}}}} \cdot \frac{\partial {\hat{{\tilde{b}}}} }{\partial {{\tilde{b}}} }=\frac{\chi ^{2}}{\left| {\nabla F} \right| }\sum K_i K_j F_{x_i x_j } =-S_\mathrm{b}. \end{aligned}$$

(127)

Appendix F: Evaluation of Eq. (50) time derivatives

Equations (37) list the parameters. The m parameter that appears in these equations is given by (79b) and

$$\begin{aligned} M_{1o}^2 =\left( {\frac{\rho V^{2}}{\gamma p}} \right) _{1o}. \end{aligned}$$

(128)

Its derivative is

$$\begin{aligned} \frac{1}{m}\,\frac{\partial m}{\partial t}=-\frac{p_{1ot} }{p_{1o} }+\frac{\rho _{1ot} }{\rho _{1o} }+2\frac{V_{1ot} }{V_{1o} }-2\frac{c_2 }{c_1 }\left( {\frac{c_1 c_{2t} -c_2 c_{1t} }{c_1^2 +c_2^2 }} \right) . \end{aligned}$$

(129)

The $\theta _t$ derivative stems from

$$\begin{aligned} \hbox {sin}\,\theta =\frac{\sum \upsilon _{1,j} F_{x_j } }{V_1 \left| {\nabla V} \right| }=\frac{c_1 }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}. \end{aligned}$$

(130a)

Since

$$\begin{aligned} \hbox {cos}\,\theta =-\frac{c_2 }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}},\quad \hbox {cot}\,\theta =-\frac{c_2 }{c_1 } \end{aligned}$$

(130b,c)

$\theta _t$ becomes

$$\begin{aligned} \theta _t =\left( {\frac{c_1 c_{2t} -c_2 c_{1t} }{c_1^2 +c_2^2 }} \right) . \end{aligned}$$

(131)

Note that the right-most term in (129) is $2\left( {\hbox {cot}\theta } \right) \theta _t$ .

With the above, the state 2 pressure derivative is

$$\begin{aligned} p= & {} \frac{2}{\gamma +1}p_{1o} Y, \end{aligned}$$

(132a)

$$\begin{aligned} \frac{\partial p}{\partial t}= & {} \frac{2}{\gamma +1}p_{1ot} Y+\frac{2\gamma }{\gamma +1}p_{1o} m_t, \end{aligned}$$

(132b)

where $m_t$ is given by (129). Similarly, the density derivative is

$$\begin{aligned} \rho= & {} \frac{\gamma +1}{2}\rho _{1o} \frac{m}{X}, \end{aligned}$$

(133a)

$$\begin{aligned} \frac{\partial \rho }{\partial t}= & {} \frac{\gamma +1}{2}\,\frac{\rho _{1o} }{X^{2}}\left[ {X\frac{m}{\rho _{1o} }\rho _{1ot} +m_t } \right] . \end{aligned}$$

(133b)

The ${{\tilde{u}}}$ derivative is

$$\begin{aligned} {{\tilde{u}}}= & {} -V_{1o} \frac{c_2 }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}, \end{aligned}$$

(134a)

$$\begin{aligned} \frac{\partial {{\tilde{u}}} }{\partial t}= & {} -\frac{c_2 V_{1o} }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}\left[ {\frac{V_{1ot} }{V_{1o} }+\frac{c_1 }{c_2 }\left( {\frac{c_1 c_{2t} -c_2 c_{1t} }{c_1^2 +c_2^2 }} \right) } \right] . \end{aligned}$$

(134b)

Finally, the ${{\tilde{\upsilon }}}$ derivative is

$$\begin{aligned} {{\tilde{\upsilon }}}= & {} \frac{2}{\gamma +1}V_{1o} \frac{X}{m}\,\frac{c_1 }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}, \end{aligned}$$

(135a)

$$\begin{aligned} \frac{\partial {{\tilde{\upsilon }}} }{\partial t}= & {} {\,}{{\tilde{\upsilon }}} \left[ {\frac{V_{1ot} }{V_{1o} }-\frac{c_2 }{c_1 }\left( {\frac{c_1 c_{2t} -c_2 c_{1t} }{c_1^2 +c_2^2 }} \right) -\frac{1}{X}\,\frac{m_t }{m}} \right] . \end{aligned}$$

(135b)

Appendix G: Evaluation of the $\partial {\hat{{\tilde{s}}}} /\partial t$ and $\partial {\hat{{\tilde{n}}}} /\partial t$ derivatives

As evident from (51), the $\partial {\hat{{\tilde{s}}}} /\partial t$ and $\partial {\hat{{\tilde{n}}}} /\partial t$ derivatives are required in terms of the ${\hat{{\tilde{s}}}} ,{\hat{{\tilde{n}}}} ,{\hat{{\tilde{b}}}}$ basis. Equations (36) provide the ${\hat{{\tilde{s}}}} \,\hbox {and}\,{\hat{{\tilde{n}}}}$ basis in terms of the time independent ${\hat{|}}_i^{*}$ basis. After differentiation, this yields

$$\begin{aligned} \frac{\partial {\hat{{\tilde{s}}}} }{\partial t}= & {} -\frac{1}{c_2^2 \left( {c_1^2 +c_2^2 } \right) ^{3/2}}\left[ {c_1 c_2 c_{1t} +\left( {c_1^2 +2c_2^2 } \right) c_{2t} } \right] \sum \left[ {c_1 F_{x_i^*}^*-\left( {c_1^2 +c_2^2 } \right) \frac{\beta _i }{V_1 }} \right] {\hat{|}}_i^{*} \nonumber \\&+ \frac{1}{{c_2 ( {c_1^2 +c_2^2 } )^{1/2}}} \sum \left\{ F_{x_i^{*}}^{*} c_{1t} +c_1 F_{x_i^{*} t}^{*} -2\left( {c_1 c_{1t} +c_2 c_{2t} } \right) \frac{\beta _i }{V_1 } {-\frac{\left( {c_1^2 +c_2^2 } \right) }{V_1^3 }\left[ {V_1^2 \,\frac{\partial \beta _i }{\partial t}-\beta _i \left( {\sum \beta _j \frac{\partial \beta _j }{\partial t}} \right) \,} \right] } \right\} {\hat{|}}_i^{*}, \nonumber \\\end{aligned}$$

(136a)

$$\begin{aligned} \frac{\partial {\hat{{\tilde{n}}}} }{\partial t}= & {} \frac{1}{\left( {c_1^2 +c_2^2 } \right) ^{3/2}}\sum \left[ {-F_{x_i^*}^*\left( {c_1 c_{1t} +c_2 c_{2t} } \right) +\left( {c_1^2 +c_2^2 } \right) F_{x_i^*t}^*} \right] {\hat{|}}_i^{*}, \end{aligned}$$

(136b)

where

$$\begin{aligned} \frac{\partial \beta _i }{\partial t}= & {} \upsilon _{1,it}^*+\frac{F_{x_i^*t}^*F_t^*}{\left( {c_1^2 +c_2^2 } \right) }+\frac{F_{x_i^*}^*F_{tt}^*}{\left( {c_1^2 +c_2^2 } \right) }-\frac{2F_{x_i^*}^*F_t^*\left( {c_1 c_{1t} +c_2 c_{2t} } \right) }{\left( {c_1^2 +c_2^2 } \right) ^{2}}, \end{aligned}$$

(137)

$$\begin{aligned} \frac{\partial }{\partial t}\left( {\frac{1}{V_1 }} \right)= & {} -\frac{1}{V_1^3 }\sum \beta _j \frac{\partial \beta _j }{\partial t}. \end{aligned}$$

(138)

For later analysis, (136) is conveniently written as

$$\begin{aligned} \frac{\partial {\hat{{\tilde{s}}}} }{\partial t}= & {} \sum \gamma _\mathrm{si} {\hat{|}}_i^{*}, \end{aligned}$$

(139a)

$$\begin{aligned} \frac{\partial {\hat{{\tilde{n}}}} }{\partial t}= & {} \sum \gamma _\mathrm{ni} {\hat{|}}_i^{*}, \end{aligned}$$

(139b)

where

$$\begin{aligned} \gamma _\mathrm{si}= & {} \frac{\left[ {c_2^3 c_{1t} -c_1 \left( {c_1^2 +2c_2^2 } \right) c_{2t} } \right] F_{x_i^*}^*}{c_2^2 \left( {c_1^2 +c_2^2 } \right) ^{3/2}}+\frac{c_1 F_{x_i^*t}^*}{c_2 \left( {c_1^2 +c_2^2 } \right) ^{1/2}} +\frac{c_1 \left( {-c_2 c_{1t} +c_1 c_{2t} } \right) }{c_2^2 \left( {c_1^2 +c_2^2 } \right) ^{1/2}}\,\frac{\beta _i }{V_1 }-\frac{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}{c_2 V_1 }\,\frac{\partial \beta _i }{\partial t} \nonumber \\&+\frac{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}{c_2 }\,\frac{\beta _i }{V_1^3 }\sum \beta _j \frac{\partial \beta _j }{\partial t}, \end{aligned}$$

(140a)

$$\begin{aligned} \gamma _\mathrm{ni}= & {} \frac{1}{\left( {c_1^2 +c_2^2 } \right) ^{3/2}}\left[ {-F_{x_i^*}^*\left( {c_1 c_{1t} +c_2 c_{2t} } \right) +\left( {c_1^2 +c_2^2 } \right) F_{x_i^*t}^*} \right] . \end{aligned}$$

(140b)

To obtain the desired form, the inverse of (35) is needed:

$$\begin{aligned} {\hat{|}}_1 =\frac{-c_2 {\hat{{\tilde{s}}}} +c_1 {\hat{{\tilde{n}}}} }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}},\quad {\hat{|}}_2 =\frac{c_1 {\hat{{\tilde{s}}}} +c_2 {\hat{{\tilde{n}}}} }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}},\quad {\hat{|}}_3 =-{\hat{{\tilde{b}}}}. \end{aligned}$$

(141)

Combined with (20), this yields

$$\begin{aligned} {\hat{|}}_i^{*} =\alpha _\mathrm{si} {\hat{{\tilde{s}}}} +\alpha _\mathrm{ni} {\hat{{\tilde{n}}}} +\alpha _\mathrm{bi} {\hat{{\tilde{b}}}}, \end{aligned}$$

(142)

where

$$\begin{aligned} \alpha _\mathrm{si} =\frac{-c_2 a_{i1} +c_1 a_{i2} }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}},\quad \alpha _\mathrm{ni} =\frac{c_1 a_{i1} +c_2 a_{i2} }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}},\quad \alpha _\mathrm{bi} =-a_{i3}. \end{aligned}$$

(143)

With the aid of (74) – (76), these simplify to

$$\begin{aligned} \alpha _\mathrm{si}= & {} \frac{c_1 F_{x_i^*}^*}{c_2 \left( {c_1^2 +c_2^2 } \right) ^{1/2}}-\frac{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}{c_2 }\,\frac{\beta _i }{V_1 }, \end{aligned}$$

(144a)

$$\begin{aligned} \alpha _\mathrm{ni}= & {} \frac{F_{x_i^*}^*}{ \left( {c_1^2 +c_2^2 } \right) ^{1/2}}, \end{aligned}$$

(144b)

$$\begin{aligned} \alpha _\mathrm{b1}= & {} \frac{1}{c_2 V_1 }\left( {\upsilon _{1,3}^*F_{x_2^*}^*-\upsilon _{1,2}^*F_{x_3^*}^*} \right) , \nonumber \\ \alpha _\mathrm{b2}= & {} \frac{1}{c_2 V_1 }\left( {\upsilon _{1,1}^*F_{x_3^*}^*-\upsilon _{1,3}^*F_{x_1^*}^*} \right) , \nonumber \\ \alpha _\mathrm{b3}= & {} \frac{1}{c_2 V_1 }\left( {\upsilon _{1,2}^*F_{x_1^*}^*-\upsilon _{1,1}^*F_{x_2^*}^*} \right) , \end{aligned}$$

(144c)

where $\beta _i$ is given by (9c) and $F_{x_i^*}^*$ by (70).

For inclusion into the Euler equations, the ${\hat{{\tilde{s}}}}$ and ${\hat{{\tilde{n}}}}$ derivatives are written as

$$\begin{aligned} \frac{\partial {\hat{{\tilde{s}}}} }{\partial t}= & {} N_\mathrm{ss} {\hat{{\tilde{s}}}} +N_\mathrm{sn} {\hat{{\tilde{n}}}} +N_\mathrm{sb} {\hat{{\tilde{b}}}}, \end{aligned}$$

(145a)

$$\begin{aligned} \frac{\partial {\hat{{\tilde{n}}}} }{\partial t}= & {} N_\mathrm{ns} {\hat{{\tilde{s}}}} +N_\mathrm{nn} {\hat{{\tilde{n}}}} +N_\mathrm{nb} {\hat{{\tilde{b}}}}, \end{aligned}$$

(145b)

where

$$\begin{aligned} N_\mathrm{ss}= & {} \sum \gamma _\mathrm{si} \alpha _\mathrm{si} ,\quad N_\mathrm{sn} =\sum \gamma _\mathrm{si} \alpha _\mathrm{ni} ,\quad N_\mathrm{sb} =\sum \gamma _\mathrm{si} \alpha _\mathrm{bi}, \end{aligned}$$

(146a)

$$\begin{aligned} N_\mathrm{ns}= & {} \sum \gamma _\mathrm{ni} \alpha _\mathrm{si} ,\quad N_\mathrm{nn} =\sum \gamma _\mathrm{ni} \alpha _\mathrm{ni} ,\quad N_\mathrm{nb} =\sum \gamma _\mathrm{ni} \alpha _\mathrm{bi}. \end{aligned}$$

(146b)

As noted in Sect. 2.10.4, $N_\mathrm{sb}$ and $N_\mathrm{nb}$ do not appear in the Euler equations and, therefore, are not needed. With the aid of (140) and (144), the four Ns of consequence are

$$\begin{aligned} N_\mathrm{ss}= & {} \frac{1}{c_2^2 }\left\{ {c_2 \left( {c_1^2 +2c_2^2 } \right) c_{1t} } -c_1 \left( {c_1^2 +3c_2^2 } \right) c_{2t}+ \frac{\left[ {-c_2 \left( {c_1^2 +c_2^2 } \right) c_{1t} +2c_1 \left( {c_1^2 -c_2^2 } \right) c_{2t} } \right] }{c_2 \left( {c_1^2 +c_2^2 } \right) V_1 }\sum F_{x_i^*}^*\beta _i\right. \nonumber \\&+\frac{c_1 }{\left( {c_1^2 +c_2^2 } \right) }\sum F_{x_i^*}^*F_{x_i^*t}^*-\frac{c_1 }{V_1 }\sum \beta _i F_{x_i^*t}^*-\frac{c_1 }{V_1 }\sum F_{x_i^*}^*\frac{\partial \beta _i }{\partial t} \left. {+\frac{c_1 }{V_1^3 }\left( {\sum F_{x_i^*}^*\beta _i } \right) \left( {\sum \beta _j \frac{\partial \beta _j }{\partial t}} \right) } \right\} , \end{aligned}$$

(147a)

$$\begin{aligned} N_\mathrm{sn}= & {} \frac{1}{c_2^3 \left( {c_1^2 +c_2^2 } \right) }\left[ {c_2^3 c_{1t} -c_1 \left( {c_1^2 +2c_2^2 } \right) c_{2t} +c_1 c_2 \sum F_{x_i^*}^*F_{x_i^*t}^*} \right. \nonumber \\&+\frac{c_1 }{V_1 }\left( {-c_2 c_{1t} +c_1 c_{2t} } \right) \sum F_{x_i^*}^*\beta _i -\frac{c_2 \left( {c_1^2 +c_2^2 } \right) }{V_1 }\sum F_{x_i^*}^*\frac{\partial \beta _i }{\partial t} \nonumber \\&\left. +{\frac{c_2 \left( {c_1^2 +c_2^2 } \right) }{V_1^3 }\left( {\sum F_{x_i^*}^*\beta _i } \right) \left( {\sum \beta _j \frac{\partial \beta _j }{\partial t}} \right) } \right] , \end{aligned}$$

(147b)

$$\begin{aligned} N_\mathrm{ns}= & {} \frac{1}{c_2 \left( {c_1^2 +c_2^2 } \right) ^{1/2}}\left[ {-\frac{c_1 \left( {c_1 c_{1t} +c_2 c_{2t} } \right) }{\left( {c_1^2 +c_2^2 } \right) ^{1/2}}} +\frac{\left( {c_1 c_{1t} +c_2 c_{2t} } \right) }{V_1 }\sum F_{x_i^*}^*\beta _i +\frac{c_1 }{V_1 }\sum F_{x_i^*}^*F_{x_i^*t}^*-\frac{1}{V_1 }\sum \beta _i F_{x_i^*t}^*\right] , \nonumber \\\end{aligned}$$

(148a)

$$\begin{aligned} N_\mathrm{nn}= & {} \frac{1}{\left( {c_1^2 +c_2^2 } \right) }\left[ {-\left( {c_1 c_{1t} +c_2 c_{2t} } \right) +\sum F_{x_i^*}^*F_{x_i^*t}^*} \right] . \end{aligned}$$

(148b)

Overall, the $N\hbox {s}$ are evaluated in the laboratory-frame system, except for the $c_1$, $c_2$, and $V_1$ parameters.