Three-dimensional curved shock theory

Abstract

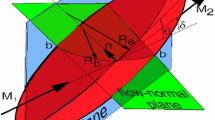
Curved shock theory is developed to characterize the flow on the downstream side of a three-dimensional shock surface. It is applied to non-symmetric, stationary, blunt-body shocks in a uniform, steady, supersonic freestream. The flow-plane-associated derivatives that are tangential and normal to the shock of pressure, density, velocity components, vorticity, and shock curvatures are presented. Relations are provided for the shock angles, flow deflection angles, intrinsic coordinates, the associated basis, pressure derivatives along these coordinates, streamline curvatures, and the reflection coefficient. A global analysis, utilizing scatterplots, is used to locate curves of sonic flow, maximum flow deflection angle, maximum vorticity, and curves for zero streamline curvature (Crocco) and zero streamwise pressure gradient (Thomas) on the back of a three-dimensional shock wave surface.

Appendices

Appendix 1: Errors in [24]

The few errors in [24] are given in terms of equation numbers in [24].

$$ \begin{array}{*{20}l} {\frac{{\partial \widehat{{\tilde{n}}}}}{{\partial \tilde{b}}} = \frac{1}{{h_{3} }} \frac{{\partial h_{3} }}{{\partial \tilde{n}}}\widehat{{\tilde{b}}}} \hfill & \qquad\qquad \qquad\qquad\qquad\qquad\,\, \qquad \qquad\qquad(43, [24]) \hfill \\ \end{array} $$

$$ \begin{aligned} c_{11} & = c_{11}^{*} a_{11}^{2} + c_{22}^{*} a_{21}^{2} + c_{33}^{*} a_{31}^{2} \\ & \quad + \frac{1}{2}\left( {c_{12}^{*} a_{11} a_{21} + c_{13}^{*} a_{11} a_{31} + c_{23}^{*} a_{21} a_{31} } \right)\qquad (72{\text{a}},[24]) \\ \end{aligned} $$

$$ \begin{aligned} c_{22} & = c_{11}^{*} a_{12}^{2} + c_{22}^{*} a_{22}^{2} + c_{33}^{*} a_{32}^{2} \\ & \quad + \frac{1}{2}\left( {c_{12}^{*} a_{12} a_{22} + c_{13}^{*} a_{12} a_{32} + c_{23}^{*} a_{22} a_{32} } \right)\qquad (72{\text{b}},[24]) \\ \end{aligned} $$

$$ \begin{aligned} c_{33} & = c_{11}^{*} a_{13}^{2} + c_{22}^{*} a_{23}^{2} + c_{33}^{*} a_{33}^{2} \\ & \quad + \frac{1}{2}\left( {c_{12}^{*} a_{13} a_{23} + c_{13}^{*} a_{13} a_{33} + c_{23}^{*} a_{23} a_{33} } \right)\quad\quad (72{\text{c}},[24]) \\ \end{aligned} $$

$$ = - \left( {\frac{{c_{1} c_{13} + c_{2} c_{23} }}{{c_{1}^{2} + c_{2}^{2} }}} \right) \qquad\qquad\qquad\qquad \qquad\qquad\,\,\quad (126{\text{b}},[24]) $$

Appendix 2: Errors in [25]

The errors in [25] are given in terms of the equation numbers in [25].

$$ d_{n}^{2} = \frac{{A^{2} \left( {1 - Ba_{s}^{2} }\right)}}{B}\qquad\qquad\qquad\qquad \qquad\quad\, \qquad \qquad(92{\text{d}},[25]) $$

$$ A_{ss,n} = - \frac{C}{{\left( {c_{1}^{2} + c_{2}^{2} }\right)^{3/2} }} = \frac{1}{2}S_{a}\quad \qquad\qquad \qquad \qquad(110{\text{b}},[25]) $$

$$ A_{ns,s} = - A_{ss,n} = - \frac{1}{2}S_{a}\qquad \qquad \qquad \qquad\qquad\,\,\,\quad(111{\text{a}},[25]) $$

$$ P_{s} = \tilde{u}\frac{{\partial \tilde{u}}}{{\partial \tilde{n}}} + \upsilon \frac{{\partial \tilde{u}}}{{\partial \tilde{n}}} - \tilde{\upsilon }\left( {\frac{1}{2}\tilde{u}S_{a} + \tilde{\upsilon }S_{n} } \right)\qquad\qquad\quad (115{\text{a}},[25]) $$

$$ P_{n} = \tilde{u}\frac{{\partial \tilde{\upsilon }}}{{\partial \tilde{s}}} + \upsilon \frac{{\partial \tilde{\upsilon }}}{{\partial \tilde{n}}} + \tilde{u}\left( {\frac{1}{2}\tilde{u}S_{a} + \tilde{\upsilon }S_{n} } \right)\qquad\qquad\quad (115{\text{b}},[25]) $$

$$ \frac{{\partial \tilde{n}}}{{\partial \tilde{s}}} = - \frac{{S_{a} }}{{\left( {c_{1}^{2} + c_{2}^{2} } \right)^{\frac{1}{2}} }}\left( {c_{2} \widehat{|}_{1} + c_{1} \widehat{|}_{2} } \right) + \frac{{c_{1} c_{32} - c_{2} c_{31} }}{{\left( {c_{1}^{2} + c_{2}^{2} } \right)}}\widehat{|}_{3} \qquad \qquad \qquad\qquad\qquad \qquad (170{\text{b}},[25]) $$

$$ \frac{{\partial \widehat{{\tilde{n}}}}}{{\partial \tilde{n}}} = \frac{{S_{n} }}{{\left( {c_{1}^{2} + c_{2}^{2} } \right)^{1/2} }}\left( {c_{2} \widehat{|}_{1} - c_{1} \widehat{|}_{2} } \right) + \frac{{c_{1} c_{31} + c_{2} c_{32} }}{{\left( {c_{1}^{2} + c_{2}^{2} } \right)}}\widehat{|}_{3} \qquad \qquad \qquad \qquad\qquad\qquad (170{\text{d}},[25]) $$

Starting with the discussion after (92e), the signs of the $a$ and $d$ coefficients are incorrect. This topic is addressed in Sect. 2.8.

Appendix 3: Parameters of an Oblique shock

$$ V_{1} = \left( {\frac{{\gamma p_{1} }}{{\rho_{1} }}} \right)^{1/2} M_{1} $$

(41)

$$ m = M_{1}^{2} \frac{{c_{1}^{2} }}{{b_{12}^{2} }} $$

(42)

$$ X = 1 + \frac{\gamma - 1}{2}m,\quad Y = \gamma m - \frac{\gamma - 1}{2},\quad Z = m - 1 $$

(43)

$$ A = - \frac{\gamma + 1}{2} \frac{{c_{1} c_{2} }}{{b_{12}^{2} }} \frac{{M_{1}^{2} }}{X} $$

(44)

$$ B = 1 + A^{2} $$

(45)

$$ \theta = {\text{sin}}^{ - 1} \left( {\frac{{c_{1} }}{{b_{12} }}} \right) $$

(46)

$$ \delta = {\text{cos}}^{ - 1} \left( {\frac{{c_{1} - c_{2} A}}{{b_{12} B^{1/2} }}} \right) $$

(47)

State variables:

$$ p_{2} = \frac{2}{\gamma + 1}p_{1} Y $$

(48)

$$ \rho_{2} = \frac{\gamma + 1}{2}\rho_{1} \frac{m}{X} $$

$$ \tilde{u}_{2} = - V_{1} \frac{{c_{2} }}{{b_{12} }} $$

(49)

The minus sign counters a negative $c_{2}$ value.

$$ \tilde{\upsilon }_{2} = \frac{2}{\gamma + 1}V_{1} \frac{{b_{12} }}{{c_{1} M_{1}^{2} }}X $$

(50)

$$ V_{2} = \frac{2}{\gamma + 1}V_{1} \frac{{c_{1} X B^{1/2} }}{{b_{12} m}} $$

(51a)

$$ V_{2} = \left( {\tilde{u}_{2}^{2} + \tilde{\upsilon }_{2}^{2} } \right)^{1/2} $$

(51b)

$$ M_{2} = \left( {\frac{{\rho_{2} }}{{\gamma p_{2} }}} \right)^{1/2} V_{2} $$

(52)

Appendix 4: Tangential derivatives

$$ \frac{\partial p}{{\partial \tilde{s}}} = - \frac{4\gamma }{{\gamma + 1}}p_{1} m \frac{{c_{2} }}{{c_{1} }} \frac{C}{{b_{12}^{3} }} $$

(53)

$$ \frac{\partial \rho }{{\partial \tilde{s}}} = - \left( {\gamma + 1} \right)\rho_{1} \frac{m}{{X^{2} }} \frac{{c_{2} }}{{c_{1} }} \frac{C}{{b_{12}^{3} }} $$

(54)

$$ \frac{{\partial \tilde{u}}}{{\partial \tilde{s}}} = - V_{1} c_{1} \frac{C}{{b_{12}^{4} }} $$

(55)

$$ \frac{{\partial \tilde{\upsilon }}}{{\partial \tilde{s}}} = \frac{2}{\gamma + 1}V_{1} \frac{{1 - \frac{\gamma - 1}{2}m}}{m}c_{2} \frac{C}{{b_{12}^{4} }} $$

(56)

$$ \frac{{\partial \tilde{w}}}{{\partial \tilde{s}}} = 0 $$

(57)

$$ \frac{\partial p}{{\partial \tilde{b}}} = \frac{4\gamma }{{\gamma + 1}}p_{1} M_{1}^{2} \frac{{c_{1}^{2} c_{2} c_{23} }}{{b_{12}^{4} }} $$

(58)

$$ \frac{\partial \rho }{{\partial \tilde{b}}} = \left( {\gamma + 1} \right)\rho_{1} \frac{{M_{1}^{2} }}{{X^{2} }}\frac{{c_{1}^{2} c_{2} c_{23} }}{{b_{12}^{4} }} $$

(59)

$$ \frac{{\partial \tilde{u}}}{{\partial \tilde{b}}} = V_{1} \frac{{c_{1}^{2} c_{23} }}{{b_{12}^{3} }} $$

(60)

$$ \frac{{\partial \tilde{\upsilon }}}{{\partial \tilde{b}}} = - \frac{2}{\gamma + 1}V_{1} \frac{{1 - \frac{\gamma - 1}{2}m}}{m} \frac{{c_{1} c_{2} c_{23} }}{{b_{12}^{3} }} $$

(61)

$$ \frac{{\partial \tilde{w}}}{{\partial \tilde{b}}} = 0 $$

(62)

Appendix 5: Normal derivatives

The $J_{i}$ parameters are first defined and evaluated. They represent curvilinear coefficients that appear in the Euler equations when written in the shock-based FP coordinates.

$$ J_{1} = \widehat{{\tilde{s}}} \cdot \frac{{\partial \widehat{{\tilde{n}}}}}{{\partial \tilde{s}}} = - \widehat{{\tilde{n}}} \cdot \frac{{\partial \widehat{{\tilde{s}}}}}{{\partial \tilde{s}}} = \frac{C}{{b_{12}^{3} }} $$

(63)

$$ J_{2} = \widehat{{\tilde{s}}} \cdot \frac{{\partial \widehat{{\tilde{n}}}}}{{\partial \tilde{n}}} = - \widehat{{\tilde{n}}} \cdot \frac{{\partial \widehat{{\tilde{s}}}}}{{\partial \tilde{n}}} = \frac{{c_{1} c_{2} \left( { - c_{11} + c_{22} } \right)}}{{b_{12}^{3} }} $$

(64)

$$ J_{3} = \widehat{{\tilde{b}}} \cdot \frac{{\partial \widehat{{\tilde{s}}}}}{{\partial \tilde{s}}} = - \widehat{{\tilde{s}}} \cdot \frac{{\partial \widehat{{\tilde{b}}}}}{{\partial \tilde{s}}} = - \frac{{c_{1}^{2} c_{23} }}{{c_{2} b_{12}^{2} }} $$

(65)

$$ J_{4} = \widehat{{\tilde{b}}} \cdot \frac{{\partial \widehat{{\tilde{s}}}}}{{\partial \tilde{b}}} = - \widehat{{\tilde{s}}} \cdot \frac{{\partial \widehat{{\tilde{b}}}}}{{\partial \tilde{b}}} = 0 $$

(66)

$$ J_{5} = \widehat{{\tilde{b}}} \cdot \frac{{\partial \widehat{{\tilde{n}}}}}{{\partial \tilde{n}}} = - \widehat{{\tilde{n}}} \cdot \frac{{\partial \widehat{{\tilde{b}}}}}{{\partial \tilde{n}}} = - \frac{{c_{2} c_{23} }}{{b_{12}^{2} }} $$

(67)

$$ J_{6} = \widehat{{\tilde{b}}} \cdot \frac{{\partial \widehat{{\tilde{n}}}}}{{\partial \tilde{b}}} = - \widehat{{\tilde{b}}} \cdot \frac{{\partial \widehat{{\tilde{b}}}}}{{\partial \tilde{b}}} = \frac{{c_{33} }}{{b_{12}^{{}} }} $$

(68)

Note that $J_{4}$ is zero because $\partial \widehat{{\tilde{b}}}/\partial \tilde{b}$ is normal to $\widehat{{\tilde{s}}}$. This does not happen with the other dot products.

$$ A_{1} = - \frac{{\partial \tilde{u}}}{{\partial \tilde{s}}} - \tilde{\upsilon }_{2 } J_{1} + \tilde{u}_{2 } J_{2} - \tilde{\upsilon }_{2} J_{6} - \frac{{\tilde{u}_{2} }}{{\rho_{2} }} \frac{\partial \rho }{{\partial \tilde{s}}} $$

(69)

$$ A_{3} = - \tilde{u}_{2} \frac{{\partial \tilde{\upsilon }}}{{\partial \tilde{s}}} + \tilde{u}_{2 }^{2} J_{1} + \tilde{u}_{2 } \tilde{\upsilon }_{2 } J_{2} $$

(70)

$$ A_{5} = - \tilde{u}_{2} \frac{\partial p}{{\partial \tilde{s}}} + \frac{{\gamma p_{2} \tilde{u}_{2} }}{{\rho_{2} }} \frac{\partial \rho }{{\partial \tilde{s}}} $$

(71)

$$ \Delta = \frac{2\gamma }{{\gamma + 1}} \frac{{p_{1} }}{{\rho_{1} }} \frac{XZ}{m} $$

(72)

$$ \frac{\partial p}{{\partial \tilde{n}}} = \frac{1}{\Delta }\left( { - \gamma p_{2} \tilde{\upsilon }_{2} A_{1} + \gamma p_{2} A_{3} - \tilde{\upsilon }_{2} A_{5} } \right) $$

(73)

$$ \frac{\partial \rho }{{\partial \tilde{n}}} = \frac{1}{\Delta }\left( { - \rho_{2} \tilde{\upsilon }_{2} A_{1} + \rho_{2} A_{3} - \frac{1}{{\tilde{\upsilon }_{2} }}A_{5} } \right) $$

(74)

$$ \frac{{\partial \tilde{u}}}{{\partial \tilde{n}}} = \frac{1}{{\tilde{\upsilon }_{2} }}\left( { - \tilde{u}_{2} \frac{{\partial \tilde{u}}}{{\partial \tilde{s}}} - \tilde{u}_{2 } \tilde{\upsilon }_{2 } J_{1} - \tilde{\upsilon }_{2 }^{2} J_{2} - \frac{1}{{\rho_{2} }} \frac{\partial p}{{\partial \tilde{s}}}} \right) $$

(75)

$$ \frac{{\partial \tilde{\upsilon }}}{{\partial \tilde{n}}} = \frac{1}{\Delta }\left( {\frac{{\gamma p_{2} }}{{\rho_{2} }}A_{1} - \tilde{\upsilon }_{2} A_{3} + \frac{1}{{\rho_{2} }}A_{5} } \right) $$

(76)

$$ \frac{{\partial \tilde{w}}}{{\partial \tilde{n}}} = \frac{1}{{\tilde{\upsilon }_{2} }}\left( { - \tilde{u}_{2 }^{2} J_{3} - \tilde{\upsilon }_{2 }^{2} J_{5} - \frac{1}{{\rho_{2} }} \frac{\partial p}{{\partial \tilde{b}}}} \right) $$

(77)

Note that $\partial \tilde{u}/\partial \tilde{n}$ and $\partial \tilde{w}/\partial \tilde{n}$ do not involve the $A_{i}$. These stem, respectively, from the $\widehat{{\tilde{s}}}$ and $\widehat{{\tilde{n}}}$ scalar momentum equations. The other three derivatives require Cramer’s rule and stem from continuity, the $\widehat{{\tilde{b}}}$ momentum equation, and a constant entropy along a streamline equation, which is used in place of an energy equation.

Appendix 6: Vorticity

$$ \overline{S}_{1} = \frac{{\gamma Z^{2} }}{XY} \frac{{c_{2}^{2} c_{11} }}{{c_{1} b_{12}^{2} }} $$

(78)

$$ \overline{S}_{2} = - \frac{{\gamma Z^{2} }}{XY} \frac{{c_{2} c_{22} }}{{b_{12}^{2} }} $$

(79)

$$ \overline{S}_{3} = - \frac{{\gamma Z^{2} }}{XY} \frac{{c_{2} c_{23} }}{{b_{12}^{2} }} $$

(80)

$$ G_{s} = - \frac{4\gamma }{{\left( {\gamma + 1} \right)^{2} }} \frac{{p_{1} }}{{\rho_{1} }} \frac{{1 + \gamma m^{2} }}{m}X\frac{{c_{2} }}{{c_{1} }} \frac{C}{{b_{12}^{3} }} $$

(81)

$$ G_{b} = \frac{4\gamma }{{\left( {\gamma + 1} \right)^{2} }} \frac{{p_{1} }}{{\rho_{1} }} \frac{{1 + \gamma m^{2} }}{m} \frac{{c_{2} c_{23} }}{{b_{12}^{2} }} $$

(82)

$$ E_{s} = \tilde{u}_{2} \frac{{\partial \tilde{u}}}{{\partial \tilde{s}}} + \tilde{\upsilon }_{2} \frac{{\partial \tilde{u}}}{{\partial \tilde{n}}} + \tilde{u}_{2 } \tilde{\upsilon }_{2 } J_{1} + \tilde{\upsilon }_{2 }^{2} J_{2} $$

(83)

$$ E_{b} = \tilde{\upsilon }_{2} \frac{{\partial \tilde{w}}}{{\partial \tilde{n}}} + \tilde{u}_{2 }^{2} J_{3} + \tilde{\upsilon }_{2 }^{2} J_{5} $$

(84)

$$ \omega_{s2} = \frac{1}{{\tilde{\upsilon }_{2} }}\left[ { - \left( {\frac{2}{\gamma + 1}} \right)^{2} \frac{{p_{1} }}{{\rho_{1} }} \frac{XY}{m}\overline{S}_{3} - G_{b} - E_{b} } \right] $$

(85)

$$ \omega_{b2} = \frac{1}{{\tilde{\upsilon }_{2} }}\left[ { - \left( {\frac{2}{\gamma + 1}} \right)^{2} \frac{{p_{1} }}{{\rho_{1} }} \frac{XY}{m} \frac{{c_{1} \overline{S}_{2} - c_{2} \overline{S}_{1} }}{{b_{12}^{2} }} + G_{s} + E_{s} } \right] $$

(86)

$$ \omega_{2} = \left( {\omega_{s2}^{2} + \omega_{b2}^{2} } \right)^{1/2} $$

(87)

Appendix 7: Intrinsic coordinate pressure derivatives

The equations for the $a_{s} , \cdots$ and $d_{s} , \cdots$ can be written as

$$ d_{s}^{2} + d_{n}^{2} + d_{b}^{2} = 1 $$

(88a)

$$ a_{s}^{2} + a_{n}^{2} + a_{b}^{2} = 1 $$

(88b)

$$ Aa_{s} + a_{n} = 0 $$

(88c)

$$ Ad_{s} + d_{n} = 0 $$

(88d)

$$ a_{s} d_{s} + a_{n} d_{n} + a_{b} d_{b} = 0 $$

(88e)

$$ \frac{\partial p}{{\partial \tilde{s}}}a_{s} + \frac{\partial p}{{\partial \tilde{n}}}a_{n} + \frac{\partial p}{{\partial \tilde{b}}}a_{b} = 0 $$

(88f)

where (88c, d, e) stem from (21). In turn, these can be written as

$$ a_{n} = - Aa_{s} $$

(89a)

$$ d_{n} = - Ad_{s} $$

(89b)

$$ Ba_{s} d_{s} + a_{b} d_{b} = 0 $$

(89c)

$$ Bd_{s}^{2} + d_{b}^{2} = 1 $$

(89d)

$$ Ba_{s}^{2} + a_{b}^{2} = 1 $$

(89e)

$$ \left( {\frac{\partial p}{{\partial \tilde{s}}} - A\frac{\partial p}{{\partial \tilde{n}}}} \right)a_{s} + \frac{\partial p}{{\partial \tilde{b}}}a_{b} = 0 $$

(89f)

Equations (89c–f) represent four equations for the unknowns $a_{s} ,a_{b} ,d_{s} , {\text{and}} \,d_{b}$. Eliminate $a_{s}$ from (89c) and (89e), to obtain

$$ a_{b} = \pm \frac{1}{D}\left( {\frac{\partial p}{{\partial \tilde{s}}} - A\frac{\partial p}{{\partial \tilde{n}}}} \right) $$

(90a)

where

$$ D = \left[ {\left( {\frac{\partial p}{{\partial \tilde{s}}} - A\frac{\partial p}{{\partial \tilde{n}}}} \right)^{2} + B\left( {\frac{\partial p}{{\partial \tilde{b}}}} \right)^{2} } \right]^{1/2} $$

(91)

Hence, $a_{S}$ becomes

$$ a_{s} = \pm \frac{1}{D} \frac{\partial p}{{\partial \tilde{b}}} $$

(90b)

and $a_{n}$ is given by (89a). Aside from sign, this determines the $a_{s}$. When $\left( {\partial p/\partial \tilde{b}} \right) = 0$, which occurs whenever $e = f$ or $z = 0\, {\text{or}}\,y = 0$, the $a_{s} , \cdots$ become,

$$ a_{s} = a_{n} = 0, a_{b} = \pm 1 $$

(92)

Similarly, the $d$ equations are

$$ d_{s} = \pm \left( {B + B^{2} \frac{{a_{s}^{2} }}{{a_{b}^{2} }}} \right)^{ - 1/2} $$

(93a)

$$ d_{n} = - Ad_{s} $$

(93b)

$$ d_{b} = - B\frac{{a_{s} }}{{a_{b} }}d_{s} $$

(93c)

where the $\pm$ sign in (93a) is not correlated with that in (90). Aside from their signs, the $a_{s} , \cdots$ and $d_{s} , \cdots$ are evaluated.

The signs in (90a) and (93a) are determined by using axial symmetry cases, i.e., $e = f$, and evaluating

$$ \frac{\partial p}{{\partial n}} = d_{s} \frac{\partial p}{{\partial \tilde{s}}} + d_{n} \frac{\partial p}{{\partial \tilde{n}}} + d_{b} \frac{\partial p}{{\partial \tilde{b}}} $$

(94)

at selected $G = 0$ points below the Crocco curve. Remember that $\left( {\partial p/\partial n} \right) < 0$ below and above it. This result then holds for when the shock is 3D.

Final results are

$$ a_{s} = - \frac{1}{D} \frac{\partial p}{{\partial \tilde{b}}} $$

(95a)

$$ a_{n} = - Aa_{s} $$

(95b)

$$ a_{b} = \frac{1}{D} \left( {\frac{\partial p}{{\partial \tilde{s}}} - A\frac{\partial p}{{\partial \tilde{n}}}} \right) $$

(95c)

$$ d_{s} = \left( {B + B^{2} \frac{{a_{s}^{2} }}{{a_{b}^{2} }}} \right)^{ - 1/2} $$

(95d)

$$ d_{n} = - Ad_{s} $$

(95e)

$$ d_{b} = - B\frac{{a_{s} }}{{a_{b} }}d_{s} $$

(95f)

where $D$ is given by (91). Notice that the sign of $a_{s}$ changes when $\partial p/\partial \tilde{b}$ changes sign as it does when $z$ changes sign. As discussed in Appendix 2, this approach differs from that in [25, Sect. 6].

Appendix 8: Data presentation

If the value of a variable $I$ is determined from a relation such as $I = I(P,x,y,z)$ where $P$ represents any number of parameters and $x,y,z$ denote the position of a point in space, and if one is interested in finding the location in space where $I$ takes on a specified value (typically on curves in a contour plot), then this relation must be inverted to obtain $z = z(I,P,x,y)$. Such an inversion is not always possible and is troublesome when the relation for $I$ is multivalued. This data problem is solved by a simple, computationally somewhat tedious yet robust plotting algorithm. This is illustrated with the steps in the task of drawing the sonic curve on the back of the shock: (1) select an arbitrary, random ($y, z$) coordinate pair for a point in the task space; (2) from the shock shape equation, G = 0, calculate the corresponding $x$-coordinate to locate the ($x, y, z$)-point on the shock; (3) calculate the shock angle at this point; (4) compare the shock angle with the sonic angle; (5) if the shock angle and the calculated angle differ by less than a specified (small) criterion, plot the ($x, y, z$)-point. This will produce a band of points in the task space that looks like a line if the criterion is small enough and if enough points are selected. Figure 14 is plotted with 300,000 points and consumed 18 min to plot on an HP Pavilion dv6 laptop computer. This technique is easily adaptable to plot variable contours and regions of specific values. Since the points in (1) are selected randomly, over the plotting surface, we call the resulting graph a scatterplot.

Appendix 9: Validation of theory and code

Four steps were taken to ensure the accuracy of the theoretical analysis and its numerical representation. The first is the many built-in checks, such as (30a, b) for the pressure gradient. The second step, which proved quite effective, is the dimensionality checking of the Sect. 2 equations. The next step is checking of the output for inconsistencies. As an example, it was noticed in early scatterplots that the Crocco curve, for a doubly curved shock, had a discontinuous slope at $z$ = 0. The error was tracked down and resulted in the changes listed in Appendix 1. The last step involved detailed checking of the Sect. 2 equation for the case:

$$ M_{1} = 3,p_{1} = 10^{5} ,\rho_{1} = 1;d = 3,e = 2,f = 1;y = 2,z = 1 $$

(96)