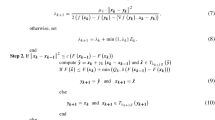Abstract
We study a novel inertial proximal-gradient method for composite optimization. The proposed method alternates between a variable metric proximal-gradient iteration with momentum and an Armijo-like linesearch based on the sufficient decrease of a suitable merit function. The linesearch procedure allows for a major flexibility on the choice of the algorithm parameters. We prove the convergence of the iterates sequence towards a stationary point of the problem, in a Kurdyka–Łojasiewicz framework. Numerical experiments on a variety of convex and nonconvex problems highlight the superiority of our proposal with respect to several standard methods, especially when the inertial parameter is selected by mimicking the Conjugate Gradient updating rule.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we consider a composite optimization problem with the following structure
where \(f_0:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is a continuously differentiable function and \(f_1:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{\infty \}\) is convex. This kind of problem is especially relevant in the framework of the variational approach to inverse problems, where a solution is obtained by minimizing a function which combines data fidelity and regularization terms.
Forward–backward (FB) methods are a class of optimization algorithms which fully exploit the structure of problem (1), namely the smoothness of \(f_0\) and the convexity of \(f_1\). They have reasonable theoretical convergence guarantees and, if implemented with some care, they exhibit good practical performances.
The general iteration of a FB method can be expressed in the following way
where \(\alpha _k\) is a positive steplength parameter, \(D_k\) is a symmetric positive definite matrix and \({\textrm{prox}}_{f_1}^D(\cdot )\) denotes the proximal operator associated to the function \(f_1\), in the metric induced by D.
Many state-of-the-art algorithms can be stated in the form (2) [1, 16, 21, 24,25,26,27,28, 49], each depending on some specific choices of the parameters \(\alpha _k,\lambda _k,D_k\) and the strategy for computing, possibly in an approximate way, the proximity operator. These methods have been extensively analyzed in convex and nonconvex frameworks and a wide numerical experience shows that they are a valid tool for solving large scale problems. In the last two decades, more variants of iteration (2) have been proposed, with the aim to overcome some known pitfalls of FB methods, as the so-called “hem stitching” effect. These FB variants introduce a kind of extrapolation, or inertial, step exploiting the two previous iterations and can be traced back to two main typologies: FISTA-like methods and Heavy-Ball ones.
FISTA-like methods are reminiscent of the seminal work [37] and can be stated as
where \(\beta _k\) is an extrapolation parameter. Method (3) has been analyzed for example in [4, 7, 10, 20, 23, 45] in the convex case. Other recent contributions on this class of methods and related developments can be found in [34, 54,55,56], where the analysis covers also the nonconvex case. The most remarkable property of method (3) is the convergence rate estimation \(f( { x}^{(k)})-f^* = o(1/k^2)\), which can be proved under suitable assumptions on the parameters \(\beta _k,\alpha _k, D_k\), when \(f_0\) is convex and has Lipschitz continuous gradient. In the same settings, the standard FB rate is 1/k and, in this sense, FISTA is optimal among all first order methods. On the other side, the implementation of (2) allows more flexibility in the choice of the parameters, which may lead to practical performances which are often comparable or even better than those of FISTA.
The second class of inertial methods, named Heavy-Ball, corresponds to the following scheme
The main idea behind iteration (4) dates back to Polyak [42] and, in the simple case when \(f_1=0\), it can be derived as a discretization of the ordinary differential equation
while the standard gradient method is related to
The connection between the above dynamical systems and the algorithms which can be obtained by discretization are investigated for example in [6, 36, 42]. Iteration (4) has also connections with the Conjugate Gradient method for quadratic unconstrained optimization and its extension to nonlinear smooth problems [32].
Heavy-Ball methods received considerable attention in recent years. In particular, the properties of iteration (4) under convexity assumptions are investigated in [5, 6, 31, 39], where the theoretical convergence rate is also provided. In the convex framework, the parameters \(\alpha _k\) and \(\beta _k\) are usually selected in order to guarantee that the optimal convergence rate estimate is achieved. From this point of view, the implementation of iteration (4) requires explicit knowledge of the minimum and maximum eigenvalues of \(\nabla ^2 f_0(x)\). This clearly implies that the method itself can be applied only to some specific class of problems and, in addition, it may result in a lack of effectiveness, e.g. when the minimum eigenvalue of the Hessian is small [6].
Other recent results can be found in [18, 35, 40, 41], where the analysis applies also to the nonconvex case, assuming that the Kurdyka–Łojasiewicz property holds. We also mention the Inertial Bregman proximal gradient methods proposed in [54, 56], which are closely related to the iteration (4). In these settings, the guidelines for selecting \(\alpha _k\), \(\beta _k\) could be different than in the convex case and adaptive rules based on a backtracking procedure have been also proposed [38, 40, 54].
Contribution. In this paper we propose the following generalization of the Heavy-Ball iteration (4)
and we analyze it in a nonconvex setting, providing also some insights on the related implementation issues.
The key feature of our proposed method is a line-search procedure to determine the steplength parameter \(\lambda _k\), in order to guarantee the sufficient decrease of a suitably defined merit function. The combination of a line-search procedure with an inertial step is, as far as we know, new. Thanks to the descent properties enforced by the line-search, we can prove the convergence of the iterates to a stationary point of problem (1), in the Kurdyka–Łojasiewicz (KL) framework.
Unlike most Heavy-Ball methods, the theoretical conditions employed to prove this result do not impose significant restrictions on the choice of the parameters \(\beta _k,\alpha _k, D_k\), which can be chosen freely within a compact set. This possibility allows to adopt acceleration strategies for improving the performances.
Indeed, as a second contribution, we also devise practical rules for selecting the algorithm parameters, by adapting some ideas proposed in the literature as acceleration strategies for the standard FB methods. In particular, for the stepsize parameter \(\alpha _k\) we propose an adaptation of the well known Barzilai–Borwein formulae [8], while for selecting the inertial parameter \(\beta _k\) we borrow the ideas behind the nonlinear Conjugate Gradient (CG) method.
Our approach encompasses also the possibility to employ an approximation of the proximal operator in (6a) and adopt a metric associated to the matrix \(D_k\) which may vary throughout the iterations.
The numerical experience described in the last section shows that these implementation choices make the algorithm competitive if compared to the most effective FB and FISTA algorithms, as well as with more standard implementations of the Heavy-Ball itself.
Related work.
Our method shares with the Heavy-Ball algorithms proposed in [38, 40] and in [54] the idea to combine an inertial step with a backtracking loop to compute some of its parameters. The key difference is that our approach consists in an actual line-search, i.e., the next iterate is found along the direction joining the current iterate and the (approximate) inertial proximal-gradient point \( {\tilde{y}}^{(k)}\) (6b). Moreover, unlike the above mentioned references, the line-search concerns only the steplength parameter \(\lambda _k\), allowing a totally different approach to the selection of the parameters \(\alpha _k,\beta _k,D_k\). On the other side, the iterates \( { x}^{(k)}\) produced by the rules (6), unlike the plain Heavy-Ball iteration (4), are not necessarily obtained as the evaluation of the proximity operator at some point. As a consequence of this, the convergence analysis of our proposed method can not be obtained as a special case of [38, 40, 54].
Alternatives to the Euclidean metric have been considered in [54, 56], where a Bregman distance is adopted. Here we adopt a scaled Euclidean metric, induced by the matrix \(D_k^{-1}\), which may vary at each iteration.
The convergence analysis of iteration (6) is performed by showing that it is a special instance of the abstract scheme presented in [18]. From this point of view, our approach shares similar convergence properties with the Heavy-Ball methods in [18, 38, 40]. More insights about the relations between our new algorithm and the existing ones are given in Sect. 3.
Moreover, our approach to the selection of the steplength \(\alpha _k\) is in the same line of [29, 30], where the authors shows that the effectiveness of line-search based FB methods of the form (2) can be significantly improved by devising clever steplength selection rules, in spite of lower theoretical rate estimates.
Paper organization. In Sect. 2 we state some basic definitions and results about subdifferential calculus in nonconvex settings and we define the KL framework. The proposed algorithm, named Phila, is described in Sect. 3, where the relations with existing algorithms are discussed. The theoretical convergence analysis is developed in Sect. 4, leading to the main result which is stated in Theorem 13. In Sect. 5 we describe and motivate the implementation choices concerning the algorithm parameters. In order to evaluate the effectiveness of these choices, we present the results of a numerical experience carried out on a variety of test problems, ranging from unconstrained quadratic to nonconvex, nonlinear problems where the proximity operator of \(f_1\) is not available in explicit form. The performances assessment is obtained comparing our approach to several state-of-the-art methods. Final remarks and perspectives are offered in Sect. 6.
2 Preliminaries
2.1 Notations
The notation \({\overline{{\mathbb {R}}}}\) denotes the extended real numbers set, i.e., \({\overline{{\mathbb {R}}}}= {\mathbb {R}}\cup \{-\infty ,+\infty \}\). Given two vectors \(x,y\in {\mathbb {R}}^n\), we denote by \(\langle x,y\rangle \) the scalar product on \({\mathbb {R}}^n\) and by \(\Vert x\Vert \) the Euclidean norm of x:
If \(x\in {\mathbb {R}}^n\) and D is a symmetric positive definite matrix, we denote by \(\Vert x\Vert _D\) the norm induced by D:
Given \(\mu >1\), we define the set \({{\mathcal {M}}}_{\mu }\) of all symmetric positive definite matrices with eigenvalues belonging to the interval \([\frac{1}{\mu }, \mu ]\):
If \(D\in {{\mathcal {M}}}_{\mu }\), then \(D^{-1}\in {{\mathcal {M}}}_{\mu }\). Moreover, for any \(D\in {{\mathcal {M}}}_{\mu }\), we also have
Given a function \(\phi :{\mathbb {R}}^n\rightarrow {\bar{{\mathbb {R}}}}\), the domain of \(\phi \) is denoted as \(\textrm{dom}(\phi ) = \{x\in {\mathbb {R}}^n:\phi (x)<+\infty \}\), and f is called proper if \(\textrm{dom}(\phi )\ne \emptyset \) and \(\phi (x)>-\infty \) for all \(x\in {\mathbb {R}}^n\). Given a proper, convex function \(\phi :{\mathbb {R}}^n\rightarrow {\overline{{\mathbb {R}}}}\), a symmetric positive definite matrix D and a point \(x\in {\mathbb {R}}^n\), the proximal operator of \(\phi \) at point x in the norm induced by D is defined as
2.2 Subdifferential calculus and KL functions
In this section, we draw the fundamental concept of subdifferential from the field of variational analysis. We refer the reader to well-known textbooks such as [47, 48] for more details.
We start with the definitions of Fréchet subdifferential and limiting-subdifferential.
Definition 1
[48, Definition 8.3] Let \(f:{\mathbb {R}}^n\rightarrow {\overline{{\mathbb {R}}}}\) and \(x\in \textrm{dom}(f)\). The Fréchet subdifferential of f at x is the set
The limiting-subdifferential (or simply subdifferential) of f at x is defined as
and \(\textrm{dom}(\partial f)=\{x\in \textrm{dom}(f):\partial f(x) \ne \emptyset \}\).
Definition 2
We say that a point \(x\in {\mathbb {R}}^n\) is stationary for \(f:{\mathbb {R}}^n\rightarrow {\overline{{\mathbb {R}}}}\) if \(x\in \textrm{dom}(f)\) and \(0\in \partial f(x)\).
Remark 3
Any (local) minimum point \(x\in {\mathbb {R}}^n\) of f is a stationary point, while the converse may not be true in general. If f is also convex, then x is a (local) minimum point if and only if x is a stationary point.
The following subdifferential calculus rule will be used later in the paper.
Lemma 4
[48, Exercise 8.8c] If \(f=f_0+f_1\) with \(f_1\) finite at x and \(f_0\) continuously differentiable on a neighbourhood of x, then
Definition 5
[57, p. 82] Let \(f:{\mathbb {R}}^n\rightarrow {\overline{{\mathbb {R}}}}\) be a proper, convex function. Given \(\epsilon \ge 0\) and \(x\in {\mathbb {R}}^n\), the \(\epsilon -\)subdifferential of f at x is the set
For our convergence analysis, we need to recall the definition of the so-called Kurdyka-Łojasiewicz inequality [13], an analytical property which has been extensively employed to ensure the convergence of iterative methods in the absence of convexity [3, 14, 18, 38].
Definition 6
[14, Definition 3] Let \(f:{\mathbb {R}}^n\rightarrow {\overline{{\mathbb {R}}}}\) be proper and lower semicontinuous. The function f satisfies the Kurdyka-Łojasiewicz (KL) inequality at the point \(x^*\in \textrm{dom}(\partial f)\) if there exist \(\nu >0\), a neighbourhood U of \(x^*\), and a continuous concave function \(\xi :[0,\nu )\rightarrow [0,+\infty ) \) such that \(\xi (0) = 0\), \(\xi \) is \(C^1\) on \((0,\nu )\), \(\xi '(s)>0\) for all \(s\in (0,\nu )\), and the following inequality holds
for all \(x\in U \cap \{y\in {\mathbb {R}}^n: \ f(x^*)< f(y) < f(x^*)+\nu \}\). If f satisfies the KL inequality for all \(x^*\in \textrm{dom}(\partial f)\), then f is called a KL function.
Remark 7
The KL inequality is trivially satisfied around nonstationary points [2, Remark 3.2], whereas it establishes a meaningful connection between the gradient norm and the function values of the objective function around stationary points. Several classes of functions arising in signal and image processing satisfy the KL inequality, including the indicator functions of semi-algebraic sets, real polynomials, \(p-\)norms and, more generally, semi-algebraic functions or real analytic functions (see [14] and references therein for more details).
3 The algorithm
In the following, we present Phila, a Proximal Heavy-ball Inexact Line-search Algorithm for solving problem (1). Our proposal is reported step by step in Algorithm 1.
Phila requires as inputs an initial guess \(x^{(0)}\in \textrm{dom}(f_1)\), the backtracking parameters \(\delta ,\sigma \in (0,1)\) and \(\gamma >0\), the constants \(0<\alpha _{min}\le \alpha _{max}\), \(\beta _{max}>0\), and \(\mu \ge 1\) related to the choice of the steplength, the inertial parameter, and the scaling matrix, respectively, and a tolerance parameter \(\tau \ge 0\) for the (possibly inexact) computation of the proximal-gradient point. Once the inputs are fixed, Phila starts an iterative process, where at each iteration k the iterate \( { x}^{(k+1)}\) is formed according to the following steps.
At Step 1, we select a steplength \(\alpha _k\in [\alpha _{min},\alpha _{max}]\), an inertial parameter \(\beta _{k}\in [0,\beta _{max}]\), and a symmetric positive definite scaling matrix \(D_k\in {\mathcal {M}}_\mu \). These three parameters contribute to the definition of the (possibly inexact) proximal-gradient point defined at the next step. No requirements are imposed on \(\alpha _k,\beta _k,D_k\), other than they must belong to compact subsets in their corresponding spaces.
At Step 2, we compute the point \( {\tilde{y}}^{(k)}\in {\mathbb {R}}^n\), which approximates or possibly coincides with the inertial proximal-gradient point \( {\hat{y}}^{(k)}= {\textrm{prox}}_{\alpha _k f_1}^{D_k}( { x}^{(k)}-\alpha _k D_k^{-1}\nabla f_0( { x}^{(k)})+\beta _k( { x}^{(k)}- { x}^{(k-1)}))\). To this aim, we define the function \(h^{(k)}(\,\cdot \,; { x}^{(k)}, { x}^{(k-1)}):{\mathbb {R}}^n\rightarrow {\bar{{\mathbb {R}}}}\) as follows
It is easy to see that the inertial proximal-gradient point \( {\hat{y}}^{(k)}\) is the unique minimum point of the strongly convex function \(h^{(k)}(\,\cdot ; { x}^{(k)}, { x}^{(k-1)})\), i.e.,
Then, we compute \( {\tilde{y}}^{(k)}\) by means of the following condition
If \(\tau = 0\), the above condition implies \( {\tilde{y}}^{(k)}= {\hat{y}}^{(k)}\), i.e., the inertial proximal-gradient point is computed exactly; otherwise, if \(\tau >0\), an approximation \( {\tilde{y}}^{(k)}\) of the exact point \( {\hat{y}}^{(k)}\) is computed. This condition has been employed for inexactly computing the proximal-gradient point in several first-order methods, see e.g. [12, 17, 18, 33]. For completeness, an explicit procedure for computing a point satisfying (10) is detailed in the Appendix. By observing that \({\hat{y}}^{(k)}\) is a minimizer of \(h^{(k)}(\cdot ;x^{(k)}, { x}^{(k-1)})\) and \(h^{(k)}(x^{(k)};x^{(k)}, { x}^{(k-1)})=0\), the above condition entails that
so that the inexactness condition can be conveniently rewritten as
with
In other words, the computation of \( {\tilde{y}}^{(k)}\) is based on a relaxation of the optimality condition (9), obtained by appropriately enlarging the subdifferential of the function \(h^{(k)}(\,\cdot ; { x}^{(k)}, { x}^{(k-1)})\) at the point \( {\tilde{y}}^{(k)}\). Even if inequality (10) and its equivalent version (11) are presented in an implicit way, there exists a well defined, explicit procedure to compute it [20, 50, 52]. For completeness, this aspect is detailed in Appendix A. We observe that the inexactness criterion based on the inclusion (11a) is employed also in [56], where the accuracy parameter \(\epsilon _k\) is chosen as a prefixed sequence instead of our adaptive rule (11b).
Once the quantity \(\Delta _k =h^{(k)}({\tilde{y}}^{(k)};x^{(k)}, { x}^{(k-1)})\) and the search direction \(d^{(k)}= {\tilde{y}}^{(k)}- { x}^{(k)}\) are assigned at Steps 3–4, an Armijo-like linesearch along the direction \(d^{(k)}\) is performed at Steps 5–6. Particularly, we compute the linesearch parameter as \(\lambda _k=\delta ^{i_k}\), where \(\delta \in (0,1)\) is the backtracking factor and \(i_k\) is the first non-negative integer such that the following Armijo-like condition holds:
Since \(\Delta _k\le 0\), we stop the backtracking procedure when the minimum between \(f( { x}^{(k)}+\delta ^{i_k}d^{(k)}) + \frac{\gamma }{2}\Vert \delta ^{i_k}d^{(k)}\Vert ^2\) and \(f( {\tilde{y}}^{(k)})+\frac{\gamma }{2} \Vert d^{(k)}\Vert ^2 \) is sufficiently smaller than the reference value \(f( { x}^{(k)}) + \frac{\gamma }{2}\Vert { x}^{(k)}- { x}^{(k-1)}\Vert ^2\). We remark that the minimum operation is not necessary from a theoretical viewpoint, as our convergence analysis still holds if we neglect the value \(f( {\tilde{y}}^{(k)})+\frac{\gamma }{2} \Vert d^{(k)}\Vert ^2\) from (12); rather, it should be seen as a way of saving unnecessary backtracking iterations. Note that we are enforcing a descent condition on the merit function \(\Phi (x,s) = f(x)+\frac{\gamma }{2}\Vert x-s\Vert ^2\), rather than on the original objective function f. This is motivated by the fact that \(d^{(k)}\) might not be a descent direction for the function f in general, so it might be unfeasible to impose the decrease of \(f( { x}^{(k)}+\lambda d^{(k)})\) for a sufficiently small \(\lambda >0\). On the other hand, it is still possible to ensure the decrease of the merit function \(\Phi \) (see Sect. 4 for more details).
Finally, Step 7 updates the next iterate as either \( { x}^{(k+1)}= { x}^{(k)}+ \lambda _k d^{(k)}\) or \( { x}^{(k+1)}= {\tilde{y}}^{(k)}\), depending on whether or not \(f( { x}^{(k)}+\lambda _kd^{(k)}) + \frac{\gamma }{2} \Vert \lambda _kd^{(k)}\Vert ^2\) is smaller than \(f( {\tilde{y}}^{(k)}) + \frac{\gamma }{2} \Vert d^{(k)}\Vert ^2\). Note that, as a consequence of Steps 5–7, the sequence generated by Phila satisfies the following inequalities
Remark 8
(Related work) The main novelty of Phila lies in the original combination between a proximal-gradient iteration with inertia and a linesearch along a prefixed direction. In particular, our line-search approach involves only the steplength parameter \(\lambda _k\), while the other parameters, \(\alpha _k\), \(D_k\), can be selected in a completely independent manner. This is in contrast with existing inertial proximal-gradient methods, where the parameters \(\alpha _k,\beta _k,D_k\) are usually prefixed, or selected through a backtracking procedure based on a local version of the Descent Lemma, see e.g. [9, 38,39,40, 43]. To the best of our knowledge, the inertial proximal-gradient method with backtracking which are more similar to ours are [18, Algorithm 3] and [55, Algorithm 1] (see also [54, Algorithm 2] for a generalization of it). All these methods employ the same merit function as Phila. However, in contrast to Phila, the algorithm in [18] introduces an auxiliary iterate \(s^{(k)}\), and computes the inexact proximal point as \( {\tilde{y}}^{(k)}\approx {\textrm{prox}}_{\alpha _k f_1}^{D_k}( { x}^{(k)}-\alpha _k D_{k}^{-1}\nabla f_0( { x}^{(k)})+\beta _k( { x}^{(k)}-s^{(k)}))\), where the term \(\beta _k( { x}^{(k)}-s^{(k)})\) may not coincide with the inertial force \(\beta _k( { x}^{(k)}- { x}^{(k-1)})\) that is typically employed in inertial proximal-gradient methods. Moreover, the backtracking procedure in [55, Algorithm 1] and [54, Algorithm 2] involves also the inertial parameter and, in addition, it is not performed along a line but along the path defined by the proximal-gradient operator. We also observe that the complexity of the backtracking procedure of these two algorithms might be more demanding, since each reduction step requires the evaluation of the proximity operator, while our approach needs it only once per outer iteration.
Our linesearch has two main advantages. On the one hand, it allows a relatively free selection of the parameters \(\alpha _k,\beta _k,D_k\), as the theoretical convergence relies on the linesearch parameter \(\lambda _k\) (see Sect. 4); on the other hand, it requires only one evaluation of the proximal operator per iteration k, as opposed to the standard backtracking loops based on the Descent Lemma that require a proximal evaluation at each backtracking step. Note also that the Armijo-like condition (12) is applied to the merit function \(\Phi (x,s)=f(x)+\frac{1}{2}\Vert x-s\Vert ^2\), rather than to the objective function f; again, this is contrast with the prior literature, where condition (12) is typically employed by setting \(\gamma = 0\) and neglecting the term \(f( {\tilde{y}}^{(k)}) + \frac{\gamma }{2}\Vert d^{(k)}\Vert ^2\) on the left-hand side of the inequality, see e.g. [17, 19, 51]. The merit function \(\Phi (x,s)\) was inspired by the works on the algorithm iPiano [38, 40], where the choice of the parameters \(\alpha _k,\beta _k,D_k\) (either prefixed or selected according to a local version of the Descent Lemma) guarantees the sufficient decrease of a similar merit function along the iterates. A backtracking loop based on the same merit function with a different acceptance rule and implementation is proposed also in [54, 55]. In these works, unlike our approach, the backtracking steps involve not only the steplength \(\alpha _k\), but also the other parameters defining the iteration rule.
4 Convergence analysis
In this section, we are interested in providing the convergence analysis for Algorithm 1. The analysis will be carried out under the following assumptions on the functions \(f_0,f_1\) appearing in problem (1).
-
[A1
] \(f_1:{\mathbb {R}}^n\rightarrow {\overline{{\mathbb {R}}}}\) is a proper, lower semicontinuous, convex function.
-
[A2
] \(f_0:{\mathbb {R}}^n\rightarrow {\mathbb {R}}\) is continuously differentiable on an open set \(\Omega _0\supset \overline{\textrm{dom}(f_1)}\).
-
[A3
] \(f_0\) has \(L-\)Lipschitz continuous gradient on \(\textrm{dom}(f_1)\), i.e., there exists \(L>0\) such that
$$\begin{aligned} \Vert \nabla f_0(x)-\nabla f_0(y)\Vert \le L\Vert x-y\Vert , \ \ \forall x,y\in \textrm{dom}(f_1). \end{aligned}$$ -
[A4
] f is bounded from below.
First, let us state some lemmas holding for the sequences \(\{ { x}^{(k)}\}_{k\in {\mathbb {N}}}\), \(\{ {\tilde{y}}^{(k)}\}_{k\in {\mathbb {N}}}\), and \(\{ {\hat{y}}^{(k)}\}_{k\in {\mathbb {N}}}\) associated to Algorithm 1, which can be seen as special cases of the results [18, Lemma 8-10].
Lemma 9
Suppose that Assumptions [A1]–[A2] hold true. Then, the following inequalities hold.
with \(\displaystyle \theta = \left( \sqrt{1+\frac{\tau }{2}}+\sqrt{\frac{\tau }{2}}\right) ^{-2}\le 1\).
Lemma 10
Suppose Assumptions [A1]–[A3] hold true. Then, there exists a subgradient \({\hat{v}}^{(k)}\in \partial f( {\hat{y}}^{(k)})\) such that
where the two constants p, q depend only on \(\alpha _{min},\alpha _{max},\beta _{max}\), \(\mu \), and the Lipschitz constant L.
Lemma 11
Suppose Assumptions [A1]–[A3] hold true. Then, there exist \(c,d,{\bar{c}},{\bar{d}} \in {\mathbb {R}}\) depending only on \(\alpha _{min}\), \(\alpha _{max}\), \(\beta _{max}\), \(\mu \), \(\tau \) such that
Next, we show that the linesearch procedure at Step 5 terminates in a finite number of steps, and that the linesearch parameter \(\lambda _k\) is bounded away from zero.
Lemma 12
Let \(\{x^{(k)}\}_{k\in {\mathbb {N}}}\) be the sequence generated by Algorithm 1 and suppose Assumptions [A1]–[A3] hold true.
-
(i)
The linesearch at Step 5 is well-defined.
-
(ii)
There exists \(\lambda _{min}>0\) depending only on \(\alpha _{min}\), \(\alpha _{max}\), \(\beta _{max}\), \(\mu \) and \(\tau \), such that the parameter \(\lambda _k\) computed at Step 6 satisfies
$$\begin{aligned} \lambda _k\ge \lambda _{min}, \ \ \forall \ k\ge 0. \end{aligned}$$(22)
Proof
Let \(\lambda \in (0,1)\). Then, we have
where the first inequality follows from the Descent Lemma and the convexity of \(f_1\), the second one from the inequality
and the third one from inequality (17). Setting \(\kappa = \dfrac{\mu \alpha _{max}}{\theta }\left( L+\gamma + \dfrac{\mu ^2\beta _{max}^2}{\gamma \alpha _{min}^2}\right) \), the last inequality writes as
Let us denote by m the smallest integer such that \(\delta ^{m}\ge (1 - \sigma )/\kappa \). Then, the parameter \(\lambda _k\) computed at Step 6 using inequality (12) satisfies \(\lambda _k\ge \delta ^m\). Therefore, (22) is satisfied with \(\lambda _{min} = \delta ^m\). \(\square \)
The main result about Phila is stated below.
Theorem 13
Let \(\{x^{(k)}\}_{k\in {\mathbb {N}}}\) be the sequence generated by Algorithm 1. Suppose that Assumptions [A1]– are satisfied and assume that the function \({\mathcal {F}}:{\mathbb {R}}^n\times {\mathbb {R}}\rightarrow {\overline{{\mathbb {R}}}}\) defined as
is a KL function. Moreover, assume that the sequence \(\{{ x}^{(k)}\}_{k\in {\mathbb {N}}}\) is bounded. Then, \(\{x^{(k)}\}_{k\in {\mathbb {N}}}\) converges to a stationary point of f.
The proof of Theorem 13 is given by showing that Phila can be cast in the framework of the abstract scheme in [18]. More precisely, we will prove Theorem 13 as a special case of [18, Theorem 5(iii)] which, for convenience, is restated below.
Theorem 14
Let \({{\mathcal {F}}}:{\mathbb {R}}^{n}\times {\mathbb {R}}^m\rightarrow {\overline{{\mathbb {R}}}}\) be a proper, lower semicontinuous KL function. Consider any sequence \(\{( { x}^{(k)},\rho ^{(k)})\}_{k\in {\mathbb {N}}}\subset {\mathbb {R}}^n\times {\mathbb {R}}^m\) and assume that there exist a proper, lower semicontinuous, bounded from below function \(\Phi :{\mathbb {R}}^n\times {\mathbb {R}}^q\rightarrow {\overline{{\mathbb {R}}}}\) and four sequences \(\{u^{(k)}\}_{{k\in {\mathbb {N}}}}\subset {\mathbb {R}}^n\), \(\{s^{(k)}\}_{{k\in {\mathbb {N}}}}\subset {\mathbb {R}}^q\), \(\{\rho ^{(k)}\}_{k\in {\mathbb {N}}}\subset {\mathbb {R}}^m\), \(\{d_k\}_{k\in {\mathbb {N}}}\subset {\mathbb {R}}_{\ge 0}\) such that the following relations are satisfied.
-
[H1
]There exists a positive real number a such that
$$\begin{aligned} \Phi ( { x}^{(k+1)},s^{(k+1)})+a d_k^2 \le \Phi ( { x}^{(k)},s^{(k)}), \quad \forall \ k\ge 0. \end{aligned}$$ -
[H2
] There exists a sequence of non-negative real numbers \(\{r_k\}_{k\in {\mathbb {N}}}\) with \(\lim \limits _{k\rightarrow \infty } r_k = 0\) such that
$$\begin{aligned} \Phi ( { x}^{(k+1)},s^{(k+1)})\le {{\mathcal {F}}}(u^{(k)},\rho ^{(k)})\le \Phi ( { x}^{(k)},s^{(k)})+r_k, \quad \forall \ k\ge 0. \end{aligned}$$ -
[H3
] There exists a subgradient \(w^{(k)}\in \partial {{\mathcal {F}}}(u^{(k)},\rho ^{(k)})\) such that
$$\begin{aligned} \Vert w^{(k)}\Vert \le b \sum _{i\in I}\theta _id_{k+1-i}, \quad \forall \ k\ge 0, \end{aligned}$$where b is a positive real number, \({{\mathcal {I}}}\subset {\mathbb {Z}}\) is a non-empty, finite index set and \(\theta _i\ge 0\), \(i\in {{\mathcal {I}}}\) with \(\sum _{i\in {{\mathcal {I}}}} \theta _i=1\) (\(d_j=0\) for \(j\le 0\)).
-
[H4
] If \(\{(x^{(k_j)},\rho ^{(k_j)})\}_{j\in {\mathbb {N}}}\) is a subsequence of \(\{( { x}^{(k)},\rho ^{(k)})\}_{k\in {\mathbb {N}}}\) converging to some \( (x^*,\rho ^*)\in {\mathbb {R}}^n\times {\mathbb {R}}^m\), then we have
$$\begin{aligned} \lim _{j\rightarrow \infty }\Vert u^{(k_j)}-x^{(k_j)}\Vert =0, \quad \lim _{j\rightarrow \infty } {{\mathcal {F}}}(u^{(k_j)},\rho ^{(k_j)}) = {{\mathcal {F}}}(x^*,\rho ^*). \end{aligned}$$ -
[H5
] There exists a positive real number \(p>0\) such that
$$\begin{aligned} \Vert { x}^{(k+1)}- { x}^{(k)}\Vert \le p d_{k}, \quad \forall \ k\ge 0. \end{aligned}$$
Moreover, assume that \(\{( { x}^{(k)},\rho ^{(k)})\}_{k\in {\mathbb {N}}}\) is bounded and \(\{\rho ^{(k)}\}_{k\in {\mathbb {N}}}\) converges. Then, the sequence \(\{( { x}^{(k)},\rho ^{(k)})\}_{k\in {\mathbb {N}}}\) converges to a stationary point of \({\mathcal {F}}\).
In the remaining of this section, we will show that the sequence generated by Phila, with a proper setting of the surrogate function \(\Phi \) and all the auxiliary sequences, satisfies the assumptions of the previous theorem.
Proposition 15
Let \(\{ { x}^{(k)}\}_{k\in {\mathbb {N}}}\) be the sequence generated by Phila and define the function \(\Phi :{\mathbb {R}}^n\times {\mathbb {R}}^n\rightarrow {\overline{{\mathbb {R}}}}\) as
If Assumptions [A1]–[A3] hold true, then for any k we have
If, in addition, Assumption is satisfied, we also have
Proof
Inequality (25) follows from (13) and from Lemma 12. Since from Assumption f is bounded from below, \(\Phi \) is bounded from below as well. Therefore, (25) implies \(-\sum _{k=0}^{\infty }\Delta _k<\infty \), which, in turn, yields \(\lim _{k\rightarrow \infty }\Delta _k=0\). Recalling (17), this implies (26). \(\square \)
Proposition 16
Let \(\{ { x}^{(k)}\}_{{k\in {\mathbb {N}}}}\) be the sequence generated by Phila and suppose that Assumptions [A1]– hold true. Let \({{\mathcal {F}}}:{\mathbb {R}}^n\times {\mathbb {R}}\rightarrow {\overline{{\mathbb {R}}}}\) be defined as in (23). Then, there exist \(\{\rho _k\}_{k\in {\mathbb {N}}},\{r_k\}_{k\in {\mathbb {N}}}\subset {\mathbb {R}}\), with \(\lim _{k\rightarrow \infty }r_k=0\), such that
where \(\Phi \) and \( {\hat{y}}^{(k)}\) are defined in (24) and (8), respectively.
Proof
From Step 8, we have
where the last inequality follows from (20) and (17). Setting
we obtain \( \Phi ( { x}^{(k+1)}, { x}^{(k)}) \le {{\mathcal {F}}}( {\hat{y}}^{(k)},\rho _k)\), which represents the left-most inequality in (27). On the other hand, from inequality (21) we obtain
Setting \(r_k = \rho _k^2/2 -{\bar{c}} h^{(k)}( {\tilde{y}}^{(k)}; { x}^{(k)}, { x}^{(k-1)}) +({\bar{d}}-\frac{\gamma }{2})\Vert { x}^{(k)}- { x}^{(k-1)}\Vert ^2 \), we can write
which is the rightmost inequality in (27). Finally, from (26) we have that \(\lim _{k\rightarrow \infty }r_k=0\). \(\square \)
Proposition 17
Let \(\{ { x}^{(k)}\}_{{k\in {\mathbb {N}}}}\) be the sequence generated by Phila and suppose that Assumptions [A1]– hold true. Let \(\rho _k\) be defined as in (28). Then, for any k, there exists a subgradient \(w^{(k)}\in \partial {{\mathcal {F}}}({black {\hat{y}}^{(k)}},\rho _k)\) such that
for some positive constant \(\theta \).
Proof
From (19) we know that for any k there exists a subgradient \({\hat{v}}^{(k)}\in \partial f(\hat{y}^{(k)})\) such that
where p, q are positive constants which do not depend on k. Setting
since \({{\mathcal {F}}}\) is separable, we have
By the triangular inequality we also obtain
Let us analyze the two terms at the right-hand side of the inequality above. From (30) we have
where the first inequality follows from the fact that \( { x}^{(k)}- { x}^{(k-1)}= \lambda _{k-1}({\tilde{y}}^{(k-1)} - { x}^{(k-1)})\), where \(\lambda _{k-1}\le 1\), the second one is a consequence of (17), and the third one follows from the definition of \(\Delta _k\). Setting \({\bar{q}} = q\cdot \max \left\{ 1, \sqrt{{2\mu \alpha _{max}}/{\theta }}\right\} \), the last inequality above yields
Reasoning as above, from (28) we obtain
where \({\bar{p}} = \sqrt{2}\max \left\{ c+ \gamma \mu \alpha _{max}/{\theta }, 2\mu d\alpha _{max} / \theta \right\} ^{\frac{1}{2}}\) and the last inequality follows from the concavity of \(\sqrt{\cdot }\). Therefore, by combining the last inequality above with (32) and (31), it follows that (29) holds with \(\eta = {\bar{q}} + {\bar{p}}\). \(\square \)
Proposition 18
Let \(\{ { x}^{(k)}\}_{k\in {\mathbb {N}}}\) be the sequence generated by Phila and define \(\rho _k\) as in (28). Assume that \(({ x}^*,\rho ^*)\) is a limit point of \(\{( { x}^{(k)},\rho _k)\}_{k\in N}\) and that \(\{(x^{(k_j)}, \rho _{k_j})\}_{j\in {\mathbb {N}}}\) is a subsequence converging to it. Then, we have
Proof
Inequalities (15) and (26) implies that
From (26) and (29), there exists a sequence \(\{w^{(k)}\}_{k\in {\mathbb {N}}}\) with \(w^{(k)}\in \partial {{\mathcal {F}}}( {\hat{y}}^{(k)},\rho _k)\) such that \(\lim _{k\rightarrow \infty }\Vert w^{(k)}\Vert = 0\). Since \({{\mathcal {F}}}\) has a separable structure, this implies that there exists a sequence \(\{v^{(k)}\}_{k\in {\mathbb {N}}}\) with \({\hat{v}}^{(k)}\in \partial f({black {\hat{y}}^{(k)}})\) such that \(w^{(k)}= ({\hat{v}}^{(k)},\rho _k)\) with \(\lim _{k\rightarrow \infty } \Vert {\hat{v}}^{(k)}\Vert = \lim _{k\rightarrow \infty }\rho _k=0\). Moreover, thanks to Lemma 4, we can write \({\hat{v}}^{(k)}= \nabla f_0( {\hat{y}}^{(k)}) + z^{(k)}\), with \(z^{(k)}\in \partial f_1({black {\hat{y}}^{(k)}})\). Hence, by continuity of \(\nabla f_0\), the assumption on the subsequence \(\{( { x}^{(k_j)},\rho _{k_j})\}_{j\in {\mathbb {N}}}\), and (33), the following implication holds
By applying the subgradient inequality to \(z^{(k)}\), and adding the quantity \(\frac{1}{2} \rho _{k_j}^2\) to both sides of the same inequality, we get
where the last equality is obtained by adding and subtracting \(f_0({\hat{y}}^{(k_j)})\) to the right-hand-side. Taking limits on both sides we obtain
which, rearranging terms, gives \(\lim _{j\rightarrow \infty }{{\mathcal {F}}}({\hat{y}}^{(k_j)},\rho _{k_j}) \le {{\mathcal {F}}}(x^*,\rho ^*)\). On the other side, by assumption, \({\mathcal {F}}\) is lower semicontinuous, therefore \(\lim _{j\rightarrow \infty }{{\mathcal {F}}}({\hat{y}}^{(k_j)},\rho _{k_j}) \ge {{\mathcal {F}}}(x^*,\rho ^*)\), which completes the proof. \(\square \)
Proof of Theorem 13
By Propositions 15, 16, and 17, we know that conditions [H1], [H2], and [H3] hold for Phila, with the merit functions defined in (23) and (24) with the following settings:
Moreover, the inequalities in [H2] are satisfied with \(\rho ^{(k)}\) and \(r_k\) set as in the proof of Proposition 16, while the inequality [H3] holds with \({{\mathcal {I}}} = \{1,2\}\), \(\theta _i = 1/2\), for \(i=1,2\), \(b = 2\eta \).
Moreover, Proposition 18 leads to conclude that [H4] holds.
Finally, condition [H5] holds as a consequence of (17) ans (14), since \(d_k= \sqrt{-\Delta _k}\). Then, Theorem 14 applies and guarantees that the sequence \(\{(x^{(k)},\rho _k)\}_{k\in {\mathbb {N}}}\) converges to a stationary point \((x^*,\rho ^*)\) of \({\mathcal {F}}\). Note that, since \({\mathcal {F}}\) is the sum of separable functions, its subdifferential can be written as \(\partial {\mathcal {F}}(x,\rho )=\partial f(x)\times \{\rho \}\). Then, \((x^*,\rho ^*)\) is stationary for \({\mathcal {F}}\) if and only if \(\rho ^*=0\) and \(0\in \partial f(x^*)\). Hence \(x^*\) is a stationary point for f and \(\{x^{(k)}\}_{k\in {\mathbb {N}}}\) converges to it. \(\square \)
5 Numerical experiments
In this section, we show the flexibility and effectiveness of our proposed algorithm on a series of optimization problems of varying difficulty, ranging from uncostrained quadratic minimization to nonconvex composite minimization (see Table 1 for a summary of the test problems presented in the following and related features). For each problem, we equip Algorithm 1 with different selection rules for the parameters \(\alpha _k\) and \(\beta _k\), and compare its numerical performance to other well-known methods available in the literature. Overall, we will see that Algorithm 1 performs best when its parameters are either partially or completely related to the nonlinear Conjugate Gradient iteration. The numerical experience is carried out on a PC equipped with 11th Gen Intel(R) Core(TM) i7 processor (16GB RAM) in Matlab (R2021b) environment.
5.1 Quadratic toy problems
5.1.1 Unconstrained quadratic problem
As a first test, we address the unconstrained minimization of a quadratic function, i.e.,
where \(n = 100\), and \(A\in {\mathbb {R}}^{n\times n}\) is a symmetric positive definite matrix with eigenvalues \(\mu _{min}=\mu _{1}<\mu _2<\ldots <\mu _n=\mu _{max}\), respectively. The test problem is generated following the same procedure described in [44]: first, we compute an orthogonal matrix \(Q\in {\mathbb {R}}^{n\times n}\) via the QR factorization of a random \(n\times n\) matrix; then, we choose the eigenvalues \(\mu _1<\mu _2<\ldots <\mu _n\) as n random values in the interval \([\mu _{min},\mu _{max}]\), and we define \(\Lambda \in {\mathbb {R}}^{n\times n}\) as the diagonal matrix where \(\Lambda _{ii} = \mu _i\), \(i=1,\ldots ,n\); finally, we define \(A = Q^T\Lambda Q\). The solution of the test problem is then defined as a random vector \(x^*\in {\mathbb {R}}^n\) and the linear term is set as \(b = Ax^*\).
In the numerical experiments we consider different implementations of our method. In order to explain the rationale behind the setting of the algorithm parameters, we first restate the iteration of Algorithm 1 applied to (34). As there is no need to compute an (inexact) proximal point, Phila reduces in this case to the two-step iterative scheme
where
The above relation shows that the Phila iteration has the same form of the preconditioned CG updating rule, with an iteration dependent preconditioner. Assume now that at the iteration k the steplength parameter \(\alpha _k\) and the scaling matrix \(D_k\) have been selected. Borrowing the ideas behind the Spectral Conjugate Gradient Method (see [11, Section 1]), we consider the following choice for the extrapolation parameter
where \(w^{(k)}= g^{(k)}-g^{(k-1)}\). The above formula with \(D_k=I\) has been proposed in [11] and is a generalization of well known strategies in the framework of the nonlinear Conjugate Gradient method (see [32] for a survey). For example, if \({s^{(k)}}^TD_k^{-1}g^{(k)}={g^{(k)}}^TD_{k-1}^{-1}g^{(k-1)}=0\) for all k, it gives the following generalization of the Fletcher–Reeves formula
Assuming that a fixed upper bound \(\beta _{max}\) is given as an input parameter of Phila, in all our experiments we set the inertial parameter as follows
where the thresholding operation is needed to comply with the theoretical prescriptions.
As for the other parameters, in the experiments we set \(D_k=I\), \(\gamma = 10^{-4}\), while we consider different choices for the steplength \(\alpha _k\), which are detailed below.
-
Phila-L: We set \(\alpha _k\) as a fixed value related to the Lipschitz constant of \(\nabla f_0\):
$$\begin{aligned} \alpha _k = \frac{1.99}{\mu _{max}}. \end{aligned}$$(38) -
Phila-BB1: Here \(\alpha _k\) is computed by means of the first BB rule, namely,
$$\begin{aligned} \alpha _k^{BB1} =\frac{{s^{(k)}}^Ts^{(k)}}{{s^{(k)}}^Tw^{(k)}}. \end{aligned}$$(39)The formula for computing \(\alpha _k\) is then the following one:
$$\begin{aligned} \alpha _k = \max \left\{ \min \left\{ \alpha _k^{BB1},\alpha _{min}\right\} \right\} . \end{aligned}$$ -
Phila-BB2: We also consider the variant corresponding to the second BB rule:
$$\begin{aligned} \alpha _k^{BB2} =\frac{{s^{(k)}}^Tw^{(k)}}{{w^{(k)}}^Tw^{(k)}}. \end{aligned}$$(40)We observed that the above quotient provided a good estimation of the inverse of the Lipschitz constant of the gradient \(1/\mu _{max}\). Then, in analogy with (38), we employ twice its value to define \(\alpha _k\)
$$\begin{aligned} \alpha _k = \max \left\{ \min \left\{ 2\alpha _k^{BB2},\alpha _{min}\right\} \right\} . \end{aligned}$$ -
Phila-CG: In this implementation we aim to closely reproduce the CG iteration. In particular, for \(k\ge 1\), we compute \(\beta ^{FR}_k\) as in (36) with \(D_k=D_{k-1} = I\) and we define \(p^{(k)}= -g^{(k)}+ \frac{\beta _k^{FR}}{\lambda _{k-1}\alpha _{k-1}}( { x}^{(k)}- { x}^{(k-1)}) \). Then, we define
$$\begin{aligned} \alpha _k^{CG} = -\frac{{p^{(k)}}^Tg^{(k)}}{{p^{(k)}}^TA p^{(k)}}, \end{aligned}$$(41)which is the optimal steplength along the direction \(p^{(k)}\), i.e., \(f( { x}^{(k)}+\alpha _k^{CG}p^{(k)}) = \min _{\alpha >0} f( { x}^{(k)}+\alpha p^{(k)})\). Finally, we set
$$\begin{aligned} \alpha _k = \max \{\min \{\alpha _k^{CG},\alpha _{max}\},\alpha _{min}\} \end{aligned}$$(42)Thus, the CG iterations are exactly reproduced when, for all k, \(\lambda _k=1\), \(\alpha _k^{CG}\in [\alpha _{min},\alpha _{max}]\) and \(\beta _k^{SGM}\in [0,\beta _{max}]\).
We observe that all the above implementations, except Phila-CG which is specifically tailored for quadratic problems, can be applied also to smooth nonlinear problems.
As a benchmark, we compare our proposed algorithm with the following state-of-the-art methods.
-
SD: this is the classical Steepest Descent, based on the iteration (2) where \(D_k=I\), \(\lambda _k=1\), and \(\alpha _k\) is computed by the exact minimization rule
$$\begin{aligned} \alpha _k = \mathop {{\text {argmin}}}\limits _{\alpha > 0} f_0( { x}^{(k)}-\alpha \nabla f_0( { x}^{(k)})) = \frac{\Vert \nabla f_0( { x}^{(k)})\Vert ^2}{\nabla f_0( { x}^{(k)})^TA\nabla f_0( { x}^{(k)})}. \end{aligned}$$ -
ISTA: with this acronym, we refer to iteration (2) with \(D_k=I\), \(\lambda _k=1\) and \(\alpha _k\equiv \alpha \) given by the constant value \(\alpha = 1.99/{\mu _{max}}\), where \(\mu _{max}\) represents the Lipschitz constant of \(\nabla f_0\) [10, 26, 28, p. 191].
-
FISTA: this is the well-known accelerated FB method (3), with the parameter setting described in [10, p.193].
-
Heavy-Ball: this consists in iteration (4) with the constant choices for the parameters proposed in [42], which are defined as follows
$$\begin{aligned} \beta _k \equiv \beta = \left( \frac{\sqrt{\kappa }-1}{\sqrt{\kappa }+1}\right) ^2, \ \ \alpha _k \equiv \alpha = \frac{(1+\sqrt{\beta })^2}{\mu _{max}}, \end{aligned}$$where \(\kappa = \mu _{max}/\mu _{min}\).
-
ADR denotes the inertial algorithm corresponding to formula (4.19) in [6].
-
VMILA: the Variable Metric Inexact Linesearch Algorithm is a FB scheme (2) first proposed in [16] where \(\alpha _k\in [\alpha _{min},\alpha _{max}]\) and \(D_k\in {\mathcal {M}}_\mu \) can be freely selected, whereas \(\lambda _k\in (0,1]\) is computed by Armijo-like backtracking. For our tests, the scaling matrix \(D_k\) is equal to the identity matrix, whereas the steplength \(\alpha _k\) is computed by alternating the two standard Barzilai–Borwein (BB) rules [8].
In Fig. 1 (left column), we show the relative decrease of the objective function with respect to the iteration number for three different values of the conditioning number of the matrix A. All implementations of Phila outperform ISTA and FISTA, while being comparable or superior to VMILA, Heavy-Ball and ADR. We note that the acceleration of Phila-L with respect to ISTA is only due to the presence of the inertial term, whereas the improvement with respect to all the inertial methods—FISTA, Heavy-Ball and ADR—can be attributed to the automated CG-like choice of the Phila inertial parameter in place of the prefixed FISTA, Heavy-Ball and ADR rules. Furthermore, the implementation Phila-CG achieves the same convergence speed of the Conjugate Gradient method, which provides the best performance among all the competitors.
Quadratic toy problems. Left column: unconstrained case with different condition numbers. Minimum eigenvalue \(\mu _{min} = 1\) and \(\mu _{max} = 10^2\) (top), \(10^3\) (middle), \(10^4\) (bottom). Right column: non-negatively constrained case with \( \mu _{min} = 1\), \(\mu _{max} = 10^3 \) and different number of active constraints at the solution \(n_a= 1\) (top), 20 (middle), 48 (bottom)
5.1.2 Non-negatively constrained quadratic problem
In this section we consider a quadratic problem constrained onto the non-negative orthant,
where \(n = 100\), \(A\in {\mathbb {R}}^{n\times n}\) is a symmetric positive definite matrix with minimum and maximum eigenvalues denoted by \(\mu _{min}\) and \(\mu _{max}\), respectively. This is a convex composite optimization problem of the form (1), where the nonsmooth term corresponds to \(f_1(x) = \iota _{{\ge 0}}(x)\). The proximal operator associated to \(f_1\) is the orthogonal projection onto the constraint set \(P_{\ge 0}(x) = \max \{x,0\}\).
We aim to evaluate the effectiveness of Phila in comparison with some existing approaches, with respect not only to the conditioning of the Hessian A, but also to the number of constraints which are active at the solution.
To this end, the test problems are defined following [44]: first, a symmetric positive definite matrix with uniformly spaced eigenvalues in \([\mu _{min},\mu _{max}]\) is computed as described in the previous section; then, we randomly define a set of indexes \({{\mathcal {I}}}_a \subset \{1,\ldots ,n \}\) of the constraints which will be active at the solution. We compute the vector \(w^*\) of the Lagrange multipliers such that \(w^*_i = 1\) if \(i\in {{\mathcal {I}}}_a\) and \(w_i^* = 0\) if \(i\notin {{\mathcal {I}}}_a\). The solution \(x^*\) is computed in a similar way as a random vector such that \(x^*_i\in (0,1)\) if \(i\notin {{\mathcal {I}}}_a \) and \(x^*_i = 0\) for \(i\in {{\mathcal {I}}}_a\). The linear term is finally computed as \(b = Ax^*-w^*\).
Also in this case we consider different implementations of Phila, which can be considered as a generalization of those described in the previous sections. Indeed, the optimality conditions of problem (43) write as
At each iteration k we compute the following set of indexes
and we define the residual vector \(r^{(k)}\in {\mathbb {R}}^n\) as
Clearly we have \(r^{(k)}\in \partial f( { x}^{(k)})\) and, in particular, \(\Vert r^{(k)}\Vert = \textrm{dist}(\partial f( { x}^{(k)}),0)\). According to the founding in [29, 30], we then propose to generalize the implementation of Phila described in the previous section with the subgradient (45) in place of the gradient of f.
-
Phila-L, Phila-BB1 and Phila-BB2 are the generalization of the corresponding algorithms described in the previous section, where \(\beta _k\) is still defined as in (37) but with
$$\begin{aligned} w^{(k)}= r^{(k)}- r^{(k-1)}, \ \ g^{(k)}= r^{(k)}\end{aligned}$$(46)in (35)–(36). Moreover, the steplength parameter for Phila-L is defined as in (38), while for Phila-BB1 and Phila-BB2 we revisit the BB rules (39), (40) by computing them with \(w^{(k)}\) as in (46).
-
Phila-CG: we compute \(\beta ^{FR}_k\) as in (36) with \(D_k=D_{k-1} = I\) and \(r^{(k)}\) in place of \(g^{(k)}\). Then, we define \(p^{(k)}= -r^{(k)}+ \frac{\beta _k^{FR}}{\lambda _{k-1}\alpha _{k-1}}( { x}^{(k)}- { x}^{(k-1)}) \) and \(\alpha _k^{CG}\) as in (41), again with \(r^{(k)}\) instead of \(g^{(k)}\). Finally, \(\alpha _k\) is defined as in (42) while the inertial parameter is
$$\begin{aligned} \beta _k= & {} \left\{ \begin{array}{ll}\min \left\{ \beta _{max},\frac{\alpha _k^{CG}\beta _k^{CG}}{\alpha _{k-1}^{CG}\lambda _{k-1}}\right\} &{} \text{ if } {{\mathcal {B}}}_{k-1}= {{\mathcal {B}}}_k\\ 0 &{} \text{ otherwise } \end{array} \right. . \end{aligned}$$
Also in this case, the implementations Phila-L, Phila-BB1 and Phila-BB2 can be directly applied to non-negatively constrained nonlinear smooth problems. The above variants of Phila are then compared with the following methods.
-
ISTA, FISTA, VMILA, Heavy-Ball and ADR with the same parameters described in the previous section. Since in this case \(f_1\ne 0\) is convex but not strongly convex, the Heavy-Ball method actually corresponds to the algorithm named iPiasco proposed in [39].
-
BCCG: we include in the comparison the Bound Constrained Conjugate Gradient method [53], which is an adaptation of the CG iteration to box constrained problems where the search direction is based on the residual vector. The convergence properties of this method are not well established, but we include it in our comparison since we observed good performances.
The results of the comparison are depicted in Fig. 1 (right column). Also in this case, Phila-BB2 achieves the overall best performances.
5.2 Image restoration problems
5.2.1 Image denoising with edge preserving Total Variation regularization
We consider the variational model for image denoising
where \(g\in {\mathbb {R}}^n\) is the noisy data, \(\rho \) is a positive parameter and the discrete, smoothed version of the Total Variation function is defined as
where \(A_i\in {\mathbb {R}}^{2\times n}\) represents the discrete image gradient operator at the i-th pixel, while \(\epsilon >0\) is a smoothing parameter.
The noisy data g has been generated by choosing a good quality image of size \(481\times 321\) (hence \(n = 154401\)), with pixels in the range [0, 255], and adding Gaussian noise with zero mean and standard deviation 25. The model parameters \(\rho \) and \(\epsilon \) have been empirically selected in order to obtain a good restoration: the values employed in the experiments are \(\rho =0.0531\) and \(\epsilon =1\). The ground truth and the noisy image are shown in Fig. 2a, b.
Problem (47) is a strongly convex, nonlinear, smooth constrained optimization problem, having a unique solution \(x^*\), where the nonsmooth term consists in \(f_1(x) = \iota _{\ge 0}(x)\).
In the numerical experiments we consider the implementations Phila-L, Phila-BB1 and Phila-BB2 exactly as described in Sect. 5.1.2. In particular, for Phila-L, we set \(\mu _{max} = 1+\rho /\epsilon \) in (38), which is motivated by the approximation of the Lipschitz constant of \(\nabla TV_\epsilon (x)\) with \( 1/\epsilon \) (see [22, Section 3.3]).
The other parameters are set as \(\gamma =10^{-4}\), \(\alpha _{min}= 10^{-5}\), \(\alpha _{max} = 10^{5}\) and \(\beta _{max} = 1.5\).
As a benchmark, we consider again ISTA, FISTA and VMILA. In particular, since the Lipschitz constant is available only as an estimation, we equip both ISTA and FISTA with a backtracking procedure to possibly adjust the steplength. Since the problem is strongly convex, we can still include in the comparison also the Heavy-Ball method and ADR. In addition, we consider also the inertial methods ABPG-LS [54], PGels [55], nmAPG-LS [34] and v-iBPG [56].
Moreover, for Phila and VMILA, we consider also a variable metric implementation, obtained by defining a diagonal scaling matrix \(D_k\) as prescribed in [58]. These implementations are denoted with the suffix ’s’ added to the algorithm name.
As a stopping criterion we adopt the average relative difference of the objective function value between two successive iterates over the last 10 steps
Since the exact solution \(x^*\) of problem (47) is not available, it has been approximated by running all the considered methods for 200 iterations or until condition (48) is satisfied with \(tol = 10^{-15}\) and then selecting the point corresponding to the lower function value. We then compare the speed of each method in approaching the optimal value.
The results of the numerical comparison are reported in Fig. 3. In the left panel, we plot the relative distance of the objective function from the optimal value with respect to the iteration number over the first 150 iterations, while the right panel plots the same quantity with respect to the computational time in seconds. All algorithms are stopped when a maximum number of 1000 iterations or 4.5 s of computing time are exceeded, As a further reference, in Table 2 we report for each method the number of iterations performed to satisfy the stopping criterion (48) with \(tol=10^{-8}\) (i.e., for a medium-high accuracy solution), the total number of function evaluations, the relative Euclidean distance between the restored and the ground truth image, the PSNR, and the corresponding computational time. Actually, iPiasco and ADR do not require the computation of the objective function, but only of its gradient. However, since the objective function evaluation can be obtained as a byproduct of the gradient, we believe that the plots in Fig. 3 and Table 2 give a clear indication about the effectiveness of the algorithms. In Fig. 2c we report the output image obtained from Phila-BB2.
Our proposed line-search based methods outperform the benchmark methods with fixed parameters (Heavy-Ball, ADR, v-iBPG) as well as those employing a backtracking procedure (ABPG_LS, PGels, nmAPG_LS). In terms of execution time, the most performing algorithm is Phila-BB2. Indeed, the presence of the scaling matrix seems to slightly reduce the number of iterations needed to achieve a given accuracy as shown in the left panel of Fig. 3, but in some cases this results in an increased number of the backtracking steps. This explains why the scaled methods generally perform better of their nonscaled version in terms of number of iterations (see left panel of Fig. 2), whereas the computational time can be larger. This can also be explained by the fact that the computation of the scaling matrix adds some complexity. However, we believe that a more reliable assessment of the algorithms based on the execution time would require an highly optimized implementation of each code, which is out of the scope of the present paper.
5.2.2 Image deblurring with bimodal nonconvex regularization
In this section we consider a simulated test problem inspired by the Helsinki Deblur Challenge (HDC) 2021. The goal is to recover an image of some text string from a noisy blurred acquisition. The target image has been generated by resizing and binarizing a randomly selected ground truth image provided by the HDC dataset (the ones acquired by Camera 1). The resulting image has size \(183\times 295\) and its pixels are zero (black) or one (white). The binary image has been convolved with a disk psf of radius 7 to simulate out-of-focus blur. Finally, Gaussian noise with zero mean and standard deviation 0.01 has been added. The restored image is obtained by solving the following optimization problem
where g is the noisy blurred data and H represents the blurring matrix corresponding to the disc psf. In addition to the TV functional, here the objective function includes also a bimodal nonconvex regularization term, whose minima are attained when each pixel value is either zero or one. This kind of regularization has been considered in [15] in the HDC framework. The ground truth image and the simulated data are reported in Fig. 4a, b, respectively. Problem (49) is a nonconvex, constrained, smooth optimization problem. Due to nonconvexity, it may have multiple stationary points.
The implementation of Phila is based on a generalization of the settings described in Sect. 5.1.2, taking into account the presence of box constraints instead of non-negativity only. In particular, for each iteration k we define the following set of indexes
and we define the residual at the iteration k as in (45) and the vectors \(w^{(k)},g^{(k)}\) as in (46). Also in this case we have \(r^{(k)}\in \partial f( { x}^{(k)})\) and \(\Vert r^{(k)}\Vert = \textrm{dist}(\partial f( { x}^{(k)}),0)\). Based on these definitions, we consider the implementations Phila-L, Phila-BB1 and Phila-BB2 as described in Sect. 5.1.2. We also set \(D_k= I\) and \(\gamma = 10^{-4}\). For the fixed stepsize version Phila-L, we adopt \(\mu _{max}=1+\rho /\epsilon + 2\chi \) as an estimate of the Lipschitz constant of \(\nabla f_0(x)\), and we define \(\alpha _k\) as in (38).
The other parameters are set exactly as in the previous section (\(\gamma =10^{-4}\), \(\alpha _{min}= 10^{-5}\), \(\alpha _{max} = 10^{5}\) and \(\beta _{max} = 1.5\)). The benchmark algorithms compared to Phila are ISTA, FISTA, VMILA, ABPG_LS, PGels, nmAPG_LS and v-iBPG as in the previous experiment. We include also FISTA, even if its convergence properties are proved only for convex problems, since in this case we observed a good behaviour anyway. In particular, for ISTA and FISTA we use the same estimate employed in Phila-L for \(\mu _{max}\) to determine the steplengh parameter; also in this case, we include a backtracking procedure as a safeguard for convergence. As a further benchmark, we include also the Heavy-Ball method iPiano [40], with constant parameters.
The results are reported in Fig. 5, where the plots show the decrease of the objective function with respect to the iteration number (left panel) and the computational time (right panel). Table 3 reports a comparison of the algorithms when the stopping condition (48) with \(tol = 10^{-8}\) is satisfied. From left to right, the columns of the table report the number of iterations, the corresponding total number of function evaluations, the Euclidean relative error, the PSNR between the restored and the clean image and the total computational time.
We can observe that all the Phila version perform well with respect to the reference algorithms: in particular, Phila-BB2 exhibits the overall best performance.
5.2.3 Image deblurring with sparsity inducing regularization on the wavelet transform
In this section we consider a different approach to the deblurring problem, leading to a convex composite \(\ell _2\)-\(\ell _1\) minimization problem. Given a blurred noisy image \(g\in {\mathbb {R}}^n\), a restoration is obtained by solving the following optimization problem
where \(H\in {\mathbb {R}}^{n\times n}\) is the blurring operator and \(R\in {\mathbb {R}}^{n\times n}\) represents an orthogonal wavelet transform. Here, the unknown \(x\in {\mathbb {R}}^n\) corresponds to the wavelet coefficients and the \(\ell _1\) regularization terms aims to induce sparsity on it. Once computed a solution \(x^*\) of the above problem, the restored image is obtained with formula \(R^T x^*\). The test problem is defined following [10, Example 5.1]: as a ground truth we take the \(256\times 256\) cameraman image and we blur it with a Gaussian psf of size \(9\times 9\) and standard deviation 4. We assume reflective boundary conditions, therefore the matrix-vector products involving the blurring operator H can be easily implemented via the dct2 transform. Finally, we add to the blurred image zero mean Gaussian noise with standard deviation \(10^{-3}\). The ground truth and the noisy blurred image are shown in Fig. 6a, b. As for the synthesis operator R we adopt a three stage Haar wavelet transform. Since R is orthogonal, the eigenvalues of the Hessian matrix can be computed using the dct2 transform. The regularization parameter \(\rho \) is set to \(2\cdot 10^{-5}\).
Problem (50) is convex, therefore the optimal value is unique.
We compare the same algorithms considered in the previous section. In particular, for the implementation of Phila we first observe that in this case we have \(f_1(x) = \rho \Vert x\Vert _1\) and

Then, using the same rationale behind the strategies proposed for non-negatively and box constrained problems, at each iteration we define the following set of indexes
and we define \(r^{(k)}\) as
so that \(r^{(k)}\in \partial f( { x}^{(k)})\) and \(\Vert r^{(k)}\Vert = \textrm{dist}(\partial f( { x}^{(k)}),0)\). Using this definition of \(r^{(k)}\) and with \(w^{(k)},g^{(k)}\) as in (46), we compute the steplength and inertial parameters as in (39), (40) and (35), leading to the corresponding implementations of Phila. Since R is orthogonal and thanks to the special structure of H, the maximum eigenvalue \(\mu _{max}\) of the Hessian employed in Phila-L, can be computed via the dct2 transform. The other parameters are set as in the previous experiments (\(\alpha _{min}=10^{-5}\), \(\alpha _{max}=10^{5}\), \(\beta _{max}=1.5\) and \(D_k=I\)).
The comparison still includes ISTA, FISTA, Heavy Ball, ADR, VMILA, ABPG_LS, PGels, nmAPG_LS and v-iBPG. In particular, ISTA and FISTA are implemented using the exact value of the Lipschitz constant \(\mu _{max}\).
The results are reported in Fig. 7, while the restoration obtained from the Phila-BB2 solution is shown in Fig. 6c. To evaluate the performances, we first obtain a numerical approximation of the optimal value \(f^*\) by running 15,000 iterations of Phila-BB2. Then, we run all methods for a maximum of 4000 iterations with a time limit of 200 s and we plot the function values with respect to the iteration number (left panel of Fig. 7) and the computational time (right panel). In Table 4 we report the results of all algorithms stopped when condition (48) with \(tol=10^{-6}\) is satisfied. In the columns of the table we list the same parameters as in Table 2 and 3 with, at the sixth column, the additional information about the number of zero components of the computed solution. Actually, FISTA, ISTA, Heavy-Ball and ADR do not require the function evaluation; however, as we noticed before, the objective function can be obtained as a byproduct of the gradient, which all methods need. Therefore, the performance assessment can be still obtained by comparing the total number of function evaluations of the backtracking methods—Phila and VMILA—with the number of iterations of the methods employing fixed stepsize—ISTA, FISTA, Heavy-Ball and ADR.
We can observe that the fastest decrease of the objective function is achieved by Phila-BB2, which also provides the sparsest solution. Also from the point of view of the effectiveness, Phila-BB2 requires very few backtracking reductions, leading to the overall best performance.
5.2.4 Image deblurring in presence of signal dependent Gaussian noise
As a last image restoration example, we consider a deblurring problem where the data \(g\in {\mathbb {R}}^n\) are affected by signal dependent Gaussian noise. In this case, the likelihood principle leads to the following fit-to-data term
where \(H\in {\mathbb {R}}^{n\times n}\) models the blurring phenomenon and \(a_i,c_i > 0\) are prefixed parameters. As a regularization term we consider the nonsmooth TV functional, given by formula (48) with \(\epsilon = 0\). This is a case where the explicit formula for the proximity operator is not available and it has to be approximated with the dual procedure described in the Appendix and detailed in Algorithm 2. Non-negativity constraints are also included in the model, therefore the nonsmooth part of the objective function reads as
We observe that \(f_0\) is nonconvex and \(\nabla f_0\) is Lipschitz continuous on \(\textrm{dom}(f_1)\), but the constant is not easy to estimate. The test problem, consisting in the ground truth and noisy blurred image shown in Fig. 8a, b, has been downloaded from [46]. Moreover, the data discrepancy parameters are \(a_i=c_i=1\) for all \(i=1,\ldots ,n\), H corresponds to a convolution with a \(7\times 7\) Gaussian kernel and the regularization parameter is \(\rho = 0.03\).
The numerical comparison includes ISTA, VMILA, iPiano (in the implementation described in [18]), the variable metric forward-backward algorithm (VMFB) proposed in [25], whose Matlab code can be downloaded from [46] and the inexact version of v-iBPG [56]. All these methods, as well as Phila, need an approximation of the proximity operator. For ISTA, VMILA, iPiano and Phila we adopt the same approach, i.e., Algorithm 2 with \(a=2.1\) and the adaptive stopping criterion (10) with \(\tau =10^{6}\) (for more details concerning this point, see Sect. A.1). The inexactness criterion in v-iBPG is very similar and it can be implemented using the same approach described above but with a different stopping criterion. In particular, at the iteration k, the inner iterations are stopped when the primal-dual gap is below the prefixed tolerance \(\nu _k = 100/(1+k^{1.1})\), fulfilling the theoretical prescriptions detailed in [56]. As for VMFB, in the code [46] the proximal gradient point is still approximated with inner dual iterations, until the relative difference of two successive iterates and corresponding dual function values are below to a fixed tolerance. Then, evaluation of the effectiveness of the considered algorithms can be measured in terms of the number of function/gradient evaluations and of the number of inner iterations required to achieve an approximate solution with similar accuracy.
In the first phase of our numerical experience, we also considered the scaled versions of VMILA and Phila based on the variable metric employed in VMFB: however, since there was no improvement in the convergence behaviour, we do not report the corresponding results. For Phila we adopt the fixed stepsize \(\alpha _k=50\), which was empirically determined. The other parameters of Phila are set exactly as in the other image restoration experiments (\(\gamma =10^{-4}\), \(\alpha _{min}= 10^{-5}\), \(\alpha _{max} = 10^{5}\) and \(\beta _{max} = 1.5\)).
The results of the comparison are shown in Fig. 9. In this case, even if the problem is nonconvex, all methods seem to converge to the same value. Therefore, for a better visual comparison we first computed an approximation of the optimal value \(f^*\) by running 20,000 iterations of VMFB, then we evaluate the relative distance from \(f^*\) at each iteration of all methods and we plot this quantity with respect to the iteration number (left panel) and the computational time (right panel). Table 5 collects some information about the effectiveness of each algorithm. The first three columns report the number of iterations, function evaluations and inner iterations needed to fulfill condition (48) with \(tol=10^{-8}\). In the last column we report a kind of optimality measure in terms of the quantity \(h_k\), which is defined as as \(h^{(k)}( {\tilde{y}}^{(k)}; { x}^{(k)}, { x}^{(k)})\) for the non inertial methods ISTA, VMILA and VMFB, while \(h_k = h^{(k)}( {\tilde{y}}^{(k)}; { x}^{(k)}, { x}^{(k-1)})\) for the three implementations of Phila and iPiano. Then, for all methods \(h_k\) is a quantity which must converge to zero, so that the smaller is \(h_k\), the closer is the algorithm to its limit. Moreover, for the inexact methods ISTA, VMILA and Phila, \(h_k\) controls the accuracy level in evaluating the proximity operator, which becomes more demanding, in terms of inner iterations, for small values of \(h_k\).
From Fig. 9 and Table 5 we can observe that condition (48) with the same tolerance stops different algorithms at a different accuracy level. In particular, the solutions provided by Phila are more accurate with respect to both the closeness to the target value \(f^*\) and the optimality measure \(h_k\). This also explains why the number of inner iterations is larger. Again, the overall best performances are obtained by Phila-BB2. The restored image provided by Phila-BB2 is shown in Fig. 8c.
6 Conclusions and future work
In this paper we proposed a new inertial proximal gradient algorithm whose convergence is guaranteed by the descent properties enforced by a suitable line-search procedure. This results in a flexible scheme where, unlike previously proposed Heavy-Ball methods, the parameters characterizing the iteration can be selected almost freely. This freedom can be exploited by adapting acceleration techniques which already demonstrated their effectiveness when combined with non inertial forward–backward methods. In particular, we adopt a variant of the Barzilai–Borwein formulae for the stepsize selection, while the inertial parameter is computed by mimicking the nonlinear Conjugate Gradient rules. The results of the numerical experience show that these practical rules make the proposed method more efficient than existing Heavy-Ball methods and competitive also with accelerated forward–backward methods, especially when seeking for a medium-high accuracy solution. Future research will concern more insights on the parameter selection from a spectral point of view.
Data availability statement
The test image watercastle in the experiments described in Sect. 5.2.1 is from the Berkley Segmentation Dataset https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/bsds/; the image used in the deblurring experiment in Sect. 5.2.2 is from the dataset released for the Helsinki Deblur Challenge 2021 https://www.fips.fi/HDCdata.php#anchor1; the cameraman image shown in Sect. 5.2.3 is included in the Matlab libraries; the jetplane one used in Sect. 5.2.4 can be downloaded from [46].
References
Abbas, B., Attouch, H.: Dynamical systems and forward-backward algorithms associated with the sum of a convex subdifferential and a monotone cocoercive operator. Optimization 64(10), 2223–2252 (2015)
Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 35(2), 438–457 (2010)
Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward-backward splitting, and regularized Gauss-Seidel methods. Math. Program. 137(1–2), 91–129 (2013)
Attouch, H., Peypouquet, J.: The rate of convergence of Nesterov’s accelerated forward-backward method is actually faster than \(1/k^2\). SIAM J. Optim. 26(3), 1824–1834 (2016)
Attouch, H., Peypouquet, J., Redont, P.: A dynamical approach to an inertial forward-backward algorithm for convex minimization. SIAM J. Optim. 24(1), 232–256 (2014)
Aujol, J.-F., Dossal, Ch., Rondepierre, A.: Convergence rates of the Heavy Ball method for quasi-strongly convex optimization. SIAM J. Optim. 32(3), 1817–1842 (2022)
Aujol, J.-F., Dossal, Ch., Rondepierre, A.: FISTA is an automatic geometrically optimized algorithm for strongly convex functions. Math. Program. 34(3), 307–327 (2023)
Barzilai, J., Borwein, J.M.: Two-point step size gradient methods. IMA J. Numer. Anal. 8(1), 141–148 (1988)
Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18(11), 2419–2434 (2009)
Beck, A., Teboulle, M.: A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2(1), 183–202 (2009)
Birgin, E.G., Martinez, J.M.: A spectral conjugate gradient method for unconstrained optimization. Appl. Math. Optim. 43, 117–128 (2001)
Birgin, E.G., Martinez, J.M., Raydan, M.: Inexact spectral projected gradient methods on convex sets. IMA J. Numer. Anal. 23(4), 539–559 (2003)
Bolte, J., Danilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17(4), 1205–1223 (2007)
Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146(1–2), 459–494 (2014)
Bonettini, S., Franchini, G., Pezzi, D., Prato, M.: Explainable bilevel optimization: An application to the Helsinki deblur challenge. Inverse Probl. Imaging 17, 925–950 (2023)
Bonettini, S., Loris, I., Porta, F., Prato, M.: Variable metric inexact line-search based methods for nonsmooth optimization. SIAM J. Optim. 26(2), 891–921 (2016)
Bonettini, S., Loris, I., Porta, F., Prato, M., Rebegoldi, S.: On the convergence of a linesearch based proximal-gradient method for nonconvex optimization. Inverse Probl. 33(5), 055005 (2017)
Bonettini, S., Ochs, P., Prato, M., Rebegoldi, S.: An abstract convergence framework with application to inertial inexact forward-backward methods. Comput. Optim. Appl. 84, 319–362 (2023)
Bonettini, S., Prato, M., Rebegoldi, S.: New convergence results for the inexact variable metric forward-backward method. Appl. Math. Comput. 392, 125719 (2021)
Bonettini, S., Rebegoldi, S., Ruggiero, V.: Inertial variable metric techniques for the inexact forward-backward algorithm. SIAM J. Sci. Comput. 40(5), A3180–A3210 (2018)
Chambolle, A.: An algorithm for Total Variation minimization and applications. J. Math. Imaging Vis. 20(1–2), 89–97 (2004)
Chambolle, A., Caselles, V., Cremers, D., Novaga, M., Pock, T.: An Introduction to Total Variation for Image Analysis. In: Fornasier, M. (ed.) Theoretical Foundations and Numerical Methods for Sparse Recovery, pp. 263–340. De Gruyter, Berlin, New York (2010)
Chambolle, A., Dossal, Ch.: On the convergence of the iterates of the “Fast Iterative Shrinkage/Thresholding Algorithm’’. J. Optim. Theory Appl. 166(3), 968–982 (2015)
Chouzenoux, E., Pesquet, J.-C.: A stochastic majorize-minimize subspace algorithm for online penalized least squares estimation. IEEE Trans. Signal Process. 65(18), 4770–4783 (2017)
Chouzenoux, E., Pesquet, J.-C., Repetti, A.: Variable metric forward-backward algorithm for minimizing the sum of a differentiable function and a convex function. J. Optim. Theory Appl. 162(1), 107–132 (2014)
Combettes, P.L., Pesquet, J.-C.: Proximal splitting methods in signal processing. In: Bauschke, H.H., Burachik, R.S., Combettes, P.L., Elser, V., Luke, D.R., Wolkowicz, H. (eds.) Fixed-Point Algorithms for Inverse Problems in Science and Engineering. Springer Optimization and Its Applications, pp. 185–212. Springer, New York, NY (2011)
Combettes, P.L., Vũ, B.C.: Variable metric forward-backward splitting with applications to monotone inclusions in duality. Optimization 63(9), 1289–1318 (2014)
Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward-backward splitting. Multiscale Model. Simul. 4(4), 1168–1200 (2005)
Crisci, S., Porta, F., Ruggiero, V., Zanni, L.: Hybrid limited memory gradient projection methods for box-constrained optimization problems. Comput. Optim. Appl. 84, 151–189 (2023)
Crisci, S., Rebegoldi, S., Toraldo, G., Viola, M.: Barzilai–Borwein-like rules in proximal gradient schemes for \(\ell _1\) regularized problems. Optim. Method Soft., in press. https://doi.org/10.1080/10556788.2023.2285489
Ghadimi, E., Feyzmahdavian, H. R., Johansson, M.: Global convergence of the Heavy-ball method for convex optimization. In: 2015 European Control Conference (ECC), pp. 310–315 (2015)
Hager, W.W., Zhang, H.: A survey of nonlinear conjugate gradient methods. Pac. J. Optim. 2(1), 35–58 (2006)
Lee, C.-P., Wright, S.J.: Inexact successive quadratic approximation for regularized optimization. Comput. Optim. Appl. 72(3), 641–674 (2019)
Li, H., Lin, Z.: Accelerated proximal gradient methods for nonconvex programming. In: Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 28. Curran Associates Inc. (2015)
Liang, J., Fadili, J., Peyré, G.: A multi-step inertial forward-backward splitting method for non-convex optimization. In: Lee, D., Sugiyama, M., Luxburg, U., Guyon, I., Garnett, R. (eds.) Advances in Neural Information Processing Systems, vol. 29. Curran Associates Inc. (2016)
Luo, H., Chen, L.: From differential equation solvers to accelerated first-order methods for convex optimization. Math. Program. 195(1–2), 735–781 (2022)
Nesterov, Y.: Smooth minimization of non-smooth functions. Math. Program. 103(1), 127–152 (2005)
Ochs, P.: Unifying abstract inexact convergence theorems and block coordinate variable metric iPiano. SIAM J. Optim. 29(1), 541–570 (2019)
Ochs, P., Brox, T., Pock, T.: iPiasco: inertial proximal algorithm for strongly convex optimization. J. Math. Imaging Vis. 53, 171–181 (2015)
Ochs, P., Chen, Y., Brox, T., Pock, T.: iPiano: inertial proximal algorithm for non-convex optimization. SIAM J. Imaging Sci. 7(2), 1388–1419 (2014)
Pock, T., Sabach, S.: Inertial proximal alternating linearized minimization (iPALM) for nonconvex and nonsmooth problems. SIAM J. Imaging Sci. 9(4), 1756–1787 (2016)
Polyak, B.: Introduction to Optimization. Optimization Software - Inc., Publication Division, New York (1987)
Polyak, B.T.: Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 4, 1–17 (1964)
Porta, F., Prato, M., Zanni, L.: A new steplength selection for scaled gradient methods with application to image deblurring. J. Sci. Comput. 65, 895–919 (2015)
Rebegoldi, S., Calatroni, L.: Scaled, inexact and adaptive generalized FISTA for strongly convex optimization. SIAM J. Optim. 32(3), 2428–2459 (2022)
Repetti, A., Chouzenoux, E.: RestoVMFB Lab: Matlab Toolbox for image restoration with the variable metric forward-backward algorithm. http://www-syscom.univ-mlv.fr/~chouzeno/Logiciel.html (2013)
Rockafellar, R.T.: Convex Analysis. Princeton University Press, Princeton, NJ (1970)
Rockafellar, R.T., Wets, R.J.-B., Wets, M.: Variational Analysis, Grundlehren der Mathematischen Wissenschaften, vol. 317. Springer, Berlin (1998)
Salzo, S.: The variable metric forward-backward splitting algorithm under mild differentiability assumptions. SIAM J. Optim. 27(4), 2153–2181 (2017)
Salzo, S., Villa, S.: Inexact and accelerated proximal point algorithms. J. Convex Anal. 19(4), 1167–1192 (2012)
Tseng, P., Yun, S.: A coordinate gradient descent method for nonsmooth separable minimization. Math. Program. 117(1–2), 387–423 (2009)
Villa, S., Salzo, S., Baldassarre, L., Verri, A.: Accelerated and inexact forward–backward algorithms. SIAM J. Optim. 23(3), 1607–1633 (2013)
Vollebregt, E.A.H.: The bound-constrained conjugate gradient method for non-negative matrices. J. Optim. Theory Appl. 162, 931–953 (2014)
Wu, Z., Li, C., Li, M., Lim, A.: Inertial proximal gradient methods with Bregman regularization for a class of nonconvex optimization problems. J. Glob. Optim. 79, 617–644 (2021)
Yang, L.: Proximal gradient method with extrapolation and line search for a class of nonconvex and nonsmooth problems. arXiv:1711.06831 (2021)
Yang, L., Toh, K.-C.: An inexact Bregman proximal gradient method and its inertial variants. arXiv:2109.05690 (2022)
Zalinescu, A.: Convex Analysis in General Vector Spaces. World Scientific Publishing, Singapore (2002)
Zanella, R., Boccacci, P., Zanni, L., Bertero, M.: Efficient gradient projection methods for edge-preserving removal of Poisson noise. Inverse Probl. 25(4), 045010 (2009)
Acknowledgements
The authors are all members of the INdAM research group GNCS, which is kindly acknowledged.
Funding
Open access funding provided by Università degli Studi di Modena e Reggio Emilia within the CRUI-CARE Agreement. The authors are partially supported by the PRIN projects 2022ANC8HL, 20225STXSB, and 2022B32J5C, under the National Recovery and Resilience Plan (NRRP) funded by the European Union – NextGenerationEU.
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design, and the theoretical content of the paper. Code implementation, data collection and analysis were performed by SB. The first draft of the manuscript was written by SB and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Conflict of interest
All authors certify that they have no affiliations with or involvement in any organization or entity with any financial interest or non-financial interest in the subject matter or materials discussed in this manuscript. The authors have no competing interests to declare that are relevant to the content of this article.
Ethics approval
The authors declare that research ethics approval was not required for this study.
Informed consent
The authors declare that informed consents were not required for this study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Computation of the inexact proximal point
Computation of the inexact proximal point
In this section we explain how to compute a point \( {\tilde{y}}^{(k)}\) such that condition (10) is satisfied, when the convex term in the objective function has the following form
where \(\phi _i:{\mathbb {R}}^{n_i}\rightarrow {{\mathbb {R}}}\cup \{+\infty \}\), \(\psi : {\mathbb {R}}^n\rightarrow {\mathbb {R}}\cup \{+\infty \}\) are lower semicontinuous convex functions and \(A_i\in {\mathbb {R}}^{n_i\times n}\). Denoting by \(\phi _i^*\) the Fenchel conjugate of \(\phi _i\) (see (51)) and the block matrix \(A = (A_1^T\ A_2^T\ \cdots \ A_p^T)^T\in {\mathbb {R}}^{m\times n}\), with \(m = n_1+\cdots +n_q\), using the same arguments in [16, 20] we can define the dual function of \(h^{(k)}(\cdot \; { x}^{(k)}, { x}^{(k-1)})\) as
where \(w\in {\mathbb {R}}^{m}\) is the dual variable partitioned as \(w = (w_1^T,\ldots ,w_p^T)^T\), with \(w_i\in {\mathbb {R}}^{n_i}\), and
By definition of the Fenchel dual, we have
for any \(y\in {\mathbb {R}}^n\) and for any \(w\in {\mathbb {R}}^m\) and the equality holds if and only if y is the minimizer of \(h^{(k)}\) (i.e., \(y= {\hat{y}}^{(k)}\)) and w is a maximum point of \({{\mathcal {Q}}}^{(k)}\). More in general, the above inequality holds for \(y= {\hat{y}}^{(k)}\) and for any \(w\in {\mathbb {R}}^m\). Therefore, if (y, w) is a primal dual pair satisfying
then y is an inexact inertial proximal gradient point in the sense of (10). The existence of such a pair is stated in the following proposition, which also indicates a way to practically compute it.
Proposition 19
Suppose that \(f_1\) is defined as in (51), \(f_1\) is continuous in its domain and \(\textrm{dom}(f_1) = \textrm{dom}(\psi )\). Let \(\{w^{(k,\ell )}\}_{\ell \in {\mathbb {N}}}\subset {\mathbb {R}}^m\) a sequence converging to a maximum point of the dual function \({{\mathcal {Q}}}^{(k)}\) such that \(\lim _{\ell \rightarrow \infty } {{\mathcal {Q}}}(w^{(k,\ell )}) = \max _{w\in {\mathbb {R}}^m} {{\mathcal {Q}}}^{(k)}(w)\). For any \(\ell \), define the corresponding primal point as
Then,
and, therefore, inequality
holds for all sufficiently large \(\ell \), for any given \(\tau >0\).
The proof of the previous proposition can be found in [20, Proposition 4.2]. In summary, an inexact inertial proximal gradient point can be computed by approximately solving the dual problem
which is a convex composite optimization problem where the smooth part is the function \(\Phi ^{(k)}(w)\), whose gradient is given by \(\nabla \Phi ^{(k)}(w) = A{\textrm{prox}}_{\alpha \psi }^{D_k}(z^{(k)}-\alpha _kD_k^{-1}A^Tw)\). Moreover, an estimation of the Lipschitz constant of \(\nabla \Phi ^{(k)}\) is \(L_{\Phi ^{(k)}}=\alpha _k\Vert A\Vert ^2\Vert D_k^{-1}\Vert \).
Therefore, the dual sequence \(w^{(k,\ell )}\) can be obtained by applying FISTA to the dual problem, setting the algorithm parameters as prescribed in [23] to guarantee the convergence. For completeness, the FISTA dual algorithm for computing the inexact inertial proximal point is detailed in Algorithm 2.
1.1 Inexact proximity operator evaluation for the test problem
In the test problem described in Sect. 5.2.4, the nonsmooth term can be written in the form (51) with \(q=n\), \(\phi _i = \rho \Vert \cdot \Vert _2\), \(A_i\in {\mathbb {R}}^{2\times n}\) representing the discrete gradient operator at pixel i, for \(i=1,\ldots ,n\), while \(\psi = \iota _{\ge 0}\). In these settings, the dual functions \(\phi _i^*\), \(i=1,\ldots ,n\) are all equal to the indicator function of the set \(B = \{w\in {\mathbb {R}}^2:\Vert w\Vert \le \rho \}\). Hence, \({\textrm{prox}}_{\phi _i^*}\) is the orthogonal projection onto B, which can be computed in closed form. Therefore, Algorithm 2 can be easily implemented in this case.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bonettini, S., Prato, M. & Rebegoldi, S. A new proximal heavy ball inexact line-search algorithm. Comput Optim Appl 88, 525–565 (2024). https://doi.org/10.1007/s10589-024-00565-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10589-024-00565-9