Skip to main content
SpringerLink
Log in

Variable Metric Forward–Backward Algorithm for Minimizing the Sum of a Differentiable Function and a Convex Function

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

We consider the minimization of a function G defined on \({ \mathbb{R} } ^{N}\), which is the sum of a (not necessarily convex) differentiable function and a (not necessarily differentiable) convex function. Moreover, we assume that G satisfies the Kurdyka–Łojasiewicz property. Such a problem can be solved with the Forward–Backward algorithm. However, the latter algorithm may suffer from slow convergence. We propose an acceleration strategy based on the use of variable metrics and of the Majorize–Minimize principle. We give conditions under which the sequence generated by the resulting Variable Metric Forward–Backward algorithm converges to a critical point of G. Numerical results illustrate the performance of the proposed algorithm in an image reconstruction application.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Notes

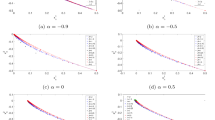
  1. We consider right derivatives when u=0.

References

  1. Chen, G.H.G., Rockafellar, R.T.: Convergence rates in forward–backward splitting. SIAM J. Optim. 7, 421–444 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  2. Tseng, P.: A modified forward–backward splitting method for maximal monotone mappings. SIAM J. Control Optim. 38(2), 431–446 (1998)

    Article  Google Scholar 

  3. Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. 116, 5–16 (2008)

    Article  MathSciNet  Google Scholar 

  4. Attouch, H., Bolte, J., Svaiter, B.F.: Convergence of descent methods for semi-algebraic and tame problems: proximal algorithms, forward–backward splitting, and regularized Gauss–Seidel methods. Math. Program. 137, 91–129 (2011)

    Article  MathSciNet  Google Scholar 

  5. Łojasiewicz, S.: Une propriété topologique des sous-ensembles analytiques réels, pp. 87–89. Editions du centre National de la Recherche Scientifique (1963)

  6. Beck, A., Teboulle, M.: Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems. IEEE Trans. Image Process. 18(11), 2419–2434 (2009)

    Article  MathSciNet  Google Scholar 

  7. Bioucas-Dias, J.M., Figueiredo, M.A.: A new TwIST: two-step iterative shrinkage/thresholding algorithms for image restoration. IEEE Trans. Image Process. 16, 2992–3004 (2007)

    Article  MathSciNet  Google Scholar 

  8. Zibulevsky, M., Elad, M.: ℓ 2–ℓ 1 optimization in signal and image processing. IEEE Signal Process. Mag. 27(3), 76–88 (2010)

    Article  MathSciNet  Google Scholar 

  9. Kowalski, M.: Proximal algorithm meets a conjugate descent. Tech. Rep. (2010). http://hal.archives-ouvertes.fr/docs/00/50/57/33/PDF/proxconj.pdf

  10. Nesterov, Y.: Gradient methods for minimizing composite objective function (2007). http://www.optimization-online.org/DB_HTML/2007/09/1784.html

  11. Bonnans, J.F., Gilbert, J.C., Lemaréchal, C., Sagastizábal, C.A.: A family of variable metric proximal methods. Math. Program. 68, 15–47 (1995)

    MATH  Google Scholar 

  12. Burke, J.V., Qian, M.: A variable metric proximal point algorithm for monotone operators. SIAM J. Control Optim. 37, 353–375 (1999)

    Article  MATH  MathSciNet  Google Scholar 

  13. Parente, L.A., Lotito, P.A., Solodov, M.V.: A class of inexact variable metric proximal point algorithms. SIAM J. Optim. 19, 240–260 (2008)

    Article  MathSciNet  Google Scholar 

  14. Lotito, P.A., Parente, L.A., Solodov, M.V.: A class of variable metric decomposition methods for monotone variational inclusions. J. Convex Anal. 16, 857–880 (2009)

    MATH  MathSciNet  Google Scholar 

  15. Combettes, P.L., Vũ, B.C.: Variable metric forward–backward splitting with applications to monotone inclusions in duality. Optimization (2013, to appear). doi:10.1080/02331934.2012.733883. arXiv:1206.6791 [math.OC]

  16. Becker, S., Fadili, J.: A quasi-Newton proximal splitting method. In: Bartlett, P., Pereira, F., Burges, C., Bottou, L., Weinberger, K. (eds.) Advances in Neural Information Processing Systems (NIPS), vol. 25, pp. 2618–2626 (2012)

    Google Scholar 

  17. Lee, J.D., Sun, Y., Saunders, M.A.: Proximal Newton-type methods for convex optimization. In: Bartlett, P., Pereira, F., Burges, C., Bottou, L., Weinberger, K. (eds.) Advances in Neural Information Processing Systems (NIPS), vol. 25, pp. 827–835 (2012)

    Google Scholar 

  18. Tran-Dinh, Q., Kyrillidis, A., Cevher, V.: Composite self-concordant minimization. Tech. Rep. (2013). http://arxiv.org/pdf/1308.2867v1.pdf

  19. Hunter, D.R., Lange, K.: A tutorial on MM algorithms. Am. Stat. 58(1), 30–37 (2004)

    Article  MathSciNet  Google Scholar 

  20. Hiriart-Urruty, J.B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms. Springer, New York (1993)

    Google Scholar 

  21. Combettes, P.L., Vũ, B.C.: Variable metric quasi-Fejér monotonicity. Nonlinear Anal. 78, 17–31 (2013)

    Article  MATH  MathSciNet  Google Scholar 

  22. Moreau, J.J.: Proximité et dualité dans un espace Hilbertien. Bull. Soc. Math. Fr. 93, 273–299 (1965)

    MATH  MathSciNet  Google Scholar 

  23. Combettes, P.L., Wajs, V.R.: Signal recovery by proximal forward–backward splitting. Multiscale Model. Simul. 4(4), 1168–1200 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  24. Combettes, P.L., Pesquet, J.C.: Proximal thresholding algorithm for minimization over orthonormal bases. SIAM J. Optim. 18(4), 1351–1376 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  25. Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17, 1205–1223 (2006)

    Article  MathSciNet  Google Scholar 

  26. Bolte, J., Daniilidis, A., Lewis, A., Shiota, M.: Clarke subgradients of stratifiable functions. SIAM J. Optim. 18(2), 556–572 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  27. Kurdyka, K., Parusinski, A.: w f -stratification of subanalytic functions and the Łojasiewicz inequality. C. R. Acad. Sci., Ser. 1 Math. 318(2), 129–133 (1994)

    MATH  MathSciNet  Google Scholar 

  28. Bertsekas, D.P.: Nonlinear Programming, 2nd edn. Athena Scientific, Belmont (1999)

    MATH  Google Scholar 

  29. Chen, K.: Matrix Preconditioning Techniques and Applications. Cambridge Monogr. Appl. Comput. Math., vol. 19. Cambridge University Press, Cambridge (2005)

    Book  MATH  Google Scholar 

  30. Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, New York (1999)

    Book  MATH  Google Scholar 

  31. Bertsekas, D.P.: Projected Newton methods for optimization problems with simple constraints. SIAM J. Control Optim. 20, 221–246 (1982)

    Article  MATH  MathSciNet  Google Scholar 

  32. Birgin, E.G., Martínez, J.M., Raydan, M.: Nonmonotone spectral projected gradient methods on convex sets. SIAM J. Optim. 10(4), 1196–1211 (2000)

    Article  MATH  MathSciNet  Google Scholar 

  33. Bonettini, S., Zanella, R., Zanni, L.: A scaled gradient projection method for constrained image deblurring. Inverse Probl. 25(1), 015002+ (2009)

    Article  MathSciNet  Google Scholar 

  34. Rockafellar, R.T., Wets, R.J.B.: Variational Analysis, 1st edn. Grundlehren der Mathematischen Wissenschaften, vol. 317. Springer, Berlin (1998)

    Book  MATH  Google Scholar 

  35. Mordukhovich, B.S.: Variational Analysis and Generalized Differentiation. I. Basic Theory. Grundlehren der Mathematischen Wissenschaften, vol. 330. Springer, Berlin (2006)

    Google Scholar 

  36. Bolte, J., Daniilidis, A., Ley, O., Mazet, L.: Characterizations of Łojasiewicz inequalities and applications. Transl. Am. Math. Soc. 362(6), 3319–3363 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  37. Erdogan, H., Fessler, J.A.: Monotonic algorithms for transmission tomography. IEEE Trans. Med. Imaging 18(9), 801–814 (1999)

    Article  Google Scholar 

  38. Healey, G.E., Kondepudy, R.: Radiometric CCD camera calibration and noise estimation. IEEE Trans. Pattern Anal. Mach. Intell. 16(3), 267–276 (1994)

    Article  Google Scholar 

  39. Tian, H., Fowler, B., Gamal, A.E.: Analysis of temporal noise in CMOS photodiode active pixel sensor. IEEE Solid State Circ. Mag. 36(1), 92–101 (2001)

    Article  Google Scholar 

  40. Janesick, J.R.: Photon Transfer, vol. PM170. SPIE, Bellingham (2007)

    Book  Google Scholar 

  41. Foi, A., Trimeche, M., Katkovnik, V., Egiazarian, K.: Practical Poissonian–Gaussian noise modeling and fitting for single-image raw-data. IEEE Trans. Image Process. 17(10), 1737–1754 (2008)

    Article  MathSciNet  Google Scholar 

  42. Li, J., Shen, Z., Jin, R., Zhang, X.: A reweighted ℓ 2 method for image restoration with Poisson and mixed Poisson–Gaussian noise. Tech. rep. (2012). UCLA Preprint. ftp://ftp.math.ucla.edu/pub/camreport/cam12-84.pdf

  43. Sorenson, H.W.: Parameter Estimation: Principles and Problems, Control and Systems Theory vol. 9, 1st edn. Dekker, New York (1980)

    Google Scholar 

  44. Dahlquist, G., Bjorck, A.: Numerical Methods. Dover, Mineola (2003)

    MATH  Google Scholar 

  45. Chaâri, L., Pustelnik, N., Chaux, C., Pesquet, J.C.: Solving inverse problems with overcomplete transforms and convex optimization techniques. In: Wavelets XIII, San Diego, CA, USA, vol. 7446. SPIE, Bellingham (2009). 14 pp.

    Chapter  Google Scholar 

  46. Elad, M., Milanfar, P., Ron, R.: Analysis versus synthesis in signal priors. Inverse Probl. 23(3), 947–968 (2007)

    Article  MATH  Google Scholar 

  47. Pustelnik, N., Pesquet, J.C., Chaux, C.: Relaxing tight frame condition in parallel proximal methods for signal restoration. IEEE Trans. Signal Process. 60(2), 968–973 (2012)

    Article  MathSciNet  Google Scholar 

  48. Combettes, P.L., Dũng, D., Vũ, B.C.: Proximity for sums of composite functions. J. Math. Anal. Appl. 380(2), 680–688 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  49. Zubal, I.G., Harrell, C.R., Smith, E.O., Rattner, Z., Gindi, G., Hoffer, P.B.: Computerized three-dimensional segmented human anatomy. Med. Phys. 21, 299–302 (1994)

    Article  Google Scholar 

  50. Slaney, M., Kak, A.: Principles of Computerized Tomographic Imaging. SIAM, Philadelphia (1988)

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire d’Informatique Gaspard Monge and CNRS UMR 8049, Université Paris-Est Marne-la-Vallée, Champs-sur-Marne, 77454, Marne-la-Vallée, France

    Emilie Chouzenoux, Jean-Christophe Pesquet & Audrey Repetti

Authors
  1. Emilie Chouzenoux
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jean-Christophe Pesquet
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Audrey Repetti
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Emilie Chouzenoux.

Additional information

Communicated by Hedy Attouch.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chouzenoux, E., Pesquet, JC. & Repetti, A. Variable Metric Forward–Backward Algorithm for Minimizing the Sum of a Differentiable Function and a Convex Function. J Optim Theory Appl 162, 107–132 (2014). https://doi.org/10.1007/s10957-013-0465-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10957-013-0465-7

Keywords

Search

Navigation