1 Introduction

Historical stone masonry structures are very vulnerable to earthquakes, and effective risk mitigation strategies require the development of suitable assessment procedures. However, the seismic performance assessments of masonry buildings are often hindered by a lack of information regarding the structure, materials and structural details. As an added complexity, interventions can increase the heterogeneity of the construction material and structural details, as these also degrade during the building’s lifespan (Lourenço 2002; Lagomarsino and Cattari 2015). Additionally, the properties of the connections between the structural elements, such as the wall-to-wall and floor-to-wall interfaces, are often unknown (Ortega et al. 2018; Solarino et al. 2019; Almeida et al. 2020; Vanin et al. 2020a; Tomić et al. 2021). At the same time, it is often not feasible to test the properties of the materials and components, either due to high costs or the limits imposed by the cultural value of the building (Borri and Corradi 2019).

The seismic response of historical masonry is further complicated for buildings that are part of aggregates, which are common in European city centres due to the centuries-long process of densification (Carocci 2012; da Porto et al. 2013; Mazzoni et al. 2018). In these aggregates, neighbouring units often share a structural wall, with the connection ensured either through interlocking stones or by a layer of mortar. These aggregates usually developed over centuries and without consistent planning or engineering, resulting in adjacent buildings that often have different material properties, floor and roof heights, and are poorly connected. Figure 1 shows an example from Central Italy where the 2016 earthquakes damaged buildings and their connection joints in an aggregate built to densify the block by ‘borrowing’ walls from the adjacent buildings.

Fig. 1
figure 1

Damage to masonry aggregates in Central Italy after the 2016 earthquake

Full size image

To simulate the behaviour of masonry and help predict seismic responses, various modelling techniques and approaches have been adopted, each with differing levels of complexity and computational burden (Roca et al. 2010; Lourenço 2013). The key pre-requisite of every model is to adequately describe the geometry, morphology, connections and boundary conditions. In addition to the challenges in accurately determining these properties, another challenge stems from the lack of clear and detailed modelling guidelines and codes for representing the interaction between adjacent building units. In the following, we review the literature on benchmark studies and existing blind prediction competitions focused on modelling unreinforced masonry (URM).

1.1 Review of past blind prediction competitions and software benchmarks

Modelling the seismic response of URM buildings in general and historical masonry aggregates in particular is challenging because it requires to perform nonlinear numerical simulations, which requires experience in nonlinear modelling (Penna et al. 2014; Lagomarsino et al. 2018; Cattari et al. 2022; D’Altri et al. 2022). Open questions on how to account for the material and modelling uncertainties and how to calibrate numerical models of URM buildings have been raised since the very first nonlinear analyses were performed (Tomaževič 1978). Since then, multiple studies have addressed material and modelling uncertainties for URM buildings, either by organising blind prediction competitions or by directly benchmarking different software packages.

A dozen studies benchmarked modelling approaches and assumptions for URM buildings (Salonikios et al. 2003; Marques and Lourenço 2011, 2014; Giamundo et al. 2014; Betti et al. 2015; Calderoni et al. 2015; Bartoli et al. 2017; De Falco et al. 2017; Cattari et al. 2018; Siano et al. 2018; Aşıkoğlu et al. 2020; Malcata et al. 2020). The large number of studies here differ by case-study size, complexity, software used and modelling approaches, but highlight a large scatter in obtained results due to the many alternatives in choosing material parameters, defining a numerical model, and interpreting results. Particularly relevant for the present work is the study by Malcata et al. (2020), which focused on a building aggregate of seven units, for which results of in-situ material tests and a detailed geometric survey were available. Two models were created; the first one was an equivalent frame method (EFM) model in 3Muri (STA DATA 2008) and the second one a solid finite element method (FEM) model in ABAQUS (Smith 2009). In the 3Muri model, the entire aggregate was modelled assuming that all units of the aggregate were fully connected to each other. On the other hand, in ABAQUS only about half of the units represented in the 3Muri model were included and constraints applied to account for the missing units. The models were calibrated using frequencies obtained from ambient vibration measurements. The authors obtained some similarities in terms of damage mechanisms, but also different base shear force capacities, with the 3Muri model having less force capacity than the ABAQUS model. This difference was attributed to the difference in constitutive models adopted in each software and to the fact that the ABAQUS model contained only half of the units. In general, for complex buildings Malcata et al. (2020) recommended using EFM due to the much shorter analysis time and their finding that this modelling approach tends to lead to more conservative results.

Cattari and Magenes (2022) presented the study from the ReLUIS project, which sought to define a set of reference structures of increasing complexity. This research program carried out by several Italian universities tested these reference structures by means of nonlinear static analyses using different software packages. Here, the focus was on the global response governed by the in-plane response of the walls and did not consider out-of-plane collapse failures. Some of the case study buildings were permanently monitored (Dolce et al. 2017), and an earthquake that hit during the project phase (Cattari et al. 2019) allowed the numerical results to be verified. To account for the various scenarios, the following properties were varied: (i) masonry typology, (ii) boundary conditions in case of wallettes (fixed-fixed and cantilever) and (iii) spandrel configurations. The spandrel configurations included in that study comprised spandrels without any tensile resistant horizontal element, spandrels with horizontal steel tie rods, spandrels coupled to reinforced concrete beams, and infinitely stiff spandrels. To limit the scatter, the following assumptions were made: (i) good wall-to-wall connections, (ii) rigid diaphragms and (iii) a perfect connection between the diaphragm and walls. While other papers stemming from the ReLUIS project elaborate on the specific results obtained on each of these case studies, Cattari and Magenes (2022) presented an overview of the benchmark structures, their purpose, and the standardized criteria for comparison of the results.

Finally, the latest study by Parisse et al. (2021) described a benchmark exercise performed as part of the European Conference on Earthquake Engineering (Magenes et al. 2018). Two three-storey buildings were considered as case studies. The first was a stone masonry building with flexible diaphragms, and the second was a brick masonry building with rigid horizontal diaphragms. A wide range of approaches was used, with participants free to choose modelling strategies, methods of analysis and criteria for attaining limit states, which were not predefined. Here, the majority of participants submitted predictions using EFMs. The results were compared in terms of capacity curves, predicted damage mechanisms and the attainment of the damage and the near collapse limit states. The study showed good agreement for damage patterns and collapse mechanisms, with some differences in failure modes. However, the scatter was very high in the capacity curves and peak ground accelerations (PGAs) required for attaining the limit state, including for the case study presenting similar masonry quality and details to the present study.

While benchmarking studies compare modelling strategies and assumptions of hypothetical structures and/or loading scenarios, blind prediction studies compare simulations to experimental results where the experimental test is carried out after the simulations have been performed. The blind predictions by Mendes et al. (2017) and Esposito et al. (2019) are the most relevant for the present study and discussed here. In both studies, participants were free to choose their modelling approach and type of analysis (static or dynamic, and linear or nonlinear). The study by Mendes et al. (2017) was organized for research groups and tested two structures with the similar geometric dimensions but with different masonry typologies (irregular stone masonry and solid brick masonry). The structures represented three walls (facade and side walls) of a single storey building and a gable on the facade wall. They were tested on a shake-table, focusing on the out-of-plane behaviour of the facade wall. The groups were asked to report a PGA value and the failure mode that would lead to the out-of-plane collapse of the specimen. Even though the average provided value was on the safe side, the coefficient of variation (CoV) was high, 63% for the stone structure and 39% for the brick structure, meaning that some of the participants were extremely conservative whereas others were unconservative. Moreover, only 9 out of 19 models predicted the failure mode correctly for the stone structure, and 6 out of 17 for the brick structure. The study by Esposito et al. (2019) was organized for engineering companies that were asked to simulate and predict the in-plane behaviour of the quasi-static cyclic test on a two-storey modern house, representative of Dutch URM building stock. Nine participants submitted 16 models but were asked to choose one final contribution per participant. The participants were requested to provide base-shear versus first and second floor displacements and a clear description and explanation of the failure mechanism. The FEM models overestimated the peak strength and underestimated the ultimate displacement capacity. On the opposite, the analytical-based model underestimated the peak strength, but overestimated the ultimate displacement capacity. Finally, EFM models generally underestimated the experimental capacity in terms of both force (at peak load) and displacement (at near collapse). Peak strength CoV was 51% and 42% for negative and positive loads, respectively. Displacement at near collapse CoV was 32% and 41% for negative and positive displacements, respectively. Only 4 out of 9 models predicted the failure mode correctly. Based on their submissions, the capacity/demand (C/D) ratio was calculated. EFM models resulted on average in smaller values of C/D, and FEM and analytical models resulted on average with larger values of C/D ratios than those computed from the experiment. For all submissions, C/D CoV was in between 26% and 69%, depending on the load direction and method for computing C/D ratio. The two blind prediction studies and the SERA AIMS study presented herein are summarized in Table 1.

Table 1 Comparison of blind prediction studies on the seismic response of unreinforced masonry buildings
Full size table

With the blind prediction study presented in this paper, we intend to contribute as follows to the existing benchmarking and blind prediction studies and their findings:

  • In the previous studies, participants were either free to choose the analysis method (Mendes et al. 2017; Esposito et al. 2019; Parisse et al. 2021) or pushover analyses were performed (Cattari and Magenes 2022). In the present study, participants were asked to perform a time-history analysis to capture the full complexity of the URM response and aggregate out-of-phase behaviour. In total, eleven out of the thirteen participants performed nonlinear time-history analysis.

  • Previous blind predictions were either focusing on in-plane (Esposito et al. 2019) or out-of-plane behaviour (Mendes et al. 2017). The present study was designed such that in-plane and out-of-plane components were expected to play an important role in the behaviour of the two units.

  • Previous studies usually narrowed the modelling choices by considering wall-to-wall and floor-to-wall connections as rigid (Cattari and Magenes 2022), or floor-to-wall connections as rigid and not specifying the properties of wall-to-wall connections (Parisse et al. 2021). The present study was designed such that a nonlinear response of the unit-unit connections and the floor-to-wall connections was expected.

  • Blind prediction studies on masonry aggregates were not yet conducted. When a unit was part of an aggregate, the influence of adjacent units on the response was either out of scope and not accounted for (Parisse et al. 2021) or accounted for in a simplified manner (Malcata et al. 2020). The principal objective of this study was the masonry aggregate behaviour and the aggregate behaviour was designed such that a nonlinear response of the interface was expected.

  • In previous benchmark studies, modelling approaches were often limited to a few different software packages. In the present study, thirteen submissions covered a wide variety of modelling approaches using various modelling approaches: three discrete element method (DEM) models, four solid FEM models, two shell FEM models, two EFM models, one limit analysis model and one hand calculation.

The following sections first describe the timeline and information on the case study aggregate that was shared with the participants of the blind prediction competition together with the nominal and actual seismic input. Second, the categories of modelling approaches used by the participants are described and discussed. Third, the statistical evaluation of the submitted results and the qualitative description of the predicted damage mechanisms are discussed and compared with experimental results. Finally, conclusions and recommendations on modelling URM aggregates are drawn.

2 Case study information shared with the participants

The chosen case study was a half-scale prototype of a masonry building aggregate, designed for the shake-table test of the SERA AIMS project. Details about the experimental campaign can be found in Tomić et al. (2022). Table 2 shows the timeline of the blind prediction competition. Participants were provided with data on mortar, stone, and masonry material properties (Table 4), data from quasi-static cyclic shear tests on wallettes of the same masonry typology, as well as data on the geometry, mass, construction details and testing sequence (Tomić et al. 2019).

Table 2 Timeline for the blind prediction competition associated with the SERA AIMS stone masonry aggregate experimental campaign in Tomić et al. (2022)
Full size table

2.1 Geometry and material properties

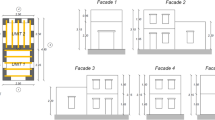
The aggregate was composed of two units. The two-storey unit (Unit 2) was built first and had a closed rectangular footprint with plan dimensions of 2.5 × 2.5 m and a total height of 3.15 m. The one-storey unit (Unit 1) had a U-shape footprint with plan dimensions of 2.5 × 2.45 m and a total height of 2.2 m. The wall thicknesses were 30 cm for Unit, 35 and 25 cm for Unit 2 for the first and second floor, respectively. The thickness of the spandrels beneath the openings was 15 cm. The floor plan and facades are shown in Fig. 2.

Fig. 2
figure 2

Case study of the stone masonry aggregate experimental campaign in Tomić et al. (2022). 3D view, floor plan with beam orientation and facade layout of the two units

Full size image

The total masses of Unit 1 and Unit 2 were 7,434 and 13,272 kg, respectively. Unit 2 had additional masses of 1500 kg evenly distributed per floor. The detailed mass distribution is displayed in Table 3.

Table 3 Specimen masses of the units of the SERA AIMS stone masonry aggregate experimental campaign in Tomić et al. (2022)
Full size table

The walls of the stone masonry aggregate were built from double-leaf irregular stone masonry. Commercial hydraulic lime mortar was used, with the addition of 2:3 volumetrically proportional expanded polystyrene (EPS) spheres to further reduce the strength and stiffness of the mortar. Stone chips were placed between the leaves. The interlocking between the leaves was poor, except near openings and corners. The masonry typology (shown in Fig. 3) and materials were chosen to be as similar as possible to the ones used in a previous test at the EUCENTRE (Senaldi et al. 2019a; Guerrini et al. 2019). Material properties of the EUCENTRE test, as shown in Table 4, were shared with all participants of the blind prediction, together with the data from quasi-static cyclic shear tests on wallettes of the same typology.

Fig. 3
figure 3

Masonry typology: detail of a corner of Unit 1 of the SERA AIMS aggregate in Tomić et al. (2022)

Full size image
Table 4 Estimates of the mortar, stone and masonry properties that were distributed to the blind prediction participants before the tests.
Full size table

The walls of Unit 2 were constructed first, representing the ‘older’ unit of the aggregate. Afterwards, a layer of mortar was applied to the interface (shown in Fig. 4) to ensure that there was no interlocking between the units, simulating a weak connection between the two units. The timber floors were simply supported on the masonry walls and were oriented differently for the two units, with the Unit 1 beams spanning in the x-direction and the Unit 2 beams spanning in the y-direction. One layer of 2 cm-thick planks was nailed to the beams by two nails at each intersection. PVC tubes were placed in the walls under the beams and alongside beams running adjacent to walls to leave the possibility of connecting the walls to the beams to prevent any out-of-plane failure during the test.

Fig. 4
figure 4

Detail of the interface between the units of the SERA AIMS aggregate in Tomić et al. (2022)

Full size image

2.2 Earthquake record

The aggregate specimen was tested under one- and two-component excitations, using the two horizontal components of the 1979 Montenegro earthquake Albatros station records displayed in Fig. 5. Note that the time axes of the ground motions are scaled by \(1/\sqrt{2}\) because the units were built at half scale (Tomić et al. 2022). The response spectra are displayed in Fig. 6. The maximum accelerations that could be applied to the specimen by the shake-table are 0.875 g in the y-direction and 0.625 g in the x-direction.

Fig. 5
figure 5

Processed acceleration time histories of the Montenegro 1979 earthquake recorded at the Albatros station, with the scaled time step in the: (a) east-west direction; (b) north-south direction (Luzi et al. 2016)

Full size image
Fig. 6
figure 6

Acceleration response spectra of the Montenegro 1979 earthquake recorded at the Albatros station for a 5% damping ratio with the scaled time step (Luzi et al. 2016)

Full size image

The theoretical specified limit was planned to be reached in four steps, with the ground motion applied at 25%, 50%, 75% and 100% of such limit. Each step consisted of three stages, comprising (i) a uni-directional test in the y-direction, (ii) a uni-directional test in the x-direction and (iii) a bi-directional test in x- and y-directions, as shown in Table 5. Varying directions of acceleration led to better understanding of the influence of bidirectional acceleration on the aggregate response. However, the actual testing sequence differed from the original plan and comprised ten steps overall, as shown in Table 6. Due to this discrepancy, Table 7 shows the list of experimental results compared with blind predictions by participants to account for differences between nominal and effective shake-table accelerations.

Table 5 Nominal SERA AIMS shake-table testing sequence
Full size table
Table 6 Actual applied testing sequence of the SERA AIMS shake-table test in Tomić et al. (2022)
Full size table
Table 7 List of experimental results compared with blind predictions by participants to account for differences between nominal and effective shake-table accelerations
Full size table

First, three additional runs at 12.5% of the shake-table capacity were added to better calibrate the table for the runs. The nominal and effective spectra for Runs 1.1 – 1.3 matched well, as shown in Fig. 7. Note that nominal Run 1.3 was composed by nominal Runs 1.1 and 1.2 combined. Components of the bi-directional run 1.3 were very similar as when applied separately in Runs 1.1 and 1.2.

Fig. 7
figure 7

Comparison of response spectra for nominal and effective records of Runs 1.1 – 1.3 in the SERA AIMS shake-table test in Tomić et al. (2022)

Full size image

After Run 2.1, the damage was widespread, so the specimen was strengthened before continuing (Tomić et al. 2022). For all subsequent runs, the run label ends therefore with an “S” to highlight that the specimen was strengthened. Overall, the nominal and effective PGA and spectral shape of the runs differed, making it challenging to compare numerical and experimental displacements and base shear. Figure 8 shows the effectively applied acceleration spectra for Run 2.1, which was the last run before strengthening measures were installed. Run 2.1 was a uni-directional excitation in y-direction. The effectively applied spectra are computed from the recorded shake-table accelerations. Figure 8 also shows the nominal excitations of Runs 2.1 and 3.1. The fundamental period of the undamaged structure were approximately 0.13 s in the longitudinal (y- direction). (Tomić et al. 2022). Comparing the effective to the nominal spectra shows that for a period range between 0.1 and 0.15 s, the effective spectra of Run 2.1 is closer to the nominal spectra of Run 3.1 rather than 2.1. At the same time, the effective spectra of Run 2.2S is closer to the nominal spectra of Run 3.2 rather than 2.2. For this reason, for displacements and base shear in the longitudinal direction we will compare in the next section the blind predictions of Run 3.1, keeping in mind, however, that the comparison is somewhat ambiguous due to differences in nominal and effective spectre and therefore rather comparing an order of magnitude of the variable. For excitation in the transversal direction, we will compare the predicted responses for Run 3.2 to experimental results of Run 2.2S. Again, the objective is to compare the predicted responses of the participants, while the experimental comparison is only to compare an order of the magnitude. However, it needs to be kept in mind that at Run 2.2S the structure was already retrofitted and heavily damaged because Run 2.1 corresponded rather to Run 3.1. In addition to comparing predicted and observed values for displacements and base shears we compare predicted and actual damage mechanisms.

Fig. 8
figure 8

Comparison of response spectra for selected nominal and effective records in the SERA AIMS shake-table test in Tomić et al. (2022)

Full size image

3 Blind prediction submissions

To derive conclusions about the influence of modelling uncertainties on the response of the models, this section first presents the submitted models by describing the modelling approach and assumptions with regard to floors, floor-to-wall connections, wall-to-wall connections, unit-to-unit connections and damping. Second, we present a statistical representation of the reported results in terms of roof displacements, interface openings and base-shear forces. To derive conclusions on the general trend that modelling approaches or assumptions exert on the results in terms of roof displacements, interface openings and base-shear forces, statistical plots are used to compare the overall values with the values from the models using some of the previously described modelling assumptions, and with the experimental results. Third, we compare the damage mechanisms reported by the participants with the actual observed mechanisms.

3.1 Submitted models

In total, 12 groups with 10 coming from academia and two from industry submitted a total of 13 models. Here, submissions are split by modelling approach and presented using tables to show modelling assumptions considered essential for the further processing of the results. Each of the important modelling choices is described in more detail. Figure 9 shows all the submitted models.

Fig. 9
figure 9

Models submitted to the SERA AIMS blind prediction competition

Full size image

Three participating groups submitted models using DEM or Finite-Discrete element method (FEM-DEM) using 3DEC (Itasca Consulting Group, Inc. 2016) and LS-DYNA (Hallquist 2006) software, which modelled the material as an assemblage of either rigid (DEM) or deformable (FEM-DEM) discrete elements with discontinuities at their boundaries. For the sake of simplicity, the nomenclature “DEM” will be used for indicating all three submissions hereinafter. The DEM 1 was developed according to the Macro-Distinct Element Model (M-DEM), a new hybrid FEM-DEM macro-element approach (Malomo and DeJong 2021a, b) where each URM member is idealized an assembly of deformable FE macro-blocks connected through zero-thickness nonlinear spring layers. Two submissions (DEM 2, DEM 3) used the simplified micro-modelling technique that does not explicitly model mortar, but instead lumps mortar properties at interfaces (Lourenco 1996), modelling each unit separately, albeit according to an equivalent masonry pattern. All the three DEM submissions modelled explicitly the two units. DEM 1 modelled floors using deformable 3D joists and link elements accounting for the in-plane stiffness of the diaphragms. DEM 2 modelled the floor slabs and beams as rigid blocks. DEM 3 modelled beams as 3D elastic elements, while the planks were not modelled. Here, the participant elaborated that, considering that the floor is very flexible, the planks were not modelled to avoid elements with small dimensions considering that the smallest finite element governs the time step in an explicit analysis, which increases the computational time (AlShawa et al. 2017). All three participants explicitly modelled floor-to-wall connections with the same interface that was used to model the connections between the blocks. DEM 2 used the same parameters for the connections between blocks and floor-to-wall and unit-to-unit connections, whereas DEM 3 used a lower tensile strength for the latter two connections. DEM 1 used the same parameters for floor-to-wall connections and connections between blocks, while the unit-to-unit connection was modelled with zero cohesion and tensile strength (compression-shear). Damping varied both in terms of whether it was mass proportional (DEM 1, DEM 2) or stiffness proportional (DEM 3) and with regards to the critical damping ratio. DEM 2 progressively lowered the damping ratio to compensate for an increase in the mass-proportional damping as damage appeared and period of the structure elongated. Table 8 summarizes modelling assumptions for the DEM submissions.

Table 8 Modelling assumptions for blind submissions to the SERA AIMS project based on Discrete - Finite Element Models (DEM-FEM)
Full size table

With six submissions, shell and solid FEM models were the most popular approach. In these models, masonry is represented as a homogenous continuous material, discretized into a mesh of finite elements of various sizes, and the nonlinear behaviour is described by material laws. Modelling choices concern the choice of element type and size, the meshing algorithm, the integration scheme, etc. Four of these submissions featured solid FEM models, of which two used DIANA (Diana 2017) and two OpenSEES (McKenna et al. 2000). Two submissions feature shell FEM models using SAP2000 (2009). FEM 1 and FEM 3 used the total strain-based crack constitutive model for masonry, with exponential and parabolic behaviour in tension and compression, respectively (Lourenco 1996). A rotating crack orientation was selected following the coaxial stress-strain approach, where stress-strain relations were evaluated in the principal directions of the strain vector. FEM 4 and FEM 5, the same model with and without floors, used a material model for masonry based on Faria et al. (1998). FEM 2 modelled the masonry as elastic/perfectly plastic in compression. In tension, masonry was modelled as linear elastic up to a cracking strain. For larger strains, a damage material law was assumed. FEM 6 did not provide additional information on the masonry material model. The submissions differed from each other with regard to assumptions for modelling floors and floor-to-wall connections. FEM 3 and FEM 5 did not model floors, ignoring their effect and replacing them with tributary masses. On the other extreme, FEM 2 modelled floors as a rigid diaphragm by applying a diaphragm constraint in their chosen software. FEM 1 modelled floors using a linear elastic orthotropic shell membrane with equivalent properties accounting for both the beams and planks, and nonlinear elastic floor-to-wall connections with normal stiffness tending to zero after exceeding a certain threshold value. FEM 4 modelled timber beams as elastic trusses, choosing a beam material that was elastic isotropic, while the planks were neglected and not modelled. The floor-to-wall connection was modelled by elastic/perfectly plastic behaviour, with material collapse after a peak displacement level. The material model accounts for pinching and cyclic degradation. The hysteretic rules were calibrated based on floor-to-wall pull-out experiments (Moreira 2015). FEM 6 also modelled only elastic beams, but with rigid floor-to-wall connections and without transferring the bending moments. The models differed also with regards to modelling the unit-to-unit interface. Only one participant modelled the units as separated (FEM 3). Two participants modelled the interaction only in compression (FEM 2, FEM 6), with the latter also modelling a gap/separation of 3 mm. Three participants (FEM 1, FEM 4, FEM 5) modelled the connection between units as a nonlinear 3D surface accounting for both the Mode I and Mode II failure at the interface (compression-shear) (Walter et al. 2005). All submissions included mass and stiffness proportional Rayleigh damping, with critical damping ratios often set to 3% (FEM 3, FEM 4, FEM 5) and 5% (FEM 2, FEM 6). An outlier was FEM 1 with a damping ratio of 10% to balance the underestimation of dissipated energy at the material level, as reported by the participant. Table 9 summarizes modelling assumptions for FEM.

Table 9 Modelling assumptions for blind submissions to the SERA AIMS project based on Finite Element Models (FEM)
Full size table

Though the use of EFM dominated in previous studies, only two participants submitted EFM predictions for this study, which were done using in-house and OpenSEES (McKenna et al. 2000) software. In these models, the structure was discretized into piers, spandrels and rigid nodes on the structural element level (Bracchi et al. 2015; Quagliarini et al. 2017). EFM 1 modelled the piers and spandrels with beams using the concentrated plasticity approach. The out-of-plane (OOP) mechanism was accounted for using a series of representative pin-ended column elements that were geometrically defined to reflect the expected one-way out-of-plane mechanism and wall section, with an appropriate tributary mass and stiffness. The capacity of the column was independent of the in-plane wall actions (similarly the in-plane capacities were treated as independent of the out-of-plane response). However, to impose the correct displacements, the out-of-plane column was slaved to the relevant floor levels. The capacity of the out-of-plane wall elements was defined a priori using a nonlinear kinematic approach, with out-of-plane collapse assumed to occur when mid-height displacements exceeded the wall thickness. Where parapet behaviour occurred, the out-of-plane displacement limit was taken as the wall thickness. Floors were modelled as nonlinear plane stress finite elements. The floor model assumed that the elements maintained their strength after yielding, but the stiffness was reduced as a function of the maximum deformation. The floor-to-wall and wall-to-wall connections were modelled as rigid, and the unit-to-unit connection was modelled with gap elements that could transfer only compression forces but no shear or tension forces. The compression stiffness of the gap element was calibrated based on: (i) the shear depth of the adjacent Unit 1 and Unit 2 piers, (ii) the pier wall thickness and (iii) the given masonry Young’s modulus value. Mass and initial stiffness proportional damping was used with a 3% critical damping ratio. EFM 2 used a newly developed macro-element (Vanin et al. 2020b) to simultaneously model in-plane and out-of-plane behaviour. Floors were modelled as linear orthotropic shell membranes, with nonlinear sliding floor-to-wall connections. Nonlinear interfaces were also used for wall-to-wall and unit-to-unit connections. Mass and initial stiffness damping was used together with a 1% critical damping ratio to avoid overdamping of the out-of-plane behaviour. Table 10 summarizes the modelling assumptions for EFM.

Table 10 Modelling assumptions for the blind submissions to the SERA AIMS project based on Equivalent Frame Models (EFM)
Full size table

Finally, one participant submitted a prediction using a simple design code-based spreadsheet calculation (also referred to as hand-calculation, HAC, or analytical approach), and one participant submitted a prediction through a limit analysis (LIM) approach using the LiABlock_3D software (Cascini et al. 2020). HAC 1 used the capacity spectrum method, performing a pushover analysis with Acceleration Displacement Response Spectrum (ADRS) (Freeman 1998). Only the ground floors were modelled, meaning that failures and nonlinearities were concentrated at the ground floor in this approach, with extrapolated roof displacements. The effective stiffness was reduced according to SIA 269/8 (Wenk 2014), the shear capacity was calculated according to SIA 266 (Pfyl-Lang et al. 2009), and the drift capacity was chosen according to Vanin et al. (2017). There were no connections between walls or units, neglecting the rotation, and floors were replaced with tributary masses.

LIM 1 predicted the aggregate response using rigid block limit analysis by mathematical programming. The structure was idealized into a three-dimensional assemblage of rigid blocks interacting via no-tension frictional interfaces, with zero cohesion and infinite compressive strength. The sliding failure was governed by a Coulomb friction criterion with zero cohesion. The beams were modelled as rigid with unilateral floor-to-wall connections, which matched what was done for the rest of the interfaces. The unit-to-unit connection used the same interfaces, but the interaction at the head joints was only considered for this connection. Table 11 summarizes the modelling assumptions for the approaches based on spreadsheet analysis method and limit analysis.

Table 11 Modelling assumptions for the blind submissions to the SERA AIMS based on analytical approach and limit analysis.
Full size table

3.2 Statistical evaluation of blind prediction submissions

Here we present the submitted maximum absolute values of the recorded relative displacements of the units in relation to the ground (Rd1-6), interface openings (Id1-4) and total base-shear forces (BSx, BSy) using statistical methods for each step. The displacements and interface openings are shown in Fig. 10. Then, the values of Rd2, Rd3, Id3, Id4, BSx, and BSy for Run 3.1 and 3.2 predicted by each participant are grouped by a modelling approach or assumption. These values are then compared with statistical representation (using boxplots) of all submissions and with the values from the comparable experimental runs. Roof displacement, interface opening, and the base shear are considered both in the longitudinal and in the transversal directions. The values reported by each participant are classified according to the following five properties of a model: (i) model class, (ii) unit-to-unit connection, (iii) floor model, (iv) floor-to-wall connection and (v) wall-to-wall connection.

Fig. 10
figure 10

Compared quantities for the blind prediction submissions. Displacements relative to the ground (Rd1-6) and interface opening (Id1-4)

Full size image

First, Fig. 11 shows the scatter of maximum values through the test steps, compared with the values from the corresponding experimental runs. The red mark indicates the median, and the box edges indicate the 25th and 75th percentile, respectively. The whiskers extend to the most extreme data points not considered outliers. The outliers are plotted separately using the ‘+’ symbol. Already for Step 1.3, the results tend to scatter significantly, and this scatter increases through the runs. The scatter is more significant for roof displacements and interface openings than for base-shear forces.

Fig. 11
figure 11

Statistical representation of the results of the blind prediction submissions in terms of peak roof displacements, interface openings and peak base-shear forces for Runs 1.3, 2.3, 3.3 and 4.3. Blind prediction Run 1.3 is compared with experimental Run 1.3

Full size image

Figure 12 shows the reported values of Rd2, Rd3, Id3, Id4, BSx, and BSy grouped according to the model class, compared with the values from the corresponding experimental runs. On average, the DEM models predict larger displacements and interface openings and lower base shear forces than the rest of the models, partially due to an outlier. All shown DEM results are outside the 25th to 75th percentile range of the predicted values but are in fact the only models to correctly capture the order of magnitude of the experimentally measured displacements. Conversely, the shell and solid FEM models show the lowest displacements and interface openings and the highest base shear forces on average, indicating that the stiffness of the aggregate was probably overestimated. Also, it should be kept in mind that in continuous FEM models it is not possible to simulate the separation of masonry portions, therefore the displacements are limited. The majority of the shell FEM models are also either close to or outside the 25th to 75th percentile range of predicted values, but on the opposite side as the DEM models. On average, the EFM models seem to be closer to the median values, but median values were not close to the experimental values. We also calculated the CoV values for predictions using the same model class for Runs 3.1 and 3.2, for model classes with more than one submission (EFM, shell FEM, solid FEM, DEM). However, Table 12 shows that CoV values did not show any clear trend and varied largely between predicted quantities. Only on the average the CoV values of the solid FEM model were lower than those of other model classes. However, these four solid FEM models were submitted by members of the same research group. CoV values computed for all submissions together were large with a CoV of 160–268% for displacement quantities and a CoV of 58–74% for base shears at near collapse. The largest CoV values were obtained for the interface openings, highlighting that the interaction between the units of an aggregate is very difficult to predict. These values are higher than those of previous blind prediction studies. Mendes et al. (2017) reported a CoV of 39–63% for the predicted PGA at collapse and Esposito et al. (2019) a CoV of 51% for the predicted peak strength and 41% for the predicted displacement at near collapse. The values of the SERA AIMS study might be higher because the analysed structure is significantly more complex than the specimens tested in Mendes et al. (2017) and Esposito et al. (2019) (Table 1).

Fig. 12
figure 12

Reported Rd2, Rd3, Id3, Id4, BSx, and BSy values for Runs 3.1 and 3.2 from the blind prediction submissions grouped according to the modelling approach, compared with the values from the corresponding experimental runs. The reported CoV value is related to all submissions

Full size image
Table 12 CoV values for predictions grouped using the same model class for Runs 3.1 and 3.2
Full size table

Figure 13 shows the reported values of Rd2, Rd3, Id3, Id4, BSx, and BSy grouped by the unit-to-unit connection type, compared with the values from the corresponding experimental runs. Models were separated in three groups. The models in the first group considered the units as completely separate, with no interaction. The models in the second group accounted for Mode 1 (interaction in compression) only, ignoring interaction in the transversal direction. The models in the third group included both Mode 1 and Mode 2 interaction (interaction in shear) by the transfer of compression and shear forces, where the maximum shear force is a function of the compression force. Some of these models also included tensile strength, which was small and therefore ignored in defining the model categories. Models with a compression-shear unit-to-unit interface show on average larger roof displacements and interface openings and lower base-shear forces than models with a compression-only interface, which is unexpected. It would be expected that models with no interaction or compression-only interaction would on average produce larger transversal openings of the interface (Id4), but this was not the case probably because of the generally stiff behaviour of these models. It is worth noting that just two models did not model the interaction between the two units, and they also differed in modelling approach (hand calculation method versus solid FEM model).

Fig. 13
figure 13

Reported Rd2, Rd3, Id3, Id4, BSx, and BSy values for Runs 3.1 and 3.2 from the blind prediction submissions grouped according to unit-to-unit connection type, compared with the values from the corresponding experimental runs. The reported CoV value is related to all submissions

Full size image

Figure 14 shows the reported values of Rd2, Rd3, Id3, Id4, BSx, and BSy grouped by floor type, compared with the values from the corresponding experimental runs. The model featuring rigid floors shows the lowest roof displacements and interface openings—close to the 25th percentile, with a base-shear force close to the 75th percentile of the predicted values. However, there is just one model featuring this property. The models with no floors average lower displacements and similar interface openings and base-shear forces compared to the models featuring flexible floor diaphragms. This is surprising as we would have expected that models with no floors lead to larger displacements than models that include the diaphragm. However, the effect of the diaphragm might have been minor because the structure was symmetric in the x-direction. Finally, comparing models featuring only beams with those featuring the entire diaphragm (therefore including the shear stiffness of the floor) presents inconclusive results due to exceptionally high scatter within the group of teams that modelled only the beams.

Fig. 14
figure 14

Reported Rd2, Rd3, Id3, Id4, BSx, and BSy values for Runs 3.1 and 3.2 from the blind prediction submissions grouped according to floor type, compared with the values from the corresponding experimental runs. The reported CoV value is related to all submissions

Full size image

Figure 15 shows the reported values of Rd2, Rd3, Id3, Id4, BSx, and BSy grouped by the floor-to-wall connection type, compared with the values from the corresponding experimental runs. The models featuring rigid floor-to-wall connections show lower roof displacements and interface openings (close to 25th percentile on average) as well as higher base-shear forces (on average larger than 75th percentile). The opposite applies for the models with nonlinear floor-to-wall connections. There are no values reported for the models with elastic floor-to-wall connections, as they only reported the results starting at Run 4.1 (100% shake-table capacity).

Fig. 15
figure 15

Reported Rd2, Rd3, Id3, Id4, BSx, and BSy values for Runs 3.1 and 3.2 from the blind prediction submissions grouped according to floor-to-wall connection type, compared with the values from the corresponding experimental runs. The reported CoV value is related to all submissions

Full size image

Figure 16 shows the reported values of Rd2, Rd3, Id3, Id4, BSx, and BSy grouped by the wall-to-wall connection type, compared with the values from the corresponding experimental runs. The models featuring nonlinear wall-to-wall connections show on average larger roof displacements and interface openings and lower base-shear forces than those with rigid wall-to-wall connections. However, in case of interface openings and base shear, this behaviour largely stems from an outlier with nonlinear wall-to-wall connections for interface openings, and an outlier with rigid wall-to-wall connections for base shear. Without outliers, the two groups of models would on average yield similar results in these two categories.

Fig. 16
figure 16

Reported Rd2, Rd3, Id3, Id4, BSx, and BSy values for Runs 3.1 and 3.2 from the blind prediction submissions grouped according to wall-to-wall connection type, compared with the values from the corresponding experimental runs. The reported CoV value is related to all submissions

Full size image

Figure 17 shows the reported values of Rd2, Rd3, Id3, Id4, BSx, and BSy grouped by the Rayleigh damping ratio, compared with the values from the corresponding experimental runs. The models do not show any correlation between the reported values and damping ratio. However, the model with 10% damping ratio predicted almost no damage even at 100% acceleration values, and therefore has reported values starting with Run 4.1.

Fig. 17
figure 17

Reported Rd2, Rd3, Id3, Id4, BSx, and BSy values for Runs 3.1 and 3.2 from the blind prediction submissions grouped according to Rayleigh damping ratio, compared with the values from the corresponding experimental runs. The reported CoV value is related to all submissions

Full size image

3.3 Qualitative description of the damage mechanisms

A qualitative evaluation was performed that compared the predicted damage mechanisms with the one observed in the experimental campaign. We analysed the damage mechanisms reported after Step 3 (75% shake-table capacity), as they were the closest match to the actual Runs 2.1 and 2.2S in terms of response spectrum and PGA. Figure 18 shows the illustrative possible damage mechanisms. Therefore in the appendix show the following rows for each participant: (i) image reporting the damage in the model (if applicable); (ii) short resume of predicted damage mechanisms reported by participant; (iii) qualitative comparison of the reported damage mechanisms to those observed in the experimental campaign.

Fig. 18
figure 18

Illustrative description of damage mechanisms. It should be noted that in-plane damage mechanisms were always illustrated as flexural mechanisms. Actual observed behaviour in the experiment was always flexural, so if a participant reported in-plane shear damage, it was counted as incorrect prediction

Full size image

The principal damage mechanism observed in the shake-table test during Run 2.1 was the in-plane flexural and out-of-plane mechanisms of Unit 2. In-plane mechanism formed in Facades 2 and 3, with the maximum residual width of the flexural cracks at the spandrels and piers of the 2nd storey 5 mm and 1.4 mm, respectively. Flexural cracks formed in the middle pier of the 1st storey of Facades 2 and 3 as well as on the spandrels of the 1st storey. The maximum residual width of the flexural cracks at spandrels and piers of the 1st storey was 1.9 mm and 1.2 mm, respectively. Out-of-plane mechanism formed in Facade 4 and 5. Horizontal out-of-plane crack formed at the floor level in Facade 4, with a residual width up to 0.55 mm. The spandrels of Facade 4 were extensively cracked. Out-of-plane cracks were also detected in Facade 5, but for the 2nd storey, instead of being placed at floor level, the horizontal crack was located at the level of the interaction with Unit 1. The wall-to-wall connections proved strong enough to trigger the flange effect, forming out-of-plane and in-plane cracks that were continuous across the connections. Signs of pounding and interaction at the unit-to-unit interface were visible, as well as the beam sliding in the upper floor of Unit 2.

After Run 2.2S Unit 2 did not show any new visible damage. In-plane flexural cracking of both the spandrels and piers of Facade 1 was observed with residual crack widths up to 3 mm and 1 mm for spandrels and piers, respectively. Hairline out-of-plane horizontal cracks were observed in Facades 2 and 3 of Unit 1, which were continuous across the orthogonal walls of Facade 1, showing a flange effect. The maximum residual thickness of these cracks was 1 mm and 0.35 mm for Facades 2 and 3, respectively.

Table 13 reviews the types of damage mechanisms reported by the participants split by unit, storey, direction and failure mode in terms of in-plane (IP) and out-of-plane (OOP) mechanism. Correctly predicted mechanisms are indicated by a green circle, and incorrectly predicted mechanisms are indicated by a red circle. Failure to indicate a correct mechanism is marked by a red x. Finally, correct predictions, false positive, and false negative predictions are summarised at the bottom rows. Not many participants correctly predicted in-plane and out-of-plane mechanisms in the x-direction of Unit 1, though a majority correctly predicted both in-plane and out-of-plane mechanisms in the y-direction of Unit 2 for both storeys. This response was the principal mechanism of the tested aggregate, so this prediction was key to correctly capturing the experimental behaviour. A common mistake was a prediction of in-plane damage in the x-direction of Unit 2 for both storeys, which was not observed in the tests.

Table 13 Damage mechanisms reported by the SERA AIMS blind prediction participants. IP = in-plane mechanism; OOP = out-of-plane mechanism. Correctly predicted mechanisms are indicated with a green circle, incorrectly predicted mechanisms with a red circle and a failure to indicate a correct mechanism with a red x
Full size table

Table 14 reviews the reported damage mechanisms according to the modelling approach, with the number of submissions in each category indicated in parentheses after the name. Correctly predicted damage mechanisms are marked by green circles, and incorrectly predicted mechanisms are marked by red circles. For each row and column, the total number of circles represents the total number of submissions of this category, and filled circles show those that reported a particular damage mechanism. DEM models seemed to miss the mechanisms in the x-direction of Unit 1, while they mostly correctly predict mechanisms in the y-direction of Unit 2. It is important to highlight that the latter mechanisms were the principal ones. EFM models generally performed well, with some incorrectly predicted mechanisms, such as an in-plane mechanism in the x-direction of Unit 2. The best prediction in terms of activated damage mechanisms came from the limit analysis submission, which correctly predicted all the mechanisms, emerging as a clear winner from this comparison.

Table 14 Damage mechanisms reported by the SERA AIMS blind prediction participants. IP = in-plane mechanism; OOP = out-of-plane mechanism. Correctly predicted damage mechanisms are marked by filled green circles, and incorrectly predicted mechanisms are marked by filled red circles
Full size table

Table 15 reviews the reported damage mechanisms according to the unit-to-unit connection type. Models with no interaction between the units and with a compression-only unit-to-unit interface seem to predict more incorrect in-plane mechanisms in the x-direction in Unit 2. At the same time, models with a compression-shear unit-to-unit interface seem to predict damage more correctly in the y-direction of Unit 2, especially for out-of-plane failure modes.

Table 15 Damage mechanisms reported by the SERA AIMS blind prediction participants divided according to unit-to-unit connection type. IP = in-plane mechanism; OOP = out-of-plane mechanism. Correctly predicted damage mechanisms are marked by filled green circles, and incorrectly predicted mechanisms are marked by filled red circles
Full size table

Table 16 reviews the reported damage mechanisms according to the floor type. Contrary to what might be expected, models with no floors predicted less out-of-plane mechanisms. Models with flexible floor diaphragms seemed to incorrectly predict an in-plane mechanism in the x-direction of Unit 2. With regards to the other mechanisms, the results are inconclusive, partially due to the large variation in total number of submissions leading to a low number of models per category.

Table 16 Damage mechanisms reported by the SERA AIMS blind prediction participants divided according to floor type. IP = in-plane mechanism; OOP = out-of-plane mechanism. Correctly predicted damage mechanisms are marked by filled green circles, and incorrectly predicted mechanisms are marked by filled red circles.
Full size table

Table 17 reviews the reported damage mechanisms according to the floor-to-wall connection type. Models with a nonlinear floor-to-wall connection better predict both the in-plane and out-of-plane damage mechanism in both storeys of Unit 2 in the y-direction. This effect is especially pronounced for the out-of-plane damage mechanisms.

Table 17 Damage mechanisms reported by the SERA AIMS blind prediction participants divided according to floor-to-wall connection type. IP = in-plane mechanism; OOP = out-of-plane mechanism. Correctly predicted damage mechanisms are marked by filled green circles, and incorrectly predicted mechanisms are marked by filled red circles.
Full size table

Table 18 reviews the reported damage mechanisms according to the wall-to-wall connection type. Models with rigid wall-to-wall connections more accurately predicted the in-plane mechanism in the x-direction of Unit 1. At the same time, they incorrectly predicted an in-plane mechanism in the x-direction of the 1st storey of Unit 2. Models with nonlinear wall-to-wall connections better predicted both in-plane and out-of-plane damage mechanisms of both storeys of Unit 2 in the y-direction. Models with nonlinear wall-to-wall connections comprise the three DEM models, an EFM model and a limit analysis model.

Table 18 Damage mechanisms reported by the SERA AIMS Blind prediction participants divided with regards to wall-to-wall connection type. IP = in-plane mechanism; OOP = out-of-plane mechanism. Correctly predicted damage mechanisms are marked by filled green circles, and incorrectly predicted mechanisms are marked by filled red circles
Full size table

4 Conclusions

This paper presents the results of a blind prediction competition organized as a part of a shake-table test within the SERA AIMS project. All available data on the unreinforced stone masonry aggregate—material, geometry, construction details, seismic input and testing sequence were shared with all the participants before the tests. The participants were asked to submit their predictions of the damage mechanisms, roof displacements, interface openings and base-shear forces for four levels of shaking. In total, 12 participants from academia and industry submitted a total of 13 models, which were well distributed with regards to modelling approaches, including discrete element models, shell and solid finite element models, equivalent frame models, a limit analysis model, and a code-based hand-calculation approach. The paper summarises the modelling approaches and describes the main modelling assumptions adopted, particularly with regard to the floor models and the unit-to-unit, floor-to-wall and wall-to wall connections.

Material properties shared with the participants were assumed based on the specimen tested in Pavia, a previous experimental campaign on an aggregate of similar typology. In addition, results of in-plane quasi-static cyclic shear tests on walls from the Basel project were shared. In the SERA AIMS project, standard material tests were carried out after the shake-table test and these material properties matched well the ones from the Basel project. Hence, we conclude that discrepancies between the predictions and experimental results are not caused by differences between assumed and actual material properties.

While the assumed and actual material properties agreed well, the actual seismic input differed from the assumed one. Comparing the effective and nominal shake-table accelerations in terms of acceleration response spectra we found that, for the range close to the fundamental periods, the demand imposed in Run 2.1 corresponded closely to the nominal demand planned for Run 3.1. For this reason, the predictions for Run 3.1 were compared to the experimental results of Run 2.1, which was the last run before strengthening measures were applied. Run 2.1 and 3.1 are tests in the longitudinal direction only. For loading in the transverse direction the predictions of Run 3.2 were compared to the experimental results of Run 2.2S, following the same argumentation as for the longitudinal direction. In Run 2.2S the test specimen was already strengthened. A comparison between and experimental results is therefore affected by the following factors: (i) discrepancies between the nominal and effective testing sequence, (ii) discrepancies between the nominal and effective shake-table accelerations, (iii) for the transverse direction, discrepancy in the model (experiment: strengthened, prediction: unstrengthened).

To account for the discrepancy between planned and effective shake-table accelerations we compared submitted predictions and experimental results as follows: (i) a quantitative statistical comparison of the submitted values and a qualitative benchmarking of the submitted values against the experimental results, and (ii) a qualitative comparison of the reported damage mechanisms with the ones observed in the experiment. In the following, we summarise the main findings of the paper.

  • Modelling uncertainty: Although uncertainties with regard to the material level and the structural element level were reduced to a minimum by providing information on the material properties and pier element response, the modelling uncertainties were very high with a CoV of 160–268% for displacement quantities and a CoV of 58–74% for base shears at the significant damage level. These CoVs are larger than those obtained in other blind prediction studies on unreinforced masonry buildings. Study by Mendes et al. (2017) reported CoV of 39–63% for predicted PGA at collapse, while study by Esposito et al. (2019) reported CoV of 51% for predicted peak strength and 41% for predicted displacement at near collapse. In both cases, they call for further blind prediction competitions and further test data of complex structures to calibrate and validate numerical models. The higher CoV values in SERA AIMS are attributed to a significantly more complex structure that included interaction between the two units. Furthermore, not only global (top displacements, base shears) but also local response quantities (interface opening) were predicted and the largest CoV values were obtained for these local response quantities.

  • Model class: The four model classes with more than one submission were the following: discrete element models, solid finite element models, shell finite element models, and equivalent frame models. The CoV values did not show a clear trend between groups of models, except that the lowest CoV was found within the solid FE models. This result might be related to all four solid FE model submissions originating from the same research group using different modelling hypotheses and two different softwares. However, there were only few submissions per model class and therefore the statistical basis for this conclusion is weak.

  • Prediction of peak displacements, base shear forces and failure modes: The DEM modelling approaches led to the best prediction in terms of displacement demands. A submission using limit analysis emerged as a winner in the prediction of the damage mechanisms, but at the same time, significantly underestimated the PGA for the initiation of the mechanisms. The FE model submissions (shell element models, solid element models and equivalent frame models) underestimated the displacement demands, most likely because these models tended to be too stiff.

  • Modelling of interface behaviour between units: Only the hand-calculation submission and one solid FE model neglected the interaction between the units, while all others accounted for the interaction between the units either assuming that the interface between units can transfer only compression forces or assuming that the interface between units can transfer compression and shear forces and the maximum shear force is a function of the compression force. Although it would be expected that the models with compression-only interfaces and no connection between the units would lead to larger transverse displacements than shear-compression interface, this was not the case. However, this is attributed to the rather stiff behaviour of the models featuring compression-only interfaces and no connection between the units.

  • Modelling of timber floors and floor-to-wall connections: Participants modelled the timber floor either modelling just the beams, or introducing elastic diaphragms, or using rigid diaphragms. As the structure was symmetric along the longitudinal axes, the choice of the diaphragm stiffness played probably a lesser role than in other studies. However, models that included rigid diaphragms predicted shear instead of flexural cracking in the spandrels because the axial elongation of the spandrels was restrained, while in the experiment the spandrels developed flexural cracks. The assumptions with regard to the floor-to-wall connections influenced the out-of-plane mechanism, with some of the models featuring rigid-wall connections predicting out-of-plane mechanisms with centre of rotation between the stories, whereas experimental overturning mechanisms involved a relative displacement between wall and timber beams. We therefore conclude that adopting the modelling assumption of nonlinear floor-to-wall connections is important for capturing the in-plane and out-of-plane failure modes correctly.

  • Damping: Although no clear trend in the results was observed with regards to chosen damping ratios, the model that applied the highest value (10%) predicted the very light damage at shake-table capacity, and no damage at acceleration values substantially affecting the physical model.

This study showed that several modelling parameters influence the response of masonry aggregates, leading to large values of CoV in reported displacement results although the uncertainties at the material level and the structural element level were small. It is concerning that the majority of the models underestimated the order of magnitude of displacements. This highlights the need for further work addressing modelling uncertainties of unreinforced masonry structures, in particular for complex typologies such as masonry aggregates.