1 Introduction

A common type of housing in old, populated areas consists of groups of houses that were built with uniform plans and designs and put out in compact configurations, most frequently along rows. In these configurations, during earthquakes the various housing units may come into direct contact with one another, which can result in failure mechanisms that can vary depending on the link between the units and their geometry (Angiolilli et al. 2021).

The seismic response of adjacent buildings, or building aggregates, has received increasing attention following the most recent earthquakes occurred, e.g., in central Italy, which largely destroyed the historic centers of several cities that were occupied by unreinforced stone masonry buildings (Penna et al. 2022). Earthquake-induced building collisions have also been observed in modern buildings (Cole et al. 2010, 2012), where the presence of unreinforced masonry is commonly indicated as the major cause of damage and casualties (So and Spence 2013).

The reasons of these collisions, also denoted as pounding, can be mainly searched in the significantly different height, period or mass of the adjacent buildings (Anagnostopoulos and Spiliopoulos 1992). Similar types of interactions can be encountered in other complex structures such as those of hospital complexes, churches and castles (Degli Abbati et al. 2019; Erdogan et al. 2019; Garofano and Lestuzzi 2016; Valente and Milani 2019), where the presence of adjacent structural units of various shape and height can trigger unexpected failures (Penna et al. 2019). Due to the cost and difficulty of execution, very few experimental investigations have explored the seismic response of unreinforced stone masonry aggregate buildings (Guerrini et al. 2019; Senaldi et al. 2019), while larger efforts have been put so far in the development of tools for assessing their capacity, see for instance (Angiolilli et al. 2021; Formisano and Massimilla 2018; Grillanda et al. 2020; Maio et al. 2015; Pujades et al. 2012; Senaldi et al. 2010).

The present study falls within the activities that were performed as part of the project Adjacent Interacting Masonry Structures (AIMS), sponsored by the Seismology and Earthquake Engineering Research Infrastructure Alliance for Europe (SERA). The main goal of the project was to provide experimental data on the seismic response of aggregate masonry buildings, by performing shake-table tests on a half-scale two-unit aggregate building under bi-directional seismic excitation (Tomić et al. 2022a). Another goal of the project was to make progress in the modelling of these structures. To this purpose, a blind prediction was organized to present and compare different modelling approaches that are nowadays accessible to the analysts (Tomić et al. 2022b). The results of the shaking table tests were then communicated, allowing the models’ validity to be evaluated and reassessed during post-test analyses.

The prototype building that was tested on the shaking table consisted in a two-unit housing configuration, with each unit having similar layout but different height (Tomić et al. 2022a). The walls of the building were made of double-leaf irregular stone masonry with mortar joints. Floors were supported by timber beams with different orientations within the two units. The interface between the two units consisted in a dry connection with no interaction, like two structures which were built next to each other but in two different ages. The prototype was tested under two-component excitations, with increasing values of peak ground acceleration.

In this study we make use of the rigid block modelling approaches presented in (Portioli et al. 2014; Portioli 2020) to simulate the response of the tested aggregate building prototype. For the discretization of the masonry walls, a simple meso-modelling approach is adopted, with rectangular blocks representing more than one masonry unit and interacting at no-tension, frictional interfaces. This modeling approach is inspired by classic methods of limit analysis that are recommended in the Italian technical standard for the analysis of local failure mechanisms (NTC18 2018). According to the standard, the structure can be schematized into a system of rigid blocks interacting at frictional interfaces with infinite compressive strength. The use of frictional rigid block models is also specifically indicated in the standard for the determination of the failure modes associated to the lowest load multiplier corresponding to the onset of mechanism.

The adopted rigid block model represents a strong simplification of the masonry behavior in the case of stoneworks with irregular units and mortar, as in the case of the investigated prototype building. However, the use of a regular texture and the assumption of no-tension, frictional contacts are attractive for practical applications in different ways, including limited computational costs, simple discretization procedures and a more restricted number of parameters characterizing the structural response. The main aim of this study is to evaluate the applicability of the proposed rigid block modeling approach to the fast code-conforming seismic assessment of failure mechanisms for the aggregate stone masonry building tested in the framework of the SERA-AIMS project. Different analysis methods, namely, the limit and pushover analysis, used in conjunction with the force- and displacement-based assessment methods contained in (NTC18 2018), along with the time-history analysis are compared using the SERA-AIMS tests as a benchmark. For this purpose, two different models were implemented.

A 3D model was implemented in the prediction phase for the limit analysis of failure mechanisms of the building (Fig. 1a, b). The model reproduced the entire geometry of the experimental mock-up and allowed prediction analyses to be performed for the unretrofitted configuration only. The outcomes were the failure modes and the lateral load multipliers corresponding to their activation. Following the Italian technical standard’s provisions for the force-based seismic assessment of existing masonry structures (NTC18 2018), the lateral load multipliers could be related to the base shears and peak ground accelerations corresponding the damage (DLS) and the life-safety limit states (LSLS).

A 2D model was generated in the post-test phase, to include the non-linear static pushover and time-history analysis of the building (Fig. 1c). The latter were conducted in the longitudinal direction of the building and both the original and retrofitted configurations were considered. The outcomes were the failure modes and the displacements and base-shear time-histories. In the case of pushover analysis, the peak ground accelerations corresponding to the ultimate displacement was calculated according to the displacement-based method contained in the Italian technical standard (NTC18 2018).

Both rigid block models were generated using in-house software tools developed within a research activity carried out at the University of Naples, in collaboration with the Universities of Genova, Minho, Roma Tre, Sheffield, and RISE Research Institutes of Sweden. The analyses were not performed in incremental way, in that they did not consider the cumulative damage of the structure, but they were meant to represent the structure at different instances of the tests based on simplified code-conforming assumptions.

Differently from other discontinuous models such as the distinct element method and the applied element method, see e.g. (Calò et al. 2021; Hart et al. 1988; Malomo et al. 2020a, b), the rigid block modelling approach adopted here relies on a variational formulation of the problems associated to the limit (Cascini et al. 2020), non-linear pushover (Portioli et al. 2021) and time-history analysis (Portioli 2020). The optimization problems were here reformulated following a unified approach, based on the equivalence with the complementarity problems corresponding to the set of equations governing the behavior of the rigid block models. Based on the adopted approach, which was inspired by similar applications in the field of non-smooth and granular contact mechanics (Huang et al. 2013; Krabbenhoft et al. 2012; Meng et al. 2018), it can be shown that the mathematical programming problems used for the non-linear pushover and limit analysis represent special cases of the optimization problem formulated for the time-history analysis. The optimization problem solved for limit analysis is a force-based optimization problem which is expressed according to the classic formulation of the lower bound theorem. Similar force-based problems are also solved for the sequential limit analysis, used here for the non-linear pushover, and time-history integrations. In all cases, the displacements corresponding to the solution of the dual displacement-based problems are derived from Lagrange multipliers associated to the solution of the same force-based problem, thus reducing the computational costs.

Fig. 1
figure 1

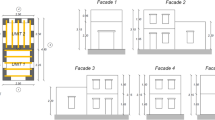
a CAD model of the aggregate masonry building with façade number; b 3D rigid block model for limit analysis used in the prediction phase, as part of the SERA-AIMS blind-prediction competition; c 2D rigid block model used for non-linear pushover and time-history analysis in the post-test phase; d rigid block idealization of external and internal forces at the generic contact point k, kinematic variables at block centroid and contact gaps

Full size image

The manuscript is organized as follows. Section 2 provides a brief description of the experimental program and results. Section 3 reports details of the optimization-based formulations adopted for the limit, pushover and time-history analyses. Section 4 discusses the results of the study undertaken during the prediction phase using the 3D limit analysis. Section 5 reports the results of the post-test study using the 2D rigid block modeling for comparisons between limit, pushover and time-history analyses, both on the original and retrofitted building configurations. Section 6 sums up the main findings of the study. It is worthwhile noticing that Sect. 4 is based on the blind-prediction competition, which was partially described in (Gagliardo et al. 2022). The present study represents a considerable extension of the contents presented therein.

2 Experimental program of the SERA-AIMS project

The masonry of the prototype aggregate building was made of two leaves of calcium-based sandstones of irregular shape with dimensions varying between 100 and 400 mm. The stones were placed on mortar joints with thickness of 5 to 20 mm. The walls of Unit 1 had a thickness of 30 cm, while those of Unit 2 were 35 and 25 cm for the first and second floor, respectively. The masonry properties shared for the blind prediction are reported in Table 1. Those were determined within a previous experimental investigation conducted at EUCENTRE and were obtained on the basis of vertical and diagonal compression tests on masonry elements made of materials similar to the ones used for the aggregate building (Senaldi et al. 2018).

Table 1 Estimates of the masonry properties based on the properties obtained from the EUCENTRE tests (Senaldi et al. 2018)
Full size table

Unit 1 had an U-shape and was built after Unit 2 with zero interlocking, in order to represent the new unit of the aggregate built adjacent to the existing one (Tomić et al. 2022a). The timber beams of the floors were simply supported on the walls. One layer of 2-cm-thick planks was nailed to the beams by two nails at each intersection. Additional masses of 1.5 tons were distributed on the two floors of Unit 2. The building was tested under one and two-component excitations using the 1979 Montenegro earthquake’s Albatros station records. A scaling factor of \(1/\sqrt{2}\) was used for the time of the ground motion considering that the aggregate was built at half scale.

The experimental program on the shaking table was organized into different steps with increasing values of the peak ground acceleration (Tomić et al. 2022a). At each step, three tests were planned, including a uni-directional shake in the y-direction, a uni-directional shake in the x-direction, and a bi-directional shake in the x- and y-directions. The applied testing sequence is reported in Table 2, where the level of shaking is expressed as a percentage of the shake-table capacity (0.875 g). Test runs were carried out both on the original configuration of the building and on the strengthened specimen after a widespread damage was observed (indicated with ‘S’ in the table).

Table 2 Testing sequence of the SERA-AIMS shake-table test (Tomić et al. 2022a)
Full size table

The largest peak ground acceleration was applied to the original aggregate in the test run # 2.1 and was equal to 0.593 g. After the run # 2.1, in-plane flexural and out-of-plane damage mechanisms were observed on Unit 2, see Fig. 2. Flexural diagonal and horizontal cracks formed on the 2nd story of façades 2 and 3 at the spandrels and piers, with residual width of about 5 mm and 1.4 mm, respectively (Tomić et al. 2022a). Flexural cracks were observed at the spandrels of façades 2 and 3 as well as in the middle pier of the 1st story, with residual width of about 1.9 mm and 1.2 mm. Horizontal cracks corresponding to the out-of-plane failure formed at the 1st floor level in façade 4 and at the level of interaction with Unit 1 in façade 5, with a residual width up to about 0.55 mm. These cracks were continuous with the orthogonal walls, thus confirming that the wall-to-wall connections were strong enough to trigger the flange effect. Signs of beam sliding in the upper floor of Unit 2 were also visible.

After the run # 2.1, the building was strengthened using steel angles and threaded rods to anchor the timber beams into the front and longitudinal walls of Unit 2 and new test runs were carried out (Fig. 2). No retrofitting intervention was applied to Unit 1, considering that no damage was observed on that unit during the tests on the unretrofitted specimen. The specimen was then subjected to uni-directional tests along the x and y-direction, with the largest peak ground accelerations corresponding to 0.425 and 0.615 g, respectively. After the run # 2.2 S, the visible damage on Unit 2 was similar to that of previous tests, with larger values of residual crack widths.

Figure 3 shows the experimental incremental dynamic analysis (IDA) curves, reporting the peak roof displacement of Unit 2 (Fig. 3a) and the interface opening between the two units along the y-direction (Fig. 3b) as a function of the inputted peak ground acceleration for test runs # 0.1, 1.1, 1.3 and 2.1, respectively. More details about the experimental mock-up and test campaign can be found in (Tomić et al. 2022a).

Fig. 2
figure 2

Annotated crack patterns (in red color) slightly shifted with respect to the original crack patterns (in black) in the graphical representation provided by the test organizers. Cracks observed in: a, b test run # 2.1, PGA = 0.593 g; c, d test run # 2.1 S, PGA = 0.615 g (Tomić et al. 2022a)

Full size image
Fig. 3
figure 3

Experimental incremental dynamic curves: a roof displacement of Unit 2 and b interface opening between Unit 1 and Unit 2, against inputted peak ground acceleration

Full size image

3 Formulations of rigid block modelling approach

According to the rigid block modelling approach, masonry is modelled as an assemblage of rigid blocks whereas deformation is concentrated at the interfaces (Fig. 1). In both the 3D and 2D models used for the present study, the blocks interact via no-tension frictional interfaces, with zero cohesion and infinite compressive strength. A point-contact model was adopted for the block interactions, with internal normal forces \({n}_{k}\) and shear forces \({t}_{k}\) associated at each contact point k located at the vertices of the interface. The normal forces are assumed to be positive when in compression. A single component of the shear force \({t}_{k}\) was considered for the 2D rigid block model (Fig. 1d), whereas two components \({t}_{1k}\) and \({t}_{2k}\) directed along a local coordinate system were used in the 3D model.

Three types of optimization problems were formulated and solved for the limit, pushover and time-history analysis.

According to the classical lower bound theorem of limit analysis, the problem solved for 3D limit equilibrium analysis can be expressed as a quadratically constrained optimization problem by the following matrix form (Portioli et al. 2014):

$$\begin{array}{ll}\text{m}\text{a}\text{x}& {\alpha }_{0}\\ \text{s}.\text{t}.& {\varvec{A}}_{0}\varvec{c}={\varvec{f}}_{\varvec{D}}+{\alpha }_{0}{\varvec{f}}_{\varvec{L}}\\ & \varvec{y}\le 0, \varvec{y}={\varvec{c}}^{\mathbf{T}}{\varvec{Y}}^{\mathbf{T}}\varvec{c}\end{array},$$
(1)

where \({\alpha }_{0}\) is the failure load multiplier at the onset of failure mechanism; \(\varvec{c}\) is the 3c \(\times\) 1 vector of the unknown internal forces, being c the number of contact points, collected into vectors for each contact point \({\varvec{c}}_{\varvec{k}}={\left[\begin{array}{ccc}{t}_{1k}& {t}_{2k}& {n}_{k}\end{array}\right]}^{\text{T}}\); \({\varvec{f}}_{\varvec{D}}\) is the 6b \(\times\) 1 vector of dead loads applied at the centroid of the blocks; \({\varvec{f}}_{\varvec{L}}\) is the vector of live loads; \({\varvec{A}}_{0}\) is the 6b \(\times\) 3c equilibrium matrix, with coefficients determined by the position of contact points and geometry of rigid blocks; \(\varvec{Y}\) is the coefficient matrix of the failure conditions corresponding to sliding failure at contact points; \(\varvec{y}\) is the vector of failure conditions. With reference to the contact point k, the matrix of failure conditions can be expressed as:

$${\varvec{Y}}_{\varvec{k}}^{\varvec{T}}=\left[\begin{array}{rrr}1& & \\ & 1& \\ & & -{\mu }^{2}\end{array}\right],$$
(2)

where \(\mu\) is the friction coefficient. The kinematic variables used for the identification of the failure modes corresponding to the solution of problem (1) are directly derived from Lagrange multipliers associated to the solution of the dual displacement-based optimization problem. Under these assumptions, it is worth noticing that sliding failures involve a dilatant behavior (associative behavior) which is related to the friction coefficient. Considering that failure multipliers corresponding to dilatant failure modes might be overestimated, an iterative solution procedure was implemented to take into account non-dilatant (non-associative) behavior, the latter corresponding to lower and hence safer collapse load multipliers. For more details, we refer to (Portioli et al. 2014).

For the 2D non-linear pushover analysis, the formulation presented in (Portioli et al. 2021) was adopted. The formulation relies more particularly on a rigid behavior and neglects the elastic behavior. A sequential solution procedure allows modelling the effects of large displacements on the lateral load multiplier and force capacity. The force-based optimization problem which is solved in this case at each increment is:

$$\begin{array}{ll}\text{m}\text{a}\text{x}& \alpha -{\varvec{g}}_{0}^{\mathbf{T}}\varvec{c}\\ \text{s}.\text{t}.& {\varvec{A}}_{0}\varvec{c}={\varvec{f}}_{\varvec{D}}+\alpha {\varvec{f}}_{\varvec{L}}\\ & \varvec{y}\le 0, \varvec{y}={\varvec{Y}}^{\mathbf{T}}\varvec{c}\end{array},$$
(3)

where \(\varvec{c}\) is the 2c \(\times\) 1 vector of unknown contact forces, collecting the subvectors \({\varvec{c}}_{\varvec{k}}={\left[\begin{array}{cc}{t}_{k}& {n}_{k}\end{array}\right]}^{\text{T}}\); \({\varvec{g}}_{0}\) is the 2c \(\times\) 1 vector collecting initial known gaps \({\left[\begin{array}{cc}0& {g}_{0k}\end{array}\right]}^{\text{T}}\) at each contact point. The expression of the matrix of failure conditions at contact point k for the 2D rigid block model is:

$${\varvec{Y}}_{\varvec{k}}^{\varvec{T}}=\left[\begin{array}{rr}1& -\mu \\ -1& -\mu \\ 0& -1\end{array}\right].$$
(4)

The optimization problem (3) reduces to the classic form of the 2D static problem of limit analysis for \({\varvec{g}}_{0}^{\mathbf{T}}\varvec{c}=0\), i.e., for the initial configuration of the block assemblage corresponding to \({\varvec{g}}_{0}=0.\)

Similarly to other analysis types, the following force-based optimization problem was solved at each time step \({t}_{0}\) of the 2D time-history analysis (Portioli 2020):

$$\begin{array}{ll}\text{m}\text{a}\text{x}& -\frac{1}{2}{\varvec{i}}^{\mathbf{T}} {\stackrel{-}{\varvec{M}}}^{-1}\varvec{i}-{\varvec{g}}_{0}^{\mathbf{T}}\varvec{c}\\ \text{s}.\text{t}.& {\varvec{i}+\varvec{A}}_{0}\varvec{c}={\stackrel{-}{\varvec{f}}}_{0}\\ & \varvec{y}\le 0, \varvec{y}={\varvec{Y}}^{\mathbf{T}}\varvec{c}\end{array},$$
(5)

where \(\varvec{i}=\stackrel{-}{\varvec{M}}\varvec{\Delta }\varvec{x}\) is the vector of the scaled inertia forces; \(\stackrel{-}{\varvec{M}}=\left(1/\varDelta {t}^{2}\right)\varvec{M}\), being \(\varvec{M}\) the diagonal matrix collecting masses and mass moment of inertia of the blocks; \({\stackrel{-}{\varvec{f}}}_{0}\) is the vector of the external scaled forces with \({\stackrel{-}{\varvec{f}}}_{0}=\varvec{f}+\stackrel{-}{\varvec{M}}{\varvec{v}}_{0}\varDelta t\), being \({\varvec{v}}_{0}\) the initial velocity at time \({t}_{0}\). The expressions of the scaled inertia forces, mass matrix and external forces are derived from the use of a time stepping scheme for the integration of the equation of motion. The scheme is based on the implicit Euler method and assumes that at time \(t={t}_{0}+\varDelta t\) accelerations and velocities are expressed as \(\varvec{a}\left(t\right)=\left(\varvec{v}-{\varvec{v}}_{0}\right)/ {\Delta }t\) and \(\varvec{v}\left(t\right)=\varvec{\varDelta }\varvec{x}/\varDelta t\), where \(\varvec{\varDelta }\varvec{x}\) is the vector collecting the displacements at the block centroids.

The integration algorithm for dynamics starts with the solution of problem (5) on the basis of known configuration and initial velocities at time \({t}_{0}\) (i.e. \({\varvec{A}}_{0}, {\varvec{g}}_{0}, {\stackrel{-}{\varvec{f}}}_{0})\). The equilibrium matrix, the vector of contact gaps and external forces are then updated based on the new configuration and a new problem (5) is set up and solved at time \(t={t}_{0}+\varDelta t\). A similar sequential solution procedure was implemented for the pushover analysis, which is based on lateral force and corresponding displacement increments at the control point. It is worth noting that the proposed time stepping involves a normal restitution coefficient (associated to translational velocities) equal to 0, which corresponds to a perfectly plastic response at impacts. As a consequence, the dissipation is only numerical and implicitly related to the size of the time step \(\varDelta t\) (Portioli 2020).

The Mosek tool (ver 9.1.10) was used to solve the linear, quadratic and quadratically constrained optimization problems formulated for the different analysis types (Andersen et al. 1996, 2003). In Mosek the quadratically constrained optimization problem (1) is converted internally into a conic form in order to save CPU time.

4 Prediction study by 3D rigid block model for limit analysis

This section presents the work undertaken for the participation to the blind-prediction competition. The 3D model used for the prediction of the test results was implemented using the in-house software ‘LiABlock_3D’ (https://doi.org/10.5281/zenodo.7051361), based on the formulation described in Sect. 3 for limit analysis. The software takes as input and analyzes models previously generated in a CAD environment, made by an assemblage of polyhedral rigid blocks. The software is provided with a simple Graphic User Interface (GUI), which can be used to assign input data, that is the weight for unit volume and friction coefficient. The GUI also allows assigning the loading and boundary conditions. The software returns the failure mechanism and the value of the load multiplier corresponding to the onset of failure.

The perimetral walls of the building were modelled as a double-leaf masonry, with transversal blocks connecting the two leaves (Fig. 1a). The irregular pattern of the masonry panels, which is an assemblage of rough stones of different size (Tomić et al. 2022a), was schematized adopting a simple meso-modeling approach using rectangular blocks. The shape and the dimensions of the blocks were selected in order to facilitate the generation of the 3D model with the developed in-house software tool as well as on the basis of some features of the masonry walls. In the case of Unit 1, rectangular blocks of dimension 15 × 15 × 15 cm interacting along the bed joints were used. For Unit 2, block dimensions were 17.5 × 15 × 15 cm and 12.5 × 15 × 15 cm, for the first and second floor, respectively. The depth of the blocks was selected in order to use two blocks for the modeling of the two-leave masonry walls (with thickness of 30 cm in Unit 1 and thickness of 35 and 25 cm in Unit 2). Considering that the stone blocks had dimensions varying between 100 and 400 mm (Senaldi et al. 2018), the height of the blocks was set equal to 150 mm to simplify the generation of the block assemblage and to reduce the computational cost. Since in rigid block models the force capacity increases as the block size ratio increases, the length of the blocks was also set equal to the height as a conservative choice. Special blocks were used to provide interlocking in the orthogonal walls, with length equal to the thickness of the walls plus the staggering length. In the interest of safety, interactions at the head joints were considered only for the interface between the two structural units. It should be noted that the sensitivity of the simple meso-modeling approach to the block shape and size might be remarkable. For these reasons, a sensitivity analysis was carried out in the post-diction study to investigate these features (Sect. 5). Various studies found that the response of masonry walls might be significantly affected by the bond pattern, see e.g. (Malomo et al. 2019; Page, 1981). Previous studies based on the adopted rigid block modeling approach showed that decreasing the block size ratio of 50% decreases the load multiplier of about 20% and slightly affects the failure mechanisms (Malena et al. 2019). Refined discontinuous meso-modeling approaches could be used to reduce the sensitivity to the block size by taking into account different failure modes in the masonry units, such as splitting and crushing. In these cases, it was shown that increasing the masonry unit size up to ten times the real size has seemingly no significant effect on the failure mechanisms and lateral strength (Pulatsu et al. 2020). Another study seems to confirm this trend (Dolatshahi et al. 2018).

The unit weight was set equal to 1980 kg/m3, according to the data provided during the competition. Considering that the material properties reported by Senaldi et al. (2018) did not include the friction coefficient and that were estimated on a masonry typology similar to the one used for the construction of the building prototype, the friction coefficient was set to 0.47, corresponding to a friction angle of 25°, according to an experimental study conducted on stone masonry piers made of a masonry typology that was also similar to the one of the mock-up (Godio et al. 2019). Another study appears to suggest a lower value, 0.34, for a more brittle masonry typology (Rezaie et al. 2020). As such, the friction coefficient used for the numerical analysis is lower than that recommended by the Italian technical standard for the verification of local failure mechanisms, which is equal to 0.58 (CNTC 2019). For simplicity, the coefficient of 0.47 was adopted also for the interfaces located at the connection between the timber beams used for the floors of the building and the masonry walls. An experimental study characterizing the mortar-timber friction in floor connections of masonry buildings shows that larger coefficients can be used, 0.47 representing a lower bound estimate of the coefficient for low contact forces (Almeida et al. 2020).

The timber joists were modelled using distinct rigid blocks. Additional masses of 1.5 tons per floor were distributed on the elements corresponding to the timber beams. As for the lateral loads \({\varvec{f}}_{\varvec{L}}\), a constant distribution of horizontal forces was applied, which was expressed as the blocks weight multiplied by the load multiplier \({\alpha }_{0}\). Two different directions were considered for the application of the lateral loads, one longitudinal (y) and one transversal (x) to the building (Fig. 1).

The failure mechanisms predicted by the model along the longitudinal directions are shown in Fig. 4a,b for forces of positive and negative sign, respectively. Both failure modes are overturning mechanisms involving the front walls and a portion of the sidewalls of Unit 2. In the case of lateral loads directed along the positive longitudinal direction, the mechanisms observed from the experimental test on façades 2 and 3 (Fig. 2a) are in quite good agreement with the numerical outcomes in terms of crack patterns (Fig. 4a). In fact, both numerical and experimental results show extensive damage concentrated in Unit 2 with the development of flexural cracks in the spandrels and the piers of the walls longitudinal to the excitation at the upper story. However, differences in the formation of flexural cracks in the piers at the first story can be noticed. In the experimental tests, diagonal flexural cracks were observed at the base of the middle pier of Unit 2, whereas flexural cracks in the outer pier are also predicted by the numerical model. The failure mechanisms corresponding to the lateral loads acting along the negative longitudinal direction were also slightly different from those observed in the experimental tests (Figs. 2b and 4b). The flexural crack which can be noted in the spandrel of the 1st story adjacent to Unit 1 in the numerical model was not observed in the experimental tests. Indeed, in this case the experimental failure mechanism in the longitudinal walls mainly involved flexural cracks in the piers of the 2nd story, due to the interaction with Unit 1. Differences in the position and distribution of the out of plane cracks can be also observed in the transversal walls of Unit 2, both for positive and negative y-direction (cf. Figs. 2 and 4). Although in the experimental tests horizontal cracks at the floor level and at the level of interaction with Unit 1 were observed on façades 4 and 5, horizontal out-of-plane cracks can be also noted in the numerical model at the ground level as well as the level of the openings of the 1st floor.

Fig. 4
figure 4

Prediction of test results by 3D rigid block model for limit analysis. Collapse mechanisms predicted by model in the positive a and negative b longitudinal directions (non-associative solution)

Full size image

The values of the predicted failure load multipliers are equal to 0.21 and 0.22 for the positive and negative y-directions respectively (Table 3). The value of the peak ground acceleration \({a}_{g}\) at the DLS and LSLS were estimated using the following expression, according to the provisions contained in the Italian technical standard for the force-based method (NTC18 2018):

$$a_{g} = \frac{{\alpha _{0} \cdot g \cdot q}}{{e^{*} \cdot CF}}$$
(6)

where \({\alpha }_{0}\) is the collapse load multiplier; \(g\) is the value of the gravity acceleration; \(q\) is the behavior factor, which is equal to 1.0 and 2.0 for the DLS and LSLS respectively; \({e}^{\text{*}}\) is the participating mass ratio; \(CF\) is the confidence factor. The participating mass ratio was calculated as follows:

$${e}^{*}= \frac{{\left[{\sum }_{k=1}^{N}{P}_{k}\cdot {\delta }_{Px,k}\right]}^{2}}{\left[{\sum }_{k=1}^{N}{P}_{k}\right]\cdot \left[{\sum }_{k=1}^{N}{P}_{k}\cdot {\delta }_{Px,k}^{2}\right]}$$
(7)

where \({P}_{k}\) is the total force applied to the block k involved in the failure mechanism; \({\delta }_{Px,k}\) is the horizontal virtual displacement corresponding to point of application of the force \({P}_{k}\). For the confidence factor \(CF\), a value equal to 1.35 was assumed, given the simplified modelling assumptions that were adopted during the blind prediction. Figure 5 shows the blocks participating in the failure modes, which were considered for the calculation of \({e}^{*}\) in Eq. (7). The values of the participating mass calculated by the model are 0.67 and 0.61 for the mechanisms in the positive (a) and negative (b) direction. Finally, the values of the corresponding base shear were estimated based on the mock-up weight and related peak ground acceleration (Table 3).

Fig. 5
figure 5

Prediction of test results by 3D rigid block model for limit analysis. Participating mass (in blue) for the collapse mechanisms in the positive a and negative b longitudinal directions (non-associative solution)

Full size image

Another set of analyses was performed to investigate the behavior of the building in the case of a lateral load applied along the transversal direction. The model parameters were the same as in the previous set of analyses. Figure 6 shows the resulting failure mechanisms and participating masses, considering both the positive and negative directions. Interestingly, the failure mode exhibits the overturning of the longitudinal wall of the shortest structural unit (Unit 1). It is worth to notice that only Unit 1 is involved in the mechanism due to the lack of box behavior which stems from the assumption of no connection between the units. Unit 2 is not affected by the failure in both load cases. In the case of the non-associative solution, the values of the collapse load multipliers obtained from the numerical simulation are equal to 0.17 for both the positive and the negative direction. The calculated values of the participating mass are equal to 0.69 and 0.71, respectively (Table 3). The peak ground accelerations along the longitudinal (y) and transversal (x) directions corresponding to the DLS appear to be comparable with the effective peak ground accelerations attained during the experimental test run # 1.3, equal to 0.208 g and 0.174 g for the y and x directions respectively, where no significant damage was observed except at the interface between the units (Tomić et al. 2022b). This is also in accordance with experimental IDA curves, showing an almost linear relationship between peak ground accelerations and control displacements for Unit 2 up to the test run # 1.3 (Fig. 3a). On the other hand, the peak ground acceleration predicted along the y-direction at the LSLS appears to be consistent with the largest experimental value obtained in the run # 2.1, equal to 0.593 g (Tomić et al. 2022b). However, the numerical value underestimates the experimental one, also because of the large value considered for the confidence factor \(CF\). Moreover, the peak ground acceleration in the test run # 2.1 corresponds to interstorey drifts that are larger than 4% (Fig. 3a). Those values appear to be comparable with the drifts that are specified in the standards for collapse limit state and with the ultimate drift obtained from the experimental tests reported in (Senaldi et al. 2018). Nevertheless, considering that only few test runs were available from the experimental investigations, the value of the experimental peak ground acceleration corresponding to test run # 2.1 is considered as a reference value for comparisons with the numerical LSLS in the following. The peak ground acceleration along the x-direction appears also to be underestimated, with no significant damage being reported from the tests up to 0.425 g. Further comparisons concerning the 3D rigid block limit analysis model are discussed in Sect. 5, where the effect of introducing contacts along the head joints is considered.

Fig. 6
figure 6

Prediction of test results by 3D rigid block model for limit analysis. Participating mass (in blue) for the collapse mechanisms in the positive a and negative b transversal directions (non-associative solution)

Full size image
Table 3 Results of the blind-prediction study using the 3D rigid block model for limit analysis
Full size table

A sensitivity analysis on the friction coefficient \(\mu\) was performed as part of the numerical investigations that were carried out during the blind prediction, in order to explore its effect on the collapse load multiplier \({\alpha }_{0}\) and failure mode predicted by the model. Figure 7 shows the outcomes of the analysis, in which the friction coefficient was varied between 0.2 and 0.7. The value of the collapse load multiplier increases with the friction coefficient, for both the associative and non-associative solutions. For all the investigated values of the friction coefficient an overturning mechanism of the front walls of the highest unit was obtained, except for \(\mu =0.2\), where the collapse mechanism slightly changed, showing a more important contribution of the horizontal sliding between the blocks. The values for \(\mu\) used in this paper and recommended by the Italian technical standard (Godio et al. 2019; Rezaie et al. 2020) differ by about 23% and lead to a change of only 5–10% in the load multipliers predicted by the model.

Fig. 7
figure 7

Prediction of test results by 3D rigid block model for limit analysis. Sensitivity analysis on the friction coefficient for a load applied in the positive a and negative b longitudinal direction

Full size image

5 Post-test study by 2D rigid block model for limit, pushover and time-history analysis

The post-test study extended the investigation initiated during the blind-prediction competition by using the 2D formulation presented in Sect. 3 for the non-linear static pushover and time-history analysis. Limit equilibrium analysis was also carried using the 2D model, allowing for the comparison with the 3D model used for the blind prediction and the other types of analysis that were conducted at this stage. Numerical analyses were carried out using the tool ‘DynABlock_2D’ (https://doi.org/10.5281/zenodo.6657392). The objective of the post-test study was to compare the experimental results corresponding to the test runs # 2.1 and # 2.1 S with the predictions obtained with the rigid block modeling approach by using other assessment methods than the force-based limit-analysis method used in the prediction study, namely, a non-linear static pushover used in conjunction with a displacement-based method, and a time-history analysis.

The 2D rigid block model used in the post-test study is a simplified version of the 3D model presented in Sect. 4, in that it represents only the longitudinal façade of the building prototype. The process undertaken to build the 2D model starting from the 3D building mock-up is shown in Fig. 8. Additional vertical loads \({P}_{i}\) were applied at each one of the blocks, indicated with corresponding colors in Fig. 8b,c, in order to include the loads transferred by the floor beams and transversal walls in the out-of-plane failure mechanism. As for the blocks corresponding to the floor beams, the vertical loads were calculated on the basis of the reactions at the supports of each joist. For the blocks corresponding to the transversal walls, the vertical loads were derived on the basis of the weight of half the length of these walls (Fig. 8a). The additional vertical load applied at each block was then calculated by dividing this weight by the number of corresponding blocks in the 2D model (Fig. 8c). The lintels in the 2D model had the same geometry than those designed for the tests, whereas in the 3D model their height was set equal to that of the masonry blocks to save modeling time.

Fig. 8
figure 8

Construction of the 2D rigid block model used in the post-test study starting from the 3D input geometry: a, c 3D and 2D models with identification of the blocks with increased load; b additional load \({P}_{i}\) applied to each block to account for the contribution of the transversal walls (values expressed in kN); d identification of the investigated building façade

Full size image

Differently from the prediction study, at this stage interactions were considered at both the bed and head joints, in order to properly take into account the impacts between the blocks and structural units occurring during the time-history analysis. For completeness, the same interactions were considered in the limit and pushover analysis. The value of the friction angle and the weight for unit volume were the same adopted in the prediction study, respectively 25° and 1980 kg/m3. In view of the comparison with the experimental tests, two control points, a and b, were selected at the left and right top of Unit 2 (Fig. 8c).

5.1 Limit and pushover analysis

A limit equilibrium analysis was carried out to preliminarily compare the 2D model with the 3D model used for the prediction study. Figure 9a shows the collapse mechanism resulting from the 2D model for the positive y-direction. Compared with the outcomes of the 3D models developed for the prediction study (cf. Fig. 4a), the mechanism obtained from the 2D model appears to be more localized, with a rigid rotation of a wedge on the right top and the development of the hinge at about middle height of the first floor.

Fig. 9
figure 9

Post-test study by 2D rigid block model. Collapse mechanisms from a, c limit analysis and b, d pushover analysis at a control displacement of 100 mm for lateral loads applied along the positive a, b and negative c, d y-direction. Different scale factors were used in a, c and b, d to display the deformation of the structure: in particular, the displacements occurring in a and c were more amplified than those displayed in b and d

Full size image

For the negative y-direction, the failure mechanism predicted by 2D limit analysis involves the out-of-plane failure of façade 1 in Unit 1 and is different from that observed in the experimental tests and from the 3D model used in the prediction study. For this reason, and also considering that the onset of failure mechanism along the y-negative direction corresponds to higher value of the load multiplier, only the results related to the positive y-direction are discussed in the following.

The collapse load multiplier resulting from the 2D limit analysis is 0.19 and the participating mass ratio is 0.66. The value of the corresponding peak ground acceleration was calculated according to the force-based method by Eq. (6). In line with the spirit of the post-test analysis, the confidence factor \(CF\) was set equal to 1.0 and, in order to refer to the LSLS, a behavior factor \(q=2.0\) was used. This results in a peak ground acceleration of 0.58 g.

During the pushover analysis, the structure was subjected to an incremental equilibrium analysis that was realized by setting a control displacement rate of 0.01 m and calculating the load factor corresponding to the updated configuration at each step. The resulting failure mechanism and pushover curve, obtained by plotting the value of the load factor versus the displacement of the control point a at the right top of Unit 2, are shown in Figs. 9b and 10a respectively. In general, as anticipated above, the failure mechanism obtained in the positive y-direction compares fairly well to the one obtained by limit analysis on the 3D model. However, here the seismic performance of Unit 2 appears to be affected by the development of a local mechanism of the top right lintel, which slides on the bottom block. When the overlapping length is attained, a local failure is produced, and this occurs before the development of the overturning mechanism of the front wall of said unit. This type of failure was not among those that were reported by the organizers (Tomić et al. 2022a). However, the cracks annotated in Fig. 2 indicate that the window corners were all cracked after the shakes. In addition, the plaster covering the lintels visibly fell off, which seems to point at a possible movement of the underlying substratum. Because of this local mechanism, the pushover curve returns a significantly lower value of the ultimate displacement (110.00 mm) when compared with the one that would be obtained in the case of a global overturning mechanism.

Fig. 10
figure 10

Post-test study by 2D rigid block model for pushover analysis. a Pushover curve; b acceleration-displacement response spectrum diagram for the definition of the predicted peak ground acceleration by the displacement-based method contained in (NTC18 2018)

Full size image

The displaced configuration corresponding to the ultimate displacement, when the lintel is about to fall, is shown in Fig. 9b. The corresponding point on the pushover curve is marked in red in Fig. 10a along with the configuration recorded right after failure.

The development of the above-described local mechanism is crucial to the definition of the response parameters to be used for the overall comparison with the experimental test and other numerical procedures. The displacement-based procedure reported in the Italian technical standard for LSLS (NTC18 2018) was applied for the calculation of the peak ground acceleration. The latter could be determined in the Acceleration-Displacement Response Spectrum (ADRS) diagram (Fig. 10b), by comparing the spectral demand with the spectral capacity. The capacity curve \({a}^{*}-{d}^{*}\) was derived starting from the pushover curve \(\alpha -d\) after calculation of the spectral acceleration \({a}^{*}\), by Eq. (6), and spectral displacement \({d}^{*}\), by \({d}^{*}=d{\varGamma }^{*},\) with \(q=1\) and \({\varGamma }^{*}=\sum {P}_{i}{\delta }_{x,i}^{2}/\left({\delta }_{x,C}\sum {P}_{i}{\delta }_{x,i}\right)\) the displacement factor. The procedure returns a value of 0.66 and 0.60 for e* and \({\varGamma }^{*}\), respectively.

The maximum spectral displacement on the capacity curve was calculated on the basis of the displacement corresponding to the activation of said mechanism. The value of the peak ground acceleration at the maximum allowable displacement was calculated by scaling the spectrum of the adopted seismic input in order to obtain a curve matching the specific displacement at a corresponding period \({T}_{LSLS}=1.68\pi \sqrt{{d}_{LSLS}^{*}/{a}_{LSLS}^{*}}\). The described approach leads to a value for the ultimate spectral displacement of 66 mm and a peak ground acceleration at the LSLS of 0.39 g.

A sensitivity analysis was carried out on the 2D pushover model in order to investigate the influence of the block size and size ratio on the failure load multiplier and ultimate displacement. To evaluate the sensitivity to the block size, the latter was varied from 10 to 20 cm, assuming a size ratio equal to 1 (Fig. 11a, b). For the sensitivity to the size ratio, blocks of dimension 15 × 20 cm and 15 × 25 cm were considered (Fig. 11c, d). The results of the sensitivity analysis showed that the value of the collapse load factor is only slightly affected by the block size and increases up to 8% as the size increases (Fig. 12a). The analysis also showed that the displacement capacity is more affected by the block size, varying between 110 mm (for large blocks) and 220 mm (for small blocks), while the block shape has a smaller influence on it (Fig. 12b). According to these results, it can be shown that the values adopted in this study bring a conservative result.

5.2 Time-history analysis

In order to run the time-history analysis, a support rigid block was added to the 2D model to simulate the shaking table and to impose the earthquake acceleration time-history. The rigid block model for time-history analysis takes as seismic input acceleration records. The test run # 2.1 was considered, with a PGA equal to 0.59 g. Both the displacements and accelerations of the shaking table were recorded during that run (Tomić et al. 2022a).

Fig. 11
figure 11

Sensitivity analysis on the block size and size ratio: displaced configurations at a roof displacement equal to 110 mm for blocks of dimension a 10 × 10 cm, b 20 × 20 cm, c 15 × 20 cm and d 15 × 25 cm

Full size image
Fig. 12
figure 12

Sensitivity analysis on the block size and size ratio: a collapse load factor \(\alpha\) versus block size and b ultimate displacement \({d}_{u}\) versus block size ratio

Full size image

A preliminary study was carried out to select the most appropriate seismic input to be used in the numerical model. The predicted and experimental displacement time history at the shaking table were compared using for seismic input the recorded accelerogram and the accelerogram obtained by deriving the experimental processed displacement record. Figure 13a shows the comparison between the experimental displacement time history at the shaking table, the numerical displacement time history obtained by applying at the support block the accelerogram derived from experimental recorded displacements and the numerical time history corresponding to the experimental recorded accelerogram. A better agreement with the experimental outcomes is observed when the analysis was performed using the accelerogram derived by the experimental displacement time-history (Fig. 13a). For this reason, this quantity was preferred to the acceleration record. To save CPU time, the time analysis was limited to the first 15 s corresponding to the main shocks.

With respect to the base shear (Fig. 13b), the experimental and numerical results are substantially in accordance, with low differences in some peaks probably due to the no-tension and no-cohesion assumption of the computational approach at the interfaces. As for the numerical model, the base shear was computed as the sum of the horizontal reactions per each step measured along the lower base of the blocks located at the foundation level. The maximum base shear predicted by the dynamic model is equal to 100.7 kN, i.e. about 50% less than the value experimentally observed. This difference could be ascribed to the large values of the rocking periods and to the non-uniform distribution of accelerations along the height of the building which are associated to the assumption of rigid, cohesionless material behavior and to consequent crumbling observed during the main shocks in the numerical analysis.

Fig. 13
figure 13

Post-test study by 2D rigid block model for time history analysis. Comparison between experimental and model seismic input motion a and base shear b. Test run # 2.1, PGA = 0.59 g.

Full size image

Figure 14 shows the evolution of failure mechanisms observed throughout the time-history analysis. At about 7.4 s, a rotation of the left side of Unit 1 can be observed (Fig. 14b): it is worth noticing that such a movement was not observed in the experimental test, where the shorter unit seems not to be involved at all in the mechanism. After this step, two main impact events are predicted by the numerical simulation, at about 9.0 (Fig. 14c) and 12.4 s (Fig. 14d), in agreement with the impacts observed in the experimental test concerning Unit 2 (Tomić et al. 2022a).

The comparison in terms of time history displacements at the control points a and b is shown in Figs. 15 and 16. In this case, the comparison is conducted in terms of both absolute displacement (Figs. 14a and 16a) and relative displacement with respect to the shaking table (Figs. 15a and 16b). The plots show that the absolute displacements predicted by the model are in good agreement with the experimental test results. In particular, the largest displacements are predicted within an error of about + 31% and + 15% in the case of point a and b respectively. The maximum displacement predicted by the numerical model refers to point a and it is equal to 131 mm. The comparison in terms of relative displacement is less satisfactory because of the time lag at which such large-amplitude oscillations occur. The rigid block model also allowed investigating one of the main topics proposed within the AIMS project, i.e., the behaviour of adjacent masonry units along their contact interface. Figure 15b shows the comparison between numerical and experimental results in terms of opening of the units’ interface. The figure shows that the main differences are related to the time lag where the maximum openings occur. However, the maximum amplitudes are in a good agreement between the numerical and experimental results. The maximum values of the interface openings are equal to 20 mm and 14 mm according to the experimental and numerical output respectively, with a difference equal to about − 34%.

Fig. 14
figure 14

Post-test study by 2D rigid block model for time history analysis (test run # 2.1 PGA = 0.59 g). a Comparison between experimental and numerical absolute displacement time-histories at the control point a; b–d deformation of the aggregate building at three different time steps of the analysis

Full size image
Fig. 15
figure 15

Post-test study by 2D rigid block model for time history analysis. Comparison between experimental and model displacement time-histories: a relative displacement at the control point a; b opening at the interface between the two masonry units

Full size image
Fig. 16
figure 16

Post-test study by 2D rigid block model for time history analysis. Comparison between experimental and model displacement time-histories: a absolute and b relative displacement at the control point b

Full size image

5.3 Numerical analysis of retrofitted building

The rigid block model of the retrofitted building is shown in Fig. 17a. Single blocks were used at the floor levels in order to represent the rigid-diaphragm constraint created by the retrofitting intervention. The mechanical properties of this model matched those of the unretrofitted model. As for the unretrofitted case, only the positive y-direction was investigated. The numerical investigation included limit equilibrium analysis, with the main objective to calculate the value of the load factor and the corresponding collapse mechanism, along with static pushover and time-history analysis. The test run # 2.1 S was considered for the time-history analysis.

Fig. 17
figure 17

Post-test study of the retrofitted building by 2D rigid block models for limit a and pushover analysis b

Full size image

The results of the limit and pushover analysis are shown in Fig. 17 in terms of collapse mechanisms. Thanks to the action of the introduced anchoring steel angles, the model is able to predict a mechanism characterized by the simple overturning of the upper floor of the Unit 2, in quite good accordance with the experimental outcomes. For the sake of comparison, the value of the peak ground accelerations corresponding to the predicted mechanism was calculated according to Eq. (6). The retrofitted model is part of the post-study analysis and, as a consequence, the value of the confidence factor was set equal to 1.0 and the behavior factor equal to 2.0. The adopted numerical procedure allowed obtaining a value of the collapse multiplier equal to 0.29, and a value of the participating mass ratio equal to 0.84. The peak ground acceleration results in 0.69 g.

Figure 18 shows the main outcomes of the pushover analysis in terms of pushover curve (Fig. 18a) and demand versus capacity (Fig. 18b). The procedure described in Sect. 5 was adopted for the development of the capacity curve, yielding a participating mass \({e}^{*}\) equal to 0.84 and a displacement factor \({\varGamma }^{*}\) equal to 0.94. The ultimate displacement results in 105 mm and the PGA in 0.40 g. As in the unretrofitted case, the pushover curve is stopped at the onset of a local failure mechanism, when the upper single-length block loses the contact with the block below and falls.

The results obtained from the time-history analysis are shown in Fig. 19. As in the unretrofitted case, the mechanism is initially represented by a rigid rotation of the left side of Unit 1, occurred at about 7.4 s and not observed in the experimental test. Next, the model shows two impact movements at about 12.4 and 13.0 s. It is worth noticing that these two movements are mainly located at the upper floor of Unit 2 thanks to the contribution provided by the intervention. As for the comparison with the experimental outcomes, these last two mechanism were also observed in the test run # 2.1 S.

The comparison between numerical and experimental results in terms of relative displacement at the control point a and opening at the interface is described in Fig. 20. Larger differences can be observed this time in terms of peak of displacements in the comparison with the experimental results (cf. Fig. 15a, b). The main reason could be ascribed to the simplified assumptions adopted to model the retrofitting interventions, using a single rigid block corresponding to the timber beams.

Fig. 18
figure 18

Post-test study of the retrofitted building by 2D rigid block model for pushover analysis. a Pushover curve; b acceleration-displacement response spectrum diagram for the definition of the predicted peak ground acceleration by the displacement-based method contained in (NTC18 2018)

Full size image
Fig. 19
figure 19

Post-test study of the retrofitted building by 2D rigid block model for non-linear time-history analysis (test run # 2.1 S, PGA = 0.61 g). a Comparison between experimental and numerical absolute displacement time-histories at the control point a; b–d deformation of the aggregate building recorded at three different instances of the analysis

Full size image
Fig. 20
figure 20

Post-test study of the retrofitted building by 2D rigid block model for time history analysis. Comparison between experimental and model displacement time-histories. Relative displacements at the control point a a and opening at the interface between the two masonry units b

Full size image

6 Discussion of results

To discuss advantages and drawbacks of the different rigid block models and assessment strategies undertaken in the pre- and post-test studies, a comparison between the experimental and numerical results is offered in Table 4 for the analyses conducted in the positive y-direction. The comparison refers to the experimental test runs # 2.1 and 2.1 S, performed respectively on the original and retrofitted building prototype. The results reported for the limit and pushover analysis refer to the values obtained for the LSLS. CPU times are included to evaluate the computational efficiency of the different analysis types. For consistency with the post-test analyses, the prediction model (denoted as ‘3D limit analysis’) was re-run after activating the interactions at both the bed and head joints, and using a confidence factor of 1.00 for the assessment. This new model brings a similar failure mechanism than that displayed by the 2D post-test model (Fig. 21), with an almost uniform rotation of the transversal walls instead of the two-way bending failure modes initially observed in the prediction study (cf. Fig. 9).

The comparison between the results achieved for the original prototype shows that limit analysis, used in conjunction with the force-based assessment method, is the most efficient and suitable analysis type among the developed rigid block models for the prediction of the failure mechanisms (Table 4). In this case, the difference between experimental and numerical peak ground accelerations and base shear is up to about + 13%. Larger differences in peak ground acceleration and base shear are observed for the pushover analysis, used in conjunction with the displacement-based method, reaching − 40%. The ultimate displacement predicted by pushover analysis is nonetheless in good accordance with the largest displacement recorded during the tests. For this reason, and considering that similar values of load multiplier and participating mass ratio for the onset of motion were obtained from the pushover and limit analysis, the difference in peak ground acceleration and base shear appears to be mainly related to the spectral displacement transformation factor \({\varGamma }^{*}\). As for the time-history analysis, the difference in terms of peak displacements and base shear is about + 30% and − 38%, respectively. However, as noticed in the comparison with the experimentally observed failure mechanisms, the pounding behavior is more accurately predicted by this type of analysis. Yet, the comparison in terms of CPU time shows differences up to four orders of magnitude between as compared to the pushover and limit analysis.

Similar considerations can be drawn for the retrofitted prototype, with the pushover analysis underestimating the acceleration capacity but quite accurately capturing the displacement capacity of the building, and all the other analysis methods giving results in line with the tests. Comparing the original with the retrofitted configuration, the results of limit and pushover analysis indicate that the retrofitting intervention only slightly affects the capacity of the building in terms of peak ground acceleration.

Fig. 21
figure 21

Failure mechanisms (non-associative solution) predicted by 3D rigid block model for limit analysis with frictional contacts at both bed and head joints for the original a and retrofitted building b

Full size image
Table 4 Results of the post-test study using the rigid block modelling approach: summary of numerical and experimental results
Full size table

This appears to agree with the testing protocol used for experimental tests, where similar values of accelerations were attained on both the original and retrofitted building prototype. Looking at the results from 3D limit analysis, the effect of the retrofitting intervention appears to be even slightly detrimental in terms of peak ground accelerations, due to the different values of participating mass ratio. Larger differences between the predicted peak ground acceleration are obtained in the case of 2D limit analysis, because of the different values obtained for the load multipliers. Generally, the comparisons in terms of maximum base shear shows that, in the case of the retrofitted building, the experimental values are even more underestimated with respect to the case of the unretrofitted configuration. It is also worth noticing that during experimental tests a remarkable increase of the base shear was measured, although a similar seismic input was applied.

7 Conclusion

The results of a numerical study using the rigid block modelling approach on an aggregate stone masonry building tested on the shaking table were presented in this paper. The models proposed here were formulated according to the simplified rigid block modelling assumptions recommended in the Italian technical standard for the analysis of local collapse mechanisms (NTC18 2018). The models offered a cross-comparison over a whole range of analysis types. This included the 3D limit analysis, used for the prediction of the experimental tests on the unretrofitted building, as well as the 2D limit, pushover and time-history analysis, used in the post-test phase on both the original and retrofitted building. The force and displacement capacity of the building prototype in the limit and pushover analysis were determined according to the force- and displacement-based seismic assessment methods for existing masonry structures contained in (NTC18 2018).

Based on the comparisons with the experimental observations, the following conclusions can be reached:

  • For the direction of lateral load that does not involve pounding effects on the tallest structural unit, the out-of-plane failure mechanisms with flange effects predicted by rigid block limit analysis model in the longitudinal walls of the aggregate building compared reasonably well with the experimental tests;

  • Limitations were found when using the limit and pushover analysis to describe the in-plane and out-of-plane failure mechanisms brought on by pounding, or the interaction between structural units. The cause could be searched in the constant distribution of horizontal forces used in these types of analysis, which, in light of the results of this study, should be reconsidered for aggregate buildings subjected to pounding;

  • In the analyses conducted in this study, interactions at the head joints had a substantial impact on the form and location of the obtained failure mechanisms, especially in the case of failure mechanisms associated to pounding;

  • In the case of the original building prototype, the peak ground acceleration and base shear produced by limit analysis for the life safety limit state, using a unitary confidence factor, were close to the ones of the test run with the largest peak ground acceleration, with differences of about + 13%. Larger differences were however obtained for the damage limit state, and in the case of the retrofitted building. Experimental and numerical investigations are undoubtedly required to promote a better definition of the limit states for stone masonry buildings and aggregates, including those retrofitted;

  • The displacement-based assessment carried out in conjunction with the 2D pushover analysis showed differences in terms of failure modes with respect to experimental outcomes, similar to those observed in the limit analysis. Moreover, peak ground acceleration and base shear were largely underestimated by the model mainly because of the small value of the calculated spectral displacement capacity. As observed in the study, this was the result of a localized failure that was predicted by the model at one of the top lintels;

  • The results of the time-history analysis conducted by the 2D rigid block model compared reasonably well with the experimental tests in terms of failure mechanisms related to pounding. However, crumbling failures of the piers and out-of-plane failure modes in the lowest unit were obtained in the numerical model, but were not visible from the test results. The modelling of the tensile and cohesive strength of the joints, although expectedly very narrow for this masonry typology, could lead the rigid block model to a better representation of the response of these structures, limiting the occurrence of sparse joint openings;

  • Differences up to about − 34% were observed between experimental and numerical displacements at the interface between the two structural units in the time-history analysis on the original building prototype. Larger differences were obtained for the relative displacements recorded at the top of the tallest unit, mainly due to the duration of oscillations with maximum amplitudes, which was overestimated in the numerical analysis. Similar scatters were observed for the retrofitted building.

Further comparisons with other experimental tests and parametric analyses should be carried out to generalize the conclusions of the present study, which are based on a single case study. Differences of the proposed rigid block models with the experimental tests can be mainly ascribed to the simplified rigid, no-tension, cohesionless contact behavior assumed at the blocks’ interfaces, whose effect on the structural response must be explored by the rigid block model. Further sources of discrepancies with the experimental tests can be ascribed to the modeling of the structural elements, such as the floors and retrofitting interventions. Introducing their elastic behavior and tensile strength at the interfaces with the walls represent a possible further development of the present study to improve the accuracy of the adopted optimization-based modeling approach.