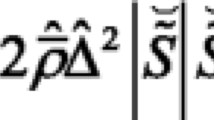An a priori DNS analysis of scale similarity based combustion models for LES of non-premixed jet flames

Abstract

In this work, recently developed finite-rate dynamic scale similarity (SS) sub-grid scale (SGS) combustion models have been a priori assessed and compared with the Eddy Dissipation Concept (EDC) and “no model” approaches based on a Direct Numerical Simulation (DNS) database of a temporally evolving non-premixed jet flame. Two different filter widths, one placed in the inertial range and the other in the near dissipation range, have been used. The analyses were carried out in two time instants corresponding to instants of maximum local extinction and re-ignition. Conditional averaged filtered chemical source terms, conditioned on different parameters in the composition space, have been presented. Improvements are observed using the dynamic SS models compared to the two other approaches in the prediction of filtered chemical source terms of individual species while using larger filter widths. However, discrepancies still exists using the dynamic SS model on the turbulent/non-turbulent interfaces of the jet, mainly in the prediction of the oxidizer consumption rate.

1 Introduction

Combustion of fossil fuels is the primary source of energy production. However, the combustion of conventional fuels is prone to pollutant formation and emissions. The formation of pollutants is an unsteady phenomenon which requires relatively detailed kinetics for its modelling. Moreover, the rapid mixing processes with high levels of turbulence intensities implemented in combustion devices may cause undesired consequences like local extinction and the subsequent re-ignition processes. These processes, in turn, increase emissions and flame instability. The extinction and re-ignition processes are unsteady phenomena which contain Finite-Rate (FR) chemistry effects. The two examples highlight the fact that FR chemistry and its interaction with turbulence are of great importance in the study of turbulent flames.

Due to increased computational power available today, Computational Fluid Dynamics (CFD) has become a promising tool in the study of processes like extinction and re-ignition, pollutants formations, or in general turbulent flames. Reynolds Average Navier-Stokes Simulation (RANS) is not usually applicable due to its time-averaged results so that unsteady effects cannot be captured. Among Direct Numerical Simulation (DNS) and Large Eddy Simulation (LES) approaches, the application of the former is limited up-to-now to low-to-medium Reynolds numbers and simple computational geometries/setups. This is due to a prohibitive computational burden of performing DNS of reactive flows with detailed chemistry. However, DNS results can be exploited to develop or assess sub-models in RANS or LES. LES of reactive flows has become more popular nowadays. Unsteady process like the two examples mentioned before can be predicted by LES. Unlike DNS which resolves all the scales of a motion, only large scales are captured directly by LES while effects of small scales need to be modelled. Detailed/FR chemistry can be directly incorporated into reactive LES codes by solving the transport equations of filtered species mass fractions. Each species filtered mass balance equation has an unclosed source term of chemistry. Sub-grid scale (SGS) combustion models are required to account for the effects of unresolved fluctuations in flow and composition fields or in general to account for turbulence-chemistry interactions (TCI). FR-TCI models in LES, namely FR-TCI-SGS models, are those with no assumption about the flow or flame, attempting to model the low-pass filtered production/consumption rates directly [1]. Some examples of FR-TCI-SGS models for non-premixed flames are the transported PDF (TPDF) models [2, 3], the Partially Stirred Reactor (PaSR) model [4], the Eddy Dissipation Concept (EDC) [5], the “Laminar FR model” or “no model” approach [6], the conditional moment closure (CMC) models [7], and the Scale Similarity (SS) models [8, 9]. The focus of the present work is on SS models.

The Scale Similarity models first were developed by Bardina et al. [10] to model the SGS stress tensor in LES for non-reactive flows. The idea was applied to develop FR-TCI-SGS models by DesJardin and Frankel [8]. They proposed two models, namely the scale similarity resolved reaction rate model (SSRRRM), hereafter model A, and the scale similarity filtered reaction rate model (SSFRRM), hereafter model B. Another FR-TCI-SGS SS model, model C, can be developed based on the idea of Germano et al. [11], which was reviewed in [12]. In the so-called non-dynamic FR-TCI-SGS SS models, the similarity coefficient is set equal to one [8, 12, 13]. Jaberi and James [9] extended the non-dynamic model A using the Germano identity to evaluate the SS coefficient dynamically. This model (hereafter DA) was tested using a DNS database of homogeneous, isotropic, reacting turbulent flow with a one-step Arrhenius reaction, showing encouraging results compared to the non-dynamic version. Shamooni et al. [14] applied the identity on models B and C and derived different variants of the dynamic FR-TCI-SGS SS models. An a priori analysis was carried out using DNS databases of temporally evolving non-premixed jet flames, experiencing high levels of local extinction followed by re-ignition, with different Reynolds numbers (the so-called cases L, M and H [15]). In their analyses using a fixed filter width (set equal to $\mathrm {\overline {\Delta }=12{\Delta }_{DNS}}\approx 12\underline {\eta }_{f}$, with Δ_DNS the DNS [15] grid size and $\underline {\eta }_{f}$ the Favre averaged Kolmogorov length scale), improvements were observed in the prediction of filtered heat release rates compared to the non-dynamic models in the highest Reynolds flame. The current work is the extension of the previous analysis in [14] which will be focused on the effect of filter width and flame regimes, i.e., the regime in which a flame experiences a high level of local extinction or when it is re-igniting. The methodology is to use DNS datasets in an a priori manner. DNS databases of reactive flows with relatively detailed chemistry can be utilised through a priori or a posteriori DNS analyses to assess/develop the combustion models for LES [16]. An a priori DNS analysis is adopted by comparing modelled targets (here filtered chemical source terms) with the exact targets (filtered DNS data). Moreover, exact LES-like quantities which were directly filtered from DNS are used as model inputs. While a priori analyses have been used in many previous studies (see e.g., [17,18,19,20,21,22,23]), the outcomes should not be overrated. One of the drawbacks of a priori analyses is that the error which is produced and propagated in dynamical systems can not be observed. The reverse is also true which means that models that fail in a priori studies may work well in real LES. Knowing the drawbacks of this type of analysis, it is chosen as a good starting point in the development phase due to the availability of LES like quantities without relying on turbulence models. In this work an a priori DNS analysis will be carried out using a well-documented DNS of a temporally evolving non-premixed syngas jet flame, the so called case H [15], which exhibits local extinction followed by re-ignition. The objective is to investigate the performance of newly developed dynamic FR-TCI-SGS SS models using filter widths either in the inertial range or when placed in the near dissipation range. Moreover, the secondary objective is to study the models’ capability in different flame conditions mentioned above.

The paper is organized as follows. In the next section, dynamic finite-rate sub-grid scale Scale Similarity models for LES (FR-TCI-SGS SS models) and the EDC model for LES will be briefly presented. Next, the DNS database will be introduced following a discussion on the choice of filter widths selected for the current analysis. The results of the a priori analysis will be presented and final conclusions will be drawn.

2 FR-TCI-SGS Models

2.1 Dynamic SS models

In Large Eddy Simulation (LES) of reactive flows with detailed kinetics, the transport equations of filtered species mass fractions are solved. The filtered mass conservation equation for species k, has a filtered production/consumption rate (the chemistry source term), i.e. $\overline {\dot {\omega } }_{k}\left (\boldsymbol {\varphi } \right )$, which needs to be modelled. In $\overline {\dot {\omega } }_{k}\left (\boldsymbol {\varphi } \right )$, φ is the composition vector together with the temperature (T) and pressure (p), and $\overline {(.)}$ a filtering operator. $\overline {(.)}^{f}$ is the Favre filtering operator defined as $\overline {\rho (.)}/\overline {\rho }$ with ρ the density. Finite-rate SGS combustion models (FR-TCI-SGS models) try to include the effects of turbulence on chemistry in such a way that $\overline {\dot {\omega }}_{k}\left (\boldsymbol {\varphi } \right )$ can be calculated by the use of filtered fields, viz. $\overline {\boldsymbol {\varphi }}^{f}$. Dynamic Scale Similarity (SS) models, are types of FR-TCI-SGS models which use the scale similarity idea of Bardina et al. [10] to directly model the filtered chemistry source terms and the Germano identity, to model the resulting coefficient of similarity. The first dynamic FR-TCI-SGS SS model is the dynamic version of SSRRRM [8], in this work called DA, which was proposed in [9]:

$$ {\overline{\dot{\omega }}}^{DA}=\dot{\omega }({\overline{\boldsymbol{\varphi }}}^{f})+C^{\overline{\Delta }}_{DA}\ {\mathcal{L}}_{{\dot{\omega }}^{A}} $$

(1)

with ${{\mathcal{L}}}_{{\dot {\omega }}^{A}}$ as:

(2)

and $C^{\overline {\Delta }}_{DA}$ computed by applying Germano’s identity:

$$ C^{\overline{\Delta }}_{DA}=\left( {\underline{{\mathrm{\Upsilon }}_{\mathrm{A}}{\mathcal{X}}_{A}}}\right)/\left( {\underline{ {\mathcal{X}}_{A}{\mathcal{X}}_{A}}}\right) $$

(3)

where $\underline {(.)}$ is a Reynolds averaging operator will be defined later. ${\mathcal {X}}_{A}$ is computed by:

(4)

and Υ_A is:

$$ {\mathrm{\Upsilon }}_{\mathrm{A}} = \widehat{\dot{\omega }}({\overline{\boldsymbol{\varphi }}}^{f}) - \dot{\omega }({\widehat{\overline{\boldsymbol{\varphi }}}}^{f}) $$

(5)

The different filters, namely the “simple filter” ($\overline {(.)}$), and the “grid filter” , have been introduced in the Appendix. Briefly, they are filters with similar filter widths equal to the grid size they are acted on, however, since the numerical implementations are different, to avoid ambiguity, different notations have been used. The “simple-grid filtered” quantities are mathematically similar to the ones already exist in the literature (see eg., [8, 9, 24,25,26,27]).

The second dynamic model, is the dynamic version of SSFRRM [8] was derived in [14]. Model DB reads:

(6)

where the residual field, viz. ${{\mathcal{L}}}_{{\dot {\omega }}^{B}}$, is:

(7)

Using Germano’s identity $C^{\overline {\Delta }}_{DB}$ can be found as:

$$ C^{\overline{\Delta }}_{DB}=\left( {\underline{{\mathrm{\Upsilon }}_{\mathrm{B}}{\mathcal{X}}_{B}}}\right)/\left( {\underline{ {\mathcal{X}}_{B}{\mathcal{X}}_{B}}}\right) $$

(8)

where Υ_B is

(9)

and

(10)

The third dynamic model is the dynamic version of a SS model in which, based on the proposals of Liu et al. [28] and Germano [11], a test filter ($\widehat {{\Delta }}=2\overline {{\Delta }}$) instead of the grid filter has been used in the similarity model formulation. In [12] this proposal was extended to calculate finite-rate formation rates of species. The dynamic version, called DC, was derived in [14] which reads:

$$ {\overline{\dot{\omega }}}^{DC}(\boldsymbol{\varphi })=\dot{\omega }({\overline{\boldsymbol{\varphi }}}^{f})+C^{\overline{\Delta }}_{DC}\ {\mathcal{L}}_{{\dot{\omega }}^{C}} $$

(11)

where

$$ {\mathcal{L}}_{{\dot{\omega }}^{C}}= {\widehat{\dot{\omega }}}(\overline{\boldsymbol{\varphi}}^{f})- {{\dot{\omega }}}(\widehat{\overline{\boldsymbol{\varphi}}}^{f}) $$

(12)

The similarity coefficient then can be calculated following [29] and writing the Germano’s identity for the two filter levels. This results in [14]:

$$ C^{\overline{\Delta }}_{DC}=\left( {\underline{{\mathrm{\Upsilon }}_{\mathrm{C}}{\mathcal{X}}_{C}}}\right)/\left( {\underline{ {\mathcal{X}}_{C}{\mathcal{X}}_{C}}}\right) $$

(13)

In Eq. 13, Υ_C is:

$$ \begin{array}{llll} {\mathrm{\Upsilon }}_{C}=\widehat{\dot{\omega }}({\overline{\boldsymbol{\varphi }}}^{f})-\dot{\omega }({\widehat{\overline{\boldsymbol{\varphi }}}}^{f}) \end{array} $$

(14)

and ${\mathcal {X}}_{C}$ is:

$$ {\mathcal{X}}_{C}=\left( \overbrace{\dot{\omega }}({\overline{\boldsymbol{\varphi }}}^{f})-\dot{\omega }({\overbrace{\overline{\boldsymbol{\varphi }}}}^{f})\right)-\left( \widehat{\widehat{\dot{\omega }}}\left( {\overline{\boldsymbol{\varphi }}}^{f}\right)-\widehat{\dot{\omega }}({\widehat{\overline{\boldsymbol{\varphi }}}}^{f})\right) $$

(15)

where $\overbrace {(.)}$ represents a spatial filter at scale $4\mathrm {\overline {\Delta }}$.

The derivations are comprehensively discussed in [14]. In Eqs. 3, 8, and 13, $\underline {(.)}$ is a Reynolds averaging operator. It must be mentioned that in the current work, the averaging operator is a spatial one. Since the case is a temporal jet (not a conventional statistically stationary jet) with two homogeneous directions (Ox and Oz), the spatial average of a quantity, q, is defined as:

$$ \underline{q}(y,t) \equiv \frac{{\sum}_{n3=1}^{n3=N_{z}}{\sum}_{n1=1}^{n1=N_{x}}q(x_{n1},y,z_{n3},t)}{N_{x}N_{z}} $$

(16)

which is a function of time and the crosswise direction,Oy. In Eq. 16, N_x and N_z are the number of computational cells or data-points in Ox and Oz homogeneous directions, respectively. Favre averaged quantities can be defined likewise as $\underline {\rho q}/\underline {\rho }$ where the Favre averaging operator is denoted by $\underline {(.)}_{f}$. The steps to compute all Favre filtered quantities needed in the models are explained in the Appendix. For simplicity, compact notations have been used in the formulas above. The exact notations are provided in Table 1 to avoid confusions. Since the Germano identity has been applied on scalar fields, the final formula to compute the similarity coefficient could be different from what has been used in Eqs. 3, 8, and 13. Both mean, viz. $C^{\overline {\Delta }}={\underline {{\mathrm {\Upsilon }}}}/{\underline { {\mathcal {X}}}}$ and local, viz. $C^{\overline {\Delta }}={{{\mathrm {\Upsilon }}}}/{{ {\mathcal {X}}}}$, methods of the evaluation of the coefficients in the three models were analysed and found to produce large errors. The least square minimization method in Eqs. 3, 8, and 13 was found to reproduce the best results. Finally, no clipping has been performed on the final coefficient except avoiding very low formation rate values in the denominator of Eqs. 3, 8, and 13.

Table 1 1D implementation of different filters used in the current study

2.2 EDC model

The Eddy Dissipation Concept (EDC) [30, 31] has been selected, as a coarse-grained finite-rate combustion model commonly used in LES of practical applications, to compare the performance of dynamic SS models.

The EDC model is based on the idea that chemical reactions take place when fuel and oxidizer are perfectly mixed on the molecular level. Originally, it was developed based on RANS arguments where the Favre mean turbulent dissipation rate, $\underline {\varepsilon }_{f}$, has been used as a mixing rate indicator. The intrinsic internal intermitteny of the instantaneous turbulent dissipation rate, ε, has been accounted for by considering reaction spaces as regions occupying only a fraction of physical space. These highly dissipative regions are called fine structures within which everything is well mixed. The step-wise turbulence cascade model [30] has been used to evaluate the scales of these regions. In terms of LES, this reads [5, 32]:

$$ \begin{array}{@{}rcl@{}} L^{*}&=&\frac{2}{3}\left( \frac{3{CD_{2}}^{3}}{{CD_{1}}^{2}}\right)^{1/4} \left( \frac{{\overline{ \nu}}^{3}}{\varepsilon_{\nu,SGS}} \right)^{1/4} \end{array} $$

(17a)

$$ \begin{array}{@{}rcl@{}} u^{*}&=&\left( \frac{{CD_{2}}}{3{CD_{1}}^{2}}\right)^{1/4} \left( {{\overline{ \nu}}}{\varepsilon_{\nu,SGS}} \right)^{1/4}, \end{array} $$

(17b)

where $\overline {\nu }$ is filtered viscosity and ε_ν,SGS is viscous dissipation of turbulent kinetic energy in sub-grid, i.e. Eq. 18. CD₁ and CD₂ are two model coefficients resulted from proportionality relations in the cascade model. CD₁ = 0.135 and CD₂ = 0.5 are common choices for RANS applications [31]. The same values have been used so far for LES applications (see e.g. [5, 32, 33]). In the current work similar values have been used.

In the a priori DNS analysis, the above mentioned scales can be directly computed by using DNS data. The exact sub-grid viscous dissipation is defined as:

$$ \varepsilon_{\nu,SGS}=\frac{1}{\overline{\rho}} \left( \overline{\tau_{ij}S_{ij}}-\overline{\tau_{ij}}\overline{S_{ij}}^{f}\right), $$

(18)

where τ_ij is the viscous stress tensor:

$$ \tau_{ij}\equiv 2\mu \left( S_{ij}- {\Delta}_{v} \delta_{ij}/3 \right), $$

(19)

with μ the molecular viscosity of mixture and S_ij the symmetric part of velocity gradient tensor, viz. $\frac {\partial u_{i}}{\partial x_{j}}$:

$$ S_{ij}\equiv\frac{1}{2}\left( \frac{\partial u_{i}}{\partial x_{j}}+\frac{\partial u_{j}}{\partial x_{i}} \right). $$

(20)

In Eq. 19, Δ_v = S_ii is the flow dilatation and δ_ij the Kronecker delta.

Using the above defined velocity and length scales, one can find the mass transfer rate between dissipative (fine) structures and surroundings per unit of mass of fine structures:

$$ {\dot{m}^{*}_{LES}} \equiv2 \frac{u^{*}}{L^{*}}, $$

(21)

so that the time scale of fine structures can be defined as:

$$ \tau^{*}_{LES} \equiv \frac{1}{\dot{m}^{*}_{LES}}. $$

(22)

Moreover, the volume fraction occupied by fine structures is computed by [5, 32]:

$$ \gamma^{*}_{LES}=\left( \frac{{u^{*}}}{{u^{SGS}}}\right)^{2}, $$

(23)

with u^SGS the velocity scale at the sub-grid level which can be calculated using the sub-grid scale turbulent kinetic energy, k_SGS:

$$ u^{SGS}=({\frac{2}{3}k_{SGS}})^{1/2}\equiv \left( \frac{2}{3}\frac{\left( \overline{u_{i}u_{i}}^{f} - \overline{u_{i}}^{f}\overline{u_{i}}^{f}\right)}{2}\right)^{1/2}. $$

(24)

Finally [5]:

$$ \overline{\dot{\omega}_{k}}=\frac{\overline{\rho}\gamma^{*}_{LES}}{1-\gamma^{*}_{LES}}\frac{\left( {Y^{F}_{k}}-{Y^{0}_{k}} \right)}{\tau^{*}_{LES}}, k=1..N_{s} $$

(25)

In Eq. 25, it is assumed that the fine structures are batch reactors with input compositions of ${Y^{0}_{k}}={\overline {{\varphi }_{k}}}^{f}$. The governing ODEs of each reactor is solved over a fine structure residence time, $\tau ^{*}_{LES}$, and the solutions, i.e. ${Y^{F}_{k}}$ will be used in Eq. 25 to evaluate filtered net production/consumption rates. OpenSMOKE++ [34] has been used for ODE integration.

As already mentioned, in the a priori analysis all of the terms introduced in the model can be computed directly from DNS databases. This will enable us to assess the model performance using exact inputs. Moreover, the fact that the model has two fitting coefficients, makes it a good candidate to be compared with the dynamic SS models where coefficients are evaluated dynamically.

3 The DNS Database

The numerical experiment (DNS) database used in the current study is a DNS of a temporally evolving non-premixed syngas jet flame [15] experiencing a high level of local extinction. The schematic of the DNS configuration is shown in Fig. 1. Finite-rate chemistry has been considered in the DNS by using a chemical kinetic mechanism with 11 species and 21 elementary reactions which can be found in [15]. Case H (a case with the highest Reynolds number among the flames studied in [15]) has been selected for the current a priori analysis. The same kinetics as the one in the DNS has been used in the current work. Reynolds number is defined as Re ≡ UH/ν_fuel = 9079, with H = 1.37mm the initial fuel jet width, U = 2 × 138m/s difference between fuel (CO/H₂) and oxidizer (O₂/N₂) streams velocities and ν_fuel initial kinematic viscosity of the fuel stream [15]. Two time instants of the DNS, i.e., t = 20t_j, t = 30t_j, has been studied. t_j = H/U = 5μs is “transient jet time” [15]. In Fig. 2a, the maximum of Favre mean temperature ($\underline {T}_{f}$) in the DNS is plotted versus simulation time with vertical red lines show the two instants selected in this study. The mean effect of extinction and re-ignition phenomenon is seen in the figure by the decreasing and increasing maximum (among the Oxz planes with different crosswise locations) of mean temperature. The first time instant (t = 20t_j) is an instant corresponding to the maximum local extinction while the second instant (t = 30t_j) is during the re-ignition process.

Fig. 1

The schematic of the temporal jet DNS case, with contours of heat release rate (back) and mass fraction of OH (front) at the maximum extinction time (t = 20t_j). Periodic boundary conditions has been used in Ox and Oz directions

Fig. 2

(a) Maximum Favre averaged temperature in [K] during the simulation with vertical lines showing the time instants selected for the current study. (b) Percentages of the resolved TKE using different filter widths versus the normalized crosswise distance from the central Oxz plane at t = 20t_j. The vertical lines show the crosswise locations of mean stoichiometric mixture fraction

In Fig. 3 the normalized 1D velocity spectra ($E_{11}^{{1D}}(\kappa _{x})$) computed in the central Oxz plane of the DNS configuration are plotted for the two time instants, with κ_x the streamwise component of the wavenumber vector. $E_{11}^{{1D}}$ is computed by the 1D Fourier transforms of the streamwise Favre fluctuations of velocity ($u^{\prime \prime }=u-\underline {u}_{f}$). Then $E_{11,norm}^{1D}(\kappa _{x} \underline {\eta }_{f})={E_{11}^{1D}(\kappa _{x})}/\left ({{\underline {\varepsilon }_{f}}^{2/3} {\underline {\eta }_{f}}^{5/3}}\right )$, with ${\underline {\varepsilon }_{f}}$ the Favre averaged turbulent kinetic energy (TKE) dissipation rate and $\underline {\eta }_{f}$ the Favre averaged Kolmogorov length scale, can be calculated. The $\kappa _{x}^{-5/3}$ scaling is also shown in the figure. The locations of the spectral cutoff filters with the same filter widths as top-hat kernels are also shown. It is observed that due to the relatively low Reynolds number of the jet, the inertial range is somehow narrow. The location of the filter with the width of $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$ can be considered to be in the inertial range, however, $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ is in the near dissipation range.

Fig. 3

Normalized 1D velocity spectrum versus the normalized wavenumber extracted from the central Oxz plane of case H at two time instants. Vertical lines show the locations of the spectral cutoff filters with the same filter width as top-hat kernels

In Fig. 2b, the corresponding percentages of the resolved TKE using each filter width are depicted. Using $\mathrm {\overline {\Delta }=8,18{\Delta }_{DNS}}$, almost 80% and 60% of the TKE will be resolved, respectively. In [35], an a posteriori analysis was carried out using the same DNS database with a filter with width of $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$. In another a posteriori analysis in [36] using the similar DNS case H, $\mathrm {\overline {\Delta }=8,16{\Delta }_{DNS}}$ were used. In [37], where an a posteriori analysis of LES-LEM models using case M (the same DNS configuration as the current study, however with lower Reynolds number of about 4478) was carried out, a filter widths of about $\mathrm {\overline {\Delta } \approx 2.5,5{\Delta }_{DNS}}$ have been used. Considering the previous analyses using the similar DNS database, $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ and $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$ are found to be reasonable choices. Although as can be seen in Fig. 3, $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ seems to be small. It is of interest to see how dynamic SS models behave when filters are located in different locations in the spectrum. Moreover, it should be taken into account that in the current study, the filter widths are chosen in such a way that future a posteriori analyses will be applicable. In LES of double shear layer configurations, enough grid points are needed inside the jet. Using $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ and $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$, 9 and 4 cells exist in the initial jet width, respectively. In the DNS test case 72 cells exist in the initial jet width.

4 Results and Discussions

4.1 Extinction time

Conditional averages of CO in the composition space conditioned on mixture fraction, CO mass fraction, and temperature are shown in Fig. 4. The “no model approach”, viz. ${\dot {\omega }}^{noModel}\left (\boldsymbol {\varphi }\right )=\dot {\omega }({\overline {\boldsymbol {\varphi }}}^{f})$, neglecting SGS effects are also shown in these figures. It should be mentioned that in the conditional mean plots, conditioned on mass fractions and also temperature, last bins are not shown due to lack of data in the composition space caused by the extinction event. The exact filtered data from the DNS database are also shown in the right plots of Fig. 4 as scatter points. As it can be seen, since the flame is in extinction mode, a small fraction of cells have reached high temperatures. This causes the divergence of the statistics in the last bins (high temperature and high CO consumption rate) of the joint PDF. This is the reason why deviations are observed in the right tail of the conditional averages (conditioned on temperature). This effect is higher when using $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$ (see the right corner of Fig. 4f) because much less data points (≈ 1/11) are available to extract conditional statistics. The reduction of data points is due to sampling on a coarse grid after applying the explicit filter (see the Appendix). Now it is obvious that using $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ there is almost no need for an SGS model for CO. Some discrepancies exist using the “no model” in the oxidizer sides (see Fig. 4a and b) which are improved using the dynamic SS models DA and DC. The EDC model also performs reasonably in the reaction zone and around stoichiometric mixture fraction (Z_st ≈ 0.42) while near the cold stream it behaves nearly similar to the “no model” approach. In Fig. 5a the conditional average of intermittency factor, γ^∗, conditioned on Favre filtered mixture fraction is shown for $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ at t = 20t_j. The factor is computed by Eq. 23 using exact extracted turbulence quantities. As can be seen, the factor is close to 0.5 so that $\frac {\gamma ^{*}}{1-\gamma ^{*}}$ in Eq. 25 is ≈ 1. In Fig. 5b the logarithm of residence time computed by Eq. 22 is shown in mixture fraction space. In this figure, high values at the left side are in laminar oxidizer region which do not affect the results. As can be seen the residence time of fine structures computed by EDC model is low so that the final consumption rate of fuel computed by EDC model is very close to the one computed by the “no model” approach. The “no model” approach uses Arrhenius instantaneous reaction rates.

Fig. 4

Conditional mean results of $\overline {\dot {\omega }}_{\text {CO}}$ [kg/m³/s] conditioned on the mixture fraction, CO mass fraction and temperature [K] using different models and compared to the DNS data. (Top) $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ and (bottom) $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$. The filtered DNS data points are also shown using scatter plots

Fig. 5

EDC parameters for computations using $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ at t = 20t_j. a Conditional mean of intermitteny factor, γ^∗ in EDC, conditioned on Favre filtered mixture fraction. b Scatter plots of logarithm of EDC residence time, τ^∗ versus Favre filtered mixture fraction

In Fig. 4d, e, and f the models are tested using larger explicit filter width of $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$. While the choice of such a large filter width seems to be aggressive for a double shear layer cases (see the fraction of resolved kinetic energy in Fig. 2b), the main reason is to assess the performance of SS model while the filter is placed in the inertial range of the spectrum (see also Fig. 3). The first observation is the failure of the EDC model in the core jet region while the other models still behave reasonably. The “no model” results are now showing increased errors compared to the results using the smaller filter width. As already mentioned, low number of available data points resulted in unconverged conditional statistics at the right tale of Fig. 4f. Similar behavior and predictions for the other fuel, i.e. H₂ and major products like CO₂ and H₂O were observed and are not reported for the sake of brevity.

In Fig. 6, the conditional mean plots for O₂ (the oxidizer) are presented. In the first row of Fig. 6 where the results using $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ are shown, again one may conclude that using this filter width, the scalar fluctuations have been almost resolved (although it is not the case for velocity fluctuations, see Fig. 3). Improvements can be observed compared to the “no model” and EDC approaches which become more pronounced in the case of using $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$ (see the Fig. 6d–f). It is interesting to see the large effect of the filter width on the EDC model by increasing it from $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ to $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$ while dynamic SS models DA and DB can almost adapt themselves. The predictions in the cold oxidizer streams (the air streams around the main fuel stream) show errors while in the jet core region (where the mean fuel stream exists) and around the Favre mean stoichiometric plane ($\underline {Z}_{f}=0.422$ [15]) are in a resealable agreement with the filtered DNS data. Among the major species only $\overline {\dot {\omega }}_{\mathrm {O_{2}}}$ failed to be correctly predicted near the cold streams and the results of, e.g., $\overline {\dot {\omega }}_{\text {CO}}$, $\overline {\dot {\omega }}_{\mathrm {H_{2}O}}$, or $\overline {\dot {\omega }}_{\mathrm {CO_{2}}}$, did not show this failure. The reason for this discrepancy in the models predictions needs more investigations as discussed below.

Fig. 6

Conditional averaged results of the dynamic SS models in the prediction of $\overline {\dot {\omega }}_{\mathrm {O_{2}}}$ [kg/m³/s] compared with the exact filtered DNS values for case H at t = 20t_j (maximum extinction instant). In the first row the filter width is $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ while in the second row $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$ has been applied. The temperature is in Kelvin. Legends are similar to Fig. 4

In Fig. 7 the contour of oxygen consumption rate, viz. $\overline {\dot {\omega }}_{\mathrm {O_{2}}}$, on the central (in Oz direction) Oxy plane of the jet at t = 20t_j is shown. All results are filtered values on the coarse (Δ = 8Δ_DNS) grid. Figure 7a is the exact filtered rate obtained from DNS while Fig. 7b is the prediction of dynamic model DA. Figure 7c is the same as Fig. 7b where only positive values are kept. The reason of focusing on these values is that the errors already observed in the conditional plots of Fig. 6 are caused by positive values of $\overline {\dot {\omega }}_{\mathrm {O_{2}}}$ (see Fig. 6c and f). Finally Fig. 7d shows the positive values of prediction of non-dynamic SS model A, i.e., C_DA = 1. In these figures the magenta lines are the isolines of stoichiometric mixture fraction, i.e. Z_st = 0.422. The outer green lines are the detected turbulent/non-turbulent (T/NT) interfaces. To detect the T/NT interface, the method in [38] has been used. The vorticity magnitude is defined as:

$$ w\equiv\sqrt{{w}_{x}^{2}+{w}_{y}^{2}+{w}_{z}^{2}}, $$

(26)

where w = (w_x,w_y,w_z) ≡∇×U with U the velocity vector. A threshold, w_threshold, is introduced based on the 10% of the mean w on the central plane of the jet [38, 39] where any region below this threshold is considered as non-turbulent. This method is applied on the filtered velocity field on the coarse grid of Δ = 8Δ_DNS and the isolines are shown in In Fig. 7 on the central (in Oz direction) Oxy plane of the jet at t = 20t_j.

Fig. 7

Contour of $\overline {\dot {\omega }}_{\mathrm {O_{2}}}$ in [kg/m³/s] with T/NT detected interface (outer green lines) and the stoichiometric mixture fraction isoline (inner magenta lines). a Exact filtered value from DNS. (b Prediction of dynamic SS DA model. c Only positive values in prediction of dynamic SS DA model. (c) Only positive values in prediction of non-dynamic SS A model. Results are at t = 20t_j for Δ = 8Δ_DNS

By comparing Fig. 7a and b it can be observed that inside the highly turbulent region (surrounded by green lines) the model performs well. Main reactions occurs near stoichiometric isolines which were captured and predicted by DA. In Fig. 7c, it is clearly observed that the wrong positive values predicted by $\overline {\dot {\omega }}_{\mathrm {O_{2}}}^{DA}$ are mainly on the T/NT interface where a sharp vorticity jump occurs. Finally, comparing Fig. 7c and d, it can be found that the source of error is in the wrong prediction of the base non-dynamic model A. If C_DA = 1 in Eq. 1, the non-dynamic SS model A will be recovered. In this model, ${{\mathcal{L}}}_{{\dot {\omega }}^{A}}$, i.e. Eq. 2 is positive at the T/NT interface and higher than the other term in Eq. 1 so that the positive values are observed in Fig. 7d. Double grid filtering of composition vector generates artificially mixed states. Near the T/NT interface, due to sharp changes, the effect is higher. This in turn causes higher consumption rates of oxygen in the right term in Eq. 2. Also note that the condition is the same for both ${{\mathcal{L}}}_{{\dot {\omega }}^{B}}$ and ${{\mathcal{L}}}_{{\dot {\omega }}^{C}}$ in Eqs. 7 and 12, respectively.

In Fig. 8 the similarity coefficient computed by DA is shown along with the mean T/NT interface location which is an indication of the external intermittency. A sharp reduction of the coefficient to -0.0007 on the right side and -0.0003 on the left side is observed which coincides with the mean interface location. This shows that the dynamic procedure could capture the effect, however, the reduction of the coefficient is not enough. This can be due to the least square minimization used for the final computation of the dynamic coefficients in Eqs. 3, 8, and 13, for dynamic models DA, DB and DC, respectively. In the current version of the implementation of the models, no limiter has been applied so that only the least square minimization produced reasonable results (see also the discussion in the last paragraph of Section 2). Conditions are the same for H radical which will be seen in the next figures. Possible solutions will be discussed in the conclusion section.

Fig. 8

Similarity coefficient computed by dynamic SS model DA at t = 20t_j for Δ = 8Δ_DNS. Vertical lines show the mean T/NT interface location

In Fig. 9, the conditional mean statistics for H radical are presented. As can be seen, for this specific radical, TCI is high even using $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$. Although there still exists errors in different conditional statistics, improvements compared the “no model” and EDC approached using dynamic SS models are clearly observed. Again a discrepancy already discussed is observed by all dynamic procedures near the cold stream (see Fig. 9c and d).

Fig. 9

Conditional averaged results of the dynamic SS models in the prediction of $\overline {\dot {\omega }}_{\mathrm {H}}$ [kg/m³/s] radical compared with the exact filtered DNS values for case H at t = 20t_j. In the first row the filter width is $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ while in the second row $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$ has been applied. Legends are similar to Fig. 4

4.2 Re-ignition time

At t = 30t_j the flame is re-igniting (see Fig. 2a where the maximum of mean temperature across the shear layers is increasing) and the main mechanism found to be the folding of burning packets onto the extinguished regions [40]. It is of interest to test the performance of dynamic FR-TCI-SGS models when the flame regime is changing.

In the investigation of the conditional plots (not reported here), it was revealed that using $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$, the turbulence effect on most of the major species source terms is small. By increasing the filter width to 18Δ_DNS, it is still observed that the “no model” approach can capture the trends while the EDC model produces larger errors. This is shown in Fig. 10 where the conditional mean of $\overline {\dot {\omega }}_{\mathrm {H_{2}}}$ and $\overline {\dot {\omega }}_{\mathrm {CO_{2}}}$, conditioned on mixture fraction are depicted. As can be see, the errors in the conditional means while using $\overline {\dot {\omega }}\left (\boldsymbol {\varphi }\right )=\dot {\omega }({\overline {\boldsymbol {\varphi }}}^{f})$ are not high, although it is clear that dynamic SS models show better predictions. The radicals, however, show stronger interactions. In Fig. 11 the conditional means (conditioned on the mixture temperature) of $\overline {\dot {\omega }}_{\mathrm {H}}$ and $\overline {\dot {\omega }}_{\mathrm {O}}$ are plotted. Using both EDC and “no model” approaches, the formation rates predictions show large error while dynamic SS models better predict radicals formation rates. Again a systematic over-prediction of $\overline {\dot {\omega }}_{\mathrm {H}}$ by all three dynamic SS models can be observed in the cold stream in Fig. 11a. As discussed before this is due to failure of base non-dynamic SS models at T/NT interfaces.

Fig. 10

Conditional average of a$\overline {\dot {\omega }}_{\mathrm {H_{2}}}$ [kg/m³/s] and b$\overline {\dot {\omega }}_{\mathrm {CO_{2}}}$[kg/m³/s], conditioned on the mixture fraction at t = 30t_j. The filter width is $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$. The DNS data points are also shown by scatter plots. The vertical axes are bounded to lower values for clarity

Fig. 11

Conditional average of a$\overline {\dot {\omega }}_{\mathrm {H}}$ [kg/m³/s] and b$\overline {\dot {\omega }}_{\mathrm {O}}$ [kg/m³/s], conditioned on temperature [K] at t = 30t_j. The filter width is $\mathrm {\overline {\Delta }=18{\Delta }_{DNS}}$. The DNS data points are also shown by scatter plots. The vertical axes are bounded to lower values for clarity. Legends are similar to Fig. 4

5 Summary and Conclusions

In this work an a priori analysis of the newly developed dynamic finite-rate scale similarity models for LES (FR-TCI-SGS SS models) was performed using a DNS database of a temporally evolving syngas non-premixed jet flame, the so-called case H [15]. Moreover, the Eddy Dissipation Concept (EDC) was a priori studied as a coarse-grained combustion model typically used in pratical applications. The a priori analysis was carried out using two explicit filters, placed in different spectral locations (in wavenumber), one in the so-called inertial range and the other in the near dissipation range. Moreover, two time instants of the time dependent DNS database were considered corresponding to an instant when the flame experiences its maximum local extinction and an instant during the re-ignition process. The objective was to study the effect of these parameters on the performance of the dynamic SS models. The performance was assessed by analyzing the predicted filtered chemistry source terms and comparing them with the exact filtered ones from the DNS databases. Comparisons have been also carried out with the “no model” and EDC approaches.

At both extinction and re-ignition times, it was observed that using $\mathrm {\overline {\Delta }=8{\Delta }_{DNS}}$ (with which the filter is placed in the near dissipation range), the interaction between turbulence and chemistry is not so high for major species. Specifically in the re-ignition phase, it seems that due to the already decayed turbulence and/or approximately homogeneous mixture, filtered net production/consumption rates of major species can be approximately predicted by using no SGS combustion model. The EDC model found to produce more reliable results using the lower filter width compared to the larger one. The dynamic models resulted in better predictions compared to the “no model” and EDC approaches in the cold stream sides of the jet. In radicals, the interactions are higher so that the “no model” and EDC approaches failed to predict correctly the conditional means while all the three variants of the dynamic models better predict the conditional means. However, discrepancies still exists in the prediction of oxygen and H radical using SS models which were found to occur on the turbulent/non-turbulent interfaces on both sides of the jet. Closer investigation of one of the dynamic models, i.e., DA, showed that the dynamic procedure can capture the average location of the issue as the rapid reduction of the similarity coefficient coincides with the mean interface locations on both side of the jet. However, the reduction of the coefficient does not suffice to account for the failure of the base non-dynamic model. This can be due to the averaging procedure in the evaluation of the dynamic SS coefficients. Future works can be focused on other alternatives rather than averaging in the full statistically stationary direction for example filtering in smaller domains. In this way one may gain more from dynamic procedures since the local attributes of the methods can be exploited. In this paper the results without using any limiter in the model are presented to highlight the conditions/locations where the SS models fail. Although it is suggested to search for other alternatives rather than least square minimization in Eqs. 3, 8, and 13 to overcome the issue in predictions on the T/NT interfaces, one can still apply the dynamic procedures with least square minimization method using limiters.

Future works will be focused on an a priori analysis of the models in different combustion regimes. The analysis should be completed by performing a posteriori one. Finally, the models can be applied in real LES of experimental setups.

Appendix: Implementation of Explicit Filters

In this work, the top-hat filter is chosen to filter the DNS fields and produce LES-like quantities explicitly. The top-hat filter corresponds to the filter implicitly associated with the discretization used in finite volume codes in LES [41]. In Table 1 the numerical implementation of different filter types using the trapezoidal rule is explained in 1D for simplicity. The equations described in Table 1 are applicable to structured meshes which is usually the case for the DNS databases.

The “simple filter”, $\overline {(.)}$, is a top-hat filter with a filter width ($\overline {{\Delta }}$), N times the grid size, viz. $\mathrm {\overline {\Delta }}=N{{\Delta }^{*}}$. The “simple filter” is usually applied on the original DNS data so that ${{\Delta }^{*}={\Delta }_{DNS}}$. Consider that the DNS grid is a uniform grid so that the filter width is uniform. The application of the “simple filter” on the DNS fields creates LES-like quantities. In a posteriori DNS analyses or real LES, there is no need to apply the “simple filter” because the solution of the filtered NS equations gives “simple filtered” quantiles. In the present a priori study and in general for the a priori analysis to be consistent [28], after the first filtering level to produce LES-like quantities, the “simple filtered” data should be sampled on a coarser grid (the hypothetical LES grid). This means for example if $\mathrm {\overline {\Delta }}=8{{\Delta }_{DNS}}$, and the DNS mesh is (N_x,N_y,N_z) = (864, 1008, 576), $\overline {q}$ will be defined only on a grid with ($\frac {864}{8},\frac {1008}{8},\frac {576}{8}$) and in the case of $\mathrm {\overline {\Delta }}=18{{\Delta }_{DNS}}$, it will be defined on mesh composed of ($\frac {864}{18},\frac {1008}{18},\frac {576}{18}$) grid cells in Ox, Oy, Oz directions, respectively. The sampling will be only done in the first filtering level to produce LES-like quantities. Due to the constraint imposed in the models, no more sampling can be done for other filtering levels. It means, for example , is defined on the same grid as $\overline {q}$, or this is also the case in $\widehat {\overline {q}}$ which is defined on the same grid as $\overline {q}$. It should be taken into account that in some unstructured LES codes, e.g. OpenFOAM [42], the similar approach (no sampling after the application of the test filter) has been used for the application of the Germano identity in dynamic turbulence models.

The 3D filtered data is computed by three consecutive applications of each 1D formula in Ox, Oy, and Oz directions, respectively. The “1^st test filter” and “2^nd test filter” are simple top-hat filters with fixed filter widths of 2 and 4, respectively. Different filtering levels can be created by applying different filters sequentially. For example the “1^st test-simple-filtered” data is computed by the application of the “1^st test filter” in already “simple filtered” fields using a kernel with $\widehat {\Delta }=2\overline {\Delta }$. In 3D, it reads:

$$ \left\{\begin{array}{llll} \overline{q}_{i,j,k}^{*}=\frac{1}{4}\left( \overline{q}_{i+1,j,k} +2\overline{q}_{i,j,k}+\overline{q}_{i-1,j,k}\right) \\ \overline{q}_{i,j,k}^{**}=\frac{1}{4}\left( \overline{q}_{i,j+1,k}^{*} +2\overline{q}_{i,j,k}^{*}+\overline{q}_{i,j-1,k}^{*}\right)\\ \widehat{\overline{q}}_{i,j,k}=\frac{1}{4}\left( \overline{q}_{i,j,k+1}^{**} +2\overline{q}_{i,j,k}^{**}+\overline{q}_{i,j,k-1}^{**}\right) \end{array}\right\} $$

(27)

The “grid filter”, , is virtually the same filter as the “simple filter” but with a different numerical implementation. In this work the method of Zang et al., [27] has been exploited. The “double grid filtered” data can be created by applying the “grid filter” to a “simple filtered” quantity (an LES-like quantity) which in 3D reads:

(28)

In the SS models presented in this paper, quantities are needed to be filtered/Favre filtered in different levels. Throughout the paper, a compact notation has been used, the exact notations as well as the sequential steps for the computation of Favre filtered quantities are explained in Table 2. Beside the Favre filtered quantities (i.e., species mass fraction and temperature), filtered source terms need to be computed in the FR-TCI-SGS SS models. To this end, first, the source terms need to be calculated using kinetics tool boxes like OpenSMOKE++ [34] or Cantera [43]. No ODE system is required to be solved; the Arrhenius reaction rates should be calculated to form the net formation rates of the individual species.

Table 2 The sequential steps to compute the Favre filtered quantities required for the FR-TCI-SGS SS models