Abstract
Vibration reduction has always been one of hot and important topics in mechanical engineering, especially for the special measurement instrument. In this paper, a novel limb-inspired bionic structure is proposed to generate negative stiffness and design a new quasi-zero stiffness isolator via torsion springs, distinguishing from the existing tension spring structures in the literature. The nonlinear mathematical model of the proposed structure is developed and the corresponding dynamic properties are further investigated by using the Harmonic Balance method and ADAMS verification. To evaluate the vibration isolation performance, typical three-springs quasi-zero stiffness (TS QZS) system is selected to compare with the proposed bionic structure. And the graphical processing unit (GPU) parallel technology is applied to perform necessary two-parameter analyses, providing more insights into the effects of parameters on the transmissibility. It is shown that the proposed structure can show advantages over the typical TS QZS system in a wider vibration isolation range for harmonic excitation case and shorter decay time for the impact excitation case.
Graphic abstract
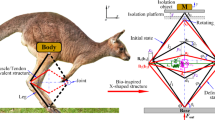
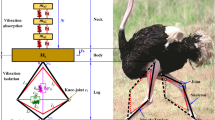
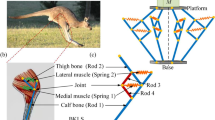
A novel limb-inspired bionic structure is proposed to generate negative stiffness and design a new quasi-zero stiffness isolator via torsion springs. To evaluate the vibration isolation performance, typical three-springs quasi-zero stiffness (TS QZS) system is selected to compare with the proposed bionic structure. It is shown that the proposed structure can show advantages over the typical TS QZS system in a wider vibration isolation range for harmonic excitation case and shorter decay time for the impact excitation case.



















Similar content being viewed by others
References
Liu, J., Ou, H., Zeng, R., et al.: Fabrication, dynamic properties and multi-objective optimization of a metal origami tube with Miura sheets. Thin-Walled Struct. 144, 106352 (2019)
Zhao, G., Liu, J., Wen, G., et al.: Stick-slip behavior of reversing the tubular woven bag covering a rigid tube-theoretical and numerical studies. Results Phys. 12, 1218–1227 (2019)
Ma, J., Chen, G., Ji, L., et al.: A general methodology to establish the contact force model for complex contacting surfaces. Mech. Syst. Signal Proc. 140, 106678 (2020)
Yin, S., Ji, J., Deng, S., et al.: Degenerate grazing bifurcations in a three-degree-of-freedom impact oscillator. Nonlinear Dyn. 97, 525–539 (2019)
Wen, G., Xu, D.: Nonlinear observer control for full-state projective synchronization in chaotic continuous-time systems. Chaos Solitons Fractals. 26, 71–77 (2005)
Omidi, E., Mahmoodi, S.N.: Nonlinear integral resonant controller for vibration reduction in nonlinear systems. Acta Mech. Sin. 32, 925–934 (2016)
Wang, F., Xu, J.: Parameter design for a vibration absorber with time-delayed feedback control. Acta Mech. Sin. 35, 624–640 (2019)
Rivin, E.I.: Passive Vibration Isolation. ASME Press, New York (2001)
Ye, K., Ji, J., Brown, T.: Design of a quasi-zero stiffness isolation system for supporting different loads. J. Sound Vib. 471, 115198 (2020)
Ibrahim, R.A.: Recent advances in nonlinear passive vibration isolators. J. Sound Vib. 314, 371–452 (2008)
Carrella, A., Brennan, M.J., Waters, T.P., et al.: Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 55, 22–29 (2012)
Xu, J., Sun, X.: A multi-directional vibration isolator based on Quasi-Zero-Stiffness structure and time-delayed active control. Int. J. Mech. Sci. 100, 126–135 (2015)
Cao, Q., Wiercigroch, M., Pavlovskaia, E. E., et al.: Archetypal oscillator for smooth and discontinuous dynamics. Phys. Rev. E 74, 046218 (2006).
Zhao, F., Ji, J., Ye, K., et al.: Increase of quasi-zero stiffness region using two pairs of oblique springs. Mech. Syst. Signal Proc. 144, 106975 (2020)
Huang, X., Liu, X., Sun, J., et al.: Effect of the system imperfections on the dynamic response of a high-static-low-dynamic stiffness vibration isolator. Nonlinear Dyn. 76, 1157–1167 (2014)
Shaw, A.D., Neild, S.A., Wagg, D.J., et al.: A nonlinear spring mechanism incorporating a bistable composite plate for vibration isolation. J. Sound Vib. 332, 6265–6275 (2013)
Zhou, N., Liu, K.: A tunable high-static–low-dynamic stiffness vibration isolator. J. Sound Vib. 329, 1254–1273 (2010)
Shan, Y., Wu, W., Chen, X.: Design of a Miniaturized Pneumatic Vibration Isolator With High-Static-Low-Dynamic Stiffness. J. Vib. Acoust. 137, 045001 (2015)
Dong, G., Zhang, X., Xie, S., et al.: Simulated and experimental studies on a high-static-low-dynamic stiffness isolator using magnetic negative stiffness spring. Mech. Syst. Signal Proc. 86, 188–203 (2017)
Zheng, Y., Zhang, X., Luo, Y., et al.: Analytical study of a quasi-zero stiffness coupling using a torsion magnetic spring with negative stiffness. Mech. Syst. Signal Proc. 100, 135–151 (2018)
Zhou, J., Wang, X., Xu, D., et al.: Nonlinear dynamic characteristics of a quasi-zero stiffness vibration isolator with cam-roller-spring mechanisms. J. Sound Vib. 346, 53–69 (2015)
Ye, K., Ji, J., Brown, T.: A novel integrated quasi-zero stiffness vibration isolator for coupled translational and rotational vibrations. Mech. Syst. Signal Proc. 149, 107340 (2021)
Li, M., Cheng, W., Xie, R.: Design and experiments of a quasi-zero-stiffness isolator with a noncircular cam-based negative-stiffness mechanism. J. Vib. Control 0, 1–13 (2020).
Meng, L., Sun, J., Wu, W.: Theoretical design and characteristics analysis of a quasi-zero stiffness isolator using a disk spring as negative stiffness element. Shock Vib. 2015, 1–19 (2015)
Sadeghi, S., Li, S.: Fluidic origami cellular structure with asymmetric quasi-zero stiffness for low-frequency vibration isolation. Smart Mater. Struct. 28, 065006 (2019)
Tuo, J., Deng, Z., Zhang, H., et al.: A 3-axis torsion quasi-zero-stiffness-based sensor system for angular vibration measurement. J. Vib. Control. 24, 4325–4336 (2017)
Zhou, J., Wang, K., Xu, D., et al.: Vibration isolation in neonatal transport by using a quasi-zero-stiffness isolator. J. Vib. Control. 24, 3278–3291 (2017)
Le, T.D., Ahn, K.K.: Experimental investigation of a vibration isolation system using negative stiffness structure. Int. J. Mech. Sci. 70, 99–112 (2013)
Ding, H., Ji, J., Chen, L.: Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics. Mech. Syst. Signal Proc. 121, 675–688 (2019)
Zhu, G., Liu, J., Cao, Q., et al.: A two degree of freedom stable quasi-zero stiffness prototype and its applications in aseismic engineering. Sci. China-Technol. Sci. 63, 496–505 (2020)
Wu, Z., Jing, X., Bian, J., et al.: Vibration isolation by exploring bio-inspired structural nonlinearity. Bioinspir Biomim. 10, 056015 (2015)
Silva-Soares, T., Mônico, A. T.: Hind limb malformation in the tree frog Corythomantis greeningi (Anura: Hylidae). Phyllomedusa. 16 (2017).
Bian. J., Jing. X.: Superior nonlinear passive damping characteristics of the bio-inspired limb-like or X-shaped structure. Mech. Syst. Signal Proc. 125, 21–51 (2019).
Wang, Y., Jing, X., Guo, Y.: Nonlinear analysis of a bio-inspired vertically asymmetric isolation system under different structural constraints. Nonlinear Dyn. 95, 445–464 (2018)
Meng, G., Peng, Z., Zhang, W., et al.: Multi-direction vibration isolator for momentum wheel assemblies. J. Vib. Acoust. 142, 1–19 (2020)
Yan, G., Wang, S., Zou, H., et al.: Bio-inspired polygonal skeleton structure for vibration isolation: design, modelling, and experiment. Sci. China Technol. Sci. 63, 1–14 (2020)
Yan, G., Zou, H., Wang, S., et al.: Large stroke quasi-zero stiffness vibration isolator using three-link mechanism. J. Sound Vib. 478, 115344 (2020)
Feng, X., Jing, X.: Human body inspired vibration isolation: beneficial nonlinear stiffness, nonlinear damping & nonlinear inertia. Mech. Syst. Signal Proc. 117, 786–812 (2019)
Feng, X., Jing, X., Xu, Z., et al.: Bio-inspired anti-vibration with nonlinear inertia coupling. Mech. Syst. Signal Proc. 124, 562–595 (2019)
Dai, H., Cao, X., Jing, X., et al.: Bio-inspired anti-impact manipulator for capturing non-cooperative spacecraft: theory and experiment. Mech. Syst. Signal Proc. 142, 106785 (2020)
Zhou, J., Xu, D., Bishop, S.: A torsion quasi-zero stiffness vibration isolator. J. Sound Vib. 338, 121–133 (2015)
Hamdan, M.N., Burton, T.D.: On the steady state response and stability of non-linear oscillators using harmonic balance. J. Sound Vib. 166, 255–266 (1993)
Yan, B., Ma, H., Jian, B., et al.: Nonlinear dynamics analysis of a bi-state nonlinear vibration isolator with symmetric permanent magnets. Nonlinear Dyn. 97, 2499–2519 (2019)
Carrella, A., Brennan, M.J., Kovacic, I., et al.: On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 322, 707–717 (2009)
Lou, J., Zhu, S., He, L., et al.: Experimental chaos in nonlinear vibration isolation system. Chaos Solitons Fractals. 40, 1367–1375 (2009)
Yin, S., Wen, G., Ji, J., et al.: Novel two-parameter dynamics of impact oscillators near degenerate grazing points. Int. J. Non-Linear Mech. 120, 103403 (2020)
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grants 11832009 and 11672104), and the Chair Professor of Lotus Scholars Program in Hunan province (Grants XJT2015408). Meanwhile, the authors are very grateful to the reviewers for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Executive Editor: Jian Xu
Appendices
Appendix 1
The coefficients in Eqs. (2)-(4) can be expressed as
Appendix 2
The coefficients in Eq. (5) can be expressed as
Appendix 3
The coefficients in Eq. (9) can be expressed as
Rights and permissions
About this article
Cite this article
Zeng, R., Wen, G., Zhou, J. et al. Limb-inspired bionic quasi-zero stiffness vibration isolator. Acta Mech. Sin. 37, 1152–1167 (2021). https://doi.org/10.1007/s10409-021-01070-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-021-01070-6