Introduction

The completion of the global constellation deployment of the BeiDou Navigation Satellite System (BDS-3) was marked by the successful launch of its final satellite on June 23, 2020. The integration of BDS-2 and BDS-3 enables the derivation of highly precise positioning solutions (Yang et al. 2019; Pan et al. 2020).

Precise point positioning (PPP) finds widespread applications in various fields, such as atmospheric monitoring and GNSS seismology (Liu et al. 2022). The IGS launched the Real-Time Pilot Project (RTPP) and began providing RT-PPP services based on the multi-GNSS experiment (MGEX) in April 2013 (Montenbruck et al. 2017). Currently, there are seven analysis centers (ACs) offering real-time BDS orbit and clock corrections, including Wuhan University (WHU) and Centre National d’Etudes Spatiales (CNES). The real-time products provided by CNES have garnered significant attention among the various analysis centers’ offerings (Wang et al. 2018; Kazmierski et al. 2020; Tao et al. 2021). In a study conducted by Kazmierski et al. (2018) on CNES RT multi-GNSS products, the three-dimensional (3D) orbit root mean square (RMS) values over a one-month period were found to be approximately 36 cm, 18 cm, and 5 cm for BDS-2 inclined geosynchronous orbit (IGSO), BDS-2 medium earth orbit (MEO), and GPS satellites, respectively. Using CNES SSRX00CNEX data, the positioning error and initialization time of BDS-only real-time PPP (RT-PPP) were found to be more significant compared to those using GPS-only observations (Wang et al. 2019; Pan et al. 2020). Currently, the majority of studies on BDS RT-PPP utilizing products from analysis centers or BDS-3 B2b signals primarily concentrate on the traditional float PPP solution, which may limit its applicability in certain high-precision scenarios (Tao et al. 2021; Xu et al. 2021).

In recent years, PPP techniques have advanced from traditional float solutions to PPP with ambiguity resolution (PPP-AR) (Geng et al. 2011). With the augmentation of phase bias products, the integer property of ambiguity would be recovered and the initialization speed can be enhanced. To facilitate user convenience, code and phase bias corrections are generally broadcasted and stored in observable-specific signal bias (OSB) format, allowing for direct application to the raw observations (Banville and Laurichesse 2017; Jiang et al. 2023). Common methods for extracting phase bias include the Integer-recovery (IRC) method and the Fractional Cycle Bias (FCB) method (Laurichesse et al. 2009; Ge et al. 2008). OSB can be derived from wide-lane (WL) and narrow-lane (NL) FCB as well as differential code bias (DCB) (Laurichesse 2012). The WL FCB can be solved with geometry-free Hatch–Melbourne–Wübbena (HMW) combinations. Usually, the WL FCB is considered stable over one day and can be solved accurately (Li et al. 2018a, b). The estimation of NL FCB or IRC requires the use of geometry-based observables. In addition to GNSS signal hardware delays, the signal-in-space ranging errors (SISRE) of precise products also have a great impact on NL FCBs (Li et al. 2015). Previous studies have primarily relied on post-processing orbits and clocks for the estimation of BDS-2/3 FCB and PPP-AR (Gu et al. 2015; Jiang et al. 2019; Li et al. 2020; Geng et al. 2020; Liu et al. 2023). In RT applications, however, which are subject to parameter estimation strategies and data quality control issues, time latency, and instability of the data stream, the RT clocks and orbits are less stable and accurate than post-processed products. Confined with factors such as the hybrid constellation, distribution of ground-based stations, and imperfect models, the RT orbital error of BDS was generally found to be higher compared to GPS (Pan et al. 2020; Wang et al. 2018). Currently, CNES provides real-time multi-GNSS OSB products for PPP-AR users. However, in the scenarios with significant RT orbit and clock offset error, only the integer nature of WL and EWL ambiguity can be reliably recovered for BDS, making NL AR unreliable (Liu et al. 2020; Du et al. 2022).

Utilizing regional GNSS reference station networks to solve IRC/FCB products can help compensate for orbital errors (Li et al. 2018a, b; Shu et al. 2021; Zhang et al. 2021). However, it is crucial to separate the reliable integer ambiguity from the undifferenced float ambiguity solution beforehand. The float ambiguity estimated using the undifferenced model is often contaminated by the significant RT orbital errors, resulting in challenging to separate integer ambiguities. This, in turn, impacts the performance of RT-PPP. PPP-AR/PPP-RTK is a relative technique for which the fixed ambiguities are essentially double-differenced (DD) ambiguities (Teunissen and Khodabandeh. 2015). Resolving the DD ambiguities within the GPS network leads to improved FCB products, enhancing positioning accuracy (Geng et al. 2012). The integer estimable frequency division multiple access (FDMA) model is derived and validated by resolving DD ambiguities with the S-system theory (Zhang et al. 2021).

To address errors in upstream RT BDS precise products, we have developed an OSB-generating method that utilizes DD ambiguity resolution. First, the undifferenced network GNSS observation model is established for the float solution, and then, the DD integer ambiguities are solved with the DD model. Finally, the ambiguity datums are determined to convert the DD ambiguities into undifferenced ambiguities, which are then used to derive the OSB products. The performance of the BDS products derived from the proposed method will be evaluated using datasets from two regional Continuous Operating Reference Station (CORS) networks from Shaanxi, China, and Europe.

Methodology

To minimize the impact of RT orbit and clock errors on ambiguity parameter estimation and improve AR reliability, a two-step AR approach has been developed and is shown in Fig. 1. The DD ambiguities are first resolved and fixed using the DD observation model. Subsequently, the undifferenced ambiguities are reconstructed using the integer ambiguity datum. The OSB generation method using a sparse GNSS reference station network based on fixed ambiguities will be introduced in this section.

Fig. 1
figure 1

Flowchart of the PPP-AR phase OSB generation aided with DD model

Full size image

Network observation model for float solution

Ionosphere-free (IF) combined GNSS observation equations are generally used for RT network processing and could be explained (Gong et al. 2018):

$$ \left\{ {\begin{array}{*{20}l} {P_{{r,{\text{if}}}}^{s} = \rho_{r}^{s} + c\left( {t_{r} - t^{s} } \right) + \alpha_{r}^{s} w_{r} + b_{{r,{\text{if}}}} - b_{if}^{s} + \varepsilon_{{P,{\text{if}}}}^{{}} \, } \hfill \\ {L_{{r{\text{,if}}}}^{s} = \rho_{r}^{s} + c\left( {t_{r} - t^{s} } \right) + \alpha_{r}^{s} w_{r} + \lambda_{1} \left( {N_{{r,{\text{if}}}}^{s} + B_{{r,{\text{if}}}} - B_{{{\text{if}}}}^{s} } \right) + \varepsilon_{{L,{\text{if}}}}^{{}} } \hfill \\ \end{array} } \right. $$
(1)

where \(P\) and \(L\) represent the pseudorange and carrier phase observations from satellite \(s\) to receiver \(r\);\(w\) is the zenith troposphere delay and can convert to slant with the mapping function \(\alpha_{r}^{s}\); \(\rho\) represents the geometric range between receiver antenna and the satellite antenna; \(\lambda\) is the wavelength; \(c\) is the speed of light in vacuum; \(N\) denotes the integer ambiguity; \(B_{{{\text{if}}}}^{s}\) and \(B_{{r,{\text{if}}}}\) are the IF phase hardware delays of the satellite and receiver; \(b_{{{\text{if}}}}^{s}\) and \(b_{{r,{\text{if}}}}\) represent the code hardware delays of the satellite and receiver; \(\varepsilon_{P}\) and \(\varepsilon_{L}\) mean the observation noise of the pseudorange and carrier phases; and\(t_{r}\) and \(t^{s}\) are the receiver and satellite clock offsets.

The equations include hardware delay terms that exhibit a linear dependence on clock and ambiguity parameters, necessitating reparameterization before estimation. In this model, a portion of the pseudorange hardware delay is incorporated into the clock offset, while the remaining portion and the carrier phase hardware delay are combined into the ambiguity parameters (Li et al. 2016). Consequently, the reparameterized estimated parameters in this model are defined as follows:

$$ \left\{ {\begin{array}{*{20}l} {P_{{r,{\text{if}}}}^{s} = \rho_{r}^{s} + c\left( {\overline{t}_{{r,{\text{if}}}} - \overline{t}_{{{\text{if}}}}^{s} } \right) + \alpha_{r}^{s} w_{r} + \varepsilon_{{P_{{{\text{if}}}} }} \, } \hfill \\ {L_{{r,{\text{if}}}}^{s} = \rho_{r}^{s} + c\left( {\overline{t}_{{r,{\text{if}}}} - \overline{t}_{{{\text{if}}}}^{s} } \right) + \alpha_{r}^{s} w_{r} + \lambda_{1} \overline{N}_{{r,{\text{if}}}}^{s} + \varepsilon_{{L_{{{\text{if}}}} }} \, } \hfill \\ \end{array} } \right. $$
(2)
$$ \left\{ {\begin{array}{*{20}l} {\overline{t}_{{r,{\text{if}}}} = t_{r} + b_{{r,{\text{if}}}} /c \, } \hfill \\ {\overline{t}_{{{\text{if}}}}^{s} = t^{s} + b_{{{\text{if}}}}^{s} /c} \hfill \\ {\overline{N}_{{r,{\text{if}}}}^{s} = N_{{r,{\text{if}}}}^{s} + d_{{r,{\text{if}}}} - d_{{{\text{if}}}}^{s} \, } \hfill \\ \end{array} } \right. $$
(3)

where \(d_{{r,{\text{if}}}}^{{}} = B_{{r{\text{,if}}}} - b_{{r,{\text{if}}}} /\lambda_{1}\) and \(d_{{{\text{if}}}}^{s} = B_{{{\text{if}}}}^{s} - b_{{{\text{if}}}}^{s} /\lambda_{1}\). During RT network processing, float undifferenced (UD) ambiguities, along with atmospheric delays, receiver clocks, and satellite clocks, can be derived after applying RT precise orbit products. To distinguish the clock parameters of the satellite and receiver, a constraint equation related to the clocks should be added. In comparison with the original observation model, the ionosphere delays are eliminated from the IF model. About 50% of ambiguity parameters for dual-frequency signals are attenuated, leading to improved network processing efficiency.

Ambiguity resolution for phase bias estimation with a DD model

Compared with GPS and Galileo, the RT SSR products for BDS have a larger error (Wang et al. 2018), which increases the difficulty of AR in the UD model. We have developed a two-step AR approach in this study. The first step involves determining DD ambiguities in the reference station network. Instead of fixing DD ambiguities in the undifferenced network model (Geng et al. 2012; Zhang et al. 2021), we directly resolved and fixed the DD ambiguities using DD baselines, which helps mitigate the impacts of various errors, e.g., RT orbit error. The equations for DD pseudorange and phase observations for a single baseline are as follows:

$$ \left\{ {\begin{array}{*{20}l} {P_{AB,k}^{pq} = \rho_{AB}^{pq} + \mu_{k} I_{AB,1}^{pq} + \alpha_{B}^{pq} w_{B} - \alpha_{A}^{pq} w_{A} + \varepsilon_{P,k} } \hfill \\ {L_{AB,k}^{pq} = \rho_{AB}^{pq} - \mu_{k} I_{AB,1}^{pq} + \alpha_{B}^{pq} w_{B} - \alpha_{A}^{pq} w_{A} + \lambda_{k} N_{AB,k}^{pq} + \varepsilon_{L,k} } \hfill \\ \end{array} } \right. $$
(4)

where \(I\) is the ionosphere delay with frequency 1, which can be converted into the frequency \(k\) using the coefficient \(\mu\) according to \(\mu_{k} = f_{1}^{2} /f_{k}^{2}\); \(A\) and \(B\) denote two reference stations of a baseline in the reference station network; \(p\) denotes the referenced satellite; and \(q\) is a non-referenced satellite.

A Kalman filter can be employed to estimate the float DD ambiguity vector, zenith troposphere delays, and slant ionosphere using measurements from BDS or multi-GNSS. The partial AR approach can be used to resolve the DD integer ambiguity (Shu et al. 2018). We assume that \(A\) and \(B\) are the master and non-master reference stations in the network, respectively. We start from the combined association of the undifferenced ambiguity with the double-differenced integer ambiguity of the reference station network. The single-differenced ambiguity of the master station \(A\) (\(N_{A,k}^{pq}\)) and, the integer double-differenced ambiguity of the baseline (\(N_{AB,k}^{pq}\)) can be used to retrieve the undifferenced ambiguities of the reference station \(B\) (\(N_{B,k}^{q}\)):

$$ N_{B,k}^{q} { = }N_{AB,k}^{pq} + N_{A,k}^{pq} + N_{B,k}^{p} $$
(5)

\(N_{B,k}^{p}\) is the ambiguity of the reference satellite for the station \(B\). Note that the DD baselines in the reference station network are usually constructed based on the Delaunay Triangulation, and there may be no direct connecting baseline between a reference station and a master reference station. In this situation, the undifferenced ambiguities of the reference station can be transferred and converted by the DD ambiguities of multiple connected baselines.

A combination of the integer NL ambiguity \(N_{r,n}^{s}\) and WL ambiguity \(N_{r,w}^{s}\) is used to define the fixed IF ambiguity in (3):

$$ N_{r,if}^{s} { = }\frac{{f_{1} }}{{f_{1} + f_{2} }}N_{r,n}^{s} { + }\frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{r,w}^{s} $$
(6)

where \(N_{r,n}^{s} = N_{r,1}^{s}\) and \(N_{r,w}^{s} = N_{r,1}^{s} - N_{r,2}^{s}\). Usually, WL ambiguities can be fixed at a high success rate with the assistance of WL FCB correction. Assuming that the WL ambiguities for all satellite and station pairs (\(N_{B,w}^{p}\),\(N_{B,w}^{q}\),\(N_{A,w}^{p}\),\(N_{A,w}^{q}\)), double-differenced NL ambiguities \(N_{AB,1}^{pq}\) are known, then the phase observations in (2) for all reference stations can be expressed as follows:

$$ \left\{ {\begin{array}{*{20}c} {L_{{B,{\text{if}}}}^{p} = \rho_{B}^{p} + c\left( {\tilde{t}_{{B,{\text{if}}}} - \tilde{t}_{{{\text{if}}}}^{p} } \right) + \alpha_{B}^{p} w_{B} + \lambda_{1} \tilde{N}_{{B,{\text{if}}}}^{p} + \varepsilon_{{L_{{{\text{if}}}} }}^{{}} } \\ {L_{{B,{\text{if}}}}^{q} = \rho_{B}^{q} + c\left( {\tilde{t}_{{B,{\text{if}}}} - \tilde{t}_{{{\text{if}}}}^{q} } \right) + \alpha_{B}^{q} w_{B} + \lambda_{1} \tilde{N}_{{B,{\text{if}}}}^{q} + \varepsilon_{{L_{{{\text{if}}}} }}^{{}} } \\ {L_{{A,{\text{if}}}}^{p} = \rho_{A}^{p} + c\left( {\tilde{t}_{{A,{\text{if}}}} - \tilde{t}_{{{\text{if}}}}^{p} } \right) + \alpha_{A}^{p} w_{A} + \lambda_{1} \tilde{N}_{{A,{\text{if}}}}^{p} + \varepsilon_{{L_{{{\text{if}}}} }}^{{}} } \\ {L_{{A,{\text{if}}}}^{q} = \rho_{A}^{q} + c\left( {\tilde{t}_{{A,{\text{if}}}} - \tilde{t}_{{{\text{if}}}}^{q} } \right) + \alpha_{A}^{q} w_{A} + \lambda_{1} \tilde{N}_{{A,{\text{if}}}}^{q} + \varepsilon_{{L_{{{\text{if}}}} }}^{{}} } \\ \end{array} } \right. $$
(7)
$$ \left\{ {\begin{array}{*{20}l} {\tilde{t}_{{B,{\text{if}}}} = \overline{t}_{{B,{\text{if}}}} + \left( {\lambda_{NL} N_{B,1}^{p} + \lambda_{1} d_{{B,{\text{if}}}} } \right)/c,\tilde{t}_{{A,{\text{if}}}} = \tilde{t}_{{A,{\text{if}}}} + \left( {\lambda_{NL} N_{A,1}^{p} + \lambda_{1} d_{{A,{\text{if}}}} } \right)/c} \hfill \\ {\tilde{t}_{{{\text{if}}}}^{q} = \overline{t}_{if}^{q} - \left( {\lambda_{NL} N_{A,1}^{pq} - \lambda_{1} d_{{{\text{if}}}}^{q} } \right)/c,\tilde{t}_{{{\text{if}}}}^{p} = \tilde{t}_{{{\text{if}}}}^{p} + \lambda_{1} d_{{{\text{if}}}}^{p} /c \, } \hfill \\ {\tilde{N}_{{B,{\text{if}}}}^{q} = \frac{{f_{1} }}{{f_{1} + f_{2} }}N_{AB,1}^{pq} + \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{B,w}^{q} ,\tilde{N}_{{B,{\text{if}}}}^{p} = \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{B,w}^{p} \, } \hfill \\ {\tilde{N}_{{A,{\text{if}}}}^{q} = \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{A,w}^{q} ,\tilde{N}_{{A,{\text{if}}}}^{p} = \frac{{f_{1} f_{2} }}{{f_{1}^{2} - f_{2}^{2} }}N_{A,w}^{p} \, } \hfill \\ \end{array} } \right. $$
(8)

where \(\lambda_{NL} = c/(f_{1} + f_{2} )\). From (7 and 8), in addition to the NL FCB of receiver and satellite, the single-differenced NL ambiguities \(N_{A,1}^{pq}\) for the master station and the undifferenced NL ambiguities of reference satellites for all stations (\(N_{A,1}^{p}\),\(N_{B,1}^{p}\)) are absorbed by the receiver and satellite clock parameters, respectively. Thus, the \(N_{A,1}^{pq}\), \(N_{A,1}^{p}\) and \(N_{B,1}^{p}\) values can be arbitrary for a specific epoch, which can be seen as integer ambiguity datum to recover the undifferenced ambiguity (Teunissen et al. 2015). In this study, \(N_{A,1}^{pq}\), \(N_{A,1}^{p}\), and \(N_{B,1}^{p}\) are solved by rounding without any ambiguity validation test, and their values along with the fixed double-differenced \(N_{AB,1}^{pq}\) and WL ambiguities are introduced into (7). To ensure the continuity of IRC/FCB products, the integer ambiguity datum remains unchanged in the absence of cycle slips. For RT products from CNES, the SISRE of the orbit errors for BDS is significantly higher than that for GPS (around 2 to 3 times larger) (Pan et al. 2020). However, the projection of satellite orbit error shows similarity across different stations in a regional GNSS network. This error can be compensated for by incorporating it into the satellite clock parameter when ambiguity is resolved accurately. The following equation is the expression of the satellite clock parameter solution:

$$ \left\{ {\begin{array}{*{20}l} {\tilde{t}_{{{\text{if}}}}^{q} = \overline{t}_{{{\text{if}}}}^{q} - \left( {\lambda_{NL} \Delta \ddot{N}_{A,1}^{pq} - \lambda_{1} d_{{{\text{if}}}}^{q} } \right)/c + O_{{{\text{region}}}}^{q} /c = \overline{t}_{{{\text{if}}}}^{q} + \lambda_{NL} \hat{d}_{NL}^{q} /c} \hfill \\ {\tilde{t}_{{{\text{if}}}}^{p} = \overline{t}_{{{\text{if}}}}^{p} + \lambda_{1} d_{{{\text{if}}}}^{p} /c + O_{{{\text{region}}}}^{p} /c = \overline{t}_{if}^{p} + \lambda_{NL} \hat{d}_{NL}^{p} /c \, } \hfill \\ \end{array} } \right. $$
(9)

where \(\hat{d}_{NL}^{p}\) means NL FCB; \(\tilde{t}_{{{\text{if}}}}^{q}\) and \(\tilde{t}_{{{\text{if}}}}^{p}\) represent the so-called integer satellite clocks, except for the float clock and hardware delay, which may include the possible inaccurate part of the SD integer ambiguity \(\Delta \ddot{N}_{A,1}^{pq}\) and the common orbit error \(O_{{{\text{region}}}}^{q}\) in a particular regional area.

Code OSB is usually derived from DCB products (Laurichesse 2012). When the DCB is ignored (as it can be absorbed by ionosphere parameters at the PPP user side), the phase OSB required for dual-frequency observations can be calculated using NL and WL FCB.

$$ \left\{ {\begin{array}{*{20}c} {b_{{L_{1} }}^{s} = \hat{d}_{NL}^{s} - \frac{{f_{2} }}{{f_{1} - f_{2} }}\hat{d}_{WL}^{s} } \\ {b_{{L_{2} }}^{s} = \hat{d}_{NL}^{s} - \frac{{f_{1} }}{{f_{1} - f_{2} }}\hat{d}_{WL}^{s} } \\ \end{array} } \right. $$
(10)
$$ \hat{d}_{NL}^{s} = c \cdot \left( {\tilde{t}_{if}^{s} - \overline{t}_{if}^{s} } \right)/\lambda_{NL} $$
(11)

where NL FCB is generated from the integer and float satellite clock.

Experiment and results analysis

The OSB product is evaluated from two perspectives on the PPP user side. First, the residual distribution of the ambiguity parameter was analyzed after the use of RT OSB products. Second, the initialization speed and positioning precision of PPP-AR were analyzed.

Data collection and processing strategies

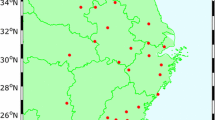
We tested the proposed method using the datasets collected from the Shaanxi and European CORS networks. The station distribution of the two networks is depicted in Fig. 2. The Shaanxi network is situated in Shaanxi province, China. It comprises 13 reference stations (red triangles) with an average baseline distance of approximately 200 km. All stations are equipped with Trimble ALLOY receivers and TRM 59900.00 antennas. The European network consists of 14 selected reference stations (red triangles) with an average baseline distance of around 300 km. All stations in this network are equipped with JAVAD TRE_3 DELTA receivers and JAVRINGANT_DM antennas. There are 5 stations designed as the rover sites (blue circles) in each network. Both networks collected dual-frequency GPS/BDS-2/BDS-3 observations from Day Of Year (DOY) 305 to 314 data in 2021, with a sampling interval of 30 s. The corresponding post-stored RT clock and orbit correction records from CNES were also collected.

Fig. 2
figure 2

Distribution of the CORS stations in Shaanxi (left) and European (right) networks. Red triangles and blue circles are the reference and rover stations, respectively

Full size image

Table 1 presents the specific processing strategies for IRC estimation assisted with the DD model. The IRC is updated with UD ambiguities, which are converted by DD ambiguities with the given datum (i.e., the proposed method, referred to as the S1 method hereafter). For comparative analysis, the IRC products are also generated using the traditional UD ambiguity rounding method (Ge et al. 2008) (referred to as the S2 method hereafter). Considering the repeated long ambiguity initialization processes in a regional network solution, the S2 method includes a coordinate-fixed PPP step to estimate ambiguity parameters for all reference stations using CNES RT precise products, and then, the integer UD ambiguities are separated and determined (see Fig. 1 in Shu et al. 2021). Except for the AR strategy, the processing strategy and data resources are the same for S1 and S2 IRC estimation. As depicted in Fig. 3, both S1 and S2 OSBs are generated using NL and WL FCBs. The NL FCB is converted from the IRC and CNES code satellite clock. The WL FCB information of the current day was obtained from the Deutsches GeoForschungs Zentrum (GFZ) MGEX precise clock file.

Table 1 Processing strategy for satellite IRC estimations at the server side (S1 method)
Full size table
Fig. 3
figure 3

S1 and S2 OSB generation flowchart

Full size image

To validate the effectiveness of regional OSB products using the proposed method (S1 OSB products), we investigate a comparison test with S2 and CNES RT OSB products in terms of the ambiguity residual distribution and PPP performance. Note that the same CNES RT orbit and clock products are used for the comparative experiment using three kinds of OSB products. The PPP performance will be conducted using the data from five rover CORSs.

Results in Shaanxi CORS network

This section shows the ambiguity residuals and PPP-AR performance in the Shaanxi CORS network. We compare the proposed DD model derived OSB with both the traditional UD model and CNES derived OSB products.

Distribution of ambiguity residuals using phase bias products

The ambiguity residual distribution is an important criterion for testing the quality of OSB products. After removing the FCB of the satellites using the estimated OSB products, the SD ambiguity between satellites for PPP users was close to the integer ambiguity. When the ambiguity parameters are initialized, the ambiguity residuals can be calculated using the discrepancy between the SD integer and float ambiguities (Liu et al. 2020; Du et al.2022).

Considering that the WL ambiguity can usually be fixed at a high success rate with OSB products (Du et al. 2022), only the NL residuals are analyzed in this study. Figure 4 shows the NL ambiguity residual histograms of BDS-2, BDS-3 and GPS during DOY 305 to 314 in 2021 after removing the influence of satellite FCBs. The corresponding statistical results under different thresholds are also given. For the OSB products from CNES, the GPS NL ambiguity residuals have an unimodal normal distribution, which cannot be found in BDS-3 and BDS-2, indicating the integer characteristics of the BDS NL ambiguities can not be recovered. The ambiguity residuals of S1 OSB show obvious advantages over that of S2 and CNES OSB. The proportion of NL residuals within ± 0.25 cycles of GPS, BDS-2, and BDS-3 for S1 OSB accounts for 96.3%, 74.4%, and 93.1%, respectively, which are 11.6%, 12.7%, and 23.1% and 16.7%, 24.5%, and 33.2% higher than that of S2 and CNES OSB, respectively. According to the statistical results, the improvement of BDS-2 and BDS-3 is more obvious than that of GPS. Compared to CNES OSB, the main reason for the improved NL ambiguity of the S1 product is that the regional IRC can effectively compensate for the orbital errors (Li et al. 2015; Shu et al. 2021). The improvement of S2 over S1 NL ambiguity residuals may be attributed to the reliability of the UD ambiguity converted from DD ambiguity at the server side. For the S1 method, the RT orbit errors are almost eliminated in the DD model and the DD ambiguity can be resolved accurately by the least-squares ambiguity decorrelation adjustment (LAMBDA) method, while the float ambiguities utilized to round UD integer ambiguities will be affected by RT orbit errors in the undifferenced model for the S2 method.

Fig. 4
figure 4

Histograms of NL ambiguity residuals for GPS, BDS-2, and BDS-3 using different OSB products: S1 (top), S2 (middle), and CNES (bottom), during the period from DOY 305 to 314 in 2021

Full size image

Figure 5 gives the statistical results of the AR inconsistency rate between the S1 and S2 methods on the server side. The inconsistency rate is calculated by counting the number of DD ambiguities converted with the S2 method that is not equal to the S1 method; only the DD ambiguity fixed by both the S1 and S2 methods is compared. The DD ambiguities of S2 are converted from UD ambiguities according to baseline information. The average inconsistency rates are 1.30% for GPS and 2.27% for BDS, respectively. Considering the reliability of the DD ambiguity of the S1 method, the inconsistency means that the UD ambiguities are wrongly fixed in the S2 method, which will reduce the quality of S2 OSB products.

Fig. 5
figure 5

Comparison of inconsistent fixed DD ambiguities in S1 and S2 for GPS (up) and BDS (bottom)

Full size image

Performance analysis of real-time PPP-AR

We have also tested the PPP-AR performance using the ten-day data at five rover stations from the Shaanxi CORS network (blue circles in Fig. 2). The S1, S2 and CNES OSB are involved in the comparison. After obtaining the WL and NL float ambiguities, satellite-differenced (SD) ambiguities can be formed to avoid the influence of the receiver FCBs. The partial ambiguity resolution (PAR) strategy is adopted to fix the SD WL and NL integer ambiguity using the LAMBDA approach (Shu et al. 2018; Teunissen et al. 1995). After WL ambiguities are fixed, the NL ambiguities begin to fix. The fixed-failure rate ratio (FF-ratio) test is applied for ambiguity validation (Verhagen et al. 2013). For the PPP-AR experiment, the rover coordinates are estimated as dynamic parameters, which are initialized with standard point positioning (SPP) results every epoch; the corresponding priori variance is set as 302 m2.

Figure 6 shows the three-dimensional (3D) kinematic PPP-AR results involved in positioning using BDS-3, BDS-2/3, and GPS on the 314th day of 2021 at the SNSY station. As depicted, ambiguity-fixed results cannot be obtained for BDS PPP using CNES OSB products, with the fixed rate of 72.6% (GPS), 1.3% (BDS-3) and 15.7% (BDS-2/3), respectively, which is more likely ascribed to larger RT clock and orbit errors for BDS (Pan et al. 2021). As a result, the positioning errors of BDS PPP are significantly greater than that of GPS. In addition, some gaps can be observed in BDS-3 only PPP results, which are mainly attributed to the low availability of CNES BDS OSB products. When the regional S1 and S2 OSB products are adopted, the performance of PPP-AR results using different GNSS observations shows a certain extent of improvement, especially for those using BDS-2/3 and BDS-3 observations. Notably, consistent with the statistical results of NL ambiguity residual distribution, the proposed S1 method shows greater stability in kinematic PPP-AR positioning sequences than the S2 method.

Fig. 6
figure 6

PPP-AR positioning results using real-time S1 (top), S2 (middle) and CNES (bottom) OSB products at the SNSY station on DOY 314, 2021. Both the float and fixed solutions are shown in the figure

Full size image

The average RMS and ambiguity-fixed rate of the five stations' PPP-AR results over ten days using three computational schemes are shown in Fig. 7. Only the GPS-only PPP-AR statistics are given because the ambiguity-fixed solution cannot be obtained for BDS using the CNES RT OSB product. For the GPS PPP-AR using CNES products, the mean RMS of the fixed solutions of the five rover stations in the E, N, and U directions is 1.8, 1.3, and 4.1 cm, respectively. The counterpart values for S1 OSB products were 0.5, 0.6, and 2.1 cm, with a decrease of 72.2%, 53.8%, and 48.8%, respectively. Compared with the results of GPS PPP-AR using S2 OSB products, the positioning error of S1 is also decreased by 44.4%, 33.3% and 25.0%, respectively. The average RMS of the BDS-2/3 PPP-AR using S1 OSB in the E, N, and U components is 0.9, 0.7, and 2.3 cm, which are 57.1%, 53.3%, and 46.5% lower than those using S2 OSB. The ambiguity-fixed rate of GPS PPP using S1 OSB is also improved compared with those using S2 OSB, with the average ambiguity-fixed rate of the five rover stations increasing from 87.5 to 92.1%. The fixed rates of BDS-2/3 and BDS-3 PPP using S1 OSB were 98.4% and 96.0%, which is better than that of GPS (92.1%).

Fig. 7
figure 7

Average RMS (in cm) of ambiguity-fixed kinematic PPP-AR using the proposed S1, S2 and CNES OSB products for 5 rover stations

Full size image

The Time-To-First-Fix (TTFF) was calculated by re-initializing the Kalman filter parameter every hour to evaluate the PPP-AR performance. Figure 8 presents boxplots of the average TTFF of five rover stations, utilizing three different OSB products from DOY 305 to 314. An observation emerges from the boxplots, indicating that the OSB products generated with the S1 method significantly outperformed their counterparts, with median TTFF of 20.5 min (GPS), 7.5 min (BDS-2/3), and 12 min (BDS-3). No obvious TTFF differences were observed for GPS when employing the three OSB products. However, for the BDS, the utilization of the S1 products exhibited significant reductions in TTFF, with notable improvements of 68.4% (BDS-2/3) and 52.0% (BDS-3) compared to those using S2 products (23.8 min (BDS-2/3), and 25 min (BDS-3)). An in-depth scrutiny of the boxplots underscored a captivating trend: The TTFF distribution using S1 OSB products showed a compelling concentration towards lower values, precisely within the ranges [13.5, 31.5], [4, 12], [9.5, 15] (GPS, BDS-2/3, BDS-3), while the corresponding results for S2 and CNES subtly gravitated toward higher values. Some outliers were present in the TTFF estimates using S1 products; however, they exhibited notably smaller magnitudes when compared to those using S2 and CNES OSB products.

Fig. 8
figure 8

Average TTFF of kinematic PPP-AR from DOY 305 to 314 for 5 rover stations. Results from GPS, BDS-2/3 and BDS-3 using OSB product of the proposed S1 (left), S2 (middle), and CNES (right)

Full size image

Results in European CORS network

We also tested the proposed method using the dataset from the European network. The coverage area and baseline distance of the European network are about 3 and 1.5 times larger than the Shaanxi network, respectively.

Distribution of ambiguity residuals using phase bias products

Figure 9 shows the NL ambiguity residuals for GPS, BDS-2, and BDS-3 using three different OSB products in the European network. Consistent with the findings in the Shaanxi network, the ambiguity residuals of S1 OSB show significant performance over that of S2 and CNES OSB. The S1 OSB exhibits a higher proportion of NL residuals within ± 0.25 cycles for GPS, BDS-2, and BDS-3, accounting for 98.1%, 97.8%, and 97.9%, respectively. These values are 8.4%, 9.9%, and 15.2% higher than those of the S2 OSB, and 13.0%, 50.9%, and 43.1% higher than those of the CNES OSB. Figure 10 presents the statistical results of the AR inconsistency rate between the S1 and S2 methods on the server side. The average inconsistency rates for GPS and BDS are 0.12% and 0.69%, respectively. Note that the AR inconsistency can only provide a partial indication of the rate of incorrectly fixed UD ambiguity. This is because there may be situations where UD ambiguity is fixed while the DD ambiguity remains unfixed. Figures 9 and 10 reveal that the NL residual distribution and the reliability of UD AR in the European network outperform the results observed in the Shaanxi network. One possible reason for this difference is the superior GNSS data quality of the European network compared to that of the Shaanxi network. Figure 11 illustrates the average cycle slip ratio of reference stations in the Shaanxi network is lower than that observed in the European network. A lower cycle slip ratio indicates a more frequent occurrence of cycle slips, which can cause ambiguity parameters to be reinitialized, thereby reducing the AR reliability, especially for the rounding AR method.

Fig. 9
figure 9

Histograms of NL ambiguity residuals for GPS, BDS-2, and BDS-3 using different OSB products: S1 (top), S2 (middle), and CNES (bottom), during the period from DOY 305 to 314 in 2021

Full size image
Fig. 10
figure 10

Comparison of inconsistent fixed DD ambiguities in S1 and S2 for GPS (up) and BDS (bottom)

Full size image
Fig. 11
figure 11

The average cycle slip ratio of reference stations in Shaanxi CORS and European CORS

Full size image

Performance analysis of real-time PPP-AR

Figure 12 shows the statistical results of ten days’ PPP-AR positioning errors and ambiguity fixing rates at five rover stations in the European network. For GPS PPP-AR, the positioning errors using S1 OSB products demonstrate superior performance compared to S2 products and CNES products. Comparing BDS-2/3 and BDS-3 PPP-AR with S2 OSB products, the 3D averaged RMS values using proposed OSB products were reduced by about 61.3% for BDS-2/3 and 62.3% for BDS-3 observations. The utilization of S1 OSB also improves ambiguity-fixing rates, with the fixed rates of 97.2% and 96.1% for BDS-2/3 and BDS-3, respectively, surpassing 95.0% of GPS. Results demonstrate the effectiveness and transferability of the proposed method to other CORS networks.

Fig. 12
figure 12

Average RMS (in cm) of ambiguity-fixed kinematic PPP-AR using the proposed S1, S2 and CNES OSB products for 5 rover stations

Full size image

Discussions

We developed an OSB product generation method and tested its performance using the data from two regional networks. The proposed method effectively mitigates orbit errors, enabling comparable positioning performance to the RTK technique when utilizing the derived products for RT PPP with BDS-only data. Nevertheless, it is important to consider that the effectiveness of compensating for orbit errors is strongly influenced by the size of the GNSS network. When applying the proposed method to a large reference network to extract correction products, it becomes feasible to extend its applicability to continental or even global areas by incorporating external orbit-correcting parameters (Ji et al. 2023) and solving simultaneously with the integer clock.

Compared to the previous experimental results (Geng et al. 2010, 2012, 2019), there is a more pronounced distinction between the UD and DD methods, particularly for the BDS system. In this study, we utilize the RT CNES orbit and clock products, which exhibit larger orbit errors compared to the final IGS products adopted in previous research. The UD float ambiguity solution is sensitive to orbit and clock error. In addition, the OSB products are derived by a Kalman filter in real-time processing mode, and the reliability of rounding AR in real-time mode is inferior to that in the post-processing mode. The benefits of the proposed method primarily stem from the high-precision ambiguity solution achieved in the DD model.

Conclusions

In this study, we proposed a real-time phase bias estimation method aided by a double-differenced model. Specifically, the reliable undifferenced ambiguities are recovered by the first fixing network DD ambiguities and given ambiguity datum, making the derived RT OSB products can mitigate the orbital errors in the BDS RT products, thereby allowing high precision, fast convergence real-time AR for the PPP users. Validated by regional Shaanxi and European CORS network, the primary findings are summarized as follows:

The NL ambiguity residuals derived from the proposed method are normally distributed and show significant improvement compared to the UD model and CNES-derived OSB products. The NL ambiguity residuals within ± 0.25 cycles for GPS, BDS-2, and BDS-3 occupy 96.3%, 74.4%, and 93.1% in Shaanxi network, showing an improvement of 11.6%, 12.7%, and 23.1%, and 16.7%, 24.5%, and 33.2% compared to UD model-derived and CNES OSB products, respectively. Comparable performance is also obtained in the European CORS network.

Additionally, reliable positioning results of the BDS-only PPP-AR can be realized using proposed method-derived OSB products, with a higher ambiguity fixed rate (96% and 98.4% for BDS-3 and BDS-2/3) and faster TTFF (12.0 and 7.5 min for BDS-3 and BDS-2/3) in Shaanxi Network. A centimeter- or even millimeter-level positioning accuracy can be achieved for BDS-2/3 PPP, with about 50% and 60% improvement compared to traditional UD model-derived OSB products in Shaanxi and European networks, respectively. The results elucidate the potential applications of BDS-only RT PPP-AR in certain high-precision requirement fields.