Crack nucleation in heterogeneous bars: h- and p-FEM of a phase field model

Abstract

Failure initiation and subsequent crack trajectory in heterogeneous materials, such as functionally graded materials and bones, are yet insufficiently addressed. The AT1 phase field model (PFM) is investigated herein in a 1D setting, imposing challenges and opportunities when discretized by h- and p-finite element (FE) methods. We derive explicit PFM solutions to a heterogeneous bar in tension considering heterogeneous E(x) and $G_{Ic}(x)$, necessary for verification of the FE approximations. $G_{Ic}(x)$ corrections accounting for the element size at the damage zone in h-FEMs are suggested to account for the peak stress underestimation. p-FEMs do not require any such corrections. We also derive and validate penalty coefficient for heterogeneous domains to enforce damage positivity and irreversibility via penalization. Numerical examples are provided, demonstrating that p-FEMs exhibit faster convergence rates comparing to classical h-FEMs. The new insights are encouraging towards p-FEM discretization in a 3D setting to allow an accurate prediction of failure initiation in human bones.

1 Introduction

Man-made functionally graded materials and nature-made bones are heterogeneous at the macro-scale, and may be regarded as linear elastic until fracture [1,2,3]. These sophisticated materials impose major challenges for failure initiation theorems (termed also crack nucleation) and for subsequent crack trajectory evolution under a complex stress state. For example, predicting hip fractures among the elderly based on clinical CT scans and maximum principal strain criterion is unsatisfactory (may be overestimated by 20%), partly due to an insufficiently accurate failure theorem [1, 3,4,5]. To the best of our knowledge, no verified and validated methods exist for predicting failure initiation with high accuracy in such heterogeneous materials, which could assist in the design of functional graded materials structures and medical applications.

In the past 25 years phase field modeling (PFM) had emerged, based on energy minimization. For simplicity, consider a heterogeneous bar $\Omega =\{x: 0\le x \le L \}$ fixed at the left end and subjected to a displacement $U_t$ at the right end, see Fig. 1.

The total potential energy in the bar with no volume forces, denoted by $\Pi$, is a sum of strain energy and dissipated damage energy [6,7,8]:

$$\begin{aligned} \Pi (u,\alpha )= & {} \underbrace{\int _{\Omega }\frac{1}{2}a(\alpha )E(x)u'{}^2 dx}_\text {elastic energy} \nonumber \\{} & {} + \underbrace{\int _{\Omega } \frac{G_{Ic}(x)}{c_w \ell _o}(w(\alpha ) + \ell _o^2 \alpha '{}^2 )dx}_\text {dissipated energy}, \quad \quad \alpha \in [0,1] \nonumber \\ \end{aligned}$$

(1)

where u(x) is the sought displacement, E(x) is the Young modulus, $G_{Ic}(x)$ is the fracture toughness, and $\alpha (x)$ is the sought phase field function ($\alpha (x) \in [0, 1]$, that represents damage) being 0 for the undamaged material and 1 for the broken material. A regularization length $\ell _o$ is introduced (smearing the crack). The material degradation is manifested via the degradation function $a(\alpha )= (1-\alpha )^2$, whereas the dissipation function is either taken as $w(\alpha )=\alpha$ denoted as the AT1 PFM, or $w(\alpha )=\alpha ^2$ denoted as the AT2 PFM. The normalization factor $c_w=8/3$ is used with the AT1 model and $c_w=2$ is used with the AT2 to associate the dissipation energy at fracture initiation with $G_{Ic}$ times the bar area. The u(x) and $\alpha (x)$ that are the minimizers of $\Pi (u,\alpha )$ (as will be formulated precisely in the sequel) are the sought solutions. Usually, one is interested in increasing $U_t$ up to the "fracture displacement" that shifts all strain energy into dissipation energy at a given $x_o$ along the bar ($\alpha (x_o)=1$). The AT1 model is more appropriate model for a linear elastic behavior until fracture, thus it is the model adopted in this manuscript,. For the AT1 model a purely elastic phase ($\alpha =0$) is realised until the stress $\sigma =\sigma _e$ corresponds to the critical stress $\sigma _c$ which is referred here as the peak stress $\sigma _p$. The AT2 model introduces slight nonlinearity in the stress–strain relation with $\alpha (x)>0$ for any $U_t > 0$.

Fig. 1

1D clamped bar subjected to $U_t$ at its right end

Fig. 2

PFM implementation for heterogeneous material in the literature. a and b represent piecewise heterogeneity while c and d represent pointwise heterogeneity

Crack propagation in structural heterogeneity (piecewise constant properties) was well predicted in many cases: matrix/inclusions/pores, cement and porous materials (see Fig. 2b, c) [9,10,11,12,13,14,15,16,17,18,19,20,21]. Material heterogeneity (continuous changing properties), has been investigated for example in [22]. Among these papers, AT1 model has only been used in [9, 17, 18]. $\Gamma$-convergence for heterogeneous material (an important consideration for crack propagation) was demonstrated in [23] for $E(x);G_{Ic}(x);\sigma _c(x)$ (critical tensile stress that is also the ultimate stress for a brittle material) and $\ell _o$ constant or a bounded function $\ell _o(x)$. $\Gamma$-convergence characterization is also provided for periodically heterogeneous material in [24]. In both cases, AT2 model was considered.

Application of PFMs aimed at predicting failure initiation necessitates to abandon the $\Gamma$-convergence requirement and be regarded as a gradient damage models. Such PFMs reconsider the regularization parameter as being a material parameter determined by $G_{Ic}$, E and $\sigma _c$. Such models grasp a rich interpretation of physical information including pointwise, length-scale, and gradient data (see e.g. [25]). Failure initiation in heterogeneous structures was shown to be well predicted by these PFM models in: lightweight concrete [9, 11, 26,27,28] (see Fig. 2a), porous rocks [29] and fiber-reinforced composites [19, 30]. Preliminary encouraging application of PFM for failure initiation prediction in material heterogeneity was documented recently for humeri bones [31, 32] (see Fig. 2d). Among these papers, AT1 model was only used in [9].

To the best of our knowledge, for heterogeneous materials PFM has not been yet rigorously investigated and efficiently implemented in a finite element (FE) code for predicting failure initiation and crack trajectories, nor has it been verified by analytical solutions to allow a rigorous assessment of the FE performance. Numerical verification, i.e. quantifying numerical errors separated from modeling ones, was not investigated for the AT1 model and heterogeneous material.

To fill this gap and to allow a rigorous numerical treatment we concentrate on a simplified 1D problem, providing herein explicit solutions for three different E(x) and $G_{Ic}(x)$ profiles (bi-linear, parabolic, bi-exponential) to serve as benchmark problems for FE solutions. These solutions are derived based on [33].

When crack nucleation in a homogeneous material is of interest, $\ell _o$ conceptually does not tend to zero and the ratio $\ell _o / h$ has to be kept large (h is the element size) so to represent well the localized solution $\alpha (x)$. For any $\ell _o / h$ ratio an overestimated fracture toughness $G_{Ic}$ [34, 35] is implied in the FE approximation. Hence for the classical h-FE discretization the mesh size is generally adjusted such that $\ell _o>h$, in [36] $\ell _o/h=5$, or such that $\ell _o \gg h$ [37]. For inhomogeneous materials the appropriate $G_{Ic}$ correction is unknown, and especially so for high-order (also denoted as p-FE) approximations [38].

Furthermore, for the AT1 PFM damage positivity i.e. $\alpha \ge 0$ must be enforced explicitly so healing should be forbidden through an irreversibility constraint . These constraints may be enforced using penalization [37], augmented Lagrangian approach [39] or Lagrange multiplier [40]. In this work the penalization technique [37] is adopted and enhanced for inhomogeneous materials.

p-FEs (large elements and high polynomial degree) was proposed for the simulation of bone’s mechanical response [41], having several advantages over conventional h-FEs: accurate surface representation, distorted elements do not pose accuracy deterioration and faster convergence rates achieved by increasing the polynomial degree of the shape functions over the same mesh thus controlling numerical errors easily [38]. Herein a feasibility study is presented aimed at investigating whether p-FEs advantages carry over to AT1 PFM for inhomogeneous 1D domains. To this end we compute explicitly analytical solutions of PFM problems in a heterogeneous bar and perform numerical studies using both h- and p-FE implementations. In Sect. 2 we present the benchmark problem and derive analytical solutions for different heterogeneity profiles for numerical verification. In Sect. 3 we address the h-FEM and investigate the error related to the numerical fracture toughness $G_{Ic}^{FE}$ and the penalization enforcing damage positivity and irreversibility. In Sect. 4 we investigate the performance of p-FEs and demonstrate their super numerical performance compared to h-FEs.

2 Explicit solutions for a heterogeneous bar

The analytical framework in [33] is used herein to compute explicit analytic solutions to the heterogeneous 1D problem stated in strong form. Three heterogeneous profiles for the material properties $E(x)=E_0 \times k(x)$ and $G_{Ic}(x)= G_{Ic_0} \times k(x)$ are studied: linear, exponential and parabolic with k(x) given in (2).

$$\begin{aligned} k(x) = \left\{ \begin{array}{ll} 1+\frac{|x-L/2|}{l_f}&{} \text {, linear} \\ \text { } \\ \exp (\frac{2|x-L/2|}{l_f}) &{} \text {, exponential} \\ \text { } \\ 1+(\frac{x-L/2}{l_f})^2 &{} \text {, parabolic} \\ \end{array} \right. \end{aligned}$$

(2)

$l_f$ is the characteristic length of heterogeneity (the smaller $l_f$ the largest E and $G_{Ic}$ at the bar ends). E(x) and $G_{Ic}(x)$ are maximum at the bar’s ends and have the same minima, respectively $E_0$ and $G_{Ic_0}$, at $x=L/2$ (see Fig. 3).

Fig. 3

Heterogeneous profiles for E(x) and $G_{Ic}(x)$ with $E_0=1$ and $G_{Ic_0}=8/15$

The solutions u(x) and $\alpha (x)$ are obtained by minimizing the total potential energy (1) with respect to displacement and damage fields under the constraint $0\le \alpha \le 1$. In the classical variational framework, it is a quasi-static evolution problem for displacement and damage fields formulated at the pseudo-time t as a first-order local minimum condition on the energy functional $\Pi$. This condition is unilateral so to ensure damage irreversibility, i.e. $\alpha _t(x)$ is non decreasing function $\forall x$. In other terms, $u_t(x)$ and $\alpha _t(x)$ are solutions of¹

$$\begin{aligned} \text {arg loc min } \{ \Pi ( u_t,\alpha _t): u_t \in \mathcal {U}, \alpha _t \in \mathcal {A}\}, \end{aligned}$$

(3)

where the admissible displacement and damage solutions are sought in the spaces $\mathcal {U}$ and $\mathcal {A}$, respectively, defined by

$$\begin{aligned} \mathcal {U} = \left\{ v \in H^1(\Omega \setminus \mathcal {S}): v(0)=0 \text { and } v(L) = U_t \right\} \end{aligned}$$

(4)

with $\mathcal {S}$ being the set of points where v is discontinuous. In our problem,

$$\begin{aligned} \mathcal {S}= & {} \left\{ x \in \Omega : \alpha _t(x)=1 \right\} \end{aligned}$$

(5)

$$\begin{aligned} \mathcal {A}= & {} \left\{ \beta \in H^1(\Omega ): \beta \in [0,1] \text { and } \dot{\beta } \ge 0\right\} \end{aligned}$$

(6)

Following the variational approach in [33, 42, 43], the evolution problem is governed by the principles of irreversibility, local stability and energy balance. Due to the irreversibility constraint $\alpha _t>\alpha _{t-1}$, the necessary optimality condition to compute the solutions $(u_t,\alpha _t)$ of the constrained minimization problem (3) is a variational inequality. These solutions should be solutions of the first-order evolution problem.

First-order evolution problem. Given the initial state ($u_0$,$\alpha _0$)=(0,0) at the pseudo-time $t=0$, find $t \rightarrow$ ($u_t$,$\alpha _t$) $\in \mathcal {U} \times \mathcal {A}$ such that:

$$\begin{aligned}{} & {} \dot{\alpha _t} \ge 0, \quad \quad \textit{irreversibility} \end{aligned}$$

(7)

$$\begin{aligned}{} & {} D\Pi (u_t,\alpha _t)(v,\beta ) \ge 0 \nonumber \\{} & {} \quad \forall (v,\beta ) \in \mathcal {V} \times \mathcal {B},\quad \textit{first-order stability} \end{aligned}$$

(8)

$$\begin{aligned}{} & {} D\Pi (u_t,\alpha _t)(\dot{u_t},\dot{\alpha _t}) \nonumber \\{} & {} \quad = \sigma _t(L) \dot{u_t}(L), \quad \textit{energy balance} \end{aligned}$$

(9)

where $D\Pi (u_t,\alpha _t)(v,\beta )$ is the directional or Gâteaux derivative of $\Pi$ at ($u_t$,$\alpha _t$) in the direction (v,$\beta$).

The superimposed dot denotes derivative with respect to pseudo-time t while $'$ denotes derivative with respect to space variable x. In (9) $\sigma _t(x)$ denotes the Cauchy stress at pseudo-time t:

$$\begin{aligned} \sigma _t(x)=E(x)(1-\alpha _t(x))^2 u_t'(x) \end{aligned}$$

(10)

The sets of admissible test functions are respectively:

$$\begin{aligned} \mathcal {V}= & {} \left\{ v(x)\in H^1(\Omega \setminus \mathcal {S}): v(0)=0 \text { and } v(L) = 0 \right\} \end{aligned}$$

(11)

$$\begin{aligned} \mathcal {B}= & {} \left\{ \beta (x)\in H^1(\Omega ): \beta (x) \ge 0 \right\} \end{aligned}$$

(12)

2.1 Explicit solutions $(u(x), \alpha (x))$

Exact (analytical) solutions can be derived [33] by realizing that the stress is constant along the bar i.e. $\sigma _t(x) \rightarrow \sigma _t$. Hence it is possible to switch the increasing prescribed displacement $U_t$ to a controlled prescribed stress $\sigma _t$ and determine analytically damage and displacement solutions [33]. We denote by elastic limit stress $\sigma _e$ the stress below which $\alpha _t^{max}(x)=0$ and denote by peak stress $\sigma _p$ the maximum possible stress. We also denote by $\sigma _u=0$ the broken bar. For a heterogeneous bar a representative stress-displacement response is shown in Fig. 4 that may represent also a snap-back phenomenon: for a given $\sigma _t$ the solutions $(u_t(x), \alpha _t(x))$ may be not unique. For $\sigma _t=1$ one can observe in Fig. 4 that it can either be associated to an undamaged bar i.e $\sigma _t=\sigma _e$ or to a partially damage bar i.e $0<\alpha _t^{max}(x)<1$ within the snap-back portion of the curve.

For $\sigma _t > 0$ and without considering the snap-back portion of the curve, three distinct damage phases occur (as opposed to only two in a homogeneous bar):

• $\sigma _t \le \sigma _e$, purely elastic phase i.e. $\alpha _t^{max}(x)=0$.

• $\sigma _e < \sigma _t \le \sigma _p$, partially damaged phase i.e. $0<\alpha _t^{max}(x)<1$,

• $\sigma _t = \sigma _u$, fully-developed crack phase i.e. $\alpha _t^{max}(x)=1 \, {\buildrel \mathrm def \over =} \alpha _u$

For the fully-developed crack phase, $\sigma _t = \sigma _u$ has a conceptual definition, because of the snap-back at $\sigma _p$ and stress decreases to 0 at fracture.

Fig. 4

Stress-displacement response for bi-linear E(x) and $G_{Ic}(x)$ with $l_f=0.4$ and $\ell _o=0.2$

In a homogeneous bar $\sigma _p = \sigma _e$, thus a “partially damage phase” is associated only with a snap-back. Heterogeneity thus induces a “stress hardening effect” ($\sigma _p > \sigma _e$) and at the same time the smeared crack width ($\delta <4\ell _o$) is smaller due to shrinking of damage profile.

Analytical solutions based on [33] for u(x) and $\alpha (x)$ for the three phases $\sigma _t = \sigma _e$, $\sigma _t = \sigma _p$ and $\sigma _t= \sigma _u$ serve to verify finite element (FE) approximations.

Purely Elastic Phase: For $\sigma _t \le \sigma _e$ the solution for the damage for the AT1 model is $\alpha _t(x)=0$, and the exact solutions for $u_t(x)$ are:

for linear profile

$$\begin{aligned}{} & {} u_t(x) = \frac{\sigma _tl_f}{E_0} \times \nonumber \\{} & {} \quad \left\{ \begin{array}{ll} \log \left( \frac{l_f+L/2}{l_f+L/2-x}\right) &{} \forall \text { } 0 \le x \le L/2\\ \log (l_f-L/2+x)+\log \left( \frac{l_f+L/2}{l_f^2}\right) &{} \forall \text { } L/2 \le x \le L\ \end{array} \right. , \nonumber \\ \end{aligned}$$

(13)

for exponential profile

$$\begin{aligned}{} & {} u_t(x) = \frac{\sigma _t l_f}{2E_0} \times \nonumber \\{} & {} \quad \quad \left\{ \begin{array}{ll} \exp (-L/l_f)\left( exp(2x/l_f) - 1\right) &{} \forall \text { } 0 \le x \le L/2 \\ 2-\exp (-L/l_f)-\exp ((L-2x)/l_f) &{} \forall \text { } L/2 \le x \le L\ \end{array} \right. , \nonumber \\ \end{aligned}$$

(14)

for parabolic profile

$$\begin{aligned} u_t(x)= & {} \frac{\sigma _t l_f}{E_0} \left( arctan\bigg ( \frac{x- L/2}{l_f} \biggr )\right. \nonumber \\{} & {} \left. + arctan\biggl (\frac{L}{2 l_f} \biggr ) \right) \forall \text { } 0 \le x \le L. \end{aligned}$$

(15)

Partially damage phase For $\sigma _e < \sigma _t \le \sigma _p$, solutions $\alpha _t(x)$ are found semi-analytically. Solutions $u_t(x)$ are computed by integrating the constitutive law using the semi-analytical solutions $\alpha _t(x)$ and the change of variable $\tilde{x}= x/\ell _o$.

$$\begin{aligned} u_t(x_i) = \frac{\sigma _t \ell _o}{E_0} \int ^{\tilde{x}_i}_0 \frac{1}{k(\tilde{x})(1-\alpha _t(\tilde{x}))^2}d\tilde{x} \quad \forall \text { } 0 \le x_i \le L. \nonumber \\ \end{aligned}$$

(16)

Fully-developed crack phase The case $\sigma _t= \sigma _u$ corresponds to a broken bar. The damage solutions are provided in [33] for the three heterogeneity profiles. $\alpha _t(x=L/2)=1$, the discontinuous field

$$\begin{aligned} u_t(x) = \left\{ \begin{array}{ll} 0, &{} 0 \le x \le L/2\\ \hat{u}, &{} L/2 \le x \le L\ \end{array} \right. \end{aligned}$$

(17)

is the displacement solution where $\hat{u}$ is the displacement at the end of the broken bar. To compare with FE solutions of displacement-controlled problem, one needs to find $\hat{u}$ value corresponding to a broken bar. It has to be higher than the maximum allowable displacement in the stress-displacement curve (see Fig. 4) so $\hat{u}= \underset{\sigma _t vs. U_t}{max}\ (U_t) + 0.01$ is a chosen.

For the linear and parabolic heterogeneity profiles (Fig. 3a and c) the (u(x),$\alpha (x)$) solutions are plotted in Figs. 5 and 6 ($L=2$, $l_f=0.4$, $\ell _o=0.2$) for the three phases $\sigma _t = \sigma _e$, $\sigma _t = \sigma _p$ and $\sigma _t = \sigma _u$. The shrinking of crack profile (Figs. 5b and 6b) with respect to homogeneous case illustrates the interplay between crack and $G_{Ic}(x)$ heterogeneity profile.

Explicit solutions u(x) and $\alpha (x)$ have been derived for all heterogeneity profiles and tabulated with a 0.0001 precision in Appendix A. These serve as benchmark problems to verify the FE approximations.

Fig. 5

Bi-linear E(x), $G_{Ic}(x)$ and solutions (u(x),$\alpha (x)$) at different $\sigma _t$ for $L=2$, $l_f=0.4$, $\ell _o=0.2$. Dashed blue line corresponds to homogeneous case i.e $l_f \rightarrow \infty$. (Color figure online)

Fig. 6

Bi-parabolic E(x), $G_{Ic}(x)$ and solutions (u(x),$\alpha (x)$) at different $\sigma _t$ for $L=2$, $l_f=0.4$, and $\ell _o=0.2$. Dashed blue line corresponds to homogeneous case i.e. $l_f \rightarrow \infty$. (Color figure online)

3 Discretization by h-FEA

In this section the approximations $u^{h}$ and $\alpha ^{h}$, in a space of low order piece-wise polynomials (h-FEM), are addressed. The problem is displacement-controlled and depicted in Fig. 1.

The minimization problem (3), (8) and (7) is casted in the coupled weak formulation (the associated strong formulation is given in Appendix B):

Weak formulation. Given the initial state ($u_0$,$\alpha _0$)=(0,0) at the pseudo-time $t=0$, find $t \rightarrow$ ($u_t$,$\alpha _t$) $\in \mathcal {U} \times \mathcal {A}$ such that $\forall (v,\beta ) \in \mathcal {V} \times \mathcal {B}$:

$$\begin{aligned}{} & {} \int _{\Omega } E(x)(1-\alpha _t)^2u'_tv' dx = 0, \quad \quad \textit{Elastic problem} \end{aligned}$$

(18)

$$\begin{aligned}{} & {} \int _{\Omega } E(x) (\alpha _t-1) \beta u_t{'}^2 dx \nonumber \\{} & {} \qquad + \frac{3}{8 \ell _o} \int _{\Omega } G_{Ic}(x) \left( \beta + 2 \ell _o ^2 \alpha _t' \beta ' \right) dx \ge 0, \quad \quad \nonumber \\{} & {} \quad \textit{Damage problem} \end{aligned}$$

(19)

The elasticity problem (18) becomes an equality because displacement is reversible and $\alpha _t \in \mathcal {A}$ satisfies the irreversibility constraint.

Two cases may be considered: a) A history-independent problem, i.e. the phase field does not evolve, so non-negativity of $\alpha _t(x)$ must be enforced (no evolution of $\alpha _t(x)$). b) A history-dependent problem i.e. the PF $\alpha _t(x)$ evolves starting from the initial state ($u_0$,$\alpha _0$)=(0,0) for $U_t=0$.

Remark 1

In both cases a constrained minimization problem is solved by the FEA. In the former damage positivity is enforced because it is not automatically satisfied for the AT1 model. In the latter, damage irreversibility is enforced from the initial state ($u_0$,$\alpha _0$)=(0,0) for $U_t=0$.

We are not interested in the loading history but in computing a "snapshot" $(u(x),\alpha (x)$) solution for a given prescribed displacement $U_t$, and focus on a fully damaged phase i.e. $\alpha _t(x)=\alpha _u(x)$ and $U_t=\hat{u}$ corresponding to a broken bar. The constraint $\alpha (x) \ge 0$ $\text { } \forall x \in [0,L]$ (positivity), also called recovery [37], is enforced by a penalty technique. Penalization technique (see [37]) consists of adding to the potential energy a penalty term that tends to infinity if the recovery condition is not respected. I.e. we seek to minimize:

$$\begin{aligned} \Pi _C(u,\alpha )= & {} \int _{\Omega }\frac{1}{2}(1-\alpha )^2E(x)u'{}^2 dx \nonumber \\{} & {} + \int _{\Omega } \frac{3G_{Ic}(x)}{8\ell _o}(\alpha + \ell _o^2 \alpha '{}^2 )dx \nonumber \\{} & {} + \underbrace{\frac{C}{2} \int _{\Omega } <\alpha >_-^2dx}_\text {penalty term} \end{aligned}$$

(20)

with $<y>_-^2 = y^2$ if $y<0$, and 0 otherwise, being the Macaulay brackets and C being the penalty constant that must be large enough ($\gg 1$) to ensure recovery without causing ill-conditioning issues. u(x) and $\alpha (x)$ are solutions of

$$\begin{aligned} \text {arg loc min } \{ \Pi _C(u(x),\alpha (x)): u(x) \in \mathcal {U}, \alpha (x) \in \mathcal {A}\} \end{aligned}$$

(21)

The penalized problem (21) is equivalent to the original minimization problem (3) in the limit of $C \rightarrow \infty$ and is an approximation of it as C is finite. Hence, the choice of this value is important for numerical verification.

The functions $u^h(x), \alpha ^h(x)$ and the test functions $v^h(x),$ $\beta ^h(x)$ are approximated by a space of piecewise polynomials spanned by shape functions $\vec {N}^T_e(x)=(N_1(x) \ N_2(x) \ \cdots$ $N_{p+1}(x))_e$ and associated elemental vectors $\vec {u}_e$, $\vec {v}_e$, $\vec {\alpha }_e$ and $\vec {\beta }_e$: $u_e^{h} =\vec {N}_e^T(x) \vec {u}_e$, $\alpha _e^{h} =\vec {N}_e^T(x) \vec {\alpha }_e$, $v_e^{h} =\vec {N}_e^T(x) \vec {v}_e$ and $\beta _e^{h} =\vec {N}_e^T(x) \vec {\beta }_e$. The subscript "e" denotes shape functions and vectors at the element level.

FE formulation. Find ($u^h$,$\alpha ^h$) $\in \mathcal {U}^h \times \mathcal {A}^h$ such that $\forall (v^h,\beta ^h) \in \mathcal {V}^h \times \mathcal {B}^h$:

$$\begin{aligned}{} & {} \int _{\Omega } E(x)(1-\alpha ^h)^2u^{h'}v^{h'} dx = 0, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} \int _{\Omega } E(x) (\alpha ^h-1) \beta ^h u^{{h'}^2} dx + \int _{\Omega } \frac{3G_{Ic}(x)}{8 \ell _o}(\beta ^h \nonumber \\{} & {} \quad + 2\ell _o^2 \alpha ^{h'} \beta ^{h'}) dx + C \int _{\Omega } <\alpha ^h>_- \beta ^h dx = 0, \end{aligned}$$

(23)

with the discretized spaces of finite dimensions, $\mathcal {U}^h \subset \mathcal {U}$, $\mathcal {A}^h \subset \mathcal {A}$, $\mathcal {V}^h \subset \mathcal {V}$ and $\mathcal {B}^h \subset \mathcal {B}$.

We use the set of nodes $\{0,h,2h,...,(N_{el}-1)h,L\}$ where $h=L_e$ is the element length and $N_{el}$ is the number of elements such as $N_{el} \times h=L$.

Since the solutions of the broken bar are localized in the center i.e. $x=L/2$ (see Figs. 5 and 6) we adopt a mesh with selective refinement (Fig. 7) in the region where the crack is expected to appear and $\alpha >0$ i.e. $[\frac{L-4\ell _o}{2}$,$\frac{L+4\ell _o}{2}$].

Fig. 7

Symmetric representation of the selectively refined mesh through h parameter while $h_{max}=L/10$ is fixed

Displacement (22) and damage (23) weak forms are solved by a weak coupling i.e. "freezing" alternatively $u^h$ and $\alpha ^h$. The equation (23) is nonlinear due to the Macaulay brackets $< >_-$ term while (22) is linear. A Newton–Raphson solver is used for (23) and for (22) without loss of generality.

The staggered solver scheme STG_solver is described in Appendix C. The numerical integration was performed by a Gauss quadrature with $N_{GP}=2$ points (u(x) and $\alpha (x)$ are both approximated by linear shape functions).

Fig. 8

Error in dissipated fracture energy $\Pi _D^{err}$ imposing damage recovery via penalization for linear and parabolic heterogeneity profile depending on $\ell _o/l_f$ (Left) and $L/\ell _o$ (Right) with $\ell _o=0.2$ and $\ell _o/h=150$. (Dashed red line) -1% tolerance error. (Color figure online)

3.1 Positivity constraint

An optimal penalty coefficient C in (23) corresponds to a minimum value $C^{opt}$ ensuring $\alpha (x)>0$ $\forall x \in \Omega$ given a prescribed tolerance avoiding ill-conditioning. For a homogeneous bar a penalty term was proposed for fully-developed crack $\alpha _u(x)$, i.e. the stress is zero and only the phase field profile was solved. A lower bound for the penalty coefficient was determined to satisfy $\Gamma -$convergence and recover the dissipated fracture energy, i.e. $\Pi _{\mathcal {D}}(\alpha _u(x))=G_{Ic}$, with a user-prescribed tolerance threshold $(1-TOL_{rec})\times 100\%$:

$$\begin{aligned} C_{opt} = \frac{9G_{Ic}\left( \frac{L}{\ell _o}-4\right) }{64\ell _o TOL_{rec}} \end{aligned}$$

(24)

A practical $TOL_{rec} = 0.01$ was suggested, because a higher penalty coefficient did not improve the results [37]. Inspecting (24) one notices:

• $C_{opt}$ depends on $L/\ell _o$. If $\ell _o=L/4$ the damage profile is along the entire bar, and no penalization is required, i.e. $C_{opt}=0$.

• $C_{opt}$ is determined under the assumption of a fully developed damage profile, hence it may be not be sufficient to enforce positivity of $\alpha (x)$ for $\alpha (x)<1$ $\forall x \in \Omega$.

Although a fully-damaged profile including penalty cannot be obtained analytically for an heterogeneous bar, $C_{het}$ should have the following properties:

• At the homogeneous limit, $C_{het}\rightarrow C_{opt}$ in (24). I.e.: $\lim \limits _{l_f \rightarrow \infty } C_{het} =\frac{9G_{Ic_0}\left( \frac{L}{\ell _o}-4\right) }{64\ell _o TOL_{rec}}$.

• $C_{het}$ should account for shrinking the compact support of the fully damaged profile and the heterogeneous $G_{Ic}(x)$ by considering $\ell _o/l_f$ and $G_{Ic}^{max}=max(G_{Ic}(x))$ contributions.

Accordingly, the expression below is proposed for minimum penalty coefficient in an heterogeneous bar:

$$\begin{aligned} C_{het}= \frac{9G_{Ic}^{max}\left( \frac{L}{\ell _o}\left( 1+\frac{\ell _o}{l_f}\right) -4\right) }{64\ell _o TOL_{rec}^{1+n\ell _o/l_f}} \end{aligned}$$

(25)

With n being a coefficient calibrated for the heterogeneity profile to recover 99% of the dissipated fracture energy, used as a criterion in [37] for homogeneous case.

Considering $\ell _o \gg h$ Fig. 8a, b show $n=1$ and $n=2$ are appropriate coefficient to ensure 99% recovery of dissipated fracture energy enforcing damage positivity for linear and parabolic profiles $G_{Ic}(x)$ (Fig. 3a and c), respectively.

To check the penalty coefficient influence when used for different h-refinements we adopt the mesh in Fig. 7. The penalty is activated only for $\alpha _u(x)<0$ that may occur outside the damage compact support $\approx ]\frac{L-4\ell _o}{2},\frac{L+4\ell _o}{2}[$ and we adopt an uniform mesh, i.e. $h_{max}=h$ in Fig. 7. Considering a linear heterogeneity profile (Fig. 3a), the proposed correction $G_{Ic}^{h}$ in (33) (see Sect. 3.3) and different mesh refinements h, we compute the error in fully-damaged profile $\alpha _u^{err}$ for different tolerances $TOL_{rec}$. These are presented in Figs. 9a, b.

Fig. 9

Error in damage half-profile $\alpha _u^{err}$ imposing damage positivity via penalization for linear heterogeneity profile and different tolerances $TOL_{rec}$ and mesh refinement, $\ell _o=0.2$, $\ell _o/l_f=0.5$ and $L/\ell _o=10$

One may notice that the mesh refinement and the penalty coefficient are independent since the error is controlled by mesh refinement inside the damage band $\approx ]\frac{L-4\ell _o}{2},\frac{L+4\ell _o}{2}[$ and by the penalty coefficient via $TOL_{rec}$ outside the damage band where positivity constraint is activated. Mesh dependency is seen where penalty is activated at $x=\frac{L+4\ell _o}{2}=1.4$ for the coarser mesh $\ell _o/h=2$ but the error is smaller. Thus, the penalty coefficient (25) is adapted for ensuring damage positivity regardless the mesh refinement as $\ell _o/h \ge 2$.

3.2 Damage evolution and irreversibility constraint

We address here an evolution process for which irreversibility constraint (7) may also be enforced via penalization [37]. Starting from the initial state ($u_0$,$\alpha _0$)=(0,0) for $U_t=0$, a penalty term is added to the potential energy functional:

$$\begin{aligned} \Pi _{C^{irr}}(u_t,\alpha _t)= & {} \int _{\Omega }\frac{1}{2}(1-\alpha _t)^2E(x)u_t'{}^2 dx \nonumber \\{} & {} + \int _{\Omega } \frac{3G_{Ic}(x)}{8\ell _o}(\alpha _t + \ell _o^2 \alpha _t'{}^2 )dx \nonumber \\{} & {} + \underbrace{\frac{C^{irr}}{2} \int _{\Omega } <\alpha _t-\alpha _{t-1}>_-^2dx}_\text {penalty term} \end{aligned}$$

(26)

Here too, an optimal penalty coefficient is derived to recover 99% of dissipated fracture energy and we consider the case for which $\alpha _{t-1}=\alpha _u$. For an homogeneous bar [37]:

$$\begin{aligned} C^{irr} = \frac{27G_{Ic}}{64\ell _o TOL_{irr}^2} \end{aligned}$$

(27)

with $TOL_{irr}=0.01$. Since $L/\ell _o$ ratio is not involved, we consider an optimal penalty coefficient for an heterogeneous bar to satisfy:

• $\lim \limits _{l_f \rightarrow \infty } C^{irr}_{het} =\frac{27G_{Ic_0}}{64\ell _o TOL_{irr}^2}$, corresponding to the homogeneous case (27).

• $C^{irr}_{het}$ accounts for heterogeneous $G_{Ic}(x)$ through $G_{Ic}^{max}=max(G_{Ic}(x))$ contribution.

Hence the expression below is proposed for minimum penalty coefficient to enforce irreversibility in a heterogeneous 1D bar.

$$\begin{aligned} C^{irr}_{het} =\frac{27G_{Ic}^{max}}{64\ell _o TOL_{irr}^2} \end{aligned}$$

(28)

Considering $\ell _o \gg h$ Fig. 10 shows the penalty coefficient (28) is satisfying to recover 99% of dissipated fracture energy enforcing damage irreversibility for linear and parabolic $G_{Ic}(x)$.

Fig. 10

Error in dissipated fracture energy $\Pi _D^{err}$ imposing damage irreversibility via penalization for linear and parabolic heterogeneity profile depending on $\ell _o/l_f$ with $\ell _o=0.2$ and $\ell _o/h=150$. (Dashed red line) −1% tolerance error. (Color figure online)

3.3 Numerical $G^{FE}_{Ic}$

$G_{Ic}$ has to be corrected in a PF formulation to overcome the overestimation of the dissipated fracture energy $\Pi _{\mathcal {D}}(\alpha _u)$ because of smearing the crack over $\ell _o = \mathcal {O}(h)$. For a homogeneous bar a correction was suggested in [34]. The dissipated fracture energy is:

$$\begin{aligned} \Pi _{\mathcal {D}}(\alpha _u)= \int _{\Omega } \frac{3G_{Ic}(x)}{8\ell _o}(\alpha _u + \ell _o^2 \alpha _u'{}^2 )dx \end{aligned}$$

(29)

For a homogeneous bar, i.e. $l_f \rightarrow \infty$ and $G_{Ic}(x) \rightarrow G_{Ic_0}$, the dissipated energy at fracture is $\Pi _{\mathcal {D}}(\alpha _u)=G_{Ic_0}$ with $\alpha _u$ the fully-damaged profile and $\alpha _u=1$ at $x^*=L/2$. The overestimation is related to the discontinuity at $x^* \in \mathcal {S}$. $u^h\in H^1(\Omega )$ is approximated by continuous shape functions ( $\mathcal {C}_0(\Omega ))$, whereas $u(x) \in H^1(\Omega /\mathcal {S}:=x^*)$. Hence, the displacement discontinuity and the damage kink at $x^*=L/2$ are approximated on an element of size h (see Fig. 11a, b for linear FE approximation).

Fig. 11

a Representation of linear FE-approximation of displacement discontinuity and b Damage kink at crack location $x^*=L/2$ (zoomed in the crack location)

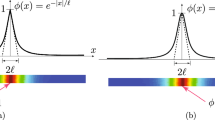
h-FE discretization in a homogeneous 1D domain results in an overestimation of dissipated energy at fracture of order $\mathcal {O}(h)$, i.e. $G_{Ic}^{h} +\mathcal {O}(h) = G_{Ic}$ (see [34] for $\ell _o = \mathcal {O}(h)$ and linear elements). As indicated in Figs. 11a, b, displacement discontinuity and damage kink is better approximated as $\ell _o/h \rightarrow \infty$, i.e. $h \rightarrow 0$.

$$\begin{aligned} G_{Ic}^{h}=\frac{G_{Ic}}{1+\biggl (\frac{3h}{8\ell _o} \biggr )} \end{aligned}$$

(30)

For a heterogeneous material a connection similar to (30) is unknown, thus former studies suggested to consider $\ell _o \ge h$ [9] to $\ell _o > 5 h$ [14, 20, 22]. The larger the ratio $\ell _o/h$, the smaller the error $\Pi _{\mathcal {D}}^{err}$. Thus, [13] suggested $\ell _o \ge (4-5)h$ and the constraint $\ell _o \gg h$ is suggested in [18]. As $\ell _o/h \rightarrow \infty$:

$$\begin{aligned} \Pi _{\mathcal {D}}^{err}= \frac{\Pi _{\mathcal {D}}^{FE}-\Pi _{\mathcal {D}}^{EX}}{\Pi _{\mathcal {D}}^{EX}} \rightarrow 0 \end{aligned}$$

(31)

$\Pi _{\mathcal {D}}^{EX}$ can be computed for the 3 different heterogeneity profiles, depending on $\ell _o/l_f$ and $\delta$ (the support of $\alpha _u(x)$) [33].

For a finite h, and considering a linear heterogeneity profile (Fig. 3a), two correction approaches are investigated.

Naive approach. The correction in [34] is applied replacing the homogeneous $G_{Ic}$ by $G_{Ic}(x)$:

$$\begin{aligned} G_{Ic}^{h}(x)=\frac{G_{Ic}(x)}{1+\biggl (\frac{3h}{8\ell _o} \biggr )} \end{aligned}$$

(32)

Alternative approach. The dissipated fracture energy corresponds to the fracture toughness at crack location, i.e. $G_{Ic}(x^*=L/2)=G_{Ic_0}$. Since $\Pi _{\mathcal {D}}(\alpha _u)$ is overestimated, $G_{Ic}(x)$ and $G_{Ic_0}$ are also. $G_{Ic}(x)$ depends on $G_{Ic_0}$ thus based on arguments of [34] and symmetry of $G_{Ic}(x)$ profile, one may apply a correction to the overestimated $G_{Ic_0}$ such that $x^*=L/2$ is at the middle of an element. More precisely,

$$\begin{aligned} G_{Ic}^h= & {} G_{Ic_0}+ 2 \cdot \int _{\frac{L}{2}}^{\frac{L+h}{2}} G_{Ic}(x) dx = G_{Ic_0}\nonumber \\{} & {} + 2 \cdot \frac{3G_{Ic_0}}{8\ell _o} \int _{\frac{L}{2}}^{\frac{L+h}{2}} \biggl (1+\frac{|x-\frac{L}{2}|}{l_f} \biggr ) dx \nonumber \\= & {} \frac{ G_{Ic_0}}{1+\frac{3h}{8\ell _o} \biggl (1+\frac{h}{4l_f}\biggr )} \end{aligned}$$

(33)

Remark 2

For a homogeneous bar, i.e. $l_f \rightarrow \infty$, the correction (33) reduces to (30) with $G_{Ic}=G_{Ic_0}$.

We investigate the proposed corrections based on the induced error in dissipated fracture energy $\Pi _{\mathcal {D}}^{err}$ and the induced error in fully-damaged profile $\alpha _u^{err}=\alpha _u^{EX}-\alpha _u^{FE}$.

Numerical examples shown in Figs. 12a, b demonstrate that the proposed "Alternative correction" reduces the overestimation of dissipated fracture energy compared to the "Naive approach". For $\ell _o/h=2$ the overestimated dissipated fracture energy is associated with fracture toughness overestimation such that partially-damaged profile occurs instead of fully-damaged profile $\alpha _u(x)$. Both Naive and Alternative approaches correct this toughening effect by well representing the fully-damaged profile $\alpha _u(x)$ (Fig. 12b).

Fig. 12

Error in dissipated fracture energy $\Pi _{\mathcal {D}}^{err}$ (Top) and in fully damaged profile (Bottom) using different correction approaches, linear profile $G_{Ic}(x)$, $\ell _o=0.2$, $\ell _o/l_f=0.5$ and $L/\ell _o=10$. (Dashed red line) 1% tolerance error. (Black line) No correction. (Dashed gray line) Naive approach. (Blue line) Alternative approach. (Color figure online)

We remark that both Naive correction and our proposed Alternative correction results in the same accuracy when approximating the damage profile (Fig. 12c). Thus, $G_{Ic}$ correction is limited to a global improvement in the fully-damaged phase. Prior to the fully-damaged phase, to better approximate the damage profile $\alpha _u(x)$, regardless the adopted correction, one needs a better numerical approximation by either refining the mesh i.e. h-version or increasing the polynomial order of the shape functions i.e. p-version.

Nucleation stress

One of the most important quantity of interest is the nucleation stress (peak stress $\sigma _p$) in a PF analysis. We demonstrate that for a heterogeneous bar an accurate dissipation energy computation does not ensure an accurate determination of the nucleation stress, and the reason for it.

We use the penalty coefficient (28) to ensure damage irreversibility and monitor $\sigma _p$. Considering the linear heterogeneity profile and the explicit solutions derived in Sect. 2, we perform $h-$extensions for $U_t=(0.25,0.5,...,N_{step},1)\times \hat{u}$ starting from the initial state ($u_0$,$\alpha _0$)=(0,0) at $U_t=0$.

The relative error in peak stress is computed by $\sigma _p^{err}=\frac{\sigma _p^{FE}-\sigma _p^{EX}}{\sigma _p^{EX}}$. $\sigma _p^{EX}=1.21$ as seen in in Fig. 5 and Table 1. $\sigma _p^{FE}$ is calculated at a Gauss point in the last element of the bar with $N_{step}=100$. The effect of $G_{Ic}$-correction approaches on $\sigma _p^{err}$ is shown in Fig. 13. One may observe that the most accurate $\sigma _p^{FE}$ is obtained without corrections of $G_{Ic}$ whereas errors are induced by the naive and alternative corrections which assure least errors in the dissipated energy. This error decreases as the correction effect decreases (Figs. 13b and 13c), i.e. $\ell _o/h\rightarrow \infty$. Since on one hand $\sigma _p$ is related to a small maximum value of $\alpha$ (minimal damaged phase), which is relatively well approximated by linear FE, and on the other hand the $G_{Ic}$ corrections are derived at the fully-damaged profile, the fracture toughness is decreased while it is not needed. Consequently the peak stress $\sigma _p^{FE}$ is underestimated using the corrected $G_{Ic}$ (Figs. 13a and c).

Fig. 13

Error in peak stress $\sigma _p^{err}$ and stress-displacement curves using different correction approaches, linear profile $G_{Ic}(x)$, $\ell _o=0.2$, $\ell _o/l_f=0.5$ and $L/\ell _o=10$. (Black line) No correction. (Gray line) Naive approach or exact stress-displacement curve. (Dashed blue line) Alternative approach. (Color figure online)

We investigate the penalization influence on $\alpha _u^{err}=\alpha _u^{EX}-\alpha _u^{FE}$ (error in fully-damaged profile) using the alternative $G_{Ic}$-correction (33) (both naive and alternative approaches are efficient only at the fully-damaged phase). Considering different mesh refinements $\alpha _u^{err}$ is computed for different tolerances $TOL_{irr}$ and $N_{step}$ ($N_{step}=5$ and $N_{step}=20$ for $\ell _o/h=2$ and $\ell _o/h=\{20;150\}$ respectively). Contrary to positivity constraint, expected to be activated outside the damage band support, irreversibility may be activated also inside the damage band (see Fig. 14 for $\ell _o/h=150$ at $x=1.3$). Hence the error may be controlled by both mesh refinement and penalty coefficient. Outside the damage band support the error is controlled by the penalty coefficient and the loading history through $\alpha _{t-1}$ in (26). That explains the differences between $\ell _o/h=2$ and $\ell _o/h=\{20;150\}$ in Fig. 14a, b since the loading history is different i.e. there are approximately 3 times more pseudo-time steps for $\ell _o/h=\{20;150\}$. We expect that $\alpha _u^{err}$ increases as $N_{step}$ increases so additional positivity constraint $\alpha \ge 0$ may be needed as mentioned in [37].

The penalty coefficient (28) for damage irreversibility is adapted for linear and parabolic heterogeneity profile and regardless the mesh refinement as $\ell _o/h \ge 2$.

4 Discretization by p-FEA

A p-FE implementation of PFM for the heterogeneous bar is investigated using hierarchic shape functions that are integrals of Legendre polynomials [44]. For a p-FE extension the mesh is fixed and the degrees of freedom (DOFs) are increased by adding additional shape functions of a higher polynomial order p to obtain convergence. Due to the hierarchical shape functions, we use the solution vector at a given polynomial order as an initial guess at the higher polynomial order, resulting in a faster convergence rate in the iterative solution scheme. The p-FE algorithm used in our implementation is described in the algorithm below.

Fig. 14

Error in damage half-profile $\alpha _u^{err}$ imposing damage irreversibility via penalization for linear heterogeneity profile, different tolerances $TOL_{irr}$ and mesh refinement. $\ell _o=0.2$, $\ell _o/l_f=0.5$ and $L/\ell _o=10$

Using polynomials up to degree 8 to approximate displacement and damage solutions u(x) and $\alpha (x)$, the numerical integration is performed using 16 Gauss points ($N_{GP}=16$).

We consider the "snap shot" solution, so we concentrate on the positivity constraint (not the irreversibility one). For illustration purposes we focus (as in Sects. 3.3 and 3.1) on the fully damaged phase i.e. $\alpha _t(x)=\alpha _u(x)$ and $U_t=\hat{u}$ corresponding to a broken bar.

The bi-linear heterogeneity profile in (Fig. 3a) is considered with $\ell _o=0.2$, $\ell _o/l_f=0.5$ and $L/\ell _o=10$.

For the p-FE analyses two meshes with different refinement types are used: the selective mesh used for the h-FE computations in Fig. 7 and a geometrically refined mesh (Fig. 15). The later is expected to be optimal for convergence, as it is for problems with singular points [45]. The selective meshis used for fixed $h_{max}=L/10$ and $\ell _o/h=10$ ratio.

Algorithm 1

Algorithm describing the implemented p-FE methodology

The geometrically refined mesh is progressively refined towards $x=L/2$ i.e. the location where crack nucleates and $\alpha _u=1$. The nodes do not consider boundary of the damage support through $\ell _o/h$ ratio and $\ell _o/h<2$ except at the vicinity of $x=L/2$. Considering the mesh symmetry at L/2, the nodes are located as follows:

$$\begin{aligned} x_0= & {} 0, x_1= \frac{L}{4}, x_2 = \frac{3L}{8}, x_3 = \frac{37L}{80},\\ x_4= & {} \frac{3955L}{8000} \text { and } x_5 = \frac{L}{2}. \end{aligned}$$

The phase field profile $\alpha _u(x)$ is shown in Figs. 16a and 16b. An excellent approximation is already achieved from $p=4$ for both selective and geometrically refined meshes (of course the selective mesh has many more elements). Because p-FEA approximates very well the phase-field profile for $p \ge 4$, a correction for $G_{Ic}(x)$ is not required.

Fig. 15

Geometrically refined mesh used for p-FEA

Fig. 16

Fully damaged phase-field profile $\alpha _u(x)$ for selective refined mesh (Left) and geometrically refined mesh (Right), linear profile $G_{Ic}(x)$ and increasing polynomial order p, $\ell _o=0.2$, $\ell _o/l_f=0.5$ and $L/\ell _o=10$

4.1 Positivity constraint

For the positivity constrain we use the penalty coefficient (25) derived for h-FEA. We investigate how does the penalty coefficient depend on the polynomial order p by computing the error for the fully-damaged profile $\alpha _u^{err}$ for different tolerances $TOL_{rec}$.

Considering for example the selective mesh we compute the error in the phase field for different polynomial orders p and two tolerance values, as shown in Fig. 17b). Similarly to h-FEA, inside the damage support band the error is controlled by the numerical approximation through p while outside the damage support band, where penalty is activated, it is controlled by the penalty coefficient.

Fig. 17

Error in phase field profile $\alpha _u^{err}$ imposing damage positivity via penalization on the selective refined mesh and linear heterogeneity profile, different tolerances $TOL_{rec}$ and polynomial order p, $\ell _o=0.2$, $\ell _o/l_f=0.5$ and $L/\ell _o=10$

4.2 Convergence analysis: a node at the crack nucleation

We investigate the numerical performance of the h- and the p-FEM by quantifying the error in dissipated energy $\Pi _D^{err}$ as the DOFs is increased. The exact solution of $\alpha (x)$ is also used to determine the numerical convergence in terms of $||\alpha _u^{err}||_2$, the $L^2$ norm error in $\alpha _u(x)$, expressed as:

$$\begin{aligned} ||\alpha _u^{err}||_2 = \sqrt{\frac{1}{N}\sum _{i=1}^{N} (\alpha _u^{EX}(x_i)-\alpha _u^{FE}(x_i))^2} \end{aligned}$$

The points $x_i=x_0,x_1,...,x_N$ where the error is calculated are the ones specified in Appendix A.

In this subsection a node is placed at the crack nucleation location $x=L/2$. The simulations were performed on a standard PC with an Intel Xeon CPU E5-1620 3.60GHz processor. For the h-FEM the alternative correction (33) is applied to $G_{Ic}(x)$ (more efficient to achieve the fully-damaged profile for coarse meshes).

Different mesh layouts are also investigated. For the h-FEM we investigate the “selective refinement” schematically presented in Fig. 7 for which the compact support of the damage zone is uniformly refined from $h=0.1$ to $h=0.002$, and also a “graded refinement” (see Fig. 18) for which the two elements closest to the nucleation at $x=L/2$, on both sides, are progressively refined (from $h=0.2$ to $h=1.2e^{-5}$). Note that the selective refinement is controlled by $\ell _0/h$. For the p-FEM the mesh is kept fixed and we choose the “selective refinement” mesh and the “geometric refinement” mesh with a ratio of 0.17 towards $x=L/2$ shown in Fig. 15.

Fig. 18

Illustration of the graded refinement meshes

One may observe in Figs. 19 and 20 a higher convergence rate of the p-FEM both with respect of the DOFs and CPU compared to the h-FEM. Using geometrically refined mesh the convergence is dramatically faster compared to h-FEM on the selective mesh.

The h-FEM on a graded refined mesh converges much faster compared to the selective refinement. However, it reaches a sort of "plateau" and further refinements do not decrease the numerical error. This is because the refinement is applied recursively on the 4 elements closest to $x=L/2$ so the numerical error associated with the other elements does not decrease. This error becomes dominant while the error associated to the crack initiation location is constantly decreasing thanks to the refinement. Hence, an optimal graded refined mesh requires an adaptive algorithm to track the dominant numerical errors and adaptively refine the mesh.

Increasing the positivity constraint i.e. $TOL_{rec}=0.001$ leads to the same conclusions.

Fig. 19

Convergence analysis of dissipated fracture energy $\Pi _D^{err}$ as a function of DOFs (Left) and CPU time in seconds (Right) for h-FE on selective refined mesh, h-FE on graded refined mesh, p-FE on selective refined mesh, and p-FE on geometrically refined mesh. Phase-field positivity is imposed via penalization and $TOL_{rec}=0.01$, $\ell _o=0.2$, $\ell _o/l_f=0.5$, $L/\ell _o=10$. (Dashed red line) 1% tolerance error

Fig. 20

Convergence analysis of the $L^2$-norm error in $\alpha _u(x)$ as a function of DOFs (Left) and CPU time in seconds (Right) for h-FE on selective refined mesh, h-FE on graded refined mesh, p-FE on selective refined mesh, and p-FE on geometrically refined mesh.. Phase-field positivity is imposed via penalization and $TOL_{rec}=0.01$, $\ell _o=0.2$, $\ell _o/l_f=0.5$, $L/\ell _o=10$

The convergence plots show that p-FEM converges faster compared to h-FEM when using a geometrically refined mesh. Decreasing $TOL_{rec}$ i.e. increasing the penalty coefficient, slightly improves the accuracy for p-FEM on a geometrically refined mesh.

4.3 Convergence analysis: crack nucleation occurs inside an element

To address cases for which the nucleation location is unknown a-priori, we present the numerical performance of the h- and the p-FEM for the same problem in the former subsection, with same meshes only that the node at $x=L/2$ is removed. I.e. an element exists in the middle of the bar so crack nucleates with a kink in $\alpha$ at the middle of the element.

Following the former subsection we present the error in dissipated energy $\Pi _D^{err}$ as the DOFs is increased in Figs. 21a, b.

Fig. 21

Convergence analysis of dissipated fracture energy $\Pi _D^{err}$,, without a node at $x=L/2$, as a function of DOFs (Left) and CPU time in seconds (Right) for h-FE on selective refined mesh, p-FE on selective refined mesh and p-FE on geometrically refined mesh. Phase-field positivity is imposed via penalization and $TOL_{rec}=0.01$, $\ell _o=0.2$, $\ell _o/l_f=0.5$, $L/\ell _o=10$. (Dashed red line) 1% tolerance error. (Color figure online)

Again, p-FEM exhibits a higher convergence rate both with respect of the DOFs and CPU compared to the h-FEM for the geometrically refined mesh. One notices, as expected, the slower convergence rate compared to the mesh with a node at the crack nucleation location.

The numerical error associated with the FE approximation, $||\alpha _u^{err}||_2$ is presented in Fig. 22.

Fig. 22

Convergence analysis of the $L^2$-norm error in $\alpha _u(x)$, without a node at $x=L/2$, as a function of DOFs (Left) and CPU time in seconds (Right) for h-FE on selective refined mesh, p-FE on selective refined mesh and p-FE on geometrically refined mesh. Phase-field positivity is imposed via penalization and $TOL_{rec}=0.01$, $\ell _o=0.2$, $\ell _o/l_f=0.5$, $L/\ell _o=10$

Compared to Fig. 20, one notices also here the slower convergence, but again p-FEM is more accurate and converges faster compared to the h-FEM using the geometrically refined mesh.

5 A pseudo three-dimensional example

A pseudo 3D extension of the heterogeneous bar is investigated using FEniCSx [46, 47]. The $G_{Ic}$ correction and the penalty coefficient $C_{opt}$ determined for the 1D case are investigated in this 3D setting. To enable us to compare the 3D approximation to the analytical solution derived for the 1D bar, we consider a 3D elastic bar, of length $L=2$ and cross-section $S=0.1 \times 0.1$ fixed at the left flat surface and subjected to a horizontal displacement $U_t$ applied to the right end surface as shown in Fig. 23.

The material properties $E(x,y,z)=E(x)$ and $G_{Ic}(x,y,$$z)= G_{Ic}(x)$ vary linearly as in the 1D case presented in the previous section with a Poisson’s ratio $\nu =0$ (this is to allow to compare the results to the exact 1D case). The 3D mesh has one element in the "thickness” direction and convergence of the dissipated energy is monitored for the h-FE on graded refined mesh and the p-FE on geometrically graded mesh.

The p-extension implemented in FEniCSx is based on Lagrange-based shape functions that are inferior to Legendre-based shape functions (the stiffness matrix has to be entirely recomputed as p-level increases and the condition number increases much faster as well). Additionally, the p-extension is isotropic (polynomial degree in all directions increases as p-level increases) while h- refinement is only performed along the longitudinal axis identically to the 1D case. Thus, numerical convergence is investigated as a function of the DOFs along the longitudinal direction (X axis). The $G_{Ic}$ correction is applied to h-FEA and the penalty coefficient is selected as in the 1D analysis. Figure 24 presents the convergence in dissipated fracture energy $\Pi _D^{err}$ for the h-FEA on a graded refined mesh (along X axis) compared to the p-FEA on a geometrically refined mesh. The h-FEA converges until a "plateau" while the p-FEA converges monotonically. These results are consistent with the ones observed for the 1D case, thus the penalty coefficient as well as the $G_{Ic}$ correction derived for the 1D case may also be applicable in a 3D setup. Since the implementation of the p-FEA is suboptimal in FEniCSx and does not include the p-prediction, we don’t consider convergence in terms of CPU.

6 Summary and conclusion

Explicit solution, displacement and phase field $(u(x),\alpha (x))$, for the AT1 phase field problem in a heterogeneous bar in tension were derived to serve as benchmark problems. We considered E(x) and $G_{Ic}(x)$ that had bi-linear, parabolic and bi-exponential profiles. These solutions were used for numerical verification of h- and p-FE approximations for heterogeneous materials. Important insights were highlighted for these heterogeneous materials when solved by finite element methods.

We investigated the performance of h- and p-FE methods for AT1 PFM enforcing positivity and irreversibility by penalization. Comparing to the explicit solutions derived:

• We proposed and verified a new correction for $G_{Ic}^{FE}(x)$ to be used in conjunction with h-FEMs and computed the phase field profile in a heterogeneous bar using coarse meshes.

• We investigated different $G_{Ic}(x)$ correction approaches and their influence on different quantities. We demonstrated that the popular correction introduced for a homogeneous bar in [34] is inappropriate for a quasi-static evolution problem, because the peak stress is underestimated.

• We proposed and verified a penalty coefficient for heterogeneity effects allowing to enforce damage positivity and irreversibility via penalization.

• For the simplified 1-D problem we demonstrated that p-FEs exhibit a faster convergence rate compared to h-FE implementation. Using a geometrically refined mesh these FE methods may be a good alternative to decrease the computational burden associated to PFM for predicting fracture in multidimensional and heterogeneous material such as FGMs and bone.

One-dimensional heterogeneity is a good surrogate to 2D/3D for a Poisson ratio $\nu =0$ and the 1D behavior is qualitatively the same for $\nu >0$ [33]. The insights observed by investigating the 1D bar are encouraging and shown to be useful in 3D domains on a pseudo 3D example. Analytical solutions for 3D PF problems in multi-dimensional heterogeneity are unknown and manufactured solutions to verify PF implementation for pointwise heterogeneous material such as FGMs or bone are yet to be developed. At the same time, since the failure initiation location is unknown a-priori,one needs to implement multilevel approaches for local space enrichment when p-FE methods are applied [48,49,50].

Fig. 23

3D clamped bar subjected to a horizontal displacement $U_t$ at its right surface

Fig. 24

Convergence analysis of dissipated fracture energy $\Pi _D^{err}$ and damage profile as a function of DOFs along X axis for h-FE on a graded refined mesh and p-FE on a geometrically refined mesh. Phase-field positivity is imposed via penalization and $TOL_{rec}=0.01$, $\ell _o=0.2$, $\ell _o/l_f=0.5$, $L/\ell _o=10$. (Dashed red line) 1% tolerance error

Appendices

PFM AT1 explicit solutions u(x) and $\alpha (x)$ for a heterogeneous bar $[0,L=2]$ with 0.0001 precision

Table 1 Bi-linear E(x) and $G_{Ic}(x)$ with $E_{0}=1$, $G_{Ic0}=8/15$, $l_f=0.4$ and $\ell _o=0.2$

Table 2 Bi-parabolic E(x) and $G_{Ic}(x)$ with $E_{0}=1$, $G_{Ic0}=8/15$, $l_f=0.4$ and $\ell _o=0.2$

Table 3 Bi-exponential E(x) and $G_{Ic}(x)$ with $E_{0}=1$, $G_{Ic0}=8/15$, $l_f=0.8$ and $\ell _o=0.2$

Strong formulation of AT1 PFM for a heterogeneous bar

Integrating by parts (18) and (19) and using the boundary conditions of $(v,\beta )$ (11), (12) leads to the strong form of PFM.

Strong formulation (AT1 model). Given the initial state ($u_0$,$\alpha _0$)=(0,0) at the pseudo-time $t=0$, find $t \rightarrow$ ($u_t$,$\alpha _t$) $\in \mathcal {U} \times \mathcal {A}$ such that:

$$\begin{aligned}{} & {} \left( E(x)(1-\alpha _t)^2 u'_t(x) \right) ' = 0 \quad \forall x \in \Omega , \quad \quad \nonumber \\{} & {} \quad \textit{Equilibrium equation} \end{aligned}$$

(B.1)

$$\begin{aligned}{} & {} E(x) (\alpha _t-1) u_t{'}^2 + \frac{3G_{Ic}(x)}{8l_0} \biggl ( 1 - 2\ell _o^2 \alpha _t'' \biggr ) \ge 0, \quad \quad \nonumber \\{} & {} \quad \textit{Damage criterion}, \end{aligned}$$

(B.2)

subject to the irreversibility condition (7).

STG_solver: staggered FE solver scheme for PF problem (22)–(23)

Newton–Raphson implies to compute for both displacement and damage problem the Jacobian terms for each element from (22) and (23). Respectively,

$$\begin{aligned} \vec {\mathcal {J}_e^{u}}{} & {} = \int _0^{L_e}E(x)(1-\vec {N}_e^T(x) \vec {\alpha }_e)^2 \vec {N}_e^{'}(x) \vec {N}_e^{'T}(x) \vec {u_e} dx \end{aligned}$$

(C.1)

$$\begin{aligned} \vec {\mathcal {J}_e^{\alpha }}{} & {} = \int _0^{L_e} \biggl ( E(x) (\vec {N}_e^T(x) \vec {\alpha }_e - 1) \vec {N}_e(x) (\vec {N}_e^{'T}(x) \vec {u_e})^2 \nonumber \\{} & {} \quad + \frac{G_c(x)}{c_w \ell _o}(\vec {N}_e(x) + 2l_0^2 \vec {N}_e^{'}(x) \vec {N}_e^{'T}(x) \vec {\alpha _e} + \nonumber \\{} & {} \quad C <\vec {N}_e^T(x) \vec {\alpha _e}>_- \vec {N}_e(x) \biggr ) dx \end{aligned}$$

(C.2)

The Jacobian terms are assembled to give the global Jacobian vectors $\vec {\mathcal {J}^{u}}$ and $\vec {\mathcal {J}^{\alpha }}$. They are also associated to residual vectors whose the norm gives $res_{u}$ and $res_{\alpha }$, respectively. The element stiffness matrix, associated to Hessian terms $[{\mathcal {H}}_e^{i}]= \partial \vec {\mathcal {J}_e^{i}}/\partial \vec {i}_e$ for $i=\{u,\alpha \}$, are computed as follows:

$$\begin{aligned}{}[{\mathcal {H}}_e^{u}]{} & {} = \int _0^{L_e}E(x)(1-\vec {N}_e^T(x) \vec {\alpha }_e)^2 \vec {N}_e^{'}(x) \vec {N}_e^{'T}(x) dx \end{aligned}$$

(C.3)

$$\begin{aligned}{} & {} = \int _0^{L_e} \biggl ( E(x) \vec {N}_e^T(x) \vec {N}_e(x) (\vec {N}_e^{'T}(x) \vec {u_e})^2 \nonumber \\{} & {} \quad + \frac{G_c(x)}{c_w}( 2\ell _o \vec {N}_e^{'}(x) \vec {N}_e^{'T}(x) + \nonumber \\{} & {} \quad C D_{<>}(\vec {N}_e^T(x) \vec {\alpha _e}) \vec {N}_e^T(x) \vec {N}_e(x) \biggr ) dx \end{aligned}$$

(C.4)

where

$$\begin{aligned} D_{<>}(y) = \left\{ \begin{array}{ll} 1 &{} \text {if } y < 0 \\ 0 &{} \text {if } y \ge 0\ \end{array} \right. \end{aligned}$$

(C.5)

The alternate minimization solving scheme is represented below.

Algorithm 2

Staggered FE solver STG_solver