A multiscale stabilized physics informed neural networks with weakly imposed boundary conditions transfer learning method for modeling advection dominated flow

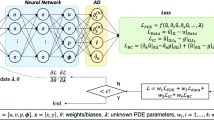
Abstract

Physics informed neural network (PINN) frameworks have been developed as a powerful technique for solving partial differential equations (PDEs) with potential data integration. However, when applied to advection based PDEs, PINNs confront challenges such as parameter sensitivity in boundary condition enforcement and diminished learning capability due to an ill-conditioned system resulting from the strong advection. In this study, we present a multiscale stabilized PINN formulation with a weakly imposed boundary condition (WBC) method coupled with transfer learning that can robustly model the advection diffusion equation. To address key challenges, we use an advection-flux-decoupling technique to prescribe the Dirichlet boundary conditions, which rectifies the imbalanced training observed in PINN with conventional penalty and strong enforcement methods. A multiscale approach under the least squares functional form of PINN is developed that introduces a controllable stabilization term, which can be regarded as a special form of Sobolev training that augments the learning capacity. The efficacy of the proposed method is demonstrated through the resolution of a series of benchmark problems of forward modeling, and the outcomes affirm the potency of the methodology proposed.

Appendix

1.1 Weights normalization for penalty method

To normalize the penalty parameter in the PINN, we run the dimension analysis for the loss function, by setting $u$ as the concentration field with the SI unit ${\text{mol}}/{{\text{m}}}^{3}$, ${a}_{i}$ as advection velocity vector component with SI unit ${\text{m}}/{\text{s}}$ and diffusivity coefficient $k$ with SI unit ${{\text{m}}}^{2}/{\text{s}}$. Here ${\text{mol}}$ indicates the mole number, ${\text{m}}$ indicates the unit meter and ${\text{s}}$ indicate the unit second. To satisfy dimension consistency, all terms in the loss function in Eq. (10) should results in same units eventually.

The unit of equilibrium equation loss ${\Pi }_{S}$ is shown below.

$${\Pi }_{S}=\frac{1}{2}{\Vert \mathcal{L}u-s\Vert }_{\Omega }^{2}=\frac{1}{2}\underset{\Omega }{\overset{}{\int }}{\left({a}_{i}{u}_{,i}-{k}_{ij}{u}_{,ij}\right)}^{2}d\Omega \propto {\text{O}}\left(\frac{{{\text{mol}}}^{2}}{{{\text{s}}}^{2}\cdot {{\text{m}}}^{4}}\right)$$

(56)

where ${\text{O}}\left(\cdot \right)$ means the order of the argument. Similarly, the Dirichlet boundary condition and Neumann boundary condition loss can be represented as:

$${\Pi }_{D}=\frac{1}{2}{\Vert u-g\Vert }_{\partial {\Omega }_{D}}^{2}=\frac{1}{2}\underset{\partial {\Omega }_{D}}{\overset{}{\int }}{\left({u}^{h}-g\right)}^{2}d\Gamma \propto {\text{O}}\left(\frac{{{\text{mol}}}^{2}}{{{\text{m}}}^{5}}\right)$$

(57)

$${\Pi }_{N}=\frac{1}{2}{\Vert \mathcal{B}u-h\Vert }_{\partial {\Omega }_{N}}^{2}=\frac{1}{2}\underset{\partial {\Omega }_{D}}{\overset{}{\int }}{\left(\left(-{a}_{i}u+{k}_{ij}{u}_{,j}\right){n}_{i}-h\right)}^{2}d\Gamma \propto {\text{O}}\left(\frac{{{\text{mol}}}^{2}}{{\text{s}}\cdot {{\text{m}}}^{3}}\right)$$

(58)

Then, in order to enforce dimension consistency between Eqs. (56)–(58), the penalty parameter ${\beta }_{D}$ and ${\beta }_{N}$ can be normailized by the Peclet number, diffusivity coefficient and the characteristic length ${L}_{c}$:

$${\beta }_{D}\propto {\text{O}}\left(\frac{{\text{m}}}{{{\text{s}}}^{2}}\right)={\text{O}}\left(\frac{P{e}^{2}{k}^{2}}{{L}_{c}}\right)$$

(59)

$${\beta }_{N}\propto {\text{O}}\left(\frac{1}{{\text{m}}}\right)={\text{O}}\left(\frac{1}{{L}_{c}}\right)$$

(60)

In the numerical testing, we then can define the following penalty parmeter by introducing a unitless coefficient ${\widehat{\beta }}_{D}$ and ${\widehat{\beta }}_{N}.$

$${\beta }_{D}={\widehat{\beta }}_{D}\frac{P{e}^{2}{k}^{2}}{{L}_{c}}$$

(61)

$${\beta }_{N}={\widehat{\beta }}_{N}\frac{1}{{L}_{c}}$$

(62)

1.2 Weights normalization for weakly enforced boundary condition method

By performing the dimension analysis for the WBC formulation for the two terms shown in Eq. (32), one obtains:

$$\frac{{C}_{a}}{4}\underset{\partial {\Omega }_{D}}{\overset{}{\int }}\left(\left|{a}_{i}{n}_{i}\right|-{a}_{i}{n}_{i}\right){\left({u}^{h}-g\right)}^{2}d\Gamma \propto {C}_{a}\cdot {\text{O}}\left(\frac{{{\text{mol}}}^{2}}{{\text{s}}\cdot {{\text{m}}}^{3}}\right)$$

(63)

$$\underset{\partial {\Omega }_{D}}{\overset{}{\int }}\frac{{C}_{k}k}{2{h}_{c}}{\left({u}^{h}-g\right)}^{2}d\Gamma \propto {C}_{k}\cdot {\text{O}}\left(\frac{{{\text{mol}}}^{2}}{{\text{s}}\cdot {{\text{m}}}^{4}}\right)\cdot $$

(64)

Then by comparing Eqs. (63) and (64) with the loss of the equilibrium Eq. (56), the dimension of the two parameters ${C}_{a}$ and ${C}_{k}$ can be expressed in terms of the Peclet number, diffusivity coefficient and the characteristic length ${L}_{c}$:

$${C}_{a}\propto {\text{O}}\left(\frac{1}{{\text{ms}}}\right)\propto {\text{O}}\left(\frac{Pe\cdot k}{{L}_{c}^{2}}\right)$$

(65)

$${C}_{k}\propto {\text{O}}\left(\frac{1}{{\text{s}}}\right)\propto {\text{O}}\left(\frac{Pe\cdot k}{{L}_{c}}\right)$$

(66)

Then, following the same logic shown in Eqs. (59) and (60), one can introduce controllable unitless coefficients ${\widehat{C}}_{a}$ and ${\widehat{C}}_{k}$ to represent ${C}_{a}$ and ${C}_{k}$

$${C}_{a}={\widehat{C}}_{a}\frac{Pe\cdot k}{{L}_{c}^{2}}$$

(67)

$${C}_{k}={\widehat{C}}_{k}\frac{Pe\cdot k}{{L}_{c}}$$

(68)

1.3 Influence of weights normalization effect for penalty method and WBC approach

The one-dimensional boundary layer problem in Sect. 2.3.1.1 is given below in Fig. 32 to perform the parameter study for both the penalty method and the WBC method. First, we select four choices of penalty parameters ${\widehat{\beta }}_{D}=0.01, 0.1, 1, 100$ (${\widehat{\beta }}_{D}=100.0$ is corresponding to unnormalized parameter ${\beta }_{D}=2.5\times {10}^{5}$, which is a large enough value to impose boundary condition) for the penalty method. It can be seen that without the WBC approach, non-convergence result is found for Peclet number equaling 100 (advection dominate case). Secondly, we perform the same study for WBC method ${\widehat{C}}_{a}={\widehat{C}}_{k}=0.01, 0.1, 1$ in comparison to an improper choice of parameter ${\widehat{C}}_{a}={\widehat{C}}_{k}=100.0$ (corresponding to unnormalized parameter ${C}_{a}={C}_{k}=2.5\times {10}^{5}$, making it large enough which make it similar to the penalty method). From the analysis, the value of ${\widehat{C}}_{a}={\widehat{C}}_{k}=100.0$ causes non-convergence solution in the $Pe=100$ case, while all other choices robustly capture the boundary layer feature. Therefore, we are assured that proper normalization is necessary for the WBC approach.

Fig. 32

One-dimensional boundary layer problem with different ${\widehat{\beta }}_{D},{\widehat{C}}_{a},{\widehat{C}}_{k}$ selection in penalty and WBC methods

1.4 Coefficient sensitivity analysis of the penalty parameter in WBC fine-tuning

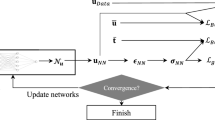
This analysis is conducted to investigate the effect of penalty coefficient ${\gamma }_{D}$ selection in the WBC fine-tuning stage, providing a reasonable selection range as well as demonstrating the solution balancing phenomenon of pre-trained solution and Dirichlet boundary conditions as mentioned in Sect. 3.1. The two-dimensional point source boundary layer problem in Sect. 2.3.1.2 with different penalty coefficients defined on the boundary are conducted and demonstrated in Fig. 33. From the result, we can see that since the pre-trained model already captures the main features of the system (advection), the second term for Dirichlet boundary condition regularization is not sensitive to the penalty coefficient ${\gamma }_{D}$ anymore. However, employing an excessively large penalty coefficient will lead to oscillation in the result as shown in Fig. 33d and therefore a reasonable range ${\gamma }_{D}\in \left[\mathrm{0,1}\right]$ is recommended.

Fig. 33

Two-dimensional point source boundary layer problem with different fine-tuning penalty coefficients

1.5 Numerical comparison of the proposed VMS-PINN with gradient-enhanced PINN (gPINN)

A numerical example is conducted to investigate the effect of parameter “${c}_{VMS}$” in Eq. (47) and VMS compared to the gPINN method [46]. The two-dimensional point source boundary layer problem (in Sect. 2.3.1.2) is used with all numerical setting remaining the same. The ${L}_{2}$ error norm in the training process is shown in Fig. 34, and both gPINN and VMS methods use 50,000 iterations for training. The gPINN implemented in this numerical example employs a loss function accordinig to [46], as shown in Eq. (69):

$$\mathcal{L}={\mathcal{L}}_{f}+w{\mathcal{L}}_{{g}_{{\varvec{x}}}}+w{\mathcal{L}}_{{g}_{t}}$$

(69)

where ${\mathcal{L}}_{{g}_{{\varvec{x}}}}$ and ${\mathcal{L}}_{{g}_{t}}$ are the gradient loss with respect to space and time and uses a penalty parameter $w=1.0$ according to the reference [46]. In this example, ${\mathcal{L}}_{{g}_{t}}$ is omitted since the problem is time independent. From the result, we can see that under the same experiment setting, the VMS has higher convergency compared with the gPINN result. It is possible that by optimal choice of the weight in the VMS gradient regularization term leads to a better result.

Fig. 34

Numerical comparison of the proposed VMS method and the gradient enhanced PINN (gPINN) formulation in [46]. Both methods conduct 50,000 iterations of training