Abstract
We introduce an immersed meshfree formulation for modeling heterogeneous materials with flexible non-body-fitted discretizations, approximations, and quadrature rules. The interfacial compatibility condition is imposed by a volumetric constraint, which avoids a tedious contour integral for complex material geometry. The proposed immersed approach is formulated under a variational multiscale based formulation, termed the variational multiscale immersed method (VMIM). Under this framework, the solution approximation on either the foreground or the background can be decoupled into coarse-scale and fine-scale in the variational equations, where the fine-scale approximation represents a correction to the residual of the coarse-scale equations. The resulting fine-scale solution leads to a residual-based stabilization in the VMIM discrete equations. The employment of reproducing kernel (RK) approximation for the coarse- and fine-scale variables allows arbitrary order of continuity in the approximation, which is particularly advantageous for modeling heterogeneous materials. The effectiveness of VMIM is demonstrated with several numerical examples, showing accuracy, stability, and discretization efficiency of the proposed method.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The accurate description of heterogeneous materials is important in a wide range of engineering problems such as composite solids and structures [1], bi-material heat conduction devices [2], bone structures in biological systems [3], among others. These problems are represented by partial differential equations (PDEs) with discontinuous material properties in space, leading to rough solution with strain discontinuities across material interfaces. The finite element method (FEM) with \( C^{0} \) continuity employs a body-fitted mesh across the material interface for proper jumps of strains across material interfaces. However, the construction of such body-fitted meshes is time-consuming, and it becomes non-trivial when material heterogeneity involves complex geometry in multi-dimensional space. As a result, methods that can handle unfitted meshes are attractive in heterogeneous material analysis.
Body-unfitted mesh approaches which employ a boundary integral on the material interface for interfacial compatibility (termed “embedded approach” hereafter) have been proposed under different embedded domain methods. Mortar FEM [4] couples unfitted meshes across the interface by enforcing the interfacial constraint with Lagrange multipliers. Unfortunately, such an approach suffers from the violation of the LBB (Ladyzhenskaya–Babuška–Brezzi, or called inf–sup) conditions [5, 6] if the function space of Lagrange multipliers is not properly selected. The violation of the LBB condition may lead to instabilities and oscillations in the interfacial traction fields [7]. Nitsche’s method by Stenberg [8] and Hansbo [9] was introduced where the Lagrange multipliers are replaced by the tractions on the interface, and a least-square type stabilization is added with a penalty parameter based on material properties. The determination of the penalty parameter is non-trivial, as a local eigenvalue analysis is often required [10]. To address this issue, the extended finite element method (XFEM) stabilized by bubble functions has been proposed [11, 12] under the embedded approach, where the displacement field is decomposed into coarse- and fine-scale fields following the variational multiscale framework [13, 14], and the fine-scale field is enriched with element bubble function, similar to the residual-free bubble approach [15]. While the bubble-stabilized XFEM [11] and Nitsche’s method [9] capture the interfacial constraint and achieve good convergence, they rely on high order quadrature over the contour integral at the material interface, which is tedious for complex geometric interfaces. Further, the employment of the interfacial constraint under the embedded framework often yields ill-conditioning due to the near-zero internal energy at the overlapping domain (also known as the fictitious domain), in which removal of additional degrees of freedom (DOF) is necessary.
The alternative to an interfacial constraint is to employ a volumetric constraint (enforcement of Dirichlet condition on the overlapping domain, termed “immersed approach” hereafter). Such an approach has been employed with various immersed frameworks, especially in the field of fluid–structure interaction. Similar to the interfacial constraint approach, the penalty method [16] and the Lagrange multiplier method [17] were implemented to enforce such constraint. Glowinski et al. [18] developed the distributed Lagrange multiplier and fictitious domain method for particulate flow, where the kinematics of rigid body motion of particles follows background fluid flow through a perturbed Lagrange multiplier. Zhang et al. [19, 20] developed the immersed finite element method (IFEM) for fluid–structure interaction problems, where the compatibility condition of solid/fluid velocity is imposed weakly through a reproducing kernel (RK) function. The volumetric constraint enforcement not only avoids ill-conditioning in the embedded method but also avoids tedious boundary integrals along with the material interfaces, although it still exhibits low order accuracy near the interface. Due to the limited literature on the application of volumetric constraints for heterogeneous solid material problems, the accuracy and robustness of the immersed approach with volumetric constraints for heterogeneous solids deserve further investigation.
Meshfree methods, such as the reproducing kernel particle method (RKPM) [21, 22], are attractive alternatives to FEM and are constructed based on a set of scattered points without any mesh connectivity, thus avoiding mesh distortion or mesh entanglement issues [21, 23, 24]. Further, the flexibility in controlling the local smoothness in the approximation is attractive for problems with varying smoothness in the problem domain. The application of the meshfree method for heterogeneous materials has been studied extensively with techniques such as element free Galerkin (EFG) [25,26,27], meshless local Petrov–Galerkin (MLPG) [2], moving least-squares (MLS) [28,29,30], reproducing kernel particle method (RKPM) [31,32,33,34,35], and Smoothed Particle Galerkin (SPG) [36], to name a few. Due to the lack of Kronecker delta properties, it is not natural for the meshfree methods to impose the compatibility condition, and various techniques have been developed to enforce the constraint strongly or weakly. A meshfree approximation with local enrichment across the material interface [26, 29, 30, 35] was constructed to enable the direct imposition of the compatibility condition, but requires additional DOFs employed on the interface for the enrichment. Wang et al. [32] used a discontinuous Galerkin formulation based on an incompatible patch-based RK approximation, such that additional DOFs are not required since the compatibility and equilibrium conditions were imposed weakly in the variational equation. Wu et al. [33, 36] introduced a meshfree discretization strategy for composite materials based on an immersed approach and employed the singular kernel method [37] for approximation such that the point-wise continuity across the material interface was naturally built-in. Koester et al. [34] employed the conforming RK shape function constructed on the boundary-fitted local triangulation, creating \( C^{0} \) approximation functions at material interfaces. Although meshfree methods have demonstrated their applicability in modeling heterogeneous materials, most of the aforementioned works are based on the embedded framework with interfacial constraints and thus have intrinsic difficulties in modeling heterogeneous materials with complex geometries.
With all the above-mentioned issues and challenges, in this work we present an immersed meshfree formulation under the variational multiscale framework for modeling heterogeneous materials using a volumetric constraint. The proposed method provides flexibility in adopting independent discretizations, approximations, and quadrature rules in the foreground and background domains and avoids the issue of ill-conditioning in the immersed discrete system. The method employs the variational multiscale formulism to enhance accuracy and has built-in stabilization to reduce the oscillations common in conventional immersed methods. One of the proposed methods with an approximated fine-scale solution requires higher order continuity in the background approximation, and methods such as isogeometric analysis (IGA) [38] and RKPM offer such regularity. In this paper, RKPM is employed due to its flexibility in adopting arbitrary smoothness and domain discretization in solving the variational multiscale equations. Interested readers can refer to [39,40,41] for a comprehensive review of RKPM and its applications.
The paper is organized as follows. The problem description of the heterogeneous, linear elasticity problem and the immersed weak form based on a volumetric constraint are introduced in Sect. 2. The variational multiscale immersed method with different approaches for obtaining the fine-scale and coarse-scale solutions are presented in Sect. 3. Domain integration and stabilization techniques for the foreground and background weak forms are also discussed in this section. Finally, benchmark problems are studied in Sect. 4 to examine the performance of the proposed method. The findings of this research are summarized in Sect. 5.
2 Basic immersed formulation for heterogeneous materials
2.1 Strong form
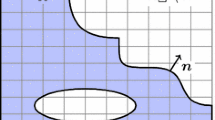
Consider a solid occupying closed subdomains \( \bar{\Omega }^{1} \) and \( \bar{\Omega }^{2} \), where \( \bar{\Omega } = \bar{\Omega }^{1} \cup \bar{\Omega }^{2} \) describes the total domain, \( \bar{\Omega }^{1} \cap \bar{\Omega }^{2} = \Gamma \) denotes the material interface, and \( \partial \Omega_{N}^{2} \) and \( \partial \Omega_{D}^{2} \). denote the Neumann and Dirichlet boundary on boundary \( \partial \Omega^{2} \), respectively, with \( \partial \Omega_{N}^{2} \cup \partial \Omega_{D}^{2} = \partial \Omega^{2} \). and \( \partial \Omega_{N}^{2} \cap \partial \Omega_{D}^{2} = \emptyset \). An illustration of the heterogeneous problem is given in Fig. 1a. To aid the development of the immersed formulation, we intruce a foreground domain \( \bar{\Omega }^{ + } = \bar{\Omega }^{1} \) and a background domain \( \bar{\Omega }^{ - } = \bar{\Omega }^{1} \cup \bar{\Omega }^{2} \), where \( \bar{\Omega }^{i} = \Omega^{i} \cup \partial \Omega^{i} \) shown in Fig. 1b.
Illustration for two-dimensional solid with heterogeneous materials: a Total domain \( \bar{\Omega } \), and b background domain \( \bar{\Omega }^{ - } \) and foreground domain \( \bar{\Omega }^{ + } \)
The strong form of the problem can be described by the following boundary value problem (BVP):
where
here \( \varvec{u}\left( \varvec{x} \right) \) is the displacement vector, \( \varvec{\varepsilon}\left( \varvec{u} \right) \) is the strain tensor, \( \varvec{n}^{0} \) is the surface normal vector corresponding to boundary \( \partial \Omega \), b is the body force vector, t and g denote the prescribed traction and displacement vectors on \( \partial \Omega_{N} \) and \( \partial \Omega_{D} \), respectively, C is the elastic stiffness, and \( \varvec{\sigma} \) is the Cauchy stress tensor. The continuity conditions on the interface \( \Gamma \) are as follows:
where \( \left[\kern-0.15em\left[ \cdot \right]\kern-0.15em\right] \) the jump operator is defined in (8) and n is the surface normal on the interface.
Remark 2.1.1
Here we classify the boundary value problem with heterogeneous materials as the problem with varying material constants; that is, C(x) is piecewise constant for the problems under consideration as described in Eq. (5). However, the proposed formation is applicable to problems where C(x) is a piecewise higher-order function.
2.2 Weak form
It can be easily seen that the conventional discretization of weak form for the setting in Fig. 1 requires a geometric conforming domain discretization and numerical integration for subdomains \( \Omega^{1} \) and \( \Omega^{2} \), which is tedious for problems involving complex geometry or evolving interfaces. In the immersed setting of Fig. 1b the weak form for this problem is first constructed as follows:
where \( \left( { \cdot , \cdot } \right) \) denotes the \( L_{2} \) inner product, and \( \varvec{u}^{ + } \) and \( \varvec{u}^{ - } \) are the displacement fields on the foreground and background domains, respectively. \( {\varvec{\mathcal{L}}}^{ - } \left( \cdot \right) = - \varvec{\nabla} \cdot \left( {\varvec{C}^{ - } : \varvec{\varepsilon}\left( \cdot \right)} \right),\;{\varvec{\mathcal{L}}}^{ + } \left( \cdot \right) = - \varvec{\nabla} \cdot \left( {\varvec{C}^{ + } : \varvec{\varepsilon}\left( \cdot \right)} \right) \) are stress divergence operators acting on the foreground and background subdomains, respectively. The imposition of the continuity jump condition (7) on the interface \( \Gamma \) in Eq. (9) yields the weak form: find \( \left( {\varvec{u}^{ + } ,\varvec{u}^{ - } } \right) \in {\varvec{\mathcal{U}}}^{ + } \times {\varvec{\mathcal{U}}}^{ - } ,\;\varvec{u}^{ - } = \varvec{u}^{ + } \;{\text{on}}\;\Gamma \), such that \( \forall \left( {\delta \varvec{u}^{ + } ,\delta \varvec{u}^{ - } } \right) \in {\varvec{\mathcal{V}}}^{ + } \times {\varvec{\mathcal{V}}}^{ - } \)
The function spaces \( {\varvec{\mathcal{U}}}^{ + } \), \( {\varvec{\mathcal{U}}}^{ - } \), \( {\varvec{\mathcal{V}}}^{ + } \), and \( {\varvec{\mathcal{V}}}^{ - } \) are given in Eq. (11)
where \( n_{d} \) is the number of spatial dimensions. The weak form associated with Eq. (10) and interfacial condition \( \varvec{u}^{ - } = \varvec{u}^{ + } \;{\text{on}}\;\Gamma \) is usually referred to as the weak form for the “embedded method,” which employs the constraint “\( \varvec{u}^{ - } = \varvec{u}^{ + } \)” on the material interface when solving the composite material system. However, the employment of an interfacial constraint requires a contour integral along material interfaces, which is tedious for complex material geometry. To remedy this issue, a volumetric constraint approach can be introduced [20] as given in the next section.
2.3 Volumetric constraint
Due to the redundancy of \( \varvec{u}^{ - } \) in \( \Omega^{ + } \), a volumetric constraint for the overlapping domain is employed in the immersed method [17]:
The employment of a volumetric constraint (12) for Eq. (10) avoids the need for front tracking and contour integrals along material interfaces [4]. With the constraint (12), the internal energy and body forces terms in Eq. (10) can be rewritten as
From Eqs. (13) and (14), the new weak form reads: find \( \left( {\varvec{u}^{ + } ,\varvec{u}^{ - } } \right) \in {\varvec{\mathcal{U}}}^{ + } \times {\varvec{\mathcal{U}}}^{ - } \), \( \varvec{u}^{ - } = \varvec{u}^{ + } \) in \( \Omega^{ + } \), such that \( \forall \left( {\delta \varvec{u}^{ + } ,\delta \varvec{u}^{ - } } \right) \in {\varvec{\mathcal{V}}}^{ + } \times {\varvec{\mathcal{V}}}^{ - } \),
The function spaces \( {\varvec{\mathcal{U}}}^{ + } \), \( {\varvec{\mathcal{V}}}^{ + } \), \( {\varvec{\mathcal{U}}}^{ - } \), and \( {\varvec{\mathcal{V}}}^{ - } \) here are given as
The imposition of the volumetric constraint in Eq. (12) can be achieved by various methods. Here three common approaches are introduced to impose the volumetric constraint: penalty method, Lagrange multiplier method, and Nitsche’s method.
-
1.
Penalty method
Find \( \left( {\varvec{u}^{ + } ,\varvec{u}^{ - } } \right) \in {\varvec{\mathcal{U}}}^{ + } \times {\varvec{\mathcal{U}}}^{ - } \) such that \( \forall \left( {\delta \varvec{u}^{ + } ,\delta \varvec{u}^{ - } } \right) \in {\varvec{\mathcal{V}}}^{ + } \times {\varvec{\mathcal{V}}}^{ - } \),
The penalty parameter \( \beta \) has been proposed in [9] as
where \( \beta_{nor} \) is the normalized penalty parameter, E is the Young’s modulus, and h is the nodal spacing.
-
2.
Lagrange multiplier method
Let \( \varvec{\lambda}\in {\varvec{\mathcal{W}}} \equiv \left[ {L^{2} \left( {\Omega^{ + } } \right)} \right]^{{n_{d} }} \), find \( \left( {\varvec{u}^{ + } ,\varvec{u}^{ - } ,\varvec{\lambda}} \right) \in {\varvec{\mathcal{U}}}^{ + } \times {\varvec{\mathcal{U}}}^{ - } \times {\varvec{\mathcal{W}}} \) such that \( \forall \left( {\delta \varvec{u}^{ + } ,\delta \varvec{u}^{ - } ,\delta\varvec{\lambda}} \right) \in {\varvec{\mathcal{V}}}^{ + } \times {\varvec{\mathcal{V}}}^{ - } \times {\varvec{\mathcal{W}}} \),
-
3.
Nitsche’s method
A standard Nitsche’s formulation [42] is constructed by selecting the Lagrange multiplier as the energy conjugate function corresponding to the jump \( \left[\kern-0.15em\left[ \varvec{u} \right]\kern-0.15em\right] \), that is, \( \varvec{\lambda}= \left[\kern-0.15em\left[ {{\varvec{\nabla }} \cdot\varvec{\sigma}\left( \varvec{u} \right)} \right]\kern-0.15em\right] \), and with an additional least-squares stabilization: find \( \left( {\varvec{u}^{ + } ,\varvec{u}^{ - } } \right) \in {\varvec{\tilde{\mathcal{U}}}}^{ + } \times {\varvec{\tilde{\mathcal{U}}}}^{ - } \), such that \( \forall \left( {\delta \varvec{u}^{ + } ,\delta \varvec{u}^{ - } } \right) \in {\varvec{\tilde{\mathcal{V}}}}^{ + } \times {\varvec{\tilde{\mathcal{V}}}}^{ - } \),
here \( \beta = \beta_{nor} \left[\kern-0.15em\left[ E \right]\kern-0.15em\right]h^{ - 2} \) works as the stabilization to ensure the coercivity of the system. Due to the stress divergence operator \( \left[\kern-0.15em\left[ {\varvec{\nabla } \cdot\varvec{\sigma}\left( \varvec{u} \right)} \right]\kern-0.15em\right] \) employed in the weak form, the function spaces \( {\varvec{\tilde{\mathcal{U}}}}^{ + } \), \( {\varvec{\tilde{\mathcal{U}}}}^{ - } \), \( {\varvec{\tilde{\mathcal{V}}}}^{ + } \) and \( {\varvec{\tilde{\mathcal{V}}}}^{ - } \) are taken as
The three methods introduced in Eqs. (17) to (21) are regarded as conventional immersed methods and their performance will be investigated and compared to the proposed VMIM in the numerical examples.
2.4 Approximation and discretization
In this work we employ the Reproducing Kernel (RK) approximation [43] for its flexibility in controlling order of continuity, order of consistency, and locality for the foreground and background displacement fields. The RK approximation is constructed based upon a set of scattered points \( \left\{ {\varvec{x}_{1} ,\varvec{x}_{2} ,\ldots \varvec{x}_{NP} } \right\} \) in the domain \( \Omega \) as shown in Fig. 2, where \( \varvec{x}_{I} \) is the position vector of node I, and NP is the total number of nodes. The RK approximation of displacement \( u_{i} \) is expressed as
where x is the spatial coordinates, \( u_{iI} \) is the associated nodal coefficient to be determined, and \( \varPsi_{I} \left( \varvec{x} \right) \) is the reproducing kernel (RK) shape function of node I expressed as:
where the basis vector \( \varvec{H}\left( {\varvec{x} - \varvec{x}_{I} } \right) \) is defined as
and \( \varvec{M}\left( \varvec{x} \right) \) is the so-called moment matrix:
Illustration of a 2D RK discretization: support coverage and nodal shape function with circular kernel
The set \( G_{\varvec{x}} = \left\{ {I|\varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) \ne 0 } \right\} \) shown in Eqs. (22) and (25) contains the nodal indexes of point \( \varvec{x}^{{\prime }} s \) neighbors, and \( \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) \) is the kernel function centered at \( \varvec{x}_{I} \) with compact support size \( a_{I} \) defined as
In the above equation, \( \tilde{c} \) is the normalized support size, and \( h_{I} \) is the nodal spacing associated with nodal point \( \varvec{x}_{I} \). The kernel function controls the order of continuity and locality of the approximation as shown in Fig. 3, where the \( C^{0} \) tent kernel function is compared with the following \( C^{2} \) cubic B-spline kernel function:
Illustration of 2D kernel functions with a normalized support of 1.5: a tent kernel and b cubic B-Spline kernel
Tent Function (\( C^{0} \)):
Cubic B-spline kernel function (\( C^{2} \)):
where \( z_{I} \) is defined as \( z_{I} = \frac{{\left\| {\varvec{x} - \varvec{x}_{I} } \right\|}}{{a_{I} }} \).
By construction, the RK shape functions satisfy the following nth order reproducing conditions:
where n is the specified order of completeness, which determines the order of consistency in the solution of PDEs.
3 Variational multiscale immersed method
To effectively account for the fine-scale features in heterogeneous materials, a variational multiscale immersed method formulated under the variational multiscale (VMS) formulation originally proposed by Hughes et al. [13, 14] is employed. Consider the following decomposition of displacement fields \( \varvec{u}^{ - h} \left( \varvec{x} \right) \) and \( \varvec{u}^{ + h} \left( \varvec{x} \right)\varvec{ } \) on the background and foreground domains, respectively, as
Here superposed “-“and “^” denote coarse and fine scale components, respectively. Here we consider a scale decomposition for the background displacement field, while the foreground displacement field is represented by the coarse-scale component only.
Remark 3.1
Note that the scale decomposition in the foreground or background domain can be introduced based on the material composition in heterogeneous materials. The fine-scale field can also be introduced to the foreground domain \( \Omega^{ + } \) or both foreground and background domains.
The following boundary conditions are imposed for the coarse-scale and fine-scale solution:
where \( {\varvec{\bar{\mathcal{U}}}}^{ - } \) and \( {\varvec {\hat{\mathcal{U}}}}^{ - } \) are the function spaces for the coarse-scale and fine-scale, respectively, and \( {\varvec{\mathcal{U}}}^{ - } = {\varvec{\bar{\mathcal{U}}}}^{ - } \oplus {\varvec{\hat{\mathcal{U}}}}^{ - } \). Following [13], we assume the Dirichlet and Neumann boundary conditions on \( \partial \Omega^{ - } \) are fully satisfied by the background coarse-scale displacement, this results in the background fine-scale homogeneous Dirichlet boundary conditions for all boundaries.
3.1 Variational multiscale immersed weak form
By introducing the multiscale decomposition in the Eq. (30) into the immersed weak form (19) with Galerkin approximation, the variational multiscale immersed Galerkin equation reads:
By the virtue of the linear independence of test functions at different scales, Eq. (35) can be decoupled into the coarse-scale equations:
and the fine-scale equation:
From Eq. (39), it can be seen that the fine-scale solution serves as a correction to the residual of the coarse-scale solution.
By introducing the boundary condition of the fine-scale solution in (32) and (34), and with integration-by-parts operations, the fine-scale Eq. (39) yields
Since the domain \( \Omega^{ + } \) is immersed in \( \Omega^{ - } \), the problem of Eq. (40) can be rewritten as
The solution of Eq. (41) can be solved with the aid of Green’s function [14], or by an approximation method to be discussed in the following sections.
Similarly, a different form can be employed for the coarse-scale background Eq. (36). Performing integration-by-parts on Eq. (36) and employing the fine-scale boundary conditions in (32) results in the following expression for the coarse-scale solution:
From Eq. (42), the fine-scale solution \( \hat{\varvec{u}}^{ - h} \) can be directly employed without taking additional differentiation.
Remark 3.1.1
The variational multiscale immersed formulation can be derived by solving the fine-scale Eq. (41) analytically, numerically, or approximately for \( \hat{\varvec{u}}^{ - h} \). The coarse-scale Eqs. (36) or (42) are then solved by incorporating the fine-scale solution into the coarse-scale equations through a static condensation. Note that Eq. (39) or (40) can both be used for solving the fine-scale solution. In this study, two approaches are introduced to solve the multiscale solutions. In the first approach, the coarse-scale Eq. (36) and the fine-scale Eq. (39) are solved by introducing the residual-free bubble method [15] for the fine-scale solution. In the second approach, the coarse-scale Eq. (42) is solved by the standard Galerkin RKPM with stabilized nodal integration, and the fine-scale Eq. (40) is solved by a collocation-type method with an approximation of the local Green’s function. Both approaches are introduced in the following sections.
Remark 3.1.2
Although the \( {\varvec{\mathcal{L}}}^{ - } \left( {\bar{\varvec{u}}^{ - h} } \right) \) in Eqs. (40) and (42) require a second order gradient performed on \( \bar{\varvec{u}}^{ - h} \), the derivatives on fine-scale terms \( \hat{\varvec{u}}^{ - h} \) are avoided, which enables the fine-scale features to be directly introduced in the static condensation process. In addition, since no numerical derivative is performed on \( \hat{\varvec{u}}^{ - h} \), it is more straightforward to employ the resolved fine-scale solution in the coarse-scale equation. The second order gradient \( {\varvec{\mathcal{L}}}^{ - } \left( {\bar{\varvec{u}}^{ - h} } \right) \) required for \( \bar{\varvec{u}}^{ - h} \) can be easily handled by RKPM as shown later.
3.2 Residual-free bubble method
One option to obtain the fine-scale solution in Eq. (39) is to employ the residual-free bubble method [15], where the \( \hat{\varvec{u}}^{ - h} \) can be approximated by an enrichment function [11] or so-called bubble function [15]. The bubble basis can be computed from the integral of the local Green’s function [13]. In the beginning, let the domain \( \bar{\Omega }^{ - } \) be subdivided into subdomains \( \bar{\Omega }_{L}^{ - } \), \( \bigcup\nolimits_{L} {\bar{\Omega }_{L}^{ - } } = \bar{\Omega }^{ - } \), with their boundaries \( \partial \Omega_{L}^{ - } = \Gamma_{L}^{ - } \). The fine-scale solution is approximated by bubble basis function \( \hat{N}_{L}^{ - } \) in each subdomain \( \Omega_{L}^{ - } \) as [15]:
and
where \( S^{ - } = \left\{ {I|\varvec{x}_{I} \in \Omega^{ - } } \right\} \) is the node set containing all nodes within domain \( \Omega^{ - } \), \( \hat{\varvec{u}}_{L}^{ - } \) is the approximation coefficient, and \( \hat{N}_{L}^{ - } \) is the nodal bubble basis function for subdomain \( \Omega_{L}^{ - } \). In this study we employ the cubic B-spline kernel function in Eq. (28) as the nodal bubble function:
The strain vector ε (in Voigt notation) for \( \hat{\varvec{u}}^{ - } \) can then be written as
where
Remark 3.2.1
The construction of nodal bubble functions can be done with conforming nodal representative domains such as Voronoi cells. Constructing such bubble functions on Voronoi cells with arbitrary geometry can be achieved by, for example, the conforming reproducing kernel [34]. In this work, we relax this condition by introducing cubic B-spline functions on the non-conforming circular nodal domain (45) to construct the bubble functions. The fine-scale homogeneous Dirichlet and Neumann boundary conditions are satisfied by using RK kernel functions as bubble functions with small support size not covering neighboring nodes.
The coarse-scale approximation for coarse-scale variables \( \bar{\varvec{u}}^{ - } \), \( \bar{\varvec{u}}^{ + } \) and λ are introduced as follows:
where \( \bar{\varvec{N}}_{I}^{ - } \), \( \bar{\varvec{N}}_{I}^{ + } \) and \( \varvec{N}_{I}^{\lambda } \) are shape function for \( \bar{\varvec{u}}^{ - } \), \( \bar{\varvec{u}}^{ + } \) and λ, respectively, \( \bar{\varvec{B}}_{I}^{ - } \) and \( \bar{\varvec{B}}_{I}^{ + } \) are gradient matrix for \( \bar{\varvec{N}}_{I}^{ - } \) and \( \bar{\varvec{N}}_{I}^{ + } \), respectively, \( S^{ + } = \left\{ {I|\varvec{x}_{I} \in \Omega^{ + } } \right\} \) is the node set containing all nodes within domain \( \Omega^{ + } \). Standard \( C^{0} \) finite element shape functions or smooth RK shape functions given in Sect. 2 can be used as the approximation in Eqs. (48) to (50). More discussion on the choice of shape functions is given in the numerical examples in Sect. 4.
The Galerkin equation of the VMIM reads: find \( \left( {\bar{\varvec{u}}^{ + h} ,\bar{\varvec{u}}^{ - h} ,\hat{\varvec{u}}^{ - h} ,\varvec{\lambda}^{h} } \right) \in {\varvec{\bar{\mathcal{U}}}}^{ + } \times {\varvec{\bar{\mathcal{U}}}}^{ - } \times {\varvec{\hat{\mathcal{U}}}}^{ - } \times {\varvec{\mathcal{W}}} \), such that \( \forall \left( {\delta \bar{\varvec{u}}^{ + h} ,\delta \bar{\varvec{u}}^{ - h} ,\delta \hat{\varvec{u}}^{ - h} ,\delta\varvec{\lambda}^{h} } \right) \in {\varvec{\bar{\mathcal{V}}}}^{ + } \times {\varvec{\bar{\mathcal{V}}}}^{ - } \times {\varvec{\hat{\mathcal{V}}}}^{ - } \times {\varvec{\mathcal{W}}} \),
The function spaces \( {\varvec{\bar{\mathcal{U}}}}^{ + } \), \( {\varvec{\bar{\mathcal{V}}}}^{ + } \), \( {\varvec{\bar{\mathcal{U}}}}^{ - } \), \( {\varvec{\bar{\mathcal{V}}}}^{ - } \), \( {\varvec{\hat{\mathcal{U}}}}^{ - } \), \( {\varvec{\hat{\mathcal{V}}}}^{ - } \) and \( {\varvec{\mathcal{W}}} \) here are given as
By using the approximation in Eqs. (43) to (51) into Eqs. (52) to (55), and invoking the arbitrariness of test function coefficients, the matrix equation of the coarse-scale and fine-scale solutions on the background and foreground are expressed as:
for all I. The matrices and vectors in Eqs. (57) to (60) are expressed in Eqs. (69) to (71):
With the static condensation of Eq. (60) into Eqs. (57) to (59), we have:
where
Equations (72) to (74) can be rearranged into a matrix form for the coarse-scale solution:
Remark 3.2.2
For a comparison of VMIM in Eq. (80), the matrix form of the conventional immersed approach with Lagrange multipliers in Eq. (19) is shown below
It can be observed that Eq. (80) naturally yields a stabilization to the Lagrange multiplier formulation Eq. (81) where the term \( \varvec{\hat{\hat{K}}}^{ - 1} \) in \( \varvec{G}_{IJ}^{\lambda *\lambda } \) plays the role of residual-based stabilization. In the conventional augmented Lagrange multiplier formulation, such stabilization is introduced through a penalization.
Remark 3.2.3
The left hand side matrix in Eq. (80) is a symmetric matrix which is expressed entirely in terms of the coarse-scale solution. The fine-scale solution is obtained from Eq. (60) using the coarse scale solution in Eq. (80).
Remark 3.2.4
In the numerical implementation, the kinematically admissible course-scale test and trial functions defined in (61) have been approximated by the employment of Nitsche’s method to weakly impose the Dirichlet boundary conditions in (31)–(34). Since the focus of this study is on the imposition of volumetric constraint and the variational multiscale decomposition, we do not include the Ntische’s terms in the Galerkin weak form to avoid distraction. The inclusion of Nitsche’s terms on the Dirichlet boundary does not affect the derivation of the proposed variational multiscale immersed method.
3.3 Approximated fine-scale solution
The second method introduced here follows the concept of stabilized Galerkin methods [14] such as stabilized upwind Petrov–Galerkin (SUPG) [44], where the fine-scale solution can be derived approximately. Due to the strong form nature on the right hand side of Eq. (40), a collocation-type method for Eq. (40) is introduced as follows:
where \( \hat{\tau }^{ - } \) is the nodal domain average of fine-scale Green functions from Eq. (41), which will be derived later. By substituting Eq. (82) into Eq. (42), we have
Rearranging Eq. (83) gives the form:
Similar to the method 1 (bubble method), substituting the fine-scale solution into the constraint Eq. (38) and rearranging gives the following equation
Then, the Galerkin equation via the approximated fine-scale solution reads: find \( \left( {\bar{\varvec{u}}^{ + h} ,\bar{\varvec{u}}^{ - h} ,\varvec{\lambda}^{h} } \right) \in {\varvec{\bar{\mathcal{U}}}}^{ + } \times {\varvec{\bar{\mathcal{U}}}}^{ - } \times {\varvec{\mathcal{W}}} \), such that \( \forall \left( {\delta \bar{\varvec{u}}^{ + h} ,\delta \bar{\varvec{u}}^{ - h} ,\delta\varvec{\lambda}^{h} } \right) \in {\varvec{\bar{\mathcal{V}}}}^{ + } \times {\varvec{\bar{\mathcal{V}}}}^{ - } \times {\varvec{\mathcal{W}}} \),
The function spaces \( {\varvec{\bar{\mathcal{U}}}}^{ + } \), \( {\varvec{\bar{\mathcal{U}}}}^{ - } \), \( {\varvec{\bar{\mathcal{V}}}}^{ + } \), \( {\varvec{\bar{\mathcal{V}}}}^{ - } \), and \( {\varvec{\mathcal{W}}} \) are given as
Note that in this construction, function spaces for the background functions are in \( H^{2} \). As such, smooth RK shape functions given in Sect. 2 are good candidates for this approach. More discussion on the fine-scale shape functions is given in the numerical examples in Sect. 4.
The stress divergence operator \( {\mathbf{\nabla }} \cdot\varvec{\sigma} \) for the coarse-scale solution \( \bar{\varvec{u}}^{ - h} \) is computed as,
where \( \varvec{\eta}_{i = 1,2,3} \) are geometric tensors expressed as
and \( \bar{\varvec{B}}_{I,i}^{ - } \) is the derivative of \( \bar{\varvec{B}}_{I}^{ - } \) with respect to \( x_{i} \):
with \( \varvec{C}^{ - } \) following the Voigt notation here. Note that (92) requires 2nd order derivatives of the shape functions, which can introduce significant computational costs when using direct derivatives. Here, the implicit gradient technique [45] is employed for \( \bar{N}_{I,i}^{ - } \) to avoid a direct derivative, and \( \bar{N}_{I,ij}^{ - } \) is then computed by the differentiation of the first-order implicit gradient \( \bar{N}_{I,i}^{ - } \) with respect to \( x_{j} \). Following [45], the implicit gradient in \( \bar{N}_{I,i}^{ - } \) is computed as:
and Di takes the following form
and \( \varvec{H}\left( {\varvec{x} - \varvec{x}_{I} } \right) \), \( \varvec{M}\left( \varvec{x} \right) \), and \( \varPhi_{a} \left( {\varvec{x} - \varvec{x}_{I} } \right) \) are given in Eqs. (24), (25) and (28), respectively.
Finally, by introducing the coarse-scale shape functions in Eqs. (48) to (50) into the weak form (86) to (88), and using the arbitrariness of the test functions, the matrix form of VMIM via the approximated fine-scale solution is obtained as
where \( \bar{\varvec{K}}_{IJ}^{ - } \), \( \bar{\varvec{K}}_{IJ}^{ + } \), \( \bar{\varvec{G}}_{IJ}^{ - \lambda } \), \( \bar{\varvec{G}}_{IJ}^{ + \lambda } \), \( \bar{\varvec{F}}_{I}^{ - } \), and \( \bar{\varvec{F}}_{I}^{ + } \) are given in Eqs. (61) to (68) and \( \hat{\varvec{G}}_{IJ}^{ - \tau } \), \( \hat{\varvec{G}}_{IJ}^{ - \tau \lambda } \), \( \varvec{G}_{IJ}^{\lambda \tau \lambda } \), \( \hat{\varvec{F}}_{I}^{\tau } \) and \( \varvec{F}_{I}^{\tau \lambda } \) are given as follows:
The remaining step in this approach is the estimate of the parameter \( \hat{\tau }^{ - } \) following [46]:
where h is the characteristic nodal distance, \( E^{ - } \) is the Young’s modulus of background matrix media, and \( c_{\tau } \) is a constant usually taken as \( c_{\tau } \in \left[ {0,1} \right] \). The parameter \( \hat{\tau }^{ - } \) is computed from the nodal domain average of the Green’s function [47]:
for a given nodal domain \( \Omega_{L} \) where \( g_{L} \left( {\varvec{x},\varvec{x}^{\prime } } \right) \) is the nodal Green’s function and \( B\left( {\varvec{x}^{\prime } } \right) = \int\limits_{{\Omega_{L} }} {g_{L} \left( {\varvec{x},\varvec{x}^{\prime } } \right)d\Omega_{x} } \) is the fine-scale basis, satisfying the following local problem:
A one-dimensional version of Eq. (103) is considered here:
where h is the size of the nodal domain and the solution of Eq. (104) can be derived:
and from Eq. (102), \( \hat{\tau }^{ - } \) can be obtained as follows
By comparing Eqs. (101) to (106), \( c_{\tau } = \frac{1}{12} \) is employed.
Remark 3.3.1
The term \( \hat{\tau }^{ - } \) represents an approximation to the fine-scale Green’s function as shown in Eq. (102). From Eq. (82), the residual (or error) of the coarse-scale equations, namely \( - {\varvec{\mathcal{L}}}^{ - } \left( {\bar{\varvec{u}}^{ - h} } \right) +\varvec{\lambda}^{h} + \varvec{b}^{ - } \), is normalized by \( \hat{\tau }^{ - } \).
Remark 3.3.2
By employing integration-by-parts for the coarse-scale internal energy terms, the combination of Eqs. (86)–(88) gives the following form in terms of the coarse-scale fields only:
which yields a Petrov–Galerkin formulation for the given immersed setting.
Remark 3.3.3
From the expression of Eq. (83), the derived VMIM via approximated fine-scale solution naturally leads to a stabilized Galerkin formulation [13] in the form of Eq. (108):
with the operator \( {\mathbb{L}} = {\varvec{\mathcal{L}}}^{ - } \) chosen to be the Galerkin/least-squares (GLS) operator [48]. The second term on the left-hand side of Eq. (108) can be regarded as a residual-based stabilization.
Remark 3.3.4
From the matrix form given in Eq. (95), method 2 (approximated fine-scale solution) can also be regarded as a stabilized Lagrange multiplier method, similar to the method 1 (bubble method).
3.4 Quadrature rule in immersed framework
A stabilized nodal integration scheme is employed for the proposed variational multiscale immersed method, where the stabilized conforming nodal integration (SCNI) [49] with naturally stabilized nodal integration (NSNI) [50] is employed for the coarse-scale equations. For comparison purposes, the same integration formulation is employed for the conventional immersed method. With this integration method, the stiffness matrices in (61) and (62) are expressed as
and \( \bar{\varvec{K}}_{IJ}^{ - SCNI} \) and \( \bar{\varvec{K}}_{IJ}^{ + SCNI} \) are integrated by the following nodal quadrature rule:
where \( V_{L} \) is the volume for \( L{\text{th}} \) nodal representative domain as shown in Fig. 4. The matrix \( \varvec{\tilde{\bar{B}}}_{I}^{ - } \left( {\varvec{x}_{L} } \right) \) is calculated by Eq. (113):
where \( \tilde{\bar{\varPsi }}_{I,i}^{ - } \left( {\varvec{x}_{L} } \right) \) is the smoothed gradient at the nodal point \( \varvec{x}_{L} \) calculated following Chen et al. [49]:
where \( n_{i} \) denotes the \( i{\text{th}} \) component of the outward unit normal vector to the smoothing domain boundary shown in Fig. 4. Same computation is applied to \( \varvec{\tilde{\bar{B}}}_{I}^{ + } \).
Voronoi cell diagram in two-dimensional domain \( \Omega \)
It was shown in [49] that with the smoothed gradient of shape function in Eq. (114), the first order integration constraint is exactly satisfied. As discussed in [51], in order to maintain linear consistency of the smoothed gradient of a linearly consistent shape function, a simple one-point Gauss integration rule can be used for the contour integral in Eq. (114). In this study, a Voronoi tessellation is employed to generate each nodal integration cell, as shown in Fig. 4.
Spurious low energy modes can still be triggered with SCNI, and therefore the naturally stabilized nodal integration (NSNI) [50] is employed. Using this technique engenders additional stabilization terms \( \bar{\varvec{K}}_{IJ}^{ - NSNI} \) and \( \bar{\varvec{K}}_{IJ}^{ + NSNI} \), expressed in Eqs. (109) and (110) below
where \( \bar{\varvec{B}}_{I,i}^{ - \nabla } \) is defined as follows:
where \( \bar{\varPsi }_{Ii,j}^{ - \nabla } \) is calculated by the direct differentiation of the first-order implicit gradient \( \bar{\varPsi }_{Ii}^{ - \nabla } \) with respect to \( x_{j} \) [50], as shown in Eqs. (93) and (94). Same computation is applied to \( \bar{\varvec{B}}_{I,i}^{ + \nabla } \). The term \( M_{iL} \) in Eqs. (115) and (116) is the second moment of inertia in each nodal integration domain, calculated from Eq. (118)
The matrices \( \bar{\varvec{K}}_{IJ}^{ - NSNI} \) and \( \bar{\varvec{K}}_{IJ}^{ + NSNI} \) are introduced to maintain coercivity of the system due to reduced nodal integration.
For the approach using the residual free bubble method (Sect. 3.2), SNNI [52] (the non-conforming version of subdomain integrated SCNI [53]) is employed for the domain integration when computing \( \varvec{\hat{\hat{K}}}_{IJ}^{ - } \) in Eq. (69) since the local bubble functions are constructed over non-conforming domains as explained in Sect. 3.2
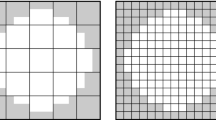
where \( S_{L}^{ - } = \left\{ {M |\varvec{x}_{L}^{M} \in \Omega_{L}^{ - } } \right\} \) is the set containing the subdomain integration points \( \varvec{x}_{L}^{M} \) of the non-conforming nodal domain \( \Omega_{L}^{ - } \) as shown in Fig. 5, \( \hat{\varvec{B}}_{I}^{ - } \left( {\varvec{x}_{L}^{M} } \right) \) is defined in Eq. (47) with each bubble function derivatives computed using smoothed gradient following (114) for each subdomain, and \( V_{L}^{M} \) is the volume of subdomain \( \Omega_{L}^{M - } \). In this study, the size of the non-conforming nodal domain is chosen such that the volume of the circular domain \( \Omega_{L}^{ - } \)(or spherical domain in 3 dimensions) is equivalent to the nodal volume \( V_{L} \) of the corresponding conformal SCNI cell at node L.
Non-conforming nodal diagram in two-dimensional domain \( \Omega \)
For all other domain integration terms, direct nodal integration is employed:
where \( V_{L} \) is the volume for Lth nodal representative domain.
4 Numerical examples
In this study, numerical examples are solved to examine the performance of the proposed variational multiscale immersed method (VMIM) for modeling heterogeneous materials. The reproducing kernel approximation with a linear basis and cubic B-spline kernel is adopted for the approximation of the coarse-scale foreground and background displacement fields and the Lagrange multipliers as shown in Eqs. (48) to (50). Circular support with a normalized support size equaling 2.0 is employed for all approximations. In VMIM, the fine-scale solution is approximated by the bubble functions and the approximated Green’s functions discussed in Sects. 3.2–3.3. The background Dirichlet boundary conditions over \( \partial \Omega_{D}^{ - } \) are imposed by Nitsche’s method with a normalized penalty parameter of 100.
The following methods with their abbreviations are given and tested:
-
(1)
IM + Penalty: Immersed method with penalty method, with a penalty parameter of 100, Eq. (17)
-
(2)
IM + LM: Immersed method with Lagrange multipliers, Eq. (20)
-
(3)
IM + Nitsches: Immersed method with Nitsche’s method, with a normalized penalty parameter of 100, Eq. (21)
-
(4)
VMIM(Bubble) + LM: Variational multiscale immersed method by the residual-free bubble method with Lagrange multipliers, Eq. (80)
-
(5)
VMIM(App) + LM: Variational multiscale immersed method by the approximated fine-scale solution with Lagrange multipliers, Eq. (95)
To assess the accuracy of different numerical schemes, the following normalized displacement and energy norms are employed:
in which the superscript “exact” denotes the exact solutions. \( \varvec{u}^{ - h} \), \( \varvec{\varepsilon}^{ - h} \), \( \varvec{\sigma}^{ - h} \) are the numerical solutions for displacement, strain, and stress from the background domain, respectively, and \( \varvec{u}^{ + h} \), \( \varvec{\varepsilon}^{ + h} \), \( \varvec{\sigma}^{ + h} \) are the numerical solutions for displacement, strain, and stress from the foreground domain, respectively. A 10 × 10 Gauss integration rule is employed to integrate the \( L_{2} \) and energy norms given in (121) and (122).
4.1 Patch test
In the first example, the linear patch test is analyzed to verify the accuracy using linear bases in the RK approximation with nodal integration for the derived variational multiscale immersed formulation. An elasticity equation is considered with the exact solution defined as a linear polynomial function:
where the problem contains a square foreground inclusion domain immersed in a square background matrix domain as shown in Fig. 6.
Computational domain for the patch test: a foreground square domain \( \Omega^{ + } \) is immersed in a background square domain \( \Omega^{ - } \)
For the patch test, the elastic moduli of the foreground and background are set to be \( \varvec{C}^{ + } = \varvec{C}^{ - } \), with Young’s modulus \( E^{ + } = E^{ - } = 1 \times 10^{3} \) and Poisson’s ratio \( \nu^{ + } = v^{ - } = 0.3 \), \( \varvec{\varepsilon}^{exact} \) is the exact strain with \( \varvec{\varepsilon}^{exact} = \left[ {0.1, 0.1, 0.175} \right]^{T} \); \( \varvec{g} = \varvec{u}^{exact} \) is enforced on \( \partial \Omega_{D}^{ - } \), and the body force is set to \( \varvec{b} = \varvec{0}. \) Next, the solution accuracy with discretization refinement under both uniform and non-uniform discretizations is examined. As shown in Fig. 7, non-uniform discretizations are generated by introducing random numbers between \( \pm 0.5h \) into the uniform discretizations, where h is the nodal distance in the uniform discretizations of a unit square.
Uniform and non-uniform discretization of a square domain with a \( 6 \times 6 \), b \( 11 \times 11 \), c \( 16 \times 16 \), and d \( 21 \times 21 \) nodes for both the background and foreground domains, where the non-uniform discretizations from (e) to (h) consist of randomized nodal distributions that correspond to the uniform nodal distributions from (a) to (d), respectively
As shown in Tables 1, 2, 3 and 4, the \( L_{2} \) and energy norm in uniform and nonuniform discretizations show that all tested methods pass the linear patch test, which demonstrates that the quadrature scheme for both the conventional immersed approach and the variational immersed approach all satisfy the integration constraint.
4.2 Heterogeneous material diffusion problems
In the second numerical example, the heterogeneous material diffusion problem given in [54] is tested, where the strong form of the heterogeneous material diffusion problem is given below
where u is the scalar variable field. \( \varvec{\nabla }^{2} = \varvec{\nabla } \cdot \varvec{\nabla } \) is the Laplacian operator, s is the source term, and q and g denote the prescribed flux and essential boundary condition on \( \partial \Omega_{N} \) and \( \partial \Omega_{D} \), respectively. f is the flux vector. Similarly, the source term s and diffusivity k can exhibit discontinuities across different subdomains, but have smooth distribution in each subdomain \( \Omega^{ + } \) and \( \Omega^{ - } \backslash \Omega^{ + } \) respectively, given as
where \( k^{ + } \) and \( k^{ - } \) are scalar diffusivities corresponding to different materials in \( \Omega^{ + } \) and \( \Omega^{ - } \backslash \Omega^{ + } \) respectively, and \( s^{ + } \) and \( s^{ - } \) are the source terms corresponding to \( \Omega^{ + } \) and \( \Omega^{ - } \backslash \Omega^{ + } \) respectively. In this study, \( k^{ + } \) and \( k^{ - } \) are taken as material constants. The following conditions apply on the interface \( \Gamma \):
and the divergence operator can also be defined for each material subdomain:
For this example, the diffusivity is set to be \( k^{ + } = 100 \) and \( k^{ - } = 1 \) and the problem is subjected to a source term \( s = s^{ + } = s^{ - } = - 4 \). The problem domain and the discretization are illustrated in Fig. 8. Since this is a scalar problem, the VMIM formulation for this heterogeneous diffusion problem is slightly modified from that in Sect. 3 and is summarized in the “Appendix”.
Illustration of heterogeneous material diffusion problem and the numerical discretization. The foreground is discretized into 401 nodes and the background is discretized into 441 nodes (regular discretization)
The exact solution of the problem reads:
where \( r_{0} = 0.5 \) is the radius of the circular inclusion. The exact solution \( g = u^{exact} \) is employed as the essential boundary condition at boundary \( \partial \Omega_{D}^{ - } . \) The performance of the conventional immersed formulation with different kinematic constraint methods is investigated. As shown in Fig. 9, large error is observed in the scalar solution inside the region \( \Omega^{ + } \) for immersed method with all three constraint enforcement methods. Also, it can be seen in Fig. 10 that flux field exhibits strong oscillation. The numerical investigation shows that the conventional immersed approach yields an unstable and inaccurate solution with each constraint enforcement method.
Numerical solution of scalar variable field along \( x_{2} = 0 \) by the immersed method with penalty, Lagrange multiplier, and Nitsche’s method, compared with the exact solution
Numerical solution of the gradient and flux fields along \( x_{2} = 0 \) by the immersed method with penalty, Lagrange multiplier, and Nitsche’s method, compared with the exact solution
On the other hand, from Fig. 11, by employing the variational multiscale immersed method, the solution becomes much more accurate. Also, the gradient field becomes much more stable near the interface, where the oscillation in the flux field is largely reduced. As shown in Fig. 12, only marginal perturbation from the exact solution near the material interface is found. The introduction of fine-scale features not only increases the accuracy of the solution but also surpresses the numerical instability.
Numerical solution of scalar variable field along \( x_{2} = 0 \) by immersed method and variational multiscale immersed method, compared with exact solution
Numerical solution of radient and flux field along \( x_{2} = 0 \) by immersed method and variational multiscale immersed method, compared with exact solution
The convergence rate and computational costs for all tested methods are given in Fig. 13. From the convergence study, the VMIM analyses show significantly improved convergence as compared to the conventional IM analyses for both \( L_{2} \) and energy norms. Additionally, the VMIM runs result in similar computational costs compared to the IM runs as shown in Fig. 13b. The computational cost of VMIM with the bubble method (method 1) is higher than that of the approximate fine-scale approach (method 2) due to the domain subdivision required to numerically integrate the fine-scale equation.
Convergence rate and computational cost of all tested methods. The values in the legends indicate the average convergence rate
Finally, the distribution of solution, its gradient and flux field are shown in Fig. 14, where it can be clearly seen that the flux fields from IM + LM are oscillatory near the interface, while the VMIM results are much more stable, although a minor perturbation from the exact solution is found in the flux field. This perturbation can be further reduced by copying the discretization of the foreground domain into the background domain, as shown in Fig. 15. Improvements are seen in the both VMIM and IM methods. Note that boolean operations provide a straigtfoward means to construct such a discretization by removing the background points and adding the foreground points in the overlapping domain as shown in the left column of Fig. 15.
Numerical results of the heterogeneous material diffusion problem: scalar variable \( u \), gradient \( u_{1} \), and flux \( f_{1} \)
Flux fields corresponding to different discretization strategies
Finally, the fine-scale solutions from the VMIM solves are shown in Fig. 16, where the peak value lies near the material interfaces. From the theory of the variational multiscale method [13], the fine-scale solution plays a role in enhancing the coarse-scale solution. Here, it can be verified that the fine-scale solution is magnified near the interface, which is where the coarse-scale solution exhibits higher errors. This indicates that the fine-scale solution can be used as a posteriori error indicator consistent with the multiscale theory [13].
Fine-scale solution \( \left| {\hat{u}^{ - } } \right| \) by a residual-free bubble method and b approximated fine-scale solution
4.3 Circular inclusion in an infinite plate subject to far-field traction
A heterogeneous, linear elasticity problem with the strong form given in Eqs. (1) to (5) is tested, where a circular inclusion with radius \( R \) in an infinite plate is subject to a far-field traction \( P \) as shown in Fig. 17. The computational domain is a truncated finite square domain with length \( L \). The Young’s modulus \( E^{ + } = 1 \times 10^{5} \) is used for the inclusion and \( E^{ - } = 1 \times 10^{3} \) is used for the background matrix media. A Poisson ratio \( v^{ + } = v^{ - } = 0.3 \) is used for both domains.
Illustration of circular inclusion problem and the numerical discretization. Foreground is discretized into 401 nodes and background is discretized into 441 nodes (regular discretization)
The plane stress condition is assumed and the exact solution [55] in the background matrix domain reads
where \( \left( {r,\theta } \right) \) are polar coordinates and \( \beta_{1} \), \( \gamma_{1} \) and \( \delta_{1} \) are expressed as
Then, the exact solution inside the inclusion are given by the following equations
where \( \beta_{2} \) and \( \delta_{2} \) are expressed as
The exact solution is prescribed as essential boundary conditions. The displacement and strain–stress solutions for the immersed methods are shown in Figs. 18 and 19, respectively. It is seen from Fig. 19b that the stress solutions exhibit strong oscillations, similar to the case observed in the heterogeneous material diffusion problem. The VMIM solutions are presented in Figs. 20 and 21 and exhibit much better accuracy. The oscillation in the stress field is largely reduced by the VMIM. The introduction of fine-scale features not only increases the accuracy of the solution but also reduces the numerical instability.
Numerical solution of x-direction displacement along \( x_{1} = 0 \) by the immersed method with the penalty, Lagrange multiplier, and Nitsche’s method, compared with the exact solution
Numerical solution of strian and stress field along \( x_{1} = 0 \) by the immersed method with the penalty, Lagrange multiplier, and Nitsche’s method, compared with the exact solution
Numerical solution of x-direction displacement along \( x_{1} = 0 \) by the immersed method and variational multiscale immersed method, compared with the exact solution
Numerical solution of strian and stress field along \( x_{1} = 0 \) by the immersed method and variational multiscale immersed method, compared with the exact solution
The convergence rates and computational costs for all methods are compared in Fig. 22. From the convergence rate results in Fig. 22a, the VMIMs exhibit significantly improved convergence rates for both L2 and energy norm compared to the IM methods. Superior computational efficiency (i.e., the accuracy versus total runtime) of VMIM over IM is also shown in Fig. 22b.
Convergence rate and computational cost of all tested methods. The values in the legends indicates the average convergence rate
Finally, the distributions of displacement, strain, and stress fields are shown in Figs. 23 and 24, where it can be clearly seen that the stress solutions from IM + LM are oscillatory, while the results from VMIM solutions are much more stable.
Numerical results of elastic inclusion under far-field tension: displacement \( u_{1} \), Strain \( \varepsilon_{11} \), and stress \( \sigma_{11} \)
Numerical results of elastic inclusion under far-field tension: displacement \( u_{2} \), Strain \( \varepsilon_{22} \), and stress \( \sigma_{22} \)
Next, the influence of the foreground and background RK shape functions constructed from kernel functions with different orders of continuity are investigated. In this study, VMIM(App) is employed due to its better accuracy than VMIM(Bubble), as have shown in Fig. 22. Three different kernel functions are adopted: \( C^{0} \) linear B-spline kernel, \( C^{1} \) quadratic B-spline kernel, and \( C^{2} \) cubic B-Spline kernel (the exact expression of the linear and quadratic B-spline kernel can be found from [41]). Different combinations of kernel functions for the background and foreground approximation are tested here.
The stress distributions under different combinations of kernel functions are shown in Figs. 25 and 26. The solution with the \( C^{0} \) linear B-spline kernel used in the background approximation is worse than all other cases. In contrast, adopting a smoother kernel for the foreground and background approximation gives the most stable result. This is due to the employment of the strong form approach in obtaining the approximated fine-scale solution.
Stress fields \( \sigma_{11} \) corresponding to different choices of kernel function used for the background and foreground RK shape function
Stress fields \( \sigma_{22} \) corresponding to different choices of kernel function used for the background and foreground RK shape function
To enhance the accuracy for VMIM, the discretization strategy employed in diffusion problem (left columns of Fig. 15) is also introduced here. As shown in Fig. 27, such modified discretization improves the solution accuracy in all methods, but VMIM again shows better accuracy and stability compared to conventional immersed methods.
Stress fields corresponding to different discretization strategies
The fine-scale solution from VMIMs is shown in Fig. 28, where the magnitude of the fine-scale solution \( \left( {\left| {\hat{\varvec{u}}} \right| = \sqrt {\left( {\hat{u}_{1}^{ - } } \right)^{2} + \left( {\hat{u}_{2}^{ - } } \right)^{2} } } \right) \) has higher error near the material interface. Since the computational domain traction is applied in the \( x_{1} \) direction, the fine-scale solution is expected to have higher contribution along the \( x_{1} \) direction.
Fine-scale solution \( \left| {\hat{\varvec{u}}} \right| \) by two VMIM approaches
4.4 Modeling of heterogeneous microstructure
Heterogeneous microstructure usually involves complex geometry which leads to a low-quality mesh for FEM, unless a very fine mesh is used, as shown in Fig. 29. The proposed immersed meshfree framework can more effectively handle the discretization for such complicated geometries while providing accurate and stable numerical solutions.
Finite element mesh of the duplex stainless-steel microstructures sample. Courtesy of [56]
In this numerical example, a microstructure with prescribed horizontal and vertical displacements to generate tensile and shear deformation, as shown in Fig. 30, is considered. The geometry of the microstructure is generated by randomly distributing 35 circular inclusions inside a square domain with unit length. The radii of the inclusions are also randomly generated from 0.05 to 0.15 units as shown in Fig. 30. The Young’s modulus and Poisson ratio for the background material and foreground inclusions are set to be \( \left( {E^{ - } ,v^{ - } } \right) = \left( {2,0.4} \right) \) and \( \left( {E^{ + } ,v^{ + } } \right) = \left( {40,0.1} \right) \), respectively. The plane stress condition is assumed. The numerical discretization for the proposed immersed method is shown in Fig. 31, where 1,108 nodes are used for the inclusions, and 1681 nodes generated from a 41 by 41 rectilinear grid are used for the background domain. The finite element discretization with a conforming mesh is also shown in Fig. 31. In this test, only VMIM with an approximated fine-scale solution is employed due to its better efficiency and accuracy as shown in the previous examples. A body-fitted FEM result with a highly refined mesh shown in Fig. 31 is employed as the reference solution. Note that when generating the FEM results in this example, a mesh size of 0.005 (corresponding to 44,258 nodes in the FEM solution) was required to avoid a low-quality mesh. In comparison, the proposed VMIM formulation only required 2,789 nodes.
Tensile and shear test of heterogeneous microstructure
Numerical discretization employed for the microstructure problem in Fig. 30
The results of the microstructure under tensile deformation can be found in Figs. 32 and 33, where it can be easily seen that the VMIM results show consistent displacement and stress distribution in the microstructure when compared to reference FEM solution. Also, VMIM produces non-oscillatory strain and stress solutions, and the results are in good agreement with the reference conforming FEM solutions even at a discretization that is 16 times coarser than the conformal mesh.
Displacement fields of the microstructure under the tensile deformation
Strain and stress field of the microstructure under the tensile deformation
The results of the microstructure under shear deformation can be found in Figs. 34 and 35. Similar to the tensile test, the VMIM produces smooth and comparable accuracy in comparison with the reference FEM solution obtained with a much finer discretization. Oscillation is observed in the stress solution in the conventional immersed method. For both the tensile and shear tests the strain concentration for nearby inclusions is smoother in the case of VMIM. This may be due to the smooth approximation employed in RKPM, and the coarser discretization used in the VMIM compared to that used in FEM.
Displacement fields of the microstructure under the shear deformation
Strain and stress field of the microstructure under the shear deformation
Finally, we present numerical results generated by copying the foreground discretization into the background discretization as before. The discretization is shown in Fig. 36 and the numerical results are shown in Fig. 37. The stress and strain field between inclusions are slightly better captured in this case compared to the solution of the other discretization in Fig. 35. However, it is observed that the concave geometry of the foreground inclusions causes local support overlap issues in the region with strong concavity. This issue can be enhanced by the conforming RK method [34] for the foreground inclusion domain.
Discretization employed for the microstructure tensile and shear test
Numerical solution by using the new discretization shown in Fig. 36
5 Summary
In this study, an immersed formulation based on the variational multiscale framework has been proposed for modeling heterogeneous materials. The weak formulation of the problem has been formulated under an immersed setting with independent foreground and background discretizations, and volumetric kinematics constraints have been imposed in the foreground and background overlapping domains. In the proposed variational multiscale immersed method (VMIM), the multiscale decomposition has been employed to better capture the fine-scale features in heterogeneous materials. The fine-scale solution serves as a correction to the residual in the coarse-scale equations. Two strategies have been employed to solve the fine-scale equations: (1) residual-free bubble method, and (2) approximated fine-scale solution. In the first method, the fine-scale equation was obtained by the introduction of nodal bubble functions. The substitution of the fine-scale solution into the coarse-scale equations naturally yields a stabilized Galerkin formulation in an immersed setting. In the second method, due to the stress divergence operator involved in the proposed VMIM with approximated fine-scale field, reproducing kernel approximations with higher-order continuity have been introduced for the solution approximation. Domain integration of the foreground and background weak forms has been accomplished via the SCNI nodal integration technique with NSNI stabilization.
The effectiveness of the proposed variational multiscale immersed meshfree framework has been validated by solving several numerical examples. VMIM showed enhanced accuracy and stability compared to the conventional immersed methods with comparable efficiency. The proposed method with an approximated fine-scale solution (method 2) exhibited better efficiency than the residual-free bubble method (method 1). Furthermore, the proposed VMIM approach has been effectively applied to material microstructures with complex geometry. The accuracy of the proposed method is shown to be in good agreement with the solution obtained from FEM with a highly refined body-fitted mesh. In conclusion, the proposed VMIM has been shown to be an effective method for modeling heterogeneous materials when compared to FEM based methods, which require tedious body-fitted mesh generation. Further, VMIM demonstrated superior performance to conventional immersed approaches. The extension of this research to fluid–structure interaction problems is currently in progress.
References
Wu C-T, Koishi M (2009) A meshfree procedure for the microscopic analysis of particle-reinforced rubber compounds. Interact Multiscale Mech 2(2):129–151
Batra R, Porfiri M, Spinello D (2004) Treatment of material discontinuity in two meshless local Petrov–Galerkin (MLPG) formulations of axisymmetric transient heat conduction. Int J Numer Methods Eng 61(14):2461–2479
Duster A, Parvizian J, Yang Z, Rank E (2008) The finite cell method for three-dimensional problems of solid mechanics. Comput Methods Appl Mech Eng 197(45–48):3768–3782
Bernardi C, Maday Y, Patera AT (1993) Domain decomposition by the mortar element method. In: Asymptotic and numerical methods for partial differential equations with critical parameters, pp 269–286. Dordrecht, Springer. https://link.springer.com/chapter/10.1007/978-94-011-1810-1_17
Babuska I (1973) The finite element method with Lagrangian multipliers. Numer Math 20(3):179–192
Brezzi F, Fortin M (2012) Mixed and hybrid finite element methods, vol 15. Springer, Berlin
Bechet E, Moes N, Wohlmuth B (2009) A stable Lagrange multiplier space for stiff interface conditions within the extended finite element method. Int J Numer Methods Eng 78(8):931–954
Stenberg R (1995) On some techniques for approximating boundary conditions in the finite element method. J Comput Appl Math 63(1–3):139–148
Hansbo P (2005) Nitsche’s method for interface problems in computational mechanics. GAMM-Mitteilungen 28(2):183–206
Fernandez-Mendez S, Huerta A (2004) Imposing essential boundary conditions in mesh-free methods. Comput Methods Appl Mech Eng 193(12–14):1257–1275
Mourad HM, Dolbow J, Harari I (2007) A bubble-stabilized finite element method for Dirichlet constraints on embedded interfaces. Int J Numer Methods Eng 69(4):772–793
Dolbow JE, Franca LP (2008) Residual-free bubbles for embedded Dirichlet problems. Comput Methods Appl Mech Eng 197(45–48):3751–3759
Hughes TJ (1995) Multiscale phenomena: Green’s functions, the Dirichlet-to-Neumann formulation, subgrid scale models, bubbles and the origins of stabilized methods. Comput Methods Appl Mech Eng 127(1–4):387–401
Hughes TJ, Feijoo GR, Mazzei L, Quincy J-B (1998) The variational multiscale method—a paradigm for computational mechanics. Comput Methods Appl Mech Eng 166(1–2):3–24
Brezzi F, Bristeau M-O, Franca LP, Mallet M, Roge G (1992) A relationship between stabilized finite element methods and the Galerkin method with bubble functions. Comput Methods Appl Mech Eng 96(1):117–129
Janela J, Lefebvre A, Maury B (2005) A penalty method for the simulation of fluid-rigid body interaction. ESAIM Proc 14:115–123
Blanco P, Feijoo R, Dari E (2008) A variational framework for fluid-solid interaction problems based on immersed domains: theoretical bases. Comput Methods Appl Mech Eng 197(25–28):2353–2371
Glowinski R, Pan T-W, Hesla TI, Joseph DD (1999) A distributed Lagrange multiplier/fictitious domain method for particulate flows. Int J Multiph Flow 25(5):755–794
Zhang L, Gerstenberger A, Wang X, Liu WK (2004) Immersed finite element method. Comput Methods Appl Mech Eng 193(21–22):2051–2067
Liu WK, Tang S, Tang S (2007) Mathematical foundations of the immersed finite element method. Comput Mech 39(3):211–222
Chen J-S, Pan C, Wu C-T, Liu WK (1996) Reproducing kernel particle methods for large deformation analysis of non-linear structures. Comput Methods Appl Mech Eng 139(1–4):195–227
Liu WK, Jun S, Zhang YF (1995) Reproducing kernel particle methods. Int J Numer Meth Fluids 20(8–9):1081–1106
Liu WK, Hao S, Belytschko T, Li S, Chang CT (1999) Multiple scale meshfree methods for damage fracture and localization. Comput Mater Sci 16(1–4):197–205
Li S, Hao W, Liu WK (2000) Mesh-free simulations of shear banding in large deformation. Int J Solids Struct 37(48–50):7185–7206
Cordes L, Moran B (1996) Treatment of material discontinuity in the element-free Galerkin method. Comput Methods Appl Mech Eng 139(1–4):75–89
Krongauz Y, Belytschko T (1998) EFG approximation with discontinuous derivatives. Int J Numer Methods Eng 41(7):1215–1233
Rabczuk T, Gracie R, Song J-H, Belytschko T (2010) Immersed particle method for fluid–structure interaction. Int J Numer Methods Eng 81(1):48–71
Masuda S, Noguchi H (2006) Analysis of structure with material interface by meshfree method. Comput Model Eng Sci 11(3):131
Yoon Y-C, Song J-H (2014) Extended particle difference method for weak and strong discontinuity problems: part I. Derivation of the extended particle derivative approximation for the representation of weak and strong discontinuities. Comput Mech 53(6):1087–1103
Yoon Y-C, Song J-H (2014) Extended particle difference method for weak and strong discontinuity problems: part II. Formulations and applications for various interfacial singularity problems. Comput Mech 53(6):1105–1128
Wang D, Chen J-S, Sun L (2003) Homogenization of magnetostrictive particle-filled elastomers using an interface-enriched reproducing kernel particle method. Finite Elem Anal Des 39(8):765–782
Wang D, Sun Y, Li L (2009) A discontinuous Galerkin meshfree modeling of material interface. Comput Model Eng Sci 45(1):57
Wu C, Guo Y, Askari E (2013) Numerical modeling of composite solids using an immersed meshfree Galerkin method. Compos B Eng 45(1):1397–1413
Koester JJ, Chen J-S (2019) Conforming window functions for meshfree methods. Comput Methods Appl Mech Eng 347:588–621
Lu H, Wan Kim D, Kam Liu W (2005) Treatment of discontinuity in the reproducing kernel element method. Int J Numer Methods Eng 63(2):241–255
Wu C, Wang D, Guo Y (2016) An immersed particle modeling technique for the three-dimensional large strain simulation of particulate-reinforced metal-matrix composites. Appl Math Model 40(4):2500–2513
Chen J-S, Wang H-P (2000) New boundary condition treatments in meshfree computation of contact problems. Comput Methods Appl Mech Eng 187(3–4):441–468
Cottrell JA, Hughes TJ, Bazilevs Y (2009) Isogeometric analysis: toward integration of CAD and FEA. Wiley, New York
Chen J-S, Hillman M, Chi S-W (2017) Meshfree methods: progress made after 20 years. J Eng Mech 143(4):04017001
Chen J-S, Liu WK, Hillman MC, Chi S-W, Lian Y, Bessa MA (2017) Reproducing Kernel particle method for solving partial differential equations. In: Encyclopedia of computational mechanics, 2nd edn, pp 1–44. https://onlinelibrary.wiley.com/doi/full/10.1002/9781119176817.ecm2104
Huang T-H, Wei H, Chen J-S, Hillman MC (2020) RKPM2D: an open-source implementation of nodally integrated reproducing kernel particle method for solving partial differential equations. Comput Part Mech 7(2):393–433
Nitsche J (1971) Uber ein Variationsprinzip zur Losung von Dirichlet-Problemen bei Verwendung von Teilraumen, die keinen Randbedingungen unterworfen sind. Abhandlungen aus dem mathematischen Seminar der Universitat Hamburg 36(1):9–15
Li S, Liu WK (2007) Meshfree particle methods. Springer, Berlin
Brooks AN, Hughes TJ (1982) Streamline upwind/Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput Methods Appl Mech Eng 32(1–3):199–259
Chen J-S, Zhang X, Belytschko T (2004) An implicit gradient model by a reproducing kernel strain regularization in strain localization problems. Comput Methods Appl Mech Eng 193(27–29):2827–2844
Hughes TJ, Franca LP, Balestra M (1986) A new finite element formulation for computational fluid dynamics: V. Circumventing the Babuska–Brezzi condition: a stable Petrov-Galerkin formulation of the Stokes problem accommodating equal-order interpolations. Comput Methods Appl Mech Eng 59(1):85–99
Nakshatrala K, Masud A, Hjelmstad K (2008) On finite element formulations for nearly incompressible linear elasticity. Comput Mech 41(4):547–561
Hughes TJ, Franca LP, Hulbert GM (1989) A new finite element formulation for computational fluid dynamics: VIII. The Galerkin/least-squares method for advective-diffusive equations. Comput Methods Appl Mech Eng 73(2):173–189
Chen J-S, Wu C-T, Yoon S, You Y (2001) A stabilized conforming nodal integration for Galerkin mesh-free methods. Int J Numer Meth Eng 50(2):435–466
Hillman M, Chen J-S (2016) An accelerated, convergent, and stable nodal integration in Galerkin meshfree methods for linear and nonlinear mechanics. Int J Numer Meth Eng 107(7):603–630
Chen J-S, Hillman M, Ruter M (2013) An arbitrary order variationally consistent integration for Galerkin meshfree methods. Int J Numer Meth Eng 95(5):387–418
Puso M, Chen J-S, Zywicz E, Elmer W (2008) Meshfree and finite element nodal integration methods. Int J Numer Meth Eng 74(3):416–446
Hillman M, Chen J-S (2016) Nodally integrated implicit gradient reproducing kernel particle method for convection dominated problems. Comput Methods Appl Mech Eng 299:381–400
Li Z, Lin T, Wu X (2003) New Cartesian grid methods for interface problems using the finite element formulation. Numer Math 96(1):61–98
Kachanov ML, Shafiro B, Tsukrov I (2013) Handbook of elasticity solutions. Springer, Berlin
Dengiz CG, Yildizli K (2020) Effect of phase shape and size on the FEM analysis of indentation test of duplex stainless steel microstructures. SN Appl Sci 2(4):1–11
Acknowledgements
The support of this work by Sandia National Laboratories to the University of California, San Diego under Contract Agreement 1655264 is greatly acknowledged. Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology and Engineering Solutions of Sandia LLC, a wholly owned subsidiary of Honeywell International Inc. for the U.S. Department of Energy’s National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: VMIM for heterogeneous material diffusion problems
Appendix: VMIM for heterogeneous material diffusion problems
The immersed weak form for the given heterogeneous material diffusion problem reads: find \( \left( {u^{ + } ,u^{ - } } \right) \in {\mathcal{U}}^{ + } \times {\mathcal{U}}^{ - } , u^{ - } = u^{ + }\, {\text{on}}\,\, \Omega^{ + } \), such that \( \forall \left( {\delta u^{ + } ,\delta u^{ - } } \right) \in {\mathcal{V}}^{ + } \times {\mathcal{V}}^{ - } \):
The function space \( {\mathcal{U}}^{ + } \), \( {\mathcal{U}}^{ - } \), \( {\mathcal{V}}^{ + } \), and \( {\mathcal{V}}^{ - } \) are given as
1.1 VMIM via residual-free bubble method
By using the residual free bubble method discussed in Sect. 3.2, the VMIM Galerkin equation reads: find \( \left( {\bar{u}^{ + h} ,\bar{u}^{ - h} ,\hat{u}^{ - h} ,\lambda^{h} } \right) \in {\bar{\mathcal{U}}}^{ + } \times {\bar{\mathcal{U}}}^{ - } \times {\hat{\mathcal{U}}}^{ - } \times {\mathcal{W}} \), such that \( \forall \left( {\delta \bar{u}^{ + h} ,\delta \bar{u}^{ - h} ,\delta \hat{u}^{ - h} ,\delta \lambda^{h} } \right) \in {\bar{\mathcal{V}}}^{ + } \times {\bar{\mathcal{V}}}^{ - } \times {\hat{\mathcal{V}}}^{ - } \times {\mathcal{W}} \),
The function space \( {\bar{\mathcal{U}}}^{ + } \), \( {\bar{\mathcal{V}}}^{ + } \), \( {\bar{\mathcal{U}}}^{ - } \), \( {\bar{\mathcal{V}}}^{ - } \), \( {\hat{\mathcal{U}}}^{ - } \), \( {\hat{\mathcal{V}}}^{ - } \) and \( {\mathcal{W}} \) are given as
Introducing the RK approximation for all solutions and statically condensing the fine-scale terms results in the matrix equations of Eqs. (142) to (144), given as follows
for all \( I \), where the matrices and vector in Eqs. (147) to (149) are expressed as
and the evaluation for each matrix and vector follows Eqs. (155) to (164).
where \( \bar{N}_{I}^{ - } \), \( \bar{N}_{I}^{ + } \) and \( N_{I}^{\lambda } \) are I-th shape function for \( \bar{u}^{ - } \), \( \bar{u}^{ + } \) and \( \lambda \), respectively. \( \hat{N}_{I}^{ - } \) us the fine-scale bubble function for node I. \( \bar{\varvec{B}}_{I}^{ - } \) and \( \bar{\varvec{B}}_{I}^{ + } \) are the gradient matrices for \( \bar{N}_{I}^{ - } \) and \( \bar{N}_{I}^{ + } \), respectively. For example, \( \bar{\varvec{B}}_{I}^{ - } \) and \( \bar{\varvec{B}}_{I}^{ + } \) in the three-dimensional case are expressed as
and \( \bar{\varvec{B}}_{I,i}^{ - } \) is the \( i \)-th derivative of \( \bar{\varvec{B}}_{I}^{ - } \)
The geometric vector \( \varvec{\eta}_{i = 1,2,3} \) for the diffusion problem is expressed as
1.2 VMIM via approximated fine-scale solution
By employing the derivation of the approximated fine-scale solution shown in Sect. 3.3, the VMIM Galerkin equation for the heterogeneous material diffusion problem reads: find \( \left( {\bar{u}^{ + h} ,\bar{u}^{ - h} ,\lambda^{h} } \right) \in {\bar{\mathcal{U}}}^{ + } \times {\bar{\mathcal{U}}}^{ - } \times {\mathcal{W}} \), such that \( \forall \left( {\delta \bar{u}^{ + h} ,\delta \bar{u}^{ - h} ,\delta \lambda^{h} } \right) \in {\bar{\mathcal{V}}}^{ + } \times {\bar{\mathcal{V}}}^{ - } \times {\mathcal{W}} \):
The function space \( {\bar{\mathcal{U}}}^{ + } \), \( {\bar{\mathcal{U}}}^{ - } \), \( {\bar{\mathcal{V}}}^{ + } \), \( {\bar{\mathcal{V}}}^{ - } \) and \( {\mathcal{W}} \) are given as
The matrix equations are given as follows
where \( \bar{K}_{IJ}^{ - } \), \( \bar{K}_{IJ}^{ + } \), \( \bar{G}_{IJ}^{ - \lambda } \), \( \bar{G}_{IJ}^{ + \lambda } \), \( \bar{F}_{I}^{ - } \), and \( \bar{F}_{I}^{ + } \) are given in Eqs. (155) to (160) and \( \hat{K}_{IJ}^{ - \tau } \), \( \hat{G}_{IJ}^{ - \tau \lambda } \), \( G_{IJ}^{\lambda \tau \lambda } \), \( \hat{F}_{I}^{\tau } \) and \( F_{I}^{\tau \lambda } \) are given as follows
The algebraic operator \( \hat{\tau }^{ - } \) can also be derived from the one-dimensional analysis in Eqs. (101) to (106) as:
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huang, TH., Chen, JS., Tupek, M.R. et al. A variational multiscale immersed meshfree method for heterogeneous materials. Comput Mech 67, 1059–1097 (2021). https://doi.org/10.1007/s00466-020-01968-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00466-020-01968-1