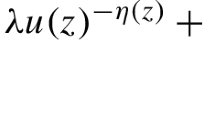(p, q)-Equations with Singular and Concave Convex Nonlinearities

Abstract

We consider a nonlinear Dirichlet problem driven by the (p, q)-Laplacian with $1<q<p$. The reaction is parametric and exhibits the competing effects of a singular term and of concave and convex nonlinearities. We are looking for positive solutions and prove a bifurcation-type theorem describing in a precise way the set of positive solutions as the parameter varies. Moreover, we show the existence of a minimal positive solution and we study it as a function of the parameter.

1 Introduction

Let $\Omega \subseteq \mathbb {R}^N$ be a bounded domain with a $C^2$-boundary $\partial \Omega$. In this paper, we study the following parametric Dirichlet (p, q)-equation

For $r\in (1,\infty )$ we denote by $\Delta _r$ the r-Laplace differential operator defined by

$$\begin{aligned} \Delta _r u ={{\,\mathrm{div}\,}}\left( |\nabla u|^{r-2} \nabla u\right) \quad \text {for all }u \in {W^{1,r}_0(\Omega )}. \end{aligned}$$

The perturbation in problem (P$_\lambda$), namely $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$, is a Carathéodory function, that is, f is measurable in the first argument and continuous in the second one. We suppose that $f(x,\cdot )$ is $(p-1)$-superlinear near $+\infty$ but it does not satisfy the well-known Ambrosetti-Rabinowitz condition which we will write AR-condition for short. Hence, we have in problem (P$_\lambda$) the combined effects of singular terms (the function $s\rightarrow \lambda s^{-\eta }$), of sublinear (concave) terms (the function $s\rightarrow \lambda s^{\tau -1}$ since $1<\tau<q<p$) and of superlinear (convex) terms (the function $s\rightarrow f(x,s)$). For the precise conditions on f we refer to hypotheses H(f) in Sect. 2. Consider the following two functions (for the sake of simplicity we drop the x-dependence)

$$\begin{aligned} f_1(s)=\left( s^+\right) ^{r-1}, \quad p<r<p^*, \qquad f_2(s) = {\left\{ \begin{array}{ll} \left( s^+\right) ^l&{}\text {if }s\le 1,\\ s^{p-1} \ln (s)+1&{}\text {if }1<s, \end{array}\right. } \quad q<l. \end{aligned}$$

Both functions satisfy our hypotheses H(f) but only $f_1$ satisfies the AR-condition.

We are looking for positive solutions and we establish the precise dependence of the set of positive solutions of (P$_\lambda$) on the parameter $\lambda >0$ as the latter varies. For the weight $a(\cdot )$ we suppose the following assumptions

• H(a): $a\in L^{\infty }(\Omega )$, $a(x)\ge a_0>0$ for a.a. $x\in \Omega$;

The main result in this paper is the following one.

Theorem 1.1

If hypotheses H(a) and H(f) hold, then there exists $\lambda ^*\in (0,+\infty )$ such that

• (a) for all $\lambda \in \left( 0,\lambda ^*\right)$, problem (P$_\lambda$) has at least two positive solutions

  $$\begin{aligned} u_0, {\hat{u}} \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) \text { with }u_0\le \hat{u} \text { and }u_0\ne {\hat{u}}; \end{aligned}$$

• (b) for $\lambda =\lambda ^*$, problem (P$_\lambda$) has at least one positive solution $u^*\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$;

• (c) for $\lambda >\lambda ^*$, problem (P$_\lambda$) has no positive solution;

• (d) for every $\lambda \in {\mathcal {L}}=\left( 0,\lambda ^*\right]$, problem (P$_\lambda$) has a smallest positive solution $u^*_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ and the map $\lambda \rightarrow u^*_\lambda$ from ${\mathcal {L}}$ into $C^1_0(\overline{\Omega })$ is strictly increasing, that is, $0<\mu <\lambda \le \lambda ^*$ implies $u^*_\lambda -u^*_\mu \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ and it is left continuous.

The study of elliptic problems with combined nonlinearities was initiated with the seminal paper of Ambrosetti–Brezis–Cerami [1] who studied semilinear Dirichlet equations driven by the Laplacian without any singular term. Their work has been extended to nonlinear problems driven by the p-Laplacian by García Azorero–Peral Alonso–Manfredi [5] and Guo–Zhang [11]. In both works there is no singular term and the reaction has the special form

$$\begin{aligned} x\rightarrow \lambda s^{\tau -1}+s^{r-1} \quad \text {for all}\, s \ge 0\, \text {with }1<\tau<p<r<p^*, \end{aligned}$$

where $p^*$ is the critical Sobolev exponent to p given by

$$\begin{aligned} p^*= {\left\{ \begin{array}{ll} \frac{Np}{N-p} &{}\text {if }p<N,\\ +\infty &{}\text {if } N \le p. \end{array}\right. } \end{aligned}$$

More recently there have been generalizations involving more general nonlinear differential operators, more general concave and convex nonlinearities and different boundary conditions. We refer to the works of Papageorgiou–Rădulescu–Repovš [23] for Robin problems and Papageorgiou–Winkert [19], Leonardi–Papageorgiou [14] and Marano–Marino–Papageorgiou [16] for Dirichlet problems. None of these works involves a singular term. Singular equations driven by the p-Laplacian and with a superlinear perturbation were investigated by Papageorgiou–Winkert [21].

We mention that (p, q)-equations arise in many mathematical models of physical processes. We refer to Benci–D’Avenia–Fortunato–Pisani [2] for quantum physics and Cherfils-Il$'$yasov [3] for reaction diffusion systems.

Finally, we mention recent papers which are very close to our topic dealing with certain types of nonhomogeneous and/or singular problems. We refer to Papageorgiou–Rădulescu–Repovš [26, 28], Papageorgiou–Zhang [22] and Ragusa–Tachikawa [30].

2 Preliminaries and Hypotheses

We denote by $L^{p}(\Omega )$ $\left( \text {or } L^p\left( \Omega ; \mathbb {R}^N\right) \right)$ and $W^{1,p}_0(\Omega )$ the usual Lebesgue and Sobolev spaces with their norms $\Vert \cdot \Vert _{p}$ and $\Vert \cdot \Vert$, respectively. By means of the Poincaré inequality we have

$$\begin{aligned} \Vert u\Vert = \Vert \nabla u\Vert _p \quad \text {for all }u \in W^{1,p}_0(\Omega ). \end{aligned}$$

For $s \in \mathbb {R}$, we set $s^{\pm }=\max \{\pm s,0\}$ and for $u \in W^{1,p}_0(\Omega )$ we define $u^{\pm }(\cdot )=u(\cdot )^{\pm }$. It is known that

$$\begin{aligned} u^{\pm } \in W^{1,p}_0(\Omega ), \quad |u|=u^++u^-, \quad u=u^+-u^-. \end{aligned}$$

Furthermore, we need the ordered Banach space

$$\begin{aligned} C^1_0(\overline{\Omega })= \left\{ u \in C^1(\overline{\Omega }): u\big |_{\partial \Omega }=0 \right\} \end{aligned}$$

and its positive cone

$$\begin{aligned} C^1_0(\overline{\Omega })_+=\left\{ u \in C^1_0(\overline{\Omega }): u(x) \ge 0 \text { for all } x \in \overline{\Omega }\right\} . \end{aligned}$$

This cone has a nonempty interior given by

$$\begin{aligned} {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) =\left\{ u \in C^1_0(\overline{\Omega })_+: u(x)>0 \text { for all } x \in \Omega , \frac{\partial u}{\partial n}(x)<0 \text { for all } x \in \partial \Omega \right\} , \end{aligned}$$

where $n(\cdot )$ stands for the outward unit normal on $\partial \Omega$. We will also use two more open cones. The first one is an open cone in the space $C^1(\overline{\Omega })$ and is defined by

$$\begin{aligned} D_+&=\left\{ u \in C^1(\overline{\Omega })_+: u(x)>0 \text { for all } x\in \Omega , \ \frac{\partial u}{\partial n}\bigg |_{\partial \Omega \cap u^{-1}(0)}<0 \right\} . \end{aligned}$$

The second open cone is the interior of the order cone

$$\begin{aligned} K_+=\left\{ u\in C_0(\overline{\Omega }): u(x) \ge 0 \text { for all }x\in \overline{\Omega }\right\} \end{aligned}$$

of the Banach space

$$\begin{aligned} C_0(\overline{\Omega })=\left\{ u\in C(\overline{\Omega }) : u\big |_{\partial \Omega }=0\right\} . \end{aligned}$$

We know that

$$\begin{aligned} {{\,\mathrm{int}\,}}K_+=\left\{ u \in K_+: c_u \hat{d} \le u \text { for some }c_u>0\right\} \end{aligned}$$

with ${\hat{d}}(\cdot )=d(\cdot ,\partial \Omega )$. Let ${\hat{u}}_1$ denote the positive $L^p$-normalized, that is, $\Vert {\hat{u}}_1\Vert _p=1$, eigenfunction of $\left( -\Delta _p,W^{1,p}_0(\Omega )\right)$. We know that $\hat{u}_1\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. From Papageorgiou–Rădulescu–Repovš [25] we have

$$\begin{aligned} c_u \hat{d}\le u \text { for some }c_u>0 \quad \text { if and only if }\quad \hat{c}_u\hat{u}_1 \le u \text { for some }\hat{c}_u>0. \end{aligned}$$

Given $u,v\in W^{1,p}_0(\Omega )$ with $u(x)\le v(x)$ for a.a.$x\in \Omega$ we define

$$\begin{aligned}{}[u,v]&=\left\{ y\in W^{1,p}_0(\Omega ): u(x) \le y(x) \le v(x) \text { for a.\,a.\,}x\in \Omega \right\} ,\\ {{\,\mathrm{int}\,}}_{\mathop {_{C^1_0(\overline{\Omega })}}} [u,v]&=\text {the interior in } \mathop {C^1_0(\overline{\Omega })} \text { of } [u,v]\cap C^1_0(\overline{\Omega }),\\ [u)&= \left\{ y\in W^{1,p}_0(\Omega ): u(x) \le y(x) \text { for a.a. }x\in \Omega \right\} . \end{aligned}$$

If $h,g \in L^{\infty }(\Omega )$, then we write $h \prec g$ if and only if for every compact set $K\subseteq \Omega$, there exists $c_K>0$ such that $c_K \le g(x)-h(x)$ for a.a. $x\in K$. Note that if $h,g \in C(\Omega )$ and $h(x)<g(x)$ for all $x\in \Omega$, then $h\prec g$.

If X is a Banach space and $\varphi \in C^1(X)$, then we denote by $K_\varphi$ the critical set of $\varphi$, that is,

$$\begin{aligned} K_\varphi =\left\{ u\in X: \varphi '(u)=0\right\} . \end{aligned}$$

Moreover, we say that $\varphi$ satisfies the “Cerami condition”, C-condition for short, if every sequence $\{u_n\}_{n \ge 1}\subseteq X$ such that $\{\varphi (u_n)\}_{n\ge 1}\subseteq \mathbb {R}$ is bounded and

$$\begin{aligned} \left( 1+\Vert u_n\Vert _X\right) \varphi '(u_n) \rightarrow 0\quad \text {in }X^* \text { as }n\rightarrow \infty , \end{aligned}$$

admits a strongly convergent subsequence.

For every $r\in (1,\infty )$, let $A_r:W^{1,r}_0(\Omega )\rightarrow W^{-1,r'}(\Omega )=W^{1,r}_0(\Omega )^*$ with $\frac{1}{r}+\frac{1}{r'}=1$ be defined by

$$\begin{aligned} \left\langle A_r(u), h\right\rangle = \int _{\Omega }|\nabla u|^{r-2} \nabla u \cdot \nabla h \,dx \quad \text {for all }u,h\in W^{1,r}_0(\Omega ). \end{aligned}$$

This operator has the following properties, see Gasiński–Papageorgiou [8, p. 279].

Proposition 2.1

The map $A_r:W^{1,r}_0(\Omega )\rightarrow W^{-1,r'}(\Omega )$ is bounded (that is, it maps bounded sets into bounded sets), continuous, strictly monotone (so maximal monotone) and of type (${{\,\mathrm{S}\,}}$)$_+$, that is,

$$\begin{aligned} u_n\overset{{{\,\mathrm{w}\,}}}{\rightarrow }u \text { in }W^{1,r}_0(\Omega ) \quad \text {and}\quad \limsup _{n\rightarrow \infty } \langle A_r(u_n),u_n-u\rangle \le 0 \end{aligned}$$

imply

$$\begin{aligned} u_n\rightarrow u \quad \text {in }W^{1,r}_0(\Omega ). \end{aligned}$$

The hypotheses on the function $f(\cdot )$ are the following ones:

• H(f): $f:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ is a Carathéodory function such that

  • (i)
    $$\begin{aligned} 0\le f(x,s) \le c_1 \left[ 1+s^{r-1}\right] \end{aligned}$$

    for a. a. $x\in \Omega$, for all  $s \ge 0$  with $c_1>0$ and $r\in (p,p^*)$;

  • (ii) if $F(x,s)=\int _0^sf(x,t)\,dt$, then

    $$\begin{aligned} \lim _{s\rightarrow +\infty } \frac{F(x,s)}{s^p}=+\infty \quad \text {uniformly for a.a. }x\in \Omega ; \end{aligned}$$

  • (iii) there exists $\mu \in \left( (r-p)\max \left\{ 1,\frac{N}{p}\right\} ,p^*\right)$ with $\mu >\tau$ such that

    $$\begin{aligned} 0<c_2 \le \liminf _{s\rightarrow +\infty } \frac{f(x,s)s-pF(x,s)}{s^\mu } \quad \text {uniformly for a.a.}\ x\in \Omega ; \end{aligned}$$
  • (iv)
    $$\begin{aligned} \lim _{s\rightarrow 0^+} \frac{f(x,s)}{s^{q-1}}=0\quad \text {uniformly for a.a. }x\in \Omega ; \end{aligned}$$

  • (v) for every $\rho >0$ there exists $\hat{\xi }_\rho >0$ such that the function

    $$\begin{aligned} s \mapsto f(x,s)+\hat{\xi }_\rho s^{p-1} \end{aligned}$$

    is nondecreasing on $[0,\rho ]$ for a.a. $x\in \Omega$.

Remark 2.2

Since our aim is to produce positive solutions and all the hypotheses above concern the positive semiaxis $\mathbb {R}_+=[0,+\infty )$, we may assume, without any loss of generality, that

$$\begin{aligned} f(x,s)=0 \quad \text {for a.a. }x\in \Omega \text { and for all }s \le 0. \end{aligned}$$

(2.1)

Note that hypothesis H(f)(iv) implies that $f(x,0)=0$ for a.a. $x\in \Omega$. From hypotheses H(f)(ii), (iii) we infer that

$$\begin{aligned} \lim _{s\rightarrow +\infty } \frac{f(x,s)}{s^{p-1}}=+\infty \quad \text {uniformly for a.a. }x\in \Omega . \end{aligned}$$

Therefore, the perturbation $f(x,\cdot )$ is $(p-1)$-superlinear for a.a. $x\in \Omega$. However, the superlinearity of $f(x,\cdot )$ is not expressed using the AR-condition which is common in the literature for superlinear problems. We recall that the AR-condition says that there exist $\beta >p$ and $M>0$ such that

$$\begin{aligned} 0&<\beta F(x,s) \le f(x,s)s \quad \text {for a.a. }x\in \Omega \text { and for all } s\ge M, \end{aligned}$$

(2.2)

$$\begin{aligned} 0&<\text {ess inf}_{x\in \Omega }\, F(x, M). \end{aligned}$$

(2.3)

In fact this is a uniliteral version of the AR-condition due to (2.1). Integrating (2.2) and using (2.3) gives the weaker condition

$$\begin{aligned} c_3 s^{\beta } \le F(x,s) \quad \text {for a.\,a.\,}x\in \Omega , \text { for all }x\ge M\text { and for some }c_3>0, \end{aligned}$$

which implies

$$\begin{aligned} c_3 s^{\beta -1} \le f(x,s) \quad \text {for a.\,a.\,}x\in \Omega \text { and for all }s \ge M. \end{aligned}$$

Hence, the AR-condition dictates that $f(x,\cdot )$ eventually has at least $(\beta -1)$-polynomial growth. In the present work we replace the AR-condition by hypothesis H(f)(iii) which includes in our framework also superlinear nonlinearities with slower growth near $+\infty$.

Hypothesis H(f)(v) is a one-sided Hölder condition. If $f(x,\cdot )$ is differentiable for a.a. $x\in \Omega$ and if for every $\rho >0$ there exists $c_\rho >0$ such that

$$\begin{aligned} f'_s(x,s)s \ge -c_\rho s^{p-1}\quad \text {for a.a. }x\in \Omega \text { and for all }0\le s \le \rho , \end{aligned}$$

then hypothesis H(f)(v) is satisfied. We introduce the following sets

$$\begin{aligned} \mathcal {L}&=\{ \lambda >0: \text {problem} \,(\text {P}_\lambda ) \text { admits a positive solution} \},\\ \mathcal {S}_\lambda&= \{ u:\,u \text { is a positive solution of}\, (\text {P}_\lambda ) \}. \end{aligned}$$

Moreover, we consider the following auxiliary Dirichlet problem

Proposition 2.3

If hypothesis H(a) holds, then for every $\lambda >0$ problem (Q$_\lambda$) admits a unique solution $\tilde{u}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Proof

We consider the $C^1$-functional $\gamma _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \gamma _\lambda (u)=\frac{1}{p}\Vert \nabla u\Vert _p^p +\frac{1}{q} \Vert \nabla u\Vert _q^q-\lambda \int _{\Omega }a(x) \left( u^+\right) ^{\tau }\,dx \quad \text {for all }u \in W^{1,p}_0(\Omega ). \end{aligned}$$

Since $\tau<q<p$ it is clear that $\gamma _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is coercive and by the Sobolev embedding theorem, we see that $\gamma _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is sequentially weakly lower semicontinuous. Hence, there exists ${\tilde{u}}_\lambda \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \gamma _\lambda \left( \tilde{u}_\lambda \right) = \min \left[ \gamma _\lambda (u): u\in W^{1,p}_0(\Omega )\right] . \end{aligned}$$

(2.4)

If $u \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ and $t>0$ then

$$\begin{aligned} \gamma _\lambda (tu) = \frac{t^p}{p} \Vert \nabla u\Vert _p^p +\frac{t^q}{q} \Vert \nabla u\Vert ^q_q-\frac{\lambda t^\tau }{\tau } \int _{\Omega }a(x) u^2\,dx. \end{aligned}$$

Since $\tau<q<p$, choosing $t\in (0,1)$ small enough, we have $\gamma _\lambda (tu)<0$ and so,

$$\begin{aligned} \gamma _\lambda \left( \tilde{u}_\lambda \right) <0=\gamma _\lambda (0), \end{aligned}$$

see (2.4), which shows that ${\tilde{u}}_\lambda \ne 0$. From (2.4) we know that $\gamma _\lambda '\left( \tilde{u}_\lambda \right) =0$, that is,

$$\begin{aligned} \langle A_p \left( {\tilde{u}}_\lambda \right) ,h\rangle +\langle A_q\left( {\tilde{u}}_\lambda \right) ,h\rangle =\lambda \int _{\Omega }a(x) \left( {\tilde{u}}_\lambda ^+\right) ^{\tau -1}h\,dx \text { for all }h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(2.5)

Choosing $h=-\tilde{u}^-_\lambda \in W^{1,p}_0(\Omega )$ in (2.5) gives

$$\begin{aligned} \left\| \nabla {\tilde{u}}^-_\lambda \right\| _p^p +\left\| \nabla {\tilde{u}}_\lambda ^-\right\| _q^q =0, \end{aligned}$$

which shows that ${\tilde{u}}_\lambda \ge 0$ with ${\tilde{u}}_\lambda \ne 0$. Therefore, (2.5) becomes

$$\begin{aligned}&-\Delta _p {\tilde{u}}_\lambda -\Delta _q {\tilde{u}}_\lambda = \lambda a(x) {\tilde{u}}_\lambda ^{\tau -1}\quad \text {in } \Omega , \qquad {\tilde{u}}_\lambda \big |_{\partial \Omega }=0. \end{aligned}$$

We know that $\tilde{u}_\lambda \in L^{\infty }(\Omega )$, see, for example Marino–Winkert [17]. Then, from the nonlinear regularity theory of Lieberman [15] we have that ${\tilde{u}}_\lambda \in C^1_0(\overline{\Omega })_+\setminus \{0\}$. Moreover, the nonlinear maximum principle of Pucci-Serrin [29, pp. 111, 120] implies that ${\tilde{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

We still have to show that this positive solution is unique. Suppose that $\tilde{v}_\lambda \in W^{1,p}_0(\Omega )$ is another solution of (Q$_\lambda$). As before we can show that $\tilde{v}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. We consider the integral functional $j:L^{1}(\Omega )\rightarrow \overline{\mathbb {R}}=\mathbb {R}\cup \{+\infty \}$ defined by

$$\begin{aligned} j(u)= {\left\{ \begin{array}{ll} \frac{1}{p}\left\| \nabla u^{\frac{1}{q}}\right\| _p^p +\frac{1}{q} \left\| \nabla u^{\frac{1}{q}}\right\| ^q_q &{}\text {if } u\ge 0, u^{\frac{1}{q}} \in W^{1,p}_0(\Omega ),\\ +\infty &{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

From Díaz–Saá [4, Lemma 1] we see that j is convex. Furthermore, applying Proposition 4.1.22 of Papageorgiou–Rădulescu–Repovš [24, p. 274], we obtain that

$$\begin{aligned} \frac{{\tilde{u}}_\lambda }{{\tilde{v}}_\lambda }, \frac{{\tilde{v}}_\lambda }{{\tilde{u}}_\lambda }\in L^{\infty }(\Omega ). \end{aligned}$$

We denote by

$$\begin{aligned} {{\,\mathrm{dom}\,}}j =\left\{ u\in L^{1}(\Omega ): j(u)<+\infty \right\} \end{aligned}$$

the effective domain of j and set $h={\tilde{u}}_\lambda ^q-{\tilde{v}}_\lambda ^q$. One gets

$$\begin{aligned} {\tilde{u}}_\lambda ^q-th \in {{\,\mathrm{dom}\,}}j \quad \text {and}\quad {\tilde{v}}_\lambda ^q+th\in {{\,\mathrm{dom}\,}}j\quad \text {for all }t\in [0,1]. \end{aligned}$$

Note that the functional $j:L^{1}(\Omega )\rightarrow \overline{\mathbb {R}}$ is Gateaux differentiable at ${\tilde{u}}_\lambda ^q$ and at ${\tilde{v}}_\lambda ^q$ in the direction h. Using the nonlinear Green’s identity, see Papageorgiou–Rădulescu–Repovš [24, Corollary 1.5.16, p. 34], we obtain

$$\begin{aligned} j'\left( {\tilde{u}}_\lambda ^q\right) (h)&=\frac{1}{q} \int _{\Omega }\frac{-\Delta _p {\tilde{u}}_\lambda -\Delta _q {\tilde{u}}_\lambda }{{\tilde{u}}_\lambda ^{q-1}}h\,dx =\frac{\lambda }{q}\int _{\Omega }\frac{a(x)}{{\tilde{u}}_\lambda ^{q-\tau }}h\,dx,\\ j'\left( {\tilde{v}}_\lambda ^q\right) (h)&=\frac{1}{q} \int _{\Omega }\frac{-\Delta _p {\tilde{v}}_\lambda -\Delta _q {\tilde{v}}_\lambda }{{\tilde{v}}_\lambda ^{q-1}}h\,dx =\frac{\lambda }{q}\int _{\Omega }\frac{a(x)}{{\tilde{v}}_\lambda ^{q-\tau }}h\,dx. \end{aligned}$$

The convexity of $j:L^{1}(\Omega )\rightarrow \overline{\mathbb {R}}$ implies the monotonicity of $j'$. Hence

$$\begin{aligned} 0 \le \frac{\lambda }{q}\int _{\Omega }a(x) \left[ \frac{1}{{\tilde{u}}_\lambda ^{q-\tau }}-\frac{1}{{\tilde{v}}_\lambda ^{q-\tau }} \right] \left[ {\tilde{u}}_\lambda ^q-{\tilde{v}}_\lambda ^q\right] \,dx\le 0, \end{aligned}$$

which implies ${\tilde{u}}_\lambda ={\tilde{v}}_\lambda$. Therefore, ${\tilde{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ is the unique positive solution of the auxiliary problem (Q$_\lambda$). $\square$

This solution will provide a useful lower bound for the elements of the set of positive solutions ${\mathcal {S}}_\lambda$.

3 Positive Solutions

Let $\tilde{u}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ be the unique positive solution of (Q$_\lambda$), see Proposition 2.3. Let $s>N$. Then $\tilde{u}_\lambda ^s\in {{\,\mathrm{int}\,}}K_+$ and so there exists $c_4>0$ such that

$$\begin{aligned} {\hat{u}}_1 \le c_4 {\tilde{u}}_\lambda ^s, \end{aligned}$$

see Sect. 2. Hence

$$\begin{aligned} {\tilde{u}}_\lambda ^{-\eta } \le c_5 {\hat{u}}_1^{-\frac{\eta }{s}}\quad \text {for some }c_5>0. \end{aligned}$$

Applying the Lemma of Lazer–McKenna [13] we have

$$\begin{aligned} {\hat{u}}_1^{-\frac{\eta }{s}} \in L^{s}(\Omega ) \end{aligned}$$

and thus

$$\begin{aligned} {\tilde{u}}_\lambda ^{-\eta } \in L^{s}(\Omega ). \end{aligned}$$

(3.1)

We introduce the following modification of problem (P$_\lambda$) in which we have neutralized the singular term

Let $\psi _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ be the Euler energy functional of problem (P$_\lambda$’) defined by

$$\begin{aligned} \psi _\lambda (u)&=\frac{1}{p}\Vert \nabla u\Vert _p^p +\frac{1}{q} \Vert \nabla u\Vert _q^q -\lambda \int _{\Omega }{\tilde{u}}_\lambda ^{-\eta } u\,dx\\&\quad -\frac{\lambda }{\tau } \int _{\Omega }a(x)\left( u^+\right) ^{\tau }\,dx-\int _{\Omega }F(x,u^+)\,dx \end{aligned}$$

for all $u \in W^{1,p}_0(\Omega )$, see (3.1). It is clear that $\psi _\lambda \in C^1(W^{1,p}_0(\Omega ))$.

Proposition 3.1

If hypotheses H(a) and H(f) hold and if $\lambda >0$, then $\psi _\lambda$ satisfies the C-condition.

Proof

Let $\{u_n\}_{n \ge 1} \subseteq W^{1,p}_0(\Omega )$ be a sequence such that

$$\begin{aligned}&\left| \psi _\lambda (u_n)\right| \le c_6 \quad \text {for all }n\in \mathbb {N}\text { and for some }c_6>0,\end{aligned}$$

(3.2)

$$\begin{aligned}&(1+\Vert u_n\Vert )\psi '_\lambda (u_n)\rightarrow 0 \quad \text {in }W^{1,p}_0(\Omega )^*=W^{-1,p'}(\Omega ) \text { with }\frac{1}{p}+\frac{1}{p'}=1. \end{aligned}$$

(3.3)

From (3.3) we have

$$\begin{aligned}&\left| \langle A_p(u_n),h\rangle +\langle A_q(u_n),h\rangle -\lambda \int _{\Omega }\tilde{u}_\lambda ^{-\eta }h\,dx-\lambda \int _{\Omega }a(x) \left( u_n^+\right) ^{\tau -1}h\,dx\right. \nonumber \\&\quad \left. -\int _{\Omega }f\left( x,u_n^+\right) h\,dx\right| \le \frac{\varepsilon _n\Vert h\Vert }{1+\Vert u_n\Vert }\quad \text {for all } h\in W^{1,p}_0(\Omega ) \text { with }\varepsilon _n\rightarrow 0^+. \end{aligned}$$

(3.4)

Choosing $h=-u_n^-\in W^{1,p}_0(\Omega )$ in (3.4) leads to

$$\begin{aligned} \left\| \nabla u_n^-\right\| _p^p \le \varepsilon _n\quad \text {for all }n \in \mathbb {N}, \end{aligned}$$

which implies

$$\begin{aligned} u_n^- \rightarrow 0\quad \text {in }W^{1,p}_0(\Omega ) \text { as }n\rightarrow \infty . \end{aligned}$$

(3.5)

Combining (3.2) and (3.5) gives

$$\begin{aligned}&\left\| \nabla u_n^+\right\| _p^p+\frac{p}{q}\left\| \nabla u_n^+\right\| _q^q -\lambda p\int _{\Omega }\tilde{u}_\lambda ^{-\eta } u_n^+\,dx-\frac{\lambda p}{\tau } \int _{\Omega }a(x) \left( u_n^+\right) ^{\tau }\,dx\nonumber \\&-\int _{\Omega }pF\left( x,u_n^+\right) \,dx \le c_7 \quad \text {for all }n\in \mathbb {N}\text { and for some }c_7>0. \end{aligned}$$

(3.6)

On the other hand, if we choose $h=u_n^+\in W^{1,p}_0(\Omega )$ in (3.4), we obtain

$$\begin{aligned}&-\left\| \nabla u_n^+\right\| _p^p-\left\| \nabla u_n^+\right\| _q^q +\lambda \int _{\Omega }\tilde{u}_\lambda ^{-\eta } u_n^+\,dx+\lambda \int _{\Omega }a(x) \left( u_n^+\right) ^\tau \,dx\nonumber \\&\quad +\,\int _{\Omega }f\left( x,u_n^+\right) u_n^+\,dx \le \varepsilon _n \quad \text {for all }n\in \mathbb {N}. \end{aligned}$$

(3.7)

Adding (3.6) and (3.7) yields

$$\begin{aligned}&\int _{\Omega }\left[ f\left( x,u_n^+\right) u_n^+-pF\left( x,u_n^+\right) \right] \,dx\nonumber \\&\quad \le \,\lambda (p-1)\int _{\Omega }\tilde{u}_\lambda ^{-\eta }u_n^+\,dx+\lambda \left[ \frac{p}{\tau }-1\right] \int _{\Omega }a(x) \left( u_n^+\right) ^\tau \,dx. \end{aligned}$$

(3.8)

By hypotheses H(f)(i), (iii) we can find $c_8>0$ such that

$$\begin{aligned} \frac{c_2}{2}s^\mu -c_8 \le f(x,s)s-pF(x,s)\quad \text {for a.a. } x\in \Omega \text { and for all }s\ge 0. \end{aligned}$$

This implies

$$\begin{aligned} \frac{c_2}{2}s^\mu \left\| u_n^+\right\| _\mu ^\mu -c_9 \le \int _{\Omega }\left[ f\left( x,u_n^+\right) u_n^+-pF\left( x,u_n^+\right) \right] \,dx \end{aligned}$$

(3.9)

for some $c_9>0$ and for all $n\in \mathbb {N}$.

Since $s>N$ we have $s'<N'\le p^*$. Hence, $u_n^+\in L^{s'}(\Omega )$. Then, taking (3.1) along with Hölder’s inequality into account, we get

$$\begin{aligned} \lambda [p-1]\int _{\Omega }\tilde{u}_\lambda ^{-\eta }u_n^+\,dx \le c_{10} \left\| \tilde{u}_\lambda ^{-\eta }\right\| _s \left\| u_n^+\right\| _{s'} \end{aligned}$$

(3.10)

for some $c_{10}=c_{10}(\lambda )>0$ and for all $n\in \mathbb {N}$. Moreover, by hypothesis H(a), we have

$$\begin{aligned} \lambda \left[ \frac{p}{\tau }-1\right] \int _{\Omega }a(x) \left( u_n^+\right) ^\tau \,dx \le c_{11} \left\| u_n^+\right\| _\tau ^\tau \end{aligned}$$

(3.11)

for some $c_{11}=c_{11}(\lambda )>0$ and for all $n\in \mathbb {N}$.

Now we choose $s>N$ large enough such that $s'<\mu$. Returning to (3.8), using (3.9), (3.10) as well as (3.11) and using the fact that $s', \tau <\mu$ by hypothesis H(f)(iii) leads to

$$\begin{aligned} \left\| u_n^+\right\| _\mu ^\mu \le c_{12}\left[ \left\| u_n^+\right\| _\mu +\left\| u_n^+\right\| _\mu ^\tau +1\right] \end{aligned}$$

for some $c_{12}>0$ and for all $n\in \mathbb {N}$. Since $\tau <\mu$ we obtain

$$\begin{aligned} \left\{ u_n^+\right\} _{n \ge 1} \subseteq L^{\mu }(\Omega ) \text { is bounded}. \end{aligned}$$

(3.12)

Assume that $N\ne p$. From hypothesis H(f)(iii) it is clear that we may assume $\mu<r<p^*$. Then there exists $t\in (0,1)$ such that

$$\begin{aligned} \frac{1}{r}=\frac{1-t}{\mu }+\frac{t}{p^*}. \end{aligned}$$

Taking the interpolation inequality into account, see Papageorgiou–Winkert [20, Proposition2.3.17, p. 116], we have

$$\begin{aligned} \left\| u_n^+\right\| _r\le \left\| u_n^+\right\| _\mu ^{1-t} \left\| u_n^+\right\| ^t_{p^*}, \end{aligned}$$

which by (3.12) implies that

$$\begin{aligned} \left\| u_n^+\right\| _r^r\le c_{13}\left\| u_n^+\right\| ^{tr} \end{aligned}$$

(3.13)

for some $c_{13}>0$ and for all $n\in \mathbb {N}$.

From hypothesis H(f)(i) we know that

$$\begin{aligned} f(x,s)s \le c_{14} \left[ 1+s^r\right] \end{aligned}$$

(3.14)

for a.a. $x\in \Omega$, for all $s\ge 0$ and for some $c_{14}>0$. We choose $h=u_n^+\in W^{1,p}_0(\Omega )$ in (3.4), that is,

$$\begin{aligned}&\left\| \nabla u_n^+\right\| _p^p+\left\| \nabla u_n^+\right\| _q^q -\lambda \int _{\Omega }\tilde{u}_\lambda ^{-\eta }u_n^+\,dx-\lambda \int _{\Omega }a(x) \left( u_n^+\right) ^{\tau }\,dx\\&\quad -\int _{\Omega }f\left( x,u_n^+\right) u_n^+\,dx\le \varepsilon _n\quad \text {for all } n\in \mathbb {N}. \end{aligned}$$

From this it follows by using (3.13), (3.14) and $1<\tau<p<r$

$$\begin{aligned} \left\| u_n^+\right\| ^p \le c_{15}\left[ 1+\left\| u_n^+\right\| ^{tr}\right] \end{aligned}$$

(3.15)

for some $c_{15}>0$ and for all $n\in \mathbb {N}$. The condition on $\mu$, see hypothesis H(f)(iii), implies that $tr<p$. Then from (3.15) we infer

$$\begin{aligned} \left\{ u_n^+\right\} _{n\ge 1} \subseteq W^{1,p}_0(\Omega ) \text { is bounded.} \end{aligned}$$

(3.16)

If $N=p$, then we have by definition $p^*=\infty$. The Sobolev embedding theorem ensures that $W^{1,p}_0(\Omega )\hookrightarrow L^{\vartheta }(\Omega )$ for all $1\le \vartheta <\infty$. So, in order to apply the previous arguments we need to replace $p^*$ by $\vartheta>r>\mu$ and choose $t \in (0,1)$ such that

$$\begin{aligned} \frac{1}{r}=\frac{1-t}{\mu }+\frac{t}{\vartheta }, \end{aligned}$$

which implies

$$\begin{aligned} tr=\frac{\vartheta (r-\mu )}{\vartheta -\mu }. \end{aligned}$$

Note that $\frac{\vartheta (r-\mu )}{\vartheta -\mu }\rightarrow r-\mu <p$ as $\vartheta \rightarrow +\infty$. So, for $\vartheta >r$ large enough, we see that $tr<p$ and again (3.16) holds.

From (3.5) and (3.16) we infer that

$$\begin{aligned} \left\{ u_n\right\} _{n \ge 1} \subseteq W^{1,p}_0(\Omega ) \text { is bounded}. \end{aligned}$$

So, we may assume that

$$\begin{aligned} u_n\overset{{{\,\mathrm{w}\,}}}{\rightarrow }u \quad \text {in }W^{1,p}_0(\Omega ) \quad \text {and}\quad u_n\rightarrow u \quad \text {in }L^{r}(\Omega ). \end{aligned}$$

(3.17)

We choose $h=u_n-u\in W^{1,p}_0(\Omega )$ in (3.4), pass to the limit as $n\rightarrow \infty$ and use the convergence properties in (3.17). This gives

$$\begin{aligned} \lim _{n\rightarrow \infty } \left[ \langle A_p(u_n),u_n-u\rangle +\langle A_q(u_n),u_n-u\rangle \right] =0 \end{aligned}$$

and since $A_q$ is monotone we obtain

$$\begin{aligned} \lim _{n\rightarrow \infty } \left[ \langle A_p(u_n),u_n-u\rangle +\langle A_q(u),u_n-u\rangle \right] \le 0. \end{aligned}$$

By (3.16) we then conclude that

$$\begin{aligned} \lim _{n\rightarrow \infty } \langle A_p(u_n),u_n-u\rangle \le 0. \end{aligned}$$

Applying Proposition 2.1 shows that $u_n\rightarrow u$ in $W^{1,p}_0(\Omega )$ and so we conclude that $\psi _\lambda$ satisfies the C-condition. $\square$

Proposition 3.2

If hypotheses H(a) and H(f) hold, then there exists $\hat{\lambda }>0$ such that for every $\lambda \in \left( 0,\hat{\lambda }\right)$ we can find $\rho _\lambda >0$ for which we have

$$\begin{aligned} \psi _\lambda (0)=0<\inf \left[ \psi _\lambda (u): \Vert u\Vert =\rho _\lambda \right] =m_\lambda . \end{aligned}$$

Proof

Hypotheses H(f)(i), (iv) imply that for a given $\varepsilon >0$ we can find $c_{16}=c_{16}(\varepsilon )>0$ such that

$$\begin{aligned} F(x,s)\le \frac{\varepsilon }{q}s^q +c_{16}s^r \quad \text {for a.a. }x\in \Omega \text { and for all }s\ge 0. \end{aligned}$$

(3.18)

Recall that $\tilde{u}_\lambda ^{-\eta } \in L^{s}(\Omega )$ with $s>N$, see (3.1). We choose $s>N$ large enough such that $s'<p^*$. Then, by Hölder’s inequality, we have

$$\begin{aligned} \lambda \int _{\Omega }{\tilde{u}}_\lambda ^{-\eta }u\,dx \le \lambda c_{17}\Vert u\Vert \quad \text {for some }c_{17}>0. \end{aligned}$$

(3.19)

Moreover, one gets

$$\begin{aligned} \frac{\lambda }{\tau } \int _{\Omega }a(x) |u|^\tau \,dx\le \frac{\lambda \Vert a\Vert _\infty }{\tau } \Vert u\Vert ^\tau . \end{aligned}$$

(3.20)

Applying (3.18), (3.19) and (3.20) leads to

$$\begin{aligned} \psi _\lambda (u) \ge \frac{1}{p} \Vert \nabla u\Vert _p^p +\frac{1}{q} \left[ \Vert \nabla u\Vert _q^q-\varepsilon \Vert u\Vert _q^q\right] -c_{18} \left[ \Vert u\Vert ^r+\lambda \left( \Vert u\Vert +\Vert u\Vert ^\tau \right) \right] \end{aligned}$$

(3.21)

for some $c_{18}>0$. Let ${\hat{\lambda }}_1(q)>0$ be the principal eigenvalue of $\left( -\Delta _q,W^{1,q}_0(\Omega )\right)$. Then, from the variational characterization of $\hat{\lambda }_1(q)$, see Gasiński–Papageorgiou [6, p. 732], we obtain

$$\begin{aligned} \frac{1}{q} \left[ \Vert \nabla u\Vert _q^q-\varepsilon \Vert u\Vert _q^q\right] \ge \frac{1}{q} \left[ 1-\frac{\varepsilon }{\hat{\lambda }_1(q)}\right] \Vert \nabla u\Vert _q^q. \end{aligned}$$

Choosing $\varepsilon \in \left( 0,\hat{\lambda }_1(q)\right)$ we infer that

$$\begin{aligned} \frac{1}{q} \left[ \Vert \nabla u\Vert _q^q-\varepsilon \Vert u\Vert _q^q\right] >0. \end{aligned}$$

(3.22)

Since $1<\tau <r$, it holds

$$\begin{aligned} \Vert u\Vert ^\tau \le \Vert u\Vert +\Vert u\Vert ^r. \end{aligned}$$

(3.23)

Applying (3.22) and (3.23) to (3.21) gives

$$\begin{aligned} \psi _\lambda (u)&\ge \frac{1}{p} \Vert u\Vert ^p -c_{18} \left[ 2\lambda \Vert u\Vert +(\lambda +1)\Vert u\Vert ^{r}\right] \nonumber \\&\ge \left[ \frac{1}{p} -c_{18} \left( 2\lambda \Vert u\Vert ^{1-p}+(\lambda +1)\Vert u\Vert ^{r-p}\right) \right] \Vert u\Vert ^p. \end{aligned}$$

(3.24)

We consider now the function

$$\begin{aligned} k_\lambda (t)=2\lambda t^{1-p}+(\lambda +1)t^{r-p}\quad \text {for all }t>0. \end{aligned}$$

It is clear that $k_\lambda \in C^1(0,\infty )$ and since $1<p<r$ we see that

$$\begin{aligned} k_\lambda (t)\rightarrow +\infty \quad \text {as }t\rightarrow 0^+ \text { and as }t\rightarrow +\infty . \end{aligned}$$

Hence, there exists $t_0>0$ such that

$$\begin{aligned} k_\lambda (t_0)=\min \left[ k_\lambda (t): t>0\right] , \end{aligned}$$

which implies that $k_\lambda '(t_0)=0$. Therefore,

$$\begin{aligned} 2\lambda (p-1)t_0^{-p}=(r-p)(\lambda +1)t_0^{r-p-1}. \end{aligned}$$

From this we deduce that

$$\begin{aligned} t_0=t_0(\lambda )=\left[ \frac{2\lambda (p-1)}{(r-p)(\lambda +1)}\right] ^{\frac{1}{r-1}}. \end{aligned}$$

We have

$$\begin{aligned} k_\lambda (t_0) =2\lambda \frac{(r-p)(\lambda +1)^{\frac{p-1}{r-1}}}{(2\lambda (p-1))^{\frac{p-1}{r-1}}} +(\lambda +1) \frac{(2\lambda (p-1))^{\frac{r-p}{r-1}}}{((r-p)(\lambda +1))^{\frac{r-p}{r-1}}}. \end{aligned}$$

Since $1<p<r$ we see that

$$\begin{aligned} k_\lambda (t_0)\rightarrow 0 \quad \text {as }\lambda \rightarrow 0^+. \end{aligned}$$

Therefore, we can find $\hat{\lambda }>0$ such that

$$\begin{aligned} k_\lambda (t_0)<\frac{1}{pc_{18}}\quad \text {for all }\lambda \in \left( 0,\hat{\lambda }\right) . \end{aligned}$$

Then, by (3.24) we see that

$$\begin{aligned} \psi _\lambda (u)>0=\psi _\lambda (0)\quad \text {for all }\Vert u\Vert =t_0(\lambda )=\rho _\lambda \text { and for all }\lambda \in \left( 0,\hat{\lambda }\right) . \end{aligned}$$

From hypothesis H(f)(ii) we see that for every $u\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ we have

$$\begin{aligned} \psi _\lambda (tu)\rightarrow -\infty \quad \text {as }t\rightarrow +\infty . \end{aligned}$$

(3.25)

Proposition 3.3

If hypotheses H(a) and H(f) hold and if $\lambda \in \left( 0,\hat{\lambda }\right)$, then problem (P$_\lambda$’) admits a solution $\overline{u}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Proof

Propositions 3.1, 3.2 and (3.25) permit the use of the mountain pass theorem. So, we can find $\overline{u}_\lambda \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \overline{u}_\lambda \in K_{\psi _\lambda }\quad \text {and}\quad \psi _\lambda (0)=0<m_\lambda \le \psi _\lambda (\overline{u}_\lambda ). \end{aligned}$$

(3.26)

From (3.26) we see that $\overline{u}_\lambda \ne 0$ and $\psi _\lambda '(\overline{u}_\lambda )=0$, that is,

$$\begin{aligned}&\langle A_p(\overline{u}_\lambda ),h\rangle +\langle A_q(\overline{u}_\lambda ),h\rangle \nonumber \\&=\lambda \int _{\Omega }\tilde{u}_\lambda ^{-\eta }h\,dx+\lambda \int _{\Omega }a(x) \left( \overline{u}_\lambda ^+\right) ^{\tau -1}h\,dx +\int _{\Omega }f\left( x,\overline{u}_\lambda ^+\right) h\,dx \end{aligned}$$

(3.27)

for all $h\in W^{1,p}_0(\Omega )$. We choose $h=-\overline{u}_\lambda ^-\in W^{1,p}_0(\Omega )$ in (3.27) which shows that

$$\begin{aligned} \left\| \overline{u}_\lambda ^-\right\| ^p \le 0. \end{aligned}$$

Thus, $\overline{u}_\lambda \ge 0$ with $\overline{u}_\lambda \ne 0$.

From (3.27) we know that $\overline{u}_\lambda$ is a positive solution of (P$_\lambda$’) with $\lambda \in \left( 0,{\hat{\lambda }}\right)$. This means

$$\begin{aligned}&-\Delta _p \overline{u}_\lambda -\Delta _q \overline{u}_\lambda = \lambda \tilde{u}_\lambda ^{-\eta }+\lambda a(x)\overline{u}_\lambda ^{\tau -1}+f(x,\overline{u}_\lambda )\quad \text {in } \Omega , \quad \overline{u}_\lambda \big |_{\partial \Omega }=0. \end{aligned}$$

As before, see the proof of Proposition 2.3, using the nonlinear regularity theory, we have $\overline{u}_\lambda \in C^1_0(\overline{\Omega })_+\setminus \{0\}$. The nonlinear maximum principle, see Pucci–Serrin [29, pp. 111, 120] implies that $\overline{u}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Proposition 3.4

If hypotheses H(a) and H(f) hold and if $\lambda \in \left( 0,{\hat{\lambda }}\right)$, then ${\tilde{u}}_\lambda \le \overline{u}_\lambda$.

Proof

We introduce the Carathéodory function $g_\lambda :\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} g_\lambda (x,s)= {\left\{ \begin{array}{ll} \lambda a(x) \left( s^+\right) ^{\tau -1} &{}\text {if }s\le \overline{u}_\lambda (x),\\ \lambda a(x) \overline{u}_\lambda (x)^{\tau -1} &{}\text {if }\overline{u}_\lambda (x)<s. \end{array}\right. } \end{aligned}$$

(3.28)

We set $G_\lambda (x,s)=\int ^s_0g_\lambda (x,t)\,dt$ and consider the $C^1$-functional $\sigma _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} \sigma _\lambda (u) = \frac{1}{p}\Vert \nabla u\Vert _p^p+\frac{1}{q}\Vert \nabla u\Vert _q^q-\int _{\Omega }G_\lambda (x,u) dx\quad \text {for all }u \in W^{1,p}_0(\Omega ). \end{aligned}$$

From (3.28) it is clear that $\sigma _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is coercive. Moreover, by the Sobolev embedding, we have that $\sigma _\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is sequentially weakly lower semicontinuous. Then, by the Weierstraß-Tonelli theorem, we can find ${\hat{u}}_\lambda \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} \sigma _\lambda \left( {\hat{u}}_\lambda \right) = \min \left[ \sigma _\lambda (u):u\in W^{1,p}_0(\Omega )\right] . \end{aligned}$$

(3.29)

Since $\tau<q<p$, we have $\sigma _\lambda \left( {\hat{u}}_\lambda \right) <0=\sigma _\lambda (0)$ which implies ${\hat{u}}_\lambda \ne 0$.

From (3.29) we have $\sigma _\lambda '\left( \hat{u}_\lambda \right) =0$, that is,

$$\begin{aligned} \langle A_p \left( {\hat{u}}_\lambda \right) ,h\rangle +\langle A_q\left( {\hat{u}}_\lambda \right) ,h\rangle =\int _{\Omega }g_\lambda \left( x,{\hat{u}}_\lambda \right) h\,dx\quad \text {for all }h\in W^{1,p}_0(\Omega ). \end{aligned}$$

(3.30)

First, we choose $h=-{\hat{u}}_\lambda ^-\in W^{1,p}_0(\Omega )$ in (3.30). Then, by the definition of the truncation in (3.28) we easily see that $\Vert {\hat{u}}_\lambda ^-\Vert ^p \le 0$ and so, ${\hat{u}}_\lambda \ge 0$ with ${\hat{u}}_\lambda \ne 0$.

Next, we choose $h=\left( {\hat{u}}_\lambda -\overline{u}_\lambda \right) ^+\in W^{1,p}_0(\Omega )$ in (3.30) which gives, due to (3.28) and $f\ge 0$,

$$\begin{aligned}&\langle A_p\left( {\hat{u}}_\lambda \right) ,\left( {\hat{u}}_\lambda -\overline{u}_\lambda \right) ^+\rangle +\langle A_q\left( {\hat{u}}_\lambda \right) ,\left( {\hat{u}}_\lambda -\overline{u}_\lambda \right) ^ +\rangle \\&\quad = \int _{\Omega }\lambda a(x) \overline{u}_\lambda ^{\tau -1} \left( {\hat{u}}_\lambda -\overline{u}_\lambda \right) ^+\,dx\\&\quad \le \int _{\Omega }\left[ \lambda {\tilde{u}}_\lambda ^{-\eta } +\lambda a(x) \overline{u}_\lambda ^{\tau -1}+f\left( x,\overline{u}_\lambda \right) \right] \left( {\hat{u}}_\lambda -\overline{u}_\lambda \right) ^+\,dx\\&\quad = \langle A_p\left( \overline{u}_\lambda \right) ,\left( {\hat{u}}_\lambda -\overline{u}_\lambda \right) ^+\rangle +\langle A_q\left( \overline{u}_\lambda \right) ,\left( {\hat{u}}_\lambda -\overline{u}_\lambda \right) ^+\rangle . \end{aligned}$$

This shows that ${\hat{u}}_\lambda \le \overline{u}_\lambda$. We have proved that

$$\begin{aligned} {\hat{u}}_\lambda \in \left[ 0,\overline{u}_\lambda \right] , {\hat{u}}_\lambda \ne 0. \end{aligned}$$

Hence, ${\hat{u}}_\lambda$ is a positive solution of (Q$_\lambda$) and due to Proposition 2.3 we know that ${\hat{u}}_\lambda ={\tilde{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. Therefore, ${\tilde{u}}_\lambda \le \overline{u}_\lambda$ for all $\lambda \in \left( 0,{\hat{\lambda }}\right)$. $\square$

Now we are able to establish the nonemptiness of the set ${\mathcal {L}}$ (being the set of all admissible parameters) determine the regularity of the elements in the solution set ${\mathcal {S}}_\lambda$.

Proposition 3.5

If hypotheses H(a) and H(f) hold, then ${\mathcal {L}}\ne \emptyset$ and, for every $\lambda >0$, ${\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Proof

Let $\lambda \in \left( 0,{\hat{\lambda }}\right)$. From Proposition 3.4 we know that ${\tilde{u}}_\lambda \le \overline{u}_\lambda$. So we can define the truncation $e_\lambda :\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ of the reaction of problem (P$_\lambda$)

$$\begin{aligned}&e_\lambda (x,s)\nonumber \\&= {\left\{ \begin{array}{ll} \lambda \left[ \tilde{u}_\lambda (x)^{-\eta }+a(x)\tilde{u}_\lambda (x)^{\tau -1}\right] +f\left( x,\tilde{u}_\lambda (x)\right) &{}\text {if }s<\tilde{u}_\lambda (x),\\ \lambda \left[ s^{-\eta }+a(x)s^{\tau -1}\right] +f(x,s) &{}\text {if }\tilde{u}_\lambda (x) \le s\le \overline{u}_\lambda (x),\\ \lambda \left[ \overline{u}_\lambda (x)^{-\eta }+a(x)\overline{u}_\lambda (x)^{\tau -1}\right] +f\left( x,\overline{u}_\lambda (x)\right) &{}\text {if }\overline{u}_\lambda (x) <s. \end{array}\right. } \end{aligned}$$

(3.31)

This is a Carathéodory function. We set $E_\lambda (x,s)=\int ^s_0 e_{\lambda }(x,t)\,dt$ and consider the $C^1$-functional $J_\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} J_\lambda (u)=\frac{1}{p} \Vert \nabla u\Vert _p^p +\frac{1}{q} \Vert \nabla u\Vert _q^q-\int _{\Omega }E_\lambda (x,u)\,dx \quad \text {for all }u \in W^{1,p}_0(\Omega ). \end{aligned}$$

From (3.31) we see that $J_\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ is coercive and the Sobolev embedding theorem implies that J is also sequentially weakly lower semicontinuous. Hence, its global minimizer $u_\lambda \in W^{1,p}_0(\Omega )$ exists, that is,

$$\begin{aligned} J_\lambda (u_\lambda )=\min \left[ J_\lambda (u):u\in W^{1,p}_0(\Omega ) \right] . \end{aligned}$$

Hence, $J_\lambda '(u_\lambda )=0$ which means that

$$\begin{aligned} \langle A_p\left( u_\lambda \right) ,h\rangle +\langle A_q\left( u_\lambda \right) ,h\rangle =\int _{\Omega }e_\lambda \left( x,u_\lambda \right) h\,dx \quad \text {for all } h \in W^{1,p}_0(\Omega ). \end{aligned}$$

(3.32)

We choose $h=\left( u_\lambda -\overline{u}_\lambda \right) ^+\in W^{1,p}_0(\Omega )$ in (3.32). Then, by using (3.31) and Propositions 3.4 and 3.3 we obtain

$$\begin{aligned}&\langle A_p\left( u_\lambda \right) ,\left( u_\lambda -\overline{u}_\lambda \right) ^+\rangle +\langle A_q\left( u_\lambda \right) ,\left( u_\lambda -\overline{u}_\lambda \right) ^+\rangle \\&\quad =\int _{\Omega }\left( \lambda \left[ \overline{u}_\lambda ^{-\eta }+a(x)\overline{u}_\lambda ^{\tau -1}\right] +f\left( x,\overline{u}_\lambda \right) \right) \left( u_\lambda -\overline{u}_\lambda \right) ^+\,dx\\&\quad \le \int _{\Omega }\left( \lambda \left[ \tilde{u}_\lambda ^{-\eta }+a(x)\overline{u}_\lambda ^{\tau -1}\right] +f\left( x,\overline{u}_\lambda \right) \right) \left( u_\lambda -\overline{u}_\lambda \right) ^+\,dx\\&\quad =\langle A_p\left( \overline{u}_\lambda \right) ,\left( u_\lambda -\overline{u}_\lambda \right) ^+\rangle +\langle A_q\left( \overline{u}_\lambda \right) ,\left( u_\lambda -\overline{u}_\lambda \right) ^+\rangle . \end{aligned}$$

This shows that $u_\lambda \le \overline{u}_\lambda$.

Next, we choose $h=\left( \tilde{u}_\lambda -u_\lambda \right) ^+\in W^{1,p}_0(\Omega )$ in (3.32). Then, by (3.31) and hypotheses H(a) as well as H(f)(i) it follows

$$\begin{aligned}&\langle A_p \left( u_\lambda \right) ,\left( \tilde{u}_\lambda -u_\lambda \right) ^+\rangle +\langle A_q\left( u_\lambda \right) ,\left( \tilde{u}_\lambda -u_\lambda \right) ^+\rangle \\&\quad =\, \int _{\Omega }\left( \lambda \left[ {\tilde{u}}^{-\eta }+a(x){\tilde{u}}_\lambda ^{\tau -1}\right] +f\left( x,{\tilde{u}}_\lambda \right) \right) \left( {\tilde{u}}_\lambda -u_\lambda \right) ^+\,dx\\&\qquad \ge \int _{\Omega }\lambda {\tilde{u}}_\lambda ^{-\eta } \left( {\tilde{u}}_\lambda -u_\lambda \right) ^+dx\\&\qquad = \langle A_p\left( {\tilde{u}}_\lambda \right) ,\left( {\tilde{u}}_\lambda -u_\lambda \right) ^+\rangle +\langle A_q\left( {\tilde{u}}_\lambda \right) ,\left( {\tilde{u}}_\lambda -u_\lambda \right) ^+\rangle . \end{aligned}$$

Hence, ${\tilde{u}}_\lambda \le u_\lambda$ and so we have proved that $u_\lambda \in \left[ {\tilde{u}}_\lambda , \overline{u}_\lambda \right]$. Then, with view to (3.31) and (3.32), we see that $u_\lambda$ is a positive solution of (P$_\lambda$) for $\lambda \in \left( 0,{\hat{\lambda }}\right)$. In particular, we have

$$\begin{aligned} -\Delta _p u_\lambda (x)-\Delta _qu_\lambda (x)=\lambda u_\lambda (x)^{-\eta }+a_\lambda (x)u_\lambda (x)^{\tau -1}+f(x,u_\lambda (x))\quad \text {for a.a. }x\in \Omega . \end{aligned}$$

The nonlinear regularity theory, see Lieberman [15], and the nonlinear maximum principle, see Pucci–Serrin [29, pp. 111 and 120] imply that $u_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Concluding we can say that $\left( 0,{\hat{\lambda }}\right) \subseteq {\mathcal {L}}$ which means that ${\mathcal {L}}$ is nonempty. Moreover, for all $\lambda >0$, ${\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. $\square$

Reasoning as in the proof of Proposition 3.4 with $\overline{u}_\lambda$ replaced by $u \in {\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$, we obtain the following result.

Proposition 3.6

If hypotheses H(a) and H(f) hold and if $\lambda \in {\mathcal {L}}$, then ${\tilde{u}}_\lambda \le u$ for all $u \in {\mathcal {S}}_\lambda$.

Moreover, the map $\lambda \rightarrow {\tilde{u}}_\lambda$ from $(0,+\infty )$ into $C^1_0(\overline{\Omega })$ exhibits a strong monotonicity property which we will use in the sequel.

Proposition 3.7

If hypotheses H(a) holds and if $0<\lambda <\lambda '$, then ${\tilde{u}}_{\lambda '}-{\tilde{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Proof

Following the proof of Proposition 3.4 we can show that

$$\begin{aligned} {\tilde{u}}_\lambda \le {\tilde{u}}_{\lambda '}. \end{aligned}$$

(3.33)

From (3.33) we have

$$\begin{aligned} -\Delta _p {\tilde{u}}_\lambda -\Delta _q{\tilde{u}}_\lambda&=\lambda a(x) {\tilde{u}}_\lambda ^{\tau -1}\nonumber \\&=\lambda 'a(x){\tilde{u}}_\lambda ^{\tau -1}-\left( \lambda '-\lambda \right) {\tilde{u}}_\lambda ^{\tau -1}\nonumber \\&\le \lambda 'a(x){\tilde{u}}_{\lambda '}^{\tau -1}\nonumber \\&= -\Delta _p {\tilde{u}}_{\lambda '}-\Delta _q{\tilde{u}}_{\lambda '}. \end{aligned}$$

(3.34)

Note that $0\prec \left( \lambda '-\lambda \right) \tilde{u}_\lambda ^{\tau -1}$. So, from (3.34) and Gasiński–Papageorgiou [9, Proposition 3.2], we have

$$\begin{aligned} {\tilde{u}}_{\lambda '}-{\tilde{u}}_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) . \end{aligned}$$

$\square$

Next we are going to show that ${\mathcal {L}}$ is an interval.

Proposition 3.8

If hypotheses H(a) and H(f) hold and if $\lambda \in {\mathcal {L}}$ and $\mu \in (0,\lambda )$, then $\mu \in {\mathcal {L}}$.

Proof

Since $\lambda \in {\mathcal {L}}$ there exists $u_\lambda \in {\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$, see Proposition 3.5. From Propositions 3.4 and 3.7 we have

$$\begin{aligned} {\tilde{u}}_\mu \le u_\lambda . \end{aligned}$$

We introduce the truncation function ${\hat{k}}_\mu :\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} {\hat{k}}_\mu (x,s) = {\left\{ \begin{array}{ll} \mu \left[ {\tilde{u}}_\mu (x)^{-\eta }+a(x)u_\mu (x)^{\tau -1}\right] +f\left( x,u_\mu (x)\right) &{}\text {if }s<{\tilde{u}}_\mu (x),\\ \mu \left[ s^{-\eta }+a(x)s^{\tau -1}\right] +f\left( x,s\right) &{}\text {if } {\tilde{u}}_\mu (x)\le s \le u_\lambda (x),\\ \mu \left[ u_\lambda (x)^{-\eta }+a(x)u_\lambda (x)^{\tau -1}\right] +f\left( x,u_\lambda (x)\right) &{}\text {if }u_\lambda (x)<s, \end{array}\right. } \end{aligned}$$

(3.35)

which is a Carathéodory function. We set $\hat{K}_\mu (x,s)=\int ^s_0 \hat{k}_\mu (x,t)\,dt$ and consider the $C^1$-functional $\hat{\sigma }_\mu :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} {\hat{\sigma }}_\mu (u)=\frac{1}{p}\Vert \nabla u\Vert ^p_p+\frac{1}{q}\Vert \nabla u\Vert _q^q-\int _{\Omega }{\hat{K}}_\mu (x,u)\,dx\quad \text {for all }u \in W^{1,p}_0(\Omega ). \end{aligned}$$

This functional is coercive because of (3.35) and sequentially weakly lower semicontinuous due to the Sobolev embedding theorem. Hence, there exists $u_\mu \in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} {\hat{\sigma }}_\mu (u_\mu )=\inf \left[ {\hat{\sigma }}_\mu (u):W^{1,p}_0(\Omega )\right] . \end{aligned}$$

Therefore, ${\hat{\sigma }}_\mu '(u_\mu )=0$ and so

$$\begin{aligned} \langle A_p\left( u_\mu \right) ,h\rangle +\langle A_q\left( u_\mu \right) ,h\rangle =\int _{\Omega }{\hat{k}}_\mu \left( x,u_\mu \right) h\,dx \end{aligned}$$

(3.36)

for all $h\in W^{1,p}_0(\Omega )$. We first choose $h=\left( u_\mu -u_\lambda \right) ^+\in W^{1,p}_0(\Omega )$ in (3.36). Then, by (3.35), $\mu <\lambda$ and since $u_\lambda \in {\mathcal {S}}_\lambda$, we obtain

$$\begin{aligned}&\langle A_p\left( u_\mu \right) ,\left( u_\mu -u_\lambda \right) ^+\rangle +\langle A_q\left( u_\mu \right) , \left( u_\mu -u_\lambda \right) ^+\rangle \\&\quad =\int _{\Omega }\left[ \mu \left( u_\mu ^{-\eta }+a(x)u_\lambda ^{\tau -1}\right) +f\left( x,u_\lambda \right) \right] \left( u_\mu -u_\lambda \right) ^+\,dx\\&\quad \le \int _{\Omega }\left[ \lambda \left( u_\lambda ^{-\eta }+a(x)u_\lambda ^{\tau -1}\right) +f\left( x,u_\lambda \right) \right] \left( u_\mu -u_\lambda \right) ^+\,dx\\&\quad =\langle A_p\left( u_\lambda \right) , \left( u_\mu -u_\lambda \right) ^+\rangle +\langle A_q\left( u_\lambda \right) ,\left( u_\mu -u_\lambda \right) ^+\rangle . \end{aligned}$$

Hence, $u_\mu \le v_\lambda$. In the same way, choosing $h=\left( {\tilde{u}}_\mu -u_\mu \right) ^+ \in W^{1,p}_0(\Omega )$, we get from (3.35), hypotheses H(a), H(f)(i) and Proposition 2.3 that

$$\begin{aligned}&\langle A_p\left( u_\mu \right) ,\left( {\tilde{u}}_\mu -u_\mu \right) ^+\rangle +\langle A_q\left( u_\mu \right) , \left( {\tilde{u}}_\mu -u_\mu \right) ^+\rangle \\&\quad =\int _{\Omega }\left[ \mu \left( {\tilde{u}}_\mu ^{-\eta }+a(x){\tilde{u}}_\mu ^{\tau -1}\right) +f\left( x,{\tilde{u}}_\mu \right) \right] \left( {\tilde{u}}_\mu -u_\mu \right) ^+ \,dx\\&\qquad \ge \int _{\Omega }\mu {\tilde{u}}_\mu ^{-\eta } \left( {\tilde{u}}_\mu -u_\mu \right) ^+\,dx\\&\qquad = \langle A_p\left( {\tilde{u}}_\mu \right) ,\left( {\tilde{u}}_\mu -u_\mu \right) ^+\rangle +\langle A_q\left( {\tilde{u}}_\mu \right) ,\left( {\tilde{u}}_\mu -u_\mu \right) ^+\rangle . \end{aligned}$$

Thus, ${\tilde{u}}_\mu \le u_\mu$. We have proved that

$$\begin{aligned} u_\mu \in \left[ \tilde{u}_\mu ,u_\lambda \right] . \end{aligned}$$

(3.37)

From (3.37), (3.35) and (3.36) it follows that

$$\begin{aligned} u_\mu \in {\mathcal {S}}_\mu \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) \text { and so }\mu \in {\mathcal {L}}. \end{aligned}$$

$\square$

Now we are going to prove that the solution multifunction $\lambda \rightarrow {\mathcal {S}}_\lambda$ has a kind of weak monotonicity property.

Proposition 3.9

If hypotheses H(a) and H(f) hold and if $\lambda \in {\mathcal {L}}, u_\lambda \in \mathcal {S}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ and $\mu \in (0,\lambda )$, then $\mu \in {\mathcal {L}}$ and there exists $u_\mu \in {\mathcal {S}}_\mu \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ such that

$$\begin{aligned} u_\lambda -u_\mu \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) . \end{aligned}$$

Proof

From Proposition 3.8 and its proof we know that $\mu \in {\mathcal {L}}$ and that we can find $u_\mu \in {\mathcal {S}}_\mu \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ such that $u_\mu \le v_\lambda$. Let $\rho =\Vert u_\lambda \Vert _\infty$ and let $\hat{\xi }_\rho >0$ be as postulated by hypothesis H(f)(v). Using $u_\mu \in {\mathcal {S}}_{\mu }$, hypotheses H(a), H(f)(v) and recalling that $\mu <\lambda$ we obtain

$$\begin{aligned}&-\Delta _p u_\mu -\Delta _q u_\mu +{\hat{\xi }}_\rho u_\mu ^{p-1}-\mu u_\mu ^{-\eta }\nonumber \\&\quad =\mu a(x) u_\mu ^{\tau -1}+f(x,u_\mu )+{\hat{\xi }}_\rho u_\mu ^{p-1}\nonumber \\&\quad =\lambda a(x) u_\mu ^{\tau -1} +f(x,u_\mu )+{\hat{\xi }}_\rho u_\mu ^{p-1} -(\lambda -\mu )a(x)u_\mu ^{\tau -1}\nonumber \\&\quad \le \lambda a(x) u_\lambda ^{\tau -1} +f(x,u_\lambda )+{\hat{\xi }}_\rho u_\lambda ^{p-1}\nonumber \\&\quad \le -\Delta _p u_\lambda -\Delta _q u_\lambda +{\hat{\xi }}_\rho u_\lambda ^{p-1}-\mu u_\lambda ^{-\eta }. \end{aligned}$$

(3.38)

We have

$$\begin{aligned} 0\prec (\lambda -\mu )a(x)u_\mu ^{\tau -1}. \end{aligned}$$

Therefore, from (3.38) and Papageorgiou–Smyrlis [18, Proposition 4], see also Proposition 7 in Papageorgiou–Rădulescu–Repovš [27, Proposition 3.2], we have

$$\begin{aligned} u_\lambda -u_\mu \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) . \end{aligned}$$

$\square$

Let $\lambda ^*=\sup {\mathcal {L}}$.

Proposition 3.10

If hypotheses H(a) and H(f) hold, then $\lambda ^*<\infty$.

Proof

From hypotheses H(a) and H(f) we can find ${\tilde{\lambda }}>0$ such that

$$\begin{aligned} {\tilde{\lambda }} a(x) s^{\tau -1}+f(x,s) \ge s^{p-1} \quad \text {for a.a. }x\in \Omega \text { and for all }s\ge 0. \end{aligned}$$

(3.39)

Let $\lambda >{\tilde{\lambda }}$ and suppose that $\lambda \in {\mathcal {L}}$. Then we can find $u_\lambda \in {\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. Consider a domain $\Omega _0\subset \subset \Omega$, that is, $\Omega _0\subseteq \Omega$ and $\overline{\Omega }_0\subseteq \Omega$, with a $C^2$-boundary $\partial \Omega _0$ and let $m_0=\min _{\overline{\Omega }_0}u_\lambda >0$. We set

$$\begin{aligned} m_0^\delta =m_0+\delta \quad \text {with}\quad \delta \in (0,1]. \end{aligned}$$

Let $\rho =\max \{ \Vert u_\lambda \Vert _\infty , m_0^1\}$ and let ${\hat{\xi }}_\rho >0$ be as postulated by hypothesis H(f)(v). Applying (3.39), hypothesis H(f)(v) and recalling that $u_\lambda \in \mathcal {S}_\lambda$ as well as ${\tilde{\lambda }}<\lambda$, we obtain

$$\begin{aligned}&-\Delta _p m_0^\delta -\Delta _q m_0^\delta +{\hat{\xi }}_\rho \left( m_0^\delta \right) ^{p-1}-{\tilde{\lambda }} \left( m_0^\delta \right) ^{-\eta }\nonumber \\&\quad \le {\hat{\xi }}_\rho m_0^{p-1}+\chi (\delta ) \quad \text {with } \chi (\delta )\rightarrow 0^+\text { as }\delta \rightarrow 0^+\nonumber \\&\quad \le \left[ {\hat{\xi }}_\rho +1\right] m_0^{p-1}+\chi (\delta )\nonumber \\&\quad \le {\tilde{\lambda }} a(x) m_0^{\tau -1}+f(x,u_0)+{\hat{\xi }}_\rho m_0^{p-1}+\chi (\delta )\nonumber \\&\quad =\lambda a(x) m_0^{\tau -1}+f(x,m_0)+{\hat{\xi }}_\rho m_0^{p-1} -\left( \lambda -{\tilde{\lambda }}\right) m_0^{\tau -1} +\chi (\delta )\nonumber \\&\quad \le \lambda a(x) m_0^{\tau -1} +f(x,m_0)+{\hat{\xi }}_\rho m_0^{p-1} \quad \text {for }\delta \in (0,1]\text { small enough}\nonumber \\&\quad \le \lambda a(x) u_\lambda ^{\tau -1}+f(x,u_\lambda ) +{\hat{\xi }}_\rho u_\lambda ^{p-1}\nonumber \\&\quad =-\Delta _p u_\lambda -\Delta _q u_\lambda +{\hat{\xi }}_\rho u_\lambda ^{p-1} -\lambda u_\lambda ^{-\eta }\nonumber \\&\quad \le -\Delta _p u_\lambda -\Delta _q u_\lambda +{\hat{\xi }}_\rho u_\lambda ^{p-1}-{\tilde{\lambda }} u_\lambda ^{-\eta }\quad \text {for a.\,a.\,}x\in \Omega _0. \end{aligned}$$

(3.40)

From (3.40) and Papageorgiou–Rădulescu–Repovš [27, Proposition 6] we know that

$$\begin{aligned} u_\lambda -m_0^\delta \in D_+ \quad \text {for }\delta \in (0,1] \text { small enough}, \end{aligned}$$

a contradiction. Therefore, $\lambda ^*\le {\tilde{\lambda }}<\infty$. $\square$

Proposition 3.11

If hypotheses H(a) and H(f) hold and if $\lambda \in (0,\lambda ^*)$, then problem (P$_\lambda$) has at least two positive solutions

$$\begin{aligned} u_0, {\hat{u}} \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) \text { with }u_0 \le {\hat{u}} \text { and }u_0\ne \hat{u}. \end{aligned}$$

Proof

Let $\vartheta \in \left( \lambda ,\lambda ^*\right)$. According to Proposition 3.9 we can find $u_\vartheta \in {\mathcal {S}}_\vartheta \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ and $u_0\in {\mathcal {S}}_\lambda \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ such that

$$\begin{aligned} u_\vartheta -u_0\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) . \end{aligned}$$

Recall that ${\tilde{u}}_\lambda \le u_0$, see Proposition 3.4. Hence $u_0^{-\eta } \in L^{s}(\Omega )$ for all $s>N$, see (3.1).

We introduce the Carathéodory function $i_\lambda :\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} i_\lambda (x,s)= {\left\{ \begin{array}{ll} \lambda \left[ u_0(x)^{-\eta }+a(x)u_0(x)^{\tau -1}\right] +f(x,u_0(x))&{}\text {if }s\le u_0(x),\\ \lambda \left[ s^{-\eta }+a(x)s^{\tau -1}\right] +f(x,s)&{}\text {if }u_0(x)<s. \end{array}\right. } \end{aligned}$$

(3.41)

We set $I_\lambda (x,s)=\int ^s_0 i_\lambda (x,t)\,dt$ and consider the $C^1$-functional $w_\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} w_\lambda (u)=\frac{1}{p} \Vert \nabla u \Vert _p^p+\frac{1}{q}\Vert \nabla u\Vert _q^q-\int _{\Omega }I_\lambda (x,u)\,dx\quad \text {for all }u\in W^{1,p}_0(\Omega ). \end{aligned}$$

Using (3.41) and the nonlinear regularity theory along with the nonlinear maximum principle we can easily check that

$$\begin{aligned} K_{w_\lambda }\subseteq [u_0)\cap {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) . \end{aligned}$$

(3.42)

Then, from (3.41) and (3.42) it follows that, without any loss of generality, we may assume

$$\begin{aligned} K_{w_\lambda }\cap \left[ u_0,u_\vartheta \right] =\{u_0\}. \end{aligned}$$

(3.43)

Otherwise, on account of (3.41) and (3.42), we see that we already have a second positive smooth solution of (P$_\lambda$) distinct and larger than $u_0$.

We introduce the following truncation of $i_\lambda (x,\cdot )$, namely, $\hat{i}_\lambda :\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} {\hat{i}}_\lambda (x,s)= {\left\{ \begin{array}{ll} i_\lambda (x,s) &{}\text {if }s\le u_\vartheta (x),\\ i_\lambda (x,u_\vartheta (x)) &{}\text {if }u_\vartheta (x)<s, \end{array}\right. } \end{aligned}$$

(3.44)

which is a Carathéodory function. We set ${\hat{I}}_\lambda (x,s)=\int ^s_0 {\hat{i}}_\lambda (x,t)\,dt$ and consider the $C^1$-functional ${\hat{w}}_\lambda :W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} {\hat{w}}_\lambda (u)=\frac{1}{p}\Vert \nabla u\Vert _p^p+\frac{1}{q}\Vert \nabla u\Vert _q^q-\int _{\Omega }{\hat{I}}_\lambda (x,u)\,dx\quad \text {for all }u\in W^{1,p}_0(\Omega ). \end{aligned}$$

From (3.41) and (3.44) it is clear that ${\hat{w}}_\lambda$ is coercive and due to the Sobolev embedding theorem we know that ${\hat{w}}_\lambda$ is also sequentially weakly lower semicontinuous. Hence, we find ${\hat{u}}_0\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} {\hat{w}}_\lambda \left( {\hat{u}}_0\right) =\min \left[ {\hat{w}}_\lambda (u):u\in W^{1,p}_0(\Omega )\right] . \end{aligned}$$

(3.45)

It is easy to see, using (3.44), that

$$\begin{aligned} K_{{\hat{w}}_\lambda }\subseteq \left[ u_0,u_\vartheta \right] \cap {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) \end{aligned}$$

(3.46)

and

$$\begin{aligned} {\hat{w}}_\lambda \big |_{\left[ 0,u_\vartheta \right] } =w_\lambda \big |_{\left[ 0,u_\vartheta \right] }, \quad {\hat{w}}'_\lambda \big |_{\left[ 0,u_\vartheta \right] } =w'_\lambda \big |_{\left[ 0,u_\vartheta \right] }. \end{aligned}$$

(3.47)

From (3.45) we have ${\hat{u}}_0\in K_{{\hat{w}}'_\lambda }$ which by (3.43), (3.46) and (3.47) implies that ${\hat{u}}_0=u_0$.

Recall that $u_\vartheta -u_0\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. So, on account of (3.47), we have that $u_0$ is a local $C^1_0(\overline{\Omega })$-minimizer of $w_\lambda$ and then $u_0$ is also a local $W^{1,p}_0(\Omega )$-minimizer of $w_\lambda$, see, for example Gasiński–Papageorgiou [7].

We may assume that $K_{w_\lambda }$ is finite, otherwise, we see from (3.42) that we already have an infinite number of positive smooth solutions of (P$_\lambda$) larger than $u_0$ and so we are done. From Papageorgiou–Rădulescu–Repovš [24, Theorem 5.7.6, p. 449] we find $\rho \in (0,1)$ small enough such that

$$\begin{aligned} w_\lambda (u_0)<\inf \left[ w_\lambda (u):\Vert u-u_0\Vert =\rho \right] =m_\lambda . \end{aligned}$$

(3.48)

If $u\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$, then by hypothesis H(f)(ii) we have

$$\begin{aligned} w_\lambda (tu)\rightarrow -\infty \quad \text {as }t\rightarrow +\infty . \end{aligned}$$

(3.49)

Moreover, reasoning as in the proof of Proposition 3.1, we show that

$$\begin{aligned} w_\lambda \text { satisfies the C-condition}, \end{aligned}$$

(3.50)

see also (3.41). Then, (3.48), (3.49) and (3.50) permit the use of the mountain pass theorem. So we can find ${\hat{u}}\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} {\hat{u}}\in K_{w_\lambda }\subseteq [u_0)\cap {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right) , \quad m_\lambda \le w_\lambda \left( {\hat{u}}\right) . \end{aligned}$$

(3.51)

From (3.51), (3.48) and (3.41) it follows that

$$\begin{aligned} {\hat{u}}\in {\mathcal {S}}_\lambda , \quad u_0\le {\hat{u}}, \quad u_0\ne \hat{u}. \end{aligned}$$

$\square$

Remark 3.12

If $1<q = 2\le \lambda <p$, then, using the tangency principle of Pucci–Serrin [29, p. 35] we can say that ${\hat{u}}-u_0\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Proposition 3.13

If hypotheses H(a) and H(f) hold, then $\lambda ^*\in {\mathcal {L}}$.

Proof

Let $\lambda _n\nearrow \lambda ^*$. With ${\hat{u}}_{n+1}\in {\mathcal {S}}_{\lambda _{n+1}}\subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ we introduce the following Carathéodory function (recall that ${\tilde{u}}_{\lambda _1}\le {\tilde{u}}_{\lambda _n}\le u$ for all $u\in {\mathcal {S}}_{\lambda _n}$ and for all $n\in \mathbb {N}$, see Propositions 3.4 and 3.7)

$$\begin{aligned}&{\tilde{t}}_n(x,s)=\\&{\left\{ \begin{array}{ll} \lambda _n\left[ {\tilde{u}}_{\lambda _1}(x)^{-\eta }+a(x){\tilde{u}}_{\lambda _1}(x)^{\tau -1} \right] +f\left( x,{\tilde{u}}_{\lambda _1}(x)\right) &{}\text {if } s<{\tilde{u}}_{\lambda _1}(x)\\ \lambda _n\left[ s^{-\eta }+a(x)s^{\tau -1}\right] +f\left( x,s\right) &{}\text {if } {\tilde{u}}_{\lambda _1}(x)\le s \le {\hat{u}}_{n+1}(x)\\ \lambda _n\left[ {\hat{u}}_{n+1}(x)^{-\eta }+a(x){\hat{u}}_{n+1}(x)^{\tau -1}\right] +f\left( x,{\hat{u}}_{n+1}(x)\right) &{}\text {if } {\hat{u}}_{n+1}(x)<s. \end{array}\right. } \end{aligned}$$

Let ${\tilde{T}}_n(x,s)=\int ^s_0 {\tilde{t}}_n(x,t)\,dt$ and consider the $C^1$-functional ${\tilde{I}}_n:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} {\tilde{I}}_n(u)= \frac{1}{p}\Vert \nabla u\Vert _p^p+\frac{1}{q}\Vert \nabla u\Vert _q^q-\int _{\Omega }{\tilde{T}}_n(x,u)\,dx\quad \text {for all }u \in W^{1,p}_0(\Omega ). \end{aligned}$$

Applying the direct method of the calculus of variations, see the definition of the truncation ${\tilde{t}}_n:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$, we can find $u_n\in W^{1,p}_0(\Omega )$ such that

$$\begin{aligned} {\tilde{I}}_n(u_n)=\min \left[ {\tilde{I}}_n(u):u\in W^{1,p}_0(\Omega )\right] . \end{aligned}$$

Hence, $\tilde{I}_n'(u_n)=0$ and so $u_n \in \left[ \tilde{u}_{\lambda _1}, \hat{u}_{n+1}\right] \cap {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$, see the definition of $\tilde{t}_n$. Moreover, $u_n\in \mathcal {S}_{\lambda _n}\subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. From Proposition 2.3 we know that

$$\begin{aligned} {\tilde{I}}_n(u_n)\le {\tilde{I}}_n\left( {\tilde{u}}_{\lambda _1}\right) <0. \end{aligned}$$

Now we introduce the truncation function ${\hat{t}}_n:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} {\hat{t}}_n(x,s)= {\left\{ \begin{array}{ll} \lambda _n\left[ {\tilde{u}}_{\lambda _1}(x)^{-\eta }+a(x){\tilde{u}}_{\lambda _1} (x)^{\tau -1}\right] +f\left( x,{\tilde{u}}_{\lambda _1}(x)\right) &{}\text {if } s\le {\tilde{u}}_{\lambda _1}(x),\\ \lambda _n\left[ s^{-\eta }+a(x)s^{\tau -1}\right] +f(x,s)&{}\text {if } {\tilde{u}}_{\lambda _1}(x)<s. \end{array}\right. } \end{aligned}$$

(3.52)

We set ${\hat{T}}_n(x,s)=\int ^s_0 {\hat{t}}_n(x,t)\,dt$ and consider the $C^1$-functional ${\hat{I}}_n:W^{1,p}_0(\Omega )\rightarrow \mathbb {R}$ defined by

$$\begin{aligned} {\hat{I}}_n(u)=\frac{1}{p}\Vert \nabla u\Vert _p^p+\frac{1}{q}\Vert \nabla u\Vert _q^q-\int _{\Omega }{\hat{T}}_n(x,u)\,dx\quad \text {for all }u\in W^{1,p}_0(\Omega ). \end{aligned}$$

It is clear from the definition of the truncation ${\tilde{t}}_n:\Omega \times \mathbb {R}\rightarrow \mathbb {R}$ and (3.52) that

$$\begin{aligned} {\hat{I}}_n\big |_{\left[ 0,{\hat{u}}_{n+1}\right] } ={\tilde{I}}_n\big |_{\left[ 0,{\hat{u}}_{n+1}\right] } \quad \text {and}\quad {\hat{I}}'_n\big |_{\left[ 0,{\hat{u}}_{n+1}\right] } ={\tilde{I}}'_n\big |_{\left[ 0,{\hat{u}}_{n+1}\right] }. \end{aligned}$$

Then from the first part of the proof, we see that we can find a sequence $u_n\in {\mathcal {S}}_{\lambda _n}\subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$, $n\in \mathbb {N}$, such that

$$\begin{aligned} {\hat{I}}_{n}(u_n)<0\quad \text {for all }n\in \mathbb {N}. \end{aligned}$$

(3.53)

Moreover we have

$$\begin{aligned} \langle {\hat{I}}_n'(u_n),h\rangle =0\quad \text {for all }h\in W^{1,p}_0(\Omega )\text { and for all }n\in \mathbb {N}. \end{aligned}$$

(3.54)

From (3.53) and (3.54), reasoning as in the proof of Proposition 3.1, we show that

$$\begin{aligned} \{u_n\}_{n\ge 1} \subseteq W^{1,p}_0(\Omega ) \text { is bounded}. \end{aligned}$$

So we may assume that

$$\begin{aligned} u_n\overset{{{\,\mathrm{w}\,}}}{\rightarrow }u^* \text { in }W^{1,p}_0(\Omega )\quad \text {and}\quad u_n\rightarrow u^*\text { in }L^{r}(\Omega ). \end{aligned}$$

As before, see the proof of Proposition 3.1, using Proposition 2.1 we show that

$$\begin{aligned} u_n\rightarrow u^* \text { in }W^{1,p}_0(\Omega ). \end{aligned}$$

Then $u^* \in {\mathcal {S}}_{\lambda ^*} \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$, recall that ${\tilde{u}}_{\lambda _1} \le u_n$ for all $n\in \mathbb {N}$. This shows that $\lambda ^*\in {\mathcal {L}}$. $\square$

According to Proposition 3.13 we have

$$\begin{aligned} {\mathcal {L}}=(0,\lambda ^*]. \end{aligned}$$

The set ${\mathcal {S}}_\lambda$ is downward directed, see Papageorgiou–Rădulescu–Repovš [27, Proposition 18] that is, if $u, {\hat{u}}\in {\mathcal {S}}_\lambda$, we can find ${\tilde{u}}\in {\mathcal {S}}_\lambda$ such that ${\tilde{u}} \le u$ and ${\tilde{u}}\le {\hat{u}}$. Using this fact we can show that, for every $\lambda \in {\mathcal {L}}$, problem (P$_\lambda$) has a smallest positive solution.

Proposition 3.14

If hypotheses H(a) and H(f) hold and if $\lambda \in {\mathcal {L}}=(0,\lambda ^*]$, then problem (P$_\lambda$) has a smallest positive solution $u_\lambda ^*\in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$.

Proof

Applying Lemma 3.10 of Hu–Papageorgiou [12, p. 178] we can find a decreasing sequence $\{u_n\}_{n \ge 1}\subseteq {\mathcal {S}}_\lambda$ such that

$$\begin{aligned} \inf _{n\ge 1} u_n=\inf {\mathcal {S}}_\lambda . \end{aligned}$$

It is clear that $\{u_n\}_{n\ge 1}\subseteq W^{1,p}_0(\Omega )$ is bounded. Then, applying Proposition 2.1, we obtain

$$\begin{aligned} u_n\rightarrow u^*_\lambda \text { in }W^{1,p}_0(\Omega ). \end{aligned}$$

Since ${\tilde{u}}_\lambda \le u_n$ for all $n\in \mathbb {N}$ it holds $u^*_\lambda \in {\mathcal {S}}_\lambda$ and $u^*_\lambda =\inf {\mathcal {S}}_\lambda$. $\square$

We examine the map $\lambda \rightarrow u^*_\lambda$ from ${\mathcal {L}}$ into $C^1_0(\overline{\Omega })$.

Proposition 3.15

If hypotheses H(a) and H(f) hold, then the map $\lambda \rightarrow u^*_\lambda$ from ${\mathcal {L}}$ into $C^1_0(\overline{\Omega })$ is

• (a) strictly increasing, that is, $0<\mu <\lambda \le \lambda ^*$ implies $u^*_\lambda -u^*_\mu \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$;

• (b) left continuous.

Proof

(a) Let $0<\mu <\lambda \le \lambda ^*$ and let $u^*_\lambda \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ be the minimal positive solution of problem (P$_\lambda$), see Proposition 3.14. According to Proposition 3.9 we can find $u_\mu \in {\mathcal {S}}_\mu \subseteq {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ such that $u^*_\lambda -u^*_\mu \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$. Since $u^*_\mu \le u_\mu$ we have $u^*_\lambda -u^*_\mu \in {{\,\mathrm{int}\,}}\left( C^1_0(\overline{\Omega })_+\right)$ and so, we have proved that $\lambda \rightarrow u^*_\lambda$ is strictly increasing.

(b) Let $\{\lambda _n\}_{n \ge 1}\subseteq \mathcal {L}=(0,\lambda ^*]$ be such that $\lambda _n \nearrow \lambda$ as $n\rightarrow \infty$. We have

$$\begin{aligned} {\tilde{u}}_{\lambda _1} \le u^*_{\lambda _1} \le u^*_{\lambda _n}\le u^*_{\lambda ^*} \quad \text {for all }n \in \mathbb {N}. \end{aligned}$$

Thus,

$$\begin{aligned} \{u^*_{\lambda _n}\}_{n\ge 1}\subseteq W^{1,p}_0(\Omega ) \text { is bounded} \end{aligned}$$

and so

$$\begin{aligned} \{u^*_{\lambda _n}\}_{n\ge 1}\subseteq L^{\infty }(\Omega )\text { is bounded}, \end{aligned}$$

see Guedda–Véron [10, Proposition 1.3]. Therefore, we can find $\beta \in (0,1)$ and $c_{19}>0$ such that

$$\begin{aligned} u^*_{\lambda _n} \in C^{1,\beta }_0(\overline{\Omega })\quad \text {and}\quad \Vert u^*_{\lambda _n}\Vert _{C^{1,\beta }_0(\overline{\Omega })}\le c_{19} \quad \text {for all }n\in \mathbb {N}, \end{aligned}$$

see Lieberman [15]. The compact embedding of $C^{1,\beta }_0(\overline{\Omega })$ into $C^{1}_0(\overline{\Omega })$ and the monotonicity of $\{u^*_{\lambda _n}\}_{n\ge 1}$, see part (a), imply that

$$\begin{aligned} u^*_{\lambda _n}\rightarrow \hat{u}^*_{\lambda } \quad \text {in }C^{1}_0(\overline{\Omega }). \end{aligned}$$

(3.55)

If ${\hat{u}}^*_\lambda \ne u^*_\lambda$, then there exists $x_0\in \Omega$ such that

$$\begin{aligned} u^*_\lambda (x_0)<\hat{u}^*_\lambda (x_0) \quad \text {for all }n\in \mathbb {N}. \end{aligned}$$

From (3.55) we then conclude that

$$\begin{aligned} u^*_\lambda (x_0)<\hat{u}^*_{\lambda _n}(x_0)\quad \text {for all }n\in \mathbb {N}, \end{aligned}$$

which contradicts part (a). Therefore, ${\hat{u}}^*_\lambda = u^*_\lambda$ and so we have proved the left continuity of $\lambda \rightarrow u^*_\lambda$. $\square$