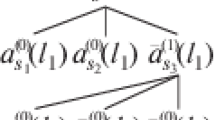Abstract
Consider the cubic nonlinear Schrödinger equation set on a d-dimensional torus, with data whose Fourier coefficients have phases which are uniformly distributed and independent. We show that, on average, the evolution of the moduli of the Fourier coefficients is governed by the so-called wave kinetic equation, predicted in wave turbulence theory, on a nontrivial timescale.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 The Kinetic equation
The central theme in the theory of non-equilibrium statistical physics of interacting particles is the derivation of a kinetic equation that describes the distribution of particles in phase space. The main example here is Boltzmann’s kinetic theory: rather than looking at the individual trajectories of N-point particles following \(N-\)body Newtonian dynamics, Boltzmann derived a kinetic equation that described the effective dynamics of the distribution function in a certain large-particle limit (so-called the Boltzmann–Grad limit).
A parallel kinetic theory for waves, being as fundamental as particles, was proposed by physicists in the past century. Much like the Boltzmann theory, the aim is to understand the effective behavior and energy-dynamics of systems where many waves interact nonlinearly according to time-reversible dispersive or wave equations. The theory predicts that the macroscopic behavior of such nonlinear wave systems is described by a wave kinetic equation that gives the average distribution of energy among the available wave numbers (frequencies). Of course, the shape of this kinetic equation depends directly on the particular dispersive system/PDE that describes the reversible microscopic dynamics.
The aim of this work is to start the rigorous investigation of such passage from a reversible nonlinear dispersive PDE to an irreversible kinetic equation that describes its effective dynamics. For this, we consider the cubic nonlinear Schrödinger equations on a generic torus of size L (with periodic boundary conditions) and with a parameter \(\lambda >0\) quantifying the importance of nonlinear effects (or equivalently via scaling, the size of the initial datum):
The spatial dimension is \(d \ge 3\). Here, and throughout the paper, we denote
where \(\beta \mathrel {\mathop :}=(\beta _1,\ldots ,\beta _d)\in [1,2]^d\), and we denote \({\mathbb {Z}}_L^d \mathrel {\mathop :}=\frac{1}{L} {\mathbb {Z}}^d\), the dual space to \({\mathbb {T}}_L^d\).
Typically in this theory, the initial data are randomly distributed in an appropriate fashion. For us, we consider random initial data of the form
for some nice (smooth and localized) deterministic function \(\phi :{\mathbb {R}}^d \rightarrow [0, \infty )\). The phases \(\vartheta _k(\omega )\) are independent random variables, uniformly distributed on [0, 1]. Notice that the normalization of the Fourier transform is chosen so that
Filtering by the linear group and expanding in Fourier series, we write
The main conjecture of wave turbulence theory is that as \(L \rightarrow \infty \) (large box limit) and \(\frac{\lambda ^2}{L^d} \rightarrow 0\) (weakly nonlinear limit), the quantity
converges to a solution of a kinetic equation. More precisely, it is conjectured that, as \(L\rightarrow \infty \), \(t\rightarrow \infty \) and \(\frac{\lambda ^2}{L^d} \rightarrow 0\), then \(\rho ^L_k(t) \sim \rho (t,k)\), where \(\rho : {\mathbb {R}}\times {\mathbb {R}}^d\rightarrow {\mathbb {R}}_+\) satisfies the wave kinetic equation
where \(\tau \sim \left( \frac{L^{d}}{\lambda ^2}\right) ^{2}\), we introduced the convention \(k_0=k\) and the notation
and finally \(\delta (\Sigma ) \delta (\Omega )\) is to be understood in the sense of distributions: \(\delta (\Sigma )\) is just the convolution integral over \(k_1-k_2+k_3=k\), whereas \(\delta (\Omega =0):=\lim _{\epsilon \rightarrow 0}\int \varphi (\frac{\Omega }{\epsilon }) dk_1 dk_2 dk_3\) for some \(\varphi \in C_c^\infty ({\mathbb {R}})\) with \(\int \varphi =1\). Note that this is absolutely continuous to the surface measure through the formula \(\delta (\Omega ) = \frac{1}{|\nabla \Omega |} d\mu _\Omega \), with \(d \mu _\Omega \) being the surface measures on \(\{ \Omega = 0\}\).
1.2 Background
In the physics literature, the wave kinetic Eq. (WKE) was first derived by Peierls [33] in his investigations of solid state physics; it was discovered again by Hasselmann [23, 24] in his work on the energy spectrum of water waves. The subject was revived and systematically investigated by Zakharov and his collaborators [38], particularly after the discovery of special power-type stationary solutions for the kinetic equation that serve as analogs of the Kolmogorov spectra of hydrodynamic turbulence. These so-called Kolmogorov–Zakharov spectra predict steady states of the corresponding microscopic system (possibly with forcing and dissipation at well-separated extreme scales), where the energy cascades at a constant flux through the (intermediate) frequency scales. Nowadays, wave turbulence is a vibrant area of research in nonlinear wave theory with important practical applications in several areas including oceanography and plasma physics, to mention a few. We refer to [31, 32] for recent reviews.
The analysis of (WKE) is full of very interesting questions, see [16, 22, 34] for recent developments, but we will focus here on the problem of its rigorous derivation. Several partial or heuristic derivations have been put forward for (WKE), or the closely related quantum Boltzmann equations [1,2,3, 10, 13, 17, 28, 30, 36]. However, to the best of our knowledge, there is no rigorous mathematical statement on the derivation of (WKE) from random data. The closest attempt in this direction is due to Lukkarinen and Spohn [29], who studied the large box limit for the discrete nonlinear Schrödinger equation at statistical equilibrium (corresponding to a stationary solution to (WKE)).
In preparation for such a study, one can first try to understand the large box and weakly nonlinear limit of (NLS) without assuming any randomness in the data. In the case where (NLS) is set on a rational torus, it is possible to extract a governing equation by retaining only exact resonances [6, 18, 20, 21]. The limiting equation is then Hamiltonian and dictates the behavior of the microscopic system (NLS on \({\mathbb {T}}^d_L\)) on the timescales \(L^2/\lambda ^2\) (up to a log loss for \(d=2\)) and for sufficiently small \(\lambda \). It is worth mentioning that such a result is not possible if the equation is set on generic tori, since most of the exact resonances are destroyed there.
Finally, we point out that there are very few instances where the derivation of kinetic equations has been done rigorously. The fundamental result of Lanford [27], later clarified in [19], deals with the N-body Newtonian dynamics, from which emerges, in the Grad limit, the Boltzmann equation. This can be understood as a classical analog of the rigorous derivation on (WKE). Another instance of such success was the case of random linear Schrödinger operators (Anderson’s model) [12, 14, 15, 35]. This can be understood as a linear analog of the problem of rigorously deriving (WKE).
1.3 The difficulties of the problem
There are several difficulties in proving the validity of (WKE) which we now enumerate:
-
(a)
The textbook derivation of the wave kinetic equation is done under the assumption that the independence of the data propagates for all time. This assumption cannot be verified for any nonlinear model. A way around this difficulty is to Taylor expand the profile \(a_k\) in terms of the initial data. Such an expansion can be represented by Feynman trees, and permits us to utilize the statistical independence of the data in computing the expected value of \(|a_k|^2\). Moreover one needs to control the errors in such an expansion to derive the kinetic equation (WKE). These calculations are presented in Sects. 4 and 5.
-
(b)
The wave kinetic equation induces an O(1) change on its initial configuration at a timescale of \(\tau \). Thus we need to establish that for solutions of (NLS), the expansion mentioned above converge up to time \(\tau \). This requires a local existence result on a timescale which is several orders of magnitude longer than what is known. This shortcoming is a main reason why our argument cannot reach the kinetic timescale \(\tau \), and we have to contend with a derivation over timescales where the kinetic equation only affects a relatively small change on the initial distribution, and as such coincides (up to negligible errors) with its first time-iterate.
Therefore, a pressing issue is to increase the length of the time interval [0, T], over which the Taylor expansion gives a good representation of solutions to the nonlinear problem. For deterministic data, the best known results that give effective bounds in terms of L come from our previous work [6] which gives a description of the solution up to times \(\sim L^2/\lambda ^2\) (up to a \(\log L\) loss for \(d=2\)) and for \(\lambda \ll 1\). Such timescale would be very short for our purposes.
To increase T, we have to rely on the randomness of the initial data. Roughly speaking, for a random field that is normalized to 1 in \(L^2({\mathbb {T}}^d_L)\), its \(L^\infty \) norm can be heuristically bounded on average by \(L^{-d/2}\). Therefore, regarding the nonlinearity \(\lambda ^{2} |u|^{2}u\) as a nonlinear potential Vu with \(V=\lambda ^{2}|u|^{2}\) and \(\Vert V\Vert _{L^\infty }\lesssim \lambda ^{2}L^{-d}\), one would hope that this should get a convergent expansion on an interval [0, T] provided that \(T \lambda ^{2}L^{-d} \ll 1\), which amounts to \(T\le \sqrt{\tau }\). This is the target in this manuscript.
The heuristic presented above can be implemented by relying on Khinchine-type improvements to the Strichartz norms of a linear solution \(e^{it\Delta _\beta } u_{0}\) with random initial data \(u_{0}\). Similar improvements have been used to lower the regularity threshold for well-posedness of nonlinear dispersive PDE. Here, the aim is to prolong the existence time and improve the Taylor approximation. The randomness gives us better control on the size of the linear solution over the interval [0, T], while an improved deterministic Strichartz estimate for \(\Vert e^{it\Delta _\beta }\psi \Vert _{L^p([0,T]\times {\mathbb {T}}^d)}\) with \(\psi \in L^2({\mathbb {T}}^d)\), allows us to maintain the random improvement for the nonlinear problem. The genericity of the \((\beta _i)\) is crucial (as was first observed in [11]), and allows us to go beyond the limiting \(T^{1/p}\) growth that occurs on the rational torus. Unfortunately, the available estimates here (including those in [11]) are not optimal for some ranges of the parameters \(\lambda \) and L, which is why, in \(d=3\), our result in Theorem 1.1 below falls short of the timescale \(\sqrt{\tau }\sim L^3/\lambda \).
-
(c)
To derive the kinetic equation in the large box limit, using the expansion for \(\rho ^L_k(t) = {\mathbb {E}} |a_k(t)|^2\), one has to prove equidistribution theorems for the quasi-resonances over a very fine scale, i.e., \(T^{-1}\). Since T could be \(\gg L^2\), such scales are much finer than the any equidistribution scale on the rational torus. Again, here the genericity of the \((\beta _i)\) is crucial. For this we use and extend a recent result of Bourgain on pair correlation for irrational quadratic forms [5].
1.4 The main result
Precise statements of our results in arbitrary dimensions \(d\ge 3\) will be given in Sect. 2. Those statements depend on several parameters coming from equidistribution of lattice points and Strichartz estimates. For the purposes of this introductory section, we present a less general theorem without the explicit appearance of these parameters.
Theorem 1.1
Consider the cubic (NLS) on the three-dimensional torus \({\mathbb {T}}^3_L\). Assume that the initial data are chosen randomly as in (1.1). There exists \(\delta >0\) such that the following holds for L sufficiently large and \(L^{-A}\le \lambda \le L^B\) (for positive A and B):
where \(\tau =\frac{1}{2}\left( \frac{L^{3}}{\lambda ^2}\right) ^{2}\) and \(T\sim \frac{L^{3-\gamma }}{\lambda ^2}\), for some \(0<\gamma <1\) stated explicitly in Theorem 2.2.
We note that the right-hand side of (1.3) is nothing but the first time-iterate of the wave kinetic Eq. (WKE) with initial data \(\phi \) (cf. (1.1)) which coincides (up to the error term in (1.3)) with the exact solution of the (WKE) over long times scales, but shorter than the kinetic timescale \(\tau \).
The proof this theorem can be split into three components:
-
(1)
Section 4: Feynman tree representation. In this section we derive the Taylor expansion of the nonlinear solution in terms of the initial data. Roughly speaking, we write the Fourier modes of the nonlinear solution \(a_k(t)\) (see (1.2)) as follows:
$$\begin{aligned} a_ k(t) = \sum \limits _{n = 0}^N {\mathcal {J}}_n(t, k)({\varvec{a}}^{(0)}) +R_{N+1}(t, k)({\varvec{a}}^{(t)}), \end{aligned}$$where \({\mathcal {J}}_n\) are sums of monomials of degree \(2n+1\) in the initial data \({\varvec{a}}^{(0)}\), and \(R_N\) is the remainder which depends on the nonlinear solution \({\varvec{a}}^{(t)}\). Each term of \({\mathcal {J}}_n\) can be represented by a Feynman tree which makes the calculations of \({\mathbb {E}}( {\mathcal {J}}_n {\mathcal {J}}_{n'})\) more transparent. Such terms appear in the expansion of \({\mathbb {E}} |a_k|^2\). The estimates in this section rely on essentially sharp bounds on quasi-resonant sums of the form
$$\begin{aligned} \sum _{\begin{array}{c} \mathbf {k} \in {\mathbb {Z}}_L^{rd}\\ \end{array}} \mathbb {1} (|\mathbf {k}|\lesssim 1) \mathbb {1}(|{\mathcal {Q}}(k)|\sim 2^{-A})\lesssim 2^{-A}L^{rd} \end{aligned}$$(1.4)where \(\mathbb {1}(S)\) denotes the characteristic function of a set S and \({\mathcal {Q}}\) is an irrational quadratic form. Since A will be taken large \(2^A\sim T \gg L^2\), such estimates belong to the realm of number theory and will be a consequence the third component of this work.
The bounds we obtain for such interaction are good up to times of order \(\sqrt{\tau }\) which is sufficient given the restrictions on the time interval of convergence imposed by the second component below.
-
(2)
Section 5: Construction of solutions. In this section we construct solutions on a time interval [0, T] via a contraction mapping argument. To maximize T while maintaining a contraction, we rely on the Khinchine improvement to the space-time Strichartz bounds, as well as the long-time Strichartz estimates on generic irrational tori proved in [11]. It is here that our estimates are very far from optimal, since there is no proof to the conjectured optimal Strichartz estimates.
-
(3)
Section 8: Equidistribution of irrational quadratic forms. The purpose of this section is two-fold. The first is proving bounds on quasi-resonant sums like those in (1.4) for the largest possible T, and the second is to extract the exact asymptotic, with effective error bounds, of the leading part of the sum. It is this leading part that converges to the kinetic equation collision kernel as \(L\rightarrow \infty \).
Here we remark, that if \({\mathcal {Q}}\) is a rational form, then the largest A for which one could hope for an estimate like (1.4) is \(2^A\sim L^2\) which reflects the fact that a rational quadratic form cannot be equidistributed at scales smaller than \(L^{-2}\) (at the level of NLS, it would yield a time interval restriction of \(T\lesssim L^2\) for the rational torus). However, for generic irrational quadratic forms, \({\mathcal {Q}}\) is actually equidistributed at much finer scales than \(L^{-2}\). Here, we adapt a recent work of Bourgain [5] which will allow us to reach equidistribution scales essentially up to \(L^{-d}\).
1.5 Notations
In addition to the notation introduced earlier for \({\mathbb {T}}_L^d = [0,L]^d\) and \({\mathbb {Z}}^d_L = \frac{1}{L} {\mathbb {Z}}^d\), we use standard notations. A function f on \({\mathbb {T}}_L^d\) and its Fourier transform \(\widehat{f}\) on \({\mathbb {Z}}^d_L\) are related by
Parseval’s theorem becomes
We adopt the following definition for weighted \(\ell ^p\) spaces: if \(p\ge 1\), \(s\in {\mathbb {R}}\), and \(b\in \ell ^p\),
Sobolev spaces \(H^s({\mathbb {T}}^d)\) are then defined naturally by
For functions defined on \({\mathbb {R}}^d\), we adopt the normalization
We denote by C any constant whose value does not depend on \(\lambda \) or L. The notation \(A \lesssim B\) means that there exists a constant C such that \(A \le C B\). We also write \( A \lesssim L^{r^+} B \), if for any \(\epsilon > 0\) there exists \(C_\epsilon \) such that \(A \le C_\epsilon L^{r+\epsilon } B\). Similarly \(A > rsim L^{r^-} B\), if for any \(\epsilon > 0\) there exists \(C_\epsilon \) such that \(A \ge C_\epsilon L^{r-\epsilon } B\). Finally we use the notation \(u =O_X(B)\) to mean \(\Vert u\Vert _X\lesssim B\).
We would like to thank Peter Sarnak for pointing us to unpublished work by Bourgain [5]. This reference helped us improve an earlier version of our work. We also would like to thank Peter and Simon Myerson for many helpful and illuminating discussions.
2 The general result
We start by writing the equations for the interaction representation \((a_k(t))_{k \in {\mathbb {Z}}^d_L}\), given in (1.2):
where we recall \( \varOmega (k,k_1,k_2,k_3) = Q(k) - Q(k_1) + Q(k_2)- Q(k_3), \) and \(\vartheta _k(\omega )\) are i.i.d. random variables that are uniformly distributed in \([0,2\pi ]\). Our results depend on two parameters: the equidistribution parameter \(\nu \), and a Strichartz parameter \(\theta _p\), which we now explain.
2.1 The Equidistribution parameter \(\nu \)
The interaction frequency \(\varOmega (k,k_1,k_2, k_3)\) above is an irrational quadratic form. Such quadratic forms can be equidistributed at scales that are much smaller than the finest scale \(\sim L^{-2}\) of rational forms.
We will denote by \(\nu \) the largest real number such that for all \(k\in {\mathbb {Z}}^d_L\), \(|k|\le 1\), and \(\epsilon >0\), there exists \(\delta >0\) such that, for \(|a|, |b|<1\) with \(b-a \ge L^{-\nu ^-}\),
Proposition 2.1
With the above definition for \(\nu \), we have
-
(i)
If \(\beta _i = 1\) for all \(i \in \{1,\ldots ,d\}\), \(\nu = 2\).
-
(ii)
If the \(\beta _i\) are generic, \(\nu = d\).
Proof
The first assertion is classical, e.g., see [6]. The second assertion is proved in Sect. 8. \(\square \)
2.2 The Strichartz parameter \(\varvec{\theta _d}\)
Our proof relies on long-time Strichartz estimates, which are used to maintain linear bounds for the nonlinear problem. The genericity of the \(\beta \)’s gives crucial improvements from the rational case. The improved estimates for generic \(\beta \)’s were proved in [11],
for some \(0\le \gamma (d,p) \le d-2\). The \(N^{\gamma }\) term can be thought of as the time it takes for a focused wave with localized wave number \(\le N\), to focus again. For the rational torus \(\gamma =0\).
Here we only need to use the \({L^4_{t,x}([0,T]\times {\mathbb {T}}_L^d)}\) norm, and therefore we introduce a parameter \(\theta _d\) to record how the constant in the \({L^4_{t,x}([0,T]\times {\mathbb {T}}_L^d)}\) estimates depends on L. By scaling, the result in [11] translates into,
where \(\theta _d:={\left\{ \begin{array}{ll} \frac{4}{13}+2, \qquad d=3\\ \frac{(d-2)^2}{2(d-1)}+ 2, \qquad d\ge 4. \end{array}\right. }\)
2.3 The approximation theorem
With these parameters defined, we state the approximation theorem for the cubic NLS in dimension \(d\ge 3\) and generic \(\beta \)’s.
Theorem 2.2
Assume the \(\beta \)’s are generic and \(d\ge 3\). Let \(\phi _0: {\mathbb {R}}^d \rightarrow {\mathbb {R}}^+\), a rapidly decaying smooth function. Suppose that \(a_k(0)=\sqrt{\phi (k)}e^{i\vartheta _k(\omega )}\) where \(\vartheta _k(\omega )\) are i.i.d. random variables uniformly distributed in \([0,2\pi ]\). For every \(\epsilon _0\), a sufficiently small constant, and \(L>L_*(\epsilon _0)\) sufficiently large, the following holds:
There exists a set \(E_{\epsilon _0, L}\) of measure \({\mathbb {P}}(E_{\epsilon _0, L})\ge 1-e^{-L^{\epsilon _0}}\) such that: if \(\omega \in E_{\epsilon _0,L}\) , then for any \(L>L_*(\epsilon _0)\), the solution \(a_k(t)\) of (NLS) exists in \(C_tH^s([0, T] \times {\mathbb {T}}^d_L)\) for
Moreover,
For \(d=3, 4\), the solutions exist globally in time [4, 26], and one has the same estimate without multiplying with \(\mathbb {1}_{E_{\epsilon _0}}\) inside the expectation.
Here we note that the error could be controlled in a much stronger norm than \(\ell ^\infty \), and that other randomizations of the data are possible (complex Gaussians for instance) without any significant changes in the proof.
3 Formal derivation of the kinetic equation
In this section, we present the formal derivation of the kinetic equation, whose basic steps we shall follow in the proof. The starting point is Eq. (2.1) integrated in time,
The derivation of the kinetic equation proceeds as follows:
Step 1: expanding in the data Noting the symmetry in (3.1) in the variables \(k_1\) and \(k_3\), we have upon integrating by parts twice, and substituting (2.1) for \(\dot{a}_k\),
where we denoted \(\varOmega (k,k_1,k_2,k_3,k_4,k_5) = Q(k) + \sum _{i=1}^5(-1)^iQ(k_i)\); we also used the convention that, if \(a=0\), \(\frac{e^{2\pi i ta} -1}{2\pi a} = it\), while, if \(a=b=0\), \(\frac{1}{2\pi a}\left( \frac{e^{2\pi i t(a+b)}-1}{2\pi (a+b)} - \frac{e^{2\pi i t a}-1}{2\pi a} \right) = -\frac{1}{2} t^2 \).
Step 2: parity pairing We now compute \({\mathbb {E}} |a_k|^2\), where the expectation \({\mathbb {E}}\) is understood with respect to the random phases (random parameter \(\omega \)). The key observation is,
(for \(k \in {\mathbb {Z}}^d_L\), we write \(\phi _k = \phi (k)\)). Computing \({\mathbb {E}}\left( |a_k|^2\right) \) with the help of the above formula, we see that, there are no terms of order \(\lambda ^2\). There are two kinds of terms of order \(\lambda ^4\) obtained as follows: either by pairing the term of order \(\lambda ^2\), namely (3.2b), with its conjugate, or by pairing one of the terms of order \(\lambda ^4\), (3.2c) or (3.2d), with the term of order 1, namely \(a_k^0\). Overall, this leads to
where degenerate cases occur for instance if k, \(k_1\), \(k_2\), \(k_3\) are not distinctFootnote 1. The details of the computation are as follows:
-
(a)
Consider first \({\mathbb {E}} |(3.2\mathrm{b})|^2 = {\mathbb {E}} (3.2\mathrm{b}) \overline{(3.2\mathrm{b})}\), and denote \(k_1,k_2,k_3\) the indices in (3.2b) and \(k_1',k_2',k_3'\) the indices in \(\overline{(3.2\mathrm{b})}\). There are two possibilities:
-
\( \{ k_1,k_3 \} = \{ k_1', k_3' \}\), in which case \(k_2=k_2'\), and \(\varOmega (k,k_1,k_2,k_3) = \varOmega (k,k_1',k_2',k_3')\).
-
\((k_2 = k_1 \; \text{ or }\; k_3) \; \text{ and }\;(k_2' = k_1' \; \text{ or } \; k_3' )\), in which case \(\varOmega (k,k_1,k_2,k_3) = \varOmega (k,k_1',k_2',k_3') = 0\).
Overall, we find, neglecting degenerate cases (which occur if k, \(k_1\), \(k_2\), \(k_3\) are not distinct),
$$\begin{aligned} {\mathbb {E}} |(3.2\mathrm{b})|^2= & {} \frac{2 \lambda ^4}{L^{4d}} \sum \limits _{k - k_1 + k_2 - k_3=0} \phi _{k_1} \phi _{k_2} \phi _{k_3} \left| \frac{\sin (\pi t\varOmega (k,k_1,k_2,k_3)) }{\pi \varOmega (k,k_1,k_2,k_3)} \right| ^2 \\&+ \frac{4 \lambda ^4}{L^{4d}} t^2 \sum \limits _{k_1,k_3} \phi _k \phi _{k_1} \phi _{k_2}. \end{aligned}$$ -
-
(b)
Consider next the pairing of \(a_k^0\) with (3.2c), which contributes \(2 {\mathbb {E}} \mathfrak {Re} \left[ (3.2\mathrm{c}) \overline{a_k^0}\right] \). The possible pairings are
-
\(\{k,k_2 \} = \{k_4,k_6 \}\), implying \(k_3=k_5\), and leading to \(\varOmega (k_1,k_4,k_5,k_6) = - \varOmega (k,k_1,k_2,k_3)\), and \(\varOmega (k,k_4,k_5,k_6,k_2,k_1)=0\).
-
\((k_3 = k_2 \; \text{ or }\; k) \; \text{ and }\; (k_5 = k_4 \; \text{ or } \; k_6)\) in which case \(\varOmega (k,k_1,k_2,k_3) = \varOmega (k_1,k_4,k_5,k_6) = 0\).
This gives, neglecting degenerate cases,
$$\begin{aligned} \begin{aligned}&2 {\mathbb {E}} \mathfrak {Re} \left[ \overline{a_k^0} (3.2\mathrm{c})\right] =\frac{8 \lambda ^4}{L^{4d}} \\&\qquad \times \sum \limits _{k - k_1 + k_2 - k_3=0} \phi _k \phi _{k_2} \phi _{k_3} \mathfrak {Re} \left[ \frac{e^{-2\pi it\varOmega (k,k_1,k_2,k_3)} - 1}{4\pi ^2 \varOmega (k,k_1,k_2,k_3)^2} \right] \\&\qquad - \frac{8 \lambda ^4}{L^{4d}} t^2 \sum \limits _{k_1,k_3} \phi _k \phi _{k_2} \phi _{k_3} \\&\quad = - \frac{2 \lambda ^4}{L^{4d}} \sum \limits _{k - k_1 + k_2 - k_3=0} \phi _k \phi _{k_1} \phi _{k_2} \phi _k \left[ \frac{1}{\phi _{k_1}} + \frac{1}{\phi _{k_3}} \right] \left| \frac{\sin (\pi t\varOmega (k,k_1,k_2,k_3))}{\pi \varOmega (k,k_1,k_2,k_3)} \right| ^2 \\&\qquad - \frac{8 \lambda ^4}{L^{4d}} t^2 \sum \limits _{k_1,k_3} \phi _k \phi _{k_2} \phi _{k_3}, \end{aligned} \end{aligned}$$where we used in the last line the symmetry between the variables \(k_1\) and \(k_3\), as well as the identity \(\mathfrak {Re} (e^{iy} - 1 ) = - 2 |\sin (y/2)|^2\), for \(y \in {\mathbb {R}}\).
-
-
(c)
Finally, the pairing of \(a_k^0\) with (3.2d) can be discussed similarly, to yield
$$\begin{aligned} 2 {\mathbb {E}} \mathfrak {Re} \left[ \overline{a_k^0} (\mathrm{3.2} \mathrm{d})\right]= & {} \frac{2 \lambda ^4}{L^{4d}} \sum \limits _{k - k_1 + k_2 - k_3=0} \phi _k \phi _{k_1} \phi _{k_3} \left| \frac{\sin (\pi t\varOmega (k,k_1,k_2,k_3))}{\pi \varOmega (k,k_1,k_2,k_3)} \right| ^2 \\&+ \frac{4 \lambda ^4}{L^{4d}} t^2 \sum \limits _{k_1,k_3} \phi _k \phi _{k_2} \phi _{k_3}, \end{aligned}$$
Summing the above expressions for \({\mathbb {E}} |(\mathrm{3.2b})|^2\), \(2 {\mathbb {E}} \mathfrak {Re} \left[ \overline{a_k^0} (\mathrm{3.2c}) \right] \) and \(2 {\mathbb {E}} \mathfrak {Re} \left[ \overline{a_k^0} (3.2\mathrm{d})\right] \) gives the desired result.
Step 3: the big box limit \(L \rightarrow \infty \) Assuming that \(\varOmega (k,k_1,k_2,k_3)\) is equidistributed on a scale
we see that, as \(L \rightarrow \infty \),
Step 4: the large time limit \(t \rightarrow \infty \) Observe thatFootnote 2\(\int \limits \frac{(\sin x)^2}{x^2} \,dx = \pi ^2\), so that, in the sense of distributions,
Therefore, as \(t \rightarrow \infty \),
Conclusion: relevant timescales for the problem Overall, we find, assuming that the above limits are justified
This suggests that the actual timescale of the problem is
and that, setting \(s = \frac{t}{\tau }\), the governing equation should read
In which regime is this approximation expected? Let T be the timescale over which we consider the equation.
-
In order for (3.4) to hold, the condition (3.3) has to hold, and the limits \(L\rightarrow \infty \) and \(T \rightarrow \infty \) have to be taken: one needs
$$\begin{aligned} T \ll L^{\nu }, \qquad L \gg 1, \qquad \text{ and } \qquad T\gg 1. \end{aligned}$$ -
In order for the nonlinear evolution of (3.5) to affect an \(O(\kappa )\) change on the initial data, the two conditions above should be satisfied; in addition T should be of the order of \(\kappa \tau \) (equivalently \(s\sim \kappa \)). Thus we find the conditions
$$\begin{aligned} 1\ll T \approx \kappa \tau \ll L^{\nu } \qquad \text{ and } \qquad \kappa ^{\frac{1}{4}}L^{d/2} \gg \lambda \gg \kappa ^{\frac{1}{4}}L^{d/2 - \nu /4}. \end{aligned}$$
4 Feynman trees: bounding the terms in the expansion
Since we are considering the problem with rapidly decaying \(\phi \), then the rapid decay of \(\phi \) yields all the bounds one needs for wave numbers \(|k|\ge L^{0^+}\), thus we might as well consider \(\phi \) to be compactly supported.
4.1 Expansion of the solution in the data
We follow mostly the notations in Lukkarinen–Spohn [29], Section 3 (see also [9]).
The iterates of \(\phi \), considered in the previous section, can be represented through trees (at least up to lower order error terms). To explain these trees, let us start with the equation satisfied by the amplitude of the wave number \(a_ k\)
where the subscript in \({\mathscr {P}}_3\) is to indicate that it is a monomial of degree 3, and where we suppressed the k dependence for convenience. The expansion can be obtained by integrating by parts on the oscillating factor \( e^{- 2\pi is \varOmega }\). Thus the first integration by parts gives the cubic expansion,
Using the equation for a, we see that \(\dot{{\mathscr {P}}}_3(a)\) consists of three monomials of degree 5, and if we denote on of them by \({\mathscr {P}}_5\), then the integral term consists of three integrals of the type,
Another integration by parts gives the quintic expansion, which consist of three terms of the form
Consequently, to compute the expansion to order N we need to integrate by parts N times on the oscillating exponentials, giving the expansion,
where \({\mathcal {J}}_n = \sum \limits _{\varvec{\ell }} {\mathcal {J}}_{n,\varvec{\ell }}\), and each \({\mathcal {J}}_{n,\varvec{\ell }}\) is a monomial of degree \(2n+1\) generated by the \(n^{th}\) integration by parts. The index \(\varvec{\ell }\) is a vector whose entries keep track of the history of how the monomial \({\mathcal {J}}_{n,\varvec{\ell }}\) was generated. \(R_{N+1}\) is the remaining time integral.
Each \({\mathcal {J}}_{n,\varvec{\ell }}\) can be represented by a tree similar to Fig. 1 below. which we now explain.
The trees will be constructed in reverse order of their usage. Therefore the labeling of the wave numbers will be done backwards: \(n-j\), \(0\le j\le n\).
The tree corresponding to \({\mathcal {J}}_{n,\varvec{\ell }}\), is given as follows.
-
There are \(n+1\) levels in the tree, the bottom level is the \(0^{th}\) level. Descending from the top to the bottom, each level is generated from the previous level by an integration by parts step. Thus level j represents the terms present after \(n-j\) integration by parts.
-
\(k_{j,m}\) denote the wave numbers present in level j, and therefore \(1\le m \le 2(n-j)+1\).
-
\(k_{j,m}\) has a parity \(\sigma _m \) due to complex conjugation. For m odd or even, \(\sigma _m= +1\) or \(\sigma _m= -1\) respectively.
$$\begin{aligned} a_{k_{j,m},\sigma _m} = {\left\{ \begin{array}{ll} a_{k_{j,m}} &{} \text{ if } \sigma _m = +1 \\ \overline{a_{k_{j,m}} }&{} \text{ if } \sigma _m = -1 \end{array}\right. }\,. \end{aligned}$$ -
For each level j, we associate a number \(\ell _j\), which signals out the wave number \( k_{j,\ell _j}\) which has 3 branches. This is the wave number of the a (or \({{\bar{a}}}\)) that was differentiated by the \(j^{th}\) integration by parts. The index vector \(\varvec{\ell }\), keeps track of the integration by parts history in the tree for \({\mathcal {J}}_{n,\ell }\). The entries \(\ell _{j}\), \(1\le j \le n\), are given by
$$\begin{aligned} \varvec{\ell }= (\ell _1,\ldots , \ell _n) \in \{1,\ldots ,2n-1\} \times \{1,\ldots ,2n-3\} \times \dots \times \{1,2,3\} \times \{1 \}. \end{aligned}$$ -
The tree has a signature \(\sigma _{\varvec{\ell }}= \prod _{j=1}^n (-1)^{\ell _j +1}\).
-
Transition rules. To go from level j to level \(j-1\), the wave numbers are related as follows
$$\begin{aligned} {\left\{ \begin{array}{ll} k_{j,m} = k_{j-1,m} &{} \text{ for } m<\ell _{j} \\ k_{j,m} = k_{j-1,m+2} &{} \text{ for } \ell _{j} < m \\ k_{j,\ell _{j}} = k_{j-1,\ell _{j}} -k_{j-1,\ell _j+1} + k_{j-1,\ell _j +2} \end{array}\right. } \end{aligned}$$(4.2)Note that for any j, \(\sum _{m=1}^{2(n-j)+1}(-1)^{m+1} k_{j,m}= k_{n,1}=k\). The wave numbers at level 0, i.e., those present in \({\mathcal {J}}_{n,\varvec{\ell }}\), are labeled
$$\begin{aligned} {\varvec{k}}= ( k_{0,1}, \dots ,k_{0,2n+1}) \in ({\mathbb {Z}}^d_L)^{2n+1}\,. \end{aligned}$$ -
At each level j, the derivative of the element with wave number \( k_{j,\ell _j}\) (due to the integration by parts), generates a oscillatory term with frequency
$$\begin{aligned} \varOmega _j({\varvec{k}}) = (-1)^{\ell _j +1}\left( Q(k_{j,\ell _j}) - Q(k_{j-1,\ell _j}) + Q(k_{j-1,\ell _j +1}) - Q(k_{j-1,\ell _j +2})\right) \,. \end{aligned}$$ -
We introduce variables \({\varvec{s}} = (s_0,\ldots ,s_n) \in {\mathbb {R}}_+^{n+1}\); \(t_j({\varvec{s}}) = \sum \limits _{k=0}^{j-1} s_k\), \(1\le j \le n\). This choice of variables can be explained as follows. Repeated integration by parts generates terms of the form
$$\begin{aligned}&\int \limits _0^t g_0(s_0) \int \limits _{s_0}^t g_1(s_1) \dots \int \limits _{s_{n-2}}^t g_{n-1}(s_{n-1}) \\&\quad =\int \limits _0^t g_0(s_0) \int \limits _{0}^{t-s_0}g_1(s_0 +s_1) \dots \quad \int \limits _0^{t- s_0-\dots -s_{n-2}} \quad g_{n-1}(s_0 + \dots + s_{n-1}) \end{aligned}$$which can be written as
$$\begin{aligned} \int _{{\mathbb {R}}_+^{n+1}}g_0(s_0) g_1(s_0 +s_1) \dots g_{n-1}(s_0 + \dots + s_{n-1}) \delta (t-\sum _{l=0}^n s_l) \end{aligned}$$
With this notation at hand,
and Fig. 1 represents \({\mathcal {J}}_{3,(2,3,1)}\). The general formula for \({\mathcal {J}}_{n, \varvec{\ell }}\) is given by
Here and throughout the manuscript we write
while \(\delta (\cdot )\) is the Dirac delta.
Finally, we write \( R_n(t, k)({{\varvec{a}}})=\sum \limits _{\varvec{\ell }}\int \limits _0^t R_{n, \varvec{\ell }}(t, s_0; k)({\varvec{a}}^{(s_0)}) ds_0, \) where
4.2 Bound on the correlation
Our aim is to prove the following proposition.
Proposition 4.1
If \(t < L^{d-\epsilon _0}\), then
Remark 4.2
The trivial estimate would be that
Indeed, \({\mathcal {J}}_{n, \varvec{\ell }} {\mathcal {J}}_{n', \varvec{\ell }'}\) comes with a prefactor \(\left( \frac{\lambda ^2}{L^{2d}} \right) ^{n+n'}\); the size of the domains where the time integration takes place is \(O(t^{n+n'})\); and the summation over \({\varvec{k}}\) and \(\varvec{k'}\) is over \(2d(n+n'+1)\) dimensions, half of which are canceled by the pairing (see below), out of which d further dimensions are canceled by the requirement that \(k_{n,1} = k\). Overall, this gives a bound \(\left( \frac{\lambda ^2}{L^{2d}} \right) ^{n+n'} \times t^{n+n'} \times L^{d(n+n')} = \left( \frac{t}{\sqrt{\tau }} \right) ^{n+n'}\).
Therefore, the above proposition essentially allows a gain of \(\frac{1}{t}\) over the trivial bound. This gain of \(\frac{1}{t}\) comes from cancelations in the “non degenerate interactions” as will be exhibited by Eq. (4.13).
Before we start the proof of Proposition 4.1, we shall classify the transitions (4.2) as degenerate if
i.e., if the parallelogram with verticies \((k_{j, \ell _j}, k_{j-1, \ell _{j} -1}, k_{j-1, \ell _j}, k_{j-1, \ell _j+2})\) degenerates into a line. In this case \(\varOmega _{\ell _j} ({\varvec{k}})=0\). When all transitions in a tree that represents \({\mathcal {J}}_{n, \varvec{\ell }}\) are degenerate we denote the term by \(D_{n, \varvec{\ell }}(t,k)\), and if one transition is non degenerate we denote it by \({\widetilde{{\mathcal {J}}}}_{n,\varvec{\ell }}(t,k) \), that is
where \(\Delta ({{\varvec{k}}})=1-\prod _{j=1}^n\delta _{\{k_{j-1, \ell _{j}+1}, k_{j-1, \ell _j+1+\sigma _{j, \ell _j}}\}}^{k_{j, \ell _j}}\). Note that \(\Delta ({{\varvec{k}}})=1\) whenever \({\widetilde{{\mathcal {J}}}}_{n,\varvec{\ell }}(t,k) \ne 0\).
4.3 Cancellation of degenerate interactions
As can be seen from a simple computation in the formula for \(D_{n, \varvec{\ell }}\), the contribution of each \({\mathbb {E}}(D_{n, \varvec{\ell }}(t,k){{\overline{D}}}_{n', \varvec{\ell }'}(t,k))\) to the sum in (4.5) is of size \(\sim \left( \frac{t}{\sqrt{\tau }} \right) ^S\), which is too large. Luckily, all those terms cancel out as shows the lemma below.
Note that this cancellation between graph expectations is essentially due to the invariance of the expectation \({\mathbb {E}}|a_k|^2\) under Wick renormalization, which is a classical trick in the analysis of the nonlinear Schrödinger equation that eliminates all degenerate interactions. However, working at the level of graph expectations might be applicable in more general contexts.
Lemma 4.3
For any \(S\ge 2\)
Proof
First we note that since each level in the tree has parity equal to 1, then
Hence by Eq. (4.7)
Thus we obtain
The result will follow once we show that
This follows by parametrizing the above sum as \(\{(n, n')=(S-j, j): j=0, \ldots S\}\), which gives
\(\square \)
4.4 Estimate on non-degenerate interactions
Proposition 4.1 now follows from the following lemma:
Lemma 4.4
Suppose \(G_{n', \varvec{\ell }'}(t,k)\in \{{\widetilde{{\mathcal {J}}}}_{n', \varvec{\ell }'}(t,k)), D_{n', \varvec{\ell }'}(t,k))\}\), then for \(0<t< L^{d-\epsilon _0}\),
Proof
We will only consider the case of \(G_{n', \varvec{\ell }'}(t,k)={\widetilde{{\mathcal {J}}}}_{n', \varvec{\ell }'}(t,k)\), since the case \(G_{n', \varvec{\ell }'}(t,k)=D_{n', \varvec{\ell }'}(t,k))\) is easier to bound. Using the identity
we can write for any \((e_0,\ldots ,e_n) \in {\mathbb {R}}^{n+1}\) and \(\eta >0\)
Thus by choosing \(\eta = \frac{1}{t}\), we have
Here we employed the notation \(\varOmega _j = 2\pi \varOmega _{j}({\varvec{k}})\).
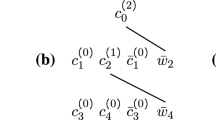
To bound \({\mathbb {E}} ({\widetilde{{\mathcal {J}}}}_{n, \varvec{\ell }}(t,k) \overline{{\widetilde{{\mathcal {J}}}}_{n', \varvec{\ell }'}(t,k)})\), we will simplify the notation by setting \(k_{0,2n+1+j}= k'_{0,j}\), which also preserves the parity convention. Consequently, we have \(2n +2n' +2\) wave numbers present in the expression for \({\mathbb {E}} ({\widetilde{{\mathcal {J}}}}_{n, \varvec{\ell }}(t,k) \overline{{\widetilde{{\mathcal {J}}}}_{n', \varvec{\ell }'}(t,k)})\) (Fig. 2).
Next, since the phases are i.i.d. with mean 0, then only specific paring of the wave numbers contribute nonzero terms, namely the paring should be between terms with the same wave number and opposite parity. For this reason we introduce \({\mathcal {P}} = {\mathcal {P}}(n,n',\varvec{\sigma },\varvec{\sigma }')\) a class of pairings indices and parities, as illustrated in Fig. 3
Furthermore, we define the pairing of wave numbers induced by \(\psi \), \(\varGamma _\psi ({\varvec{k}},{\varvec{k}}') = \prod _{j=1}^{2n+2n'+2} \delta ^{k_{0,j}}_{ k_{0,\psi (j)}}. \) By the independence of the phases \(\vartheta _{k_{0,j}}(\omega )\), we have,
Hence we obtain
where \({\mathscr {A}}_{\psi }({\varvec{k}},{\varvec{k}}')=\delta ^{k_{n,1}}_k\delta _{ k'_{n',1}}^k\Delta ({{\varvec{k}}})\Delta ({{\varvec{k}}'}) \varGamma _\psi ({\varvec{k}},{\varvec{k}}') \prod _{j=1}^{2n+1} \sqrt{\phi (k_{0,j})} \prod _{j'=1}^{2n'+1} \sqrt{\phi (k_{0,j'}')} \).
By Hölder’s inequality, for any \(m \ge 1\) and \(b_1,\ldots ,b_{n'+1} \in {\mathbb {R}}\),
and applying this bound to the \(\alpha '\) integral yields
Let \(p=p({\varvec{k}})\) be the smallest integer such that \(k_{p+1, \ell _p}\notin \{k_{p, \ell _{p}+1}, k_{p, \ell _p+1+\sigma _{p+1, \ell _p}}\}\), i.e., in the tree for \({\widetilde{{\mathcal {J}}}}_{n, \varvec{\ell }}\) the transition from level \(p+1\) to level p is not degenerate. Note that \(0 \le p \le n-1\), and
We now set
Note that, by definition of p,
The figure below illustrate all the introduced notations and parings for the product of two non degenerate terms.
We distinguish three cases depending on the values of the numbers \(J_i\).
Case 1: \(J_1,J_2,J_3 \ge 2n+2\) For a fixed p and \(\psi \) we sum over all wave numbers in \( {\mathfrak {I}}_{p,\psi }\) that yield degenerate transitions, i.e., wave numbers generated in rows \(0\le l \le p-1\). This contributes \(L^{dp}\) to the bound,
where \(\sum ^*\) stands for the sum over \(k_{p,j}\), where \(1 \le j \le 2(n-p) + 1\) and \(j \notin \{ I_1,I_2,I_3 \}\), and \(k'_{0, j'}\) for \(1\le j'\le 2n'+1\) with \(j' \notin \{J_1, J_2,J_3\}\).
The contribution of the above integral is acceptable as long as the denominator is \(O(\langle \alpha \rangle ^{-2})\). Therefore, it suffices to prove the desired bound when the domain of integration reduces to \(\alpha \in [-R,R]\), for some \(R>0\), since the resonance moduli \(\varOmega _i\) are bounded. Furthermore by bounding the integrand by \(\frac{t^{n-1}}{|\alpha -\varOmega _{p+1} - \dots - \varOmega _{n} + \frac{i}{t}| |\alpha + \frac{i}{t}|}\), matters reduce to estimating
By the identity \( k_{p+1,I_1} - k_{p,I_2} = \sigma _{p,I_1} (k_{p,I_3} - k_{p,I_1})\), this can also be written
and since \(\sum _{j=1}^{2(n-p)+1}\sigma _{p, j}k_{p, j}=k_{n,1}=k\), we note that
where C depends only on k and the variables \(k_{p, j}\) with \(j\notin \{I_1, I_2, I_3\}\).
By setting \(P= k_{p,I_3}\) and \(R=k_{p,I_1}\), for \(t < L^{\nu }\) we bound
using the equidistribution result in Sect. 8. If \(| -Q(P) + Q(R) - Q(N+P-R) + C| \le t^{-1}\), we have by Corollary 8.5
Whereas for \(| -Q(P) + Q(R) - Q(N+P-R) + C| \ge t^{-1}\), we bound
Therefore, we can bound (4.11) by
The sum \(\sum ^*\) is over \(2(n+n'-p-2)\) variables; however, because of the pairing \(\varGamma _\psi \), half of them drop out, so that the remaining sum is \(\lesssim L^{d(n+n'-p-2)}\). Ans since \(\int _{-R}^R \frac{d\alpha }{ |\alpha + \frac{i}{t}|} \lesssim \log t\), the above expression can be bounded by,
which gives the stated bound.
Case 2: only two of \(J_1,J_2,J_3\hbox { are }\ge 2n+2\) Suppose for instance that \(J_2\le 2n+1\). Then, there exists \(I_4\le 2(n-p)+1\) such that \(\psi (I_4) = J_4 \ge 2n+2\) (such an index exists because there is an odd number of elements in the set of elements in \(\{1, \ldots , 2(n-p)+1\}\setminus \{I_1, I_2, I_3, J_2\}\), so they cannot be paired together completely). One can then follow the above argument replacing \(I_2\) by \(I_4\).
Case 3: two of \(J_1,J_2,J_3\) are \(\le 2n+1\) Assume for instance that \(J_1, J_3 \le 2n+1\) Proceeding as in Case 1, it suffices to bound
where \(\Sigma ^*\) is the sum over \(k_{p,j}\), with \(j \in \{1,\ldots ,2(n-p)+1\} \setminus \{I_1,I_3,J_1,J_3\}\), and over \(k_{0,j'}\), with \(j' \in \{1,\ldots ,2n'+1\}\).
A crucial observation is that, since \(\sum _{j=1}^{2(n-p)+1}\sigma _{p, j}k_{p, j}=k_{n,1}=k\), the wave numbers \(k_{p,I_1}\) and \(k_{p,I_3}\) do not contribute to this sum since the paring \(k_{p,I_1} = k_{p,J_1}\) and \(k_{p,I_3} = k_{p,J_3}\), causes them to cancel one another. Furthermore, \(0\le p \le n-2\) since \(J_1,J_3 \le 2n+1\), and therefore we bound the integrand by \(\frac{t^{n-1}}{| \alpha -\varOmega _{p+2} - \dots - \varOmega _{n} + \frac{i}{t}||\alpha + \frac{i}{t}|}\). Overall, we can bound the above by
From Eq. (4.12), we conclude
where C only depends on the variables in \(\sum ^*\). Applying (4.13) enables us to bound the inner sum by \(L^{2d} \log t\), and the \(\alpha \) integral by \(\log t\). Finally, the number of variables in \(\sum ^*\) is \(2(n+n'-p-1)\). By pairing them there are only \(n+n'-p-1\), and fixing \(k_{n,1}=k\) brings their number down to \(n+n'-p-2\). Thus \(\sum ^*\) will contribute \(\lesssim L^{d(n+n'-p-2)}\). Overall, we obtain the bound
which is the desired estimate. \(\square \)
5 Deterministic local well-posedness
Local or long time existence existence of smooth solutions is usually carried out by using Strichartz estimates to bound solutions. The known Strichartz estimates for our problem (2.2) are not sufficient to allow us to prove existence of solutions for a long time interval where the wave kinetic Eq. (WKE) emerges. However, if the data is assumed to be random, then one has improved estimates due to Khinchin’s inequality [7]. Based on this, we first present a local well-posedness theorem provided the data satisfies a certain estimate. In Sect. 6, we show that such an improved estimate occurs with high probability.
Moreover, to use the results from Sects. 4 and 8, we will restrict discussion to the case \(T < L^{d-\epsilon _0}\).
5.1 Strichartz estimate
Recall Eq. (2.2) , which can be written as,
Moreover if we denote the characteristic function of the unit cube centered at \(j \in {\mathbb {Z}}^d\) by \(\mathbb {1}_{B_j}\), and define
Then, using the Galilean invariance \(\left| e^{-it \Delta _\beta } \psi _{B_j}(x)\right| = \left| [e^{-it \Delta _\beta } (e^{2\pi i j x}\psi )_{B_0}](x-2tj)\right| \), we have
Converting this estimate to its dual, and applying the Christ–Kiselev inequality, one gets
for an appropriate choice of \(C_{d,\epsilon }\) used in the definition of \( S_{d,\epsilon }\).
5.2 A priori bound in \(\varvec{Z_T^s}\) and energy
Let \(Z_T^s\) denote the function space defined by the norm,
then the \(Z^s_T\) norm of the nonlinearity is bounded.
Lemma 5.1
Fix \(s > \frac{d}{2}\). For every \(\epsilon _0 >0\), and an appropriate choice of \(C_{d,\epsilon _0}\), we have
Proof
Consider \(v\in L^{\frac{4}{3}}_{t,x}([0,T]\times {\mathbb {T}}^d_L)\), and let \({\widetilde{v}}(s, x)= \int _s^Te^{i(s-s')\Delta _\beta }v(s') ds'\), then
Using Eq. (5.3), we have for every \(\epsilon _0 >0\),
and therefore
Consequently, for \(s>d/2\), we have
proving Eq. (5.5). \(\square \)
Lemma 5.2
(A priori energy estimates)
Proof
By duality, we have
Applying the Strichartz estimate (5.1) yields
This establishes the stated bound. \(\square \)
5.3 Existence theorem
Local well-posedness for (NLS) will be established in the space \(Z^s_T\), with data f of size at most \({\mathscr {I}}\),
This seemingly strange normalization is actually well adapted to the problem we are considering. Indeed, consider for simplicity initial data f supported on Fourier frequencies \(\lesssim 1\), whose \(L^2\) norm is of size \(L^{\epsilon _0} \), and with random Fourier coefficients of uncorrelated phases. Then we expect \(e^{it\Delta _\beta } f\) to be evenly spread over \({\mathbb {T}}_L^d\). By conservation of the \(L^2\) norm, this corresponds to \( \Vert e^{it\Delta _\beta } f \Vert _{Z^s_T} \sim {\mathscr {I}}\).
Theorem 5.3
Let \(f\in Z_T^s\) with \({\mathscr {I}}\) and \(S_*\) defined in Eqs. (5.7) and (5.5) respectively, then
is locally well-posed in \(Z^s_T\), provided
The solution \(u\in Z^s_T\), satisfies \(\Vert u \Vert _{Z_T^s} \le 2{\mathscr {I}}\). Moreover
Remark 5.4
The time scale T over which the solution can be constructed would be equal to \(\sqrt{\tau }\), up to subpolynomial losses in L, if the long-time Strichartz estimate conjectured in [11] for \(p=4\) could be established. Since it is currently not known to be true, the result stated above gives a shorter time scale, with a more complicated numerology.
Proof
This theorem is proved by using a contraction mapping argument, to find a fixed point of the map,
in \(\{ u\in Z^s_T \bigm |\Vert u\Vert _{Z^s_T } \le 2 {\mathscr {I}}\}\). Consequently \(u = \lim _{N\rightarrow \infty } \varPhi ^N(0)\), where \(\varPhi ^N\) stands for the N-th iterate of \(\varPhi \):
To check that \(\varPhi \) is a contraction on \(B_{Z^s_T} (0, 2{\mathscr {I}})\), note that by Eq. (5.5),
and thus \(\varPhi \) maps \(B_{Z^s_T} (0, 2{\mathscr {I}})\) into itself. Again, by Eq. (5.5),
Therefore \(\varPhi \) is a contraction on \(\{ u\in Z^s_T \bigm |\Vert u\Vert _{Z^s_T } \le 2 {\mathscr {I}}\}\), and the \(H^s\) estimate follows from the a priori energy bound. \(\square \)
Besides the established bounds on u, we need to investigate the rate of convergence of \(\varPhi ^N(u) \rightarrow u \).
Corollary 5.5
Under the conditions of Theorem 5.3, there holds
Proof
Since \(\varPhi \) is a contraction with modulus R, then
Moreover the energy estimate (5.6) gives
Consequently by writing \(u - \varPhi ^N(0) = \sum \limits _{j=N}^\infty \varPhi ^{j+1}(0) - \varPhi ^j (0)\), we bound
\(\square \)
Next we establish an energy bound for the Feynman trees,
Corollary 5.6
Under the conditions of Theorem 5.3,
Proof
Since \(U_{n, \varvec{\ell }}\) is the linear propagator of \({\mathcal {J}}_{n, \varvec{\ell }}\) in physical space, then they can be represented by the following iterative procedure: Set \(v_0^m = e^{2\pi it\Delta _\beta } u_0\) for \(0 \le m \le 2n+1\) and for any \(1 \le j\le n\) we define \(v^j_m\) for \(0\le m \le 2(n-j)+1\) as \(v_j^m= v_{j-1}^m\) if \(m < \ell _j\), and \( v_j^m= v_{j-1}^{m+2} \) if \(m > \ell _j\), where we set
Hence we have \(U_{n, \varvec{\ell }} = v_n^1\).
Using the energy estimate (5.6), we bound
We can then descend down the tree by estimating \(v_{n-j}^{\ell _{n-j}}\) using the \(Z^s\) estimate (5.5). This leads to the stated bound. \(\square \)
6 Improved integrability through randomization
Recall that
where the \(\vartheta _k(\omega )\) are independent random variables, uniformly distributed on \([0,2\pi ]\).
For any t, s, \(\omega \), we have
In other words, the randomization of the angles of the Fourier coefficients does not have any effect on \(L^2\) based norms. This is not the case for Lebesgue indices larger than 2.
Theorem 6.1
Assume that \(|\phi (k)| \lesssim \langle k \rangle ^{-s}\), with \(s>\frac{d}{2}\). Then
-
(i)
\({\mathbb {E}} \left\| e^{it\Delta _{\beta }}u_0 \right\| _{L^4_{t,x}([0,T]\times {\mathbb {T}}^d_L)}^4 \lesssim \frac{T}{L^d} \Vert u_0 \Vert _{L^2_x}^4\)
-
(ii)
(large deviation estimate)
$$\begin{aligned} {\mathbb {P}} \left[ \left\| e^{it\Delta _{\beta }}u_0 \right\| _{L^4_{t,x}([0,T]\times {\mathbb {T}}^d_L)}^4 > \lambda \right] \lesssim \exp \left( - c \left( \frac{\lambda }{T^{1/4} L^{-d/4}} \right) ^2 \right) \end{aligned}$$
Proof
- (i):
-
The proof is more or less standard. See [7] for instance.
- (ii):
-
We follow the argument in [7]. By Minkowski’s inequality (for \(p \ge 4\)) and Khinchin’s inequality,
$$\begin{aligned} \left\| e^{it\Delta _{\beta }}u_0 \right\| _{L^p_\omega (\varOmega ,L^4_{t,x}([0,T]\times {\mathbb {T}}^d_L))}&\lesssim \left\| e^{it\Delta _{\beta }}u_0 \right\| _{L^4_{t,x}([0,T]\times {\mathbb {T}}^d_L,L^p_\omega (\varOmega )))} \\&\lesssim \frac{\sqrt{p}}{L^d} \left\| \left( \sum \phi (k) \right) ^{1/2} \right\| _{L^4_{t,x}([0,T]\times {\mathbb {T}}^d_L)}\\&\lesssim \sqrt{p} T^{1/4} L^{-d/4}. \end{aligned}$$By Chebyshev’s inequality,
$$\begin{aligned} {\mathbb {P}} \left[ \left\| e^{it\Delta _{\beta }}u_0 \right\| _{L^p_{t,x}([0,T]\times {\mathbb {T}}^d_L)} > \lambda \right] \lesssim \lambda ^{-p} (C_0 \sqrt{p} T^{1/4} L^{-d/4})^p. \end{aligned}$$The desired inequality is then obvious if \(\lambda < 2eC_0 T^{1/4} L^{-d/4}\); if not, it follows upon choosing \(p = \left( \frac{\lambda }{C_0 T^{1/4} L^{-d/4} e} \right) ^2\). \(\square \)
As a consequence, we deduce the following proposition.
Proposition 6.2
Let \(\epsilon _0>0\), \( \alpha >s + \frac{d}{2}\), and assume that \(|\phi (k)| \lesssim \langle k \rangle ^{-2\alpha } \). Then, for two constant \(C,c>0\),
Proof
Applying Theorem 6.1 to \((u_0)_{B_j}\),
Therefore, for L sufficiently large,
\(\square \)
7 Proof of the main theorem
Fix \(\epsilon _0 > 0\) sufficiently small, and recall that \(T\le L^d\), with
-
1)
Excluding exceptional data. Let \(E_{\epsilon _0,L}\) be the event \(\{ \left\| e^{it\Delta _{\beta }}u_0 \right\| _{Z^s} \le {\mathscr {I}}\}\), and \(F_{\epsilon _0,L}\) its contrary: \(\{ \left\| e^{it\Delta _{\beta }}u_0 \right\| _{Z^s} > {\mathscr {I}}\}\). By Proposition 6.2,
$$\begin{aligned} {\mathbb {P}} (F_{\epsilon _0,L}) \lesssim e^{-c L^{\epsilon _0}}. \end{aligned}$$This is the set appearing in the statement of Theorem 2.2. By conservation of mass
$$\begin{aligned} {\mathbb {E}} \left( |a_k(t)|^2 \right) = {\mathbb {E}} \left( |a_k(t)|^2 \; | \; E_{\epsilon _0,L} \right) + O_{\ell ^\infty }( e^{-c L^{\epsilon _0}} L^d). \end{aligned}$$ -
2)
Iterative resolution. To ensure that \(R\le \frac{1}{2}\) we restrict the range of the parameters \(\lambda \), T relative to L. There are two regimes depending on the Strichartz constant \(S_*\) and the number theory restriction \(t\le L^{d-\epsilon _0}\) (see Remark 8.2).
-
\(L^{ \theta _d}\lesssim T \lesssim L^{d}\). The condition \(R\le \frac{1}{2}\) translates into \(T\sim \lambda ^{-2}L^{\frac{d+ \theta _d}{2}-4\epsilon _0}\). Therefore we restrict \(\lambda \) to
$$\begin{aligned} L^{\frac{-d+ \theta _d -8\epsilon _0}{4}}\lesssim \lambda \lesssim L^{\frac{d- \theta _d -8\epsilon _0}{4}}\, . \end{aligned}$$For this range of parameters, the energy inequality (5.9) implies \(\Vert u\Vert _{L_t^\infty H_x^s ([0,T]\times {\mathbb {T}}^d_L)} \lesssim 1\).
-
\(T\lesssim L^{ \theta _d}\). In this case the condition on R restricts \(T \sim \min (L^{ \theta _d}, \lambda ^{-4}L^{d-8\epsilon _0})\), and therefore
$$\begin{aligned} L^\frac{d -\theta _d-8\epsilon _0}{4}\lesssim \lambda . \end{aligned}$$Here the energy inequality also implies \(\Vert u\Vert _{L_t^\infty H_x^s ([0,T]\times {\mathbb {T}}^d_L)} \lesssim 1\).
Note that for these ranges of parameters \(T\le L^{-2\delta }\sqrt{\tau }\), where \(\delta \) is that of Theorem 8.1.
With these restrictions on the range of the parameters we proceed by writing \(u = \varPhi ^N(0) + u - \varPhi ^N(0)\). Note that since \(\varPhi ^N(0)\) is a polynomial of degree \(3^N\), we write
$$\begin{aligned} u = \sum \limits _{n=0}^N U_{n, \varvec{\ell }} + \sum \limits _{(n,\ell ) \in S^N} U_{n, \varvec{\ell }} + u - \varPhi ^N(0), \end{aligned}$$where \(S^N\) includes all the terms in \(\varPhi ^N(0)\) of degree greater than N. By Corollary 5.5 and Proposition 5.6, this implies that
$$\begin{aligned} u = \sum \limits _{n=1}^N \sum \limits _\ell U_{n, \varvec{\ell }} + O_{L^\infty _tH^s_x} \left( R^N\right) \end{aligned}$$where the constant depends on N. In terms of Fourier variables this can be written as,
$$\begin{aligned} |a_k(t)|^2 \!=\! \left| \sum \limits _{n=1}^N \sum \limits _\ell J_{n, \varvec{\ell }} \right| ^2 \!+\! O_{\ell _L^{1,2s}} \left( R^N\right) \!=\!\left| \sum \limits _{n=1}^N \sum \limits _\ell J_{n, \varvec{\ell }} \right| ^2 + O_{\ell ^{\infty }} \left( L^d R^N\right) . \end{aligned}$$ -
-
3)
Pairing. By Proposition 4.1,
$$\begin{aligned} \left| \sum \limits _{n=1}^N \sum \limits _\ell J_{n, \varvec{\ell }} \right| ^2&= {\mathbb {E}} \left[ |J_1(k)|^2 + J_0(k) \overline{J_2(k)} + \overline{J_0(k)} J_2(k) \right] \\&\quad + O \left( \frac{t}{\tau } \frac{t \log t}{\sqrt{\tau }} \right) \\&= \phi _k + \frac{2 \lambda ^4}{L^{4d}} \sum \limits _{k - k_1 + k_2 - k_3=0} \phi _k \phi _{k_1} \phi _{k_2} \phi _{k_3} \left[ \frac{1}{\phi _k} - \frac{1}{\phi _{k_1}} + \frac{1}{\phi _{k_2}} - \frac{1}{\phi _{k_3}} \right] \\&\quad \times \left| \frac{\sin (t \pi \varOmega (k,k_1,k_2,k_3))}{\pi \varOmega (k,k_1,k_2,k_3)} \right| ^2 + O_{\ell ^\infty } \left( \frac{t}{\tau } \frac{t \log t}{\sqrt{\tau }} \right) \end{aligned}$$ -
4)
Large box limit \(L \rightarrow \infty \). By the equidistribution Theorem 8.1, we have for \(t < L^{d- \epsilon }\)
$$\begin{aligned}&\frac{2 \lambda ^4}{L^{4d}} \sum \limits _{k - k_1 + k_2 - k_3=0} \phi _k \phi _{k_1} \phi _{k_2} \phi _{k_3} \left[ \frac{1}{\phi _k} - \frac{1}{\phi _{k_1}} + \frac{1}{\phi _{k_2}} - \frac{1}{\phi _{k_3}} \right] \left| \frac{\sin (t \pi \varOmega (k,k_1,k_2,k_3))}{\pi \varOmega (k,k_1,k_2,k_3)} \right| ^2 \\&\quad = \frac{2 \lambda ^4}{L^{2d}} \int \limits \delta (\varSigma ) \phi (k) \phi (k_1) \phi (k_2) \phi (k_3) \left[ \frac{1}{\phi (k)} - \frac{1}{\phi (k_1)} + \frac{1}{\phi (k_2)} - \frac{1}{\phi (k_3)} \right] \\&\qquad \times \left| \frac{\sin (\pi t\varOmega (k,k_1,k_2,k_3))}{\pi \varOmega (k,k_1,k_2,k_3)} \right| ^2 \,dk_1 \, dk_2 \,dk_3 +O_{\ell ^\infty }(\frac{t}{\tau }L^{-\delta } ). \end{aligned}$$ -
5)
Large time limit \(t \sim T \rightarrow \infty \). Since for a smooth function f,
$$\begin{aligned} \int \left| \frac{\sin (\pi t x)}{x} \right| ^2 f(x)\,dx = \pi ^2t f(0) + O(1), \end{aligned}$$then, with \( \tau =\frac{L^{2d}}{2\lambda ^4}\), we have
$$\begin{aligned}&\frac{2 \lambda ^4}{L^{2d}} \int \limits \delta (\varSigma ) \phi (k) \phi (k_1) \phi (k_2) \phi (k_3) \left[ \frac{1}{\phi (k)} - \frac{1}{\phi (k_1)} + \frac{1}{\phi (k_2)} - \frac{1}{\phi (k_3)} \right] \\&\quad \times \left| \frac{\sin (\pi t\varOmega (k,k_1,k_2,k_3))}{\pi \varOmega (k,k_1,k_2,k_3)} \right| ^2 \,dk_1 \, dk_2 \,dk_3 = \frac{t}{\tau } {\mathcal {T}}(\phi ,\phi ,\phi ) + O\left( \frac{1}{\tau } \right) . \end{aligned}$$
Consequently, for \(\epsilon _0\) sufficiently small and \(t\le T\le L^{d-\epsilon _0}\), we choose \(L\ge L_1(\epsilon _0)\) to bound the error term in Step 1 by \(\frac{t}{\tau }L^{-\epsilon _0}\). Also, since \(R\le \frac{1}{2}\) then by picking N large enough we can bound the error in Step 2 by \(O(\frac{t}{\tau }L^{-\epsilon _0})\). Similarly, since \(t\log t \le L^{-\delta }\sqrt{\tau }\), then the error for Steps 3, 4, and 5, are of order \(O_{\ell ^\infty }(\frac{t}{\tau }L^{-\delta } )\), and this concludes the Proof of Theorem 2.2.
8 Number theoretic results
Our aim in this section is to prove the asymptotic formula for the following Riemann sum,
Theorem 8.1
Given \(\phi \in {\mathscr {S}}({\mathbb {R}}^d)\) and \(\epsilon >0\), there exists a \(\delta >0\) such that if \(0<t\le L^{d -\epsilon }\), then
where we recall \(\varSigma (k,k_1,k_2,k_3) = k - k_1 + k_2 - k_3\).
The difficulty in proving this theorem is that \(\varOmega \) can be very small, while the stated time interval for the validity of the asymptotic formula is very large. In fact if we restrict ourselves to a timescale which is not too long, then the asymptotic formula is straight forward as will be demonstrated in Proposition 8.10. However to prove this theorem as stated we need to generalize a result of Bourgain on pair correlations of generic quadratic forms [5].
Bourgain considered a positive definite diagonal form,
for generic \(\beta =(\beta _1,\ldots ,\beta _d)\in [1,2]^d\), and proved that for \(d=3\) the lattice points in the region,
are equidistributed at a scale of \(\frac{1}{L^{\rho }}\), for \(0< \rho <d-1\). Specifically, he proved,
provided \(|a|, |b|<O(1)\) and \(L^{-\rho }< b-a<1\). Here \({\mathcal {H}}^{2d-1}\) is the \(2d-1\) Hausdorff measure.
Our quadratic form \(\varOmega \), restricted to \(\varSigma \), can be transformed to Q(p, q), given in (8.1), as follows. Rescale time \(\mu \mathrel {\mathop :}=tL^{-2}\), let \(K_i = Lk_i\in {\mathbb {Z}}\), and denote by
Then the sum can be expressed as
By defining
then
where
Hence the sum can be expressed as
The quadratic form \(Q_0\) can be diagonalized by making the change of coordinates
where \(p_i\) and \(q_i\) are either both even or both odd, i.e.
Consequently, the sum (8.3), can be written as four different sums of the form,
where Q(p, q) is given byFootnote 3 (8.1), and where we suppressed the dependence of W on k for convenience.
Remark 8.2
Note that we do not exclude the points when \(p_i^2=q_i^2\) for all \(i\in [1,\ldots ,n]\), as Bourgain did. These points contribute \(O(L^d)\) to the sum and will be considered as lower order terms. They also explain the \(O(L^d)\) term in Theorem 8.1.
It is this fact that prevents us from using the full strength of our equidistribution result which holds for \(\mu =tL^{-2} \le L^{d-1 -\epsilon }\), and we use the result for \(t\le L^{d -\epsilon }\). This ensures that \(O(L^d)\) term is an error in the asymptotic formula.
To prove the asymptotic formula given in Theorem 8.1, with \(0< \mu = tL^{-2} \le L^{d-1 -\epsilon }\), we proceed as follows: 1) identify which part of the sum contributes the leading order term and which part contributes error terms; 2) prove equidistribution of lattice points on a coarse scale; 3) present Bourgain’s theorem on equidistribution on a fine scale; and finally 4) prove Theorem 8.1.
8.1 Identifying main terms vs error terms
To identify the leading order term in the equidistribution formula, we first obtain upper bounds on lattice sums that are optimal up to sub-polynomial factor.
For generic \(\beta =(\beta _1,\ldots ,\beta _d)\in [1,2]^d\), a good upper bound for the linear form \(\beta \cdot n\in [a,b]\), where \(n={\mathbb {Z}}^d\) is a consequence of the pigeonhole principle:
Lemma 8.3
The linear form \(\beta \cdot n\in [a,b]\) satisfies the following bound
Proof
Since \(\beta = (\beta _1,\ldots ,\beta _d)\) are generic, then for \(0<|n| \le M\) (see for example [8], Chapter VII)
For arbitrary \(n^{(1)}\ne n^{(2)}\in {\mathbb {Z}}^d\) satisfying \(a\le \beta \cdot n^{(i)} \le b\) and \(0<\left| n^{(i)}\right| \le M\),
By the pigeonhole principle we obtain (8.5). \(\square \)
An upper bound on the cardinality of the set,
can be obtained by bounding the number of lattice points in subsets of the form,
using Lemma 8.3, and by using the divisor bound \(d(k)\lesssim _\epsilon k^\epsilon \).
Lemma 8.4
For \(\ell =1,\dots d\) the cardinality of \(R_{{\mathbb {Z}}\ell }\) satisfies the bound
Proof
Define \(k_i=(p_i-q_i)(p_i+q_i)\), for \(1\le i \le \ell \). Since \(p_i=q_i\), for \(\ell +1\le i \le d\), we conclude
By the divisor bound
and by (8.5), with \(M=L^2\), we obtain
and (8.6) follows. \(\square \)
Corollary 8.5
The number of elements in \(R_{{\mathbb {Z}}}\), can be bounded by
Moreover, if we further assume \(\left| a\right| ,\left| b\right| \le 1\), then we have the improved bound
Proof
It suffices to apply the Lemma 8.4, and to observe that \(\ell \in \{ 1,\ldots ,d \}\) since \(p=q\) is excluded. (8.8) follows from noting that if \(\left| a\right| ,\left| b\right| \le 1\), then \(R_{{\mathbb {Z}}1}\) is empty. \(\square \)
Remark 8.6
Note, that in terms of the first estimate (8.7), the second term may be treated as an error as long as \(b-a\ge L^{-(d-1) + \epsilon _0}\) for some \(\epsilon _0>0\). Analogously, the second term of (8.8) may be treated as an error assuming \(b-a\ge L^{-d + \epsilon _0}\).
Following this remark on identifying the leading order term, we can now identify subsets of \(R_{{\mathbb {Z}}}\) that contribute error terms only. The first such subsets are when \(|p_i-q_i|\lesssim L^{1-\delta }\) for some fixed \(\delta >0\) and some i that we may without loss of generality assume to be 1.
Lemma 8.7
For \(\left| a\right| ,\left| b\right| \le 1\), the number of elements in \(R_{{\mathbb {Z}}}\) satisfying \(|p_1-q_1|\lesssim L^{1-\delta }\) satisfy the following bound
Proof
If \(p_{i}=q_{i}\) for at least one i, then by Corollary 8.5 with d replaced by \(d-1\), we have
which is lower order. Moreover, if \(p_i \ne q_i\) for all i, and \(|p_1-q_1| \lesssim L^{1-\delta }\), then the sum over \(2\le i \le d\) can be bounded by \(L^{2(d-2)^+}(b-a) + L^{0^+}\), using Lemma 8.4, while the sum over \(p_1\) and \(q_1\) can be by \(L^{2-\delta }\). This gives a bound of \(L^{2-\delta } \left( L^{2(d-2)^+}(b-a) + L^{0^+}\right) \), which is lower order if \(d\ge 3\). \(\square \)
Next we show that if one \(p_i\) or \(q_i\) is less than \(L^{1-\delta }\), where we may again assume \(i=1\), then the contribution to the number of elements in \(R_{{\mathbb {Z}}}\) is lower order.
Lemma 8.8
For \(\left| a\right| ,\left| b\right| \le 1\), we have the following estimate
Proof
If both \(|p_1| \lesssim L^{1-\delta }\) and \(|q_1| \lesssim L^{1-\delta }\) or \(p_i =q_i\) for at least one i, then by Lemma 8.7 we have the stated bound. Otherwise, the sum over \(2\le i \le d\) contributes \(L^{2(d-2)^+}(b-a) + L^{0^+}\), while the sum over \(p_1\) and \(q_1\) contributes \(L^{2-\delta }\). \(\square \)
From Lemmas 8.7 and 8.8, we have
Corollary 8.9
Setting
Then, for \(\left| a\right| ,\left| b\right| \le 1\), we have the following cardinality bound on the set difference \(R_{{\mathbb {Z}}}\setminus R_{{\mathbb {Z}}\delta }\)
8.2 Asymptotic formula on a coarse scale
These upper bounds, in particular Corollary 8.5 allow us to present a simple proof of the asymptotic formula for \(\# R_{{\mathbb {Z}}}\) on a coarser scale, e.g. \(b-a = L^{\frac{4}{3}}\). Note hat this is still better then the trivial Riemann sum scale of \(b-a= O(L^2)\).
Proposition 8.10
Fix \(\delta >0\) sufficiently small, then if \(L^{1+4\delta } \le b-a\le L^{2-\delta }\), we have the asymptotic formula
Proof
First we will smooth the characteristic functions by extending the region to a slightly bigger region with a controlled error term. This is done as follows. Let \(w_L\in C_c^\infty ([-L^{\delta },L+L^{\delta }])\) be a bump function satisfying \(w_L(x)=1\) for \(x\in [0,L]\) and
Then by setting \(W_L(x, y)= \prod _{i=1}^d w_L(L x_i) w_{L}(y_i)\), we have,
Moreover, if we denote by \(h_L\in C_c^\infty ([a-L^{1+2\delta },b+L^{1+2\delta }])\) a bump function \(h_L(x)=1\) for \(x\in [a, b]\) and
then by Corollary 8.5, we have
assuming that \(b-a\ge L^{1+4\delta }\). Thus, it is sufficient to obtain the asymptotic formula for
Using Fourier transform, we express \({\mathcal {S}}\) as
Applying Poisson summation we may rewrite S(s) as
where \(z = (x,y)\), and \(\ell = (m,n)\).
The term \(\ell =0\) contributes the asymptotic formula
where we used \((b-a)<L^{2-\delta }\) in replacing \(h_L(L^2Q)\)) by \(\delta _{dirac}(Q)\). So it remains to show that the sum for \(\ell \ne 0\) can be treated as error. First we estimate the sum for \(s \le \frac{1}{L^{1+\delta }}\). In this case we write \( \Phi (z,\ell ,s) = L^2Q(z)s-L \ell \cdot z,\) and note that since \(|s| \le \frac{1}{L^{1+\delta }}\) and \(|z|\lesssim 1\), then \(\left| \nabla _z \Phi (z,m,s)\right| \ge \frac{L\left| \ell \right| }{2}\), where
and thus upon integrating (8.11) by parts, we obtain
Since each derivative of \(W_L\) contributes \(L^{1-\delta }\), then each integration by parts contributes a factor of \(\frac{1}{L^{\delta }\left| \ell \right| }\). Applying a sufficient number of integrations by parts, and using the fact that \(|{\widehat{h}}_L(s)|\lesssim b-a\), we may ensure that the contribution for \(\ell \ne 0\) and \(|s| \le \frac{1}{L^{1+\delta }}\) is arbitrarily small.
For \(|s|\ge \frac{1}{L^{1+\delta }}\) we note that
for all N, and thus this term can be treated as an error. This concludes the stated result. \(\square \)
8.3 Bourgain’s theorem
Now we present Bourgain’s proof of equidistribution.
Theorem 8.11
Fix \(\epsilon >0\), then for \(\delta >0\) sufficiently small the following statement is true: Suppose \(I_j,J_j\subset [0,L]\), \(j=1,\ldots ,d\) for \(d\ge 3\) are intervals with length satisfying
Then for a, b satisfying \(\left| a\right| ,\left| b\right| \le 1\) and \({L^{-d+1+\epsilon }}<b-a<L^{-\epsilon }\) we have
In order to prove Theorem 8.11, we first make a series of reductions.
Step 1: Restrict to dyadic lengths and discrete intervals (a,b) We first show that it sufficient to assume dyadic lengths \(L=2^{N_1}\) for \(N_1\in {\mathbb {N}}\) and that \((a,b)=(N_2 L^{-d+1+\varepsilon },(N_2+1) L^{-d+1+\varepsilon })\), for \(N_2\in {\mathbb {Z}}\) such that \(\left| N_2\right| \le 2L^{d-1-\varepsilon }\). The restriction to dyadic lengths \(L=2^{N_1}\) is valid since it only has potential effect of modifying the implicit constants in the theorem. Now suppose (8.15) is satisfied for all such L and (a, b) as described above and suppose we are given another interval \((a',b')\) such that \(a',b'\) satisfies \(\left| a'\right| ,\left| b'\right| \le 1\) and \({L^{-d+1+2\epsilon }}<b'-a'<L^{-\epsilon }\). Then, by assuming \(\delta \) is sufficiently small (depending on \(\varepsilon \)), and summing over intervals of the form \((N_2 L^{-d+1+\varepsilon },(N_2+1) L^{-d+1+\varepsilon })\) we obtain
Thus, by again taking \(\delta \) smaller if needed, we obtain Theorem 8.11 with \(\varepsilon \) replaced by \(2\varepsilon \), i.e. up to a relabeling of \(\varepsilon \), we obtain Theorem 8.11.
Step 2: Ignore intervals that contribute lower order sums Set \({\tilde{\delta }}= 4d\delta \), then by Corollary 8.9 we have for \({\tilde{\delta }}\) sufficiently small,
where we have used the restriction of \(a-b\) and assumed \(\delta \) to be sufficiently small compared to \(\epsilon \).
Thus we restrict our attention to the case where
-
(a)
\(\forall p_i\in E_i, \text{ and } \forall q_i\in F_i, \text{ we } \text{ have } |p_i|> L^{1-{\tilde{\delta }}}, |q_i|>L^{1-{\tilde{\delta }}}\),
-
(b)
\(\text {distance}(E_i,F_i) > L^{1-{\tilde{\delta }}}\).
With this reduction at hand, we divide each interval into at most \(L^{3{\tilde{\delta }}}\) intervals, \(E_i=\cup _{\alpha }I^\alpha _i\) and \(F_i=\cup _{\alpha }J^\alpha _i\) each satisfying
-
(c)
\(\frac{1}{2} L^{1-3{\tilde{\delta }}} \le \left| I^\alpha _i\right| ,\left| J^\alpha _i\right| \le L^{1-3{\tilde{\delta }}}\),
and prove that for intervals \(I^{\alpha }_i\) and \(J^{\alpha }_i\), satisfying Conditions (a), (b), and (c) we have
Summing in \(\alpha \) and using (8.16) we have
Using that \({\tilde{\delta }}= 4d\delta \) and
we conclude (8.15).
Summarizing, if by abuse of notation, we drop the index \(\alpha \) and replace \({\tilde{\delta }}\) with \(\delta \), we have reduced the proof of Theorem 8.11 to proving the following proposition.
Proposition 8.12
Fix \(\epsilon >0\), then for \(\delta >0\) sufficiently small the following statement is true: Suppose \(I_j,J_j\subset [-L,L]\), \(j=1,\ldots ,d\) for \(d\ge 3\) are intervals satisfying
-
(1)
\(\forall p_i\in I_i, \text{ and } \forall q_i\in J_i, \text{ we } \text{ have } |p_i|> L^{1-\delta }, |q_i|>L^{1- \delta }\).
-
(2)
\(\text{ distance }(I_i,J_i) > L^{1-\delta }\).
-
(3)
\(\frac{1}{2} L^{1-3\delta } \le \left| I_i\right| ,\left| J_i\right| \le L^{1-3\delta }\)
Then for a, b satisfying \(\left| a\right| ,\left| b\right| \le 1\) and \({L^{-d+1+\epsilon }}<b-a<L^{-\epsilon }\) we have
Let us now suppose \(I_j\) and \(J_j\) satisfy the hypothesis of Proposition 8.12.
Step 3: Transform the region of summation The sum can be written as,
By writing \(I_d=[u-\Delta u,u+\Delta u]\), and \(J_d=[v-\Delta v,v+\Delta v]\), and utilizing the fact that \(|u- v| > L^{1-{\delta }}\), we express the region \(R_{{\mathbb {Z}}}\) as,
since
Setting \(\xi = \frac{b+a}{2}\) and \(\eta = \frac{b-a}{2}\), then by taking logarithms and Taylor expanding \(\ln (x)\) around \(x=1\) we obtain
here we assumed, without loss of generality, \(\sum _{j=1}^{d-1}\beta _j (p_j^2-q_j^2) -\xi > 0\) and \(p_d^2-q_d^2 > 0\).
Step 4: Replace the sum with an analogous sum
Instead of considering the sum over the region \(R_{{\mathbb {Z}}}\), we will consider the sum over the region \(S_{{\mathbb {Z}}}\), defined as
In order to make this reduction, we need a bound on cardinality of (p, q) satisfying
Such a bound would follow as a consequence of a version of a weaker version of Proposition 8.12 with the asymptotic formula (8.18) replaced with a sharp upper bound, i.e.,
Proposition 8.13
Fix \(\epsilon >0\), then for \(\delta >0\) sufficiently small the following statement is true: Suppose \(I_j\) and \(J_j\) satisfy the hypothesis of Proposition 8.12, then for a, b satisfying \(\left| a\right| ,\left| b\right| \le 1\) and \({L^{-d+1+\epsilon }}<b-a<L^{-\epsilon }\) we have
We note that for Proposition 8.12 compared with Proposition 8.13 we may require a stricter smallness criteria on \(\delta \) relative to the choice of \(\epsilon \). With this in mind, applying Proposition 8.13, the difference in summing in p and q satisfying (8.20) and computing the cardinality of \(S_{{\mathbb {Z}}}\) is of order \(O(L^{2(d-1)-(3d+1)\delta }(b-a))\) and hence can be treated as an error. We remark that such arguments will be used later to bound analogous error terms.
By the arguments above, the sum in Proposition 8.13 may be estimated from above by the cardinality of \(S_{{\mathbb {Z}}}\) with \(\eta \) replaced by \(2\eta \) in the set’s definition. Hence up to a factor of 2 in the definition of \(S_{{\mathbb {Z}}}\), to prove both Propositions 8.13 and 8.12, it suffices to obtain an asymptotic formula for \(S_{{\mathbb {Z}}}\).
If we set
then we can rewrite the cardinality of \(S_{{\mathbb {Z}}}\) as
For a technical reason (as will be seen in Step 7), we replace \(\mathbb {1}_{[-A,A]}\) by a smooth approximation. Let \(\phi :{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a smooth, non-negative, symmetric Friedrich mollifier, that is monotonically decreasing on \({\mathbb {R}}^+\). Setting \(\phi _\varepsilon (x)=\varepsilon ^{-1}\phi (\frac{x}{ \varepsilon })\). Then, we have
In an analogous argument to showing that the cardinality of \(R_{{\mathbb {Z}}}\) can well approximated by the cardinality of \(R_{{\mathbb {Z}}}\), we may show that sum II can be estimated up to an acceptable error.
Step 5: Expressing the sum using Fourier Transform The number \(\#S_{{\mathbb {Z}}}\) can be expressed using the Fourier transform as follows. Let
and write
where,
Step 6: A scaling argument As mentioned earlier, if A is large compared to \(L^{-1}\), then comparing the sum over \(S_{{\mathbb {Z}}}\) and the area of S is relatively simple. For this reason we split our sum by scaling with a factor \(\frac{A}{A_0}\), where \(A_0 = \frac{L^{4/3}}{\left| u^2-v^2\right| }\), i.e., split the integral into two terms,
Ignoring the factor \(\widehat{\phi _{L^{-100d}}}\), the first integral is counting p, q such that
As in Step 4, the factor \(\widehat{\phi _{L^{-100d}}}\) can be ignored, up to a suitable contributing error. Then, one is reduced to counting
Again, applying a similar upper/lower bounding argument to that used in Step 4 with the use of Proposition 8.13 replaced by the use of Proposition 8.10, we obtain
For the purpose of proving Proposition 8.13, one simply observes that the first term is of order \(O(L^{2(d-1)-3d\delta }(b-a))\). Thus in order to complete the proof of Propositions 8.12, 8.13, and by implication Theorem 8.11, it suffices to estimate IV.
Step 7: Replace \(S_2\) with a sum involving smooth cut-offs
We now replace the sum \(S_2\) with a sum involving smooth cut-offs. This is a preparatory step, that will be needed for Step 10, in order to apply an argument involving the Mellin transform and Riemann zeta function estimates.
We rewrite \(S_2\) in terms of the coordinates \(m=p_d-q_d\), \(n=p_d+q_d\) and the set
Then \(S_2\) becomes
Without loss of generality, we may assume \(\Delta u\le \Delta v\). Let us cover K by disjoint intervals \(M_j\) of length \( L^{1-100d{\delta }}\) and define \(w_j\) to be the center of \(M_j\). It is not difficult to show that that may be achieved such that \(\# \{M_j\}\lesssim L^{100d{\delta }}\) we have the following bound on the set difference
Thus we have
Using that \(M_j\) is of length \( L^{1-100d{\delta }}\), we may also replace m with the midpoints \(w_j\) in order to obtain the estimate
and hence
Again, up to an allowable error we may also replace the sharp cut-off cutoff functions with a smooth cut-off \(\psi \equiv 1\) on \([-1+L^{-100d\delta },1-L^{-100d\delta }]\) and supported on the interval \([-1,1]\), i.e.
Finally, the sum in m can be replaced be a sum involving a smooth cut-off, up to an allowable error
We now decompose IV as
By (8.27) we have
Observe that
and for any N we have
Thus using that \(A\lesssim (b-a)L^{-2+2\delta }\), we have
which is an acceptable error.
Step 8: V is an error Now consider V, we aim to show that
for a set of \((\beta _2, \beta _d)\) of full measure, independent of our choice of length \(L=2^{N_1}\) and interval \((a,b)=(N_2 L^{-d+1+\varepsilon },(N_2+1) L^{-d+1+\varepsilon })\). By Chebyshev’s inequality, it suffices to show
To see this, define
By Chebyshev’s inequality we have
Recall that \(\eta =L^{-d+1+\varepsilon }\), then, since
we obtain (8.30) for a set of \((\beta _2, \beta _d)\) of full measure, where the implicit constant depends on \((\beta _2, \beta _d)\).
Applying (8.28) and (8.29) we have
Averaging in \(\beta _2\) and \(\beta _d\), and using Plancherel’s theorem for the integral in \(\beta _d\), we have from the bounds \(A=\eta L^{-2+2{\delta }}\) and \(A_0= L^{-\frac{2}{3}+2{\delta }}\)
where we have used the trivial bound \(\# {\tilde{S}}_2\le \# I_d \#J_d \le L^{2-6\delta }\).
Step 9: Bounding VII To bound \(\left\| S_1\right\| _{L^2_{\beta _2}}\), we rewrite
where
for \(d>3\) or \( \psi _1= \psi _2=\xi \) for the case \(d=3\). Setting
we have
then for \(t\le L^4\), and by taking the sup over indices \(3\le i\le d-1\), we have
Here we a using the trivial bound for the case \(1\ge |t|\inf _{\beta _2}|\partial _{\beta _2}\Psi |\), otherwise we use Van der Corput’s Lemma (see for example [37] Chapter 8, Proposition 2). For the former case, to apply the proposition, we split the integral into regions for which \(\partial _{\beta _2}\Phi \) is monotonic in \(\beta _2\).
Set \((p_i-q_i)(p_i+q_i)=w_i\) and \((r_i-s_i)(r_i+s_i)=z_i\), and sum over fixed \(w_i\) and \(z_i\) using the divisor bound \(d(k)\lesssim _\epsilon |k|^\epsilon \), we obtain
The above sum can rearranged by summing first over the set,
and then over \((k,w_2,z_2)\) to obtain,
Now we estimate \(\#{\mathscr {A}}_{\psi }(k,w_2,z_2)\) for a fixed \((k,w_2,z_2)\). Assume \({\mathscr {A}}_{\psi }(k,w_2,z_2) \ne \emptyset \), then there exists \(w_0\) and \(z_0\), such that, \(L^{2-2{\delta }}\le \left| w_0-\psi _2\right| \le L^2\) and \(L^{2-2\delta }\le \left| z_0-\psi _1\right| \le L^2\) and
Thus
Since \({\widetilde{w}}_1\in {\mathbb {Z}}\) then \(\#{\mathscr {A}}_{\psi }\lesssim 1+\frac{L^2 \gcd (w_2,z_2)}{z_2}\), and consequently
Hence, applying this bound to VII yields
where we used that \(\eta =L^{-d+1+\varepsilon }\), \(\delta \) is sufficiently small and \(d\ge 3\).
Step 10: Bounding VIII Now consider VIII, we have
We proceed to estimate \(\left| S_j\right| \), defined in (8.26). Defining
and letting \({\hat{\chi }}\) denote Mellin transform of \(\chi \), then
Shifting the contour to \(\mathfrak {R}s=\frac{1}{2}\) we pick up the residue
which for \(\left| t\right| \ge L^{\frac{1}{3}}\) is order \(O(L^{-N})\) for any N due to the decay of \({\hat{\chi }}\) and that \(\Delta u\) and \(\Delta v\) are of comparable size. Then using \(\Delta u\sim L^{1-3{\delta }}\)
Again, using the rapid decay of \({\hat{\psi }}\), we have
We now utilize following classical \(L^4\) bound of the zeta function in the critical strip [25]
Using the above bound yields
Thus we obtain
An analogous argument also yields
Using the decomposition (8.26) and the bound \(\# \{M_j\}\lesssim L^{100d{\delta }}\), we have
Thus, combining the above estimate on \(S_2\) with (8.31), we obtain
where we used that \(\eta =L^{-d+1+\varepsilon }>L^{2}\) since \(d\ge 3\). Thus assuming \(\delta \) to be sufficiently small, then
and hence
as desired.
8.4 Proof of Theorem 8.1
First we note that the sum in Theorem 8.1 can be simplified as follows,
-
(1)
Ignore all pairs (p, q) such that \(\left| p_j\right| =\left| q_j\right| \) for each j. The sum of such pairs such that \(\left| p\right| ,\left| q\right| \le L^{1+\delta }\) is of order O(\(t^2L^{d(1+\delta )})\) and hence contributes to an admissible error, where here we used the restriction \(t\le L^{d -\epsilon }\).
-
(2)
We restrict the sum to the positive sector \(p,q\in {\mathbb {Z}}^d_+\cap [0,L^{1+\delta }]\) for \(p\ne q\). Here we are using that the subset of (p, q) such that \(p_j=0\) or \(q_j=0\) for some j is an admissible error. This follows as a consequence of Lemma 8.8. To rigorously carry out such an estimate, one must split the contributions when \(\left| Q(p,q)\right| \le \mu ^{-1}\) and \(\left| Q(p,q)\right| > \mu ^{-1}\). Assuming without of loss of generality that \(p_1=0\), then splitting up the later part dyadically in the size of \(\left| Q(p,q)\right| \) and using \(\left| g(x)\right| \lesssim \frac{1}{\left| x\right| ^2}\) one obtains the estimate
$$\begin{aligned} t^2 \sum _{ \begin{array}{c} (p,q)\in {\mathbb {Z}}_+^{2d}\\ p_1=0,~p\ne q \end{array}}\left| W\left( \frac{p}{L},\frac{q}{L}\right) g(\mu Q(p,q))\right|&\lesssim t^2\left( \frac{L^{2(d-1)^+ -2\delta }}{\mu }+ L^{(d-1)^+}\right) \lesssim tL^{2d-\delta }\, , \end{aligned}$$
where W was defined in (8.4).
With all these reductions in mind, proving Theorem 8.1 will follow as a consequence of the following theorem.
Theorem 8.14
(Equidistribution) Fix \(\epsilon >0\) and let \(\delta >0\) be sufficiently small. Then for generic \(\beta \in [1,2]^d\), we have that for any function \(W \in {\mathscr {S}}({\mathbb {R}}^d)\), the following holds,
where \(1< \mu \le L^{d-1 -\epsilon }\).
We remark that the above theorem is actually stronger than required: in view of the restriction on t in the hypothesis of Theorem 8.1, we need only consider \(\mu \) within the range \(0<\mu \le L^{d-2 -\epsilon }\).
Before we prove Theorem 8.14, we will need a couple of auxiliary lemmas. The following lemma is helpful in bounding errors to the asymptotic formula.
Lemma 8.15
Let \(\epsilon >0\). Given a generic quadratic from Q(p, q) as defined in (8.1), we have the following estimate
for \(a\ge L^{-d+\epsilon }\)
Proof
We begin by dyadically subdividing the interval \([a,CL^2]\), for some large C, we define
Applying Lemma 8.4 yields
\(\square \)
The following lemma will be useful localizing the sum in Theorem 8.14.
Lemma 8.16
Fix \(\epsilon >0\), then for \(\delta >0\) sufficiently small the following statement is true: Suppose \(I_j,J_j\subset \mathbb [0,L]\) for \(j=1,\ldots ,n\) are intervals with length satisfying
and define
Then for \(\mu \) satisfying \(L^{\epsilon }\le \mu \le L^{d-\epsilon }\) we have
Proof
First note that by Lemma 8.15
Define the sum A(y) and the integral \({\tilde{A}}\) as follows
Then in the sense of distributions
where in the last inequality we applied Lemma 8.4 and the bound \(L^{\epsilon }\le \mu \le L^{d-\epsilon }\). Writing \(A={\tilde{A}}+(A-{\tilde{A}})\), we have
By Theorem 8.11 (by choosing \(\delta \) smaller than the \(\delta \) used in the theorem) it follows that assuming \(y\ge L^{-d+\epsilon }\) then
For \(y\le L^{-d+\epsilon }\) by the trivial bound
Using the trivial bound \(g'(z)\lesssim 1\) we have
where in the last inequality we used \(\mu \le L^{d-\epsilon }\). Choosing \(\delta \) sufficiently small in relation to \(\epsilon \), this constitutes an allowable error. The proof concludes by noting that by integration by parts
\(\square \)
Proof of Theorem 8.14
We first note that by symmetry, it is sufficient to restrict ourselves to the positive sector \(p,q\in {\mathbb {Z}}^d_+\). Note that Lemma 8.8 implies the subset of (p, q) such that \(p_j=0\) or \(q_j=0\) may be treated as an admissible error. Thus, it suffices to show
Divide \([0,L^{\delta }]^d\times [0,L^{\delta }]^d\) into products of cubes \(M_j,N_k\subset {\mathbb {R}}_+^d\) of length \(L^{-10d\delta }\). Define \(W_{j,k}\) to be the average of W over \(M_j\times N_k\):
Note that if \((x,y)\in M_j\times N_k\) then from the smoothness of W
Hence using Lemma 8.15
Applying Lemma 8.16 (taking \(\delta \) to be sufficiently small) we obtain
\(\square \)
Notes
Degenerate cases, like higher order terms, have smaller order of magnitude, on the timescales we consider as will be illustrated in Sect. 4.
This follows from Plancherel’s theorem, and the fact that the Fourier transform of \(\frac{1}{\pi } \frac{\sin x}{x}\) is the characteristic function of \([-\frac{1}{2\pi },\frac{1}{2\pi }]\).
There are factors of 2 missing due to sums over even terms. However, this has no impact since \(\beta \) is generic.
References
Benedetto, D., Castella, F., Esposito, R., Pulvirenti, M.: Some considerations on the derivation of the nonlinear quantum Boltzmann equation. J. Statist. Phys. 116(1–4), 381–410 (2004)
Benedetto, D., Castella, F., Esposito, R., Pulvirenti, M.: Some considerations on the derivation of the nonlinear quantum Boltzmann equation. II. The low density regime. J. Stat. Phys. 124(2—-4), 951–996 (2006)
Benedetto, D., Castella, F., Esposito, R., Pulvirenti, M.: From the \(N\)-body Schrödinger equation to the quantum Boltzmann equation: a term-by-term convergence result in the weak coupling regime. Comm. Math. Phys. 277(1), 1–44 (2008)
Bourgain, J.: Fourier transform restriction phenomena for certain lattice subsets and applications to nonlinear evolution equations I Schrödinger equations. Geom. Funct. Anal. 3(2), 107–156 (1993)
Bourgain, J.: On pair correlation for generic diagonal forms. arXiv e-printsarXiv:1606.06173 (June 2016)
Buckmaster, T., Germain, P., Hani, Z., Shatah, J.: Effective dynamics of the nonlinear Schrödinger equation on large domains. Comm. Pure Appl. Math. 71(7), 1407–1460 (2018)
Burq, N., Tzvetkov, N.: Random data Cauchy theory for supercritical wave equations. I. Local theory. Invent. Math. 173(3), 449–475 (2008)
Cassels, J.W.S.: An introduction to Diophantine approximation. Hafner Publishing Co., New York, : Facsimile reprint of the, 1957th edn., p. 45. Cambridge Tracts in Mathematics and Mathematical Physics (1972)
Christ, M.: Power series solution of a nonlinear Schrödinger equation. In: Mathematical Aspects of Nonlinear Dispersive Equations, vol. 163 Ann. Math. Stud., pp. 131–155. Princeton University Press, Princeton, NJ (2007)
de Suzzoni, A., Tzvetkov, N.: On the propagation of weakly nonlinear random dispersive waves. Arch. Ration. Mech. Anal. 212(3), 849–874 (2014)
Deng, Y., Germain, P., Guth, L.: Strichartz estimates for the Schrödinger equation on irrational tori. J. Funct. Anal. 273(9), 2846–2869 (2017)
Erdős, L.: Lecture notes on quantum brownian motion. In: Quantum Theory from Small to Large Scales, pages 3–98. Oxford University Press, (2012)
Erdős, L., Salmhofer, M., Yau, H.: On the quantum Boltzmann equation. J. Statist. Phys. 116(1–4), 367–380 (2004)
Erdős, L., Salmhofer, M., Yau, H.: Quantum diffusion of the random Schrödinger evolution in the scaling limit. II. The recollision diagrams. Comm. Math. Phys. 271(1), 1–53 (2007)
Erdős, L., Salmhofer, M., Yau, H.: Quantum diffusion of the random Schrödinger evolution in the scaling limit. Acta Math. 200(2), 211–277 (2008)
Escobedo, M., Velázquez, J.J.L.: On the theory of weak turbulence for the nonlinear Schrödinger equation. Mem. Amer. Math. Soc. 238(1124), v+107 (2015)
Faou, E.: Linearized wave turbulence convergence results for three-wave systems. Commun. Math. Phys. 378, 807–849 (2020). https://doi.org/10.1007/s00220-020-03799-w
Faou, E., Germain, P., Hani, Z.: The weakly nonlinear large-box limit of the 2D cubic nonlinear Schrödinger equation. J. Am. Math. Soc. 29, 915–982 (2016)
Gallagher, I., Saint-Raymond, L., Texier, B.: From Newton to Boltzmann: hard spheres and short-range potentials. Zurich Lectures in Advanced Mathematics. Eur. Math. Soc. (EMS), Zürich, (2013)
Germain, P., Hani, H., Thomann, L.: On the continuous resonant equation for NLS, II: Statistical study. Anal. PDE 8(7), 1733–1756 (2015)
Germain, P., Hani, H., Thomann, L.: On the continuous resonant equation for NLS. I. Deterministic analysis. J. Math. Pures Appl. (9) 105(1), 131–163 (2016)
Germain, P., Ionescu, A.D., Tran, M.-B.: Optimal local well-posedness theory for the kinetic wave equation. J. Funct. Anal. 279(4), 108570 (2020). https://doi.org/10.1016/j.jfa.2020.108570
Hasselmann, K.: On the non-linear energy transfer in a gravity-wave spectrum Part 1. General theory. J. Fluid Mech. 12(04), 481–500 (1962)
Hasselmann, K.: On the non-linear energy transfer in a gravity wave spectrum. II. Conservation theorems; wave-particle analogy; irreversibility. J. Fluid Mech. 15, 273–281 (1963)
Heath-Brown, D.R.: The fourth power moment of the Riemann zeta function. Proc. London Math. Soc. (3) 38(3), 385–422 (1979)
Ionescu, A.D., Pausader, B.: The energy-critical defocusing NLS on \({\mathbb{T}}^3\). Duke Math. J. 161(8), 1581–1612 (2012)
Lanford, O.E.: III.: Time Evolution of Large Classical Systems. Springer, Berlin (1975)
Lukkarinen, J., Spohn, H.: Not to normal order-notes on the kinetic limit for weakly interacting quantum fluids. J. Stat. Phys. 134(5), 1133–1172 (2009)
Lukkarinen, J., Spohn, H.: Weakly nonlinear Schrödinger equation with random initial data. Invent. Math. 183(1), 79–188 (2011)
Majda, A.J., McLaughlin, D.W., Tabak, E.G.: A one-dimensional model for dispersive wave turbulence. J. Nonlinear Sci. 7(1), 9–44 (1997)
Nazarenko, S.: Wave turbulence. Lecture Notes in Physics, vol. 825. Springer, Heidelberg (2011)
Newell, A.C., Rumpf, B.: Wave turbulence: a story far from over. In: Advances in wave turbulence, volume 83 of World Sci. Ser. Nonlinear Sci. Ser. A Monogr. Treatises, pp. 1–51. World Scientific Publishing, Hackensack, NJ, (2013)
Peierls, R.: Zur kinetischen theorie der wärmeleitung in kristallen. Annalen der Physik 395(8), 1055–1101 (1929)
Soffer, A., Tran, M.-B.: On the energy cascade of 3-wave kinetic equations: beyond Kolmogorov–Zakharov solutions. Commun. Math. Phys. 376, 2229–2276 (2020). https://doi.org/10.1007/s00220-019-03651-w
Spohn, H.: Derivation of the transport equation for electrons moving through random impurities. J. Statist. Phys. 17(6), 385–412 (1977)
Spohn, H.: The phonon Boltzmann equation, properties and link to weakly anharmonic lattice dynamics. J. Stat. Phys. 124(2–4), 1041–1104 (2006)
Stein, E.: Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals, volume 43 of Princeton Mathematical Series. Princeton University Press, Princeton, NJ, (1993). With the assistance of Timothy S. Murphy, Monographs in Harmonic Analysis, III. ISBN: 9780691032160
Zakharov, V., L’vov, V., Falkovich, G.: Kolmogorov Spectra of Turbulence I: Wave Turbulence. Springer Science & Business Media, Berlin (2012)
Acknowledgements
TB was supported by the National Science Foundation Grant DMS-1820764. PG was supported by the National Science Foundation Grant DMS-1301380. JS was supported by the National Science Foundation Grant DMS-1363013. ZH was supported by National Science Foundation Grant DMS-1852749, NSF CAREER award DMS-1654692, and a Sloan Fellowship.
Author information
Authors and Affiliations
Corresponding author
Additional information
We dedicate this manuscript to the memory of Jean Bourgain (1954–2018).
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Buckmaster, T., Germain, P., Hani, Z. et al. Onset of the wave turbulence description of the longtime behavior of the nonlinear Schrödinger equation. Invent. math. 225, 787–855 (2021). https://doi.org/10.1007/s00222-021-01039-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00222-021-01039-z