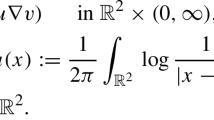Stability of Regularized Hastings–Levitov Aggregation in the Subcritical Regime

Abstract

We prove bulk scaling limits and fluctuation scaling limits for a two-parameter class ALE$({\alpha },\eta )$ of continuum planar aggregation models. The class includes regularized versions of the Hastings–Levitov family HL$({\alpha })$ and continuum versions of the family of dielectric-breakdown models, where the local attachment intensity for new particles is specified as a negative power $-\eta$ of the density of arc length with respect to harmonic measure. The limit dynamics follow solutions of a certain Loewner–Kufarev equation, where the driving measure is made to depend on the solution and on the parameter ${\zeta }={\alpha }+\eta$. Our results are subject to a subcriticality condition ${\zeta }\leqslant 1$: this includes HL$({\alpha })$ for ${\alpha }\leqslant 1$ and also the case ${\alpha }=2,\eta =-1$ corresponding to a continuum Eden model. Hastings and Levitov predicted a change in behaviour for HL$({\alpha })$ at ${\alpha }=1$, consistent with our results. In the regularized regime considered, the fluctuations around the scaling limit are shown to be Gaussian, with independent Ornstein–Uhlenbeck processes driving each Fourier mode, which are seen to be stable if and only if ${\zeta }\leqslant 1$.

1 Introduction

1.1 Hastings–Levitov aggregation

In many physical contexts there appear clusters whose shape is complex, formed apparently by some mechanism of random growth. It has long been a challenge to account for the observed variety of complex cluster shapes, starting from plausible physical principles governing the aggregation of individual microscopic particles. For clusters which are essentially two-dimensional, there is an approach introduced by Carleson and Makarov [4] and Hastings and Levitov [10], in which clusters are encoded as a composition of conformal maps, one for each particle. In this approach, a growing cluster is modelled by an increasing sequence of compact sets $K_n\subseteq \mathbb {C}$ which are assumed to be simply connected. We will take the initial set $K_0$ to be the closed unit disk $\{|z|\leqslant 1\}$. The increments $K_n\setminus K_{n-1}$ are then thought of as a sequence of particles added to the cluster. The idea is to study the clusters $K_n$ via the conformal isomorphisms

$$\begin{aligned} \Phi _n:D_0\rightarrow D_n \end{aligned}$$

where $D_n$ is the complementary domain $\mathbb {C}\setminus K_n$ and $\Phi _n$ is normalized by $\Phi _n(\infty )=\infty$ and $\Phi _n'(\infty )>0$. Then $\Phi _0(z)=z$ for all z and $K_n$ has logarithmic capacity $\Phi _n'(\infty )>1$ for all $n\geqslant 1$. This formulation is convenient because the harmonic measure from $\infty$ on the boundary $\partial D_n$, which provides a natural way to choose the location of the next particle, is then simply the image under $\Phi _n$ of the uniform distribution on $\partial D_0=\{|z|=1\}$. Having chosen a random angle ${\Theta }_{n+1}$ to locate the next particle, and a model particle $P_{n+1}$ attached to $K_0$ at $e^{i{\Theta }_{n+1}}$, for example a small disk tangent to $K_0$, the cluster map is updated to

$$\begin{aligned} \Phi _{n+1}=\Phi _n\circ F_{n+1} \end{aligned}$$

(1)

where $F_{n+1}$ is the conformal isomorphism $D_0\rightarrow D_0\setminus P_{n+1}$, normalized similarly to $\Phi _n$. Then $\Phi _{n+1}$ encodes the cluster

$$\begin{aligned} K_{n+1}=K_n\cup \Phi _n(P_{n+1}). \end{aligned}$$

Thus, once we specify distributions for the angles ${\Theta }_n$ and model particles $P_n$, we have specified a mechanism to grow a random cluster.

We will write

$$\begin{aligned} {{\text {cap}}}(K_n)=\log \Phi '(\infty ),\quad c_n=\log F_n'(\infty ) \end{aligned}$$

and we will refer to ${{\text {cap}}}(K_n)$ as the capacity¹ of $K_n$ and $c_n$ as the capacity of $P_n$. Then

$$\begin{aligned} {{\text {cap}}}(K_n)=c_1+\dots +c_n. \end{aligned}$$

We will be looking for scaling limits where the particle capacities $c_n$ and the associated particles $P_n$ become small, but where n is chosen sufficiently large that the cluster capacities ${{\text {cap}}}(K_n)$ grow macroscopically.

A simple case is to choose ${\Theta }_{n+1}$ uniformly distributed on the unit circle and to take $P_{n+1}=e^{i{\Theta }_{n+1}}P$, where P is a small disk tangent to the unit disk at 1, of radius r(c), chosen so that P has capacity c. Then in fact $r(c)/\sqrt{c}$ has a positive limit as $c\rightarrow 0$. The location of the new particle $\Phi _n(P_{n+1})$ is then distributed according to harmonic measure on $\partial K_n$. However, if we assume that $\partial K_n$ is approximately linear on the scale of P, then we would have

$$\begin{aligned} \Phi _n(P_{n+1})\approx \Phi _n(e^{i{\Theta }_{n+1}})+\Phi _n'(e^{i{\Theta }_{n+1}})P \end{aligned}$$

(2)

so we would add an approximate disk of diameter proportional to $\sqrt{c}|\Phi _n'(e^{i{\Theta }_{n+1}})|$.

In order to compensate for this distortion, Hastings and Levitov proposed the HL$({\alpha })$ family of models where, once ${\Theta }_{n+1}$ is chosen, we choose $P_{n+1}$ to be a particle of capacity

$$\begin{aligned} c_{n+1}=|\Phi _n'(e^{i{\Theta }_{n+1}})|^{-{\alpha }}c. \end{aligned}$$

Then, in the case ${\alpha }=2$, the particles added to the cluster would be approximately of constant size. The approximation (2) is in fact misleading, at least on a microscopic level, because $\partial K_n$ develops inhomogeneities on the scale of the particles. Nevertheless, HL(2) has been considered as a variant of diffusion-limited aggregation (DLA) [28], with some justification, see [10], derived from numerical experiments.

In general, the HL$({\alpha })$ model offers a convenient mechanism for such experiments, and moves away from the lattice formulation of [28] which has been shown to lead to unphysical effects on large scales (see for example [8]). Moreover, it might be hoped that an evolving family of conformal maps would present a more tractable framework for the analysis of scaling limits than other growth models, while potentially sharing the same bulk scaling limit and fluctuation universality class. That is the direction explored in this paper.

Besides the mechanism of diffusive aggregation, based on harmonic measure, there is another one-parameter family of models, conceived originally in the lattice case, called dielectric breakdown models [20], which interpolates between DLA and the Eden model [7]. In the Eden model, each boundary site is chosen with equal probability. In the continuum setting, for an Eden-type model we would choose an attachment point on the boundary according to normalized arc length, which has density proportional to $|\Phi _n'(e^{i{\theta }})|$ with respect to harmonic measure. We can widen our family of models to include a continuum analogue of dielectric breakdown models (DBM) by choosing

$$\begin{aligned} \mathbb {P}({\Theta }_{n+1}\in d{\theta }|\Phi _n)\propto |\Phi _n'(e^{i{\theta }})|^{-\eta }d{\theta }. \end{aligned}$$

The case $\eta =-1$ then provides a continuum variant of the Eden model.

In a law-of-large-numbers regime, it might be guessed that bulk characteristics of the cluster for the model incorporating both the ${\alpha }$ and $\eta$ modifications would depend only on their sum ${\zeta }={\alpha }+\eta$ since, once this is fixed, up to a global time-scaling, the growth rate of capacity due to particles attached near $e^{i{\theta }}$ does not depend further on ${\alpha }$ or $\eta$. We will show, in the regime which we can address, that this is indeed true.

In this paper we investigate the two-parameter family of models just described, but modified by the introduction of a regularization parameter ${\sigma }>0$, which controls the minimum length scale over which feedback occurs through $c_{n+1}$ and ${\Theta }_{n+1}$. Specifically, we require

$$\begin{aligned} \mathbb {P}({\Theta }_{n+1}\in d{\theta }|\Phi _n)\propto |\Phi _n'(e^{\sigma + i{\theta }})|^{-\eta }d{\theta }, \quad c_{n+1}=|\Phi _n'(e^{\sigma + i{\Theta }_{n+1}})|^{-{\alpha }}c. \end{aligned}$$

(3)

This model was introduced in [27] as the (discrete-time) aggregate Loewner evolution model. We will require throughout that ${\sigma }\gg \sqrt{c}$ (and sometimes more) and we will restrict attention to the subcritical regime ${\zeta }\leqslant 1$. This includes the Eden case (${\alpha }=2$, $\eta =-1$) but excludes continuum DLA (${\alpha }=2$, $\eta =0$). In the regularized models, we will show fluctuation behaviour which is universal over all choices of particle family. Our first main result shows that, in this regime, in the limit $c\rightarrow 0$, disks are stable, that is, an initial disk cluster remains close to a disk as particles are added and its capacity becomes large. Our second main result is to prove convergence of the normalized fluctuations of the cluster around its deterministic limit, to an explicit Gaussian process. The constraint ${\zeta }\leqslant 1$ appears sharp for this behaviour: we see an explicit dependence of the fluctuations on ${\alpha }$ and $\eta$ and, in particular, an exponential instability of rate $({\zeta }-1)k$ in the kth Fourier mode if we formally take ${\zeta }>1$.

1.2 Statement of results

In this section, we define the continuous-time ALE$({\alpha },\eta )$ model, which is our object of study, and we specify our standing assumptions for individual particles. We then state our main results.

Our model is constructed as a composition of univalent functions on the exterior unit disk $D_0=\{|z|>1\}$. Each of these functions corresponds to a choice of attachment angle ${\theta }\in [0,2\pi )$ and a basic particle P. Recall that $K_0=\{|z|\leqslant 1\}$. By a basic particle P we mean a non-empty subset of $D_0$ such that $K_0\cup P$ is compact and simply connected. Set $D=D_0\setminus P$. By the Riemann mapping theorem, there is a $c\in (0,\infty )$ and a conformal isomorphism $F:D_0\rightarrow D$ with Laurent expansion of the form

$$\begin{aligned} F(z)=e^c\left( z+\sum _{k=0}^\infty a_kz^{-k}\right) . \end{aligned}$$

(4)

Then F is uniquely determined by P, and P has capacity c. Our model depends on three parameters ${\alpha },\eta \in \mathbb {R}$ and ${\sigma }\in (0,\infty )$, along with the choice of a family of basic particles $(P^{(c)}:c\in (0,\infty ))$ with $P^{(c)}$ of capacity c. The associated maps $F_c:D_0\rightarrow D^{(c)}$ then have the form (4) with $a_k=a_k(c)$ for all k. We assume throughout that $F_c$ extends continuously to $\{|z|\geqslant 1\}$. We require that our particle family is nested

$$\begin{aligned} P^{(c_1)}\subseteq P^{(c_2)}\quad \text {for}\, c_1<c_2 \end{aligned}$$

(5)

and satisfies, for some ${\Lambda }\in [1,\infty )$,

$$\begin{aligned} {\delta }(c)\leqslant {\Lambda }r_0(c)\quad \text {for all}\,\, c \end{aligned}$$

(6)

where

$$\begin{aligned} r_0(c)=\sup \{|z|-1:z\in P^{(c)}\},\quad {\delta }(c)=\sup \{|z-1|:z\in P^{(c)}\}. \end{aligned}$$

In our results, only small values of c are of interest. For such c, the last condition (6) forces our particles $P^{(c)}$ to concentrate near the point 1 while never becoming too flat against the unit circle.

The following are all examples of particle families satisfying both conditions (5) and (6):

$$\begin{aligned} P^{(c)}_{{\text {slit}}}=(1,1+{\delta }(c)],\quad P^{(c)}_{{\text {bump}}}=\{z\in D_0:|z-1|\leqslant {\delta }(c)\} \end{aligned}$$

and

$$\begin{aligned} P^{(c)}_{{\text {disk}}}=\{z\in D_0:|z-1-r(c)|\leqslant r(c)\},\quad r(c)={\delta }(c)/2 \end{aligned}$$

where in each case ${\delta }$ is a suitable increasing homeomorphism of $(0,\infty )$.

It will be convenient to place our aggregation models from the outset in continuous time. By a (continuous-time) aggregate Loewner evolution of parameters ${\alpha },\eta \in \mathbb {R}$, or ALE$({\alpha },\eta )$, we mean a finite-rate, continuous-time Markov chain $(\Phi _t)_{t\geqslant 0}$ taking values in the set of univalent functions $D_0\rightarrow D_0$, starting from $\Phi _0(z)=z$, which, when in state $\phi$, jumps to $\phi \circ F_{c({\theta },\phi ),{\theta }}$ at rate ${\lambda }({\theta },\phi )d{\theta }/(2\pi )$, where

$$\begin{aligned} F_{c,{\theta }}(z)=e^{i{\theta }}F_c(e^{-i{\theta }}z),\quad c({\theta },\phi )=c|\phi '(e^{{\sigma }+i{\theta }})|^{-{\alpha }},\quad {\lambda }({\theta },\phi )=c^{-1}|\phi '(e^{{\sigma }+i{\theta }})|^{-\eta }.\nonumber \\ \end{aligned}$$

(7)

Since ${\sigma }>0$, the rate ${\lambda }({\theta },\phi )$ is continuous in ${\theta }$, so the total jump rate is finite. The model may be thought of equivalently in term of the random process of compact sets $(K_t)_{t\geqslant 0}$ given by

$$\begin{aligned} K_0=\{|z|\leqslant 1\},\quad K_t=K_0\cup \{z\in D_0:z\not \in \Phi _t(D_0)\}. \end{aligned}$$

The effect of the jump just described is then to add to the current cluster the set $\phi (e^{i{\theta }}P^{(c({\theta },\phi ))})$ thereby increasing its capacity by $c({\theta },\phi )$.

An explicit realisation of this Markov chain can be constructed as follows. Given a univalent function $\phi : D_0\rightarrow D_0$, define the normalising constant

$$\begin{aligned} Z_\phi = \int _0^{2 \pi } |\phi '(e^{\sigma +i\theta })|^{-\eta } d\theta . \end{aligned}$$

Starting from $\Phi _0(z) = z$, suppose that a realisation of $(\Phi _s)_{0 \leqslant s \leqslant t}$ has been constructed up to some $t \geqslant 0$, and that $\Phi _t = \phi$. Sample independently a random time $T \sim \textrm{Exp}(c^{-1} Z_\phi / (2 \pi ))$ and random angle $\Theta$ with density function $|\phi '(e^{\sigma +i\theta })|^{-\eta }/ Z_\phi$. Then set $\Phi _s = \phi$ for $t< s < t+T$, and $\Phi _{t+T}=\phi \circ F_{c({\Theta },\phi ),{\Theta }}$. It is straightforward to verify that this construction gives a Markov chain with distribution corresponding to the specification above.

Denote the jump times of the Markov chain by $T_k$, $k=1, 2, \dots$. By the explicit construction,

$$\begin{aligned} \Phi _{T_{n+1}}=\Phi _{T_n}\circ F_{n+1} \end{aligned}$$

where $F_n=F_{C_n,{\Theta }_n}$, for capacity $C_n$ and attachment angle ${\Theta }_n$ satisfying

$$\begin{aligned} \mathbb {P}({\Theta }_{n+1}\in d{\theta }|\Phi _{T_n})\propto |\Phi _{T_n}'(e^{\sigma + i{\theta }})|^{-\eta }d{\theta }, \quad C_{n+1}=|\Phi _{T_n}'(e^{\sigma + i{\Theta }_{n+1}})|^{-{\alpha }}c. \end{aligned}$$

Therefore, if $T_n \leqslant t < T_{n+1}$, we have

$$\begin{aligned} \Phi _t=F_1\circ \dots \circ F_n, \end{aligned}$$

as in Fig. 1. Moreover, the capacity ${{\mathcal {T}}}_t$ of the cluster $K_t$ is then given by

$$\begin{aligned} {{\mathcal {T}}}_t=\log \Phi _t'(\infty )=C_1+\dots +C_n. \end{aligned}$$

Fig. 1

Cluster map with n particles

For certain parameter values, the process $(\Phi _t)_{t\geqslant 0}$ may explode, that is, may take infinitely many jumps in a finite time interval. We will show in Proposition A.1 that explosion occurs if and only if both $\eta <0$ and ${\zeta }={\alpha }+\eta <0$, and in this case we also have ${{\mathcal {T}}}_t\rightarrow \infty$ at the explosion time. This phenomenon is however irrelevant to our main results on scaling limits, since explosion is excluded by these results (with high probability) over the relevant time interval. Hence we will make no attempt to define $\Phi _t$ beyond explosion.

By reference to (1) and (3), it is immediate that the jump-chain $(\Phi _{T_n})_{n\geqslant 0}$ is exactly the discrete-time aggregate Loewner evolution process $(\Phi _n)_{n\geqslant 0}$ in the introductory discussion. In particular, in the case $\eta =\sigma =0$, $(\Phi _t)_{t\geqslant 0}$ is the original Hastings–Levitov process embedded in continuous time as a Poisson process with jumps of rate $c^{-1}$. For clarity, from now on we denote the discrete-time process by $(\Phi ^{{\text {disc}}}_n)_{n\geqslant 0}$. Prior work on ALE models [21, 27] was framed in terms of this discrete-time process. The continuous-time framework allows a more local specification of the dynamics, without the need to normalise the distribution of attachment angles. It further allows us to organise the computation of martingales in terms of a standard calculus for Poisson random measures.

We can now state our first main result. Define

$$\begin{aligned} t_{\zeta }= {\left\{ \begin{array}{ll} \infty ,&{}\text {if}\, {\zeta }\geqslant 0,\\ |{\zeta }|^{-1},&{}\text {if}\, {\zeta }<0. \end{array}\right. } \end{aligned}$$

and for $t<t_{\zeta }$ set

$$\begin{aligned} {\tau }_t= {\left\{ \begin{array}{ll} t,&{}\text {if}\, {\zeta }=0,\\ {\zeta }^{-1}\log (1+{\zeta }t),&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

Note that ${\tau }_t\rightarrow \infty$ as $t\rightarrow t_{\zeta }$ for all ${\zeta }$.

Fig. 2

Domain of stability for ALE$({\alpha },\eta )$

The result identifies the small-particle scaling limit of $K_t$ in the case ${\zeta }\leqslant 1$ as a disk of radius $e^{{\tau }_t}$, with quantified error estimates. It is proved in Proposition 5.7. The range of parameter values to which the result applies is indicated by the region shaded red in Fig. 2, with diagonal lines showing parameter pairs $({\alpha },\eta )$ sharing a common bulk scaling limit. Recall that ${{\mathcal {T}}}_t=\log \Phi _t'(\infty )$, which is the capacity of $K_t$, and set

$$\begin{aligned} {\hat{\Phi }}_t(z)=\Phi _t(z)/e^{{{\mathcal {T}}}_t}. \end{aligned}$$

Theorem 1.1

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, for all ${\varepsilon }\in (0,1/3]$ and $\nu \in (0,{\varepsilon }/4]$, for all $m\in \mathbb {N}$ and $T\in [0,t_{\zeta })$, there is a constant $C=C({\alpha },\eta ,{\Lambda },{\varepsilon },\nu ,m,T)<\infty$ with the following property. In the case ${\zeta }<1$, for all $c\leqslant 1/C$ and all ${\sigma }\geqslant c^{1/2-{\varepsilon }}$, with probability exceeding $1-c^m$, for all $t\leqslant T$,

$$\begin{aligned} |{{\mathcal {T}}}_t-{\tau }_t| \leqslant C\left( c^{1/2-\nu }+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) \end{aligned}$$

and, for all $|z|=r\geqslant 1+c^{1/2-{\varepsilon }}$,

$$\begin{aligned} |{\hat{\Phi }}_t(z)-z| \leqslant C\left( c^{1/2-\nu }+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) . \end{aligned}$$

Moreover, in the case ${\zeta }=1$, for all $c\leqslant 1/C$ and all ${\sigma }\geqslant c^{1/3-{\varepsilon }}$, with probability exceeding $1-c^m$, for all $t\leqslant T$,

$$\begin{aligned} |{{\mathcal {T}}}_t-{\tau }_t| \leqslant C\left( c^{1/2-\nu }+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) \end{aligned}$$

and, for all $|z|=r\geqslant 1+c^{1/2-{\varepsilon }}$,

$$\begin{aligned} |{\hat{\Phi }}_t(z)-z| \leqslant C\left( c^{1/2-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{1/2} +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{5/2}\right) . \end{aligned}$$

We will show a similar result for the discrete-time process $(\Phi _n^{{\text {disc}}})_{n\geqslant 0}$. Set

$$\begin{aligned} {{\mathcal {T}}}^{{\text {disc}}}_n=\log (\Phi ^{{\text {disc}}}_n)'(\infty ),\quad {\hat{\Phi }}^{{\text {disc}}}_n(z)=\Phi ^{{\text {disc}}}_n(z)/e^{{{\mathcal {T}}}^{{\text {disc}}}_n}. \end{aligned}$$

Define

$$\begin{aligned} n_{\alpha }= {\left\{ \begin{array}{ll} \infty ,&{}\text {if}\, {\alpha }\geqslant 0,\\ |{\alpha }|^{-1},&{}\text {if}\, {\alpha }<0 \end{array}\right. } \end{aligned}$$

and for $n<n_{\alpha }/c$ set

$$\begin{aligned} {\tau }^{{\text {disc}}}_n= {\left\{ \begin{array}{ll} cn,&{}\text {if}\, {\alpha }=0,\\ {\alpha }^{-1}\log (1+{\alpha }cn),&{}\text {otherwise}. \end{array}\right. } \end{aligned}$$

(8)

The following result is proved at the end of Sect. 5.2. The case ${\alpha }=0$ is Theorem 1.1 in [21] but with an improvement to the constraints on r and $\sigma$, and the corresponding upper bound, in the $\eta =1$ case.

Theorem 1.2

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, for all ${\varepsilon }\in (0,1/3]$ and $\nu \in (0,{\varepsilon }/4]$, for all $m\in \mathbb {N}$ and $N\in [0,n_{\alpha })$, not necessarily an integer, there is a constant $C=C({\alpha },\eta ,{\Lambda },{\varepsilon },\nu ,m,N)<\infty$ with the following property. In the case ${\zeta }<1$, for all $c\leqslant 1/C$ and all ${\sigma }\geqslant c^{1/2-{\varepsilon }}$, with probability exceeding $1-c^m$, for all $n\leqslant N/c$,

$$\begin{aligned} |{{\mathcal {T}}}^{{\text {disc}}}_n-{\tau }^{{\text {disc}}}_n| \leqslant Cc^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2 \end{aligned}$$

and, for all $|z|=r\geqslant 1+c^{1/2-{\varepsilon }}$,

$$\begin{aligned} |{\hat{\Phi }}^{{\text {disc}}}_n(z)-z| \leqslant C\left( c^{1/2-\nu }+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) . \end{aligned}$$

Moreover, in the case ${\zeta }=1$, for all $c\leqslant 1/C$ and all ${\sigma }\geqslant c^{1/3-{\varepsilon }}$, with probability exceeding $1-c^m$, for all $n\leqslant N/c$,

$$\begin{aligned} |{{\mathcal {T}}}^{{\text {disc}}}_n-{\tau }^{{\text {disc}}}_n| \leqslant Cc^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2 \end{aligned}$$

and, for all $|z|=r\geqslant 1+c^{1/2-{\varepsilon }}$,

$$\begin{aligned} |{\hat{\Phi }}^{{\text {disc}}}_n(z)-z| \leqslant C\left( c^{1/2-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{1/2}+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{5/2}\right) . \end{aligned}$$

We turn to our second main result, which describes the limiting fluctuations of ALE$({\alpha },\eta )$. Denote by ${{\mathcal {H}}}$ the set of all holomorphic functions on $D_0=\{|z|>1\}$ which are bounded at $\infty$. We equip ${{\mathcal {H}}}$ with the metric

$$\begin{aligned} d(f,g)=\sum _{n=0}^\infty 2^{-n}\left( \sup _{|z|\geqslant 1+1/n}|f(z)-g(z)|\wedge 1\right) . \end{aligned}$$

Then ${{\mathcal {H}}}$ is a complete separable metric space. Define for $t<t_{\zeta }$

$$\begin{aligned} {\hat{\Psi }}_t(z)={\hat{\Phi }}_t(z)-z,\quad \Psi ^{{\text {cap}}}_t={{\mathcal {T}}}_t-{\tau }_t. \end{aligned}$$

Let $(B_t)_{t\geqslant 0}$ be a (real) Brownian motion. Let $(B_t(k))_{t\geqslant 0}$ for $k\geqslant 0$ be a sequence of independent complex Brownian motions, independent of $(B_t)_{t\geqslant 0}$. We can define continuous Gaussian processes $({\Gamma }_t(k))_{t<t_{\zeta }}$ and $({\Gamma }^{{\text {cap}}}_t)_{t<t_{\zeta }}$ by the following Ornstein–Uhlenbeck-type stochastic differential equations

$$\begin{aligned} d{\Gamma }_t(k)&=e^{-{\alpha }{\tau }_t}\left( \sqrt{2}e^{-\eta {\tau }_t/2}dB_t(k) -(1+(1-{\zeta })k){\Gamma }_t(k)e^{-\eta {\tau }_t}dt\right) ,\quad {\Gamma }_0(k)=0,\\ d{\Gamma }^{{\text {cap}}}_t&=e^{-{\alpha }{\tau }_t}\left( e^{-\eta {\tau }_t/2}dB_t -{\zeta }{\Gamma }^{{\text {cap}}}_te^{-\eta {\tau }_t}dt\right) ,\quad {\Gamma }^{{\text {cap}}}_0=0. \end{aligned}$$

We show in Sect. 6.2 that the series

$$\begin{aligned} {\hat{{\Gamma }}}_t(z)=\sum _{k=0}^\infty {\Gamma }_t(k)z^{-k} \end{aligned}$$

converges in ${{\mathcal {H}}}$, uniformly on compacts in $[0,t_{\zeta })$, almost surely. In fact $({\hat{{\Gamma }}}_t)_{t<t_{\zeta }}$ satisfies the following stochastic differential equation in ${{\mathcal {H}}}$

$$\begin{aligned} d{\hat{{\Gamma }}}_t=e^{-{\alpha }{\tau }_t}\left( \sqrt{2}e^{-\eta {\tau }_t/2}d{\hat{B}}_t-(Q_0+1){\hat{{\Gamma }}}_te^{-\eta {\tau }_t}dt\right) ,\quad {\hat{{\Gamma }}}_0=0 \end{aligned}$$

where $Q_0f(z)=-(1-{\zeta })zf'(z)$ and

$$\begin{aligned} {\hat{B}}_t(z)=\sum _{k=0}^\infty B_t(k)z^{-k}. \end{aligned}$$

The following two results are proved in Sect. 6.

Theorem 1.3

Assume that ${\zeta }={\alpha }+\eta \in (-\infty ,1]$. Fix $T\in [0,t_{\zeta })$ and ${\varepsilon }>0$ and consider the limit $c\rightarrow 0$ with ${\sigma }\rightarrow 0$ subject to the constraint

$$\begin{aligned} {\sigma }{\geqslant } {\left\{ \begin{array}{ll} c^{1/4-{\varepsilon }},&{}\text {if}\, {\zeta }<1,\\ c^{1/5-{\varepsilon }},&{}\text {if}\, {\zeta }=1. \end{array}\right. } \end{aligned}$$

Then

$$\begin{aligned} c^{-1/2}({\hat{\Psi }}_t,\Psi ^{{\text {cap}}}_t)_{t\leqslant T}\rightarrow ({\hat{{\Gamma }}}_t,{\Gamma }^{{\text {cap}}}_t)_{t\leqslant T} \end{aligned}$$

weakly in the Skorokhod space $D([0,T],{{\mathcal {H}}}\times \mathbb {R})$.

As in the bulk scaling limit, we can deduce an analogous discrete-time fluctuation theorem. The case ${\alpha }=0$ recovers Theorem 1.2 in [21]. Define for $t\geqslant 0$

$$\begin{aligned} {\hat{\Psi }}^{{\text {disc}}}_t(z)={\hat{\Phi }}^{{\text {disc}}}_{\lfloor t\rfloor }(z)-z. \end{aligned}$$

We have seen already in Theorem 1.2, for $N<n_{\alpha }$, that $({{\mathcal {T}}}^{{\text {disc}}}_n-{\tau }^{{\text {disc}}}_n)_{n\leqslant N/c}$ does not fluctuate at scale $\sqrt{c}$. We can define a continuous Gaussian process $({\hat{{\Gamma }}}^{{\text {disc}}}_t)_{t<n_{\alpha }}$ in ${{\mathcal {H}}}$ by

$$\begin{aligned} d{\hat{{\Gamma }}}^{{\text {disc}}}_t=\frac{\sqrt{2}d{\hat{B}}_t-(Q_0+1){\hat{{\Gamma }}}^{{\text {disc}}}_tdt}{1+{\alpha }t},\quad {\hat{{\Gamma }}}^{{\text {disc}}}_0=0. \end{aligned}$$

Theorem 1.4

Assume that ${\zeta }={\alpha }+\eta \in (-\infty ,1]$. Fix $N\in [0,n_{\alpha })$, not necessarily an integer, and fix ${\varepsilon }>0$. In the limit $c\rightarrow 0$ with ${\sigma }\rightarrow 0$ considered in Theorem 1.3, we have

$$\begin{aligned} c^{-1/2}({\hat{\Psi }}^{{\text {disc}}}_{t/c})_{t\leqslant N}\rightarrow ({\hat{{\Gamma }}}^{{\text {disc}}}_t)_{t\leqslant N} \end{aligned}$$

weakly in $D([0,N],{{\mathcal {H}}})$.

1.3 Commentary and review of related work

Hastings and Levitov [10] introduced the family of planar aggregation models HL(${\alpha }$), which are the cases $\eta ={\sigma }=0$ of our ALE$({\alpha },\eta )$ model. They discovered by numerical experiments that, for small particles, the models underwent a transition at ${\alpha }=1$: for ${\alpha }\leqslant 1$ the cluster grows like a disk, while for ${\alpha }>1$ it exhibits fractal properties. There are two natural scaling-limit regimes under which mathematical results have been established: capacity rescaling and the small-particle limit. Under capacity-rescaling, the particle capacity parameter c is kept fixed, and the cluster is rescaled to have logarithmic capacity 1, before the limit is taken as the number of particles goes to infinity. This corresponds to studying the limit of the map $\hat{\Phi }_n^{{{\text {disc}}}}(z)$ as $n \rightarrow \infty$. Under the small-particle limit, the parameter $c \rightarrow 0$, but the rate at which particles arrive is increased to ensure a non-trivial limit. This is the regime followed in the present paper, and corresponds to studying the limit of the process $(\Phi ^{{\text {disc}}}_{n(t)}(z))_{t \geqslant 0}$ as $c \rightarrow 0$, where n(t) is a suitable embedding of arrival times into continuous time. In most results to date, the embedding $n(t) = \lfloor t/c \rfloor$ has been used.

The HL(0) model is the most mathematically tractable model in the Hastings–Levitov family as in this case the particle maps, $F_n$, are i.i.d. It has been investigated rigorously in a series of works [24] (existence of a bulk scaling limit under capacity rescaling), [22] (bulk small-particle scaling limit), [26] (fluctuation small-particle scaling limit). Several variants exist, for example [1, 2] (versions of HL(0) grown in the upper half-plane) and [14, 17] (anisotropic versions of HL(0)). The ${\sigma }$-regularized variant of HL$({\alpha })$ was proposed in [15], where it was shown for slit maps that, if ${\sigma }\gg (\log (1/c))^{-1/2}$, there is disk-like behaviour in the small-particle limit for all ${\alpha }\geqslant 0$: it appeared that the observed fractal properties of HL$({\alpha })$ for ${\alpha }>1$ were suppressed by strong regularization. In contrast, for the weaker regularization used in the present paper, the conjectured phase transition at ${\alpha }=1$ (or ${\zeta }=1$) becomes visible at the level of fluctuations. The method of [15] used a comparison with an HL(0)-type model which breaks down for smaller values of ${\sigma }$. Regularized versions of HL$(\alpha )$ under capacity-rescaling are considered in [24] (estimates for the dimension) and [16] (fluctuation limit when $0< \alpha < 2$ and $\sigma = \infty$).

The regularized ALE$({\alpha },\eta )$ model first appeared in [27] where it was shown that, for slit maps, if $\alpha \geqslant 0$ and $\eta > 1$, ${\sigma }$-regularized ALE$(\alpha ,\eta )$ converges to a growing slit in the small-particle limit, provided $\sigma \rightarrow 0$ sufficiently fast as $c\rightarrow 0$. This result is a consequence of the singularities of the derivative of the slit map on the cluster boundary, which causes the cluster growth to concentrate at the tips of particles. Similar degeneracies are exploited in two recent papers [12, 13]. In [12] it was shown that, when $\eta < -2$, ALE$(0,\eta )$ converges to a $\text {SLE}_4$ curve. It is conjectured that, by making appropriate choices of particle shape, one can get convergence to $\text {SLE}_\kappa$ for any $\kappa \geqslant 4$. In [13], it is shown that ALE$(0, \eta )$, initiated from a needle-like configuration, converges to a Laplacian-path model [5]. Another model that fits into this framework is Quantum Loewner Evolution (QLE) [19]. The paper [27] contains a comprehensive discussion of connections between these and related models, so we do not repeat this here.

A new approach was begun in [21], treating regularized ALE$(0,\eta )$ as a Markov chain in univalent functions. By martingale arguments, a bulk small-particle scaling limit and fluctuation scaling limit were shown, subject to the constraint $\eta \leqslant 1$ and to restrictions on ${\sigma }$ as a fractional power of c. These limits (in contrast to those above) turn out not to depend on the details of individual particle shapes. In this paper, we extend the analysis of [21] to ALE$({\alpha },\eta )$, subject now to the constraint ${\zeta }={\alpha }+\eta \leqslant 1$. Thus we now include regularized HL$({\alpha })$ for ${\alpha }\leqslant 1$. Hastings and Levitov had argued that there should be a trade-off between ${\alpha }$ and $\eta$, with only ${\zeta }$ affecting the bulk scaling limit, and on this basis proposed HL(1), that is ALE(1, 0), as a continuum variant of the Eden model. A more direct continuum analogue of the Eden model is ALE$(2,-1)$. Our results, in the regularized case, both justify the trade-off argument and show a disk scaling limit whenever ${\zeta }\leqslant 1$. On the other hand, we show that ALE(1, 0) and ALE$(2,-1)$ have different fluctuation behaviour. As in [21], the behaviour of fluctuations as a function of ${\zeta }$ is consistent with the conjectured transition in behaviour at ${\zeta }=1$. We emphasise that scaling limits for the conjectured supercritical regime $\zeta >1$ lie outside the scope of the present paper.

Hastings and Levitov [10] identify a Loewner–Kufarev-type equation, which they propose as governing the small-particle limit of HL$({\alpha })$, citing a discussion of Shraiman and Bensimon [25] for the Hele–Shaw flow, where ${\alpha }$ is taken to be 2. This is the LK$({\alpha })$ equation, which is the subject of the next section. As noted by Sola in a contribution to [18], there is a lack of mathematical theory for the LK$({\alpha })$ equation, except in the case ${\alpha }=2$ when some special techniques become available (we refer the reader to [11] and to the monograph [9] which contains an extensive list of references). In this paper, since our focus is on clusters initiated as a disk, we are able to use an explicit solution of the equation, along with its linearization around that solution, so we do not rely on a general theory. However, the particle interpretation established here offers some evidence that for ${\alpha }\leqslant 1$, the LK$({\alpha })$ equation may have a suitable existence, uniqueness and stability theory, and that it may be possible to derive the equation as a limit of particle models.

Our results depend on constraints on the regularization parameter ${\sigma }$, though substantially weaker ones than those used in [15]. These constraints limit the interactions of individual particles and place us in the simplest case of Gaussian fluctuations. At a technical level, for Theorem 1.1, these constraints come from the need to have ${\bar{{\delta }}}(e^{\sigma })\leqslant c^{\varepsilon }$ in Proposition 5.3, while for Theorem 1.3 they are needed to show that the Poisson integral process $(\Pi _t)_{t\geqslant 0}$ is a good approximation to the fluctuations in Proposition 5.7. In the case ${\zeta }=1$, the regularizing operator Q obtained by linearization of the LK$({\zeta })$ equation collapses from a fixed multiple of the Cauchy operator to ${\sigma }$ times the second derivative. In general, for scaling regimes where ${\sigma }\rightarrow 0$ faster than our fluctuation results allow, it remains possible that ALE$({\alpha },\eta )$ has different universal fluctuation behaviour, such as KPZ, as has been conjectured for the lattice Eden model.

1.4 Structure of the paper

In the next section, we discuss the Loewner–Kufarev equation for the limit dynamics. Then, in Sect. 3, we derive an interpolation formula between ALE$({\alpha },\eta )$ and solutions of the limit equation. The terms in this formula are estimated in Sect. 4. Equipped with these estimates, we show the bulk scaling limit in Sect. 5 and the fluctuation scaling limit in Sect. 6. We collect in Appendix A some further estimates needed in the course of the paper, including estimates on the conformal maps which encode single particles and particle families.

2 Loewner–Kufarev Equation

Let ${{\mathcal {S}}}$ denote the set of univalent holomorphic functions $\phi$ on $\{|z|>1\}$ with $\phi (\infty )=\infty$ and $\phi '(\infty )\in (0,\infty )$. Then each $\phi \in {{\mathcal {S}}}$ has the form

$$\begin{aligned} \phi (z)=e^c\left( z+\sum _{k=0}^\infty a_kz^{-k}\right) \end{aligned}$$

for some $c\in \mathbb {R}$ and some sequence $(a_k:k\geqslant 0)$ in $\mathbb {C}$. Fix parameters ${\zeta }\in \mathbb {R}$ and ${\sigma }\geqslant 0$. Given $\phi _0\in {{\mathcal {S}}}$, consider the following Cauchy problem for $(\phi _t)_{t\geqslant 0}$ in ${{\mathcal {S}}}$

$$\begin{aligned} {\dot{\phi }}_t=a(\phi _t) \end{aligned}$$

(9)

where

The case ${\sigma }=0$ of this equation is the equation proposed by Hastings and Levitov as scaling limit for HL$({\zeta })$, which we will call the LK$({\zeta })$ equation. When ${\zeta }=0$, the value of ${\sigma }$ is immaterial and there is a unique solution given by

$$\begin{aligned} \phi _t(z)=\phi _0(e^tz). \end{aligned}$$

When ${\zeta }=2$ and ${\sigma }=0$, (9) is the Loewner–Kufarev equation associated to the Hele–Shaw flow. For ${\sigma }>0$, we will refer to (9) as the ${\sigma }$-regularized LK$({\zeta })$ equation. We will be interested in the subcritical case ${\zeta }\in (-\infty ,1]$.

The general form of the Loewner–Kufarev equation is given by

$$\begin{aligned} {\dot{\phi }}_t(z)=z\phi '_t(z)\int _0^{2\pi }\frac{z+e^{i{\theta }}}{z-e^{i{\theta }}}\,\mu _t(d{\theta }) \end{aligned}$$

with $(\mu _t:t\geqslant 0)$ a given family of measures on $[0,2\pi )$. Thus the ${\sigma }$-regularized LK$({\zeta })$ equation is obtained by requiring that the driving measures are given by

$$\begin{aligned} \mu _t(d{\theta })=\left| \phi '_t(e^{{\sigma }+i{\theta }})\right| ^{-{\zeta }}d{\theta }/(2\pi ). \end{aligned}$$

Note that, when ${\zeta }={\alpha }+\eta$, the density of these driving measures is the product of the density of the local attachment rate and the local particle capacity (7) for ALE$({\alpha },\eta )$. By the Loewner–Kufarev theory, for any solution $(\phi _t)_{t\geqslant 0}$ of (9), the sets

$$\begin{aligned} K_t=\mathbb {C}\setminus \{\phi _t(z):|z|>1\} \end{aligned}$$

form an increasing family of simply-connected compacts, with capacities given by

$$\begin{aligned} {\tau }_t={{\text {cap}}}(K_t)=\log \phi _t'(\infty )=\log \phi _0'(\infty )+\int _0^t\mu _s([0,2\pi ))ds. \end{aligned}$$

2.1 Linearization

We compute the linearization of (9) around a solution $(\phi _t)_{t\geqslant 0}$. For $\psi$ holomorphic in $\{|z|>1\}$, we have

$$\begin{aligned} (\nabla a(\phi )\psi )(z) =\left. \frac{d}{d{\varepsilon }}\right| _{{\varepsilon }=0}a(\phi +{\varepsilon }\psi )(z) =z\psi '(z)h(z)-{\zeta }z\phi '(z)g(z) \end{aligned}$$

where

and, setting $\rho =\psi '/\phi '$,

(10)

Note that first-order variations in ${{\mathcal {S}}}$ have the form

$$\begin{aligned} \psi (z)={\delta }z+\sum _{k=0}^\infty \psi _kz^{-k},\quad {\delta }\in \mathbb {R},\quad \psi _k\in \mathbb {C}. \end{aligned}$$

The process of first-order variations $(\psi _t)_{t\geqslant 0}$ around a solution $(\phi _t)_{t\geqslant 0}$ can be expected to satisfy the linearized equation

$$\begin{aligned} {\dot{\psi }}_t=\nabla a(\phi _t)\psi _t. \end{aligned}$$

2.2 Linear stability of disk solutions in the subcritical case

Fix ${\tau }_0\in (0,\infty )$. A trial solution $\phi _t(z)=e^{{\tau }_t}z$ for (9) leads to the equation

$$\begin{aligned} {\dot{{\tau }}}_t=e^{-{\zeta }{\tau }_t}. \end{aligned}$$

We solve to obtain $({\tau }_t)_{t<t_{\zeta }}$, with ${\tau }_t\rightarrow \infty$ as $t\rightarrow t_{\zeta }$, given by

$$\begin{aligned} {\tau }_t= {\left\{ \begin{array}{ll} {\tau }_0+t,&{}\text {if}\, {\zeta }=0,\\ {\zeta }^{-1}\log (e^{{\zeta }{\tau }_0}+{\zeta }t),&{}\text {otherwise} \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} t_{\zeta }= {\left\{ \begin{array}{ll} \infty ,&{}\text {if}\, {\zeta }\geqslant 0,\\ e^{{\zeta }{\tau }_0}/|{\zeta }|,&{}\text {if}\, {\zeta }<0. \end{array}\right. } \end{aligned}$$

For the associated solutions $(\phi _t)_{t<t_{\zeta }}$, the the sets $K_t$ form a growing family of disks. We call such a $(\phi _t)_{t<{\tau }_{\zeta }}$ a disk solution.

For disk solutions, we have $\phi _t'(z)=e^{{\tau }_t}$ for all z, so we can evaluate the integral (10) to obtain

$$\begin{aligned} (\nabla a(\phi _t)\psi )(z) =-Q\psi (z){\dot{{\tau }}}_t \end{aligned}$$

where

$$\begin{aligned} Q\psi (z)=-z\psi '(z)+{\zeta }z\psi '(e^{\sigma }z)=-D\psi (z)+{\zeta }e^{-{\sigma }}D\psi (e^{\sigma }z). \end{aligned}$$

(11)

Here and below, we write $D\psi (z)$ for the radial derivative $z\psi '(z)$. Consider the action of Q on the set of holomorphic functions on $\{|z|>1\}$ which are bounded at infinity. Then Q is a multiplier operator

$$\begin{aligned} Q\psi (z)=\sum _{k=0}^\infty q(k)\psi _kz^{-k},\quad \psi (z)=\sum _{k=0}^\infty \psi _kz^{-k} \end{aligned}$$

where

$$\begin{aligned} q(k)=k(1-{\zeta }e^{-{\sigma }(k+1)}). \end{aligned}$$

It is straightforward to obtain the following lower bounds. We have

$$\begin{aligned} q(k)\geqslant {\left\{ \begin{array}{ll} k,&{}\text {if}\, {\zeta }\leqslant 0,\\ k/(1-{\zeta }),&{}\text {if}\, {\zeta }\in (0,1),\\ (1-1/e)(({\sigma }k^2)\wedge k),&{}\text {if}\, {\zeta }=1. \end{array}\right. } \end{aligned}$$

Define for ${\tau }\geqslant 0$

$$\begin{aligned} P({\tau })=e^{-{\tau }Q}. \end{aligned}$$

(12)

At least formally, at a disk solution, the linearized equation ${\dot{\psi }}_t=\nabla a(\phi _t)\psi _t$ has solution given by

$$\begin{aligned} \psi _t(z)=P({\tau }_t-{\tau }_0)\psi _0(z). \end{aligned}$$

(13)

In the case ${\sigma }=0$, we have $q(k)=(1-{\zeta })k$ so $P({\tau })\psi (z)=\psi (e^{(1-{\zeta }){\tau }}z)$ for suitable $\psi$. Thus, if ${\zeta }>1$, as for example in the Hele–Shaw case when ${\zeta }=2$, we see that $\psi _t$ is holomorphic in $\{|z|>1\}$ only if $\psi _0$ extends to a holomorphic function in the larger domain $\{|z|>e^{(1-{\zeta })({\tau }_t-{\tau }_0)}\}$. On the other hand, if ${\zeta }\leqslant 1$, then $P({\tau }_t-{\tau }_0)$ preserves the set of holomorphic first-order variations, so the variation $\psi _t$ as given by (13) remains holomorphic for all t. We will show that this stability property in fact also holds whenever ${\sigma }\geqslant 0$ and ${\zeta }\leqslant 1$.

Define for $r>1$

For a multiplier operator M, given by

$$\begin{aligned} M\psi (z)=\sum _{k=0}^\infty m(k)\psi _kz^{-k},\quad \psi (z)=\sum _{k=0}^\infty \psi _kz^{-k} \end{aligned}$$

let us write $A=A(M)$ for the smallest constant such that

$$\begin{aligned} |m(0)|\leqslant A,\quad \sum _{k=0}^\infty |m(k+1)-m(k)|\leqslant A. \end{aligned}$$

The Marcinkiewicz multiplier theorem is recalled in Sect. A.3. This implies in particular that, for all $p\in (0,\infty )$, there is a constant $C=C(p)<\infty$ such that, for all $r>1$, we have

$$\begin{aligned} \Vert M\psi \Vert _{p,r}\leqslant CA(M)\Vert \psi \Vert _{p,r}. \end{aligned}$$

We use this criterion to obtain some estimates on the operators $P({\tau })$ and $DP({\tau })$ for ${\tau }\geqslant 0$. Note that, if $0\leqslant m(k)\leqslant m^*$, then $A(M)\leqslant N(M)m^*$ where N(M) is the number of maximal intervals of constant sign in the sequence of increments $(m(k+1)-m(k):k\geqslant 0)$.

Lemma 2.1

For all $n\geqslant 0$ and all $p\in (1,\infty )$, there is a constant $C=C(n,p)<\infty$ such that, for all ${\sigma }\geqslant 0$, for all holomorphic functions $\psi$ on $\{|z|>1\}$ bounded at $\infty$, all ${\tau }\geqslant 0$ and all $r>1$, we have, for ${\zeta }<1$,

$$\begin{aligned} \Vert D^nP({\tau })\psi \Vert _{p,r}\leqslant \frac{C\Vert \psi \Vert _{p,r}}{(1-{\zeta }^+)^n{\tau }^n} \end{aligned}$$

and for ${\zeta }=1$

$$\begin{aligned} \Vert D^nP({\tau })\psi \Vert _{p,r}\leqslant \frac{Ce^{{\sigma }n}\Vert \psi \Vert _{p,r}}{{\tau }^n\wedge ({\sigma }{\tau })^{n/2}}. \end{aligned}$$

Proof

Consider first the case where ${\zeta }\leqslant 0$. We split

$$\begin{aligned} q(k)=q_1(k)+q_2(k),\quad q_1(k)=k,\quad q_2(k)=|{\zeta }|ke^{-{\sigma }(k+1)}. \end{aligned}$$

Then, with obvious notation, $P({\tau })=P_1({\tau })P_2({\tau })$ so

$$\begin{aligned} \Vert D^nP({\tau })\Vert _{p,r}\leqslant \Vert D^nP_1({\tau })\Vert _{p,r}\Vert P_2({\tau })\Vert _{p,r}. \end{aligned}$$

The sequence of multipliers $k^ne^{-{\tau }k}$ for $(-D)^nP_1({\tau })$ is bounded by $(n/{\tau })^n$ and its increments change sign at most once, so $A(D^nP_1({\tau }))\leqslant 2(n/{\tau })^n$. The sequence of multipliers $e^{-{\tau }q_1(k)}$ for $P_2({\tau })$ is bounded by 1 and its increments change sign at most once, so $A(P_2({\tau }))\leqslant 2$. Hence $\Vert D^nP({\tau })\Vert _{p,r}\leqslant C/{\tau }^n$ as claimed.

Consider next the case ${\zeta }\in (0,1)$. We make another split

$$\begin{aligned} q(k)=q_1(k)+q_2(k),\quad q_1(k)=(1-{\zeta })k,\quad q_2(k)={\zeta }k(1-e^{-{\sigma }(k+1)}). \end{aligned}$$

Then $P({\tau })=P_1({\tau })P_2({\tau })$ again, where the notation now corresponds to the new split. We have $A(D^nP_1({\tau }))\leqslant 2(n/((1-{\zeta }){\tau }))^n$ by the argument used for $D^nP_1$ in the case ${\zeta }\leqslant 0$. The sequence of multipliers $e^{-{\tau }q_1(k)}$ for $P_2({\tau })$ is bounded by 1 and is decreasing, so $A(P_2({\tau }))\leqslant 1$. Hence $\Vert D^nP({\tau })\Vert _{p,r}\leqslant C/((1-{\zeta }){\tau })^n$ as claimed.

Consider finally the case ${\zeta }=1$. We now write

$$\begin{aligned} q(k)={\hat{q}}(k)+q_3(k),\quad {\hat{q}}(k)=e^{-(1+{\sigma })}(q_1(k)\wedge q_2(k)),\quad q_1(k)=k,\quad q_2(k)={\sigma }k^2 \end{aligned}$$

and write ${\hat{P}}({\tau })$ for the operator with multipliers $e^{-{\tau }{\hat{q}}(k)}$ and so on. As already observed, the sequence of multipliers $k^ne^{-{\tau }k}$ for $(-D)^nP_1({\tau })$ is bounded by $(n/{\tau })^n$ and its increments change sign at most once, so $A(D^nP_1({\tau }))\leqslant 2(n/{\tau })^n$. The sequence of multipliers $k^ne^{-{\tau }{\sigma }k^2}$ for $(-D)^nP_2({\tau })$ is bounded by $(n/({\sigma }{\tau }))^{n/2}$ and its increments also change sign at most once, so $A(DP_2({\tau }))\leqslant 2$. We use the inequality

$$\begin{aligned} |a_1\vee b_1-a_2\vee b_2|\leqslant |a_1-a_2|\vee |b_1-b_2| \end{aligned}$$

to deduce that $A(D{\hat{P}}({\tau }))\leqslant Ce^{{\sigma }n}/({\tau }^n\wedge ({\sigma }{\tau })^{n/2})$. Finally, it is straightforward to check that the sequence of multipliers $e^{-{\tau }q_3(k)}$ for $P_3({\tau })$ is bounded by 1 and decreasing, so $A(P_3({\tau }))\leqslant 1$. Hence $\Vert D^nP({\tau })\Vert _{p,r}\leqslant \Vert D^n{\hat{P}}({\tau })\Vert _{p,r}\Vert P_3({\tau })\Vert _{p,r}\leqslant Ce^{{\sigma }n}/({\tau }^n\wedge ({\sigma }{\tau })^{n/2})$ as claimed. $\square$

2.3 Transformation to (Schlicht function, capacity) coordinates

Write ${{\mathcal {S}}}_1$ for the set of ‘Schlicht functions at $\infty$’ on $\{|z|>1\}$, given by

$$\begin{aligned} {{\mathcal {S}}}_1=\{\phi \in {{\mathcal {S}}}:\phi '(\infty )=1\}. \end{aligned}$$

It will be convenient to use coordinates $({\hat{\phi }},{\tau })$ on ${{\mathcal {S}}}$, given by

$$\begin{aligned} {\hat{\phi }}(z)=e^{-{\tau }}\phi (z),\quad {\tau }=\log \phi '(\infty ). \end{aligned}$$

Then ${\hat{\phi }}\in {{\mathcal {S}}}_1$ and ${\tau }\in \mathbb {R}$. It is straightforward to show that, for a solution $(\phi _t)_{t\geqslant 0}$ to (9), the transformed variables $({\hat{\phi }}_t,{\tau }_t)_{t\geqslant 0}$ satisfy

$$\begin{aligned} (\dot{{\hat{\phi }}}_t,{\dot{{\tau }}}_t) =b({\hat{\phi }}_t,{\tau }_t)=({\hat{b}},b^{{\text {cap}}})({\hat{\phi }}_t,{\tau }_t) \end{aligned}$$

(14)

where

On linearizing (14) around a solution $({\hat{\phi }}_t,{\tau }_t)_{t\geqslant 0}$, we obtain equations for first-order variations $({\hat{\psi }}_t,\psi ^{{\text {cap}}}_t)_{t\geqslant 0}$ in the new coordinates, where now ${\hat{\psi }}_t$ is bounded at $\infty$ for all t, reflecting the normalization of ${\hat{\phi }}_t$. These are then related to the first-order variations $(\psi _t)_{t\geqslant 0}$ in the old coordinates by

$$\begin{aligned} \psi _t(z)=e^{{\tau }_t}({\hat{\psi }}_t(z)+\psi ^{{\text {cap}}}_t{\hat{\phi }}_t(z)). \end{aligned}$$

For a disk solution $(\phi _t)_{t<t_{\zeta }}$, we have ${\hat{\phi }}_t(z)=z$ and $b({\hat{\phi }}_t,{\tau })=(0,e^{-{\zeta }{\tau }})$. The equations for first-order variations are then given by

$$\begin{aligned} \dot{{\hat{\psi }}}_t(z)=-(Q+1){\hat{\psi }}_t(z){\dot{{\tau }}}_t,\quad {\dot{\psi }}^{{\text {cap}}}_t=-{\zeta }\psi ^{{\text {cap}}}_t{\dot{{\tau }}}_t \end{aligned}$$

with solutions

$$\begin{aligned} {\hat{\psi }}_t(z) =e^{-({\tau }_t-{\tau }_0)}P({\tau }_t-{\tau }_0){\hat{\psi }}_0(z),\quad \psi ^{{\text {cap}}}_t=e^{-{\zeta }({\tau }_t-{\tau }_0)}\psi ^{{\text {cap}}}_0. \end{aligned}$$

3 Interpolation Formula for Markov Chain Fluid Limits

We use an interpolation formula between continuous-time Markov chains and differential equations, which we first review briefly in a general setting. This formula is then applied to an ALE(${\alpha },\eta$) aggregation process $(\Phi _t)_{t\geqslant 0}$ with capacity parameter c, regularization parameter ${\sigma }$ and particle family $(P^{(c)}:c\in (0,\infty ))$, taking as limit equation the ${\sigma }$-regularized LK$({\zeta })$ equation with ${\zeta }={\alpha }+\eta$. We use (Schlicht function, capacity) coordinates for both the process and the limit equation.

3.1 General form of the interpolation formula

Let $(X_t)_{t\geqslant 0}$ be a continuous-time Markov chain with state-space E and transition rate kernel q, starting from $x_0$ say. Suppose for this general discussion that $E=\mathbb {R}^d$. Let b be a vector field on E with continuous bounded derivative $\nabla b$. Write $(\xi _t(x):t\geqslant 0,x\in E)$ for the flow of b. The compensated jump measure of $(X_t)_{t\geqslant 0}$ is the signed measure ${\tilde{\mu }}^X$ on $E\times (0,\infty )$ given by

$$\begin{aligned} {\tilde{\mu }}^X(dy,dt)=\mu ^X(dy,dt)-q(X_{t-},dy)dt,\quad \mu ^X=\sum _{t:X_t\not =X_{t-}}{\delta }_{(X_t,t)}. \end{aligned}$$

Set $x_t=\xi _t(x_0)$ and define, for $s\in [0,t]$,

$$\begin{aligned} Z_s=x_t+\nabla \xi _{t-s}(x_s)(X_s-x_s). \end{aligned}$$

Then $Z_0=x_t$ and $Z_t=X_t$ and, on computing the martingale decomposition of $(Z_s)_{s\leqslant t}$, we obtain the interpolation formula

$$\begin{aligned} X_t-x_t=M_t+A_t \end{aligned}$$

(15)

where

$$\begin{aligned} M_t=\int _{E\times (0,t]}\nabla \xi _{t-s}(x_s)(y-X_{s-}){\tilde{\mu }}^X(dy,ds) \end{aligned}$$

and

$$\begin{aligned} A_t=\int _0^t\nabla \xi _{t-s}(x_s)({\beta }(X_s)-b(x_s)-\nabla b(x_s)(X_s-x_s))ds \end{aligned}$$

where ${\beta }$ is the drift of $(X_t)_{t\geqslant 0}$, given by

$$\begin{aligned} {\beta }(x)=\int _E(y-x)q(x,dy). \end{aligned}$$

The identification of martingales associated with finite-rate continuous-time Markov chains is standard. The particular pathwise formulation in terms of the jump measure used here is developed in detail in [6]. We will use this formula in a case where the state-space E is infinite-dimensional. Rather than justify its validity generally in such a context, in the next section, we will prove directly the special case of the formula which we require. Note that the integrands in $M_t$ and $A_t$ depend on t. Nevertheless, we will call $M_t$ the martingale term and $A_t$ the drift term.

3.2 Proof of the formula for ALE(${\alpha },\eta$)

Let $(\Phi _t)_{t\geqslant 0}$ be an ALE(${\alpha },\eta$) aggregation process with capacity parameter c, regularization parameter ${\sigma }$ and particle family $(P^{(c)}:c\in (0,\infty ))$. See Sect. 1.2 and (7) for the specification of this process. We use (Schlicht function, capacity) coordinates, as in Sect. 2.3, to obtain a continuous-time Markov chain $(X_t)_{t\geqslant 0}=({\hat{\Phi }}_t,{{\mathcal {T}}}_t)_{t\geqslant 0}$ in ${{\mathcal {S}}}_1\times [0,\infty )$. When in state $x=({\hat{\phi }},{\tau })$, for all ${\theta }\in [0,2\pi )$, this process makes a jump of size $(\Delta ({\theta },z,c({\theta }),{\hat{\phi }}),c({\theta }))$ at rate ${\lambda }({\theta })d{\theta }/(2\pi )$, where

$$\begin{aligned} \Delta ({\theta },z,c,{\hat{\phi }})=e^{-c}{\hat{\phi }}(F_c({\theta },z))-{\hat{\phi }}(z) \end{aligned}$$

and

$$\begin{aligned} c({\theta })= & {} c({\theta },{\hat{\phi }},{\tau })=ce^{-{\alpha }{\tau }}|{\hat{\phi }}'(e^{{\sigma }+i{\theta }})|^{-{\alpha }},\\ {\lambda }({\theta })= & {} {\lambda }({\theta },{\hat{\phi }},{\tau })=c^{-1}e^{-\eta {\tau }}|{\hat{\phi }}'(e^{{\sigma }+i{\theta }})|^{-\eta }. \end{aligned}$$

We can and do assume that the process is constructed from a Poisson random measure $\mu$ on $[0,2\pi )\times [0,\infty )\times (0,\infty )$ of intensity $(2\pi )^{-1}d{\theta }dvdt$ by the following stochastic differential equation:

$$\begin{aligned} {\hat{\Phi }}_t(z)= & {} \int _{E(t)}H_s({\theta },z)1_{\{v\leqslant {\Lambda }_s({\theta })\}}\mu (d{\theta },dv,ds),\\ {{\mathcal {T}}}_t= & {} \int _{E(t)}C_s({\theta })1_{\{v\leqslant {\Lambda }_s({\theta })\}}\mu (d{\theta },dv,ds) \end{aligned}$$

where

$$\begin{aligned} E(t)=[0,2\pi )\times [0,\infty )\times (0,t] \end{aligned}$$

and

$$\begin{aligned} H_s({\theta },z)= & {} \Delta ({\theta },z,C_s({\theta }),{\hat{\Phi }}_{s-}),\quad C_s({\theta })=c({\theta },{\hat{\Phi }}_{s-},{{\mathcal {T}}}_{s-}),\\ {\Lambda }_s({\theta })= & {} {\lambda }({\theta },{\hat{\Phi }}_{s-},{{\mathcal {T}}}_{s-}). \end{aligned}$$

We use the vector field $b=({\hat{b}},b^{{\text {cap}}})$ of the ${\sigma }$-regularized LK$({\zeta })$ equation (14), written in (Schlicht function, capacity) coordinates. Consider the disk solution $(x_t)_{t\geqslant 0}=({\hat{\phi }}_t,{\tau }_t)_{t<t_{\zeta }}$ with initial capacity ${\tau }_0=0$, which is given by

$$\begin{aligned} {\hat{\phi }}_t(z)=z,\quad {\tau }_t = {\left\{ \begin{array}{ll} t,&{}\text {if}\, {\zeta }=0,\\ {\zeta }^{-1}\log (1+{\zeta }t),&{}\text {if}\, {\zeta }\not =0, \end{array}\right. } \quad t_{\zeta }= {\left\{ \begin{array}{ll} \infty ,&{}\text {if}\, {\zeta }\geqslant 0,\\ |{\zeta }|^{-1},&{}\text {if}\, {\zeta }<0. \end{array}\right. } \end{aligned}$$

(16)

We will compute the form of the interpolation formula in this case and then prove directly that it holds. Note that

$$\begin{aligned} b(x_t)=({\hat{b}},b^{{\text {cap}}})({\hat{\phi }}_t,{\tau }_t)=(0,e^{-{\zeta }{\tau }_t}) \end{aligned}$$

and, for $y=({\hat{\psi }},\psi ^{{\text {cap}}})$,

$$\begin{aligned} \nabla b(x_t)y =-e^{-{\zeta }{\tau }_t}((Q+1){\hat{\psi }},{\zeta }\psi ^{{\text {cap}}}) \end{aligned}$$

and the first-order variation at time t due to a variation y at time $s\leqslant t$ is given by

$$\begin{aligned} \nabla \xi _{t-s}(x_s)y=(e^{-({\tau }_t-{\tau }_s)}P({\tau }_t-{\tau }_s){\hat{\psi }},e^{-{\zeta }({\tau }_t-{\tau }_s)}\psi ^{{\text {cap}}}). \end{aligned}$$

Write ${\tilde{\mu }}$ for the compensated Poisson random measure

$$\begin{aligned} {\tilde{\mu }}(d{\theta },dv,ds)=\mu (d{\theta },dv,ds)-(d{\theta }/2\pi )dvds. \end{aligned}$$

Fix $t\geqslant 0$ and set ${\bar{{\tau }}}_s={\tau }_t-{\tau }_s$. We alert the reader to the concealed dependence of ${\bar{{\tau }}}_s$ on t. The martingale term $M_t=({\hat{M}}_t,M^{{\text {cap}}}_t)$ in the interpolation formula may then be written

$$\begin{aligned} {\hat{M}}_t(z)&=\int _{E(t)}e^{-{\bar{{\tau }}}_s}P({\bar{{\tau }}}_s)H_s({\theta },z) 1_{\{v\leqslant {\Lambda }_s({\theta })\}}{\tilde{\mu }}(d{\theta },dv,ds),\\ M^{{\text {cap}}}_t&=\int _{E(t)}e^{-{\zeta }{\bar{{\tau }}}_s}C_s({\theta }) 1_{\{v\leqslant {\Lambda }_s({\theta })\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

The drift ${\beta }=({\hat{{\beta }}},{\beta }^{{\text {cap}}})$ for $({\hat{\Phi }},{{\mathcal {T}}})$ is given by

Write ${\hat{\Psi }}_s(z)={\hat{\Phi }}_s(z)-{\hat{\phi }}_s(z)={\hat{\Phi }}_s(z)-z$ and $\Psi ^{{\text {cap}}}_s={{\mathcal {T}}}_s-{\tau }_s$. Then we have formally

$$\begin{aligned} \nabla b(x_s)(X_s-x_s)=-e^{-{\zeta }{\tau }_s}((Q+1){\hat{\Psi }}_s,{\zeta }\Psi ^{{\text {cap}}}_s) \end{aligned}$$

and so

$$\begin{aligned} \nabla \xi _{t-s}(x_s)\nabla b(x_s)(X_s-x_s)=-e^{-{\zeta }{\tau }_s}(e^{-{\bar{{\tau }}}_s}P({\bar{{\tau }}}_s) (Q+1){\hat{\Psi }}_s,e^{-{\zeta }{\bar{{\tau }}}_s}{\zeta }\Psi ^{{\text {cap}}}_s). \end{aligned}$$

The following interpolation identities may then be obtained formally by splitting equation (15) into its Schlicht function and capacity components.

Proposition 3.1

For all $t<t_{\zeta }$ and all $|z|>1$, we have

$$\begin{aligned} {\hat{\Psi }}_t(z)={\hat{M}}_t(z)+{\hat{A}}_t(z),\quad \Psi ^{{\text {cap}}}_t=M^{{\text {cap}}}_t+A^{{\text {cap}}}_t \end{aligned}$$

(17)

where

$$\begin{aligned} {\hat{A}}_t(z)&=\int _0^te^{-{\bar{{\tau }}}_s}P({\bar{{\tau }}}_s)\left( {\hat{{\beta }}}({\hat{\Phi }}_s, {{\mathcal {T}}}_s)+e^{-{\zeta }{\tau }_s}(Q+1){\hat{\Psi }}_s\right) (z)ds,\\ A^{{\text {cap}}}_t&=\int _0^te^{-{\zeta }{\bar{{\tau }}}_s}\left( {\beta }^{{\text {cap}}}({\hat{\Phi }}_s,{{\mathcal {T}}}_s)-e^{-{\zeta }{\tau }_s} +{\zeta }e^{-{\zeta }{\tau }_s}\Psi ^{{\text {cap}}}_s\right) ds. \end{aligned}$$

Proof

Fix $t<t_{\zeta }$. For $x\in [0,t]$, recall that ${\bar{{\tau }}}_x={\tau }_t-{\tau }_x$ and define for $|z|>1$

$$\begin{aligned} {\hat{\Psi }}_{x,t}(z)=e^{-{\bar{{\tau }}}_x}P({\bar{{\tau }}}_x)({\hat{\Phi }}_x-{\hat{\phi }}_x)(z),\quad \Psi ^{{\text {cap}}}_{x,t}=e^{-{\zeta }{\bar{{\tau }}}_x}({{\mathcal {T}}}_x-{\tau }_x). \end{aligned}$$

Set

$$\begin{aligned} {\hat{M}}_{x,t}(z)&=\int _{E(x)}e^{-{\bar{{\tau }}}_s}P({\bar{{\tau }}}_s)H_s({\theta },z)1_{\{v\leqslant {\Lambda }_s({\theta })\}} {\tilde{\mu }}(d{\theta },dv,ds),\\ M^{{\text {cap}}}_{x,t}&=\int _{E(x)}e^{-{\zeta }{\bar{{\tau }}}_s}C_s({\theta })1_{\{v\leqslant {\Lambda }_s({\theta })\}}{\tilde{\mu }}(d{\theta },dv,ds) \end{aligned}$$

and

$$\begin{aligned} {\hat{A}}_{x,t}(z)&=\int _0^xe^{-{\bar{{\tau }}}_s}P({\bar{{\tau }}}_s)\left( {\hat{{\beta }}}({\hat{\Phi }}_s,{{\mathcal {T}}}_s) +e^{-{\zeta }{\tau }_s}(Q+1){\hat{\Psi }}_s\right) (z)ds,\\ A^{{\text {cap}}}_{x,t}&=\int _0^xe^{-{\zeta }{\bar{{\tau }}}_s}\left( {\beta }^{{\text {cap}}}({\hat{\Phi }}_s,{{\mathcal {T}}}_s)-e^{-{\zeta }{\tau }_s} +{\zeta }e^{-{\zeta }{\tau }_s}\Psi ^{{\text {cap}}}_s\right) ds. \end{aligned}$$

We will show that, for all $x\in [0,t]$ and all $|z|>1$,

$$\begin{aligned} {\hat{\Psi }}_{x,t}(z)={\hat{M}}_{x,t}(z)+{\hat{A}}_{x,t}(z),\quad \Psi ^{{\text {cap}}}_{x,t}=M^{{\text {cap}}}_{x,t}+A^{{\text {cap}}}_{x,t}. \end{aligned}$$

The case $x=t$ gives the claimed identities. In the case $x=0$, all terms are 0. The left-hand and right-hand sides are piecewise continuously differentiable in x, except for finitely many jumps, at the jump times of $(\Phi _x)_{0\leqslant x\leqslant t}$, which occur when $\mu$ has an atom at $({\theta },v,x)$ with $v\leqslant {\Lambda }_x({\theta })$. It will suffice to check that the jumps and derivatives agree. Now ${\hat{A}}_{x,t}(z)$ and $A^{{\text {cap}}}_{x,t}$ are continuous in x and, at the jump times of $\Phi _x$, the jumps in ${\hat{\Psi }}_{x,t}(z)$ and $\Psi ^{{\text {cap}}}_{x,t}$ are given by

$$\begin{aligned} \Delta {\hat{\Psi }}_{x,t}(z)&=e^{-{\bar{{\tau }}}_x}P({\bar{{\tau }}}_x)\Delta {\hat{\Phi }}_x(z)\\&=e^{-{\bar{{\tau }}}_x}P({\bar{{\tau }}}_x)(e^{-C_x({\theta })}{\hat{\Phi }}_{x-}\circ F_{C_x({\theta })}({\theta },.)-{\hat{\Phi }}_{x-})(z)\\&=e^{-{\bar{{\tau }}}_x}P({\bar{{\tau }}}_x)H_x({\theta },z) =\Delta {\hat{M}}_{x,t}(z) \end{aligned}$$

and

$$\begin{aligned} \Delta \Psi ^{{\text {cap}}}_{x,t} =e^{-{\zeta }{\bar{{\tau }}}_x}\Delta {{\mathcal {T}}}_x =e^{-{\zeta }{\bar{{\tau }}}_x}C_x({\theta }) =\Delta M^{{\text {cap}}}_{x,t}. \end{aligned}$$

So it remains to check the derivatives. We will use a spectral calculation for the semigroup of multiplier operators $P({\tau })=e^{-{\tau }Q}$, whose justification is straightforward. Recall that ${\dot{{\tau }}}_t=e^{-{\zeta }{\tau }_t}$. We have

$$\begin{aligned} \frac{d}{dx}{\bar{{\tau }}}_x=-e^{-{\zeta }{\tau }_x},\quad \frac{d}{dx}e^{-{\bar{{\tau }}}_x}=e^{-{\bar{{\tau }}}_x}e^{-{\zeta }{\tau }_x},\quad \frac{d}{dx}e^{-{\zeta }{\bar{{\tau }}}_x}={\zeta }e^{-{\zeta }{\bar{{\tau }}}_x}e^{-{\zeta }{\tau }_x} \end{aligned}$$

and

$$\begin{aligned} \frac{d}{dx}P({\bar{{\tau }}}_x)=e^{-{\zeta }{\tau }_x}QP({\bar{{\tau }}}_x). \end{aligned}$$

So, between the jump times, we have

$$\begin{aligned} \frac{d}{dx}{\hat{\Psi }}_{x,t}(z)= & {} e^{-{\zeta }{\tau }_x}e^{-{\bar{{\tau }}}_x}P({\bar{{\tau }}}_x)(Q+1){\hat{\Psi }}_x(z),\\ \frac{d}{dx}\Psi ^{{\text {cap}}}_{x,t}(z)= & {} -e^{-{\zeta }{\bar{{\tau }}}_x}e^{-{\zeta }{\tau }_x}(1-{\zeta }\Psi ^{{\text {cap}}}_x) \end{aligned}$$

and

and

$$\begin{aligned} \frac{d}{dx}{\hat{A}}_{x,t}(z)&=e^{-{\bar{{\tau }}}_x}P({\bar{{\tau }}}_x)\left( {\hat{{\beta }}}({\hat{\Phi }}_x,{{\mathcal {T}}}_x)+e^{-{\zeta }{\tau }_x}(Q+1){\hat{\Psi }}_x\right) (z),\\ \frac{d}{dx}A^{{\text {cap}}}_{x,t}&=e^{-{\zeta }{\bar{{\tau }}}_x}\left( {\beta }^{{\text {cap}}}({\hat{\Phi }}_x,{{\mathcal {T}}}_x)-e^{-{\zeta }{\tau }_x}+{\zeta }e^{-{\zeta }{\tau }_x}\Psi ^{{\text {cap}}}_x\right) . \end{aligned}$$

Hence, between the jump times,

$$\begin{aligned} \frac{d}{dx}{\hat{\Psi }}_{x,t}(z) =\frac{d}{dx}({\hat{M}}_{x,t}(z)+{\hat{A}}_{x,t}(z)),\quad \frac{d}{dx}\Psi ^{{\text {cap}}}_{x,t} =\frac{d}{dx}(M^{{\text {cap}}}_{x,t}+A^{{\text {cap}}}_{x,t}) \end{aligned}$$

as required. $\square$

4 Estimation of Terms in the Interpolation Formula

We obtain some estimates on the terms in the interpolation formula (17) for ALE(${\alpha },\eta$) when it is close to the disk solution (16) of the LK$({\zeta })$ equation, with ${\zeta }={\alpha }+\eta$. For ${\delta }_0\in (0,1/2]$, define

$$\begin{aligned} T_0=T_0({\delta }_0)=\inf \big \{t\in [0,t_{\zeta }):\sup _{{\theta }\in [0,2\pi )}|{\hat{\Psi }}_t'(e^{{\sigma }+i{\theta }})|>{\delta }_0 \text { or }|\Psi ^{{\text {cap}}}_t|>{\delta }_0\big \}. \end{aligned}$$

We estimate first the martingale term and then the drift term.

4.1 Estimates for the martingale terms

Recall that the martingale term $({\hat{M}}_t,M^{{\text {cap}}}_t)$ in the interpolation formula is given by

$$\begin{aligned} {\hat{M}}_t(z)&=\int _{E(t)}e^{-{\bar{{\tau }}}_{t,s}}P({\bar{{\tau }}}_{t,s})H_s({\theta },z)1_{\{v\leqslant {\Lambda }_s({\theta })\}} {\tilde{\mu }}(d{\theta },dv,ds),\\ M^{{\text {cap}}}_t&=\int _{E(t)}e^{-{\zeta }{\bar{{\tau }}}_{t,s}}C_s({\theta })1_{\{v\leqslant {\Lambda }_s({\theta })\}}{\tilde{\mu }}(d{\theta },dv,ds) \end{aligned}$$

where $E(t)=[0,2\pi )\times [0,\infty )\times (0,t]$ and

$$\begin{aligned} {\bar{{\tau }}}_{t,s}={\tau }_t-{\tau }_s,\quad C_s({\theta })=c({\theta },{\hat{\Phi }}_{s-},{{\mathcal {T}}}_{s-}),\quad {\Lambda }_s({\theta })={\lambda }({\theta },{\hat{\Phi }}_{s-},{{\mathcal {T}}}_{s-}) \end{aligned}$$

(18)

with

$$\begin{aligned} c({\theta },{\hat{\phi }},{\tau })=ce^{-{\alpha }{\tau }}|{\hat{\phi }}'(e^{{\sigma }+i{\theta }})|^{-{\alpha }},\quad {\lambda }({\theta },{\hat{\phi }},{\tau })=c^{-1}e^{-\eta {\tau }}|{\hat{\phi }}'(e^{{\sigma }+i{\theta }})|^{-\eta } \end{aligned}$$

and

$$\begin{aligned} H_s({\theta },z)=\Delta ({\theta },z,C_s({\theta }),{\hat{\Phi }}_{s-}),\quad \Delta ({\theta },z,c,{\hat{\phi }})=e^{-c}{\hat{\phi }}(F_c({\theta },z))-{\hat{\phi }}(z). \end{aligned}$$

Consider the following approximations to ${\hat{M}}_t(z)$ and $M_t^{{\text {cap}}}$, which are obtained by replacing ${\hat{\Phi }}_{s-}$ by ${\hat{\phi }}_s$, ${{\mathcal {T}}}_{s-}$ by ${\tau }_s$ and $e^{-c}F_c({\theta },z)-z$ by $2cz/(e^{-i{\theta }}z-1)$. (Under our assumptions on the particle family, the last approximation becomes good in the limit $c\rightarrow 0$. See Sect. A.2 and in particular equation (110).) Define

$$\begin{aligned} {\hat{\Pi }}_t(z)&=\int _{E(t)}e^{-{\bar{{\tau }}}_{t,s}}P({\bar{{\tau }}}_{t,s})H({\theta },z) 2c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds), \end{aligned}$$

(19)

$$\begin{aligned} \Pi ^{{\text {cap}}}_t&=\int _{E(t)}e^{-{\zeta }{\bar{{\tau }}}_{t,s}}c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds) \end{aligned}$$

(20)

where

$$\begin{aligned} c_s=ce^{-{\alpha }{\tau }_s},\quad {\lambda }_s=c^{-1}e^{-\eta {\tau }_s} \end{aligned}$$

and

$$\begin{aligned} H({\theta },z)=\frac{z}{e^{-i{\theta }}z-1}=\sum _{k=0}^\infty e^{i(k+1){\theta }}z^{-k}. \end{aligned}$$

(21)

Lemma 4.1

For all ${\alpha },\eta \in \mathbb {R}$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,p,T)<\infty$, such that, for all $c\in (0,1]$, all ${\sigma }\geqslant 0$ and all ${\delta }_0\in (0,1/2]$,

$$\begin{aligned} \big \Vert \sup _{t\leqslant T_0({\delta }_0)\wedge T}|M^{{\text {cap}}}_t|\big \Vert _p\leqslant C\sqrt{c} \end{aligned}$$

and

$$\begin{aligned} \big \Vert \sup _{t\leqslant T_0({\delta }_0)\wedge T}|M^{{\text {cap}}}_t-\Pi ^{{\text {cap}}}_t|\big \Vert _p\leqslant C(c+\sqrt{c{\delta }_0}). \end{aligned}$$

Proof

We write $T_0$ for $T_0({\delta }_0)$ in the proofs. Consider the martingale $(M_t)_{t<t_{\zeta }}$ given by

$$\begin{aligned} M_t=\int _{E(t)}e^{{\zeta }{\tau }_s}C_s({\theta })1_{\{v\leqslant {\Lambda }_s({\theta }),\,s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

By an inequality of Burkholder, for all $p\geqslant 2$, there is a constant $C(p)<\infty$ such that, for all $t\geqslant 0$,

$$\begin{aligned} \Vert M_t^*\Vert _p\leqslant C(p)\left( \Vert \langle M \rangle _t\Vert _{p/2}^{1/2}+\Vert (\Delta M)^*_t\Vert _p\right) . \end{aligned}$$

(22)

We write here $M^*_t$ for $\sup _{s\leqslant t}|M_s|$ and similarly for other processes. See [3, Theorem 21.1] for the discrete-time case. The continuous-time case follows by a standard limit argument. Now

and

$$\begin{aligned} \Delta M_t=|M_t-M_{t-}|\leqslant e^{{\zeta }{\tau }_t}\sup _{{\theta }\in [0,2\pi )}C_t({\theta }). \end{aligned}$$

For all $t\leqslant T_0\wedge T$ and all ${\theta }\in [0,2\pi )$, we have

$$\begin{aligned} e^{{\zeta }{\tau }_t}\leqslant C,\quad C_t({\theta })\leqslant Cc,\quad {\Lambda }_t({\theta })\leqslant C/c \end{aligned}$$

(23)

so $\langle M \rangle _t\leqslant Cc$ and $(\Delta M)^*_t\leqslant Cc$. Here and below, we write C for a finite constant of the dependence allowed in the statement. The value of C may vary from one instance to the next. We remind the reader that $C_t({\theta })$ and ${\Lambda }_t({\theta })$ are defined at (18). Hence

$$\begin{aligned} \Vert M^*_t\Vert _p\leqslant C\sqrt{c}. \end{aligned}$$

Since $M^{{\text {cap}}}_t=e^{-{\zeta }{\tau }_t}M_t$ for all $t\leqslant T_0$, the first claimed estimate follows.

For the second estimate, we use instead the martingale $(M_t)_{t\geqslant 0}$ given by

$$\begin{aligned} M_t=\int _{E(t)}e^{{\zeta }{\tau }_s}\left( C_s({\theta })1_{\{v\leqslant {\Lambda }_s({\theta })\}}-c_s1_{\{v\leqslant {\lambda }_s\}}\right) 1_{\{s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Then

For $t\leqslant T_0\wedge T$ and ${\theta }\in [0,2\pi )$, we have

$$\begin{aligned} |C_t({\theta })-c_t|\leqslant Cc{\delta }_0,\quad |{\Lambda }_t({\theta })-{\lambda }_t|\leqslant C{\delta }_0/c \end{aligned}$$

(24)

so

$$\begin{aligned} \int _0^\infty \left( C_t({\theta })1_{\{v\leqslant {\Lambda }_t({\theta })\}}-c_t1_{\{v\leqslant {\lambda }_t\}}\right) ^2dv\leqslant Cc{\delta }_0. \end{aligned}$$

(25)

Then $\langle M \rangle _t\leqslant Cc{\delta }_0$ and $(\Delta M)_t\leqslant Cc$. Hence, by Burkholder’s inequality,

$$\begin{aligned} \Vert M_t^*\Vert _p\leqslant C(c+\sqrt{c{\delta }_0}). \end{aligned}$$

Since $M^{{\text {cap}}}_t-\Pi ^{{\text {cap}}}_t=e^{-{\zeta }{\tau }_t}M_t$ for all $t\leqslant T_0$, the second claimed estimate follows. $\square$

Note that, since ${\hat{\Phi }}_t$ takes values in ${{\mathcal {S}}}_1$, the holomorphic function ${\hat{\Psi }}_t(z)={\hat{\Phi }}_t(z)-z$ is bounded at $\infty$ and hence has a limiting value ${\hat{\Psi }}_t(\infty )$. The same is true for the terms ${\hat{M}}_t$ and ${\hat{A}}_t$ in the interpolation formula. Instead of estimating these terms directly, we estimate first their values at $\infty$ and then their radial derivatives $D{\hat{M}}_t$ and $D{\hat{A}}_t$, since this gives the best control of the derivative of ${\hat{\Phi }}_t$ near the unit circle, which drives the dynamics of the process.

Lemma 4.2

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },p,T)<\infty$, such that, for all $c\in (0,1]$, all ${\sigma }\geqslant 0$, all ${\delta }_0\in (0,1/2]$ and all $t\leqslant T$,

$$\begin{aligned} \big \Vert \sup _{s\leqslant T_0({\delta }_0)\wedge t}|{\hat{M}}_s(\infty )|\big \Vert _p^p \leqslant Cc^{p/2}\bigg (1+\int _0^t\Vert {\hat{\Psi }}_{s-}(\infty )1_{\{s\leqslant T_0({\delta }_0)\}}\Vert _p^pds\bigg ) \end{aligned}$$

and

$$\begin{aligned}{} & {} \big \Vert \sup _{s\leqslant T_0({\delta }_0)\wedge t}|{\hat{M}}_s(\infty )-{\hat{\Pi }}_s(\infty )|\big \Vert _p^p\\{} & {} \quad \leqslant C\bigg (\left( c+\sqrt{c{\delta }_0}\right) ^p+c^{p/2}\int _0^t\Vert {\hat{\Psi }}_{s-}(\infty )1_{\{s\leqslant T_0({\delta }_0)\}}\Vert _p^pds\bigg ). \end{aligned}$$

Proof

By considering the Laurent expansions of $F_c$ and ${\hat{\phi }}$, we have

$$\begin{aligned} \Delta ({\theta },\infty ,c,{\hat{\phi }})=a_0(c)e^{i{\theta }}+(e^{-c}-1){\hat{\psi }}(\infty ),\quad {\hat{\psi }}(z)={\hat{\phi }}(z)-z. \end{aligned}$$

(26)

Consider the martingale $(M_t)_{t<t_{\zeta }}$ given by

$$\begin{aligned} M_t=\int _{E(t)}e^{{\tau }_s}\left( a_0(C_s({\theta }))e^{i{\theta }}+(e^{-C_s({\theta })}-1){\hat{\Psi }}_{s-}(\infty )\right) 1_{\{v\leqslant {\Lambda }_s({\theta }),\,s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Then ${\hat{M}}_t(\infty )=e^{-{\tau }_t}M_t$ for all $t\leqslant T_0$. By Proposition A.5, $|a_0(c)|\leqslant Cc$ for all c. Hence

and, for $p\geqslant 2$, since

$$\begin{aligned} |(\Delta M)^*_t|^p\leqslant \int _{E(t)} e^{p{\tau }_s}\left| a_0(C_s({\theta }))e^{i{\theta }}+(e^{-C_s({\theta })}-1){\hat{\Psi }}_{s-}(\infty )\right| ^p 1_{\{v\leqslant {\Lambda }_s({\theta }),s\leqslant T_0\}}\mu (d{\theta },dv,ds) \end{aligned}$$

we have

The first claimed estimate then follows from Burkholder’s inequality (22).

For the second estimate, we consider instead the martingale $(M_t)_{t<t_{\zeta }}$ given by

$$\begin{aligned} M_t&=\int _{E(t)}e^{{\tau }_s}\Big (\left( a_0(C_s({\theta }))1_{\{v\leqslant {\Lambda }_s({\theta })\}}-2c_s1_{\{v\leqslant {\lambda }_s\}}\right) e^{i{\theta }}\\&\quad +(e^{-C_s({\theta })}-1){\hat{\Psi }}_{s-}(\infty )1_{\{v\leqslant {\Lambda }_s({\theta })\}} \Big )1_{\{s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Then ${\hat{M}}_t(\infty )-{\hat{\Pi }}_t(\infty )=e^{-{\tau }_t}M_t$ for all $t\leqslant T_0$. By Proposition A.5, we have $|a_0(c)-2c|\leqslant Cc^{3/2}$. We combine this with (23) and (24) to see that

$$\begin{aligned} \int _0^\infty \left| a_0(C_t({\theta }))1_{\{v\leqslant {\Lambda }_t({\theta })\}}-2c_t1_{\{v\leqslant {\lambda }_t\}}\right| ^pdv \leqslant C(c^{3p/2-1}+c^{p-1}{\delta }_0) \leqslant C(c^p+c^{p-1}{\delta }_0). \end{aligned}$$

The second estimate then follows by Burkholder’s inequality as above. $\square$

Recall that, for $p\in [1,\infty )$ and $r>1$, we set

For a measurable function $\Psi$ on ${\Omega }\times \{|z|>1\}$, we set

Lemma 4.3

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, all ${\varepsilon }\in (0,1/2)$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\varepsilon },{\Lambda },p,T)<\infty$ such that, for all $c\in (0,1]$, all ${\sigma }\geqslant 0$, all ${\delta }_0\in (0,1/2]$ and all $t\leqslant T$, for all $r\geqslant 1+c^{1/2-{\varepsilon }}$, for $\rho =(1+r)/2$, we have, in the case ${\zeta }<1$,

(27)

and

(28)

while in the case ${\zeta }=1$ the same bounds hold with $\left( \frac{r}{r-1}\right)$ replaced in the first term on the right-hand side by $\left( \frac{r}{r-1}\right) +\frac{1}{\sqrt{\sigma }}\left( \frac{r}{r-1}\right) ^{1/2}$.

Proof

Recall that we write $T_0$ for $T_0({\delta }_0)$. Fix $t\leqslant T<t_{\zeta }$. For $s\in [0,t]$, we will write ${\bar{{\tau }}}_s$ for ${\bar{{\tau }}}_{t,s}={\tau }_t-{\tau }_s$. Consider for $|z|>1$, the martingale $(M_x(z))_{0\leqslant x\leqslant t}$ given by

$$\begin{aligned} M_x(z)= & {} \int _{E(x)}{\tilde{H}}_s({\theta },z)1_{\{v\leqslant {\Lambda }_s({\theta }),\,s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds),\\ {\tilde{H}}_s({\theta },z)= & {} e^{-{\bar{{\tau }}}_s}DP({\bar{{\tau }}}_s)H_s({\theta },z). \end{aligned}$$

By Burkholder’s inequality, for $p\geqslant 2$ and all $|z|>1$,

$$\begin{aligned} \Vert M_t(z)\Vert _p \leqslant C(p)\left( \Vert \langle M(z) \rangle _t\Vert _{p/2}^{1/2}+\Vert (\Delta M(z))^*_t\Vert _p\right) . \end{aligned}$$

(29)

On the event $\{t\leqslant T_0\}$, we have $D{\hat{M}}_t(z)=M_t(z)$ so, on taking the $\Vert .\Vert _{p,r}$-norm in (29), we obtain

(30)

Now

and

$$\begin{aligned} (\Delta M(z))^*_t \leqslant \sup _{s\leqslant T_0\wedge t,{\theta }\in [0,2\pi )}|{\tilde{H}}_s({\theta },z)|. \end{aligned}$$

(31)

Also

$$\begin{aligned} |(\Delta M(z))^*_t|^p \leqslant \int _{E(t)}|{\tilde{H}}_s({\theta },z)|^p1_{\{v\leqslant {\Lambda }_s({\theta }),s\leqslant T_0\}}\mu (d{\theta },dv,ds) \end{aligned}$$

so

We have ${\Lambda }_s({\theta })\leqslant C/c$ for all $s\leqslant T_0$ and ${\theta }\in [0,2\pi )$. Hence

(32)

and

(33)

Similarly,

(34)

We will split the jump $\Delta ({\theta },z,c,{\hat{\phi }})$ as the sum of several terms, and thereby split $H_s({\theta },z)$ and hence $M_t$ also as a sum of terms. For each of these terms, we will use one of the inequalities (32), (33) and one of (31), (34) to obtain a suitable upper bound for the right-side of (30). These bounds will combine to prove the first claimed estimate.

Recall that ${\hat{\phi }}(z)=z+{\hat{\psi }}(z)$, so

$$\begin{aligned} \Delta ({\theta },z,c,{\hat{\phi }}) =\Delta _0({\theta },z,c)+\left( e^{-c}{\hat{\psi }}(F_c({\theta },z))-{\hat{\psi }}(z)\right) \end{aligned}$$

(35)

where

$$\begin{aligned} \Delta _0({\theta },z,c)=e^{-c}F_c({\theta },z)-z. \end{aligned}$$

We further split the second term by expanding in Taylor series, using an interpolation from z to $F_c({\theta },z)$. For $u\in [0,1]$, define

$$\begin{aligned} F_{c,u}({\theta },z)=e^{uf_c({\theta },z)}z,\quad f_c({\theta },z)=\log (F_c({\theta },z)/z). \end{aligned}$$

Then $F_{c,0}({\theta },z)=z$ and $F_{c,1}({\theta },z)=F_c({\theta },z)$. Fix c, ${\theta }$ and z and set

$$\begin{aligned} g(u)=e^{-cu}{\hat{\psi }}(F_{c,u}({\theta },z)) \end{aligned}$$

then

$$\begin{aligned} g^{(k)}(u)=e^{-cu}\sum _{j=0}^k\left( {\begin{array}{c}k\\ j\end{array}}\right) (-c)^{k-j}f_c({\theta },z)^jD^j{\hat{\psi }}(F_{c,u}({\theta },z)). \end{aligned}$$

Set $m=\lceil 1/(8{\varepsilon })\rceil$ and recall that our constants C are allowed to depend on ${\varepsilon }$. Then

$$\begin{aligned} e^{-c}{\hat{\psi }}(F_c({\theta },z))-{\hat{\psi }}(z)&=g(1)-g(0)\nonumber \\&=\sum _{k=1}^m\frac{g^{(k)}(0)}{k!}+\int _0^1\frac{(1-u)^m}{m!}g^{(m+1)}(u)du\nonumber \\&=\sum _{k=1}^{m+1}\Delta _k({\theta },z,c,{\hat{\psi }}) \end{aligned}$$

(36)

where, for $k=1,\dots ,m$,

$$\begin{aligned} \Delta _k({\theta },z,c,{\hat{\psi }}) =\frac{1}{k!}\sum _{j=0}^k\left( {\begin{array}{c}k\\ j\end{array}}\right) (-c)^{k-j}f_c({\theta },z)^jD^j{\hat{\psi }}(z) \end{aligned}$$

and

$$\begin{aligned}{} & {} \Delta _{m+1}({\theta },z,c,{\hat{\psi }})=\frac{1}{m!}\int _0^1(1-u)^me^{-cu}\\{} & {} \quad \sum _{j=0}^{m+1} \left( {\begin{array}{c}m+1\\ j\end{array}}\right) (-c)^{m+1-j}f_c({\theta },z)^jD^j{\hat{\psi }}(F_{c,u}({\theta },z))du. \end{aligned}$$

Let us write

$$\begin{aligned} H^0_s({\theta },z)= & {} \Delta _0({\theta },z,C_s({\theta })),\\ H^k_s({\theta },z)= & {} \Delta _k({\theta },z,C_s({\theta }),{\hat{\Phi }}_{s-}),\quad k=1,\dots ,m+1 \end{aligned}$$

and

$$\begin{aligned} {\tilde{H}}_s^k({\theta },z)=e^{-{\bar{{\tau }}}_s}DP({\bar{{\tau }}}_s)H_s^k({\theta },z) \end{aligned}$$

and

$$\begin{aligned} M^k_x(z)=\int _{E(x)}{\tilde{H}}^k_s({\theta },z)1_{\{v\leqslant {\Lambda }_s({\theta }),s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

We consider first the contribution of

$$\begin{aligned} \Delta _0({\theta },z,c)=e^{-c}F_c({\theta },z)-z. \end{aligned}$$

We make the further split $\Delta _0=\Delta _{0,0}+\Delta _{0,1}$, where

$$\begin{aligned} \Delta _{0,0}({\theta },z,c) =\frac{a_0(c)z}{e^{-i{\theta }}z-1} =a_0(c)\sum _{k=0}^\infty e^{i(k+1){\theta }}z^{-k} \end{aligned}$$

and

$$\begin{aligned} \Delta _{0,1}({\theta },z,c) =e^{-c}F_c({\theta },z)-z-\frac{a_0(c)z}{e^{-i{\theta }}z-1}. \end{aligned}$$

We will exploit the more explicit form of $\Delta _{0,0}$, which is the main term as $c\rightarrow 0$ under our particle assumptions (4), (5) and (6), to obtain better estimates. We have, with obvious notation,

$$\begin{aligned} H_s^{0,0}({\theta },z)=a_0(C_s({\theta }))\sum _{k=0}^\infty e^{i(k+1){\theta }}z^{-k} \end{aligned}$$

so, for ${\tau }\geqslant 0$,

$$\begin{aligned} DP({\tau })H_s^{0,0}({\theta },z)=a_0(C_s({\theta }))\sum _{k=1}^\infty e^{i(k+1){\theta }}(-k)e^{-{\tau }q(k)}z^{-k}. \end{aligned}$$

By Proposition A.5, $|a_0(c)|\leqslant Cc$ for all c. So, for $|z|=r$ and ${\tau }\geqslant 0$,

$$\begin{aligned} |DP({\tau })H_s^{0,0}({\theta },z)| \leqslant Cc\sum _{k=1}^\infty kr^{-k} \leqslant \frac{Cc}{r}\left( \frac{r}{r-1}\right) ^2 \end{aligned}$$

(37)

and

Hence we have

We used the facts that $(d/ds){\bar{{\tau }}}_s=-{\dot{{\tau }}}_s$ and ${\dot{{\tau }}}_s=e^{-{\zeta }{\tau }_s}$ and $e^{{\zeta }{\tau }_s}\leqslant C$ to see that, for all ${\lambda }>0$,

$$\begin{aligned} \int _0^t{\lambda }e^{-{\lambda }{\bar{{\tau }}}_s}ds\leqslant C\int _0^t{\lambda }e^{-{\lambda }{\bar{{\tau }}}_s}{\dot{{\tau }}}_s ds\leqslant C. \end{aligned}$$

(38)

We will use similar estimates for other integrals of $({\bar{{\tau }}}_s)_{s\leqslant t}$ without further explanation. Now $q(k)\geqslant (1-{\zeta }^+)k$ so we obtain, for ${\zeta }<1$,

$$\begin{aligned} \langle M^{0,0}(z) \rangle _t\leqslant \frac{Cc}{r^2}\left( \frac{r}{r-1}\right) ^2. \end{aligned}$$

On the other hand, for ${\zeta }=1$, we have $q(k)\geqslant (({\sigma }k^2)\wedge k)/C$ so we obtain

$$\begin{aligned} \langle M^{0,0}(z) \rangle _t\leqslant \frac{Cc}{r^2}\bigg (\left( \frac{r}{r-1}\right) ^2+\frac{1}{{\sigma }}\left( \frac{r}{r-1}\right) \bigg ). \end{aligned}$$

We use (31) and (37) to obtain, for $|z|=r>1$,

$$\begin{aligned} |(\Delta M^{0,0}(z))^*_t| \leqslant \sup _{s\leqslant T_0\wedge t,{\theta }\in [0,2\pi )}|DP({\bar{{\tau }}}_s)H_s^{0,0}({\theta },z)| \leqslant \frac{Cc}{r}\left( \frac{r}{r-1}\right) ^2. \end{aligned}$$

On substituting the estimates for $\langle M^{0,0}(z) \rangle _t$ and $(\Delta M^{0,0}(z))^*_t$ into (30), we obtain for $r\geqslant 1+\sqrt{c}$ and $p\geqslant 2$, for ${\zeta }<1$,

(39)

while, for ${\zeta }=1$,

(40)

We turn to the contribution of $\Delta _{0,1}$. For $s\leqslant T_0$ and all ${\theta }\in [0,2\pi )$, we have

$$\begin{aligned} C_s({\theta })\leqslant Cc. \end{aligned}$$

(41)

By Proposition A.6, there is a family of functions $(Q_u:u\in [0,1])$, each holomorphic on $\{|z|>1\}$, such that

$$\begin{aligned} |Q_u(z)|\leqslant \frac{C\sqrt{u}|z|}{|z-1|^2} \end{aligned}$$

(42)

and such that

$$\begin{aligned} H^{0,1}_s({\theta },z) =\Delta _{0,1}({\theta },z,C_s({\theta })) =e^{-C_s({\theta })}\int _0^{C_s({\theta })}Q_u({\theta },z)du \end{aligned}$$

(43)

where $Q_u({\theta },z)=e^{i{\theta }}Q_u(e^{-i{\theta }}z)$. We use the Laurent series

$$\begin{aligned} Q_u(z)=\sum _{k=1}^\infty a_u(k)z^{-k} \end{aligned}$$

to write

$$\begin{aligned} DP({\tau })H^{0,1}_s({\theta },z)=e^{-C_s({\theta })}\sum _{k=1}^\infty (-k)e^{-{\tau }q(k)}e^{i(k+1){\theta }}z^{-k}\int _0^{C_s({\theta })}a_u(k)du. \end{aligned}$$

Hence we obtain, for $|z|=r>1$,

$$\begin{aligned} |DP({\tau })H^{0,1}_s({\theta },z)| \leqslant \int _0^{Cc}\sum _{k=1}^\infty kr^{-k}|a_u(k)|du \leqslant \frac{Cc^{3/2}}{r}\left( \frac{r}{r-1}\right) ^3 \end{aligned}$$

where we used

$$\begin{aligned} \sum _{k=1}^\infty kr^{-k}|a_u(k)|du \leqslant \left( \sum _{k=1}^\infty k^2(r/\rho )^{-2k}\right) ^{1/2} \left( \sum _{k=1}^\infty |a_u(k)|^2\rho ^{-2k}\right) ^{1/2} \end{aligned}$$

and

$$\begin{aligned} \sum _{k=1}^\infty |a_u(k)|^2\rho ^{-2k}=\Vert Q_u\Vert _{2,\rho }^2\leqslant \frac{Cu}{r^2}\left( \frac{r}{r-1}\right) ^3. \end{aligned}$$

Now

so, using again (38),

Hence, using the same lower bounds for q(k) as above, we obtain, for ${\zeta }<1$,

and, for ${\zeta }=1$,

Hence, for $|z|=r>1$ and ${\zeta }<1$, we have

while, for ${\zeta }=1$, similarly,

$$\begin{aligned} \langle M^{0,1}(z) \rangle _t \leqslant \frac{Cc^2}{r^2}\bigg (\left( \frac{r}{r-1}\right) ^4+\frac{1}{{\sigma }}\left( \frac{r}{r-1}\right) ^3\bigg ). \end{aligned}$$

Also, for all $s\leqslant T_0$ and $|z|=r>1$, we have

$$\begin{aligned} |\Delta M^{0,1}_s(z)| \leqslant \sup _{s\leqslant T_0}|DP({\bar{{\tau }}}_s)H_s^{0,1}({\theta },z)| \leqslant \frac{Cc^{3/2}}{r}\left( \frac{r}{r-1}\right) ^3. \end{aligned}$$

Hence we obtain, for $p\geqslant 2$ and $r\geqslant 1+\sqrt{c}$, for ${\zeta }<1$,

(44)

and, for ${\zeta }=1$, similarly,

(45)

We consider next, for $k=1,\dots ,m$, the contribution of

$$\begin{aligned} \Delta _k({\theta },z,c,{\hat{\psi }}) =\frac{1}{k!}\sum _{j=0}^k\left( {\begin{array}{c}k\\ j\end{array}}\right) (-c)^{k-j}f_c({\theta },z)^jD^j{\hat{\psi }}(z). \end{aligned}$$

In order to avoid the appearance of a spurious log term in the case ${\zeta }=1$ we treat this contribution a little differently. We take an additional derivative, estimate the derivative and finally integrate that estimate. We have

$$\begin{aligned} f_c({\theta },z)=\int _0^cL_u({\theta },z)du \end{aligned}$$

where $L_u({\theta },z)=e^{i{\theta }}L_u(e^{-i{\theta }}z)$ and $L_u(z)$ is given by (117). Then

$$\begin{aligned}{} & {} H^k_s({\theta },z) =\Delta _k({\theta },z,C_s({\theta }),{\hat{\Psi }}_{s-})\nonumber \\{} & {} \quad =\frac{1}{k!}\sum _{j=0}^k\left( {\begin{array}{c}k\\ j\end{array}}\right) (-C_s({\theta }))^{k-j}\left( \int _0^{C_s({\theta })}L_u({\theta },z)du\right) ^jD^j{\hat{\Psi }}_{s-}(z) \end{aligned}$$

(46)

so

$$\begin{aligned}&D^2P({\tau })H_s^k({\theta },z)\\&\quad =\frac{1}{k!}(-C_s({\theta }))^kD^2P({\tau }){\hat{\Psi }}_{s-}(z)+\frac{1}{k!}\sum _{j=1}^k\left( {\begin{array}{c}k\\ j\end{array}}\right) (-C_s({\theta }))^{k-j}\\&\qquad \int _0^{C_s({\theta })}\dots \int _0^{C_s({\theta })}D^2P({\tau }) (L_{u_1,\dots ,u_j}({\theta },.)D^j{\hat{\Psi }}_{s-})(z)du_1\dots du_j \end{aligned}$$

where

$$\begin{aligned} L_{u_1,\dots ,u_j}({\theta },z)=\prod _{i=1}^jL_{u_i}({\theta },z). \end{aligned}$$

Hence, for $s\leqslant T_0$,

$$\begin{aligned}&|D^2P({\tau })H_s^k({\theta },z)|\leqslant Cc^k|D^2P({\tau }){\hat{\Psi }}_{s-}(z)|\\&\quad +C\sum _{j=1}^kc^{k-j}\int _0^{Cc}\dots \int _0^{Cc}|D^2P({\tau })(L_{u_1,\dots ,u_j} ({\theta },.)D^j{\hat{\Psi }}_{s-})(z)|du_1\dots du_j \end{aligned}$$

so

where

By Proposition A.6, for $|z|=r\geqslant 1+\sqrt{c}$ and $u\leqslant Cc$,

$$\begin{aligned} |L_u(z)| \leqslant \frac{C|z|}{|z-1|} \end{aligned}$$

so

$$\begin{aligned} \Vert L_{u_1,\dots ,u_j}\Vert _{p,r} \leqslant C\left( \frac{r}{r-1}\right) ^{j-1/p} \end{aligned}$$

and so by Proposition A.7, for $j=1,\dots ,k$ and $\rho =(r+1)/2$ and $\rho '=(3r+1)/4$, for ${\zeta }<1$,

$$\begin{aligned}&\Vert h_{s,u_1,\dots ,u_j}\Vert _{p,r} \leqslant \Vert D^2P({\bar{{\tau }}}_s)\Vert _{p,\rho '\rightarrow r}\Vert L_{u_1,\dots ,u_j}\Vert _{2,\rho '}\Vert D^j{\hat{\Psi }}_{s-}\Vert _{p,\rho '}\\&\quad \leqslant C\left( \left( \frac{r}{r-1}\right) ^2\wedge \frac{1}{{\bar{{\tau }}}_s^2}\right) \left( \frac{r}{r-1}\right) ^{j-1/2}\left( \frac{r}{r-1}\right) ^{j-1}\Vert D{\hat{\Psi }}_{s-}\Vert _{p,\rho }. \end{aligned}$$

In estimating $\Vert D^2P({\tau })\Vert _{p,\rho '\rightarrow r}$, we used the better of two estimates – either the case $n=0$ of Lemma 2.1 in conjunction with (119) or the case $n=2$ of Lemma 2.1. A similar but easier estimate holds for $\Vert h_s\Vert _{p,r}$. Now

so, for $r\geqslant 1+\sqrt{c}$ and ${\zeta }<1$,

$$\begin{aligned}&\Vert \langle DM^k(.) \rangle _t\Vert _{p/2,r} \\&\quad \leqslant \frac{C}{c}\int _0^{T_0\wedge t} \bigg (c^k\Vert h_s\Vert _{p,r}+\sum _{j=1}^kc^{k-j}\int _0^{Cc}\dots \int _0^{Cc} \Vert h_{s,u_1,\dots ,u_j}\Vert _{p,r}du_1\dots du_j\bigg )^2ds\\&\quad \leqslant Cc^{2k-1}\left( \frac{r}{r-1}\right) ^{4k-3} \int _0^{T_0\wedge t}\bigg (\left( \frac{r}{r-1}\right) ^4\wedge \frac{1}{{\bar{{\tau }}}_s^4}\bigg ) \Vert D{\hat{\Psi }}_{s-}\Vert _{p,\rho }^2ds\\&\quad \leqslant Cc\left( \frac{r}{r-1}\right) \int _0^{T_0\wedge t}\bigg (\left( \frac{r}{r-1}\right) ^4\wedge \frac{1}{{\bar{{\tau }}}_s^4}\bigg )\Vert D{\hat{\Psi }}_{s-}\Vert _{p,\rho }^2ds \end{aligned}$$

and so

We used here the inequality

$$\begin{aligned} \int _0^\infty a^p\wedge s^{-p}ds\leqslant \left( \frac{p}{p-1}\right) a^{p-1} \end{aligned}$$

(47)

which holds for all $a>0$ and all $p>1$, to see that

$$\begin{aligned} \int _0^t\bigg (\left( \frac{r}{r-1}\right) ^4\wedge \frac{1}{{\bar{{\tau }}}_s^4}\bigg )ds \leqslant C\int _0^t\bigg (\left( \frac{r}{r-1}\right) ^4\wedge \frac{1}{{\bar{{\tau }}}_s^4}\bigg ){\dot{{\tau }}}_sds \leqslant C\left( \frac{r}{r-1}\right) ^3. \end{aligned}$$

For $p\geqslant 2$ and $r>1$, we have

and, from (46), for $r\geqslant 1+\sqrt{c}$, estimating as above but now using the second estimate of Proposition A.7, we get

$$\begin{aligned} \Vert D^2P({\bar{{\tau }}}_s)H_s^k({\theta },.)\Vert _{p,r}&\leqslant Cc^k\bigg (\left( \frac{r}{r-1}\right) ^2\wedge \frac{1}{{\bar{{\tau }}}_s^2}\bigg )\left( \frac{r}{r-1}\right) ^{2k-1-1/p}\Vert D{\hat{\Psi }}_{s-}\Vert _{p,\rho }\\&\leqslant Cc\bigg (\left( \frac{r}{r-1}\right) ^2\wedge \frac{1}{{\bar{{\tau }}}_s^2}\bigg )\left( \frac{r}{r-1}\right) ^{1-1/p}\Vert D{\hat{\Psi }}_{s-}\Vert _{p,\rho } \end{aligned}$$

so, for $r\geqslant 1+\sqrt{c}$,

(48)

On substituting the estimates for $\langle DM^k(z) \rangle _t$ and $(\Delta DM^k(.))^*_t$ into (30), we obtain for $r\geqslant 1+\sqrt{c}$ and $p\geqslant 2$, for ${\zeta }<1$,

(49)

In the case ${\zeta }=1$, we have to modify the above estimation in using

$$\begin{aligned} \Vert D^2P({\tau })\psi \Vert _{p,r}\leqslant C\bigg (\left( \frac{r}{r-1}\right) ^2\wedge \left( \frac{1}{{\tau }^2}\vee \frac{1}{{\sigma }{\tau }}\right) \bigg )\Vert \psi \Vert _{p,\rho }. \end{aligned}$$

We obtain in this case

(50)

Now, since the holomorphic functions $M^k_t$ and ${\hat{\Psi }}_{s-}$ vanish at $\infty$, we have

$$\begin{aligned} M_t^k(z)=-\int _1^\infty \frac{DM_t^k(az)}{a}da \end{aligned}$$

and, for $a\geqslant 1$,

$$\begin{aligned} \Vert {\hat{\Psi }}_{s-}\Vert _{p,a\rho }\leqslant \frac{C}{a}\Vert {\hat{\Psi }}_{s-}\Vert _{p,\rho } \end{aligned}$$

so, on integrating (49) and (50) we obtain, for ${\zeta }<1$,

(51)

while, for ${\zeta }=1$,

(52)

(We remark that, if a similar argument is used to estimate directly, then one obtains the same estimate (51) for ${\zeta }<1$ but one faces in the case ${\zeta }=1$ the integral

$$\begin{aligned} \int _0^t\left( \frac{r}{r-1}\right) \wedge \frac{1}{{\sigma }{\bar{{\tau }}}_s}ds. \end{aligned}$$

The $p=1$ case of (47) then generates a log term, which our method avoids.)

We consider finally the contribution of

$$\begin{aligned} \Delta _{m+1}({\theta },z,c,{\hat{\psi }})= & {} \frac{1}{m!}\int _0^1(1-u)^me^{-cu}\sum _{j=0}^{m+1}\left( {\begin{array}{c}m+1\\ j\end{array}}\right) \\{} & {} (-c)^{m+1-j}f_c ({\theta },z)^jD^j{\hat{\psi }}(F_{c,u}({\theta },z))du. \end{aligned}$$

Then

$$\begin{aligned}&H_s^{m+1}({\theta },z)=\Delta _{m+1}({\theta },z,C_s({\theta }),{\hat{\Psi }}_{s-})\\&\quad =\frac{1}{m!}\int _0^1(1-u)^me^{-C_s({\theta })u}\sum _{j=0}^{m+1}\left( {\begin{array}{c}m+1\\ j\end{array}}\right) \\&\qquad (-C_s({\theta }))^{m+1-j}f_{C_s({\theta })}({\theta },z)^jD^j{\hat{\Psi }}_{s-}(F_{C_s({\theta }),u}({\theta },z))du. \end{aligned}$$

By Proposition A.5, we have

$$\begin{aligned} |f_c({\theta },z)|\leqslant \frac{Cc|z|}{|e^{-i{\theta }}z-1|}. \end{aligned}$$

Hence, for $s\leqslant T_0$ and ${\tau }\geqslant 0$,

$$\begin{aligned}&\Vert DP({\tau })H_s^{m+1}({\theta },.)\Vert _{p,r}\\&\quad \leqslant Cc^{m+1}\Vert DP({\tau }){\hat{\Psi }}_{s-}\Vert _{p,r} +C\Vert DP({\tau })\Vert _{p,\rho '\rightarrow r}\\&\qquad \sum _{j=1}^{m+1}c^{m+1-j}\Vert f_{C_s({\theta })}({\theta },.)^j\Vert _{p,\rho '} \Vert D^j{\hat{\Psi }}_{s-}(F_{C_s({\theta }),u}({\theta },.))\Vert _{\infty ,\rho '}. \end{aligned}$$

By Lemma 2.1, for ${\zeta }<1$,

$$\begin{aligned} \Vert DP({\tau })\Vert _{p,\rho '\rightarrow r}\leqslant C\left( \frac{r}{r-1}\right) \wedge \frac{1}{{\tau }}. \end{aligned}$$

We have

$$\begin{aligned} \Vert f_{C_s({\theta })}({\theta },.)^j\Vert _{p,\rho '}\leqslant Cc^j\left( \frac{r}{r-1}\right) ^{j-1/p} \end{aligned}$$

and, since $|F_{c,u}({\theta },z)|\geqslant |z|$, we have

$$\begin{aligned} \Vert D^j{\hat{\Psi }}_{s-}(F_{C_s({\theta }),u}({\theta },.))\Vert _{\infty ,\rho '} \leqslant \Vert D^j{\hat{\Psi }}_{s-}\Vert _{\infty ,\rho '} \leqslant C\left( \frac{r}{r-1}\right) ^{j-1+1/p}\Vert D{\hat{\Psi }}_{s-}\Vert _{p,\rho }. \end{aligned}$$

Hence, for ${\zeta }<1$, we have

$$\begin{aligned} \Vert DP({\tau })H_s^{m+1}({\theta },.)\Vert _{p,r} \leqslant Cc^{m+1} \bigg (\left( \frac{r}{r-1}\right) \wedge \frac{1}{{\tau }}\bigg ) \left( \frac{r}{r-1}\right) ^{2m+1} \Vert D{\hat{\Psi }}_{s-}\Vert _{p,\rho } \end{aligned}$$

so, using (33),

$$\begin{aligned} \Vert \langle M^{m+1}(.) \rangle _t\Vert _{p/2,r} \leqslant Cc^{2m+1}\left( \frac{r}{r-1}\right) ^{4m+2} \int _0^{T_0\wedge t} \bigg (\left( \frac{r}{r-1}\right) ^2\wedge \frac{1}{{\bar{{\tau }}}_s^2}\bigg )\Vert D{\hat{\Psi }}_s\Vert _{p,\rho }^2ds \end{aligned}$$

and so

Here we have used our choice of $m\geqslant 1/(8{\varepsilon })$ and the assumption $r\geqslant 1+c^{1/2-{\varepsilon }}$ to see that

$$\begin{aligned} c^{2m}\left( \frac{r}{r-1}\right) ^{4m+1}\leqslant C. \end{aligned}$$

The bound (48) remains valid with $M^{m+1}$ in place of $M^k$. Hence for ${\zeta }<1$

(53)

For ${\zeta }=1$, given the weaker bound for $\Vert DP({\tau })\Vert _{p,r}$ in Lemma 2.1, we adapt the argument as above to obtain

where $\log$ term has been absorbed using our choice of m, and then

(54)

Now

$$\begin{aligned} M_t=M^{0,0}_t+M^{0,1}_t+\sum _{k=1}^{m+1}M^k_t \end{aligned}$$

and we have shown that all terms on the right-hand side can be bounded by the right-hand side in (27), so this first estimate is now proved.

It remains to show the second estimate. Fix $t\geqslant 0$ and consider, for $|z|>1$, the martingale $(\Pi _x(z))_{x\geqslant 0}$ given by

$$\begin{aligned} \Pi _x(z)=\int _{E(x)}e^{-{\bar{{\tau }}}_s}P({\bar{{\tau }}}_s)DH({\theta },z)2c_s1_{\{v\leqslant {\lambda }_s,\,s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Set ${\tilde{M}}_x(z)=M^{0,0}_x(z)-\Pi _x(z)$. Then

$$\begin{aligned} {\tilde{M}}_x(z)&=\int _{E(x)}e^{-{\bar{{\tau }}}_s}\left( a_0(C_s({\theta }))1_{\{v\leqslant {\Lambda }_s({\theta })\}} -2c_s1_{\{v\leqslant {\lambda }_s\}}\right) \\&\quad DP({\bar{{\tau }}}_s)H({\theta },z) 1_{\{s\leqslant T_0\}}{\tilde{\mu }}(d{\theta },dv,ds) \end{aligned}$$

and

$$\begin{aligned} D({\hat{M}}_t-{\hat{\Pi }}_t)=M_t-\Pi _t={\tilde{M}}_t+M^{0,1}_t+\sum _{k=1}^{m+1}M^k_t. \end{aligned}$$

For all but the first term on the right, the bounds (44), (45), (51), (52), (53), (54), are sufficient for (28). It remains to show a suitable bound on ${\tilde{M}}_t$. We use the estimate (25) to see that, for ${\zeta }<1$,

while for ${\zeta }=1$ we obtain similarly

$$\begin{aligned} \langle {\tilde{M}}(z) \rangle _t \leqslant \frac{Cc{\delta }_0}{r^2}\bigg (\left( \frac{r}{r-1}\right) ^2+\frac{1}{{\sigma }}\left( \frac{r}{r-1}\right) \bigg ). \end{aligned}$$

Otherwise we can proceed as for $M^{0,0}$ to arrive as the following estimates, which suffice for (28). For ${\zeta }<1$, we have

while for ${\zeta }=1$

$\square$

4.2 Estimates for the drift terms

We turn to the drift terms, beginning with estimates for the drift $({\hat{{\beta }}},{\beta }^{{\text {cap}}})$ of the ALE$({\alpha },\eta )$ process. Recall that $({{\mathcal {T}}}_t)_{t\geqslant 0}$ has drift given by

where

$$\begin{aligned} c({\theta },{\hat{\phi }},{\tau })=ce^{-{\alpha }{\tau }}|{\hat{\phi }}'(e^{{\sigma }+i{\theta })}|^{-{\alpha }},\quad {\lambda }({\theta },{\hat{\phi }},{\tau })=c^{-1}e^{-\eta {\tau }}|{\hat{\phi }}'(e^{{\sigma }+i{\theta })}|^{-\eta }. \end{aligned}$$

Lemma 4.4

For all ${\zeta }\in \mathbb {R}$ and all $T<t_{\zeta }$, there is a constant $C({\zeta },T)<\infty$ such that, for all ${\delta }_0\in (0,1/2]$, all $t\leqslant T$, all ${\hat{\phi }}\in {{\mathcal {S}}}_1$ and all ${\tau }\geqslant 0$, we have

$$\begin{aligned} |{\beta }^{{\text {cap}}}({\hat{\phi }},{\tau })-e^{-{\zeta }{\tau }_t}+{\zeta }e^{-{\zeta }{\tau }_t}\psi ^{{\text {cap}}}_t|\leqslant C{\delta }_0^2 \end{aligned}$$

whenever $|\psi ^{{\text {cap}}}_t|\leqslant {\delta }_0$ and $|{\hat{\psi }}'(e^{{\sigma }+i{\theta }})|\leqslant {\delta }_0$ for all ${\theta }$, where $\psi ^{{\text {cap}}}_t={\tau }-{\tau }_t$ and ${\hat{\psi }}(z)={\hat{\phi }}(z)-z$.

Proof

We have

$$\begin{aligned} c({\theta },{\hat{\phi }},{\tau }){\lambda }({\theta },{\hat{\phi }},{\tau }) =e^{-{\zeta }{\tau }}|{\hat{\phi }}'(e^{{\sigma }+i{\theta })}|^{-{\zeta }} =e^{-{\zeta }{\tau }_t}e^{-{\zeta }\psi ^{{\text {cap}}}_t}|1+{\hat{\psi }}'(e^{{\sigma }+i{\theta })}|^{-{\zeta }} \end{aligned}$$

and, for $|w|\leqslant 1/2$,

$$\begin{aligned} |1+w|^{-{\zeta }}=1-{\zeta }{\text {Re}}w+{\varepsilon }(w),\quad |{\varepsilon }(w)|\leqslant C|w|^2 \end{aligned}$$

so

$$\begin{aligned} c({\theta },{\hat{\phi }},{\tau }){\lambda }({\theta },{\hat{\phi }},{\tau }) =e^{-{\zeta }{\tau }_t}\left( 1-{\zeta }\psi ^{{\text {cap}}}_t-{\zeta }{\text {Re}}{\hat{\psi }}'(e^{{\sigma }+i{\theta }})+{\gamma }_t({\theta },{\hat{\phi }},{\tau })\right) \end{aligned}$$

(55)

where

$$\begin{aligned} |{\gamma }_t({\theta },{\hat{\phi }},{\tau })|\leqslant C{\delta }_0^2 \end{aligned}$$

(56)

whenever $|\psi ^{{\text {cap}}}_t|\leqslant {\delta }_0$ and $|{\hat{\psi }}'(e^{{\sigma }+i{\theta }})|\leqslant {\delta }_0$ for all ${\theta }$. For ${\hat{\phi }}\in {{\mathcal {S}}}_1$, ${\hat{\psi }}$ is holomorphic in $\{|z|>1\}$ and bounded at $\infty$, so

(57)

The claimed estimate follows on integrating (55) in ${\theta }$. $\square$

Recall that the drift of $({\hat{\Phi }}_t)_{t\geqslant 0}$ is given by

where

$$\begin{aligned} \Delta ({\theta },z,c,{\hat{\phi }}) =e^{-c}{\hat{\phi }}(F_c({\theta },z))-{\hat{\phi }}(z),\quad F_c({\theta },z)=e^{i{\theta }}F_c(e^{-i{\theta }}z). \end{aligned}$$

It is convenient in the following statement to use the notation

$$\begin{aligned} \Vert \phi \Vert _{p,r,0}=\Vert \phi -\phi (\infty )\Vert _{p,r} \end{aligned}$$

for functions $\phi$ holomorphic in $\{|z|>1\}$ and bounded at $\infty$.

Lemma 4.5

For all ${\alpha },\eta \in \mathbb {R}$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },T)<\infty$ with the following property. For all $c\in (0,1/C]$, all ${\sigma }>0$, all ${\delta }_0\in (0,1/2]$, all $t\leqslant T$, all ${\hat{\phi }}\in {{\mathcal {S}}}_1$ and all ${\tau }\geqslant 0$, we have

$$\begin{aligned} |{\hat{{\beta }}}({\hat{\phi }},{\tau })(\infty )+e^{-{\zeta }{\tau }_t}(Q+1){\hat{\psi }}(\infty )| \leqslant C({\delta }_0\sqrt{c}+{\delta }_0^2)+C(c+{\delta }_0)|{\hat{\psi }}(\infty )| \end{aligned}$$

(58)

whenever $|\psi ^{{\text {cap}}}_t|\leqslant {\delta }_0$ and $|{\hat{\psi }}'(e^{{\sigma }+i{\theta }})|\leqslant {\delta }_0$ for all ${\theta }$, where $\psi ^{{\text {cap}}}_t={\tau }-{\tau }_t$ and ${\hat{\psi }}(z)={\hat{\phi }}(z)-z$.

Moreover, for all ${\alpha },\eta \in \mathbb {R}$, all ${\varepsilon }\in (0,1/2]$, all $p\geqslant 2$ and all $T<{\tau }_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },{\varepsilon },p,T)<\infty$ with the following property. For all $c\in (0,1/C]$, all ${\sigma }>0$, all ${\delta }_0\in (0,1/2]$, all $t\leqslant T$, all ${\hat{\phi }}\in {{\mathcal {S}}}_1$ and all ${\tau }\geqslant 0$, for all $r\geqslant 1+c^{1/2-{\varepsilon }}$ and $\rho =(3r+1)/4$, we have

$$\begin{aligned}&\Vert {\hat{{\beta }}}({\hat{\phi }},{\tau })+e^{-{\zeta }{\tau }_t}(Q+1){\hat{\psi }}\Vert _{p,r,0}\nonumber \\&\quad \leqslant \frac{C{\delta }_0^2}{r}\left( 1+\log \left( \frac{r}{r-1}\right) \right) +\frac{C{\delta }_0}{r}\left( 1+\log \left( \frac{r}{r-1}\right) \right) r\Vert D{\hat{\psi }}\Vert _{p,\rho }\nonumber \\&\qquad +\frac{C{\delta }_0\sqrt{c}}{r}\left( \frac{r}{r-1}\right) +\frac{Cc}{r}\left( \frac{r}{r-1}\right) r\Vert D{\hat{\psi }}\Vert _{p,\rho } \end{aligned}$$

(59)

whenever $|\psi ^{{\text {cap}}}_t|\leqslant {\delta }_0$ and $|{\hat{\psi }}'(e^{{\sigma }+i{\theta }})|\leqslant {\delta }_0$ for all ${\theta }$.

Proof

We use the split (35) and the Taylor expansion (36) to write

$$\begin{aligned} \Delta ({\theta },z,c,{\hat{\phi }}) =\Delta _0({\theta },z,c)+\sum _{k=1}^{m+1}\Delta _k({\theta },z,c,{\hat{\psi }}) \end{aligned}$$

where $m=\lceil 1/(8{\varepsilon })\rceil$. We further split

$$\begin{aligned} \Delta _0({\theta },z,c)=\frac{2cz}{e^{-i{\theta }}z-1}+{\tilde{\Delta }}_0({\theta },z,c) \end{aligned}$$

(60)

and

$$\begin{aligned} \Delta _1({\theta },z,c,{\hat{\psi }}) =c(D{\hat{\psi }}(z)-{\hat{\psi }}(z))+{\tilde{\Delta }}_1({\theta },z,c,{\hat{\psi }}). \end{aligned}$$

Note that we now split $\Delta _0$ slightly differently to the split $\Delta _0=\Delta _{0,0}+\Delta _{0,1}$ used for the martingale term: where before we had $a_0(c)$ we now approximate by 2c, putting an additional error into the remainder term ${\tilde{\Delta }}_0$. Set

$$\begin{aligned} {\tilde{\Delta }}({\theta },z,c,{\hat{\phi }})={\tilde{\Delta }}_0({\theta },z,c)+{\tilde{\Delta }}_1({\theta },z,c,{\hat{\psi }}) +\sum _{k=2}^{m+1}\Delta _k({\theta },z,c,{\hat{\psi }}) \end{aligned}$$

and note that

$$\begin{aligned} e^{-c}{\hat{\phi }}(F_c({\theta },z))-{\hat{\phi }}(z) =c\left( \frac{2z}{e^{-i{\theta }}z-1}+D{\hat{\psi }}(z)-{\hat{\psi }}(z)\right) +{\tilde{\Delta }}({\theta },z,c,{\hat{\psi }}). \end{aligned}$$

(61)

We use equation (55) to write

Now ${\hat{\psi }}'(z)\rightarrow 0$ as $z\rightarrow \infty$, so

Hence

(62)

and

(63)

We will estimate the terms on the right-hand sides of (62) and (63), assuming from now on that t, ${\hat{\phi }}$ and ${\tau }$ are chosen so that $|\psi ^{{\text {cap}}}_t|\leqslant {\delta }_0$ and $|{\hat{\psi }}'(e^{{\sigma }+i{\theta }})|\leqslant {\delta }_0$ for all ${\theta }$.

From (55) and (56), we have $|{\gamma }_t({\theta },{\hat{\phi }},{\tau })|\leqslant C{\delta }_0^2$ and

We use (26) to see that

$$\begin{aligned} {\tilde{\Delta }}({\theta },\infty ,c,{\hat{\psi }})= & {} \Delta ({\theta },\infty ,c,{\hat{\psi }})-2ce^{i{\theta }}+c{\hat{\psi }}(\infty )\\= & {} (a_0(c)-2c)e^{i{\theta }}+(e^{-c}-1+c){\hat{\psi }}(\infty ). \end{aligned}$$

Write $c({\theta })$ for $c({\theta },{\hat{\phi }},{\tau })$ and ${\lambda }({\theta })$ for ${\lambda }({\theta },{\hat{\phi }},{\tau })$. Then

$$\begin{aligned} |c({\theta })-c_t|\leqslant C{\delta }_0c,\quad |{\lambda }({\theta })-{\lambda }_t|\leqslant C{\delta }_0c^{-1} \end{aligned}$$

and, by Proposition A.5, we have

$$\begin{aligned} |a_0(c({\theta }))-2c({\theta })|\leqslant Cc^{3/2},\quad |(a_0(c({\theta }))-2c({\theta }))-(a_0(c_t)-2c_t)|\leqslant Cc^{3/2}{\delta }_0. \end{aligned}$$

We can now estimate in (62) to obtain (58).

It remains to prove (59). For $|z|=r>1$, we have

(64)

Since ${\hat{\psi }}$ is bounded at $\infty$, by Marcinkiewicz’s multiplier theorem, $\Vert {\hat{\psi }}\Vert _{p,r,0}\leqslant C\Vert D{\hat{\psi }}\Vert _{p,r}$ for all $p>1$ and $r>1$. Hence

(65)

It remains to deal with the final term in (63). We first estimate the function obtained on replacing $c({\theta },{\hat{\phi }},{\tau })$ and ${\lambda }({\theta },{\hat{\phi }},{\tau })$ in that term by $c_t=ce^{-{\alpha }{\tau }_t}$ and ${\lambda }_t=c^{-1}e^{-\eta {\tau }_t}$. Note that, in the case $F_c(z)=e^cz$ and $m=1$, the Taylor expansion (36) has the form

$$\begin{aligned} e^{-c}{\hat{\phi }}(e^cz)-{\hat{\phi }}(z)= & {} c(D{\hat{\psi }}(z)-{\hat{\psi }}(z))\\{} & {} +\,c^2\int _0^1(1-u)e^{-cu}(D^2{\hat{\psi }} (e^{cu}z)\\{} & {} -2D{\hat{\psi }}(e^{cu}z)+{\hat{\psi }}(e^{cu}z))du. \end{aligned}$$

On the other hand, by Cauchy’s theorem,

Hence, on integrating in ${\theta }$ in (61), we see that

so, for $r>1$ and $\rho =(3r+1)/4$,

(66)

It remains to deal with the error made in replacing $c({\theta },{\hat{\phi }},{\tau })$ and ${\lambda }({\theta },{\hat{\phi }},{\tau })$ by $c_t$ and ${\lambda }_t$. We make a further split

$$\begin{aligned} {\tilde{\Delta }}_0({\theta },z,c)={\tilde{\Delta }}_{0,0}({\theta },z,c)+{\tilde{\Delta }}_{0,1}({\theta },z,c),\quad {\tilde{\Delta }}({\theta },z,c)={\bar{\Delta }}({\theta },z,c)+{\tilde{\Delta }}_{0,1}({\theta },z,c) \end{aligned}$$

where

$$\begin{aligned} {\tilde{\Delta }}_{0,0}({\theta },z,c)=e^{-c}F_c({\theta },z)-z-\frac{a_0(c)z}{e^{-i{\theta }}z-1},\quad {\tilde{\Delta }}_{0,1}({\theta },z,c)=\frac{(a_0(c)-2c)z}{e^{-i{\theta }}z-1}. \end{aligned}$$

Thus ${\tilde{\Delta }}_{0,0}=\Delta _{0,1}$, as considered in estimating the martingale terms, and ${\tilde{\Delta }}_{0,1}$ is the additional error introduced by the new split (60). We first estimate the ${\tilde{\Delta }}_{0,1}$ term. Since $|\psi ^{{\text {cap}}}_t|\leqslant {\delta }_0$ and $|{\hat{\psi }}'(e^{{\sigma }+i{\theta }})|\leqslant {\delta }_0$ for all ${\theta }$, we have

$$\begin{aligned} |c({\theta },{\hat{\phi }},{\tau })-c_t|\leqslant Cc{\delta }_0,\quad |{\lambda }({\theta },{\hat{\phi }},{\tau })-{\lambda }_t|\leqslant C{\delta }_0/c. \end{aligned}$$

Hence, by Proposition A.5, for $c\leqslant 1/C$,

$$\begin{aligned} |(a_0(c({\theta },{\hat{\phi }},{\tau }))-2c({\theta },{\hat{\phi }},{\tau })){\lambda }({\theta },{\hat{\phi }},{\tau }) -(a_0(c_t)-2c_t){\lambda }_t|\leqslant C{\delta }_0\sqrt{c} \end{aligned}$$

and, estimating as for (64), we obtain

$$\begin{aligned}{} & {} \Vert {\tilde{\Delta }}_{0,1}({\theta },.,c({\theta },{\hat{\phi }},{\tau })){\lambda }({\theta },{\hat{\phi }},{\tau }) -{\tilde{\Delta }}_{0,1}({\theta },.,c_t){\lambda }_t\Vert _{p,r,0}\nonumber \\{} & {} \quad \leqslant \frac{C{\delta }_0\sqrt{c}}{r}\left( 1+\log \left( \frac{r}{r-1}\right) \right) . \end{aligned}$$

(67)

By Proposition A.5, for $c\leqslant 1/C$,

$$\begin{aligned} |{\tilde{\Delta }}_{0,0}({\theta },z,c)|\leqslant \frac{Cc^{3/2}|z|}{|e^{-i{\theta }}z-1|^2} \end{aligned}$$

and, for $c_1,c_2\in (0,c]$ and $|z|\geqslant 1+\sqrt{c}$,

$$\begin{aligned} |{\tilde{\Delta }}_{0,0}({\theta },z,c_1)-{\tilde{\Delta }}_{0,0}({\theta },z,c_2)| \leqslant \frac{C\sqrt{c}|c_1-c_2||z|}{|e^{-i{\theta }}z-1|^2} \end{aligned}$$

so

$$\begin{aligned} |{\tilde{\Delta }}_{0,0}({\theta },z,c({\theta },{\hat{\phi }},{\tau })){\lambda }({\theta },{\hat{\phi }},{\tau }) -{\tilde{\Delta }}_{0,0}({\theta },z,c_t){\lambda }_t| \leqslant \frac{C{\delta }_0\sqrt{c}|z|}{|e^{-i{\theta }}z-1|^2} \end{aligned}$$

so, for $|z|=r\geqslant 1+\sqrt{c}$,

(68)

We have

$$\begin{aligned} {\tilde{\Delta }}_1({\theta },z,c,{\hat{\psi }}) =\left( \log \left( \frac{F_c({\theta },z)}{z}\right) -c\right) D{\hat{\psi }}(z) \end{aligned}$$

so, by Proposition A.5, for $c\leqslant 1/C$,

$$\begin{aligned} |{\tilde{\Delta }}_1({\theta },z,c,{\hat{\psi }})| \leqslant \frac{Cc}{|e^{-i{\theta }}z-1|}|D{\hat{\psi }}(z)| \end{aligned}$$

and, for $c_1,c_2\in (0,c]$ and $|z|\geqslant 1+\sqrt{c}$,

$$\begin{aligned} |{\tilde{\Delta }}_1({\theta },z,c_1,{\hat{\psi }})-{\tilde{\Delta }}_1({\theta },z,c_2,{\hat{\psi }})| \leqslant \frac{C|c_1-c_2|}{|e^{-i{\theta }}z-1|}|D{\hat{\psi }}(z)| \end{aligned}$$

so

$$\begin{aligned} |{\tilde{\Delta }}_1({\theta },z,c({\theta },{\hat{\phi }},{\tau })){\lambda }({\theta },{\hat{\phi }},{\tau })-{\tilde{\Delta }}_1({\theta },z,c_t){\lambda }_t| \leqslant \frac{C{\delta }_0}{|e^{-i{\theta }}z-1|}|D{\hat{\psi }}(z)| \end{aligned}$$

so, for $|z|=r\geqslant 1+\sqrt{c}$,

(69)

For $k=2,\dots ,m$, we have

$$\begin{aligned} \Delta _k({\theta },z,c,{\hat{\psi }}) =\frac{1}{k!}\sum _{j=0}^k\left( {\begin{array}{c}k\\ j\end{array}}\right) (-c)^{k-j}f_c({\theta },z)^jD^j{\hat{\psi }}(z) \end{aligned}$$

where $f_c({\theta },z)=\log (F_c({\theta },z)/z)$. By Proposition A.5, for $c\leqslant 1/C$ and $|z|=r>1$,

$$\begin{aligned} |f_c({\theta },z)|\leqslant \frac{Ccr}{|e^{-i{\theta }}z-1|} \end{aligned}$$

and, for $c_1,c_2\in (0,c]$ and $|z|=r\geqslant 1+\sqrt{c}$,

$$\begin{aligned} |f_{c_1}({\theta },z)-f_{c_2}({\theta },z)|\leqslant \frac{C|c_1-c_2|r}{|e^{-i{\theta }}z-1|} \end{aligned}$$

so, for $j=0,1,\dots ,k$,

$$\begin{aligned} |c_1^{k-j}f_{c_1}({\theta },z)^j-c_2^{k-j}f_{c_2}({\theta },z)^j| \leqslant \frac{Cc^{k-1}|c_1-c_2|r^j}{|e^{-i{\theta }}z-1|^j} \end{aligned}$$

so

$$\begin{aligned} |\Delta _k({\theta },z,c,{\hat{\psi }})| \leqslant Cc^k\sum _{j=0}^k\frac{r^j}{|e^{-i{\theta }}z-1|^j}|D^j{\hat{\psi }}(z)| \end{aligned}$$

and

$$\begin{aligned}{} & {} |\Delta _k({\theta },z,c_1,{\hat{\psi }})-\Delta _k({\theta },z,c_2,{\hat{\psi }}) |\\{} & {} \quad \leqslant Cc^{k-1}|c_1-c_2|\sum _{j=0}^k\frac{r^j}{|e^{-i{\theta }}z-1|^j}|D^j{\hat{\psi }}(z)| \end{aligned}$$

so

$$\begin{aligned}{} & {} |\Delta _k({\theta },z,c({\theta },{\hat{\phi }},{\tau })){\lambda }({\theta },{\hat{\phi }},{\tau })-\Delta _k({\theta },z,c_t){\lambda }_t|\\{} & {} \quad \leqslant Cc^{k-1}{\delta }_0\sum _{j=0}^k\frac{r^j}{|e^{-i{\theta }}z-1|^j}|D^j{\hat{\psi }}(z)| \end{aligned}$$

so

and so, for $r\geqslant 1+2\sqrt{c}$,

(70)

where we used the inequality $\Vert {\hat{\psi }}\Vert _{p,r,0}\leqslant C\Vert D{\hat{\psi }}\Vert _{p,r}$ in the $j=0$ term.

In the final step, we use our assumption that $r\geqslant 1+c^{1/2-{\varepsilon }}$ and our choice of $m=\lceil 1/(8{\varepsilon })\rceil$ to see that

$$\begin{aligned} c^m\left( \frac{r}{r-1}\right) ^{2m+1+1/p} \leqslant Cc\left( \frac{r}{r-1}\right) ^2. \end{aligned}$$

Recall that

$$\begin{aligned} \Delta _{m+1}({\theta },z,c,{\hat{\psi }})= & {} \frac{1}{m!}\int _0^1(1-u)^me^{-cu}\sum _{j=0}^{m+1}\left( {\begin{array}{c}m+1\\ j\end{array}}\right) \\{} & {} (-c)^{m+1-j} f_c({\theta },z)^jD^j{\hat{\psi }}(F_{c,u}({\theta },z))du \end{aligned}$$

and, for $|z|=r>1$, since $|F_{c,u}({\theta },z)|\geqslant r$, by (118), we find, for $\rho '=(7r+1)/8$,

$$\begin{aligned} |D^j{\hat{\psi }}(F_{c,u}({\theta },z))|\leqslant C \left( \frac{r}{r-1}\right) ^{1/p} \Vert D^j{\hat{\psi }}\Vert _{p,\rho '}. \end{aligned}$$

So, for $|z|=r>1$,

$$\begin{aligned} |\Delta _{m+1}({\theta },z,c,{\hat{\psi }})| \leqslant Cc^{m+1} \left( \frac{r}{r-1}\right) ^{1/p} \left( \frac{r}{|e^{-i{\theta }}z-1|}\right) ^{m+1} \Vert D^{m+1}{\hat{\psi }}\Vert _{p,\rho '} \end{aligned}$$

so

and so

(71)

The claimed estimate is obtained by combining (64), (65), (66), (67), (68), (69), (70) and (71). $\square$

Recall that the drift term $({\hat{A}}_t,A^{{\text {cap}}}_t)$ in the interpolation formula (17) is given by

$$\begin{aligned} {\hat{A}}_t(z)&=\int _0^te^{-({\tau }_t-{\tau }_s)}P({\tau }_t-{\tau }_s)\left( {\hat{{\beta }}}({\hat{\Phi }}_s,{{\mathcal {T}}}_s) +e^{-{\zeta }{\tau }_s}(Q+1){\hat{\Psi }}_s\right) (z)ds,\\ A^{{\text {cap}}}_t&=\int _0^te^{-{\zeta }({\tau }_t-{\tau }_s)}\left( {\beta }^{{\text {cap}}}({\hat{\Phi }}_s,{{\mathcal {T}}}_s) -e^{-{\zeta }{\tau }_s}+{\zeta }e^{-{\zeta }{\tau }_s}\Psi ^{{\text {cap}}}_s\right) ds \end{aligned}$$

where $\Psi ^{{\text {cap}}}_s={{\mathcal {T}}}_s-{\tau }_s$ and ${\hat{\Psi }}_s(z)={\hat{\Phi }}_s(z)-z$. Recall also that

$$\begin{aligned} T_0({\delta }_0)=\inf \big \{t\in [0,t_{\zeta }):\sup _{{\theta }\in [0,2\pi )}|{\hat{\Psi }}_t'(e^{{\sigma }+i{\theta }})|>{\delta }_0\text { or }|\Psi ^{{\text {cap}}}_t|>{\delta }_0\big \}. \end{aligned}$$

Lemma 4.6

For all ${\zeta }\in \mathbb {R}$ and all $T<t_{\zeta }$, there is a constant $C({\zeta },T)<\infty$ such that, for all ${\sigma }>0$, all ${\delta }_0\in (0,1/2]$ and all $t\leqslant T_0({\delta }_0)\wedge T$, we have

$$\begin{aligned} |A^{{\text {cap}}}_t|\leqslant C{\delta }_0^2. \end{aligned}$$

Proof

For all $t\leqslant T_0({\delta }_0)\wedge t_{\zeta }$ and all ${\theta }$, we have $|\Psi ^{{\text {cap}}}_t|\leqslant {\delta }_0$ and $|{\hat{\Psi }}'_t(e^{{\sigma }+i{\theta }})|\leqslant {\delta }_0$ for all ${\theta }$. Hence, by Lemma 4.4, for $t\leqslant T_0({\delta }_0)\wedge T$,

$$\begin{aligned} |A^{{\text {cap}}}_t|\leqslant e^{-{\zeta }{\tau }_t}\int _0^te^{{\zeta }{\tau }_s}|{\beta }^{{\text {cap}}}({\hat{\Phi }}_s,{{\mathcal {T}}}_s)-e^{-{\zeta }{\tau }_s}+{\zeta }e^{-{\zeta }{\tau }_s}\Psi ^{{\text {cap}}}_s|ds\leqslant C{\delta }_0^2. \end{aligned}$$

$\square$

Lemma 4.7

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },T)<\infty$ with the following property. For all $c\in (0,1/C]$, all ${\sigma }>0$, all ${\delta }_0\in (0,1/2]$ and all $t\leqslant T$,

$$\begin{aligned} \sup _{s\leqslant t\wedge T_0({\delta }_0)}|{\hat{A}}_s(\infty )| \leqslant C({\delta }_0\sqrt{c}+{\delta }_0^2)+C(c+{\delta }_0)\int _0^{t\wedge T_0({\delta }_0)}|{\hat{\Psi }}_s(\infty )|ds. \end{aligned}$$

(72)

Moreover, for all such ${\alpha },\eta$ and T, for all ${\varepsilon }\in (0,1/2]$ and all $p\geqslant 2$, there is a constant $C({\alpha },\eta ,{\Lambda },{\varepsilon },p,T)<\infty$ with the following property. For all $c\in (0,1/C]$, all ${\sigma }\geqslant 0$, all ${\delta }_0\in (0,1/2]$ and all $t\leqslant T$, for all $r\geqslant 1+c^{1/2-{\varepsilon }}$, for $\rho =(1+r)/2$, we have in the case ${\zeta }<1$

(73)

while for ${\zeta }=1$ the estimate (73) holds with the first factor of $1+\log (\tfrac{r}{r-1})$ replaced by $1+\log (\tfrac{r}{r-1})+\tfrac{1}{\sqrt{\sigma }}$ in each term on the right.

We remark that some of the log terms in (73) can be avoided when ${\zeta }<1$ by the same strategy used for (51). However, this does not work in the case ${\zeta }=1$ because that strategy also replaces the term $\frac{1}{\sqrt{\sigma }}$ by $\frac{1}{{\sigma }}$ which, for our main results, leads to a weaker conclusion. The $\frac{1}{\sqrt{\sigma }}$ in (51) arises in a different way. Since spurious log terms for ${\zeta }<1$ do not affect the main results, and to economise the argument, we will not present the slightly stronger estimates than (73) that are available for ${\zeta }<1$.

Proof

The estimate (72) follows immediately from (58). Set $\rho '=(3r+1)/4$. For ${\zeta }<1$, by Lemma 2.1, we have

(74)

By Lemma 4.5, for $s\leqslant T_0$,

$$\begin{aligned}&\Vert {\hat{{\beta }}}({\hat{\Phi }}_s,{{\mathcal {T}}}_s)+e^{-{\zeta }{\tau }_s}(Q+1){\hat{\Psi }}_s\Vert _{p,\rho ',0}\\&\quad \leqslant \frac{C{\delta }_0^2}{r}\left( 1+\log \left( \frac{r}{r-1}\right) \right) +\frac{C{\delta }_0}{r}\left( 1+\log \left( \frac{r}{r-1}\right) \right) r\Vert D{\hat{\Psi }}_s\Vert _{p,\rho }\\&\qquad +\frac{C{\delta }_0\sqrt{c}}{r}\left( \frac{r}{r-1}\right) +\frac{Cc}{r}\left( \frac{r}{r-1}\right) r\Vert D{\hat{\Psi }}_s\Vert _{p,\rho } \end{aligned}$$

so, for $s\leqslant t$,

Since

$$\begin{aligned} \int _0^t\left( \frac{r}{r-1}\right) \wedge \frac{1}{{\bar{{\tau }}}_s}ds\leqslant C\left( 1+\log \left( \frac{r}{r-1}\right) \right) \end{aligned}$$

these estimates combine to prove (73). In the case ${\zeta }=1$, the estimate of Lemma 2.1 leads to a different integral on the right in (74), for which we have the following bound

$$\begin{aligned} \int _0^t\left( \frac{r}{r-1}\right) \wedge \left( \frac{1}{{\bar{{\tau }}}_s}\vee \frac{1}{\sqrt{{\sigma }{\bar{{\tau }}}_s}}\right) ds \leqslant C\bigg (1+\log \left( \frac{r}{r-1}\right) +\frac{1}{\sqrt{\sigma }}\bigg ). \end{aligned}$$

Hence we obtain the modified form of (73) claimed for ${\zeta }=1$. $\square$

5 Bulk Scaling Limit for ALE$({\alpha },\eta )$

Recall that we write our ALE(${\alpha },\eta$) process $(\Phi _t)_{t\geqslant 0}$ in (Schlicht function, capacity) coordinates $({\hat{\Phi }}_t,{{\mathcal {T}}}_t)$, and that we set

$$\begin{aligned} {\hat{\Psi }}_t(z)={\hat{\Phi }}_t(z)-{\hat{\phi }}_t(z),\quad \Psi ^{{\text {cap}}}_t={{\mathcal {T}}}_t-{\tau }_t \end{aligned}$$

where $({\hat{\phi }}_t,{\tau }_t)_{t<t_{\zeta }}$ is the disk solution to the LK$({\zeta })$ equation with initial capacity ${\tau }_0=0$. We obtained the following interpolation formula (17)

$$\begin{aligned} {\hat{\Psi }}_t(z)={\hat{M}}_t(z)+{\hat{A}}_t(z),\quad \Psi ^{{\text {cap}}}_t=M^{{\text {cap}}}_t+A^{{\text {cap}}}_t \end{aligned}$$

and have estimated the terms on the right-hand sides in the preceding section. We now put these estimates together to obtain first $L^p$-estimates and then pointwise high-probability estimates which allow us to prove Theorems 1.1 and 1.2.

5.1 $L^p$-estimates

Recall that

$$\begin{aligned} T_0({\delta }_0)=\inf \big \{t\in [0,t_{\zeta }):\sup _{{\theta }\in [0,2\pi )}|{\hat{\Psi }}_t'(e^{{\sigma }+i{\theta }})|>{\delta }_0\text { or }|\Psi ^{{\text {cap}}}_t|>{\delta }_0\big \}. \end{aligned}$$

Proposition 5.1

For all ${\alpha },\eta \in \mathbb {R}$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,p,T)<\infty$ such that, for all $c\in (0,1]$ and all ${\delta }_0\in (0,1/2]$,

$$\begin{aligned} \big \Vert \sup _{t\leqslant T\wedge T_0({\delta }_0)}|\Psi ^{{\text {cap}}}_t|\big \Vert _p\leqslant C(\sqrt{c}+{\delta }_0^2) \end{aligned}$$

and

$$\begin{aligned} \big \Vert \sup _{t\leqslant T\wedge T_0({\delta }_0)}|\Psi ^{{\text {cap}}}_t-\Pi ^{{\text {cap}}}_t|\big \Vert _p \leqslant C(c+\sqrt{c{\delta }_0}+{\delta }_0^2) \end{aligned}$$

and

$$\begin{aligned} \big \Vert \sup _{t\leqslant T\wedge T_0({\delta }_0)}|{\hat{\Psi }}_t(\infty )|\big \Vert _p\leqslant C(\sqrt{c}+{\delta }_0^2) \end{aligned}$$

and

$$\begin{aligned} \big \Vert \sup _{t\leqslant T\wedge T_0({\delta }_0)}|{\hat{\Psi }}_t(\infty )-{\hat{\Pi }}_t(\infty )|\big \Vert _p \leqslant C(c+\sqrt{c{\delta }_0}+{\delta }_0^2). \end{aligned}$$

Proof

The first two estimates follow immediately from Lemmas 4.1 and 4.6. From Lemmas 4.2 and 4.7, we obtain, for all $t\leqslant T$,

$$\begin{aligned} \big \Vert \sup _{s\leqslant t\wedge T_0({\delta }_0)}|{\hat{\Psi }}_t(\infty )|\big \Vert _p^p \leqslant C(\sqrt{c}+{\delta }_0^2)^p+C\int _0^t\Vert {\hat{\Psi }}_s(\infty )1_{\{s\leqslant T_0({\delta }_0)\}}\Vert _p^pds \end{aligned}$$

from which the third estimate follows by Gronwall’s lemma. The fourth estimate follows from the third, together with Lemmas 4.2 and 4.7. $\square$

Fix ${\sigma }>0$ and set

$$\begin{aligned} R=\frac{r}{r-1},\quad L=1+\log R,\quad R_1=R+\frac{\sqrt{R}}{\sqrt{\sigma }},\quad L_1=L+\frac{1}{\sqrt{\sigma }}. \end{aligned}$$

Define

$$\begin{aligned} {\delta }(r)&=(\sqrt{c}R+{\delta }_0^2L^2+{\delta }_0\sqrt{c}LR)/r,\quad {\bar{{\delta }}}(r)=\sqrt{c}R+{\delta }_0L^2, \end{aligned}$$

(75)

$$\begin{aligned} {\delta }_1(r)&=(\sqrt{c}R_1+{\delta }_0^2LL_1+{\delta }_0\sqrt{c}L_1R)/r,\quad {\bar{{\delta }}}_1(r)=\sqrt{c}R_1+{\delta }_0LL_1. \end{aligned}$$

(76)

The next estimates follow immediately from Lemmas 4.3 and 4.7.

Proposition 5.2

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, all ${\varepsilon }\in (0,1/2]$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },{\varepsilon },p,T)<\infty$ with the following property. For all $c\in (0,1]$, all ${\delta }_0\in (0,1/2]$, all $r,e^{\sigma }\geqslant 1+c^{1/2-{\varepsilon }}$ and all $t\leqslant T$, setting $\rho =(1+r)/2$, we have, for ${\zeta }<1$,

(77)

while, for ${\zeta }=1$,

(78)

The preceding estimate may be improved by an iterative argument to obtain the following result.

Proposition 5.3

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, all ${\varepsilon }\in (0,1/2]$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },{\varepsilon },p,T)<\infty$ with the following property. In the case ${\zeta }<1$, for all $c\in (0,1]$, all $r,e^{\sigma }\geqslant 1+c^{1/2-{\varepsilon }}$ and all $t\leqslant T$, for all $\nu \in (0,{\varepsilon }/2]$, setting ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1)$, we have

Moreover, in the case ${\zeta }=1$ and ${\varepsilon }\leqslant 1/3$, for all $c\in (0,1]$, all $r\geqslant 1+c^{1/2-{\varepsilon }}$, all $e^{\sigma }\geqslant 1+c^{1/3-{\varepsilon }}$ and all $t\leqslant T$, for $\nu \in (0,{\varepsilon }/2]$, setting ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1)$, we have

(79)

Proof

We begin with a crude estimate which allows us to restrict further consideration to small values of c. The function ${\hat{\Phi }}_t(z)$ is univalent on $\{|z|>1\}$, with ${\hat{\Phi }}_t(z)\sim z$ as $z\rightarrow \infty$. So, by a standard distortion estimate, for all $|z|=r>1$,

$$\begin{aligned} |{\hat{\Phi }}_t'(z)-1| \leqslant \frac{1}{r^2-1} \end{aligned}$$

and so

$$\begin{aligned} \Vert D{\hat{\Psi }}_t\Vert _{p,r} =r\Vert {\hat{\Phi }}_t'-1\Vert _{p,r} \leqslant \frac{1}{r-1}. \end{aligned}$$

(80)

It is straightforward to check that this implies the claimed estimates in the case where $c>1/C$, for any given constant C of the allowed dependence. Hence it will suffice to consider the case where $c\leqslant 1/C$.

Consider first the case ${\zeta }<1$. On substituting the chosen value of ${\delta }_0$ in (75), we obtain

$$\begin{aligned} {\delta }(r)&=\frac{1}{r}\bigg (\sqrt{c}R+c^{1-2\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2L^2+c^{1-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) LR\bigg ),\\ {\bar{{\delta }}}(r)&=\sqrt{c}R+c^{1/2-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) L^2. \end{aligned}$$

Note that, for $\rho =(1+r)/2$, we have $R(\rho )\leqslant 2R(r)$ and $L(\rho )\leqslant 2L(r)$, so ${\bar{{\delta }}}(\rho )\leqslant 4{\bar{{\delta }}}(r)$ and ${\bar{{\delta }}}(\rho )\leqslant 4{\bar{{\delta }}}(r)$. Note also that, for $r\geqslant 1+c^{1/2-{\varepsilon }/2}$ and $e^{\sigma }\geqslant 1+c^{1/2-{\varepsilon }}$, for all sufficiently small c,

$$\begin{aligned} C^*{\bar{{\delta }}}(r)\leqslant 2C^*(c^{{\varepsilon }/2}+c^{{\varepsilon }/2}(1+\log (1/c))^2)\leqslant c^{{\varepsilon }/3}\leqslant 1 \end{aligned}$$

where $C^*$ is the constant in Proposition 5.2. We restrict to such c. Set $C_0=1$ and for $k\geqslant 0$ define recursively $C_{k+1}=2^{k+1}C_k+1$. We will show that, for all $k\geqslant 0$, all $r\geqslant 1+2^kc^{1/2-{\varepsilon }/2}$ and all $t\leqslant T$,

(81)

The case $k=0$ is implied by (80). Suppose inductively that (81) holds for k, for all $r\geqslant 1+2^kc^{1/2-{\varepsilon }/2}$ and all $t\leqslant T$. Take $r\geqslant 1+2^{k+1}c^{1/2-{\varepsilon }/2}$ and $t\leqslant T$. Then $\rho =(r+1)/2\geqslant 1+2^k c^{1/2-{\varepsilon }/2}$ so, for all $s\leqslant t$,

Since $r\geqslant 1+c^{1/2-{\varepsilon }/2}$, we can use Proposition 5.2 with ${\varepsilon }$ replaced by ${\varepsilon }/2$ and substitute the last inequality into (77) to obtain

Hence (81) holds for $k+1$ and the induction proceeds. Choose now $k=\lceil 3/{\varepsilon }\rceil$. Then

$$\begin{aligned} \frac{(C^*{\bar{{\delta }}}(r))^k}{r-1}\leqslant \frac{c^{{\varepsilon }k/3}}{r-1}\leqslant \frac{c}{r-1}\leqslant {\delta }(r). \end{aligned}$$

For c sufficiently small, we have $c^{{\varepsilon }/2}\leqslant 2^{-k/2}$. Then, for all $r\geqslant 1+c^{1/2-{\varepsilon }}$, we have $r\geqslant 1+2^kc^{1/2-{\varepsilon }/2}$, so we obtain

For c sufficiently small, we have

$$\begin{aligned} c^{1-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) LR\leqslant \sqrt{c}R \end{aligned}$$

so this is a bound of the claimed form.

We turn to the case ${\zeta }=1$. On substituting the chosen value of ${\delta }_0$ in (76), we obtain

$$\begin{aligned} {\delta }_1(r)&=\frac{1}{r}\bigg (\sqrt{c}R_1+c^{1-2\nu }R(e^{\sigma })^2LL_1+c^{1-\nu }R(e^{\sigma })L_1R\bigg ),\\ {\bar{{\delta }}}_1(r)&=\sqrt{c}R_1+c^{1/2-\nu }R(e^{\sigma })LL_1. \end{aligned}$$

Note that, for $\rho =(1+r)/2$, we have $R_1(\rho )\leqslant 2R_1(r)$ and $L_1(\rho )\leqslant 2L_1(r)$, so ${\bar{{\delta }}}_1(\rho )\leqslant 4{\bar{{\delta }}}_1(r)$ and ${\bar{{\delta }}}_1(\rho )\leqslant 4{\bar{{\delta }}}_1(r)$. Note also that, for $r\geqslant 1+c^{1/2-{\varepsilon }/2}$ and $e^{\sigma }\geqslant 1+c^{1/3-{\varepsilon }}$, for all sufficiently small c,

$$\begin{aligned} C^*{\bar{{\delta }}}(r)\leqslant 4C^*(c^{{\varepsilon }/2}+c^{{\varepsilon }/2}(1+\log (1/c))^2)\leqslant c^{{\varepsilon }/3}\leqslant 1 \end{aligned}$$

where $C^*$ is the constant in Proposition 5.2. We restrict to such c. Set $C_0=1$ and for $k\geqslant 0$ define recursively $C_{k+1}=2^{2k+1}C_k+1$. Then, by an analogous inductive argument, we obtain, for all $k\geqslant 0$, all $t\leqslant T$ and all $r\leqslant 1+2^kc^{1/2}$,

(82)

Choose now $k=\lceil 1/{\varepsilon }\rceil$ and assume that $r\geqslant 1+c^{1/2-{\varepsilon }}$. Then

$$\begin{aligned} \frac{{\bar{{\delta }}}_1(r)^k}{r-1}\leqslant \frac{c^{{\varepsilon }k}}{r-1}\leqslant \frac{c}{r-1}\leqslant {\delta }_1(r). \end{aligned}$$

and, for c sufficiently small, we have $c^{\varepsilon }\leqslant 2^{-k}$, so $r\geqslant 1+2^kc^{1/2}$ and so

$\square$

We note also the following estimates, which are deduced from (28) and (73) using the estimates of Proposition 5.3

Proposition 5.4

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, all ${\varepsilon }\in (0,1/2]$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },{\varepsilon },p,T)<\infty$ with the following property. In the case ${\zeta }<1$, for all $c\in (0,1]$, all $r,e^{\sigma }\geqslant 1+c^{1/2-{\varepsilon }}$ and all $t\leqslant T$, for all $\nu \in (0,{\varepsilon }/2]$, setting ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1)$, we have

Moreover, in the case ${\zeta }=1$ and ${\varepsilon }\leqslant 1/3$, for all $c\in (0,1]$, all $r\geqslant 1+c^{1/2-{\varepsilon }}$, all $e^{\sigma }\geqslant 1+c^{1/3-{\varepsilon }}$ and all $t\leqslant T$, for $\nu \in (0,{\varepsilon }]$, setting ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1)$, we have

We turn now to some estimates needed for the discrete-time results Theorems 1.2 and 1.4. Write ${{\mathcal {V}}}_t$ for the number of particles added by time t and define for $t<t_{\zeta }$

$$\begin{aligned} \nu _t={\alpha }^{-1}((1+{\zeta }t)^{{\alpha }/{\zeta }}-1). \end{aligned}$$

It is straightforward to see that, for all ${\alpha },\eta \in \mathbb {R}$, we have $\nu _t\rightarrow n_{\alpha }$ as $t\rightarrow t_{\zeta }$. Also

$$\begin{aligned} c{{\mathcal {V}}}_t=\int _{E(t)}c1_{\{v\leqslant {\Lambda }_s({\theta })\}}\mu (d{\theta },dv,ds),\quad \nu _t=\int _0^te^{-\eta {\tau }_s}ds. \end{aligned}$$

(83)

Proposition 5.5

For all ${\alpha },\eta \in \mathbb {R}$, all $p\geqslant 2$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,p,T)<\infty$ such that, for all $c\in (0,1]$ and all ${\delta }_0\in (0,1/2]$,

$$\begin{aligned} \big \Vert \sup _{t\leqslant T\wedge T_0({\delta }_0)}|c{{\mathcal {V}}}_t-\nu _t|\big \Vert _p\leqslant C(\sqrt{c}+{\delta }_0^2). \end{aligned}$$

Proof

Recall from Sect. 3.2 that

$$\begin{aligned} {{\mathcal {T}}}_t=\int _{E(t)}C_s({\theta })1_{\{v\leqslant {\Lambda }_s({\theta })\}}\mu (d{\theta },dv,ds),\quad {\tau }_t=\int _0^te^{-\zeta {\tau }_s}ds \end{aligned}$$

where

$$\begin{aligned} C_s({\theta })=c|\Phi _{s-}'(e^{{\sigma }+i{\theta }})|^{-{\alpha }},\quad {\zeta }={\alpha }+\eta . \end{aligned}$$

If we substitute the explicit appearances of ${\alpha }$ in the preceding line by 0, then $C_s({\theta })$ becomes c and $e^{-{\zeta }{\tau }_s}$ becomes $e^{-\eta {\tau }_s}$. Then, applying these substitutions in the line above, we recover the integral representations (83) of $c{{\mathcal {V}}}_t$ and $\nu _t$. The claimed estimate results from following through this modification in the calculations leading to Proposition 5.1. The details are left to the reader. $\square$

We can also improve on the estimate of ${{\mathcal {T}}}_t$ by ${\tau }_t$ in Proposition 5.1. Define, for $c{{\mathcal {V}}}_t<n_{\alpha }$,

$$\begin{aligned} {\tilde{{{\mathcal {T}}}}}_t={\tau }^{{\text {disc}}}_{{{\mathcal {V}}}_t} \end{aligned}$$

where ${\tau }_n^{{\text {disc}}}={\alpha }^{-1}\log (1+{\alpha }cn)$ as at (8). We leave any modifications needed for the case ${\alpha }=0$ to the reader. By allowing ${\tilde{{{\mathcal {T}}}}}_t$ to depend on the random time-scale of particle arrivals, we remove the main source of error when estimating ${{\mathcal {T}}}_t$ by ${\tau }_t$.

Proposition 5.6

For all ${\alpha },\eta \in \mathbb {R}$, all $p\geqslant 2$, all $T<t_{\zeta }$ and all $N<n_{\alpha }$, there is a constant $C({\alpha },\eta ,p,T,N)<\infty$ such that, for all $c\leqslant 1/C$ and all ${\delta }_0\in (0,1/2]$,

$$\begin{aligned} \big \Vert \sup _{t\leqslant T\wedge T({\delta }_0),\,c{{\mathcal {V}}}_t\leqslant N}|{{\mathcal {T}}}_t-{\tilde{{{\mathcal {T}}}}}_t|\big \Vert _p\leqslant C(c+{\delta }_0^2). \end{aligned}$$

Proof

Set

$$\begin{aligned} {\tilde{C}}_t={\tau }^{{\text {disc}}}_{{{\mathcal {V}}}_{t-}+1}-{\tau }^{{\text {disc}}}_{{{\mathcal {V}}}_{t-}}={\alpha }^{-1}\log \left( 1+\frac{{\alpha }c}{1+{\alpha }c{{\mathcal {V}}}_{t-}}\right) . \end{aligned}$$

Then

$$\begin{aligned} {\tilde{{{\mathcal {T}}}}}_t=\int _{E(t)}{\tilde{C}}_s1_{\{v\leqslant {\Lambda }_s({\theta })\}}\mu (d{\theta },dv,ds) \end{aligned}$$

so

We have, for $c{{\mathcal {V}}}_t\leqslant N$,

$$\begin{aligned} |{\tilde{C}}_t-ce^{-{\alpha }{\tilde{{{\mathcal {T}}}}}_{t-}}|\leqslant Cc^2 \end{aligned}$$

and, for $t\leqslant T_0({\delta }_0)$, as in the proof of Lemma 4.4,

$$\begin{aligned} |C_t({\theta })-ce^{-{\alpha }{{\mathcal {T}}}_{t-}}(1+{\alpha }{\text {Re}}{\hat{\Psi }}_{t-}'(e^{{\sigma }+i{\theta }}))|&\leqslant Cc{\delta }_0^2,\\ |c{\Lambda }_t({\theta })-e^{-\eta {{\mathcal {T}}}_{t-}}(1+\eta {\text {Re}}{\hat{\Psi }}_{t-}'(e^{{\sigma }+i{\theta }}))|&\leqslant C{\delta }_0^2,\\ |C_t({\theta }){\Lambda }_t({\theta })-e^{-{\zeta }{{\mathcal {T}}}_{t-}}(1+{\zeta }{\text {Re}}{\hat{\Psi }}_{t-}'(e^{{\sigma }+i{\theta }}))|&\leqslant C{\delta }_0^2 \end{aligned}$$

so

$$\begin{aligned} |C_t({\theta })-{\tilde{C}}_t|\leqslant Cc|{{\mathcal {T}}}_{t-}-{\tilde{{{\mathcal {T}}}}}_{t-}|+Cc{\delta }_0 \end{aligned}$$

and, using (57),

and

and so

Set

$$\begin{aligned} f(t)=\mathbb {E}\left( \sup _{s\leqslant t\wedge T_0({\delta }_0),\,c{{\mathcal {V}}}_s\leqslant N}|{{\mathcal {T}}}_s-{\tilde{{{\mathcal {T}}}}}_s|^p\right) \end{aligned}$$

Then, by Burkholder’s and Jensen’s inequalities, for $p\geqslant 2$, and all $t\leqslant T$,

$$\begin{aligned} f(t)\leqslant C(c^p+{\delta }_0^{2p})+C\int _0^tf(s)ds \end{aligned}$$

and the claimed estimate follows by Gronwall’s lemma. $\square$

5.2 Spatially-uniform high-probability estimates

We now pass from the $L^p$-estimates of the preceding section to pointwise estimates which hold with high probability on the function ${\hat{\Psi }}_t(z)={\hat{\Phi }}_t(z)-z$, uniformly in $t\in [0,T]$ and $|z|\geqslant r(c)$ as $c\rightarrow 0$, for a suitable function r(c), which is specified in the next result, and tends to 1 as $c\rightarrow 0$. In order to show the desired uniformity, we combine the usual $L^p$-tail estimate with suitable dissections of [0, T] and $\{|z|\geqslant r(c)\}$, choosing p large to deal with an increasing number of terms as $c\rightarrow 0$. We see at the same time that the event $\{T_0({\delta }_0)>T\}$, to which our previous estimates were restricted, is in fact an event of high probability as $c\rightarrow 0$, thus closing the argument for convergence to a disk. The following result contains Theorem 1.1.

Proposition 5.7

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$, all ${\varepsilon }\in (0,1/2]$ and all $\nu \in (0,{\varepsilon }/4]$, all $m\in \mathbb {N}$ and all $T<t_{\zeta }$, there is a constant $C({\alpha },\eta ,{\Lambda },{\varepsilon },\nu ,m,T)<\infty$ with the following property. In the case ${\zeta }<1$, for all $c\leqslant 1/C$, for $e^{\sigma }\geqslant 1+c^{1/2-{\varepsilon }}$ and ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1)$, there is an event ${{\Omega }_0\subseteq \{T_0({\delta }_0)>T\}}$ of probability exceeding $1-c^m$ on which, for all $t\leqslant T$ and all $|z|=r\geqslant 1+c^{1/2-{\varepsilon }}$,

$$\begin{aligned} |\Psi ^{{\text {cap}}}_t| \leqslant C\bigg (c^{1/2-\nu }+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\bigg ) \end{aligned}$$

(84)

and

$$\begin{aligned} |{\hat{\Psi }}_t(z)| \leqslant C\bigg (c^{1/2-\nu }+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\bigg ) \end{aligned}$$

(85)

and

$$\begin{aligned} |D{\hat{\Psi }}_t(z)| \leqslant \frac{C}{r}\bigg (c^{1/2-\nu }\left( \frac{r}{r-1}\right) +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\bigg ) \end{aligned}$$

(86)

and

$$\begin{aligned} |\Psi ^{{\text {cap}}}_t-\Pi ^{{\text {cap}}}_t| \leqslant C\bigg (c^{3/4-2\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{1/2}+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\bigg ) \end{aligned}$$

(87)

and

$$\begin{aligned} |{\hat{\Psi }}_t(z)-{\hat{\Pi }}_t(z)| \leqslant Cc^{3/4-2\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{1/2} +Cc^{1-4\nu }\bigg (\left( \frac{r}{r-1}\right) +\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\bigg ).\nonumber \\ \end{aligned}$$

(88)

Moreover, in the case ${\zeta }=1$ with ${\varepsilon }\in (0,1/3]$, for all $c\leqslant 1/C$, for $e^{\sigma }\geqslant 1+c^{1/3-{\varepsilon }}$ and ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1)$ there is an event ${{\Omega }_0\subseteq \{T_0({\delta }_0)>T\}}$ of probability exceeding $1-c^m$ on which, for all $t\leqslant T$, the estimates (84) and (87) hold and, for all $|z|=r\geqslant 1+c^{1/2-{\varepsilon }}$,

$$\begin{aligned} |{\hat{\Psi }}_t(z)| \leqslant C\bigg (c^{1/2-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{1/2}+c^{1-4\nu } \left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{5/2}\bigg ) \end{aligned}$$

and

$$\begin{aligned} |D{\hat{\Psi }}_t(z)| \leqslant \frac{C}{r}\bigg (c^{1/2-\nu }\bigg (\left( \frac{r}{r-1}\right) +\frac{1}{\sqrt{\sigma }}\left( \frac{r}{r-1}\right) ^{1/2}\bigg ) +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{5/2}\bigg ) \end{aligned}$$

and

$$\begin{aligned} |{\hat{\Psi }}_t(z)-{\hat{\Pi }}_t(z)| \leqslant Cc^{3/4-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) +Cc^{1-4\nu }\bigg (\left( \frac{r}{r-1}\right) +\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{5/2}\bigg ). \end{aligned}$$

(89)

Proof

We will give details for the case ${\zeta }\in [0,1)$. Some minor modifications are needed for the case ${\zeta }=1$ because of the weaker $L^p$-estimate (79) which applies in that case, and also for the case ${\zeta }<0$. These are left to the reader.

Fix ${\alpha },\eta ,{\varepsilon },\nu ,m$ and T as in the statement. By adjusting the value of ${\varepsilon }$, it will suffice to consider the case where $e^{\sigma }\geqslant 1+2c^{1/2-{\varepsilon }}$, and to find an event ${{\Omega }_0\subseteq \{T_0({\delta }_0)>T\}}$, of probability exceeding $1-c^m$, on which the claimed estimates holds whenever ${r\geqslant 1+2c^{1/2-{\varepsilon }}}$ and $t\leqslant T$. There is a constant $C<\infty$ of the desired dependence, such that ${\delta }_0\leqslant 1/2$ whenever $c\leqslant 1/C$. We restrict to such c. Set

$$\begin{aligned} {\delta }=c^{m+3},\quad t(n)={\delta }n,\quad N=\lfloor T/{\delta }\rfloor ,\quad N_0=\lfloor (T_0({\delta }_0)\wedge T)/{\delta }\rfloor . \end{aligned}$$

Recall that ${{\mathcal {V}}}_t$ denotes the number of particles added to the cluster by time t. Consider the event

$$\begin{aligned} {\Omega }_1=\{{{\mathcal {V}}}_{t(n)}-{{\mathcal {V}}}_{t(n-1)}\leqslant 1\text { for all}\, n\leqslant N_0\, \text {and }{{\mathcal {V}}}_{t(N_0)}={{\mathcal {V}}}_{T_0({\delta }_0)\wedge T}\}. \end{aligned}$$

Note that, on ${\Omega }_1$, for all $t\leqslant T_0({\delta }_0)\wedge T$, there exists $n\in \{1,\dots ,N_0\}$ such that ${\hat{\Psi }}_t={\hat{\Psi }}_{t(n)}$. Since ${\delta }_0\leqslant 1/2$, there is a constant $C<\infty$ of the desired dependence such that the process $({{\mathcal {V}}}_t)_{t\leqslant T_0({\delta }_0)}$ is a thinning of a Poisson process of rate C/c. Hence

$$\begin{aligned} \mathbb {P}({\Omega }_1^c)\leqslant N(C/c)^2{\delta }^2+(C/c)/{\delta }\leqslant C{\delta }/c^2=Cc^{m+1} \end{aligned}$$

and hence $\mathbb {P}({\Omega }_1^c)\leqslant c^m/3$ for all $c\leqslant 1/(3C)$. We restrict to such c.

Fix an integer $p\geqslant 2$, to be chosen later, depending on m and $\nu$. By Proposition 5.1, there is a constant $C<\infty$ of the desired dependence such that, for $\mu _0=C\left( \sqrt{c}+{\delta }_0^2\right)$, we have

$$\begin{aligned} \big \Vert \sup _{t\leqslant T_0({\delta }_0)\wedge T}|\Psi ^{{\text {cap}}}_t|\big \Vert _p\leqslant \mu _0,\quad \big \Vert \sup _{t\leqslant T_0({\delta }_0)\wedge T}|{\hat{\Psi }}_t(\infty )|\big \Vert _p\leqslant \mu _0. \end{aligned}$$

Set ${\lambda }_0=(6c^{-m})^{1/p}$ and consider the event

$$\begin{aligned} {\Omega }_2=\{|\Psi ^{{\text {cap}}}_t|\leqslant {\lambda }_0\mu _0\text { and }|{\hat{\Psi }}_t(\infty )|\leqslant {\lambda }_0\mu _0\text { for all }t\leqslant T_0({\delta }_0)\wedge T\}. \end{aligned}$$

Then $\mathbb {P}({\Omega }_2^c)\leqslant 2{\lambda }_0^{-p}=c^m/3$. We choose $p\geqslant m/\nu$. Then, since $e^{\sigma }\geqslant 1+2c^{1/2-{\varepsilon }}$ and $\nu \leqslant {\varepsilon }$, there is a constant $C<\infty$ of the desired dependence such that, for $c\leqslant 1/C$, on the event ${\Omega }_2$, for all $t\leqslant T_0({\delta }_0)\wedge T$,

$$\begin{aligned} |\Psi ^{{\text {cap}}}_t| \leqslant {\lambda }_0\mu _0 \leqslant Cc^{-\nu }(\sqrt{c}+{\delta }_0^2) =C\left( c^{1/2-\nu }+c^{1-3\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) \leqslant {\delta }_0. \end{aligned}$$

(90)

We restrict to such c. Set

$$\begin{aligned} K=\min \{k\geqslant 1:2^{k}c^{1/2-{\varepsilon }}\geqslant 1\}. \end{aligned}$$

Then $K\leqslant \lfloor \log (1/c)\rfloor +1$. For $k=1,\dots ,K$, set

$$\begin{aligned} r(k)=1+2^{k}c^{1/2-{\varepsilon }},\quad \rho (k)=\frac{r(k)+1}{2}. \end{aligned}$$

Then $\rho (k)\geqslant \rho (1)=1+c^{1/2-{\varepsilon }}$ for all k and $r(K)\in [2,4]$. By Proposition 5.3, there is a constant $C<\infty$ of the desired dependence such that, for $k=1,\dots ,K$ and all $t\leqslant T$,

where

$$\begin{aligned} \mu (r)=\frac{C}{r}\left( \sqrt{c}\left( \frac{r}{r-1}\right) +c^{1-3\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) . \end{aligned}$$

Set ${\lambda }=\left( 3KTc^{-2m-3}\right) ^{1/p}$ and consider the event

$$\begin{aligned} {\Omega }_3=\bigcap _{n=1}^N\bigcap _{k=1}^K\{\Vert D{\hat{\Psi }}_{t(n)}\Vert _{p,\rho (k)}1_{\{t(n)\leqslant T_0({\delta }_0)\}}\leqslant {\lambda }\mu (r(k))\}. \end{aligned}$$

Then

$$\begin{aligned} \mathbb {P}(\Vert D{\hat{\Psi }}_{t(n)}\Vert _{p,\rho (k)}1_{\{t(n)\leqslant T_0({\delta }_0)\}}>{\lambda }\mu (r(k)))\leqslant {\lambda }^{-p} \end{aligned}$$

so

$$\begin{aligned} \mathbb {P}({\Omega }_3^c)\leqslant KN{\lambda }^{-p}\leqslant KT{\lambda }^{-p}/{\delta }=c^m/3. \end{aligned}$$

Fix $r\geqslant 1+2c^{1/2-{\varepsilon }}$. Then $r(k)\leqslant r<r(k+1)$ for some $k\in \{1,\dots ,K\}$, where we set $r(K+1)=\infty$. Note that $zD{\hat{\Psi }}_t(z)$ is a bounded holomorphic function on $\{|z|>\rho (1)\}$. We use the inequality (118) to see that, on the event ${\Omega }_3$, for $n\leqslant N_0$,

$$\begin{aligned} r\Vert D{\hat{\Psi }}_{t(n)}\Vert _{\infty ,r}&\leqslant r(k)\Vert D{\hat{\Psi }}_{t(n)}\Vert _{\infty ,r(k)}\\&\leqslant \left( \frac{r(k)+1}{r(k)-1}\right) ^{1/p}r(k)\Vert D{\hat{\Psi }}_{t(n)}\Vert _{p,\rho (k)} \leqslant (2c^{-1/2})^{1/p}r(k){\lambda }\mu (k) \end{aligned}$$

so

$$\begin{aligned} \Vert D{\hat{\Psi }}_{t(n)}\Vert _{\infty ,r} \leqslant (2c^{-1/2})^{1/p}{\lambda }\mu (r(k)) \leqslant 2(2c^{-1/2})^{1/p}{\lambda }\mu (r). \end{aligned}$$

We choose $p\geqslant (2m+4)/\nu$. Then there is a constant $C<\infty$ of the desired dependence such that, for $c\leqslant 1/C$, on ${\Omega }_3$, for $n=1,\dots ,N_0$ and all $r\geqslant 1+2c^{1/2-{\varepsilon }}$, we have

$$\begin{aligned} \Vert D{\hat{\Psi }}_{t(n)}\Vert _{\infty ,r} \leqslant \frac{C}{r}\left( c^{1/2-\nu }\left( \frac{r}{r-1}\right) +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) \end{aligned}$$

and

$$\begin{aligned} \Vert {\hat{\Psi }}'_{t(n)}\Vert _{\infty ,e^{\sigma }}\leqslant c^{1/2-\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ={\delta }_0. \end{aligned}$$

We restrict to such c. Set

$$\begin{aligned} {\Omega }_0={\Omega }_1\cap {\Omega }_2\cap {\Omega }_3. \end{aligned}$$

Then $\mathbb {P}({\Omega }_0^c)\leqslant c^m$ and, on the event ${\Omega }_0$, for all $t\leqslant T_0({\delta }_0)\wedge T$ and all $r\geqslant 1+2c^{1/2-{\varepsilon }}$,

$$\begin{aligned} \Vert D{\hat{\Psi }}_t\Vert _{\infty ,r} \leqslant \frac{C}{r}\left( c^{1/2-\nu }\left( \frac{r}{r-1}\right) +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) \end{aligned}$$

and

$$\begin{aligned} \Vert {\hat{\Psi }}'_t\Vert _{\infty ,e^{\sigma }}\leqslant {\delta }_0. \end{aligned}$$

In conjunction with (90), this forces $T_0({\delta }_0)>T$ on ${\Omega }_0$ and so concludes the proof of (84) and (86).

We deduce (85) using the identity

$$\begin{aligned} \psi (z)=\psi (\infty )-\int _1^\infty D\psi (sz)s^{-1}ds. \end{aligned}$$

On the event ${\Omega }_2$, for all $t\leqslant T_0({\delta }_0)\wedge T$,

$$\begin{aligned} |{\hat{\Psi }}_t(\infty )|\leqslant C\left( c^{1/2-\nu }+c^{1-3\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) . \end{aligned}$$

On the other hand, ${\Omega }_0\subseteq {\Omega }_2$ and on ${\Omega }_0$ we have $T_0({\delta }_0)>T$ and, using (86), for $t\leqslant T$ and $|z|=r\geqslant 1+c^{1/2-{\varepsilon }}$,

$$\begin{aligned} \int _1^\infty |D{\hat{\Psi }}_t(sz)|s^{-1}ds&\leqslant \int _1^\infty \frac{C}{rs}\left( c^{1/2-\nu }\left( \frac{sr}{sr-1}\right) +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) s^{-1}ds\\&\leqslant \frac{C}{r}\left( c^{1/2-\nu }\left( 1+\log \left( \frac{r}{r-1}\right) \right) +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) . \end{aligned}$$

Since $r\geqslant 1+c^{1/2}$, the $\log$ factor can be absorbed in $c^{1/2-\nu }$ by adjustment of $\nu$. Then, on combining the last two estimates, we obtain (85).

The estimate (87) may now be deduced from Proposition 5.1 using standard $L^p$ tail estimates. The details are left to the reader.

For the estimate (88), define

$$\begin{aligned} {\tilde{\mu }}_0=C(c+\sqrt{c{\delta }_0}+{\delta }_0^2) \end{aligned}$$

where C is the constant in Proposition 5.1, and define

$$\begin{aligned} {\tilde{\mu }}(r) =\frac{C}{r}\left( c\left( \frac{r}{r-1}\right) ^2+\sqrt{c{\delta }_0}\left( \frac{r}{r-1}\right) +{\delta }_0^2\left( 1+\log \left( \frac{r}{r-1}\right) \right) \right) . \end{aligned}$$

where C is the constant of Proposition 5.4. Set ${\tilde{{\Omega }}}_0={\Omega }_1\cap {\tilde{{\Omega }}}_2\cap {\tilde{{\Omega }}}_3$, where

$$\begin{aligned} {\tilde{{\Omega }}}_2={\Omega }_2\cap \{|{\hat{\Psi }}_t(\infty )-{\hat{\Pi }}_t(\infty )|\leqslant {\lambda }_0{\tilde{\mu }}_0\text { for all }t\leqslant T_0({\delta }_0)\wedge T\} \end{aligned}$$

and

$$\begin{aligned} {\tilde{{\Omega }}}_3={\Omega }_3\cap \bigcap _{n=1}^N\bigcap _{k=1}^K\{\Vert D({\hat{\Psi }}_{t(n)} -{\hat{\Pi }}_{t(n)})\Vert _{p,\rho (k)}1_{\{t(n)\leqslant T_0({\delta }_0)\}}\leqslant {\lambda }{\tilde{\mu }}(r(k))\}. \end{aligned}$$

We follow a similar argument to above to see that $\mathbb {P}({\tilde{{\Omega }}}_0^c)\leqslant 2c^m$ and on ${\tilde{{\Omega }}}_0$ we have $T_0({\delta }_0)>T$ and for $t\leqslant T$

$$\begin{aligned} |{\hat{\Psi }}_t(\infty )-{\hat{\Pi }}_t(\infty )|\leqslant C\left( c^{3/4-3\nu /2}\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{1/2} +c^{1-3\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) \end{aligned}$$

and for $|z|=r\geqslant 1+2c^{1/2-{\varepsilon }}$,

$$\begin{aligned} \Vert D({\hat{\Psi }}_t-{\hat{\Pi }}_t)\Vert _{\infty ,r}\leqslant & {} \frac{C}{r}\left( c^{1-\nu }\left( \frac{r}{r-1}\right) ^2 +c^{3/4-3\nu /2}\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^{1/2}\right. \\{} & {} \left. \left( \frac{r}{r-1}\right) +c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) . \end{aligned}$$

Finally we can integrate as above to deduce (88). $\square$

Proof of Theorem 1.2

We will write the argument for the case ${\zeta }<1$, omitting the modifications needed for ${\zeta }=1$, which are left to the reader. Since $N<n_{\alpha }$, we can choose ${\delta }={\delta }({\alpha },\eta ,N)>0$ and $T<t_{\zeta }$ such that $\nu _T=N+{\delta }$. Choose ${\delta }_0$ and ${\Omega }_0$ as in Proposition 5.7, with the choice of T just made. Write C for the constant appearing in Proposition 5.7 and set

$$\begin{aligned} \Delta =C\left( c^{1/2-\nu }+c^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2\right) . \end{aligned}$$

Then, for all $|z|\geqslant 1+c^{1/2-{\varepsilon }}$ and all $t\leqslant T$, on the event ${\Omega }_0$, we have $|{\hat{\Phi }}_t(z)-z|\leqslant \Delta$. Then, by Propositions 5.5 and 5.6, choosing ${\delta }_0$ as in Proposition 5.7 and using an $L^p$-tail estimate for suitably large p, there is an event ${\Omega }_1\subseteq {\Omega }_0$, of probability exceeding $1-2c^m$, on which, for all $t\leqslant T$, both $|c{{\mathcal {V}}}_t-\nu _t|\leqslant \Delta$ and, provided $c{{\mathcal {V}}}_t\leqslant N$, also

$$\begin{aligned} |{{\mathcal {T}}}_t-{\tilde{{{\mathcal {T}}}}}_t|\leqslant Cc^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2. \end{aligned}$$

We can choose C so that, for $c\leqslant 1/C$, we have $\Delta \leqslant {\delta }$, so $c{{\mathcal {V}}}_T\geqslant N+{\delta }-\Delta \geqslant N$ always on ${\Omega }_1$. Now, for all $n\leqslant N/c$, we have ${{\mathcal {V}}}_t=n$ for some $t\leqslant T$ with $c{{\mathcal {V}}}_t\leqslant N$, so on ${\Omega }_1$, for all $|z|\geqslant 1+c^{1/2-{\varepsilon }}$, we have

$$\begin{aligned} |{\hat{\Phi }}_n^{{\text {disc}}}(z)-z|\leqslant \Delta ,\quad |{{\mathcal {T}}}^{{\text {disc}}}_n-{\tau }^{{\text {disc}}}_n|\leqslant Cc^{1-4\nu }\left( \frac{e^{\sigma }}{e^{\sigma }-1}\right) ^2. \end{aligned}$$

$\square$

6 Fluctuation Scaling Limit for ALE$({\alpha },\eta )$

Given an ALE$({\alpha },\eta )$ process $(\Phi _t)_{t\geqslant 0}$, recall that

$$\begin{aligned} {\hat{\Phi }}_t(z)=\Phi _t(z)/e^{{{\mathcal {T}}}_t},\quad {{\mathcal {T}}}_t=\log \Phi _t'(\infty ). \end{aligned}$$

The fluctuations in these coordinates are given by

$$\begin{aligned} {\hat{\Psi }}_t(z)={\hat{\Phi }}_t(z)-z,\quad \Psi ^{{\text {cap}}}_t={{\mathcal {T}}}_t-{\tau }_t,\quad {\tau }_t={\zeta }^{-1}\log (1+{\zeta }t). \end{aligned}$$

Recall that we write ${{\mathcal {H}}}$ for the set of holomorphic functions on $\{|z|>1\}$ which are bounded at $\infty$, and we use on ${{\mathcal {H}}}$ the topology of uniform convergence on $\{|z|\geqslant r\}$ for all $r>1$. In this section we prove Theorem 1.3 and then, at the end, we deduce Theorem 1.4.

6.1 Reduction to Poisson integrals

Our starting point is the interpolation formula (17)

$$\begin{aligned} {\hat{\Psi }}_t(z)={\hat{M}}_t(z)+{\hat{A}}_t(z),\quad \Psi ^{{\text {cap}}}_t=M^{{\text {cap}}}_t+A^{{\text {cap}}}_t. \end{aligned}$$

As a first step, we study the approximations ${\hat{\Pi }}_t(z)$ and $\Pi ^{{\text {cap}}}_t$ to ${\hat{M}}_t(z)$ and $M^{{\text {cap}}}_t$ which have a simple form and which prove to be the dominant terms in the considered limit. Set

$$\begin{aligned} H({\theta },z)=\frac{z}{e^{-i{\theta }}z-1}=\sum _{k=0}^\infty e^{i(k+1){\theta }}z^{-k}. \end{aligned}$$

Recall the multiplier operator $P({\tau })$ defined at (12). Then

$$\begin{aligned} P({\tau })H({\theta },z)=\sum _{k=0}^\infty e^{-q(k){\tau }}e^{i(k+1){\theta }}z^{-k}. \end{aligned}$$

Recall that $c_t=ce^{-{\alpha }{\tau }_t}$ and ${\lambda }_t=c^{-1}e^{-\eta {\tau }_t}$, and that we define for $|z|>1$

$$\begin{aligned} {\hat{\Pi }}_t(z)&=\int _{E(t)}e^{-({\tau }_t-{\tau }_s)}P({\tau }_t-{\tau }_s)H({\theta },z)2c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds), \end{aligned}$$

(91)

$$\begin{aligned} \Pi ^{{\text {cap}}}_t&=\int _{E(t)}e^{-{\zeta }({\tau }_t-{\tau }_s)}c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

(92)

The following result allows us to deduce the weak limit of the normalized fluctuations from that of the Poisson integrals $({\hat{\Pi }}_t,\Pi ^{{\text {cap}}}_t)_{t\geqslant 0}$.

Proposition 6.1

For all ${\alpha },\eta \in \mathbb {R}$ with ${\zeta }={\alpha }+\eta \leqslant 1$,

$$\begin{aligned} c^{-1/2}({\hat{\Psi }}_t-{\hat{\Pi }}_t,\Psi ^{{\text {cap}}}_t-\Pi ^{{\text {cap}}}_t)\rightarrow 0 \end{aligned}$$

in ${{\mathcal {H}}}\times \mathbb {R}$ uniformly on compacts in $[0,t_{\zeta })$, in probability, in the limit $c\rightarrow 0$ and ${\sigma }\rightarrow 0$ considered in Theorem 1.3.

Proof

In Theorem 1.3, for ${\zeta }<1$, we restrict to ${\sigma }\geqslant c^{1/4-{\varepsilon }}$ and take ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1)$ with $\nu \leqslant {\varepsilon }/4$. On the other hand, for ${\zeta }=1$, we restrict to ${\sigma }\geqslant c^{1/5-{\varepsilon }}$ and take ${\delta }_0=c^{1/2-\nu }e^{\sigma }/(e^{\sigma }-1))$. In both cases, the right-hand sides in (87), (88) and (89) are therefore small compared to $\sqrt{c}$ in the considered limit. The claim thus follows from Proposition 5.7. $\square$

Since the integral (91) converges absolutely for all ${\omega }$, we can exchange limits to see that

$$\begin{aligned} {\hat{\Pi }}_t(z)=\sum _{k=0}^\infty \Pi _t(k)z^{-k} \end{aligned}$$

where

$$\begin{aligned} \Pi _t(k)=2\int _{E(t)}e^{-(1+q(k))({\tau }_t-{\tau }_s)}e^{i(k+1){\theta }}c_s1_{\{v\leqslant {\lambda }_s\}} {\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Set $q_0(k)=(1-{\zeta })k$ and define, for all ${\zeta }\in (-\infty ,1]$ and $t<t_{\zeta }$,

$$\begin{aligned} \Pi ^0_t(k)=2\int _{E(t)}e^{-(1+q_0(k))({\tau }_t-{\tau }_s)}e^{i(k+1){\theta }}c_s1_{\{v\leqslant {\lambda }_s\}} {\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Proposition 6.2

For all ${\alpha },\eta \in \mathbb {R}$ with ${\alpha }+\eta ={\zeta }\leqslant 1$, and all $t<t_{\zeta }$, there is a constant $C({\alpha },\eta ,t)<\infty$ such that, for all $k\geqslant 0$,

$$\begin{aligned} \Big \Vert \sup _{s\leqslant t}|\Pi _s(k)|\Big \Vert _2\leqslant C\sqrt{c},\quad \Big \Vert \sup _{s\leqslant t}|\Pi ^{{\text {cap}}}_s|\Big \Vert _2\leqslant C\sqrt{c} \end{aligned}$$

and

$$\begin{aligned} \Big \Vert \sup _{s\leqslant t}|\Pi _s(k)-\Pi ^0_s(k)|\Big \Vert _2\leqslant Ck^2{\sigma }\sqrt{c}. \end{aligned}$$

Moreover, C may be chosen so that, for all $h\in [0,1]$ and all stopping times $T\leqslant t-h$,

$$\begin{aligned} \Vert \Pi ^0_{T+h}(k)-\Pi ^0_T(k)\Vert _2\leqslant C\sqrt{c}(\sqrt{h}+kh),\quad \Vert \Pi ^{{\text {cap}}}_{T+h}-\Pi ^{{\text {cap}}}_T\Vert _2\leqslant C\sqrt{ch}. \end{aligned}$$

Proof

The estimates for $(\Pi ^{{\text {cap}}}_t)_{t<t_{\zeta }}$ are standard and are left to the reader. For $(\Pi _t(k))_{t<t_{\zeta }}$, we use time-dissection to obtain estimates with good dependence on k. Set ${\kappa }=1+q(k)$ and define

$$\begin{aligned} M_t(k) =e^{{\kappa }{\tau }_t}\Pi _t(k) =\int _{E(t)}e^{{\kappa }{\tau }_s}e^{i(k+1){\theta }}2c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Set $n=\lceil {\kappa }{\tau }_t\rceil$ and $t(n)=t$. Set $t(i)=i/{\kappa }$ for $i=0,1,\dots ,n-1$. Then $t(i+1)-t(i)\leqslant 1/{\kappa }$ for all i. We have

$$\begin{aligned} \mathbb {E}(|M_t(k)|^2) =4\int _0^t e^{2{\kappa }{\tau }_s}c_s^2{\lambda }_sds \leqslant Cc\int _0^te^{2{\kappa }{\tau }_s}{\dot{{\tau }}}_sds \leqslant Cce^{2{\kappa }{\tau }_t}/{\kappa }\end{aligned}$$

so, by Doob’s $L^2$-inequality,

$$\begin{aligned} \Big \Vert \sup _{s\leqslant t}|M_s(k)|\Big \Vert _2 \leqslant Ce^{{\kappa }{\tau }_t}\sqrt{c/{\kappa }}. \end{aligned}$$

Now, for $t(i)\leqslant s\leqslant t(i+1)$,

$$\begin{aligned} |\Pi _s(k)|\leqslant e^{-{\kappa }{\tau }_{t(i)}}|M_s(k)| \end{aligned}$$

so

$$\begin{aligned} \Big \Vert \sup _{t(i)\leqslant s\leqslant t(i+1)}|\Pi _s(k)|\Big \Vert _2 \leqslant Ce^{-{\kappa }{\tau }_{t(i)}}\Big \Vert \sup _{s\leqslant t(i+1)}|M_s(k)|\Big \Vert _2 \leqslant C\sqrt{c/{\kappa }} \end{aligned}$$

and so

$$\begin{aligned} \Big \Vert \sup _{s\leqslant t}|\Pi _s(k)|\Big \Vert _2\leqslant C\sqrt{c}. \end{aligned}$$

(93)

For the second estimate, set ${\kappa }_0=1+(1-{\zeta })k$ and note that

$$\begin{aligned} 0\leqslant |{\kappa }-{\kappa }_0|=|{\zeta }|k(1-e^{-{\sigma }(k+1)})\leqslant |{\zeta }|k(k+1){\sigma }. \end{aligned}$$

Restrict for now to the case ${\zeta }\geqslant 0$, when ${\kappa }\geqslant {\kappa }_0$, and define

$$\begin{aligned} M^0_t(k)=\int _{E(t)}e^{{\kappa }_0{\tau }_s}e^{i(k+1){\theta }}2c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds) \end{aligned}$$

and

$$\begin{aligned} {\tilde{M}}_t(k) =M_t(k)-M_t^0(k) =\int _{E(t)}(e^{{\kappa }{\tau }_s}-e^{{\kappa }_0{\tau }_s})e^{i(k+1){\theta }}2c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Note that

$$\begin{aligned} 0\leqslant e^{{\kappa }{\tau }_s}-e^{{\kappa }_0{\tau }_s}\leqslant ({\kappa }-{\kappa }_0){\tau }_se^{{\kappa }{\tau }_s} \end{aligned}$$

so, by a similar argument,

$$\begin{aligned} \Big \Vert \sup _{s\leqslant t}|e^{-{\kappa }{\tau }_s}{\tilde{M}}_s(k)|\Big \Vert _2 \leqslant C({\kappa }-{\kappa }_0)\sqrt{c}. \end{aligned}$$

Now

$$\begin{aligned} \Pi _s(k)-\Pi ^0_s(k)=e^{-{\kappa }{\tau }_s}{\tilde{M}}_s(k)+(e^{-{\kappa }{\tau }_s}-e^{-{\kappa }_0{\tau }_s})M_s^0(k) \end{aligned}$$

so

$$\begin{aligned} |\Pi _s(k)-\Pi ^0_s(k)|\leqslant e^{-{\kappa }{\tau }_s}|{\tilde{M}}_s(k)|+({\kappa }-{\kappa }_0){\tau }_s|\Pi ^0_s(k)| \end{aligned}$$

and so

$$\begin{aligned} \Big \Vert \sup _{s\leqslant t}|\Pi _s(k)-\Pi ^0_s(k)|\Big \Vert _2 \leqslant C({\kappa }-{\kappa }_0)\sqrt{c}\leqslant Ck^2{\sigma }\sqrt{c}. \end{aligned}$$

For $\Pi ^0_s(k)$, we used the estimate (93) with ${\kappa }$ replaced by ${\kappa }_0$, which is the special case ${\sigma }=0$. A similar argument holds in the case ${\zeta }<0$, with the roles of ${\kappa }$ and ${\kappa }_0$ interchanged, which leads to the same estimate. It remains to show the third estimate, which we will do for general ${\sigma }\geqslant 0$. We have

$$\begin{aligned} \Pi _{T+h}(k)-\Pi _T(k)&=e^{-{\kappa }{\tau }_{T+h}}M_{T+h}(k)-e^{-{\kappa }{\tau }_T}M_T(k)\\&=e^{-{\kappa }{\tau }_{T+h}}{\tilde{M}}_h(k)-(e^{-{\kappa }({\tau }_{T+h}-{\tau }_T)}-1)\Pi _T(k) \end{aligned}$$

where we redefine

$$\begin{aligned} {\tilde{M}}_h(k) =M_{T+h}(k)-M_T(k) =\int _{E(T+h)\setminus E(T)}e^{{\kappa }{\tau }_s}e^{i(k+1){\theta }}2c_s1_{\{v\leqslant {\lambda }_s\}}{\tilde{\mu }}(d{\theta },dv,ds). \end{aligned}$$

Now

$$\begin{aligned} \mathbb {E}(|{\tilde{M}}_h(k)|^2|T)=4\int _T^{T+h}e^{2{\kappa }{\tau }_s}c_s^2{\lambda }_sds \end{aligned}$$

so

$$\begin{aligned} \mathbb {E}(|e^{-{\kappa }{\tau }_{T+h}}{\tilde{M}}_h(k)|^2)\leqslant Cch. \end{aligned}$$

On the other hand, since $T\leqslant t$,

$$\begin{aligned} \Vert (e^{-{\kappa }({\tau }_{T+h}-{\tau }_T)}-1)\Pi _T(k)\Vert _2 \leqslant C{\kappa }h\Big \Vert \sup _{s\leqslant t}|\Pi _s(k)|\Big \Vert _2 \leqslant C(k+1)h\sqrt{c}. \end{aligned}$$

The claimed estimate follows. $\square$

6.2 Gaussian limit process

By Proposition 6.1, in order to compute the weak limit of $c^{-1/2}({\hat{\Psi }}_t,\Psi ^{{\text {cap}}}_t)_{t<t_{\zeta }}$, it suffices to compute the weak limit of $c^{-1/2}({\hat{\Pi }}_t,\Pi ^{{\text {cap}}}_t)_{t<t_{\zeta }}$. This process is a deterministic linear function of the compensated Poisson random measure ${\tilde{\mu }}$. We are guided to find the weak limit process by replacing ${\tilde{\mu }}$ in (91) and (92) by a Gaussian white noise on $[0,2\pi )\times [0,\infty )\times (0,\infty )$ of the same intensity. At the same time, we set ${\sigma }=0$ in the limit,² replacing the multiplier operator $P({\tau })$ by the corresponding operator $P_0({\tau })$ when ${\sigma }=0$. Then, using the scaling properties of white noise, we arrive at candidate limit processes $({\hat{{\Gamma }}}_t(z))_{t<t_{\zeta }}$ and $({\Gamma }^{{\text {cap}}}_t)_{t<t_{\zeta }}$ which are defined as follows. Let W be a Gaussian white noise on $[0,2\pi )\times (0,\infty )$ of intensity $(2\pi )^{-1}d{\theta }dt$. Define for each $|z|>1$ and $t\in [0,t_{\zeta })$

$$\begin{aligned} {\hat{{\Gamma }}}_t(z)&=2\int _0^t\int _0^{2\pi }e^{-({\tau }_t-{\tau }_s)}P_0({\tau }_t-{\tau }_s) H({\theta },z)e^{-({\alpha }+\eta /2){\tau }_s}W(d{\theta },ds),\nonumber \\ {\Gamma }^{{\text {cap}}}_t&=\int _0^t\int _0^{2\pi }e^{-{\zeta }({\tau }_t-{\tau }_s)}e^{-({\alpha }+\eta /2){\tau }_s}W(d{\theta },ds) \end{aligned}$$

where these Gaussian integrals are understood by the usual $L^2$ isometry. Define for $t\geqslant 0$ and $k\geqslant 0$

$$\begin{aligned} B_t(k)=\sqrt{2}\int _0^t\int _0^{2\pi }e^{i(k+1){\theta }}W(d{\theta },ds),\quad B_t=\int _0^t\int _0^{2\pi }W(d{\theta },ds). \end{aligned}$$

We can and do choose versions of $(B_t(k))_{t\geqslant 0}$ and $(B_t)_{t\geqslant 0}$ which are continuous in t. Then $(B_t(k))_{t\geqslant 0}$ is a complex Brownian motion for all k, $(B_t)_{t\geqslant 0}$ is a real Brownian motion, and all these processes are independent. Note that, almost surely, for all $t<t_{\zeta }$,

$$\begin{aligned} {\Gamma }^{{\text {cap}}}_t=\int _0^te^{-{\zeta }({\tau }_t-{\tau }_s)}e^{-({\alpha }+\eta /2){\tau }_s}dB_s. \end{aligned}$$

Define for $t\in [0,t_{\zeta })$ and $k\geqslant 0$

$$\begin{aligned} {\Gamma }_t(k)=\sqrt{2}\int _0^te^{-(1-{\zeta })k({\tau }_t-{\tau }_s)}e^{-({\alpha }+\eta /2){\tau }_s}dB_s(k). \end{aligned}$$

The following estimate may be obtained by (a simpler version of) the argument used for Proposition 6.2.

Proposition 6.3

For all ${\alpha },\eta \in \mathbb {R}$ with ${\alpha }+\eta ={\zeta }\leqslant 1$, and all $t<t_{\zeta }$, there is a constant $C({\alpha },\eta ,t)<\infty$ such that, for all $k\geqslant 0$,

$$\begin{aligned} \Big \Vert \sup _{s\leqslant t}|{\Gamma }_s(k)|\Big \Vert _2\leqslant C. \end{aligned}$$

The following identity holds in $L^2$ for all $|z|>1$ and $t<t_{\zeta }$

$$\begin{aligned} {\hat{{\Gamma }}}_t(z)=\sum _{k=0}^\infty {\Gamma }_t(k)z^{-k}. \end{aligned}$$

(94)

By Proposition 6.3, almost surely, the right-hand side in (94) converges uniformly on compacts in $[0,t_{\zeta })$, uniformly on $\{|z|\geqslant r\}$, for all $r>1$. So we can and do use (94) to choose a version of ${\hat{{\Gamma }}}_t(z)$ for each $t<t_{\zeta }$ and $|z|>1$ such that $({\hat{{\Gamma }}}_t)_{t<t_{\zeta }}$ is a continuous process in ${{\mathcal {H}}}$ and (94) holds for all ${\omega }$.

The processes $({\Gamma }_t(k))_{t<t_{\zeta }}$ and $({\Gamma }^{{\text {cap}}}_t)_{t<t_{\zeta }}$ are also characterized by the following Ornstein–Uhlenbeck-type stochastic differential equations

$$\begin{aligned} d{\Gamma }_t(k)&=e^{-{\alpha }{\tau }_t}\left( \sqrt{2}e^{-\eta {\tau }_t/2}dB_t(k)-(1+(1-{\zeta })k){\Gamma }_t(k)e^{-\eta {\tau }_t}dt\right) ,\quad {\Gamma }_0(k)=0,\\ d{\Gamma }^{{\text {cap}}}_t&=e^{-{\alpha }{\tau }_t}\left( e^{-\eta {\tau }_t/2}dB_t-{\zeta }{\Gamma }^{{\text {cap}}}_te^{-\eta {\tau }_t}dt\right) ,\quad {\Gamma }^{{\text {cap}}}_0=0. \end{aligned}$$

These equations can be put in a simpler form by switching to the time-scale

$$\begin{aligned} \nu _t=\int _0^te^{-\eta {\tau }_s}ds \end{aligned}$$

which arises as the limit as $c\rightarrow 0$ of a time-scale where particles arrive at a constant rate. Write $\nu \mapsto t(\nu ):[0,n_{\alpha })\rightarrow [0,t_{\zeta })$ for the inverse map and set

$$\begin{aligned} {\tilde{{\Gamma }}}_\nu (k)={\Gamma }_{t(\nu )}(k),\quad {\tilde{{\Gamma }}}^{{\text {cap}}}_\nu ={\Gamma }^{{\text {cap}}}_{t(\nu )} \end{aligned}$$

and

$$\begin{aligned} {\tilde{{\tau }}}_\nu ={\tau }_{t(\nu )},\quad {\tilde{B}}_\nu (k)=\int _0^{t(\nu )}e^{-\eta {\tau }_s/2}dB_s(k),\quad {\tilde{B}}_\nu =\int _0^{t(\nu )}e^{-\eta {\tau }_s/2}dB_s. \end{aligned}$$

Then $e^{-{\alpha }{\tilde{{\tau }}}_\nu }=(1+{\alpha }\nu )^{-1}$. Also $({\tilde{B}}_\nu (k))_{\nu <n_{\alpha }}$ is a complex Brownian motion for all k, $({\tilde{B}}_\nu )_{\nu <n_{\alpha }}$ is a real Brownian motion, and these processes are independent. Then we have

$$\begin{aligned} d{\tilde{{\Gamma }}}_\nu (k)&=(1+{\alpha }\nu )^{-1}\left( \sqrt{2}d{\tilde{B}}_\nu (k)-(1+(1-{\zeta })k) {\tilde{{\Gamma }}}_\nu (k)d\nu \right) ,\quad {\tilde{{\Gamma }}}_0(k)=0,\nonumber \\ d{\tilde{{\Gamma }}}^{{\text {cap}}}_\nu&=(1+{\alpha }\nu )^{-1}\left( d{\tilde{B}}_\nu -{\zeta }{\tilde{{\Gamma }}}^{{\text {cap}}}_\nu d\nu \right) ,\quad {\tilde{{\Gamma }}}^{{\text {cap}}}_0=0. \end{aligned}$$

(95)

We can define a Brownian motion $({\tilde{B}}_\nu )_{\nu <n_{\alpha }}$ in ${{\mathcal {H}}}$ by

$$\begin{aligned} {\tilde{B}}_\nu (z)=\sum _{k=0}^\infty {\tilde{B}}_\nu (k)z^{-k}. \end{aligned}$$

Set

$$\begin{aligned} {\tilde{{\Gamma }}}_\nu (z)=\sum _{k=0}^\infty {\tilde{{\Gamma }}}_\nu (k)z^{-k}={\hat{{\Gamma }}}_{t(\nu )}(z). \end{aligned}$$

On summing the equations (95), we see that $({\tilde{{\Gamma }}}_\nu )_{\nu <n_{\alpha }}$ satisfies the following stochastic integral equation in ${{\mathcal {H}}}$

$$\begin{aligned} {\tilde{{\Gamma }}}_\nu (z)=\int _0^\nu \frac{\sqrt{2}d{\tilde{B}}_s(z) -{\tilde{{\Gamma }}}_s(z)ds+(1-{\zeta })D{\tilde{{\Gamma }}}_s(z)ds}{1+{\alpha }s}. \end{aligned}$$

6.3 Convergence

Given Proposition 6.1, the following result will complete the proof of Theorem 1.3.

Proposition 6.4

For all ${\alpha },\eta \in \mathbb {R}$ with ${\alpha }+\eta ={\zeta }\leqslant 1$ and all $T<t_{\zeta }$, we have

$$\begin{aligned} c^{-1/2}({\hat{\Pi }}_t,\Pi ^{{\text {cap}}}_t)_{t\geqslant 0}\rightarrow ({\hat{{\Gamma }}}_t,{\Gamma }^{{\text {cap}}}_t)_{t\leqslant T} \end{aligned}$$

weakly in ${{D([0,T],{{\mathcal {H}}}\times \mathbb {R})}}$ as $c\rightarrow 0$ and ${\sigma }\rightarrow 0$ as in Theorem 1.3.

Proof

By Proposition 6.2, it will suffice to show the claimed limit with $({\hat{\Pi }}_t)_{t\leqslant T}$ replaced by $({\hat{\Pi }}^0_t)_{t\leqslant T}$. We first show that

$$\begin{aligned} c^{-1/2}((\Pi ^0_t(k):k\geqslant 0),\Pi ^{{\text {cap}}}_t)_{t\leqslant T}\rightarrow (({\Gamma }_t(k):k\geqslant 0),{\Gamma }^{{\text {cap}}}_t)_{t\leqslant T} \end{aligned}$$

in the sense of finite-dimensional distributions. For all $n\geqslant 1$, all $k_1,\dots ,k_n\geqslant 0$ and all $t_1,\dots ,t_n\leqslant T$, any real-linear function of $c^{-1/2}(\Pi ^0_{t_j}(k_j),\Pi ^{{\text {cap}}}_{t_j}:j=1,\dots ,n)$ can be written in the form

$$\begin{aligned} F=\int _{E(T)}{\tilde{f}}_t({\theta })1_{\{v\leqslant {\lambda }_t\}}{\tilde{\mu }}(d{\theta },dv,dt) \end{aligned}$$

where

$$\begin{aligned} {\tilde{f}}_t({\theta })=c^{-1/2}f_t({\theta })c_t \end{aligned}$$

and $({\theta },t)\mapsto f_t({\theta }):[0,2\pi )\times (0,T]\rightarrow \mathbb {R}$ is bounded, measurable and independent of c. Set

The same linear function applied to $({\Gamma }_{t_j}(k_j),{\Gamma }^{{\text {cap}}}_{t_j}:j=1,\dots ,n)$ gives the random variable

$$\begin{aligned} G=\int _0^T\int _0^{2\pi }{\tilde{f}}_t({\theta }){\lambda }_t^{1/2}W(d{\theta },dt) =\int _0^T\int _0^{2\pi }f_t({\theta })e^{-({\alpha }+\eta /2){\tau }_t}W(d{\theta },dt). \end{aligned}$$

Then

and, using the Campbell–Hardy formula, as $c\rightarrow 0$,

The claimed convergence of finite-dimensional distributions follows, by convergence of characteristic functions.

Now, Proposition 6.2 shows that the processes $(\Pi ^0_t(k))_{t\leqslant T}$ and $(\Pi ^{{\text {cap}}}_t)_{t\leqslant T}$ all satisfy Aldous’s tightness criterion in $D([0,T],\mathbb {C})$. Hence

$$\begin{aligned} c^{-1/2}((\Pi ^0_t(k):k\geqslant 0),\Pi ^{{\text {cap}}}_t)_{t\leqslant T}\rightarrow (({\Gamma }_t(k):k\geqslant 0),{\Gamma }^{{\text {cap}}}_t)_{t\leqslant T} \end{aligned}$$

weakly in $D([0,T],\mathbb {C}^{\mathbb {Z}^+}\times \mathbb {R})$ as $c\rightarrow 0$. Hence, for all $K\geqslant 0$,

$$\begin{aligned} c^{-1/2}(p_K({\hat{\Pi }}^0_t),\Pi ^{{\text {cap}}}_t)_{t\leqslant T}\rightarrow (p_K({\hat{{\Gamma }}}_t),{\Gamma }^{{\text {cap}}}_t)_{t\leqslant T} \end{aligned}$$

weakly in $D([0,T],{{\mathcal {H}}}\times \mathbb {R})$ as $c\rightarrow 0$, where, for $f(z)=\sum _{k=0}^\infty a_kz^{-k}$,

$$\begin{aligned} p_K(f)(z)=\sum _{k=0}^Ka_kz^{-k}. \end{aligned}$$

For $|z|=r$, we have

$$\begin{aligned} |(f-p_K(f))(z)|\leqslant \sum _{k=K+1}^\infty |a_k|r^{-k}. \end{aligned}$$

Hence, it will suffice to show, for $r>1$ and all ${\varepsilon }>0$, that

$$\begin{aligned} \lim _{K\rightarrow \infty }\limsup _{c\rightarrow 0}\mathbb {P}\left( c^{-1/2}\sup _{t\leqslant T}\sum _{k=K+1}^\infty |\Pi ^0_t(k)|r^{-k}>{\varepsilon }\right) =0. \end{aligned}$$

But, since ${\alpha }+\eta ={\zeta }\leqslant 1$, by Proposition 6.2, there is a constant $C({\alpha },\eta ,T)<\infty$ such that, for all $c>0$ and all $r>1$,

$$\begin{aligned} \left\| c^{-1/2}\sup _{t\leqslant T}\sum _{k=K}^\infty |\Pi ^0_t(k)|r^{-k}\right\| _2\leqslant \frac{Cr^{-K}}{r-1}. \end{aligned}$$

The desired limit follows. $\square$

Proof of Theorem 1.4

We will argue via the Skorokhod representation theorem. It will suffice to show the claimed convergence for all sequences $c_k\rightarrow 0$ and ${\sigma }_k\rightarrow 0$ subject to the constraint assumed in Theorem 1.3. Given $N<n_{\alpha }$, choose ${\delta }>0$ and $T<t_{\zeta }$ such that $\nu _T=N+{\delta }$, as in the proof of Theorem 1.2. By Theorem 1.3 and Propositions 5.5 and 5.7, and since $D([0,T],{{\mathcal {H}}})$ is a complete separable metric space, there is a probability space on which are defined a sequence of ALE$({\alpha },\eta )$ processes $(\Phi _t^{(k)})_{t\geqslant 0}$, with common particle family $(P^{(c)}:c\in (0,\infty ))$, and a Gaussian process $({\hat{{\Gamma }}}_t)_{t<t_{\zeta }}$ with the following properties:

• (a) $(\Phi _t^{(k)})_{t\geqslant 0}$ has capacity parameter $c_k$ and regularization parameter ${\sigma }_k$,

• (b) $({\hat{{\Gamma }}}_t)_{t<t_{\zeta }}$ has the distribution of the limit Gaussian process in Theorem 1.3,

• (c) almost surely, as $k\rightarrow \infty$,

  $$\begin{aligned} \sup _{t\leqslant T}|c{{\mathcal {V}}}^{(k)}_t-\nu _t|\rightarrow 0 \end{aligned}$$

  and, for all $r>1$,

  $$\begin{aligned} \sup _{t\leqslant T}\sup _{|z|\geqslant r}\left| c^{-1/2}{\hat{\Psi }}^{(k)}_t(z)-{\hat{{\Gamma }}}_t(z)\right| \rightarrow 0. \end{aligned}$$

Here, ${{\mathcal {V}}}^{(k)}_t$ denotes the number of particles added in $(\Phi _t^{(k)})_{t\geqslant 0}$ by time t. Define for $n\geqslant 0$ and $\nu <n_{\alpha }$

$$\begin{aligned} J^{(k)}_n=\inf \{t\geqslant 0:{{\mathcal {V}}}^{(k)}_t=n\},\quad t(\nu )={\zeta }^{-1}((1+{\alpha }\nu )^{{\zeta }/{\alpha }}-1). \end{aligned}$$

From (c), we deduce that, almost surely, as $k\rightarrow \infty$,

$$\begin{aligned} \sup _{n\leqslant N/c}|J^{(k)}_n-t(cn)|\rightarrow 0 \end{aligned}$$

and, for $\nu \in [0,N]$ and $n=\lfloor \nu /c\rfloor$, the following limit holds in ${{\mathcal {H}}}$

$$\begin{aligned} c^{-1/2}{\hat{\Psi }}^{(k),{{\text {disc}}}}_{\nu /c} =c^{-1/2}{\hat{\Psi }}^{(k),{{\text {disc}}}}_n =c^{-1/2}{\hat{\Psi }}^{(k)}_{J^{(k)}_n}\rightarrow {\hat{{\Gamma }}}_{t(\nu )}. \end{aligned}$$

But $({\hat{{\Gamma }}}_{t(\nu )})_{\nu <n_{\alpha }}$ has the same distribution as $({\hat{{\Gamma }}}^{{\text {disc}}}_\nu )_{\nu <n_{\alpha }}$. Hence

$$\begin{aligned} c^{-1/2}({\hat{\Psi }}^{(k),{{\text {disc}}}}_\nu )_{\nu \leqslant N}\rightarrow ({\hat{{\Gamma }}}^{{\text {disc}}}_\nu )_{\nu \leqslant N} \end{aligned}$$

weakly in $D([0,N],{{\mathcal {H}}})$. $\square$

Miscellaneous Estimates

1.1 Explosion in continuous-time ALE(${\alpha },\eta$)

In this paper we adopted a continuous-time formulation of ALE. When the cluster is in state $\phi$, we add a particle with harmonic measure coordinate ${\theta }\in [0,2\pi )$ at rate $c^{-1}|\phi (e^{{\sigma }+i{\theta }})|^{-\eta }d{\theta }/(2\pi )$. In previous works, this process had been considered in discrete time, that is, jump by jump. Besides being mathematically convenient, the continuous-time formulation has physical meaning since it considers the process in the natural physical time-scale. We now determine exactly for which parameter values ${\alpha }$ and $\eta$ there is pathwise explosion for ALE. The definition and running assumptions (5) and (6) for ALE(${\alpha },\eta$) are given in Sect. 1.2.

Proposition A.1

Let $(\Phi _t)_{t\geqslant 0}$ be an ALE(${\alpha },\eta$) process. Denote by $({{\mathcal {T}}}_t)_{t\geqslant 0}$ the associated process of capacities and by Z the explosion time of $(\Phi _t)_{t\geqslant 0}$. Then, on the event $\{Z<\infty \}$, we have ${{\mathcal {T}}}_t\rightarrow \infty$ as $t\rightarrow Z$. Moreover, if $\eta \geqslant 0$ or ${\zeta }={\alpha }+\eta \geqslant 0$, then $Z=\infty$ almost surely, while if $\eta <0$ and ${\zeta }<0$ then $Z<\infty$ almost surely.

Proof

The total jump rate ${\lambda }(\phi )$ at a state $\phi$ is given by

so, by distortion estimates, there is a constant $C(\eta ,{\sigma })<\infty$ such that

$$\begin{aligned} c^{-1}e^{-\eta {\tau }}/C\leqslant {\lambda }(\phi )\leqslant Cc^{-1}e^{-\eta {\tau }} \end{aligned}$$

where ${\tau }=\phi '(\infty )$. Similarly, there is a constant $C({\alpha },{\sigma })<\infty$ such that the next jump in capacity $\Delta {\tau }$ satisfies

$$\begin{aligned} ce^{-{\alpha }{\tau }}/C\leqslant \Delta {\tau }\leqslant Cce^{-{\alpha }{\tau }}. \end{aligned}$$

The upper bound in the first estimate implies that the jump rate is bounded if $\eta \geqslant 0$, and is bounded on compacts in ${\tau }$ if $\eta <0$. Hence $Z=\infty$ almost surely if $\eta \geqslant 0$, and if $\eta <0$ then $Z<\infty$ only if ${{\mathcal {T}}}_t\rightarrow \infty$ as $t\rightarrow Z$. Moreover, using also the upper bound of the second estimate, we see that

$$\begin{aligned} {{\mathcal {T}}}_t-C^2\int _0^te^{-{\zeta }{{\mathcal {T}}}_s}ds \end{aligned}$$

is a local supermartingale up to Z. Hence $Z=\infty$ almost surely if ${\zeta }\geqslant 0$.

It remains to show that $Z<\infty$ almost surely in the case when $\eta <0$ and ${\zeta }<0$. For this we use the lower bounds in the estimates above. Set

$$\begin{aligned} {\delta }({\tau })=(c/C)e^{-{\alpha }{\tau }},\quad {\lambda }({\tau })=(c^{-1}/C)e^{-\eta {\tau }},\quad F({\tau })={\tau }+{\delta }({\tau }). \end{aligned}$$

It will be convenient to choose $C\geqslant {\alpha }c$ so that F is increasing on $[0,\infty )$. We know that ${{\mathcal {T}}}_t$ jumps up by at least ${\delta }({{\mathcal {T}}}_{t-})$ at rate at least ${\lambda }({{\mathcal {T}}}_{t-})$. Consider the Markov chain $(X_t)_{t\geqslant 0}$ starting from 0 which jumps up by ${\delta }(X_{t-})$ at rate ${\lambda }(X_{t-})$. Since $\eta <0$, for as long as $X_{t-}\leqslant {{\mathcal {T}}}_{t-}$, we may couple these processes so that $(X_t)_{t\geqslant 0}$ jumps whenever $({{\mathcal {T}}}_t)_{t\geqslant 0}$ does. But $X_0={{\mathcal {T}}}_0=0$ and at each jump of $X_t$ we have $X_t=F(X_{t-})$ and ${{\mathcal {T}}}_t\geqslant F({{\mathcal {T}}}_{t-})$. Since F is increasing, the inequality $X_t\leqslant {{\mathcal {T}}}_t$ extends to all $t<Z$. It will therefore suffice to show that $(X_t)_{t\geqslant 0}$ explodes. Now the sequence of values $(x(n):n\geqslant 0)$ taken by $(X_t)_{t\geqslant 0}$ is given by

$$\begin{aligned} x(n+1)=x(n)+{\delta }(x(n)),\quad x(0)=0 \end{aligned}$$

and the holding times of $(X_t)_{t\geqslant 0}$ are independent exponential random variables of parameters $({\lambda }(x(n)):n\geqslant 0)$. Hence $(X_t)_{t\geqslant 0}$ explodes if and only if

$$\begin{aligned} \sum _{n=0}^\infty {\lambda }(x(n))^{-1}<\infty . \end{aligned}$$

Note that, if ${\alpha }\leqslant 0$, then $x(n)\geqslant cn/C$ for all n so

$$\begin{aligned} \sum _{n=0}^\infty {\lambda }(x(n))^{-1} \leqslant Cc\sum _{n=0}^\infty e^{\eta cn/C}<\infty . \end{aligned}$$

Assume then that ${\alpha }>0$. For $x\geqslant 0$, define $(\psi _t(x):t\geqslant 0)$ by

$$\begin{aligned} {\dot{\psi }}_t(x)={\delta }(\psi _t(x)),\quad \psi _0(x)=x. \end{aligned}$$

We can solve to obtain

$$\begin{aligned} \psi _t(x)=\frac{1}{{\alpha }}\log (e^{{\alpha }x}+{\alpha }ct/C). \end{aligned}$$

Since ${\alpha }>0$ and $\psi _t(x)$ is increasing in t,

$$\begin{aligned} \psi _1(x(n))=x(n)+(c/C)\int _0^1e^{-{\alpha }\psi _s(x(n))}ds\leqslant x(n)+{\delta }(x(n))=x(n+1). \end{aligned}$$

Since $\psi _t(x)$ is increasing in x, it follows by induction that, for all n,

$$\begin{aligned} x(n)\geqslant \psi _n(0)=\frac{1}{{\alpha }}\log (1+{\alpha }cn/C). \end{aligned}$$

Hence

$$\begin{aligned} e^{\eta x(n)}\leqslant (1+{\alpha }cn/C)^{\eta /{\alpha }}. \end{aligned}$$

But ${\alpha }+\eta ={\zeta }<0$ so $\eta /{\alpha }<-1$ and so

$$\begin{aligned} \sum _{n=0}^\infty {\lambda }(x(n))^{-1} \leqslant Cc\sum _{n=0}^\infty (1+{\alpha }cn/C)^{\eta /{\alpha }}<\infty \end{aligned}$$

as required. $\square$

1.2 Estimates for single-particle maps

Let P be a basic particle and let

$$\begin{aligned} F(z)=e^c\left( z+\sum _{k=0}^\infty a_kz^{-k}\right) \end{aligned}$$

be the associated conformal map $D_0\rightarrow D_0\setminus P$. We assume that F extends continuously to $\{|z|\geqslant 1\}$. Set

$$\begin{aligned} r_0&=r_0(P)=\sup \{|z|-1:z\in P\},\\ {\delta }&={\delta }(P)=\inf \{r\geqslant 0:|z-1|\leqslant r\text { for all }z\in P\}. \end{aligned}$$

We assume throughout that ${\delta }\leqslant 1$. We use the following well known estimates on the capacity c. There is an absolute constant $C<\infty$ such that

$$\begin{aligned} r_0^2/C\leqslant c\leqslant C{\delta }^2. \end{aligned}$$

(96)

The lower bound relies on Beurling’s projection theorem and a comparison with the case of a slit particle. The upper bound follows from a comparison with the case $P_{\delta }=S_{\delta }\cap D_0$, where $S_{\delta }$ is the closed disk whose boundary intersects the unit circle orthogonally at $e^{\pm i{\theta }_{\delta }}$ with ${\theta }_{\delta }\in [0,\pi ]$ is determined by $|e^{i{\theta }_{\delta }}-1|={\delta }$. See Pommerenke [23].

Write

$$\begin{aligned} \log \left( \frac{F(z)}{z}\right) =u(z)+iv(z) \end{aligned}$$

where we understand the argument to be determined for each $z\in D_0$ so that the left-hand side is holomorphic in $D_0$ and such that $v(z)\rightarrow 0$ as $z\rightarrow \infty$. Then u and v are bounded and harmonic in $D_0$, with continuous extensions to $\{|z|\leqslant 1\}$, and $u(z)\rightarrow c$ as $z\rightarrow \infty$. Note also that

$$\begin{aligned} 0\leqslant u(e^{i{\theta }})\leqslant \log (1+r_0)\leqslant r_0\quad \text { for all}\, {\theta }. \end{aligned}$$

(97)

Lemma A.2

Assume that $16{\delta }\leqslant \pi$. Then

$$\begin{aligned} u(e^{i{\theta }})=0\quad \text {whenever}\, |{\theta }|\in [16{\delta },\pi ] \end{aligned}$$

(98)

and

$$\begin{aligned} |v(e^{i{\theta }})|\leqslant 16{\delta }\quad \text { for all}\, {\theta }. \end{aligned}$$

(99)

Proof

Set

$$\begin{aligned} p_{\delta }=\mathbb {P}_\infty (B\text { hits }S_{\delta }\text { before leaving }D_0) \end{aligned}$$

where B is a complex Brownian motion. Consider the conformal map f of $D_0$ to the upper half-plane $\mathbb {H}$ given by

$$\begin{aligned} f(z)=i\frac{z-1}{z+1}. \end{aligned}$$

Set $b=f(e^{-i{\theta }_{\delta }})=\sin {\theta }_{\delta }/(1+\cos {\theta }_{\delta })$. Since ${\delta }\leqslant 1$, we have

$$\begin{aligned} {\theta }_{\delta }\leqslant {\delta }\pi /3 \end{aligned}$$

(100)

and then $b\leqslant 2\pi {\delta }/9$. By conformal invariance,

$$\begin{aligned} p_{\delta }=\mathbb {P}_i(B\text { hits}\, f(S_{\delta }) \text {before leaving} \mathbb {H}) =2\int _0^{2b/(1-b^2)}\frac{dx}{\pi (1+x^2)}. \end{aligned}$$

Hence

$$\begin{aligned} p_{\delta }\leqslant 4b/\pi \leqslant 8{\delta }/9. \end{aligned}$$

(101)

Now $e^{i\pi }$ is not a limit point of P so $e^{i\pi }=F(e^{i(\pi +{\alpha })})$ for some ${\alpha }\in \mathbb {R}$. Then $u(e^{i(\pi +{\alpha })})=0$ and we can and do choose ${\alpha }$ so that ${\alpha }+v(e^{i(\pi +{\alpha })})=0$. Set

$$\begin{aligned} {\theta }^+=\sup \{{\theta }\leqslant \pi +{\alpha }:u(e^{i{\theta }})>0\},\quad {\theta }^-=\inf \{{\theta }\geqslant \pi +{\alpha }:u(e^{i{\theta }})>0\}-2\pi . \end{aligned}$$

Then ${\theta }^-\leqslant {\theta }^+$. We will show that $|{\theta }^\pm |\leqslant 16{\delta }$, which then implies (98). For ${\theta }\in [{\theta }^-,{\theta }^+]$, we have $F(e^{i{\theta }})\in S_{\delta }$ so $|{\theta }+v(e^{i{\theta }})|\leqslant {\theta }_{\delta }$. Set $P^*=\{F(e^{i{\theta }}):{\theta }\in [{\theta }^-,{\theta }^+]\}$. Then $P^*\subseteq S_{\delta }$ so, by conformal invariance,

$$\begin{aligned} \frac{{\theta }^+-{\theta }^-}{2\pi } =\mathbb {P}_\infty (B\text { hits}\, P^*\, \text {on leaving} D_0\setminus P) \leqslant p_{\delta }. \end{aligned}$$

On the other hand, for ${\theta },{\theta }'\in [{\theta }^+,{\theta }^-+2\pi ]$ with ${\theta }\leqslant {\theta }'$, by conformal invariance,

$$\begin{aligned} \frac{{\theta }'-{\theta }}{2\pi }= & {} \mathbb {P}_\infty \big (B\text { hits}\, \big [e^{i({\theta }+v(e^{i{\theta }}))},e^{i({\theta }'+v(e^{i{\theta }'}))}\big ]\, \text {on leaving}\, D_0\setminus P\big ) \\\leqslant & {} \frac{{\theta }'+v(e^{i{\theta }'})-{\theta }-v(e^{i{\theta }})}{2\pi } \end{aligned}$$

so v is non-decreasing on $[{\theta }^+,{\theta }^-+2\pi ]$, and so

$$\begin{aligned} {\alpha }+v(e^{i{\theta }^+}) \leqslant {\alpha }+v(e^{i(\pi +{\alpha })})=0 \leqslant {\alpha }+v(e^{i{\theta }^-}). \end{aligned}$$

Hence

$$\begin{aligned} {\theta }^+-{\alpha }\leqslant 2\pi p_{\delta }+{\theta }^--{\alpha }\leqslant 2\pi p_{\delta }+{\theta }_{\delta }-v(e^{i{\theta }^-})-{\alpha }\leqslant 2\pi p_{\delta }+{\theta }_{\delta }\end{aligned}$$

(102)

and similarly

$$\begin{aligned} {\theta }^--{\alpha }\geqslant -2\pi p_{\delta }-{\theta }_{\delta }. \end{aligned}$$

(103)

So we obtain, for all ${\theta }\in [{\theta }^-,{\theta }^+]$,

$$\begin{aligned} |{\alpha }+v(e^{i{\theta }})|\leqslant 2{\theta }_{\delta }+2\pi p_{\delta }. \end{aligned}$$

(104)

Since v is continuous and is non-decreasing on the complementary interval, this inequality then holds for all ${\theta }$. Now v is bounded and harmonic in $D_0$ with limit 0 at $\infty$, so

$$\begin{aligned} \int _0^{2\pi }v(e^{i{\theta }})d{\theta }=0. \end{aligned}$$

Hence

On combining this with (102), (103) and (104), we see that

$$\begin{aligned} |{\theta }^\pm |\leqslant 4{\theta }_{\delta }+4\pi p_{\delta },\quad |v(e^{i{\theta }})|\leqslant 4{\theta }_{\delta }+4\pi p_{\delta }\quad \text {for all}\, {\theta }. \end{aligned}$$

But $4{\theta }_{\delta }+4\pi p_{\delta }\leqslant 44\pi {\delta }/9\leqslant 16{\delta }$ by (100) and (101), so we have shown the claimed inequalities. $\square$

Proposition A.3

There is an absolute constant $C<\infty$ with the following properties. In the case where ${\delta }={\delta }(P)\leqslant 1/C$, for all $|z|>1$,

$$\begin{aligned} \left| \log \left( \frac{F(z)}{z}\right) -c\right| \leqslant \frac{C{\delta }}{|z|} \end{aligned}$$

(105)

and, for all $|z|>1$ with $|z-1|\geqslant C{\delta }$,

$$\begin{aligned} \left| \log \left( \frac{F(z)}{z}\right) -c-\frac{2c}{z-1}\right| \leqslant \frac{C{\delta }c|z|}{|z-1|^2} \end{aligned}$$

(106)

and

$$\begin{aligned} |a_0-2c|\leqslant C{\delta }c \end{aligned}$$

(107)

and

$$\begin{aligned} \left| \log \left( \frac{F(z)}{z}\right) -c-\frac{a_0}{z-1}\right| \leqslant \frac{C{\delta }c}{|z-1|^2}. \end{aligned}$$

(108)

Proof

Since $z\log (F(z)/z)$ is bounded and holomorphic in $\{|z|>1\}$, (105) follows from (97) and (99) by the maximum principle. The inequality (107) follows from (106) on letting $z\rightarrow \infty$, since $z(\log (F(z)/z)-c)\rightarrow a_0$. Moreover, since $(z-1)^2(\log (F(z)/z)-c)-a_0z$ is bounded and holomorphic on $\{|z|>1\}$, (108) follows from (106) by the maximum principle, at the cost of replacing C by 6C, say. We will show (106) holds whenever $|z-1|\geqslant 3a$, where $a=16{\delta }$.

Since u is bounded and harmonic with $u(z)\rightarrow c$ as $z\rightarrow \infty$, we have

and, for all $|z|>1$,

Let ${\alpha }\in (-\pi ,\pi ]$ and $\rho >0$ be defined by

We use (98) to see that $|{\alpha }|\leqslant a$ and $\rho \in [\cos a,1)$. Now

For $|z-1|\geqslant 2a$ and any ${\theta }$ such that $u(e^{i{\theta }})>0$, we have

$$\begin{aligned} |z-e^{i{\alpha }}|\geqslant |z-1|/2,\quad |z-e^{i{\theta }}|\geqslant |z-1|/2,\quad |e^{i{\theta }}-e^{i{\alpha }}|\leqslant 2a. \end{aligned}$$

Hence, for $|z|>1$ with $|z-1|\geqslant 2a$,

and

$$\begin{aligned} \left| \frac{2}{z-1}-\frac{2\rho e^{i{\alpha }}}{z-e^{i{\alpha }}}\right| \leqslant \frac{2(1-\rho +|\rho e^{i{\alpha }}-1||z|)}{|z-1||z-e^{i{\alpha }}|} \leqslant \frac{12a|z|}{|z-1|^2} \end{aligned}$$

and hence

$$\begin{aligned} \left| u(z)-c-{\text {Re}}\left( \frac{2c}{z-1}\right) \right| \leqslant \frac{Cac|z|}{|z-1|^2}. \end{aligned}$$

(109)

We can extend F to a holomorphic function in $\{|z-1|>a\}$ by setting $F({\bar{z}}^{-1})=\overline{F(z)}^{-1}$. Then u and v also extend and it is straightforward to check that the estimate (109) remains valid for all $|z-1|\geqslant 2a$. Since $v(z)\rightarrow 0$ as $z\rightarrow \infty$, a standard argument allows us to deduce from (109) that, for $|z-1|\geqslant 3a$,

$$\begin{aligned} \left| v(z)-{\text {Im}}\left( \frac{2c}{z-1}\right) \right| \leqslant \frac{Cac|z|}{|z-1|^2} \end{aligned}$$

and hence

$$\begin{aligned} \left| \log \left( \frac{F(z)}{z}\right) -c-\frac{2c}{z-1}\right| \leqslant \frac{Cac|z|}{|z-1|^2}. \end{aligned}$$

$\square$

We sometimes use exponentiated versions of the inequalities just proved, which are straightforward to deduce and are noted here for easy reference. There is an absolute constant $C<\infty$ with the following properties. Suppose that ${\delta }\leqslant 1/C$. Then, for all $|z|>1$,

$$\begin{aligned} |e^{-c}F(z)-z|\leqslant C{\delta }\end{aligned}$$

and, in the case $|z-1|\geqslant C{\delta }$,

$$\begin{aligned} \left| e^{-c}F(z)-z-\frac{2cz}{z-1}\right| \leqslant \frac{C{\delta }c|z|^2}{|z-1|^2} \end{aligned}$$

(110)

and

$$\begin{aligned} \left| e^{-c}F(z)-z-\frac{a_0z}{z-1}\right| \leqslant \frac{C{\delta }c|z|}{|z-1|^2}. \end{aligned}$$

Proposition A.4

There is an absolute constant $C<\infty$ with the following properties. Let $P_1,P_2$ be basic particles with $P_1\subseteq P_2$. For $i=1,2$, write $F_i$ for the associated conformal map $D_0\rightarrow D_0\setminus P_i$ and write $c_i$ for the capacity of $P_i$. Set ${\delta }_i={\delta }(P_i)$ and $a_{0,i}=a_0(P_i)$ and set

$$\begin{aligned} {\varepsilon }_i(z)=\log \left( \frac{F_i(z)}{z}\right) -c_i-\frac{2c_i}{z-1},\quad {\varepsilon }_{0,i}(z)=\log \left( \frac{F_i(z)}{z}\right) -c_i-\frac{a_{0,i}}{z-1}. \end{aligned}$$

Assume that ${\delta }_2\leqslant 1/C$. Then

$$\begin{aligned} |a_{0,2}-a_{0,1}-2(c_2-c_1)|\leqslant C{\delta }_2(c_2-c_1) \end{aligned}$$

(111)

and, for all $|z|>1$ with $|z-1|\geqslant C{\delta }_2$,

$$\begin{aligned} \left| {\varepsilon }_1(z)-{\varepsilon }_2(z)\right| \leqslant \frac{C{\delta }_2(c_2-c_1)|z|}{|z-1|^2} \end{aligned}$$

(112)

and

$$\begin{aligned} \left| {\varepsilon }_{0,1}(z)-{\varepsilon }_{0,2}(z)\right| \leqslant \frac{C{\delta }_2(c_2-c_1)}{|z-1|^2}. \end{aligned}$$

(113)

Proof

The inequalities (112) and (113) follow from (111) by the same argument used to deduce (107) and (108) from (106). Set ${\tilde{P}}=F_1^{-1}(P_2\setminus P_1)$. Write ${\tilde{F}}$ for the associated conformal map $D_0\rightarrow D_0\setminus {\tilde{P}}$ and write ${\tilde{c}}$ for the capacity of ${\tilde{P}}$. Then

$$\begin{aligned} F_2=F_1\circ {\tilde{F}},\quad c_2=c_1+{\tilde{c}}. \end{aligned}$$

Note that, for $z\in {\tilde{P}}$, we have $F_1(z)\in P_2$, so $|F_1(z)-1|\leqslant {\delta }_2$. But $|e^{-c_1}F_1(z)-z|\leqslant C{\delta }_1$ for all $|z|>1$ and $c_1\leqslant C{\delta }_1^2$. Hence $|z-1|\leqslant C{\delta }_2$ for all $z\in {\tilde{P}}$ and so

$$\begin{aligned} {\tilde{{\delta }}}={\delta }({\tilde{P}})\leqslant C{\delta }_2. \end{aligned}$$

Hence, for C sufficiently large and ${\delta }_2\leqslant 1/C$, for all $|z|>1$ with $|z-1|\geqslant C{\delta }_2$,

$$\begin{aligned} \left| \log \left( \frac{{\tilde{F}}(z)}{z}\right) -{\tilde{c}}-\frac{2{\tilde{c}}}{z-1}\right| \leqslant \frac{C{\delta }_2{\tilde{c}}|z|}{|z-1|^2} \end{aligned}$$

(114)

and in particular

$$\begin{aligned} \left| \log \left( \frac{{\tilde{F}}(z)}{z}\right) \right| \leqslant \frac{C{\tilde{c}}|z|}{|z-1|}. \end{aligned}$$

(115)

Set $z_t=z\exp (t\log ({\tilde{F}}(z)/z))$ and $f(t)=\log (F_1(z_t)/F_1(z))$. Then

$$\begin{aligned} \log \left( \frac{F_2(z)}{F_1(z)}\right) =f(1)-f(0) =\int _0^1\dot{f}(t)dt =\log \left( \frac{{\tilde{F}}(z)}{z}\right) \int _0^1F_1'(z_t)\left( \frac{F_1(z_t)}{z_t}\right) ^{-1}dt \end{aligned}$$

so

$$\begin{aligned}&{\varepsilon }_2(z)-{\varepsilon }_1(z)\\&\quad =\log \left( \frac{F_2(z)}{F_1(z)}\right) -{\tilde{c}}-\frac{2{\tilde{c}}}{z-1}\\&\quad =\log \left( \frac{{\tilde{F}}(z)}{z}\right) \int _0^1F_1'(z_t)\left( \frac{F_1(z_t)}{z_t}\right) ^{-1}dt -{\tilde{c}}-\frac{2{\tilde{c}}}{z-1}\\&\quad =\log \left( \frac{{\tilde{F}}(z)}{z}\right) -{\tilde{c}}-\frac{2{\tilde{c}}}{z-1} +\log \left( \frac{{\tilde{F}}(z)}{z}\right) \int _0^1\left( F_1'(z_t)\left( \frac{F_1(z_t)}{z_t}\right) ^{-1}-1\right) dt. \end{aligned}$$

Now $|\log ({\tilde{F}}(z)/z)|\leqslant C{\delta }_2$, so $|z_t-z|\leqslant C{\delta }_2$ for all t. Hence, for C sufficiently large and $|z-1|\geqslant C{\delta }_2$, we have $|z_t-1|\geqslant C_0{\delta }_1$ for all t, where $C_0$ is the constant from Proposition A.3. Then

$$\begin{aligned} |e^{-c_1}F_1(z_t)-z_t|\leqslant C{\delta }_1,\quad |e^{-c_1}F_1'(z_t)-1|\leqslant \frac{C{\delta }_1}{|z-1|} \end{aligned}$$

where we used Cauchy’s integral formula for the second inequality, adjusting the value of C if necessary. On combining these estimates with (114) and (115), we see that

$$\begin{aligned} |{\varepsilon }_2(z)-{\varepsilon }_1(z)|\leqslant \frac{C{\delta }_2(c_2-c_1)|z|}{|z-1|^2} \end{aligned}$$

as claimed. $\square$

The following is a straightforward consequence of (96) and Propositions A.3 and A.4.

Proposition A.5

Let $(P^{(c)}:c\in (0,1])$ be a family of basic particles and suppose that the associated conformal maps $F_c$ are given by

$$\begin{aligned} F_c(z)=e^c\left( z+\sum _{k=0}^\infty a_k(c)z^{-k}\right) . \end{aligned}$$

Fix ${\Lambda }\in [1,\infty )$ and assume that ${\delta }(c)\leqslant {\Lambda }r_0(c)$ for all c. Then there is a constant $C({\Lambda })<\infty$ such that, for all $c\leqslant 1/C$,

$$\begin{aligned} |a_0(c)-2c|\leqslant Cc^{3/2} \end{aligned}$$

and, for all $|z|>1$,

$$\begin{aligned} \left| \log \left( \frac{F_c(z)}{z}\right) -c\right| \leqslant \frac{Cc}{|z-1|} \end{aligned}$$

and

$$\begin{aligned} \left| \log \left( \frac{F_c(z)}{z}\right) -c-\frac{a_0(c)}{z-1}\right| \leqslant \frac{Cc^{3/2}}{|z-1|^2} \end{aligned}$$

and

$$\begin{aligned} \left| e^{-c}F_c(z)-z-\frac{a_0(c)z}{z-1}\right| \leqslant \frac{Cc^{3/2}|z|}{|z-1|^2}. \end{aligned}$$

Moreover, if $(P^{(c)}:c\in (0,1])$ is nested, then C may be chosen so that, for all $c_1,c_2\in (0,c]$,

$$\begin{aligned} |(a_0(c_1)-2c_1)-(a_0(c_2)-2c_2)|\leqslant Cc^{1/2}|c_1-c_2| \end{aligned}$$

and, for all $|z-1|\geqslant C\sqrt{c}$,

$$\begin{aligned} \left| \left( \log \left( \frac{F_{c_1}(z)}{z}\right) -c_1\right) -\left( \log \left( \frac{F_{c_2}(z)}{z}\right) -c_2\right) \right| \leqslant \frac{C|c_1-c_2|}{|z-1|} \end{aligned}$$

and

$$\begin{aligned} \left| \left( \log \left( \frac{F_{c_1}(z)}{z}\right) -c_1-\frac{a_0(c_1)}{z-1}\right) -\left( \log \left( \frac{F_{c_2}(z)}{z}\right) -c_2-\frac{a_0(c_2)}{z-1}\right) \right| \leqslant \frac{C\sqrt{c}|c_1-c_2|}{|z-1|^2} \end{aligned}$$

and

$$\begin{aligned} \left| \left( e^{-c_1}F_{c_1}(z)-z-\frac{a_0(c_1)z}{z-1}\right) -\left( e^{-c_2}F_{c_2}(z)-z-\frac{a_0(c_2)z}{z-1}\right) \right| \leqslant \frac{C\sqrt{c}|c_1-c_2||z|}{|z-1|^2}. \end{aligned}$$

For our final particle estimates, we use the following integral representation for the family of particle maps

$$\begin{aligned} F_c(z)=z+\int _0^cDF_t(z)\int _0^{2\pi }\frac{z+e^{i{\theta }}}{z-e^{i{\theta }}}\mu _t(d{\theta })dt \end{aligned}$$

for some measurable family of probability measures $(\mu _t:t\in (0,\infty ))$, with $\mu _t$ supported on $\{{\theta }:|e^{i{\theta }}-1|\leqslant {\delta }(t)\}$ for all t. This follows from our requirements that the particles $P^{(c)}$ have capacity c, are contained in $\{|z-1|\leqslant {\delta }(c)\}$ and are nested, by the Loewner–Kufarev theory. Our condition (6) and the inequality (96) then give a constant $C({\Lambda })<\infty$ such that

$$\begin{aligned} {\text {supp}}\mu _t\subseteq \{{\theta }:|e^{i{\theta }}-1|\leqslant C\sqrt{t}\}. \end{aligned}$$

(116)

Define holomorphic functions $L_t$ and $Q_t$ on $\{|z|>1\}$ by

$$\begin{aligned} L_t(z)=\int _0^{2\pi }l_t({\theta },z)\mu _t(d{\theta }),\quad Q_t(z)=\int _0^{2\pi }q_t({\theta },z)\mu _t(d{\theta }) \end{aligned}$$

(117)

where

$$\begin{aligned} l_t({\theta },z)=\left( D\log \left( \frac{F_t(z)}{z}\right) +1\right) \frac{z+e^{i{\theta }}}{z-e^{i{\theta }}},\quad q_t({\theta },z)=DF_t(z)\frac{z+e^{i{\theta }}}{z-e^{i{\theta }}}-e^tz-\frac{2e^te^{i{\theta }}z}{z-1}. \end{aligned}$$

Note that $l_t({\theta },z)\rightarrow 1$ and $q_t({\theta },z)\rightarrow 0$ as $z\rightarrow \infty$, uniformly in ${\theta }$. It is then straightforward to show the integral representations

$$\begin{aligned} \log \left( \frac{F_c(z)}{z}\right) =\int _0^cL_t(z)dt,\quad e^c\left( e^{-c}F_c(z)-z-\frac{a_0(c)z}{z-1}\right) =\int _0^cQ_t(z)dt. \end{aligned}$$

Proposition A.6

There is a constant $C({\Lambda })<\infty$ with the following property. For all $t\leqslant 1/C$ and all $|z|>1$,

$$\begin{aligned} |L_t(z)|\leqslant \frac{C|z|}{|z-1|}+\frac{C\sqrt{t}|z|}{|z-1|^2},\quad |Q_t(z)|\leqslant \frac{C\sqrt{t}|z|}{|z-1|^2}. \end{aligned}$$

Proof

We give the details for the second estimate, leaving the first which is similar but simpler to the reader. We split $q_t({\theta },z)=g_t({\theta },z)+h_t({\theta },z)$, where

$$\begin{aligned} g_t({\theta },z)=(DF_t(z)-e^tz)\frac{z+e^{i{\theta }}}{z-e^{i{\theta }}},\quad h_t({\theta },z)=e^tz\left( \frac{z+e^{i{\theta }}}{z-e^{i{\theta }}}-1-\frac{2e^{i{\theta }}}{z-1}\right) . \end{aligned}$$

Now

$$\begin{aligned} \frac{z+e^{i{\theta }}}{z-e^{i{\theta }}}-1-\frac{2e^{i{\theta }}}{z-1} =\frac{2e^{i{\theta }}(e^{i{\theta }}-1)}{(z-e^{i{\theta }})(z-1)} \end{aligned}$$

so, on the support of $\mu _t$, we have, for $|z-1|\geqslant 2C\sqrt{t}$,

$$\begin{aligned} |h_t({\theta },z)|\leqslant \frac{2C e^t\sqrt{t}|z|}{|z-1|^2} \end{aligned}$$

where C is the constant in (116). On the other hand, we showed above that, for all $|z|>1$,

$$\begin{aligned} |F_t(z)-e^tz|\leqslant C\sqrt{t} \end{aligned}$$

and $F_t$ extends by reflection to a holomorphic function on $\{|z-1|>C\sqrt{t}\}$ satisfying the same inequality. Hence, by Cauchy’s integral formula, for $|z-1|\geqslant 2C\sqrt{t}$,

$$\begin{aligned} |DF_t(z)-e^tz|\leqslant \frac{C\sqrt{t}|z|}{|z-1|} \end{aligned}$$

and so, for ${\theta }$ in the support of $\mu _t$,

$$\begin{aligned} |g_t({\theta },z)|\leqslant \frac{C\sqrt{t}|z|}{|z-1|^2}. \end{aligned}$$

We have shown that, for all $|z-1|\geqslant C\sqrt{t}$,

$$\begin{aligned} |Q_t(z)|\leqslant \frac{C\sqrt{t}|z|}{|z-1|^2}. \end{aligned}$$

$\square$

1.3 Operator inequalities

Recall that, for a measurable function f on $\{|z|>1\}$, for $p\in [1,\infty )$ and $r>1$, we set

Suppose that f is holomorphic and is bounded at $\infty$. It is standard that, for $\rho \in (1,r)$,

$$\begin{aligned} \Vert f\Vert _{p,r}\leqslant \Vert f\Vert _{p,\rho },\quad \Vert f\Vert _{\infty ,r}\leqslant \left( \frac{\rho }{r-\rho }\right) ^{1/p}\Vert f\Vert _{p,\rho }. \end{aligned}$$

(118)

Moreover, there is an absolute constant $C<\infty$ such that

$$\begin{aligned} \Vert Df\Vert _{p,r}\leqslant \frac{C\rho }{r-\rho }\Vert f\Vert _{p,\rho } \end{aligned}$$

(119)

where $Df(z)=zf'(z)$. The function f has a Laurent expansion

$$\begin{aligned} f(z)=\sum _{k=0}^\infty f_kz^{-k}. \end{aligned}$$

Let M be an operator which acts as multiplication by $m_k$ on the the kth Laurent coefficient. Thus

$$\begin{aligned} Mf(z)=\sum _{k=0}^\infty m_k f_kz^{-k}. \end{aligned}$$

Assume that there exists a finite constant $A>0$ such that, for all $k\geqslant 0$,

$$\begin{aligned} |m_k|\leqslant A \end{aligned}$$

and, for all integers $K\geqslant 0$,

$$\begin{aligned} \sum _{k=2^K}^{2^{K+1}-1}|m_{k+1}-m_k|\leqslant A. \end{aligned}$$

Then, by the Marcinkiewicz multiplier theorem [29, Vol. II, Theorem 4.14], for all $p\in (1,\infty )$, there is a constant $C=C(p)<\infty$ such that, for all $r>1$,

$$\begin{aligned} \Vert Mf\Vert _{p,r}\leqslant CA\Vert f\Vert _{p,r}. \end{aligned}$$

(120)

We will use also the following estimate.

Proposition A.7

Let f and g be holomorphic in $\{|z|>1\}$ and bounded at $\infty$. Let M be a multiplier operator and let $p\geqslant 2$. Set

$$\begin{aligned} f_{\theta }(z)=f(e^{-i{\theta }}z). \end{aligned}$$

and

Then, for all $r,\rho >1$, we have

$$\begin{aligned} \Vert h_2\Vert _{p,r}\leqslant \Vert M\Vert _{p,\rho \rightarrow r}\Vert g\Vert _{p,\rho }\Vert f\Vert _{2,\rho } \end{aligned}$$

and

$$\begin{aligned} \Vert h_p\Vert _{p,r}\leqslant \Vert M\Vert _{p,\rho \rightarrow r}\Vert g\Vert _{p,\rho }\Vert f\Vert _{p,\rho } \end{aligned}$$

where

$$\begin{aligned} \Vert M\Vert _{p,\rho \rightarrow r}=\sup \{\Vert Mf\Vert _{p,r}:\Vert f\Vert _{p,\rho }\leqslant 1\}. \end{aligned}$$

Proof

The second estimate is straightforward and is left to the reader. For the first, we can write

$$\begin{aligned} f(z)=\sum _{k=0}^\infty f_kz^{-k},\quad g(z)=\sum _{k=0}^\infty g_kz^{-k},\quad Mf(z)=\sum _{k=0}^\infty m_k f_kz^{-k}. \end{aligned}$$

Then

$$\begin{aligned} M(f_{\theta }.g)(z)=\sum _{k=0}^\infty \sum _{j=0}^\infty m_{j+k}f_kg_je^{i{\theta }k}z^{-(k+j)} \end{aligned}$$

so

$$\begin{aligned} h_2(z)^2=\sum _{k=0}^\infty |f_k|^2|M(\tau _kg)(z)|^2 \end{aligned}$$

where $\tau _kg(z)=z^{-k}g(z)$. Hence

$$\begin{aligned} \Vert h_2\Vert _{p,r}^2 =\Vert h_2^2\Vert _{p/2,r}&\leqslant \sum _{k=0}^\infty |f_k|^2\Vert M(\tau _kg)\Vert ^2_{p,r} \leqslant \sum _{k=0}^\infty |f_k|^2\Vert M\Vert ^2_{p,\rho \rightarrow r}\Vert \tau _kg\Vert ^2_{p,\rho }\\&=\sum _{k=0}^\infty |f_k|^2\rho ^{-2k}\Vert M\Vert ^2_{p,\rho \rightarrow r}\Vert g\Vert ^2_{p,\rho } =\Vert M\Vert ^2_{p,\rho \rightarrow r}\Vert f\Vert ^2_{2,\rho }\Vert g\Vert ^2_{p,\rho }. \end{aligned}$$

$\square$