Skip to main content
SpringerLink
Log in

Hastings–Levitov Aggregation in the Small-Particle Limit

  • Published:
Communications in Mathematical Physics Aims and scope Submit manuscript

Abstract

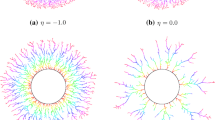
We establish some scaling limits for a model of planar aggregation. The model is described by the composition of a sequence of independent and identically distributed random conformal maps, each corresponding to the addition of one particle. We study the limit of small particle size and rapid aggregation. The process of growing clusters converges, in the sense of Carathéodory, to an inflating disc. A more refined analysis reveals, within the cluster, a tree structure of branching fingers, whose radial component increases deterministically with time. The arguments of any finite sample of fingers, tracked inwards, perform coalescing Brownian motions. The arguments of any finite sample of gaps between the fingers, tracked outwards, also perform coalescing Brownian motions. These properties are closely related to the evolution of harmonic measure on the boundary of the cluster, which is shown to converge to the Brownian web.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ball R.C., Brady R.M., Rossi G., Thompson B.R.: Anisotropy and cluster growth by diffusion-limited aggregation. Phys. Rev. Lett. 55, 1406–1409 (1985)

    Article  ADS  Google Scholar 

  2. Bazant, M.Z., Crowdy, D.: Conformal mapping methods for interfacial dynamics. In: Yip, S. ed., Handbook of Materials Modeling, Berlin-Heidleberg-NewYork:Springer, 2005, pp. 1417–1451

  3. Carleson L., Makarov N.: Aggregation in the plane and Loewner’s equation. Commun. Math. Phys. 216(3), 583–607 (2001)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  4. Carleson, L., Makarov, N.: Laplacian path models. J. Anal. Math. 87, 103–150 (2002). (Dedicated to the memory of Thomas H. Wolff)

    Google Scholar 

  5. Davidovitch B., Hentschel H.G.E., Olami Z., Procaccia I., Sander L.M., Somfai E.: Diffusion limited aggregation and iterated conformal maps. Phys. Rev. E (3) 59(2, part A), 1368–1378 (1999)

    Article  MathSciNet  ADS  Google Scholar 

  6. Eden, M.: A two-dimensional growth process. In: Proc. 4 th Berkeley Sympos. Math. Statist. and Prob. Vol. IV, Berkeley, CA: Univ. California Press, 1961, pp. 223–239

  7. Fontes L.R.G., Isopi M., Newman C.M., Ravishankar K.: The Brownian web: characterization and convergence. Ann. Probab. 32(4), 2857–2883 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  8. Hastings M.B.: Fractal to nonfractal phase transition in the dielectric breakdown model. Phys. Rev. Lett. 87, 175502 (2001)

    Article  ADS  Google Scholar 

  9. Hastings M.B., Levitov L.S.: Laplacian growth as one-dimensional turbulence. Physica D 116(1–2), 244 (1998)

    Article  ADS  MATH  Google Scholar 

  10. Jensen M.H., Levermann A., Mathiesen J., Procaccia I.: Multifractal structure of the harmonic measure of diffusion-limited aggregates. Phys. Rev. E 65, 046109 (2002)

    Article  MathSciNet  ADS  Google Scholar 

  11. Viklund F.J., Sola A., Turner A.: Scaling limits of anisotropic Hastings-Levitov clusters. Ann. Inst. H. Poincaré Probab. Stat. 48, 235–257 (2012)

    Article  ADS  MATH  Google Scholar 

  12. Kesten H.: Hitting probabilities of random walks on Z d. Stoch. Proc. Appl. 25(2), 165–184 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  13. Meakin P., Ball R.C., Ramanlal P., Sander L.M.: Structure of large two-dimensional square-lattice diffusion-limited aggregates: Approach to asymptotic behavior. Phys. Rev. A 35, 5233–5239 (1987)

    Article  ADS  Google Scholar 

  14. Niemeyer L., Pietronero L., Wiesmann H.J.: Fractal dimension of dielectric breakdown. Phys. Rev. Lett. 57(5), 650 (1986)

    Article  ADS  Google Scholar 

  15. Norris, J., Turner, A.G.: Planar aggregation and the coalescing Brownian flow. http://arxiv.org/abs/0810.0211v1 [math.PR], 2008

  16. Norris, J., Turner, A.G.: Weak convergence of the localized disturbance flow to the coalescing Brownian flow. http://arxiv.org/abs/1106.3252v3 [math.PR], 2012

  17. Rohde S., Zinsmeister M.: Some remarks on Laplacian growth. Topology Appl. 152(1-2), 26–43 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  18. Witten T.A., Sander L.M.: Diffusion-limited aggregation, a kinetic critical phenomenon. Phys. Rev. Lett. 47(19), 1400–1403 (1981)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Statistical Laboratory, Centre for Mathematical Sciences, Wilberforce Road, Cambridge, CB3 0WB, UK

    James Norris

  2. Department of Mathematics and Statistics, Lancaster University, Lancaster, LA1 4YF, UK

    Amanda Turner

Authors
  1. James Norris
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Amanda Turner
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to James Norris.

Additional information

Communicated by H. Spohn

James Norris: Research supported by EPSRC grant EP/103372X/1.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Norris, J., Turner, A. Hastings–Levitov Aggregation in the Small-Particle Limit. Commun. Math. Phys. 316, 809–841 (2012). https://doi.org/10.1007/s00220-012-1552-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00220-012-1552-6

Keywords

Search

Navigation