Combined algorithms of high-frequency topographical effects for the boundary-value problems based on Helmert's second condensation method

Abstract

The Helmert’s second condensation method is usually used to condense the topographical masses outside the boundary surface in the determination of the geoid and quasi-geoid based on the boundary-value theory. The condensation of topographical masses produces direct and indirect topographical effects. Nowadays, the Remove-Compute-Restore (RCR) technique has been widely utilized in the boundary-value problems. In view of spectral consistency, high-frequency direct and indirect topographical effects should be used in the Hotine-Helmert/Stokes–Helmert integral when the Earth gravitational model serves as the reference model in determining the (quasi-) geoid. Thus, the algorithms for high-frequency topographical effects are investigated in this manuscript. First, the prism methods for near-zone direct and indirect topographical effects are derived to improve the accuracies of near-zone effects compared with the traditional surface integral methods. Second, the Molodenskii spectral methods truncated to power H⁴ are put forward for far-zone topographical effects. Next, the "prism + Molodenskii spectral-spherical harmonic" combined algorithms for high-frequency topographical effects are further presented. At last, the effectiveness of the combined algorithms for the high-frequency topographical effects are verified in a mountainous test area.

1 Introduction

The geoid and quasi-geoid are two kinds of height reference surfaces used widely by countries around the world nowadays. The vertical distance between the geoid and the reference ellipsoid is known as geoidal height (i.e., geoid undulation), while the distance between the quasi-geoid and the reference ellipsoid is termed height anomaly. Thus, geoidal height and height anomaly are usually utilized to represent the geoid and quasi-geoid models, respectively. The high-precision (quasi-) geoid model can be constructed based on the second or third geodetic boundary-value theory (Heiskannen and Moritz 1967; Hofmann-Wellenhof and Moritz, 2006). The geodetic boundary-value theory assumes no topographical masses exist outside the boundary surface. Therefore, the topographical masses outside the boundary surface need to be condensed or shifted onto the boundary surface or into its internal space. The effects of the condensation or shift of topographical masses can be categorized into direct effect on gravity and indirect effect on (quasi-) geoid (cf. Martinec 1998). Since the Helmert's second condensation method produces relatively small indirect effect, it is widely used in the determination of the geoid and quasi-geoid (cf. Nahavandchi and Sjöberg 2001; Heck 2003; Vaníček 2008; Ellmann and Vaníček 2007; Wang et al. 2012; Huang and Véronneau 2013).

The direct and indirect topographical effects are functions of the difference between the topographical potential produced by actual topographical masses and that generated by condensed topographical masses. Geodetic scholars have achieved some representative research results in the algorithms for gravitational attraction and potential generated by actual topographical masses, which are instrumental in the research on the direct and indirect topographical effects conducted in this paper. As is known, the height data are stored in discrete grids. However, the surface integral formulae for gravitational attraction and potential take the form of continuous double integration. Mader (1951) and Nagy et al. (2000) studied prism methods for gravitational attraction and potential generated by actual topographical masses to reduce the effects of the discretization of the integral formulae. Heck and Seitz (2007) provided an approximate solution of the spherical tesseroid (spherical prism) integrals based on Taylor series expansions including third-order terms. Tsoulis et al. (2009) indicated that the results of the first-order radial derivatives of the gravitational potential by the prismatic and tesseroidal modeling methods converge to the same values, even at complex mountainous terrain. However, the tesseroidal method provides results in shorter computational times. Grombein et al. (2013) presented optimized formulas with fourth-order Taylor truncation error for the gravitational potential of a homogeneous tesseroid and its derivatives up to second-order, resulting in a computational time reduction by approximately 45%.

International geodesists have also made a series of research achievements in the algorithms of direct and indirect topographical effects. Nahavandchi (1999) pointed out that the topographical effects calculated by the surface integral and spherical harmonic methods differ obviously, which is due to the different errors and frequency characteristics of the two methods. The integrals for the direct and indirect topographical effects are singular in the innermost area. The singularities in the integrals for the direct and indirect topographical effects in the innermost area are removable, as shown by Heiskanen and Moritz (1967), Martinec and Vaníček (1994a, b) and Martinec (1998). The integrals for the indirect topographical effect are Taylor-expanded to power H³ (H represents topographical elevation) by Sjöberg and Nahavandchi (1999). The surface integrals for the direct and indirect topographical effects are Taylor-expanded to terms H² by Sjöberg (2000). A formula of the direct topographical effect is derived by combing the classical formula for the near zone and a set of spherical harmonics of the topography to degree and order 360 for the far zone by Nahavandchi (2000). The formulae for the far-zone topographical effects on gravity and the geoid in the Stokes-Helmert scheme are put forward by using a spherical harmonic model of the global topography and a Molodenskii-type spectral approach by Novák (2000) and Novák et al. (2001). In addition, the formulae for the far-zone effects on gravity and geoidal heights using Helmert’s first and second methods of condensation as well as the Airy-Heiskanen model are presented in Makhloof and Ilk (2008). The direct and indirect topographical effects of Helmert’s second method of condensation can be also computed by the closed integral formulae for the near zone of half degree and one-dimensional fast Fourier transform method for the outer zone (Wang 2011). The formulae for the spherical and spheroidal harmonic expansion of the gravitational potential of the topographical masses are developed by Wang and Yang (2013), which can provide references for the research and application of the spherical harmonic formula for the residual topographical potential.

To circumvent the global Hotine/Stokes integral in practical applications, the Remove-Compute-Restore (RCR) technique in application of gravitational model is widely used nowadays. For the Hotine/Stokes integral in the RCR scheme, the high-frequency gravity data are the input and the high-frequency geoidal heights or high-frequency height anomalies are the output. According to spectral consistency, the high-frequency direct and indirect topographical effects should be applied in the Hotine-Helmert/Stokes-Helmert integral when the Earth gravitational model acts as the reference model. For this purpose, in-depth research on the algorithms of the high-frequency topographical effects are conducted based on the previous studies for direct and indirect topographical effects in this manuscript. First, the global region for the topographical effects is divided into the near and far zones in view of the computational accuracy and efficiency. Second, formulae for prism model for near-zone topographical effects are derived to enhance computational accuracy. Third, the Molodenskii spectral methods for the far-zone topographical effects are put forward based on the Taylor series expanded to order H⁴. Next, subtracting the low-frequency global topographical effects, which are calculated by the spherical harmonic methods, from the sum of the near- and far-zone effects yields the high-frequency effects. The combined algorithms are succinctly referred to as “prism + Molodenskii spectral－spherical harmonic” algorithms. Last, the effectiveness of the algorithms of topographical effects is verified by numerical examples.

2 Surface integral methods for topographical effects

When the Helmert’s 2nd condensation method is used to condense the topographical masses outside the boundary surface, a certain condensation criteria need to be followed. Throughout this paper, the criterion of mass conservation is adopted and the surface density of the Helmert condensation layer is defined in spherical approximation as Heck (2003); Martinec (1998)

$$ \sigma = \rho h\left( {1 + \frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}} \right) $$

(1)

where $\sigma$ is surface density of the Helmert condensation layer, $\rho$ is density of topographical mass, $R$ is mean radius of the Earth, and $h$ is topographical height.

The direct and indirect topographical effects are both functions of residual topographical potential, which is the difference between real topographical potential and condensed topographical potential. In spherical coordinates, the formula for the residual topographical potential is written as Heck (2003), Sjöberg and Nahavandchi (1999) and Martinec (1998)

$$ \delta V\left( P \right) = V^{t} \left( P \right) - V^{c} \left( P \right) = G\iint\limits_{{\Omega_{0} }} {\int\limits_{r = R}^{R + h} {\frac{\rho }{{\ell_{P} }}r^{2} {\text{d}}r} {\text{d}}\Omega } - G\iint\limits_{{\Omega_{0} }} {\frac{\sigma }{{\ell_{P0} }}R^{2} {\text{d}}\Omega } $$

(2)

where $P$ is ground evaluation point, $\delta V$ is residual topographical potential, $V^{t}$ is gravitational potential of real topographical masses, $V^{c}$ is gravitational potential of condensed topographical masses, $G$ is the Newton's gravitational constant, $\Omega_{0}$ represents the global integral region, $r$ is radial distance of the integration point, and $\ell_{{\text{P}}}$ and $\ell_{{{\text{P0}}}}$ are the distances between the computation point and integration points on the ground and on the boundary surface, respectively. $\ell_{P}$ and $\ell_{P0}$ are defined by

$$ \begin{aligned} &\ell_{{{P}}} = \sqrt {r^{2} + r_{{{P}}}^{2} - 2rr_{{{P}}} \cos \psi } \\&\ell_{{{{P0}}}} = \sqrt {r_{{{P}}}^{2} + R^{2} - 2r_{{{P}}} R\cos \psi } \end{aligned}$$

(3)

where $r_{{\text{P}}}$ is radial distance of the evaluation point, and $\psi$ is the angular distance between the integration point and the evaluation point.

The topographical effects are related to residual topographical potential by Martinec (1998), Sjöberg (2000) and Wang (2011)

$$ \begin{aligned}&\delta A = \frac{\partial \delta V\left( P \right)}{{\partial r_{{{P}}} }},\quad\, \delta S = \frac{2}{{r_{{{P}}} }}\delta V\left( P \right)\\ &\delta \zeta = \frac{\delta V\left( P \right)}{\gamma },\quad \, \delta N = \frac{{\delta V\left( {P_{0} } \right)}}{{\gamma_{0} }}\end{aligned} $$

(4)

where $P_{0}$ is projection point of the evaluation point $P$ on the boundary surface of $r = R$, $\delta A$ is direct effect, $\delta S$ is secondary indirect effect on the ground gravity, $\delta \zeta$ is indirect effect on height anomaly, $\delta N$ is indirect effect on geoidal height, $\gamma$ is normal gravity at the telluroid point, and $\gamma_{0}$ is normal gravity at the ellipsoidal point. According to Eq. (4), the secondary indirect effect is related to the indirect effect on height anomaly by

$$ \delta S = \frac{2\gamma }{{r_{P} }}\delta \zeta $$

(5)

According to Eq. (5), it is straightforward to derive the formulae for secondary indirect effect from the formulae for indirect effect on height anomaly. Given the straightforward nature of this derivation and to maintain focus on the primary contributions of this manuscript, the explicit formulae for the secondary indirect effect are intentionally omitted in this manuscript.

The surface integral for the direct effect on the ground point is Martinec (1998) and Wang (2011)

$$\begin{aligned}\delta A &= G\iint\limits_{{\Omega_{0} }} \rho \left[ \frac{{rr_{P} \left( {1 - 6\cos^{2} \psi } \right) + \left( {3r_{P}^{2} + r^{2} } \right)\cos \psi }}{{\ell_{{\text{P}}} }}\right. \\ &\quad\left.- \frac{{Rr_{P} \left( {1 - 6\cos^{2} \psi } \right) + \left( {3r_{P}^{2} + R^{2} } \right)\cos \psi }}{{\ell_{{{\text{P0}}}} }}\right. \\ &\quad\left. + \left( {3\cos^{2} \psi - 1} \right)r_{{\text{P}}} \ln \frac{{r - r_{{\text{P}}} \cos \psi + \ell_{{\text{P}}} }}{{R - r_{{\text{P}}} \cos \psi + \ell_{{{\text{P0}}}} }} \right. \\ &\quad\left. + R^{2} h\left( {1 + \frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}} \right)\frac{{r_{P} - R\cos \psi }}{{\ell_{p0}^{3} }}{\text{d}}\Omega \right] \end{aligned}$$

(6)

The closed integral for the indirect effect on height anomaly is

$$ \begin{aligned}\delta \zeta &= \frac{G}{\gamma }\iint\limits_{{\Omega_{0} }} \rho \left[ \frac{{r + 3r_{{\text{P}}} \cos \psi }}{2}\ell_{{\text{P}}} - \frac{{R + 3r_{{\text{P}}} \cos \psi }}{2}\ell_{P0} \,\right.\\ &\quad\left.+ \frac{{3\cos^{2} \psi - 1}}{2}r_{{\text{P}}}^{2} \ln \frac{{r - r_{{\text{P}}} \cos \psi + \ell_{{\text{P}}} }}{{R - r_{{\text{P}}} \cos \psi + \ell_{{{\text{P0}}}} }}\right.\\ &\quad\left. - \frac{{R^{2} h}}{{\ell_{{{\text{P0}}}} }}\left( {1 + \frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}} \right)\right]\,{\text{d}}\Omega \end{aligned}$$

(7)

The integral of the indirect effect on geoidal height can be derived from Eq. (7) by setting $r_{P} = R$ and $\gamma = \gamma_{0}$, that is, Martinec (1998) and Wang (2011)

$$ \begin{aligned}\delta N &= \frac{G}{{\gamma_{0} }}\iint\limits_{{\Omega_{0} }} \rho \left[ \frac{r + 3R\cos \psi }{2}\ell - \frac{1 + 3\cos \psi }{2}R\ell_{0} \right.\\ &\quad\left.+ \frac{{3\cos^{2} \psi - 1}}{2}R^{2} \ln \frac{r - R\cos \psi + \ell }{{R - R\cos \psi + \ell_{0} }}\right.\\ &\quad\left. - \frac{{R^{2} h}}{{\ell_{0} }}\left( {1 + \frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}} \right) \right]{\text{d}}\Omega \end{aligned}$$

(8)

where $\ell$ and $\ell_{0}$ are the distances between $P_{0}$ and the integration points on the ground and on the boundary surface, respectively. $\ell$ and $\ell_{0}$ are defined by

$$ \ell = \sqrt {r^{2} + R^{2} - 2Rr\cos \psi } ,\quad \, \ell_{0} = 2R\sin \left( {{\psi \mathord{\left/ {\vphantom {\psi 2}} \right. \kern-0pt} 2}} \right) $$

(9)

The integral formulae for the direct and indirect effects are singular at $\psi = 0$. The singularities of the integral formulae in the innermost grid can be sidestepped by splitting the terrain into Bouguer shells and roughness terms (cf. Martinec 1998). Alternatively, the topographical effects induced by the non-innermost grids are calculated by the aforementioned integral formulae, while the effects stemming from the innermost grid are computed by the prism methods presented below.

3 Spherical harmonic methods for global topographical effects

The spherical harmonic formulae for the residual topographical potentials are derived in Appendix A. According to Eqs. (4), (A.4) and (A.9), the spherical harmonic formulae for direct and indirect topographical effects without Taylor truncation errors reduce to Martinec (1998)

$$ \begin{aligned} \delta A =&\, - \frac{2\pi G}{{r_{{\text{P}}} }}\sum\limits_{n = 0}^{\infty } {\left( {n + 1}\right)\left( {\frac{R}{{r_{{\text{P}}} }}} \right)^{n + 1} }\sum\limits_{m = - n}^{n} {\delta V_{nm}^{e} } \overline{Y}_{nm}\left( {\Omega_{{\text{P}}} } \right) \hfill \\ \delta \zeta =&\,\frac{2\pi G}{\gamma }\sum\limits_{n = 0}^{\infty } {\left({\frac{R}{{r_{{\text{P}}} }}} \right)^{n + 1} } \sum\limits_{m = -n}^{n} {\delta V_{nm}^{e} } \overline{Y}_{nm} \left({\Omega_{{\text{P}}} } \right) \hfill \\ \delta N =&\, \frac{2\pi G}{{\gamma_{0} }}\sum\limits_{n = 0}^{\infty } {\sum\limits_{m = -n}^{n} {\delta V_{nm}^{i} } \overline{Y}_{nm} \left({\Omega_{{\text{P}}} } \right)} \hfill \\ \end{aligned}$$

(10)

where $\delta V_{nm}^{e}$ and $\delta V_{nm}^{i}$ are spherical harmonic coefficients with degree $n$ and order $m$ for the residual topographical potentials on the Earth’s surface and on the boundary surface of $r =R$, respectively. Equations (A.5) and (A.10) are the non-Taylor expansion formulas for $\delta V_{nm}^{e}$ and $\delta V_{nm}^{i}$, respectively.According to Eqs. (A.6) and (A.11), the spherical harmonic coefficients for the two residual topographical potentials Taylor-expanded to term H⁴ can be obtained as (cf. Huang and Véronneau 2013)

$$ \begin{gathered} \delta V_{nm}^{e} =\frac{n}{2n + 1}\left[ {H_{nm}^{2} + \frac{n + 3}{{3R}}H_{nm}^{3} +\frac{{\left( {n + 1} \right)\left( {n + 2} \right)}}{{12R^{2}}}H_{nm}^{4} } \right] \hfill \\ \delta V_{nm}^{i} = \frac{n +1}{{2n + 1}}\left[ { - H_{nm}^{2} + \frac{n - 2}{{3R}}H_{nm}^{3} +\frac{{n\left( {1 - n} \right)}}{{12R^{2} }}H_{nm}^{4} } \right]\hfill \\ \end{gathered} $$

(11)

where $H_{nm}^{k}$is height-related spherical harmonic coefficient with degree $n$ and order $m$.The coefficient $H_{nm}^{k}$is computed by

$$ H_{nm}^{k} = \frac{1}{4\pi }\iint\limits_{{\Omega_{0} }} {\rho h^{k} \overline{Y}_{nm} \left(\Omega \right){\text{d}}\Omega },\,k = 2,3,4 $$

(12)

4 Derivation of prism methods for near-zone topographical effects

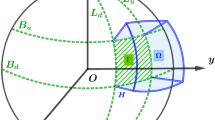
To mitigate the errors arising from the discretization of the integral formulae for the direct and indirect effects, the prism methods for the topographical effects are further deduced below. A three-dimensional Cartesian coordinate system, whose origin is the projection point of the evaluation point on the boundary surface, is established. Figure 1 is a schematic diagram of the prism model for the $i$th discrete geographical grid in the near area of the computation point in the Cartesian coordinates.

Fig. 1

Prism model for the $i$th discrete geographical grid

In Fig. 1, $h_{i}$ is height of the $i$th geographical grid element, $x_{i}$, $x_{i + 1}$, $y_{i}$ and $y_{i + 1}$ are coordinate values of the boundaries of its prism model on x- and y-axis, respectively. Adding the topographical effects generated by condensation of the near-zone prisms together yields the near-zone topographical effects, that is,

$$ \delta A_{{{\text{near}}}} = \sum\limits_{i} {\delta A_{i} } ,\quad \delta \zeta_{{{\text{near}}}} = \sum\limits_{i} {\delta \zeta_{i} } ,\quad \delta N_{{{\text{near}}}} = \sum\limits_{i} {\delta N_{i} } $$

(13)

where $\delta A_{{{\text{near}}}}$ is near-zone direct effect, $\delta \zeta_{{{\text{near}}}}$ is near-zone indirect effect on height anomaly, $\, \delta N_{{{\text{near}}}}$ is near-zone indirect effect on geoidal height, $\delta A_{i}$, $\delta \zeta_{i}$ and $\delta N_{i}$ are topographical effects induced by the $i$th near-zone geographical grid element. The specific formulae for topographical effects of the $i$th geographic grid are derived below.

According to the definition of direct effect, the triple integral formula for $\delta A_{i}$ in the three-dimensional Cartesian coordinate system is

$$ \begin{aligned} \delta A_{i} &= G\rho_{i}\int\limits_{{x_{i} }}^{{x_{i + 1} }} \int\limits_{{y_{i} }}^{{y_{i + 1} }} \int\limits_{0}^{{h_{i} }} \frac{\partial }{{\partial h_{{\text{P}}} }}\hfill \\ & \quad \left[ {\frac{1}{{\sqrt {x^{2} +y^{2} + \left( {h - h_{{\text{P}}} } \right)^{2} } }}} \right]{\text{d}}h{\text{d}}y{\text{d}}x \hfill \\ & \quad - G\rho_{i}h_{i} \left( {1 + \frac{{h_{i} }}{R} + \frac{{h_{i}^{2} }}{{3R^{2}}}} \right)\hfill \\ &\quad{\int\limits_{{x_{i} }}^{{x_{i + 1} }} \int\limits_{{y_{i} }}^{{y_{i + 1} }} {\frac{\partial }{{\partial h_{{\text{P}}} }}\left[ {\frac{1}{{\sqrt {x^{2} + y^{2}+ h_{{\text{P}}}^{2} } }}} \right]{\text{d}}y{\text{d}}x} }\end{aligned} $$

(14)

where $\rho_{i}$is terrain density of the $i$th grid element. The double-integration form of Eq. (14) is expressed as

$$ \begin{aligned} \delta A_{i} &= G\rho_{i}\int\limits_{{x_{i} }}^{{x_{i + 1} }} \int\limits_{{y_{i} }}^{{y_{i + 1} }} \left[ \frac{1}{{\sqrt {x^{2} + y^{2} + h_{P}^{2} } }}\right.\\ &\quad \left.- \frac{1}{{\sqrt {x^{2} + y^{2} + \left({h_{i} - h_{P} } \right)^{2} } }} \right. \hfill \\ \, &\quad \left. { + h_{i} \left( {1 + \frac{{h_{i} }}{R} + \frac{{h_{i}^{2}}}{{3R^{2} }}} \right)\frac{{h_{P} }}{{\left( {x^{2} + y^{2} +h_{P}^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right.\kern-0pt} 2}}} }}} \right]dydx \hfill \\ \end{aligned}$$

(15)

By using Eqs. (B.1) and (B.2), Eq. (15) is rewritten in the single integral form as

$$ \begin{aligned} \delta A_{i} &= G\rho_{i} \int\limits_{{x_{i} }}^{{x_{i + 1} }} \left[ \ln \left( {y + \sqrt {x^{2} + y^{2} + h_{P}^{2} } } \right) \right.\\ &\quad\left.- \ln \left( {y + \sqrt {x^{2} + y^{2} + \left( {h_{i} - h_{P} } \right)^{2} } } \right)\left. \left. + h_{i} \left( {1 + \frac{{h_{i} }}{R} + \frac{{h_{i}^{2} }}{{3R^{2} }}} \right)\frac{{h_{P} y}}{{\left( {x^{2} + h_{P}^{2} } \right)\sqrt {x^{2} + y^{2} + h_{P}^{2} } }} \right] \right|_{{y_{i} }}^{{y_{i + 1} }} {\text{d}}x \right.\end{aligned} $$

(16)

Employing Eqs. (B.3) and (B.4), Eq. (16) yields the prism formula for direct effect as

$$ \begin{aligned} \delta A_{i} &= G\rho_{i} \left[ x\ln \frac{{y + \ell_{{{\text{P0}}}}^{*} }}{{y + \ell_{{\text{P}}}^{*} }} + y\ln \frac{{x + \ell_{{{\text{P0}}}}^{*} }}{{x + \ell_{{\text{P}}}^{*} }} \right.\\ &\quad+ \left( {h_{i} - h_{{\text{P}}} } \right)\arctan \frac{xy}{{\left( {h_{i} - h_{{\text{P}}} } \right)\ell_{{\text{P}}}^{*} }}\left. {\left. {\left. { + \left( {h_{i} + \frac{{h_{i}^{2} }}{R} + \frac{{h_{i}^{3} }}{{3R^{2} }} - h_{P} } \right)\arctan \frac{xy}{{h_{{\text{P}}} \ell_{{{\text{P0}}}}^{*} }}} \right]} \right|_{{y_{i} }}^{{y_{i + 1} }} } \right|_{{x_{i} }}^{{x_{i + 1} }} \end{aligned}$$

(17)

where

$$ \ell_{{\text{P}}}^{*} = \sqrt {x^{2} + y^{2} + \left( {h_{i} - h_{{\text{P}}} } \right)^{2} } ,\quad \ell_{{{\text{P0}}}}^{*} = \sqrt {x^{2} + y^{2} + h_{{\text{P}}}^{2} } $$

(18)

The following identity of definite integral is used in the derivation process of Eq. (17)

$$ \left. {\left. {f\left( x \right)} \right|_{{x_{1} }}^{{x_{2} }} } \right|_{{y_{1} }}^{{y_{2} }} = 0,\quad \left. {\left. {\left. {g\left( {x,y} \right)} \right|_{{x_{1} }}^{{x_{2} }} } \right|_{{y_{1} }}^{{y_{2} }} } \right|_{{z_{1} }}^{{z_{2} }} = 0 $$

(19)

where $f\left( x \right)$ refers to an arbitrary one-variable function, and $g\left( {x,y} \right)$ represents an arbitrary two-variable function. $x_{1}$, $x_{2}$, $y_{1}$, $y_{2}$, $z_{1}$ and $z_{2}$ represent arbitrary constant boundary coordinates on the three axes.

The indirect effect on height anomaly in the local Cartesian coordinate system is expressed as

$$ \begin{gathered} \delta \zeta_{i} = \frac{{G\rho_{i} }}{{\gamma_{i} }}\int\limits_{{x_{i} }}^{{x_{i + 1} }} {\int\limits_{{y_{i} }}^{{y_{i + 1} }} {\int\limits_{0}^{{h_{i} }} {\frac{1}{{\sqrt {x^{2} + y^{2} + \left( {h - h_{P} } \right)^{2} } }}} {\text{d}}h{\text{d}}y{\text{d}}x} } \hfill \\ \, - \frac{{G\rho_{i} }}{{\gamma_{i} }}h_{i} \left( {1 + \frac{{h_{i} }}{R} + \frac{{h_{i}^{2} }}{{3R^{2} }}} \right)\int\limits_{{x_{i} }}^{{x_{i + 1} }} {\int\limits_{{y_{i} }}^{{y_{i + 1} }} {\frac{1}{{\sqrt {x^{2} + y^{2} + h_{{\text{P}}}^{2} } }}{\text{d}}y{\text{d}}x} } \hfill \\ \end{gathered} $$

(20)

where $\gamma_{i}$ is the normal gravity at the midpoint of the $i$ th grid on its top surface. The prism formula for $\delta \zeta_{i}$ is obtained by applying Eqs. (B.5), (B.11), and (19) as

$$ \begin{aligned} \delta \zeta_{i} = & \,\frac{{G\rho_{i} }}{{\gamma_{i} }}\left\{ {xy\ln \frac{{\ell_{{{P}}}^{*} + h_{i} - h_{{{P}}} }}{{\ell_{{{{P0}}}}^{*} - h_{{{P}}} }} + x\left( {h_{i} - h_{{{P}}} } \right)\ln \left( {y + \ell_{{{P}}}^{*} } \right) + y\left( {h_{i} - h_{{{P}}} } \right)\ln \left( {x + \ell_{{{P}}}^{*} } \right)} \right. \\ & + xh_{{{P}}} \ln \left( {y + \ell_{{{{P0}}}}^{*} } \right) + yh_{P} \ln \left( {x + \ell_{{{{P0}}}}^{*} } \right) - \frac{{\left( {h_{i} - h_{{{P}}} } \right)^{2} }}{2}\arctan \frac{xy}{{\left( {h_{i} - h_{{{P}}} } \right)\ell_{{{P}}}^{*} }} - \frac{{h_{{{P}}}^{2} }}{2}\arctan \frac{xy}{{h_{{{P}}} \ell_{P0}^{*} }} \\ & - \frac{{x^{2} }}{2}\arctan \frac{{y\left( {h_{i} - h_{{{P}}} } \right)}}{{x\ell_{{{P}}}^{*} }} - \frac{{x^{2} }}{2}\arctan \frac{{yh_{{{P}}} }}{{x\ell_{{{{P0}}}}^{*} }} - \frac{{y^{2} }}{2}\arctan \frac{{x\left( {h_{i} - h_{{{P}}} } \right)}}{{y\ell_{{{P}}}^{*} }} - \frac{{y^{2} }}{2}\arctan \frac{{xh_{P} }}{{y\ell_{{{{P0}}}}^{*} }} \\ & \left. {\left. {\left. { - h_{i} \left( {1 + \frac{{h_{i} }}{R} + \frac{{h_{i}^{2} }}{{3R^{2} }}} \right)\left[ {x\ln \left( {y + \ell_{{{{P0}}}}^{*} } \right) + y\ln \left( {x + \ell_{{{{P0}}}}^{*} } \right) - h_{{{P}}} \arctan \frac{xy}{{h_{{{P}}} \ell_{{{{P0}}}}^{*} }}} \right]} \right\}} \right|_{{y_{i} }}^{{y_{i+1} }} } \right|_{{x_{i} }}^{{x_{i+1} }} \\ \end{aligned} $$

(21)

Setting the computation point $P$ in Eq. (21) on the boundary surface yields the prism formula for $\delta N_{i}$ as follows.

$$ \begin{aligned} \delta N_{i} & = \frac{{G\rho _{i} }}{{\gamma _{0i} }}\left\{ {xy\ln \frac{{\ell ^{*} + h_{i} }}{{\ell _{0}^{*} }} + xh_{i} \ln\left( {y + \ell ^{*} } \right) + yh_{i} \ln \left( {x + \ell ^{*} } \right)} \right. \\ & - \frac{{h_{i}^{2} }}{2}\arctan \frac{{xy}}{{h_{i} \ell ^{*} }} - \frac{{x^{2} }}{2}\arctan \frac{{yh_{i} }}{{x\ell ^{*} }} - \frac{{y^{2} }}{2}\arctan \frac{{xh_{i} }}{{y\ell ^{*} }} \\ & \left. {\left. {\left. { - h_{i} \left( {1 + \frac{{h_{i} }}{R}+\frac{{h_{i}^{2} }}{{3R}^{2}}} \right)\left[ {x\ln \left( {y + \ell _{0}^{*} } \right) + y\ln \left( {x + \ell _{0}^{*} } \right)} \right]} \right\}} \right|_{{y_{i} }}^{{y_{i+1} }} } \right|_{{x_{i} }}^{{x_{i+1} }} \\ \end{aligned} $$

(22)

where $\gamma_{0i}$ is the normal gravity of the projection position of the computation point on the reference ellipsoid, and the distances $\ell^{*}$ and $\ell_{0}^{*}$ are defined by

$$ \ell^{*} = \sqrt {x^{2} + y^{2} + h_{i}^{2} } ,\quad \ell_{0}^{*} = \sqrt {x^{2} + y^{2} } $$

(23)

As is known, the Earth is approximate to a sphere with radius $R$. However, the near zone is treated as a plane for prism model. This approach inevitably introduces planar approximation errors. To avoid the planar approximation errors, it is essential to factor in the Earth's curvature. According to Forsberg (1984), a straightforward correction can be applied by adjusting the height of computation point to one considering the Earth's curvature, that is,

$$ \overline{h}_{{\text{P}}} = h_{{\text{P}}} + \frac{{\ell_{0}^{2} }}{2R} $$

(24)

where $\overline{{h_{{\text{P}}} }}$ is height of computation point considering the Earth’s curvature and $\ell_{0}$is the horizontal distance between the integration point and the computation point. Replacing $h_{P}$ in Eqs. (17) and (21) by $\overline{h}_{P}$ yields the prism methods for $\delta A_{i}$ and $\delta \zeta_{i}$ considering the Earth's curvature, respectively. Since Eq. (22) is a simplified form of Eq. (21) with $h_{{\text{P}}} = 0$, the prism algorithm for $\delta N_{i}$ considering the Earth's curvature is obtained by substituting ${{\ell_{0}^{2} } \mathord{\left/ {\vphantom {{\ell_{0}^{2} } {\left( {2R} \right)}}} \right. \kern-0pt} {\left( {2R} \right)}}$ for $h_{P}$ and $\gamma_{0i}$ for $\gamma_{i}$ in Eq. (21). That is,

$$ \begin{aligned} \delta N_{i} = & \frac{{G\rho _{i} }}{{\gamma _{{0i}} }}\left\{ {xy\ln \frac{{\ell _{{P_{0} }}^{*} + h_{i} - h_{{P_{0} }} }}{{\ell _{{P_{0} 0}}^{*} - h_{{P_{0} }} }} + x\left( {h_{i} - h_{{P_{0} }} } \right)\ln \left( {y + \ell _{{P_{0} }}^{*} } \right) + y\left( {h_{i} - h_{{P_{0} }} } \right)\ln \left( {x + \ell _{{P_{0} }}^{*} } \right)} \right. \\ & + xh_{{P_{0} }} \ln \left( {y + \ell _{{P_{0} 0}}^{*} } \right) + yh_{{P_{0} }} \ln \left( {x + \ell _{{P_{0} 0}}^{*} } \right) - \frac{{\left( {h_{i} - h_{{P_{0} }} } \right)^{2} }}{2}\arctan \frac{{xy}}{{\left( {h_{i} - h_{{P_{0} }} } \right)\ell _{{P_{0} }}^{*} }} - \frac{{h_{{P_{0} }}^{2} }}{2}\arctan \frac{{xy}}{{h_{{P_{0} }} \ell _{{P_{0} 0}}^{*} }} \\ & - \frac{{x^{2} }}{2}\arctan \frac{{y\left( {h_{i} - h_{{P_{0} }} } \right)}}{{x\ell _{{P_{0} }}^{*} }} - \frac{{x^{2} }}{2}\arctan \frac{{yh_{{P_{0} }} }}{{x\ell _{{P_{0} 0}}^{*} }} - \frac{{y^{2} }}{2}\arctan \frac{{x\left( {h_{i} - h_{{P_{0} }} } \right)}}{{y\ell _{{P_{0} }}^{*} }} - \frac{{y^{2} }}{2}\arctan \frac{{xh_{{P_{0} }} }}{{y\ell _{{P_{0} 0}}^{*} }} \\ & \left. {\left. {\left. { - h_{i} \left( {1 + \frac{{h_{i} }}{R} + \frac{{h_{i}^{2} }}{{3R^{2} }}} \right)\left[ {x\ln \left( {y + \ell _{{P_{0} 0}}^{*} } \right) + y\ln \left( {x + \ell _{{P_{0} 0}}^{*} } \right) - h_{{P_{0} }} \arctan \frac{{xy}}{{h_{{P_{0} }} \ell _{{P_{0} 0}}^{*} }}} \right]} \right\}} \right|_{{y_{i} }}^{{y_{{i + 1}} }} } \right|_{{x_{i} }}^{{x_{{i + 1}} }} \\ \end{aligned} $$

(25)

where the distances $\ell_{{{\text{P}}_{{0}} }}^{*}$ and $\ell_{{{\text{P}}_{{0}} {0}}}^{*}$ are defined by

$$ \ell_{{{\text{P}}_{{0}} }}^{*} = \sqrt {x^{2} + y^{2} + \left( {h_{i} - h_{{{\text{P}}_{{0}} }} } \right)^{2} } ,\quad \, \ell_{{{\text{P}}_{{0}} {0}}}^{*} = \sqrt {x^{2} + y^{2} + h_{{{\text{P}}_{{0}} }}^{2} } $$

(26)

where $h_{{{\text{P}}_{{0}} }}$ is equal to ${{\ell_{0}^{2} } \mathord{\left/ {\vphantom {{\ell_{0}^{2} } {2R}}} \right. \kern-0pt} {2R}}$.

Similar to the prism methods for the topographical effects produced by actual topographical masses (Nagy et al. 2000), the prism methods for the direct and indirect effects encounter singularities when the evaluation point coincides with the latitude or longitude lines that define the boundaries of the integration grid. In these specific scenarios, the integral methods for the topographical effects are nonsingular. Thus, the integral methods can be applied to calculate the direct and indirect topographical effects produced by grids whose boundaries align with the evaluation point's latitude or longitude.

The prism approach is an analytical form of the integral, whereas the tesseroid method based on Taylor series expansion is not analytical. With use of high resolution topographical data, the results computed by the prism and tesseroid methods differ very little. Since the tesseroid method boasts superior computation efficiency, the derivation of the tesseroid formulae for the direct and indirect topographical effects will be the further research topic.

5 Molodenskii spectral methods expanded to power H ⁴ for far-zone topographical effects

The far-zone topographical effects with use of Molodenskii spectral method (Molodenskii et al. 1962) are derived below based on the Taylor series expansions in Appendix C. According to Eq. (C.4), the far-zone direct effect expanded to the fourth power of height can be expressed as

$$ \begin{aligned} \delta A_{{{\text{far}}}} = & - \frac{G}{{r_{{{P}}} }}\iint\limits_{{\Omega_{0} - C_{0} }} {\rho \left( {h^{2} R_{2} + h^{3} R_{3} + h^{4} R_{4} } \right){\text{d}}\Omega } \\ & = - \frac{G}{{r_{{{P}}} }}\iint\limits_{{\Omega_{0} }} {\rho \left( {h^{2} \overline{R}_{2} + h^{3} \overline{R}_{3} + h^{4} \overline{R}_{4} } \right){\text{d}}\Omega } \\ \end{aligned} $$

(27)

where $\delta A_{{{\text{far}}}}$ is far-zone direct effect, $\Omega_{0} - C_{0}$ represents the far integral zone, and kernel functions $\overline{R}_{2}$, $\overline{R}_{3}$ and $\overline{R}_{4}$ are related to $R_{2}$, $R_{3}$ and $R_{4}$, whose specific expressions are given in Eq. (C.5), by

$$ \overline{R}_{k} = \left\{ {\begin{array}{*{20}c} {0,} & {0 < \psi \le \psi_{0} } \\ {R_{k} ,} & {\psi_{0} < \psi \le \pi } \\ \end{array} } \right.\quad k = 2,3,4 $$

(28)

where $\psi_{0}$ is the radius of the near-zone cap. The Legendre’s polynomials for discontinuous functions $\overline{R}_{k}$ ($k = 2,3,4$) are

$$ \overline{R}_{k} = \sum\limits_{n = 0}^{\infty } {\frac{2n + 1}{2}Q_{n}^{k} P_{n} \left( {\cos \psi } \right)} $$

(29)

where $Q_{n}^{k}$ is Molodenskii truncation coefficient of degree $n$ for kernel function $R_{k}$. $Q_{n}^{k}$ is computed by

$$ Q_{n}^{k} = \int\limits_{{\psi = \psi_{0} }}^{\pi } {R_{k} P_{n} \left( {\cos \psi } \right)\sin \psi d\psi } $$

(30)

As can be seen, $Q_{n}^{k}$ is related with the height of the computation point. The continuous integral for $Q_{n}^{k}$ are to be discretized in the process of computation (similarly hereinafter). Since Eq. (30) is a single integral, the discretization has a little influence on the computational efficiency. In addition, the integral domain of Eq. (30) is in the far distance from $\psi_{0}$ to $\pi$, so the discretization error introduced is very small. Substituting Eq. (29) into Eq. (27), together with Eqs. (12) and (A.3), gives the Molodenskii spectral algorithm for $\delta A_{{{\text{far}}}}$ as

$$ \begin{gathered} \delta A_{{{\text{far}}}} = - \frac{2\pi G}{{r_{P} }}\sum\limits_{n = 0}^{\infty } {\left[ {Q_{n}^{2} \sum\limits_{m = - n}^{n} {H_{nm}^{2} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} + Q_{n}^{3} \sum\limits_{m = - n}^{n} {H_{nm}^{3} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} } \right.} \hfill \\ \quad\quad\quad\left. { \, + Q_{n}^{4} \sum\limits_{m = - n}^{n} {H_{nm}^{4} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} } \right] \hfill \\ \end{gathered} $$

(31)

According to Eq. (C.7), the far-zone indirect effect on height anomaly expanded to H⁴ is written as

$$ \begin{aligned} \delta \zeta_{{{\text{far}}}} = &\, \frac{G}{\gamma }\iint\limits_{{\Omega_{0} - C_{0} }} {\rho \left( {h^{2} F_{2} + h^{3} F_{3} + h^{4} F_{4} } \right){{d}}\Omega } \\ = &\,\frac{G}{\gamma }\iint\limits_{{\Omega_{0} }} {\rho \left( {h^{2} \overline{F}_{2} + h^{3} \overline{F}_{3} + h^{4} \overline{F}_{4} } \right){{d}}\Omega } \\ \end{aligned} $$

(32)

where $\delta \zeta_{{{\text{far}}}}$ is far-zone indirect effect on height anomaly, and kernel functions $\overline{F}_{2}$, $\overline{F}_{3}$ and $\overline{F}_{4}$ are related to $F_{2}$, $F_{3}$ and $F_{4}$, whose specific formulae are shown in Eq. (C.8), by

$$ \overline{F}_{k} = \left\{ {\begin{array}{*{20}c} {0,} & {0 < \psi \le \psi_{0} } \\ {F_{k} ,} & {\psi_{0} < \psi \le \pi } \\ \end{array} } \right.\quad k = 2,3,4 $$

(33)

The Legendre’s polynomials for discontinuous functions $\overline{F}_{k}$ ($k = 2,3,4$) are

$$ \overline{F}_{k} = \sum\limits_{n = 0}^{\infty } {\frac{2n + 1}{2}X_{n}^{k} P_{n} \left( {\cos \psi } \right)} $$

(34)

where $X_{n}^{k}$, which is computed by the following formula, is Molodenskii truncation coefficient of degree $n$ for kernel function $F_{k}$

$$ X_{n}^{k} = \int\limits_{{\psi = \psi_{0} }}^{\pi } {F_{k} P_{n} \left( {\cos \psi } \right)\sin \psi {\text{d}}\psi } $$

(35)

Analogously, substituting Eq. (34) into Eq. (32),along with Eqs. (12) and (A.3), yields the Molodenskii spectral algorithm for $\delta \zeta_{{{\text{far}}}}$expanded to power H⁴ as

$$ \begin{aligned} \delta \zeta_{{{\text{far}}}} =&\, \frac{2\pi G}{\gamma }\sum\limits_{n =0}^{\infty } \left[ X_{n}^{2}\sum\limits_{m = - n}^{n} {H_{nm}^{2}\overline{Y}_{nm} \left( {\Omega_{P} } \right)}\right.\\&\left. + X_{n}^{3}\sum\limits_{m = - n}^{n} {H_{nm}^{3} \overline{Y}_{nm} \left({\Omega_{{\text{P}}} } \right)}+ X_{n}^{4} \sum\limits_{m = - n}^{n}{H_{nm}^{4} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} \right]\end{aligned} $$

(36)

Similarly, the Molodenskii spectral algorithm for the far-zone indirect effect on geoidal height expanded to term H⁴is

$$\begin{aligned} \delta N_{{{\text{far}}}} =\,\,& \frac{2\pi G}{{\gamma_{0} }}\sum\limits_{n = 0}^{\infty } \left[ Z_{n}^{2}\sum\limits_{m = - n}^{n} {H_{nm}^{2} \overline{Y}_{nm} \left({\Omega_{{\text{P}}} } \right)} \right.\\&\left.+\,\, Z_{n}^{3} \sum\limits_{m = -n}^{n} {H_{nm}^{3} \overline{Y}_{nm} \left( {\Omega_{P} } \right)} +Z_{n}^{4} \sum\limits_{m = - n}^{n} {H_{nm}^{4} \overline{Y}_{nm}\left( {\Omega_{{\text{P}}} } \right)} \right]\end{aligned}$$

(37)

where $\delta N_{{{\text{far}}}}$ is far-zone indirect effect on geoidal height, and $Z_{n}^{k}$is the Molodenskii truncation coefficient of degree $n$related to kernel function $T_{{\text{k}}}$,which are expressed in Appendix (C.12), by

$$ Z_{n}^{k} = \int\limits_{{\psi = \psi_{0}}}^{\pi } {T_{k} P_{n} \left( {\cos \psi } \right)\sin \psi {{d}}\psi } $$

(38)

The derivation method based on binomial series for far-zone topographical effects, used by Novak et al. (2001) and Makhloof et al. (2008), is somewhat complex. By comparison, the method based on Legendre series expansion in this paper significantly simplifies the derivation process. In terms of the truncated height power, the far-zone effects were expanded to power H² by Novak et al. (2001) and Makhloof et al. (2008), while the effects are further expanded to power H⁴ in this paper. In a word, the study not only reduces complexity but also extends the term of Taylor series expansions.

6 Combined algorithms for high-frequency topographical effects

The accurate assessment of direct and indirect topographical effects is crucial in the determination of the geoid and quasi-geoid based on the Stokes-Helmert or Hotine-Helmert boundary-value theory. The formulae for the Stokes-Helmert boundary-value problem are

$$ \begin{gathered} \zeta = \frac{R}{4\pi \gamma }\iint\limits_{{\Omega_{0} }} {\left( {\Delta g + \delta A + \delta S} \right)^{*} S\left( {r_{P} ,\psi } \right){{d}}\Omega } + \delta \zeta \hfill \\ N = \frac{R}{{4\pi \gamma_{0} }}\iint\limits_{{\Omega_{0} }} {\left( {\Delta g + \delta A + \delta S} \right)^{*} S\left( \psi \right){{d}}\Omega } + \delta N \hfill \\ \end{gathered} $$

(39)

where $\zeta$ is height anomaly (the distance between the quasi-geoid and reference ellipsoid surface), $N$ is geoidal height (the distance between the geoid and reference ellipsoid surface), $\Delta g$ is measured gravity anomaly on the ground, $\Omega_{0}$ is global integration domain, $S\left( {r_{{{P}}} ,\psi } \right)$ is extended Stokes kernel function, $S\left( \psi \right)$ is non-extended Stokes kernel function, and $^{*}$ represents the downward continuation process of converting the ground gravity value into the corresponding gravity value on the boundary surface. Nowadays, the orthometric height data, such as SRTM data (Jarvis et al. 2008), is widely used in the determination of the (quasi-) geoid. The ground gravity anomaly $\Delta g$ is usually obtained by subtracting the normal gravity calculated using the orthometric height of the ground point from the absolute gravity value of the ground point.

The Hotine/Stokes integral requires global integration in theory. Due to the difficulty in obtaining global gravity data and time-consuming computation involved with global integration, the RCR technique is widely adopted in the Hotine/Stokes integral. The Stokes-Helmert integral in the RCR scheme is formulated as

$$ \begin{aligned} \zeta = &\frac{R}{4\pi \gamma }\iint\limits_{{C_{1} }} \left( {\Delta g - \Delta g_{M} + \delta A^{{{\text{high}}}} + \delta S^{{{\text{high}}}} } \right)^{*}\\& \,S\left( {r_{P} ,\psi } \right)d\Omega + \delta \zeta^{{{\text{high}}}} + \zeta_{M} \hfill \\ N = &\frac{R}{{4\pi \gamma_{0} }}\iint\limits_{{C_{1} }} \left( {\Delta g - \Delta g_{M} +\delta A^{{{\text{high}}}} + \delta S^{{{\text{high}}}} }\right)^{*} \\&\, S\left( \psi \right)d\Omega + \delta N^{{{\text{high}}}} + N_{M} \hfill \\ \end{aligned}$$

(40)

where $C_{1}$denotes near-zone integration domain, $\Delta g_{M}$ represents ground model gravity anomaly, $\delta A^{{{\text{high}}}}$ is high-frequency direct effect, $\delta S^{{{\text{high}}}}$ is high-frequency secondary indirect effect, $\delta \zeta^{{{\text{high}}}}$ is high-frequency indirect effect on height anomaly, $\delta N^{{{\text{high}}}}$ is high-frequency indirect effect on geoidal height, $\zeta_{M}$is model height anomaly, and $N_{M}$is model geoidal height. $\Delta g_{M}$, $\zeta_{M}$and $N_{M}$are calculated with the use of the Earth gravitational model truncated to degree $L$(cf. Rapp 1997). The difference of the measured gravity anomaly and the model gravity anomaly $\Delta g - \Delta g_{M}$, i.e. the high-frequency gravity anomaly, contains errors originating from the two kinds of gravity data. The errors of $\Delta g -\Delta g_{M}$ propagated into the (quasi-) geoid can be reduced effectively by adding an appropriate spectral weight to the Stokes’ kernel (cf. Jiang and Wang 2016; Huang and Véronneau 2013).

The Hotine-Helmert integral in application of the RCR technique is written as

$$ \begin{aligned} \zeta = \;&\frac{R}{\,4\pi \gamma }\iint\limits_{{C_{1} }} {\left( {\delta g - \delta g_{M} + \delta A^{{{\text{high}}}} } \right)^{*} H\left( {r_{P} ,\psi }\right){{d}}\Omega } \\&+ \delta \zeta^{{{\text{high}}}} +\zeta_{M} \hfill \\ N =\;& \frac{R}{{\,4\pi \gamma_{0} }}\iint\limits_{{C_{1} }}{\left( {\delta g - \delta g_{M} + \delta A^{{{\text{high}}}} }\right)^{*} H\left( \psi \right){{d}}\Omega } \\ &+ \delta N^{{{\text{high}}}} + N_{M} \hfill \\ \end{aligned}$$

(41)

where $\delta g$ is ground gravity disturbance, $H(r_P,\psi)$ is extended Hotine kernel function, $H (\psi)$ is non-extended Hotine kernel function, and $\delta g_{M}$ is model gravity disturbance on the ground computed using the Earth gravitational model truncated to degree $L$.

The high-frequency topographical effects in Eqs. (40) and (41) can be calculated by a combined method of subtracting the low-frequency topographical effects from full-frequency effects. That is,

$$ \begin{gathered} \delta A^{{{\text{high}}}} = \delta A^{{{\text{full}}}} - \delta A^{{{\text{low}}}} \hfill \\ \delta S^{{{\text{high}}}} = \delta S^{{{\text{full}}}} - \delta S^{{{\text{low}}}} \hfill \\ \delta \zeta^{{{\text{high}}}} = \delta \zeta^{{{\text{full}}}} - \delta \zeta^{{{\text{low}}}} \hfill \\ \delta N^{{{\text{high}}}} = \delta N^{{{\text{full}}}} - \delta N^{{{\text{low}}}} \hfill \\ \end{gathered} $$

(42)

where $\delta A^{{{\text{full}}}}$ and $\delta A^{{{\text{low}}}}$ are full- and low-frequency direct effects, $\delta S^{{{\text{full}}}}$ and $\delta S^{{{\text{low}}}}$ are full- and low-frequency secondary indirect effects, $\delta \zeta^{{{\text{full}}}}$ and $\delta \zeta^{{{\text{low}}}}$ are full- and low-frequency indirect effects on height anomaly, $\delta N^{{{\text{full}}}}$ and $\delta N^{{{\text{low}}}}$ are full- and low-frequency indirect effects on geoidal height, respectively.

The spherical harmonic methods and far-zone Molodenskii spectral methods for topographical effects have the advantages of computational simplicity and fast processing speed. The height-related spherical harmonic coefficients applied by these two methods can be exploited repeatedly once computed. According to Nyquist sampling theorem, the frequency band of the grid data is related to the grid resolution. The higher the resolution of grid data, the greater the truncation degree of the computed spherical harmonic coefficients. Computation of spherical harmonic coefficients with high truncation degree requires computer’s fast processing power and great storage capacity. Thus, the spherical harmonic methods and far-zone Molodenskii methods are particularly well-suited for the calculation of low-frequency topographical effects. In view of this, the low-frequency topographical effects in Eq. (42) is calculated by the spherical harmonic methods specifically, i.e.,

$$ \begin{aligned} \delta A^{{{\text{low}}}} &= - \frac{2\pi G}{{r_{P} }}\sum\limits_{n = 0}^{L} {\left( {n + 1} \right)\left( {\frac{R}{{r_{P} }}} \right)^{n + 1} } \sum\limits_{m = - n}^{n} {\delta V_{nm}^{e} } \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right) \\ \delta S^{{{\text{low}}}} &= \frac{4\pi G}{{r_{P} }}\sum\limits_{n = 0}^{L} {\left( {\frac{R}{{r_{P} }}} \right)^{n + 1} } \sum\limits_{m = - n}^{n} {\delta V_{nm}^{e} } \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right) \\ \delta \zeta^{{{\text{low}}}} &= \frac{2\pi G}{\gamma }\sum\limits_{n = 0}^{L} {\left( {\frac{R}{{r_{P} }}} \right)^{n + 1} } \sum\limits_{m = - n}^{n} {\delta V_{nm}^{e} } \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right) \\ \delta N^{{{\text{low}}}} &= \frac{2\pi G}{{\gamma_{0} }}\sum\limits_{n = 0}^{L} {\sum\limits_{m = - n}^{n} {\delta V_{nm}^{i} } \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} \end{aligned} $$

(43)

where $L$ is the truncation degree of the spherical harmonic coefficients, which equals to the truncation degree of gravitational model.

The full-frequency topographical effects in Eq. (42) contain high-frequency and low-frequency information. Theoretically, both high-frequency and low-frequency topographical effects ought to contain global information. Considering the far-zone high-frequency information is minimal and negligible, the full-frequency topographical effects can be approximated as the sum of near-zone full-frequency effects and far-zone low-frequency effects, i.e.,

$$ \begin{gathered} \delta A^{{{\text{full}}}} \approx \delta A_{{{\text{near}}}}^{{{\text{full}}}} + \delta A_{{{\text{far}}}}^{{{\text{low}}}} \hfill \\ \delta S^{{{\text{full}}}} \approx \delta S_{{{\text{near}}}}^{{{\text{full}}}} + \delta S_{{{\text{far}}}}^{{{\text{low}}}} \hfill \\ \delta \zeta^{{{\text{full}}}} \approx \delta \zeta_{{{\text{near}}}}^{{{\text{full}}}} + \delta \zeta_{{{\text{far}}}}^{{{\text{low}}}} \hfill \\ \delta N^{{{\text{full}}}} \approx \delta N_{{{\text{near}}}}^{{{\text{full}}}} + \delta N_{{{\text{far}}}}^{{{\text{low}}}} \hfill \\ \end{gathered} $$

(44)

where $\delta A_{{{\text{near}}}}^{{{\text{full}}}}$ and $\delta S_{{{\text{near}}}}^{{{\text{full}}}}$ are near-zone full-frequency direct effect and secondary indirect effect, $\delta \zeta_{{{\text{near}}}}^{{{\text{full}}}}$ and $\delta N_{{{\text{near}}}}^{{{\text{full}}}}$ are near-zone full-frequency indirect effects on height anomaly and on geoidal height, $\delta A_{{{\text{far}}}}^{{{\text{low}}}}$ and $\delta S_{{{\text{far}}}}^{{{\text{low}}}}$ are far-zone low-frequency direct effect and secondary indirect effect, $\delta \zeta_{{{\text{far}}}}^{{{\text{low}}}}$ and $\delta N_{{{\text{far}}}}^{{{\text{low}}}}$ are far-zone low-frequency indirect effects on height anomaly and geoidal height, respectively.

Surface integral methods offer a versatile approach to calculating topographical effects, whether near-zone,far-zone, or global. The scope of these calculations can be readily adjusted by defining the integration domain to match the region of interest. However, when it comes to the computational efficiency of far-zone topographical effects, the Molodenskii spectral method holds a distinct advantage over traditional integral methods. Thus, the Molodenskii spectral method is chosen to calculate the far-zone low-frequency topographical effects for our combined algorithms, i.e.,

$$ \begin{aligned} \delta A_{{{\text{far}}}}^{{{\text{low}}}} =& - \frac{2\pi G}{{r_{P}}}\sum\limits_{n = 0}^{L} \left[ Q_{n}^{2} \sum\limits_{m = -n}^{n} {H_{nm}^{2} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} }\right)} \right.\\ &\left.+ Q_{n}^{3} \sum\limits_{m = - n}^{n} {H_{nm}^{3}\overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} + Q_{n}^{4}\sum\limits_{m = - n}^{n} {H_{nm}^{4} \overline{Y}_{nm} \left({\Omega_{{\text{P}}} } \right)} \right] \hfill \\ \delta S_{{{\text{far}}}}^{{{\text{low}}}} =& \frac{4\pi G}{{r_{P}}}\sum\limits_{n = 0}^{L} \left[ X_{n}^{2} \sum\limits_{m = -n}^{n} {H_{nm}^{2} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} }\right)} \right.\\ &\left.+ X_{n}^{3} \sum\limits_{m = - n}^{n} {H_{nm}^{3}\overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} + X_{n}^{4}\sum\limits_{m = - n}^{n} {H_{nm}^{4} \overline{Y}_{nm} \left({\Omega_{{\text{P}}} } \right)} \right] \hfill \\ \delta \zeta_{{{\text{far}}}}^{{{\text{low}}}} =& \frac{2\pi G}{\gamma }\sum\limits_{n = 0}^{L} \left[ X_{n}^{2} \sum\limits_{m = -n}^{n} {H_{nm}^{2} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} }\right)}\right.\\ & \left.+ X_{n}^{3} \sum\limits_{m = - n}^{n} {H_{nm}^{3}\overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} + X_{n}^{4}\sum\limits_{m = - n}^{n} {H_{nm}^{4} \overline{Y}_{nm} \left({\Omega_{{\text{P}}} } \right)} \right] \hfill \\ \delta N_{{{\text{far}}}}^{{{\text{low}}}} =& \frac{2\pi G}{{\gamma_{0}}}\sum\limits_{n = 0}^{L} {\left[ {Z_{n}^{2} \sum\limits_{m = -n}^{n} {H_{nm}^{2} \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} }\right)} } \right.}\\&+ Z_{n}^{3} \sum\limits_{m = - n}^{n} {H_{nm}^{3}\overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} \\&\left. { + Z_{n}^{4} \sum\limits_{m = - n}^{n} {H_{nm}^{4}\overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)} } \right]\hfill \\ \end{aligned} $$

(45)

The near-zone full-frequency topographical effects can be computed by either integral methods or prism methods with use of near-zone high-resolution terrain data. As is stated above, the prism methods can reduce effectively the discretization effects of the surface integral. Therefore, the prism methods for the near-zone full-frequency effects are utilized in the combined algorithms.

In summary, the combined algorithms of high-frequency topographical effects in the Hotine-Helmert/Stokes-Helmert integral using the RCR technique are as follows. First, the prism methods, the Molodenskii spectral methods and the spherical harmonic methods are used to calculate near-zone full-frequency topographical effects, far-zone low-frequency effects and global low-frequency effects, respectively. Subsequently the high-frequency topographical effects are obtained by subtracting the global low-frequency topographical effects from the sum of the near-zone full-frequency effects and far-zone low-frequency effects. For the sake of brevity, the combined algorithms for high-frequency topographical effects can be denoted by “prism + Molodenskii spectral-spherical harmonic” algorithms. Given the small magnitude of the near-zone ellipsoidal correction, it is deemed unnecessary to calculate the ellipsoidal correction for the high-frequency topographical effects.

7 Numerical investigation

As is known, the absolute magnitudes of topographical effects are typically pronounced at elevated altitudes and comparatively minor in flat plains. A mountainous area, delimited by longitudes 103° E and 106° E and latitudes 32° N and 35° N, is chosen as the test area in this article. The height data used for the numerical investigation is SRTM data. The terrain undulation of the test area is shown in Fig. 2.

Fig. 2

the topographical map of test area

The terrain in the test area fluctuates from 490.64 to 4761.69 m with an average of 2348.13 m and an RMS of 2527.08 m in 2′-grid resolution. The SRTM height data limited by longitudes 101°E and 108°E and latitudes 30° N and 37 °N with the resolutions of 3′′ × 3′′ and 2′ × 2′ are prepared for testing the methods for near-zone topographical effects. Besides, the global SRTM data in 5′-grid and 30′-grid resolutions are prepared for testing the methods of far-zone and global topographical effects.

7.1 Near-zone topographical effects: surface integrals versus prism methods

Both the surface integral methods and the prism methods are used to calculate the near-zone topographical effects, including direct effect, secondary indirect effect, indirect effect on height anomaly and indirect effect on geoidal height. The prism methods considering the Earth’s curvature are used in the test to circumvent the planar approximation errors. Since the integral formulae are singular in the innermost grid, the innermost topographical effects are always calculated by the prism methods in the test. As stated above, the prism methods are singular when the evaluation point is located on the latitude or longitude lines defining the boundaries of the integration grid. For the several near-zone grids where the prism methods encounter singularity, the topographical effects are calculated by the integral methods instead in the test. Table 1 gives the statistics for 2′-grid near-zone topographical effects within the range of 1° calculated by 3′′ × 3′′ and 2′ × 2′ height data, respectively.

Table 1 Near-zone topographical effects within the range of 1°

As is shown in Table 1, the near-zone direct effects are notably large in magnitude. There are obvious differences in the near-zone direct effects by 3′′-grid and 2′-grid data. The spectral discrepancies between height data in the two resolutions are predominantly in high-frequency band, implying that direct effects have high-frequency dominant spectral characteristics. Compared with the direct effects, the near-zone secondary indirect effects are minimal. The computation point $P$ for the indirect effect on height anomaly is situated on the ground, while the computation point $P_{0}$ for the indirect effect on geoidal height is located on the geoid. During the process of mass condensation, topographical masses recede from $P$ while approaching $P_{0}$, resulting in the two indirect effects exhibiting opposite signs in Table 1. According to Table 1, the near-zone indirect effects by 3′′-grid and 2′-grid data differ slightly, which indicates the indirect effects contain a small quantity of high-frequency information. Figure 3 depicts the geographical distributions of the near-zone topographical effects calculated by height data in 3′′-grid resolution.

Fig. 3

Distribution of near-zone topographical effects

The results in Table 1 are the near-zone topographical effects calculated by height data within the range of 1°. To illustrate the variation of the near-zone topographical effects with range, the topographical effects induced by the topography within the range between 1° and 2° are shown in Table 2.

Table 2 Near-zone topographical effects within the range from 1° to 2°

According to Eq. (2), the topographical effects are functions of the residual topographical potential, whose integration kernel is positively correlated with the reciprocal of the distance between the computation point and the integration point. The reciprocal distance decreases rapidly as the distance between the two points increases. Thus, the topographical effects induced by elevation data within the range of 1° to 2° are small in magnitude as shown in Table 2. The boundary for defining the near and far ranges of topographical effects is set at 1° in the following test. Table 1 shows that the differences of near-zone topographical effects calculated by 3′′-grid data with use of the two methods are relatively small, whereas the discrepancies between the methods become more pronounced for 2″-grid data. Table 3 details statistics for the differences of the near-zone topographical effects by integral methods and those by prism methods.

Table 3 Differences of near-zone topographical effects by integral and prism methods

The discrepancies between the topographical effects computed by the integral and prism methods can serve as an approximation of the discretization effects associated with the integral methods. Table 3 reveals that the discretization errors of the integral formulae are tiny for the near-zone topographical effects calculated with use of 3′′ × 3′′ data. The RMS values of the differences of the near-zone topographical effects in 2′-grid resolution by the two methods are 6.27 mGal for direct effect, 0.004mGal for secondary indirect effect, 1.32 cm for indirect effect on height anomaly, and 2.91 cm for indirect effect on geoidal height in the test area, implying the effects of discretization should not be ignored for 2′ × 2′ height data. It can be concluded by Table 3 that either the integral or the prism methods are viable for calculating the near-zone topographical effects when using high-resolution data. However, when the resolution of near-zone height data is moderate or low, the prism methods are preferable in consideration of the effects of the discretization.

7.2 Far-zone topographical effects: surface integrals versus Molodenskii spectral methods

In order to apply the Molodenskii spectral methods and subsequent spherical harmonic methods, the height-related spherical harmonic coefficients (i.e., $H_{nm}^{2}$, $H_{nm}^{3}$ and $H_{nm}^{4}$) are precomputed. 2160-degree spherical harmonic coefficients can be computed using grid data in 5′ × 5′ or higher resolution,while the computation of 360-degree spherical harmonic coefficients requires grid data in 30′ × 30′ or higher resolution. To facilitate the comparison of the methods based on the spherical harmonic coefficients and the methods using the grid data, the height-related spherical harmonic coefficients truncated to degrees 360 and 2160 are computed according to Eq. (24) using the global height data in 30′-grid and 5′-grid resolutions in this paper, respectively. During the calculation process, the density of the land masses is consistently set as the mean topographical density constant (i.e., 2.67 g/cm³). Besides, the column-wise recurrence formula (Xing et al. 2020) is used to compute the fully normalized associated Legendre functions so as to avoid overflow problem. The far zone in our numerical investigation represents the remaining area of the global scale removing the near zone of 1°. The far-zone topographical effects generated by 5′-grid and 30′-grid data are calculated by the integral and the Molodenskii spectral methods expanded to power H⁴, respectively. The statistics for the far-zone effects are shown in Table 4.

Table 4 Far-zone topographical effects

In accordance with Nyquist theorem, the far-zone topographical effects induced by 30′-grid and 5′-grid data contain frequency information up to spherical harmonic degrees of 360 and 2160, respectively. The far-zone topographical effects calculated by 5′-grid data using the Molodenskii spectral methods vary from 1.40 to 4.30 mGal for direct effects, from -1.89 × 10⁻² mGal to − 1.64 × 10⁻² mGal for secondary indirect effects, from − 6.15 to − 5.34 cm for indirect effects on height anomalies, and from − 7.29 to − 5.74cm for indirect effects on geoidal heights. Figure 4 plots the distributions of far-zone effects by 5′-grid data using the Molodenskii spectral methods.

Fig. 4

Far-zone topographical effects by 5'-grid data using Molodenskii spectral methods

The gentle fluctuations of far-zone topographical effects shown in Fig. 4 are indicative of their low-frequency dominant spectral characteristics. Table 4 reveals that the integral and Molodenskii methods have a high degree of consistency in calculating the far-zone topographical effects. Table 5 gives statistics of the differences of the far-zone topographical effects by Molodenskii spectral methods expanded to term H⁴ and integral methods.

Table 5 Differences of far-zone topographical effects by Molodenskii and integral methods

Since the absolute values of integration kernels of the integral formulae in the far area are tiny and decrease very slowly with the increase of angular distance $\psi$, the far-zone discretization effects of the integral formulae are negligible. As shown in Table 5, the far-zone topographical effects by Molodenskii spectral methods expanded to term H⁴ and integral methods differ slightly, proving the effectiveness of the Molodenskii methods expanded to term H⁴ presented in this paper.

In order to illustrate the variation of the far-zone effects with the radius of the near-zone cap, the far-zone effects in the frequency bands of degrees 0–2160, 0–360, and 361–2160 with use of various integration radii are plotted in Fig. 5. The Molodenskii spectral method expanded to power H⁴ is used and the highest location (103.85°E and 32.65°N with the height of 4761.69m) of study region is chosen as the test point for Fig. 5. Due to the small magnitude of the secondary indirect effect and its variation resembling that of the indirect effect on height anomaly, the variation of far-zone secondary indirect effect with the near-zone integration radius is not plotted in Fig. 5.

Fig. 5

Variation of far-zone topographical effects with the radius of near-zone cap

As shown in Fig. 5, the far-zone topographical effects in the frequency band of 0–2160 are tightly close to those in the frequency band of 0–360. The far-zone effects in the frequency band from degree 361 to degree 2160 approaches 0, implying that the far-zone high-frequency effects are small. When it comes to the combined algorithms presented in this paper, the far-zone truncation errors only exist in the highfrequency band and are thus minimal.

7.3 Global topographical effects: surface integrals, ‘prism + Molodenskii’ algorithms versus spherical harmonic methods

The traditional far-zone and global topographical effects are expanded to power H² or H³, while the effects are expanded to power H⁴ in this paper. Truncating the residual topographical potentials expanded to power H⁴ in Eq. (11) to terms H² and H³ yields the residual topographical potentials expanded to power H² and H³, respectively. The differences between the global topographical effects calculated by the spherical harmonic methods with Taylor series expansion (Eqs. (10) and (11)) and the spherical harmonic methods without Taylor series expansion (Eqs. (10), (A.5) and (A.10)) reflect Taylor truncation errors. Prior to applying the spherical harmonic methods without Taylor series expansion, the spherical harmonic coefficients for residual topographical potentials (i.e. $\delta V_{nm}^{e}$ and $\delta V_{nm}^{i}$) truncated to degrees 360 and 2160 are calculated according to Eqs. (A.5) and (A.10) through a process analogous to that used for $H_{nm}^{k}$. Tables 6 and 7 show the Taylor truncation errors of the 2160- and 360-degree global topographical effects in the test area, respectively.

Table 6 Taylor truncation errors of 2160-degree global topographical effects

Table 7 Taylor truncation errors of 360-degree global topographical effects

For 2160-degree global topographical effects, the accuracies Taylor-expanded to power H³ and H⁴ are close, which are one order of magnitude higher than the accuracies Taylor-expanded to power H², according to Table 6. As the power number $k$ increases, the global height data of power $k$ undulate more violently and the errors of its spherical harmonic coefficients get greater. The results indicate the third- or fourth-order Taylor expansion is suitable for global topographical effects truncated to degree 2160. For 360-degree global topographical effects, the accuracies Taylor-expanded to power H³ are sufficiently high and the accuracies expanded to power H⁴ significantly exceed the accuracy requirements of boundary-value solution, according to Table 7. It can thus be concluded that the third-, fourth-order Taylor expansions and non-Taylor expansion forms are all applicable for the global topographical effects in the boundary-value problem. In the following tests, the spherical harmonic methods Taylor-expanded to power H⁴ (i.e. Equations (10) and (11)) are applied to calculated the global topographical effects, which is consistent with the methods for the far-zone topographical effects.

The global topographical effects can be calculated either by spherical harmonic methods or by adding the near- and far-zone topographical effects together. Our tests have demonstrated that the discrepancies between the far-zone topographical effects calculated by the integrals and Molodenskii methods are negligible. In view of the above-mentioned facts, only integral methods, “prism + Molodenskii” algorithms (i.e., the prism methods for near-zone effects and Molodenskii spectral methods for far-zone effects) and spherical harmonic methods are tested for the global topographical effects. Table 8 shows statistics for global topographical effects induced by the condensation of 5′-grid and 30′-grid topography using the three algorithms, respectively.

Table 8 Global topographical effects

Likewise, the topographical effects calculated using the global data in 5′ and 30′ resolutions encompass global frequency information up to degrees 2160 and 360, respectively. The three algorithms used in Table 8 exhibit relatively high consistency in calculating global topographical effects, indicating that the three algorithms are all effective. In terms of computational efficiency, the spherical harmonic method outperforms the others, with the integral method being the least efficient. For instance, computing the direct effects in 5′ resolution consumed 1433.81 s, 768.92 s and 652.64 s for the integral, “prism + Molodenskii” and spherical harmonic methods, respectively. Thus, the spherical harmonic methods are superior for the low-frequency topographical effects. Figure 6 is the distribution map of the global topographical effects calculated by the spherical harmonic methods truncated to degree 2160.

Fig. 6

Global topographical effects by spherical harmonic methods truncated to degree 2160

The different error sources of the three algorithms result in the differences in the obtained topographical effects. To provide a detailed comparison of the global topographical effects calculated by the three algorithms, Table 9 gives the statistics for the differences of the global topographical effects calculated by the integrals, “prism + Molodenskii” algorithms and the effects by spherical harmonic methods, respectively.

Table 9 Differences of global topographical effects by integral, “prism + Molodenskii” and effects by spherical harmonic methods

Table 9 shows that the “prism + Molodenskii” methods have higher levels of consistency with spherical harmonic methods than integral methods in calculating the global topographical effects using 5′-grid data. In terms of global direct effects calculated using 30′-grid data, the “prism + Molodenskii” algorithm is more consistent with spherical harmonic method than the integral method. However, the integral methods exhibit slightly better consistency for global indirect effects using 30′-grid data. Since direct effect has the spectral characteristics of a small amount of low-frequency information and a significant amount of high-frequency information, the inconsistency of direct effects in the low-frequency band has very little influence on the calculation of high-frequency direct effect. According to the above analysis, the global topographical effects calculated by “prism + Molodenskii” algorithms are more consistent with those obtained by the spherical harmonic methods than those calculated by the integral methods on the whole.

7.4 High-frequency topographical effects: "prism + Molodenskii spectral-spherical harmonic" combined algorithms

The test on “prism + Molodenskii spectralspherical harmonic” combined algorithms for high-frequency topographical effects is conducted following the above numerical experiments and analysis. SRTM data in 3′′ × 3′′ resolution are utilized for the prism computation of the combined algorithms.The height-related spherical harmonic coefficients truncated to degrees 360 and 2160 are both used for the Molodenskii spectral computation and spherical harmonic computation of the combined algorithms. In consequence, the frequency bands in the computed high-frequency topographical effects are degrees from 361 to 216,000 and from 2161 to 216,000, respectively. Table 10 is a statistic for the high-frequency topographical effects in 2′ × 2′ resolution by our combined algorithms.

Table 10 High-frequency topographical effects

Table 10 reveals that the cutoff degree of spherical harmonic coefficients has a relatively small impact on the range of high-frequency direct effects, whereas its influence on the range of high-frequency indirect effects are great. The truncation degree of the height-related spherical harmonic coefficients should be set equal to the cutoff degree of the reference gravity field in solving the boundary-value problems using the Helmert’s 2nd condensation method in the RCR scheme. Besides, the high-frequency secondary indirect effects are quite small and thus the term of secondary indirect effects can be ignored in the determination of the (quasi-) geoid by the Stokes-Helmert method in the RCR scheme. Figure 7 depicts the geographical distribution of high-frequency topographical effects with the frequency domain of degrees 2161–21,6000.

Fig. 7

High-frequency topographical effects with the frequency domain from degree 2161–216,000

In order to reflect the variation of high-frequency topographical effects with low truncation degree, the high-frequency effects at the highest point in the test area with use of various low truncation degrees are plotted in Fig. 8. The variation of high-frequency secondary indirect effect with low truncation degree is also not plotted below for the same reason as Fig. 5.

Fig. 8

Variation of high-frequency topographical effects with low truncation degree

Figure 8 demonstrates that the low truncation degree has a marked impact on the magnitude of high-frequency topographical effects. At the highest point of the test area, the absolute values of all the high-frequency topographical effects decrease as the low truncation degree rises.

7.5 The determination of the quasi-geoid based on Stokes–Helmert boundary value theory

In order to investigate the effectiveness of the high-frequency topographical effects in determining the (quasi-) geoid in application of the RCR technique, a test based on the Stokes-Helmert boundary value theory is conducted in this section. Since the height system used in the test area is the normal height system, the quasi-geoid rather than the geoid is solved for the test. The area is delimited by longitudes 106.5°E and 115.5°E and latitudes 26.5°N and 33.5°N.The SRTM height data in 2′-grid resolution change from 12.92m to 2721.95m with an average of 506.34m and an RMS of 672.85m for the area. The measured gravity anomalies in 2′ grid vary from − 129.48 to 175.16 mGal with an average of− 25.50 mGal and an RMS of 38.39 mGal. The reference gravitational model is EIGEN-6C4 model (Förste et al. 2016) truncated to degrees 360 and 2160, respectively. The 360-degree model gravity anomalies fluctuate from − 88.64 to 73.16 mGal with an average of − 18.09 mGal and an RMS of 27.49 mGal. The 2160-degree model gravity anomalies range from -106.14mGal to 156.41mGal with an average of -18.48mGal and an RMS of 32.77mGal. The secondary indirect effect is ignored due to its small magnitude. The region of the direct effect is the same as that of the gravity data. Table 11 shows the statistics for near-zone direct effects, global low-frequency direct effects, far-zone direct effects and high-frequency direct effects, respectively. The near-zone direct effects are calculated with the use of 3′′-grid SRTM data. For both the global low-frequency direct effects and the far-zone direct effects, the truncation degree of the height-related spherical harmonic coefficients (i.e. $L$) is set to 360 and 2160, respectively.

Table 11 Direct effects (unit: mGal)

As shown in Table 11, the amplitude of the global direct effects in the frequency band of 0–2160 is significantly greater than that in the frequency band of 0–360. The far-zone direct effects in the frequency band of 0–2160 are small in magnitude and close to those in the frequency band of 0–360. Table 12 presents the statistics for different kinds of indirect effects on height anomaly when $L$ is set to 360 and 2160, respectively. The region of the indirect effect is the same as that of the quasi-geoid, specifically bounded by longitudes 108.5°E and 113.5°E and latitudes 28.5°N and 31.5°N. Similarly, the SRTM data in 3′′-grid resolution is used to calculate the near-zone indirect effects.

Table 12 Indirect effects on height anomaly (unit: m)

According to Table 12, the global indirect effects in the frequency band of 0–2160 are somewhat close to those in the frequency band of 0–360. The differences of the far-zone indirect effects in the two frequency bands are tiny. The topographical effects obtained above are used to calculate the quasi-geoid in the test area according to Eq. (40). To begin with, the high-frequency gravity anomalies are computed by subtracting the model gravity anomalies from the measured values. The ground Helmert high-frequency gravity anomalies are then obtained by adding the high-frequency gravity anomalies and high-frequency direct effects together. The ground Helmert high-frequency gravity anomalies are converted to the boundary Helmert high-frequency gravity anomalies through the process of downward continuation. The Helmert high-frequency height anomalies are then obtained by performing the extended Stokes integral on the boundary Helmert high-frequency gravity anomalies. Low-degree cosine modified Stokes’ kernel (cf. Huang and Véronneau 2013) is adopted in the test. The radius of the near-zone cap of the integral for downward continuation is set to 1°, so is that of the extended Stokes integral. The model height anomalies are computed using the EIGEN-6C4 model subsequently. The 360-degree model height anomalies fluctuate from − 32.96 m to − 14.31 m with an average of − 22.38 m and an RMS of 22.68 m. The 2160-degree model height anomalies range from − 32.86 m to − 14.34 m with an average and RMS that match those of the 360-degree model values. The sum of the Helmert high-frequency height anomalies, the model height anomalies, and the high-frequency indirect effects on height anomaly results in the gravimetric quasi-geoid.

Finally, the effectiveness of the high-frequency topographical effects in the Stokes-Helmert integral using the RCR technique is validated. For this purpose, the topographical effects in Eq. (40) are set to the global full-frequency topographical effects (the sum of near-zone and far-zone topographical effects), the near-zone full-frequency topographical effects (including low- and high-frequency information), and the high-frequency topographical effects calculated by the combined algorithms, respectively. The accuracies of the obtained quasi-geoids are checked by comparison with GNSS leveling points. Table 13 lists statistics for the accuracies of the gravimetric quasi-geoids using different types of topographical effects.

Table 13 Accuracies of the gravimetric quasi-geoids (unit: m)

Table 13 demonstrates that the high-frequency instead of full-frequency topographical effects are suitable for the Stokes-Helmert/Hotine-Helmert integral when an Earth gravitational model is used as the reference model.When the truncation degree is set to 360, the accuracy of the quasi-geoid in the test area using the high-frequency topographical effects is 4.90 cm, which is a notable improvement of 10.58% over that using the global full-frequency effects and 12.19% over that using the near-zone full-frequency effects. When the truncation degree is set to 2160, the accuracy of the quasi-geoid in the test area with the use of the high-frequency topographical effects is 12.14% and 13.96% higher than that using the global full-frequency effects and that using the near-zone full-frequency effects, respectively. If a Helmert gravitational model rather than an Earth gravitational model is used as the reference model, the full-frequency topographical effects are supposed to be applied in the Stokes-Helmert/Hotine-Helmert integral according to spectral consistency. The Helmert gravitational model is obtained by subtracting the consistently scaled spherical harmonic coefficients for the residual topographical potential from the corresponding spherical harmonic coefficients for the Earth gravitational model. In fact, the scheme with use of the Earth gravitational model is equivalent to that with use of the Helmert gravitational model.

8 Conclusions

The geodetic boundary-value theory for constructing the geoid and quasi-geoid requires that there are no topographical masses outside the boundary surface. To satisfy the demands, the topographical masses outside the boundary surface are generally condensed into a mass layer covering the boundary surface according to the Helmert’s second condensation method. The condensation of topographical masses results in direct effect and secondary indirect effects on gravity as well as indirect effects on the (quasi-) geoid.The high-frequency topographical effects should be applied when an Earth gravitational model serves as the reference model in the Hotine-Helmert/Stokes-Helmert integral. This necessity has motivated the study and development of algorithms for high-frequency topographical effects based on the existing methods of topographical effects.

The prism methods for near-zone topographical effects are derived to reduce the discretization effect of integral method and improve the accuracies of near-zone topographical effects. In consideration of the computational efficiency and accuracy of far-zone topographical effects, the Molodenskii spectral methods truncated to power H⁴, compared with power H² or H³ for the traditional Molodenskii methods, are derived. Subsequently, new combined algorithms, denoted as "prism + Molodenskii spectral-spherical harmonic" algorithms, are put forward for the high-frequency topographical effects in this manuscript.

Numerical investigation in a mountainous area is conducted to assess the effectiveness of different algorithms of topographical effects. With the use of high-resolution height data, the near-zone topographical effects calculated by the integral methods and prism methods differ slightly, substantiating the validity of the prism methods. When the resolution of height data is not exceedingly high, the prism methods are recommended for near-zone topographical effects due to their ability to reduce discretization effects. The far-zone topographical effects computed using Molodenskii spectral methods closely match those obtained by the integral methods, confirming the validity of the Molodenskii methods. The Molodenskii spectral methods are superior to the integral methods in calculating the far-zone topographical effects considering the computational efficiency.The global topographical effects calculated by the spherical harmonic methods are consistent with those obtained by integral methods and those computed by “prism + Molodenskii” algorithms,indicating the effectiveness of the spherical harmonic methods for the global low-frequency topographical effects. When an Earth gravitational model serves as the reference model in determining the (quasi-) geoid based on Helmert’s second condensation method, the high-frequency topographical effects calculated by the "prism + Molodenskii spectral-spherical harmonic" algorithms are demonstrated to be preferable to full-frequency topographical effects.

Appendices

Appendix A: Derivation of the spherical harmonic methods of residual topographical potentials

For $r_{{\text{P}}} > r$ and $r_{{\text{P}}} > R$, the Legendre’s polynomials for the reciprocals of $\ell_{{\text{P}}}$ and $\ell_{{{\text{P0}}}}$ in Eq. (3) are written as

$$ \frac{1}{{\ell_{{\text{P}}} }} = \frac{1}{{r_{{\text{P}}} }}\sum\limits_{n = 0}^{\infty } {\left( {\frac{r}{{r_{{\text{P}}} }}} \right)^{n} P_{n} \left( {\cos \psi } \right)} , \, \frac{1}{{\ell_{{{\text{P0}}}} }} = \frac{1}{{r_{{\text{P}}} }}\sum\limits_{n = 0}^{\infty } {\left( {\frac{R}{{r_{{\text{P}}} }}} \right)^{n} P_{n} \left( {\cos \psi } \right)} $$

(A.1)

Substituting Eq. (A.1) into Eq. (2) yields the Legendre series for the residual topographical potential of the ground point $P$, that is,

$$ \begin{aligned} &\delta V\left( P \right) =G\iint\limits_{{\Omega_{0} }} {\int\limits_{r = R}^{R + h} {\rho \frac{1}{{r_{P} }}\sum\limits_{n = 0}^{\infty } {\left({\frac{r}{{r_{P} }}} \right)^{n} } P_{n} \left( {\cos \psi }\right)r^{2} {\text{d}}r} {\text{d}}\Omega } \hfill \\ &\qquad\, -G\iint\limits_{{\Omega_{0} }} {\rho h\left( {1 + \frac{h}{R} +\frac{{h^{2} }}{{3R^{2} }}} \right)\frac{1}{{r_{P} }}\sum\limits_{n = 0}^{\infty } {\left( {\frac{R}{{r_{P} }}} \right)^{n} } P_{n}\left( {\cos \psi } \right)R^{2} {\text{d}}\Omega } \hfill \\ &\quad\, =GR^{2} \iint\limits_{{\Omega_{0} }} {\rho \sum\limits_{n =0}^{\infty } {\left( {\frac{R}{{r_{P} }}} \right)^{n + 1} \left\{{\frac{1}{n + 3}\left[ {\left( {1 + \frac{h}{R}} \right)^{n + 3} -1} \right]} \right.} } \hfill \\ &\qquad\left. { \, - \frac{h}{R}\left( {1 + \frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}} \right)} \right\}P_{n}\left( {\cos \psi } \right)e\Omega \hfill \\ \end{aligned}$$

(A.2)

where $P_{{\text{n}}}$is the Legendre function of degree $n$. The Legendre function is related to the spherical harmonics by the Laplace addition theorem as

$$ P_{n} \left( {\cos \psi } \right) =\frac{1}{2n + 1}\sum\limits_{m = - n}^{n} {\overline{Y}_{nm} \left({\Omega_{P} } \right)} \overline{Y}_{nm} \left( \Omega \right)$$

(A.3)

where $\overline{Y}_{nm}$is fully normalized spherical harmonic function of degree $n$ and order $m$,$\Omega_{{\text{P}}}$denotes spherical coordinate of the computation point,$\Omega$denotes spherical coordinate of the integration point. The spherical harmonic representation of residual topographical potential on the Earth’s surface can be thus obtained by substituting Eq. (A.3) into Eq. (A.2) as

$$ \delta V\left( P \right) = 2\pi G\sum\limits_{n = 0}^{\infty } {\left( {\frac{R}{{r_{{\text{P}}} }}}\right)^{n + 1} } \sum\limits_{m = - n}^{n} {\delta V_{nm}^{e} }\overline{Y}_{nm} \left( {\Omega_{{\text{P}}} } \right)$$

(A.4)

where $\delta V_{nm}^{e}$ is the spherical harmonic coefficient with degree $n$ and order $m$ for the residual topographical potential on the Earth’s surface, and the superscript "$e$"represents the exterior space of the Earth’s surface. The formula for $\delta V_{nm}^{e}$ is written as Martinec (1998) and Wang et al. (2012)

$$ \begin{aligned} \delta V_{nm}^{e} =&\frac{{R^{2} }}{{2\pi \left( {2n + 1}\right)}}\iint\limits_{{\Omega_{0} }} \rho \left\{{\frac{1}{{\left( {n + 3} \right)}}\left[ {\left( {1 + \frac{h}{R}}\right)^{n + 3} - 1} \right]} \right.\\&\left. { \, -\frac{h}{R}\left( {1 + \frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}}\right)} \right\}\overline{Y}_{nm} \left( \Omega \right){\text{d}}\Omega \hfill \\ \end{aligned}$$

(A.5)

It can be seen from Eq. (A.5) that $\delta V_{nm}^{e}$ is zero for $n =0$.There are no Taylor truncation errors in Eq. (A.5). Taylor expanding the term $\left( {1 + {h \mathord{\left/ {\vphantom {h R}} \right. \kern-0pt} R}} \right)^{n +3}$ in Eq. (A.5) to a specific power of topographical height yields the formula for $\delta V_{nm}^{e}$ with Taylor truncation errors. The formula for $\delta V_{nm}^{e}$ Taylor-expanded to the fourth power of height is

$$ \begin{aligned} \delta V_{nm}^{e} =&\frac{{R^{2} }}{{4\pi \left( {2n + 1}\right)}}\iint\limits_{{\Omega_{0} }} {\rho \left[ {n\frac{{h^{2}}}{{R^{2} }} + \frac{{n\left( {n + 3} \right)}}{3}\frac{{h^{3}}}{{R^{3} }}} \right.} \hfill \\ & \left. +{\frac{{n\left( {n + 1}\right)\left( {n + 2} \right)}}{12}\frac{{h^{4} }}{{R^{4} }}}\right]\overline{Y}_{nm} \left( \Omega \right){\text{d}}\Omega \hfill \\ \end{aligned} $$

(A.6)

For $r > R$, the Legendre’s polynomials for the reciprocals of $\ell$ and $\ell_{0}$ in Eq. (9) are expressed as

$$ \frac{1}{\ell } = \frac{1}{r}\sum\limits_{n = 0}^{\infty } {\left( \frac{R}{r} \right)^{n} P_{n} \left( {\cos \psi } \right)} , \, \frac{1}{{\ell_{0} }} = \frac{1}{R}\sum\limits_{n = 0}^{\infty } {P_{n} \left( {\cos \psi } \right)} $$

(A.7)

The Legendre formula for the residual topographical potential of point $P_{0}$on the surface of $r = R$is

$$ \begin{aligned} \delta V\left( {P_{0} }\right) = &\,G\iint\limits_{{\Omega_{0} }} {\int\limits_{r = R}^{R + h}{\frac{\rho }{\ell }r^{2} {\text{d}}r} {\text{d}}\Omega } -G\iint\limits_{{\Omega_{0} }} {\frac{\sigma }{{\ell_{0} }}R^{2}{\text{d}}\Omega } \hfill \\ \, =&\, G\iint\limits_{{\Omega_{0} }}{\int\limits_{r = R}^{R + h} {\rho \sum\limits_{n = 0}^{\infty }{\frac{{R^{n} }}{{r^{n - 1} }}P_{n} \left( {\cos \psi } \right)}{\text{d}}r} {\text{d}}\Omega } \hfill \\ \,& -G\iint\limits_{{\Omega_{0} }} {\rho \frac{h}{R}\left( {1 +\frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}} \right)\sum\limits_{n =0}^{\infty } {P_{{\text{n}}} \left( {\cos \psi } \right)} R^{2}{\text{d}}\Omega } \hfill \\ \end{aligned}$$

(A.8)

The spherical harmonic form of $\delta V\left({P_{0} } \right)$ is obtained by substituting Eq. (A.3) into Eq. (A.8) as

$$ \delta V\left( {P_{0} } \right) = 2\pi G\sum\limits_{n = 0}^{\infty } {\sum\limits_{m = - n}^{n} {\delta V_{nm}^{i} } \overline{Y}_{nm} \left( {\Omega_{{\text{P}}} }\right)} $$

(A.9)

where $\delta V_{nm}^{i}$ is the spherical harmonic coefficient with degree $n$ and order $m$ for the residual topographical potential on the boundary surface of $r =R$, and the superscript "$i$" denotes the interior space of the Earth’s topography. The coefficient $\delta V_{nm}^{i}$ is given by Martinec (1998) and Wang et al. (2012)

$$ \begin{aligned} \delta V_{nm}^{i} = \left\{ {\begin{array}{ll} \frac{{R^{2} }}{{2\pi \left( {2n + 1} \right)}}\iint\limits_{{\Omega_{0} }} \rho \left\{ \frac{1}{2 - n}\left[ {\left( {1 + \frac{h}{R}} \right)^{2 - n} - 1} \right]\right.\\\qquad\left. -\frac{h}{R}\left( {1 + \frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}}\right) \right\}\overline{Y}_{nm} \left( \Omega \right){\text{d}}\Omega & {n \ne 2} \\ \frac{{R^{2} }}{{2\pi \left( {2n + 1} \right)}}\iint\limits_{{\Omega_{0} }} \rho \left[\ln \left( {1 + \frac{h}{R}} \right) \right.\\ \left.\qquad- \frac{h}{R}\left( {1 +\frac{h}{R} + \frac{{h^{2} }}{{3R^{2} }}} \right)\right]\overline{Y}_{nm} \left( \Omega \right){\text{d}}\Omega \,& {n = 2} \\ \end{array} } \right. \hfill \\ \end{aligned}$$

(A.10)

Analogously, no Taylor truncation errors exist in Eq. (A.10). Taylor-expanding Eq. (A.10) to term H⁴ yields the following unified (i.e., applicable for both $n = 2$ and $n \ne 2$) form of spherical harmonic equation for $\delta V_{nm}^{i}$.

$$ \delta V_{nm}^{i} = \frac{{R^{2} }}{{4\pi \left( {2n + 1} \right)}}\iint\limits_{{\Omega_{0} }} {\rho \left[ { - \left( {n + 1} \right)\frac{{h^{2} }}{{R^{2} }} + \frac{{n^{2} - n - 2}}{3}\frac{{h^{3} }}{{R^{3} }} + \frac{{n - n^{3} }}{12}\frac{{h^{4} }}{{R^{4} }}} \right]\overline{Y}_{nm} \left( \Omega \right){\text{d}}\Omega } $$

(A.11)

Appendix B: Indefinite integrals for derivation of the prism methods of topographical effects

The indefinite integral formulae used in the derivation of prism methods for topographical effects are listed as follows.

$$ \int {\frac{1}{{\sqrt {x^{2} + a^{2} } }}{\text{d}}x} = \ln \left( {x + \sqrt {x^{2} + a^{2} } } \right) + C $$

(B.1)

$$ \int {\frac{1}{{\left( {x^{2} + a^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}} {\text{d}}x = \frac{x}{{a^{2} \sqrt {x^{2} + a^{2} } }} + C $$

(B.2)

$$ \begin{aligned} &\int {\ln \left( {y +\sqrt {x^{2} + y^{2} + z^{2} } } \right)} {\text{d}}x\\ &\quad = x\ln \left({y + \sqrt {x^{2} + y^{2} + z^{2} } } \right) + y\ln \left( {x +\sqrt {x^{2} + y^{2} + z^{2} } } \right) \hfill \\ &\qquad \, - z\arctan \frac{xy}{{z\sqrt {x^{2} + y^{2} + z^{2} } }} - x + z\arctan \frac{x}{z} + C \hfill \\ \end{aligned}$$

(B.3)

$$\int {\frac{xy}{{x^{2} + z^{2} }}} \cdot \frac{{{\text{d}}z}}{{\sqrt {x^{2} + y^{2} + z^{2} } }} = \arctan \frac{yz}{{x\sqrt {x^{2} + y^{2} + z^{2} } }} + C $$

(B.4)

where $C$denotes an arbitrary constant.

The double and triple integrals of ${1 \mathord{\left/ {\vphantom {1 {\sqrt {x^{2} + y^{2} + z^{2} } }}}\right. \kern-0pt} {\sqrt {x^{2} + y^{2} + z^{2} }}}$ in the Cartesian coordinate system are required for the prism methods for indirect effects. Using Eqs. (B.1) and (B.3) , its double integral reduces to

$$ \begin{aligned} &\int {\int {\frac{1}{{\sqrt {x^{2} + y^{2} + z^{2} } }}{\text{d}}y{\text{d}}x}} \hfill \\ &\quad= \int {\ln \left( {y + \sqrt {x^{2} + y^{2} + z^{2} } }\right){\text{d}}x} \hfill \\ &\quad= x\ln \left( {y + \sqrt {x^{2} +y^{2} + z^{2} } } \right) + y\ln \left( {x + \sqrt {x^{2} + y^{2} +z^{2} } } \right) \hfill \\ &\qquad\, - z\arctan \frac{xy}{{z\sqrt {x^{2} +y^{2} + z^{2} } }} - x + z\arctan \frac{x}{z} + C \hfill \\\end{aligned} $$

(B.5)

The specific derivation process of the triple indefinite integral of ${1 \mathord{\left/ {\vphantom {1 {\sqrt {x^{2} + y^{2} + z^{2} } }}} \right. \kern-0pt} {\sqrt {x^{2} + y^{2} + z^{2} } }}$ is presented below. To start with, its triple integral is converted to

$$ \begin{gathered} \int {\int {\int {\frac{{{\text{d}}x{\text{d}}y{\text{d}}z}}{{\sqrt {x^{2} + y^{2} + z^{2} } }}} } } = \frac{1}{2}\int {\int {\int {\left[ {\frac{{x^{2} + y^{2} }}{{\left( {x^{2} + y^{2} + z^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}} \right.} } } + \hfill \\ \left. { \, \frac{{x^{2} + z^{2} }}{{\left( {x^{2} + y^{2} + z^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }} + \frac{{y^{2} + z^{2} }}{{\left( {x^{2} + y^{2} + z^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}} }}} \right]{\text{d}}x{\text{d}}y{\text{d}}z \hfill \\ \end{gathered} $$

(B.6)

Using

$$ \frac{{x^{2} + y^{2} }}{{\left( {x^{2} +y^{2} + z^{2} } \right)^{{{3 \mathord{\left/ {\vphantom {3 2}}\right. \kern-0pt} 2}}} }} = \frac{\partial }{\partial z}\left({\frac{z}{{\sqrt {x^{2} + y^{2} + z^{2} } }}} \right)$$

(B.7)

together with Eqs. (B.1) and (B.3), the triple integral of ${{\left( {x^{2} + y^{2} } \right)}\mathord{\left/ {\vphantom {{\left( {x^{2} + y^{2} } \right)}{\left( {x^{2} + y^{2} + z^{2} } \right)^{{{3 \mathord{\left/{\vphantom {3 2}} \right. \kern-0pt} 2}}} }}} \right. \kern-0pt}{\left( {x^{2} + y^{2} + z^{2} } \right)^{{{3 \mathord{\left/{\vphantom {3 2}} \right. \kern-0pt} 2}}}}}$ in (B.6) can be written as

$$ \begin{aligned} &\int {\int {\int {\frac{{x^{2} + y^{2} }}{{\left( {x^{2} + y^{2} + z^{2} }\right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt}2}}} }}} } } {\text{d}}x{\text{d}}y{\text{d}}z = \int {\int {\frac{z}{{\sqrt {x^{2} + y^{2} + z^{2} } }}} }{\text{d}}x{\text{d}}y \hfill \\ &\quad= z\int {\ln \left( {y + \sqrt {x^{2} + y^{2} + z^{2} } } \right){\text{d}}x} \hfill \\ &\quad= xz\ln \left( {y + \sqrt {x^{2} + y^{2} + z^{2} } } \right) + yz\ln \left({x + \sqrt {x^{2} + y^{2} + z^{2} } } \right) \hfill \\ &\qquad\, - z^{2}\arctan \frac{xy}{{z\sqrt {x^{2} + y^{2} + z^{2} } }} - xz + z^{2}\arctan \frac{x}{z} + C \hfill \\ \end{aligned}$$

(B.8)

Eq. (B.8) can be rearranged to give

$$ \begin{aligned} &\int {\int {\int {\frac{{y^{2} + z^{2} }}{{\left( {x^{2} + y^{2} + z^{2} }\right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt}2}}} }}} } } {\text{d}}x{\text{d}}y{\text{d}}z \hfill \\ &\quad= xz\ln \left( {y + \sqrt {x^{2} + y^{2} + z^{2} } } \right) + xy\ln \left({z + \sqrt {x^{2} + y^{2} + z^{2} } } \right) \hfill \\ &\qquad\, - x^{2}\arctan \frac{yz}{{x\sqrt {x^{2} + y^{2} + z^{2} } }} - xy + x^{2}\arctan \frac{y}{x} + C \hfill \\ \end{aligned}$$

(B.9)

$$ \begin{aligned} &\int {\int {\int {\frac{{z^{2} + x^{2} }}{{\left( {x^{2} + y^{2} + z^{2} }\right)^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt}2}}} }}} } } {\text{d}}x{\text{d}}y{\text{d}}z \hfill \\ &\quad= xy\ln \left( {z + \sqrt {x^{2} + y^{2} + z^{2} } } \right) + yz\ln \left({x + \sqrt {x^{2} + y^{2} + z^{2} } } \right) \hfill \\ &\qquad\, - y^{2}\arctan \frac{xz}{{y\sqrt {x^{2} + y^{2} + z^{2} } }} - yz + y^{2}\arctan \frac{z}{y} + C \hfill \\ \end{aligned}$$

(B.10)

Substituting Eqs. (B.8), (B.9) and (B.10) into (B.6) yields

$$ \begin{aligned} &\int {\int {\int {\frac{{{\text{d}}x{\text{d}}y{\text{d}}z}}{{\sqrt {x^{2} + y^{2} +z^{2} } }}} } } \hfill \\ &\quad= xy\ln \left( {z + \sqrt {x^{2} + y^{2} +z^{2} } } \right) + xz\ln \left( {y + \sqrt {x^{2} + y^{2} + z^{2} }} \right)\\ &\qquad + yz\ln \left( {x + \sqrt {x^{2} + y^{2} + z^{2} } }\right) - \frac{{z^{2} }}{2}\arctan \frac{xy}{{z\sqrt {x^{2} + y^{2} + z^{2} } }} \\ &\qquad- \frac{{x^{2} }}{2}\arctan \frac{yz}{{x\sqrt {x^{2} + y^{2} + z^{2} } }} - \frac{{y^{2}}}{2}\arctan \frac{xz}{{y\sqrt {x^{2} + y^{2} + z^{2} } }} \hfill \\&\qquad- \frac{xz + xy + yz}{2} + \frac{{z^{2} }}{2}\arctan \frac{x}{z} \\&\qquad+\frac{{x^{2} }}{2}\arctan \frac{y}{x} + \frac{{y^{2} }}{2}\arctan \frac{z}{y} + C \hfill \\ \end{aligned}$$

(B.11)

Appendix C: The Taylor series expanded to power H ⁴ of topographical effects

The Taylor series of topographical effects truncated to terms of H² and H³ have already been put forward by former scholars. The Taylor expansions to power H⁴ are further deduced below.

Taking the first- through fourth-order radial derivatives of the Legendre’s polynomials for $1/\ell_{{\text{P}}}$ with respect to $r_{{\text{P}}}$yields

$$ \begin{aligned} &\sum\limits_{n =0}^{\infty } {\left( {\frac{R}{{r_{{{P}}} }}} \right)^{n + 1}P_{{{n}}} \left( {\cos \psi } \right)} \hfill \quad=\frac{R}{{\ell_{{{{P0}}}} }} \\ &\sum\limits_{n =0}^{\infty } {\left( {n + 1} \right)\left( {\frac{R}{{r_{{{P}}}}}} \right)^{n + 1} P_{{{n}}} \left( {\cos \psi } \right)} =\frac{{Rr_{{{P}}} \left( {r_{{{P}}} - R\cos \psi }\right)}}{{\ell_{{{{P0}}}}^{3} }} \hfill \qquad\\ &\sum\limits_{n =0}^{\infty } {\left( {n + 1} \right)\left( {n + 2} \right)\left({\frac{R}{{r_{{{P}}} }}} \right)^{n + 1} P_{n} \left( {\cos \psi } \right)} = - \frac{{Rr_{{{P}}}^{2}}}{{\ell_{{{{P0}}}}^{3} }} \\ & \quad + \frac{{3Rr_{{{P}}}^{2} \left({r_{{{P}}} - R\cos \psi } \right)^{2}}}{{\ell_{{{{P0}}}}^{5} }} \hfill \qquad\\ &\sum\limits_{n =0}^{\infty } {\left( {n + 1} \right)\left( {n + 2} \right)\left( {n + 3} \right)\left( {\frac{R}{{r_{{{P}}} }}} \right)^{n + 1}P_{{{n}}} \left( {\cos \psi } \right)} \hfill \\ &\quad = -\frac{{9Rr_{{{P}}}^{3} \left( {r_{P} - R\cos \psi }\right)}}{{\ell_{{{{P0}}}}^{5} }} +\frac{{15Rr_{{{P}}}^{3} \left( {r_{{{P}}} - R\cos \psi }\right)^{3} }}{{\ell_{{{{P0}}}}^{7} }} \hfill \qquad\\ &\sum\limits_{n = 0}^{\infty } {\left( {n + 1} \right)\left( {n + 2} \right)\left({n + 3} \right)\left( {n + 4} \right)\left({\frac{R}{{r_{{{P}}} }}} \right)^{n + 1} P_{n} \left( {\cos \psi } \right)} \hfill \\ &\quad = \frac{{9Rr_{{{P}}}^{4}}}{{\ell_{{{{P0}}}}^{5} }} - \frac{{90Rr_{{{P}}}^{4}\left( {r_{{{P}}} - R\cos \psi } \right)^{2}}}{{\ell_{{{{P0}}}}^{7} }} + \frac{{105Rr_{P}^{4} \left({r_{{{P}}} - R\cos \psi } \right)^{4} }}{{\ell_{P0}^{9} }}\hfill \\ \end{aligned} $$

(C.1)

According to Eqs. (10) and (11), the Taylor series expanded to power H⁴ of the residual topographical potential of point $P$ on the Earth’s surface takes the following Legendre form

$$ \begin{aligned} \delta V\left( P \right) =\,&G\iint\limits_{{\Omega_{0} }} {\rho \left[ {h^{2} \sum\limits_{n =0}^{\infty } {\frac{n}{2}\left( {\frac{R}{{r_{{{P}}} }}}\right)^{n + 1} P_{n} \left( {\cos \psi } \right)} } \right.}\\ & +h^{3} \sum\limits_{n = 0}^{\infty } {\frac{{n\left( {n + 3}\right)}}{6R}\left( {\frac{R}{{r_{{{P}}} }}} \right)^{n + 1} } P_{{{n}}} \left( {\cos \psi }\right)\hfill \\ \, &\left. +\, h^{4} \sum\limits_{n = 0}^{\infty } {\frac{{n\left( {n +1} \right)\left( {n + 2} \right)}}{{24R^{2} }}\left({\frac{R}{{r_{{{P}}} }}} \right)^{n + 1} P_{{{n}}} \left({\cos \psi } \right)} \right]{{d}}\Omega \hfill \\\end{aligned} $$

(C.2)

By using the functional relationship between the residual topographical potential and direct effect, the Taylor expansion to power H⁴ of direct effect in Legendre’s polynomial form is obtained as

$$ \begin{aligned} \delta A =& -\frac{G}{{r_{{{P}}} }}\iint\limits_{{\Omega_{0} }} {\rho \left[{h^{2} \sum\limits_{n = 0}^{\infty } {\frac{{n\left( {n + 1}\right)}}{2}\left( {\frac{R}{{r_{{{P}}} }}} \right)^{n + 1}P_{{{n}}} \left( {\cos \psi } \right)} } \right.}\\ & + h^{3}\sum\limits_{n = 0}^{\infty } {\frac{{n\left( {n + 1} \right)\left({n + 3} \right)}}{6R}} \left({\frac{R}{{r_{{{P}}} }}} \right)^{n + 1} P_{{{n}}} \left({\cos \psi } \right)\hfill \\ \,& \left. { +\, h^{4} \sum\limits_{n = 0}^{\infty }{\frac{{n\left( {n + 1} \right)^{2} \left( {n + 2}\right)}}{{24R^{2} }}\left( {\frac{R}{{r_{P} }}} \right)^{n + 1}P_{{{n}}} \left( {\cos \psi } \right)} }\right]{{d}}\Omega \hfill \\ \end{aligned}$$

(C.3)

Substituting Eqs. (C.1) into (C.3) results in the Taylor expansion to power H⁴ of direct effect in closed form, that is,

$$ \delta A = - \frac{G}{{r_{{\text{P}}}}}\iint\limits_{{\Omega_{0} }} {\rho \left( {h^{2} R_{2} + h^{3}R_{3} + h^{4} R_{4} } \right){\text{d}}\Omega }$$

(C.4)

where

$$ \begin{aligned} R_{2} =&\, \sum\limits_{n =0}^{\infty } {\frac{{n\left( {n + 1} \right)}}{2}\left({\frac{R}{{r_{{\text{P}}} }}} \right)^{n + 1} P_{{\text{n}}} \left({\cos \psi } \right)} \hfill \\ \, = &\,- \frac{{Rr_{{\text{P}}} \left({3r_{{\text{P}}} - 2R\cos \psi }\right)}}{{2\ell_{{{\text{P0}}}}^{3} }} +\frac{{3Rr_{{\text{P}}}^{2} \left( {r_{P} - R\cos \psi } \right)^{2}}}{{2\ell_{{{\text{P0}}}}^{5} }} \hfill \\ R_{3} =&\, \sum\limits_{n =0}^{\infty } {\frac{{n\left( {n + 1} \right)\left( {n + 3}\right)}}{6R}} \left( {\frac{R}{{r_{{\text{P}}} }}} \right)^{n + 1}P_{{\text{n}}} \left( {\cos \psi } \right) \hfill \\ \, =&\,\frac{{r_{{\text{P}}} R\cos \psi }}{{3\ell_{{{\text{P0}}}}^{3} }} -\frac{{r_{{\text{P}}}^{2} \left( {5r_{{\text{P}}} - 2R\cos \psi }\right)\left( {r_{{\text{P}}} - R\cos \psi }\right)}}{{2\ell_{{{\text{P0}}}}^{5} }}\\&\, + \frac{{5r_{{\text{P}}}^{3}\left( {r_{{\text{P}}} - R\cos \psi } \right)^{3}}}{{2\ell_{{{\text{P0}}}}^{7} }} \hfill \\ R_{4} =&\, \sum\limits_{n =0}^{\infty } {\frac{{n\left( {n + 1} \right)^{2} \left( {n + 2}\right)}}{{24R^{2} }}\left( {\frac{R}{{r_{{\text{P}}} }}} \right)^{n + 1} P_{{\text{n}}} \left( {\cos \psi } \right)} \hfill \\ \, =&\, -\frac{{r_{{\text{P}}}^{2} }}{{4R\ell_{{{\text{P0}}}}^{3} }} +\frac{{3r_{P}^{2} \left( {9r_{{\text{P}}}^{2} - 10Rr_{{\text{P}}}\cos \psi + 2R^{2} \cos^{2} \psi }\right)}}{{8R\ell_{{{\text{P0}}}}^{5} }} \hfill \\ \, &-\frac{{15r_{{\text{P}}}^{3} \left( {r_{{\text{P}}} - R\cos \psi }\right)^{2} \left( {2r_{{\text{P}}} - R\cos \psi }\right)}}{{4R\ell_{{{\text{P0}}}}^{7} }} + \frac{{35r_{P}^{4} \left({r_{{\text{P}}} - R\cos \psi } \right)^{4}}}{{8R\ell_{{{\text{P0}}}}^{9} }} \hfill \\ \end{aligned}$$

(C.5)

Applying Bruns’s formula to Eq. (C.2) leads to the Taylor expansion to power H⁴ of indirect effect on height anomaly in the following Legendre form.

$$ \begin{aligned} \delta \zeta =&\,\frac{G}{\gamma }\iint\limits_{{\Omega_{0} }} \rho \left[ {h^{2}\sum\limits_{n = 0}^{\infty } {\frac{n}{2}\left({\frac{R}{{r_{{{P}}} }}} \right)^{n + 1} P_{{{n}}} \left({\cos \psi } \right)} } \right. \\ &+ h^{3} \sum\limits_{n = 0}^{\infty } {\frac{{n\left( {n + 3} \right)}}{6R}\left({\frac{R}{{r_{{{P}}} }}} \right)^{n + 1} } P_{{{n}}} \left( {\cos \psi } \right)\hfill \\ \,&\left. +\, h^{4}\sum\limits_{n = 0}^{\infty } {\frac{{n\left( {n + 1} \right)\left({n + 2} \right)}}{{24R^{2} }}\left( {\frac{R}{{r_{{{P}}} }}}\right)^{n + 1} P_{{{n}}} \left( {\cos \psi } \right)}\right]{{d}}\Omega \hfill \\ \end{aligned}$$

(C.6)

Substituting Eqs. (C.1) into (C.6) yields the Taylor series expanded to order H⁴ of indirect effect on height anomaly in close form, that is,

$$ \delta \zeta = \frac{G}{\gamma }\iint\limits_{{\Omega_{0} }} {\rho \left( {h^{2} F_{2} + h^{3}F_{3} + h^{4} F_{4} } \right){\text{d}}\Omega }$$

(C.7)

where

$$ \begin{aligned} F_{2} = &\sum\limits_{n =0}^{\infty } {\frac{n}{2}\left( {\frac{R}{{r_{{\text{P}}} }}}\right)^{n + 1} P_{{\text{n}}} \left( {\cos \psi } \right)}\\ =& -\frac{R}{{2\ell_{{{\text{P0}}}} }} + \frac{{Rr_{{\text{P}}} \left({r_{{\text{P}}} - R\cos \psi } \right)}}{{2\ell_{{{\text{P0}}}}^{3}}} \hfill \\ F_{3} = &\sum\limits_{n = 0}^{\infty } {\frac{{n\left({n + 3} \right)}}{6R}} \left( {\frac{R}{{r_{{\text{P}}} }}}\right)^{n + 1} P_{{\text{n}}} \left( {\cos \psi } \right)\\ =& -\frac{1}{{3\ell_{{{\text{P0}}}} }} - \frac{{r_{{\text{P}}}^{2}}}{{6\ell_{{{\text{P0}}}}^{3} }} + \frac{{r_{{\text{P}}}^{2} \left({r_{{\text{P}}} - R\cos \psi } \right)^{2}}}{{2\ell_{{{\text{P0}}}}^{5} }} \hfill \\ F_{4} = &\sum\limits_{n =0}^{\infty } {\frac{{n\left( {n + 1} \right)\left( {n + 2}\right)}}{{24R^{2} }}\left( {\frac{R}{{r_{{\text{P}}} }}} \right)^{n + 1} P_{{\text{n}}} \left( {\cos \psi } \right)} \hfill \\ \, =&\frac{{r_{{\text{P}}}^{2} }}{{8R\ell_{{{\text{P0}}}}^{3} }} -\frac{{3r_{{\text{P}}}^{2} \left( {r_{{\text{P}}} - R\cos \psi }\right)\left( {2r_{{\text{P}}} - R\cos \psi }\right)}}{{8R\ell_{{{\text{P0}}}}^{5} }}\\ & +\frac{{5r_{{\text{P}}}^{3} \left( {r_{{\text{P}}} - R\cos \psi }\right)^{3} }}{{8R\ell_{{{\text{P0}}}}^{7} }} \hfill \\\end{aligned} $$

(C.8)

For $r_{{\text{P}}} =R$, Eq. (C.1) can be rewritten as

$$ \begin{aligned} &\sum\limits_{n =0}^{\infty } {P_{{\text{n}}} \left( {\cos \psi } \right)} =\frac{R}{{\ell_{0} }} \hfill \\ &\sum\limits_{n = 0}^{\infty }{\left( {n + 1} \right)P_{{\text{n}}} \left( {\cos \psi } \right)} =\frac{{R^{3} \left( {1 - \cos \psi } \right)}}{{\ell_{0}^{3} }}\hfill \\ &\sum\limits_{n = 0}^{\infty } {\left( {n + 1}\right)\left( {n + 2} \right)P_{{\text{n}}} \left( {\cos \psi }\right)} = - \frac{{R^{3} }}{{\ell_{0}^{3} }} + \frac{{3R^{5} \left({1 - \cos \psi } \right)^{2} }}{{\ell_{0}^{5} }} \hfill \\&\sum\limits_{n = 0}^{\infty } {\left( {n + 1} \right)\left( {n + 2}\right)\left( {n + 3} \right)P_{{\text{n}}} \left( {\cos \psi }\right)} \hfill \\ \, &\quad= - \frac{{9R^{5} \left( {1 - \cos \psi }\right)}}{{\ell_{0}^{5} }} + \frac{{15R^{7} \left( {1 - \cos \psi }\right)^{3} }}{{\ell_{0}^{7} }} \hfill \\ \end{aligned}$$

(C.9)

The Taylor expansion to term H⁴ of the residual topographical potential of point $P_{0}$on the boundary surface of $r =R$ can be obtained from Eqs. (10) and (11) in the following Legendre form.

$$ \begin{aligned} \delta V\left( {P_{0} }\right) = &G\iint\limits_{{\Omega_{0} }} \rho \left[ h^{2}\sum\limits_{n = 0}^{\infty } {\frac{ - n - 1}{2}} P_{n} \left({\cos \psi } \right)\right.\\& + h^{3} \sum\limits_{n = 0}^{\infty }{\frac{{n^{2} - n - 2}}{6R}P_{{\text{n}}} \left( {\cos \psi }\right)} \\&\left. { + h^{4} \sum\limits_{n = 0}^{\infty }{\frac{{n - n^{3} }}{{24R^{2} }}P_{n} \left( {\cos \psi } \right)} }\right]{\text{d}}\Omega \hfill \\ \end{aligned}$$

(C.10)

Analogously, the Taylor series expanded to power H⁴ of indirect effect on geoidal height in close form is expressed as

$$ \delta N = \frac{G}{{\gamma_{0}}}\iint\limits_{{\Omega_{0} }} {\rho \left( {h^{2} T_{2} + h^{3}T_{3} + h^{4} T_{4} } \right){\text{d}}\Omega }$$

(C.11)

where

$$ \begin{aligned} T_{2} = &\sum\limits_{n =0}^{\infty } {\frac{ - n - 1}{2}} P_{{\text{n}}} \left( {\cos \psi }\right) = - \frac{{R^{3} \left( {1 - \cos \psi }\right)}}{{2\ell_{0}^{3} }} \hfill \\ T_{3} = &\sum\limits_{n =0}^{\infty } {\frac{{n^{2} - n - 2}}{6R}P_{{\text{n}}} \left( {\cos \psi } \right)}\\ =& \frac{{R^{4} \left( {1 - \cos \psi } \right)^{2}}}{{2\ell_{0}^{5} }} - \frac{{R^{2} \left( {5 - 4\cos \psi }\right)}}{{6\ell_{0}^{3} }} \hfill \\ T_{4} = &\sum\limits_{n =0}^{\infty } {\frac{{n - n^{3} }}{{24R^{2} }}P_{n} \left( {\cos \psi } \right)} = - \frac{{5R^{5} \left( {1 - \cos \psi }\right)^{3} }}{{8\ell_{0}^{7} }}\\& + \frac{{3R^{3} \left( {1 - \cos \psi } \right)\left( {3 - 2\cos \psi } \right)}}{{8\ell_{0}^{5} }} -\frac{{R\left( {2 - \cos \psi } \right)}}{{4\ell_{0}^{3} }} \hfill \\ \end{aligned} $$

(C.12)