Keywords

1 Introduction

The interest in controlled atmosphere heat treatment processes is to increase energy efficiency as much as possible. At first, it would seem that bringing the heating elements closer to the part being treated would increase irradiation and thus energy efficiency. However, the proximity of the heating elements to the treated part causes temperature gradients, which is detrimental to thermal homogeneity and increases the total process time. On the other hand, moving the heating elements away from the part improves thermal homogeneity, but requires an increase in supplied power to achieve a given heating rate. Therefore, it is necessary to find a strategy that can simultaneously satisfy the requirements of adequate thermal homogeneity and irradiation in this type of process [1]. In this sense, this work presents a simulation-based methodology to determine the optimal configuration of the heating elements in controlled atmosphere heat treatment furnaces. This methodology only applies to treatments controlled by radiation and with thermal homogeneity requirements, such as stress relief, annealing, tempering, or normalizing in inert atmospheres. Furthermore, to facilitate the understanding of the reader, the methodology is explained with a practical example: stress relief treatment of a real Francis runner for hydraulic generation in a vault-type furnace heated with radiant tubes.

2 Methodology

To implement the methodology proposed in this document, it is necessary to develop a mathematical model for the heat transfer processes that take place inside the furnace. Additionally, since the optimization process requires multiple simulations of the heat treatment, it is necessary to strike a balance between the detail of the thermal model and the computational time required to solve it. As mentioned above, stress relief treatment for a Francis runner will be studied. This process consists of three fundamental stages: heating, holding, and cooling. During the heating period, the heating elements radiate heat to the part so that the part increases its temperature at a specified rate until the so-called holding temperature is reached. At this point, the holding period is given in which the piece maintains its constant temperature for a given time. Finally, the heating elements are turned off so that the cooling stage can take place, in which the piece reduces its temperature to a safe value to be removed from the furnace.

Fig. 1.
figure 1

Diagram of the EPM vault-type controlled atmosphere heat treatment furnace. a) isometric and b) top view.

Full size image

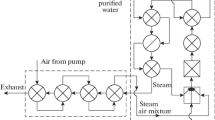
Figure 1 shows a schematic of the controlled atmosphere treatment furnace that includes the walls, a door, a roof, a floor, and 13 cylindrical radiant tubes. For these elements, the energy balances must be solved, making simplifications that obey the reality of the specific treatment process, and it is also necessary to consider the criterion of thermal homogeneity. In this sense, the control systems of this type of furnace are based on a set of thermocouples located at key points of the piece, between which there must be a controlled temperature difference. Thus, if said temperature difference is below a value ΔTmax, the part is heated; however, if this value is exceeded, a homogenization period begins in which the average temperature remains constant until the temperature difference between the gradient measurement points reaches a value ΔTmin. Therefore, a strategy proposed in this work consists of dividing the piece into surfaces whose temperatures must be controlled. For the specific case of the Francis runner in this study, a subdivision is made into 6 surfaces as shown in Fig. 2.

Fig. 2.
figure 2

Sectional view of the Francis runner and surfaces of interest.

Full size image

The energy balance equation for each of the twelve surfaces inside the runner is given by the following equation

$${\rho }_{i}dr{A}_{i}{C}_{pi}\frac{d{T}_{i}}{dt}={F}_{t,i}{\dot{Q}}_{tubos}+{A}_{i}*{\sum }_{j=1}^{12}{F}_{ij}*\left({J}_{j}-{J}_{i}\right)-h{A}_{i}\left({T}_{i}-{T}_{Ar}\right)-\sum\nolimits_{k=7}^{12}\frac{\left({T}_{i}-{T}_{k}\right)}{{R}_{ik}}$$
(1)

where \({\rho }_{i}\) is the density, \({A}_{i}\) is the surface area, \({C}_{pi}\) is the heat capacity, \({T}_{i}\) is the temperature, \({F}_{ij}\) is the view factor, \(J\) is the radiosity, \(h\) is the convective heat transfer coefficient inside the furnace, \({\dot{Q}}_{tubos}\) is the net power radiated by the tubes, \({F}_{t,i}\) is the view factor from the radiant tubes to the surface \(i\), \({R}_{ik}\) is the thermal resistance to conduction between two surfaces i and k of the piece. The model also considers the one-dimensional conduction equation inside the furnace walls, roof, door and floor, and the heat transfer by radiation between the surfaces of walls, roof, door and floor in a similar way to Eq. (1). Additionally, to emulate the control system of the thermal homogeneity of the furnace, the following function will be used by sections

$$\dot{W}=\left\{\begin{array}{l}\sum_{i=1}^{{N}_{r}}{F}_{i}{\dot{Q}}_{tubos}+{\dot{Q}}_{p{\acute{e} }rdidas} \quad si \quad {T}_{max}-{T}_{min}\le {\Delta T}_{max}\\ {\dot{Q}}_{p{\acute{e} }rdidas} \quad\quad\quad\quad\;\; si \quad\quad {{\Delta T}_{max}\ge T}_{max}-{T}_{min}\ge {\Delta T}_{min}\end{array}\right.$$
(2)

This expression establishes that when the temperature difference between two surfaces does not exceed an established maximum value, the energy supplied is equal to that required to raise the impeller temperature at the rate established by the treatment and additionally compensate energy losses to the surroundings. On the other hand, when the maximum temperature difference allowed between two surfaces is exceeded, the so-called homogenization period takes place and the radiant tubes deliver only the energy necessary to compensate the thermal losses with the environment, that is, to maintain the average temperature constant. Finally, when a temperature difference between the two surfaces ΔTmin is reached, the heating of the part continues. Thus, it is established that the maximum temperature difference between any surface of the impeller and surfaces 1, 2, and 3 must not exceed 5 ℃. On the other hand, the maximum temperature difference between any surface of the impeller and surfaces 4, 5, and 6 must not exceed 10 ℃. It is worth mentioning that there are two different values of ΔTmax due to the requirements of the specific heat treatment studied in this work since depending on the zone of the Francis runner there are different levels of risk of failure.

3 Predictions of the Heat Transfer Model

The numerical model was solved to simulate the heating of the piece during a heat treatment cycle with an average rate of 23 ℃/h until the piece reaches an average temperature of 620 ℃. Subsequently, a holding period of 12 h is carried out. Finally, the radiant tubes are turned off so that the piece cools down by exchanging heat with the environment. The simulations carried out were compared with the predictions of a steady-state model built with commercial finite-volume software and maximum deviations of 5% were found, with computational times up to 1000 times less for the model proposed here, which proves that it achieves to capture the physics of the treatment process. The parameters used during simulations are reported elsewhere [2].

Fig. 3.
figure 3

Predictions of power supply for different configurations.

Full size image

Figure 3 shows the predicted power profiles for dimensions S of 1058 mm and 703 mm. In these curves, it can be seen that there are some abrupt drops in power, which correspond to the periods of homogenization. However, without taking these periods into account, the supplied power increases with time because the energy losses with the surroundings increase with the increase in temperature. An interesting behavior that we can observe in this figure is that for the configuration with the best irradiation (S = 703 mm), the power supply is always below that of the configuration with S = 1058 mm for the same instant of the process (except, clearly, the periods of homogenization). This is because a better irradiation to the piece implies a lower energy requirement to obtain a given heating rate. However, the configuration with better irradiation requires that the total process time be greater because more periods of homogenization are necessary. Consequently, the best irradiation of the part implies longer process times and lower power supplies, which implies that there is a geometric configuration that simultaneously allows optimal process times and power supplies. Now, if we analyze the total energy consumed in the treatment, we have that this can be calculated from the following expression

$$E={\int }_{0}^{{t}_{final}}\dot{W}dt$$
(3)

Based on Eq. (3), it is clear that the thermal energy consumed in the process is no more than the area under the power curve shown in Fig. 3. In this way, we see that the better irradiation associated with the proximity of the radiant tubes to the piece implies a lower “height” of the polygon formed by the Power vs. time curve; however, it also implies a “horizontal elongation” of this polygon. In this sense, it is concluded that there must be a configuration that allows obtaining a minimum area under the curve, i.e., an optimal value of energy consumption. In other words, the objective function is given by the minimization of the total energy consumed:

$$FO=Min \; E$$
(4)

The great advantage of using Eq. (4) as an objective function is that it is capable of simultaneously taking into account the effects of irradiation and thermal gradients in the part, which avoids the need to use two objective functions for these two variables. Additionally, it is essential to mention that the appearance of said optimal value is mainly due to the ability of the proposed mathematical model to reproduce the homogenization times, which are the ones that generate the so-called “horizontal elongation” of the Power vs. time curve. Finally, to obtain an optimal configuration of the heating elements inside the furnace, the final step of the methodology consists in varying the location of the radiant tubes inside the furnace until a minimum value of energy consumption is obtained.

4 Results

To determine the optimal configuration of the heating elements, the dimensions A, B, C, and S (see Fig. 1a) of the furnace were varied. The first dimension that was analyzed was the separation S and, as seen in Fig. 4, a minimum consumption value appears for S = 950 mm. This same analysis can be carried out for the variation of any other level inside the furnace. Thus, after taking 1560 view factor data by using commercial software of finite volumes for different locations of the radiant tubes inside the furnace, it was found that the optimal elevations of the furnace are as follows: A = 6403 mm; B = 6900 mm; C = 2880 mm and S = 950 mm.

Fig. 4.
figure 4

Effect of dimension S on energy consumption.

Full size image

5 Conclusions

A new method was created to improve the design of controlled atmosphere heat treatment furnaces. It uses a heat transfer model to emulate the temperature gradients in the piece, resulting in minimum energy consumption without additional optimization criteria. The proposed model was found to have deviations of only 5% compared to a commercial finite volume model, and its computation time is 1000 times faster, making it more practical for optimization processes. The method was applied to optimize a vault-type furnace for a Francis turbine runner, resulting in minimum energy consumption during treatment.