Some consequences of nonstandard Lagrangians with time-dependent coefficients in general relativity

Abstract

Nonstandard Lagrangians entitled ‘nonnaturals’ by Arnold have recently gained increasing importance both in applied mathematics and in physical theories. These types of Lagrangians appear in some group of dissipative dynamical systems, and they play an important role in a number of field theories. However, the role of nonstandard Lagrangians in geometric theories like general relativity is still absent. In this communication, we would like to discuss the relevance of nonstandard Lagrangians in general relativity using the principles of calculus of variations. In fact, nonstandard Lagrangians came in different forms, features, and characteristics, depending on the nature of the dynamical problem under study. In this work, we will be concerned with time-dependent Lagrangians of the form L^{1 + γ(t)}. After deriving the modified geodesic equation using the basic techniques of Riemannian differential geometry which will be used to axiomatize a large part of our work, we show that many interesting consequences will be raised accordingly when applied to FRW cosmology.

Background

In recent years, the topic of nonstandard Lagrangians (NSLs) has attracted attention due to its wide applications in different branches of applied mathematics and theoretical physics. In reality, NSL is not new and its origin dated back to 1978 when Arnold entitled them ‘nonnatural’[1]. The topic was completely ignored until 1984 when Alekseev and Arbuzov used NSL to describe large-distance interactions in the field of applicability of classical theory within the framework of Yang-Mills field theory, a problem which is directly related to color confinement issue[2]. In fact, in years of progress, it was realized that NSL plays an important role in nonlinear differential equations like the nonlinear second-order Riccati equation[3] and the Lienard-type nonlinear differential equation[4, 5]. Interest in NSL increases gradually with time, and more applications were discussed in dissipative dynamical systems[6–10], quantum field theory[11, 12], and cosmology[13, 14].

Although the topic of NSL was addressed generally in classical dynamical systems, its implications in differential geometry and astrophysics are still ignored, and to the best of our knowledge, the topic is completely missed. This paper aims to explore how NSL can help bridge the gap between NSL physics and applied differential geometry. Recently, we have discussed the problem of finding a nonstandard Lagrangian description for a large class of dynamical systems[15–17]. A good number of NSLs which have been overlooked in the existing literature were derived and solved. For the sake of clarity, it should be emphasized that in our approach the term NSL refers principally to any ‘standard Lagrangian function that modify the Euler-Lagrange equations and accordingly Hamilton's equations of motion’. In fact, two different types of NSL were introduced: the exponential NSL and the power-law NSL. In this communication, we will deal with the power-law NSL (PNSL) with time-dependent coefficient, and we keep the second one for a future work. We will show that the presence of a time-dependent coefficient in PNSL is in fact connected to a time-dependent gravitational potential (TDGP). In reality, an assumption that in the universe there is a time-dependent gravitational potential was proposed in[18, 19] and discussed in[20–23]. It is an interesting attempt as it explains the Hubble redshift and the anomalous acceleration from the spacecraft Pioneer 10 and 11 mainly when TDGP decreases linearly with time. A TDGP also has many astrophysical impacts as its change modify the planetary orbits which were proven to be not axially symmetric. Moreover, it was observed that if the gravitational potential is time-dependent, the distant galaxies' velocity is not extremely fast as it is currently considered. In fact, the change of the gravitational potential is most likely caused by the change of the dark energy density, but nothing is confirmed about it. One naturally expects a violation of the strong and weak equivalence principle of general relativity. This violation was discussed in many theoretical aspects[24–41]. It is noteworthy that general relativity has been systematically tested on solar system scales. Therefore, it is unsurprising if we try to correct the theory at galactic and cosmological scales. One interesting recent anthropic argument suggests that the equivalence principle is violated at a small level[42]. This approach motivates the demand for enhanced tests of the equivalence principle. Some interesting points concerning the violation of the equivalence principle and violation of diffeomorphism invariance in connection with emergent gravity were discussed in[43, 44] and references therein.

The paper is organized as follows: in the section ‘PNSL and the modified geodesic equation’, PNSL with time-dependent coefficient is revised, and the corresponding modified geodesic equation is introduced. In the section ‘A cosmological application of G → G + H/ρa’, we discuss some main astrophysical and cosmological consequences. Finally in the last section, conclusions and perspectives are presented.

PNSL and the modified geodesic equation

The PNSL that will be considered in this paper is$L^{1+\gamma \left(t\right)}\left(t,\dot{q}\left(t\right),q\left(t\right)\right)$ (γ is a time-dependent parameter), and the corresponding action functional is$S={\displaystyle {\int }_a^b{L}^{1+\gamma \left(t\right)}\left(t,\dot{q}\left(t\right),q\left(t\right)\right)\mathit{dt}}$. Here$\left(t,\dot{q},q\right)\to L\left(t,\dot{q},q\right)$ is assumed to be a C² function,  q ∈ C¹([a, b]; ℝⁿ) is the generalized coordinate,$\dot{q}=\mathit{dq}/\mathit{dt}$, and$L\left(t,\dot{q},q\right)\in C^2\left(\left[a,b\right]\times {ℝ}^n\times {ℝ}^n;ℝ\right)$ is the Lagrangian. It is easy to check that any admissible function q ∈ C¹[a, b] subject to given boundary conditions q(a) = q _a and q(b) = q _b for which the action functional has an extremum satisfies the following Euler-Lagrange equations[17]:

$$\frac{\partial L}{\partial q}-\frac{d}{\mathit{dt}}\left(\frac{\partial L}{\partial \dot{q}}\right)=\frac{\gamma \left(t\right)}{L}\frac{\partial L}{\partial \dot{q}}\left(\frac{\partial L}{\partial t}+\dot{q}\frac{\partial L}{\partial q}+\ddot{q}\frac{\partial L}{\partial \dot{q}}\right)+\frac{1}{1+\gamma \left(t\right)}\frac{\mathit{d\gamma }\left(t\right)}{\mathit{dt}}\frac{\partial L}{\partial \dot{q}}$$

(1)

We would like to apply this result to compute the geodesics for a given metric. The mathematical translation from classical mechanics to differential geometry is discussed in any graduate textbook (see[42] for details). We use the Einstein summation convention in which we sum over repeated indices which occur as a subscript and superscript pair. In order to obtain the modified geodesic equation, we use naturally the variational principle. In the language of differential geometry, the variational principle states that any freely falling test particles follow a certain path between two fixed points in curved spacetime which extremize the proper time. This is one of the basic postulates of Einstein's general relativity (EGR). In what follows, we set for convenience τ the proper time. Besides, we work in units ℏ = c = 1 with a metric sign (-, +, +, +).

In EGR, the action is maximum for straight paths and the path length is S = ∫Ldτ where$L=\left(1/2\right)g_{\mathit{\mu \nu }}{\dot{x}}^{{}^{\mu }}{\dot{x}}^{{}^{\nu }}$, where g _μν is the covariant spacetime metric tensor. The jump from classical mechanics to differential geometry is therefore realized by making the change$\left(t,\dot{q},q\right)\to \left(\tau ,{\dot{x}}^{\mu },x^{\mu }\right)$ where${\dot{x}}^{\mu }=d{x}^{\mu }/\mathit{d\tau }$. In this context, we can rewrite Equation 1 as

$$\frac{\partial L}{\partial x^{\alpha }}-\frac{d}{\mathit{d\tau }}\left(\frac{\partial L}{\partial {\dot{x}}^{\alpha }}\right)=\frac{\gamma \left(\tau \right)}{L}\frac{\partial L}{\partial {\dot{x}}^{\alpha }}\left(\frac{\partial L}{\partial \tau }+{\dot{x}}^{\alpha }\frac{\partial L}{\partial x^{\alpha }}+{\ddot{x}}^{\alpha }\frac{\partial L}{\partial {\dot{x}}^{\alpha }}\right)+\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}\frac{\partial L}{\partial {\dot{x}}^{\alpha }}$$

(2)

After replacing$L=\left(1/2\right)g_{\mathit{\mu \nu }}{\dot{x}}^{\mu }{\dot{x}}^{\nu }$ into Equation 2, we find after simple algebra

$$\begin{array}{l}\underset{\mathrm{standard}\mathrm{part}}{\underbrace{{\ddot{x}}^{\nu }+{\Gamma }_{\mathit{\gamma \delta }}^{\nu }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }}}\\ +\underset{\text{extra}‒\text{part}}{\underbrace{\frac{2\gamma \left(\tau \right)}{g_{\mathit{\mu \nu }}{\dot{x}}^{\mu }}\left(\frac{1}{2}{g}_{\mathit{\gamma \delta },\alpha }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }{\dot{x}}^{\alpha }+{\ddot{x}}^{\alpha }{g}_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }\right)+\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}{\dot{x}}^{\nu }}}=0\end{array}$$

(3)

Here${\Gamma }_{\mathit{\alpha \beta }}^{\nu }$ are the Christoffel connection coefficients of the metric g _αβ defined by[45]

$${\Gamma }_{\mathit{\alpha \beta }}^{\nu }=\frac{1}{2}{g}^{\mathit{\nu \gamma }}\left[g_{\mathit{\alpha \gamma },\beta }+g_{\mathit{\gamma \beta },\alpha }-g_{\mathit{\alpha \beta },\gamma }\right]$$

(4)

where g_αβ,γ = ∂g _αβ /∂x^γ and so on.

Remark 1 The well-known reparametrization invariance procedure is unable to bring the equations of motion (3) into the standard form even on-shell. Therefore, we expect new physics to be obtained from the present approach by choosing a different action for particles in relativity.

The calculation is straightforward: in fact, from$L=\frac{1}{2}{g}_{\mathit{\mu \nu }}{\dot{x}}^{\mu }{\dot{x}}^{\nu }$, we get$\partial L/\partial {\dot{x}}^{\alpha }=g_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }$ and$\partial L/\partial x^{\alpha }=g_{\mathit{\gamma \delta },\alpha }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }/2$. After replacing into Equation 2, we find

$$\begin{array}{l}\frac{1}{2}{g}_{\mathit{\gamma \delta },\alpha }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }-\frac{d}{\mathit{d\tau }}{g}_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }=\frac{2\gamma \left(\tau \right)}{g_{\mathit{\mu \nu }}{\dot{x}}^{\mu }{\dot{x}}^{\nu }}{g}_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }\\ \times \left(\frac{1}{2}{g}_{\mathit{\gamma \delta },\alpha }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }{\dot{x}}^{\alpha }+{\ddot{x}}^{\alpha }{g}_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }\right)\\ +\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}{g}_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }\end{array}$$

(5)

Using$d{g}_{\mathit{\gamma \alpha }}/\mathit{d\tau }=g_{\mathit{\gamma \alpha },\delta }{\dot{x}}^{\delta }$, multiplying both sides of Equation 5 by g^να and using$g^{\mathit{\nu \alpha }}{g}_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }={\dot{x}}^{\nu }$, we find

$$\begin{array}{l}{\ddot{x}}^{\nu }-g^{\mathit{\nu \alpha }}\left(\frac{1}{2}{g}_{\mathit{\gamma \delta },\alpha }-g_{\mathit{\gamma \alpha },\delta }\right){\dot{x}}^{\gamma }{\dot{x}}^{\delta }\\ +\frac{2\gamma \left(\tau \right)}{g_{\mathit{\mu \nu }}{\dot{x}}^{\mu }{\dot{x}}^{\nu }}{\dot{x}}^{\nu }\left(\frac{1}{2}{g}_{\mathit{\gamma \delta },\alpha }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }{\dot{x}}^{\alpha }+{\ddot{x}}^{\alpha }{g}_{\mathit{\gamma \alpha }}{\dot{x}}^{\gamma }\right)\\ +\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}{\dot{x}}^{\nu }=0\end{array}$$

(6)

With the help of$g_{\mathit{\gamma \alpha },\delta }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }=g_{\mathit{\alpha \delta },\gamma }{\dot{x}}^{\gamma }{\dot{x}}^{\delta }$ and Equation 4, we effortlessly find Equation 3 which may also be written in the following useful form:

$$\begin{array}{l}\frac{d{x}^{\mu }}{\mathit{d\tau }}\left(\underset{\mathrm{standard}\mathrm{part}}{\underbrace{\frac{d^2{x}^{\nu }}{d{\tau }^2}+{\Gamma }_{\mathit{\gamma \delta }}^{\nu }\frac{d{x}^{\gamma }}{\mathit{d\tau }}\frac{d{x}^{\delta }}{\mathit{d\tau }}}}\right)\\ +\underset{\mathrm{extra}\mathrm{part}}{\underbrace{\begin{array}{l}\frac{2\gamma \left(\tau \right)}{g_{\mathit{\mu \nu }}}\left(\frac{1}{2}{g}_{\mathit{\gamma \delta },\alpha }\frac{d{x}^{\gamma }}{\mathit{d\tau }}\frac{d{x}^{\delta }}{\mathit{d\tau }}\frac{d{x}^{\alpha }}{\mathit{d\tau }}+g_{\mathit{\gamma \alpha }}\frac{d{x}^{\gamma }}{\mathit{d\tau }}\frac{d^2{x}^{\alpha }}{d{\tau }^2}\right)\\ +\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}\frac{d{x}^{\mu }}{\mathit{d\tau }}\frac{d{x}^{\nu }}{\mathit{d\tau }}\end{array}}}=0\end{array}$$

(7)

It is obvious that for γ = 0, Equation 7 is reduced to the standard geodesic form. The importance of the last term in Equation 7 which concerns the variation of γ (τ) with time will be appreciated in the next subsection.

Remark 2 If we set γ(τ) ∝ τ^- x, x > 0, then Equation 7 is reduced for a very large time to its standard form as$\underset{\tau \to \infty }{lim}\gamma \left(\tau \right)\to 0$ and$\underset{\begin{array}{l}\tau \to \infty \\ x>0\end{array}}{\text{lim}}\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}=\underset{\begin{array}{l}\tau \to \infty \\ x>0\end{array}}{\text{lim}}-\frac{x}{1+{\tau }^x}\frac{1}{\tau }\to 0$.

We consider the motion of a particle of mass m assumed to be slowly moving in a time-dependent stationary field. The limit of slow motion reduces the Christoffel symbol to:

$${\Gamma }_{00}^{\nu }=\frac{1}{2}{g}^{\mathit{\nu \alpha }}\left[g_{0\alpha ,0}+g_{\alpha 0,0}-g_{00,\alpha }\right]=-\frac{1}{2}{g}^{\mathit{\nu i}}{g}_{00,i}+\frac{1}{2}{g}^{\nu 0}{g}_{00,0}$$

(8)

We follow the standard formalism and perform the perturbation g _αβ (xⁱ, τ) = η _αβ  + h _αβ (xⁱ, τ) (small deviation from a Minkowski flat spacetime) with g^αβ(xⁱ, τ) = η^αβ - h^αβ(xⁱ, τ) since g _δβ g^αβ = δ^α _δ with |h _αβ (xⁱ, τ)|  <   <  1. The Minkowski metric η is constant, whereas h _αβ (xⁱ, τ) is time-dependent since the gravitational field is assumed to be nonstationary. To the first order, the Christoffel symbol takes the form

$${\Gamma }_{00}^{\nu }=-\frac{1}{2}{\eta }^{\mathit{\nu i}}{h}_{00,i}+\frac{1}{2}{\eta }^{\nu 0}{\widehat{h}}_{00,0}$$

(9)

In fact we assumed that$h_{00}\left(x^i,\tau \right)=h_{00}\left(x^i\right)+{\widehat{h}}_{00}\left(\tau \right)$, where${\widehat{h}}_{00}\left(\tau \right)$ is expected to be the time-dependent gravitational potential correction to h₀₀(xⁱ). We accordingly find${\Gamma }_{00}^0=\frac{1}{2}{\eta }^{00}{\widehat{h}}_{00,0}$ and${\Gamma }_{00}^j=-\frac{1}{2}{\eta }^{\mathit{ji}}{h}_{00,i}$. For ν = 0, since dxⁱ/dτ = O(ϵ), we get

$$\begin{array}{l}\left(1+2\gamma \left(\tau \right)\right)\frac{d^2{x}^0}{d{\tau }^2}+\left(-\frac{1}{2}+\gamma \left(\tau \right)\frac{1}{h_{00}-1}\right){\widehat{h}}_{00,0}\frac{d{x}^0}{\mathit{d\tau }}\frac{d{x}^0}{\mathit{d\tau }}\\ +\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}\frac{d{x}^0}{\mathit{d\tau }}=0\end{array}$$

(10)

As in general |h₀₀|  <   <  1, we can approximate Equation 10 by

$$\frac{d^2{x}^0}{d{\tau }^2}-\left(\frac{1}{2}{\widehat{h}}_{00,0}\frac{d{x}^0}{\mathit{d\tau }}-\frac{1}{\left(1+\gamma \left(\tau \right)\right)\left(1+2\gamma \left(\tau \right)\right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}\right)\frac{d{x}^0}{\mathit{d\tau }}=0$$

(11)

For ν = j and then i = j, we get with |h _ii | < < 1

$$\begin{array}{l}\frac{d^2{x}^i}{d{\tau }^2}-\frac{1}{2}{h}_{00,i}\frac{d{x}^0}{\mathit{d\tau }}\frac{d{x}^0}{\mathit{d\tau }}+2\gamma \left(\tau \right)\left(\frac{1}{2}{\widehat{h}}_{00,0}\frac{d{x}^0}{\mathit{d\tau }}\frac{d{x}^0}{\mathit{d\tau }}-\frac{d^2{x}^0}{d{\tau }^2}\right)\\ +\frac{1}{1+\gamma \left(\tau \right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}\frac{d{x}^0}{\mathit{d\tau }}=0\end{array}$$

(12)

Using Equation 11, we can rewrite Equation 12 as

$$\frac{d^2{x}^i}{d{\tau }^2}-\left(\frac{1}{2}{h}_{00,i}\frac{d{x}^0}{\mathit{d\tau }}-\frac{4\gamma \left(\tau \right)+1}{\left(1+\gamma \left(\tau \right)\right)\left(1+2\gamma \left(\tau \right)\right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}\right)\frac{d{x}^0}{\mathit{d\tau }}=0$$

(13)

Up to this stage, the situation seems complicated as we ignore the form of γ(τ) of which we are aware from the beginning that it may take a large number of forms. However, one particular class of solution may be extracted from Equation 11. If we set the factor inside the parenthesis equal to zero, then${\ddot{x}}^0\equiv d^{2}t/d{\tau }^2=0$, i.e.,${\dot{x}}^0\equiv \mathit{dt}/\mathit{d\tau }=k=$ constant. In that case, we have

$$\frac{1}{\left(1+\gamma \left(\tau \right)\right)\left(1+2\gamma \left(\tau \right)\right)}\frac{\mathit{d\gamma }\left(\tau \right)}{\mathit{d\tau }}=\frac{k}{2}{\widehat{h}}_{00,0}$$

(14)

and therefore, after simple integration, we get

$${\widehat{h}}_{00}\left(\tau \right)=\frac{2}{k}log\frac{2\gamma \left(\tau \right)+1}{\gamma \left(\tau \right)+1}$$

(15)

where we assumed that when γ(τ) = 0,${\widehat{h}}_{00}=0$. This solution seems interesting as in that case Equation 13 is simplified directly to

$$\frac{d^2{x}^i}{d{\tau }^2}-\frac{1}{2}{h}_{00,i}+\left(4\gamma \left(\tau \right)+1\right)\frac{k}{2}{\widehat{h}}_{00,0}=0$$

(16)

This equation may be written in the following useful form

$$\frac{d^2{x}^i}{d{\tau }^2}=\frac{1}{2}{\nabla }_i{h}_{00}-\left(4\gamma \left(\tau \right)+1\right)\frac{k}{2}\frac{d{\widehat{h}}_{00}}{\mathit{d\tau }}\equiv \frac{1}{2}{\nabla }_i{h}_{00}+{\Delta }_{\tau }{h}_{00}$$

(17)

where

$${\Delta }_{\tau }{h}_{00}=-\left(4\gamma \left(\tau \right)+1\right)\frac{k}{2}\frac{d{\widehat{h}}_{00}}{\mathit{d\tau }}$$

(18)

is the time-dependent gravitational potential correction to h ₀₀ . It is noticeable that if h ₀₀ is time-independent, then Equation 17 is reduced to its standard from. If now we expect that near the spherical body the gravitational potential in spherical symmetry is Φ(r) = - MG/r, then we get h₀₀ = - 2Φ(r). As discussed in the introductory text of this work, the assumption that the time-dependent gravitational potential correction decreases linearly or almost linearly with time is very appealing due to what it may explain at both the astrophysical and cosmological levels. Motivated by this argument, we postulate that

$$\gamma \left(\tau \right)=-\frac{e^{\tau }-1}{2e^{\tau }-1}$$

(19)

which gives making use of Equation 16${\widehat{h}}_{00}\left(\tau \right)=-2\tau /k$ which is a linearly decreasing time-dependent gravitational potential. In that case, Equation 17 is reduced to

$$\frac{d^2{x}^i}{d{\tau }^2}-\frac{1}{2}{h}_{00,i}+\frac{2e^{\tau }-3}{2e^{\tau }-1}\frac{2}{k}=0$$

(20)

To find k, we follow the arguments of[15, 16]: for a light starting from a certain star with a frequency ν₀(τ = 0), then its frequency at time τ is given according to the principle of general relativity by$\nu \left(\tau \right)=\nu \left(\tau =0\right)\left(1+\tau \left((d{\widehat{h}}_{00}/\mathit{d\tau }\right)\right)$. Now for R = τ, we get$\nu \left(\tau \right)=\nu \left(\tau =0\right)\left(1+R\left((d{\widehat{h}}_{00}/\mathit{d\tau }\right)\right)$. If we compare this equation with the Hubble law ν(τ) = ν(τ = 0)(1 - RH)) where H ≈ 60–70 km/s/Mpc is the Hubble constant, then we find$d{\widehat{h}}_{00}\left(\tau \right)/\mathit{d\tau }=-2/k=-H$, i.e., k = 2/H. In that case, we can now write Equation 20 as

$$\frac{d^2{x}^i}{d{\tau }^2}+{\nabla }_i\Phi +\frac{2e^{\tau }-3}{2e^{\tau }-1}H=0$$

(21)

This equation represents the modified Newton's law in the PNSL approach with a time-dependent coefficient. We can define the total gravitational potential by

$${\Phi }_{\mathrm{total}}\left(x^i,\tau \right)=\Phi +\frac{2e^{\tau }-3}{2e^{\tau }-1}H{x}^i$$

(22)

so that Equation 21 is reduced to

$$\frac{d^2{x}^i}{d{\tau }^2}+{\nabla }_i{\Phi }_{\mathrm{total}}=0$$

(23)

At a very large time, Φ_total(xⁱ, ∞) = Φ + Hxⁱ, whereas at the origin of time, we find Φ_total(xⁱ, 0) = Φ - Hxⁱ. In units where c ≠ 1, we find Φ_total(xⁱ, ∞) = Φ + Hcxⁱ and Φ_total(xⁱ, 0) = Φ - Hcxⁱ. During the cosmological evolution of the universe, the effective gravitational potential can change sign.

Remark 3 In Cartesian coordinates, i.e., xⁱ = (x, y, z), we can write in units c ≠ 1

$$\begin{array}{l}{\Phi }_{\mathrm{total}}\left(x^i,\tau \right)=-\frac{\mathit{MG}}{x^i}+\frac{2e^{\tau }-3}{2e^{\tau }-1}\mathit{Hc}{x}^i\\ =-\frac{M\left(G+G_{\mathrm{effective}}\right)}{x^i}\end{array}$$

(24)

where

$$G_{\mathrm{effective}}=-\frac{2e^{\tau }-3}{2e^{\tau }-1}\mathit{cH}\frac{x^i{x}^i}{M}$$

(25)

If we model the universe as a ball of radius α and mass M ∝ ρa³, then xⁱxⁱ ∝ a² because the distance to an object that is receding with the expansion of the universe is proportional to the cosmic scale factor α. In that case and mainly at a very large time, |G_effective| ∝ Hca²/ρa³ = Hc/ρa, i.e., ρ|G_effective| ∝ Hc/a. This equation is interesting as it shows that the effective gravitational constant varies with time since it depends on the evolution of the scale factor and the density of the universe. A cosmological implication of the effective gravitational constant is discussed in the next section.

Remark 4 In fact, the complete dynamical description, i.e., the presence of matter and energy curves of the ambient spacetime is obtained making use of Einstein's field equation (EFE) which is nothing else but the general relativity analog of the Poisson equation. In other words, EFE reduces to Newton's law of gravity by using both the weak-field and the slow-motion approximations, i.e., time derivatives are much smaller than spatial derivatives and, consequently, the gravitational coupling constant appears in the EFE which takes the form[45]: R _αβ  - g _αβ R/2 = 8πGT _αβ where R _αβ is the Riemann tensor, R is the Ricci tensor, T _αβ is the stress energy tensor defined by T _αβ  = (p + ρ)u _α u _β  + pg _αβ for matter component, p and ρ are respectively the pressure of the perfect barotropic fluid, and μ _α is the fluid rest frame four-velocity. In our approach, EFE is not modified and keeps its standard form.

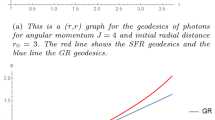
From an astrophysical point of view, it is recognizable that the Schwarzschild spacetime metric is a solution of EFE that describes a gravitational field exterior to an isolated sphere assumed to be at rest. In fact, this special solution has played an important role in general relativity. It should be stressed at this stage that if we assume the usual Schwarzschild spacetime characterized in symmetric spherical coordinates by the metric$d{s}_{\mathrm{static}}^2=-e^{2m\left(r\right)}d{t}^2+e^{2n\left(r\right)}d{r}^2+r^2\left(d{\theta }^2+{sin}^2\mathit{\theta d}{\varphi }^2\right)$then the metric is time-independent, and from Equation 14, it follows that γ(τ) is constant. In such a case, the system results in the standard Schwarzschild solution. However, it was argued that a Schwarzschild spacetime with a time-dependent metric is suitable for the description of the interior black hole solution[46]. At the interior of a black hole Schwarzschild solution, nature changes its properties. A remarkable switch occurs between the external spatial radial and temporal coordinates[47–50]. That is the main reason an interior solution is time-dependent and far from being stationary. A singularity occurs at a space like a hypersurface at the origin of time, and accordingly, observing the physical effects of this singularity is somewhat not viable. Therefore, one expects that solutions obtained at this stage will be practical if one would like to describe a particular spacetime characterized by the metric$d{s}_{\mathrm{time}‒\mathrm{dependent}}^2=-e^{2m\left(t\right)}d{t}^2+e^{2n\left(t\right)}d{r}^2+t{}^2\left(d{\theta }^2+{sin}^2\mathit{\theta d}{\varphi }^2\right)$[46] which is suitable for the description of the interior black hole solution. It is not the aim of the present work to discuss the physics inside a black hole, yet it is an interesting topic that deserves a future analysis.

A cosmological application of G → G + H/ρa

To illustrate, we discuss briefly for completeness the gravitational relaxation on the flat Friedmann-Robertson-Walker (FRW) metric given by ds² = - dτ² + a²(τ)[dr² + r²(dθ² + sin ²θdφ²)] where α(τ) is the scale factor. Mainly, we will concentrate on the late-time dynamics. We stress that our aim is not to discuss the whole cosmological scenario but simply to present the basic consequences of G → G + H/ρa.

With the replacement G → G + H/ρa, the first of the Friedmann equation in the presence of a time-dependent cosmological constant Λ(τ) is[51]

$$H^2=\frac{{\dot{a}}^2}{a^2}=\frac{8\mathit{\pi G\rho }}{3}+\frac{\Lambda \left(\tau \right)}{3}+\frac{8\mathit{\pi H}}{3a}$$

(26)

where$H=\dot{a}/a$ is the Hubble parameter, and ρ is the energy density of the (perfect) cosmological fluid. The dot represents the derivative with respect to τ. We shall assume that the equation of state for the cosmological matter is p = γρ, where γ is a constant and p is the corresponding pressure. To leading order, the corrections to the Friedmann equation can be parameterized - H/a. In what follows, we conjecture that the cosmological constant varies as Λ = 8πH/a. There exist in the literature lots of phenomenological ansatzs for the variation of the cosmological constant with time ([52] and references therein). However, to the best of our knowledge, the ansatz introduced here is completely new. The usual conservation of the energy-momentum tensor$T_{;\beta }^{\mathit{\alpha \beta }}=0$ results in two useful relations:$\dot{\rho }+3H\left(p+\rho \right)=0$ and$\dot{\Lambda }+8\pi \dot{G}\rho =0$. The first equation gives ρ(a) = ρ₀(a/a₀)^{- 3(1 + γ)} where ρ₀ = ρ(a = a₀), whereas the second equation may be written after performing the following replacement:

$$\dot{G}\to -\frac{\dot{H}}{\mathit{\rho a}}+\frac{H\dot{\rho }}{{\rho }^{2}a}-\frac{H\dot{a}}{\rho a^2},$$

(27)

as

$$2\frac{\dot{H}}{H}-2\frac{\dot{a}}{a}-\frac{\dot{\rho }}{\rho }=0$$

(28)

Equation 28 after simple integration gives H² = Cρa² where C is an integration constant. The cosmological constant varies subsequently as$\Lambda =8\mathit{\pi H}/a\propto \sqrt{\rho }$. Accordingly, Equation 26 takes the form

$$\frac{{\dot{a}}^2}{a^2}=\frac{8\mathit{\pi G\rho }}{3}+A\sqrt{\rho }$$

(29)

where A = 16πC/3. This equation is interesting as it is similar to the Cardassian model proposed by Freese and Lewis to explain the current accelerated expansion of the universe[53]. The effective gravitational constant is then replaced by G → G + Cρ^-1/2. Now with the help of ρ(a) = ρ₀(a/a₀)^{- 3(1 + γ)}, we can write Equation 29 as

$${\dot{a}}^2=B{a}^{-\left(1+3\gamma \right)}+A{a}^{\left(1-4\gamma \right)/2}$$

(30)

where B = 8πGρ₀(1/a₀)^{- 3(1 + γ)}. We set for convenience A = B = 1. This equation seems interesting as for γ = 0 (pressureless matter), the solution of${\dot{a}}^2=a^{-1}+a^{1/2}$ with the initial condition α(0) = 0 is a(τ) ∝ τ^4/3 which corresponds to an accelerated universe without the need of the dark energy component. In general, one expects that the term$A\sqrt{\rho }$ is initially negligible, but it dominates the universe at redshift z ≈ O(1), as indicated by supernova observations[54, 55]. Once it dominates, the universe starts it accelerated expansion, and in that case, we can neglect the first term on the RHS of Equation 29 with respect to$A\sqrt{\rho }$. Therefore, the scale factor evolves like${\dot{a}}^2\propto a^{\left(1-4\gamma \right)/2}$. For γ = 0, we find a(t) ∝ τ^4/3 as it is expected. Accordingly, the energy density decays like ρ ∝ a^- 3 = τ^- 4, whereas the cosmological constant and the effective gravitational constant vary respectively as Λ ∝ τ^- 2 and G_effective ∝ τ ². In reality, a number of authors have argued in favor of the decaying law Λ ∝ τ^- 2 ([52] and references therein). The time variation of the gravitational constant is not new and is well discussed largely in literature ([52] and references therein).

It is interesting to fall into the Cardassian model from nonstandard Lagrangians and mainly the PNSL with a time-dependent coefficient. This model has been confronted largely by cosmic observations, and for recent result, the authors are referred to[56].

Conclusions and perspectives

In this work, we have tried to prove that nonstandard Lagrangians are extremely important and deserve special attention. Starting from a power-law nonstandard Lagrangian characterized by a time-dependent coefficient, we have applied the basic machinery of the calculus of variations to differential geometry and in particular to general relativity. We have derived the modified geodesic equation and have proven that the presence of a time-dependent coefficient is directly connected to a time-dependent gravitational potential. As a TDGP is typical for the description of the interior black hole solution, we expect that our approach will have a large number of applications. We have proven as well that for the case of an expanding universe, the gravitational constant is replaced by G → G + H/ρa and that the resulting FRW cosmological model is similar to the Cardassian cosmology without referring to quantum corrections or brane approach. We anticipate that our formalism can be applied effectively to a wide range of astrophysical and cosmological problems. It is noteworthy that nonstandard Lagrangians introduced in this manuscript as well as by other authors are simply generating functions of different equations of motions. One naturally asks if they have any obvious meaning, and therefore it seems that they are more interesting for mathematicians than for physicists. In fact, this is an open problem which is still in its infancy and much work is required. Obtaining most dynamical equations through generating Lagrangian functions have been shown by mathematicians, who have also demonstrated that there is an infinite number of such functions. In this work, we have just found one of them out of an infinite set.

It would be interesting to consider in a future work more generalized forms of NSL, to discuss their implications in different approaches in cosmology and astrophysics, and to compare them with new approaches[57–61]. Finally, it was observed that nonstandard Lagrangians result in the violation of the weak equivalence principle. It is notable at the end that in[62], it was argued that nonconservative gravitational field equations result in a cosmological model with a locally varying Einstein's lambda. A number of phenomenological theories do not hold this property; however, they are also motivating[63]. This problem should be addressed carefully as well in the future.