1 Introduction

Einstein’s field equations in general relativity predict that the curvature is produced not only by the distribution of mass-energy but also by its motion [4]. Candidate metric geometries that can intrinsically describe the motion are the Finsler and Finsler-like geometries which constitute metrical generalizations of Riemannian geometry and depend on position and velocity/momentum/scalar coordinates. These are dynamic geometries that can describe locally anisotropic phenomena and Lorentz violations [5,6,7,8,9,10,11,12,13,14,15] as well as with field equations, FRW and Raychaudhuri equations, geodesics, dark matter and dark energy effects [16,17,18,19,20,21]. By considering this approach, the gravitational field is interpreted as the metric of a generalized spacetime and constitutes a force-field which contains the motion. This possibility reveals the Finslerian geometrical character of spacetime.

In the framework of applications of Finsler geometry, many works in different directions of geometrical and physical structures have contributed to the extension of research for theoretical and observational approaches during the last years. We cite some works from the literature of the applications of Finsler geometry [7, 8, 13, 21,22,23,24,25,26,27,28,29,30,31,32].

In the first period of development of applications of Finsler geometry to Physics, especially to General Relativity, remarkable works were published by Randers [33], Horváth [34] and Moór [35]. Later, Einstein’s field equations were formulated in the Finslerian framework by the works of Horváth [34, 35], Takano [36] and Ikeda [37]. In these studies, the field equations had been considered without calculus of variations. Asanov [38] explored the Finslerian gravitational field by using Riemannian osculating methods and derived Einstein field equations using the variational principle. A class of Finsler spaces (FR standing for Finsler–Randers) originated by Randers [33] who studied the physical properties of spacetime with an asymmetrical metric which provides the uni-direction of time-like intervals. This consideration gives a particular interest in a generalized metric structure of the Riemannian spacetime. Based on this form of spacetime, it is possible to investigate the gravitational field with more degrees of freedom in the framework of a tangent/vector/scalar bundle [31, 39, 40]. The FR cosmological model was first introduced in [41, 42]. It is of special interest since the Friedmann equations include an extra geometrical term that acts as a dark energy-fluid. The Finsler–Randers-type spacetime can be considered as a direction-dependent motion of the Riemannian/FRW model.

The local anisotropic structure of spacetime affects the gravitational field and leads to modified cosmological considerations. Based on Finsler or Finsler-like cosmologies, the Friedmann equations include extra terms which influence the cosmological evolution [17, 20, 31, 39]. When Lorentz symmetry holds, the spacetime is isotropic in the sense that all directions and uniform motions are equivalent. The introduction of a vector field in the structure of spacetime causes relativity violations and local anisotropy which arise from breaking the Lorentz symmetry and which affect the metric, curvature, geodesics and null cone [43,44,45,46,47,48,49,50].

In the framework of modified gravitational theories with Finsler–Randers type structure, two fundamental theories of investigation for the gravitation and cosmology can be developed. The first one is connected with the Friedmann–Finsler–Randers cosmological model and the second one is related to the study of SFR spacetime.

The introduction of a force field causes an asymmetry to a pseudo-Finslerian metric. Asymmetrical and locally anisotropic models such as Finsler–Randers spacetime can be connected with the chiral fields in Cosmology for descriptions of the inflationary epoch and the present accelerated expansion of the Universe [51].

An FR space has a metric function of the form

$$\begin{aligned} F(x,y) = (-a_{\mu \nu }(x)y^{\mu }y^{\nu })^{1/2} + u_{\alpha }y^{\alpha } \end{aligned}$$
(1)

where \(u_{\alpha }\) is a covector with \(||u_{\alpha }||\ll 1\), \(y^{\alpha }=\frac{dx^{\alpha }}{d\tau }\) and \(a_{\mu \nu }(x)\) is a pseudo-Riemannian metric for which the Lorentzian signature \((-,+,+,+)\) has been assumed and the indices \(\mu , \nu , \alpha \) take the values 0, 1, 2, 3. The geodesics of this space can be produced by (1) and the Euler–Lagrange equations. If \(u_{\alpha }\) denotes a force field \(f_{\alpha }\) and \(y^{\alpha }\) is substituted with \(d x^{\alpha }\) then \(f_{\alpha }dx^{\alpha }\) represents the spacetime effective energy produced by the anisotropic force field \(f_{\alpha }\), therefore Eq. (1) is written as

$$\begin{aligned} F(x,dx) = \left( -a_{\mu \nu }(x)dx^{\mu }dx^{\nu }\right) ^{1/2} + f_{\alpha }dx^{\alpha } \end{aligned}$$
(2)

This form of metric provides a dynamical effective structure of spacetime. A small differentiation is presented between GR and the FR gravitation model. This is because of the work provided by the one-form \(A_{\gamma }\) which gives an external motion to the Riemannian spacetime. This motion is an internal concept for the FR spacetime.

A cosmological model can be introduced by Eq. (2) if we assume the FRW cosmological metric instead of the general type of the Riemannian one [41, 42]. In this case, we get a Friedmann–Finsler–Randers cosmological model in the following form

$$\begin{aligned} a_{\mu \nu }(x) = \textrm{diag}\left[ -1,\frac{a^2}{1-\kappa r^{2}},a^{2}r^{2}, a^{2}r^{2}\sin ^{2}\theta \right] \end{aligned}$$
(3)

This model was also further studied later in [9, 21, 52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68].

In this work, we will follow the SFR model presented in [1]. The metric \(g_{\mu \nu }\) is the classic Schwarzschild one:

$$\begin{aligned} g_{\mu \nu }\textrm{d}x^\mu \textrm{d}x^\nu = -fdt^2 + \frac{dr^2}{f} + r^2 d\theta ^2 + r^2 \sin ^{2}\theta \, d\phi ^2 \end{aligned}$$
(4)

with \(f=1-\frac{R_s}{r}\) and \(R_s=2GM\) the Schwarzschild radius (we assume units where the speed of light \(c=1\)).

Hereafter, we consider an \(\alpha \)-Randers type metric as the one in Eq. (1) which is distinguished from the \(\beta \)-Randers type metric that is investigated in the Standard Model Extension (SME) [7, 8, 11, 46].

The metric \(v_{\alpha \beta }\) is derived from a metric function \(F_v\) of the \(\alpha \)-Randers type [1]:

$$\begin{aligned} F_v = \sqrt{-g_{\alpha \beta }(x)y^\alpha y^\beta } + A_\gamma (x) y^\gamma \end{aligned}$$
(5)

where \(g_{\alpha \beta }=g_{\mu \nu }{\tilde{\delta }}^{\mu }_{\alpha }{\tilde{\delta }}^{\nu }_{\beta }\) is the Schwarzschild metric from Eq. (4) and \(A_{\gamma }(x)\) is a covector which expresses a deviation from general relativity, with \(|A_\gamma (x)|\ll 1\), i.e., we assume that the deviation is small. In this work, we continue the investigation of the Schwarzschild–Finsler–Randers spacetime (SFR) which has been studied in previous works by a subset of the present authors [1, 2].

In this article, we examine the influence of extra gravitational effect which is imprinted in the geodesics of an SFR spacetime and we compare it with that of GR case. We prove that the additional amount of energy included in the equation of geodesics (see Eqs. (28)–(31)) stems from the geometry and the form of the SFR model.

This approach is also applied in the Newtonian gravitational theory and we obtain an interesting relation between the fundamental term \(A_{0}(r)\) of SFR gravitational theory and the Newtonian potential. This relation also provides a physical interpretation of the extra term \(A_{0}(r)\) in the Newtonian framework.

In addition, we calculate the deflection angle for the SFR model and we compare its value with that of the GR case. We also show that there is a relation between the deflection angle of SFR and of Shapiro et al. [3] observational result of the deflection angle for very small angles (\(\phi \approx 0\)) near a fiducial geodesic.

The present work is organized as follows. The structure of the model is given in Sect. 2. In this framework, the geodesics are studied and a dynamical analysis is presented in Sect. 3. We also compare our results with GR and discuss the corresponding similarities and differences and we give an application to the Newtonian framework. A dynamical analysis for the effective potential of this spacetime is provided in the Sect. 4, where upon suitable assumptions, the phase portraits of both models (SFR and GR) are presented. In Sect. 5, we study the deflection angle of the SFR spacetime and we compare it with very small values of the deflection angle of Shapiro et al. [3]. Finally, the conclusions of our study and some possible directions for future exploration are presented in Sect. 6.

2 Basic structure of the model

In this section, we briefly present the underlying geometry of the SFR gravitational model, as well as the field equations for the SFR metric. The solution of these equations for this metric is presented at the end of the section. An extended study of this model can be found in [1, 40]. The Lorentz tangent bundle TM is a fibered 8-dimensional manifold with local coordinates \(\{x^\mu ,y^\alpha \}\) where the indices of the x variables are \(\kappa ,\lambda ,\mu ,\nu ,\ldots = 0,\ldots ,3\) and the indices of the y variables are \(\alpha ,\beta ,\ldots ,\theta = 4,\ldots ,7\). The tangent space at a point of TM is spanned by the so-called adapted basis \(\{E_A\} =\,\{\delta _\mu ,{\dot{\partial }}_\alpha \} \) with

$$\begin{aligned} \delta _\mu = \dfrac{\delta }{\delta x^\mu }= \dfrac{\partial }{\partial x^\mu } - N^\alpha _\mu (x,y)\dfrac{\partial }{\partial y^\alpha } \end{aligned}$$
(6)

and

$$\begin{aligned} {\dot{\partial }}_\alpha = \dfrac{\partial }{\partial y^\alpha } \end{aligned}$$
(7)

where \(N^\alpha _\mu \) are the components of a nonlinear connection \(N=N^{\alpha }_{\mu }(x,y)\,\textrm{d}x^{\mu }\otimes \dot{\partial }_{\alpha }\).

The nonlinear connection induces a split of the total space TTM into a horizontal distribution \(T_HTM\) and a vertical distribution \(T_VTM\). The above-mentioned split is expressed with the Whitney sum:

$$\begin{aligned} TTM = T_HTM \oplus T_VTM \end{aligned}$$
(8)

The anholonomy coefficients of the nonlinear connection are defined as

$$\begin{aligned} \varOmega ^\alpha _{\nu \kappa } = \dfrac{\delta N^\alpha _\nu }{\delta x^\kappa } - \dfrac{\delta N^\alpha _\kappa }{\delta x^\nu } \end{aligned}$$
(9)

A Sasaki-type metric [69, 70] \(\mathcal {G}\) on TM is:

$$\begin{aligned} \mathcal {G} = g_{\mu \nu }(x,y)\,\textrm{d}x^\mu \otimes \textrm{d}x^\nu + v_{\alpha \beta }(x,y)\,\delta y^\alpha \otimes \delta y^\beta \end{aligned}$$
(10)

where we have defined the metrics \(g_{\mu \nu }\) and \(v_{\alpha \beta }\) to be pseudo-Finslerian.

A pseudo-Finslerian metric \( f_{\alpha \beta }(x,y) \) is defined as one that has a Lorentzian signature of \((-,+,+,+)\) and that also obeys the following form:

$$\begin{aligned} f_{\alpha \beta }(x,y) = \pm \frac{1}{2}\dfrac{\partial ^2 F^2}{\partial y^\alpha \partial y^\beta } \end{aligned}$$
(11)

where the function F satisfies the following conditions [69]:

  1. 1.

    F is continuous on TM and smooth on \( \widetilde{TM}\equiv TM\setminus \{0\} \), i.e., the tangent bundle minus the null set \( \{(x,y)\in TM | F(x,y)=0\}\) .

  2. 2.

    F is positively homogeneous of first degree on its second argument:

    $$\begin{aligned} F(x^\mu ,ky^\alpha ) = kF(x^\mu ,y^\alpha ), \qquad k>0 \end{aligned}$$
    (12)
  3. 3.

    The form

    $$\begin{aligned} f_{\alpha \beta }(x,y) = \dfrac{1}{2}\dfrac{\partial ^2 F^2}{\partial y^\alpha \partial y^\beta } \end{aligned}$$
    (13)

    defines a non-degenerate matrix:

    $$\begin{aligned} \det \left[ f_{\alpha \beta }\right] \ne 0 \end{aligned}$$
    (14)

where the plus-minus sign in (11) is chosen so that the metric has the correct signature.

In the following, we choose a non-linear connection with the following form:

$$\begin{aligned} N^\alpha _\mu = \frac{1}{2}y^\beta g^{\alpha \gamma }\partial _\mu g_{\beta \gamma } \end{aligned}$$
(15)

The metric tensor \(v_{\alpha \beta }\) is derived from (5) by using (11), after omitting higher order terms \(O(A^2)\):

$$\begin{aligned} v_{\alpha \beta }(x,y) = g_{\alpha \beta }(x) + h_{\alpha \beta }(x,y) \end{aligned}$$
(16)

where

$$\begin{aligned} h_{\alpha \beta } =&\,\, \frac{1}{\tilde{a}}(A_{\beta }g_{\alpha \gamma }y^\gamma + A_{\gamma }g_{\alpha \beta }y^\gamma + A_{\alpha }g_{\beta \gamma }y^\gamma ) \nonumber \\&+ \frac{1}{\tilde{a}^3}A_{\gamma }g_{\alpha \epsilon }g_{\beta \delta }y^\gamma y^\delta y^\epsilon \end{aligned}$$
(17)

with \(\tilde{a} = \sqrt{-g_{\alpha \beta }y^{\alpha }y^{\beta }}\). The total metric defined in the previous steps is called the Schwarzschild–Finsler–Randers (SFR) metric. As we can see, the term \(h_{\alpha \beta }(x,y)\) can be considered as a perturbation of the Schwarzschild metric since \(|A_\gamma (x)|\ll 1\).

The nonzero coefficients of a canonical and distinguished \(d-\)connection \(\mathcal D\) on TM are:

$$\begin{aligned} L^\mu _{\nu \kappa }&= \frac{1}{2}g^{\mu \rho }\left( \delta _kg_{\rho \nu } + \delta _\nu g_{\rho \kappa } - \delta _\rho g_{\nu \kappa }\right) \end{aligned}$$
(18)
$$\begin{aligned} L^\alpha _{\beta \kappa }&= \dot{\partial }_\beta N^\alpha _\kappa + \frac{1}{2}v^{\alpha \gamma }\left( \delta _\kappa v_{\beta \gamma } - v_{\delta \gamma }\,\dot{\partial }_\beta N^\delta _\kappa - v_{\beta \delta }\,\dot{\partial }_\gamma N^\delta _\kappa \right) \end{aligned}$$
(19)
$$\begin{aligned} C^\mu _{\nu \gamma }&= \frac{1}{2}g^{\mu \rho }\dot{\partial }_\gamma g_{\rho \nu } \end{aligned}$$
(20)
$$\begin{aligned} C^\alpha _{\beta \gamma }&= \frac{1}{2}v^{\alpha \delta }\left( \dot{\partial }_\gamma v_{\delta \beta } + \dot{\partial }_\beta v_{\delta \gamma } - \dot{\partial }_\delta v_{\beta \gamma }\right) \end{aligned}$$
(21)

See Appendix A for more details.

The field equations for our model have been derived in previous works and can be found in Appendix B. The solution of the field equations (B.29), (B.30) and (B.31) to first order in \(A_\gamma (x)\) in vacuum (\(T_{\mu \nu } = Y_{\alpha \beta } = \mathcal Z^\kappa _\alpha = 0\)) is [1]:

$$\begin{aligned} A_\gamma (x) = \left[ {\tilde{A}}_0 \left( 1-\frac{R_S}{r}\right) ^{1/2}, 0, 0, 0 \right] =\left[ {\tilde{A}}_0 f^{1/2}, 0, 0, 0 \right] \nonumber \\ \end{aligned}$$
(22)

with \({\tilde{A}}_0\) a constant. While this is an approximate solution, it will be sufficient for our purposes given the assumption \(|A_\gamma (x)|\ll 1\).

3 Geodesics

In this section, we will study the geodesics of the SFR and perform a dynamical analysis. We compare our results with the corresponding ones of GR. From the definition of the metric function (5) we have:

$$\begin{aligned} F(x,dx) = \left( -g_{\mu \nu }(x)dx^{\mu }dx^{\nu }\right) ^{1/2} + A_{\gamma }(x)dx^{\gamma } \end{aligned}$$
(23)

where \(g_{\mu \nu }(x)\) is the Schwarzschild metric and \(A_{\gamma }(x)\) is a one-form vector field with \(|A_\gamma (x)|\ll 1\).

By using the rel. (4), the rel. (23) is written as:

$$\begin{aligned} F(x,dx) =&\,\,\Big [fdt^2 - \frac{dr^2}{f} - r^2 d\theta ^2 - r^2 \sin ^{2}\theta \, d\phi ^2\Big ]^{1/2}\nonumber \\&+ A_{\gamma }(x)dx^{\gamma } \end{aligned}$$
(24)

We define the Lagrangian

$$\begin{aligned} L(x,\dot{x}) = F(x,\dot{x}) =&\,\, \Big [f\dot{t^{2}} - \frac{\dot{r^{2}}}{f}-r^{2}{\dot{\theta }}^{2}-r^{2}sin^{2}\theta \dot{\phi ^2}\Big ]^{1/2} \nonumber \\&+\tilde{A_{0}}f^{1/2}\dot{t} \end{aligned}$$
(25)

where we denote \(\dot{x}=\frac{dx}{d\tau }\) and we have used Eqs. (24) and (22). From the Euler–Lagrange equations

$$\begin{aligned} \frac{d}{d\tau }\frac{\partial L}{\partial \dot{x}^{\mu }}=\frac{\partial L}{\partial x^{\mu }} \end{aligned}$$
(26)

we find the equations for the geodesics:

$$\begin{aligned} \ddot{x}^{\lambda }+\varGamma ^{\lambda }_{\mu \nu }\dot{x}^{\mu }\dot{x}^{\nu }+g^{\kappa \lambda }\varPhi _{\kappa \mu }\dot{x}^{\mu }=0 \end{aligned}$$
(27)

where \(\varGamma ^{\lambda }_{\mu \nu }\) are the Christoffel symbols of Riemann geometry, \(\dot{x}^{\mu }=\frac{dx^{\mu }}{d\tau }\) and \(\varPhi _{\kappa \mu }=\partial _{\kappa }A_{\mu }-\partial _{\mu }A_{\kappa }\) and \(A_{\mu }\) is the solution rel. (22). We notice that from the definition of \(\varPhi _{\kappa \mu }\) we get a rotation form of geodesics. If \(A_{\mu }\) is a gradient of a scalar field, \(A_{\mu }=\dfrac{\partial \varPhi }{\partial x^{\mu }}\) then \(\varPhi _{\kappa \mu }=0\) and the geodesics of our model are identified with the Riemannian ones.

The geodesics of our model can then be explicitly written in the form:

$$\begin{aligned}&\ddot{t} + \frac{1-f}{rf}\dot{r} \dot{t} =-\tilde{A}_{0}\dot{r}\frac{f^{-3/2}(1-f)}{2r} \end{aligned}$$
(28)
$$\begin{aligned}&\ddot{r} + \frac{f(1-f)}{2r} \dot{t}^2 - \frac{1-f}{2rf} \dot{r}^2 \nonumber \\&\qquad - rf \big ( {\dot{\theta }}^2 + \sin ^2 \theta {\dot{\phi }}^2 \big )=-\tilde{A}_{0}\dot{t}\frac{f^{1/2}(1-f)}{2r} \end{aligned}$$
(29)
$$\begin{aligned}&\ddot{\theta }+ \frac{2}{r} {\dot{\theta }} \dot{r} - \frac{1}{2}\sin 2\theta \, {\dot{\phi }}^2=0 \end{aligned}$$
(30)
$$\begin{aligned}&\ddot{\phi }+ \frac{2}{r} {\dot{\phi }} \dot{r} + 2\cot \theta \, {\dot{\theta }} {\dot{\phi }}=0 \end{aligned}$$
(31)

From the relations (28)–(31), we notice that the first two dynamical equations involve a contribution of extra terms particular to the SFR spacetime while the last two relations are the same as in GR. From the above mentioned relations, we notice that the Riemannian geodesics are affected by a contribution that involves the curl of the force field in the SFR spacetime which can be interpreted as extra energy for the content of GR. We can notice that the geodesics of SFR are destroyed at the singular value \(r=0\) as in the GR case, this can be seen from the relations (28)–(31). In our case, the singularity is inherited from the Schwarzschild spacetime of GR. Moreover, it is evident from their dynamical form that the equations are not meaningful for \(r \le R_S\) in the context of the presently considered Schwarzschild metric, hence we only consider radial displacements past this singular point.

We now make a key assumption regarding the angular dependence of the model. Namely, by using \(\theta =\frac{\pi }{2}\) we notice that Eq. (30) is satisfied and equations (28), (29) and (31) can be written as:

$$\begin{aligned}&\ddot{t} + \frac{1-f}{rf}\dot{r} \dot{t} =-\tilde{A}_{0}\dot{r}\frac{f^{-3/2}(1-f)}{2r} \end{aligned}$$
(32)
$$\begin{aligned}&\ddot{r} + \frac{f(1-f)}{2r} \dot{t}^2 - \frac{1-f}{2rf} \dot{r}^2 - rf{\dot{\phi }}^2 =-\tilde{A}_{0}\dot{t}\frac{f^{1/2}(1-f)}{2r} \end{aligned}$$
(33)
$$\begin{aligned}&\ddot{\phi }+ \frac{2}{r} {\dot{\phi }} \dot{r}=0 \end{aligned}$$
(34)

From Eq. (34) we find:

$$\begin{aligned} r^{2}\dot{\phi }=J=const. \end{aligned}$$
(35)

where J is the angular momentum and the relevant equation represents its conservation law. If we use the relation \(f'=\frac{1-f}{r}\) where \(f=1-\frac{2GM}{r}\) and the Leibniz chain-rule \(\frac{d}{d\tau }=\frac{dr}{d\tau }\frac{d}{dr}=\dot{r} \frac{d}{dr}\), then Eq. (32) can be written as:

$$\begin{aligned} f\ddot{t} + \frac{df}{d\tau }\dot{t} = -\tilde{A}_{0}\frac{df^{1/2}}{d\tau } \end{aligned}$$
(36)

which, in turn, gives us

$$\begin{aligned} f\dot{t}+\tilde{A}_{0}f^{1/2} = \mathcal {E}_R=const. \end{aligned}$$
(37)

where \(\mathcal {E}_R\) is the energy of the particle moving along the geodesic. We notice that the first term constitutes the energy for a particle moving along the geodesics in general relativity, \(\mathcal {E}_{GR}=f\dot{t}\) and we can rewrite the relevant expression as:

$$\begin{aligned} \mathcal {E}_{GR}+\tilde{A}_{0}f^{1/2}=\mathcal {E}_{R}. \end{aligned}$$
(38)

By using Eq. (33) with (35), and (37), we arrive at the (effectively one-degree-of-freedom) radial equation:

$$\begin{aligned} \ddot{r} + \frac{1-f}{2rf}(\mathcal {E}_{R}^{2}-\dot{r}^{2}) -\frac{fJ^{2}}{r^{3}}=\tilde{A}_{0}\mathcal {E}_{R}\frac{f^{-1/2}(1-f)}{2r} \end{aligned}$$
(39)

where we omitted \(O({\tilde{A}}_{0}^{2})\) terms. As before, we use the relation \(f'=\frac{1-f}{r}\) in (39) to bring it to the equivalent form:

$$\begin{aligned} \ddot{r} + \frac{f'}{2f}(\mathcal {E}_{R}^{2}-\dot{r}^{2})-\frac{fJ^{2}}{r^{3}}=\frac{{\tilde{A}}_{0}\mathcal {E}_{R}}{2}f^{-1/2}f' \end{aligned}$$
(40)

We can further simplify the Eq. (40) by using the Leibniz chain-rule \(\frac{d}{d\tau }=\frac{dr}{d\tau }\frac{d}{dr}=\dot{r} \frac{d}{dr}\) and upon deriving the first integral of the motion, we obtain:

$$\begin{aligned} \dot{r}^{2} + f\left( \frac{J^{2}}{r^{2}}+\epsilon \right) +2\tilde{A}_{0}\mathcal {E}_{R}f^{1/2}=\mathcal {E}_{R}^{2} \end{aligned}$$
(41)

where \(\epsilon \) is a constant and for \(\epsilon = 0\) we have null geodesics. It is important to indicate here that for each value of \(\epsilon \), we obtain a different curve of this “first integral” of Eq. (41) and the inclusion of all of the admissible (r,\(\dot{r}\)) curves will provide us with the phase portraits presented below. The first two terms from (41) constitute the total energy in general relativity (GR), \(\mathcal {E}^{2}_{GR}=\dot{r}^{2} + f(\frac{J^{2}}{r^{2}}+\epsilon )\) and the third term emerges from the structure of SFR spacetime and its energetic contribution. Therefore Eq. (41) can be written as:

$$\begin{aligned} \mathcal {E}^{2}_{GR}+2\tilde{A}_{0}\mathcal {E}_{R}f^{1/2}=\mathcal {E}_{R}^{2} \end{aligned}$$
(42)

Equation (42) shows that the term \(A_{\gamma }(x)\) from (22) provides an additional energy contribution to the system of GR.

For a particle moving along the geodesics in the SFR spacetime with metric function \(F_v(x,dx)\) (rel. 24), we have extra gravitational effect (energy) compared to GR. An amount of energy comes from the gravitational field of total space in the SFR model. Therefore, from the rel. (37) and (42), the second term \(\tilde{A}_{0}f^{1/2}\) can be interpreted as the difference of energy between \(\mathcal {E}_{R}\) and \(\mathcal {E}_{GR}=f\dot{t}\).

Remark 1

The action of a vector field in the pseudo-Riemannian structure of space-time can give a vector-dependent gravitational field of Finsler–Randers (FR) type which can describe the asymmetry and the locally anisotropic form of spacetime that the Riemannian geometry is unable to provide. In this approach, because of broken Lorentz symmetry, particles and forces interact with this vector field.

In the following, we give an application for the weak gravitational field where we show that the term \(A_{0}(r)\) in the Eq. (22) is connected to the gravitational potential \(\varPhi \).

Application to the Newtonian limit

In the Newtonian gravitational theory, we can consider the second term of rel.(2) of the manuscript in the following form:

$$\begin{aligned} f_a dx^a = \frac{GmM}{r^2}dr \end{aligned}$$
(43)

The gravitational potential is given by

$$\begin{aligned} U = \frac{ W}{m} = \frac{1}{m}\int f_a dx^a \!=\! \frac{1}{m}\int ^r_\infty \frac{GmM}{r^2}dr \!=\! -\frac{GM}{r} \!=\! \varPhi \nonumber \\ \end{aligned}$$
(44)

where W represents the gravitational potential energy to be done to bring a unit mass m from infinity to a point and r is the distance from a mass M. This means that the work is converted to gravitational potential energy. In addition, from the relations (4) and (22) we have

$$\begin{aligned} g_{00} = - \left( 1 - \frac{R_S}{r} \right) = -f \end{aligned}$$
(45)

and

$$\begin{aligned} A_0(r) = \tilde{A}_0 \left( 1 - \frac{R_S}{r} \right) ^{1/2} = {\tilde{A}}_0 f^{1/2} \end{aligned}$$
(46)

From the relations (44), (45) and (46), we obtain

$$\begin{aligned} A_0(r) = {\tilde{A}}_0 \sqrt{-g_{00}} = {\tilde{A}}_0 \left( 1 - \frac{\varPhi }{2} \right) ^{1/2} \end{aligned}$$
(47)

where we have used \(R_S = 2GM\). The rel. (47) gives a physical interpretation in the geometrical term \(A_0(r)\) because of its dependence on the gravitational potential \(\varPhi \). The term \(A_0(r)\) is included in the relations (37), (38), (42) giving a physical meaning to these equations.

Remark 2

The relation (47) is also related to gravitational redshift of photons in the SFR spacetime (Ref. [2, paragraph 6]). In that case, we have proved that:

$$\begin{aligned} \frac{E_{rec}}{E_{emit}}= \frac{\nu _{rec}}{\nu _{emit}}\approx \tilde{A_{0}}f^{1/2} \end{aligned}$$
(48)

where \(\nu _{rec},\nu _{emit}\) denote the frequencies of receiver and emitter.

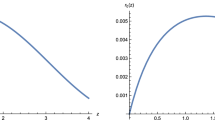
Below, we give the Figs. 1 and 2 for the geodesics of GR and SFR we have obtained by solving the Eqs. (28)–(31). The relevant ordinary differential equations are solved via a standard solver within Mathematica and \((r,\phi )\) are presented as a function of \(\tau \), while Fig. 2 presents the evolution in the original (x, y) plane. In our case, we assume \(R_{s}=2\) and initial radial distance \(r_{0}=3\), so the photons are found on the photonsphere with \(r_{ph}=\frac{3}{2}R_{s}=3\) in the GR case. The deviation between the trajectories of the SFR and those of the GR is clearly discernible in both figures.

Fig. 1
figure 1

These are the graphs for the GR and SFR geodesics of photons for angular momentum \(J=4\) and initial radial distance \(r_0=3\)

Full size image

From Fig. 1a, we can see that the radial component in the SFR model takes lower values compared to the GR one which remains constant. This difference between the r-components of SFR and GR can be interpreted as the increase of the radius of the photonsphere due to the one-form \(A_{\gamma }\) as we have shown in [2]. This leads the orbit of the photon to fall inside the event horizon because the initial distance \(r_{0}=3\) and energy are not sufficient to allow circular orbits of the photonsphere. That means for an orbit with r constant in the SFR model, the particle needs more energy compared to the GR case. In Fig. 2, the geodesics of GR and SFR are depicted. In the case of GR, the photons move in circular orbits around the black hole. In the SFR model, the photons follow a spiral orbit and fall inside the event horizon.

It is important to remind the reader here that underlying these results is the key assumption of \(\theta =\frac{\pi }{2}\) which allows the reduction of the model to an effective single degree-of-freedom system. It is important in future work to consider how deviations from this equilibrium value (and the corresponding incorporation of the full dynamical system) may affect the conclusions presented above. However, as the latter is outside the scope of the present study, we now focus on the further analysis of the effective potential of the SFR model and its implications for the phase portrait of the relevant system.

Fig. 2
figure 2

This is an x–y graph for the geodesics of photons for angular momentum \(J=4\) and initial radial distance \(r_{0}=3\). The red line shows the SFR geodesics and the blue line the GR geodesics

Full size image

4 Effective potential of SFR model

In this section, we will study the effective potential of the SFR model and compare it with the effective potential of GR. The equation of the energy in GR reads:

$$\begin{aligned} \dot{r}^{2} + f\left( \frac{J^{2}}{r^{2}}+\epsilon \right) =\mathcal {E}_{GR}^{2} \end{aligned}$$
(49)

We see from (49) that the effective potential energy landscape is given by:

$$\begin{aligned} V_{eff,GR}=\frac{1}{2}f \left( \frac{J^{2}}{r^{2}}+\epsilon \right) \end{aligned}$$
(50)

In Fig. 3a, we show the graph for the effective potential in GR for angular momentum \(J=3,J=4\) and \(J=5\) to examine its variation for different values of the angular momentum. Our effective potential (here and in what follows in Fig. 3a) solely bears a maximum at a finite \(r>0\). Based on the general theory of dynamical systems for the conservative type of problems considered herein, the relevant fixed point will be a saddle, as will be confirmed in the corresponding phase portraits below (where the attracting direction of the stable manifold and the repelling direction of the unstable manifold will be evident).

We now recall the key difference (and associated additional contribution) to the energetics of the SFR model. In particular, the energy equation for the latter, derived from Eq. (40), is given as:

$$\begin{aligned} \dot{r}^{2} + f\left( \frac{J^{2}}{r^{2}}+\epsilon \right) + 2\tilde{A}_{0}\mathcal {E}_{R}f^{1/2}= \mathcal {E}_{R}^{2} \end{aligned}$$
(51)

In (51) the effective potential can be written in the form

$$\begin{aligned} V_{eff,SFR}=\frac{1}{2}f \left( \frac{J^{2}}{r^{2}}+\epsilon \right) + \tilde{A}_{0}\mathcal {E}_{R}f^{1/2} \end{aligned}$$
(52)

The graph for the effective potential in the SFR model \((V_{eff},r)\) is depicted in Fig. 3a, in this case for different values of angular momentum.

In Fig. 3c, d we show the effective potentials of the SFR and GR models comparing the two for \(J=1\) and \(J=5\). As we can see in Fig. 3c, the difference between GR and SFR is bigger than that of Fig. 3d. Notably, when the contribution of the angular momentum is weaker, the difference between the two models is more substantial/clearly discernible. When the angular momentum becomes large, the relevant difference is rather weak and the \(V_{eff}\) of the two models become proximal.

Fig. 3
figure 3

These are the graphs for the \(V_{eff}(r)\) in the GR and SFR models for various angular momenta

Full size image

In Fig. 3 we observe the phase portraits associated with the effective potentials depicted above. These phase portraits reflect the existence of an energy barrier whose precise height depends on the value of the angular momentum. Energies below this barrier height result in reflection from the outside and trapping from the inside. On the other hand, energies higher than those of the barrier result in reaching the Schwarzschild radius (if the particle is coming from the outside) or reaching infinity (if the particle is moving outward from the inside). The latter figure demonstrates the differences between the two phase portraits which are quantitative but not qualitative (Figs. 4, 5).

Fig. 4
figure 4

These are phase plots for the radial geodesics of the GR and SFR models

Full size image
Fig. 5
figure 5

This is a comparison between the radial phase portraits of the GR (blue) and SFR (yellow) models

Full size image

5 Deflection angle

In this section, we will deal with the deflection angle of the SFR model and we will compare our findings with the corresponding ones of the GR model. In this consideration, we take into account photons that pass close to a central mass M. From Eq. (41) for photons, we put \(\epsilon =0\) and we get:

$$\begin{aligned} \frac{\dot{r}^{2}}{J^2}+\frac{f}{r^{2}}+ \frac{2\tilde{A_{0}}f^{1/2}}{Jb}=\frac{1}{b^2} \end{aligned}$$
(53)

where \(b=J/\mathcal {E}_{R}\) is a composite constant formed by the ratio of the angular momentum J divided by the energy of the particle moving along the geodesic \(\mathcal {E}_{R}\).

By using the Leibniz chain-rule \(\dot{\phi }=\frac{d\phi }{d\tau }=\frac{d\phi }{dr}\frac{dr}{d\tau }=\frac{d\phi }{dr}\dot{r}\) with the relations (35) and (53) we have:

$$\begin{aligned} \frac{\dot{r}^{2}}{\dot{\phi }^{2}}=r^{4}\left( \frac{1}{b^2}-\frac{f}{r^{2}}- \frac{2\tilde{A_{0}}f^{1/2}}{Jb}\right) \end{aligned}$$
(54)

After some rearrangements we find:

$$\begin{aligned} \frac{d\phi }{dr}=\frac{1}{r^2}\left( \frac{1}{b^2}-\frac{f}{r^{2}}- \frac{2\tilde{A_{0}}f^{1/2}}{Jb}\right) ^{-1/2} \end{aligned}$$
(55)

The deflection angle is calculated by the integration of (55):

$$\begin{aligned} \varDelta \phi _{SFR}&=2\int _{r_1}^{\infty }\frac{dr}{r^2}\left[ \frac{1}{b^2}-\frac{1}{r^{2}}\left( 1-\frac{2GM}{r}\right) \right. \nonumber \\&\quad \left. - \frac{2\tilde{A_{0}}}{Jb}\left( 1-\frac{2GM}{r}\right) ^{1/2}\right] ^{-1/2} \end{aligned}$$
(56)

where we have used \(f=1-\frac{2GM}{r}\).

We perform a change of variables in the integral of Eq. (56):

$$\begin{aligned} \varDelta \phi _{SFR}&= 2\int ^{w_{1}}_{0}dw\left[ 1-w^{2}\left( 1-{\frac{2GM}{b}}w\right) \right. \nonumber \\&\quad \left. -2a\left( 1-{\frac{2GM}{b}}w\right) ^{1/2}\right] ^{-1/2} \end{aligned}$$
(57)

where we have set \(w=\frac{b}{r}\) and \(a=\frac{\tilde{A_{0}}b}{J}\).

If we expand the integral in powers of \(\frac{2GM}{b}\) and a we find:

$$\begin{aligned} \varDelta \phi _{SFR}\approx 2\int _{0}^{w_1}dw\frac{1+\frac{GM}{b}w}{\left[ \left( 1-2a\right) +\frac{2GM}{b}w-w^{2}\right] ^{1/2}} \end{aligned}$$
(58)

where we have omitted second order terms.

By evaluating the integral in Eq. (58) we get (see Appendix 3):

$$\begin{aligned} \varDelta \phi _{SFR}=\pi +\frac{4GM}{b}\frac{1-a}{\sqrt{1-2a}} \end{aligned}$$
(59)

The deflection angle \(\delta \phi _{SFR}\) can be found as:

$$\begin{aligned}&\delta \phi _{SFR}=\varDelta \phi _{SFR}-\pi \Rightarrow \nonumber \\&\delta \phi _{SFR}=\frac{4GM}{b}\frac{1-a}{\sqrt{1-2a}} \end{aligned}$$
(60)

If we expand Eq. (60) in powers of \(a=\frac{\tilde{A}_{0}b}{J}\) the deflection angle can be written as:

$$\begin{aligned} \delta \phi _{SFR}\approx \left( 1+\frac{a^{2}}{2} \right) \frac{4GM}{b} \end{aligned}$$
(61)

The deflection angle \(\delta \phi \) of GR [4, 71] is given by:

$$\begin{aligned} \delta \phi _{GR}=\frac{4GM}{b} \end{aligned}$$
(62)

Therefore, we notice that the deflection angle of SFR includes a small additional Randers contribution term a which shows a small deviation from GR because \(|\tilde{A_0}|\ll 1\). We can see from Eq. (60) that:

$$\begin{aligned} \lim _{\tilde{A_0}\rightarrow 0}\delta \phi _{SFR}=\delta \phi _{GR} \end{aligned}$$
(63)

The small difference of the deflection angle of the SFR model from the GR one can plausibly be attributed to the Lorentz violations [7] or on the small amount of energy which is added to the gravitational potential of SFR.

Shapiro et al. [3] have shown that the deflection angle for a light ray is:

$$\begin{aligned} \theta \simeq \frac{(1+\gamma )GM}{c^{2}b}(1+cos\phi ) \end{aligned}$$
(64)

where M is the mass of the Sun, G is the gravitational constant, \(\phi \) is the angle between the source and the Sun for an observer on Earth and \(\gamma \) is the PPN parameter that characterizes the contribution of space curvature to gravitational deflection and is estimated to be \(\gamma _{Shap}=0.9998\pm 0.0004\). We compare this observational result of Shapiro et al. with Eq. (55) of our model in order to obtain some constraints for the parameter \(\alpha \). If we do this we find:

$$\begin{aligned} 2 \left( 1 + \frac{\alpha ^{2}}{2}\right) \simeq 1 + \gamma _{Shap} \end{aligned}$$
(65)

where we have taken \(\phi \simeq 0\) for an infinitesimal neighbourhood of a fiducial geodesic. By solving for \(\alpha \) we get:

$$\begin{aligned} \alpha \simeq \pm \sqrt{-1+\gamma _{Shap}} \end{aligned}$$
(66)

which gives the values for \(\alpha \simeq \pm 0.0141421\). This result provides an interesting relation between the deflection angle of a light ray in the SFR model and the approach to the deflection angle used in [3].

Remark 3

By considering the following relation, we can connect the geometrical concept of the curvature \(\kappa _{\phi }=\frac{d\phi }{d\tau }\) of a path with the deflection angle \(\delta \phi \) in the following way:

$$\begin{aligned} \dot{\phi }=\frac{d\phi }{d\tau }&=\frac{d\phi }{dr}\frac{dr}{d\tau }=\frac{d\phi }{dr}\dot{r}\Rightarrow \end{aligned}$$
(67)
$$\begin{aligned}&\kappa _{\phi }=\frac{d\phi }{dr}\dot{r}\Rightarrow \end{aligned}$$
(68)
$$\begin{aligned}&\delta \phi =\int \frac{\kappa _{\phi }}{\dot{r}} dr \end{aligned}$$
(69)

This form of curvature can be called deflection curvature.

6 Conclusions and future challenges

In this article, we investigated the analytic form of the geodesics of the model SFR which was introduced in previous works [1, 2]. A dynamical analysis was presented based on the energy and angular momentum of a particle along of geodesics (null or timelike) of the SFR spacetime. Comparisons between the SFR and GR were provided. We found that there is a small deviation from the GR model which is due to the dynamical term \(A_{\gamma }(x)\). We also formulated and studied an effective potential of our model and we compared the one of the SFR case once again with the effective potential of GR attributing the small but discernible differences to the specific structure of (and perturbation incorporated within) the SFR spacetime. The relevant differences in the trajectories were illustrated both in the evolution over the time-variable \(\tau \) and in the (x, y) plane. In addition, we calculated the deflection angle for the SFR spacetime and we compared with the corresponding one of GR. The result is a small difference of the SFR model from GR, it is possibly caused by Lorentz violations or by the small amount of energy which is added to the gravitational potential of SFR spacetime.

In addition, we found an interesting relation between the observational data of [3] and the SFR model’s prediction for the deflection angle of a null geodesic. Finally, we presented an application which relates the covector field \(A_\gamma (x)\) of the SFR model with the Newtonian gravitational potential.

It is important to note that this work opens a number of interesting directions of further study for the future. On the one hand, the traditional assumption of \(\theta =\pi /2\) made over here is clearly a restrictive one that simplifies the equations of motion automatically satisfying the dynamics for the angular variable \(\theta \) with the latter being at steady state. However, more generally, one can straightforwardly envision scenarios where this condition is no longer satisfied. It is then of interest to explore if one starts in the vicinity of \(\pi /2\) whether one stays in that neighborhood or perhaps if one deviates away from this steady state and how the associated dynamics of the full 4-degree-of-freedom space is accordingly explored. Another aspect that is also worth further exploring is that of the small amplitude covector deviation from the General Relativity standard model. Here, we have limited our considerations to the realm of associated small amplitude perturbations (where leading order expansions of the field would suffice). However, it would also be of interest to explore the situation when one gradually deviates from the realm of this approximation as well. In addition, applications of geodesics of the SFR model can be pursued for more concrete cosmological studies such as, e.g., for the case of the S2 stars orbiting the black hole in Sagittarius A* in which the geodesics of the star are perturbed from the classical Keplerian orbits because of the distribution of stellar remnants. Indeed, our hope is that this work may pave the way towards testing the Schwarzschild–Finsler–Randers gravitational model which incorporates features going beyond the standard Riemannian geometry of spacetime. In this vein, some of the above topics are presently under consideration and associated results will be presented in future publications.