Skip to main content
SpringerLink
Log in

Evolution of Lifshitz metric anisotropies in Einstein–Proca theory under the Ricci–DeTurck flow

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

By starting from a Perelman entropy functional and considering the Ricci–DeTurck flow equations, we analyze the behavior of Einstein–Hilbert and Einstein–Proca theories with Lifshitz geometry as functions of a flow parameter. In the former case, we found one consistent fixed point that represents flat space-time as the flow parameter tends to infinity. Massive vector fields in the latter theory enrich the system under study and have the same fixed point achieved at the same rate as in the former case. The geometric flow is parametrized by the metric coefficients and represents a change in anisotropy of the geometry toward an isotropic flat space-time as the flow parameter evolves. Indeed, the flow of the Proca fields depends on certain coefficients that vanish when the flow parameter increases, rendering these fields constant. We have been able to write down the evolving Lifshitz metric solution with positive, but otherwise arbitrary, critical exponents relevant to geometries with spatially anisotropic holographic duals. We show that both the scalar curvature and matter contributions to the Ricci–DeTurck flow vanish under the flow at a fixed point consistent with flat space-time geometry. Thus, the behavior of the scalar curvature always increases, homogenizing the geometry along the flow. Moreover, the theory under study keeps positive-definite, but decreasing, the entropy functional along the Ricci–DeTurck flow.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data Availability Statement

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

Notes

  1. And in particular, Ricci flows.

  2. Like Massive vector field, supergravity and string theory [21].

  3. See for example [23] for some applications of Ricci flows in General Relativity.

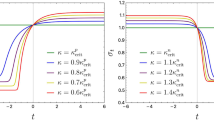
  4. We mentioned in the introduction section that, within the holographic framework, the so-called critical exponents \(z_{i}\) of a Lifshitz geometry are to be related with order parameters in quantum critical points of a dual field theory. So far these order parameters are found to be positive in real field theories. Therefore, we considered the corresponding \(z_{i}>0\). However, some or all of these critical exponents can be negative, leading to a scaling that can be compensated by the dilatation of the corresponding \(x_{i}\) coordinates. Therefore, under the evolution of the Ricci flow parameter \(\lambda\), the metric tends to the same fixed point, independently of the sign of the \(\gamma _{i}\) coefficients.

  5. In principle, one can integrate Eq. (4.7a) and get linear in r expression supplemented by an exponential term for the DeTurck vector field. However, there is no way to get rid of this term in Eq. (4.7c) without trivializing the vector field. Hence, this case reduces to the one treated in Sect. 3.

References

  1. R.S. Hamilton, Three-manifolds with positive Ricci curvature. J. Differ. Geom. 17(2), 255–306 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  2. M. Headrick, T. Wiseman, Ricci flow and black holes. Class. Quantum Grav. 23, 6683–6708 (2006). hep-th/0606086

    Article  ADS  MathSciNet  MATH  Google Scholar 

  3. J. Samuel, S.R. Chowdhury, Geometric flows and black hole entropy. Class. Quantum Grav. 24, F47–F54 (2007). arXiv:0711.0428

    Article  MathSciNet  MATH  Google Scholar 

  4. J. Samuel, S.R. Chowdhury, Energy, entropy and the Ricci flow. Class. Quantum Grav. 25, 035012 (2008). arXiv:0711.0430

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. V. Husain, S.S. Seahra, Ricci flows, wormholes and critical phenomena. Class. Quantum Grav. 25, 222002 (2008). arXiv:0808.0880

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. R. Cartas-Fuentevilla, A. Herrera-Aguilar, J.A. Olvera-Santamaría, Evolution and metric signature change of maximally symmetric spaces under the Ricci flow. Eur. Phys. J. Plus 133(6), 235 (2018). arXiv:1707.07235

    Article  Google Scholar 

  7. R. Cartas-Fuentevilla, A. Herrera-Aguilar, J.A. Herrera-Mendoza, Constructing Lifshitz spaces using the Ricci flow. Ann. Phys. 415, 168093 (2020). arXiv:1812.06239

    Article  MathSciNet  MATH  Google Scholar 

  8. G. Perelman, The entropy formula for the Ricci flow and its geometric applications. arXiv Mathematics e-prints (2002). math/0211159

  9. D.M. DeTurck, Deforming metrics in the direction of their Ricci tensors. J. Differ. Geom. 18(1), 157–162 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  10. J. de Boer, E.P. Verlinde, H.L. Verlinde, On the holographic renormalization group. JHEP 08, 003 (2000). hep-th/9912012

    Article  MathSciNet  MATH  Google Scholar 

  11. D. Friedan, Nonlinear models in \(2+\epsilon\) dimensions. Phys. Rev. Lett. 45, 1057–1060 (1980)

    Article  ADS  MathSciNet  Google Scholar 

  12. I. Heemskerk, J. Polchinski, Holographic and Wilsonian renormalization groups. JHEP 06, 031 (2011). arXiv:1010.1264

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. E.T. Akhmedov, A Remark on the AdS/CFT correspondence and the renormalization group flow. Phys. Lett. B 442, 152–158 (1998). hep-th/9806217

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. V. Balasubramanian, P. Kraus, Space-time and the holographic renormalization group. Phys. Rev. Lett. 83, 3605–3608 (1999). hep-th/9903190

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. T. Faulkner, H. Liu, M. Rangamani, Integrating out geometry: holographic Wilsonian RG and the membrane paradigm. JHEP 08, 051 (2011). arXiv:1010.4036

    ADS  MathSciNet  MATH  Google Scholar 

  16. P. Mikula, M.E. Carrington, G. Kunstatter, Nonequilibrium approach to holographic superconductors using gradient flow. Phys. Rev. D 100(4), 046004 (2019). arXiv:1902.08669

    Article  ADS  MathSciNet  Google Scholar 

  17. S.A. Hartnoll, A. Lucas, S. Sachdev, Holographic quantum matter. arXiv:1612.07324

  18. S. Kachru, X. Liu, M. Mulligan, Gravity duals of Lifshitz-like fixed points. Phys. Rev. D 78, 106005 (2008). arXiv:0808.1725

    Article  ADS  MathSciNet  Google Scholar 

  19. M. Taylor, Non-relativistic holography. arXiv:0812.0530

  20. R. Cartas-Fuentevilla, A. Herrera-Aguilar, V. Matlalcuatzi-Zamora, U. Noriega, J.M. Romero, Anisotropic Lifshitz holography in Einstein–Proca theory with stable negative mass spectrum. Eur. Phys. J. Plus 135(2), 155 (2020). arXiv:1804.02278

    Article  Google Scholar 

  21. R. Gregory, S.L. Parameswaran, G. Tasinato, I. Zavala, Lifshitz solutions in supergravity and string theory. JHEP 12, 047 (2010). arXiv:1009.3445

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. H. Braviner, R. Gregory, S.F. Ross, Flows involving Lifshitz solutions. Class. Quantum Grav. 28, 225028 (2011). arXiv:1108.3067

    Article  ADS  MathSciNet  MATH  Google Scholar 

  23. E. Woolgar, Some applications of Ricci flow in physics. Can. J. Phys. 86, 645–651 (2008). arXiv:0708.2144

    Article  ADS  Google Scholar 

Download references

Acknowledgements

All authors have been benefited from the CONACYT Grant No. A1-S-38041, while RCF and AHA were supported by the VIEP-BUAP Grants Nos. 113 and 122. MCL thanks the financial assistance provided by a CONACYT postdoctoral Grant No. 30563. JAHM acknowledges support from CONACYT through a PhD Grant No. 750974. DFHB is also grateful to CONACYT for a Postdoc por México Grant No. 372516.

Author information

Authors and Affiliations

  1. Instituto de Física, Benemérita Universidad Autónoma de Puebla, Apartado Postal J-48, 72570, Puebla, Mexico

    Roberto Cartas-Fuentevilla, Manuel de la Cruz, Alfredo Herrera-Aguilar, Jhony A. Herrera-Mendoza & Daniel F. Higuita-Borja

Authors
  1. Roberto Cartas-Fuentevilla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Manuel de la Cruz
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Alfredo Herrera-Aguilar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jhony A. Herrera-Mendoza
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Daniel F. Higuita-Borja
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alfredo Herrera-Aguilar.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cartas-Fuentevilla, R., de la Cruz, M., Herrera-Aguilar, A. et al. Evolution of Lifshitz metric anisotropies in Einstein–Proca theory under the Ricci–DeTurck flow. Eur. Phys. J. Plus 137, 1379 (2022). https://doi.org/10.1140/epjp/s13360-022-03606-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-022-03606-6

Search

Navigation